Abstract
Here, we introduce an electronic circuit that mimics the functionality of a biological spiking neuron following the Fitzhugh–Nagumo (FN) model. The circuit consists of a tunnel diode that exhibits negative differential resistance (NDR) and an active inductive element implemented by a single MOSFET. The FN neuron converts a DC voltage excitation into voltage spikes analogous to biological action potentials. We predict an energy cost of 2 aJ/cycle through detailed simulation and modeling for these FN neurons. Such an FN neuron is CMOS compatible and enables ultralow power oscillatory and spiking neural network hardware. We demonstrate that FN neurons can be used for oscillator-based computing in a coupled oscillator network to form an oscillator Ising machine (OIM) that can solve computationally hard NP-complete max-cut problems while showing robustness toward process variations.
Introduction
Biological brains can perform computational tasks at an ∼100,000× efficiency compared to the digital computers.1−6 A typical biological neuron has a surface area of ∼10 μm2, spends ∼10 pJ energy to generate each spike, and operates at a frequency of ∼100 Hz, which translates to a power cost of ∼1 nW for biological systems.3,4,6 The first set of efforts in emulating biological neurons dates back to 1960s following the FN model using voltage controlled NDR devices7,8 paired with inductors to produce relaxation oscillations similar to neuronal spiking behavior.9−11 The inductor element is the main scaling bottleneck of this circuit implementation of spiking neuron, as coil-based passive inductors are difficult to fabricate at nanoscale with the required inductance values. The emergence of current-controlled NDR devices featuring metal–insulator phase transition materials has enabled generation of relaxation oscillations using capacitors, leading to considerable progress in artificial spiking neurons.12−23 There have been other approaches to producing NDR, such as band to band tunneling, resonant tunneling, Gunn effect, real space electron transfer in III–V heterostructures, body biasing of MOSFET, exploiting graphene’s unique dispersion relationship near its Dirac point, using trap-based recombination processes, redox behavior of molecular junctions, and multiple circuits.7,8,24−42 Recently, we have shown that a graphene–silicon photodetector can show voltage-dependent NDR behavior under optical illumination while operating in the photovoltaic regime.43 This photosensor coupled with an inductive circuit element generates optically driven voltage oscillations similar to those of ganglion cells in the retina, following the FN model of spiking neurons. Using a frequency multiplexed parallel computing approach, these oscillatory retinal neurons (ORNs) were then used to demonstrate ultralow-power in-sensor neuronal computing for machine vision. Purely electronic oscillatory neurons can extend the ability of FN neurons to different types of sensors and enable the construction of deep oscillator-based neural networks. In addition, electronic oscillatory neurons are instrumental to traditional oscillatory neural networks (ONNs), where a network of coupled oscillators can be used as associative memory44−58 or an engine for convolution-like operations.44,45,59−62 However, there are three important challenges to achieving ultralow power oscillator-based computing: (1) scalability, (2) energy consumption, and (3) variability of the oscillatory neurons. These neurons serve as the smallest unit of computation in oscillator networks similar to the different logic gates in digital computing systems. Therefore, a cohesive effort is necessary to improve the design of individual neuron circuits and the algorithms that would allow the employment of these neurons for the promised excellent performance of the brain-inspired computing architectures.
In this work, we have introduced an FN neuron implementation with a tunnel diode and an active inductor. The scaling bottleneck presented by passive inductors is removed in this implementation of the FN neuron by using the active inductor that can easily be fabricated at nanoscale by traditional CMOS processes. The active inductor emulates the behavior of a passive coil-based inductor by taking advantage of an active element: a single MOSFET, and a resistor. Through circuit simulations, we demonstrated the oscillation behavior of the FN neuron implemented using this active inductor and predicted the scalability limits. The key feature of this neuron is that it is expected to generate voltage spikes with ∼2 aJ/cycle energy cost, whereas the Mott transition-based neurons consume an electrical energy of ∼50 pJ/cycle, and the state-of-the-art CMOS neuron consumes ∼4 fJ/cycle.12,14,17−21,23 These FN neurons can generate firing patterns similar to biological neurons. We have then used FN neurons to form a coupled oscillator network onto which a computationally hard combinatorial problem such as max-cut problem can be mapped in an Ising machine-like fashion. This OIM can then minimize the Ising Hamiltonian associated with the max-cut problem and identify correct solutions while consuming a small electrical energy.
Results and Discussion
The spiking behavior of biological neurons was first described by the Hodgkin–Huxley (HH) model. The HH model interprets the dynamics of ion flows across neuronal membrane and the resulting generation and propagation of action potentials through a set of coupled differential equations. The Fitzhugh–Nagumo (FN) model reduces the complexity of the HH model by using just two variables: the membrane potential and the recovery variable. Despite its simplicity, the FN model captures some of the essential features of the Hodgkin–Huxley model, such as the concept of a threshold for firing an action potential and the recovery of the membrane potential after firing. Moreover, the FN model can reproduce many of the behaviors observed in the Hodgkin–Huxley model such as the propagation of action potentials and the refractory period. Dynamics of Fitzhugh–Nagumo neurons can be described by the following coupled differential equations:63
Here, v is reminiscent
of the membrane potential
of a neuron, which is excited by an external stimulus iext analogous to the ion pump current through a nonlinear
medium f(v). f(v) can be simplified as a third-order polynomial. Such an
excitation is then dissipated through a slower sink w. Figure S1a shows the nullclines and
the trajectory of the system for 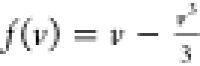 for parameter values of (a, b, r, τ, iext) = (0.7,
0.8, 0.5, 12.5, 0.4). Figure S1b shows the waveforms obtained for the Fitzhugh–Nagumo neurons
for different values of iext , showing
that action potentials or spikes are not generated for under-excitation
or over-excitation conditions. Figure S2 shows the nullclines and trajectories of the system under different
parameter values.
for parameter values of (a, b, r, τ, iext) = (0.7,
0.8, 0.5, 12.5, 0.4). Figure S1b shows the waveforms obtained for the Fitzhugh–Nagumo neurons
for different values of iext , showing
that action potentials or spikes are not generated for under-excitation
or over-excitation conditions. Figure S2 shows the nullclines and trajectories of the system under different
parameter values.
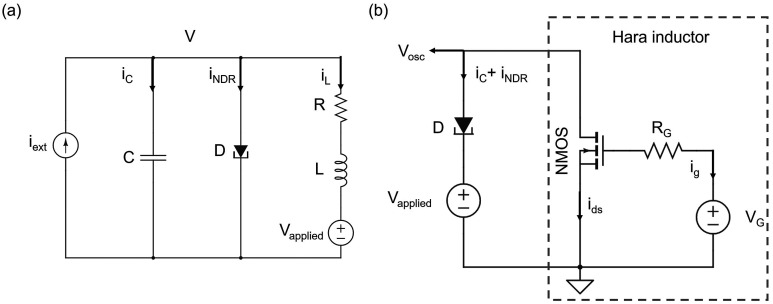
Here, we develop a circuit to emulate FN neurons, with the equivalent circuit shown in Figure 1a, with the third-order nonlinear element f(v) approximated by a tunnel diode, a circuit element that exhibits negative differential resistance. The following coupled differential equations describe the dynamics of this circuit:
Figure 1.
Implementation of an FN neuron. (a) Equivalent circuit of an FN neuron using a tunnel diode. (b) Circuit schematic of an FN neuron using Hara inductor.
These equations are equivalent to those of the Fitzhugh–Nagumo neurons and differ only by a scaling factor. In the absence of the resistor R and the offset DC voltage Vapplied, this circuit would simplify to a more traditional Van der Pol oscillator.64−66 While such a circuit accurately captures the description of a Fitzhugh–Nagumo neuron, the presence of an inductor in the circuit limits its implementation and scalability.
To overcome this challenge, we explore the effect of implementing
this circuit with a Hara active inductor comprising a single FET and
a resistor.67−69Figure 1b shows the circuit schematic for an FN neuron by using the Hara
inductor and a tunnel diode. The parasitic capacitance of the tunnel
diode (C) is implicit here. There are two sources
of electrical power in this circuit: VG and Vapplied. However, impedance of
the series RG–Cgs branch is 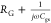 , which blocks any DC current flow, and
therefore power consumption in the VG source
is zero. Therefore, all of the power in this neuron comes from the
source, Vapplied. This power can be calculated
from
, which blocks any DC current flow, and
therefore power consumption in the VG source
is zero. Therefore, all of the power in this neuron comes from the
source, Vapplied. This power can be calculated
from
where T is the period of
one fundamental oscillation. Here, the capacitive current integrates
to zero over a full cycle of oscillation. The energy in each cycle
can be calculated from 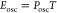 . As a rule of thumb, the power consumptions
in both the tunnel diode and active inductor are ∼IpeakVpeak, where Ipeak is the peak current of the tunnel diode before the
start of the NDR regime, and Vpeak is
the voltage at which Ipeak is observed.
Since Ipeak decreases linearly with tunnel
diode device area, any reduction in power and energy consumption requires
us to scale down the diode to the smallest possible size.
. As a rule of thumb, the power consumptions
in both the tunnel diode and active inductor are ∼IpeakVpeak, where Ipeak is the peak current of the tunnel diode before the
start of the NDR regime, and Vpeak is
the voltage at which Ipeak is observed.
Since Ipeak decreases linearly with tunnel
diode device area, any reduction in power and energy consumption requires
us to scale down the diode to the smallest possible size.
The nonlinear element in the FN neuron does not necessarily have to be a tunnel diode, as there are many different CMOS compatible circuit topologies that allow NDR with a small footprint. However, a tunnel diode is also a CMOS compatible device that allows aggressive scaling to the nanometer scale. Figure S3a shows the experimentally measured J–V and C–V curves of a silicon tunnel diode.70 We have considered a linear scaling behavior between diode current and physical diode area, which is a reasonable assumption for tunnel diodes as discussed in Section S2.1. This silicon tunnel diode is composed of a vertically stacked p++ (∼1020 cm–3)/n++ (∼1020 cm–3) silicon homojunction, completely compatible with CMOS fabrication processes. As discussed in Section S2.2, a large peak current density of 1.75 μA/μm2 indicates that a tunnel diode can be scaled down to 100 nm × 100 nm size while keeping a ∼30 dB signal-to-noise ratio at 1 GHz bandwidth. In addition to tunnel diodes that achieve NDR behavior through band-to-band tunneling, resonant tunneling diodes (RTDs) utilizing the resonant tunneling phenomenon in multiple quantum well-like structures can also be used in this implementation of FN neurons. Due to the near unity transmission probability for carriers, Si/SiGe-based RTDs can achieve a much higher NDR peak current density (2.18 mA/μm2)42 compared to tunnel diodes while maintaining similar capacitance per area. As a result, an RTD-based oscillator can potentially reach a much higher oscillation frequency.36,38,39,41 Recently, RTDs have therefore been explored for designing spiking neurons for applications in neuromorphic computing.35,37,40 However, fabrication of RTDs is more complicated, since RTDs are heterojunction devices. It is also more difficult to achieve NDR behavior in RTDs at room temperature due to its inherent physics. On the other hand, the simplified fabrication process, increased variation tolerance, and comparatively smaller susceptibility to thermal noise of silicon tunnel diodes make them better candidates for practical implementation of FN neurons.
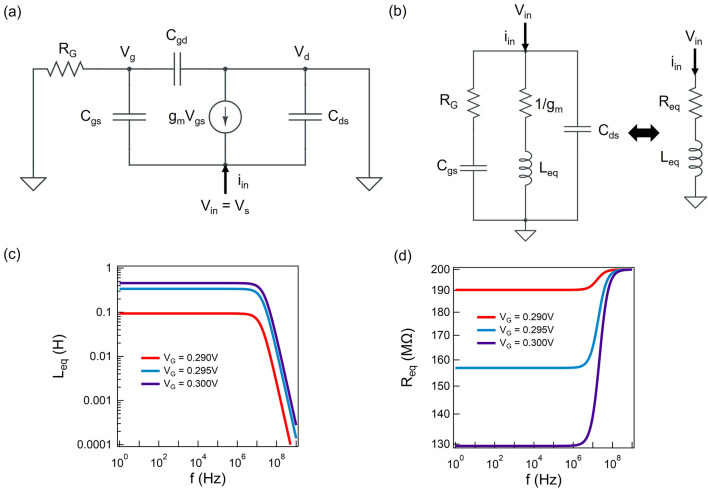
Figure 2a,b shows
a small signal equivalent circuit for the Hara inductor. The small
signal model gives us an equivalent inductance of 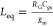 , where RG is
the series resistance to the gate, Cgs is the gate to source capacitance of the FET, and gm is the transconductance of the FET.67,69 The DC voltage source in series to the gate determines the bias
point and consequently gm of the FET.
However, it is important to note that the spiking neuron operation
can lead to voltage swings of ∼100 mV, and the small signal
model would not be applicable in that case. Nevertheless, it is a
good starting point to design the neuron circuit regardless of the
nonidealities introduced by the large signal voltage swings. Figure 2c shows Leq as a function of operating frequency for a 65 nm CMOS
process MOSFET with W/L = 1 at different
bias voltages and RG = 200 MΩ. Figure 2d shows the equivalent
resistance seen at the input terminal. These results show that Leq can be tuned by the bias voltage. However,
an active inductor has a positive equivalent inductance only within
a certain frequency range, which puts certain design constraints on
the FN neuron.
, where RG is
the series resistance to the gate, Cgs is the gate to source capacitance of the FET, and gm is the transconductance of the FET.67,69 The DC voltage source in series to the gate determines the bias
point and consequently gm of the FET.
However, it is important to note that the spiking neuron operation
can lead to voltage swings of ∼100 mV, and the small signal
model would not be applicable in that case. Nevertheless, it is a
good starting point to design the neuron circuit regardless of the
nonidealities introduced by the large signal voltage swings. Figure 2c shows Leq as a function of operating frequency for a 65 nm CMOS
process MOSFET with W/L = 1 at different
bias voltages and RG = 200 MΩ. Figure 2d shows the equivalent
resistance seen at the input terminal. These results show that Leq can be tuned by the bias voltage. However,
an active inductor has a positive equivalent inductance only within
a certain frequency range, which puts certain design constraints on
the FN neuron.
Figure 2.
Small signal behavior of the Hara inductor. (a) Small signal model for Hara inductor and (b) equivalent circuit. (c) Equivalent inductance and (d) series resistance of Hara inductor using a 65 nm process MOSFET with W/L = 1 and RG = 200 MΩ.
Using the established behavior of the individual
elements, we combine
them to form the FN neuron, as shown in Figure 1a. We have performed circuit simulations
for a FN neuron using the I–V curve and device capacitance obtained from the experimental data
of a silicon tunnel diode and an ideal inductor with no series resistance
(ideal Van der Pol oscillator case). The experimentally obtained I–V curve was first mathematically
fit and then interpolated to generate a lookup table. Using a lookup
table allows us to speed up simulations by avoiding evaluation of
the nonlinear function as we solve the system of ordinary differential
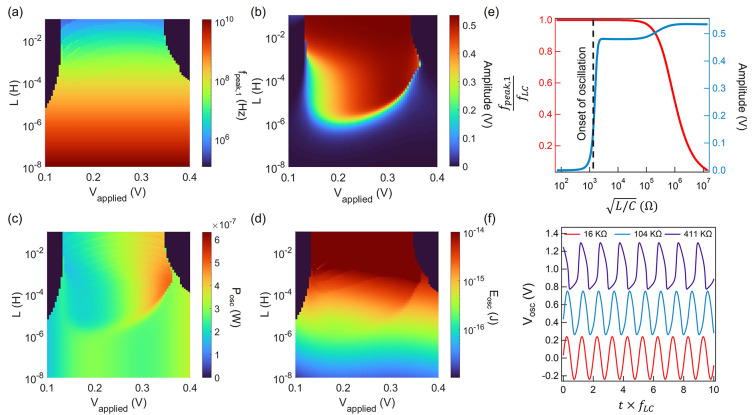
equations at each time step. Figure 3a–d shows the colormaps
for oscillation amplitude, frequency, power consumption, and energy
consumption, respectively, for a diode of 1 μm2 device
area. We observe from these colormaps that oscillation is only possible
within certain applied voltage ranges, and the oscillation amplitude
is significant after a threshold inductance. These values are functions
of the tunnel diode I–V curve
as oscillations can only be sustained at the voltages for which NDR
behavior exists. We have then introduced a normalized quantity 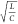 analogous to the characteristic impedance
of a transmission line. When the device area (A)
decreases, both the current and capacitance of the diode decrease
linearly. This quantity captures the effect of scaling both the device
area and inductance. Figure 3e shows the fundamental oscillation frequency (fpeak,1) normalized to the resonant frequency of the LC
circuit (
analogous to the characteristic impedance
of a transmission line. When the device area (A)
decreases, both the current and capacitance of the diode decrease
linearly. This quantity captures the effect of scaling both the device
area and inductance. Figure 3e shows the fundamental oscillation frequency (fpeak,1) normalized to the resonant frequency of the LC
circuit (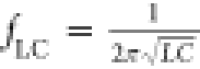 ) and oscillation amplitude for Vapplied = 0.4 V. We can observe a sharp increase
in oscillation amplitude at
) and oscillation amplitude for Vapplied = 0.4 V. We can observe a sharp increase
in oscillation amplitude at 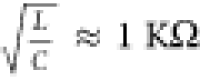 clearly marking the onset of oscillation.
It is noteworthy that such an oscillator approximates an LC oscillator
for
clearly marking the onset of oscillation.
It is noteworthy that such an oscillator approximates an LC oscillator
for 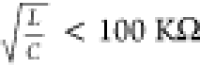 , where
, where 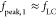 . Figure 3f shows some example oscillation waveforms for the
FN neurons at different values of
. Figure 3f shows some example oscillation waveforms for the
FN neurons at different values of 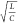 , where we can observe the emergence of
sharp spikes as we keep increasing
, where we can observe the emergence of
sharp spikes as we keep increasing  . As we scale the tunnel diode down to smaller
sizes, both I and C will scale linearly,
and we would need to increase the inductance L linearly
to maintain the same oscillation threshold and frequency. For a tunnel
diode with an area of 1 μm2, C =
25 fF, we would need an inductance of ∼100 nH to start the
oscillations.
. As we scale the tunnel diode down to smaller
sizes, both I and C will scale linearly,
and we would need to increase the inductance L linearly
to maintain the same oscillation threshold and frequency. For a tunnel
diode with an area of 1 μm2, C =
25 fF, we would need an inductance of ∼100 nH to start the
oscillations.
Figure 3.
Simulated oscillation behavior of a silicon tunnel-diode-based
FN neuron. Colormaps of (a) fundamental oscillation frequency, (b)
amplitude, (c) power, and (d) energy consumption in the FN neuron
using passive inductors. (e) Normalized fundamental oscillation frequency
and amplitude of the FN neuron. (f) Typical oscillation waveforms
at different 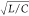 values.
values.
In order to understand the scaling limits of this
FN neuron, we
have then simulated the Hara inductor-based neurons using the 65 nm
CMOS process-based MOSFET.71 It is important
to note that while a 65 nm MOSFET has been used here for these simulations,
quantitatively similar results can be obtained by using any other
FET such as 5 nm FINFETs. Since the inductive load depends on RG, Cgs, and gm (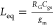 ), FETs of different sizes and processes
can achieve the same inductance by adjusting their transconductance
(gm) by applying an appropriate VG so that
), FETs of different sizes and processes
can achieve the same inductance by adjusting their transconductance
(gm) by applying an appropriate VG so that 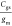 ratio remains constant. In addition, the
capacitive load seen by the oscillator is a parallel combination of
the parasitic capacitance of the diode and the drain-to-source capacitance
(Cds) of the FET. Since Cds is typically much smaller (∼100×) compared
to diode capacitance, the operational frequency of the oscillator
will not be affected significantly by using different FETs as long
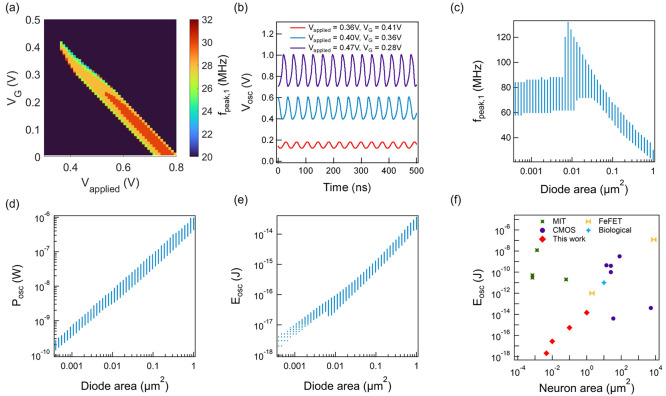
as Cdiode ≫ Cds. Figure 4a shows the oscillation frequency colormap for a FN neuron comprising
a 1 μm2 tunnel diode and RG = 200 MΩ. As shown in Figure 4a, there is a particular range of VG and Vapplied values at which
spiking neural behavior can be sustained. A decrease in VG decreases the inductance and increases the series resistance.
As a result, we see a larger oscillation frequency at a smaller VG. However, the increasing series resistance
requires us to increase Vapplied to sustain
oscillation. Figure 4b shows some oscillation waveforms for different VG and Vapplied. We then performed
the same simulation for tunnel diodes of different device areas between
400 nm2 and 1 μm2. Figure 4c shows fpeak,1 as a function of diode area, showing an ∼80 MHz oscillation
frequency for the smallest devices. Figure 4d,e shows the Posc and Eosc for the FN neuron for a minimum
oscillation amplitude of 50 mV. Posc and Eosc are calculated using the following equations,
ratio remains constant. In addition, the
capacitive load seen by the oscillator is a parallel combination of
the parasitic capacitance of the diode and the drain-to-source capacitance
(Cds) of the FET. Since Cds is typically much smaller (∼100×) compared
to diode capacitance, the operational frequency of the oscillator
will not be affected significantly by using different FETs as long
as Cdiode ≫ Cds. Figure 4a shows the oscillation frequency colormap for a FN neuron comprising
a 1 μm2 tunnel diode and RG = 200 MΩ. As shown in Figure 4a, there is a particular range of VG and Vapplied values at which
spiking neural behavior can be sustained. A decrease in VG decreases the inductance and increases the series resistance.
As a result, we see a larger oscillation frequency at a smaller VG. However, the increasing series resistance
requires us to increase Vapplied to sustain
oscillation. Figure 4b shows some oscillation waveforms for different VG and Vapplied. We then performed
the same simulation for tunnel diodes of different device areas between
400 nm2 and 1 μm2. Figure 4c shows fpeak,1 as a function of diode area, showing an ∼80 MHz oscillation
frequency for the smallest devices. Figure 4d,e shows the Posc and Eosc for the FN neuron for a minimum
oscillation amplitude of 50 mV. Posc and Eosc are calculated using the following equations,
Figure 4.
Simulated oscillation behavior of FN neuron implemented with the Hara inductor. (a) Colormap of fundamental oscillation frequency. (b) Example oscillation waveforms at different conditions. (c) Fundamental oscillation frequency, (d) power, and (e) energy consumption as a function of diode area. (f) Energy cost comparison with other artificial spiking neuron technologies.
Here, T is the fundamental oscillation period. The decrease in Posc and Eosc is linear to the neuron area until the MOSFET area becomes the limiting factor. For a 0.0046 μm2 neuron area (20 nm × 20 nm diode, 65 nm × 65 nm MOSFET), we estimate a Posc of 1.4 nW and a Eosc of 2 aJ, which is the lowest among reported energy per oscillation cycle for different electronic neurons.6,12−15,17,18,22,34,72−78 It is important to note that the spread in the data comes from all possible oscillation conditions at different VG and Vapplied. The current flow and operation voltage for this FN neuron implementation depend on the tunnel diode I–V characteristics. As discussed in more detail in Section S5, we do not expect any significant influence of the FET sizing or process on the oscillation frequency or amplitude and therefore also on power and energy consumption. Figure 4f shows the comparison between the energy consumption per cycle for different types of neurons found in the literature. There are mainly three other approaches to making an artificial neuron: (1) metal–insulator transition (MIT) memristors and a capacitor, (2) circuit-based techniques implemented with CMOS technology, and (3) ferroelectric FETs (FeFETs) with a regular FET. While the MIT neurons can be scaled down to ∼1000 nm2, the minimum energy cost is ∼50 pJ for oscillation, which is significantly larger compared to that of biological neurons.6,12−15,17,18,22,72 CMOS-based neurons have a large distribution of power and energy costs depending on the circuit techniques used for implementing the spiking neural behavior.34,73−78 Current state-of-the-art spiking neuron75 has a 35 μm2 area with a 4 fJ energy consumption, whereas a typical biological neuron of ∼10 μm2 area has an energy consumption of ∼10 pJ. FeFET neurons also demonstrate promise in achieving oscillation with an energy cost of ∼1 pJ. In contrast to all these artificial neurons, our proposed FN neuron consumes an electrical energy of 2 aJ, which can further the state-of-the-art of this field.
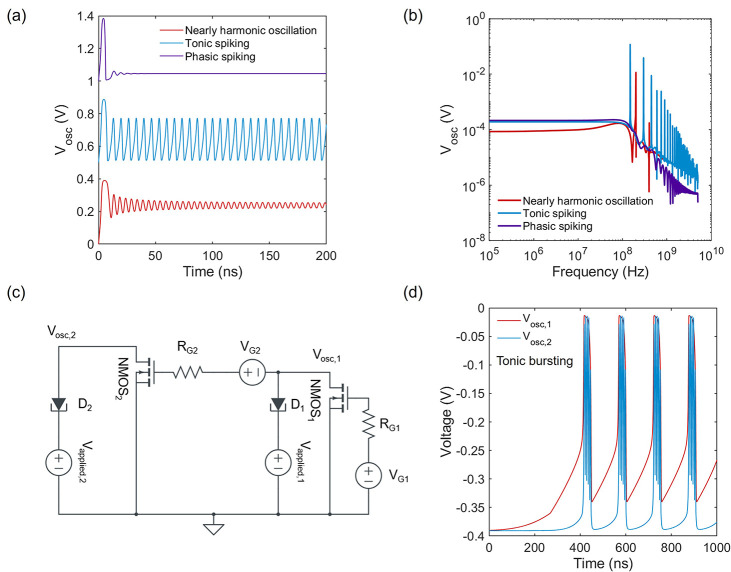
An FN neuron is a two-dimensional dynamical system capable of showing several biological neuron-like firing patterns, such as phasic and tonic spiking. Excitability of an FN neuron is dependent on the design parameters. Figure 5a shows three different operations of an FN neuron with a diode area of 0.02 μm2, RG = 110 MΩ, Vapplied = 0.39 V, and three different values of VG. At smaller VG (0.1 V), transconductance of the FET is smaller, and the Hara inductor presents a large inductive impedance. As a result, the nonlinear term in the FN neuron model becomes smaller, and the FN neuron shows nearly harmonic oscillations. As VG becomes larger (0.2 V), inductive impedance becomes smaller, and the oscillations become more nonlinear with sharper spiking nature. This is similar to tonic spiking in biological neurons. When VG becomes even larger (0.35 V), the neuron shows a transient spike, followed by overdamped oscillations similar to phasic spiking patterns. Figure 5b shows the corresponding FFT spectra of the oscillation time series shown in Figure 5a. As expected, the nearly harmonic oscillations show much smaller high harmonic peaks compared to the fundamental frequency, while the tonic spiking pattern shows significantly larger high harmonic contents. The phasic spiking pattern does not show any significant frequency peak as the oscillation dies away with time. It is important to note that FN neuron model inherently lacks the capability to generate bursting patterns due to its limited dimensionality. However, it is possible to cascade two FN neurons, as shown in Figure 5c to increase the dimensionality and generate tonic bursting patterns (Figure 5d). Essentially, when the oscillations generated by one neuron are much slower than the other (RG1 = 100RG2 = 11 GΩ), it is possible to modulate the VG2 input of the second neuron using the output of the first neuron (Vosc,1). As a result, the second neuron only fires when the first neuron provides the necessary voltage. Therefore, it is possible to generate different firing patterns by designing electronic circuits with multiple FN neurons.
Figure 5.
Biological neuron-like firing patterns. (a) Firing patterns of a single FN neuron showing tonic and phasic spiking and (b) corresponding FFT spectra. (c) Circuit schematic of two cascaded FN neurons. (d) Tonic bursting patterns generated by the cascaded circuit.
FN neurons can be used to create traditional spiking neural networks (SNNs) for performing tasks typical of artificial neural networks (ANNs). These traditional SNN architectures encode information in the timing (temporal encoding) or frequency (rate encoding) of spiking patterns and make use of all-or-nothing spiking dynamical behavior of neurons to process information.79−81 These architectures typically mimic the behavior of ANNs while utilizing the low energy consumption behavior of spiking neurons. Performance of these networks has been further limited by their incompatibility with backpropagation methods of learning. The dimensionality of these networks is reduced due to their all-or-nothing spiking nature. On the other hand, oscillator-based computing approaches utilizing synchronization behavior of oscillator networks through interaction can potentially make use of a much richer computational space to perform more versatile tasks. A liquid state machine comprising a network of oscillators is theoretically capable of performing all tasks doable by a Turing machine without resorting to any learning mechanism.82−87 OIMs have been used to solve computationally hard combinatorial problems by exploiting the oscillation dynamics of a coupled oscillator network. In our previous work, we have shown that it is possible to perform massively parallel computing by multiplexing operations in the frequency domain. SNNs are therefore a subset of the massive computational space offered by computing systems by using oscillator dynamics.
While an oscillatory neuron is the building block for neuromorphic
oscillatory computing, the actual computation emerges from the macroscopic
behavior of a network of coupled oscillators. Harnessing these emergent
computational behaviors is contingent on the construction of the coupling
network. There have been prior works on associative memory property
of coupled oscillators where the oscillator phases settle to certain
values resulting from the minimization of the “energy”
of the system.44,45,47,50,55,61,62 OIM is a special case
of such a phase-based computation scheme, where a computationally
hard combinatorial optimization problem can be mapped to the coupling
impedances of the oscillator network. Under certain circumstances,
the oscillators would then settle to a combination of binary phases
(0 or π) that result in a minimization of the system energy
that corresponds to the Ising Hamiltonian of the problem.55−58 Typically, the oscillator phases can take continuous values between
0 and π. However, if the oscillators are externally injected
with a signal with twice their fundamental oscillation frequency,
it is possible to force them to have binary phase differences of 0
or π because of subharmonic injection locking (SHIL).55−57 Detailed mathematical analysis on mapping NP-hard and NP-complete
combinatorial problems to OIMs has been carried out elsewhere.44,55−58,62 This work focuses on how FN neurons
can be utilized for oscillator-based computing, and we have chosen
to demonstrate how an FN neuron-based OIM can be used to solve an
NP-complete problem such as the “max-cut” problem. If
we have a graph with N-nodes and the nodes have M-edges between them
with different weights, then the max-cut problem aims to find a binary
partition between the N-nodes that results in the maximum number of
cuts to the edge weights. For the sake of simplicity, let us consider
a graph with 2-nodes with a single edge with unity weight. Then, partitioning
the two nodes into different groups results in the max-cut of 1 (Figure S5a). Figure S5b shows how this problem can be mapped on two FN neurons coupled
with a resistor, Rcoupling. When Rcoupling is too small, the oscillators are always
in phase, and there is no partition between the oscillators. On the
other hand, when Rcoupling is large, the
oscillators are almost uncoupled, and therefore they do not maintain
a specific phase difference between them. However, for intermediate
values of Rcoupling, they would always
couple with a phase difference of π, resulting in a partition.
We have performed simulations for X different random
initial conditions for the FN neurons for a given Rcoupling and then calculated the probability of finding correct solution
as 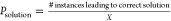 . Figure S5c shows Psolution as a function of Rcoupling for Vinj = 0.5 V
and RSHIL = 50 MΩ (X = 1000). Figure S5d shows evolution of
the oscillation waveform toward the correct solution, i.e., coupling
antiphase. It is noteworthy that the symbol of oscillator includes
the FN neuron as well as an externally applied SHIL signal, as shown
in Figure S6a.
. Figure S5c shows Psolution as a function of Rcoupling for Vinj = 0.5 V
and RSHIL = 50 MΩ (X = 1000). Figure S5d shows evolution of
the oscillation waveform toward the correct solution, i.e., coupling
antiphase. It is noteworthy that the symbol of oscillator includes
the FN neuron as well as an externally applied SHIL signal, as shown
in Figure S6a.
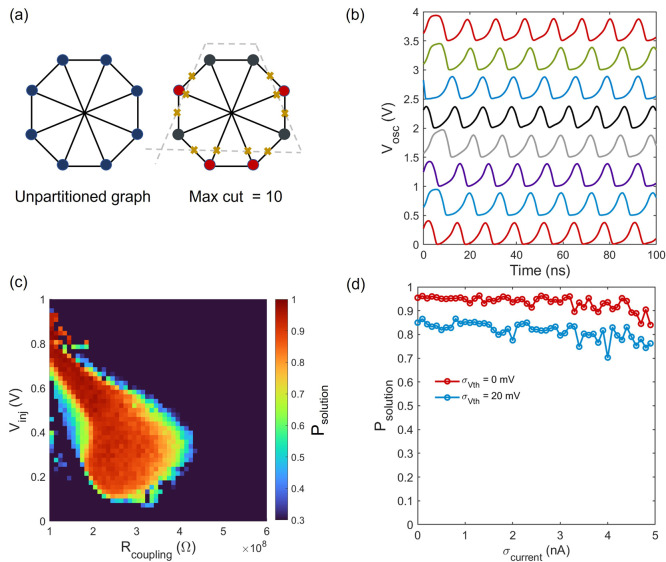
Figure 6a shows
the graph for an 8-node max-cut problem and the solution that yields
maximum cuts of 10. Figure S6b shows the
circuit schematic implementing this max-cut problem. Here, we consider Rij = Rcoupling for
all values of (i,j). Figure 6b shows the evolution of oscillator
phases toward the partition that gives us maximum cuts. This result
was achieved for Rcoupling = 150 MΩ, RSHIL = 50 MΩ, and Vinj = 0.5 V for fSHIL = 150 MHz.
It is important to note that Psolution is heavily dependent on the parameters of the coupling network.
The correct partition between oscillators depends critically on two
factors: (1) the ability to achieve phase bipartition and (2) the
ability to achieve the correct order of phase bipartition. While phase
bipartition ability comes explicitly from the SHIL signal and therefore
depends on the strength of Vinj, the correct
order of phase bipartition comes from the coupling between different
oscillators and hence on Rcoupling. Figure 6c shows the colormap
of Psolution as a function of Rcoupling and Vinj for RSHIL = 50 MΩ (X = 768). As shown in Figure 6c, high values of Psolution can
be achieved only when the combination of Rcoupling and Vinj is within a certain range.
However, one of the key issues with implementing OIMs is the variation
between the oscillators. Since the phase bipartition is very sensitive
to the oscillation dynamics, variations in oscillators can lead to
significant degradation of Psolution.
For nanoscale devices, these variations are more pronounced due to
random dopant fluctuation, lithography-based size variations, etc.
Random dopant variation is most pronounced since ion implantation
in CMOS processes is inherently a stochastic process, and such variation
leads to significant spread in threshold voltages across different
MOSFETs. In addition, the tunnel diodes also feature heavily doped
p++ (>1019 cm–3) and n++ regions (>1019 cm–3). Therefore,
we can also expect some variations in the tunnel diode current levels.
However, when there is current flow in a diode, its capacitance is
dominated by the charge transport capacitance or diffusion capacitance.
This capacitance is directly proportional to current, and therefore,
such current variations also lead to linear variations in device capacitance.
As discussed in Section S6, when there
is a variation in both device current and capacitance, the differential
equation governing the oscillation dynamics remains immune to these
fluctuations when the fluctuations are small. We have then introduced
a Gaussian variation in both device current and capacitance of the
tunnel diodes for the 8-node max-cut circuit and simulated the OIM
oscillation dynamics. Figure 6d shows Psolution as a function
of standard deviation (σcurrent) in tunnel diode
peak current, showing the insensitivity of Psolution as σcurrent increases. When we consider
variations in Vth (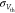 = 20 mV), as experimentally observed in
a previous study on 65 nm MOSFETs,88 there
is a slight degradation in Psolution as
shown in Figure 5d.
These results clearly show the promise of FN neurons in oscillator-based
computing. While CMOS compatibility and scalability would allow realization
of large scale coupled oscillator networks, electrical energy consumption
of such networks can also be minimized because of the superior energy
efficiency of FN neurons.
= 20 mV), as experimentally observed in
a previous study on 65 nm MOSFETs,88 there
is a slight degradation in Psolution as
shown in Figure 5d.
These results clearly show the promise of FN neurons in oscillator-based
computing. While CMOS compatibility and scalability would allow realization
of large scale coupled oscillator networks, electrical energy consumption
of such networks can also be minimized because of the superior energy
efficiency of FN neurons.
Figure 6.
Implementation of an Ising machine with FN neurons. (a) A 8-node graph for max-cut problem and its solution. (b) Evolution of oscillation waveforms toward correct solution from random initial conditions. (c) Colormap of solution probability as a function of Rcoupling and Vinj without considering any variation. (f) Robustness of Psolution to variations in tunnel diode current.
Conclusion
In conclusion, we have demonstrated an active inductor-based implementation for an FN neuron and predicted the scaling behavior of this neuron through simulations. Our simulations show that it is possible to generate the oscillation behavior in these neurons at an extremely low energy cost of 2 aJ per cycle. These FN neurons can generate firing patterns similar to biological neurons, such as tonic and phasic spiking. Firing patterns unachievable by a single FN neuron, such as bursting patterns, can also be generated by designing appropriate circuits with these neurons. FN neurons can be used in a coupled oscillator network to form an Ising machine and solve NP-complete combinatorial problems such as the max-cut problem while being robust to process variations. This work shows a roadmap to designing and implementing FN neurons through voltage controlled NDR devices, replacing the real inductor with the MOSFET-based inductor, generation of oscillations with ultralow electrical energy, and possible application in large scale variation insensitive oscillator-based computing systems.
Acknowledgments
R.A. acknowledges USC Provost Graduate Fellowship. Z.W. acknowledges Viterbi Graduate School Fellowship.
Data Availability Statement
The data that support the plots within this paper and other findings of this study are publicly available at https://doi.org/10.6084/m9.figshare.25405207.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.3c09936.
Additional details about theoretical modeling of FN neuron and Ising machine; nullclines and trajectory of a FN neuron (Figure S1); FN neuron nullclines and trajectories for different values of Iext (Figure S2); experimentally measured J–V and C–V curves of a silicon tunnel diode, peak current density of silicon homojunction, and GaSb/InAs heterojunction tunnel diodes of different diode areas (Figure S3); oscillation, frequency, amplitude, power consumption, and energy consumption for different NMOS areas (Figure S4); simple 2-node max-cut problem and mapping 2-node max-cut problem to FN neurons (Figure S5); symbol for oscillator circuit and the actual circuit (Figure S6) (PDF)
Author Contributions
R.A. and R.K. conceived the project. R.A., Z.W., and S.A.A.J performed the simulations. All authors contributed to analyzing the data. R.A. and R.K. wrote the paper while all the authors provided feedback.
1. Department of Energy Grant No. DE-SC0022248. 2. National Science Foundation Award No. 2004791. 3. Office of Naval Research Grant No. N00014–21–1–2634. 4. Air Force Office of Scientific Research Grant No. FA9550–21–1–0305.
The authors declare no competing financial interest.
Supplementary Material
References
- Benjamin B. V.; Gao P.; McQuinn E.; Choudhary S.; Chandrasekaran A. R.; Bussat J.-M.; Alvarez-Icaza R.; Arthur J. V.; Merolla P. A.; Boahen K. Neurogrid: A Mixed-Analog-Digital Multichip System for Large-Scale Neural Simulations. Proc. IEEE 2014, 102 (5), 699–716. 10.1109/JPROC.2014.2313565. [DOI] [Google Scholar]
- Liu S. C.; Delbrück T.. Introduction to Neuromorphic and Bio-Inspired Mixed-Signal VLSI; California Institute of Technology: Pasadena, CA, 2007. [Google Scholar]
- Attwell D.; Laughlin S. B. An Energy Budget for Signaling in the Grey Matter of the Brain. J. Cereb. Blood Flow Metab. 2001, 21 (10), 1133–1145. 10.1097/00004647-200110000-00001. [DOI] [PubMed] [Google Scholar]
- Lennie P. The Cost of Cortical Computation. Curr. Biol. 2003, 13 (6), 493–497. 10.1016/S0960-9822(03)00135-0. [DOI] [PubMed] [Google Scholar]
- Oliveira A.. The digital mind: how science is redefining humanity; MIT Press, 2017. [Google Scholar]
- Poon C.-S.; Zhou K. Neuromorphic silicon neurons and large-scale neural networks: challenges and opportunities. Front. Neurosci. 2011, 5, 108. 10.3389/fnins.2011.00108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Esaki L. New Phenomenon in Narrow Germanium p-n Junctions. Phys. Rev. 1958, 109 (2), 603–604. 10.1103/PhysRev.109.603. [DOI] [Google Scholar]
- Gunn J. B. Microwave oscillations of current in III–V semiconductors. Solid State Commun. 1963, 1 (4), 88–91. 10.1016/0038-1098(63)90041-3. [DOI] [Google Scholar]
- Nagumo J.; Arimoto S.; Yoshizawa S. An active pulse transmission line simulating nerve axon. Proc. IRE 1962, 50 (10), 2061–2070. 10.1109/JRPROC.1962.288235. [DOI] [Google Scholar]
- Nishizawa J.-I.; Hayasaka A. Two-line neuristor with active element in series and in parallel. Int. J. Electron. 1969, 26 (5), 437–469. 10.1080/00207216908938173. [DOI] [Google Scholar]
- Crane H.. The neuristor; IEEE, 1961; Vol. 4, pp 30–31.. [Google Scholar]
- Duan Q.; Jing Z.; Zou X.; Wang Y.; Yang K.; Zhang T.; Wu S.; Huang R.; Yang Y. Spiking neurons with spatiotemporal dynamics and gain modulation for monolithically integrated memristive neural networks. Nat. Commun. 2020, 11 (1), 1–13. 10.1038/s41467-020-17215-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Z.; Joshi S.; Savel’ev S.; Song W.; Midya R.; Li Y.; Rao M.; Yan P.; Asapu S.; Zhuo Y.; et al. Fully memristive neural networks for pattern classification with unsupervised learning. Nat Electron. 2018, 1 (2), 137–145. 10.1038/s41928-018-0023-2. [DOI] [Google Scholar]
- Jerry M.; Parihar A.; Grisafe B.; Raychowdhury A.; Datta S.. Ultra-low power probabilistic IMT neurons for stochastic sampling machines; IEEE, 2017; pp T186–T187.. [Google Scholar]
- Tuma T.; Pantazi A.; Le Gallo M.; Sebastian A.; Eleftheriou E. Stochastic phase-change neurons. Nat. Nanotechnol. 2016, 11 (8), 693–699. 10.1038/nnano.2016.70. [DOI] [PubMed] [Google Scholar]
- Lim H.; Ahn H.-W.; Kornijcuk V.; Kim G.; Seok J. Y.; Kim I.; Hwang C. S.; Jeong D. S. Relaxation oscillator-realized artificial electronic neurons, their responses, and noise. Nanoscale 2016, 8 (18), 9629–9640. 10.1039/C6NR01278G. [DOI] [PubMed] [Google Scholar]
- Lee D.; Kwak M.; Moon K.; Choi W.; Park J.; Yoo J.; Song J.; Lim S.; Sung C.; Banerjee W.; et al. Various threshold switching devices for integrate and fire neuron applications. Adv. Electron. Mater. 2019, 5 (9), 1800866. 10.1002/aelm.201800866. [DOI] [Google Scholar]
- Pickett M. D.; Medeiros-Ribeiro G.; Williams R. S. A scalable neuristor built with Mott memristors. Nat. Mater. 2013, 12 (2), 114–117. 10.1038/nmat3510. [DOI] [PubMed] [Google Scholar]
- Stoliar P.; Tranchant J.; Corraze B.; Janod E.; Besland M. P.; Tesler F.; Rozenberg M.; Cario L. A leaky-integrate-and-fire neuron analog realized with a Mott insulator. Adv. Funct. Mater. 2017, 27 (11), 1604740. 10.1002/adfm.201604740. [DOI] [Google Scholar]
- Mehonic A.; Kenyon A. J. Emulating the electrical activity of the neuron using a silicon oxide RRAM cell. Front. Neurosci. 2016, 10, 57. 10.3389/fnins.2016.00057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gupta I.; Serb A.; Khiat A.; Zeitler R.; Vassanelli S.; Prodromakis T. Real-time encoding and compression of neuronal spikes by metal-oxide memristors. Nat. Commun. 2016, 7 (1), 1–9. 10.1038/ncomms12805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang H.-M.; Yang R.; Tan Z.-H.; He H.-K.; Zhou W.; Xiong J.; Guo X. Quasi-Hodgkin–Huxley Neurons with Leaky Integrate-and-Fire Functions Physically Realized with Memristive Devices. Adv. Mater. 2019, 31 (3), 1803849. 10.1002/adma.201803849. [DOI] [PubMed] [Google Scholar]
- Ignatov M.; Ziegler M.; Hansen M.; Petraru A.; Kohlstedt H. A memristive spiking neuron with firing rate coding. Front. Neurosci. 2015, 9, 376. 10.3389/fnins.2015.00376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hess K.; Morkoç H.; Shichijo H.; Streetman B. G. Negative differential resistance through real-space electron transfer. Appl. Phys. Lett. 1979, 35 (6), 469–471. 10.1063/1.91172. [DOI] [Google Scholar]
- Ho C.-L.; Wu M.-C.; Ho W.-J.; Liaw J.-W. Light-induced negative differential resistance in planar InP/InGaAs/InP double-heterojunction p-i-n photodiode. Appl. Phys. Lett 1999, 74 (26), 4008–4010. 10.1063/1.123243. [DOI] [Google Scholar]
- Vega-González V.; Gutiérrez-Domínguez E.; Guarin F.. A negative differential resistance effect implemented with a single MOSFET from 375 k down to 80 k. In 2013 Proceedings of the European Solid-State Device Research Conference (ESSDERC); IEEE, 2013; pp 330–333.. DOI: 10.1109/ESSDERC.2013.6818885. [DOI] [Google Scholar]
- Sharma P.; Bernard L. S.; Bazigos A.; Magrez A.; Ionescu A. M. Room-Temperature Negative Differential Resistance in Graphene Field Effect Transistors: Experiments and Theory. ACS Nano 2015, 9 (1), 620–625. 10.1021/nn5059437. [DOI] [PubMed] [Google Scholar]
- Wu Y.; Farmer D. B.; Zhu W.; Han S.-J.; Dimitrakopoulos C. D.; Bol A. A.; Avouris P.; Lin Y.-M. Three-Terminal Graphene Negative Differential Resistance Devices. ACS Nano 2012, 6 (3), 2610–2616. 10.1021/nn205106z. [DOI] [PubMed] [Google Scholar]
- Chen H.; Nie H.; Guo L. Interface trap-induced negative differential resistance in nMOSFET with floating source. Phys. Lett. A 2020, 384 (17), 126342. 10.1016/j.physleta.2020.126342. [DOI] [Google Scholar]
- Hourdakis E.; Kaidatzis A.; Niarchos D.; Nassiopoulou A. G. Voltage-controlled negative differential resistance in metal-sputtered alumina-Si structures. J. Phys. D: Appl. Phys. 2019, 52 (8), 085101. 10.1088/1361-6463/aaf499. [DOI] [Google Scholar]
- Liu W.; Guo H.; Li W.; Wan X.; Bodepudi S. C.; Shehzad K.; Xu Y. Light-induced negative differential resistance in gate-controlled graphene-silicon photodiode. Appl. Phys. Lett. 2018, 112 (20), 201109. 10.1063/1.5026382. [DOI] [Google Scholar]
- Wang X.; Wang Y.; Feng M.; Wang K.; Bai P.; Tian Y. Light-induced negative differential resistance effect in a resistive switching memory device. Curr. Appl. Phys. 2020, 20 (3), 371–378. 10.1016/j.cap.2019.12.008. [DOI] [Google Scholar]
- Chen J.; Reed M. A.; Rawlett A. M.; Tour J. M. Large On-Off Ratios and Negative Differential Resistance in a Molecular Electronic Device. Science 1999, 286 (5444), 1550–1552. 10.1126/science.286.5444.1550. [DOI] [PubMed] [Google Scholar]
- Zhao F.; Jia C.; Guo W.; Xie S.; Chen Y.; Tee C. A. T. H.; Huo D.; Chang Y.; Jiang H. Silicon neuron transistor based on CMOS negative differential resistance (NDR). IEICE Electron. Express 2020, 17 (24), 20200316–20200316. 10.1587/elex.17.20200316. [DOI] [Google Scholar]
- Hejda M.; Alanis J. A.; Ortega-Piwonka I.; Lourenço J.; Figueiredo J.; Javaloyes J.; Romeira B.; Hurtado A. Resonant tunneling diode nano-optoelectronic excitable nodes for neuromorphic spike-based information processing. Phys. Rev. Appl. 2022, 17 (2), 024072. 10.1103/PhysRevApplied.17.024072. [DOI] [Google Scholar]
- Cimbri D.; Wang J.; Al-Khalidi A.; Wasige E. Resonant tunneling diodes high-speed terahertz wireless communications-A review. IEEE Trans. Terahertz Sci. Technol. 2022, 12 (3), 226–244. 10.1109/TTHZ.2022.3142965. [DOI] [Google Scholar]
- Ortega-Piwonka I.; Piro O.; Figueiredo J.; Romeira B.; Javaloyes J. Bursting and excitability in neuromorphic resonant tunneling diodes. Phys. Rev. Appl. 2021, 15 (3), 034017. 10.1103/PhysRevApplied.15.034017. [DOI] [Google Scholar]
- Feiginov M. Frequency limitations of resonant-tunnelling diodes in sub-THz and THz oscillators and detectors. J. Infrared, Millimeter, Terahertz Waves 2019, 40 (4), 365–394. 10.1007/s10762-019-00573-5. [DOI] [Google Scholar]
- Izumi R.; Suzuki S.; Asada M.. 1.98 THz resonant-tunneling-diode oscillator with reduced conduction loss by thick antenna electrode. In 2017 42nd International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz); IEEE, 2017; pp 1–2.. [Google Scholar]
- Romeira B.; Javaloyes J.; Ironside C. N.; Figueiredo J. M.; Balle S.; Piro O. Excitability and optical pulse generation in semiconductor lasers driven by resonant tunneling diode photo-detectors. Opt. Express 2013, 21 (18), 20931–20940. 10.1364/OE.21.020931. [DOI] [PubMed] [Google Scholar]
- Suzuki S.; Teranishi A.; Hinata K.; Asada M.; Sugiyama H.; Yokoyama H. Fundamental oscillation of up to 831 GHz in GaInAs/AlAs resonant tunneling diode. Appl. Phys. Express 2009, 2 (5), 054501. 10.1143/APEX.2.054501. [DOI] [Google Scholar]
- Chung S.-Y.; Yu R.; Jin N.; Park S.-Y.; Berger P. R.; Thompson P. E. Si/SiGe resonant interband tunnel diode with f/sub r0/20.2 GHz and peak current density 218 kA/cm/sup 2/for K-band mixed-signal applications. IEEE Electron Device Lett. 2006, 27 (5), 364–367. 10.1109/LED.2006.873379. [DOI] [Google Scholar]
- Ahsan R.; Chae H. U.; Jalal S. A. A.; Tao J.; Das S.; Liu H.; Wu J.-B.; Cronin S.; Wang H.; Sideris C.; Kapadia R.. Ultra-low power in-sensor neuronal computing with oscillatory retinal neurons for frequency-multiplexed, parallel machine vision; Research Square, 2023. [DOI] [PubMed] [Google Scholar]
- Csaba G.; Raychowdhury A.; Datta S.; Porod W.. Computing with coupled oscillators: Theory, devices, and applications. In 2018 IEEE International Symposium on Circuits and Systems (ISCAS); IEEE, 2018; pp 1–5.. [Google Scholar]
- Raychowdhury A.; Parihar A.; Smith G. H.; Narayanan V.; Csaba G.; Jerry M.; Porod W.; Datta S. Computing with networks of oscillatory dynamical systems. Proc. IEEE 2019, 107 (1), 73–89. 10.1109/JPROC.2018.2878854. [DOI] [Google Scholar]
- Pourahmad V.; Manipatruni S.; Nikonov D.; Young I.; Afshari E. Nonboolean pattern recognition using chains of coupled CMOS oscillators as discriminant circuits. IEEE J. Explor. Solid-State Comput. Devices Circuits 2017, 3, 1–9. 10.1109/JXCDC.2017.2654300. [DOI] [Google Scholar]
- Nikonov D. E.; Csaba G.; Porod W.; Shibata T.; Voils D.; Hammerstrom D.; Young I. A.; Bourianoff G. I. Coupled-oscillator associative memory array operation for pattern recognition. IEEE J. Explor. Solid-State Comput. Devices Circuits 2015, 1, 85–93. 10.1109/JXCDC.2015.2504049. [DOI] [Google Scholar]
- Shibata T.; Zhang R.; Levitan S. P.; Nikonov D. E.; Bourianoff G. I.. CMOS supporting circuitries for nano-oscillator-based associative memories. In 2012 13th International Workshop on Cellular Nanoscale Networks and their Applications; IEEE, 2012; pp. 1–5.. [Google Scholar]
- Delacour C.; Carapezzi S.; Abernot M.; Todri-Sanial A.. Energy-Performance Assessment of Oscillatory Neural Networks based on VO2 Devices for Future Edge AI Computing; IEEE, 2022. [DOI] [PubMed] [Google Scholar]
- Núñez J.; Avedillo M. J.; Jiménez M.; Quintana J. M.; Todri-Sanial A.; Corti E.; Karg S.; Linares-Barranco B. Oscillatory Neural Networks Using VO2 Based Phase Encoded Logic. Front. Neurosci. 2021, 15, 655823. 10.3389/fnins.2021.655823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corti E.; Cornejo Jimenez J. A.; Niang K. M.; Robertson J.; Moselund K. E.; Gotsmann B.; Ionescu A. M.; Karg S. Coupled VO2 oscillators circuit as analog first layer filter in convolutional neural networks. Front. Neurosci. 2021, 15, 628254. 10.3389/fnins.2021.628254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackson T.; Pagliarini S.; Pileggi L.. An oscillatory neural network with programmable resistive synapses in 28 nm CMOS. In 2018 IEEE International Conference on Rebooting Computing (ICRC); IEEE, 2018; pp 1–7.. [Google Scholar]
- Jackson T. C.; Sharma A. A.; Bain J. A.; Weldon J. A.; Pileggi L. Oscillatory neural networks based on TMO nano-oscillators and multi-level RRAM cells. IEEE J. Emerging Sel. Top. Circuits Sys. 2015, 5 (2), 230–241. 10.1109/JETCAS.2015.2433551. [DOI] [Google Scholar]
- Vaidya J.; Surya Kanthi R.; Shukla N. Creating electronic oscillator-based Ising machines without external injection locking. Sci. Rep. 2022, 12 (1), 981. 10.1038/s41598-021-04057-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dutta S.; Khanna A.; Assoa A.; Paik H.; Schlom D. G.; Toroczkai Z.; Raychowdhury A.; Datta S. An Ising Hamiltonian solver based on coupled stochastic phase-transition nano-oscillators. Nat. Electron. 2021, 4 (7), 502–512. 10.1038/s41928-021-00616-7. [DOI] [Google Scholar]
- Wang T.; Roychowdhury J.. OIM: Oscillator-based Ising machines for solving combinatorial optimization problems. In Unconventional Computation and Natural Computation: 18th International Conference, UCNC 2019, Tokyo, Japan, June 3–7, 2019, Proceedings; Springer, 2019; pp 232–256.. [Google Scholar]
- Chou J.; Bramhavar S.; Ghosh S.; Herzog W. Analog coupled oscillator based weighted Ising machine. Sci. Rep. 2019, 9 (1), 14786. 10.1038/s41598-019-49699-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang T.; Wu L.; Roychowdhury J.. New computational results and hardware prototypes for oscillator-based ising machines. In Proceedings of the 56th Annual Design Automation Conference 2019; arXiv, 2019; pp 1–2.. [Google Scholar]
- Nikonov D. E.; Kurahashi P.; Ayers J. S.; Li H.; Kamgaing T.; Dogiamis G. C.; Lee H.-J.; Fan Y.; Young I. Convolution inference via synchronization of a coupled CMOS oscillator array. IEEE J. Explor. Solid-State Comput. Devices Circuits 2020, 6 (2), 170–176. 10.1109/JXCDC.2020.3046143. [DOI] [Google Scholar]
- Nikonov D. E.; Young I. A.; Bourianoff G. I.. Convolutional networks for image processing by coupled oscillator arrays; arXiv. 2014. [Google Scholar]
- Koo M.; Pufall M.; Shim Y.; Kos A. B.; Csaba G.; Porod W.; Rippard W.; Roy K. Distance computation based on coupled spin-torque oscillators: Application to image processing. Phys. Rev. Appl. 2020, 14 (3), 034001. 10.1103/PhysRevApplied.14.034001. [DOI] [Google Scholar]
- Csaba G.; Porod W. Coupled oscillators for computing: A review and perspective. Appl. Phys. Rev. 2020, 7 (1), 011302. 10.1063/1.5120412. [DOI] [Google Scholar]
- Izhikevich E. M.; FitzHugh R. Fitzhugh-nagumo model. Scholarpedia 2006, 1 (9), 1349. 10.4249/scholarpedia.1349. [DOI] [Google Scholar]
- Cveticanin L. On the Van der Pol oscillator: An overview. Appl. Mech. Mater. 2013, 430, 3–13. 10.4028/www.scientific.net/AMM.430.3. [DOI] [Google Scholar]
- Kanamaru T. Van der Pol oscillator. Scholarpedia 2007, 2 (1), 2202. 10.4249/scholarpedia.2202. [DOI] [Google Scholar]
- Keener J. P. Analog circuitry for the van der Pol and FitzHugh-Nagumo equations. IEEE Trans. Syst. Man Cybern. 1983, 5, 1010–1014. 10.1109/TSMC.1983.6313098. [DOI] [Google Scholar]
- Broad-band monolithic microwave active inductor and its application to miniaturized wide-band amplifiers. IEEE Transactions on Microwave Theory and Techniques; IEEE, 1988. Vol. 36( (12), ). pp 1920–1924.. [Google Scholar]
- Anuar N.Supply clock generation (driver) circuit for 2PASCL: hara active inductor equivalent circuit and simulation, https://nazrulanuar.com/author/wp-content/uploads/2009/04/zemi_main141.pdf. [Google Scholar]
- Yuan F.CMOS active inductors and transformers. In Principle, implementation, and applications; Springer, 2008. [Google Scholar]
- Yan Y.; Zhao J.; Liu Q.; Zhao W.; Seabaugh A.. Vertical tunnel diodes on high resistivity silicon. In Conference Digest [Includes’ Late News Papers’ volume] Device Research Conference, 2004. 62nd DRC; IEEE, 2004; pp 27–28.. [Google Scholar]
- Sicard E.; Aziz S. M.. Introducing 65 nm technology in Microwind3; HAL open science, 2011. [Google Scholar]
- Al-Shedivat M.; Naous R.; Cauwenberghs G.; Salama K. N. Memristors empower spiking neurons with stochasticity. IEEE J. Emerging Sel. Top. Circuits Sys. 2015, 5 (2), 242–253. 10.1109/JETCAS.2015.2435512. [DOI] [Google Scholar]
- Seo J.-S.; Brezzo B.; Liu Y.; Parker B. D.; Esser S. K.; Montoye R. K.; Rajendran B.; Tierno J. A.; Chang L.; Modha D. S.. A 45nm CMOS neuromorphic chip with a scalable architecture for learning in networks of spiking neurons. In 2011 IEEE Custom Integrated Circuits Conference (CICC); IEEE, 2011; pp 1–4.. [Google Scholar]
- Indiveri G.; Chicca E.; Douglas R. A VLSI array of low-power spiking neurons and bistable synapses with spike-timing dependent plasticity. IEEE Trans. Neural Networks 2006, 17 (1), 211–221. 10.1109/TNN.2005.860850. [DOI] [PubMed] [Google Scholar]
- Sourikopoulos I.; Hedayat S.; Loyez C.; Danneville F.; Hoel V.; Mercier E.; Cappy A. A 4-fJ/Spike Artificial Neuron in 65 nm CMOS Technology. Front. Neurosci. 2017, 11, 247370. 10.3389/fnins.2017.00123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Indiveri G.. A low-power adaptive integrate-and-fire neuron circuit. In Proceedings of the 2003 International Symposium on Circuits and Systems; IEEE; 2003, Vol. 4, pp IV–IV.. [Google Scholar]
- Mahowald M.; Douglas R. A silicon neuron. Nature 1991, 354 (6354), 515–518. 10.1038/354515a0. [DOI] [PubMed] [Google Scholar]
- Wijekoon J. H.; Dudek P. Compact silicon neuron circuit with spiking and bursting behaviour. Neural Networks 2008, 21 (2–3), 524–534. 10.1016/j.neunet.2007.12.037. [DOI] [PubMed] [Google Scholar]
- Yamazaki K.; Vo-Ho V.-K.; Bulsara D.; Le N. Spiking neural networks and their applications: A Review. Brain Sci. 2022, 12 (7), 863. 10.3390/brainsci12070863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tavanaei A.; Ghodrati M.; Kheradpisheh S. R.; Masquelier T.; Maida A. Deep learning in spiking neural networks. Neural Networks 2019, 111, 47–63. 10.1016/j.neunet.2018.12.002. [DOI] [PubMed] [Google Scholar]
- Zenke F.; Ganguli S. Superspike: Supervised learning in multilayer spiking neural networks. Neural Comput. 2018, 30 (6), 1514–1541. 10.1162/neco_a_01086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wijesinghe P.; Srinivasan G.; Panda P.; Roy K. Analysis of liquid ensembles for enhancing the performance and accuracy of liquid state machines. Front. Neurosci. 2019, 13, 504. 10.3389/fnins.2019.00504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamazaki T.; Tanaka S. The cerebellum as a liquid state machine. Neural Networks 2007, 20 (3), 290–297. 10.1016/j.neunet.2007.04.004. [DOI] [PubMed] [Google Scholar]
- Roy S.; Basu A.; Hussain S.. Hardware efficient, neuromorphic dendritically enhanced readout for liquid state machines; IEEE, 2013; pp 302–305.. [Google Scholar]
- Schrauwen B.; D’Haene M.; Verstraeten D.; Van Campenhout J.. Compact hardware for real-time speech recognition using a liquid state machine; IEEE, 2007; pp 1097–1102.. [DOI] [PubMed] [Google Scholar]
- Maass W.; Natschläger T.; Markram H. Real-time computing without stable states: A new framework for neural computation based on perturbations. Neural Comput. 2002, 14 (11), 2531–2560. 10.1162/089976602760407955. [DOI] [PubMed] [Google Scholar]
- Maass W.. On the Computational Power of Recurrent Circuits of Spiking Neuron; Technische Universität Graz, 2000. [Google Scholar]
- Agarwal K.; Nassif S.. Characterizing process variation in nanometer CMOS. In Proceedings of the 44th annual Design Automation Conference; IEEE, 2007; pp 396–399.. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the plots within this paper and other findings of this study are publicly available at https://doi.org/10.6084/m9.figshare.25405207.