How Robust Is the Ligand Binding Transition State?

Abstract

For many drug targets, it has been shown that the kinetics of drug binding (e.g., on rate and off rate) is more predictive of drug efficacy than thermodynamic quantities alone. This motivates the development of predictive computational models that can be used to optimize compounds on the basis of their kinetics. The structural details underpinning these computational models are found not only in the bound state but also in the short-lived ligand binding transition states. Although transition states cannot be directly observed experimentally due to their extremely short lifetimes, recent successes have demonstrated that modeling the ligand binding transition state is possible with the help of enhanced sampling molecular dynamics methods. Previously, we generated unbinding paths for an inhibitor of soluble epoxide hydrolase (sEH) with a residence time of 11 min. Here, we computationally modeled unbinding events with the weighted ensemble method REVO (resampling of ensembles by variation optimization) for five additional inhibitors of sEH with residence times ranging from 14.25 to 31.75 min, with average prediction accuracy within an order of magnitude. The unbinding ensembles are analyzed in detail, focusing on features of the ligand binding transition state ensembles (TSEs). We find that ligands with similar bound poses can show significant differences in their ligand binding TSEs, in terms of their spatial distribution and protein–ligand interactions. However, we also find similarities across the TSEs when examining more general features such as ligand degrees of freedom. Together these findings show significant challenges for rational, kinetics-based drug design.

Graphical Abstract

1. INTRODUCTION

Structure-based drug design (SBDD) has matured over the past few decades from a handful of success stories^1–5 into a near-ubiquitous tool to guide the discovery and optimization of potential drug molecules.⁶ SBDD approach–sincluding docking- and AI-assisted virtual screens,^7,8 Molecular Mechanics Poisson–Boltzmann Surface Area (MM-PBSA) methods,⁹ and free energy perturbation^10,11—all utilize the knowledge of the 3D structure of a target protein and its probable binding site to design potential drug molecules by optimizing the binding free energy or approximations thereof. In principle, this provides an incomplete picture of the drug–target interaction; since the in vivo environment is far from thermodynamic equilibrium, the binding kinetics are also necessary to thoroughly model drug efficacy.^12–14 In practice, it has been shown that the residence tim–the average duration of a given drug–target binding event–can be the central feature related to drug efficacy in some systems,¹⁵ including soluble epoxide hydrolase (sEH),^16,17 studied here. In contrast to the binding free energy, which is a path-independent state function relying only on the bound and unbound states, the unbinding rate constant depends on the details of the transition path ensemble of (un)binding events. Specifcally, it is related by the Arrhenius equation to the free energy of activation of the unbinding event, which is the difference in free energy of the bound state and the ligand binding transition state. Hence, to fully engage the tools of SBDD for kinetics-based rational design, we need to consider the molecular structures of both the bound state and the transition state.

This poses a monumental challenge because unlike ligand bound states, for which there are hundreds of thousands of available experimentally determined structures, there are no experimental observations of ligand binding transition state structures, due to their extremely short lifetimes. Ligand binding transition states are also challenging to model in silico. Although the transition state lifetimes are short, they are often at the top of extremely large energy barriers with mean first passage times (MFPTs) of unbinding events that range up to minutes or even hours in duration. This is 6–8 orders of magnitude beyond the current capabilities of even specialized supercomputers for molecular dynamics, which are still restricted to the μs to ms regime.¹⁸ Also, transition state ensembles (TSEs) for ligand binding are likely to be much more diverse than bound ensembles and are unable to be captured in a single structure. There is substantial possibility of a ligand unbinding from a protein using multiple pathways, and within each pathway, there are conformational fluctuations that change particular ligand–protein interactions.^19–23 This requires not just generation of a single unbinding event but of a representative ensemble of unbinding events. Finally, even with an ensemble of (un)binding transition paths, identification of the TSE requires additional analysis techniques that calculate the unbinding committor probability²⁴ for each conformation. The introduction of biasing forces in methods such as metadynamics²⁵ and τ-random acceleration molecular dynamics²⁶ introduces further uncertainty to the definition of the transition state, as biasing forces can change the underlying energy landscapes. Recent studies have sought to bypass explicit identification of the TSE by combining biased dynamics methods with machine learning approaches that can identify relevant structural features of the transition in a data-driven manner.^27–30 While these could be promising approaches to predict rates for specific systems, it is difficult to extract direct structural insight into the TSE of the unbiased transition paths.

Here, we apply an alternative enhanced sampling method that can generate long-time scale ligand unbinding events without applying biasing forces. The weighted ensemble method³¹ is a general framework for path sampling where an ensemble of trajectories, each with an associated statistical weight, is evolved forward together in time.³² Periodically, the ensemble of trajectories is “resampled”: the number copies of each trajectory are changed in order to better direct the computational effort toward a predefined objective,³³ here, the generation of ligand unbinding events. We have previously shown that variants of the weighted ensemble algorithm^34,35 can efficiently generate a thorough sampling of possible ligand unbinding transition paths.^19,35–37 As these paths are all generated using the unbiased energy function, this provides us with the clearest window through which to examine properties of the TSE. We analyze the resulting trajectory sets with Markov state models (MSMs)^38–40 that are constructed using the trajectory weights from the Weighted Ensemble (WE) sampling method and are history-augmented (haMSM⁴¹) in that they only include trajectories originating from the bound state. This allows for quantitative predictions of ligand unbinding rate constants (k_off) both through the MSMs and directly from the WE simulations.^42–44

The target protein studied here is the enzyme sEH, which is present in mammalian tissues and metabolizes epoxy fatty acids (EpFAs) to their corresponding dihydroxy fatty acids.⁴⁵ EpFAs are a novel class of lipid mediators that play critical roles in blood pressure regulation, inflammation, pain perception, and endoplasmic reticulum stress.⁴⁶ Epoxyeicosatrienoic acid (EET), one of the most studied EpFAs, is antihypertensive, anti-inflammatory, analgesic, and neuroprotective.⁴⁷ Inhibitors of sEH can raise EET levels and thus have been developed as potential treatments for these medical conditions.^48,49 As it has been previously shown that the residence time is a key quantity for determining the efficacy of sEH inhibitors in these contexts,^16,17 our long-term goal is the development of new molecules with longer sEH residence times.

The binding site of sEH is large and deeply buried inside the protein. The reference crystal structure (PDBID: 4OD0), which is used in our study, reveals that the large binding site of sEH is separated into two compartments by a center pinch, resulting from two flexible loops of the protein (Figure 1C). Previously we also used weighted ensemble simulation techniques to simulate the unbinding mechanism and estimate unbinding rates for 1-trifluoromethoxyphenyl-3-(1-propionylpiperidin-4-yl)-urea (TPPU), achieving a rough agreement with the experimental rate (42 s predicted vs 660 s experimental), and offering the first structural hints for the TSE.³⁶ We found that while the TSE was structurally diverse, there were a small number of specific protein ligand interactions that could potentially be targeted for kinetic-driven SBDD. However, a key question remained: could we extend this information to give us insight into the transition states of other structurally related inhibitors? Put another way, how robust is the ligand binding transition state?

Figure 1.

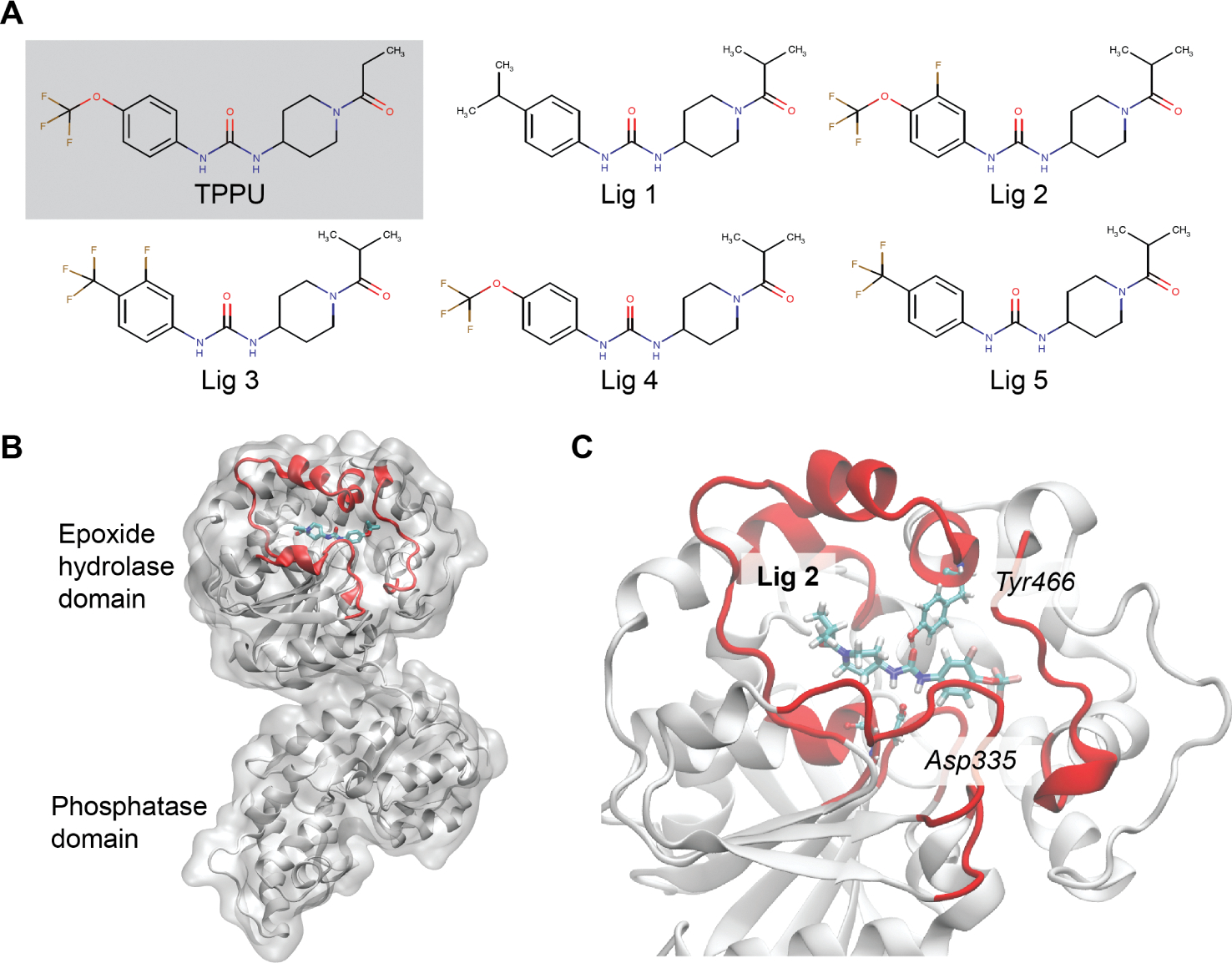
sEH protein and its inhibitors: (A) 2D representation of sEH inhibitors; (B) the combined epoxide-phosphatase domain: the binding region is highlighted in red; (C) the Ligand2 bound sEH protein with the two most interacting residues in the bound state.

Here, we tackle this question using simulations of five sEH inhibitors that are structurally related to TPPU. Their inhibition constants and residence times were measured experimentally and directly compared to residence times from simulations. We developed broad models of the ligand binding energy landscape for each ligand by maximizing the average agreement with experimental residence times. The transition path ensembles are then identified, analyzed, and compared across the set of ligands, focusing on (1) spatial location, (2) ligand–protein interactions, and (3) internal ligand degrees of freedom. We then discuss the implications of these results for kinetics-driven SBDD.

2. METHODS

2.1. Soluble Epoxide Hydrolase Inhibitors.

The inhibitors studied here share a common piperidyl phenylurea scaffold with a few different functional groups at the open-ends of the scaffold. The N atom of the piperidine group connects to a secondary keto-alkyl group. On the other side of the scaffold, the phenyl group has substitution in the meta and/or para position. Figure 1 describes the chemical structure of the inhibitor candidates. The inhibitor candidates (ligands 1, 2, 3, 4, and 5) are numbered without any particular order of significance.

2.2. Experimental Determination of Rates.

General information about the sourcing, synthesis, and characterization of the ligand compounds is given in Supplemental Methods. The measurement of unbinding rates (k_off) for ligands 2–5 was previously reported.^16,50 The unbinding rate for ligand 1 is reported here and was determined using the same FRET-displacement assay. The sEH enzyme (8 μM) was preincubated with the selected inhibitor (8.8 μM, 100 mM PB buffer, pH 7.4, 0.01% gelatin) for 1.5 h at room temperature. The sEH-inhibitor complex was diluted 40 times with ACPU (20 μM, 100 mM sodium phosphate buffer, pH 7.4, 0.01% gelatin). The fluorescence (λ_excitation at 280 nm, λ_emission at 450 nm) intensity was monitored immediately every 30 s up to 5100 s. The resulting λ_emission versus time curve was fitted to a single exponential growth equation to calculate the relative k_off.

To prevent the leaching of fluorescence impurities from the plastic tube and loss of sEH inhibitors due to nonspecific binding, the inhibitor stock solution (10 mM, DMSO) was stored in glass vials. All buffer used in this assay was filtered with a sterilized filtration unit (Millipore Durapore PVDF Membrane, pore size: 0.22 μm). All the measurements for the FRET-based displacement assays in a 96-well plate format were done in a Biotek Synergy Neo Plate Reader. To prevent nonspecific binding of sEH or inhibitor on the 96-well plate, the 96-well plates were preincubated with PB buffer with 0.1% gelatin overnight at room temperature. The gelatin coats the plate and prevents the nonspecific binding of sEH and sEH inhibitors to the plate. The buffer was discarded, and the plate was dried before use.

2.3. System Preparation for Molecular Dynamics.

The bound pose of the inhibitors inside sEH was obtained by aligning the central scaffold of each inhibitor with the bound pose of TPPU in sEH from our previous study³⁶ and then minimizing with the CHARMM36 force field.⁵¹ This conserves the previously mentioned important bound pose interactions between the ligand and protein amino acids (Asp334, Tyr383, and Tyr466). The structure from PDB ID4OD0was used to generate initial conformations for all ligands examined here.¹⁶ The catalytic domain was isolated by selecting residues 231–547 and preserving the positions of associated water molecules in the crystal structure. The ligands were parametrized using CGenFF.^52,53 We ensured that the key previously reported protein–ligand nonbonded interactions in the bound pose are conserved after alignment across all the ligands. A representation of the bound pose of one of the ligands (ligand 2) is provided in Figure 1C. The systems were solvated in TIP3 water up to a cutoff of 10 Å from the protein to the edge of the periodic box. The systems were then charge neutralized in slightly different ways across the ligand sets. Ligand 1 used 7 sodium atoms, ligands 2 and 3 used 7 potassium atoms, and ligands 4 and 5 added 17 potassium and 10 chlorine atoms to achieve an ionic strength of 150 mM. We do not expect that these differences had a significant impact on the kinetics or the transition paths.

The OpenMM simulation engine⁵⁴ was used for all of the minimization and dynamics steps in this work. CHARMM-GUI was used to generate the systems, as well as the scripts for minimization and heating.⁵⁵ The system was energy minimized by using the Limited-memory Broyden, Fletcher, Goldfarb, and Shanno (L-BFGS) algorithm with a maximum number of 5000 steps and an energy tolerance of 100 kcal/mol. The system was run at 303.15 K for 1 ns using a 0.001 ps time step with harmonic positional restraints on the protein backbone (force constant 400 kJ/mol/nm²) and protein side chains (force constant 40 kJ/mol/nm²). A force switch method was used to handle the nonbonded interactions with a switch-on distance of 10 Å and a switch-off distance of 12 Å. The particle mesh Ewald method was used to handle the electrostatic cutoff with an error tolerance of 0.0005. All covalent bonds with hydrogens were constrained. The protein restraints were then removed, and the system was equilibrated for 10 ns using a 0.002 ps time step. An isotropic Monte Carlo barostat was used to maintain a constant pressure of 1.0 bar with a pressure coupling frequency of 100 steps. The final structure was used to initialize subsequent weighted ensemble simulations, which used the same simulation conditions as the second equilibration step.

2.4. Generation of Ligand Unbinding Paths with the REVO Weighted Ensemble Method.

As mentioned above, weighted ensemble methods seek to shift the focus of the ensemble toward undersampled regions. It achieves this by “cloning” certain members of the ensemble, dividing the weight of the parent walker to be distributed evenly across the clones. Typically, trajectories are run with a stochastic integrator, such as a Langevin integrator, so that the clones diverge to explore independent paths as the simulation continues. To save computational expense, pairs of trajectories can also be “merged”. This typically occurs in oversampled regions of space near local or global free energy minima. When two trajectories A and B are merged, the resulting walker takes on the sum of the weights $\left(w_A+w_B\right)$ and adopts either the conformation of walker $A$ (with probability $w_A/\left(w_A+w_B\right)$) or walker $B(\text{with}\text{probability}{w}_B/\left(w_A+w_B\right))$. The exact nature of this random choice is important to ensure that the expectation value of the flow of probability is zero between any two regions of space.⁵⁶

The resampling of ensembles by variation optimization (REVO) algorithm is a particular implementation of the weighted ensemble that was designed to efficiently sample rare events while using an ensemble size that is as small as possible.³⁵ It achieves this by using a fixed ensemble size (here, 48) and proposing coupled merging and cloning events that are either accepted or rejected. To decide whether to accept these events, it computes the value of an objective variable termed the “trajectory variation”, $V$:

$$V=\sum _i \sum _j \frac{{d_{ij}}^{\alpha }}{d_0}{\varphi }_i{\varphi }_j$$

both before and after the proposed events. This quantifies the variation between members of the trajectory set using a measurement of distance $d_{ij}$, which is discussed in the next paragraph. The constant $d_0$ is a characteristic distance to make the variation unitless but does not affect resampling outcomes. The function ${\varphi }_i$ determines the importance of individual trajectories and is defined as a function of the walker weight: $\varphi \left(w_i\right)=\mathrm{l}\mathrm{o}\mathrm{g}\left(w_i\right)-\mathrm{l}\mathrm{o}\mathrm{g}\left(p_{\mathrm{m}\mathrm{i}\mathrm{n}}/\mathrm{C}\right)$, where $p_{\mathrm{m}\mathrm{i}\mathrm{n}}$ is a predefined minimum walker weight allowed in the simulation and C is a constant, set here to 100 following previous work.^57–59 If the proposed cloning and merging event increases the value of $V$, then it is executed, and another coupled merging and cloning event is proposed. This continues until $V$ reaches a local maximum, at which point the ensemble is propagated forward in time by the molecular dynamics integrator. Here, a round of 20 ps of dynamics (10 000 MD steps with 0.002 ps of integrator timestep) for each trajectory followed by a round of resampling is called a “cycle”. For each ligand, we run between 5 and 6 independent runs, each containing at least 2000 cycles with an ensemble size of 48. We store the frames after each “cycle” for each walker. The ensemble size was chosen to be large enough to capture a diversity of snapshots along the ligand unbinding pathway while being as small as possible to enable extension of the runs as far as possible in time. For efficient implementation, an ensemble size that is divisible by the number of GPU cards on a node (in our case, 8) is also ideal. A summary of the number of cycles in each run is given in Table 1. In total, the results presented here combined 82.9 μs of the total sampling time.

Table 1.

Length of the REVO Simulations Run for Each Ligand^a

Lig. ID	num. walkers	run index	num. cycles	aggregated sampling (μs)
Lig1	48	0	2986	2.97
		1	2751	2.64
		2	2453	2.35
		3	2224	2.13
		4	2450	2.35
		5	2470	2.37
Lig2	48	0	3257	3.13
		1	3295	3.16
		2	3274	3.14
		3	3294	3.16
		4	3275	3.14
Lig3	48	0	4000	3.84
		1	4000	3.84
		2	3885	3.73
		3	4000	3.84
		4	4000	3.84
Lig4	48	0	4000	3.84
		1	4000	3.84
		2	3414	3.28
		3	2799	2.69
		4	3518	3.38
Lig5	48	0	3400	3.26
		1	3400	3.26
		2	3400	3.26
		3	3400	3.26
		4	3400	3.26

^aThe aggregated sampling is summed across all trajectories in a given run.

The distance between trajectories $\left(d_{ij}\right)$ is calculated by aligning the binding site residues of the two trajectories and computing the rootmean-square (RMSD) distance between the ligand atoms. The set of binding site residues are defined as those within a cutoff of 5.0 Å from the ligand in the equilibrated bound pose. This distance metric captures both (1) movements of the ligand with respect to the binding site and (2) movement of ligand internal degrees of freedom. By maximizing the variation with respect to this distance, we can enhance observations of not only one unbinding path but also a broad ensemble of ligand unbinding paths.

The simulations were run with recycling boundary conditions, where all trajectories originate in the bound state and are terminated when they cross into the unbound state, which at run time was defined as having at least 10 Å of clearance between the ligand and the protein. Trajectories that unbind are reinitialized in the bound state but keeping the same weight. In practice, these are quickly merged into other high-weight trajectories in the bound state by the resampling algorithm. The simulations were conducted using the Wepy software,⁶⁰ which is a Python implementation of the REVO resampler.

2.5. Markov State Modeling and Transition State Definition.

An overview of the Markov state modeling workflow is given in Figure 2. Each frame of each trajectory is projected onto a set of features, which form the basis of the MSMs used to define the TSEs and calculate the unbinding rates. The features are a set of 336 distances calculated between a set of 56 backbone atoms in the binding site from residues Phe267, Asp335, Trp336, Ile363, Phe381, Tyr383, Gln384, Phe387, Met419, Leu328, Tyr466, Val498, Leu499, and Met503 and six ligand atoms (as shown in Figure S1) for all the frames in each simulation trajectories. The ligand atoms were chosen along the common central scaffold to facilitate a comparison of features between ligands.

Figure 2.

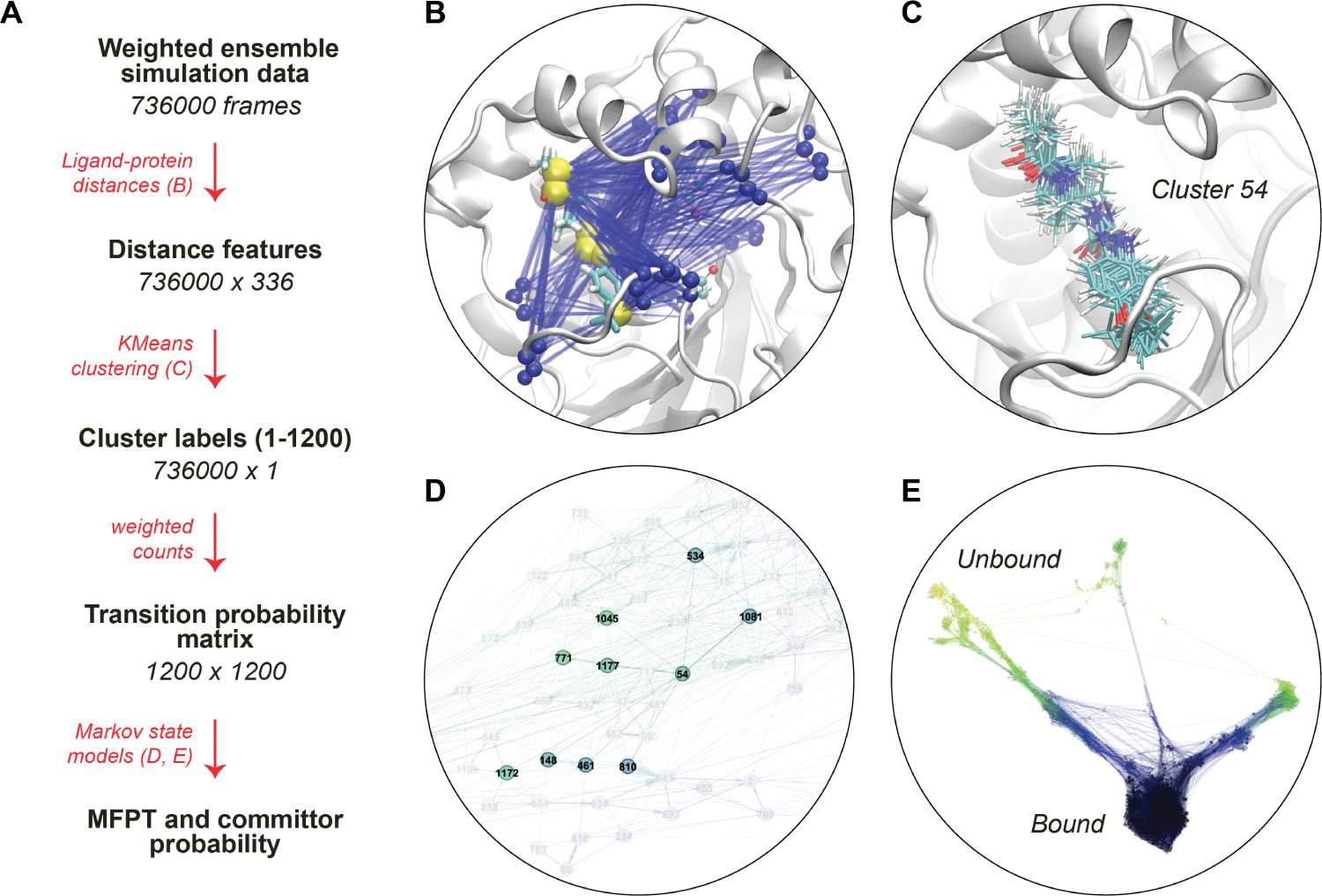
(A) The scheme of extracting TSE from weighted ensemble MD data with MSMs. (B) Visual representation of the interatomic ligand-binding site distance features for a ligand, which are later used to cluster the simulation data. The yellow spheres are ligand–atom representations, and blue spheres are the backbone atoms of the residues constituting the binding site. (C) All ligand conformations from a particular microstate after clustering all the frames based on distance features. (D) Microstates and their connectivity from a transition probability matrix. (E) CSN of ligand 4, with ligand RMSD being the scale of color. The densely populated bound state is shown in dark blue, and the sparsely connected unbound states are shown in yellow/red.

For analyses where time-independent component analysis (tICA^61,62) is used, we process the features into a Deeptime⁶³ time-lagged data set object using the sliding_windows function from Wepy. The size of the time-lagged data sets ranges from 736 000 (ligand 1) to 954 500 (ligand 3) data points, depending upon the total simulation time (Table 2). Separately for each ligand, we randomly choose a subset of 500 000 data points from the time-lagged data set members to train a tICA model, which is then used to transform the entire data set for that ligand. The reduced tICA variables are clustered into a number of states using the KMeans algorithm, and each frame of the trajectories is labeled with a cluster index. For analyses where tICA is not used, the complete set of feature vectors is used as the basis for clustering with KMeans.

Table 2.

Details of REVO Simulation Unbinding Events for Each Ligand^a

Lig. ID	cumulative sim. time (μs)	no. of unb. events	Runsunb/Runstotal	total unb. weight	weight fraction (left pathway)	weight fraction (right pathway)
Lig1	14.72	34	2/6	3.39e-10	0.000	1.000
Lig2	15.74	7	2/5	1.19e-11	0.499	0.501
Lig3	19.09	4	1/5	6.92e-12	1.000	0.000
Lig4	17.02	8	3/5	3.28e-10	0.993	0.007
Lig5	16.32	4	2/5	1.45e-07	0.000	1.000

^aThe cumulative simulation time for each ligand is combined over all 48 trajectories in each independent run. Runs_unb and Runs_total show the number of runs with unbinding events and the total number of runs, respectively, for each ligand. The total unbinding weight is the sum of the weights of all of the trajectories at the point of unbinding. Specific unbinding events were manually labeled as utilizing either the “left” or “right” pathway to determine the weight fractions.

In both cases, transition count matrices are built by counting the interstate transitions between two states across a lag time of 20 ps, again using the sliding_windows function from Wepy. Unless specified otherwise below, transitions contribute to the count matrix according to the weight of the trajectory at the end of the time interval. These are used to generate conformation space network (“CSN”) objects from the CSNAnalysis package.⁶⁴ For all clusters, we compute the average ligand RMSD to the initial reference structure. If this RMSD value is less than 2.5 Å, then the cluster is labeled as “bound”. We also compute the minimum distance $d_{\text{unb-min}}$ between the ligand and the sEH binding site for each frame in the simulation. If any members of a cluster have $d_{\text{unb-min}}>5.0\mathrm{\AA }$, then the cluster is labeled as “unbound”. Note that this is a more relaxed definition than the minimum distance of 10 Å used during run time. We consider the $d_{\text{unb-min}}>5.0\mathrm{\AA }$ to be more appropriate for describing unbinding rates that are measured by competitive binding assays, as it is more sensitive to whether the binding site has been vacated. Using these definitions of the bound and unbound basins, unbinding committor probabilities²⁴ and the unbinding MFPTs are computed using the calc_committors and calc_mfpt functions of CSNAnalysis, respectively. The calc_mfpt function creates a first-passage time distribution at intervals of 2ⁱτ, where τ is the lag time of the underlying transition probability matrix and i is an integer that increases until 99.9% of the trajectory population has reached the unbound state. We then average over the first-passage times from the bound basin to unbound basin in the unit of lag times. Subsequently, multiplying this by the lag time provides us the MFPT for the bound to unbound state.

The committor probability is a quantity from the transition path theory that measures the likelihood of an intermediate state in a two-basin system of next visiting (or “committing to”) one basin versus the other. In a ligand unbinding system, these are the bound and unbound basins. All states outside of these basins have unbinding committor probabilities that range from ~0 for states that are very close to the bound basin to ~1 for states that are close to the unbound basin. TSEs were chosen by selecting all conformations belonging to clusters within a given committor range across an unbinding committor of 0.5.

2.6. Direct Rate Calculation.

In addition to the rates from the MSMs, we also directly calculate unbinding rates using the flux into the unbound state. The flux is simply calculated as the sum of the weights of the unbinding trajectories divided by the elapsed time.

$$k_{\text{off}}=\frac{{\sum }_{\left(i,t\right)\in u}{w}_{i,t}}{T}$$ (2)

where $𝒰$ is the set of tuples denoting the trajectory indices $i$ and the time points $t$ where the unbinding events occurred, $w_{i,t}$ is the weight of the trajectory at that time point, and $T$ is the total elapsed time of the simulation. Equation 2 is also known as “Hill’s equation.”

For comparison, we also compute the fluxes corresponding to the more relaxed unbound state definition: $d_{\text{unb-min}}>5.0\mathrm{\AA }$, defined in Section 2.5. This is done by identifying the set of crossing points in the relaxed unbound state $({𝒰}^{\mathrm{*}})$. To mimic an absorbing boundary condition, we add crossing points starting from cycle 0 and only add a new crossing point if none of its predecessors have been added to ${𝒰}^{\mathrm{*}}$.

3. RESULTS

3.1. Unbinding Pathways of Five sEH Ligands.

For each of the five ligands, we performed a set of weighted ensemble simulations with the REVO algorithm that starts from an equilibrated bound pose. We observed unbinding events for all five ligands that we simulated. In our study, a ligand is defined to be unbound from the protein when it has a minimum distance of 5 Å or more from the residues that make up the binding site (Figure S2). The number of unbinding events for each ligand along with the cumulative unbinding weights and simulation time are provided in Table 2. The number of cycles in each run varies, ranging from 2224 to 4000 (see Table 1), with all the ligands having achieved at least 14.7 μs of combined sampling.

Upon inspection of the unbinding trajectories for each ligand, we noticed that the ligand unbinding in sEH can be broadly divided into two categories: (i) Unbinding through the right side of the cavity and (ii) unbinding through the left side of the cavity of sEH. For ligands 1 and 5, all of their unbinding events occur through the right side of the cavity, whereas ligand 3 accesses the left side only during unbinding. Ligands 2 and 4 have at least one unbinding pathway on either side of the cavity. The right and left sides of the sEH cavity are highlighted in Figure S3, and exemplary unbinding trajectories through each cavity are shown in Figure S4. In a weighted ensemble simulation, the cavity specificity of a ligand should not be determined based on the mere existence of binding paths but should take into account the relative weights of the trajectories that exit through those pathways. For example, the weight fractions from Table 2 indicate that despite having at least one unbinding pathway through the right, ligand 4 will almost always preferentially unbind through the left cavity. In contrast, we find that ligand 2 has an almost equal probability of unbinding through either of the cavities.

Figure 3 shows the CSNs of all the ligands, where each node represents a particular cluster of ligand–protein conformations. These are obtained from the same transition probability matrices used to build MSMs, as described in Section 2.5. Each network shows 1200 nodes that are colored according to the ligand RMSD, with the dark blue clusters corresponding to the bound states. The networks are oriented such that the left and right branches extending from the bound region in each network correspond to structures with the ligand occupying the left and right cavities. This reveals that although ligands 3 and 5 did not register full unbinding trajectories through the right and left cavities, respectively, we were able to sample trajectories that progressed along both directions. In contrast, ligand 1 only accesses the right side of the cavity and hence has no left branch.

Figure 3.

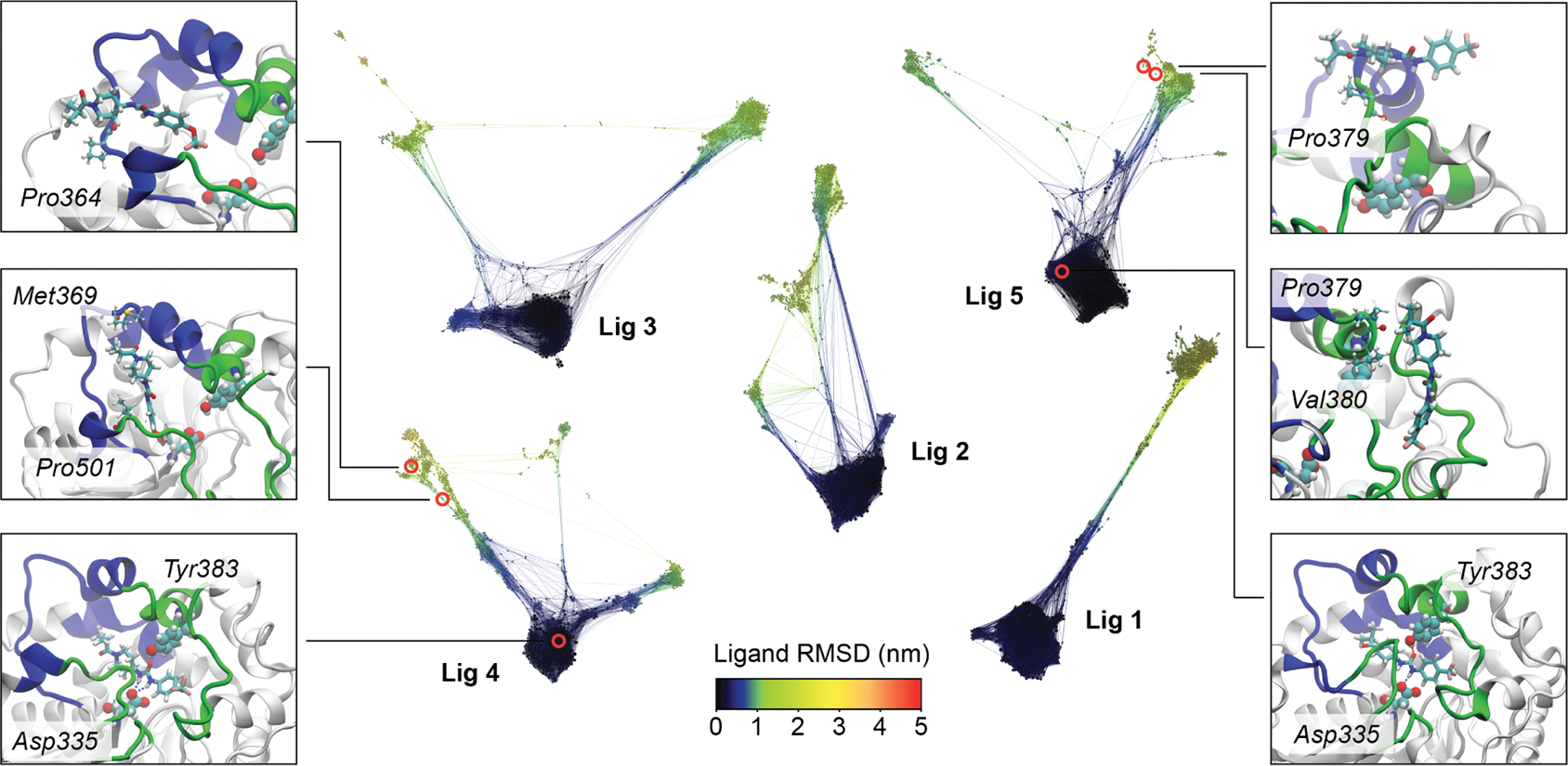
CSNs of ligand unbinding from sEH in the scale of the ligand RMSD. The networks are arranged and oriented according to pathway specificity. Three frames from the most probable unbinding pathways are highlighted for ligand 4 (cavity specificity: left) and ligand 5 (cavity specificity: right). The states corresponding to those frames are highlighted in the CSNs. In each panel, the ligands are shown in licorice while the amino acid residues within 2.5 Å of the ligands are depicted in CPK representation, with the binding site Asp335 and Tyr383 highlighted in vdW representation.

The unbinding pathways with the highest weights contribute most strongly to the transition path ensemble. We present three snapshots from the highest-weighted unbinding pathways obtained for ligand 5 (right panels) and ligand 4 (left panels) in Figure 3. The snapshots at the bottom show the bound pose for both of the ligands. The middle snapshots on each side show vertical ligand poses inside the cavity, which is a characteristic feature for all unbinding pathways of all the ligands. The top snapshots are further along the pathway and show only sparse interactions with the outer surface of the protein. Additional sets of snapshots for ligands 1 and 2 are shown in Figure S5. Interestingly, ligand 3 has an equal unbinding probability in all four of its pathways. These unbinding events all originated from the same starting trajectory, sharing a common vertical pose as an unbinding intermediate (Figure S6).

We observe a slight correlation between the total weight of the unbinding trajectories and the number of unbinding events generated. Opposing this trend, ligand 5 showed the highest total unbinding weight but registered only four unbinding events. As trajectories within a run are interrelated through cloning and merging events in the weighted ensemble algorithm, not all of the unbinding events are independent observations. However, unbinding events between runs can be considered to be completely independent. For all ligands except for ligand 3, we obtained unbinding events from at least two runs.

3.2. Kinetics of Ligand Unbinding.

Rates of unbinding can be calculated either directly from the sum of the transition rates (eq 2) or indirectly through the construction of a MSM. These can be compared with unbinding rates determined experimentally using a FRET-displacement assay, which correspond to MFPTs ranging from 14 to 32 min. We note that these MFPTs are at least tens of millions of times longer than the cumulative simulation times from our MD simulations. Despite this extreme difference of time scales, we are able to achieve RMSLEs of 2.3 for our direct rate calculations and 0.9 for our MSM results. The latter indicates an average agreement with experimental quantities that is within an order of magnitude. Values for experimental and computational MFPTs are summarized in Table 3, and log-scale RMSEs are shown in Figure 4. It should be noted from Hill’s relation that the cumulative weight of unbinding events (Table 2, column 5) is related to the direct MFPT estimation (Table 3, column 3) in case we have the same amount of the total simulation time. However, the number of unbinding events does not have any correlation with the unbinding MFPTs.

Table 3.

MFPT (Residence Time, in Minutes) of Ligand Unbinding by Experimental Assay, Hill’s Equation, and Markov State Modeling^a

	expt. residence time	comp. MFPT	comp. MFPT	comp. MFPT	comp. MFPT
Lig. ID	(unbinding kinetics assay)	(Hill’s eq., 5 Å cutoff)	(Hill’s eq., 10 Å cutoff)	(WE-MSM, best model)	(WE-MSM, median)
Lig1	14.25	723.44	1346.9	3.1	3.9
Lig2	31.75	21984.8	40971.1	227.1	27.5
Lig3	17.31	45952.9	45952.9	282.1	54.7
Lig4	27.14	864.1	1083.3	1.2	1.0
Lig5	25.37	1.87	12512.8	11.6	0.1

^aThe “best model” for the WE-MSM uses the full feature set (without tICA) and 1200 clusters.

Figure 4.

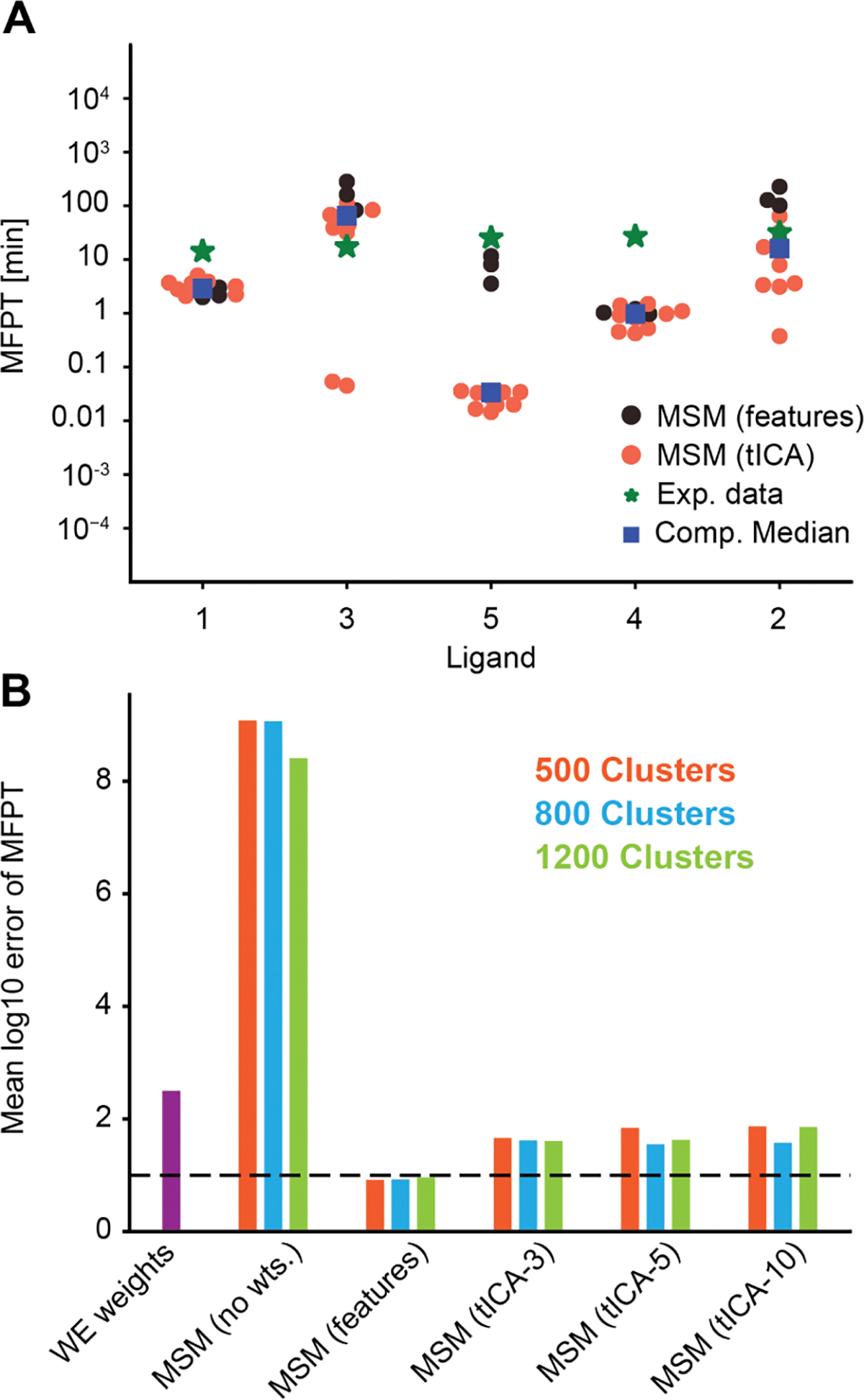
(A) Computational prediction of MFPTs for each ligand with all MSMs is plotted together as a swarmplot. The full feature space MSMs (black circles) perform better compared to tICA-based MSMs (red circles). The experimental data (green asterices) are plotted along with the medians of all computational estimates (blue boxes). The ligands are ordered in the ascending order of experimental residence times. (B) Comparison of the root mean squared log-10 error plotted for various MSMs (red, blue, and green) and direct estimates from WE weights (violet). The MSM using the full feature set has the lowest RMS log-10 error, while the unweighted MSM has the highest RMS log-10 error. The horizontal line marks an average error of 1 order of magnitude.

The larger error in our direct rate calculations is primarily due to the inadequate sampling of exit points. In the direct rate calculation method, the rates are entirely dependent on the weights of the unbinding trajectories. Although we observe unbinding events for all the ligands, the number of these events is limited to only a handful (a range of 4–34) per ligand. On the contrary, MSMs are not as susceptible to the sampling of the unbinding events, as they are built with all the simulation data and consider the nonreactive trajectories as well. Hence, trajectories far away from the bound pose that may not go on to unbind because of the finite length of the simulation will still contribute statistically in rates determined from the MSM.

While predicting the MFPTs, we have considered both (i) tICA-based MSMs and (ii) feature-distance-based MSMs. Figure 4A is a swarmplot showing MFPTs estimated from all MSMs constructed for each ligand. The experimental data and medians of the computational estimates are also plotted. The Root Mean Squared Log Error (RMSLE) between the experimental data and the computational medians is 0.97. We observe that the tICA-based models perform worse than the full feature distance clustered MSMs, particularly for ligand 5. We discuss possible reasons for this in Section 4. We also calculated MFPTs from MSMs where the transitions in the counts matrix were not scaled by the weighted ensemble probability; rather, all transitions between microstates were given an equal weight of 1. As shown in Figure 4B, unweighted MSMs deviate from the MFPTs by over 8 orders of magnitude. This is due to a systematic underestimation of the MFPT, resulting from improper weighting of state-to-state transitions in the MSM.

Both types of weighted MSMs perform significantly better than the MFPT calculated from only the unbinding flux. The feature-distance-based MSMs (“no-TICA”) have an RMSLE of 0.93 averaged over all three different cluster numbers, while tICA-based MSMs have a higher average RMSLE of 1.63. In examining different numbers of clusters for the no-TICA MSMs, we find that 500, 800, and 1200 all have similarly low RMSLEs. We find no-TICA MSMs with 1200 clusters have the highest Spearman’s rank coefficient and Kendall’s rank coefficient (Table S1). MFPTs from these MSMs are shown in Table 3 as the “WE-MSM best model”.

To examine the sensitivity of the K-means algorithm to the amount of data used, we examine MFPTs resulting from randomly chosen subsets of the training data. These varied from 20% to 90% of the full feature set using the “WE-MSM best model.” We then constructed a transition matrix using the full data set in each case. We notice that the MFPTs obtained from the subsequent transition probability matrices do not vary significantly (Figure S7) in most cases, even though we use as small as 20% of the total feature data. For each ligand, at each percentage, we carry out five iterations to obtain a standard deviation and average of the estimates. This is an indication that the clustering algorithm is not sensitive toward the amount of the data used, although, as expected, the standard deviation of the five iterations increases as we decrease the size of the data set.

3.3. Robustness of Transition State Ensembles.

The structural determinants that underlie the unbinding rates are found in the TSEs for each ligand. We developed a workflow to isolate and characterize the TSEs from the weighted ensemble simulation data (Figure 2), which was guided by the kinetics results in Section 3.2. We use a MSM constructed using the complete set of distance features (e.g., no tICA) and 1200 states, as it resulted in the best agreement with experimental unbinding rates. However, the number of states was not found to significantly impact the location of the TSE (Figure S8). We also estimated the variance among the TSE ligand poses and their average RMSD to the bound state and observed that those structural parameters are similar across MSMs built with different numbers of microstates (Tables S2 and S3).

Density volume maps for all of the TSEs in sEH are illustrated in Figure 5. These TSEs were constructed using all trajectory frames that were assigned to a cluster with a committor probability in the range (0.3, 0.7). Figure 5 (bottom) shows the distribution of probabilities of these trajectory frames, which were computed using the equilibrium probabilities of the clusters computed from the MSM. Although the ligands share a common scaffold, the spatial densities of the TSEs show a significant variation. These densities are in accordance with the variety of unbinding pathways reported earlier for each ligand. Ligands 1 and 5 have spatial density primarily on the right side of the cavity, and ligand 3 is mostly to the left side, while ligands 2 and 4 are distributed across both sides. The numbers of snapshots in the TSEs range from 140 to 5000. Higher numbers of snapshots indicate better sampling of transition paths, though not necessarily higher unbinding rates. We do not observe a strong relationship between the number of shapshots and the volume of the TSE density plots. This is expected as the TSEs are generated probabilistically using the MSM weights, and the density plots show only the regions of space with a probability density above a cutoff of 0.05 for all ligands. Generally, we find that the TSEs of all the ligands are structurally closer to the unbound ensemble compared to the bound ensemble. This can be observed in the probability distributions of ligand RMSDs within the bound, TS, and unbound ensembles (Figure S9). The heterogeneity in the TSEs can lead to a wide variety of specific sEH-ligand interactions, which we study next.

Figure 5.

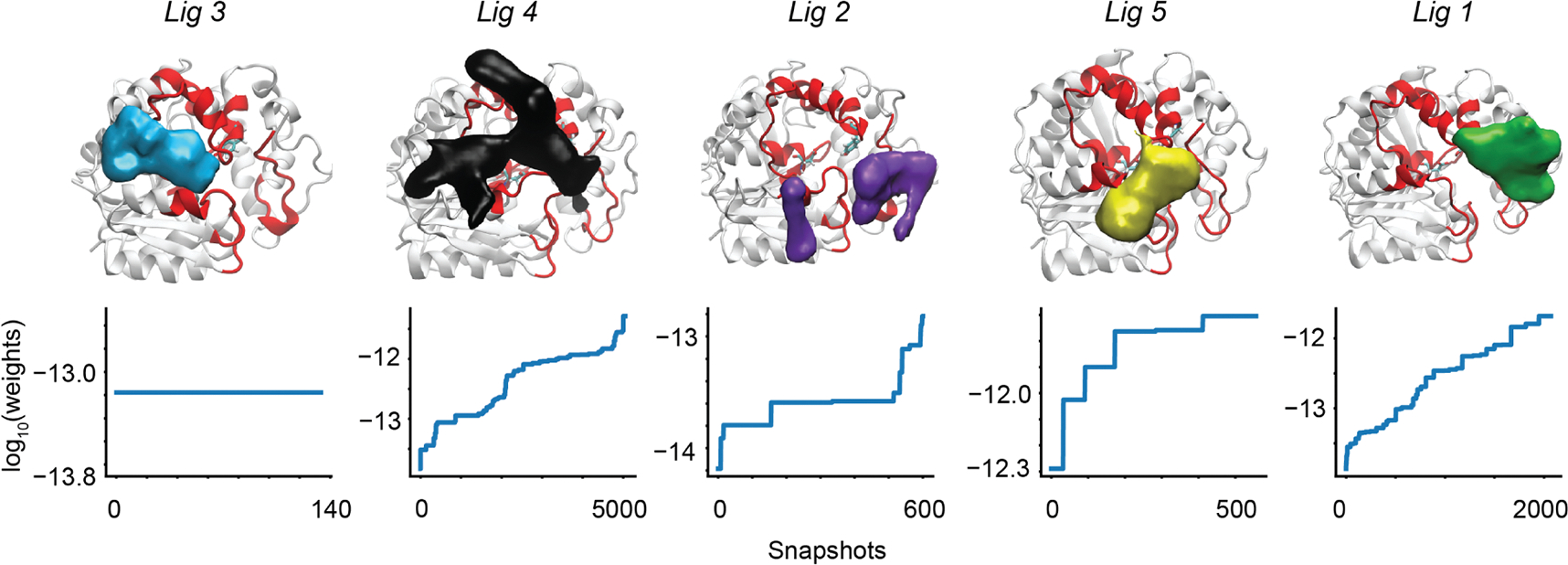
(Top row) Density plots of the ligand unbinding TSEs: different ligands are plotted in different colors. The two binding site residues Asp335 and Tyr383 are shown in the licorice representation, while the overall binding region is highlighted by a red color. Each surface is plotted in VMD using the same density cutoff (“isovalue”) of 0.05. (Bottom row) Weights of conformations used to build the TS ensembles are plotted on a log-scale for each ligand. The horizontal axis shows the number of independent snapshots in the TSE. The vertical axis shows the log₁₀ of the weight of that snapshot.

Figure 6A shows the protein residues with the most stable contacts with the ligand for the bound ensemble and the TSE. We define a contact to be present when the minimum distance for a residue–ligand pair is below 2.5 Å; the fraction of frames in which the contact is formed is shown as a heatmap. The cutoff is carefully chosen based on the maximum range of the H-bond (2.2 Å) and VdW (~3.0 Å) interatomic distances. For both the bound state and the transition state, we show all residues that have a probability of interaction greater than 5% for at least one of the ligands. The horizontal axis denotes the ligand IDs with the right cavity specific ligands (1, 2, and 5) positioned first followed by the left cavity specific ligands (3 and 4). For the TSE heatmap, the residues are arranged so as to move from residues in the left cavity (on top) to the middle region to the right cavity (on the bottom). In the bound ensemble, the protein–ligand interactions are largely consistent from one ligand to another, with binding site residues Tyr383 and Asp335 having the maximum probabilities of contact formation. The protein–ligand interactions are substantially more varied in the TS ensembles. The types of amino acids and atomic interactions also change considerably: we notice that nonpolar amino acids such as VAL(380, 500, 416), PRO(364, 379, 501), ILE(363), LEU(499), and PHE(497) are more highly represented in the TSE, in contrast to interactions with polar amino acids. This is quantified in Figure 6B, which shows protein–ligand interactions based on the type of the amino acids, averaged over all the ligands. It is evident that—moving from the bound ensemble to the TSE—there is a significant increase (18%) in the interactions with nonpolar residues, which are predominantly hydrophobic interactions. Visual representations of some of the most probable contacts in ligands 1, 3, and 5 are provided in Figure 6C. These snapshots show the high ligand-to-ligand variation in the specific interactions formed in the TSE as well as the predominance of hydrophobic interactions. Interestingly, although the specific interactions vary from ligand-to-ligand, the shift toward hydrophobic protein–ligand interactions in the TSE is consistent across the set of ligands examined here (Figure S10).

Figure 6.

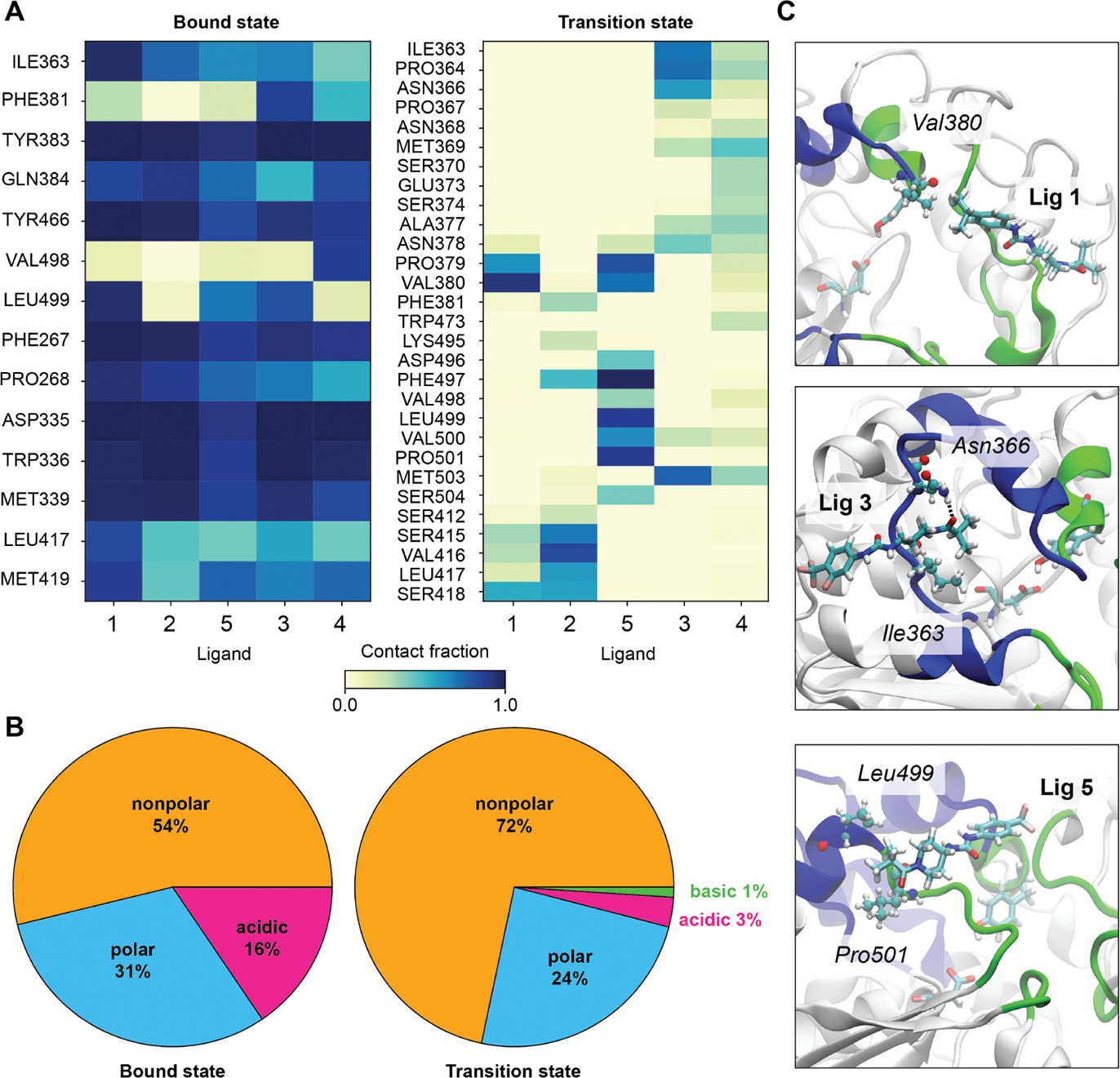
Protein–ligand interactions in the ligand unbinding TS ensembles of sEH: (A) Heatmap of interaction probabilities in bound and TSE for the ligands; colorbar denotes the measure of probability. The ligands which unbind through the right side of the cavity (ligands 1, 2, and 5) are placed first in the horizontal axis, followed by the ligands unbinding through the left side of the cavity (ligands 3 and 4). (B) Pie chart describing the category of protein–ligand interactions based on the type of the amino acids, averaged over all the ligands. (C) Representations of a few of the most probable interactions in TS ensembles for ligands 1, 3, and 5.

Irrespective of the cavity preference of the ligand unbinding TSEs, all ligands have substantial hydrophobic interactions with sEH. The nonpolar isopropyl group attached to the aryl end of ligand 1 has a higher hydrophobicity compared to mildly lipophilic –OCF3 or –CF3 counterparts connected to other ligands. Consistently, we find that this isopropyl group has stable hydrophobic interactions with sEH nonpolar residues such as Pro379 and Val380 (Figure 6A,C) in the ligand 1 TSE, while in other ligand TSEs, the piperidyl end primarily accounts for the protein–ligand hydrophobic interactions. Figure 6C illustrates the interactions between the piperidyl end of ligands 3 and 5 with nonpolar residues such as Ile363, Leu499, and Pro501. Interestingly, we notice that protein–ligand interactions mediated by –OCF3 or –CF3 groups are not significant in the TSE. The probable consequences of these functional groups are discussed in detail in Section 4 from the perspective of rational kinetics driven drug discovery.

In the context of SBDD, it is also important to understand the changes in the ligand degrees of freedom along the transition pathway. For instance, differences in the orientation of a rotatable bond, i.e., dihedral angle, between the bound state and TSE could be exploited to destabilize transition states, leading to longer residence times. Here, we examine a set of eight common dihedral angles, and we measure their corresponding angular probability distributions in both the bound and TSEs. All the dihedrals are illustrated in Figure S11, with the four constituent atoms highlighted. Wasserstein distances are computed between the bound and TS probability distributions for each dihedral across all the ligands (Figure S12). This is a metric of dissimilarity between two histograms, with a higher value indicating a higher dissimilarity between the distributions. We find that the C1–N2–C2–C3 dihedral angle has the most significant dissimilarity in the bound and TS ensemble (Figure 7). This angle is more restricted in the bound ensemble due to steric effects for all of the ligands examined here. In the TSE, these distributions are substantially broadened (Figure 7B), showing a more heterogeneous ensemble of conformations. It is interesting to note that the variation in the dihedral in TSEs is unidirectional in nature; i.e., the lower bound of the angle decreases in the TSE compared to the bound ensemble. We plot the dihedral angle along the most probable unbinding pathway of ligand 1 in Figure 7C. The average value of the angle in the bound ensemble of this trajectory is ~ −70°, while in the TSE, the average dihedral angle is ~ −130°. Two representative conformations of the dihedral from the bound and TS ensemble are provided in Figure 7D. The differences between these distributions imply that making chemical changes that hinder or freeze this rotational degree of freedom could entropically destabilize the transition state (as well as the unbound state) with respect to the bound state.

Figure 7.

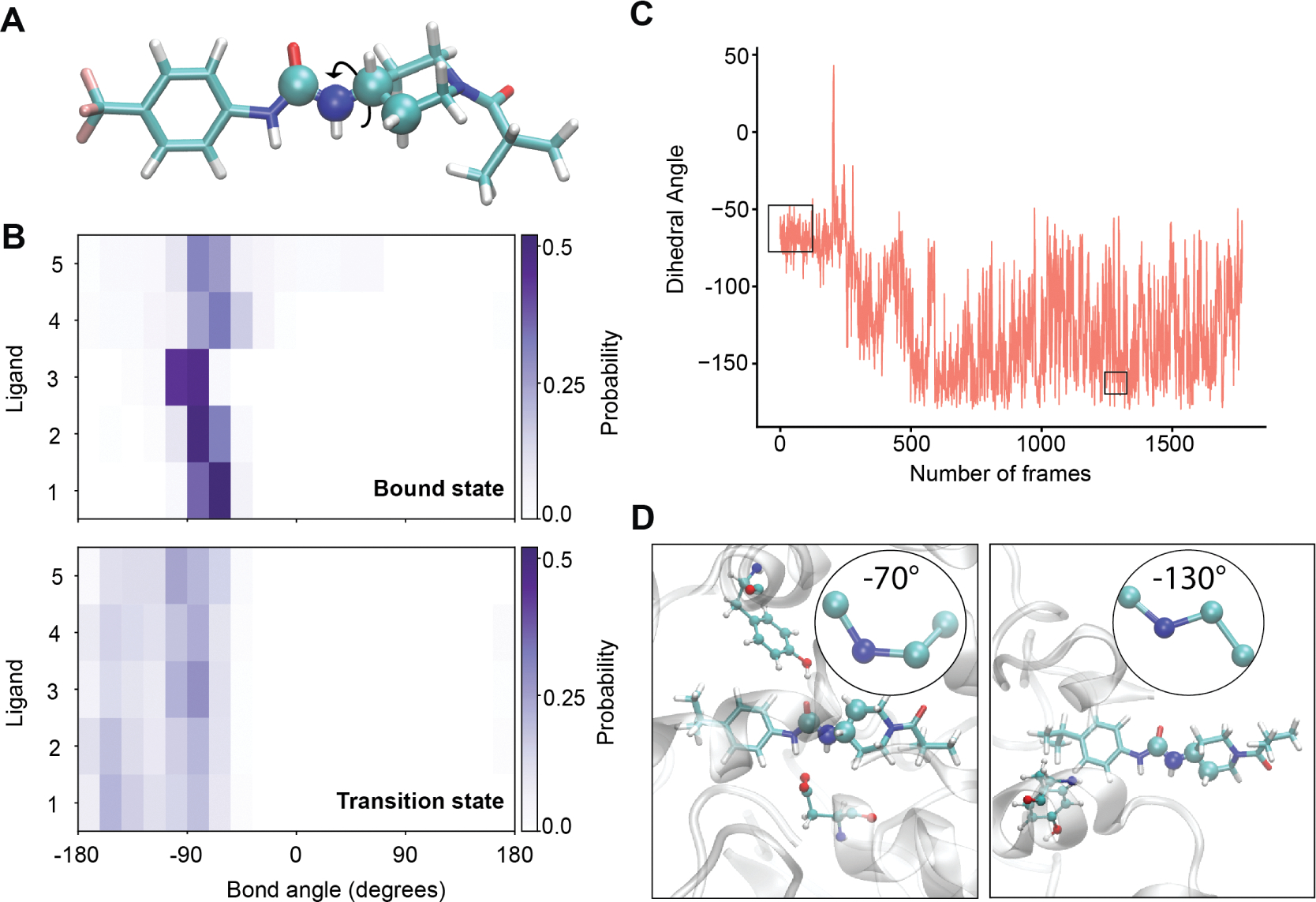
(A) The atoms corresponding to the rotatable bond with the largest difference between the bound ensemble and the TSE are shown in the van der Waals representation, with other atoms in licorice representation. (B) Probability distributions of this angle are shown for each ligand in both the bound ensemble (top) and TSE (bottom). (C) The value of this dihedral angle is shown over the course of the most probable unbinding trajectory for ligand 1. The black boxes indicate the frames corresponding to the bound (left) and TS (right) ensembles. (D) Representative snapshots of the bound (left) and TS (right) ensembles, showing the dihedral angle in the insets.

4. CONCLUSION

MFPTs of pharmacologically relevant ligands often occur on time scales ranging up to hours in length. Although molecular dynamics can be a powerful tool to characterize biomolecular processes and predict MFPTs, it is still a challenge even for state-of-the-art enhanced sampling methods to model long-time scale unbinding events with statistical significance. We have previously found that the enhanced sampling method used here (“REVO”) performs excellently for standard millisecond-time scale protein–ligand unbinding events such as trypsin-benzamidine. Unbinding transition rates for this system quickly and reproducably converged to within an order of magnitude of the experimental value.^19,35 The sEH-inhibitor systems studied here pose additional challenges, as the ligands are larger, with more rotatable bonds, and the sEH binding pocket is deeply buried, which requires a multistep unbinding process. These systems thus display significantly increased complexity and variety in the unbinding mechanism. In addition, the experimental values for these MFPTs are six orders of magnitude larger than the trypsin-benzamidine system. Here, using a combination of REVO and Markov state modeling, our RMSLE in the unbinding rate averaged 0.94, indicating that our average agreement with the experiment was also within an order of magnitude. This was much better than we originally anticipated given that our individual trajectories are only tens of nanoseconds in length. It should be noted that, following our previous works, we have used CHARMM36⁵¹ as our force field for the MD simulations and the CGenFF tool^52,53 to generate ligand parameters. While it has been shown that ligand parameters such as torsion angles can have significant impacts on binding modes and mechanisms,⁶⁵ investigating the effects of different force fields on the ligand (un)binding mechanisms examined here would incur a significant computational cost. More targeted ways to examine the impact of different force fields, perhaps by examining snapshots along transition pathways, would be an interesting direction for future work.

With a total of 82.9 μs of ligand unbinding REVO simulations, we obtain a handful of unbinding events for five pharmacologically relevant ligands from the sEH protein. Although the weights of these trajectories can be used to directly compute MFPTs using the Hill relation, the low number of trajectories results in a high uncertainty and increased RMSLE > 2 compared to experimental values. This is consistent with previous results on the sEH-TPPU system studied with the WExplore algorithm,^34,36 where the MFPT (42 s) underestimated the experimental value (660 s) by more than 15 times. As all of the underlying trajectories are generated without biasing forces, we can use them to build a history-augmented MSM (“haMSM”⁴¹) where all trajectories originate in the bound state. The rates calculated by these haMSMs are potentially more accurate and robust, as they take into account not only the small set of fully reactive trajectories but also all of the transitions from the nonreactive trajectories as well. Here, we find that the RMSLEs of MFPTs in the MSM-REVO scheme are significantly lower by more than an order of magnitude than the directly estimated MFPTs from the weights of reactive trajectories. An important note is that the trajectory weights from the REVO simulations were used to build the transition count matrix of the haMSM. This led to a dramatic reduction in the RMSLE and demonstrated the powerful synergy of weighted ensemble methods with Markov state modeling.

In the context of Markov state modeling, dimensionality reduction is particularly important to account for redundancy and noise in the features before they are clustered. For studying kinetic properties associated with slow dynamical motions in biological systems, tICA has been an excellent tool to identify important collective variables.^66,67 When dimension reduction is carried out with 3, 5, or 10 time-lagged independent components, we notice that tIC-1 separates the bound and unbound frames and tIC-2 distinguishes the cavity specificity consistently for all the ligands (Figure S13). However, the RMSLE in MFPTs obtained from haMSMs built with clustered tICA data is higher compared to that of its full feature space counterpart. Moreover, the variation of MFPTs obtained from tIC-clustered MSMs is much larger compared to the variation of MFPTs obtained from the full feature space MSMs (Figure 4A). Although we are unable to identify a particular reason behind the lower accuracy of MSMs with tICA components, it should be noted that our feature space itself (the set of ligand–protein distances) is carefully chosen to describe the ligand unbinding process. Hence, although our feature set was highly redundant, we found that the transformation into a smaller set of linearly independent components decreased the quality of the clustering, likely grouping together trajectories that were less similar in their unbinding committor values. Dimension reduction schemes, including tICA, but also machine learning approaches⁶⁸ such as VAMPnets⁶⁹ or RAVE⁷⁰ could be more useful for more heterogeneous sets of input features, such as those that describe solvation, ion densities, distances, and ligand degrees of freedom. These approaches and their combination with weighted ensemble sampling algorithms are the subject of ongoing work.

The MFPT depends upon the bound to the transition state activation energy barrier. Hence, to engineer ligands with a higher residence time, one needs to understand how changes to the ligand will differentially affect the bound and TSEs. This can include both protein–ligand molecular interactions and conformational changes of the ligand. The five ligands have identical aryl piperidyl-urea scaffolds, which may lead to the assumption that the transition states along the ligand unbinding pathways could be similar for these ligands. However, in our molecular simulations, we find many differences between the transition paths. We did not observe a connection between the path specificity and the MFPT; ligands with both shorter (ligand 1) and longer (ligand 2) MFPTs were found to unbind through the right-side transition path. The location of the transition state as well as the specific ligand–protein interactions formed varied considerably from ligand-to-ligand. However, we find a number of similarities in the TSEs that could be exploited for kinetic-driven drug design. Although not completely conserved, the most probable protein–ligand contacts in the TSEs show some common elements. Ligands 1, 2, and 5 unbind through the right side of the sEH cavity and have substantial contacts with Pro379, Val380, and Phe497, while the ligands preferring the left side of the cavity (3 and 4) have contacts with Pro364 and Met503. TSEs for all of the ligands show an increased extent of hydrophobic interactions, primarily through the piperidyl end of the ligands. However, ligand 1 has hydrophobic TSE interactions through the isopropyl group only in the aryl end only. For other ligands, the –OCF3 and –CF3 groups in the aryl end do not interact with the protein and hence do not add any extra stabilization to the TSE. From the perspective of rational kinetics-driven drug discovery, to increase the residence time, one can consider chemical changes to the ligand that destabilize favorable interactions in the TSE. The shift from isopropyl to –OCF3 or –CF3 groups could be seen in this context, where –OCF3 or –CF3 disrupt some favorable transition state interactions without destabilizing the bound ensemble, thus contributing to a longer residence time. Finally, the probability distributions along the C1–N2–C2–C3 dihedral angle show a similar shift between the ligands. The broadening of the dihedral distribution in the TS ensemble compared to the bound ensemble is unidirectional toward a more “anti”-like TSE structures.

These findings present a mixed outlook for kinetic-oriented drug design. On the one hand, the diversity of specific protein–ligand interactions formed in the TSE from ligand-to-ligand makes attempts to rationally modulate the strength of TSE interactions unfeasible. More rigorous attempts such as free energy perturbation calculations for entire ensembles of bound and transition state structures will likely also suffer from poor overlap of the TSEs between ligands. On the other hand, we have identified some structural properties of the TSEs that are consistent across all ligands examined here. The rotatable bond C1–N2–C2–C3 is rigid in the bound ensemble but shows considerable fluctuation in the TSE. This suggests that restricting the rotation of this bond could stabilize the bound state with respect to the transition state, increasing the free energy barrier to dissociation.

A characteristic feature of the sEH binding pocket is a deeply buried binding cavity. As a result, ligand unbinding is hindered by multiple stable interactions along the pathway. The depth of the binding site in the cavity could increase the number of probable unbinding pathways, making it difficult to thoroughly sample the TSE. Moreover, contrary to intuition, we observe that even when the bound state ligand–protein contacts are completely broken, the ligands can still be far from committing to the unbound states. This results in TS ensembles for all the ligands that are closer to the unbound state on the surface of the protein. It remains to be seen whether TSEs from shallower protein–ligand interactions will have similar characteristics, in terms of solvent accessibility and conformational heterogeneity. It is possible that the TSE of a moiety unbinding from a protein with a shallower binding site can be more robust with a more focused set of unbinding pathways.