Electrokinetic Convection-Enhanced Delivery of Solutes to the Brain

Abstract

Pressure-induced infusion of solutions into brain tissue is used both in research and in medicine. In medicine, convection enhanced delivery (CED) may be used to deliver agents to localized areas of the brain, such as with gene therapy to functional targets or with deep tumors not readily amenable to resection. However, clinical trials have demonstrated mixed results from CED. CED is limited by a lack of control of the infusion flow path and may cause damage or even neurological deficits due to neuronal distortion. In laboratory research, infusions may be achieved using pressure or using brief bursts of electrical current in iontophoresis. Electrokinetic convection enhanced delivery (ECED) has the potential to deliver drugs and other bioactive substances to local regions in the brain with improved control and lower applied pressures than pressure-based CED. ECED improves control over the infusion profile because the fluid follows the electrical current path and thus can be directed. Both small molecules and macromolecules can be delivered. Here we demonstrate proof-of-principal that electrokinetic (electroosmosis and electrophoresis) convection-enhanced delivery is a viable means for delivering solutes to the brain. We assessed the volume of tissue exposed to the infusates tris(2,2′-bipyridine)ruthenium(II) and fluorescent dextrans. Control of the direction of the transport was also achieved over distances ranging from several hundred micrometers to more than 4 mm. Electrokinetic delivery has the potential to improve control over infusions.

Graphical Abstract

INTRODUCTION

Pressure driven flow is important in laboratory neuroscience and clinical medicine. In neurochemical research laboratories, push–pull perfusion is used to obtain samples of the extracellular space.^1–4 In this technique, the chief objective is to acquire samples of the extracellular space, thus the volumes perfused are very small. In fact, the “push” can sometimes be eliminated and samples of extracellular space may be obtained with “pull” only.¹ In clinical work, delivery of substances directly into the central nervous system (CNS) can be accomplished using convection-enhanced delivery (CED).^5-7 CED has gained traction due to significant limitations with delivering therapeutic agents systemically due to the blood-brain and blood-tumor barriers.^8,9 While it is true that systemic delivery of substances to the brain is not always problematic¹⁰ and focused ultrasound may be used to weaken that barrier allowing for solute delivery in some scenarios,^11–13 CED promises, in principle, the ultimate in control of delivery to a localized area. Direct delivery into the human brain by CED has been applied to the delivery of drugs to gliomas not readily amenable to resection.^14–16 The volume of tissue in which infused solutes are delivered is larger and the distribution is more homogeneous than delivery by diffusion alone.¹⁷

Despite clear efficacy in localized delivery of infusates into the central nervous system, one major limitation of pressure-driven CED is backflow of the infusate along the implanted cannula tracts that limits the applied pressure, thus the flow rates, which extends procedural times. This has required the development of specialized cannula designs.^7,18 More generally, there is also a need to control where the fluid goes when it is infused^18–20 because of the permeability properties of the tissue and even the type of tumor²¹ or drug being delivered.²²

Electroosmosis is fluid flow induced by an electrical current passing through a conducting solution surrounded by charged walls. Here, we consider tissue in which the extracellular space contains the conducting solution and the “charged walls” comprise cellular surface functional groups and the extracellular matrix. Electrophoresis is the movement of ions through a solution passing an electrical current. Therefore, the electrokinetic velocity of a solute is the sum of the electroosmotic velocity of the fluid and the electrophoretic velocity of the solute. Notably, neutral molecules can be driven through a porous medium with charged walls. Electroosmosis has been observed in skin²³ and has also been suspected in corneal transport.²⁴ We first described electroosmosis in brain tissue (organotypic hippocampal slice cultures (OHSCs)) and established that electroosmotic flow is in the same direction as the electrophoresis of cations.^25,26 Thus, electrophoretic transport of cations in OHSCs is enhanced by electroosmosis. For many anions, the electroosmotic mobility is larger in magnitude than the electrophoretic mobility, so the net direction of anion transport induced by an electric current may also be in the direction of cation electrophoresis in brain tissue. In a homogeneous porous medium, there is no pressure drop accompanying electroosmotic flow of interstitial fluid or an infusate.²⁷ We have applied this phenomenon to the perfusion of OHSCs to investigate ectoenzyme activity.^27–33 Therefore, CED may be theoretically achieved without external pressure using electrokinetic transport. We postulated that electrokinetic transport may solve some of the clinical and scientific limitations described above.

More quantitatively, the relationship in eq 1 can be used to predict the volume of infusion fluid delivered into brain tissue by electroosmosis:

$$Q=I{\mu }_{\text{EO}}/{\sigma }_{\text{CSF}}$$ (1)

where Q is the observed fluid volume flow rate, I is the electrical current, μ_EO is the electroosmotic mobility, and σ_CSF is the conductivity of the extracellular fluid. A solute contained in the infused solution will demonstrate an apparent infusion volume, Q_app, that accounts for the electrophoresis of the solute in addition to the electroosmotic flow:

$$Q_{\text{app}}=I{\mu }_{\text{T}}/{\sigma }_{\text{CSF}}$$ (2)

Here, ${\mu }_{\text{T}}$ the total mobility, is the sum of the electrophoretic and electroosmotic mobilities. The former depends on the molecular/particle size, analogous to the effect on diffusion,³⁴ and charge. The volumes stipulated by the product of eq 2 and time are extracellular volumes. With a typical brain tissue porosity of 0.2,³⁵ the volume of tissue affected would be five times the volume infused. We also note that electrophoresis is generally described in terms of an applied electric field. Here, we use current. The applied current creates an electric field as it passes through a medium with a certain conductivity, so the two descriptions are equivalent. However, as a practical matter describing electrokinetic movement in terms of current is convenient. The electroosmotic flow rate in a conduit is independent of the cross-sectional area of the conduit and independent of temperature at constant current, but this is not the case for a constant electric field.

This work seeks to address some of the aforementioned obstacles encountered with pressure-driven CED. We describe the use of fused silica cannulas, of similar size and material used in pressure-driven delivery, to induce electrokinetic convection-enhanced delivery (ECED) to deliver a solute to large tissue areas in vivo. These cannulas, or capillaries, are hollow permitting both current and fluid flow. The electrodes supporting the fluid flow are in vessels outside the brain. Control of directional transport was ultimately achieved from cannula tips over distances ranging from several hundred micrometers to more than four millimeters. Furthermore, this work demonstrates directionality and quantification of the volume of distributions of the infusate in vivo from ECED in the adult rat brain as a proof-of-principle. Finally, we developed a computational model to simulate ECED and analogous pressure-induced infusions. Experimental results demonstrate that the ECED approach may address certain limitations and perhaps even augment pressure-driven CED, including the ability to direct infusions along electrical current paths in brain tissue, in congruence with our prior studies.²⁸

RESULTS AND DISCUSSION

Electrokinetic Infusions In Vivo.

Three fluorescent compounds were infused electrokinetically into the thalamus of an adult male rat in 11 separate experiments. The infusate contained either a fluorescent dextran, 10 kDa BODIPY10 (n = 3) or 70 kDa TR70 (n = 4), or the chloride salt of tris(bipyridine)ruthenium(II), Ru(bpy)₃²⁺ (n = 4). These fluorescent species were selected because of their dissimilar molecular weights and electrophoretic mobilities,³³ which are shown in Table 1 along with μ_T, their total mobilities. We carried out experiments at two sets of conditions, namely, short, 45 min infusions at 25 μA and longer, 5-h infusions at a higher current of 75 μA.

Table 1.

Solute Mobilities and Volume of Tissue Infused

infusate	kDaa	μ ep b	μ T c	Vd,pred (μL)	Vd,expt (μL)
TR70	70	−0.74	20.2	3.8	0.62 ± 0.04 (N = 4)
BODIPY10	10	−1.2	19.7	3.7	1.71 ± 0.12 (N = 3)
Ru(bpy)32+	0.57	35	56	10.6	13.0 ± 2.0 (N = 4)

^aMolecular weight.

^bElectrophoretic mobility divided by 10 ⁻⁹ m²/(Vs) at 37 °C.

^cTotal mobility divided by the same factor as above.

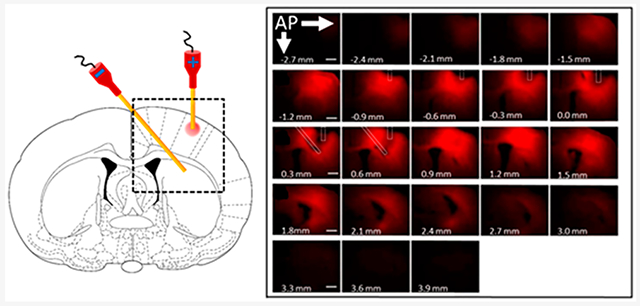
Figure 1A shows data from one of the four animals receiving an infusion of Ru(bpy)₃²⁺ for 45 min at 25 μA. Figure 1B identifies brain regions and probe track while Figure 1C shows the cannula placement for the electrokinetic infusions. For all experiments, a vessel containing one of three infusates was attached to a cannula, which was then inserted into the thalamus of a male rat. A similar vessel and cannula containing only the isotonic buffered saline medium was placed in the contralateral thalamus (Figure 1C). The vessels were connected to a current source with positive voltage in the vessel containing the infusate solution. Solutions containing each of the three fluorophores were infused in separate experiments for 45 min with 25 μA of current.

Figure 1.

Typical in vivo ejection of Ru(bpy)₃²⁺ into the rat thalamus from a 100 μm inner diameter fused silica infusion cannula with 25 μA applied current for 45 min. (A) Fluorescence images overlaid upon bright field images. The combined images are presented left-to-right from anterior (top left) to posterior (bottom right). The scale bars are 1 000 μm. Note triangles indicating probe track from −4.0 to −4.6 mm. (B) Closeup of the image at −4.0 mm from bregma identifying brain regions. (C) Scheme of the experimental setup.

Recall that the fluid is infused into the extracellular space, which is about 20% of the volume of the brain tissue.³⁵ In order to compare the calculated volume of tissue containing infusate to the observed distribution of fluorescence, we have multiplied the fluid volume calculated from eq 2 by a factor of 5. The volumes in the tissue were measured by defining a boundary within which intensity of fluorescence was measured. To determine the boundary, we took into consideration the effectiveness of an infusion of a drug. Each drug has a particular therapeutic index, the ratio of the maximum safe concentration to the minimum effective concentration of a drug.^36–38 If we had defined the boundary to be at the extremes of what is visible, the volume infused would be relatively large. However, this effective volume would only be relevant for a small number of agents with a large therapeutic index. Thus, the boundary was defined as the distance from the point of maximum intensity to the point at which the intensity is 25% of the maximum which is suitable for agents with a therapeutic index greater than 4. The boundary was determined at eight points separated by 45° and then calculating the average radius, r, from the eight measurements. The value of r and the thickness was used to calculate a volume in each slice. Slice volumes were summed to arrive at a total. Note that the 25% criterion for the boundary is quite conservative. The volume inside the 25%-of-maximum boundary of a two-dimensional Gaussian shape representing an idealized image from one of our slices is only 40% of the total volume. An example of the thresholding process is shown as Figure S3.

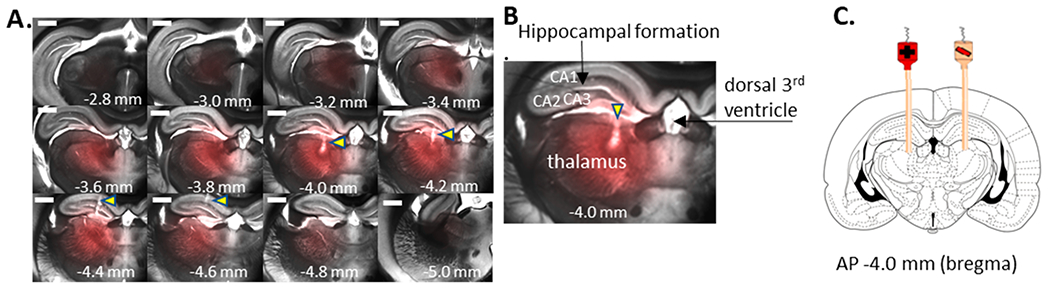
Table 1 contains both measured (as described above) and calculated observed infusion volumes in mm³. The calculated volumes have not been adjusted to be in line with the 40% factor explained above. The polymeric fluorophores (dextrans) have a small electrophoretic mobility opposing the electroosmostic flow, In addition, their large molecular weight gives them a further disadvantage because large molecules suffer from a large apparent tortuosity.³⁴ Figure 2 shows the infusion of the two dextrans in one section of tissue for 45 min at 25 μA (see Figure S5 for all sections). The observed volumes are lower than the predicted volumes for these fluorophores. While the smaller Bodipy 10 volume is in line with the approximate 40% factor, the larger TR 70s volume is lower than that. This is likely due to their molecular size increasing the apparent tortuosity³⁵ and decreasing their transport. Ru(bpy)₃²⁺ has a large electrophoretic mobility, favoring delivery both by electroosmosis and electrophoresis. Table 1 shows that significantly more of the latter solute is delivered than that of the dextrans. Unlike the larger dextran solutes, diffusion of Ru(bpy)₃²⁺ during the time between infusion and imaging may increase the observed volume. We can approximate the effect of diffusion by considering the added variance from diffusion based on taking the diffusion time postsacrifice (15 min) and the effective diffusion coefficient of the solute in the tissue (1.3 × 10⁻¹⁰m² s⁻¹). Based on this and the variance of the observed infusions such as those in Figure 1, we estimate that diffusion increases the apparent volume by about 25%. Correcting for this puts the experimental volume at about 10 μL. Once again, considering the 40% factor, the infused volume is somewhat greater than expected after accounting for diffusion.

Figure 2.

Typical in vivo infusion of Bodipy 10 and TR 70 into the rat thalamus from a 100 μm inner diameter fused silica infusion cannula for 45 min with 25 μA applied current (left) and 0 current (right). Top, brightfield; middle, Bodipy; bottom, TR. Filters wavelength/bandpass (nm): Bodipy 10, Ex 490/20, Em 525/36; TR 70, Ex 560/25, Em 625/26.

The uncertainties in V_d presented in Table 1 ranged from roughly 5 to 15%. Some of the irreproducibility arises from our making the approximation that the area in each cross section is a circle with an average radius determined from the eight apparent radii measured at 45° intervals. The relative error of the volume distribution was highest for Ru(bpy)₃²⁺. This may be because the small cation most readily encountered the tissue margins due to its large infusion areas. To control for infusion from the cannula tip by gravity-induced flow and diffusion, an identical 100 μm inner diameter fused silica cannula was filled with the fluorophore solutions and implanted into the rat thalamus for 45 min with no applied current. For TR70, Bodipy10, and Ru(bpy)₃²⁺, no fluorescence was observed in the brain tissue around the cannula implantation site, indicating that gravity and diffusion were not the driving forces for delivery of any of the solutes. It is possible that our measurements would be affected by clearance from the given volume of brain tissue. The flow rate of cerebrospinal fluid in vivo ranges from approximately 0.2 μL min⁻¹ mL⁻¹ or a fractional value of approximately 2 × 10⁻⁴ min⁻¹.³⁹ Our experiments took 45 min, so the net effect of natural convective flow in the brain would have been imperceptible.

Directional Control of Electrokinetic Infusions In Vivo.

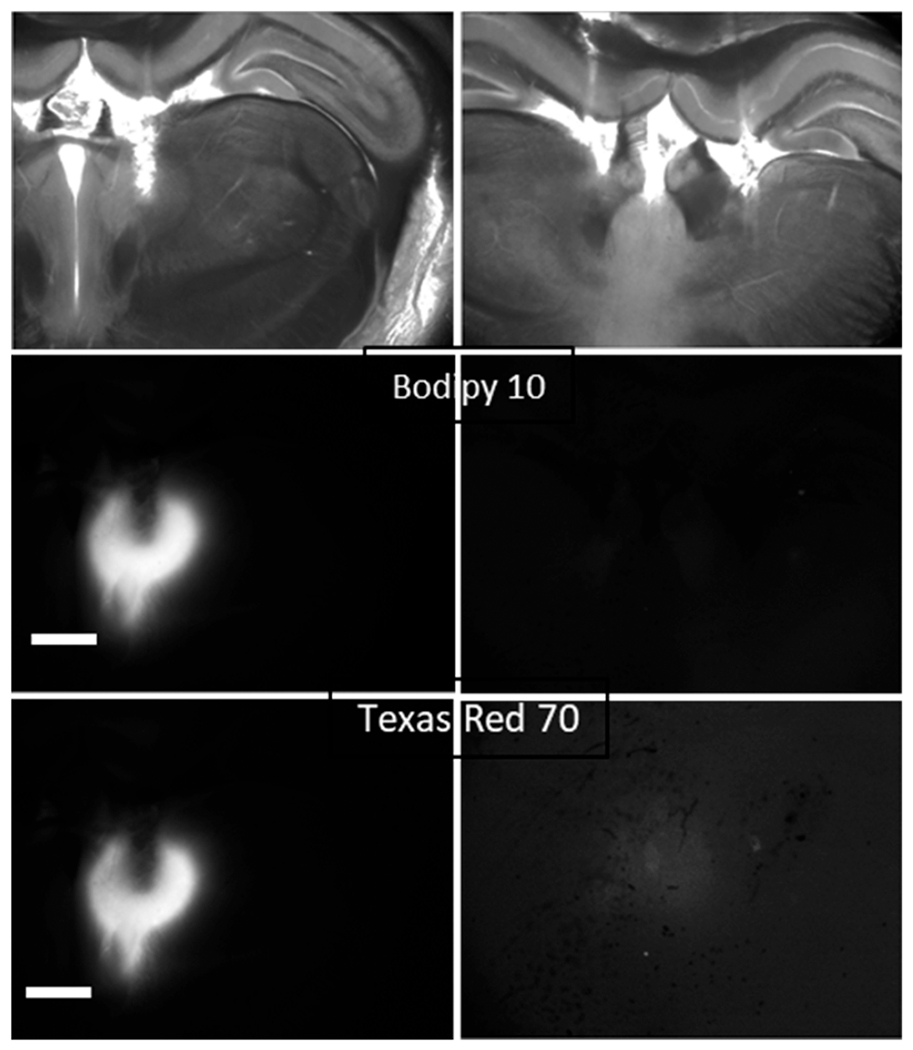
Several interesting observations were noted during electrokinetic infusions into the rat brain. Figure 3 shows an image following infusion of Ru(bpy)₃²⁺ for 45 min at 25 μA. In this experiment, the counter cannula was positioned in the opposite hemisphere from the source cannula to determine whether transport would occur through the massa intermedia (interthalamic adhesion). Figure 3 contains a plot of the fluorescence intensity from two line scans indicated on the image. The maximum intensity (100%) is near the tip of the cannula. The intensity at the terminus of the nearly horizontal line scan near “A”, which is in the opposite hemisphere to the source, is 25% of the maximum intensity. This example provides some additional evidence that electrokinetic transport may be directed in vivo, with migration of a solute along a current path toward a counter cannula. Similar observations were made in the corpus callosum and hippocampus (Figure S1 and S2).

Figure 3.

Example in vivo ejection of Ru(bpy)₃²⁺ from a 100 μm inner diameter fused silica infusion cannula into the rat thalamus (AP, 4 mm from bregma) with 25 μA applied current for 45 min with the counter cannula in the contralateral hemisphere as in Figure 1. Images are brightfield (top left) and fluorescence (bottom left). The asterisk in the brightfield image denotes the third ventricle. The right panels represent the fluorescence intensity along the skewed vertical (top) and skewed horizontal (bottom) white line scans. The “A” corresponds to the distance of 0 on the plots also denoted as “A”. Dotted lines in the plots are the standard error. The scale bar is 1 000 μm.

The foregoing examples had the counter electrode/cannula in the contralateral hemisphere and infused for 45 min at 25 μA It is of interest to know whether it is possible to transport solute in the dorsal-ventral direction across the corpus callosum and whether infusions can be carried out for a longer time. Based on neuroanatomical fiber orientation through the corpus callosum, pressure-induced transport of Ru(bpy)₃²⁺ may occur along axonal tracts of the corpus callosum because of a lower resistance to pressure-induced flow.⁴⁰ Figure 4, left, shows the experimental arrangement. The expectation is that the electrokinetic CED-induce flux will proceed from the neocortex into the striatum across the corpus callosum. The blue arrows on the right hemisphere of the atlas image show a plausible path for flow which, if significant, may be problematic. Although transport along the corpus callosum occurs to a small degree (rows B and C), there is no evidence that this rather low permeability path prevents material from being infused into the striatum (rows D and E). In this experiment, the time and current are greater than in the foregoing figures so the infusion volume is relatively larger at 46.1 ± 2.2 μL (N = 3). It is important to note that the current is confined to the region between the source and sink cannulas. A disadvantage of this fact is that, while the direction of current flow certainly dictates the direction of solute motion, diffusion will carry solute away from the region between the cannulas. However, an advantage of electrokinetic delivery to a region between a source and a sink cannula is the insensitivity of the process to the porosity of the tissue. Thus, electrokinetic delivery should be effective in infusion into “denser” brain areas such as deep brain nuclei targets for functional and restorative neurosurgery or malignancies in neuro-oncology. To date, this has not been possible with pressure-driven CED.

Figure 4.

Typical example of directionality in vivo of Ru(bpy)₃²⁺, from the prefrontal cortex to the striatum with 75 μA applied for 5 h from a 100 μA inner diameter fused silica infusion cannula. (Left) Schematic of the experimental design with the cannula placement in a coronal section at AP = bregma − 0.3 mm. The source has the positive electrode. Black dashed box represents the area of the fluorescence images in the right panel. Major brain regions are identified in the left half of the coronal section. The blue arrows within the black dashed box show the potential path to- and along the corpus callosum. Right: Fluorescence images of the 300 μm-thick slices. Asterisks represents the lateral ventricle. Bregma coordinates for each 300-μm slice are indicated at the bottom left of each image. Letters A–E identify sequential rows of slices. Cannulas are outlined in white dashed marks. The track of the infusion capillary can be seen in bregma coordinates 0.9 mm to −0.6 mm. The plane of the counter cannula is best seen at −0.3 and −0.6 mm from bregma. Scale bar is 1,000 μm. Fluorescence images superimposed onto bright field images are shown in Figure S2, and surface intensity plots are in Figure S3.

We have contrasted electrically driven flow with pressure driven flow, but it is important to point out that an electric current through a cannula and porous medium can actually induce pressure gradients. Equations 1 and 2 for electroosmotic flow are accurate for a system in which the current flowing in the aqueous electrolyte goes through spaces with a single and homogeneous electroosmotic mobility. Estimating the electrokinetic flow rate is not trivial in cases where there are varying ζ-potentials. The ζ-potential of the fused silica cannula is roughly −50 to −60 mV^26,41 while the ζ-potential of the OHSC (approximately −22 mV²⁶) was used as an estimate for the in vivo thalamus. The discontinuous ζ-potential creates a slight positive pressure^41,42 at the source cannula opening/brain tissue interface and a slight negative pressure at the brain tissue/sink capillary opening interface. The more negative ζ-potential of the cannula augments the flow rate in the tissue by an amount that depends on the ability of the source/sink capillaries to support the induced pressure differences. Calculations shown below for the system described here indicate that the pressure is about 200 Pa or about 0.2% of an atmosphere, a very low pressure. No visible tissue deformation due to increased pressure was observed at the infusion cannula implantation site in any of our experiments. Also, our calculations based on electrokinetic mobility alone are in good agreement with experimental observations, thus the pressure flow induced by the ζ-potential mismatch between the cannula and the tissue has only a minimal influence on the distribution of infused solute shown here.

The current density for a 100 μm diameter cannula tip with 25 μA of applied current, as utilized in vivo, is 3 180 A/m² at the tip. In contrast, the current density for previously published 0.5 μA ejections from an approximately 4 μm diameter cannula tip was 39 790 A/m² (at the tip⁴³). No appreciable cell death in OHSCs, as evident by propidium iodide staining, was visible at this current density.⁴³ Currents in the milliamps range are regularly used in patients with deep brain stimulation (DBS), with a 25.5 mA current passed through a 0.06 cm² electrode surface resulting in a current density of roughly 4 250 A/m². Therefore, there is some latitude to increase the flow rate from the cannula by using modestly higher current with the existing cannula or by increasing the surface area and current together, e.g., with a hollow fiber at the tip.

Finite Element Calculations to Simulate Electro-kinetic Infusions.

In order to compare the delivery profile of pressure-driven CED and ECED on transporting solutes across the white matter fibers of the corpus callosum, we developed finite element computational models for pressure-driven and electrokinetic infusions with either one or two cannulas.⁴⁴ In all four models, a representative coronal slice was adapted from the Paxinos and Watson rat atlas⁴⁵ and reproduced in the COMSOL geometry workspace. The two-dimensional profile of the slice was extended in the third dimension to create a three-dimensional shape consisting of the ventricles, corpus callosum, and brain parenchyma. A curvilinear coordinate system was created for the corpus callosum to simulate the directional anisotropy of the white matter fibers (Figure S7). Two hollow cylinders were used to represent the infusion and counter cannulas. For pressure-driven flow, the applied pressure was chosen such that the flow rate in the infusion cannula was comparable to that for ECED. For an applied current of 75 μA, the calculated infusion fluid flow rate is ~55 nL/min. A comparable flow rate in the infusion cannula is achieved with an external pressure of ~3 000 Pa (above atmospheric pressure). Computational results for the distribution of Ru(bpy)₃²⁺ are summarized in Figure 5. Images of the geometry and tables of parameters for the calculations are in Figures S7–S9 and Tables S1–S7.

Figure 5.

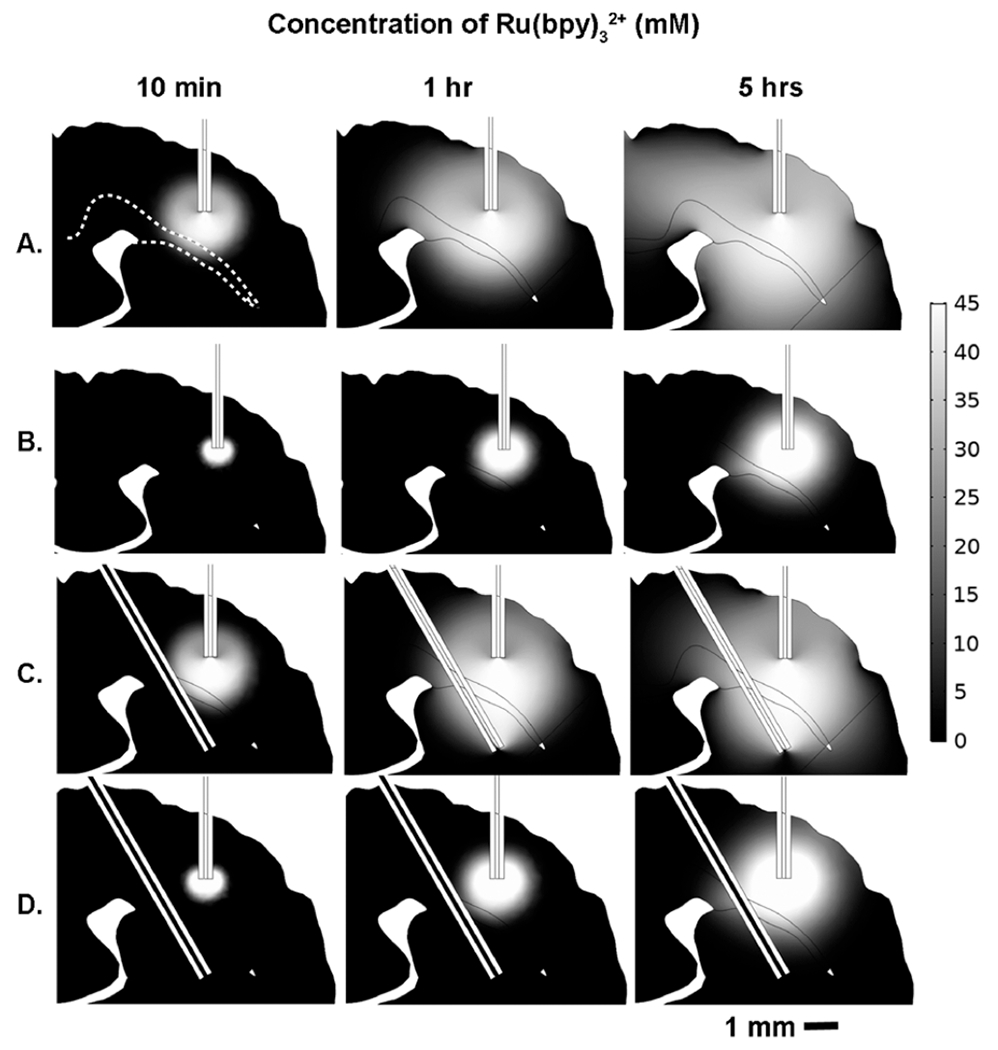
2D representative slice of the 3D geometry COMSOL calculation showing the evolution of Ru(bpy)₃²⁺ transport over time for ECED (A, C) vs pressure-driven CED (B, D). Parts A and B are single-cannula models, while parts C and D are two-cannula models. The infusion cannula is located in the cortex while the counter cannula is positioned beneath the corpus callosum in the striatum. As indicated by the scale bar, white indicates the maximum concentration, 45 mM, while black indicates zero concentration in the ECS. The corpus callosum is outlined by a white dashed line in the top left figure in part A. Snapshots of concentration profiles at three different time points are displayed for each model: 10 min, 1 h, and 5 h. Pressure boundary conditions for CED and applied potential for ECED were chosen such that the fluid flow rates in the infusion cannulas were equal in all models, ~55 nL/min.

Despite having the same fluid flow rate from the infusion cannula, ECED infuses Ru(bpy)₃²⁺ into a larger region of the brain (Figure 5A,C), in the same amount of time, than its pressure counterpart (Figure 5B,D). There are three reasons why the distribution of the solute is different for the two motivating forces: current and pressure. One is the electrophoresis of the Ru(bpy)₃²⁺. The electrophoretic mobility is 1.7× the electroosmotic mobility (Table 1). Another is that there is a ζ-potential mismatch between the cannulas and the tissue so there is a slight pressure gradient that forms²⁷ in the electrokinetic delivery. Specifically, there is a positive pressure at the tissue-infusion cannula interface and a negative pressure at the tissue-counter cannula interface. This pressure gradient is dependent on the tissue permeability and increases proportionally with the current.⁴⁴ For an applied current of 75 μA, the estimated pressure drop is approximately 200 Pa between the cannula tip and tissue. The calculated pressure drop for pressure-induced flow in the tissue is 1700 Pa. Recalling Table 1 and the discussion of the infused volume of Ru(bpy)₃²⁺, this pressure-induced flow was not included in the calculated volumes. It contributes to the fact that the predicted volume of tissue affected is lower than the experimentally realized volume. The tissue permeability (which can be related to porosity and tortuosity) affects the flow rate at constant pressure to a greater degree than it affects the flow rate at constant current.⁴⁴ Finally, it is important to distinguish the apparent volume affected by the infusion and the amount of solute introduced. Careful inspection of Figure 5 shows that the Ru(bpy)₃²⁺ is more widely dispersed with current than pressure, but its concentration decreases more rapidly away from the source than in the case of pressure.

The current-induced infusion displays some directionality. When the counter cannula is placed in the contralateral hemisphere, ECED occurs laterally, on average. (Note that in row A of Figure 5 at 5 h, the solute has proceeded beyond the boundary of the image.) When the counter cannula is placed below the source cannula, the ECED occurs, on average, vertically in the same coronal plane (Figure 5A,C). As seen in Figure 5B,D, when pressure is the main driving force, there is obvious flow along the axonal fibers of the corpus callosum and toward the ventricle. However, the effect is smaller than expected based on the relative tortuosities alone (see Table S5), which would be about 25% greater progress along the corpus callosum than in the thalamus. This is likely due to lateral diffusion causing some averaging of the velocities of molecules in and adjacent to the corpus callosum. Thus, it is possible that some infusate is being delivered along low-pressure resistance pathways. Nonetheless, it is apparent from Figure 4C that transport of Ru(bpy)₃²⁺ is, on average, orthogonal to the fibers of the corpus callosum and toward the counter cannula along the directed current path.

The preferential transport of a solute through the tissue may be contrasted with pressure-driven infusion,^{6,7,18,20,46–49} in which tissue deformation and tearing, backflow along vascular and/or cannula tracts, and the overall propensity for fluid to move along paths of least pressure resistance are limiting. In none of the electrokinetic infusions was tissue deformation visible nor did we see tissue tearing due to the volume of infusate. Of course, as with traditional CED cannulas, there was residual damage from implantation of the infusion and counter cannulas.

DISCUSSION

ECED offers an alternative to traditional pressure-driven CED and may also even augment standard techniques. By using an electric current, the infusion path is dictated by current density and tissue resistivity. Pressure-driven CED is beholden to low-resistance pressure pathways, leading to backflow along a cannula, across ependymal linings, or into cerebrospinal fluid (CSF) cisterns or the ventricular system. In contrast, ECED infusions favor regions with the highest electric fields (i.e., between electrodes).

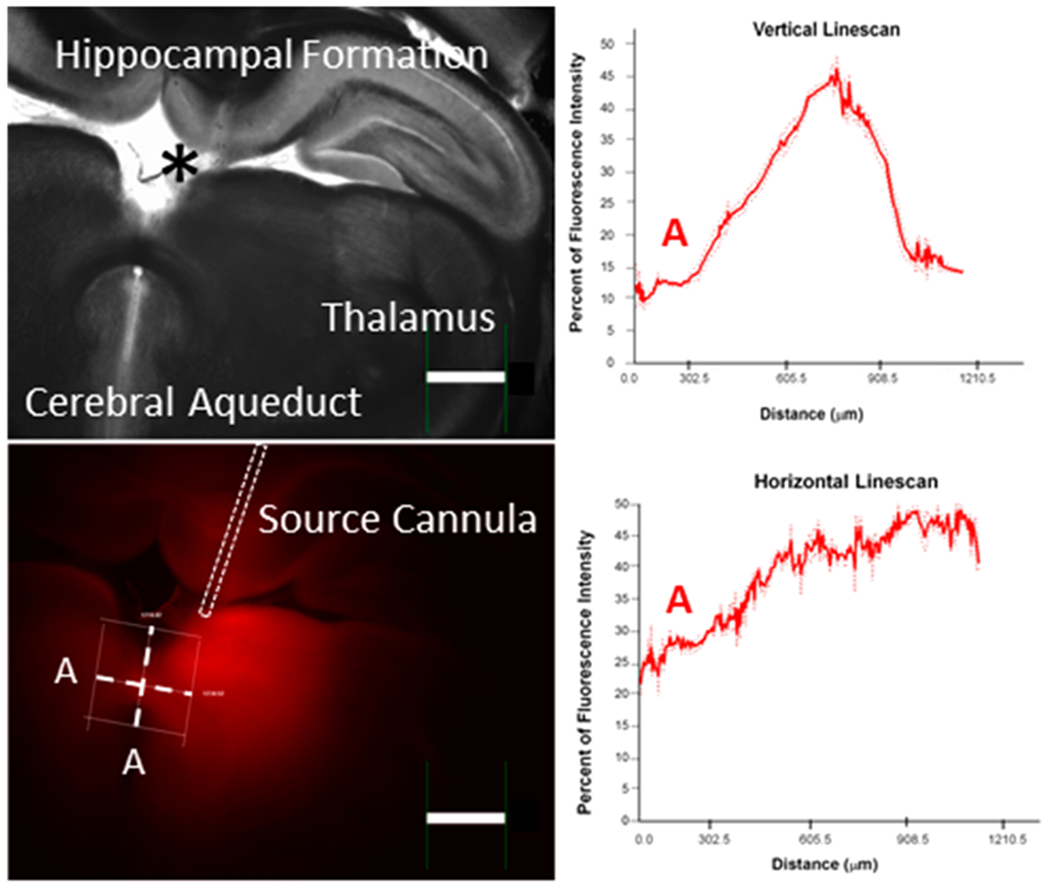
The porosity and tortuosity of brain tissue are important to molecular and fluidic transport and fortunately values are widely available.³⁵ Our calculations used single values for each (porosity, 0.20; tortuosity, 1.6) in the regions portrayed in Figure 4 except for the corpus callosum. For the electroosmotic mobility, which depends upon the tissue ζ-potential, we used the only measurement that we are aware of in brain tissue, as measured in organotypic hippocampal slice cultures.²⁵ Thus, it is useful to compare the computations with the experiments to clarify the adequacy of these assumptions. Figure 6 shows images of sections at AP coordinates near the cannula insertion from Figure 3 and compares them with the calculated solute distribution for the 5-h infusion of Ru(bpy)₃²⁺. The agreement is quite good implying that the choices of ζ-potential, tortuosity, and porosity are adequate.

Figure 6.

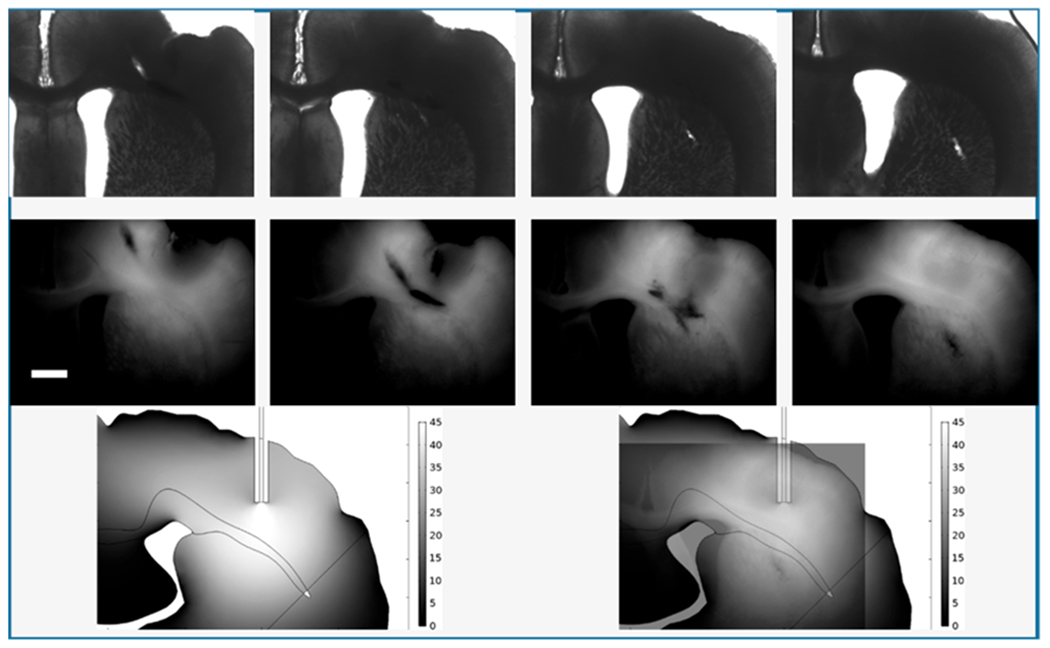
Comparison of experiment and theory. Top row: slices 10–13 from Figure 3. Bottom left: Calculation from Figure 4. Bottom right: Overlay of the fluorescence image from slice 13 with 50% transparency and of the calculation to show the portion of the image of the calculation that overlaps the images of the tissue. Note that the contrast of the experimental images has been increased for visibility. Unaltered images are shown as Figure S6.

ECED represents a novel methodology for the delivery of solutes to the central nervous system. This approach has certain advantages over pressure-driven CED, including the ability to direct infusion along current paths with potentially substantial clinical and scientific benefits.²⁸ Moreover, ECED may even direct solutes against a tissue density gradient. Unlike pressure-driven flow, the electrophoretic mobility of a solute is important. This can be a disadvantage, but it also provides a means to increase a solute’s velocity in an electric field by attaching a cationic tag. Molecular size also influences the effectiveness of electrokinetic transport. In theory, this effect is related to the tortuosity of the paths taken by the solute and thus would be similar to that experienced in pressure flow.⁴¹ Directed transport was observed in which a solute was directed toward the contralateral side (and counter cannula) through tissue connections. This results from conveyance of the electrical current through the tissue toward the contralateral side rather than into adjacent ipsilateral tissue or CSF spaces. To increase V_d, it may be possible to use higher current densities in vivo than were examined in the present work; however, this would require a deeper understanding of the effect of an electrical current on brain tissue and further preclinical safety studies. Therefore, there may be considerable opportunity to increase the applied electrical current and longer infusion times as instrumentation and safety parameters allow. While we have focused on physical transport here, there are other electrically controlled procedures such as localized electroporation that could be carried out in conjunction with localized infusions. In future applications, it may be possible to perfuse a surgical resection bed or natural tissue cavity by passing current through in implanted, doped hydrogel to provide rapid conveyance of a solute to wider areas of tissue.

METHODS

Chemicals and Solutions.

The following materials were purchased from Sigma (St. Louis, MO) and used as received, unless otherwise noted. Solutions were prepared with Millipore Synthesis A10 system 18 M purified water (Millipore, Billerica, MA). Glucose-free HEPES-buffered salt solution (GF-HBSS) contained in mM: 143.4 NaCl, 5 HEPES, 5.4 KCl, 1.2 MgSO₄, 1.2 NaH₂PO₄, and 2.0 CaCl₂. GF-HBSS was filtered, stored frozen, warmed to room temperature, and ultrasonicated for 10 min prior to use. HBSS obtained the same component concentrations as GF-HBSS, with an additional 10 mM d-(+)-glucose and underwent the same preparation and storage process. GBSS was made up of 27.5 mM d-(+)-glucose and 2.7 mM MgSO₄ supplemented to Gey’s Balanced Salt solution. GBSS was filtered, stored in the refrigerator, and warmed to 37 °C prior to use. The OHSC culture medium contained the following components from Gibco (Invitrogen, Eugene, OR): 50% Opti-MEM, 25% heat-inactivated horse serum, and 25% Hanks’ Balanced Salt Solution, supplemented with 2% vitamin B-27, and 1% d-(+)-glucose. The medium was filtered, stored in the refrigerator, and warmed to 37 °C prior to use. Tris(2,2′-bipyridine)ruthenium (abbreviated Ru-(bpy₃²⁺) was obtained from Sigma and diluted to make a solutions of 1.3 mM Ru(bpy)₃²⁺ in 150 mM aqueous NaCl supplemented with 5 mM HEPES buffered at pH 7.4.

Electrokinetic Infusions In Vivo.

The following procedures were approved by the University of Pittsburgh Institutional Animal Care and Use Committee. Male Sprague–Dawley rats (Hilltop, Scottsdale, PA), with weights ranging from 260 to 290 g, were anesthetized with isoflurane and wrapped in a 37 °C homeothermic blanket (EKEG Electronics, Vancouver, BC, Canada). An incisor bar was set at 0 mm at the interaural line. Using a stereotaxic instrument, rats underwent a single craniotomy surgery that allowed for positioning of both a dye and counter catheter. Catheters were made from 10 cm-long, 100 μm inside diameter, 360 μm outside diameter polyimide-coated fused silica capillaries (Polymicro Technologies, Phoenix, AZ). Craniotomies were performed to position an infusion (dye) capillary and counter capillary into the brain bilaterally (from bregma: 4.0 mm lateral, 1.3 mm posterior, and 5.0 mm below the dura) for volumetric analysis. A solution of 45 mM Ru(bpy)₃²⁺ was again chosen for its electrokinetic properties. Currents of 25 and 75 μA were applied for a span of 45 min and 5 h, respectively. In order to minimize the extent of diffusion of infused dyes prior to imaging, two people worked together with one managing the tissue and slicing while the other took the tissue to the microscope and did the imaging. After completion of the infusion, rats were perfused transcardially with 250 mL of 4% paraformaldehyde in phosphate buffered saline solution. The brain was then quickly removed from the rat and sliced into 4 mm coronal slices. Using a vibratome, the 4 mm slices were sectioned into 200 or 300 μm thick slices. Two to three slices were taken for imaging while the slicing continued. Images were taken using an Olympus IX-71 inverted fluorescence microscope. The time between infusion completion and imaging was approximately 20 min.

Imaging.

Images were acquired with an Olympus IX-81 inverted fluorescence microscope with a high resolution charged-coupled device camera (ORCA-ER). Filters used were (center wavelength/bandwidth in nanometer): Ru(bpy)₃²⁺ 475/30 excitation and 605/52 emission. Bodipy 10: ex 490/20, em 525/36. TR 70: ex 560/25, em 625/26. A 1.25× Olympus objective lens with a numerical aperture of 0.04 was used for imaging. The fluorescence intensity values were between 0 and 4 095. Image sequences were acquired using MetaMorph 7.6.2.0 software (MDS Analytical Technologies, Sunnyvale, CA). The MetaMorph software triggered the initiation and termination of the signal during image acquisition.

Volume of Distribution Calculations.

The volumes of distribution from the infusions shown in Figure 1 were determined using the following procedure with Metamorph Imaging Software Systems (Universal Imaging Corporation, Molecular Devices), except for Figure 2. The fluorescence intensities were evaluated by determining for each rat the overall maximum fluorescence intensity (I₀) at the infusion capillary implantation site. The distances along eight radii were measured from the point of maximum fluorescence intensity in each slice to the point where the fluorescence intensity was 25% of I₀. The eight radii were averaged together to arrive at a radius to determine the approximately circular area of tissue impacted by the infusions. The coronal area within each slice was multiplied by the thickness of the slice to arrive at a volume per tissue slice. The volumes of each slice were summed to arrive at a final volume of distribution for each rat and fluorophore. In Figure 2, the volume of distribution was determined in 200 or 300 μm thick slices using NIS Elements Advanced Research software version 4.0 (Nikon Instruments Inc.). The total area of Ru(bpy)₃²⁺ was selected as the region of interest (ROI), and this area was expressed as a percentage of the total area using the binary-threshold tool of NIS Elements. The data are reported as volume of all sections containing Ru(bpy)₃²⁺ and the standard error of the mean.

Finite Element Calculations.

All simulations were performed in COMSOL Multiphysics v5.3. The model was drawn in the COMSOL geometry workspace. The measurements from the rat atlas were used as the general outline for the 2D brain, which was then extruded in the rostral/caudal direction to generate a 3D geometry that mimicked the brain in the left/right and dorsal/ventral directions. The ventricles were generated in a similar fashion using 2D measurements from the rat atlas and extruding into a 3D shape. This volume was subtracted from the first volume using Boolean operations to represent the ventricular space. The corpus callosum was generated in a similar fashion. A curvilinear coordinate system was created in order to simulate accurately the difference in tortuosities along and perpendicular to the axonal tracts.³⁵ Two hollow cylinders were used to represent the infusion and counter cannula lumens. The “Electric Currents” module was used to calculate the potential in the tissue as a result of applied current. The “Free and Porous Media” module was used to calculate the flow rate for ECED model while the “Darcy’s Law” module was used to calculate flow rate for the pressure-driven CED model. For both pressure and electrokinetic flow, the “Transport of Diluted Species” was used to calculate evolution of Ru(bpy)₃²⁺ concentration over time. All boundary conditions are further described in the Supporting Information.