Smoothed Nested Testing on Directed Acyclic Graphs

Summary

We consider the problem of multiple hypothesis testing when there is a logical nested structure to the hypotheses. When one hypothesis is nested inside another, the outer hypothesis must be false if the inner hypothesis is false. We model the nested structure as a directed acyclic graph, including chain and tree graphs as special cases. Each node in the graph is a hypothesis and rejecting a node requires also rejecting all of its ancestors. We propose a general framework for adjusting node-level test statistics using the known logical constraints. Within this framework, we study a smoothing procedure that combines each node with all of its descendants to form a more powerful statistic. We prove a broad class of smoothing strategies can be used with existing selection procedures to control the familywise error rate, false discovery exceedance rate, or false discovery rate, so long as the original test statistics are independent under the null. When the null statistics are not independent but are derived from positively-correlated normal observations, we prove control for all three error rates when the smoothing method is arithmetic averaging of the observations. Simulations and an application to a real biology dataset demonstrate that smoothing leads to substantial power gains.

1. Introduction

We consider a structured multiple testing problem with a large set of null hypotheses structured along a directed acyclic graph. Each null hypothesis corresponds to a node in the graph and a node contains a false hypothesis only if all ancestors are false. The inferential goal is to maximize power while preserving a target error rate on the entire graph and rejecting hypotheses in a manner that obeys the graph structure. We will focus on boosting power in existing structured testing procedures by using the graph to share statistical strength between the node-level test statistics.

The graph-structured testing problem is motivated by modern biological experiments that collect a large number of samples on which to simultaneously test hundreds or even thousands of hypotheses. In genetics, for example, biologists are building genetic interaction maps (Costanzo et al., 2019). These large networks outline how different genes rely on each other to produce or prevent certain phenotypes such as cell growth and death. Recent advances such as CRISPR-Cas9 (Wang et al., 2014) and Perturb-Seq (Dixit et al., 2016) enable biologists to experimentally disable hundreds of genes, both in isolation and in subsets of two or even three genes at once (Kuzmin et al., 2018). Testing the thousands of candidate sets of genes for differences from a control population is a classic multiple hypothesis testing problem.

Unlike the classical multiple testing problem, there is a rich structure to genetic interaction experiments. The biologist wishes to understand the sets as they relate to individual genes and subsets. For example, two genes may not produce a decrease in cell survival rates if only one of them is knocked out. However, knocking both out simultaneously in the same cell may lead to a sudden drop in survival rate (Costanzo et al., 2019). In these cases, the biologist would consider the two genes to be interacting and thus the pair would be known as a synthetic lethal combination.

Beyond discovering the exact combination that leads to lethality, the biologist would also now flag the individual genes as having the potential to contribute to synthetic lethality, even though the genes cannot do so on their own. This potential has scientific and medicinal importance. For the scientist, if a gene is known to have the potential to contribute to cell death, it may be worth investigating it in the context of other knocked out genes that have not yet been considered. In medicine, if a specific type of cancer is seen to have a mutation in the first gene, a drug may be developed that inhibits the second gene, thereby killing the tumor cells. Thus, it is important to learn not just the exact lethal combinations, but also the entire ontology of genetic effects.

Modern biological experiments aim to test not just individual genes or gene sets, but all entries in this ontology. In this structured testing problem, lower-level hypotheses are nested within higher-order hypotheses: if a gene or set of genes is truly associated with a change in phenotype, it logically entails that the subsets are also associated. Here we consider this nested testing problem in the general case, where a directed acyclic graph encodes an ontology of logically nested hypotheses; we will return to the genetic interact map example in Section 5.

The key insight in this paper is that knowing the graph structure should increase power in the testing procedure. If every node in the graph represents an independent hypothesis test, then nodes should be able to borrow statistical strength from their ancestors and descendants. The signal at a non-null node may be too weak to detect on its own, but the strength of evidence when combined with the evidence from its non-null children may be sufficient to reject the null hypothesis. This strength sharing can also flow in the opposite direction, with non-null parent nodes boosting power to detect non-null children. For instance, if the non-null signal attenuates smoothly as a function of depth in the graph, it may be possible to learn this function. The test statistic for a node can then be adjusted using the estimated signal predicted by the function learned from the ancestors. Whether using the descendants, ancestors, or both, sharing statistical strength creates dependence between test statistics and therefore must be carried out thoughtfully so as to enable control of the target error rate.

This leads us to develop a smoothing approach that implements this sharing of statistical strength between connected test statistics in the directed acyclic graph while still controlling the target error rate. We focus on descendant smoothing as it requires less prior knowledge of the graph and is thus more broadly applicable. We prove that the descendant smoothing approach yields adjusted $p$-values that are compatible with three different selection algorithms from the literature on nested testing with directed acyclic graphs (Meijer & Goeman, 2015; Genovese & Wasserman, 2006; Ramdas et al., 2019a). Together, these techniques enable us to smooth the $p$-values and control the familywise error rate, the false discovery rate, or the false exceedance rate. Simulated and real data experiments confirm that smoothing yields substantially higher power across a wide range of alternative distributions and graph structures.

2. Background

There is a wealth of recent work on structured and adaptive testing. We focus on the most relevant work and refer the reader to Lynch (2014) for a comprehensive review of testing with logically nested hypotheses.

Preserving the logical nesting structure after selection is the domain of structured testing (Shaffer, 1995). Methods for structured testing can be categorized based on their assumptions about the structure of the graph and the type of target error rate. For familywise error rate control, Rosenbaum (2008) propose a generic test on a chain graph; Meinshausen (2008) propose a procedure for testing on trees in the context of variable selection for linear regression; Goeman & Mansmann (2008) propose the focus-level method, blending Holm’s procedure (Holm, 1979) and closed testing (Marcus et al., 1976), for testing on general directed acyclic graphs; and Meijer & Goeman (2015) propose a more flexible method for arbitrary directed acyclic graphs based on the sequential rejection principle which unifies the aforementioned tests (Goeman & Solari, 2010). For false discovery rate control, the Selective Seqstep (Barber & Candès, 2015), Adaptive Seqstep (Lei & Fithian, 2016), and accumulation tests (Li & Barber, 2017) enforce the logical constraint on the rejection set for chain graphs, though they do not require the logical constraint to actually hold; Yekutieli (2008) propose a recursive procedure for testing on trees which provably controls the false discovery rate up to a computable multiplicative factor; Lynch & Guo (2016) adapt the generalized step-up procedure to handle trees, which is further extended by Ramdas et al. (2019a) to general directed acyclic graphs.

There is a nascent literature on adaptive testing methods that preserve nested hypothesis structure. Lei et al. (2017) describe an interactive adaptive procedure that partially masks $p$-values, enabling the scientist to explore the data and unveil its structure, then use the masked bits to perform selection while controlling the false discovery rate at the target level. This interactive approach is able to preserve the nested hypothesis structure and take advantage of covariates, but comes at the cost of splitting the $p$-values, potentially costing power. Further, the method is only able to control the false discovery rate for independent $p$-values; we will consider a much broader class of error metrics as well as some dependent $p$-value scenarios. The application of descendant smoothing was also studied in Vovk & Wang (2020) for familywise error rate control and in Ramdas et al. (2019b) for false discovery rate control, though the latter requires a conservative correction to handle the dependence induced by aggregation. A suite of methods (Scott et al., 2015; Xia et al., 2017; Tansey et al., 2018; Lei & Fithian, 2018; Li & Barber, 2019) enable machine learning models to leverage side information like covariates that learn a prior over the probability of coming from the alternative; however, these methods do not enforce the logical constraint on the rejection set.

Other methods go beyond classical error metrics, defining and controlling a structured error metric. Benjamini & Bogomolov (2014) propose a method to control the average false discovery proportion over selected groups for a two-level graph, which is further extended by Bogomolov et al. (2017) to general graphs. The p-filter (Barber & Ramdas, 2017) and the multilayer knockoff filter (Katsevich & Sabatti, 2019) are able to control the group-level false discovery rate simultaneously for potentially-overlapping partitions of hypotheses. Unlike the methods described in the last paragraph, for which the internal node in the graph can encode an arbitrary hypothesis, these four works seek to handle a special hierarchy where each internal node encodes the intersection of a subset of hypotheses on the leaf nodes. Our proposed approach is fundamentally different from these methods since we allow internal nodes to encode non-intersection hypotheses and our goal is to control the overall target error rate.

Rather than competing with methods for structured testing, our smoothing procedures are complementary. As we will show in Section 4, the descendant smoothing procedure is compatible with controlling familywise error rate via Meijer & Goeman (2015), the false exceedance rate via an extension to the method of Genovese & Wasserman (2006), and the false discovery rate via the method of Ramdas et al. (2019a). In the case of the latter method, we explicitly show that the smoothed $p$-values are positive regression dependent on the subset of nulls (Benjamini & Yekutieli, 2001), resolving the issue of dependence under the null after smoothing and hence avoiding conservative corrections as suggested by Ramdas et al. (2019a). The benefit of smoothing is not to enable a new structured hypothesis testing procedure, but to make existing principled methods such as these more powerful by leveraging the structure of the problem.

3. Smoothing Nested Test Statistics

3.1. Smoothed p-values

Let $\left\{H_1,\dots ,H_n\right\}$ be a large set of null hypotheses. For each $v\in \{1,\dots ,n\}$ we observe a random variable $p_v$; if the null hypothesis $H_v$ holds, we assume that $p_v$ is super-uniform, i.e. $\text{pr}\left(p_v\le c\right)\le c$ for any $c\in [0,1]$. In some cases, we will assume the null $p$-value is uniform in [0, 1]. We will use $𝒱=\{1,\dots ,n\}$ to index all of the null hypotheses, and let

$$\stackrel{-}{𝒮}=\left\{v\in 𝒱:H_v\text{ is true }\right\},𝒮=𝒱\setminus \stackrel{-}{𝒮}=\left\{v\in 𝒱:H_v\text{ is false }\right\}$$

denote the unknown set of null hypotheses which hold and do not hold, respectively.

Our task is to estimate which hypotheses are false: to produce an estimator $\widehat{𝒮}$ of the set $𝒮$ from the random variables ${\left\{p_v\right\}}_{v\in 𝒱}$. To help estimate $𝒮$, we have access to a directed acyclic graph $𝒢=(𝒱,ℰ)$ whose edges encode constraints on the hypotheses in the following way: if $H_v$ is false and $w$ is an ancestor of $v$ in $𝒢$, then $H_w$ must also be false. We would like to use these logical constraints to our advantage in estimating $𝒮$.

To do so, we will use the graph $𝒢$ to transform the $p$-values into a new set of values and then apply existing structured testing procedures to the transformed values. We call the transformed values smoothed $p$-values (denoted $\tilde{p}$), because they will be formed by various kinds of averages of the original $p$-values. In the most general sense, the transformed values are created by the following process. First, we select an arbitrary collection of smoothing functions $f_v:{\mathbb{R}}^{\left|𝒱\right|}\to \mathbb{R}$ (specific examples are given below). For each $v\in 𝒱$ let ${𝒞}_v$ denote the union of $v$ with all of its descendants in the graph $𝒢$. The smoothed $\tilde{p}$-value for node $v$ is then given by

$$F_v\left(c;x_{𝒱\setminus {𝒞}_v}\right)\triangleq \text{pr}\left(f_v\left(u_{{𝒞}_v},x_{𝒱\setminus {𝒞}_v}\right)\le c\right),{\tilde{p}}_v\triangleq F_v\left(f_v\left(p_{{𝒞}_v},p_{𝒱\setminus {𝒞}_v}\right);p_{𝒱\setminus {𝒞}_v}\right),$$ (1)

where $u_{{𝒞}_v}={\left\{u_w\right\}}_{w\in {𝒞}_v}$ are independent and identically distributed as Uniform[0, 1]. For the tailored functions $f_v$ discussed in Section 3.2, $F_v$ has a closed form expression. In general, it can be computed to arbitrary accuracy for any $f_v$ using Monte Carlo simulations. The resulting random variable ${\tilde{p}}_v$ is a valid $p$-value for the hypothesis $H_v$,

Lemma 1 ($\tilde{p}$-values are super-uniform). Assume that the null $p$-values are mutually independent and independent of non-null $p$-values.

1. If the null p-values are independent and identically distributed as as Uniform[0, 1], ${\tilde{p}}_v$ is super-uniform for every $v\in \stackrel{-}{𝒮}$.

2. If the null p-values are super-uniform and $f_v$ is nondecreasing in $p_{{𝒞}_v}$ for any value of $p_{𝒱\setminus {𝒞}_v}$, then ${\tilde{p}}_v$ is super-uniform for every $v\in \stackrel{-}{𝒮}$.

We defer the proof to the appendix. Lemma 1 allows us to construct a hypothesis test with Type I error control using the smoothed $\tilde{p}$-values. The value at ${\tilde{p}}_v$ is a function of $p_v$ and all its ancestors and descendants. This enables $\tilde{p}$-values to borrow statistical strength from each other and, depending on the choice of $\left\{f_v\right\}$, can lead to more powerful hypothesis tests.

3.2. Descendant smoothing via merging

The optimal smoothing functions ${\left\{f_v\right\}}_{v\in 𝒱}$ are application specific. They depend on the structure of the graph, alternative hypothesis, and prior knowledge about the experiments. We focus our investigation on smoothing functions that use only the descendants at each node. Methods using ancestor nodes are left for future work. For notational convenience, we will write $f_v\left(p_{{𝒞}_v}\right)$ for $f_v\left(p_{{𝒞}_v},p_{𝒱\setminus {𝒞}_v}\right)$ for descendant smoothing hereafter.

Descendant smoothing functions combine the $p$-values of descendant nodes with the current node to obtain smoothed $p$-values. Many different strategies for combining $p$-values have been proposed in the literature, and it is beyond the scope of this work to investigate how each of them might perform as a descendant smoothing function. We instead consider a general class of smoothing functions derived by merging,

$$f_v\left(p_{{𝒞}_v}\right)=G_v\left\{\sum _{c\in {𝒞}_v}{H}_{v,c}^{-1}\left(p_c\right)\right\}.$$

This merging strategy covers many well-known methods for merging (independent) $p$-values. For instance, a Stouffer smoothing strategy would merge $p$-values following the method of Stouffer et al. (1949), converting the $p$-values to $z$-scores and adding them,

$$f_v\left(p_{{𝒞}_v}\right)=\sum _{c\in {𝒞}_v}{\Phi }^{-1}\left(p_c\right)$$

where ${\Phi }^{-1}(\cdot )$ is the distribution function of a standard normal. If $v$ corresponds to a null hypothesis, the logical constraint implies that $\left\{p_c:c\in {𝒞}_v\right\}$ are independent and uniformly distributed. As a result, $F_v(\cdot )$ is the distribution of a mean-zero normal distribution with variance $\left|{𝒞}_v\right|$.

A Fisher smoothing strategy would merge using the method of Fisher (1925) by considering the product of the $p$-values,

$$f_v\left(p_{{𝒞}_v}\right)=\sum _{c\in {𝒞}_v}2\text{ log}\left(p_c\right).$$

When $H_v$ is null, $-f_v\left(p_{{𝒞}_v}\right)$ has a chi-square distribution with degree of freedom $2\left|{𝒞}_v\right|$. Fisher’s method tends to have high power in a wide range of scenarios (e.g. Littell & Folks, 1971), though other methods will be more powerful for certain alternative distributions. Other popular methods include Tippett’s method, which takes the minimum $p$-values (Tippett, 1931; Bonferroni, 1936); Rüger’s method, which is based on an order statistic (Rüger, 1978); Simes’ method (Simes, 1986) or higher criticism method (Donoho et al., 2004), which combine all order statistics; the Cauchy combination, which aggregates inverse-Cauchy transformed $p$-values (Liu & Xie, 2020); and the generalized mean aggregation method which aggregates monomial-transformed $p$-values (Vovk & Wang, 2020; Vesely et al., 2021). Heard & Rubin-Delanchy (2018) provide a Neyman-Pearson analysis of optimal alternative hypotheses for each smoothing function; see also Vovk et al. (2020) for an admissibility analysis of different $p$-value aggregation methods under general dependence.

This class of descendant smoothing functions are convenient to work with both computationally and mathematically. Many have a closed form distribution that enables fast calculation of the smoothed statistic. As we will see, theoretical properties for a large class of smoothing methods can also be proven, making them compatible with a broad set of selection methods.

4. Testing with Smoothed Statistics

4.1. Familywise error rate control

The familywise error rate, controlled at level $\alpha$, ensures the probability that even one null hypothesis was rejected is at most $\alpha$, i.e. $\text{pr}\left(\right|\widehat{𝒮}\cap \stackrel{-}{𝒮}|\ge 1)\le \alpha$. It is a stringent error metric for multiple testing and useful in high-stakes decision-making where false positives are prohibitive.

To estimate $𝒮$ while controlling the familywise error rate, we can directly apply the algorithm of Meijer and Goeman to the $\tilde{p}$-values (Meijer & Goeman (2015)), outlined in Appendix 2.2. The procedure provably controls the familywise error rate so long as the null p-values are marginally all super-uniform. Therefore, by Lemma 1, even though the smoothed p-values are dependent, this correction is still valid.

The Lemma 1 result is very general for controlling the familywise error rate. It admits any choice of function over the descendant and ancestor $p$-values. This is possible because the innerloop of the Meijer & Goeman (2015) algorithm relies on a Bonferroni correction. The union bound strategy of the Bonferroni correction places no requirement on the dependency structure of the statistics.

4.2. False exceedance rate control

The false exceedance rate, controlled at level $(\gamma ,\alpha )$, ensures the false discovery proportion is greater than $\gamma$ with probability no greater than $\alpha$, i.e. $\text{pr}\left(\right|\widehat{𝒮}\cap \stackrel{-}{𝒮}|/|\widehat{𝒮}|>\gamma )\le \alpha$. It is less stringent than the familywise error rate.

Genovese & Wasserman (2006) propose a generic procedure that turns a familywise error control method into a false exceedance rate control method. Specifically, starting from any rejection set ${\widehat{𝒮}}_0$ that controls the familywise error rate at level $\alpha$, we can append any subset ${𝒮}^{\prime }\subset 𝒱\setminus {\widehat{𝒮}}_0$ onto ${\widehat{𝒮}}_0$. Then the expanded rejection set ${\widehat{𝒮}}_0\cup {\widehat{𝒮}}^{\prime }$ controls the false exceedance rate if $\left|{\widehat{𝒮}}^{\prime }\right|\le \left|{\widehat{𝒮}}_0\right|\gamma /(1-\gamma )$ (Genovese & Wasserman, 2006, Theorem 1). The proof is straightforward: on the event that ${\widehat{𝒮}}_0$ contains no false discovery, which has probability at least $1-\alpha$, the false discovery proportion is at most $\left|{\widehat{𝒮}}^{\prime }\right|/\left(\left|{\widehat{𝒮}}^{\prime }\right|+\left|{\widehat{𝒮}}_0\right|\right)\le \gamma$.

To guarantee that $\widehat{𝒮}$ satisfies the logical constraint, we apply Meijer & Goeman (2015)’s method to obtain ${\widehat{𝒮}}_0$, and then append another subset which does not violate the constraint. Since there is no restriction on ${\widehat{𝒮}}^{\prime }$, we can greedily add hypotheses based on the topological ordering to maintain the constraint. The procedure is outlined in Appendix 2.3.

4.3. False discovery rate control

The false discovery rate, controlled at level $\alpha$, ensures the expected proportion of rejected hypotheses that are actually null is at most $\alpha$, i.e. $\mathbb{E}\left[\right|\widehat{𝒮}\cap \stackrel{-}{𝒮}|/(1\vee \left|\widehat{𝒮}\right|\left)\right]\le \alpha$. This is one of the most popular error metrics in large scale inference.

To estimate $𝒮$ while controlling the false discovery rate, we apply the Greedily Evolving Rejections on Directed Acyclic Graphs method proposed by Ramdas et al. (2019a). The method works with the original test statistics by extending the Benjamini & Hochberg (1995) procedure to directed acyclic graphs. As with Benjamini & Hochberg (1995), it is only guaranteed to control the false discovery rate if the $\tilde{p}$-values satisfy a special property: positive regression dependence on the subset of nulls. Specifically, for any $x,y\in {\mathbb{R}}^m$, let $x⪯y$ signify that $x_i\le y_i$ for each $i$. A set $D\in {\mathbb{R}}^m$ is called non-decreasing if $x⪯y,x\in D⟹y\in D$. A random object $X\in {\mathbb{R}}^m$ is said to satisfy positive regression dependence on $T\subset \{1,\cdots ,m\}$ if $t\mapsto \mathbb{P}\left(X\in D\mid X_i=t\right)$ is non-decreasing for every non-decreasing set $D$ and every index $i\in T$.

Various multiple testing procedures have been proven to control the false discovery rate under positive regression dependence. However, only a few concrete examples have been shown to satisfy this condition, such as the one-sided testing problem with nonnegatively correlated Gaussian statistics and the two-sided testing problem with t-statistics derived from uncorrelated z-values (Benjamini & Yekutieli, 2001). This limits the practical usefulness of the theoretical guarantees established under this condition.

In Appendix 1, we establish a general theory of positive regression dependence on the subset of nulls based on classical stochastic ordering theory, a widely studied area in reliability theory (e.g. Efron, 1965; Kamae et al., 1977; Block et al., 1987). In Section 3.2, we introduced a class of $p$-values derived from descendant smoothing techniques. Theorem 1 shows that a broad class of these smoothed $p$-values satisfy positive regression dependence on the subset of nulls.

Theorem 1. Assume that the null $p$-values are uniformly distributed in [0, 1], mutually independent and independent of all non-null $p$-values. For each node $v$ and its descendant $c\in {𝒞}_v$, let $H_{v,c}\left(x\right):\mathbb{R}\mapsto \left[\mathrm{0,1}\right]$ be a monotone increasing function with the first-order derivative $H_{v,c}^{\prime }\left(x\right)$ being log-concave, and $G_v\left(x\right):\mathbb{R}\mapsto \mathbb{R}$ be a monotone increasing function. Further let

$$f_v\left(p_{{𝒞}_v}\right)=G_v\left\{\sum _{c\in {𝒞}_v}{H}_{v,c}^{-1}\left(p_c\right)\right\}.$$

Then the smoothed $p$-values are positive regression dependence on the subset of nulls.

Theorem 1 covers a broad class of descendant smoothing functions. For Stouffer smoothing, $G_v\left(x\right)=x,H_{v,c}\left(x\right)=\Phi \left(x\right)$ and $H_{v,c}^{\prime }\left(x\right)=\text{exp}\left\{-x^2/2\right\}/\sqrt{2\pi }$, which is log-concave; for Fisher smoothing, $G_v\left(x\right)=x,H_{v,c}\left(x\right)=\text{exp}\{x/2\}$ and $H_{v,c}^{\prime }\left(x\right)=\text{exp}\{x/2\}/2$, which is log-concave; for generalized mean smoothing (Vovk & Wang, 2020), $G_v\left(x\right)={\left(x/\left|{𝒞}_v\right|\right)}^{1/r},H_{v,c}\left(x\right)=x^{1/r}$ and $H_{v,c}^{\prime }\left(x\right)=x^{1/r-1}/r$, which is log-concave if $0<r\le 1$. For all these smoothing methods, Theorem 1 covers their weighted versions with $H_{v,c}\left(x\right)$ replaced by $a_{v,c}{H}_{v,c}\left(x\right)$ for arbitrary $a_{v,c}\ge 0$, since the log-concavity of the derivative continues to hold.

Theorem 2 presents another class of smoothed $p$-values based on order statistics. It includes Tippett’s method with $G_v\left(x\right)=\left|{𝒞}_v\right|x$ and $k_v=1$ and Rüger’s method with $G_v\left(x\right)=\left|{𝒞}_v\right|x/k$ and $k_v=k$.

Theorem 2. Under the same assumptions as in Theorem 1, the smoothed $p$-values satisfy positive regression dependence on the subset of nulls if

$$f_v\left(p_{{𝒞}_v}\right)=G_v\left(p_{{𝒞}_v,\left(k_v\right)}\right)$$

where $p_{{𝒞}_v,\left(1\right)}\le p_{{𝒞}_v,\left(2\right)}\le \dots \le p_{{𝒞}_v,\left(\left|{𝒞}_v\right|\right)}$ denote the order statistics of $p_{{𝒞}_v}$ and $k_v\in \left[1,\left|{𝒞}_v\right|\right]$ is an arbitrary integer.

Taken together, Theorems 1 and 2 establish that the Ramdas et al. (2019a) method will control the false discovery rate at the nominal level for most smoothing methods outlined in Section 3.2.

4.4. Dependent null statistics with Gaussian copulas

So far we have assumed that $p_{\stackrel{-}{𝒮}}$ are independent and (super-)uniform. If this does not hold, the smoothed $\tilde{p}$ values are not guaranteed to be super-uniform. This limits our ability to use these $\tilde{p}$-values for hypothesis testing. However, if anything is known about the dependency structure of the $p$-values then it may be possible to use this knowledge to create conservative bounds yielding super-uniform $\tilde{p}$-values. For instance, when the dependency structure between $p$-values is known, Fisher smoothing can be made valid by adjusting the critical value (Brown, 1975; Kost & McDermott, 2002). However, when the correlation structure is unknown, Fisher smoothing is not recommended as it will likely lead to inflated false discovery rates.

In this section we consider the case that $p_{\stackrel{-}{𝒮}}$ carries a Gaussian copula with unknown correlation matrix $R$. In other words, letting ${\Phi }^{-1}$ denote the quantile function of the standard normal and letting $Z_v={\Phi }^{-1}\left(p_v\right)$, we will assume that $Z_{\stackrel{-}{𝒮}}~𝒩(0,R)$. This case arises naturally if the $p$-values come from correlated $z$-scores.

When the copula is Gaussian, we can still control any of the three target error metrics by using a method we dub conservative Stouffer smoothing,

$${\tilde{p}}_v\leftarrow \left\{\begin{array}{ll}1& \text{if }\sum _{w\in {𝒞}_v}{\pi }_{vw}{Z}_w\ge 0\\ \Phi \left(\sum _{w\in {𝒞}_v}{\pi }_{vw}{Z}_w\right)& \text{otherwise.}\end{array}\right.$$

where $\Phi$ is the cumulative distribution function of the standard normal and $\pi$ satisfies ${\pi }_{vw}\ge 0,{\sum }_{w\in {𝒞}_v}{\pi }_{vw}=1$.

For familywise error rate and false exceedance rate, it suffices to show that the smoothed $\tilde{p}$-values are marginally super-uniform.

Lemma 2 (marginal validity for Gaussian copulas). Conservative Stouffer smoothing on marginally uniform $p$-values with any Gaussian copula yields super-uniform smoothed $\tilde{p}$-values, i.e. $pr\left({\tilde{p}}_v\le \alpha \right)\le \alpha$ for all $v\in \stackrel{-}{𝒮}$.

If we know that the nulls are all non-negatively correlated, we can prove the following result, implying that the Ramdas et al. (2019a) method can control the false discovery rate.

Lemma 3 (positive regression dependence for conservative Stouffer smoothing). Let $R$ be a correlation matrix with no negative entries. Conservative Stouffer smoothing on marginally uniform $p$-values with any Gaussian copula of correlation $R$ yields smoothed $\tilde{p}$-values which are positive regression dependent on the subset of nulls on $\stackrel{-}{𝒮}$.

Appendix 3.1 shows several examples where this smoothing method yields improved power.

5. Results

5.1. Simulations

To benchmark the power gains for smoothing, we run a set of simulations under different graph structures, alternative hypotheses, and target error metrics. In each case, we use Fisher smoothing on descendants. We consider the following directed acyclic graph structures:

• Deep tree. A tree graph with depth 8 and branching factor 2.

• Wide tree. A tree graph with depth 3 and branching factor 20.

• Bipartite graph. A two-layer graph with 100 roots and 100 leaves. Each root is randomly connected to 20 leaves.

• Hourglass graph. A three-layer graph with 30 roots, 10 middle nodes, and 30 leaves. Each (root, middle) and (middle, leaf) edge is added with probability 0.2. The graph is then post-processed to ensure each node is connected to at least one node, with middle nodes having at least one incoming and one outgoing node.

We generate one-sided $p$-values from $z$-scores with the null $z$-scores drawn from a standard normal. For each structure, we consider two scenarios:

• Global alternative. The alternative distribution at each nonnull node is $𝒩(2,1)$. directed acyclic graphs are populated starting at the leaves and null nodes are flipped to nonnull with probability 0.5.

• Incremental alternative. The alternative distribution at each nonnull node is $𝒩(1+0.3\times (D-d),1)$, where $d$ is the depth of the node and $D$ is the maximum depth of the directed acyclic graph. The graph is populated starting at the leaves with nonnull probability 0.5 and internal nodes are intersection hypotheses that are null if and only if all their child nodes are null.

For each simulation, we run 100 independent trials and report empirical estimates of power, familywise error rate, false exceedance rate, and false discovery rate at

$$\alpha =\left(0.01,0.02,0.03,0.04,0.05,0.08,0.1,0.15,0.2,0.25\right).$$

For the false exceedance rate, we fix $\gamma =0.1$ for all experiments. We compare performance with and without Fisher smoothing using the method of Meijer & Goeman (2015) for familywise error rate control, Meijer & Goeman (2015) with Algorithm 3 for false exceedance rate control, and Ramdas et al. (2019a) for false discovery rate control. Both structured testing methods are the current state of the art for testing on directed acyclic graphs, with both showing the highest power to-date relative to other methods targeting the same error rate. We also compare to the structureless method of Benjamini & Hochberg (1995), though this method does not preserve nesting structure. However, performance relative to this baseline illustrates how smoothing turns the graph structure into an advantage rather than just a constraint.

Figure 1 presents empirical estimates of power for each simulation. In each scenario, Fisher smoothing boosts the power of all three methods. Moreover, in all simulations the Ramdas et al. (2019a) method actually performs as well or better than Benjamini & Hochberg (1995). This is particularly promising since Ramdas et al. (2019a) found that the Benjamini & Hochberg (1995) method almost always had higher power and only in very limited scenarios would the structured method outperform. This is completely reversed in the smoothed case, with the Benjamini & Hochberg (1995) method generally having lower power due to being unaware of the structure of the method.

Fig. 1:

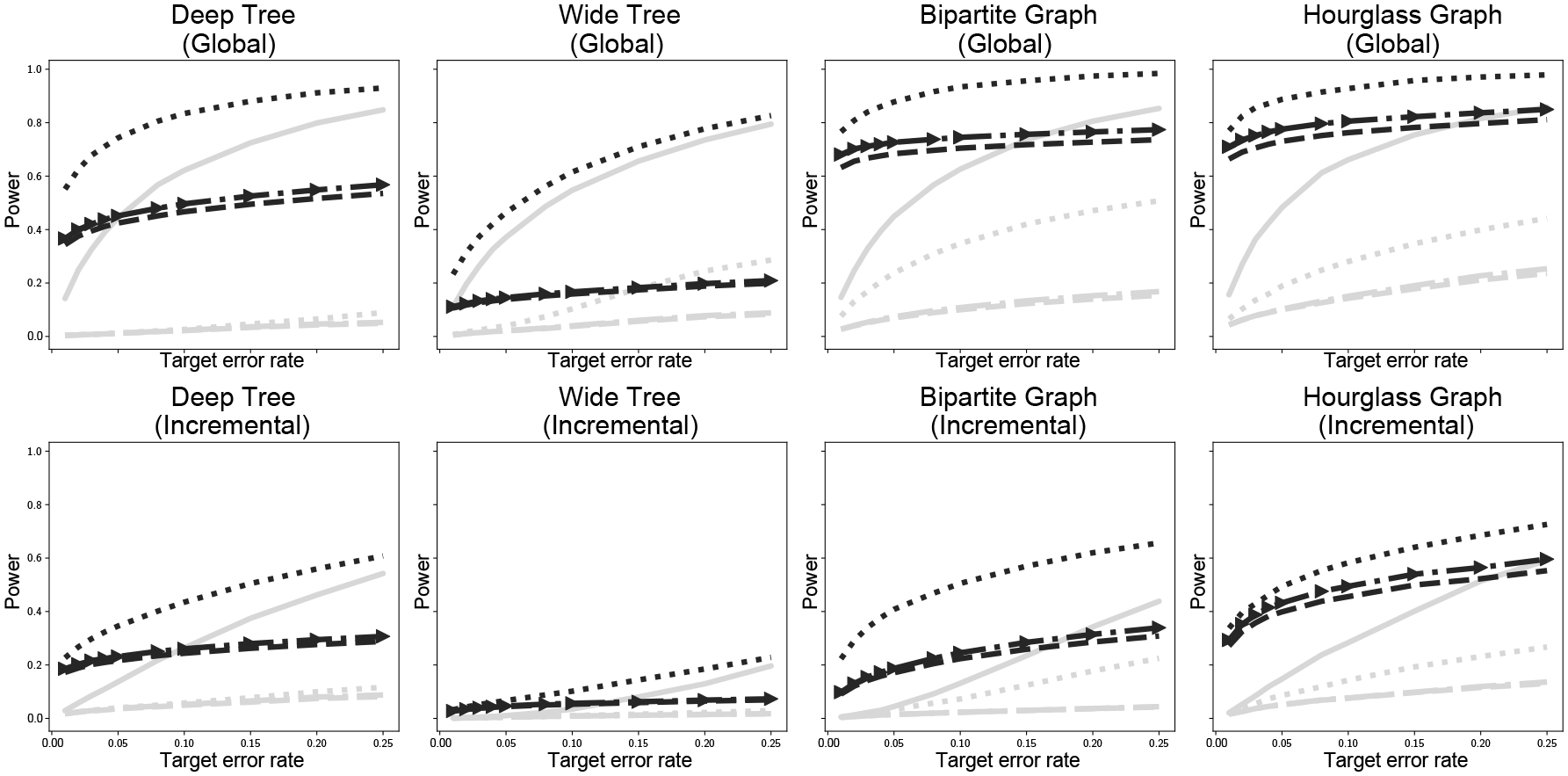
Empirical power in each simulation as a function of target error rate. Gray lines are unsmoothed results, black lines are smoothed results; dashed lines use Meijer & Goeman (2015), dashed lines with arrows use Meijer & Goeman (2015) with Algorithm 3, and dotted lines use Ramdas et al. (2019a); the solid gray line is the structureless method of Benjamini & Hochberg (1995).

Figure 2 confirms that indeed all methods conserve their target error rates empirically. In general, smoothing makes each method less conservative but not to the point of violating the target rate. This is precisely the desired outcome: given a budget for errors, one would prefer to make full use of the budget in order to maximize the number of discoveries.

Fig. 2:

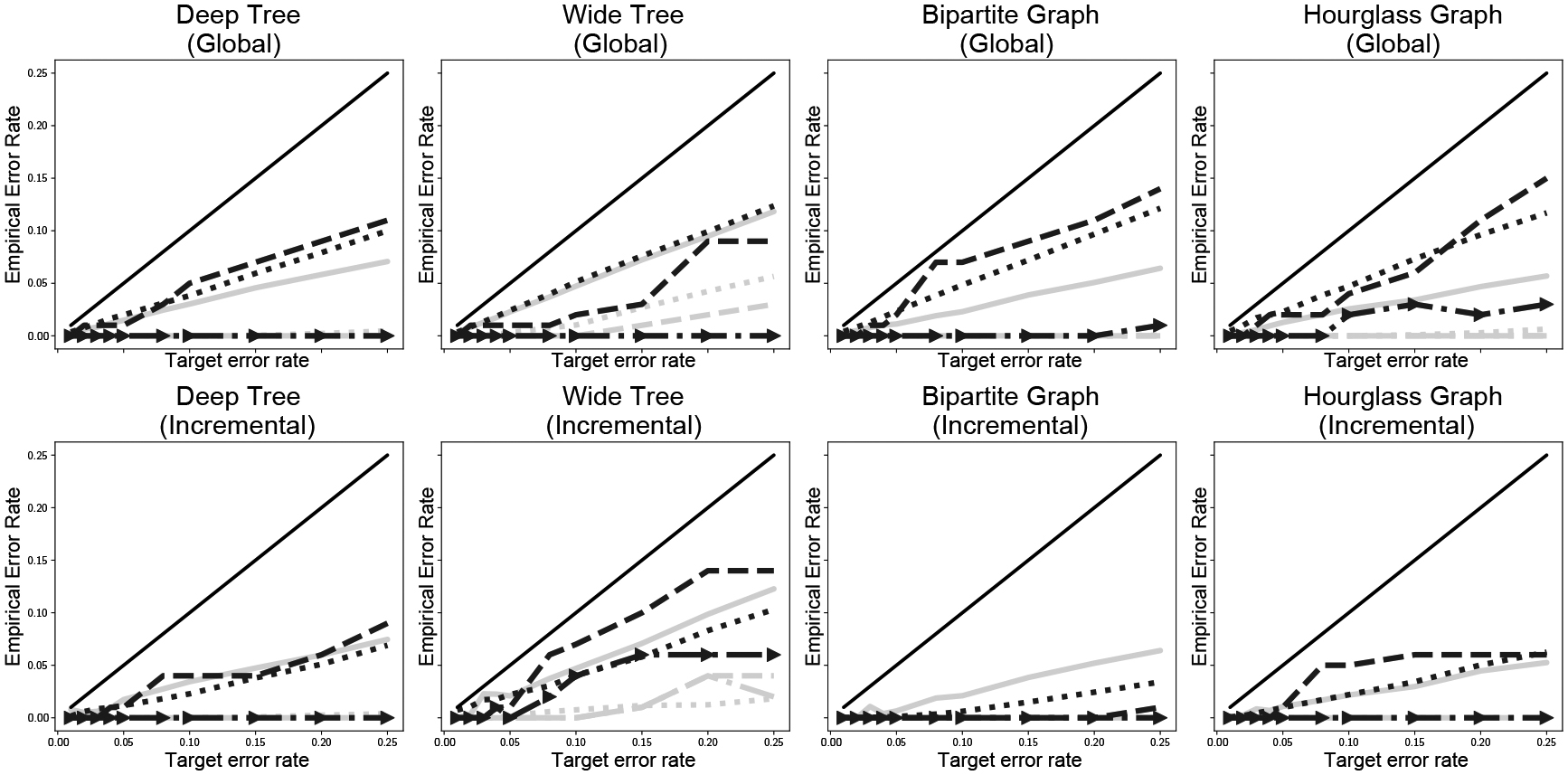
Empirical target error rates in each simulation. Lines match those in Fig. 1; the solid black line is the (0, 1) line (maximum allowable error). To facilitate comparison, each method is plotted using its specific target error metric: dashed lines target familywise error rate, dashed lines with arrows target false exceedance rate, and solid and dotted lines target false discovery rate.

Fisher smoothing is not guaranteed to increase the power of any of these algorithms, though for any given scenario there is always some form of smoothing which will increase power. Smoothing methods can help most when the smoothed values for non-null hypotheses are most heavily influenced by $p$-values from other non-null hypothesis. Appendix 3.2 contains intuition and numerical experiments which may help users select smoothing functions which are appropriate for their data.

5.2. Application to Genetic Interaction Maps

We demonstrate the gains of smoothed testing on a real dataset of genetic interactions in yeast cells (Kuzmin et al., 2018). The data measure the effects of treatments on cell population “fitness”– the population size after a fixed incubation window, relative to the initial population size before treatment. The treatment in each experiment is a gene knockout screen that disables a specified set of genes in the population; experiments in the dataset include gene knockout sets of size 1, 2, and 3. For experiments with more than a single gene knocked out, the goal is to determine whether there is any added interaction between the genes that affects fitness. The outcome of interest is the fitness beyond what is expected from independent effects,

$${ϵ}_{ij}={\delta }_{ij}-\left({\delta }_i{\delta }_j\right)$$

$${\tau }_{ijk}={\delta }_{ijk}-\left({\delta }_i{\delta }_j{\delta }_k\right)-{ϵ}_{ij}{\delta }_k-{ϵ}_{ik}{\delta }_j-{ϵ}_{jk}{\delta }_i,$$

where ${\delta }_i$ is the fitness of the population when knocking out the $i^{\text{th}}$ gene. The pair score ${ϵ}_{ij}$ and triplet score ${\tau }_{ijk}$ capture the added effect on fitness of knocking out the entire set. In words, ${ϵ}_{ij}$ and ${\tau }_{ijk}$ model the interaction between the genes in the target set above what would be expected by chance if there were no unique interaction between all genes in the set. A set of genes with a negative interaction score is known as a synthetic lethal set. See Figure 1 in Kuzmin et al. (2018) for detailed experimental procedures and details on the definition of $\delta ,ϵ$, and $\tau$.

The scientific goal in the yeast dataset is to determine which gene sets have the potential to contribute to synthetic lethality if disabled. Individual genes may not always reflect this. DNA damage repair mechanisms and other cellular machinery may compensate for an individual knocked out gene to lead to minuscule effects on fitness. If that machinery is also disabled via a second knockout, the signal may become clearer. If a knockout of a pair $(i,j)$ leads to an interaction that produces a synthetic lethal result, the implication is that genes $i$ and $j$ both have the potential to contribute to synthetic lethality.

Fig. 3 shows the implied directed acyclic graph encoding the null hypotheses in the yeast dataset. The graph has three levels. Individual gene knockouts form the root nodes, pair knockouts form the middle, and triplet knockouts form the leaves. If any of the leaf nodes is rejected, it implies every constituent pair has the potential to contribute to synthetic lethality.

Fig. 3:

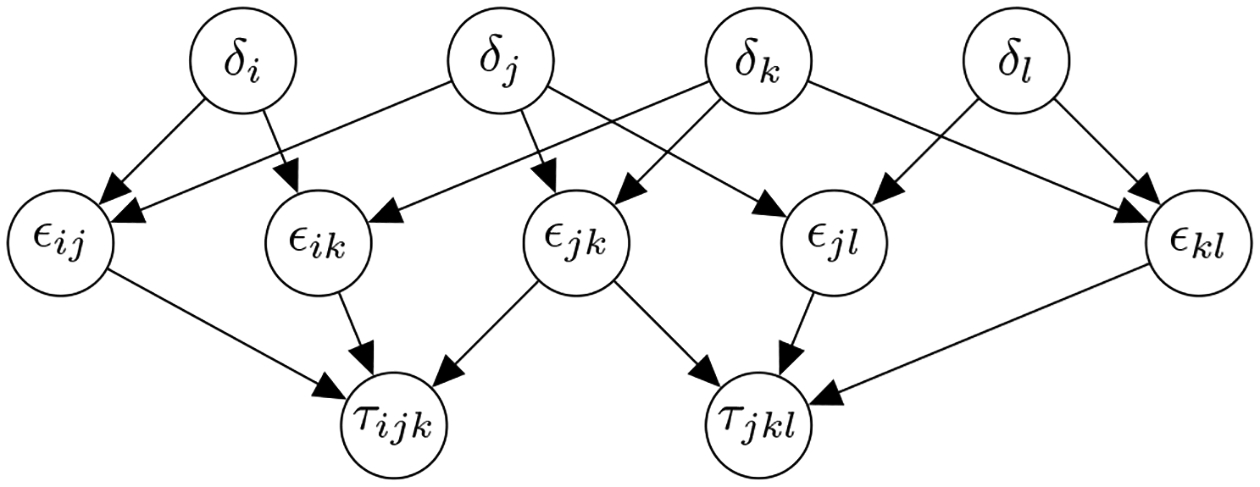
Example directed acyclic graph for the genetic interaction study. Individual gene knockouts $\delta$ s are the top of the graph, pair knockouts $\tau$ are in the middle, and triplet knockouts $ϵ$ are the leaves. Each node corresponds to an experiment conducted independently and has an independent $p$-value. If any set of genes potentially contributes to synthetic lethality, the null hypothesis at that node is rejected; all subsets must implicitly be rejected as well.

The yeast dataset has 338 single-gene experiments, 31092 pair experiments, and 5451 triplet experiments. This leads to a graph with 36881 nodes and 78519 edges. Each experiment is conducted independently across four replicates. A $t$-test is run for each target outcome variable (${\delta }_i,{ϵ}_{ij}$, or ${\tau }_{ijk}$) to compare the mean population size to the expected population size.

We use Fisher smoothing and perform selection with familywise error rate control via Meijer & Goeman (2015) and false discovery rate control via Ramdas et al. (2019a), each at the target error levels,

$$\alpha =\left(0.01,0.02,0.05,0.1,0.15,0.2,0.25,0.3,0.35\right).$$

Figure 4 shows the results and comparison to the same methods on the original test statistics. As in the simulations, the power gains are substantial: between 1.8x and 2.4x more discoveries after smoothing. Further, the smoothed the Ramdas et al. (2019a) method power is slightly higher than Benjamini & Hochberg (1995); without smoothing, the Ramdas et al. (2019a) method would be substantially lower power than Benjamini & Hochberg (1995). Smoothing therefore has the important effect of recovering or even surpassing the power of Benjamini & Hochberg (1995) while preserving the logical nesting structure.

Fig. 4:

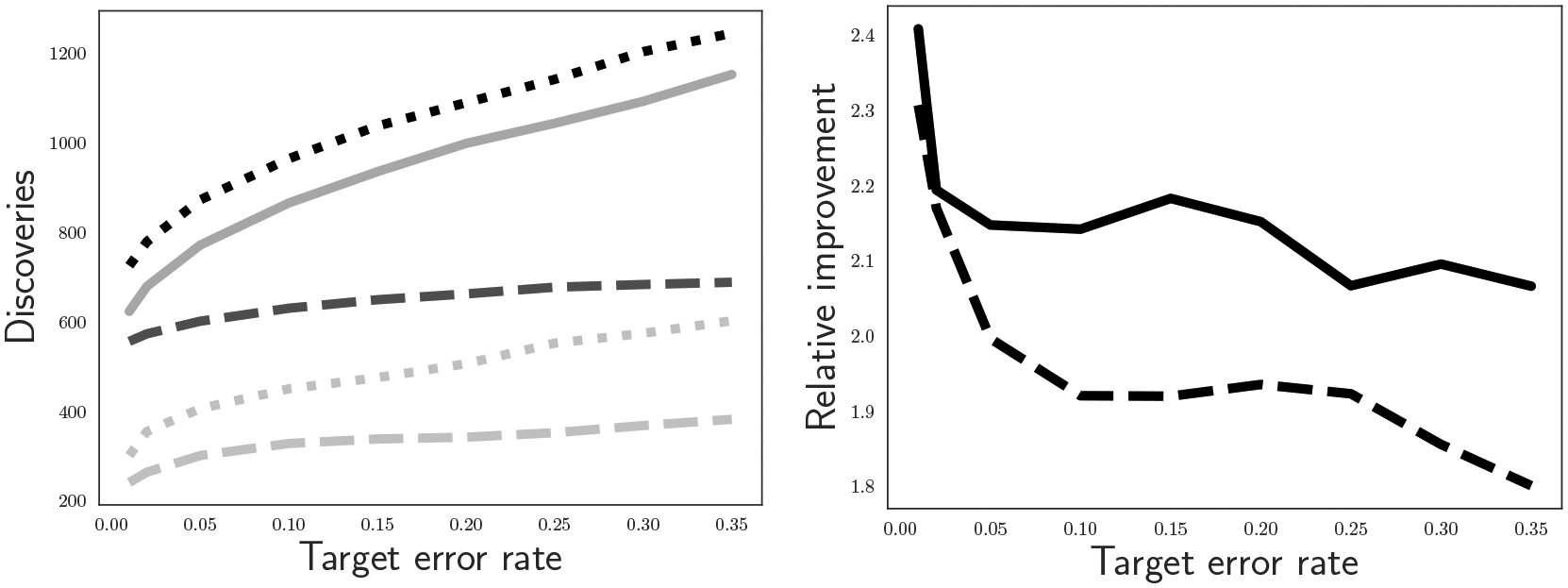
Performance comparison of raw $p$-values versus smoothed $\tilde{p}$-values on a biological dataset. Left: total discoveries reported by each method at varying error rates. Solid gray line: Benjamini & Hochberg (1995); dotted black line: Fisher smoothing with the Ramdas et al. (2019a) method, dashed dark gray line: Fisher smoothing with the method of Meijer & Goeman (2015); light gray lines at bottom are the same two methods without smoothing. Right: relative gain of using smoothed $\tilde{p}$-values over raw $p$-values. Solid black line: relative improvement for the Ramdas et al. (2019a) method; dashed black line: relative improvement for the method of Meijer & Goeman (2015).

6. Discussion

6.1. Reshaping for false discovery rate control under dependence

When targeting control of the false discovery rate, we relied on the Ramdas et al. (2019a) method for selection after smoothing. There are actually two variants of this method, each extending structureless testing methods to the directed acyclic graph testing scenario. We focused on the version which extends Benjamini & Hochberg (1995) and requires positive regression dependence. Another version extends the Benjamini & Yekutieli (2001) procedure to directed acyclic graphs by reshaping the node-level test statistics.

As in the structureless procedure, reshaping controls the false discovery rate regardless of any dependency structure among the statistics, so long as they are marginally super-uniform. This reshaping procedure can be applied directly to the smoothed $\tilde{p}$-values to control the false discovery rate. However, the reshaping procedure raises the bar for rejection, often leading to low power, and will always lead to strictly lower power than the Benjamini & Hochberg (1995) extension. Nevertheless, the reshaping variant could be used to control the false discovery rate when using smoothing functions for which no positive regression dependence guarantee is available. In these cases, false discovery rate control would be feasible if the smoothing functions led to $\tilde{p}$-values that were marginally super-uniform; proving this for a given smoothing function may require some knowledge of the dependency structure.

6.2. More powerful procedures for false exceedance control

In section 4.2, we proposed a greedy algorithm, outlined in Appendix 2.3, by combining the method of Meijer & Goeman (2015) and the generic procedure of Genovese & Wasserman (2006). Since any data-dependent topological ordering suffices, it is ideal to choose one that yields the highest power. Intuitively, we could iteratively add the most “promising” hypothesis, like the one with smallest p-values, which does not break the logical constraint. More generally, we could move beyond greedy algorithms by defining a loss function on each subset in $𝒱\setminus {\widehat{𝒮}}_0$ with cardinality $\left|{\widehat{𝒮}}_0\right|\gamma /(1-\gamma )$ and finding one that minimizes the loss via a combinatorial optimization algorithm. For instance, the loss function can be defined as the sum of p-values.

6.3. Ancestor smoothing functions

We described a general framework for smoothing test statistics on directed acyclic graphs by sharing statistical strength between related nodes. Our current work focused on descendant smoothing functions, which ignore the information contained in ancestor nodes. An alternative class of smoothing functions uses ancestor nodes to smooth the node statistics. These ancestor smoothing functions use prior knowledge about the experiment to adapt their test statistic based on the data in ancestral nodes. Ancestor smoothing functions construct ${\tilde{p}}_v$ by fixing all ancestor $p$-values of $p_v$ and fitting a model to the ancestor values. The model requires prior knowledge of the alternative hypothesis, such as knowing that the alternative signal attenuates with the depth of the graph. We expect this to be the case for many real-world scenarios where shallower nodes represent more complex mechanisms or stronger interventions.

Ancestor functions have the appeal of potentially incorporating prior knowledge to gain higher power, but come with substantial trade-offs. First, they typically do not have a closed form null distribution. This makes them computationally expensive, as they require many Monte Carlo simulations in which for every trial the adaptive procedure must be re-run. They are also much more difficult to analyze theoretically, since the the joint distribution of ancestor-smoothed $p$-values involves contributions from variables associated with false hypotheses. Pragmatically, we have not found any practical examples where the prior knowledge is so strong that it leads to meaningful increases in performance over descendant smoothing. We leave investigation of ancestor smoothing and hybrid ancestor-descendant smoothing functions to future work.