PSI-BLAST searches using hidden Markov models of structural repeats: prediction of an unusual sliding DNA clamp and of β-propellers in UV-damaged DNA-binding protein

Abstract

We have designed hidden Markov models (HMMs) of structurally conserved repeats that, based on pairwise comparisons, are unconserved at the sequence level. To model secondary structure features these HMMs assign higher probabilities of transition to insert or delete states within sequence regions predicted to form loops. HMMs were optimized using a sampling procedure based on the degree of statistical uncertainty associated with parameter estimates. A PSI-BLAST search initialized using a checkpoint-recovered profile derived from simulated sequences emitted by such a HMM can reveal distant structural relationships with, in certain instances, substantially greater sensitivity than a normal PSI-BLAST search. This is illustrated using two examples involving DNA- and RNA-associated proteins with structurally conserved repeats. In the first example a putative sliding DNA clamp protein was detected in the thermophilic bacterium Thermotoga maritima. This protein appears to have arisen by way of a duplicated β-clamp gene that then acquired features of a PCNA-like clamp, perhaps to perform a PCNA-related function in association with one or more of the many archaeal-like proteins present in this organism. In the second example, β-propeller domains were predicted in the large subunit of UV-damaged DNA-binding protein and in related proteins, including the large subunit of cleavage-polyadenylation specificity factor, the yeast Rse1p and human SAP130 pre-mRNA splicing factors and the fission yeast Rik1p gene silencing protein.

INTRODUCTION

A major goal in computational biology is to predict a protein’s structure and function from its sequence. To accomplish this, various approaches have been taken, including structural threading methods, ab initio structure prediction, homology modeling and multiple alignment and profile search methods (for a review see 1). In the case of multiple alignment and search methods, which is the focus of this analysis, two concerns need to be considered: the accuracy of the alignment and the sensitivity and selectivity of the search. Here we address these concerns by combining a multiple alignment procedure based on hidden Markov models (HMMs) (reviewed in 2) that incorporates rather specific structural features with a PSI-BLAST search (3) initialized with a profile corresponding to the HMM alignment. One reason for taking this hybrid approach is that it provides a well-established measure of significance based on the PSI-BLAST statistics. Of course, converting the HMM alignment into a PSI-BLAST profile discards the specific structural features of the HMM, which are useful for constructing the alignment. This is not necessarily a drawback, however, because relaxing these structural constraints during a search may avoid over-training, where the model incorporates features of the training sequences that are absent from distant relatives. Indeed, distantly related proteins often diverge from typical family members in unexpected ways, so that searching with a less constrained PSI-BLAST profile could be advantageous in some instances.

During construction of the HMM we use two approaches to incorporating structural information. First, we take advantage of structural symmetry by focusing on protein families characterized by the presence of structurally conserved repeats that are unconserved at the sequence level based on pairwise comparisons. Modeling of structural repeats, as opposed to modeling the full-length sequences, increases the effective size of the sequence training set, leading to improved estimates for the residue emission probabilities. Second, we rely on secondary structure information when assigning insert or delete transition probabilities for the HMM in order to better align the sequences in a manner consistent with the overall structural features of the protein family.

Although structurally conserved repeats may be only very weakly conserved at the sequence level, these can often be detected and aligned using multiple alignment methods based on Gibbs sampling (4–7). Gibbs sampling is a Monte Carlo procedure that, starting from an arbitrary alignment, iteratively realigns individual sequences against an evolving alignment model or HMM with probability proportional to the quality of the realignment. This process is analogous to a thermodynamic system coming to equilibrium. Just as a chemical reaction comes to completion faster at room temperature than near absolute zero, probabilistic sampling, by facilitating maneuvering around locally optimal traps in alignment space, converges on near optimum alignments faster than steepest descent methods. Early Gibbs sampling alignment procedures were block based (4,6) but have recently been modified to allow for limited gapping (8). Here we further generalize these methods to allow sampling of repeats using a HMM; this method incorporates a simplified sampling protocol based on the degree of statistical uncertainty associated with parameter estimates.

We illustrate our approach using two examples relating to DNA replication and repair proteins. The first example (sliding DNA clamps) illustrates how a HMM for a set of proteins of known structure can be used to predict the structure of a distantly related protein, which in this case has also led to interesting evolutionary insights. The second example (sequences related to the large subunit of UV-damaged DNA-binding protein) illustrates how a HMM for a set of proteins of unknown structure can be used to detect distantly related proteins of known structure.

Sliding DNA clamps are ring-shaped proteins that allow DNA polymerase to achieve high processivity during chromosome replication by tethering the polymerase catalytic subunit to DNA. From the crystal structures of these proteins it appears that they can encircle duplex DNA without steric hindrance, a property that presumably allows them to non-specifically attach to and move rapidly along DNA without dissociating (for reviews see 9–12). The structures of three distinct families of sliding clamps are available and include the Escherichia coli β-clamp (13), the human and yeast proliferating cell nuclear antigen (PCNA) (14,15) and the bacteriophage RB69 and T4 sliding clamp proteins (16,17). All of these structures share a 12-fold symmetry around the ring consisting of a simple β-α-β-β-β structural repeat (13), though there is structural divergence in some of the repeats. Bacterial β-clamps contain six β-α-β-β-β repeats per subunit with two subunits per ring while the eukaryotic and bacteriophage clamps contain four repeats per subunit with three subunits per ring. Pairs of these repeats form a domain, which has been termed the ‘processivity fold’ (18); thus the ring of the sliding clamp contains six domains and therefore is often described as having 6-fold symmetry (19). A structural representative of a fourth family of processivity fold proteins, namely the herpes simplex virus UL42 protein, is also available (18). UL42 does not form a ring-shaped clamp, however, but rather functions as a monomer and interacts with DNA quite differently than do sliding clamps; it has been suggested that UL42 resembles a primitive ancestor of sliding clamps (see 18 and references therein). Despite their structural similarity, proteins in each of these four families lack significant pairwise sequence similarity to proteins in the other families, suggesting that additional, unrelated processivity fold proteins remain to be found. Sensitive sequence analysis methods offer an opportunity to identify additional sliding clamps. For example, the fission yeast DNA repair proteins Rad1p, Rad9p and Hus1p were recently predicted to be distant relatives of PCNA using PSI-BLAST and similar procedures (20–22).

Another protein believed to be involved in DNA repair is UV-damaged DNA-binding (UV-DDB) protein, which is associated with the hereditary disease xeroderma pigmentosum group E (XP-E). Xeroderma pigmentosum (XP) is characterized by extreme sensitivity to UV light and a high disposition to skin cancer and XP cells are defective in nucleotide excision repair (for reviews see 23,24). In humans UV-DDB purifies as a heterodimer of 127 and 48 kDa subunits (25) and, when injected into XP-E cells that normally lack this protein, can correct the DNA repair defect (26). However, the exact function of UV-DDB remains unknown. Sequences related to the UV-DDB 127 kDa subunit (UV-DDB-127) fall into several subfamilies, the characterized proteins of which all appear to be components of DNA- or RNA-associated complexes. Components of complexes that appear to be DNA associated include the fission yeast Rik1p protein, which plays a role in gene silencing at certain centromeric regions and in chromosome segregation (27), and UV-DDB-127 itself. Components of RNA-associated complexes include the 160 kDa subunit of cleavage and polyadenylation specificity factor, which is required for 3′-end processing of mRNA precursors, and certain pre-mRNA splicing factors. These pre-mRNA splicing factors are required for pre-spliceosome assembly and include the yeast Rse1p protein (28) and the mammalian SAP 130 protein (29), which is associated with interchromatin granule clusters (30).

Here we use PSI-BLAST searches based on HMMs of subtly conserved repeats to detect a putative sliding DNA clamp that shares sequence features with both archaeal PCNAs and bacterial β-clamps and to predict β-propeller domains in proteins belonging to the UV-DDB-127 family. By capturing the inherent structural symmetry present in these proteins this approach was able to recognize sequence similarities that are very difficult to detect by standard methods.

MATERIALS AND METHODS

Our strategy for modeling structurally conserved repeats combines features of several standard computational methods with a new procedure for sampling gapped alignments that assigns HMM transition probabilities based on secondary structure predictions. The overall strategy consists of the following steps. First, a HMM (2) corresponding to subtle repeats characteristic of a protein family of interest is constructed. We require that the modeled repeats be conserved at the structural level but, in general, lack significant pairwise similarity to other repeats within the same sequence. During construction of the HMM, the optimum alignment and number of the repeats are determined via a Gibbs sampling procedure with two stages of refinement. In the first stage, repeats are detected and aligned using an ungapped alignment procedure similar to that previously described (5). In the second stage, a gapped alignment of the repeats is constructed based on a HMM. This gapped sampling routine is conceptually very simple and works by first sampling residue emission probability parameters for the HMM from the posterior Dirichlet distribution and then optimally aligning a given sequence against this sampled HMM using dynamic programming. During alignment the transition probabilities for the HMM are based on secondary structure propensities such that transitions to insert or delete states within sequence regions predicted to form loops are assigned higher probabilities. In a second step, we emit a large number of simulated sequences having a characteristic number of repeats using the optimum HMM obtained in the first step. In a third step, these simulated sequences are used to construct a corresponding PSI-BLAST checkpoint file (3). (As described in the PSI-BLAST documentation, a checkpoint file stores a profile derived during a previous search for use as the starting point for a subsequent search.) Finally, a protein database is searched using PSI-BLAST initialized with this checkpoint file. The significance of matching database sequences is assessed using the PSI-BLAST statistics, although some care must be taken to eliminate potential false positives due to subject sequences with detectable internal repeats (as explained below). The programs implementing these procedures and instructions for their use are available via anonymous ftp at ftp.cshl.org in the subdirectory pub/science/neuwald. These procedures are described in more detail in the following sections.

Construction of HMMs for structural repeats

HMMs were constructed as follows. An initial alignment of repeats was obtained using ungapped, block-based multiple alignment procedures (5,6) based on Gibbs sampling (4). The initial alignment was further refined using gapped procedures that are an extension of an earlier ungapped Gibbs sampling strategy (6) and that represents an alternative to a previously described ‘steepest descent’ approach (8). For these refinement procedures we decided to deviate from a rigorous Gibbs sampling approach for several reasons. First, we found that the large number of possible gapped alignments compared to ungapped alignments makes straightforward Gibbs sampling computationally expensive. Second, the number of unlikely alignments is so great that their total probabilities often appear to be substantially greater than the total probabilities associated with optimal and near optimal alignments. As a result, the sampler tends to fall into an ‘entropic hole’ of improbable alignments. Third, although in theory this entropic effect might be overcome by sampling at lower temperatures, finding the right temperature is difficult and, in any case, a gapped alignment space appears to contain many locally optimal traps, thereby substantially lengthening convergence. Finally, we found that an alternative, less rigorous sampling approach appears to work well in practice. This approach, which will be generalized for a variety of multiple alignment problems elsewhere (A.F.Neuwald and A.Poleksic, unpublished results), is outlined here specifically for alignment of relatively short repeats.

Just as painting a picture typically requires an initial crude sketch prior to filling in of the details, we find that alignment of distantly related sequences typically requires construction of an initial ungapped, block-based alignment prior to the introduction of insertions and deletions. This is because delineation of the gross characteristics of the alignment during the ungapped stage helps avoid becoming trapped in suboptimal alignments during the gapped stage. Here we push this strategy one step further by applying two gapped refinement steps. The first step applies fixed affine gap penalties, while the second step applies position-specific penalties based on secondary structure propensities, as described below. These penalties are formulated as transition probabilities for a HMM. Because the ungapped sampling procedure results in an initial alignment that is more or less correct, the subsequent gapped-based refinement procedures require only limited sampling flexibility. After the sampler converges, however, it is often necessary to lower the sampling ‘temperature’ (in a process called simulated annealing) in order to find an optimal alignment. In a thermodynamic context, the effect of simulated annealing is to increase the population of the lowest energy states of the Boltzmann distribution; for multiple alignments this corresponds to increasing the likelihood of sampling the more probable alignments.

Both of the refinement steps use a sampling strategy based on the inherent uncertainty in the parameter estimates of the HMM. This is illustrated through the following simple example. Consider an alignment of four sequences with only two types of residues, A and B. Assume that at a given position in the alignment four As are observed. The frequency of A at this position (which, for the HMM, corresponds to the match emission probability for A) can be estimated from this data in various ways. A maximum likelihood approach would assign a probability of 1 to A and 0 to B. This is clearly a poor assumption, however, as four observations are too few to jump to the conclusion that B never occurs at this position. The usual way around this problem is to use a Bayesian approach, which adds a certain number of pseudocounts for each residue type along with the observed counts and then takes the most probable parameter value from the posterior distribution, a procedure called maximum a posteriori (MAP) estimation. Thus, for this simple example, a Bayesian approach may add one pseudocount each for A and B to obtain a MAP estimate of 1/(4 + 1 + 1) ≈ 0.167 for the probability of the HMM emitting a B.

Rather than taking the MAP estimate, however, our procedure samples parameter values from the posterior (Dirichlet) distribution before each realignment step. [Pseudocounts corresponding to prior probabilities are obtained using the method of Henikoff and Henikoff (31); although this method does not conform to a strict Bayesian formulation, it works well in practice.] This sampling procedure can easily be extended to sample transition probabilities, but currently only residue emission probabilities are sampled. [A similar parameter sampling routine applied to DNA sequences was recently described (32).] Using the sampled HMM parameters, an optimum gapped alignment against the sequence being realigned is found by dynamic programming, which for a HMM corresponds to the Viterbi algorithm (2). After convergence, simulated annealing is applied to find a (hopefully global) optimum. During simulated annealing, and prior to sampling the HMM parameters from the posterior Dirichlet distribution, the temperature is lowered by raising the sum of the observed counts and pseudocounts to a power greater than one. This has the effect of increasing the total number of counts, which causes the Dirichlet distribution to tighten up and favors sampling nearer the most probable value. At zero degrees the sampler uses MAP parameter estimates and is therefore equivalent to a ‘steepest descent’ approach. During sampling, aligned sequences are weighted for redundancy (33).

Sampling repeats

To concurrently determine the optimum parameters of the HMM and the optimum number of corresponding gapped repeats within a set of sequences, we generalized an earlier sampling algorithm for ungapped repeats (5). This algorithm iteratively samples candidate sequence regions in and out of the alignment proportional to the likelihood that a given sequence region contains a repeat. Hence, it is important to be able to compute this likelihood for a specific sequence region. This can be done by comparing the overall MAP estimate for an alignment that includes the sequence in question with the MAP estimate for an alignment that excludes that sequence. The formula for MAP estimation for ungapped multiple alignments has been given previously (7) and it would be helpful to have an analogous MAP formula for our HMMs.

The full Bayesian approach for doing this would be to find the posterior probability of an alignment given the input sequences by integrating over all the possible parameters of the HMM. Unfortunately, this is a difficult, unsolved computational problem. As an alternative, we determine the likelihood of an alignment given the parameters of the HMM, which are estimated from the alignment itself. Using this approach, possible alignments can be explored (via sampling) to find an alignment with maximum probability given the corresponding HMM. In this case the alignment likelihood (or, more specifically, the logarithm of the likelihood) is obtained by computing the log-likelihood of each sequence being emitted by the HMM and then summing all of these. In order to speed up this calculation, an estimate is obtained by summing the log-likelihoods for the previously sampled alignment tracebacks rather than by integrating over all possible paths through the HMM. This heuristic approach is similar to computing the sum of the pairwise scores for assessing the quality of an alignment, only it sums the sequence-to-HMM log-likelihood scores instead. For each sequence a likelihood ratio is obtained by dividing the HMM emission probability (which is obtained from these log-likelihoods) by its emission probability under the null HMM (which consists of a single insert state). These likelihood ratios are used to probabilistically sample sequence regions in and out of the alignment. The probability of an insert-to-insert transition for the null HMM is set so that it emits sequences with an average length equal to that observed for the aligned sequences. Residue emission probabilities for the null HMM are based on the overall residue frequencies in the sequences being aligned.

HMM transition probabilities based on secondary structure predictions

Transition probabilities between insertion, match and deletion states of the HMM are based on secondary structure propensity, which is computed using the DSC method (34). In addition, observed secondary structure states for specific sequences whose structures are known can be used to update the DSC-derived probabilities using Bayes’ theorem. We chose this approach because the alternative approach of estimating transition probabilities based on observed numbers of insertions and deletions at each position in an alignment is typically unreliable due to the sparseness of data. Basing transition probabilities on secondary structure predictions indirectly provides an estimate of the likelihood of insertions and deletions because gaps are inherently more likely in loops than in helices or strands. Our procedure starts with pairs of transition probabilities (one probability for loops and another for helices and strands) for each of four transitions: match-to-insert, match-to-delete, insert-to-insert and delete-to-delete. The probabilities associated with the other transitions (match-to-match, insert-to-match and delete-to-match) are derived from these based on the constraint that the transitions out of any state must sum to unity.

The probability of a specific transition at a given position in the HMM is computed from the secondary structure prediction at that position via linear interpolation between the input transition probability pair. For example, assume that the secondary structure prediction at a specific position in the alignment is 0.2 for a helix or strand and 0.8 for a loop and that the input probability pair for a match-to-delete transition is 0.4 for a helix or strand and 0.6 for a loop. Then the computed match-to-delete transition probability at this position is (0.2 × 0.4) + (0.8 × 0.6) = 0.56. Thus, the higher the loop probability, the higher the probability of a deletion. Transition probabilities either to or from insert states are based on the average of the secondary structure predictions on either side of the insertion. For computational convenience, transition probabilities are specified as the logarithms of the probabilities.

The parameter values used for the starting transition probability pairs were determined empirically, based on alignments of proteins of known structure. These settings result in either an insertion or a deletion in about half of randomly simulated sequences with likelihood scores comparable to that of actual family members.

PSI-BLAST searches based on simulated checkpoint files

After constructing a HMM of a repeat unit from known family members, the protein database is searched for structurally related proteins using PSI-BLAST (3) with the checkpoint recovery option and with a checkpoint file derived from simulated sequences emitted by the HMM. (A checkpoint file stores a profile derived during a previous search for use as the starting point for a subsequent search.) We used PSI-BLAST in this way rather than searching with the HMM itself because a PSI-BLAST search is fast and the statistics are thoroughly tested. Nevertheless, preliminary studies indicate that assessing statistical significance by fitting the HMM scores to an extreme value distribution (35) may work as well or better (at least in some instances) and we are currently exploring this alternative approach. By starting the search with a checkpoint file based on the HMM, however, the PSI-BLAST procedure should still benefit from the enhanced quality of the HMM alignment.

Simulated sequences were emitted without insertions or deletions and with a fixed spacing between adjacent repeats; this spacing was set equal to the average spacing observed for repeats in the training set. Although it is straightforward to emit simulated sequences from a HMM with insertions and deletions characteristic of a particular protein family, this is unnecessary in this case because PSI-BLAST profiles use fixed, family-independent gap penalties. More importantly, generating simulated sequences that lack insertions and deletions makes it easier for the PSI-BLAST algorithm to set the checkpoint file ‘residue emission’ parameters closer to those of the HMM. For the examples described here, 1000 simulated sequences were used. The number of repeats in the simulated sequences was chosen to reflect the characteristic number found for that protein family. If desired, the training sequences used to construct the HMM can be included, along with the simulated sequences, in the initial PSI-BLAST search to create the checkpoint file. For each iteration of PSI-BLAST during this initial search, an E value of 0.05 was used as the cut-off for inclusion of detected sequences in the profile. A consensus sequence for the protein family is used as the query. The degree of similarity between sequences is often too weak for the standard BLAST heuristic to detect otherwise significant relationships. Therefore both the simulated searches and subsequent database searches used a word threshold score of 7 rather than the default value of 11. Note that from run to run there can be significant variability in the E value for a specific matching sequence due to the stochastic nature both of the HMM optimization procedure and of the simulated sequences used for the checkpoint. The variability in the simulated sequences (which is probably more significant than that associated with HMM optimization) can easily be eliminated by creating a PSI-BLAST profile directly from the HMM within the PSI-BLAST code itself, but this has not yet been implemented.

Statistical significance

The statistical significance of database hits is obtained directly from PSI-BLAST. It should be stressed, however, that the occurrence of repeats within a sequence or profile can lead to misleading results unless some care is taken in the statistical analysis (5). In particular, weak similarity between repeats within a database sequence and repeats within a profile will be amplified proportional to the level of similarity that the internal repeats share with each other. As a result, otherwise non-significant similarity between the database sequence and the profile can be amplified to a level that appears to be significant and thereby lead to false positives. (This is a potential problem for profile searches in general and not just for the searches described here.) As a safeguard against this, sequences with detectable internal repeats were eliminated from consideration during a search. More specifically, sequences were eliminated if any matching regions had detectable pairwise similarity with other matching regions in the same sequence (E value < 0.01 for the single sequence using the ungapped BLAST algorithm; 36). For similar reasons, care was taken to eliminate potential false positives due to coiled-coils (37) and compositional biased regions (38). Coiled-coil regions were detected using both the method of Lupas (39) and BLAST searches against either a single sequence consisting of tandem copies of a coiled-coil heptad consensus repeat (‘LEEELEE’) or known coiled-coil proteins.

RESULTS AND DISCUSSION

Testing our approach

Detection of distant relationships between distinct classes of known β-propeller domains. As a check of the ability of our method to detect distant structural relationships we applied our approach to nitrite reductases, a class of β-propeller domain proteins (see for example 40). We chose this protein family because it is structurally related to WD40 repeat proteins, which we predict below to share structural features with the UV-DDB-127 family. A HMM of nitrite reductase β-propeller repeats was used in a PSI-BLAST simulated checkpoint search of the NCBI non-redundant protein database. Among the sequences detected (E value < 0.01 and lacking pairwise significant internal repeats or problematical regions) were 10 families of WD40 repeat proteins. The E values obtained for the detected sequences ranged from 0.01 to 0.0000002. No other such proteins were detected with E values < 0.01 except, of course, for the nitrite reductases themselves. PSI-BLAST searches were used to confirm the presence of WD40 repeats in matching regions of those proteins not previously reported to harbor WD40 repeats. Thus, in this analysis our approach detects known structural relationships between nitrite reductases and WD40 proteins without picking up false positives.

Example 1: sliding DNA clamps

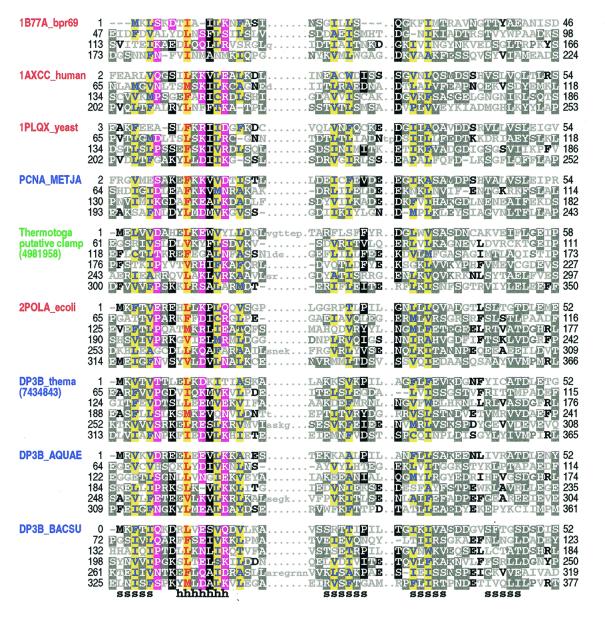
Alignment of sliding DNA clamp repeats. Application of our sampling procedure to the construction of a HMM for sliding DNA clamps resulted in a corresponding alignment of processivity fold β-α-β-β-β repeats (Fig. 1) that is consistent with what is known about the structures of these proteins (Fig. 2). The first strand and helix of the repeat corresponds to the most conserved region in the alignment and, therefore, these appear to serve important structural and/or functional roles. The second and third strands are less conserved, while the fourth strand is poorly conserved and, as a result, was misaligned for some repeats in several sliding clamps of known structure. In general, the most conserved positions correspond mainly to hydrophobic residues constituting the core of the repeat, but also include several surface residues that may perform non-structural roles (Fig. 2a). Within their respective families both the PCNA-like clamps and the bacterial β-clamps are relatively highly conserved along their entire lengths and across diverse taxonomic groups, suggesting that many additional functional constraints, beyond those needed to maintain the processivity fold itself, are acting on these distinct clamp families. As reported in the next section, however, weakly conserved features of both families appear to be present within an unusual putative sliding DNA clamp that nonetheless lacks detectable pairwise similarity to either family.

Figure 1.

Representative alignment of known and putative processivity fold proteins. Names of proteins of known structure are shown in red, of previously predicted clamp proteins in blue and of a putative clamp protein from T.maritima in green (see text). Proteins of known structure are designated by their pdb identifiers; other sequences are designated by their SwissProt identifiers or gi numbers. Abbreviations used for organism names are: bpr69, bacteriophage R69; METJA, Methanococcus jannaschii; ecoli, Escherichia coli; thema, Thermotoga maritima; AQUAE, Aquifex aeolicus; BACSU, Bacillus subtilis. The transition probability pairs (expressed in 200th nats) used to obtain the HMM parameters from secondary structure propensities are: match-to-insert, 350–1700; insert-to-insert, 20–150; match-to-delete, 400–500; delete-to-delete, 40–700 (see Materials and Methods). The first repeat in 1B77A_bpr69, which was not found by the sampler, was determined through optimum alignment against a HMM of four repeats. For each aligned column, elevated residues (i.e. with binomial tail probabilities <0.01) and related, marginally conserved residues (with tail probabilities <0.05) are indicated using the following automated hierarchical coloring scheme (see 8). Columns with ≥1.25 bits of information and hydrophobic, red on yellow highlight. Columns with 0.75–1.25 bits of information: hydrophobic, blue on yellow highlight; non-hydrophobic, magenta highlight. Other columns: ≥70% hydrophobic, yellow highlight; >66% conserved, black highlight; 50–66% conserved, dark gray highlight; 33–50% conserved, black; <33% conserved, dark gray; unconserved, light gray. Note that this coloring scheme is based on the full alignment of about 475 repeats. Consensus structural assignments based on known structures are shown below the alignment (h, helix; s, strand).

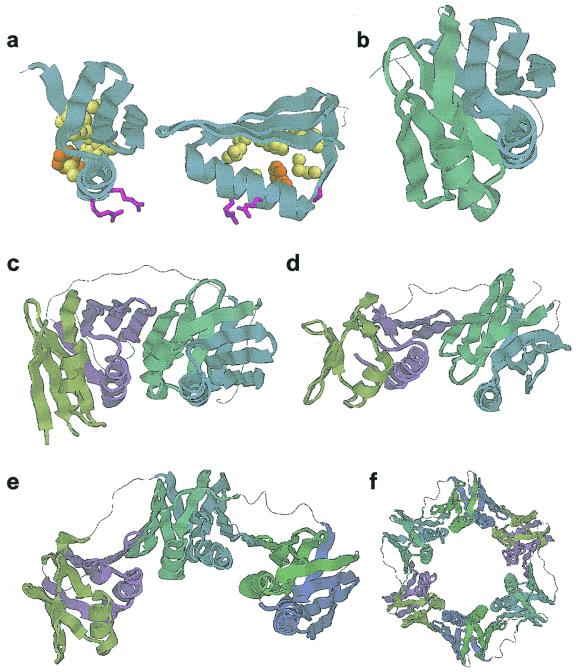
Figure 2.

Processivity fold structural repeats. (a) A single structural repeat. The unit shown corresponds to the third repeat (residues 134–186) of human PCNA (pdb 1AXC). Conserved residues involved in internal packing are shown as spheres and conserved surface residues as sticks. Side chain colors correspond to the alignment in Figure 1. (b) Arrangement of the processivity fold domain (repeats 3 and 4 of 1AXC). Adjacent repeats are related to each other through a 180° rotation around the y-axis. (c) The four repeat subunit of PCNA. (d) The four repeat subunit of the clamp from bacteriophage RB69. (e) The six repeat subunit of the E.coli β-clamp (pdb 2POL). (f) The two subunit E.coli β-clamp ring.

Database searches. We performed a PSI-BLAST simulated checkpoint search based on a HMM that was trained on sequences from three sliding clamp families with known structures: PCNAs, bacterial β-clamps and bacteriophage clamps. We chose to model simulated sliding clamp proteins as having six β-α-β-β-β repeats, in order to facilitate full alignment against either four or six repeat subunits. This search detected an uncharacterized protein from Thermotoga maritima (E value ≈ 0.0003) which lacks pairwise similarity to any other sequence. Thermotoga maritima is a thermophilic bacterium whose genome consists of 24% archaeal-like genes, which may have been acquired through lateral gene transfer, and 76% typical eubacterial genes (41). In addition to the putative clamp subunit, this bacterium also has a typical β-clamp; both of these proteins harbor six repeats (Fig. 1). Moreover, both the length of the putative clamp subunit (350 amino acids) and the spacing between its adjacent repeats are similar to that of known β-clamps. Thus, it seems that duplication of the Thermotoga β-clamp gene may have generated the putative clamp.

To further explore the possibility of gene duplication and divergence, we performed another PSI-BLAST simulated checkpoint search based on a HMM trained only on the six repeats in the Thermotoga putative clamp protein. Interestingly, sequences detected below the default PSI-BLAST E value cut-off of 0.001 (several of which were highly significant) (Fig. 3) included β-clamp proteins from two thermophilic bacteria (Aquifex aeolicus and T.maritima itself) and three PCNA-like clamps from various thermophilic archaeal organisms (Methanococcus jannaschii, Thermococcus fumicolans and Aeropyrum pernix). A fourth PCNA-like clamp from a thermophilic archaeal organism (Pyrococcus horikoshii) was the highest scoring hit (E value ≈ 0.002) above the cut-off. Similarly, we performed a PSI-BLAST simulated checkpoint search based on a HMM trained using the bacterial β-clamps with the Thermotoga β-clamp as the query. This search detected the putative Thermotoga clamp protein at a high level of significance (E value ≈ 6 × 10^–7). A similar simulated checkpoint search that substitutes the Aquifex for the Thermotoga β-clamp detects the putative Thermotoga clamp protein at an even higher level of significance (E value ≈ 1 × 10^–8). (All of these searches were performed against the NCBI non-redundant database.) Taken together, these findings suggest that the putative Thermotoga clamp arose via duplication of the β-clamp and then diverged, taking on some of the structural and functional characteristics of the thermophilic archaeal PCNA clamps. This may have occurred in order to allow this protein to perform the role of a PCNA-like sliding clamp needed for function of one or more of the archaeal-like proteins present in this organism. What this function might be is not necessarily limited to DNA replication, as PCNA performs other roles as well (42).

Figure 3.

Sequences detected in a PSI-BLAST simulated checkpoint search based on a HMM trained using the six repeats of the Thermotoga putative clamp protein. The transition probability pairs used to obtain the HMM parameters from secondary structure propensities are as for Figure 1. The NCBI non-redundant database was searched. Sequences with pairwise significant internal repeats, coiled-coil regions and compositionally biased regions were eliminated from the search and are not shown (see Materials and Methods).

Though we failed to detect known viral processivity factors in our simulated checkpoint search of the entire protein database, a separate search of only these viral processivity factors tested the specific hypothesis that these proteins possess the processivity fold. This search yielded the cytomegalovirus DNA polymerase accessory protein ICP36/UL44 (43) and related proteins, including the murine cytomegalovirus protein pp50 (44) (E values ≈ 0.001–0.0001). This suggests that these proteins are structurally related to sliding DNA clamps, even though the relationship is admittedly quite weak. The greater difficulty in detecting these viral proteins may be due to the high rate of sequence divergence for rapidly evolving phage and viral genomes and to unusual structural and sequence constraints. For instance, the herpes simplex virus UL42 protein behaves as a monomer in solution and forms a heterodimer with HSV polymerase and, therefore, appears not to form a clamp. Furthermore, as for the bacteriophage T4 gp45 sliding clamp (45), association of UL42 with polymerase or DNA occurs in the absence of clamp loaders or ATP hydrolysis (for references see 18). In contrast, an active process is required for removing (and loading) PCNA and β-clamps (46) due to their greater stability in solution and on DNA. Moreover, the gp45 clamp has been recruited as a transcriptional activator (47,48) and interacts with the gp55 late σ factor and RNA polymerase (49). For these reasons phage and viral proteins may yield poor matches to our HMM compared with bacterial, archaeal and eukaryotic sliding DNA clamps.

Example 2: β-propeller domains

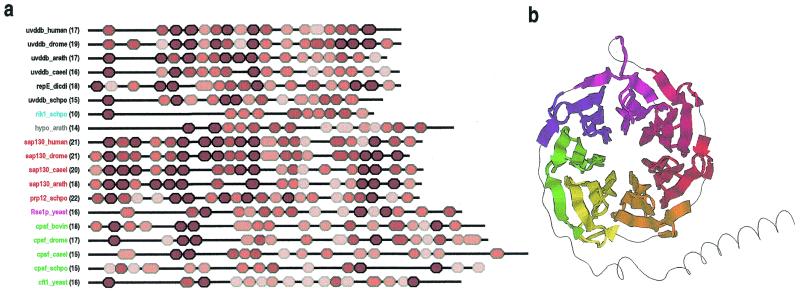
Alignment of UV-DDB-127 repeats. Repeats present within sequences in the UV-DDB-127-family were detected and multiply aligned as described in Materials and Methods. These repeats are quite subtle and have not been previously reported for these proteins. Representative sequences from the alignment are shown in Figure 4. The domain architectures for these proteins are shown in Figure 5a. The repeats are ∼40 residues in length and are predicted by the DSC algorithm to correspond to an unstructured N-terminal region followed by three β-strands. The most conserved positions correspond mainly to hydrophobic residues within the last two predicted strands and to small, mostly hydrophilic residues in the predicted loop regions between strands. The high sequence conservation in the last two predicted strands suggests an important structural role. In contrast, the N-terminal region and the first predicted strand are weakly conserved, suggesting that these may correspond to surface residues involved in family-specific interactions (see below).

Figure 4.

Representative sequences in the multiple alignment corresponding to the HMM for the UV-DDB-127 repeats. Regions predicted to form strands with >65% probability are indicated below the alignment. The coloring scheme is described in the legend to Figure 1. See the legend to Figure 5 for sequence identifiers and organism names.

Figure 5.

(a) Domain architectures for UV-DDB-127 repeat proteins. Repeats are colored red proportional to their likelihood scores using lighter shades for less conserved repeats. Protein names are color coded according to families. The number of repeats are indicated in parentheses. GenBank identifiers for the sequences are: uvddb_human, 4503279; uvddb_drome, 4928452; uvddb_arath, 7267302; uvddb_caeel, 7506084 ; repE_dicdi, 2130171; uvddb_schpo, 7492324; rik1_schpo, 7493406; hypo_arath, 6671952; sap130_human, 3540219; sap130_drome, 7292001; sap130_caeel, 7505161; sap130_arath, 7019653; prp12_schpo, 6451681; Rse1p_yeast, 6323592; cpsf_bovin, 1706101; cpsf_drome, 7303176; cpsf_caeel, 7105681; cpsf_schpo, 7492482; cft1_yeast, 6320507. Abbreviations used for organism names are: drome, Drosophila melanogaster; arath, Arabidopsis thaliana; caeel, Caenorhabditis elegans; dicdi, Dictyostelium discoideum; schpo, Schizosaccharomyces pombe. The transition probability pairs (expressed in 200th nats) used to obtain the HMM parameters from secondary structure propensities are: match-to-insert, 150–1300; insert-to-insert, 10–70; match-to-delete, 200–600; delete-to-delete, 150–350 (see Materials and Methods). (b) Structural regions of a WD40 repeat protein (human transducin β-chain, pdb 1GG2B) (55) that align with seven UV-DDB-127 repeats defined by the HMM corresponding to the alignment in Figure 4. A randomly shuffled transducin sequence was appended to the original sequence to increase the likelihood of misalignment. All seven UV-DDB-127 HMM repeats (shown using seven distinct colors in the figure) align with the transducin WD40 repeats in a manner consistent with the proposed structural arrangement (see text).

Database search. A PSI-BLAST simulated checkpoint search based on a HMM of the UV-DDB-127 repeat yielded numerous matches to WD40 β-propeller domains and related proteins in the NCBI non-redundant database. (For construction of the checkpoint file, simulated sequences with 10 repeats were emitted.) To ensure a stringent test for the statistical significance of these matches, we required that both the sequences used to construct the PSI-BLAST checkpoint files and the subject sequences detected in the search lack internal repeats detectable by pairwise analysis methods (see Materials and Methods). The UV-DDB sequences and the simulated sequences meet this criterion as assessed by searching for significant internal repeats (see Materials and Methods). In contrast, many of the matching database sequences contained pairwise significant internal repeats that may substantially amplify the apparent significance of the match if the correlation between repeats is sufficiently strong. We therefore focused on those matching subject sequences that lack significant internal repeats. Based on this criterion, the search yielded matches to many protein families that either were previously reported to contain WD40 repeats or that clearly can be linked to known WD40 repeat proteins through BLAST or PSI-BLAST searches (Fig. 6). Other types of β-propeller domains were not detected in the search, suggesting that the UV-DDB-127 repeats share similarity primarily to WD40 repeats. Corroborating evidence was obtained from PSI-BLAST searches using the UV-DDB-127 repeat sequences as seeds. This yielded several weak hits to WD40-related proteins (E values < 0.05 but above the default PSI-BLAST cut-off of 0.001). This also reveals that a PSI-BLAST simulated checkpoint search is at least several orders of magnitude more sensitive in this instance than a normal PSI-BLAST search (Fig. 6).

Figure 6.

WD40 proteins detected in a PSI-BLAST simulated checkpoint search based on a HMM of UV-DDB-127 repeats. One representative sequence is shown for each of 32 distinct protein families that were detected (E value < 0.001) in a search of the NCBI non-redundant database. (The criterion for clustering any two sequences into the same family was a pairwise gapped BLAST score with an E value < 1 × 10^–10.) All of the families detected are known to contain WD40 repeats except for two small families of uncharacterized proteins that (aside from our analysis) appear to be unrelated to other proteins. Sequences with descriptions in gray harbor marginally significant internal repeats (with 0.001 < E value < 0.01, as indicated in the far right column). Additional WD40 protein families were detected in the search but are not shown because the corresponding sequences all harbor clearly significant internal repeats (E values < 0.001), which may significantly inflate their computed statistical significance (see Materials and Methods).

Implications of UV-DDB-127 β-propeller domains. β-Propellers are composed of 4–8 structural repeats (or blades), each of which consists of four antiparallel strands that radiate out from the center of the propeller. β-Propellers fall into several families, the largest of which consists of the WD40 repeat proteins (50,51), which our analysis suggests are related to UV-DDB-127 repeats. The WD40 family is so named because the repeats are typically ∼40 residues in length and are characterized by a conserved WD dipeptide motif near their C-terminal regions (reviewed in 50). There are also several other patterns conserved within the WD40 family (50,52). The UV-DDB-127 repeats diverge from WD40 repeats in this regard, as the WD motif and these other patterns are absent. The UV-DDB-127 repeats also appear to harbor more insertions and deletions and are less well conserved relative to each other than is the case for most WD40 repeats. Indeed, additional, undetected repeats seem likely to be structurally present in members of the UV-DDB-127 family. Notably, the p48 subunit of UV-DDB contains seven WD40 repeats (data not shown), one of which was reported previously (53).

What might the presence of β-propeller domains tell us about these proteins? It appears that sequences related to UV-DDB-127 typically have around 16–21 repeats. Assuming that WD40 β-propellers are composed of about seven blades, this suggests that these proteins may have between two and three β-propeller domains each. The less conserved N-terminal region of the UV-DDB-127 repeats may correspond to the outermost strand of the blade based on analogy to typical WD40 β-propellers, for which the outermost strand is encoded in a variable length N-terminal region. This region appears to be less conserved due to the different functional constraints acting at the surface of each type of propeller domain (54). Furthermore, for an alignment of typical WD40 repeats the DSC algorithm predicts an unstructured state for this N-terminal region (not shown), just as is obtained for an alignment of UV-DDB-127 repeats. Another weakly conserved region of the UV-DDB-127 repeat corresponds to the first predicted strand and this may correspond to the innermost strand lining the propeller’s central tunnel, as is the case for WD40 repeats (54). Finally, the last two predicted strands seem likely to correspond to the internal two strands of the propeller blade, as suggested by their higher levels of sequence conservation. Further evidence for this structural arrangement is suggested by alignment of a HMM for seven UV-DDB-127 repeats against the human G protein β subunit, a WD40 protein of known structure (55; Fig. 5b).

Some possible cellular functions for the UV-DDB-127 repeats are suggested by considering β-propeller components in other DNA- and RNA-associated complexes. For example, WD40 repeats occur in the p48 subunit of mammalian chromatin assembly factor 1 (CAF-1), which, in addition to its role in chromatin assembly, is also involved in nucleotide excision repair of UV-damaged DNA (56). CAF-1 p48 binds to histone H4 and is a known subunit of a histone deacetylase; it has also been suggested that CAF-1 p48 and closely related WD40 proteins may function as chaperones that bring proteins to histones (57). Similarly, it has been suggested that UV-DDB may play a role in the repair of DNA within chromatin (58). Thus, there appear to be functional similarities between CAF-1 and the UV-DDB complex. Furthermore, in addition to imparting resistance to UV damage, subunits of the yeast CAF-I complex, which are homologous to the mammalian CAF-1 subunits, are associated with gene silencing near telomeres (59,60). This is reminiscent of the fission yeast rik1p protein, which belongs to the UV-DDB-127 family and is also involved in gene silencing (61) and in localization of the chromo domain protein Swi6p (62). Possible chromatin remodeling functions are performed by other WD40 repeat proteins, such as yeast Hir1p, which functions as a transcriptional co-repressor (63). The UV-DDB-127-related proteins associated with RNA complexes may similarly function to bring together protein components that localize to RNA.

CONCLUSION

By modeling repetitive structural elements that are very weakly conserved at the sequence level, the HMMs constructed in our analysis have yielded substantial improvements in both the corresponding multiple sequence alignments and in database search sensitivity. These alignments suggest subtly conserved structural features, as assessed through comparisons with proteins of known structure. We believe that a key property of the HMMs in this regard is the assignment of transition probabilities based on secondary structure predictions. PSI-BLAST checkpoint-recovered searches based on simulated sequences emitted from the HMMs predict novel distant relationships not readily detected by standard methods. Indeed, in several instances the statistical significance is substantially enhanced. One drawback of the current approach, however, is variability in the measure of significance due to the use of simulations. Future implementations can eliminate this problem, however, by modifying PSI-BLAST so that it constructs a profile directly from the HMM. The overall strategy described here is applicable to other protein families with repetitive structural units.