Rapidly tunable tensile stiffness enables localized shape adaptations in next-generation robotic materials.
Abstract
The emerging generation of robots composed of soft materials strives to match biological motor adaptation skills via shape-shifting. Soft robots often harness volumetric expansion directed by strain limiters to deform in complex ways. Traditionally, strain limiters have been inert materials embedded within a system to prescribe a single deformation. Under changing task demands, a fixed deformation mode limits adaptability. Recent technologies for on-demand reprogrammable deformation of soft bodies, including thermally activated variable stiffness materials and jamming systems, presently suffer from long actuation times or introduce unwanted bending stiffness. We present fibers that switch tensile stiffness via jamming of segmented elastic fibrils. When jammed, tensile stiffness increases more than 20× in less than 0.1 s, but bending stiffness increases only 2×. When adhered to an inflating body, jamming fibers locally limit surface tensile strains, unlocking myriad programmable deformations. The proposed jamming technology is scalable, enabling adaptive behaviors in emerging robotic materials that interact with unstructured environments.
INTRODUCTION
Biological organisms are able to adjust their anatomical structures, stiffness, and behaviors to accommodate a variety of tasks and environmental demands (1). Octopus tentacles, for example, can access nearly infinite trajectories, yet also form joint-like structures to adapt articulated limb control strategies for precise point-to-point movements (2, 3). Caterpillars undulate and engage in inchworm gaits but can rapidly curl into a wheel form and propel themselves away from predators (4, 5). Rapid reconfiguration capabilities make a body versatile; they are a hallmark of biological systems that thrive in the natural, unstructured world. Yet, these capabilities have long eluded conventional robots, which are limited by rigid structures and discrete joints.
To extend reconfiguration capabilities to artificial systems, researchers have leveraged continuously deformable materials to create soft robot bodies and actuators. Commonly, multiple actuators are patterned into a soft robot body, and a subset of those actuators is activated to achieve a desired body configuration (6–10). For example, several works have presented three–degree of freedom actuator modules containing three pneumatic actuators evenly spaced in a cylindrical configuration (11–15). These pneumatic multi-actuator systems are capable of bending in various directions, yet multiple chambers take up substantial radial space and make miniaturizing such systems difficult for applications like minimally invasive surgery, where a smaller outer diameter is desired (16, 17).
As an alternative to multichamber actuators, a single volumetrically expanding soft body can achieve controlled and complex motion when coupled with thin strain-limiting components (like woven meshes or fibers) that bias deformation in a programmed way (18–21). Several recent studies have attempted to create inflatable soft actuators with reprogrammable strain-limiting layers, thereby enabling a single actuator to attain multiple trajectories by controlling material properties at the actuator surface. One approach used reconfigurable tensile strain-limiting adhesive patches that can be manually repositioned over the soft body to direct inflation (22). Other approaches relied on thermally responsive materials, such as low–melting point alloy (LMPA) particulate composites (23, 24) and shape memory polymer (SMP) (25, 26) that change stiffness upon heating to influence the trajectory of pneumatic actuators. Although thermally activated variable stiffness mechanisms are disposed to large modulus changes and require no human intervention, they often suffer from long response times (27). Furthermore, when in the rigid, bulk state (28, 29), materials like LMPA and SMP compromise the deformation ability of soft systems because they have coupled tensile and bending stiffnesses. Electrostatic clutches can also modulate tensile stiffness (30, 31). However, these clutches require high voltages (>300 V) to operate, posing risks for human-orientated applications, and the nonstretchable, two-dimensional (2D) components of the clutches limit their free bending in 3D.
A growing body of work seeks to use jamming, the sudden change of modulus due to interactions of many constituent parts within a system, to achieve rapid stiffness change in soft robots (32–35). Existing jamming technologies predominately trigger interactions between subcomponents by applying a vacuum to a sealed domain of material, inducing a compressive force that drives the material together. There are three established classes of jamming—granular jamming, layer jamming, and fiber jamming. Each class is associated with a different dimensionality and tunes stiffness along particular axes (Fig. 1D). Granular jamming tunes the compressive and bending stiffnesses of a consolidated volume of particles (36–40). Vacuum-packed granules are unable to resist tensile force that exceeds the vacuum pressure, making granular jamming unsuitable for constraining tensile strain on an inflating actuator. Layer jamming tunes the bending stiffness of surfaces consisting of stacked, flexible sheets (41–43). Traditional layer jamming does not have any degrees of freedom in-plane because the layers are stiff and homogeneously connected to all sides of the system. Layer jamming thus cannot be used to tune tensile stiffness from the surface. Fiber jamming changes the bending stiffness of 1D elements composed of flexible fibers (44–47). Similar to layer jamming, fiber jamming designs in the literature have used homogeneous, inextensible fibers connected to both ends of a system and consequently cannot be used to modulate tensile stiffness. Moreover, current fiber jamming systems have a relatively high bending stiffness (even in the unjammed state) due to the incorporation of stiff fibers. High bending stiffness impedes large deformations and creates an undesirable rigid interface. Although all three jamming systems have been integrated with actively actuating structures like soft inflating bodies, their applications have been primarily restricted to locking shape (37, 40, 45, 48) or varying bending angles (42, 49, 50). The inability to independently tune tensile stiffness impedes current jamming systems from actively regulating the surface strains of soft systems to shift shape.
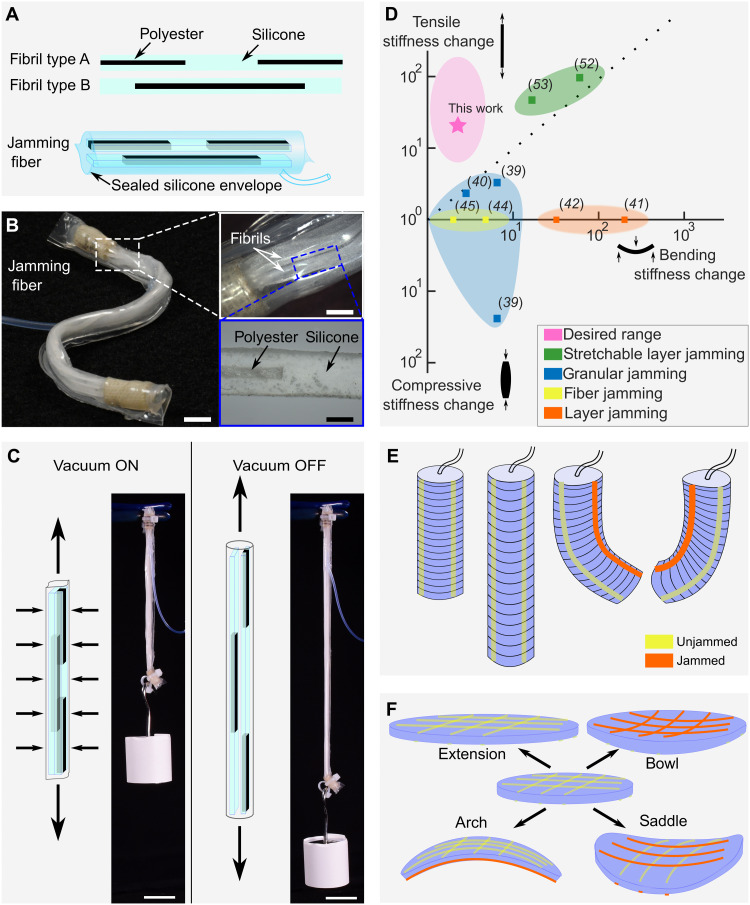
Fig. 1. Tensile jamming fiber with SEFs.
(A) Schematic of SEFs and jamming fiber. Only two SEFs are shown inside the jamming fiber for clarity. Real system has 4 to 10 SEFs. Detailed fabrication process in fig. S2. (B) Jamming fiber with eight SEFs inside is highly flexible (scale bars, 1 cm). Fibers are 12 cm long. Close-up images of SEFs and a single polyester-silicone interface [scale bars, 900 μm (top) and 500 μm (bottom)]. (C) Upon application of vacuum, SEFs agglomerate and overlapping polyester sections yield high shear strength through friction, increasing tensile stiffness of the fiber. At atmospheric pressure, SEFs in the fiber can individually stretch and slide over each other. With a mass of 200 g attached to its end, the unjammed fiber (atmospheric pressure) stretched to 88% strain, while the jammed fiber (−80 kPa) stretched to only 4% strain. Scale bars, 2 cm. (D) Stiffness change ratios of jamming systems. Tensile jamming fibers occupy the desired range: low bending stiffness change and large tensile stiffness change. (E) Radially constrained pneumatic actuator with three jamming fibers around its perimeter. The actuator executes different trajectories depending on which fibers are jammed. (F) A pneumatic membrane with jamming fibers attached to the top and bottom orthotropically expands when fibers are unjammed (top left). By jamming certain fibers, the membrane can attain shapes with zero (bottom left), positive (top right), and negative (bottom right) Gaussian curvatures. Photo credit: Robert Baines, Yale University.
A recent variant of layer jamming technology, which we will refer to as “stretchable layer jamming,” allows the tuning of tensile stiffness (51–53). In this technology, individual layers are not connected to all sides of the device, enabling the layers to slide past each other when pulled. Stretchable layer jamming could potentially be applied to modulate moderate tensile strains (<40%) but at the cost of markedly increased bending stiffness (see Fig. 1D), which severely limits the achievable curvature if it is incorporated as a strain limiter. Stretchable layer jamming sheets also cannot bend in all directions in space—even if made into long, narrow sheets resembling a fiber, these sheets only bend easily along the axis with minimal second moment of area and thus would constrain the potential deformations of the soft system. The ability to control tensile stiffness while retaining low bending stiffness in any direction is crucial for jamming-based strain-limiting technology and remains an unsolved problem.
In this work, we introduce “tensile jamming fibers,” a system that rapidly modulates its tensile stiffness while maintaining low bending stiffness in all directions. Tensile jamming fibers are the first technology to occupy the desired range in Fig. 1D. A jamming fiber comprises a collection of segmented elastic fibrils (SEFs) (Fig. 1C). One SEF consists of an alternating pattern of inextensible polyester thread and elastic springs (see Fig. 1, A and B). The segmented design of SEFs allows a jamming fiber to be highly stretchable—up to 200% of its original length without failure (fig. S5)—in the absence of vacuum (unjammed). When vacuum is applied, the SEFs press together, and the interfaces between overlapping sections with embedded polyester thread generate high shear force that resists tensile loads (jammed).
After affixing these jamming fibers to the surface of a single-chamber inflatable actuator, we tune the local tensile stiffness to rapidly and predictably change its trajectory (Fig. 1E). In addition, we integrate our jamming fibers into a planarly expanding actuator to create a rapidly shape-shifting bilayer capable of forming surfaces with zero, positive, and negative Gaussian curvatures (Fig. 1F). These demonstrations pave the way for shape-shifting robots and dynamic camouflage systems.
RESULTS
Segmented elastic fibrils
The technology underpinning tensile jamming fibers is the SEFs. We developed two SEF architectures, each consisting of different interspersed segments of polyester and silicone, labeled as “type A” and “type B” in Fig. 1A. To make a jamming fiber, equal numbers of type A and type B SEFs are aligned and joined at their ends. They are then placed inside a sealed silicone envelope and connected to a vacuum source. Further manufacturing details can be found in Materials and Methods, while an illustration of the process can be found in fig. S2. Within each type of SEF, the length of polyester content is higher than 50% of the total SEF length. This way, there will be overlapping polyester sections when the two types of SEF are placed adjacent to one another in the silicone envelope.
We conducted tension tests on SEFs with varying polyester length percentages (γ) to understand how γ influences stiffness and maximum elongation before failure (fig. S3). As γ increases, so does the stiffness, which is consistent with our understanding of the mechanics of an SEF from the rule of mixtures
| (1) |
where ESEF is the Young’s modulus of an SEF, and Ef and Em are Young’s moduli of polyester and silicone matrix, respectively.
Tensile jamming fibers
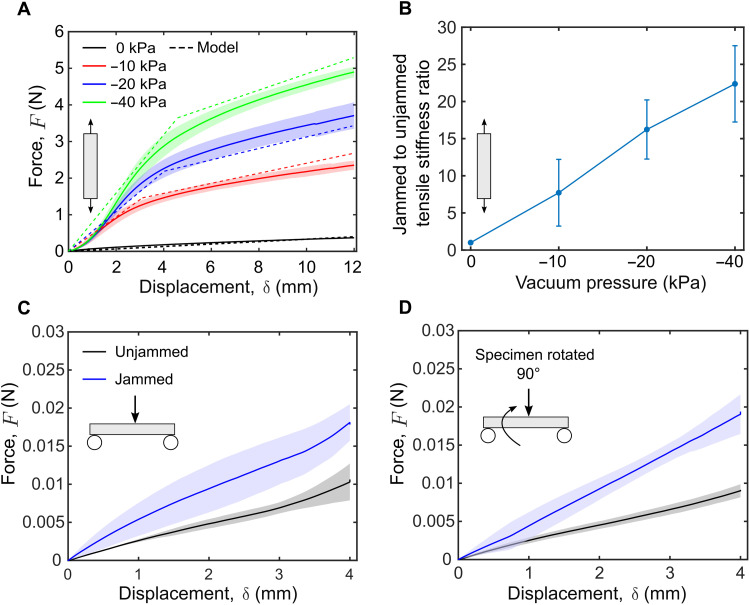
We found that we could tune the tensile force (F) required to stretch a tensile jamming fiber to a prescribed displacement (δ) and thereby the fiber’s tensile stiffness () by varying the magnitude of vacuum (ΔP) (Fig. 2A). The ratio of jammed to unjammed stiffness rises to a maximum of more than 20× with increasing pressure (Fig. 2B). Despite this high tensile stiffness ratio, the fibers retain low bending stiffness in two orthogonal directions (Fig. 2, C and D). Three-point bending tests (details in note S1) reveal that the system has a bending stiffness of 0.0021 and 0.0048 N/mm when unjammed and jammed at −85 kPa, respectively. Thus, transitioning from unjammed to jammed, the bending stiffness increases about 2×. Note that these bending stiffnesses (unjammed and jammed) are less than 1/80 of the reported stiffnesses of a benchmark fiber jamming system with similar dimensions (44).
Fig. 2. Mechanical characterization of jamming fibers.
(A) Tensile behavior at selected jamming pressures for fibers with the parameters of 70% polyester length fraction and eight SEFs (70% N8). Each solid line represents the average behavior of three specimens. Clouds indicate 1 SD from the mean. Dashed lines are predictions from the analytical model. (B) Ratio of jammed stiffness over unjammed tensile stiffness as a function of vacuum pressure for the 70% N8 specimens. Average of three specimens reported. Bars represent 1 SD above and below the mean. (C and D) Three-point bending of tensile jamming fibers. When jammed (at vacuum pressure of −85 kPa), the fiber is approximately 2× stiffer than when unjammed. However, the magnitude of the forces it sustains when deforming is still very low. (D) is test conducted with specimen rotated 90° from (C). Approximately the same force values are reached, testifying to the fact that the tensile jamming fiber has isotropic bending stiffness. Confidence cloud shows SD. Solid line indicates the mean.
Other design parameters contribute to a tensile jamming fiber’s effectiveness. We therefore derived a relationship between k and design parameters including γ, vacuum pressure, and number of SEFs (N) (see note S2). The analytical model considers the interfacial shear stiffness (kshear) between SEFs as the primary contribution to the overall tensile stiffness (see fig. S1). We express the interfacial stiffness as
| (2) |
where α is the effective contact ratio (a fitting parameter to account for imperfect contact), G is the shear modulus of silicone (, where E is Young’s modulus and ν is the Poisson ratio), A is the area of contact, and t is the thickness of the silicone under shear on one fibril. t is a function of the applied pressure, because pressure will squeeze and flatten the silicone in the linear elastic regime according to , where t0 is the initial thickness of the silicone interface. Because the shear interfaces are parallel, the total stiffness of the jamming fiber is the sum of kshear from all interfaces (eqs. S13 to S17).
In the model, we also considered SEF slippage that captures the nonlinearity of the force-displacement response. Slip happens when the shear force in the interface exceeds the maximum static friction that can be sustained by the silicone interface between polyester threads in adjacent fibrils. After slip, some interfacial stress is relieved (eqs. S18 and S19).
With only three fitting parameters [effective contact ratio (α), shear area ratio (e), and coefficient of friction (μ)], our model is able to predict the jamming behavior reasonably well. The model predicts that jamming fiber stiffness will increase with increasing γ, N, and ΔP. This prediction is consistent with uniaxial quasistatic tension tests conducted on jamming fibers while varying the same parameters (fig. S4, A and B). Theoretical predictions from the model are plotted in Fig. 2A as a dashed line. The average percentage error of force prediction at the maximum tested displacement of 8 mm is 8.60%. On the basis of the results of the tension tests, we chose to proceed with γ = 70% and N = 8 (referred to as 70% N8 in subsequent text) for further testing and demonstrations because it exhibited the highest tensile stiffness ratio, 22.2, between the jammed and unjammed states for ΔP = −40 kPa (fig. S4, C and D).
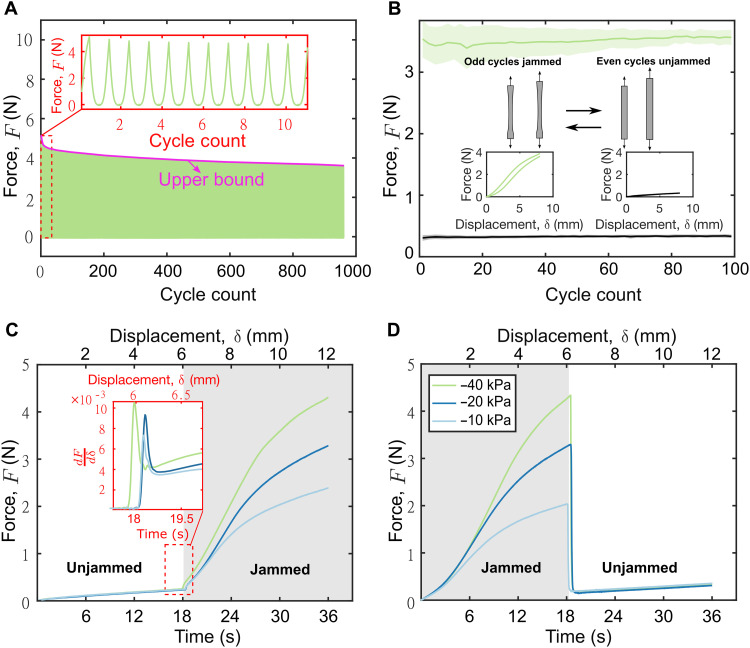
Having quantified the influence of critical design variables on a jamming fiber’s tensile stiffness, we evaluated the reliability of the fiber jamming mechanism in two ways. First, to assess how well the jammed fibers could induce the same actuator trajectory multiple times, we kept a fiber jammed and subjected it to 1000 cyclic tensile loads. After 1000 cycles, the fiber retained more than 70% of its original tensile force (dropping from 5.1 to 3.6 N) (Fig. 3A). Second, to test how well the fibers would fare in reconfigurable applications (jamming and then unjamming to facilitate different sets of motions), we applied vacuum every other cycle for 100 cycles of tensile load. Throughout the 100 cycles of intermittent jamming and unjamming, we observed negligible change in F, despite reaching the same δ each cycle (Fig. 3B). The effective maintenance of k throughout the jam-unjam cycles gave us confidence that jamming fibers could be jammed and unjammed repeatedly to perform reconfiguration tasks.
Fig. 3. Cyclic and dynamic behavior of jamming fibers.
(A) Cyclic tensile testing up to a displacement of 8 mm while jammed at −40 kPa. (B) Cyclic tensile testing up to a displacement of 8 mm, jammed at −40 kPa and unjammed for every other cycle. Average of three specimens reported. Error clouds represent 1 SD from the mean. Top green curve shows the jammed response, and bottom black curve shows the unjammed response. Insets show the force versus displacement curve for the last two cycles (jammed and unjammed). (C) Dynamic transition from unjammed to jammed at displacement of 6 mm during a tensile pull to 12 mm. Inset shows the derivative of force with regard to displacement (instantaneous stiffness) plotted against time to display the rapid time scale of the stiffness response. (D) Dynamic transition from jammed to unjammed at displacement of 6 mm during a tensile pull to 12 mm. In (C) and (D), data from only one of the three specimens tested are plotted for clarity. Additional data in fig. S6.
To quantify the time scale of stiffness change in a jamming fiber, we initiated jamming partway through a tensile test while monitoring the mechanical response (see Fig. 3C and additional data in fig. S6A). The jamming transition was rapid, stiffening the fiber within 1/10 of a second and stabilizing in the new jammed state in less than half of a second (see inset of Fig. 3C). The reverse process, going from the jammed state to the unjammed state, was also rapid and exhibited no residual forces (see Fig. 3D and additional data in fig. S6B). From this test, we also observed that force sustained in the jammed state appears to be independent of the prestrain on a fiber at the onset of jamming. For example, the maximum value attained by curves in the two gray shaded regions in Fig. 3 (C to H) is within 5% of one another. Invariance in the mechanical response of jamming fibers to moderate prestrains allows stiffness changes during inflation of an actuator, as shown in movie S4.
Modular variable trajectory actuator
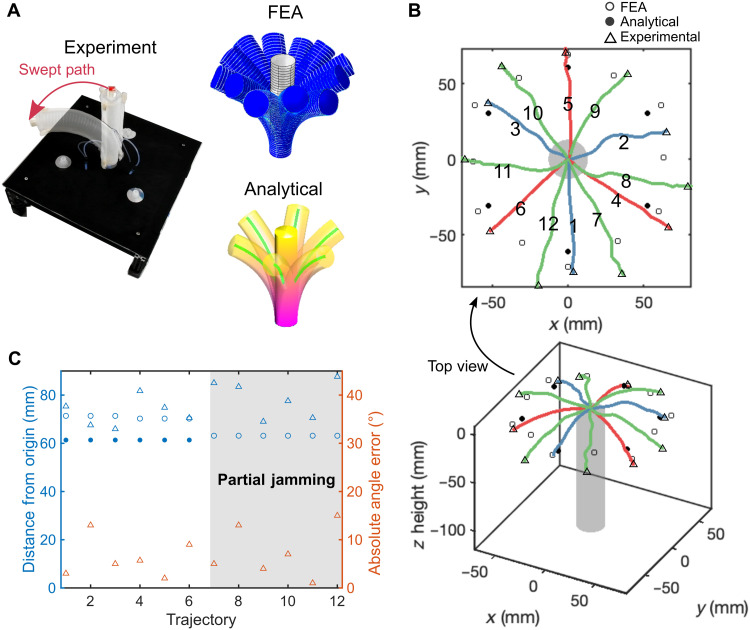
To achieve multiple trajectories using a single actuator, we integrated three jamming fibers around the circumference of a modular, vertically extending pneumatic chamber. By applying vacuum to subsets of the jamming fibers, the actuator could bend along various trajectories (Fig. 4A). The range of attainable trajectories grows combinatorially with increased resolution in pressures: Even with only two levels of pressure (P = −10 and −40 kPa), the actuator generated 12 distinct swept trajectories (Fig. 4B). Beyond the rapidity of reconfiguration, attaining 12 distinct trajectories sets us apart from multitrajectory actuators based on phase-change materials like LMPA (23, 24), where only two states—ON and OFF—are available. Our demonstration represents a single-core soft actuator with the largest number of programmable trajectories to date. With finer variations in pressure, the actuator is able to bend in more directions, without requiring additional pneumatic chambers. As a conceptual illustration, we generated 24 distinct trajectories by varying the stiffness of fibers further in finite-element (FE) simulation (fig. S8 and note S5).
Fig. 4. Modular variable trajectory actuator.
(A) Experimental setup and simulation visualizations. The FEA model generated 12 trajectories, including some configurations with two different pressures and thus two sets of stiffness, as was done in the experiment. However, our analytical model could only account for one stiffness, limiting it to prediction of six of the tested trajectories. (B) Comparison of motion capture data for the actuator’s end effector and the predictions from the analytical and FEA models. We labeled the trajectories 1 to 12, corresponding to combinations of jammed fibers. Trajectories 1 to 3 (blue) are achieved by jamming a single fiber to P = 40 kPa, 4 to 6 (red) by jamming two adjacent fibers to P = 40 kPa, and 7 to 12 (green) by jamming two adjacent fibers at different pressures (P = 10 and 40 kPa and vice versa). (C) Left axis and blue markers show final resting distance of the end effector from the origin. Right axis and orange markers show error between the measured bending angle of the actuator (as projected into the x-y plane) and the angles expected from an ideal subdivision of the plane into 12 equal parts.
Analytical and FE models were used to predict the deformation trajectories of the single actuator outfitted with jamming fibers (Fig. 4A). For derivation and simulation details, see notes S3 and S5. With the analytical model, we can predict fairly well both the bending direction and the bending curvature of the actuator. The bending direction can be approximated by calculating the geometric circumferential midpoint of the jammed fibers, while a hyperelastic constitutive model reasonably predicts the magnitude of curvature (fig. S7 and note S3). With the FE model, we were able to capture more nuanced phenomena. These include how jamming multiple fibers to bisect a trajectory decreases curvature at a fixed pressure and how jamming at intermediate pressures can be used to further hone bending angle and direction. We juxtaposed the end effector distances defined by the Euclidean distance, , from its starting position with those predicted by the models (Fig. 4C, left axis). The small discrepancies suggest that both models are useful in the design of variable trajectory actuators. However, while the analytical model offers predictions with less required computation, it cannot predict the effects of jamming at intermediate pressures.
We also calculated the angular deviation of the actuator’s swept path from the intended path, which was to divide the hemisphere into 12 equal parts (Fig. 4D, right axis). The trajectories with least absolute angle error (1, 5, and 11) arose from different jamming configurations: single fiber jammed, two fibers jammed, and fiber partially jammed, respectively. This result suggests that a desired direction—whether it is along the direction of one fiber or in between two fibers—can be achieved with high accuracy. By the same token, the result suggests that deformation trajectories, and in our case, angular deviations from perfect divisions of the x-y plane, are sensitive to fiber placement and actuator dynamics (see oscillations of swept paths projected in the x-y plane in Fig. 4B, especially trajectories 2, 3, 7, and 12).
Enhancing performance by combinations of modules
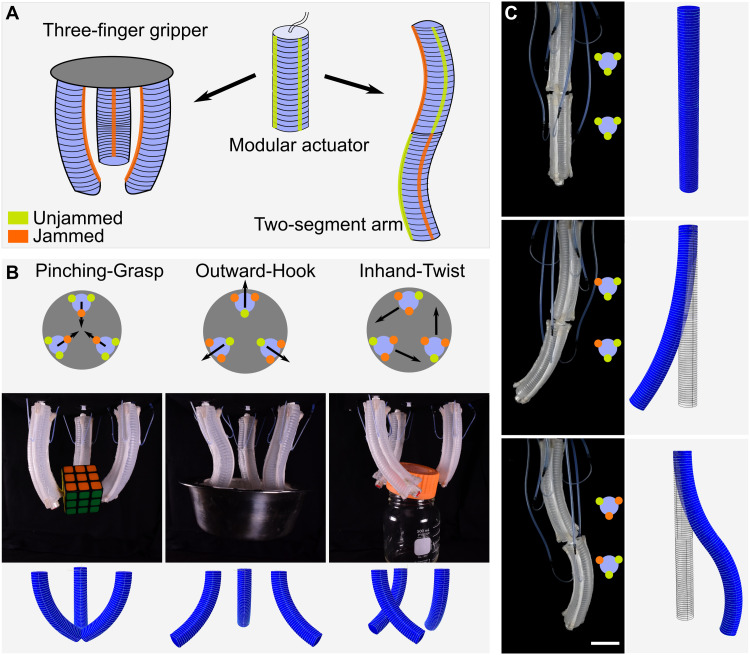
Jamming fiber–enabled modular variable trajectory actuators can be combined to create agile, reconfigurable soft robots. The resulting systems have myriad deformation modes, enabled by the versatility and modularity of individual variable trajectory actuators. To demonstrate potential applications for this principle, we created a multimodal gripper and a multitrajectory continuum arm (Fig. 5A).
Fig. 5. Modular actuators combined to make multimodal three-finger gripper and two-segment continuum arm.
(A) Schematics for the modular actuators. (B) Three grasping modes enabled by fiber jamming. Top row depicts jamming states of the three actuators. Middle row shows pictures from grasping trials: pinching a Rubik’s cube, hooking a metal bowl, and twisting a lid. Bottom row shows the FEA-simulated prediction of actuator positions in the absence of an object. (C) Multimodal two-segment arm. Left column shows the final shapes the arm attained after jamming different sets of fibers (scale bar, 4 cm). Right column shows the simulated arm position prediction with FEA. Photo credit: Bilige Yang, Yale University.
To make a multimodal gripper, we mounted three actuators (each equipped with three jamming fibers) in parallel to an acrylic base plate (Fig. 5B). Depending on the set of fibers that was jammed, the fingers engaged in three kinematically distinct grasping modes. When the fibers on the inside of the fingers were jammed, the gripper executed a “pinching grasp” for picking up relatively small objects. Jamming the outside fibers of each actuator led to an “outward-hooking” motion for latching onto the inside of concave objects. Last, when two fibers on the oblique side of the fingers were jammed, the gripper executed a “twisting” motion. Using the three grasp modes separately, the gripper was able to pick up a Rubik’s cube, lift a bowl, and twist the cap off of a jar. We also show how two grasping motions (pinching and outward-hooking) can be combined in sequence to execute a pick-and-place operation (movie S3). The ability to achieve diverse grasping modes within the same gripper with a single positive pressure input shows the enhanced reprogrammability of motion trajectories enabled by tensile jamming. A superposition of these grasp modes, or optimization of fiber placement, could potentially open up a wider grasping space.
In addition to the parallel configuration embodied by the gripper, we joined two actuators in series to create a continuum manipulator with seven controllable degrees of freedom (six fibers and one contiguous inflating core) (Fig. 5C). By jamming the fibers of each segment on the same side, the whole manipulator bent to that side; by jamming fibers on different sides of each segment, the manipulator bent into more complex configurations. Such motions are reminiscent of the variety of deformation modes of biological hydrostats (54, 55). In each case, the deformed state was predicted well by FE analysis (FEA), reinforcing its utility as a design tool for jamming fiber–based robots.
Shape-changing membrane
The ability to adapt shape to environmental and developmental triggers is a core function of living beings and a grand challenge for artificial machines (1). Many studies, those in both simulation (56) and hardware (10, 57–61), attest to the benefits shape change confers on robots under changing task demands. Soft robots, in particular, hold promise as the next generation of shape-changing robots due to their capability to undergo large deformations. Inspired by botany [unfolding of flowers (62) and natural curling of seed pods (63)], researchers have programmed thin, planar sheets to morph into complex surfaces through in-plane growth and out-of-plane buckling (64). Such an arrangement enables local control of the shape tensor, thereby giving rise to a rich diversity of shapes.
Current artificial shape-changing sheets—those made from composite hydrogels (65) or elastomers (66), for example—often have only one programmed shape and a slow response time. Recent work on liquid crystal elastomer composite shape-morphing surfaces increased the number of possible deformations with a single system but still required minutes to switch between shapes (61). Fast shape-changing systems can be achieved by applying jamming fibers to planar inflatable geometries. The capability of the fibers to tune tensile stiffness on a higher magnitude than bending stiffness allows effective redistribution of the elastic energy on the thin sheet between stretching and bending, thus effectively altering the resulting shape within seconds. Here, we demonstrate this concept by applying jamming fibers in a grid-like arrangement on each side of a planar pneumatic bladder (Fig. 6).
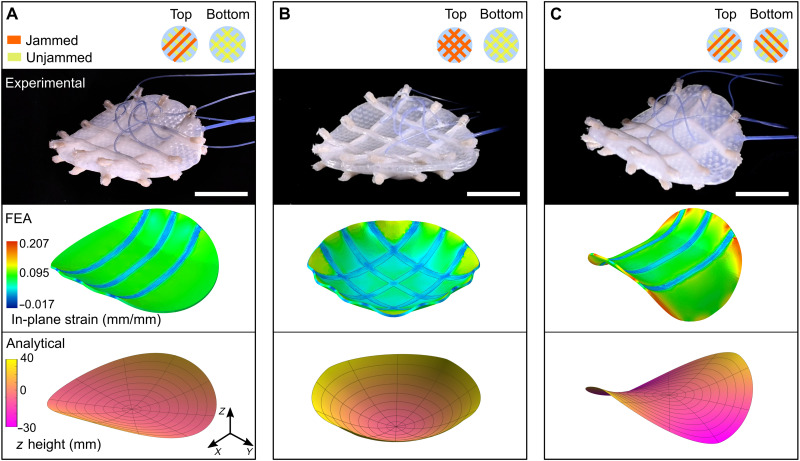
Fig. 6. Shape-changing membrane enabled by tensile jamming fibers.
A circular planarly expanding actuator was made and equipped with grids of jamming fibers. By jamming different sets of fibers, this unit was able to manifest ranges of Gaussian curvatures. FEA and analytical modeling were used to predict and understand the effect of varied tensile stiffness on the 2D actuator. (A) Top longitudinal fibers jammed to create an arch (zero Gaussian curvature). (B) Top longitudinal and latitudinal fibers jammed to create a bowl (positive Gaussian curvature). (C) Top longitudinal and bottom latitudinal fibers jammed to create a saddle shape (negative Gaussian curvature). Scale bars, 4 cm. Photo credit: Bilige Yang, Yale University.
The top and bottom faces of the bladder are connected by silicone pillars, preventing expansion through the thickness and creating a membrane that expands in-plane orthotropically (see fig. S9 and note S4). When the membrane’s surface is asymmetrically or anisotropically constrained by jamming fibers during inflation, the membrane bends out of plane as it equilibrates to a minimum energy state. For example, by jamming the top longitudinal fibers, the inflated bladder bent around a single axis into a cylindrical arch (zero Gauss curvature; Fig. 6A). Jamming the bottom longitudinal and bottom latitudinal fibers, the bladder assumed the shape of a bowl or dome (positive Gauss curvature; Fig. 6B). Last, jamming the top longitudinal and bottom latitudinal fibers yielded a saddle shape (negative Gauss curvature; Fig. 6C). This is the first demonstration of a bilayer that is able to independently switch between all three types of Gaussian curvatures within seconds.
The qualitative deformation behavior of the bladder outfitted in jamming fibers is described well by FEA, while analytical methods reasonably predict deformation of the midplane (notes S4 and S5). We expect that the local control of shape furnished by the jamming fibers will propel the field of shape-morphing structures to the next level. As a demonstration of concept, we simulated a large-scale membrane with patterned jamming fibers and found that it was able to morph to distinct and complex topologies contingent on the subsets of locally jammed fibers (fig. S10).
DISCUSSION
The ability to actively tune stiffness is critical to devising next-generation robots that replicate the control and fluidity of biological organisms’ motions and shape changes. In lieu of traditional approaches that rely on strain limiters with immutable material properties, here, we introduce controllable tensile strain limiters. Jamming fibers combine the desirable features from many different existing stiffness modulation techniques, such as state-of-the-art jamming and thermally activated variable stiffness materials. Jamming fibers exhibit marked tensile stiffness changes, rapid response times, minimal contribution to system bulk properties or weight, and highly isolated material changes. They stand in contrast to thermal stiffness-changing systems, where heat diffusion leads to undesired local interference, and stretchable layer jamming, where bending stiffness and tensile stiffness are coupled. At atmospheric pressure, the jamming fibers stretch with low tensile stiffness, having little influence on the trajectory of an actuator. When vacuum is applied, the jamming fibers’ tensile stiffness increases by more than 20× in less than 1/10 of a second, imposing strong directional bias while retaining flexibility in bending.
Tensile jamming technology demonstrates far-reaching potential in soft robotics, enabling great improvements to the workspaces of single-chamber, volumetrically expanding soft actuators without adding large volume or inducing high bending stiffness. With rapid response and an ability to influence actuator dynamics mid-inflation, such multimodal actuators are more responsive in applications compared to thermally activated strain-limiting components and safer for human-oriented applications than high voltage–activated clutches. This improvement in control of trajectories without undesired increases in volume is especially relevant for applications where the cross-sectional area of the actuator needs to be minimized, such as in endoscopic minimally invasive surgery. Our radially constrained single-chamber actuator, with small-footprint 1D elements (tensile jamming fibers), can potentially be made more slender than current multichamber actuators (16, 17) and avoid the large radial expansion needed for multichamber actuators to achieve bending.
In the surface (2D) cases, varying tensile stiffness (coupled with underlying inflation) allows control of Gaussian curvature. The result is the first demonstration of active transition between three types of Gaussian curvatures—on the order of seconds—within the same system. The ability of the tensile jamming fibers to increase tensile stiffness while maintaining a low bending stiffness enables a redistribution between bending energy and stretching energy for the thin surface, which facilitates marked shape change. Theoretically, with sufficient number of jamming fibers, an inflating 2D sheet can grow into any target surface (64) and then change between such shapes. This demonstration paves the way for next-generation shape-shifting robots with ability to adapt to environmental demands and adopt shapes for dynamic camouflage.
Beyond the robotics space, we foresee jamming fibers as a useful technology in exosuit-assisted rehabilitation, where selective mobility is tantamount to patient recovery. Additional possible use cases include on-demand sizing for smart garments and other applications where predictable, rapid, and localized tensile stiffness changes are desired.
MATERIALS AND METHODS
Manufacturing of fibers
Each SEF had segments of polyester thread embedded discontinuously in a thin silicone substrate (Ecoflex 50, Smooth-On). Several SEFs were stacked and glued together on both ends with a silicone-based adhesive (Sil-Poxy, Smooth-On). A small amount of cornstarch was applied to the surfaces of SEFs to prevent adhesion of silicone. The bundle of SEFs was put inside a silicone membrane and sealed with Sil-Poxy. The detailed manufacturing process is depicted in fig. S2. Several designs were manufactured, with different linear loading fractions of SEF (γ = 0, 60, 70, and 100%) and different numbers of SEFs per fiber (N = 4, 6, 8, and 10).
Mechanical testing
Quasistatic tensile testing of jamming fibers was done using an Instron 3345 material tester. For pull-to-failure and nondynamic tensile tests, extension was applied at 20 mm/min. For three-point bending, compression was applied at 1 mm/min. For cyclic testing, extension was applied at 60 mm/min. Additional details and results regarding characterization are presented in the Supplementary Materials.
Fabrication of actuators
The omnidirectional actuators were made by first creating a silicone (Ecoflex 50, Smooth-On) membrane with embedded parallel polyester threads and then wrapping the membrane into a cylinder, as described in previous work (22). Jamming fibers were attached on the outside of this cylinder, at even spacing (every 120°). A modular connection, made out of acrylic and Luer lock connectors (51525K123 and 51525K213, McMaster-Carr), was added to each end of the cylindrical actuator using Sil-Poxy. For the gripper demonstration, three modules were attached to an acrylic plate, in a circular pattern (radius of 300 mm), at equal spacing (120°). The continuum arm was manufactured by attaching two omnidirectional actuators in series and mounting the free end of one of them to a base plate. The shape-shifting membrane was fabricated by casting silicone (Ecoflex 30, Smooth-On) in an acrylic mold (fig. S9) and attaching 3 × 3 grids of jamming fibers on both sides of the membrane with Sil-Poxy. The resulting bilayer membrane is about 10 mm thick.
Acknowledgments
We thank S. Y. Kim for discussion regarding direction of the work. Funding: This material is based upon work supported by the NSF under grant no. EFMA-1830870. D.S. was supported by a NASA Space Technology Research Fellowship (80NSSC17K0164). R.B. was supported by an NSF Graduate Research Fellowship (DGE-1333468). Author contributions: R.K.-B. and D.S. conceived the project. B.Y. and R.B. managed the research. B.Y. and E.T. designed and manufactured the hardware. B.Y., R.B., and D.S. ran experiments on the hardware and mechanical testing. R.B., B.Y., and M.V. conducted analytical modeling. S.P. performed FEA simulations. All authors drafted the manuscript. All authors contributed to, and agree with, the content of the final version of the manuscript. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper are available at https://doi.org/10.7910/DVN/UZNRLS.
Supplementary Materials
This PDF file includes:
Notes S1 to S5
Tables S1 to S3
Figs. S1 to S10
Legends for movies S1 to S5
References
Other Supplementary Material for this manuscript includes the following:
Movies S1 to S5
REFERENCES AND NOTES
- 1.Shah D., Yang B., Kriegman S., Levin M., Bongard J., Kramer-Bottiglio R., Shape changing robots: Bioinspiration, simulation, and physical realization. Adv. Mater. 33, 2002882 (2020). [DOI] [PubMed] [Google Scholar]
- 2.Sumbre G., Fiorito G., Flash T., Hochner B., Motor control of flexible octopus arms. Nature 433, 595–596 (2005). [DOI] [PubMed] [Google Scholar]
- 3.Sumbre G., Fiorito G., Flash T., Hochner B., Octopuses use a human-like strategy to control precise point-to-point arm movements. Curr. Biol. 16, 767–772 (2006). [DOI] [PubMed] [Google Scholar]
- 4.Brackenbury J., Caterpillar kinematics. Nature 390, 453 (1997). [Google Scholar]
- 5.Brackenbury J., Fast locomotion in caterpillars. J. Insect Physiol. 45, 525–533 (1999). [DOI] [PubMed] [Google Scholar]
- 6.S. Tadokoro, S. Yamagami, M. Ozawa, T. Kimura, T. Takamori, K. Oguro, Soft micromanipulation device with multiple degrees of freedom consisting of high polymer gel actuators, in Proceedings of the Technical Digest. IEEE International MEMS 99 Conference. Twelfth IEEE International Conference on Micro Electro Mechanical Systems (Cat. No. 99CH36291) (IEEE, 1999), pp. 37–42. [Google Scholar]
- 7.Hawkes E., An B., Benbernou N. M., Tanaka H., Kim S., Demaine E. D., Rus D., Wood R. J., Programmable matter by folding. Proc. Natl. Acad. Sci. U.S.A. 107, 12441–12445 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Nguyen C. T., Phung H., Nguyen T. D., Jung H., Choi H. R., Multiple-degrees-of-freedom dielectric elastomer actuators for soft printable hexapod robot. Sens. Actuator A Phys. 267, 505–516 (2017). [Google Scholar]
- 9.Zhou J., Yi J., Chen X., Liu Z., Wang Z., Bcl-13: A 13-dof soft robotic hand for dexterous grasping and in-hand manipulation. IEEE Robot. Autom. Lett. 3, 3379–3386 (2018). [Google Scholar]
- 10.Shah D. S., Yuen M. C., Tilton L. G., Yang E. J., Kramer-Bottiglio R., Morphing robots using robotic skins that sculpt clay. IEEE Robot. Autom. Lett. 4, 2204–2211 (2019). [Google Scholar]
- 11.Suzumori K., Iikura S., Tanaka H., Applying a flexible microactuator to robotic mechanisms. IEEE Control Syst. 12, 21 (1992). [Google Scholar]
- 12.B. Shih, D. Drotman, C. Christianson, Z. Huo, R. White, H. I. Christensen, M. T. Tolley, Custom soft robotic gripper sensor skins for haptic object visualization, in Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (IEEE, 2017), pp. 494–501. [Google Scholar]
- 13.Robertson M. A., Paik J., New soft robots really suck: Vacuum-powered systems empower diverse capabilities. Sci. Robot. 2, eaan6357 (2017). [DOI] [PubMed] [Google Scholar]
- 14.Martinez R. V., Branch J. L., Fish C. R., Jin L., Shepherd R. F., Nunes R. M., Suo Z., Whitesides G. M., Robotic tentacles with three-dimensional mobility based on flexible elastomers. Adv. Mater. 25, 205–212 (2013). [DOI] [PubMed] [Google Scholar]
- 15.R. Xie, M. Su, Y. Zhang, Y. Guan, 3D-PSA: A 3d pneumatic soft actuator with extending and omnidirectional bending motion, in Proceedings of the 2018 IEEE International Conference on Robotics and Biomimetics (ROBIO) (IEEE, 2018), pp. 618–623. [Google Scholar]
- 16.Elsayed Y., Vincensi A., Lekakou C., Geng T., Saaj C., Ranzani T., Cianchetti M., Menciassi A., Finite element analysis and design optimization of a pneumatically actuating silicone module for robotic surgery applications. Soft Robot. 1, 255–262 (2014). [Google Scholar]
- 17.Runciman M., Darzi A., Mylonas G. P., Soft robotics in minimally invasive surgery. Soft Robot. 6, 423–443 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.K. C. Galloway, P. Polygerinos, C. J. Walsh, R. J. Wood, Mechanically programmable bend radius for fiber-reinforced soft actuators, in Proceedings of the 2013 16th International Conference on Advanced Robotics (ICAR) (IEEE, 2013), pp. 1–6. [Google Scholar]
- 19.Y. Sun, Y. S. Song, J. Paik, Characterization of silicone rubber based soft pneumatic actuators, in Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems (IEEE, 2013), pp. 4446–4453. [Google Scholar]
- 20.Deimel R., Brock O., A novel type of compliant and underactuated robotic hand for dexterous grasping. Int. J. Rob. Res. 35, 161–185 (2016). [Google Scholar]
- 21.Connolly F., Walsh C. J., Bertoldi K., Automatic design of fiber-reinforced soft actuators for trajectory matching. Proc. Natl. Acad. Sci. U.S.A. 114, 51–56 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kim S. Y., Baines R., Booth J., Vasios N., Bertoldi K., Kramer-Bottiglio R., Reconfigurable soft body trajectories using unidirectionally stretchable composite laminae. Nat. Commun. 10, 3464 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Buckner T. L., Yuen M. C., Kim S. Y., Kramer-Bottiglio R., Enhanced variable stiffness and variable stretchability enabled by phase-changing particulate additives. Adv. Funct. Mater. 29, 1903368 (2019). [Google Scholar]
- 24.Tonazzini A., Mintchev S., Schubert B., Mazzolai B., Shintake J., Floreano D., Variable stiffness fiber with self-healing capability. Adv. Mater. 28, 10142–10148 (2016). [DOI] [PubMed] [Google Scholar]
- 25.A. Firouzeh, M. Salerno, J. Paik, Soft pneumatic actuator with adjustable stiffness layers for multi-dof actuation, in Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (IEEE, 2015), pp. 1117–1124. [Google Scholar]
- 26.Santoso J., Skorina E. H., Salerno M., de Rivaz S., Paik J., Onal C. D., Single chamber multiple degree-of-freedom soft pneumatic actuator enabled by adjustable stiffness layers. Smart Mater. Struct. 28, 035012 (2019). [Google Scholar]
- 27.Wang L., Yang Y., Chen Y., Majidi C., Iida F., Askounis E., Pei Q., Controllable and reversible tuning of material rigidity for robot applications. Mater. Today 21, 563–576 (2018). [Google Scholar]
- 28.Rich S., Jang S.-H., Park Y.-L., Majidi C., Liquid metal-conductive thermoplastic elastomer integration for low-voltage stiffness tuning. Adv. Mater. Technol. 2, 1700179 (2017). [Google Scholar]
- 29.McEvoy M. A., Correll N., Thermoplastic variable stiffness composites with embedded, networked sensing, actuation, and control. J. Compos. Mater. 49, 1799–1808 (2015). [Google Scholar]
- 30.S. Diller, C. Majidi, S. H. Collins, A lightweight, low-power electroadhesive clutch and spring for exoskeleton actuation, in Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA) (IEEE, 2016), pp. 682–689. [Google Scholar]
- 31.Hinchet R., Shea H., High force density textile electrostatic clutch. Adv. Mater. Technol. 5, 1900895 (2020). [Google Scholar]
- 32.E. Steltz, A. Mozeika, J. Rembisz, N. Corson, H. Jaeger, Jamming as an enabling technology for soft robotics, in Electroactive Polymer Actuators and Devices (EAPAD) 2010 (International Society for Optics and Photonics, 2010), vol. 7642, p. 764225. [Google Scholar]
- 33.Manti M., Cacucciolo V., Cianchetti M., Stiffening in soft robotics: A review of the state of the art. IEEE Robot. Autom. Mag. 23, 93–106 (2016). [Google Scholar]
- 34.S. G. Fitzgerald, G. W. Delaney, D. Howard, A review of jamming actuation in soft robotics, in Actuators (Multidisciplinary Digital Publishing Institute, 2020), vol. 9, p. 104. [Google Scholar]
- 35.B. Aktaş, R. D. Howe, Tunable anisotropic stiffness with square fiber jamming, in Proceedings of the 2020 3rd IEEE International Conference on Soft Robotics (RoboSoft) (IEEE, 2020), pp. 879–884. [Google Scholar]
- 36.Brown E., Rodenberg N., Amend J., Mozeika A., Steltz E., Zakin M. R., Lipson H., Jaeger H. M., Universal robotic gripper based on the jamming of granular material. Proc. Natl. Acad. Sci. U.S.A. 107, 18809–18814 (2010). [Google Scholar]
- 37.N. G. Cheng, M. B. Lobovsky, S. J. Keating, A. M. Setapen, K. I. Gero, A. E. Hosoi, K. D. Iagnemma, Design and analysis of a robust, low-cost, highly articulated manipulator enabled by jamming of granular media, in Proceedings of the 2012 IEEE International Conference on Robotics and Automation (IEEE, 2012), pp. 4328–4333. [Google Scholar]
- 38.Cianchetti M., Ranzani T., Gerboni G., Nanayakkara T., Althoefer K., Dasgupta P., Menciassi A., Soft robotics technologies to address shortcomings in today’s minimally invasive surgery: The STIFF-FLOP approach. Soft Robot. 1, 122–131 (2014). [Google Scholar]
- 39.Jiang A., Ranzani T., Gerboni G., Lekstutyte L., Althoefer K., Dasgupta P., Nanayakkara T., Robotic granular jamming: Does the membrane matter? Soft Robot. 1, 192–201 (2014). [Google Scholar]
- 40.Ranzani T., Gerboni G., Cianchetti M., Menciassi A., A bioinspired soft manipulator for minimally invasive surgery. Bioinspir. Biomim. 10, 035008 (2015). [DOI] [PubMed] [Google Scholar]
- 41.J. Ou, L. Yao, D. Tauber, J. Steimle, R. Niiyama, H. Ishii, jamsheets: Thin interfaces with tunable stiffness enabled by layer jamming, in Proceedings of the 8th International Conference on Tangible, Embedded and Embodied Interaction (Association for Computing Machinery, 2014), pp. 65–72. [Google Scholar]
- 42.Narang Y. S., Vlassak J. J., Howe R. D., Mechanically versatile soft machines through laminar jamming. Adv. Funct. Mater. 28, 1707136 (2018). [Google Scholar]
- 43.Vasios N., Narang Y., Aktaş B., Howe R., Bertoldi K., Numerical analysis of periodic laminar and fibrous media undergoing a jamming transition. Eur. J. Mech. - A/Solids 75, 322–329 (2019). [Google Scholar]
- 44.M. Brancadoro, M. Manti, S. Tognarelli, M. Cianchetti, Preliminary experimental study on variable stiffness structures based on fiber jamming for soft robots, in Proceedings of the 2018 IEEE International Conference on Soft Robotics (RoboSoft) (IEEE, 2018), pp. 258–263. [Google Scholar]
- 45.Brancadoro M., Manti M., Grani F., Tognarelli S., Menciassi A., Cianchetti M., Toward a variable stiffness surgical manipulator based on fiber jamming transition. Front. Robot. AI 6, 12 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Brancadoro M., Manti M., Tognarelli S., Cianchetti M., Fiber jamming transition as a stiffening mechanism for soft robotics. Soft Robot. 7, 663–674 (2020). [DOI] [PubMed] [Google Scholar]
- 47.Jadhav S., Majit M. R. A., Shih B., Schulze J. P., Tolley M. T., Variable stiffness devices using fiber jamming for application in soft robotics and wearable haptics. Soft Robot. (2021). [DOI] [PubMed] [Google Scholar]
- 48.Kim Y.-J., Cheng S., Kim S., Iagnemma K., A novel layer jamming mechanism with tunable stiffness capability for minimally invasive surgery. IEEE Trans. Robot. 29, 1031–1042 (2013). [Google Scholar]
- 49.Yang Y., Zhang Y., Kan Z., Zeng J., Wang M. Y., Hybrid jamming for bioinspired soft robotic fingers. Soft Robot. 7, 292–308 (2020). [DOI] [PubMed] [Google Scholar]
- 50.Wang X., Wu L., Fang B., Xu X., Huang H., Sun F., Layer jamming-based soft robotic hand with variable stiffness for compliant and effective grasping. Cognit. Comput. Syst. 2, 44–49 (2020). [Google Scholar]
- 51.Choi I., Corson N., Peiros L., Hawkes E. W., Keller S., Follmer S., A soft, controllable, high force density linear brake utilizing layer jamming. IEEE Robot. Autom. Lett. 3, 450–457 (2017). [Google Scholar]
- 52.Choi W. H., Kim S., Lee D., Shin D., Soft, multi-dof, variable stiffness mechanism using layer jamming for wearable robots. IEEE Robot. Autom. Lett. 4, 2539–2546 (2019). [Google Scholar]
- 53.Shah D. S., Yang E. J., Yuen M. C., Huang E. C., Kramer-Bottiglio R., Jamming skins that control system rigidity from the surface. Adv. Funct. Mater. 31, 2006915 (2020). [Google Scholar]
- 54.Chapman G., The hydrostatic skeleton in the invertebrates. Biol. Rev. 33, 338–371 (1958). [Google Scholar]
- 55.Kier W. M., Smith K. K., Tongues, tentacles and trunks: The biomechanics of movement in muscular-hydrostats. Zool. J. Linn. Soc. 83, 307–324 (1985). [Google Scholar]
- 56.S. Kriegman, S. Walker, D. Shah, M. Levin, R. Kramer-Bottiglio, J. Bongard, Automated shapeshifting for function recovery in damaged robots. arXiv:1905.09264 [cs.RO] (22 May 2019).
- 57.Ishida M., Drotman D., Shih B., Hermes M., Luhar M., Tolley M. T., Morphing structure for changing hydrodynamic characteristics of a soft underwater walking robot. IEEE Robot. Autom. Lett. 4, 4163–4169 (2019). [Google Scholar]
- 58.Shah D. S., Powers J. P., Tilton L. G., Kriegman S., Bongard J., Kramer-Bottiglio R., A soft robot that adapts to environments through shape change. Nat. Mach. Intell. 3, 51–59 (2021). [Google Scholar]
- 59.Lee D.-Y., Kim S.-R., Kim J.-S., Park J.-J., Cho K.-J., Origami wheel transformer: A variable-diameter wheel drive robot using an origami structure. Soft Robot. 4, 163–180 (2017). [DOI] [PubMed] [Google Scholar]
- 60.Lin H.-T., Leisk G. G., Trimmer B., Goqbot: A caterpillar-inspired soft-bodied rolling robot. Bioinspir. Biomim. 6, 026007 (2011). [DOI] [PubMed] [Google Scholar]
- 61.Liu K., Hacker F., Daraio C., Robotic surfaces with reversible, spatiotemporal control for shape morphing and object manipulation. Sci. Robot. 6, eabf5116 (2021). [DOI] [PubMed] [Google Scholar]
- 62.Reyssat E., Mahadevan L., Hygromorphs: From pine cones to biomimetic bilayers. J. R. Soc. Interface 6, 951–957 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Armon S., Efrati E., Kupferman R., Sharon E., Geometry and mechanics in the opening of chiral seed pods. Science 333, 1726–1730 (2011). [DOI] [PubMed] [Google Scholar]
- 64.van Rees W. M., Vouga E., Mahadevan L., Growth patterns for shape-shifting elastic bilayers. Proc. Natl. Acad. Sci. U.S.A. 114, 11597–11602 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Gladman A. S., Matsumoto E. A., Nuzzo R. G., Mahadevan L., Lewis J. A., Biomimetic 4d printing. Nat. Mater. 15, 413–418 (2016). [DOI] [PubMed] [Google Scholar]
- 66.Boley J. W., van Rees W. M., Lissandrello C., Horenstein M. N., Truby R. L., Kotikian A., Lewis J. A., Mahadevan L., Shape-shifting structured lattices via multimaterial 4d printing. Proc. Natl. Acad. Sci. U.S.A. 116, 20856–20862 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.A. G. Holzapfel, Nonlinear Solid Mechanics II (John Wiley & Sons, Inc., 2000). [Google Scholar]
- 68.R. R. Craig, Mechanics of Materials (John Wiley & Sons, Inc., 2011). [Google Scholar]
- 69.Efrati E., Sharon E., Kupferman R., Buckling transition and boundary layer in non-Euclidean plates. Phys. Rev. E 80, 016602 (2009). [DOI] [PubMed] [Google Scholar]
- 70.Efrati E., Sharon E., Kupferman R., Elastic theory of unconstrained non-euclidean plates. J. Mech. Phys. Solids 57, 762–775 (2009). [Google Scholar]
- 71.D. J. Struik, Lectures on Classical Differential Geometry (Courier Corporation, 1961). [Google Scholar]
- 72.Klein Y., Efrati E., Sharon E., Shaping of elastic sheets by prescription of non-Euclidean metrics. Science 315, 1116–1120 (2007). [DOI] [PubMed] [Google Scholar]
- 73.Timoshenko S., Analysis of bi-metal thermostats. J. Opt. Soc. Am. 11, 233 (1925). [Google Scholar]
- 74.Pezzulla M., Smith G. P., Nardinocchi P., Holmes D. P., Geometry and mechanics of thin growing bilayers. Soft Matter 12, 4435–4442 (2016). [DOI] [PubMed] [Google Scholar]
- 75.J. K. Lee, N. Stoffel, K. Fite, Electronic packaging of sensors for lower limb prosthetics, in Proceedings of the 2012 IEEE 62nd Electronic Components and Technology Conference (IEEE, 2012), pp. 86–91. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Notes S1 to S5
Tables S1 to S3
Figs. S1 to S10
Legends for movies S1 to S5
References
Movies S1 to S5