A mechanistic model of gossip, reputations, and cooperation

Significance

Those who help others may earn good reputations, making them more likely to receive help themselves. This feedback loop—called indirect reciprocity—fosters cooperation provided people agree on who is in good or bad standing. Gossip has long been thought to produce such agreement. But how much gossip is required to generate sufficient consensus and stabilize cooperation? To study this problem, we develop a game-theoretic model of behavior along with a mechanistic model of gossip about social standing. We analyze how the amount of gossip required for stable cooperation depends on the costs and benefits of helping others, as well as errors and transmission biases. Our account underscores the importance of communication for sustaining systems of social status that support cooperation.

Abstract

Social reputations facilitate cooperation: those who help others gain a good reputation, making them more likely to receive help themselves. But when people hold private views of one another, this cycle of indirect reciprocity breaks down, as disagreements lead to the perception of unjustified behavior that ultimately undermines cooperation. Theoretical studies often assume population-wide agreement about reputations, invoking rapid gossip as an endogenous mechanism for reaching consensus. However, the theory of indirect reciprocity lacks a mechanistic description of how gossip actually generates consensus. Here, we develop a mechanistic model of gossip-based indirect reciprocity that incorporates two alternative forms of gossip: exchanging information with randomly selected peers or consulting a single gossip source. We show that these two forms of gossip are mathematically equivalent under an appropriate transformation of parameters. We derive an analytical expression for the minimum amount of gossip required to reach sufficient consensus and stabilize cooperation. We analyze how the amount of gossip necessary for cooperation depends on the benefits and costs of cooperation, the assessment rule (social norm), and errors in reputation assessment, strategy execution, and gossip transmission. Finally, we show that biased gossip can either facilitate or hinder cooperation, depending on the direction and magnitude of the bias. Our results contribute to the growing literature on cooperation facilitated by communication, and they highlight the need to study strategic interactions coupled with the spread of social information.

Reputations and social norms are critical for cooperation in large human societies (1–3). Individuals can improve their reputations by behaving altruistically, making others more likely to help them in the future. According to a large body of theoretical work (4–7), this feedback loop, termed indirect reciprocity, can maintain cooperation even among strangers. There is also ample empirical evidence that reputations facilitate altruistic behavior: In laboratory settings, people are more likely to offer help when others are observing them (8) or when others have knowledge of their behavioral history (9); field studies show that individuals of higher social status are more likely to gain cooperative partners (10, 11).

Indirect reciprocity facilitates cooperation only when individuals agree about each other’s social standing. The standard theory of indirect reciprocity assumes by fiat that reputations are common knowledge so that the entire population agrees about the reputation of each individual (12–14). Consensus about reputations helps maintain cooperation, as individuals choose to cooperate with those of good social standing, thereby earning good reputations for themselves.

However, when people hold private opinions about each other’s social standing, disagreements can lead to the perception of unjustified behavior that eventually undermines cooperation (15–21). Theoretical studies have proposed several mechanisms that could help maintain cooperation even when reputations are held privately—including empathetic perspective taking (22), generous moral evaluation (23, 24), nuanced quantitative assessments (25), and a monitoring system that broadcasts public information about reputations (26).

Nonetheless, the most common justification for assuming consensus about reputations (7, 17, 18, 20, 22, 26–30) is an endogenous mechanism of rapid gossip within a population—that is, the exchange of information about the social standings of others (31–33). According to this reasoning, even if individuals initially disagree about each other’s standing, rapid gossip will eventually lead to consensus. The role of gossip in cooperation also has empirical support, as laboratory (32, 34–39) and field (40) studies show that people tend to cooperate more when (they believe) their peers gossip about their behavior.

Despite the intuitive appeal of gossip and empirical studies of its effects, the theory of indirect reciprocity lacks a mechanistic description of how gossip produces consensus about social standings in a population. Existing work on gossip has focused on how gossip allows recipients to detect potential cheaters and selectively avoid them (partner choice; 34, 37, 41, 42) or how honest or dishonest gossip can incentivize cooperation or punish free riders (gossip strategies; 38, 39, 43, 44, 45). But how gossip produces consensus about reputations—and thereby stabilizes cooperation—has received less attention (20, 46). Several key questions remain unanswered: How much gossip is required to support cooperation? How does the structure of gossip transmission govern convergence to consensus? How will noise or bias in transmission deteriorate the effects of gossip?

Here, we address these questions by developing a model of indirect reciprocity that integrates a mechanistic description of gossip about social reputations. We consider two forms of gossip: exchanging information with randomly selected peers or consulting a single gossip source. We show that these two gossip processes are mathematically equivalent under an appropriate transformation of parameters. We then derive an analytical expression for the minimum amount of gossip required to stabilize cooperation, and we discuss how this critical gossip duration depends on model parameters, including the benefit-to-cost ratio for cooperation, the assessment rule (social norm), and the rates of error in reputation assessment, strategy execution, and gossip transmission. We conclude by showing that biased gossip—that is, sharing false information about another individual’s social standing—can either facilitate or hinder cooperation, depending on its direction (positive or negative) and magnitude.

A Model of Gossip, Reputations, and Social Behavior

Social Interactions.

We build on a well-established framework for modeling cooperation by indirect reciprocity (18, 47). A large, well-mixed population of individuals engage in pairwise social interactions. Each interaction takes the form of a one-shot donation game. In each game, the donor chooses whether or not to cooperate with the recipient by paying a cost $c>0$ to provide a benefit $b>c$. If the donor defects, she incurs no cost and provides no benefit to the recipient.

Whether or not a donor cooperates depends on her current behavioral strategy. We consider the three strategies that are most common in studies of indirect reciprocity (22, 27, 47): always cooperate (ALLC), which means the donor intends to cooperate with any recipient; always defect (ALLD), which means the donor defects against any recipient; and discriminate (DISC), which means the donor intends to cooperate when the recipient has a good reputation but defect when the recipient has a bad reputation. We allow for errors in strategy execution (18, 19, 47): With probability $0<u_e<1/2$ (execution error rate), a donor erroneously defects while intending to cooperate.

The resulting payoffs of cooperators (ALLC), defectors (ALLD), and discriminators (DISC) are given by

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\pi }_{\text{ALLC}}& =\left(1-u_e\right)[b\left(f_{\text{ALLC}}+f_{\text{DISC}}·r_{\text{ALLC}}\right)-c],\hfill \\ \hfill {\pi }_{\text{ALLD}}& =\left(1-u_e\right)[b\left(f_{\text{ALLC}}+f_{\text{DISC}}·r_{\text{ALLD}}\right)],\hfill \\ \hfill {\pi }_{\text{DISC}}& =\left(1-u_e\right)[b\left(f_{\text{ALLC}}+f_{\text{DISC}}·r_{\text{DISC}}\right)-c·r],\hfill \end{array}\end{array}$$ [1]

where $f_s$ is the frequency of strategic type $s\in S=\{\text{ALLC},\text{ALLD},\text{DISC}\}$ in the population, satisfying $\sum _{s\in S}{f}_s=1$. Here, $r_s$ denotes the average reputation of type $s$, i.e., the fraction of the population that views an individual of type $s$ as good; and $r=\sum _{s\in S}{f}_s·r_s$ is the average reputation in the population.

Reputation Updates (Fast Timescale).

After a round of pairwise game play—that is, after every individual interacts with every other individual, serving once as a donor and once as a recipient—individuals then privately assess the reputation of each donor by observing her action toward a randomly selected recipient (Fig. 1 A and B). At this point, individuals may disagree about the reputation of a given donor because they assessed the donor based on her interaction with potentially different recipients. In addition, we assume there is a small probability of error $0<u_a<1/2$ (assessment error rate) for each assessment (19, 48), which occurs independently for each person who assesses a donor.

Fig. 1.

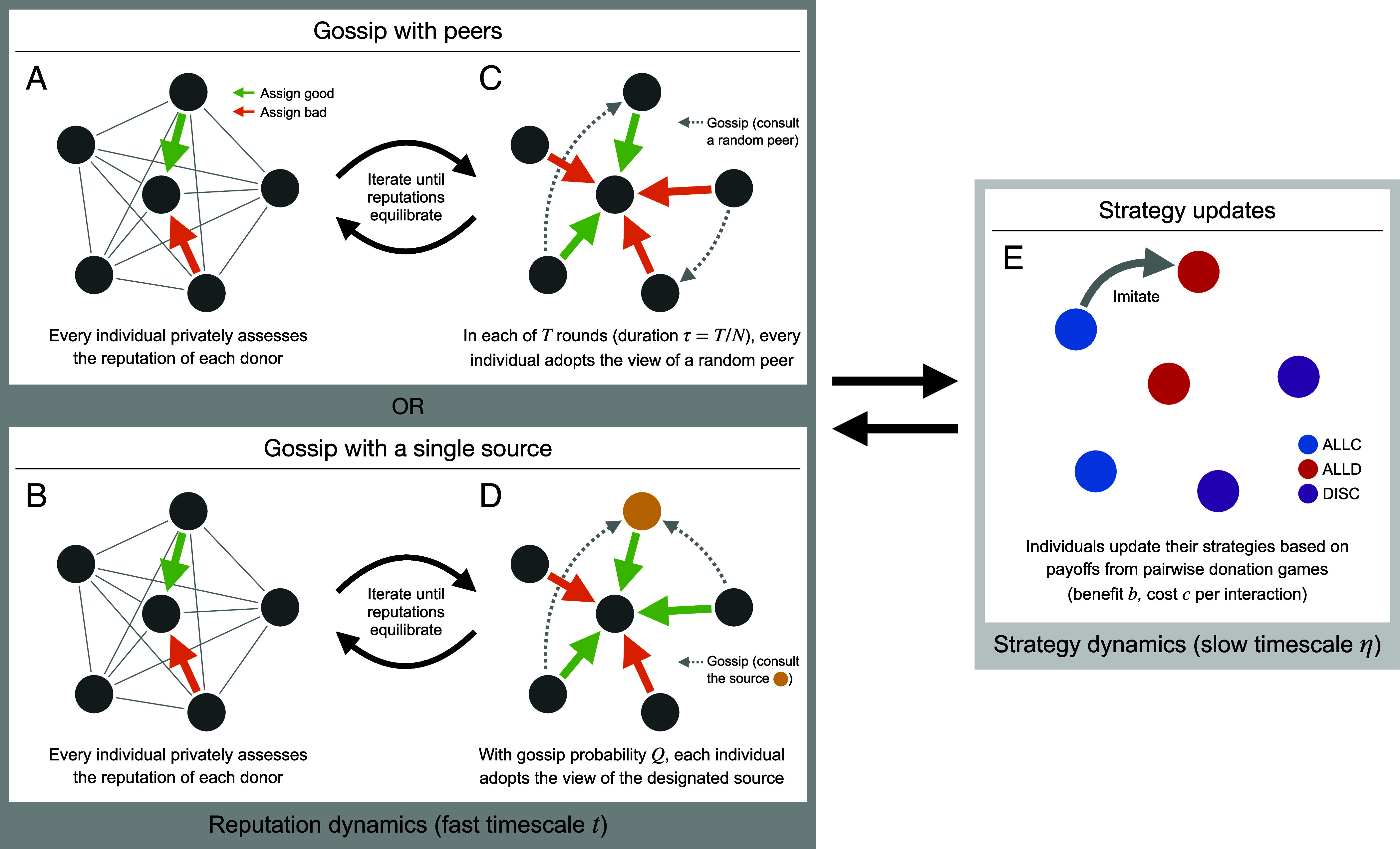
A model of gossip, reputations, and social behavior. We consider a large, well-mixed population of individuals (nodes) engaged in pairwise social interactions (edges). (A and B) After a round of pairwise social interactions, individuals privately assess each donor’s reputation by judging her action toward a randomly selected recipient. As a result of independent observations, individuals may disagree about the reputation of a given donor (orange and green arrows). (C and D) Private assessments are followed by a period of gossip, governed by one of two mechanisms. (C) Gossip with peers. In each of $T$ rounds (equivalent to scaled duration $\tau =T/N$, where $N$ is the population size), each individual consults a randomly selected peer (dotted arrows) and adopts her view of the focal individual. (D) Gossip with a single source. With probability $Q$, each observer consults the same, designated gossip source (dotted arrows toward the yellow node) and adopts her view of the focal individual. (E) Periods of private observations and periods of gossip (steps A and C or steps B and D) repeat until reputations equilibrate. Once reputations reach equilibrium, individuals update their behavioral strategies by payoff-biased imitation. Colors indicate the three possible behavioral strategies: ALLC (blue), ALLD (red), and DISC (purple).

Private assessments are then followed by a period of gossip about reputations (Fig. 1C or D), which tends to increase agreement (see below). After the gossip period, there is yet another round of private assessments. Subsequent periods of private assessments and periods of gossip occur iteratively until reputations equilibrate.

Under these assumptions, the average reputation of each strategic type $s$ changes according to the ODEs (SI Appendix, section 4; 49),

$$\begin{array}{c}\hfill \frac{d{r}_s}{\mathit{dt}}=p_s(t)-r_s(t),s\in S=\{\text{ALLC},\text{ALLD},\text{DISC}\},\end{array}$$ [2]

where $p_s(t)$ is the probability that an individual of strategic type $s$ will be assigned a good reputation by an observer, which depends on the current reputations in the population as follows (Materials and Methods):

$$\begin{array}{cc}\hfill p_{\text{ALLC}}(t)& =r(t)P_{\mathit{GC}}+\left(1-r(t)\right)P_{\mathit{BC}},\hfill \\ \hfill p_{\text{ALLD}}(t)& =r(t)P_{\mathit{GD}}+\left(1-r(t)\right)P_{\mathit{BD}},\hfill \\ \hfill p_{\text{DISC}}(t)& ={\tilde{g}}_2(t)P_{\mathit{GC}}+{\tilde{d}}_2(t)\left(P_{\mathit{BC}}+P_{\mathit{GD}}\right)+{\tilde{b}}_2(t)P_{\mathit{BD}},\hfill \\ \hfill r(t)& \triangleq {\displaystyle \sum _{s\in S}}{f}_s·r_s(t).\hfill \end{array}$$ [3]

The terms $P_{\mathit{XY}}$ in these equations correspond to reputation assignments during private assessment. In particular, $P_{\mathit{XY}}$ denotes the probability that an observer will assign a focal individual a good reputation after she takes action $X\in \{\text{Cooperate}(C),\text{Defect}(D)\}$ against a recipient who has reputation $Y\in \{\text{Good}(G),\text{Bad}(B)\}$ in the eyes of the observer. This quantity depends on the assessment and execution error rates ($u_a$ and $u_e$), as well as the social norm, a set of rules that govern how an observer judges a donor’s reputation based on her action toward a recipient (7, 13, 14, 19, 27). We consider three second-order social norms that are most common in studies of indirect reciprocity (22, 26, 29, 47): Stern Judging, Simple Standing, and Shunning (see Materials and Methods for definitions).

The terms ${\tilde{g}}_2$, ${\tilde{b}}_2$, and ${\tilde{d}}_2$ in Eq. 3 quantify the degree of agreement and disagreement about social reputations: ${\tilde{g}}_2$ denotes the probability that, after a period of gossip, two randomly selected individuals agree that a third individual is good; ${\tilde{b}}_2$ denotes the probability that, after gossip, two individuals agree that a third individual is bad; and $2{\tilde{d}}_2$ denotes the probability that, after gossip, two individuals disagree about the reputation of a third. The expressions for the average reputations of the three strategic types (Eq. 3) have the same form as in prior models of private reputations (22, 26, 29), except that the terms ${\tilde{g}}_2$, ${\tilde{d}}_2$, and ${\tilde{b}}_2$ differ from prior studies as the result of the gossip process, as we will describe below.

We refer to $r_s$ evaluated at the equilibrium of Eq. 2 as the equilibrium reputation of strategic type $s$, and we compute the agreement level at the reputation equilibrium as ${\tilde{g}}_2+{\tilde{b}}_2=\sum _s{f}_s{r}_s^2+\sum _s{f}_s{\left(1-r_s\right)}^2$. As we will see below, gossip does not change the reputation dynamics or the equilibrium reputations for individuals using strategy ALLD or ALLC, but it will tend to increase the level of agreement in the population about such reputations. By contrast, gossip can change the equilibrium reputation of discriminators ($r_{\text{DISC}}$) in the population, in addition to increasing the level of agreement about such reputations.

Gossip.

The dynamics described above include terms that account for gossip, which tends to increase agreement about reputations. We develop models for two forms of gossip: pairwise gossip between random peers or gossip with a single source. We analyze how gossip modifies the level of agreement in the population about each other’s reputations.

In the absence of gossip, there are classical expressions for the probability that two independent private observers will agree a given focal individual is good ($g_2=\sum _{s\in S}{f}_s{r}_s^2$), agree a focal individual is bad ($b_2=\sum _{s\in S}{f}_s{\left(1-r_s\right)}^2$), or disagree about the reputation of a focal individual ($2d_2=2\sum _{s\in S}{f}_s{r}_s\left(1-r_s\right)$). These expressions assume independent observations of the focal individual’s action toward a random recipient (22, 29). By contrast, the levels of agreement and disagreement after a period of gossip, denoted ${\tilde{g}}_2$, ${\tilde{b}}_2$, and ${\tilde{d}}_2$, will depart from the classical case of independent assessment, as described below.

Peer-to-peer gossip.

We model gossip as a process in which the reputation of a focal individual (the subject of gossip) spreads from peer to peer (Fig. 1C). We consider a large population of $N$ individuals engaged in gossip. In each of $T$ rounds during this gossip process, and for each focal individual $i$, every individual randomly selects a peer and adopts her view of $i$’s reputation. The gossip dynamics for a focal individual are therefore described by a biallelic haploid Wright–Fisher process, which keeps track of how many individuals view the focal individual as good (allele one) or bad (allele two) over discrete generations (rounds) of gossip. In each generation, the choice of the peer from whom to receive gossip corresponds to the choice of parentage in a neutral coalescent (Materials and Methods). The Wright–Fisher processes describing gossip about different focal individuals are assumed independent.

At the start of the gossip process, the fraction $r_i$ of the population who view a focal individual $i$ of type $s$ as good is given by fraction $r_s(t)$ of the population who view type $s$ as good in the context of the reputation ODEs that track the average reputations of different types (Eq. 2). After $T$ rounds (Wright–Fisher generations) of peer-to-peer gossip, the agreement and disagreement terms are modified as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\tilde{g}}_2& =g_2+d_2·\left(1-e^{-\tau }\right),\hfill \\ \hfill {\tilde{b}}_2& =b_2+d_2·\left(1-e^{-\tau }\right),\hfill \\ \hfill {\tilde{d}}_2& =d_2·e^{-\tau },\hfill \end{array}\end{array}$$ [4]

where we define $\tau \triangleq T/N$ as the scaled gossip duration, and where again $g_2$, $b_2$, $d_2$ denote corresponding agreement and disagreement terms from private observations before gossip (22, 29). These expressions for the effect of gossip are derived from the loss of heterozygosity over time in a Wright–Fisher process (Materials and Methods). In SI Appendix, section 4, we also derive this mean-field model as a formal limit of a finite-population process.

The number of gossip rounds, $T$, quantifies the amount of peer-to-peer gossip that occurs in between periods of private observations. Thus, the duration of each gossip period, $T$, can be thought of as the relative rate of gossip versus private observation. The case $\tau \to \infty$ (infinitely long period of peer-to-peer gossip) is equivalent to public information about reputations, with no disagreements (${\tilde{d}}_2=0$).

Gossip with a single source.

As an alternative model of gossip, we consider a process in which the reputation of a focal individual spreads from a single source (Fig. 1D). This single source could represent, for example, an influential individual in a neighborhood, or a member of an adolescent social group who is at the center of the flow of social information within her community.

In this case, we suppose that a randomly selected individual serves as the sole source of gossip. In each period of gossip, each individual decides either to retain their private view of a donor’s reputation (with probability $1-Q$, $0\le Q\le 1$) or to consult the gossip source (with probability $Q$) and adopt the source’s view of the donor. Decisions on whether or not to consult the source are made independently for each individual’s view of each individual.

The resulting rates of agreement and disagreement after one period of single-source gossip are given by (Materials and Methods)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\tilde{g}}_2& =\left(1-Q^2\right)·g_2+Q^2·r,\hfill \\ \hfill {\tilde{b}}_2& =\left(1-Q^2\right)·b_2+Q^2·(1-r),\hfill \\ \hfill {\tilde{d}}_2& =\left(1-Q^2\right)·d_2.\hfill \end{array}\end{array}$$ [5]

Here, $Q^2$ represents the probability that a random observer and a random donor have both consulted the gossip source. The quantity $Q^2$ is mathematically equivalent to the probability of unilateral empathetic assessment studied in ref. 22 (SI Appendix, section 1). In SI Appendix, section 4, we also derive this mean-field model as a formal limit of a finite-population process.

Note that the case $Q=1$ (assured consultation of the gossip source) is equivalent to public information about reputations, with no disagreements. (In fact, since $r=g_2+d_2$ and $1-r=b_2+d_2$, the expressions for ${\tilde{g}}_2$, ${\tilde{b}}_2$, and ${\tilde{d}}_2$ in Eq. 5 match the corresponding expressions in Eq. 4 in the limit of public information, i.e., $Q=1$ or $\tau \to \infty$.)

Strategy Updates (Slow Timescale).

Reputations change through iterated periods of private observations and gossip, eventually reaching equilibrium values for each strategic type, given by the equilibrium of Eq. 3. After reputations equilibrate, individuals then update their strategies by payoff-biased imitation [Fig. 1E; 50). This modeling framework assumes a separation of timescales, motivated by the idea that reputations change quickly, whereas people are slow to change their behavior. That is, we assume that reputations equilibrate before individuals update behavioral strategies, as is standard in studies of indirect reciprocity (15, 18, 19, 47).

We describe the dynamics of competing strategies using replicator-dynamic ODEs (51),

$$\begin{array}{c}\hfill \frac{d{f}_s}{d\eta }=f_s(\eta )\left({\pi }_s(\eta )-\overline{\pi }\right(\eta )),\end{array}$$ [6]

where ${\pi }_s(\eta )$ denotes the payoff to an individual of strategic type $s$ (Eq. 1) and $\overline{\pi }(\eta )=\sum _{s\in S}{f}_s(\eta ){\pi }_s(\eta )$ denotes the average payoff of the population, at time $\eta$. We use a different notation for time, $\eta$, to describe the strategy dynamics in order to distinguish this process from the reputation dynamics. The reputation dynamics occur on a faster timescale, denoted $t$, and they reach equilibrium (and influence payoffs) before any strategic changes occur.

Results

Gossip with a Single Source Is Equivalent to Peer-to-Peer Gossip.

Both proposed mechanisms of gossip—consulting a single source or transferring reputation information between peers—will tend to increase agreement about reputations across the population. To gain some intuition for this effect, we will start by comparing the two models of gossip to one another before considering their downstream impact on behavioral evolution.

The duration of peer-to-peer gossip ($\tau$) governs the extent of agreement that peer-to-peer gossip induces, as does the probability of consulting the source ($Q$) under the single-source gossip model. By comparing the expressions for ${\tilde{g}}_2$, ${\tilde{d}}_2$, and ${\tilde{b}}_2$ in Eq. 4 (peer-to-peer model; Fig. 1A and C) and Eq. 5 (single-source model; Fig. 1B and D), we see that the two models of gossip are, in fact, mathematically equivalent, with the following mapping between the duration of peer-to-peer gossip $\tau$ and the probability $Q$ of consulting the single source:

$$\begin{array}{c}\hfill \tau =-log(1-Q^2).\end{array}$$ [7]

The classical case of fully private information (18) corresponds to no peer-to-peer gossip ($T=0$) or, equivalently, to no consultation with the single source ($Q=0$). By contrast, the case of fully public information (18) corresponds to the limit of an infinitely long duration of peer-to-peer gossip ($T\to \infty$) or, equivalently, assured consultation of the single source ($Q\to 1$); in this limit, there will be no disagreement about reputations (${\tilde{d}}_2=0$). Thus, these mechanistic models of gossip span continuously between public and private information about reputations.

Eq. 7 provides some quantitative intuition about the relationship between single-source and peer-to-peer gossip. For example, peer-to-peer gossip for duration $\tau =1/100$ (e.g., one Wright–Fisher generation in a population of $100$ individuals, or $100$ peer-to-peer gossip events) corresponds to single-source gossip with $Q=0.0998$ (i.e., $\approx$10% chance of consulting the gossip source per individual), whereas peer-to-peer gossip for duration $\tau =1$ ($N$ Wright–Fisher generations in a population of $N$ individuals, or $N^2$ peer-to-peer gossip events) corresponds to $Q=0.795$ (i.e., $\approx$80% chance of consulting the gossip source per individual) (SI Appendix, Fig. S1).

Gossip Stabilizes Cooperation.

We will use the peer-to-peer model (Eq. 4) to study how gossip impacts reputations and cooperation. All our results can be translated into the language of the single-source model using the transformation given by Eq. 7. We focus on understanding how gossip can stabilize cooperation under the Stern Judging norm—because this norm provides the highest rates of cooperation under public information, but it renders cooperation vulnerable to invasion by defectors when reputations are assessed privately without any gossip (18). In SI Appendix, we report corresponding results for the Simple Standing and Shunning norms (SI Appendix, sections 2.2 and 2.3 and Fig. S2).

When reputations are assessed privately without gossip, competition among cooperators (ALLC), defectors (ALLD), and discriminators (DISC) will always lead to a population of pure defectors under the Stern Judging norm. That is, the only stable strategic equilibrium is $f_{\text{ALLD}}=1$, regardless of the benefits and costs of cooperation ($b$ and $c$) or the rates of erroneous action or assessment ($u_e$ and $u_a$) (18). Gossip can qualitatively change this outcome. For example, when gossip occurs for duration $\tau =0.4$ (Fig. 2A), both ALLD and DISC are stable strategic equilibria; indeed, there is a large basin of initial conditions that lead the population to the DISC equilibrium, which supports high levels of cooperation. This basin disappears in the absence of gossip ($\tau =0.0$; Fig. 2C). Stochastic simulations in finite populations show agreement with these analytical predictions derived from the infinite-population replicator-dynamic ODEs (Eq. 6; Fig. 2B and D). Thus, at least under Stern Judging, gossip can sometimes stabilize cooperation.

Fig. 2.

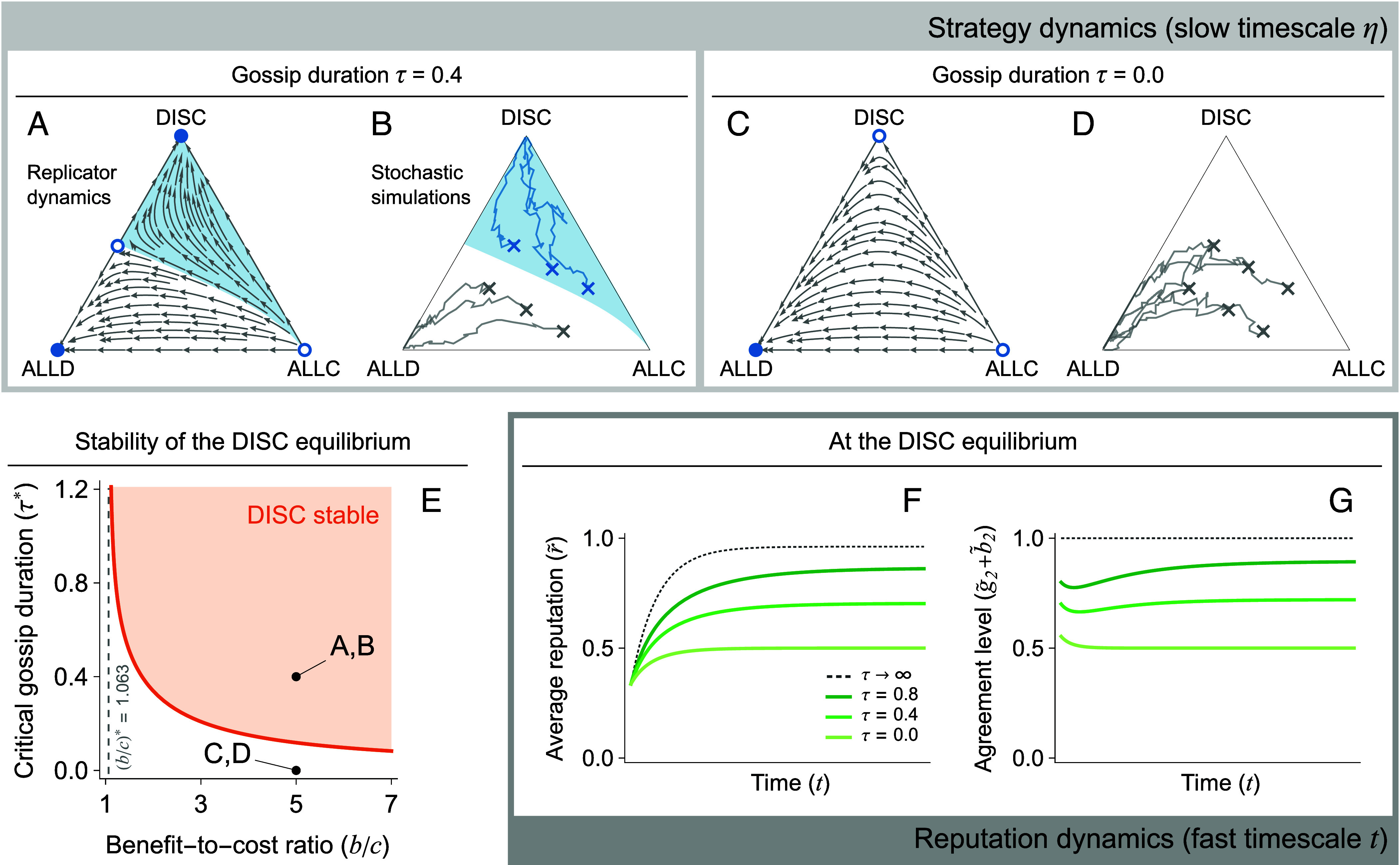
Sufficiently long gossip stabilizes cooperation. (A–D) Dynamics of competition among strategies ALLC, ALLD, and DISC under the Stern Judging norm, with a fixed benefit-to-cost ratio ($b/c=5$). (A and C) Gradients of selection (arrows) in the replicator dynamics (Eq. 6)). There is a basin of attraction toward the DISC vertex (shaded region) when $\tau =0.4>{\tau }^{\ast }$ (A) but not when $\tau =0.0<{\tau }^{\ast }$ (C). (B and D) Trajectories of stochastic simulations in a finite population ($N=100$), with x’s indicating different initial conditions (Materials and Methods). The long-term behavior of the stochastic simulations is consistent with the analytical predictions of the replicator-dynamic ODEs (B vs. A; D vs. C): When $\tau =0.4>{\tau }^{\ast }$ (B), trajectories starting from initial conditions above the separatrix tend to converge to the DISC vertex (the shaded region denotes the basin of attraction in A). When $\tau =0.0<{\tau }^{\ast }$ (D), all six trajectories converge to the ALLD vertex. (E) The discriminator-only equilibrium ($f_{\text{ALLD}}=1$) is locally stable only if the scaled gossip duration $\tau$ exceeds a critical value ${\tau }^{\ast }$ (solid orange curve defined by condition ii) and $b/c$ exceeds a critical value ${(b/c)}^{\ast }$ (dashed gray line defined by condition i). The orange region indicates parameter values where both these conditions are satisfied. The critical gossip duration ${\tau }^{\ast }$ decreases with the benefit-to-cost ratio, $b/c$. (F and G) The average reputation and agreement level as a function of time $t$ during the process of reputation dynamics by independent observations and gossip (Eq. 2). These quantities are evaluated at the DISC vertex ($f_{\text{DISC}}=1$) with a fixed benefit-to-cost ratio ($b/c=5$). Colors correspond to different values for the duration of gossip periods, $\tau$. The lightest green corresponds to $\tau =0.0$ (no gossip), which is equivalent to private reputations. The gray dashed curves correspond to $\tau \to \infty$ (infinitely long gossip), which is equivalent to public reputations. Other parameters: $u_a=u_e=0.02$. Analogous results for the Simple Standing and Shunning norms are shown in SI Appendix, Fig. S2.

The key question remains: How much gossip is required to sustain cooperation? Is an arbitrarily small but positive amount of gossip sufficient? To answer these questions, we derive an analytical condition for the stability of the discriminator equilibrium. First, to compute the equilibrium reputations, we substitute the agreement and disagreement terms from the peer-to-peer gossip process (Eq. 4) into the expressions in Eq. 3, and we set the right-hand side of the fast-time reputation ODEs (Eq. 2) to zero. These equilibrium reputations in turn determine the payoffs to strategic types (Eq. 1), which we substitute into the replicator-dynamic ODEs (Eq. 6). Linear stability analysis (Linear Stability Analysis in Materials and Methods) shows that the discriminator equilibrium ($f_{\text{DISC}}=1$) is locally stable under the Stern Judging norm if and only if the following conditions are both satisfied:

• (i) $\begin{array}{c}\frac{b}{c}>{\left(\frac{b}{c}\right)}^{\ast }=\frac{1}{\left(1-2u_a\right)(1-u_e)}\text{and}\hfill \end{array}$
• (ii) $\begin{array}{c}\tau >{\tau }^{\ast }=log\left[\left(2-\frac{\left(\frac{b}{c}\right)}{\left(\frac{b}{c}\right)-\frac{1}{2(1-u_a)}}\right)\left(\frac{\left(\frac{b}{c}\right)}{\left(\frac{b}{c}\right)-{\left(\frac{b}{c}\right)}^{\ast }}\right)\right].\hfill \end{array}$

The first condition above is identical to the minimum benefit-to-cost ratio ${(b/c)}^{\ast }$ required to stabilize the discriminator equilibrium under fully public information (dashed line in Fig. 2E), which is already known in the literature (29). The second condition gives, in addition, the critical gossip duration ${\tau }^{\ast }$ required to stabilize cooperation. Note that ${\tau }^{\ast }$ is a decreasing function of the benefit-to-cost ratio ($\partial {\tau }^{\ast }/\partial (b/c)<0$)—which means that less gossip is required to stabilize cooperation when the benefits of mutual cooperation are greater (Fig. 2E). The duration of gossip required ${\tau }^{\ast }$ approaches infinity as $b/c\to {(b/c)}^{\ast }$, meaning that no amount of gossip can outperform fully public information (at least when there is no bias in gossip transmission, an assumption we will later relax). Conversely, ${\tau }^{\ast }$ approaches zero as $b/c\to \infty$, which means that a positive amount of gossip is always required to stabilize cooperation, except in the limit of an infinite benefit-to-cost ratio.

$$\begin{array}{cc}& \mathbb{E}[R_{i,\tau }|R_{i,0}=r_{i,0}]=\left(r_{i,0}-\frac{\nu }{\mu +\nu }\right)e^{-\left(\mu +\nu \right)\tau }+\frac{\nu }{\mu +\nu }\hfill \\ \hfill & \mathrm{Var}(R_{i,\tau }|R_{i,0}=r_{i,0})=\frac{\nu }{\mu +\nu }\left(1-\frac{\nu }{\mu +\nu }\right)·\frac{1}{1+2\left(\mu +\nu \right)}\left(1-e^{-\left(2\left(\mu +\nu \right)+1\right)\tau }\right)\hfill \\ \hfill & +\left(1-\frac{2\nu }{\mu +\nu }\right)\left(r_{i,0}-\frac{\nu }{\mu +\nu }\right)\frac{1}{1+\left(\mu +\nu \right)}·e^{-\left(\mu +\nu \right)\tau }\left(1-e^{-\left(\left(\mu +\nu \right)+1\right)\tau }\right)-{\left(r_{i,0}-\frac{\nu }{\mu +\nu }\right)}^2{e}^{-2\left(\mu +\nu \right)\tau }\left(1-e^{-\tau }\right)\hfill \end{array}$$ [8]

Gossip stabilizes cooperation because it increases agreement about reputations—even in the presence of errors—and consequently improves how discriminators view each other on average. To demonstrate this, we plot the average reputation (Fig. 2F) and average agreement level (Fig. 2G) in the population at the discriminator-only equilibrium ($f_{\text{DISC}}=1$) as a function of time $t$ for different durations of gossip $\tau$. In the absence of gossip ($\tau =0$), both quantities equilibrate at $1/2$, in agreement with results under fully private information (22). As the gossip duration $\tau$ increases, both agreement and average reputation increase. In the limit of infinitely long gossip ($\tau \to \infty$), we achieve the same average reputation and agreement level as under fully public information (dashed curves in Fig. 2 F and G). In this sense, our model of gossip spans the spectrum from fully private to fully public information about social reputations.

Conditions (i) and (ii) also reveal how errors modulate the effects of gossip. Since errors in either reputation assessment or strategy execution increase the possibility of misassigned reputations and therefore disagreement, we might expect that gossip would need to proceed for longer to counteract their destabilizing effects. Indeed, we can prove that ${\tau }^{\ast }$ is monotonically increasing with the error rates: $\partial {\tau }^{\ast }/\partial u_a>0$ and $\partial {\tau }^{\ast }/\partial u_e>0$ whenever condition (i) is satisfied (SI Appendix, section 2.1 and Fig. S3).

Noisy Gossip Is Less Beneficial for Cooperation.

We have assumed that reputation information is transmitted faithfully during peer-to-peer gossip. However, in reality, gossip transmission is a noisy and possibly even biased process, just like in the game of telephone: An individual might hear from a source that a focal individual is good, but that individual might convey the opposite information to the next individual in line, either accidentally (e.g., misunderstanding) or intentionally (e.g., preferential treatment or malice).

To account for noise in transmission, we introduce the possibility of “mutation” in the Wright–Fisher process describing peer-to-peer gossip over subsequent rounds (or “generations”). Suppose that, in round $T$, there are $\ell$ individuals who believe a given focal individual $i$ is good and $N-\ell$ who believe individual $i$ is bad. We now assume that an individual who consults a peer who believes $i$ is good will, with probability $u$, adopt the opposite opinion (“mutate”) in round $T+1$. Likewise, an individual who consults a peer who believes $i$ is bad will, with probability $v$, adopt the opposite opinion. In the absence of mutation ($u=v=0$), we recover the model of noiseless gossip.

We let $R_{i,T}\in \{0,1/N,\cdots ,\left(N-1\right)/N,1\}$ be a random variable that tracks the frequency of individuals who view individual $i$ as good in round $T$. Assuming that 1) $N$ is large, 2) $u$ and $v$ are small, and 3) a fraction $r_{i,0}$ view $i$ as good at the start of gossip ($T=0$), we can approximate the mean and variance after $T$ generations of peer-to-peer gossip (equivalent to duration $\tau \triangleq T/N$, as before) about focal individual $i$ as Eq. 8, where $\mu =Nu$ and $\nu =Nv$ are scaled mutation rates (SI Appendix, section 3; 52, 53).

As in the case of noiseless gossip described earlier, we assume that the gossip occurs independently for each focal individual and that the fraction of the population who view a focal individual $i$ of type $s$ as good at the start of a gossip period is equal the fraction of the population who view type $s$ as good in the context of reputation ODEs in Eq. 2 (i.e., if individual $i$ is of type $s$, then $r_{i,0}=r_s$). Agreement and disagreement terms after a period of gossip of duration $\tau$ can then be computed as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\tilde{g}}_2& =\sum _s{f}_s·\mathbb{E}[R_{i,\tau }^2|R_{i,0}=r_s],\hfill \\ \hfill {\tilde{b}}_2& =\sum _s{f}_s·\mathbb{E}[{(1-R_{i,\tau })}^2|R_{i,0}=r_s],\hfill \\ \hfill {\tilde{d}}_2& =\sum _s{f}_s·\mathbb{E}[R_{i,\tau }(1-R_{i,\tau })|R_{i,0}=r_s],\hfill \end{array}\end{array}$$ [9]

where $\mathbb{E}[R_{i,\tau }^2|R_{i,0}=r_s]$, $\mathbb{E}[{(1-R_{i,\tau })}^2|R_{i,0}=r_s]$, and $\mathbb{E}[R_{i,\tau }(1-R_{i,\tau })|R_{i,0}=r_s]$ can be expressed in terms of the mean and variance of $R_{i,T}$ (Eq. 8; SI Appendix, section 3).

Importantly, in the case of noisy transmission, gossip affects not only the variance but also the mean proportion of the population who view a focal individual as good (Eq. 8). To account for this, we must replace the expressions for $p_s$ (Eq. 3), the probability that an individual of strategic type $s$ earns a good reputation, with the following:

$$\begin{array}{cc}\hfill p_{\text{ALLC}}(t)& =\tilde{r}(t)P_{\mathit{GC}}+\left(1-\tilde{r}(t)\right)P_{\mathit{BC}},\hfill \\ \hfill p_{\text{ALLD}}(t)& =\tilde{r}(t)P_{\mathit{GD}}+\left(1-\tilde{r}(t)\right)P_{\mathit{BD}},\hfill \\ \hfill p_{\text{DISC}}(t)& ={\tilde{g}}_2(t)P_{\mathit{GC}}+{\tilde{d}}_2(t)\left(P_{\mathit{BC}}+P_{\mathit{GD}}\right)+{\tilde{b}}_2(t)P_{\mathit{BD}},\hfill \end{array}$$ [10]

where $\tilde{r}$ is the average reputation in the population after gossip of duration $\tau$:

$$\begin{array}{cc}\hfill \tilde{r}& ={\displaystyle \sum _s}{f}_s·\mathbb{E}[R_{i,\tau }|R_{i,0}=r_s]\hfill \\ \hfill & =\left(r-\frac{\nu }{\mu +\nu }\right)e^{-\left(\mu +\nu \right)\tau }+\frac{\nu }{\mu +\nu }.\hfill \end{array}$$ [11]

We recover the case of noiseless gossip (Eq. 3) by letting $\mu =\nu =0$ and $0/0:=1$ (53); in particular, in the absence of noise, gossip does not affect the average reputation in the population ($\tilde{r}=r$).

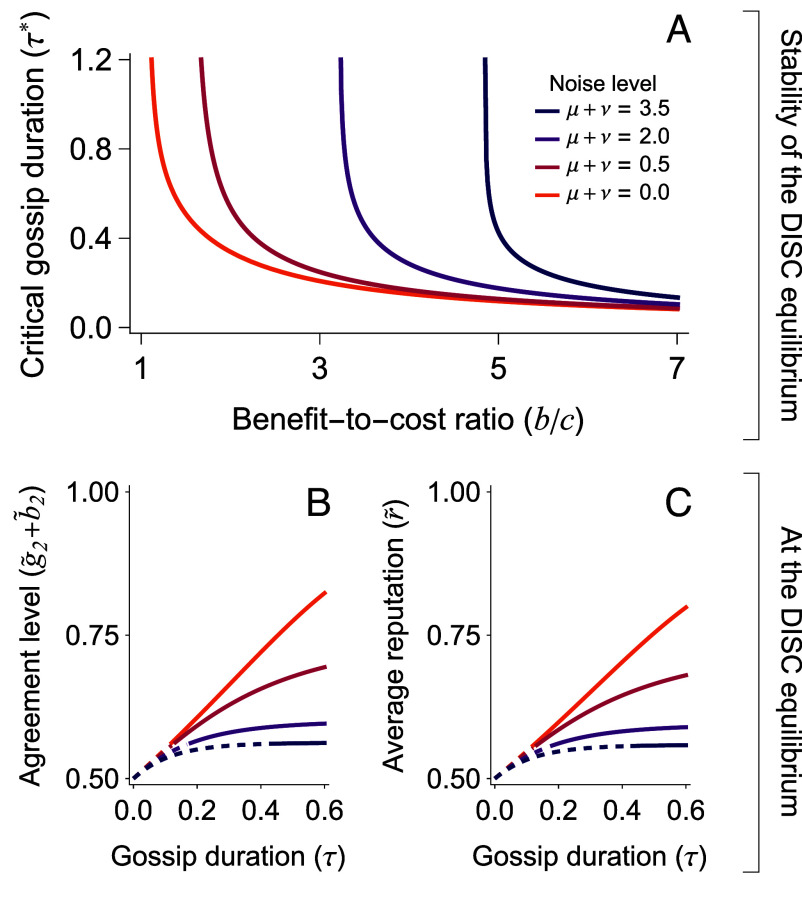
Noise in gossip transmission makes it more difficult to stabilize cooperation (Fig. 3). Under the Stern Judging norm and for a given benefit-to-cost ratio $b/c$, the duration of gossip ${\tau }^{\ast }$ required to stabilize cooperation increases with the amount of noise ($\mu +\nu$), even when there is no bias in transmission ($\mu =\nu$; Fig. 3A). In other words, as gossip becomes more prone to noise in transmission, the population must engage in gossip for longer in order to stabilize the all-DISC equilibrium. This is because transmission noise, much like errors in assessment or execution, decreases the level of agreement in the population (Fig. 3C) and, consequently, decreases the average reputation of discriminators (Fig. 3B). Importantly, noisy gossip hinders cooperation even in the limit that otherwise corresponds to public information: The higher the level of noise, the higher the minimum benefit-to-cost ratio $b/c$ required to sustain cooperation in the limit of infinitely long gossip (the vertical asymptotes in Fig. 3A).

Fig. 3.

Noise in gossip transmission tends to destabilize cooperation. (A) The critical gossip duration ${\tau }^{\ast }$ required to stabilize cooperation as a function of the benefit-to-cost ratio $b/c$, under the Stern Judging norm. Colors denote different amounts of unbiased noise in gossip ($\mu +\nu$). The orange curve indicates the critical gossip duration for noiseless transmission ($\mu =\nu =0$; Fig. 2E). (B and C) The equilibrium average reputation and agreement level at the DISC vertex as a function of scaled gossip duration $\tau$, evaluated with a fixed benefit-to-cost ratio ($b/c=5$). Colors are as indicated in A. Solid (dashed) segments denote parameters for which the DISC-only equilibrium is locally stable (unstable). Other parameters: $u_a=u_e=0.02$. Analogous results for the Simple Standing and Shunning norms are shown in SI Appendix, Fig. S4.

Biased Gossip Can Facilitate Cooperation.

In real-world scenarios, gossip is not only noisy, but it may also be biased: Someone who directly judges a focal individual as good or learns this through gossip may nonetheless report the individual as bad in a subsequent round of peer-to-peer gossip. Or, conversely, gossip may be biased toward reporting bad individuals as good. Biases may arise either by mistake (such as a cognitive bias toward a pessimistic or optimistic view of people’s reputations) or by design (such as malice or forgiveness). In either case, we wish to understand how biased gossip affects reputations in a population and, in turn, modifies the stability of cooperation.

To study the effects of bias, we fix the total magnitude of noise in transmission ($\mu +\nu$), and we compute the critical gossip duration ${\tau }^{\ast }$ required to stabilize cooperation (at $f_{\text{DISC}}=1$) as a function of the gossip bias $\beta \triangleq 2(\frac{\nu }{\mu +\nu }-\frac{1}{2})\in [-1,1]$. Here, $\beta =-1$ indicates maximally negative bias (i.e., any noise in gossip transmits a positive reputation as a negative reputation), $\beta =+1$ indicates maximally positive bias, and $\beta =0$ indicates no bias.

Under the Stern Judging norm, biased gossip has asymmetric and sometimes even nonmonotonic effects on the duration of gossip required for cooperation (Fig. 4). When the overall amount of transmission noise is small ($\mu +\nu =0.5$, Fig. 4A), the critical gossip duration ${\tau }^{\ast }$ decreases monotonically with bias: The more positive the bias, the less gossip is required to stabilize the cooperation, as individuals converge toward more positive views of each other and are more likely to cooperation. But the effect of bias becomes nonmonotonic when gossip is more noisy ($\mu +\nu =2.0$, Fig. 4B; or $\mu +\nu =3.5$, Fig. 4C). Positive bias ($\beta >0$) is still increasingly beneficial for cooperation with increasing magnitude; however, a small amount of negative bias is detrimental to cooperation, whereas a large negative bias is actually beneficial for cooperation. The basic intuition is that large amounts of noise cause disagreement and tend to destabilize cooperation for a given duration of gossip, but this effect can be counterbalanced by either positive bias or strong negative bias.

Fig. 4.

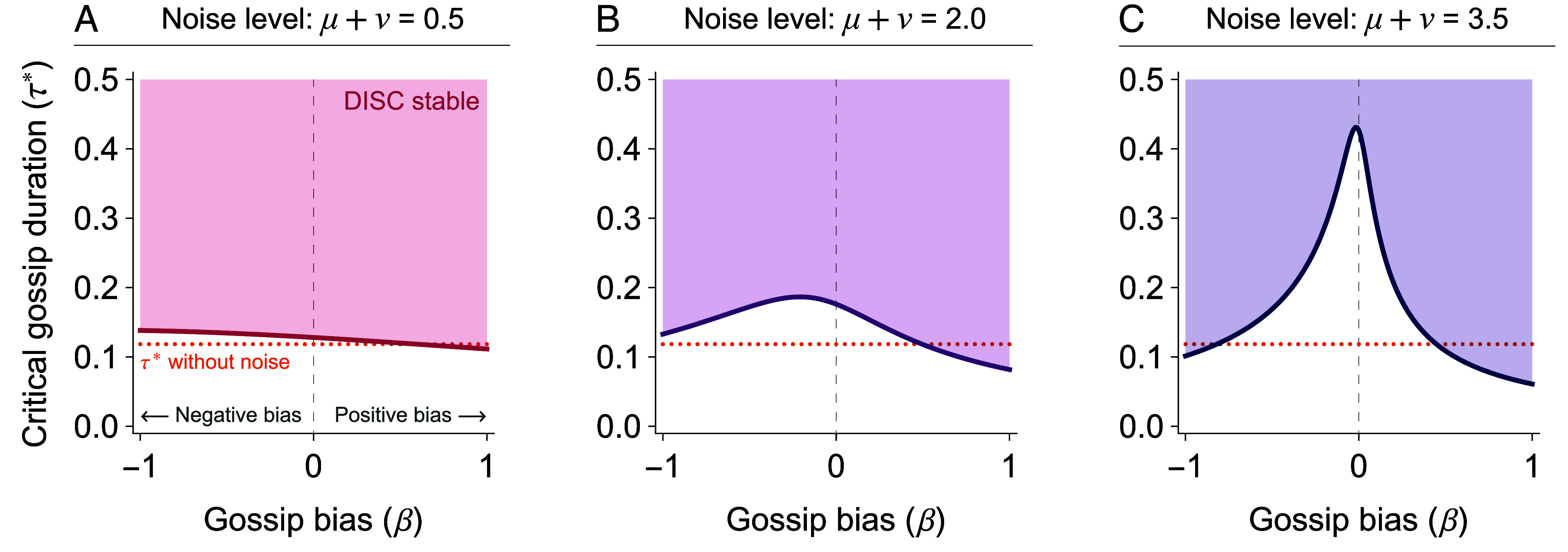
Biased gossip can facilitate or impede cooperation. Critical gossip duration ${\tau }^{\ast }$ required for stable cooperation (solid curves) as a function of the strength of gossip bias $\beta$, under the Stern Judging norm. Colors denote different amounts of noise, as in Fig. 3: $\mu +\nu =0.5$ (A), $\mu +\nu =2.0$ (B), and $\mu +\nu =3.5$ (C). Shaded regions indicate parameter regimes where the DISC-only equilibrium is locally stable. Dotted orange lines (identical across panels) indicate the baseline critical gossip duration ${\tau }^{\ast }$ in the absence of transmission noise ($\mu =\nu =0$; Fig. 2E). Other parameters: $b/c=5$, $u_a=u_e=0.02$. Analogous results for the Simple Standing and Shunning norms are shown in SI Appendix, Fig. S6.

We can understand these patterns in terms of the effects of bias on agreement and disagreement levels (SI Appendix, Fig. S5). When noise is rare ($\mu +\nu =0.5$), the quantity ${\tilde{g}}_2$ increases monotonically with the transmission bias $\beta$ whereas the quantities ${\tilde{b}}_2$ and ${\tilde{d}}_2$ decrease monotonically (compare SI Appendix, Fig. S5 A–C with Fig. 4A). But when gossip is more noisy ($\mu +\nu =2.0,3.5$), ${\tilde{d}}_2$ becomes nonmonotonic in $\beta$ (SI Appendix, Fig. S5 F and I), producing a nonmonotonic effect of bias on the stability of cooperation (Fig. 4B and C).

Whereas unbiased noise tends to destabilize cooperation (Fig. 3), biased noisy transmission can expand the region of stable cooperation, compared even to the case of no noise. In other words, the critical gossip duration ${\tau }^{\ast }$ required for stable cooperation may be shorter for noisy transmission with a strong bias than for noiseless gossip (Fig. 1; dotted orange lines in Fig. 4B and C). This is because when individuals overwhelmingly tend to transmit either positive (or even negative) gossip, the population will come to an agreement more quickly than if positive and negative noise are equally likely.

We have also analyzed the impact of biased gossip under the Simple Standing and Shunning norms (SI Appendix, Fig. S6). Unlike the case of Stern Judging, for Simple Standing (SI Appendix, Fig. S6 A–C) and Shunning (SI Appendix, Fig. S6 D–F), the duration of gossip ${\tau }_{\text{ALLD}}^{\ast }$ required to stabilize DISC against ALLD decreases monotonically with gossip bias $\beta$. This monotonicity reflects the fact that, unlike Stern Judging, Simple Standing and Shunning do not distinguish between justified and unjustified behavior toward individuals with bad reputations. Thus, for these two norms, increasing the magnitude of negative bias increases the frequency of bad reputations in the population, and cooperation becomes more difficult to sustain (i.e., ${\tau }_{\text{ALLD}}^{\ast }$ increases).

Discussion

We have developed a mechanistic model of gossip about social reputations and studied the effects of gossip on cooperative behaviors. In our analysis, individuals privately assess each other’s reputations, and then they modify their views either by consulting a designated source of gossip or, equivalently under a transformation of parameters, by exchanging views with randomly selected peers. Iterative periods of private observation and gossip eventually produce equilibrium reputations that determine the payoffs achieved by three different behavioral strategies. Individuals can then imitate each other’s strategies on a slower timescale, which may lead to long-term stable cooperation. This integrated model of gossip and indirect reciprocity spans continuously between the classical cases of fully private and fully public information. This approach allows us to analyze how the quantity and quality of gossip transmission affect long-term behavior and collective welfare.

We have shown that sufficiently long periods of gossip can stabilize cooperation. Gossip increases agreement about reputations, even in the presence of erroneous actions and assessments. The increased agreement, in turn, reduces the likelihood that a cooperative action is judged as unjustified behavior, and it improves the reputations in the population as a whole. In other words, even when reputations are assessed privately without any top–down public institution to enforce agreement, a bottom–up process based on peer-to-peer gossip can build consensus in the population, and if gossip periods are sufficiently long, stable cooperation can be restored. In this sense, our model offers a mechanistic justification for the common assertion that gossip can facilitate cooperation by indirect reciprocity (7, 17, 18, 20, 22, 26–30). Whereas prior work has explored gossip-based cooperation using agent-based simulations (20, 46, 54), our mean-field analysis provides an analytical expression for the minimum amount of gossip required to sustain cooperation—which allows us to understand how errors in action and assessment, as well as cooperative benefits and costs, govern the amount of gossip necessary for cooperation.

A key insight from our analysis is that peer-to-peer gossip stimulates consensus about reputations only if it occurs in a finite population. Indeed, if the population size were infinite, then no (finite) amount of gossip could ever change the level of agreement. We can understand this insight mathematically in Eq. 16, where, regardless of the gossip duration $T<\infty$, the levels of agreement before and after gossip are identical in the infinite-population limit ($\underset{N\to \infty }{lim}{\tilde{g}}_2=g_2$). Because of this, our model accounts for a finite population when describing the dynamics of peer-to-peer gossip, whereas it describes the dynamics of strategic changes (on a slower timescale) in an infinite population. This mixture of finite- and infinite-population treatments mirrors models of indirect reciprocity that track reputations using finite ‘image matrices’ while tracking strategy frequencies using replicator dynamic ODEs (15, 16). We have confirmed that the predictions of our analytical treatment based on this approach are consistent with the behavior of the corresponding discrete stochastic simulations in finite populations (Fig. 2).

Our account of how gossip facilitates cooperation by fostering consensus about reputations complements a larger literature on how gossip facilitates partner choice. The theory of reputation-based partner choice posits that when individuals must compete for interaction partners, players are motivated to cooperate more because those with good reputations tend to attract more cooperative partners in the future (34, 37, 41, 42). This theory hinges on the ability of individuals to alter their social ties, whereas our analysis shows that gossip can promote cooperative behavior even when the social environment is fixed and everyone must interact with everyone else.

Our results raise several unresolved questions about the role of population structure in gossip-based cooperation. Our single-source gossip model, as the name suggests, assumes that only one individual initiates gossip. In reality, however, multiple sources within a population may spread different and potentially conflicting information about others. Future research could explore how the number of gossip sources and the algorithm by which receivers integrate received information impacts cooperation. In addition, our peer-to-peer model assumes that players can exchange gossip with anyone (i.e., a complete gossip network), and as a result, the population approaches full consensus as gossip duration increases. But under what conditions (e.g., modular or dynamic gossip networks) would the population split into different camps that view a focal individual differently? When a population is structured into disjoint subgroups with high rates of within-group gossip and low rates of between-group gossip, for example, local consensus would be achieved more quickly than global consensus, so that individuals may cooperate more often with in-group members than out-group. Exploring how the structure of information flow affects reputations, including the possibility of polarization, remains an important direction for future research. Likewise, while our model assumes well-mixed interactions in addition to well-mixed gossip, interactions could instead be networked. It would also be interesting to compare how the structure of a gossip network impacts behavior versus the structure of the interaction network.

One limitation of gossip is that reputations are not always transmitted faithfully (40, 44, 45). Noise during transmission can either be unbiased (e.g., accidental errors) or biased (e.g., intentional misrepresentation). We have shown that unbiased noise tends to undercut the benefits of gossip. This result is perhaps unsurprising because, much like errors in assessment or execution (19), transmission noise impedes agreement in the population. It is notable, however, that biased gossip can sometimes stabilize cooperation relative to unbiased gossip or relative even to noiseless gossip. This is true for all norms studied when gossip is biased toward positive reports. In addition, under the Stern Judging norm, a strong negative bias can also stabilize cooperation, compared to noiseless gossip. While this is potentially good news—cooperation does not necessarily unravel even when gossip is biased—our analysis has been limited to populations with uniform tendencies to transmit false or manipulated information. An important extension for future research is to study heterogeneity in how bias is applied. For example, in a population with group structure, individuals may have different levels of bias when gossiping about in-group versus out-group members (e.g., ${\beta }_{\text{in-group}}>0$ and ${\beta }_{\text{out-group}}<0$).

We have assumed that the propensity to gossip is both uniform across the population and exogenously fixed. But competition between gossip strategies may complicate the picture. For example, a recent study has found that mixtures of individuals who do and do not gossip can give rise to opportunistic cooperators—individuals who cooperate with gossipers but defect against nongossipers—which, in turn, can stimulate the use of gossip as a mechanism to deter opportunistic defection (54). Previous work has also found that dishonest gossip strategies—where gossipers deterministically transmit false information (i.e., pure bias, akin to $u=1$ or $v=1$)—can outperform honest gossip strategies under certain conditions, although dishonest gossip tends to undermine cooperation (43, 44, 55). A natural question, then, is whether the amount and quality of gossip that stabilizes cooperation would naturally evolve if individuals were allowed to adjust the frequency and fidelity with which they transmit information. A recent study on the role of empathy in indirect reciprocity has found that populations can evolve empathetic evaluation under the right conditions (22)—which implies that single-source gossip ($Q>0$) can also evolve under the same conditions. However, several questions about the evolution of peer-to-peer gossip remain unresolved. If the degrees of noise and bias are subject to selection, will individuals evolve to share information truthfully and accurately? How will the long-term dynamics change if gossip transmission is inherently costly or if the recipients of gossip can choose to adopt the opposite view of the information they receive? Future research on the evolution of gossip strategies may guide the design of incentives for individuals to adopt gossip behaviors that ultimately promote collective welfare.

Communication has long been recognized as a key factor in human cooperation (56, 57). And there is already an extensive literature on how opinions spread in a population through peer-to-peer communication, including the complications of explicit population structure and complex modes of contagion (58–61). Despite this, only recently have researchers begun to develop mathematically tractable frameworks to study strategic evolution coincident with opinion spread (e.g., refs. 44 and 62). Our study provides a minimal, mechanistic description of how gossip facilitates consensus about reputations—a critical component of cooperation by indirect reciprocity. There remains a large, uncharted realm of research that combines the complex dynamics of belief contagion with the dynamics of social behaviors conditioned on individuals’ beliefs.

Materials and Methods

Here, we provide additional details of our mathematical model (A Model of Gossip, Reputations, and Social Behavior). We refer the reader to SI Appendix, section 4 for detailed derivations.

Social Norms.

A social norm is a set of assessment rules used to assign reputations. A norm is considered “first-order” if it updates a donor’s reputation based solely on the action of the donor, and ‘second-order’ if it uses both the donor’s action and the recipient’s reputation to assess the donor. In the main text, we focus on second-order norms, which typically support as much cooperation as even third-order norms (27). In SI Appendix, section 5, we extend our analysis of gossip and indirect reciprocity to the “leading eight" norms (13), where we exploit the fact that a third-order norm can be represented as a mixture of two second-order norms, conditioned on how the observer views the donor.

We consider three second-order social norms that are most common in studies of indirect reciprocity (22, 26, 29, 47): Stern Judging $\left(\begin{array}{cc}G& B\\ B& G\end{array}\right)$, Simple Standing $\left(\begin{array}{cc}G& G\\ B& G\end{array}\right)$, and Shunning $\left(\begin{array}{cc}G& B\\ B& B\end{array}\right)$. In each binary matrix, the rows indicate the donor’s action (row one for cooperation, two for defection), the columns indicate the recipient’s reputation (column one for good, two for bad), and the entries indicate how the donor is assessed ($G$ for good, $B$ for bad) under the corresponding norm (22).

Each of the three norms can be parameterized as $(p,q)$, where the parameter $p$ ($q$) denotes the probability that cooperating with (defecting against) a bad recipient yields a good standing. We have $(p,q)=(0,1)$ for Stern Judging, $(1,1)$ for Simple Standing, and $(0,0)$ for Shunning.

Reputation Assessments.

Next, we derive the probability $p_s$ that an individual of strategic type $s$ earns a good reputation after gossip (Eq. 3), following the approach described in refs. 22, 26, and 29.

Recall that $\tilde{r}$ is the average reputation in the population after gossip; ${\tilde{g}}_2$ (${\tilde{b}}_2$) is the probability, after gossip, that two randomly selected individuals agree that a third individual is good (bad); and ${\tilde{d}}_2$ is the probability, after gossip, that the first thinks the third is good but the second thinks the third is bad. For convenience, we also define the following quantities (29):

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill P_{\mathit{GC}}& =\left(1-u_e\right)\left(1-u_a\right)+u_e{u}_a\triangleq \epsilon ,\hfill \\ \hfill P_{\mathit{GD}}& =u_a,\hfill \\ \hfill P_{\mathit{BC}}& =p\left(\epsilon -u_a\right)+q\left(1-\epsilon -u_a\right)+u_a,\hfill \\ \hfill P_{\mathit{BD}}& =q\left(1-2u_a\right)+u_a,\hfill \end{array}\end{array}$$ [12]

where $P_{\mathit{XY}}$ is the probability that a donor who intends to $Y\in${cooperate ($C$), defect ($D$)} with a recipient viewed as $X\in${good ($G$), bad ($B$)} by the observer is assigned a good reputation.

Cooperators (ALLC).

A cooperator (ALLC) gains a good reputation by either 1) interacting with someone with a good reputation (with probability $\tilde{r}$), intending to cooperate, and successfully being assigned a good reputation (with probability $P_{\mathit{GC}}$); or 2) interacting with someone with a bad reputation (with probability $1-\tilde{r}$), intending to cooperate, and erroneously being assigned a good reputation (with probability $P_{\mathit{BC}}$).

Thus, the probability that a cooperator earns a good reputation is given by

$$\begin{array}{c}\hfill p_{\text{ALLC}}=\tilde{r}{P}_{\mathit{GC}}+(1-\tilde{r})P_{\mathit{BC}}.\end{array}$$ [13]

Defectors (ALLD).

Similarly, a defector (ALLD) gains a good reputation by either 1) interacting with someone with a good reputation (with probability $\tilde{r}$), intending to defect, and erroneously being assigned a good reputation (with probability $P_{\mathit{GD}}$); or 2) interacting with someone with a bad reputation (with probability $1-\tilde{r}$), intending to defect, and successfully being assigned a good reputation (with probability $P_{\mathit{BD}}$).

Thus, the probability that a defect earns a good reputation is given by

$$\begin{array}{c}\hfill p_{\text{ALLD}}=\tilde{r}{P}_{\mathit{GD}}+(1-\tilde{r})P_{\mathit{BD}}.\end{array}$$ [14]

Discriminators (DISC).

Finally, a discriminator (DISC) gains a good reputation by

• 1)interacting with someone who has a good reputation in the eyes of both the donor and the observer (with probability ${\tilde{g}}_2$), intending to cooperate, and being assigned a good reputation (with probability $P_{\mathit{GC}}$);
• 2)interacting with someone who has a good reputation in the eyes of the donor but a bad reputation in the eyes of the observer (with probability ${\tilde{d}}_2$), intending to cooperate, and being assigned a good reputation (with probability $P_{\mathit{BC}}$);
• 3)interacting with someone who has a bad reputation in the eyes of the donor but a good reputation in the eyes of the observer (with probability ${\tilde{d}}_2$), intending to defect, and being assigned a good reputation (with probability $P_{\mathit{GD}}$); or
• 4)interacting with someone who has a bad reputation in the eyes of both the donor and the observer (with probability ${\tilde{b}}_2$), intending to defect, and being assigned a good reputation (with probability $P_{\mathit{BD}}$).

Thus, the probability that a discriminator earns a good reputation is given by

$$\begin{array}{c}\hfill p_{\text{DISC}}={\tilde{g}}_2{P}_{\mathit{GC}}+{\tilde{d}}_2\left(P_{\mathit{BC}}+P_{\mathit{GD}}\right)+{\tilde{b}}_2{P}_{\mathit{BD}}.\end{array}$$ [15]

Agreement and Disagreement After Gossip.

Here we derive the levels of agreement and disagreement about reputations in the population.

Pairwise gossip with peers (without noise).

We consider a large population of $N$ individuals engaged in pairwise gossip. In this model, the gossip process for each focal individual $i$ is described by the Wright–Fisher process in a population of haploid individuals: In each round of gossip $T$, every individual independently and randomly selects a gossip source (equivalent to parentage in the Wright–Fisher model) from the population and adopts the source’s view of the focal individual $i$. The two “alleles” in the Wright–Fisher model therefore correspond to those individuals who view the focal individual $i$ as good and those who view $i$ as bad. The gossip processes for different focal individuals $i$ are assumed to be independent.

Each gossip process is initialized as follows: At the start of each gossip period ($T=0$), we assume that the fraction $r_i$ who view a given focal individual $i$ of type $s$ as good is identical to the fraction $r_s$ of the population who view type $s$ as good in the context of the reputation ODEs (Eq. 2). This fraction $r_i$ will be used as the initial “allele frequency" in the gossip process about individual $i$.

Under this model, we can express the agreement and disagreement terms after $T$ rounds of gossip (i.e., $N·T$ pairwise gossip events) as follows. As a reminder, $g_2$ denotes the probability that two independent private observers (in the absence of gossip) will agree a given focal individual is good, $b_2$ denotes the probability that they agree a focal individual is bad, and $2d_2$ denotes the probability that they disagree about the reputation of a focal individual. The probability after $T$ gossip rounds that two randomly selected individuals will agree a focal individual is good is given by

$$\begin{array}{cc}\hfill {\tilde{g}}_2& ={\displaystyle \sum _s}{f}_s\left[r_s^2+r_s\left(1-r_s\right)\left(1-{\left(1-\frac{1}{N}\right)}^T\right)\right]\hfill \\ \hfill & =g_2+d_2\left[1-{\left(1-\frac{1}{N}\right)}^T\right].\hfill \end{array}$$ [16]

Similarly, the probability that the two agree that the focal individual is bad is given by

$$\begin{array}{cc}\hfill {\tilde{b}}_2& ={\displaystyle \sum _s}{f}_s\left[{\left(1-r_s\right)}^2+r_s\left(1-r_s\right)\left(1-{\left(1-\frac{1}{N}\right)}^T\right)\right]\hfill \\ \hfill & =b_2+d_2\left[1-{\left(1-\frac{1}{N}\right)}^T\right].\hfill \end{array}$$ [17]

Finally, the probability that the first of the two views the focal individual as good but the second does not is

$$\begin{array}{cc}\hfill {\tilde{d}}_2& ={\displaystyle \sum _s}{f}_s\left[r_s\left(1-r_s\right){\left(1-\frac{1}{N}\right)}^T\right]\hfill \\ \hfill & =d_2{\left(1-\frac{1}{N}\right)}^T.\hfill \end{array}$$ [18]

Assuming $N$ is large but finite, we use the fact that ${(1-1/N)}^T\approx e^{-T/N}$ and let $\tau \triangleq T/N$ to obtain the simplified expressions in Eq. 4.

Gossip with a single source.

We consider a large population of $N$ individuals engaged in gossip. We assume that a single source of gossip is selected randomly from the population. The probability that the gossip source views a randomly selected focal individual as good after a round of private reputation assessments is equivalent to the average reputation $r$ of the population.

We assume that every individual has a probability $Q$ of consulting the gossip source to (possibly) revise their view of each individual’s reputation. With probability $Q^2$, then, two individuals randomly selected from the population will have consulted the gossip source (and adopted the source’s view) about a focal individual. In this case, the two are guaranteed to agree on the status of the focal individual (view her as good with probability $r$). Whereas with probability $1-Q^2$, at least one of the two will not have consulted the gossip source. In this scenario, the probability that the two individuals agree (or disagree) about the status of the focal individual is identical to the case with fully private information, since we assume that observations are made independently; in particular, the gossip source and the two individuals have made independent observations. (We neglect the case when the source is one of the two randomly selected individuals because the probability that the pair includes the source is small for a large population size $N$.)

In total, the probability after the round of gossip that two randomly selected individuals agree a focal individual is good is given by

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\tilde{g}}_2& =\left(1-Q^2\right)·g_2+Q^2·r.\hfill \end{array}\end{array}$$ [19]

Similarly, the probability that the two agree that the focal individual is bad is given by

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\tilde{b}}_2=\left(1-Q^2\right)·b_2+Q^2·(1-r).\end{array}\end{array}$$ [20]

Finally, the probability that the first of the two views the focal individual as good but the second does not is

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\tilde{d}}_2& =\left(1-Q^2\right)·d_2.\hfill \end{array}\end{array}$$ [21]

These quantities satisfy ${\tilde{g}}_2+{\tilde{b}}_2+2{\tilde{d}}_2=1$, as required.

Linear Stability Analysis.

To determine when gossip can sustain cooperation, we compute the Jacobian of the replicator equations (Eq. 6) at the discriminator equilibrium ($f_{\text{DISC}}=1$):

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill J=& \left[\begin{array}{cc}{\lambda }_{\text{ALLC}}& 0\\ 0& {\lambda }_{\text{ALLD}}\end{array}\right]{|}_{f_{\text{DISC}}=1},\text{with}\hfill \\ \hfill & {\lambda }_{\text{ALLC}}=(1-u_e)\left((b{r}_{\text{ALLC}}-c)-\left(b-c\right)r_{\text{DISC}}\right),\hfill \\ \hfill & {\lambda }_{\text{ALLD}}=(1-u_e)\left(b{r}_{\text{ALLD}}-\left(b-c\right)r_{\text{DISC}}\right),\hfill \end{array}\end{array}$$ [22]

where $r_{\text{ALLC}}$, $r_{\text{ALLD}}$, and $r_{\text{DISC}}$ are evaluated after reputations have reached their equilibrium (i.e., the equilibrium of the ODEs given by Eq. 2). Since $r_{\text{ALLC}},r_{\text{ALLD}},r_{\text{DISC}}\in [0,1]$, the eigenvalues of $J$, which are simply its diagonal entries here, have no imaginary parts, regardless of the social norm. Therefore, the discriminator equilibrium is locally stable if and only if the eigenvalues are negative.

We focus on the stability of the discriminator equilibrium in the main text because it is the only equilibrium under Stern Judging and Shunning that supports cooperation. However, the Simple Standing norm admits a stable mixed equilibrium along the ALLC–DISC axis, so that cooperation can be sustained as long as an all-DISC population can resist invasion by defectors, i.e., ${\lambda }_{\text{ALLD}}{|}_{f_{\text{DISC}}=1}<0$. We visualize this condition in SI Appendix, Fig. S2 in order to facilitate a meaningful comparison across norms.

While our analysis in the main text focuses on competition among cooperators, defectors, and discriminators, prior work has shown that paradoxical discriminators (pDISC)—who cooperate with bad individuals and defect against good individuals—can facilitate cooperation under a public reputation scheme with Stern Judging, due to the symmetry of this norm (63, 64). In SI Appendix, to expand our model to include four strategies (ALLC, ALLD, DISC, and pDISC), and we analyze the stability of the discriminator and paradoxical discriminator equilibria under Stern Judging (SI Appendix, section 2.4).

Stochastic Simulations.

To verify that our analysis provides a good approximation of a discrete, finite population, we performed a series of Monte Carlo simulations implemented in Julia 1.8.2 (65). Each population consists of $N=100$ individuals, each with a strategy $s\in \{\text{ALLC},\text{ALLD},\text{DISC}\}$. Each individual also has a private view of everyone in the population. Generations are partitioned into the following discrete processes, in this order: private assessments, gossip, interactions, and strategy updating.

Private assessments.

Each observer $i$ updates their view of each donor $j$ as follows. For each $i,j$ pair, a random recipient $k$ is selected. Each $i$ checks $j$’s most recent action toward $k$ and their own opinion of $k$, and then assigns $j$ the corresponding reputational value from a social norm matrix. Then, for each pair $i,j$, a random number is generated; if it is less than $u_a$, then $i$’s view of $j$ is flipped from good to bad or vice versa.

Gossip.

The following procedure is iterated $T{N}^3/2$ times. A random triplet $i,j,k$ is chosen. Individual $i$ then adopts $j$’s view of $k$. The $N^3$ comes from rescaling so that one unit of “time” corresponds to each individual engaging, on average, in one gossip event; the factor of $1/2$ comes from the fact that heterozygosity decreases twice as quickly in the Moran process as in the Wright–Fisher process used in our analytic treatment.

Interactions.

Each donor $i$ interacts with each recipient $j$ according to $i$’s strategy. If $i$ is ALLC, they cooperate; if $i$ is ALLD, they defect; and if $i$ is DISC, they access their view of recipient $j$, cooperating if that view is good and defecting if it is bad. A random number is selected for each action: if it is less than $u_e$, cooperation is flipped to defection (but not vice versa). Payoffs are updated accordingly: $i$ accrues a benefit $b$ for every coplayer who cooperated with $i$ and pays a cost $c$ for every coplayer with whom $i$ cooperated.

Strategy updating.

A random pair $i,j$ is chosen. Individual $i$ copies $j$’s strategy with probability $1/(1+exp[\omega ({\mathrm{\Pi }}_i-{\mathrm{\Pi }}_j)])$, where ${\mathrm{\Pi }}_i$ and ${\mathrm{\Pi }}_j$ are their payoffs and $\omega$ is the strength of selection (66); unless otherwise stated, we set $\omega =1$ in our simulations.

We initialize each replicate simulation with a prespecified number of individuals for each strategy, and with random views and interactions. We then iterate every step of the evolutionary process except strategy updating $100$ times, to ensure that reputations and interactions converge to an equilibrium. Finally, we iterate the entire evolutionary process until one strategy has fixed. Example trajectories of strategy frequencies over time are shown in Fig. 2C and D.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

All scripts for simulations, analysis, and figure generation are available in public GitHub repositories at https://github.com/tkessinger/NeutralGossip [scripts for simulations (67)] and https://github.com/marikawakatsu/gossip-reputations-cooperation [scripts for analysis and figure generation (68)].