Scoring functions and their evaluation methods for protein-ligand docking: recent advances and future directions

Abstract

The scoring function is one of the most important components in structure-based drug design. Despite considerable success, accurate and rapid prediction of protein-ligand interactions is still a challenge in molecular docking. In this perspective, we have reviewed three basic types of scoring functions (force-field, empirical, and knowledge-based) and the consensus scoring technique used in protein-ligand docking. The commonly-used criteria/methods and publicly available protein-ligand databases that are used to evaluate the performance of scoring functions are also depicted and discussed. We end with a discussion of the challenges faced by existing scoring functions and possible future directions for developing improved scoring functions.

1. Introduction

As the number of three-dimensional protein structures determined by experimental techniques grows, computational tools such as molecular docking have played an increasing role in the functional study of proteins and structure-based drug design.^1–6 In all the computational methodologies, one important problem is the development of an energy scoring function that can rapidly and accurately describe the interaction between protein and ligand. Several reviews on scoring are available in the literature.^7–11

There are three important applications of scoring functions in molecular docking. The first of these is the determination of the binding mode and site of a ligand on a protein.⁹ Given a protein target, molecular docking generates hundreds of thousands of putative ligand binding orientations/conformations at the active site around the protein. A scoring function is used to rank these ligand orientations/conformations by evaluating the binding tightness of each of the putative complexes. An ideal scoring function would rank the experimentally determined binding mode most highly. Given the determined binding mode of a ligand, scientists would be able to gain a deep understanding of the molecular mechanism of ligand binding and to further design an efficient drug by modifying the protein or ligand.⁹

The second application of a scoring function, which is related to the first application, is to predict the absolute binding affinity between protein and ligand. This is particularly important in lead optimization.⁴ Lead optimization refers to the process to improve the tightness of binding for low-affinity hits or lead compounds that have been identified. During this process, an accurate scoring function can greatly increase the optimization efficiency and save costs by computationally predicting the binding affinity between the protein and modified ligands before the much more expensive step of ligand synthesis and experimental testing.

The third application, perhaps the most important one in structure-based drug design, is to identify the potential drug hits/leads for a given protein target by searching a large ligand database, i.e. virtual database screening.⁶ A reliable scoring function should be able to rank known binders most highly according to their binding scores during database screening. Given the expensive cost of experimental screening and sometimes unavailability of high-throughput assays, virtual database screening has played an increasingly important role in drug discovery.

All of these three applications, ligand binding mode identification, binding affinity prediction, and virtual database screening, are related to each other. Presumably, an accurate scoring function would perform equally well on each of them. Despite over a decade of development, scoring is still an open question. Many existing scoring functions perform well only on one or two of the three applications. Roughly, the scoring functions can be grouped into three basic types according to how they are derived: force field-based, empirical, and knowledge-based. In this perspective, we have reviewed several important aspects of scoring functions for protein-ligand docking, as outlined in Figure 1. Specifically, we will first briefly review different categories of scoring functions in Section 2. We will then describe the commonly used criteria that are used to evaluate the performance of a scoring function in Section 3. We also review the publicly available protein-ligand databases for developing and validating a scoring function in Section 4. Finally, challenges and future directions for scoring function development will be discussed in the Conclusion and Discussions.

Figure 1:

An illustration of categories and evaluations for scoring functions in protein-ligand docking.

2. Brief review of scoring functions

Over the years, different scoring functions have been developed that exhibit different accuracies and computational efficiencies. In this section, we will briefly review the scoring functions in literature developed for protein-ligand interactions in molecular docking. Some of the commonly-used scoring functions are summarized in Table 1 and grouped into three broad categories.

Table 1:

Types of scoring functions.

Type	Scoring function
Force field-based	DOCK,12 DOCK3.5(PB/SA),13,14 DOCK/GBSA(SDOCK),15–17 AutoDock,18,19 GOLD,20 SYBYL/D-Score,12 SYBYL/G-Score20
Empirical	FlexX,21 Glide,22 ICM,23 LUDI,24,25 PLP,26,27 ChemScore,28 SCORE,29 X-Score,30 Surflex,31 SYBYL/F-Score,21 LigScore,32 MedusaScore,33 AIScore,34 SFCscore35
Knowledge-based	ITScore,36–38 PMF,39,40 DrugScore,41,42 DFIRE,43 SMoG,44,45 BLEEP,46,47 MScore,48 GOLD/ASP,49 KScore50

2.1. Force field scoring function

Force field (FF) scoring functions are developed based on physical atomic interactions,⁵¹ including van der Waals (VDW) interactions, electrostatic interactions, and bond stretching/bending/torsional forces. Force field functions and parameters are usually derived from both experimental data and ab initio quantum mechanical calculations according to the principles of physics. Despite its lucid physical meaning, a major challenge in the force field scoring functions is how to treat the solvent in ligand binding.

One typical force field scoring function in molecular docking is the scoring function of DOCK whose energy parameters are taken from the Amber force fields.^12,52,53 The scoring function is composed of two energy components of Lennard-Jones VDW and an electrostatic term

$$E=\underset{i}{\Sigma }\underset{j}{\Sigma }\left(\frac{A_{ij}}{r_{ij}^{12}}-\frac{B_{ij}}{r_{ij}^6}+\frac{q_i{q}_j}{\epsilon (r_{ij})r_{ij}}\right)$$ (1)

where r_ij stands for the distance between protein atom i and ligand atom j, A_ij and B_ij are the VDW parameters, and q_i and q_j are the atomic charges. Here, the effect of solvent is implicitly considered by introducing a simple distance-dependent dielectric constant ε(r_ij) in the Coulombic term. Despite the computational efficiency of the force field scoring function of DOCK, the distance-dependent dielectric factor cannot account for the desolvation effect, an important solvent effect that charged groups favor aqueous environments whereas non-polar groups tend to stay in non-aqueous environments. The desolvation energy is a many-body interaction term and depends on specific geometric and chemical surrounding environments of the considered solute atoms. If the desolvation effect is ignored, a scoring function would be biased on Coulombic electrostatic interactions and therefore would tend to select highly charged ligands.

A rigorous method to account for the solvent effect such as free energy perturbation (FEP) and thermodynamic integration (TI) is to treat water molecules explicitly (see refs 3 and 54 for review). However, these methods, together with their simplified approaches such as LIE, PROFEC and OWFEG (see ref 3 and references therein) are too computationally expensive to be used in virtual database screening. In addition, while simulations with explicit waters is theoretically ideal/rigorous, the accuracy of the results may be limited by the high computational cost of sampling due to the inclusion of water molecules in real applications. To reduce the computational expense, some accelerated force field models have been developed for scoring use in molecular docking by treating water as a continuum dielectric medium. Typical examples of such implicit solvent models include the Poisson-Boltzmann/surface area (PB/SA) model^55–57 and the generalized-Born/surface area (GB/SA) model,^58–60 that are often used in post-scoring of docking programs. Shoichet and colleagues applied a modified Born equation to calculate the electrostatic component of ligand solvation.^13,14 In their study, the electrostatic potential of the protein is calculated by using the finite-difference Poisson-Boltzmann (PB) method implemented in DelPhi,^12,55 and partial atomic charges are calculated with the Gasteiger algorithm⁶¹ implemented in the program SYBYL (Tripos) or with the semi-empirical quantum mechanical approach implemented in the program AMSOL.⁶² The desolvation energy penalty for the ligand was calculated by assuming full desolvation of each ligand atom or of the whole ligand. The method was validated by screening the Available Chemicals Directory (ACD) against T4 lysozyme mutants and dihydrofolate reductase (DHFR).

The PB/SA^63–69 and GB/SA^{15–17,70–77} approaches have been successfully used for relative potency studies and virtual screening tests. For example, Zou et al. accounted for the solvation effect in ligand binding free energy calculations using a GB/SA approach.^15,16 Specifically, the solvent-screened electrostatic interactions and the electrostatic desolvation costs are calculated with the GB model. The hydrophobic contributions for non-polar atoms are estimated using the solvent-accessible surface areas (SA) of the atoms. The van der Waals energies are calculated using Lennard-Jones potentials. Then the weights for the electrostatic, van der Waals, and hydrophobic contributions to the free energy of binding are optimized so that the predicted binding scores agree well with the experimental affinity data for known inhibitors and known inhibitors are distinguished from random molecules in database screening. The GB/SA formulation implemented in DOCK^78,79 as SDOCK was validated on three systems: dihydrofolate reductase (DHFR), trypsin, and a fatty acid-binding protein. To enhance the computational efficiency, a pairwise format of GB was parameterized for protein-ligand docking,^16,17 which takes only about 0.5s per orientation (with minimization) on a Silicon Graphics Octane R12000 workstation.

After thorough and systematic comparison between PB and GB on protein-ligand complexes with a wide range of electrostatic component of binding energies (from −5 to 25 kcal/mol), Zou and colleagues showed that being able to reproduce the solvation energy of a ligand or a protein calculated with PB is not necessarily suitable for ligand binding calculations. Additional quantities should be used for evaluation, particularly quantities such as the partial desolvation energy of the receptor.^17,70 To warrant the accuracy and efficiency, they proposed a multiscale GB approach for the use of virtual screening. In this approach atoms are divided into two groups: The few atoms in the first group are most likely to be critical to binding electrostatics; their contributions are calculated with accurate GB models at the sacrifice of speed. The rest atoms (second group) may be treated with a fast GB method.⁷⁰

In addition to the challenge in rapidly and accurately accounting for the solvent effect in electrostatics, how to combine individual energy terms is also difficult. Usually, empirical weighting coefficients have to be introduced because each energy component is calculated from unrelated methods.^15,16,18,19 For example, the electrostatic component can be calculated with Coulombic, PB or GB approaches. The VDW energy component is commonly represented by Lennard-Jones potentials. The hydrophobic interaction term is often approximated as being proportional to the change of solvent-accessible surface area. These terms have quite different scales, and thereby cannot be added up without weighting factors. The weighting factors are obtained by fitting experimental binding data, etc. There may be more than one set of empirical weighting coefficients to achieve comparable answers.^15,16 Although it is possible to find appropriate weighting coefficients for a specific protein or protein family, it is difficult to obtain a universal set for diverse protein-ligand complexes. Furthermore, even accurate electrostatic energy calculations can be blown off by poor treatment of entropic contributions. Finally, it is well-known that individual free energy terms may not be additive.⁸⁰

2.2. Empirical scoring function

A second kind of scoring functions are empirical scoring functions, which estimate the binding affinity of a complex on the basis of a set of weighted energy terms

$$\Delta G=\underset{i}{\Sigma }{W}_i\cdot \Delta G_i$$ (2)

where ΔG_i represents different energy terms such as VDW energy, electrostatics, hydrogen bond, desolvation, entropy, hydrophobicity, etc. The corresponding coefficients W_i are determined by fitting the binding affinity data of a training set of protein-ligand complexes with known three-dimensional structures.^{24–30,32–35,81,82}. Compared to the force field scoring functions, the empirical scoring functions are much faster in binding score calculations due to their simple energy terms.

By calibrating with a dataset of 45 protein-ligand complexes, Böhm developed an empirical scoring function (SCORE1) consisting of four energy terms: hydrogen bonds, ionic interactions, the lipophilic protein-ligand contact surface, and the number of rotatable bonds in the ligand.²⁴ This empirical scoring function was further improved by expanding the dataset to 82 protein-ligand complexes with known 3D structures and binding constants and by considering the energy parameters for the following terms: the number and geometry of intermolecular hydrogen bonds and ionic interactions, the size of the lipophilic contact surface, the flexibility of the ligand, the electrostatic potential in the binding site, water molecules in the binding site, cavities along the protein-ligand interface, and specific interactions between aromatic rings.²⁵ Eldridge et al. presented an empirical scoring function referred to as ChemScore by taking into account hydrogen bonds, metal atoms, the lipophilic effects of atoms, and the effective number of rotatable bonds in the ligand.²⁸ The scoring function was calibrated using 82 ligand-receptor complexes with known binding affinities and was tested using two other sets of 20 and 10 protein-ligand complexes, respectively. Based on a larger set of 200 protein-ligand complexes, Wang et al. developed a new empirical scoring function, X-Score, consisting of four energy terms including VDW interactions, hydrogen bonds, hydrophobic effects and effective rotatable bonds.³⁰

By including different empirical energy terms, empirical scoring functions have been used in many well-known protein-ligand docking programs such as FlexX²¹ and Surflex³¹. How to avoid double-counting problems is a difficult issue for empirical scoring functions with many energy terms. Their general applicability may also depend on the training set due to their nature of fitting binding affinities of a small dataset. With the rapid increase in the number of protein-ligand complexes with known 3D structures and binding affinities, it is possible to develop a relatively general empirical scoring function by training with known binding constants of thousands of diverse protein-ligand complexes.

In addition to fitting a set of weighted energy terms to the binding affinities of a training set, recently, inspired by the knowledge-based scoring functions, a knowledge-based quantitative structure-activity relationship (QSAR) approach has been introduced for scoring protein-ligand interactions.⁸³ In the knowledge-based QSAR method, the atom pair occurrence and distance-dependent atom pair features are used to generate the interaction potentials by using a machine-learning method to fit the binding affinities of a training set. One advantage of the machine-learning method is that it can fit the binding affinities of a very large training set due to the inclusion of more parameters through knowledge-based atom pair features. For, example, in a very recent study by Ballester and Mitchell,⁸⁴ the derived scoring function (RF-Score) by a machine-learning method yielded a high correlation (R = 0.953) on a large training set of 1105 protein-ligand complexes.

2.3. Knowledge-based scoring function

A third kind of scoring functions are knowledge-based scoring functions (also referred to as statistical-potential based scoring functions), which employ energy potentials that are derived from the structural information embedded in experimentally determined atomic structures.^85–87 The principle behind knowledge-based scoring functions is simple: Pairwise potentials are directly obtained from the the occurrence frequency of atom pairs in a database using the inverse Boltzmann relation.^88–91 For protein-ligand studies, the potentials are calculated by

$$w(r)=-k_{B}T\text{ln[}g\text{(}r\text{)],}\hspace{1em}g\text{(}r\text{)}\text{=}\rho \text{(}r\text{)/}\rho *\text{(}r\text{)}$$ (3)

where k_B is the Boltzmann constant, T is the absolute temperature of the system, ρ(r) is the number density of the protein-ligand atom pair at distance r, and ρ*(r) is the pair density in a reference state where the interatomic interactions are zero.

The idea of the inverse Boltzmann method for knowledge-based potentials comes from statistical mechanics in the physics field.⁹¹ According to the analytical integral equation for the pair distribution function g(r) in the simple fluid system, the interaction potentials by the inverse Boltzmann method are actually the mean-force potentials rather than the true potentials.^91,92 In addition, The protein system is also much different from the simple fluid system in statistical mechanics due to the effects of atomic connectivity, excluded volume, composition, etc.⁹⁰ Therefore, the knowledge-based potentials are also not the true mean-force potentials in the physics of the simple fluid system. Howerer, despite these limitations, the inverse Boltzmann method provides a simple and effective alternative method to derive the interaction scores from the structural information for complicated protein systems.^92,93 Since the pioneering work by Tanaka and Scheraga,⁸⁵ a large number of knowledge-based scoring functions have been developed and widely applied to protein structure prediction and protein-ligand studies (see ref 94 for review).

Compared to the force field and empirical scoring functions, the knowledge-based scoring functions offer a good balance between accuracy and speed. Because the potentials in eqn 3 are extracted from the structures rather than from attempting to reproduce the known affinities by fitting, and because the training structural database can be large and diverse, the knowledge-based scoring functions are quite robust and relatively insensitive to the training set.^36,37,39,40 Their pairwise characteristic also enables the scoring process to be as fast as empirical scoring functions.

However, there is a challenge in deriving knowledge-based scoring functions, which is the reference state (see eqn 3). As pointed out by Thomas and Dill⁹⁰ and other groups, an accurate reference state is not achievable. Therefore, how to calculate ρ*(r) of the reference state becomes a longstanding hurdle in deriving knowledge-based potentials. Below we will use the reference state treatment to classify various knowledge-based scoring functions.

Most of the current knowledge-based scoring functions approximate the reference state with an atom-randomized state by ignoring the effects of excluded volume, interatomic connectivity, etc.⁹⁰ Gohlke et al. developed a knowledge-based scoring function (DrugScore) based on 17 atom types and 1376 protein-ligand complex structures.⁴¹ The scoring function consists of a distance-dependent pair-potential term and a surface-dependent singlet-potential term. It was validated by using two sets of protein-ligand complexes (91 and 68 complexes in each set). A further comparative evaluation of DrugScore and AutoDock shows that DrugScore yields slightly superior results in flexible docking.⁹⁵ Recently, an improved version (DrugScore^CSD)⁴² was also developed based on the Cambridge Structural Database (CSD) of small molecules,⁹⁶ which contain low-molecular-weight structures with higher resolution than huge-molecular-weight structures in the Protein Data Bank (PDB).⁹⁷ Mitchell et al. presented a statistical potential model, BLEEP, using 40 atom types.⁴⁶ This model was tested on nine serine protease-inhibitor complexes and obtained a correlation coefficient of 0.71 (or R² = 0.50) between the calculated energy scores and the experimental binding data. A further test on a set of 90 protein-ligand complexes shows a good correlation (R = 0.74 or R² = 0.55) in affinity predictions.⁴⁷ Application of BLEEP to the 77 complexes used by Muegge and Martin³⁹ yields a correlation of R² = 0.28.⁹⁸ Based on 725 protein-ligand complexes from the PDB, Ishchenko and Shakhnovich presented an improved version of SMoG⁴⁴ (referred to as SMoG2001).⁴⁵ SMoG2001 uses 13 atom types, two distance intervals, and a reference state determined by a self-consistent method. Applying SMoG2001 to Muegge and Martin’s test set gives a correlation coefficient of 0.68 (or R² = 0.46).⁴⁵ Yang et al. presented a new knowledge-based scoring function M-Score to account for the mobility of protein atoms based upon 2331 protein-ligand complexes.⁴⁸ M-Score describes the location of each protein atom by a Gaussian distribution based upon the isotropic B-factors, which results in a smoothing effect on the pairwise distribution functions and thereby smoothen its knowledge-based potentials.

In addition to adopting the traditional atom-randomized reference state, researchers have also tried to improve the accuracy of the reference state by introducing some corrections or scalings. The potential model by Muegge and Martin, PMF (potential of mean force), was the first knowledge-based scoring function to be extensively tested for affinity predictions.³⁹ Based on 34 ligand atom types and 16 protein atom types, the distance-dependent pair potentials were derived using 697 protein-ligand structures in which a ligand volume factor is introduced to correct the reference state. The model was tested on a diverse set of 77 protein-ligand complexes with known binding affinities and outperformed LUDI²⁴ and SMoG⁴⁴, yielding a high correlation (R² = 0.61) between the calculated scores and the experimental binding constants. The PMF scoring function was also successfully applied to docking/scoring studies of weak ligands for the FK506 binding protein⁹⁹ and inhibitors for matrix metalloprotease MMP-3¹⁰⁰. Recently, a newer version of PMF (PMF04) has been developed using a much larger database of 7152 protein-ligand complexes from the PDB and received similar results.⁴⁰ Zhang et al. developed a knowledge-based statistical energy function for protein-ligand, protein-protein, and protein-DNA complexes by using 19 atom types and a distance-scale finite ideal-gas reference state (DFIRE).⁴³ The scoring function obtained a correlation coefficient of 0.63 on 100 protein-ligand complexes, 0.73 for 82 protein-protein complexes, and 0.83 for 45 protein-DNA complexes, respectively.

No matter whether one chooses to use an atom-randomized state or a more physical approximation, the accuracy of the reference state remains a problem in knowledge-based scoring functions. The problem is more prominent for binding mode predictions and virtual screening, as the pairwise potentials, which are derived from nicely-bound structures, are not sufficiently sensitive to different ligand positions and may give good scores even to bad/wrong modes. Attempting to solve this problem, Huang and Zou have recently developed a new kind of knowledge-based scoring function (referred to as ITScore) using an iterative method so as to circumvent the accurate calculation of the reference state.^{36,37,101–103} The basic idea of the iterative method is to adjust the pair potentials u_ij(r) by iteration until the interaction potentials reproduce the experimentally determined pair distribution function in the training set, yielding a set of potentials discriminating the native structures from decoys.^104–107 During the iteration procedure, the improvement for the potentials is guided through the difference between the predicted and experimentally observed pair distribution functions instead of through accurate calculation of the aforementioned reference state, where the predicted pair distribution function g_ij(r) is calculated from the ensemble of the native structures and a set of well-sampled decoys according to the Boltzmann probability. In such a way, the iterative method circumvents the reference state problem faced by traditional knowledge-based scoring functions. Another major advantage of the iterative method is that it considers the full binding energy landscape of the complexes by including both the native structures and decoys during the calculation of g_ij(r), instead of considering only the energy minima (i.e., native structures) like what conventional knowledge-based scoring functions do. Extensive evaluations on diverse test sets showed that ITScore yielded good performances on predictions of ligand binding modes and affinities and on virtual screening of compound databases.^36,37 Very recently, Huang and Zou have included the solvation effect and configurational entropy in ITScore. The new scoring function, referred to as ITScore/SE, has further improved the performance of ITScore.³⁸

2.4. Consensus scoring

Despite a large and ever increasing number of scoring functions developed, none of them is perfect in terms of accuracy and general applicability. Every existing scoring function has its advantage and limitation. To make use of the advantages and balance out the errors from different scoring functions, the consensus scoring technique has been introduced to improve the probability in finding correct solutions by combing the scores from multiple scoring functions.¹⁰⁸ The most important/challenging task in consensus scoring is how to make an appropriate consensus scoring strategy of individual scores so that the true modes/binders can be discriminated from others according to the consensus strategy.^109,110 Commonly used consensus scoring strategies include vote-by-number, numberby-number, rank-by-number, average rank, and linear combination, etc.¹¹¹ Examples of consensus scoring have MultiScore,¹¹² X-Cscore,³⁰ GFscore,¹¹³ SCS,¹¹⁴ and SeleX-CS,¹¹⁵

3. Criteria for evaluating scoring functions

In response to the three important applications of a scoring function as described in Introduction, three related but independent criteria are commonly used to evaluate the performance of a scoring function for its ability in binding mode identification, binding affinity prediction, and virtual database screening.

One of the essential measures for the performance of a scoring function is its ability to distinguish native binding modes from decoys. Namely, given a set of decoys for a protein-ligand complex, a reliable scoring function should be capable of ranking the native structure to the top by the calculated binding scores. In docking applications, successful prediction of a native binding mode is commonly defined by the rmsd value between the top ligand conformations and the experimentally observed (native) structure. If rmsd is ≤ 2.0 Å, the prediction is considered successful. Because it is simple and easy to implement, the rmsd criterion for binding mode prediction has been widely used and accepted in the field. However, this criterion could be problematic in some cases. For example, small or nearly symmetrical ligands always have good rmsd values when they are randomly placed in a small active site. On the contrary, for a large flexible ligand, the large rmsd value due to a solvent-exposed irrelevant group may hide the correctness of the overall binding mode. To overcome these limitations, several alternative methods have been presented for pose evaluations, such as relative displacement error (RDE),¹¹⁶ interaction-based accuracy classification (IBAC),¹¹⁷ real space R-factor (RSR),¹¹⁸ and Generally Applicable Replacement for rmsD (GARD).¹¹⁹

A second important measure for a scoring function is its ability to predict the binding affinity of a complex, i.e. how tightly the ligand binds the protein. It is generally difficult to achieve a score scale similar to experimental binding data. (Certainly, one may scale the calculated scores to fit the normal affinity range.) Therefore, the commonly-used criterion for affinity prediction is the Peason correlation between the calculated scores and the experimental data, which is calculated as follows:

$$R\text{=}\frac{{\sum }_{k=1}^N\left(x_k-\langle x\rangle \right)\left(y_k-\langle y\rangle \right)}{\sqrt{\left[{\sum }_{k=1}^N{\left(x_k-\langle x\rangle \right)}^2\right]\left[{\sum }_{k=1}^N{\left(y_k-\langle y\rangle \right)}^2\right]}}$$ (4)

where N is the number of tested complexes. x_k and y_k are the experimentally determined binding energy and the calculated score for k-th complex, respectively. 〈⋯〉 is an arithmetic average over all the complexes. Yet, the correlation between the predicted and experimental binding energies does not have to be linear for a scoring function. Therefore, the Spearman correlation coefficient, which calculates the correlation between two sets of rankings, is also often used in the binding affinity prediction evaluation as

$$R_{\text{s}}=1-\frac{6{\sum }_{k=1}^N{d}_k^2}{N(N^2-1)}$$ (5)

where the complexes in the test set are ranked by their known affinities and calculated scores, respectively, and d_k is the difference in two rankings for the k-th complex. Compared to binding mode prediction, binding affinity prediction is more challenging to be evaluated. One major reason is the uncertainties of the collected experimental affinity data that may come from different experimental conditions by different research groups or the inherent experimental error of an assay.

The third criterion for assessing a scoring function is its capability of selecting potential binders (hits) from a large database of compounds for a given protein target. The practical application is virtual screening in computer-based drug design, which is often used to identify lead compounds in drug discovery. Virtual database screening tests whether or not a scoring function is able to rank the known binders/inhibitors above many inactive compounds in a database. The enrichment test is a commonly-used criterion to quantify the performance of a scoring function in virtual database screening. The enrichment is defined as the accumulated rate of active inhibitors/binders found above a certain percentile of the ranked database that includes the active binders and inactive ligands. The higher enrichment corresponds to a better scoring function at a fixed percentage of the ranked database. Another measurement for virtual database screening is the receiver operating characteristic (ROC).^120,121 This method is normally more appropriate when the number of inactive ligands is comparable to the number of active binders.

Theoretically, an accurate scoring function should be able to perform equally well on all of the three criteria on any test set. However, due to the inherent limitations, most of the existing scoring functions usually perform well on only one or two of the criteria and fail on others. For example, as shown in a previous study³⁷ that SYTYL/F-Score yields a good success rate (74%) in binding mode prediction on the test set of 100 protein-ligand complexes constructed by Wang et al.¹²² (Table 2), but the F-Score performs poor with a correlation coefficient of R = 0.30 in binding affinity prediction on the same set (Table 3). Similar examples can also be found in the comparative assessment of 16 scoring functions on a larger test set of 195 protein-ligand complexes by Cheng et al.¹²³ To be successful in virtual database screening usually requires good performance in both binding mode and affinity predictions. A scoring function that yields a good correlation in binding affinity prediction does not necessarily perform well in database ranking.¹²⁴ For example, PMF-Score yielded a high correlation (R² = 0.61) in binding affinity prediction on the PMF validation set of 77 complexes (Figure 2), but performed much less satisfactorily in virtual database screening and failed to identify any binder on two of four tested targets at the 5% of the ranked database (Table 4). In addition, the performances of scoring functions are test set-dependent. For example, ITScore and PMF-Score perform significantly better on the PMF validation set than on the Wang at al.’s set in binding affinity prediction (Figure 2 and Table 3). For the PMF validation set, all of the tested scoring functions perform better on the serine protease than the others (Figure 2). Therefore, to fully evaluate the performance of a scoring function, all of the three criteria should be examined on multiple test sets.

Table 2:

Success rates of 16 scoring functions for Wang et al.’s test set of 100 diverse protein-ligand complexes, using the criterion of rmsd ≤ 2.0 Å (from Huang and Zou, 2010).³⁸

Scoring function	Type of scoringa	Success rate (%)
ITScore/SE38	K	91
DrugScoreCSD42	K	87
ITScore37	K	82
Cerius2/PLP26,27	E	76
SYBYL/F-Score21	E	74
Cerius2/LigScore32	E	74
DrugScorePDB41	K	72
Cerius2/LUDI24,25	E	67
X-Score30	E	66
AutoDock18	F	62
DFIRE43	K	58
DOCK/FF12	F	58
Cerius2/PMF39	K	52
SYBYL/G-Score20	F	42
SYBYL/ChemScore28	E	35
SYBYL/D-Score12	F	26

^a“K” stands for knowledge-based scoring functions, “E” for empirical scoring functions, and “F” for force field scoring functions, respectively.

Table 3:

Correlation coefficients between the experimentally determined binding energies and the calculated binding scores of 17 scoring functions for Wang et al.’s test set of 100 complexes (from Huang and Zou, 2010).³⁸

Scoring function	Function type	Correlation (R)
ITScore/SE	K	0.65
ITScore	K	0.65
X-Score	E	0.64
DFIRE	K	0.63
DrugScoreCSD	K	0.62
DrugScorePDB	K	0.60
Cerius2/PLP	E	0.56
SYBYL/G-Score	F	0.56
KScore	K	0.49
SYBYL/D-Score	F	0.48
SYBYL/ChemScore	E	0.47
Cerius2/PMF	K	0.40
DOCK/FF	F	0.40
Cerius2/LUDI	E	0.36
Cerius2/LigScore	E	0.35
SYBYL/F-Score	E	0.30
AutoDock	F	0.05

Figure 2:

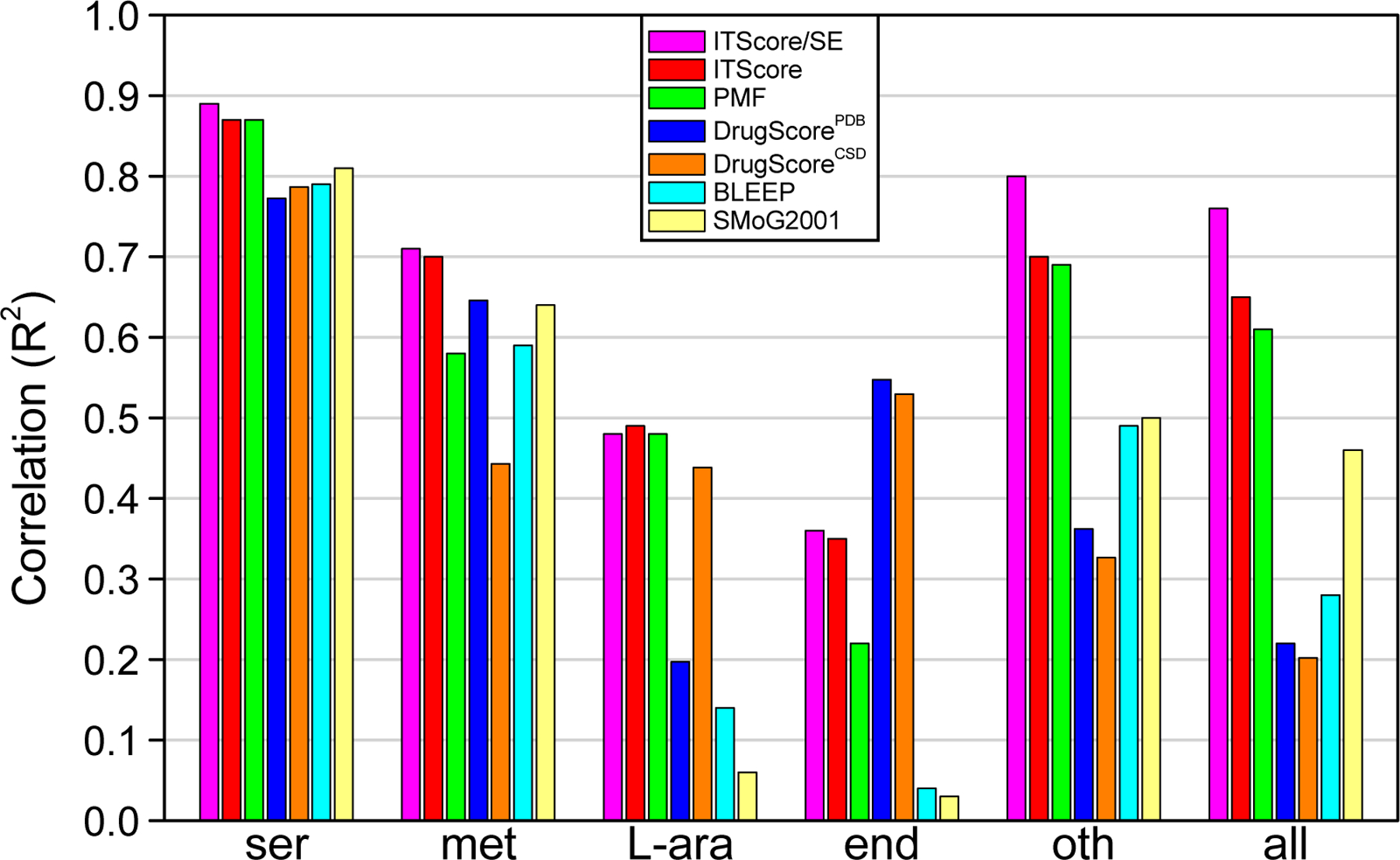
Correlations of binding affinity predictions for 7 knowledge-based scoring functions with the PMF validation set of 77 protein-ligand complexes (all) that consists of five classes: 16 serine protease (ser), 15 metalloprotease (met), 18 L-arabinose binding protein (L-ara), 11 endothiapepsin (end), and 17 diverse protein-ligand complexes (oth).³⁹ The correlation parameter here is the square of correlation coefficient (R²) rather than correlation coefficient itself (R) to maintain consistency with the original data. The correlation data for ITScore/SE, ITScore, BLEEP and SMoG2001 are taken from our previous study,³⁸ and those for DrugScore^PDB and DrugScore^CSD were calculated by the DrugScore^ONLINE server (http://pc1664.pharmazie.uni-marburg.de/drugscore/).

Table 4:

Enrichments of nine scoring functions at the top 5% of the ranked databases^a on four targets of ERα, MMP3, fXa, and AChE (from Huang and Zou, 2006).³⁷

		Enrichment at the top 5% (%)
Scoring function	Function type	ERα	MMP3	fXa	AChE
ITScore	iterative/knowledge-based	19.2	68.3	34.9	37.0
DOCK/FF12	force-field-based	2.7	56.7	14.0	7.4
ICM-Score23	empirical	38.4	36.7	29.5	0.0
ICM-PMF23	knowledge-based	9.6	20.0	19.4	1.9
SYBYL/F-Score21	empirical	23.3	31.7	26.4	1.9
SYBYL/G-Score20	force-field-based	0.7	31.7	31.8	11.1
SYBYL/ChemScore28	empirical	0.0	73.3	23.3	9.3
SYBYL/PMF-Score39	knowledge-based	0.0	5.0	21.7	0.0
SYBYL/D-Score12	force-field-based	0.0	0.0	16.3	0.0
Maximum enrichmentsb		39.2	88.3	43.7	97.5

^aFor each protein target, the constructed database includes known inhibitors (146 for ERα, 60 for MMP3, 129 for fXa, and 54 for AChE) and 999 random, diverse drug-like molecules served as a set of inactive compounds.

^bThe last row lists the maximum theoretically possible enrichments at the top 5% of the ranked database, given the compositions of the databases including active and inactive compounds.

4. Databases for evaluating scoring functions

In addition to the success criteria for evaluating scoring functions, another important issue in developing an efficient scoring function is the construction of an appropriate training/test set. Commonly-used (but not limited) criteria for constructing an appropriate training/test set include: The complexes in the set should be high quality structures with no atomic clashes (e.g. crystal structures with high resolutions); The set of complexes should cover a wide range of proteins and binding affinities; The ligands should be drug-like and non-covalent with the protein. Examples of the protein-ligand complex databases that can be used to construct the training/test set include:

1. LPDB (http://lpdb.chem.lsa.umich.edu/)¹²⁵

2. PLD (http://chemistry.st-andrews.ac.uk/staff/jbom/group/PLD.xls)¹²⁶

3. Binding DB (http://www.bindingdb.org/bind/)¹²⁷

4. PDBbind (http://sw16.im.med.umich.edu/databases/pdbbind/)^128,129

5. Binding MOAD (http://www.bindingmoad.org/)¹³⁰

6. AffinDB (http://www.agklebe.de/affinity)¹³¹

5. Conclusion and Discussions

We have reviewed the scoring functions currently used for protein-ligand interactions in molecular docking and the commonly-used criteria/methods for evaluating the performance of scoring functions in three different applications: binding mode prediction, binding affinity prediction, and database screening. The criteria for constructing an appropriate training/test set and publicly available protein-ligand databases for evaluating a scoring function are also briefly depicted.

Despite considerable progress, current scoring functions are still far from being universally accurate, considering the test set-dependency of their performance and the fact that many of the scoring functions failed on one or two of the three widely-used criteria. To improve the universal applicability of the empirical scoring functions, a large training set of complexes with known affinity data are desired for parameter fitting. For force field and knowledge-based scoring functions, explicit and accurate inclusion of the desolvation and entropic effects is requisite to improve the accuracy. The categorization of atom types with a good balance of the statistics of the pair occurrences and the number of atom types is also important for knowledge-based scoring functions. Extension of the pairwise potentials to many-body potentials theoretically will help improve the accuracy of knowledge-based scoring functions but practically remains unknown because of the introduction of many more parameters to be determined. Lack of a universal set of weighting coefficients for different energy terms for diverse protein-ligand complexes is a challenge for force field scoring functions. What is even more challenging, neglect or inaccurate treatment of entropic effect may easily render the hard efforts on accurate electrostatic calculations in force field scoring. Transition metal ions such as zinc impose great parameterization difficulty for all scoring functions. Another issue is how to evaluate the increasing number of scoring functions being developed.¹³² Comparing different scoring functions is not always possible if they are tested on different sets. Although some comparison studies have been done by researchers,^{122,124,133–136} publicly available benchmarks such as CCDC/Astex set,¹³⁷ CSAR (http://www.csardock.org/), and DUD (http://dud.docking.org/)¹³⁸ are invaluable for development of new and existing scoring functions.