Ketamine can produce oscillatory dynamics by engaging mechanisms dependent on the kinetics of NMDA receptors

Significance

Ketamine is an N-methyl-D-aspartate (NMDA)-receptor antagonist that can produce sedation, analgesia and dissociation at low doses and profound unconsciousness at high doses. It can generate gamma oscillations (>25 Hz) in the electroencephalogram which, at high-doses, are interrupted by slow-delta oscillations (0.1–4 Hz). Ketamine’s molecular targets and oscillatory dynamics have been characterized. However, how ketamine’s actions at the subcellular level give rise to the oscillatory dynamics at the network level remains unknown. Using a biophysical model of cortical circuits, we demonstrate how NMDA-receptor antagonism by ketamine produces the oscillatory dynamics recorded in humans and non-human primates. Our model analysis delivers general mechanisms that offer insight into brain dynamics, ketamine’s action on brain circuits, and ketamine’s therapeutic use for depression.

Abstract

Ketamine is an N-methyl-D-aspartate (NMDA)-receptor antagonist that produces sedation, analgesia, and dissociation at low doses and profound unconsciousness with antinociception at high doses. At high and low doses, ketamine can generate gamma oscillations (>25 Hz) in the electroencephalogram (EEG). The gamma oscillations are interrupted by slow-delta oscillations (0.1 to 4 Hz) at high doses. Ketamine’s primary molecular targets and its oscillatory dynamics have been characterized. However, how the actions of ketamine at the subcellular level give rise to the oscillatory dynamics observed at the network level remains unknown. By developing a biophysical model of cortical circuits, we demonstrate how NMDA-receptor antagonism by ketamine can produce the oscillatory dynamics observed in human EEG recordings and nonhuman primate local field potential recordings. We have identified how impaired NMDA-receptor kinetics can cause disinhibition in neuronal circuits and how a disinhibited interaction between NMDA-receptor-mediated excitation and GABA-receptor-mediated inhibition can produce gamma oscillations at high and low doses, and slow-delta oscillations at high doses. Our work uncovers general mechanisms for generating oscillatory brain dynamics that differs from ones previously reported and provides important insights into ketamine’s mechanisms of action as an anesthetic and as a therapy for treatment-resistant depression.

Ketamine is an N-methyl-D-aspartate-receptor (NMDA_R) antagonist that has analgesic, dissociative, and hypnotic properties (1–4). When administered at low doses, it causes analgesia and dissociation in patients and can be used for procedural sedation in a physician’s office or in the emergency room. When administered at high doses, it causes antinociception and profound unconsciousness and, therefore, can be used to create a state of general anesthesia in the operating room. In addition, ketamine is now being used as a therapy for treatment-resistant depression. Its antidepressant effects last long after the drug clears (5). An excited brain state has been reported under these clinical conditions. At low doses, gamma oscillations (above 25 Hz) can be expressed in the frontal electroencephalogram (EEG). At high doses, strong gamma oscillations are expressed in the frontal EEG and can be interrupted by slow-delta oscillations (below 4 Hz) to produce down-states in the rhythmic activity (1).

Ketamine has been postulated to produce an excited brain state through disinhibition (6–8). In particular, ketamine has been proposed to preferentially antagonize NMDA receptors of inhibitory neurons to drive a surge in excitation (6, 9–11). It is in this disinhibited brain state that the oscillatory dynamics have been characterized (1, 3, 12). However, taking into account this disinhibition, it remains unknown how the action of ketamine at the subcellular level can give rise to the oscillatory dynamics at the network level. We report neural circuit mechanisms that are engaged by NMDA_R antagonism under ketamine and that result in its oscillatory dynamics.

To examine these mechanisms, we developed a biophysical model of a cortical network exposed to ketamine. When we introduce ketamine as an NMDA_R antagonist, our model replicates the brain dynamics in human subjects and nonhuman primates administered ketamine and reveals brain mechanisms underlying the generation of these dynamics. Our model incorporates detailed kinetics for NMDA_R dynamics that underlie these mechanisms. By dissecting the model through simulations, we report three advances.

First, we have established that NMDA_R antagonism under ketamine can terminate spiking in active neurons with subthreshold background excitation. We find that, even when NMDA_Rs are antagonized nonpreferentially across all neurons, global disinhibition can emerge when tonic inhibition is provided by interneurons with subthreshold background excitation or high resting membrane potential. Second, we have identified an NMDA_R-dependent mechanism that can generate gamma oscillations in a cortical network, through an interaction between NMDA- and GABA-receptor-mediated currents. As NMDA_R closing is known to be slow, this mechanism stands in contrast to established mechanisms for gamma generation that rely on fast AMPA- and GABA-receptor transmission, such as the pyramidal-interneuronal gamma mechanism (13). Third, we have identified an NMDA_R-dependent mechanism that can generate slow-delta oscillations in a cortical network, also through an interaction between NMDA- and GABA-receptor-mediated currents. This mechanism relies on an imbalance between excitatory and inhibitory activity and stands in contrast to established mechanisms for slow-delta generation that rely on membrane channels, such as sodium-activated (14) and ATP-activated (15) potassium channels.

Through these findings, we explain how the effects of ketamine extend from the subcellular level to the network level to produce the oscillatory dynamics observed in brain activity. Our work proposes general mechanisms for generating brain dynamics, provides insight into the mechanism of action of ketamine, and suggests mechanisms by which ketamine can provide therapeutic effects that go beyond anesthesia, dissociation, and analgesia. Notably, ketamine has been established to produce antidepressant effect, that last long after drug clearance. Through our work, we find that the gamma oscillations could produce resonance in a subpopulation of interneurons expressing the vasoactive intestinal peptide. We believe that an excessive release of this peptide can trigger a cascade of synaptic changes and network reconfigurations that could enable or enhance the antidepressant effects of ketamine.

Results

Ketamine Administration Induces Oscillatory Dynamics in Brain Activity.

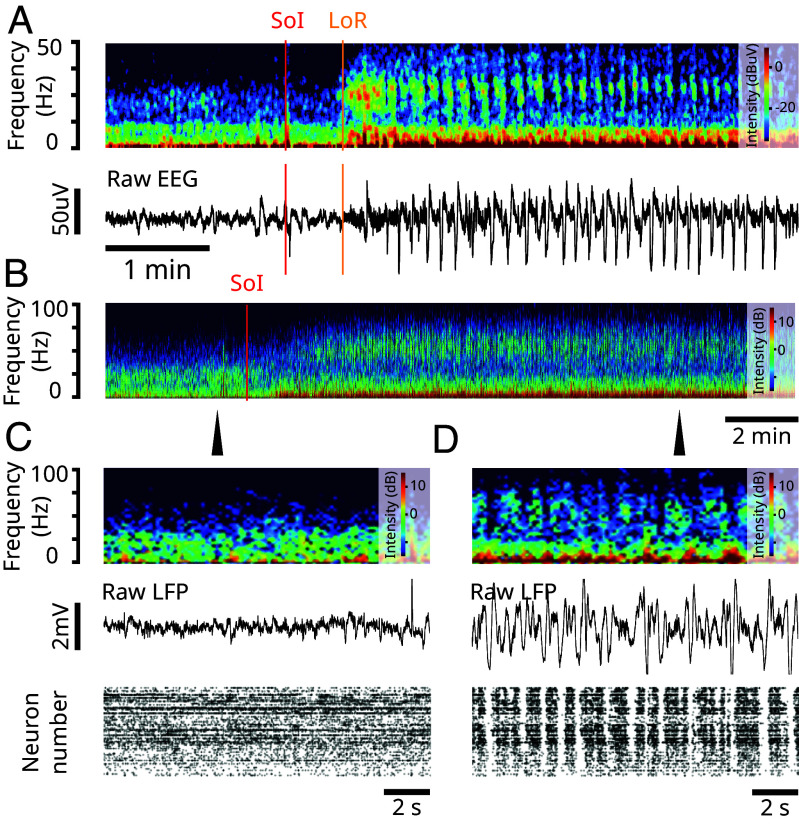
In Fig. 1A, a volunteer subject was administered a bolus of ketamine (SoI, red), with a dose high enough to produce general anesthesia (Materials and Methods). The EEG of the subject shows a surge in gamma oscillations that coincides with a loss of response (LoR, yellow). These gamma oscillations appear in bursts and are interrupted by down-states in EEG activity. Throughout these bursts, the subject is unconsciousness. As the drug begins to clear from the system, brain dynamics typically transition from gamma oscillation bursts to stable gamma oscillations. These dynamics (Fig. 1A) are representative and are described in ref. 1.

Fig. 1.

Ketamine produces gamma oscillations and up/down-states in humans and nonhuman primates. (Experimental data). (A) (Top) Spectrogram of frontal EEG of a volunteer subject administered a bolus of ketamine. SoI (red) denotes the start of infusion. LoR (orange) denotes the loss of response. (Bottom) Corresponding raw EEG. The red and orange lines denote the SoI and LoR, respectively. (B) Spectrogram of LFP recording from a nonhuman primate administered a ketamine bolus. SoI (red) denotes the start of infusion. (C) Close-up at the time-point indicated by the arrow in (B). (Top) Raster plot of spiking activity before ketamine administration. (Middle) LFP trace before ketamine administration. (Bottom) Spectrogram of LFP before ketamine administration. (D) Close-up at the time-point indicated by the arrow in (B). Same as (C) but after administering a bolus of ketamine.

Similar brain dynamics can be observed in nonhuman primates. In Fig. 1B, a rhesus macaque was also administered a bolus of ketamine, with a dose high enough to produce general anesthesia (Materials and Methods). The local field potential (LFP) in the prefrontal cortex of the nonhuman primate shows a surge in gamma oscillations that become interrupted by down-states in LFP activity, where gamma oscillations are absent (Fig. 1B–D). The up- and down-states observed in the LFP also extend to spiking activity. The down-states in gamma oscillations coincide with down-states in spiking activity (Fig. 1D, Bottom). Throughout these up- and down-states, the nonhuman primate is unconsciousness. These dynamics (Fig. 1B–D) are representative and are described in ref. 16.

Biophysical Network Modeling with Detailed NMDA_R Kinetics Can Produce the Oscillatory Dynamics Under Ketamine When NMDA_R Are Antagonized.

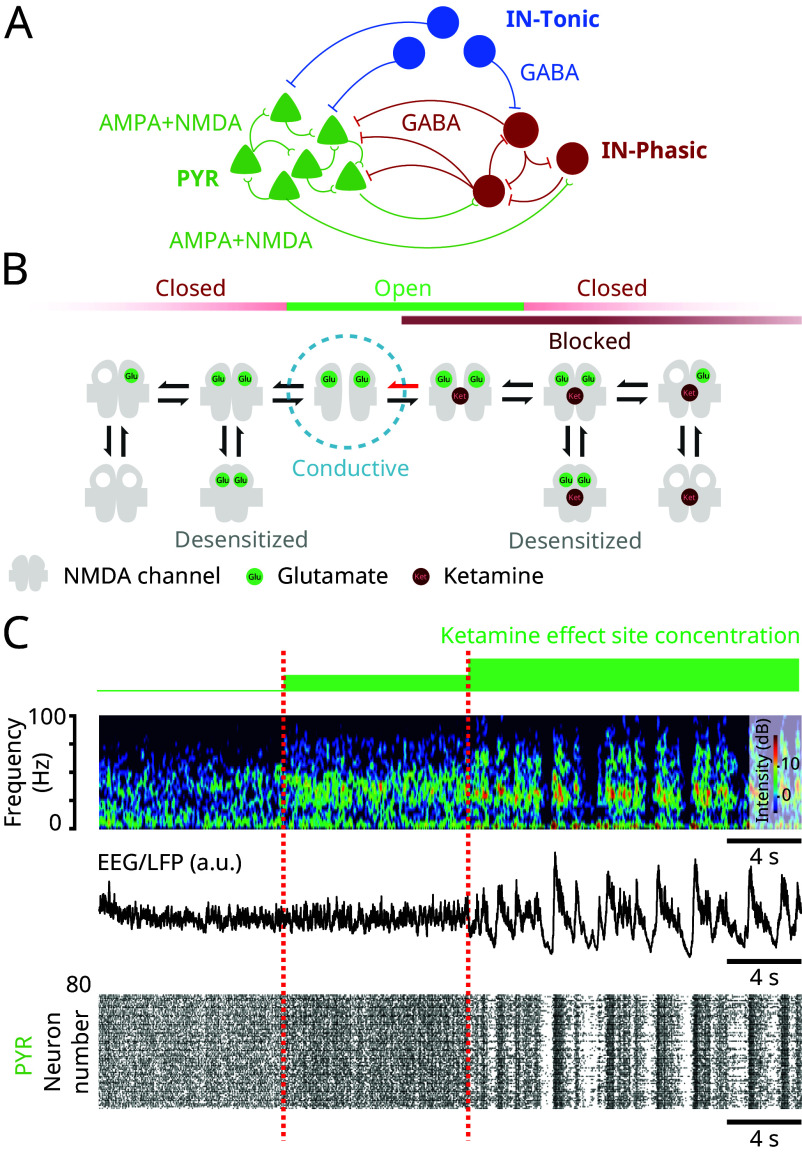
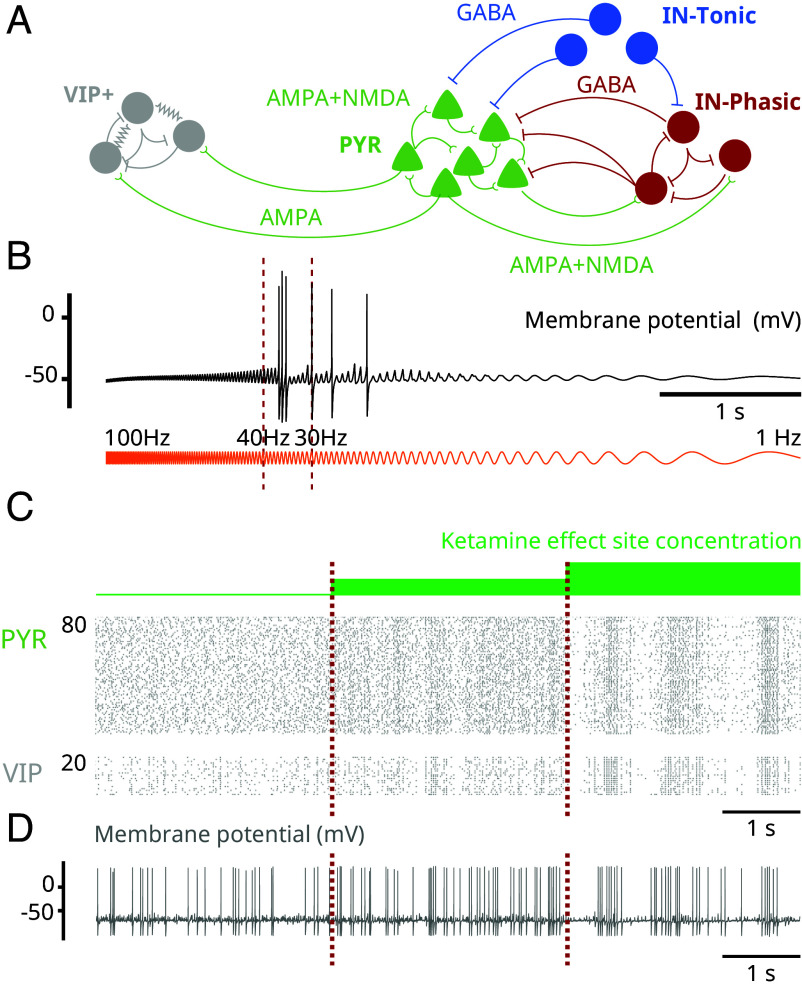
To elucidate the brain mechanisms that generate the oscillatory dynamics under ketamine, shown in Fig. 1 and observed more generally (1, 2), we developed a biophysical network model of a cortical circuit (Fig. 2A). The model consists of interacting excitatory pyramidal neurons (PYR) and inhibitory interneurons (IN-Phasic and IN-Tonic) (Materials and Methods). While systemic administration of ketamine alters circuits throughout the brain, we focused on a minimal cortical network to show that elementary local network dynamics can give rise to the complexity of the dynamics under ketamine.

Fig. 2.

NMDA_R antagonism in a biophysical model reproduces the oscillatory dynamics under ketamine (Model simulations). (A) Schematic of the biophysical network model. (B) Schematic of the 10-state model of NMDA_R kinetics. NMDA_R antagonism under ketamine was modeled as a decrease in the probability of NMDA_R channels unblocking (red arrow). (C) (Top) Spectrogram of an EEG/LFP generated from a simulation of the biophysical model, under different effect site concentrations of ketamine. (Middle) Corresponding EEG/LFP trace. (Bottom) Corresponding raster plot of spiking activity.

Our findings are driven by a detailed model of NMDA_R kinetics and the biophysical effect of ketamine on these kinetics (Fig. 2B). We implemented a 10-state probabilistic model of NMDA_R kinetics, adapted from ref. 17. In this model, a closed NMDA_R channel can become open when two glutamate molecules bind to the receptor. However, an open channel does not always conduct ionic current. An open channel can be blocked with magnesium to become nonconductive. The channel becomes conductive once the magnesium is unblocked. Unblocking is a voltage-dependent mechanism and higher membrane potentials promote unblocking. NMDA_R channels can also close when blocked, a mechanism known as trapping. Finally, excessive usage of the receptor (channel blocked or unblocked) through glutamate binding can desensitize the receptor, and the channel enters a nonconducting state. This model then consists of five unblocked and five blocked states. More details on the NMDA_R kinetics are described in Materials and Methods.

Ketamine, like magnesium, is an NMDA_R channel blocker. However, it is more effective at blocking than magnesium. To model different ketamine effect site concentrations, we decrease the rate of unblocking of the NMDA_R channel (Fig. 2B) (Materials and Methods). As we increase ketamine effect site concentration, we find that the network exhibits the oscillatory dynamics characteristic of ketamine (Fig. 2C). At baseline, brain dynamics do not show preference to an oscillation. Introducing ketamine then gives rise to continuous gamma oscillations which, at higher effect site concentration, become interrupted by down-states in activity. These dynamics are observed at the level of the spectrogram (Fig. 2C, Top), the simulated EEG/LFP (Fig. 2C, Middle), and the spiking activity (Fig. 2C, Bottom). These dynamics are preserved under randomized connectivity and initial conditions, as observed in five different simulations (SI Appendix, Figs. S1–S5).

While ketamine is primarily an NMDA_R antagonist, it is known to alter other channels such as hyperpolarization-activated nucleotide-gated (HCN) channels (18). However, we decided to focus only on NMDA_R antagonism to show that, by itself, it can give rise to the range of brain dynamics under ketamine.

Ketamine Can Decrease Activity of Interneurons by Impairing the Slow-Unblock Kinetics of NMDA_R Channels to Cause Disinhibition.

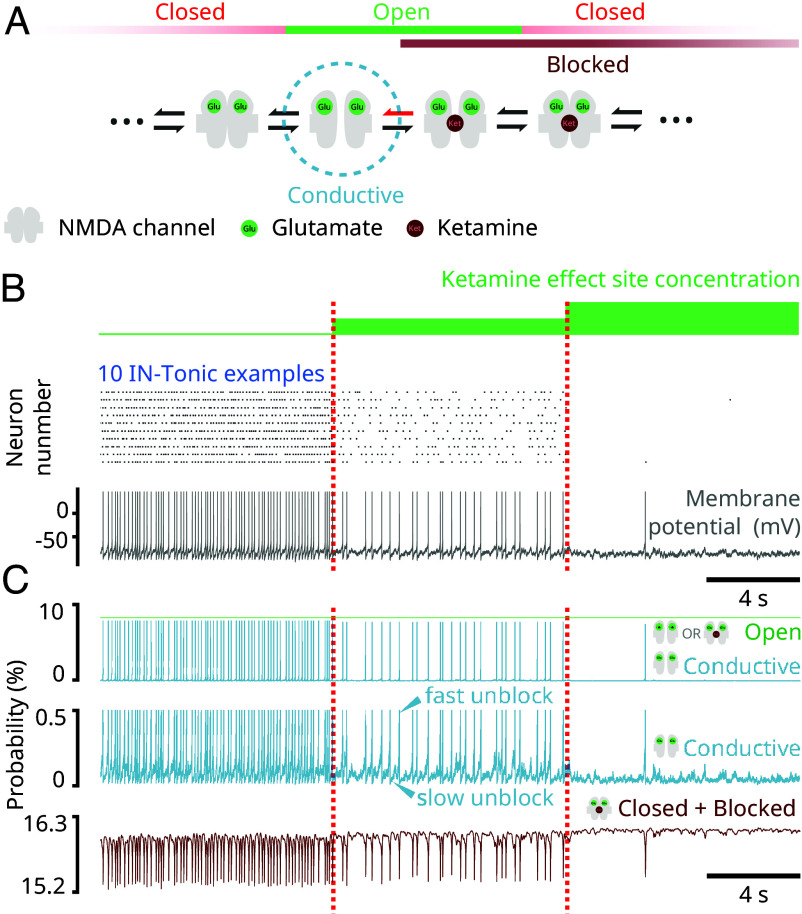
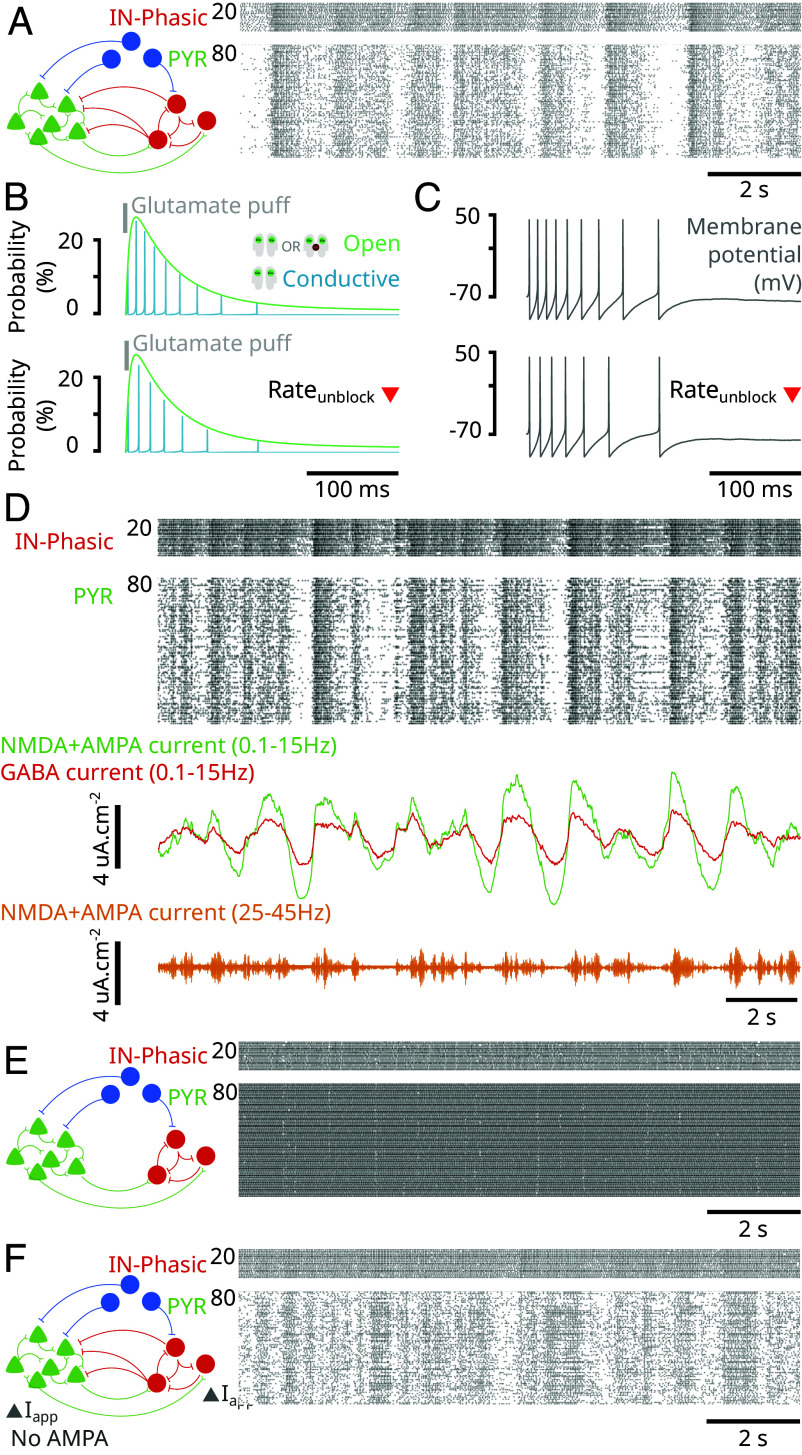
Despite antagonizing excitatory transmission, ketamine induces an excited brain state (2). This phenomenon has been explained by the disinhibition hypothesis (6), in which ketamine is postulated to preferentially antagonize inhibitory neurons leading to greater excitation (7, 8). To explain this antagonism, ketamine has been proposed to have a higher affinity to block subunits of NMDA_R channels preferentially expressed on inhibitory neurons (6, 9–11). With our modeling, we find that even when NMDA_R kinetics are impaired equally among all neurons (without preferential targeting) some neurons with subthreshold background excitation can be shut down. When the neurons that are shut down are inhibitory, providing tonic inhibition onto circuits, this can lead to global disinhibition. As a first advance, we establish that NMDA_R antagonism can hyperpolarize neurons with subthreshold background excitation to stop them from firing, despite having their NMDA_R channels open, to be blocked or unblocked (Fig. 2B).

In our modeling, this shutdown depends on the mechanism of unblocking in NMDA_R channels (Fig. 3A). Unblocking is a voltage-dependent mechanism and admits two regimes: a fast unblock and a slow unblock (17). High levels of depolarizations quickly relieve a magnesium block in NMDA_R channels. We call this a “fast unblock.” At low levels of depolarizations, such as subthreshold ranges, unblocking is still possible, although less likely. At these levels, unblocking of NMDA_R channels induces a small inward current that slowly depolarizes the neuron, that then leads to more unblocking and increases the inward current through positive feedback. We call this a “slow unblock.” By decreasing the probability of unblocking, ketamine impairs both fast and slow unblocks. In particular, ketamine decreases the inward current enabled by a subthreshold slow unblock. Neurons having subthreshold background excitations can rely on this current to sustain firing. In our model, these are represented by IN-Tonic neurons (Materials and Methods). We find that by administering ketamine, we decrease the firing rate of IN-Tonic neurons to a level at which we induce a complete shutdown (Fig. 3B). When tonic inhibition is mediated by such neurons, we find that ketamine leads to disinhibition.

Fig. 3.

NMDA_R antagonism can shut down activity of neurons with subthreshold background excitation (Model simulations). (A) Schematic showing parts of the 10-state model of NMDA_R kinetics. The red arrow represents the probability of unblocking, which was decreased. (B) (Top) Raster plot of IN-Tonic activity at different ketamine effect site concentrations. Only 10 representative examples were selected. (Bottom) Membrane potential of a representative example IN-Tonic neurons. (C) (Top) Representative example from a neuron showing the probability of an NMDA_R channel being conductive (blue) and being open (blocked or unblocked; green) at different ketamine effect site concentrations. (Middle) Scaled trace (blue) showing the probability of being conductive at different ketamine effect site concentrations. The slow ramp-up of probability indicates a slow-unblock (upper arrow) and a fast sudden-jump in probability indicates a fast-unblock (lower arrow). (Bottom) Representative example from the same neuron at top showing the probability of the NMDA_R channel being closed and blocked with 2 bound glutamate (brown).

The effect of ketamine on IN-Tonic neurons can be observed in the evolution of their NMDA_R channel state probabilities (Fig. 3C). The probability of an NMDA_R channel being conductive shows a stable fluctuation interrupted by sudden jumps that coincide with action potentials (Fig. 3C, Top and Middle). The stable fluctuations indicate periods of slow unblock during subthreshold membrane potentials, whereas the sudden surges indicate periods of fast unblock caused by high depolarization. The inward NMDA_R current is proportional to this probability (Materials and Methods). As ketamine effect site concentration increases, we find that the probability of an NMDA_R channel being conductive decreases (Fig. 3C, Top and Middle), indicating a decrease in slow unblock current. However, this decrease occurs while the probability of a channel being open remains unchanged (Fig. 3C, Top), indicating that the probability of being in a blocked state increases. Indeed, this decrease also coincides with an increase in the probability of NMDA_R channel being closed and blocked (Fig. 3C). Overall, this pushes neurons into a less excitable state.

We studied this effect of ketamine on network activity by providing IN-Tonic neurons with constant and maximal access to glutamate (Materials and Methods). However, we also find that this effect is recreated when we modify the network to have IN-Tonic neurons directly receive local glutamate input from PYR neurons (SI Appendix, Fig. S6A). Additionally, we find that the oscillatory dynamics (SI Appendix, Fig. S6 B, Bottom) replicate those of the original model (Fig. 2 A and B and SI Appendix, Figs. S1–S5) as ketamine effect site concentration increases. Furthermore, our findings can also be replicated if subthreshold background excitation is replaced by high resting membrane potential (SI Appendix, Fig. S6 C and D) by altering the potassium leak current. Low-threshold spiking interneurons exhibit high resting membrane potentials (19) and include interneurons expressing somatostatin (SOM). In fact, SOM+ neurons have been found to be preferentially silenced by ketamine (20). IN-Tonic neurons might comprise SOM+ neurons.

Ketamine Can Engage an NMDA_R-Dependent Network Mechanism to Generate Gamma Oscillations.

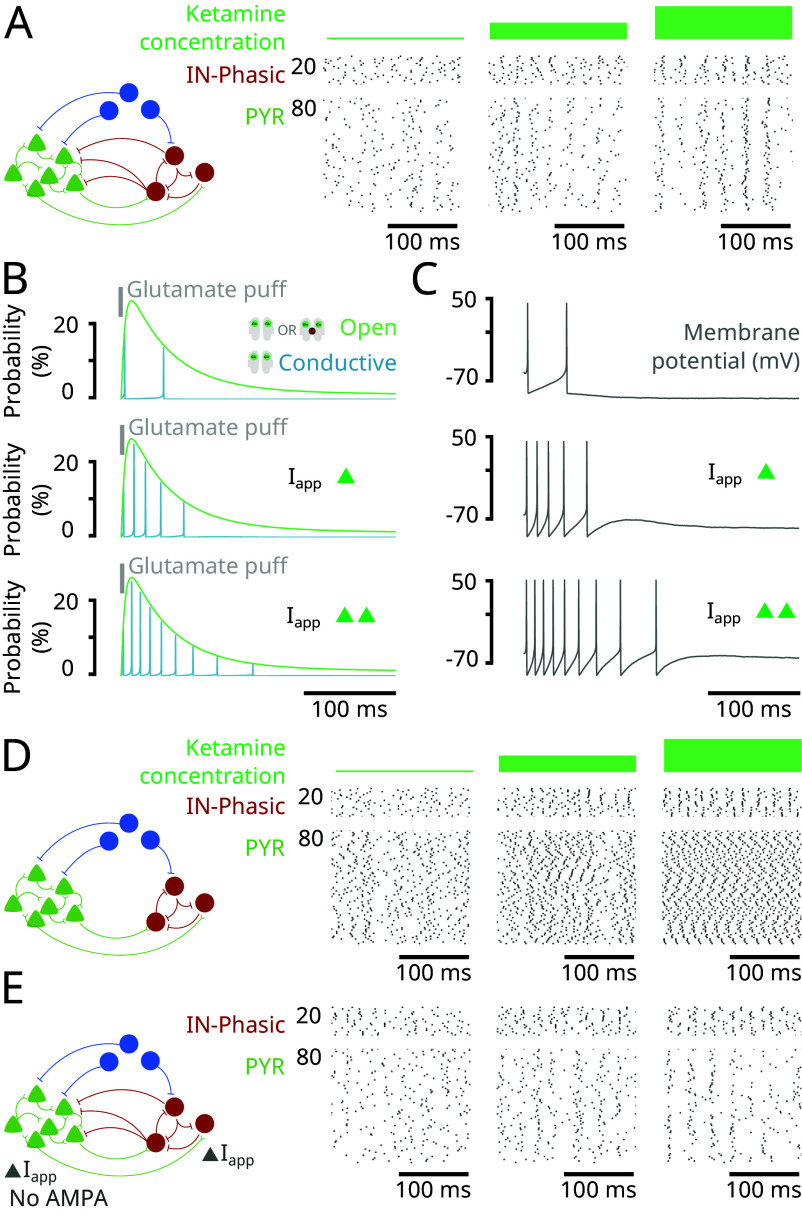
A central signature of ketamine action is that the excitable brain state leads to an overexpression of gamma oscillations. Through our model, as a second advance, we find that NMDA_R antagonism by administering ketamine can yield gamma oscillations (Fig. 4A). As we will explain, we find that disinhibition allows NMDA_R channels to unblock at a gamma time-scale (Fig. 4B) and trigger bursts of spikes at a gamma time-scale in single neurons (Fig. 4C). These spikes are synchronized across neurons with GABA inhibition to form gamma oscillations (Fig. 4D). This mechanism is substantially different from pyramidal-interneuronal gamma (PING) that relies on the interaction of AMPA- and GABA-receptor-mediated currents (13). Indeed, we obtain the gamma oscillations in our model even in the absence of AMPA-receptors in the network (Fig. 4E).

Fig. 4.

NMDA_R antagonism generates gamma oscillations through an NMDA_R-dependent mechanism (Model simulations). (A) (Left) Schematic of the network in Fig. 2. (Right) Closed-up at the raster plot of spiking activity from the simulation in Fig. 2 at different ketamine effect site concentrations. (B) Probability for an NMDA_R channel of an isolated neuron to be conductive (blue) and open (blocked or unblocked; green) following an initial puff of glutamate (gray), under different levels of background excitation (Iapp). (C) Membrane potentials (gray) corresponding to the conditions in (B). (D) (Left) Schematic of the network where GABA input to PYR neurons was removed. (Right) Raster plots of spiking activity for IN-Phasic and PYR neurons under the conditions in (Left), at different ketamine effect site concentrations. (E) (Left) Schematic of the network where AMPA receptors are removed from the network (while NMDA receptors are kept) and background current (Iapp) is adjusted to rectify the loss of excitation. (Right) Raster plots of spiking activity for IN-Phasic and PYR neurons under the conditions in (Left), at different ketamine effect site concentrations.

A core principle in this mechanism is that not all GABAergic neurons are inhibited under ketamine. In our model, some GABAergic neurons are disinhibited and then recruited to produce gamma oscillations. Indeed, once ketamine decreases the activity of IN-Tonic neurons, it relieves the inhibition onto PYR and IN-Phasic neurons. The slow unblock current of NMDA_R channels becomes more effective at depolarizing PYR and IN-Phasic neurons without this inhibition to counter it. Once an NMDA_R channel is open but blocked, depolarization can happen more rapidly, causing the membrane potential to reach the threshold and triggering an action potential. Specifically, by applying a puff of glutamate onto an isolated neuron (Materials and Methods), we find that, as we increased the background excitation of the neuron, NMDA_R channel unblocking is facilitated (Fig. 4B) and can cause a neuron to go from two spikes to a longer burst of spiking at a gamma time-scale (Fig. 4C). Through this mechanism triggered by disinhibition, NMDA_R channels can produce gamma oscillations at the level of a single neuron. The on-going excitatory activity in the network ensures that gamma bursts are expressed at the level of single neurons, PYR or IN-Phasic. But gamma oscillations at the level of a single neuron do not automatically translate to gamma oscillations at the level of the population. They need to be synchronized.

Synchrony is primarily achieved through inhibition from IN-Phasic neurons. Indeed, we find that if we remove the IN-Phasic to PYR projection, we lose synchrony in PYR neurons (Fig. 4D). However, by doing so, we keep the synchrony in IN-Phasic neurons (Fig. 4D). If we additionally remove IN-Phasic to IN-Phasic projections, we also lose synchrony in IN-Phasic neurons (SI Appendix, Fig. S7A). Nevertheless, NMDA_R kinetics also have a role in ensuring synchrony. Once PYR neurons are synchronized, their activity also fosters synchrony in IN-Phasic neurons. Indeed, if we remove IN-Phasic to IN-Phasic projections while keeping IN-Phasic to PYR projections, we find that PYR synchrony is preserved and IN-Phasic synchrony is recovered (SI Appendix, Fig. S7B). In fact, it is the synchronous opening of NMDA_R channels on IN-Phasic neurons that preserves the synchrony. Indeed, if we remove PYR input to IN-Phasic neurons and replace it with constant glutamate exposure, we lose the IN-Phasic synchrony (SI Appendix, Fig. S7C). Whenever PYR neurons fire together, they reopen (blocked or unblocked) NMDA_R channels across all neurons, making it more likely for all neurons to immediately fire again, together.

Ketamine Can Engage an NMDA_R-Dependent Network Mechanism to Generate Up- and Down-States.

At high doses of ketamine, gamma oscillations are interrupted by down-states of activity. Through our model, as a third advance, we find that NMDA_R antagonism by administering ketamine can yield up- and down-states in activity (Fig. 5A). As we will explain, we find that it is the further impaired NMDA_R kinetics that push the dynamics into the slow-delta oscillatory regime.

Fig. 5.

NMDA_R antagonism generates up- and down-states through an NMDA_R-dependent mechanism (Model simulations). (A) (Left) Schematic of the network in Fig. 2. (Right) Close-up at the raster plot of spiking activity for PYR and IN-Phasic neurons from the simulation in Fig. 2, at high ketamine effect site concentration. (B) (Top) Probability for an NMDA_R channel of an isolated neuron to be conductive (blue) and open (blocked or unblocked; green) following a puff of glutamate (gray), under high background excitation (disinhibited) at the baseline rate of unblocking for NMDA_R channels. (Bottom) Same as (Top) but using the high-dose rate of unblocking. (C) (Top and Bottom) Membrane potentials (gray) corresponding to the conditions in (B). (D) (Top) Raster plot of spiking activity from Fig. 2. (Middle) Filtered excitatory (green) and inhibitory (red) currents input into PYR neurons. (Bottom) Gamma oscillations in the EEG/LFP obtained through band-pass filtering. (E) (Left) Schematic of the network where GABA input to PYR neurons was removed (Right) Raster plots of spiking activity for IN-Phasic and PYR neurons under the conditions in (Left), at high ketamine effect site concentration. (F) (Left) Schematic of the network where AMPA receptors are removed (while NMDA receptors are kept) and background current (Iapp) is adjusted to rectify the loss of excitation. (Right) Raster plots of spiking activity for IN-Phasic and PYR neurons under the conditions in (Left), at high ketamine effect site concentration.

When ketamine is administered in our model, the probability of NMDA_R channels unblocking decreases. This has the effect of decreasing the slow unblock current of NMDA_Rs. For neurons with subthreshold background excitation that rely on it, this leads to a decrease in firing and eventual shutdown. For the remaining neurons, we find that this leads to a slowing of the timescale of the firing burst. Specifically, when unblocking decreases for isolated neurons, we find that the burst timescale slows down (Fig. 5 B and C). In such a situation, the gamma oscillations in PYR neurons cannot be sustained indefinitely under gamma inhibition from IN-Phasic neurons.

This weakening produces up- and down-states following three steps. First, gamma oscillations are weakened and the activity of PYR neurons decreases with time, up to a point where it ceases. Second, once PYR activity decreases and ceases, IN-Phasic activity that is momentarily sustained by NMDA_R kinetics begins to decrease due to the absence of glutamate. Third, once IN-Phasic activity decreases enough, the inhibition onto PYR weakens, and we see re-emergence of PYR activity. These fluctuations are observed in the average excitatory (green) and inhibitory (red) currents in Fig. 5D. In this cycle, inhibition from IN-Phasic neurons also plays a key role. Without it, synchrony is lost and the PYR neurons continuously spike (Fig. 5E). These up- and down-states also do not rely on AMPA receptors, as we can recreate them by removing AMPA receptors from the network (Fig. 5F). AMPA receptors do however play a role in enabling sharp transitions between the up- and down-states (e.g., compare Fig. 5F to 5A) due to their opening and closing kinetics that are faster than those of NMDA receptors.

Ketamine Can Engage VIP+ Neurons through Resonance to Gamma Oscillations.

Many interneurons that express the vasoactive intestinal peptide (VIP) are thought to express D-type potassium channels that conduct a D-current (21). Through this D-current, we know that these VIP+ neurons can naturally produce bursts of gamma oscillations (22, 23). This raises the possibility that the gamma oscillations produced by ketamine can recruit these VIP+ neurons through resonance. To investigate this, we modeled VIP+ neurons and introduced them into the network (Fig. 6A). When isolated VIP+ neurons receive a sinusoidal current with constant amplitude but increasing frequency (ZAP current), we find that they produce a burst of gamma in the range 30 to 40 Hz where gamma oscillations under ketamine are expressed (Fig. 6B). When we introduce VIP+ neurons in the network to receive PYR input, we find that they are entrained by PYR neurons (Fig. 6C). By examining membrane potentials, we find that VIP+ neurons spike sparsely at baseline and begin producing gamma bursts of oscillations as ketamine effect site concentration increases (Fig. 6C). Experimentally, the vasoactive intestinal peptide is found to have neurotrophic effects (24), and the rate of its release is tied to the stimulation frequency of VIP+ neurons (25). Recruiting these neurons through resonance may underlie the long-term therapeutic effects of ketamine, particularly its antidepressant effects.

Fig. 6.

NMDA_R antagonism can engage VIP+ neurons through gamma resonance (Model simulations). (A) Schematic of the augmented network including VIP+ neurons. (B) Membrane potential (black) of a representative VIP+ neuron in the network, where each receives a ZAP current (orange) as input instead of AMPA input from PYR neurons. The ZAP current sweeps from 100 to 1 Hz and has constant amplitude throughout. (C) Raster plots showing PYR and VIP+ neuron spiking activity at different effect site concentrations. (D) Membrane potential of a representative VIP+ neuron at different effect site concentrations.

Discussion

Ketamine Can Produce the Oscillatory Dynamics through NMDA_R Antagonism.

Using biophysical modeling, we have identified mechanisms by which NMDA_R antagonism can generate the oscillatory brain dynamics observed under ketamine. These mechanisms connect the actions of ketamine at the subcellular level to the population activity through cellular and network effects. To derive them, we have focused on the action of NMDA_R antagonism on a cortical network. In our work, we report three advances.

First, we have established that NMDA_R antagonism can hyperpolarize neurons with subthreshold background excitation to terminate spiking under ketamine by impairing the “slow-unblock” current of NMDA_R channels, despite these neurons being active before ketamine administration. We find that, even when NMDA_Rs are antagonized equally among all neurons, disinhibition can emerge when tonic inhibition is provided by interneurons with subthreshold background excitation or high resting membrane potential. The weakened activity of these interneurons can lead to global disinhibition.

Second, we have identified an NMDA_R-dependent mechanism that can generate gamma oscillations in a cortical network. Once the network is disinhibited by ketamine, we find that the gamma oscillations are generated at the single-neuron level by unblocking mechanisms in NMDA_R kinetics and are synchronized at the population level by GABA-receptor inhibition. This mechanism relies on the interaction of NMDA- and GABA-receptor-mediated currents and differs from known mechanisms such as the pyramidal-interneuronal gamma mechanism that relies on AMPA- and GABA-receptor-mediated currents (13).

Third, we have identified an NMDA_R-dependent mechanism that can generate slow-delta oscillations in a cortical network. Once NMDA_R kinetics are severely altered by high doses of ketamine, we find that up- and down-states emerge in three steps: Pyramidal cell activity cannot be sustained and is shut down by inhibition, starting a down-state; interneuron activity which is sustained by NMDA_R currents begins to weaken after losing input from pyramidal cells; and once inhibition is weak enough, pyramidal cell activity re-emerges, starting an up-state. This mechanism also relies on the interaction of NMDA- and GABA-receptor-mediated currents and differs from known mechanisms reliant on membrane channels such as the sodium-activated (14) and ATP-activated (15) potassium channels.

Through these mechanisms, we find that the oscillatory dynamics could recruit additional populations of interneurons expressing VIP through gamma resonance. The increased activity of VIP+ neurons may increase the release of VIP. This peptide has neurotrophic effects (24) and its overrelease may underlie the antidepressant effects of ketamine.

We believe that these mechanisms are more general and can be engaged in conditions beyond antagonized NMDA_R. In fact, unblocking of NMDA_R is voltage-dependent and can then be modulated by changes in neuronal excitability. As a result, we expect a momentary disinhibition or activation of neuronal populations, which is possible in normal conditions, to engage these mechanisms to generate gamma or slow-delta oscillations. Therefore, our findings contribute an NMDA_R-centric viewpoint for generating brain oscillations in the cortex that is complementary to what has been confined to AMPA- and GABA-receptor currents generating gamma oscillations and membrane channels generating slow-delta oscillations.

Our results rely on a detailed 10-state model of NMDA_R kinetics adapted from ref. 17. This level of detail allows us to directly impair the unblocking mechanism of NMDA_R, by decreasing the rate of unblocking as a function of ketamine effect site concentration. This is in contrast to an alternate 4-state model of NMDA_R that has been proposed but encapsulates the unblocking mechanism as a gating variable (26). In fact, ref. (27) examines mechanisms of ketamine action by decreasing the maximal conductance of NMDA_R channels, as modeled by Jahr and Stevens (26), as a function of ketamine effect site concentration. This leaves NMDA_R kinetics unchanged under ketamine. We believe that NMDA_R channel unblocking and trapping mechanisms, and their effects on kinetics, are essential to ketamine action and should be explicitly considered.

Therapeutic Effects through Gamma Resonance under Ketamine.

Administering ketamine at low dose has been found to have antidepressant effects (5). These effects are also long lasting. They have been proposed to emerge from a number of mechanisms: NMDA_R antagonism (5), activation of AMPA receptors (28), ketamine metabolites (29), and effects on opioid receptors (30). Downstream of these mechanisms, the antidepressant effects have been found to need brain-derived neurotrophic factor (BDNF) signaling (31, 32). Under ketamine, BDNF may be activated through a number of mechanisms to trigger the antidepressant effects.

Through our model, we find that the gamma oscillations could recruit neurons expressing the vasoactive intestinal peptide (VIP) through resonance to produce gamma bursts. This prediction would need to be verified experimentally. If correct, it would suggest a network mechanism for ketamine’s antidepressant effect. We know that VIP+ neurons corelease VIP alongside GABA (33). The rate of VIP release also increases with the rate of stimulation of VIP+ neurons (25). These peptides have been found to have neurotrophic effects (24) that may lead to activation of BDNF (34). The overrelease of this peptide can trigger a cascade of synaptic changes and network reconfigurations that could enable or enhance the antidepressant clinical effects under ketamine.

If this is true, then the gamma oscillations generated by ketamine would be critical for its antidepressant effects. Enhancing gamma oscillations under ketamine to further activate VIP+ neurons may then enhance ketamine’s therapeutic effects. Finally, that VIP+ activation is neurotrophic suggests that ketamine may be used as a therapy for conditions beyond treatment-resistant depression.

Additional Mechanisms for Generating Oscillatory Dynamics under Ketamine.

In our work, we showed how NMDA_R antagonism in a simple cortical network can give rise to gamma and slow-delta oscillations. However, ketamine can have molecular effects other than NMDA_R antagonism. Furthermore, systemic administration of ketamine will affect all structures in the central nervous system.

The interaction between the cortex, the thalamus, and the brainstem can contribute to slow-delta oscillatory dynamics. Indeed, removing significant excitatory input from the brainstem to the cortex can result in slow-delta oscillations (35). Ketamine can also decrease the activity in excitatory arousal pathways from the parabrachial nucleus and the medial pontine reticular formation in the brainstem to the thalamus and basal forebrain through NMDA_R antagonism (36). The coordination of down-states observed between the cortex and thalamus suggests a mechanistic coordination between these two structures (16). All of these indicate that other slow-delta oscillatory mechanisms can come into play to enhance or complement the mechanisms mediated by NMDA_R antagonism at the cortical level.

Ketamine can also alter hyperpolarization-activated nucleotide-gated (HCN) channels (18) for slow-delta oscillatory contributions. In fact, low doses of ketamine have been found to produce 3 Hz oscillations in posteromedial cortex (3, 12). These 3 Hz oscillations have been found to rely on HCN channels (3). Ketamine may act on these channels either indirectly through NMDA_R antagonism (3) or directly by inhibiting them (18) to produce these oscillations. Again, these mechanisms can enhance or complement the mechanisms mediated by NMDA_R antagonism at the cortical level.

Disinhibition under Ketamine.

Although ketamine antagonizes excitatory transmission, it induces an excited brain state. To explain this, ketamine has been proposed to preferentially target inhibitory neurons, decreasing their activity and causing disinhibition (6–8). To explain this targeting, ketamine has been proposed to have a higher affinity to block subunits of NMDA_R channel preferentially expressed on inhibitory neurons (6, 9–11). However, through our modeling, we find that disinhibition can also be realized without preferential targeting of NMDA_R on inhibitory neurons. Neurons, excitatory or inhibitory, with subthreshold background excitation that rely on their slow-unblock current to fire can stop firing under ketamine despite being heavily active before administration. These neurons are the IN-Tonic neurons in our model.

Background excitation for a neuron can be set by network dynamics and connections. As a result, different neuronal populations may be positioned to have different levels of background excitation through synaptic connections. Membrane channels also alter neuronal excitability and different populations of neurons can express different channels. For instance, SOM+ neurons are low-threshold spiking neurons known to have high resting membrane potentials (19). They have also been found to be preferentially silenced by ketamine (20). The IN-Tonic population in our network model may be composed of SOM+ neurons.

While the disinhibition hypothesis suggests a weakening of GABAergic activity under ketamine, not all inhibitory neurons have to be weakened. Emerging experimental evidence shows that some inhibitory neurons are activated under ketamine (37). In fact, our modeling suggests that some inhibitory neurons are activated and recruited to produce the gamma oscillations under ketamine. These neurons are the IN-Phasic neurons in our model.

Altered Balance of Inhibition and Excitation under Ketamine.

Overall, our mechanisms suggest that ketamine disrupts and alters the balance in excitation and inhibition as a function of dosage, producing switches in neuronal states. As the ketamine dose increases, the balance is first tilted to excess excitation then to more balanced inhibition at an excited regime to enable transitions between up- and down-states. The tilt in balance and switches in neuronal states set up the brain for the altered processing found under ketamine. The inhibition of neurons represented by IN-Tonic neurons can impair the brain’s ability to regulate dynamics. The disinhibition of the remaining population, represented by PYR or IN-Phasic neurons, can activate networks normally inhibited and enhance neurocognitive processes normally suppressed. The mechanisms that generate gamma oscillations also enhance synchronicity in neuronal populations. Spatially, this synchronicity can impair the formation of small natural cell assemblies and enhance the formation of large artificial ones. These changes in cell assemblies can alter perception and give rise to hallucinations (38–40). Temporally, the synchronicity can override the expression of lower and higher frequency oscillations. This restricted expression of oscillations can stabilize dynamics, limiting the range of brain processing and leading to sedation. Finally, at high doses, the mechanisms that generate down-states in activity produce regular shutdowns across large populations of neurons. These down-states will regularly interrupt the continuity of brain processing and promote a state of unconsciousness. Ketamine’s dissociative effects have been tied to a 3 Hz oscillation in the posteromedial cortex arising from altered HCN channels (3). By altering the balance of inhibition and excitation, the mechanisms engaged by NMDA_R antagonism may interact with HCN channel alterations to further promote dissociation.

In future work, we will test experimentally how changes to the altered balance in excitation and inhibition under ketamine can change the expression of oscillations. Our findings suggest that gamma oscillations could be abolished by further shutting down inhibitory neurons, particularly neurons that represent IN-Phasic neurons. Our findings also suggest that slow-delta oscillations could also be abolished by causing further disinhibition in neuronal circuits. If this relationship between the effect of inhibition and the expression of oscillations is correct, then it can begin to inform us how other anesthetics, particularly GABAergic agents that potentiate GABAergic receptors, might interact with ketamine. Our findings also suggest a role for VIP+ neurons tied to the gamma oscillations. By recording from these neurons and manipulating them, we can begin to examine their effects on oscillatory dynamics and therapeutic effects. In summary, these next directions will examine approaches to alter the expression of oscillatory dynamics under ketamine which could change the effects of ketamine at a set dose for enhanced or different therapeutic effects.

Materials and Methods

Human Volunteer Data.

All data collection and experimental protocols in human subjects reported here were approved by the Mass General Brigham Human Research Committee (Institutional Review Board). All participants provided informed consent.

The EEG was acquired from a volunteer subject (26-y-old male, 58.9 kg) administered solely ketamine to induce general anesthesia. Ketamine was administered as a single bolus of 2 mg/kg intravenously. The subject was instructed to click a mouse button when they heard auditory stimuli. Auditory stimuli were randomly presented every 4 to 8 s. All auditory stimuli were 1 s long and were delivered using headphones (ER2; Etymotic Research). Loss of response was determined once the subject stopped clicking the mouse button following the auditory stimuli. EEG was recorded using a 64-channel ANT-Neuro system (Ant-Neuro, Philadelphia, PA) sampled at 250 Hz. Channel F3 was selected and analyzed. The EEG signal was bandpass filtered between 0.1 and 50 Hz and plotted. The spectrogram was derived using the multitaper method (41).

Nonhuman Primate Data.

All procedures in nonhuman primates reported here followed the guidelines of the NIH and were approved by the Massachusetts Institute of Technology’s Committee on Animal Care.

The LFP was recorded from a rhesus macaque (Macaca mulatta) aged 8 y (female, 6.6 kg). Ketamine was administered as a single 20 mg/kg bolus intramuscular dose. Fifteen minutes prior to ketamine administration, glycopyrrolate (0.01 mg/kg) was delivered to reduce salivation and airway secretions. The LFP was recorded from an 8 × 8 iridium-oxide contact microelectrode array (“Utah array,” MultiPort: 1.0 mm shank length, 400 μm spacing, Blackrock Microsystems, Salt Lake City, UT) implanted in the frontal cortex (vlPFC). The LFP was continuously recorded from 1 to 5 min prior to ketamine injection up to 18 to 20 min following ketamine injection. The LFP recorded at 30 kHz, was low-pass filtered to 250 Hz and then downsampled to 1 kHz. The LFP was bandpass filtered between 0.5 and 100 Hz using a second-order butterworth filter and plotted. The spectrogram was derived using the discrete Fourier transform.

Biophysical Modeling.

All neurons are modeled using a single compartment with Hodgkin–Huxley-type dynamics. The voltage change in each neuron is described by:

$$c_m\frac{\mathit{dv}}{\mathit{dt}}=-\sum I_{\mathit{membrane}}-\sum I_{\mathit{synaptic}}+I_{\mathit{app}}+I_{\mathit{noise}}.$$

All neurons display a fast sodium current ($I_{\mathit{Na}}$), a fast potassium current ($I_k$), a leak current ($I_L$) for membrane currents ($I_{\mathit{membrane}}$). VIP+ neurons additionally displayed a D-current and an M-current. The synaptic currents ($I_{\mathit{synaptic}}$) depend on the connectivity. The applied current ($I_{\mathit{app}}$) is a constant that represents background excitation and the noise current ($I_{\mathit{noise}}$) corresponds to a Gaussian noise. The aggregate population activity (EEG/LFP) was defined as the sum of AMPA-receptor and NMDA-receptor synaptic currents into PYR neurons, bandpass filtered between 0.5 and 100 Hz. Modeling details and parameters are provided in SI Appendix.

Model of NMDA Receptor Kinetics.

We implemented a 10-state probabilistic model of NMDA_R kinetics, adapted from ref. 17. The probability of being a certain state can be interpreted as the fraction of NMDA receptors in the particular state. State i transitions to state j with a rate $q_{\mathit{ij}}$, denoting a conditional transition probability. The notation for the states and the rates are provided in SI Appendix, Fig. S8. If Q is the 10 × 10 transition matrix and $P(t)$ is the probability vector of being in each of the 10 states, then:

$$\begin{array}{c}\hfill \frac{dP(t)}{\mathit{dt}}=Q.P(t).\end{array}$$ [1]

For example, for the conductive state ${\text{O}}_{\text{AA}}$, we get:

$$\begin{array}{c}\hfill \frac{d{\text{O}}_{\text{AA}}}{\mathit{dt}}=\beta {\text{C}}_{\AA }+k_{\text{unblock}}(V){\text{O}}_{\text{AA}}-\alpha {\text{C}}_{\text{AA}}-k_{\text{block}}(V){\text{O}}_{\text{AA}},\end{array}$$ [2]

where:

$$\begin{array}{cc}\hfill k_{\text{unblock}}(V)& =5.4exp(V/47){\text{ms}}^{-1},\hfill \end{array}$$ [3]

$$\begin{array}{cc}\hfill k_{\text{block}}(V)& =0.61exp(-V/17){\text{ms}}^{-1}.\hfill \end{array}$$ [4]

Each NMDA_R synaptic connection consists of such a probabilistic model. NMDA_R channels open following agonist (glutamate) binding. The concentration [Glu] denotes the amount of glutamate available at the synapse that can bind to NMDA receptors. Binding rates are determined by this concentration (SI Appendix, Fig. S8). This concentration is given by:

$$\begin{array}{c}\hfill \text{[Glu]}={\text{[Glu]}}_{max}exp(-t/{\tau }_{\text{[Glu]}}),\end{array}$$ [5]

where t denotes the time of the last spike from the presynaptic neuron. We then modeled the NMDA current ($I_{\mathit{NMDA}}$) as:

$$\begin{array}{c}\hfill I_{\text{NMDA}}=g_{\text{NMDA}}{s}_{\text{NMDA}}(V-E_{\text{NMDA}}).\end{array}$$ [6]

The gating variables $s_{\text{NMDA}}$ is the sum:

$$\begin{array}{c}\hfill s_{\text{NMDA}}=\frac{1}{N}{\displaystyle \sum _{k=1}^N}{\text{O}}_{\text{AA}(k\to j)},\end{array}$$ [7]

where N is the number of presynaptic neurons and ${\text{O}}_{{\text{AA}}_{(k\to j)}}$ is the probability of being in state ${\text{O}}_{\text{AA}}$ for NMDA_R synaptic connection $k\to j$.

Network Connectivity.

PYR and IN-Phasic neurons receive excitatory projections (AMPA- and NMDA-receptors) from PYR neurons. PYR and IN-Phasic neurons receive inhibitory projections (GABA-receptors) from IN-Phasic neurons. IN-Tonic neurons do not receive projections, but are modeled to have NMDA-receptors. The concentration [Glu] for NMDA_R is fixed constant for IN-Tonic neurons, to simulate constant input, which would allow NMDA_R kinetics to open and close. The concentration [Glu] for NMDA_R for PYR and IN-Phasic neurons is derived from presynaptic activity. We fixed the [Glu] concentration for IN-Tonic neurons to examine the slow-unblock current without closed-loop effects. However, the results are unchanged if that concentration is instead from presynaptic PYR activity (SI Appendix, Fig. S6A).

Modeling the Effect of Ketamine.

The effect of ketamine was modeled by decreasing $k_{\text{unblock}}(0)$ from $5.4{\text{ms}}^{-1}$ at baseline by $15\%$ to $4.6{\text{ms}}^{-1}$ and then by $30\%$ to $3.8{\text{ms}}^{-1}$ at the highest effect site concentration. This decrease was applied to all NMDA receptors of all the neurons in the network.

Modeling Glutamate Puffs on an Isolated Neuron.

An isolated PYR neuron for NMDA_R kinetics simulations was formed by removing all projections. Glutamate puffs were simulated by setting $\text{[Glu]}=1$ and letting the concentration decay following Eq. 5.

Simulations and Analysis.

Our network model was programmed in C++ and compiled using GNU gcc. The differential equations were integrated using a fourth-order Runge–Kutta algorithm. The integration time step was 0.01 ms. The model output was analyzed using Python 3.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

All study data are included in the article and/or SI Appendix.