Abstract
Machine learning may aid the choice of optimal combinations of anticancer drugs by explaining the molecular basis of their synergy. By combining accurate models with interpretable insights, explainable machine learning promises to accelerate data-driven cancer pharmacology. However, owing to the highly correlated and high-dimensional nature of transcriptomic data, naively applying current explainable machine-learning strategies to large transcriptomic datasets leads to suboptimal outcomes. Here by using feature attribution methods, we show that the quality of the explanations can be increased by leveraging ensembles of explainable machine-learning models. We applied the approach to a dataset of 133 combinations of 46 anticancer drugs tested in ex vivo tumour samples from 285 patients with acute myeloid leukaemia and uncovered a haematopoietic-differentiation signature underlying drug combinations with therapeutic synergy. Ensembles of machine-learning models trained to predict drug combination synergies on the basis of gene-expression data may improve the feature attribution quality of complex machine-learning models.
Acute myeloid leukaemia (AML) is the most commonly diagnosed form of leukaemia in adults and carries a poor prognosis1. Although survival has improved over the past several decades for younger patients, older patients have not seen a similar improvement. This gap in survival has motivated the development of molecularly targeted combination therapies for patients who do not qualify for intensive induction chemotherapy2. Discovering optimal combinations of anticancer drugs is a difficult problem, however, as the space of all possible combinations of drugs and patients is large. Although potentially synergistic drug combinations have traditionally been tested on the basis of either biological or clinical expert knowledge3, more systematic approaches are necessary to effectively explore this space. Even systematic experimental approaches such as high-throughput screening are potentially insufficient, as there are hundreds of thousands of possible combinations of all anticancer drugs currently in development, each of which may have a different response in different patients3,4. Therefore, predictive approaches are necessary to make the immense space of possible anticancer drug combinations manageable.
State-of-the-art predictive approaches fall short along another axis, however, by failing to provide biological insight into the molecular mechanisms underlying drug response, which is essential to facilitate the discovery of new and effective anticancer therapies5–7. Although a wide variety of computational methods have historically been employed for drug combination prediction8–12, recent work has demonstrated increased predictive performance using complex, nonlinear machine-learning (ML) models. For example, all of the winning teams in the AstraZeneca-Sanger Drug Combination Prediction DREAM Challenge utilized complex models in some part of their approach, including ensembles of random forest classifiers and gradient boosted machines (GBMs)13. Additionally, it has been shown that deep neural networks outperform less sophisticated models such as linear models, achieving state-of-the-art performance at predicting the synergy of anticancer drug combinations in 39 cell lines14. A major weakness of these complex ML models is their ‘black box’ nature; despite their high predictive accuracy, these models’ inner workings are opaque, making it challenging to gain mechanistic insights into the molecular basis of drug synergies. In cases where model interpretability is important, researchers resort to simpler, less accurate models such as linear regression. For example, to identify genomic and transcriptomic markers associated with drug sensitivity, both the Cancer Genome Project15 and the Cancer Cell Line Encyclopedia16 used penalized elastic net regression.
In this Article, we present the EXPRESS (explainable predictions for gene expression data) framework to understand the relationship between accuracy and interpretability in biological models and build models that are both accurate ‘and’ biologically interpretable. A recent approach to understand the patterns learned by biological models involves ‘explaining’ complex predictive models using ‘feature attribution methods’, such as Shapley values17–20, to provide an importance score for each input feature (here, a gene). The Shapley value is a concept from game theory designed to fairly allocate credit to players in coalitional games21. By considering input features as players and the model’s output as the reward to be allocated17, the most important features can be identified for complex models that would otherwise be uninterpretable. Unfortunately, the application of off-the-shelf feature attribution methods is unlikely to be successful in the context of large cancer ‘omics data. These methods are known to struggle in the setting of high-dimensional and highly correlated features, such as those present in transcriptome-wide gene expression measurements22. Furthermore, whereas complex ML models have been shown to achieve increased predictive performance when compared to simpler models, recent work has raised the concern that models with higher predictive performance do not necessarily have higher-quality attributions on the same tasks23,24. Our results investigate the relationship between predictive performance and feature attribution quality and demonstrate how a simple approach based on model ensembles can improve the feature attribution quality of complex ML models in the life sciences.
First, using 240 synthetic datasets, we benchmark both classical and novel approaches and demonstrate how nonlinearity and correlation in the data can impede the discovery of biologically relevant features. We then demonstrate that under conditions representative of typical biological applications, all existing approaches tend to perform poorly and show how explaining ensembles of models improves the quality of feature attributions (Fig. 1a). Finally, we describe EXPRESS, which uses Shapley values to explain an ‘ensemble’ of complex models trained to predict drug combination synergy on a dataset of 133 combinations of 46 anticancer drugs tested in ex vivo tumour samples from 285 patients with AML (Fig. 1b and Extended Data Fig. 1). In addition to building highly accurate predictive models, our ensemble interpretability approach identifies relevant biological signals underlying drug synergy patterns, most notably a gene expression signature related to haematopoietic differentiation.
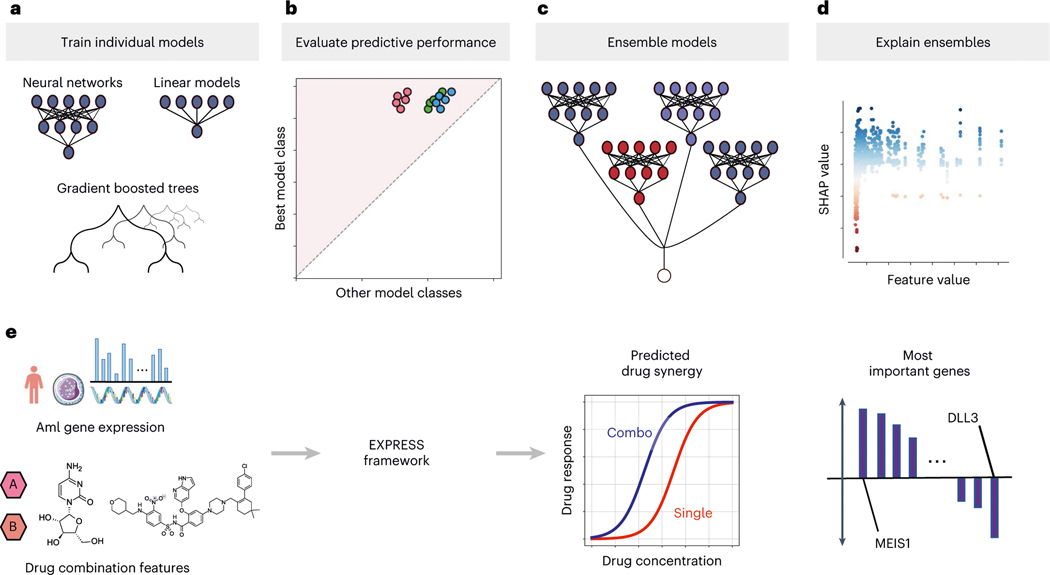
Fig. 1 |. Overview of the study design.
a–e, Our framework, EXPRESS, for learning reliable explanations of cancer therapeutic ML models trained on high-dimensional gene expression data. After training a variety of individual models across multiple model classes (a), predictive performance is evaluated to select a best-performing model class (b). Multiple models from that class are then ensembled (c) to produce more reliable and biologically meaningful explanations (d). We apply our pipeline to a dataset of ex vivo anticancer drug synergy measurements for patients with AML (e), attaining not only superior prediction performance but also identifying biological processes that are important for the determination of drug synergy.
Although individualized treatment for AML based on cancer genomic signatures is already becoming an important aspect of clinical practice6, our approach identifies a novel ‘expression’-based signature that is predictive of synergy across a broad class of drugs and their combinations in AML.
Results
Current state-of-the-art explainable AI falls short on correlated features
Explainable AI (XAI) is a recent development in the ML community that attempts to provide a human-interpretable basis for the predictions of complex, ‘black box’ models such as neural networks. In particular, feature attribution methods are a class of methods that identify the relative importance of each input feature (for example, the expression level of a gene) for a particular model17,25. One popular feature attribution method involves applying Shapley values to interpret these complex models by measuring how much the model’s output changes on average when a feature is added to all other possible coalitions of features (see Methods).
Although applying XAI techniques to complex models has become a popular practice in the life sciences26–35, applying these methods in the context of gene expression data is particularly difficult. Each patient will have a transcriptomic profile with tens of thousands of features with a high degree of feature interdependence (for example, see the feature covariance matrix for AML transcriptomic data in Fig. 2, top right). This makes the task of accurate feature attribution harder for Shapley value algorithms, which ideally would operate on statistically independent features17. In the presence of correlated features, many models with diverse mechanisms could potentially fit the data equivalently well36,37. Thus, even if we could explain a single model perfectly, that model might not correspond well to the true biological relationships between features and outcome.
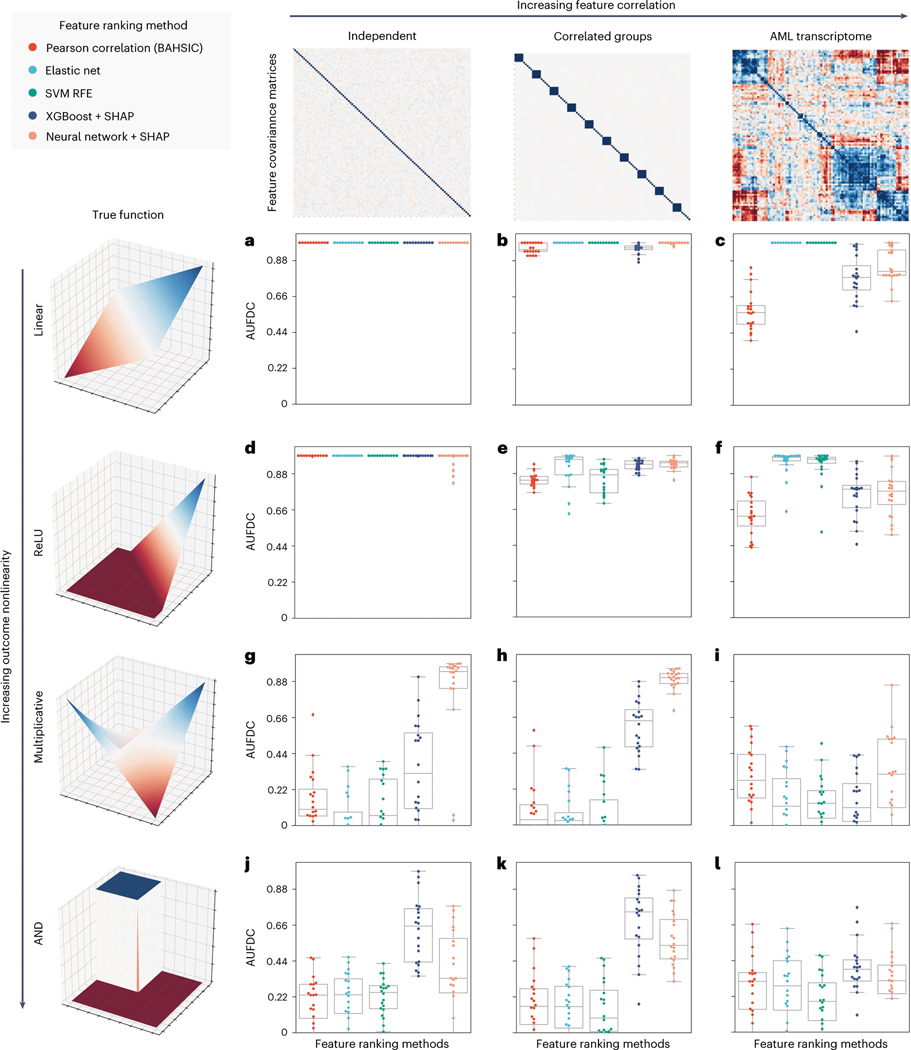
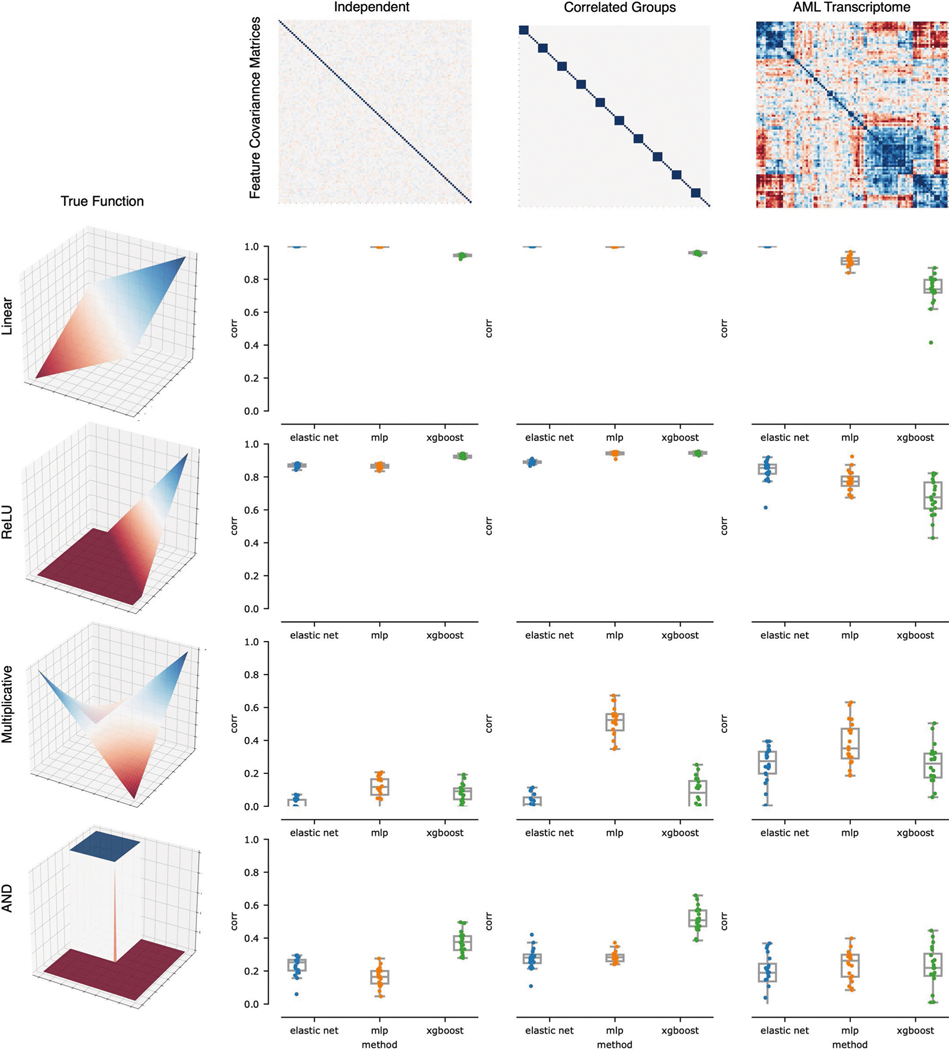
Fig. 2 |. Benchmark metric reveals the impact of nonlinearity and correlation on feature discovery.
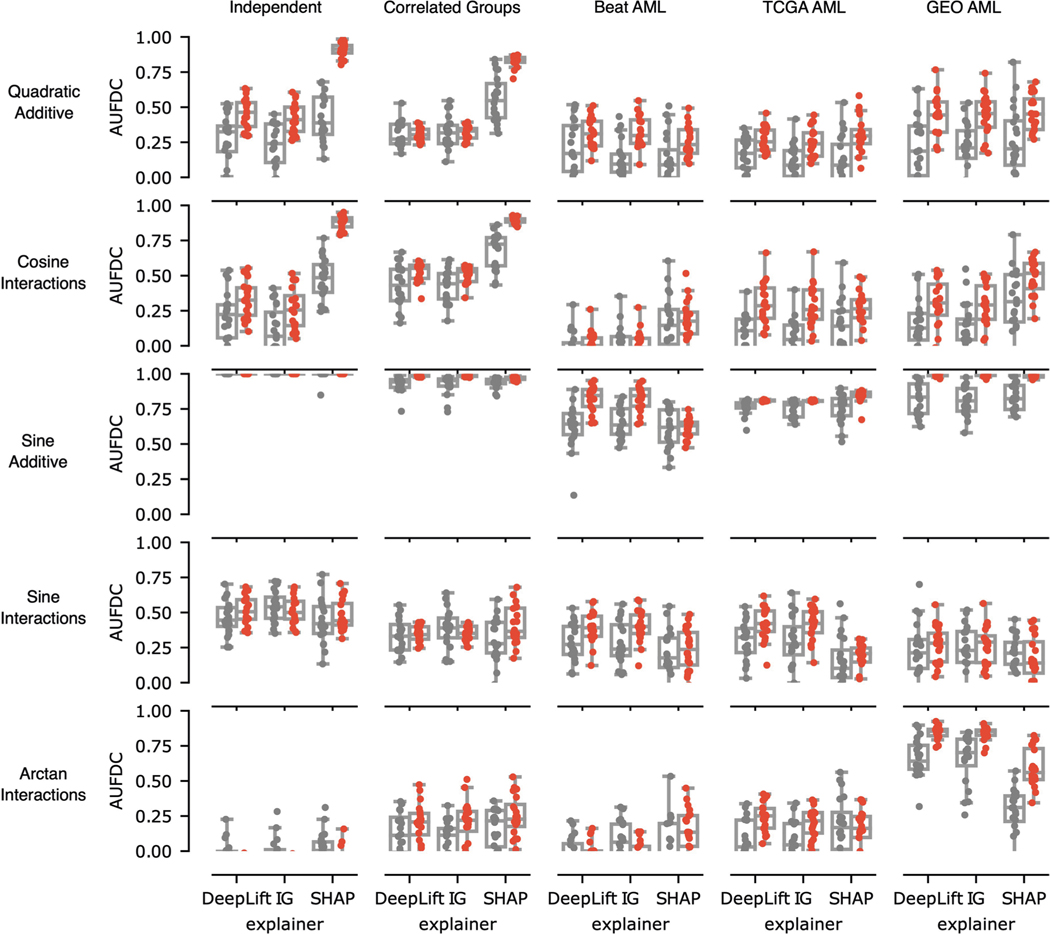
Each point in the boxplots represents the benchmark score achieved by one of five feature ranking methods applied to one of 240 datasets generated from 12 synthetic or semi-synthetic dataset types (each subplot represents one dataset type). The rows (left) are sorted from top to bottom by increasing nonlinearity of the true feature-outcome relationship (that is, all datasets in the first row (a–c) have a linear relationship between input features and outcome, all datasets in the second row (d–f) use ReLU functions, all datasets in the third row use multiplicative functions (g–i), all datasets in the last row (j–l) use AND functions), whereas the columns are sorted from left to right by the increasing extent of the correlation between features in the dataset (for example, all datasets in the last column (c,f,i,l) have real AML bulk RNA-seq features). The metric plotted in each boxplot is the AUFDC (see Methods), where a higher score indicates better performance (0 represents random performance and 1 represents perfect performance). The boxes mark the quartiles (25th, 50th and 75th percentiles) of the distribution, and the whiskers extend to show the minimum and maximum of the distribution (excluding outliers). For each dataset type (a pair of feature-outcome relationship and inter-feature correlation), 20 independent datasets are generated by randomly regenerating features. Although all approaches achieve perfect performance on simple linear data with independent features (a), all models have worse performance as features become more correlated and outcomes become more nonlinear (l).
Since these conditions are ubiquitous in biological datasets, it is essential to understand how the efficacy of both Shapley value-based attributions and more conventional methods will be impacted in the setting of high-dimensional, highly correlated features. Measuring this efficacy is difficult, however, as existing benchmarks of feature attribution methods are designed to either measure the influence of features on the ‘particular model’ being explained18, or to measure the ‘predictive performance’ of selected sets of features38.
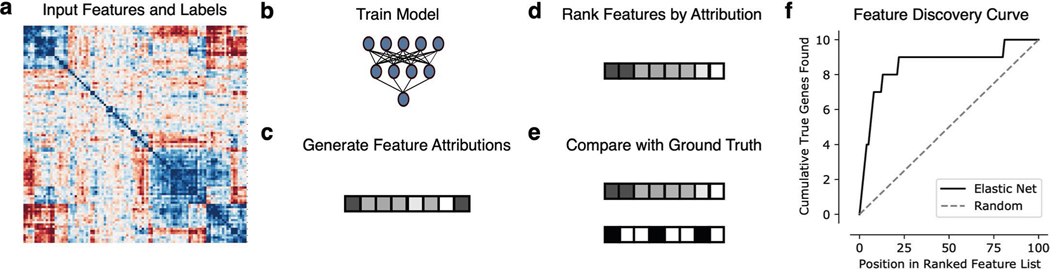
We therefore design a simple benchmark for this application (Fig. 2, Methods and Extended Data Fig. 2). To evaluate the effects of data correlation and nonlinearity on feature attribution, we use 240 unique datasets. As input data, we consider synthetic datasets with independent features and synthetic datasets with multivariate normal covariance structure, as well as datasets with real gene expression measurements sampled from AML patients7. Since the goal of our benchmark is to define how well different methods recover ‘true features’, we create synthetic labels, allowing the ground truth to be recovered and measured. These labels are created by randomly sampling input features and relating them to the outcome using functions ranging from simple linear univariate relationships to complex nonlinear step functions with interactions between features (see Methods). For our metric of feature discovery performance, we measure how many ‘true features’ are found cumulatively at each point in the lists of features ranked by each feature attribution method (see Methods and Extended Data Fig. 2; predictive performance of models reported in Extended Data Fig. 3). Using this benchmark, we then evaluate five different methods for ranking biologically important features, including two complex ML methods (GBMs, neural networks) explained using Shapley values, as well as three more traditional linear methods: ranking features by their Pearson correlation with the outcome39, ranking features by their elastic net coefficients40 and recursive feature elimination using support vector machines41.
When the outcome has a simple linear relationship with the input features, all approaches recover the true features well (see the perfect performance across all methods in the top left experiment in Fig. 2a). When there is nonlinearity in the data, however (see Fig. 2g–l), the complex ML models interpreted with Shapley values substantially outperform the linear approaches. For example, neural networks explained with Shapley values attain a higher area under the feature discovery curve (AUFDC) than elastic net coefficients when the true outcome is multiplicative and the features are independent (two-sided Mann−Whitney -test, , ) or in correlated groups (, ). Likewise, XGBoost models explained with Shapley values attain a higher AUFDC than elastic net coefficients when the true outcome is a pairwise AND function and the features are independent (, ) or in correlated groups (, ). Importantly, however, as the correlation between input features increases to the level seen in real AML transcriptomic data (Fig. 2c,f,i,l), all methods tend to perform poorly and there is a high degree of variance in the performance of each model class.
Ensembling overcomes variability in individual models
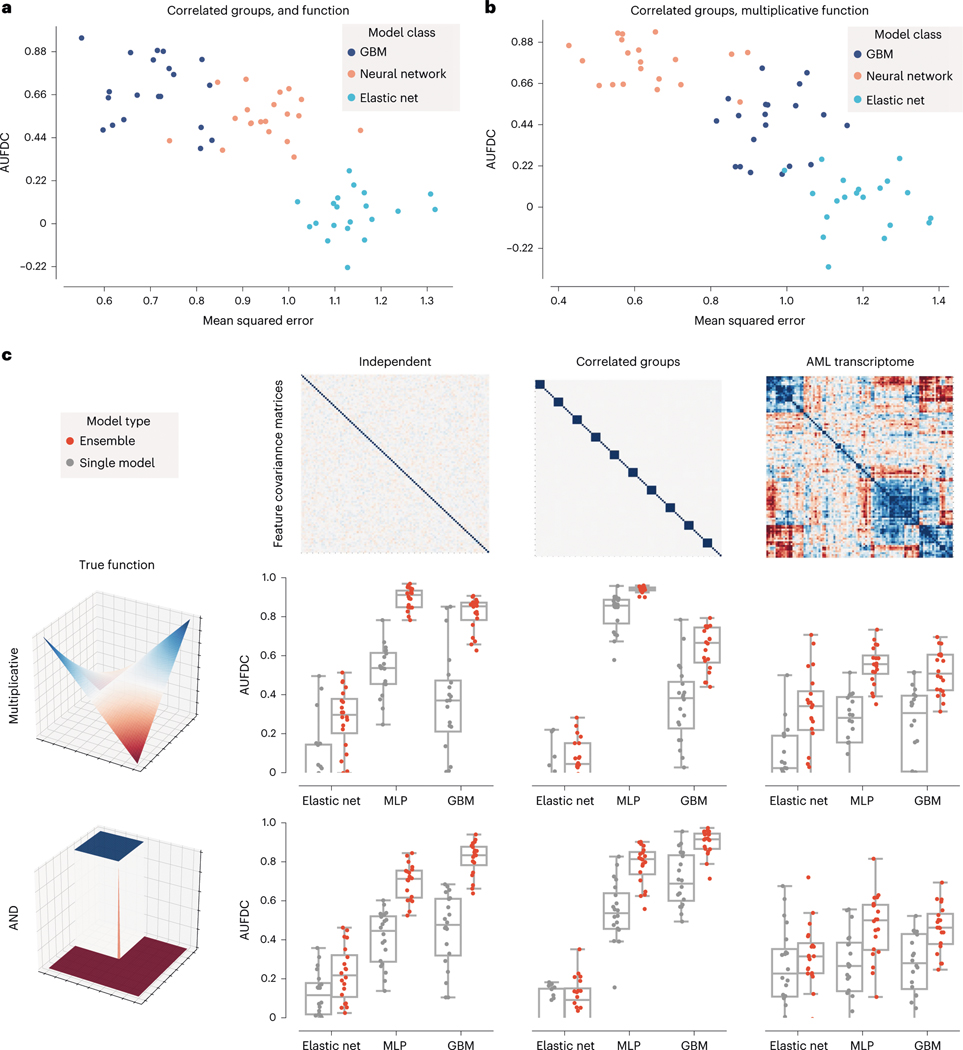
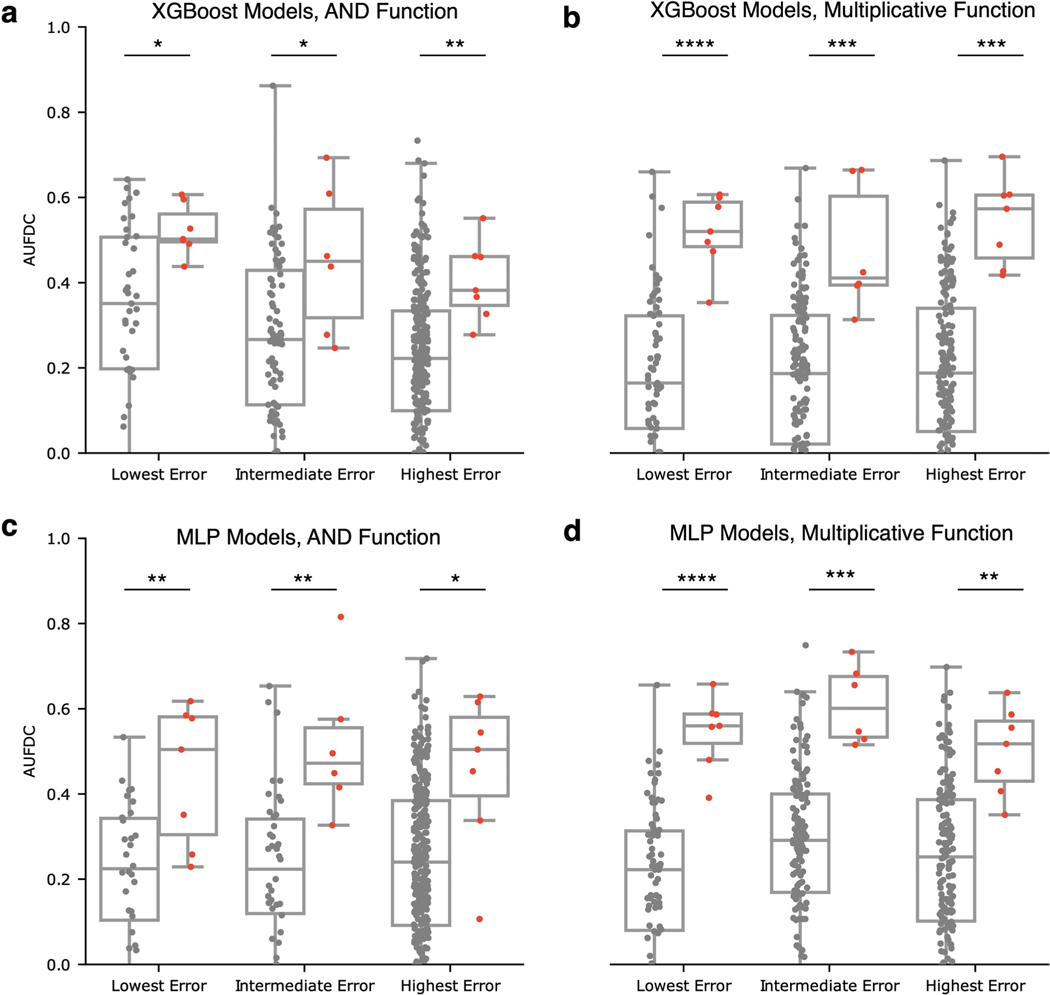
Given the observed variability of different models in terms of benchmark performance, a natural question that arises is how to select the predictive model that will attain the best performance at feature discovery. An intuitive solution is to simply pick the model with the best predictive performance. When we examine the relationship between predictive performance and feature discovery, however, we see that this is not necessarily a reliable strategy. For each of three popular model classes (linear models, feed-forward neural networks and GBMs), we train 20 independent models on bootstrap resampled versions of the same dataset and measure test set prediction error and feature discovery performance. Although there was significant overall correlation between test error and feature discovery (step function dataset: two-sided Pearson’s , , ; multiplicative dataset: two-sided Pearson’s , , ), within each model class, test error was ‘not’ significantly correlated with feature discovery performance (elastic net + step function dataset: two-sided Pearson’s , , ; neural network + step function dataset: two-sided Pearson’s , , ; XGBoost + step function dataset: Pearson’s , , ; elastic net + multiplicative dataset: two-sided Pearson’s , , ; neural network + multiplicative dataset: two-sided Pearson’s , , ; XGBoost + multiplicative dataset: two-sided Pearson’s , , ; see Fig. 3a,b). Therefore, although predictive performance may help to select a ‘model class’, it will not necessarily help to select which model within that class has the most biologically relevant explanations.
Fig. 3 |. Explaining ensembles helps overcome instability in feature discovery performance for single models.
a,b, Relationship between test error and feature discovery performance on bootstrap resampled versions of two synthetic datasets. Both datasets had clusters of highly correlated features; one had a step function outcome (a) and the second had a multiplicative outcome (b). Although there is a high overall correlation between test error and feature discovery performance for both datasets, there is no significant correlation after conditioning on model class (see Supplementary Table 1 for full statistical comparisons across model classes including XGBoost models (GBMs), multilayer perceptron neural network models (MLPs) and elastic net regression). c, Comparison of feature discovery performance between individual models and ensemble models using synthetic and semi-synthetic datasets from our benchmark. The boxes mark the quartiles (25th, 50th and 75th percentiles) of the distribution, and the whiskers extend to show the minimum and maximum of the distribution (excluding outliers). Results for the rest of the datasets and for additional feature attribution methods can be found in Extended Data Figs. 5 and 6.
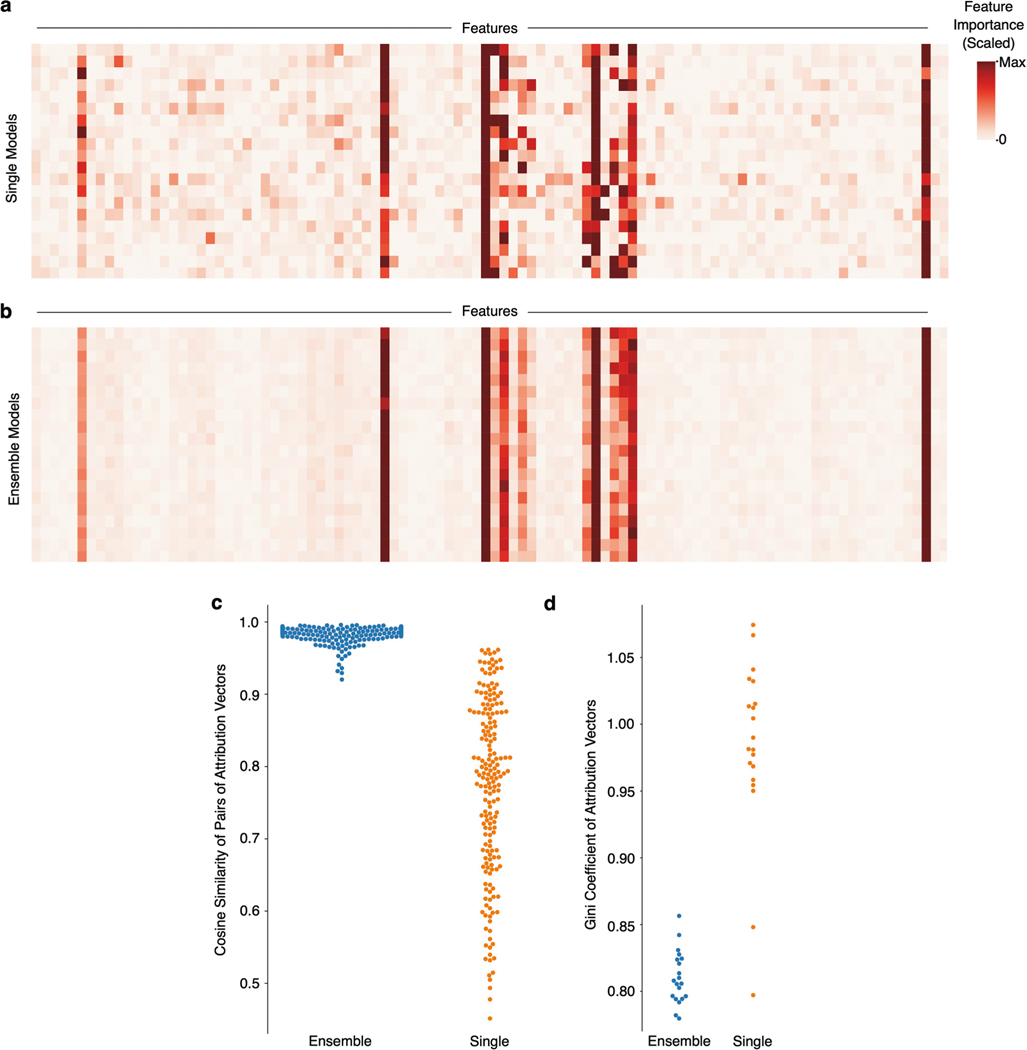
Furthermore, when we examine the feature attributions across individual models within a single model class, we observe that they vary substantially from model to model (Extended Data Fig. 4). This indicates a lack of stability in the attributions: minor perturbations to the training set (such as bootstrap resampling) can lead to substantial variability in the features identified as most important by the model36, and previous work in machine learning applied to human genomics and epigenomics has suggested the necessity of considering multiple models when analysing explanations42,43. Likewise, recent work on feature selection for black box predictive models in healthcare has pointed out the need to select robust features44.
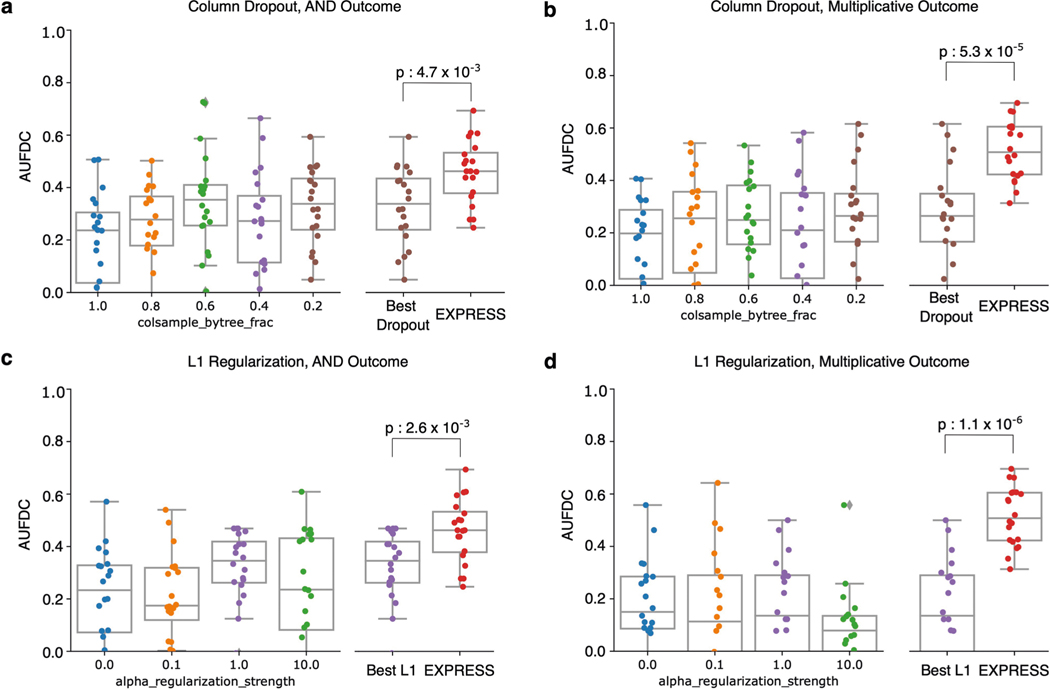
Although ensembling ML models is classically known to increase the accuracy of models by increasing stability of predictors, it remains to be demonstrated whether ensembling can improve biological hypothesis generation. We therefore created ensembles of models for all of the datasets in the original benchmark task, and found that ensembling not only decreases the variance in feature discovery performance, but also significantly increases the average feature discovery performance of the ensemble models (Fig. 3c; associated statistics in Supplementary Dataset 1). Not only does this improvement occur consistently across dataset types and model classes (see Extended Data Figs. 5 and 6 for results on 12 main benchmark dataset types and Extended Data Figs. 7 and 8 for results on 25 supplementary benchmark dataset types), but this effect is independent of an increase in predictive performance (see Extended Data Fig. 9). Furthermore, this effect is greater than that seen by adding explicit regularization to models (see Extended Data Fig. 10).
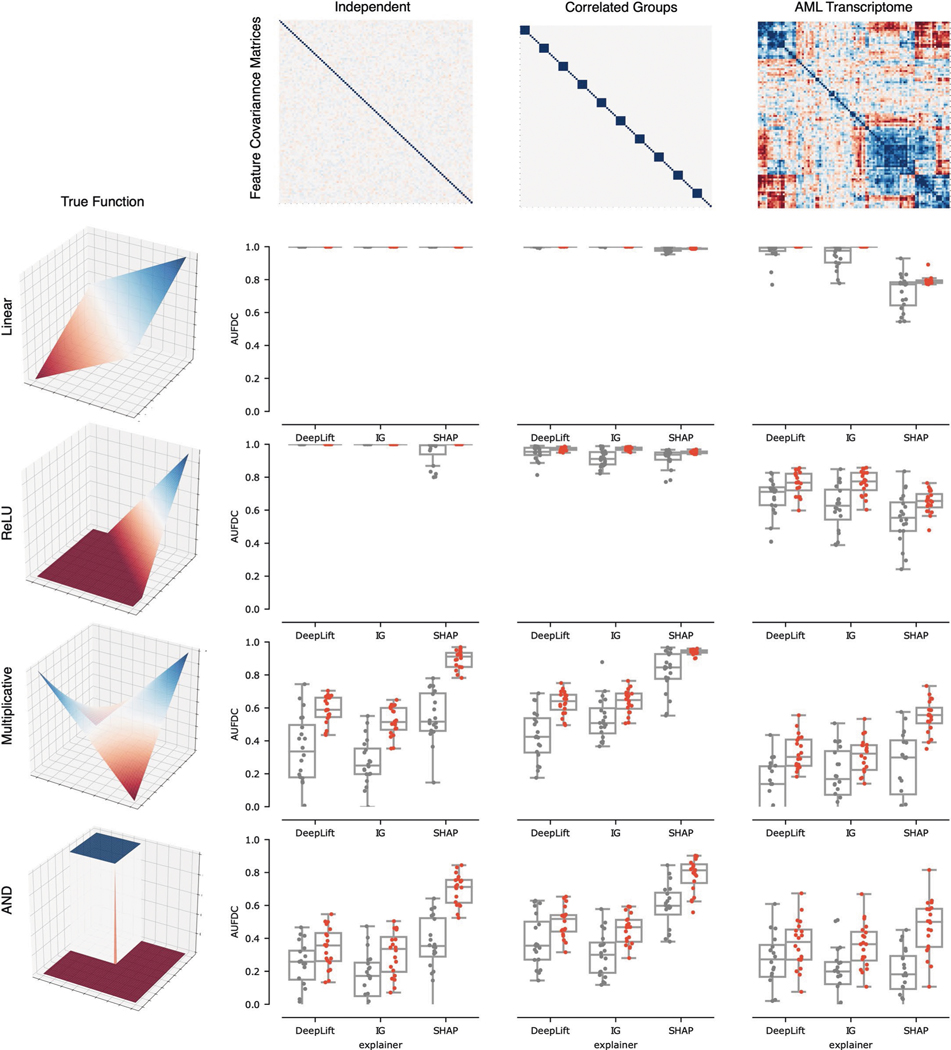
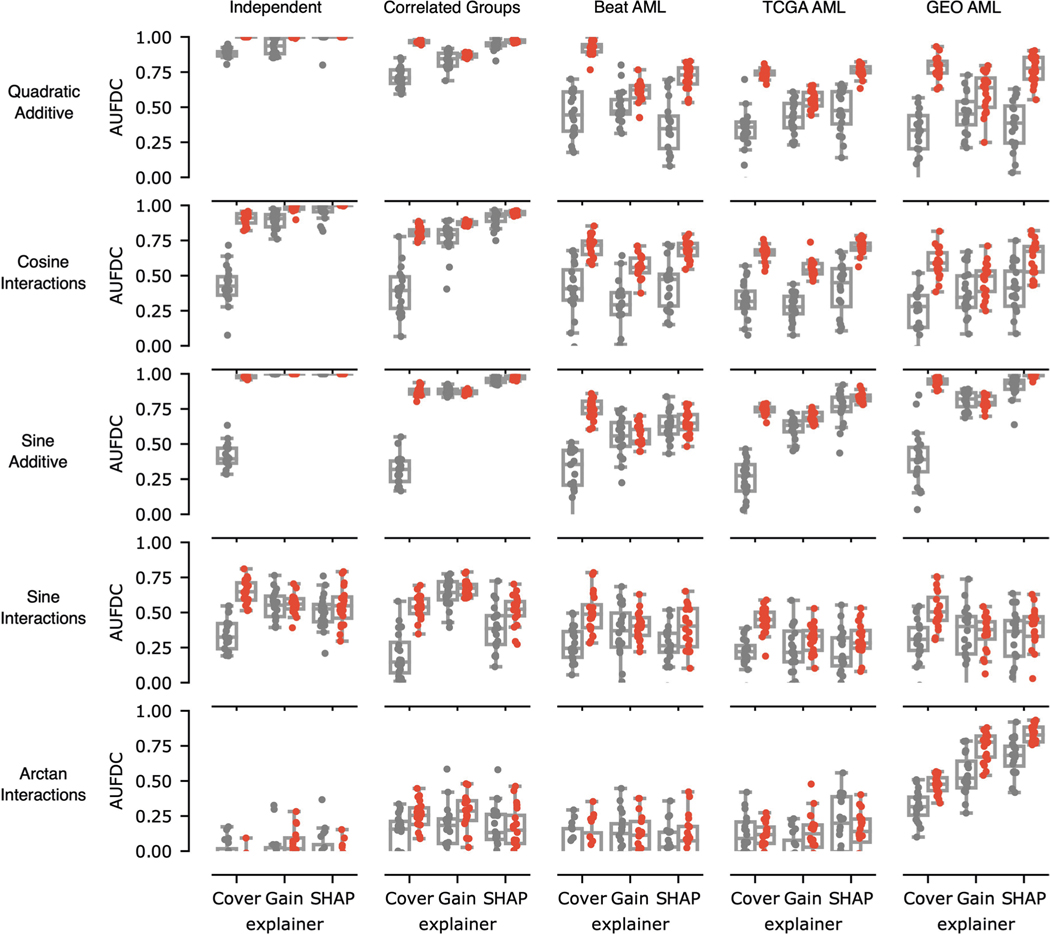
To understand how the ensembled models differed from the individual models, we analysed the difference between the attributions attained by a variety of ensembled models and the individual models. We see that the variability in attributions across bootstrap resampled versions of the dataset decreases, with an average pairwise cosine similarity between attributions across models increasing from 0.77 to 0.98 after ensembling (, ; see Extended Data Fig. 4). Furthermore, when compared to the single models, the ensemble models tend to place more weight on a small set of important features and attribute less importance to spurious correlates: spurious correlations cancel out over repeated model trainings, whereas the true signal remains consistent (Extended Data Fig. 4). In addition to carrying out this experiment for the other two ‘true functions’ evaluated in the original benchmark in Fig. 2, we also verified that the improvement seen with ensembling holds when other feature attribution methods such as DeepLift19 and Integrated Gradients20 are used (Extended Data Figs. 5 and 6).
These results suggest a natural approach for applying XAI techniques to complex biological datasets (see Fig. 1a). A variety of model classes should be compared in terms of predictive performance, and following the selection of the best-performing model class, the set of well-performing models from that class should be ensembled for explanation.
Complex GBMs accurately predict drug synergy in AML samples
After determining the importance of model class selection and model ensembling from our benchmark, we applied our framework to publicly available data provided by the Beat AML collaboration7. These data consist of the gene expression profiles of primary tumour cells from 285 patients with AML, as well as drug synergy measured for these cells in an ex vivo sensitivity assay for 131 pairs of 46 distinct drugs, spanning a variety of cancer subtypes and anticancer drug classes (Extended Data Fig. 1, and Supplementary Datasets 2 and 3). The input features of each sample thus comprise ‘gene expression features’ that describe the corresponding patient’s tumour’s molecular profile, and ‘drug features’ that describe the two drugs in that combination in terms of the gene targets of each of the two drugs (Fig. 1b and Methods). In addition to literature-derived gene target features, we also investigated describing the drug combinations with structural and physicochemical features, but found the gene target features to lead to superior predictive performance (see Supplementary Fig. 1 and Methods).
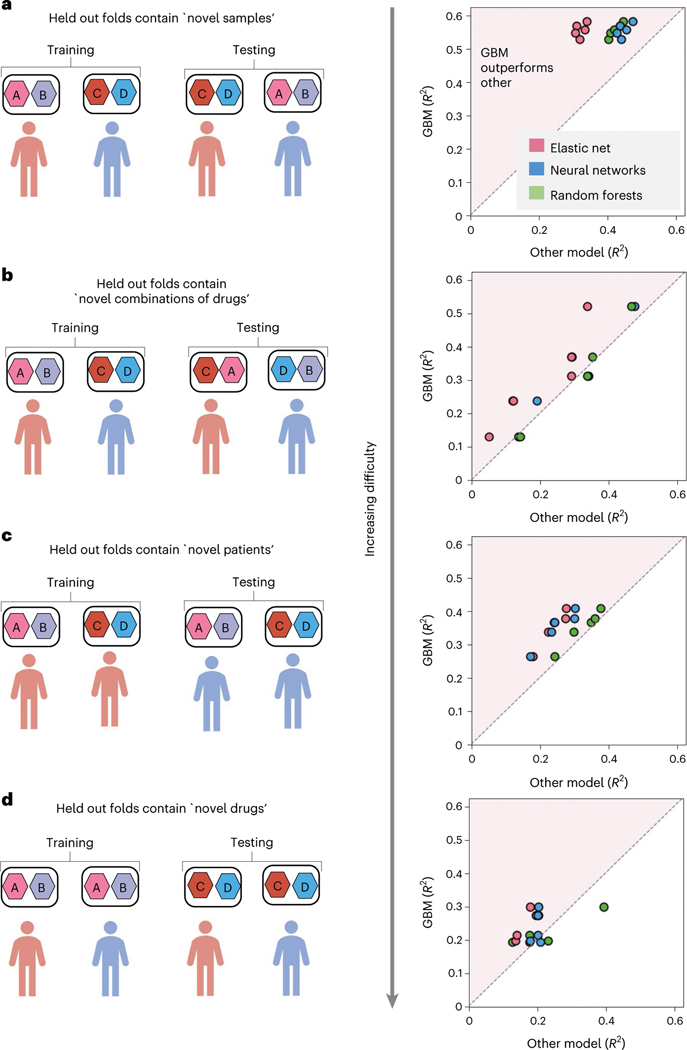
EXPRESS begins by comparing multiple model classes: elastic net40, deep neural networks14, random forests45 and extreme gradient boosting (XGBoost)46, in terms of the test error calculated using 5-fold cross-validation tests. To rigorously evaluate the predictive performance of the models, we performed comparisons using four different schemes for stratifying samples into train and test sets. Each different stratification assesses the generalization performance for a different possible application scenario (see Fig. 4 and Methods)14,47. Across these four settings, XGBoost shows better performance in 53 comparisons out of 60 (=4 × 3 × 5) comparisons from four settings, with three alternative methods and for five test folds. Elastic net, random forests and deep neural networks show better performance in 4, 27 and 30 comparisons, respectively. Our framework therefore selects XGBoost as the optimal model class for further downstream interpretive analysis. This finding aligns well with contemporary work on machine learning for tabular datasets (such as gene expression data), which has empirically demonstrated that tree models such as XGBoost tend to outperform deep learning models48.
Fig. 4 |. Comparison of predictive performance between model classes across four stratification settings.
Each point in the plots on the right represents an evaluation of model performance after a different split of the data. To consider a variety of potentially useful application settings, samples were stratified in four ways. Each sample comprises primary tumour cells from a patient with AML and a pair of anticancer drugs. In a, samples are randomly split into 5 different train test folds. In b, samples are split on the basis of the drug combinations, so that held-out test folds contain novel drug combinations that were not present in the training data. In c, samples are split on the basis of patients, so that held-out test folds contain patients that were not present in the training data. In d, samples are split on the basis of individual drugs, so that held-out test folds contain drugs that were not present in the training data.
Ensembled attributions reveal important genes for anti-AML drug synergy
After identifying GBMs as the best-performing model class for our dataset, we ensembled individual models until the ensemble model attributions were stable, leading to a final ensemble of 100 XGBoost models (see Supplementary Fig. 2 and Methods). We then analysed the resultant ensemble model attributions to look for genes with ‘global’ importance for drug combination synergy, that is, genes whose expression is related to synergy across many different drug pairs in our dataset18. Genes that impact global synergy could belong to pathways with outsized importance to cancer biology which are targeted by many drugs in the dataset, such as MAPK signalling or PI3K-Akt signalling (see Supplementary Dataset 3 for a list of targets for each drug), or could be related to larger-scale transcriptional changes impacting many pathways simultaneously, such as the degree of differentiation of leukaemic cells49.
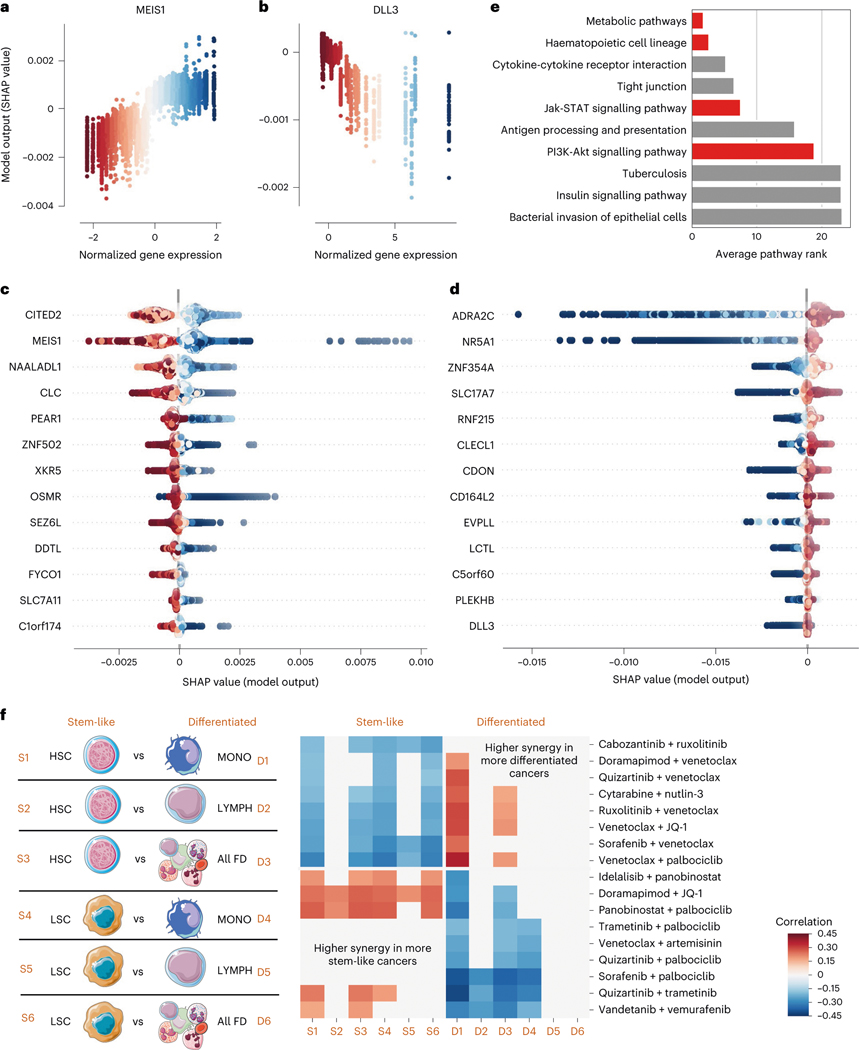
We first visualize genes with monotonic relationships with synergy across all samples in the dataset, measured by the strength of the Spearman correlation between expression and attribution values, by plotting these robust attributions in a dependence plot. For example, a strong positive correlation between the expression level of MEIS1 (the second strongest relationship out of 15,377 genes tested), and its attribution value indicates that patients with higher levels of MEIS1 expression are predicted to respond more synergistically to the drug pairs tested in this dataset (Fig. 5a). MEIS1 has been shown to be upregulated in mixed-lineage leukaemia (MLL)-rearranged AML50, while also driving leukaemogenesis independently of MLL-rearrangement51. Recently, high MEIS1 expression has been observed within Venetoclax-resistant AML subclones with ‘monocytic’ characteristics52. Because AML in different patients may manifest in different developmental stages52, the importance of MEIS1 suggests that our model may be learning a differentiation-related expression signature underlying the synergistic ability of certain drugs to overcome resistance to others.
Fig. 5 |. Transcriptomic factors affecting anti-AML drug combination synergy.
a,b, SHAP dependency plots for MEIS1 and DLL3. Each point represents a single sample (one patient with a pair of anticancer drugs), the axis and colour coding represent the normalized gene expression values, and the axis represents the feature attribution value (change in predicted drug synergy attributable to that feature). c,d, SHAP summary plots for the transcripts with the strongest positive (c) and negative (d) relationships with anti-AML drug synergy. Each point still represents a single sample and the colour coding still represents normalized gene expression values, but the axis now represents the feature attribution value (plotted on the axis in the corresponding analysis in a and b). e, Biological pathways most highly enriched in the list of most important gene expression features, sorted by their average ranking across several top gene thresholds. Red bars indicate pathways discussed further in the text. f, For 12 separate differential gene expression profiles created by pairing gene expression measurements from a more stem-like haematopoietic lineage cell population (HSCs or LSCs) with a more differentiated haematopoietic lineage cell population (monocytes, lymphocytes, or all fully differentiated cells), we measured the correlation between the average expression of that profile and the synergy for each drug combination. After FDR correction, we plotted all combinations with significant correlations across at least two profiles. We find that some combinations of drugs tend to have higher synergy in more differentiated cancers, and that some combinations of drugs tend to have higher synergy in more stem-like cancers.
EXPRESS can identify other genes showing such trends and visualize many of these feature attribution relationships at once by assembling the marginal distributions of the expression-attribution dependence plots into a summary plot. Figure 5c,d shows two summary plots: one for the genes where higher expression correlates with higher predicted synergy, and another for the genes with negatively correlated relationships (see Supplementary Dataset 4 for an exhaustive list). One of the top negatively correlated genes was DLL3 (Fig. 5b), a member of the Notch signalling pathway, which has been shown to have prognostic importance in patients with AML: patients with higher DLL3 expression have been shown to have lower overall survival53. We find that many of the top genes underlying synergy in both directions have been related to different stages of haematopoietic development. For example, CITED2 (the top positively correlated gene) is known to be essential for the maintenance of adult haematopoietic stem cells54. Additionally, CITED2-mediated haematopoietic stem cell maintenance has also been shown to be critical for the maintenance of AML55. Other genes in this list, such as OSMR, have further been shown to be essential for the maintenance of normal haematopoiesis56. Still other top genes, such as SLC7A11 and SLC17A7, have been linked to prognosis of AML57–59.
In addition to considering genes whose expression consistently impacts synergy either positively or negatively across all drug combinations, we additionally ranked genes by the magnitude of their global attribution values. This analysis allows genes that are important for multiple combinations to be ranked highly, even if higher expression levels of these genes are linked with higher synergy for some combinations and lower synergy for other combinations. When EXPRESS ranks all genes by the magnitude of their global attribution values (see Methods and Supplementary Dataset 5), we again find genes that are related to haematopoietic development and AML prognosis. In particular, IL-4 (top-ranked gene by non-directional magnitude) is an important cytokine regulating the tumour microenvironment that has been shown to be specifically downregulated in AML compared with normal myeloid cells60. STAT6 (ranked 31st) is a transcriptional regulator known to be a key mediator of cytokine signalling61. It has previously been experimentally demonstrated using CRISPR-Cas9 genomic engineering that STAT6 specifically mediates IL-4-induced apoptosis in AML62. Furthermore, expression of STAT6 has been shown to be high in haematopoietic stem cells, but not in more differentiated progenitors63. Other top genes in this list, such as SLC51A and RNF213 (ranked second and sixth overall, respectively), have been previously linked to AML and familial myelodysplasia via genome-wide association studies64,65.
Pathway explanations identify global importance of a differentiation signature
Although attributions and trends for individual genes are informative, to gain systems-level insights into the processes important to drug synergy prediction, we can also use pathway databases to systematically check whether genes from certain pathways are over-represented in EXPRESS’s top-ranked genes. When we test the top-ranked genes for pathway enrichment, we find that the top pathway (Fig. 5e) is related to cellular metabolism. Expression programmes regulating cancer metabolism have previously been linked to resistance to a variety of the drugs tested in this dataset. For example, AML cells that are resistant to the tyrosine kinase inhibitor Cabozantinib have been shown to have higher glucose uptake, GAPDH activity and lactate production than Cabozantinib-sensitive cells66.
Furthermore, consistent with our hypothesis that the importance of MEIS1 for synergy may be linked to a differentiation signature, the second most highly enriched pathway contains genes that control differentiation along the haematopoietic cell lineage ( from hypergeometric test, false discovery rate (FDR) correction using Benjamini-Hochberg procedure). Previous studies have shown that leukaemic stem cell signatures associate with worse clinical outcomes67,68, and cells at different differentiation stages have been shown to respond differently to particular combination therapies69,70. The differentiation signature and metabolic signature may in fact be related, as previous work has shown that less-differentiated leukaemic cells have unique metabolic dependencies71, and has even proposed metabolic changes as a mechanism mediating anticancer drug combination resistance specifically in stem-like leukaemic cells72.
To further explore the importance of differentiation signatures as a global pattern underlying drug combination synergy, we used RNA-sequencing data generated from specific subpopulations of haematopoietic cells to create gene lists that are relatively more (or less) expressed in either haematopoietic stem cells (HSCs) or leukaemic stem cells (LSCs) compared with more differentiated populations, such as monocytes, lymphocytes and all fully differentiated blood cells (Methods)73. Considering six pairs of cell types (Fig. 5f, left) leads to 12 gene lists; six of the gene lists represent more stem-like expression states, whereas the other six lists represent more differentiated signatures (see Methods for more details). For each gene list, we measured the correlation between the average expression of the genes in the list and drug synergy for each drug pair (Fig. 5f, right), and plotted correlations that were significant after multiple hypothesis testing correction.
Remarkably, we found two distinct sets of drug combinations: combinations that were more synergistic when applied to tumour samples with more stem-like expression profiles and combinations that were more synergistic when applied to tumour samples with more differentiated expression profiles (Fig. 5f, right). For instance, many combinations containing the BCL-2 inhibitor Venetoclax were associated with increased synergy when a more differentiated signature was present. Specifically, these were most strongly associated with a monocytic expression signature (Signature D1). Recent studies have demonstrated that in some patients, AML subclones with a monocytic differentiation signature exist next to subclones with a more primitive, stem-like transcriptional profile52,70. Monocytic subclones have been shown to be relatively resistant to Venetoclax52,70, raising the possibility that the drugs paired with Venetoclax in the identified combinations could be helping to overcome this resistance. For example, our approach identifies the combination of Ruxolitinib, a JAK inhibitor, with Venetoclax as having more synergy in more differentiated cancers. The capacity of Ruxolitinib to synergize with Venetoclax, specifically by targeting and overcoming monocytic resistance, has recently been demonstrated in several studies70,74. EXPRESS identifies a number of additional drugs that may be combined with Venetoclax to the same effect, including the p38 MAP kinase inhibitor Doramapimod, the tyrosine kinase inhibitors Quizartinib and Sorafenib, the cyclin-dependent kinase 4/6 inhibitor Palbociclib and the BET bromodomain inhibitor JQ-1. Interestingly, EXPRESS also identifies a handful of combinations not containing Venetoclax for which synergy is also associated with a differentiation signature, including the combination of Cabozantinib and Ruxolitinib, as well as the combination of MDM2 inhibitor Nutlin-3 and the chemotherapeutic cytosine analogue cytarabine. To verify the importance of haematopoietic differentiation for AML drug sensitivity, we analysed the significance of these differentiation signatures in an additional, external dataset (Supplementary Fig. 3). Using the AML cell line expression data and experimentally measured genetic dependency from the DepMap database, we found a significant association between the cancer cell line dependency of the genetic targets of the drug combinations in Fig. 5 and the expression of our differentiation signatures (empirical values 0.001, 0.001 and 0.026 according to three separate null models).
These results show that the exact position of AML cells on a haematopoietic differentiation spectrum predicts the synergy that can be achieved with specific therapy combinations. Assessment of an AML stemness (or differentiation) signature may therefore be useful in guiding therapy choices in the clinic.
Feature interactions identify drug-specific gene expression signatures
In addition to identifying expression signatures that are generally relevant for drug synergy across many combinations, our approach can also identify genes and pathways that are relevant for ‘specific’ drugs. To quantify these drug-specific mechanisms, we used an extension of the Shapley value called the Shapley interaction index18,75, which extends attributions for single features to interactions between pairs of features (see Methods). Intuitively, expression of a particular gene may be more important when one of the drugs in a combination is specifically targeting that gene. Likewise, expression of a particular gene may be less important when neither drug targets that gene. Therefore, to quantify which genes were important for specific drugs, we measured the interaction values between each drug feature label and all gene features.
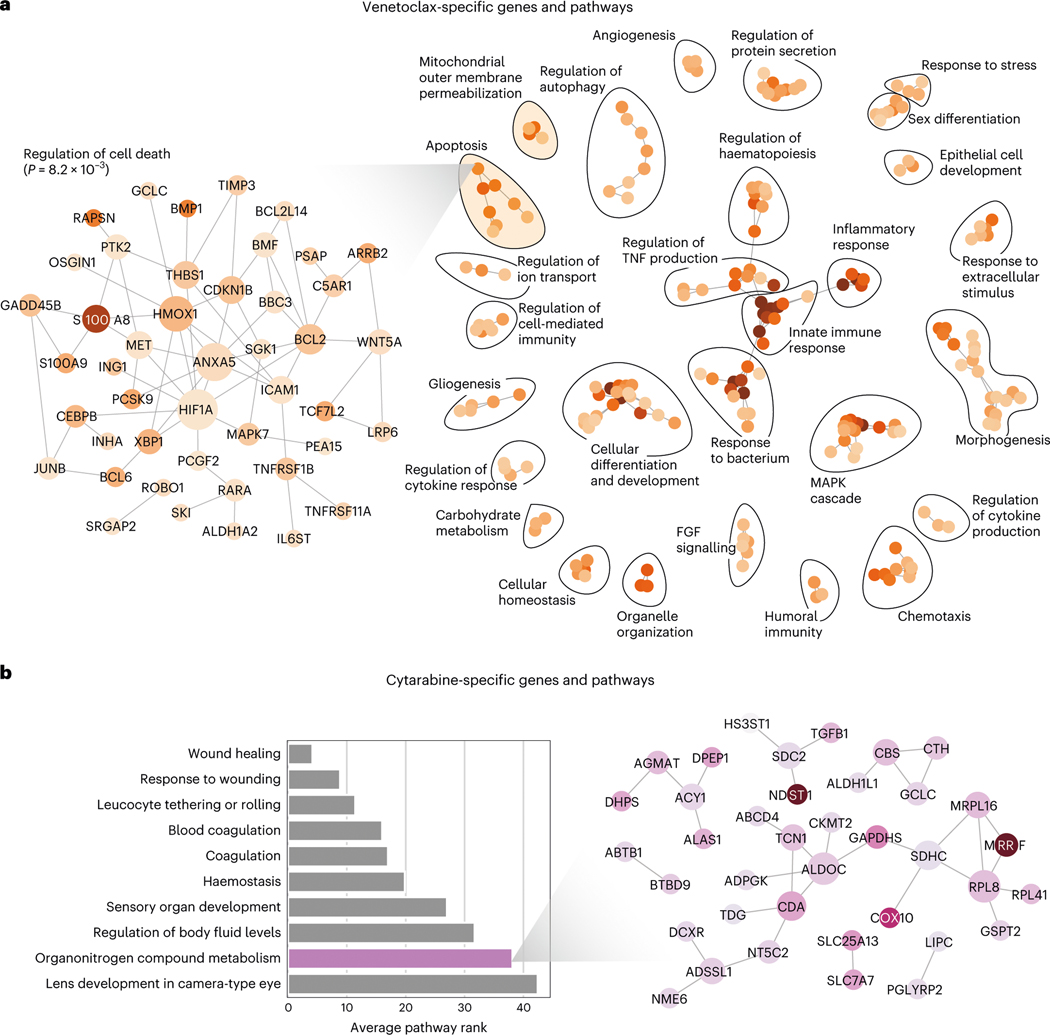
By analysing the most important genes for each drug ranked by the average magnitude of their interactions (see Methods), EXPRESS can reveal the specific biological processes related to synergy for a particular drug. After generating interaction values between all genes and drugs, we tested each list of global drug-specific gene attributions for pathway enrichment (see Methods). We found that these enrichments aligned with previous knowledge of the mechanisms of the drugs in question (Fig. 6).
Fig. 6 |. Transcriptomic factors affecting synergy of combinations including specific drugs.
a, The top pathway enrichments in the set of transcripts affecting synergy of drug combinations including the drug Venetoclax. Each node in the graph on the right represents a single pathway, where the colour indicates the strength of the enrichment, and edges indicate significant overlap in terms of the set of genes in each pathway. The zoomed inset graph on the left shows the genes in one pathway, ‘Regulation of cell death’, from the cluster of apoptosis-related pathways. In the left inset graph, each node is a gene, and the edges represent known protein-protein interactions. b, The top pathway enrichments in the set of transcripts affecting synergy of drug combinations including the drug cytarabine. The bar plot (left) shows the top pathways, and the inset graph on the right shows the relevant genes from one pathway, ‘Organonitrogen compound metabolism’.
For instance, EXPRESS pinpoints genes involved in apoptosis as important determinants of synergy for pairs of drugs containing Venetoclax (Fig. 6a, right), a drug which functions by restoring apoptotic function in malignant cells via inhibition of the gene B Cell Lymphoma-2 (BCL-2)76. Examining the individual genes in one of the enriched pathway modules for Venetoclax (Fig. 6a left, ‘Regulation of cell death’ term, FDR-corrected ) reveals Venetoclax’s specific target BCL-2 to be an important predictive gene. Measuring the strength and direction of the relationship between BCL-2 expression and Venetoclax-specific BCL-2 attribution values, we find that increased BCL-2 expression is associated with markedly increased drug synergy in the context of Venetoclax treatment (Spearman , two-sided ). Other genes in this module include S100A8 and S100A9, both genes having been previously linked to patient response to Venetoclax as well as differential expression in haematopoietic stem cells compared to more differentiated populations77,78. Other important biological processes detected by the Venetoclax-specific attributions include the MAPK cascade, which has been linked to Venetoclax resistance through stabilization of MCL179 and fibroblast growth factor (FGF) signalling (see Fig. 6a, right). Interestingly, FGF2 release by dying cells has recently been implicated as a transient, non-heritable mechanism of Venetoclax resistance80, highlighting the power of transcriptomic analysis to discover phenomena not observable in mutational data alone.
As another example, one of the most enriched biological process terms for cytarabine, an organonitrogen compound, is the ‘metabolism of organonitrogen compounds’ (Fig. 6b, from hypergeometric test, FDR correction using the Benjamini-Hochberg procedure). The individual genes in this module include CDA and NT5C2, two genes responsible for the metabolism of cytarabine that have previously been shown to be important genetic factors determining the response to cytarabine therapy81. We conducted the interaction drug-specific feature attribution analysis and pathway enrichment characterization for all drugs, which can serve as a resource for researchers interested in the particular mechanisms underlying AML response to these drugs (Supplementary Datasets 6–23). This analysis demonstrates that EXPRESS can identify not only expression trends important for large sets of combinations, but also for specific drugs.
Discussion
By ensembling complex models, the EXPRESS framework enables accurate predictive performance and robust and biologically meaningful explanations. Although previous work has been able to attain high accuracy with complex models14, our approach can provide explanations to assure patients, clinicians and scientists of the biological soundness of our predictions, even when models have high-dimensional input features with a high degree of feature correlation. The importance of interpretability in the context of biomedical AI is increasingly being recognized. Model explanations can help identify when apparently accurate ‘black box’ models may in fact be relying on unreliable confounders (also known as ‘shortcuts’82,83). Explanations also allow physicians to communicate the logic of algorithmic decisions with patients, which can increase patient trust in the treatment process84. Finally, by displaying the logic underlying model decisions, explainable AI can enable better collaboration between physicians and AI models. For example, when applied to the Beat AML dataset7, our model was optimized without respect to the cost or FDA approval status of different drug combinations. Where a ‘black box’ model can only provide physicians with a synergy score for drug combinations, the mechanistic explanations provided by our model could help a physician to choose combinations with a similar predicted mechanism that might be preferable in terms of cost or FDA approval status.
As the application of explainable AI in the life sciences continues to grow, we anticipate that our framework will be broadly helpful to researchers. As observed in previous work, model prediction and model explanation are not always identical tasks85,86, and understanding how to create approaches that work for both of these goals is important given the popularity of Shapley value-based explanations for complex models. By demonstrating the high degree of variability in explanations within a class of models (Figs. 2 and 3), we hope to discourage users from naively selecting a single model to explain, and instead encourage users to explain ensembles of models. Although our work focused on transcriptomic data, the high degree of feature correlation and dimensionality is also characteristic of many other forms of ‘omics data, indicating the broad impact of these results. We envision that future work on more efficient approaches to create ensemble models, which can be computationally costly, will be valuable. Currently, applying this approach to very large models, such as those used in the field of natural language processing, would not likely be feasible. Likewise, further theoretical characterization of the feature attributions of complex models, such as deep neural networks and GBMs, will probably be important. Although recent work has theoretically characterized the heterogeneity in feature importance across different well-performing models from the same model class, this work has thus far been limited to a small number of simple model classes (linear regression, logistic regression and simple decision trees)37.
In parallel to this work on improving the quality of attributions for black-box models, another thread of contemporary research focuses on incorporating previous biological knowledge into the modelling process. This includes methods such as MERGE, which regularizes the coefficients of linear models using multi-omic previous information87, as well as Attribution Priors, which uses an efficient and axiomatic feature attribution method to align deep neural network attributions with biological priors during the training process88,89. Other methods to incorporate previous biological information focus on structurally modifying neural network architectures, limiting interaction to genes that are known to share biological processes90,91. Determining the best way to attribute feature importance in the context of the structurally modified models will be important future work. Similarly, understanding how explainable AI can be optimally combined with the ‘unsupervised’ deep learning models that have been successful in the context of single-cell gene expression data will be another important line of future work92,93.
When applied to a large dataset of ex vivo drug synergy measurements in primary tumour cells from patients with AML, EXPRESS can both accurately predict drug synergy, as well as uncover a differentiation-related expression signature underlying the predictions for many combinations. Although mutational status is increasingly considered in the clinical management of AML, our study demonstrates how useful tumour expression data can be for the prediction of drug combination synergy. Our experiments show that the extent of haematopoietic differentiation of AML cells is an important factor for the prediction of the synergy that can be achieved with specific therapy combinations, which has potential clinical application. Whereas our approach generated gene-expression feature attributions for each individual combination of drugs and patients in the Beat AML dataset, our analysis primarily focused on expression markers of synergy that were common over many combinations of drugs. Further analysis of important biomarkers for particular subgroups will probably represent interesting future work. One limitation of the current study is that our approach was applied to a dataset of drug-synergy measurements in bulk tumour samples, rather than synergy assayed in specific purified tumour cell populations. As more studies come out measuring the specific effects of anticancer drugs on the heterogeneous individual cells and subpopulations comprising AML52,70, applying EXPRESS to these datasets may yield interesting additional mechanistic insights.
Methods
Shapley values
The Shapley value is a concept from coalitional game theory designed to fairly distribute the total surplus or reward attained by a coalition of players to each player in that coalition21. For an arbitrary coalitional game, (where is the set of players and indicates the powerset), the Shapley value for a player is defined as the marginal contribution of that player averaged over the set of all ! possible orderings of the players in :
| (1) |
where indicates the set of players in preceding player in order .
To use this value to allocate credit to features in a ML model, the model must first be defined as a coalitional game. Deciding exactly how to define a model as a game is non-trivial, and a variety of different approaches have been suggested17,25,94,95. The most popular, SHAP (SHapley Additive exPlanations)17, defines the game as the conditional expectation of the output of a model for a particular input sample given that the features in have been observed:
| (2) |
Because modelling an exponential number of arbitrary conditional distributions is often intractable, in practice the simplifying assumption that input features are independent is often made, allowing the expected value to be calculated over the marginal distributions of the features not in each given set, rather than the conditional distributions17.
In our benchmark experiments, because comparable attributions are desirable for both the GBM and neural network models, and because we want ‘global’ attributions (features which are important across all samples in the dataset), we used the SAGE software package to generate attributions. SAGE values define the coalitional game as the average reduction in test error when a set of features are included as compared to the base rate prediction :
| (3) |
Since the SAGE package uses a sampling approach over possible coalitions of features to estimate Shapley values, it is important to ensure that the estimates are well-converged. To ensure convergence for the synthetic benchmark experiments, 102,400 permutations were used for all experiments (see Supplementary Fig. 4).
For experiments using the full BEAT AML dataset, we explained models using TreeSHAP18. TreeSHAP is a model-specific algorithm that leverages the structure of tree-based ML models (such as XGBoost, the best-performing model class for the problem) to quickly calculate SHAP values in polynomial time. TreeSHAP tries to approximate the conditional expectations using the conditional distribution defined by the tree structure. In instances where we needed global TreeSHAP attributions, we followed ref. 18. and defined the global attribution as the average magnitude of the local explanations over the whole dataset :
| (4) |
In instances where we wanted global attributions that were also directional, we considered the correlation between the SHAP attributions for a feature and that feature’s underlying value:
| (5) |
Other attribution methods for complex models
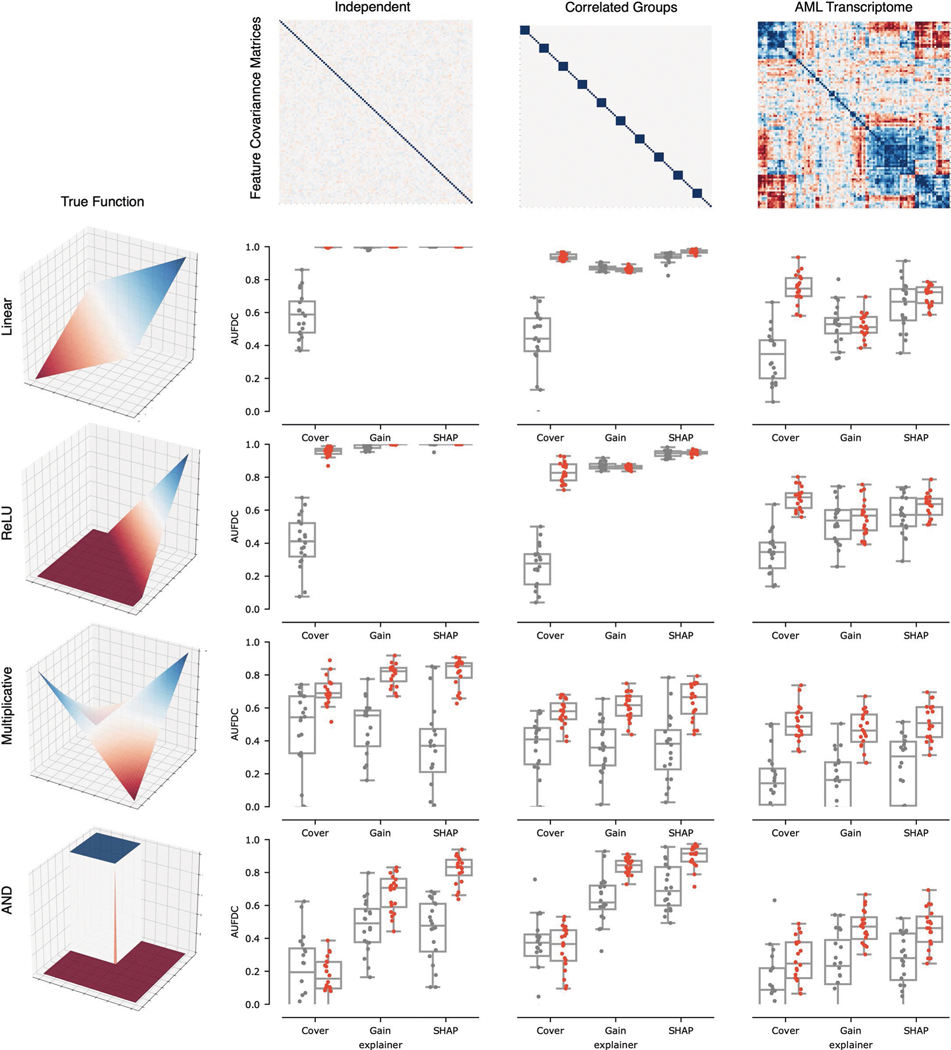
In addition to Shapley values, we also considered five other feature attribution methods in various experiments. Implementations of DeepLift and Integrated Gradients were from the Captum library96, whereas implementations of Gain and Cover were default feature importance methods in the XGBoost library. Another model agnostic method, LIME97, was considered, but ultimately could not be used because of computational efficiency problems. For example, explaining even a single sample from the Beat AML dataset (which consists of 12,362 samples) took over 30 min with LIME. In contrast, explaining ‘all’ 12,362 samples (each having 15,535 features) of the same model with TreeSHAP took 5.62 s on our CPU server (96 CPUs).
Nonlinear models explained with attributions in benchmark experiment
In our benchmark tests, we evaluated two complex model classes explained using Shapley values. The first model class consisted of feed-forward neural networks. To train these networks, we used the PyTorch deep learning library98. To tune the models, we did a grid search across the following parameters: we used between 2 and 4 fully connected layers with either ‘ELU’ or ‘ReLU’ activations; we used a number either 64, 128 or 256 nodes in the first hidden layer and considered both a ‘decreasing’ and a ‘non-decreasing’ architecture (where ‘decreasing’ reduced the number of nodes in each successive layer by a factor of 2, and non-decreasing maintained a constant number of nodes across layers). We then trained the networks using the Adam optimizer with a learning rate of 0.001 for a maximum of 1,000 epochs. Early stopping was used to stop the training process if the mean squared error loss did not improve after 50 epochs. The second model class consisted of GBMs. To train these models, we used the XGBoost library46. To tune the models, we again did a grid search across several parameters: we considered a max tree depth of either 2, 10, 18, 26, 34 or 42; we also considered a range of ‘eta’ parameters including either 0.3, 0.2, 0.1, 0.05, 0.01 or 0.005. All models were boosted for 1,000 rounds, and the saved model with the best validation error was used for downstream prediction and explanation.
Classical feature attribution methods
In addition to Shapley values (and methods such as Integrated Gradients and DeepLift) applied to neural networks and GBMs, we also compared to a baseline of three more classical feature attribution methods used in biological feature discovery. The first involves ranking features according to their Pearson correlation with the outcome of interest :
| (6) |
Ranking features in this way can be viewed as a special case of a family of feature selection algorithms known as backward elimination with the Hilbert-Schmidt independence criterion (BAHSIC)39. We also ranked features according to the magnitude of their coefficients in an elastic net regression, which is a linear regression where both the and norm of the coefficient vector are penalized in the loss function40. To train elastic net regression models, we used the ElasticNetCV function in the scikit-learn library with number of folds set to 5 (ref. 99). Finally, we also tested a procedure known as recursive feature elimination using support vector machines (SVM-RFE)41. As an estimator for this algorithm, we used the epsilon-Support Vector Regression function in scikit-learn with a linear kernel, then used the RFE function from the same library to select features with the parameters ‘n_features_to_select’ and ‘step’ set to 1.
Benchmark-evaluation metric
To evaluate how well different approaches recover biologically relevant signal, we designed a simple benchmark metric to evaluate the concordance between a list of features ranked by ML approaches and a ground truth list of features. As contemporary work shows, it is essential to evaluate attributions using benchmarks that reflect performance on the desired downstream task100. Therefore, it was necessary to design a new benchmark metric because existing metrics tend to evaluate how well feature attributions identify the features that are important for a particular ML model18. Our feature discovery benchmark measures how well each approach recovers biological signal by plotting the number of ‘true features’ cumulatively found at each point in the list of features ranked by that approach, then summarizing this curve by measuring the area beneath it using the ‘auc’ function in scikit-learn99 (see Extended Data Fig. 2). A larger AUFDC corresponds to better performance. A perfect score for a model with 10 true features out of 100 true features would be 950, whereas a random ordering would be expected to achieve an AUFDC of 500 on average. To make this score more intuitive, we subtracted the random score of 500 and divided the difference by the maximum possible area greater than random (450) so that the scores are scaled between 0 and 1, where 0 now means random performance and 1 means perfect performance. Although this metric is not sensitive to differences in ranking ‘within’ the set of relevant features, the AUFDC is a good metric in our case because the relevant task in biomarker discovery from transcriptomic data is to differentiate relevant features from a large number of irrelevant features.
Synthetic datasets
To use our benchmark-evaluation metric to systematically determine how well different approaches could uncover underlying biological signal, it was essential to define datasets where the ground truth is known101,102. Creating synthetic datasets also gave us the direct control needed to gain deeper understanding of the factors impacting the success of these algorithms, such as feature correlation, noise and outcome type18. Synthetic and semi-synthetic datasets are necessary, as this type of systematic quantitative evaluation would require having access to ground-truth annotations for each of the roughly 20,000 genes in the human genome indicating whether their expression is relevant to the synergy of drug response for each of the 133 drug combinations tested in our dataset, which is not currently feasible. We tested feature discovery performance on 240 total synthetic or semi-synthetic datasets in the main text benchmark, and on an additional 500 synthetic and semi-synthetic datasets in the supplementary benchmark experiments. Each dataset comprised a feature matrix , where represented the number of samples and represented 100 input features, and an outcome vector which is some function of the original features ().
We considered three groups of distributions for the feature matrices in the main text benchmark. The first group was 1,000 samples of 100 independent Gaussian features randomly generated to have 0 mean and unit variance. The second group was 1,000 samples of 100 Gaussian features with 10 groups of 5 tightly correlated features (Pearson’s ). The final group involved 223 real patient gene expression samples from the Beat AML Dataset, where the gene features were sampled to equal in number to the fully synthetic datasets7. We considered two additional feature distributions in the supplementary benchmark, using features drawn from real AML patient gene expression samples from The Cancer Genome Atlas (TCGA AML) and the Gene Expression Omnibus (GEO AML; for more details, see Methods section on Additional benchmark AML datasets).
For the main text benchmark, we considered four different functions by which the features were related to the outcome . The first function was a linear function with 10 non-zero coefficients,. The second function was the sum of 10 univariate ReLU functions, ReLU(). The third function was the sum of 10 pairwise multiplicative interactions,. The final function was the sum of 10 pairwise AND functions,. For each of the 12 possible pairwise combinations of feature matrices and outcome functions, we created 20 specific datasets meeting the specifications, where the only difference was that the features were randomly regenerated (or randomly resampled from the full transcriptome in the case of the AML features), and the features selected as true features were re-selected.
In the supplementary benchmark experiments (Extended Data Figs. 7 and 8), we considered an additional five functions relating features to outcome. The first was an additive function, where the outcome is the sum of quadratic terms of individual features, (‘quadratic additive’). The second was a non-additive function, where the outcome was the sum of 10 pairwise cosine interactions,. The third was an additive function, where the outcome was the sum of 10 features transformed by the sine function,. The fourth was a non-additive function (‘sine interactions’), where the outcome is of the form . This was then added to another randomly selected five variables so that the full outcome is the function of 10 variables, such as the other datasets. The fifth was a non-additive function (‘arctan interactions’), where the outcome was of the form , which is again added to additional sets of randomly selected variables so that the full outcome is the function of 10 variables.
Comparing ensembles and individual models
To train ensemble models for comparison in our benchmark experiments, we used the method of bootstrap aggregation, or ‘bagging’103. This method involved first bootstrapping the data, or resampling the dataset with replacement until the bootstrapped dataset had as many samples as the original, then training a model on the bootstrap resampled dataset. We repeated the process of bootstrapping and training models 20 times. Since our benchmark is a regression problem, the 20 model outputs were then aggregated by a simple mean. This method is known to improve predictors by increasing their stability. The number of models needed for a particular ensemble to ensure attribution stability can be evaluated by measuring the percentage overlap in the final list of top genes and the cumulative list of top genes as additional models are added to the ensemble (see Supplementary Fig. 2).
Although deep neural networks can, in general, be slow to train, the architecture proposed in ref. 14 is relatively fast to train, making these networks amenable to an ensemble approach. According to the original code published to train these models (https://github.com/KristinaPreuer/DeepSynergy), each epoch for these models takes 13 s, meaning the models take 3.5 h in total for 1,000 epochs of training. Creating ensembles of the deep learning models in question therefore took 1 week of training on a single graphics processing unit (GPU) to create an ensemble of 50 models, or 2 weeks of training on a single GPU to create an ensemble of 100 models.
To understand the difference in quality of the individual model attributions and the ensemble model attributions, we considered two separate objective metrics. The first was to assess the ‘stability’ of the attributions. We measured the pairwise cosine similarity of 20 ensemble models’ attributions trained on bootstrap resampled versions of each dataset, then measured the pairwise cosine similarity of 20 individual models’ attributions trained on bootstrap resampled versions of the same datasets:
| (7) |
The next metric aimed to understand how much importance was put on truly important features compared to how much was potentially placed on spurious correlates. We therefore measured the Gini index of each global attribution vector to understand how ‘sparse’ of an attribution was learned by each model:
| (8) |
Beat AML dataset
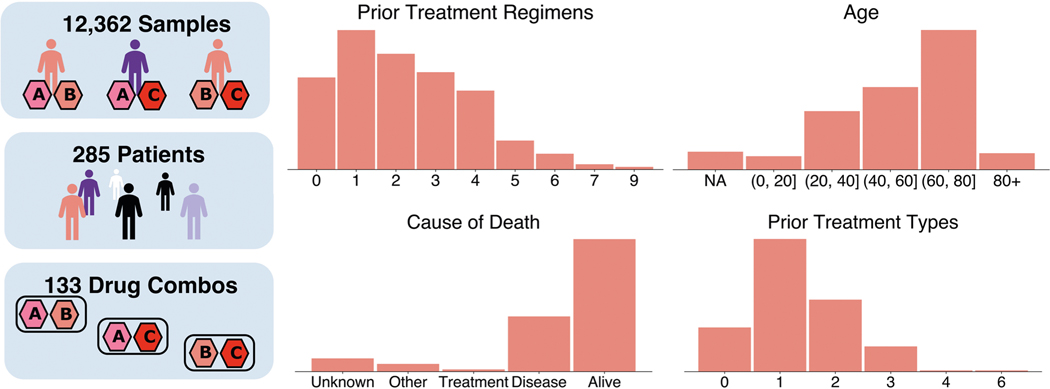
The Beat AML programme comprises a large cohort of AML patient tumour samples for which ex vivo anticancer drug sensitivity has been measured. Since our project aimed to uncover the transcriptomic factors underlying anticancer drug synergy, we only included patients from the cohort whose tumours had been characterized by RNA sequencing, for which measurement pairs of anticancer drugs had been tested. Our final dataset contained the RNA-sequencing expression data from 285 patients with myeloid malignancy and drug synergy measured on a subset of patients for 131 combinations of 46 distinct drugs.
The input features used in modelling each of 12,362 samples (where a sample is one patient and one combination of two anticancer drugs) were represented as a vector . This vector was constructed by concatenating three other vectors. First, we described each patient’s tumour sample using a vector of gene expression values (RNA-seq data), (see RNA-seq pre-processing section for more information). We described each drug combination using a feature vector, , of drug identity labels where each element was equal to 1 if the th drug was present in the combination and 0 otherwise. We also incorporated drug target information for each drug combination, using information compiled from DrugBank plus a supplementary literature search for reliable drug targets, for a total set of 146 targets. We then described the drug targets of each combo with a vector, , where each element was equal to 2 if the th target was targeted by both drugs, equal to 1 if the th target was targeted by only one of the drugs and equal to 0 if the th target was not targeted by either drug.
To ensure that these drug target features were an adequate representation of the function of the drugs in the Beat AML dataset compared to structural or physicochemical features, we re-ran our hyperparameter tuning experiment from Fig. 4, comparing the predictive performance attained by XGBoost models trained with our drug target featurization to XGBoost models trained with a similar physicochemical/structural featurization to that used in previous work (see Supplementary Fig. 1). For these physicochemical and structural features, we followed ref. 14 and used a much larger feature vector to describe each drug combination (1,838 total features for each 2-drug combination, with 919 features for each drug, including both structural toxicophore features and physicochemical features generated with ChemoPy, a Python library for generating the commonly used structural and physicochemical features). We found that in 17 out of 20 cases, our drug target featurization matched or increased predictive performance compared with using physicochemical or structural features.
RNA-seq pre-processing
To ensure a quality signal for prediction while removing noise and batch effects, it is necessary to carefully pre-process the RNA-seq gene expression data. In this study, the RNA-seq data were pre-processed as follows. First, raw transcript counts were converted to fragments per kilobase of exon model per million mapped reads (FPKM). FPKM is more reflective of the molar amount of a transcript in the original sample than raw counts, as it normalizes the counts for different RNA lengths and for the total number of reads. FPKM was calculated as follows:
| (9) |
where represents the raw counts for a transcript, is the effective length of the transcript and is the total number of counts.
After converting counts to FPKM, we removed any non-protein-coding transcripts from the dataset. We also removed transcripts that were not meaningfully observed in our dataset by dropping any transcript where greater than 70% of measurements across all samples were equal to 0. We then log-transformed the data and standardized each transcript across all samples, such that the mean for that transcript was equal to zero and the variance of the transcript was equal to one. Finally, we corrected for batch effects in the measurements using the ComBat tool available in the sva R package104.
Additional benchmark AML datasets
For the GEO AML dataset, we downloaded all publicly available gene expression datasets from the National Center for Biotechnology Information (NCBI) GEO database generated by either the Affymetrix GeneChip Human Genome U133 Plus 2.0 (Affy HG-U133 Plus 2.0) microarray platform or the Affymetrix GeneChip Human Genome U133A 2.0 (Affy HG-U133A 2.0) microarray platform105, using the keywords ‘AML’. We then manually curated our dataset to look for incorrectly included or excluded samples, such as gene expression samples from healthy tissues or patients with cancer types other than AML. Additionally, we manually excluded cell line expression samples, which are likely to have low expression variance when the same cell line is sequenced across different studies, and only used patient samples. This led to a total of 6,534 samples. For each synthetic dataset generated using these features, 200 patients were sampled.
To integrate data from various platforms, we converted platform-specific probe IDs to gene symbols using the probe ID to gene symbol conversion lists for each platform available in GEO. A study might have different sample batches submitted on different dates indicated in the ‘submission_date’ field. We corrected for these potential batch effects within each study using the ComBat tool available in the sva R package104, where different batches correspond to data subsets submitted at different dates. We log-transformed the expression measurements, standardized (that is, 0 mean and unit variance) each gene in each dataset to ensure that different input features (that is, gene expression levels) were on the same scale, and applied mean imputation to impute missing gene-level measurements. We also excluded duplicate samples with the same GEO IDs. We concatenated all datasets and applied batch effect correction, once again using ComBat with the same parameters, considering each study to be a separate batch to minimize the effect of potential study-specific confounders.
For the TCGA AML dataset, we downloaded RSEM-normalized log2-transformed RNA-seq expression matrices for patients with AML from the Broad Institute data v2016_01_28 (https://gdac.broadinstitute.org/) and generated by the TCGA Research Network (https://www.cancer.gov/tcga/). We pre-processed the TCGA samples with the same pipeline we used for pre-processing GEO expression datasets: we selected the overlapping sets of genes and standardized each gene to 0 mean and unit variance.
Drug-synergy metric
The outcome in our model was drug synergy: whether a number of drugs exhibit more anticancer activity in combination than would be expected simply by adding their individual activities together. We therefore calculated synergy using the combination index (CI) of the two drugs:
| (10) |
where is the dose of drug required to reduce cell viability to 50% when used alone and IC50combination is the dose of drug required to reduce cell viability to 50% when used in combination with the other drug we are measuring106. When a drug combination is synergistic, the CI will be less than 1 (it will be equal to 1 when the combination is additive and greater than 1 when the combination is antagonistic). In our model, we log-transformed the CI measure to help manage the skewness of the original distribution, and then scaled the measure to make the distribution have 0 mean and unit variance. We also multiplied by −1 for ease of interpretation: more synergistic combinations thus have a larger score.
Although previous studies have made use of response-surface analysis, which involves measuring the volume between an idealized additive response surface and a measured actual response surface, these measures could not be applied to the ‘diagonal’ measurements present in the Beat AML Dataset. A major drawback to response-surface analyses is that they require a ‘checkerboard’ of measurements at different drug concentrations, where the ratios and doses of each drug in a combination is varied. This consumes many more cancer cells, which is problematic when using primary cells from patients, as the amount of sample that can be collected is more limited than when using cell lines.
Cross-validation and sample stratification
In addition to the model parameters which are learned from data, ML models also rely on hyperparameters, which must be tuned to a specific task in question to attain optimal predictive performance. To estimate the true generalization error of a model (that is, how well that model is likely to perform on unseen data), it is essential that model parameters and hyperparameters be learned and chosen on the basis of training data, whereas predictive performance is evaluated on a held-out test set that is never used for hyperparameter selection or model training. Hyperparameters are typically picked through a cross-validation procedure that determines the optimal hyperparameters for the model by validating them through a number of internal training and validation fold pairs randomly chosen from the set of training samples used for learning the model parameters.
To effectively train our models and evaluate predictive performance, we therefore utilized a nested 5-fold cross-validation procedure, whereby the data were split into 5 separate test folds. For each of these test folds, we trained our synergy prediction model using the four remaining folds and evaluated it on the held-out test fold. To properly tune the hyperparameters of the models trained for each test fold, three of the four training folds were used as an internal training set, whereas the remaining fold was used as a validation set. The hyperparameters were selected by an inner loop, where for each hyperparameter set of interest, the model was trained on the internal training set and tested on the validation set. The hyperparameters giving the best performance on the validation set were then used to train a model on the entire training data, which was then finally evaluated on the held-out test fold. The grid of hyperparameters tested for each model type are as follows. For the sklearn elastic net implementation, the ‘alpha’ parameter was tuned over values ranging from 0.1 to 100, whereas the ‘l1_ratio’ parameter was tuned from 0.25 to 0.75. For the sklearn random forest implementation, the ‘n_estimators’ parameter was tuned from 128 trees to 2,048 trees, whereas the ‘max_features’ parameter was set to be either ‘log2’, ‘sqrt’ or ‘256’. For XGBoost, ‘max_depth’ was tuned between 4 and 8, ‘subsample’ was tuned to values between 0.1 and 0.8, and learning rate was tuned between 0.05 and 0.1. For deep neural networks, hyperparameters were tuned following the grid given in ref. 14, where an additional data pre-processing step that would optionally transform the RNA-seq features with a hyperbolic tangent function in addition to standardization was also included as a hyperparameter. Code for tuning these networks can be found at https://github.com/KristinaPreuer/DeepSynergy. For both deep neural networks and GBMs, early stopping based on validation set error was used to choose the number of epochs/estimators.
To evaluate the model’s performance for a variety of hypothetical uses, we stratified our data into training and testing sets in four different ways (Fig. 4). Each sample in our dataset consists of a synergy measurement for a 2-drug combination tested in a patient’s tumour cells. In the first stratification setting, we ensured that any sample (2-drug combination and patient) present in the test data would never be present in the training data. The second setting maintains the first setting’s requirement that each sample in the test data be novel, but additionally ensures that any combination of drugs in the test data would never be present in the training data. The third setting maintains the first setting’s requirement that each sample in the test data be novel, but additionally ensures that any patient in the test data would never be present in the training data. Finally, the fourth setting maintains the first and second settings’ requirements, while additionally ensuring that for any combination of drugs in the test data, at least one of the drugs in that combination would never have been present in the training data. Each of these settings should be increasingly difficult to predict, as each setting requires progressively more generalizable trends in the data to have been learned.
XGBoost model ensembles
After selecting XGBoost as the best-performing model class for the prediction of anti-AML drug synergy, we then wanted to account for the full diversity of possible good XGBoost models fit to the highly correlated AML gene expression data. We therefore trained 100 models and explained the ensemble model. Each individual model had both row and column subsampling turned on for each additional tree fit, and the difference between the models in the ensemble was the random seed given to generate the subsampling.
In practice, instead of explaining the entire ensemble (the average output of each of the 100 models), we instead explained each individual model and averaged the explanations. This is possible due to the linearity property of Shapley values107. This property states that for the convex combination of any two coalitional games and , the attribution for player will be the convex combination of the attributions that player would attain in each individual game and :
| (11) |
Overall pathway analysis
The highest-ranked genes in the lists ordered by global Shapley values were tested for pathway enrichments using the StringDB package in R108. The package was initialized using the arguments: ‘version’ = ‘10’, ‘species’ = ‘9606’ and ‘score_threshold’ set to the default of 400. We used the set of pathways from the Kyoto Encyclopedia of Genes and Genomes (KEGG) for enrichment tests. The actual enrichments were calculated by a hypergeometric test implemented in the ‘get_enrichment’ method. To ensure that pathway enrichments were robust to the threshold used for selecting the highest-ranked genes, we averaged the enrichment test results over a variety of different thresholds, ranging from 200 to 800 top genes. FDR correction was applied using the Benjamini-Hochberg procedure109.
Generation of differential-expression stemness profiles and measurement of synergy correlation
To generate expression signatures related to more or less-differentiated states of cells in the haematopoietic cell lineage, we downloaded RNA-seq data from isolated cells from particular levels of developmental transitions73. We then used the R package DESeq2, which tests for differential expression in RNA-seq data on the basis of a negative binomial model, to generate lists of genes upregulated in particular populations of cells as compared to other populations110. The populations we compared were as follows: monocytes vs haematopoietic stem cells (HSCs), lymphocytes vs HSCs, all fully differentiated cells (which included erythroblasts, T cells, B cells, NK cells and monocytes) vs HSCs, monocytes vs leukaemic stem cells (LSCs), lymphocytes vs LSCs, and all fully differentiated cells vs LSCs. The immunophenotypes used to sort HSCs and LSCs were Lin− CD34+ CD38− CD90+ CD10− and Lin− CD34+ CD38− TIM3+ CD99+, respectively. Gene expression profiles for these populations were the same as used in ref. 73. The multiple testing-adjusted value used as a significance threshold for differentially regulated genes was 0.05.
When we tested for association between our differential expression profiles and synergy for particular combinations of drugs, we first considered only samples containing the drug combination in question. We then averaged gene expression over all genes in the differential expression profile. Finally, we measured the Pearson correlation between the average expression profile and the drug combination synergy for those samples. Since we had many combinations of drugs and many differential expression profiles to test, we corrected for multiple testing using the Benjamini-Hochberg FDR correction procedure109. We then displayed only correlations that are significant after correction. Additionally, we only wanted to consider correlations that are robust to the differences in the particular stemness-differentiation profiles, so we only plotted correlations for drugs that are significant across at least two profiles.
Cancer-dependency-map analysis
To externally validate the importance of the haematopoietic differentiation expression signature for the drug combinations identified in Fig. 5f, we used data from the Cancer Dependency Map (DepMap) database. Specifically, we downloaded the Genetic Dependency CRISPR assays (DepMap 21Q4 Public+Score, Chronos, ‘CRISPR_gene_effect. csv’) and the expression data (21Q4 Public, ‘CCLE_expression.csv’), as well as the metadata in the Cell Line Sample Info file (‘sample_info. csv’), from the DepMap portal. After downloading these data, we filtered them so that only cell lines with the lineage subtype ‘AML’ were present in the analysis. Then, we tested for association between the average expression of the signature with the most associated drug combinations from Fig. 5f (S1/D1) and the genetic dependency of the targets of the drug combinations listed in Fig. 5f.
To assess the significance of the associations, we designed three null models. First, we generated a null distribution by randomizing the genes that were averaged to calculate the expression signature 1,000 times, and measuring the average magnitude of the Spearman correlation of these random signatures with the genetic dependency Chronos scores of the genetic targets of the drug combinations listed in Fig. 5f (‘Randomize Pathway Genes’ null). Second, we generated a null distribution by randomly permuting the rows (cell lines) in the gene expression matrix 1,000 times, before measuring the average magnitude of the Spearman correlation of the average expression of the haematopoietic differentiation expression signature with the genetic dependency Chronos scores of the genetic targets of the drug combinations listed in Fig. 5f (‘Permute Pathway Expression’ null). Third, we generated a null distribution by leaving the expression matrix unpermuted and unrandomized and measuring the average magnitude of the Spearman correlation of the average expression of the haematopoietic differentiation expression signature with the genetic dependency Chronos scores of random sets of genes (where the random sets were constrained to be the same size as the number of true targets of the set of combinations in Fig. 5f; ‘Randomize Targets’ null).
Across all three null models, we found that the true expression signature is significantly associated with cancer cell line genetic dependency on the drug targets of the drugs in Fig. 5f (empirical values 0.001, 0.001 and 0.026 for the ‘Randomize Pathway Genes’, ‘Permute Pathway Expression’ and ‘Randomize Targets’ nulls, respectively).
Drug-specific pathway analysis
To analyse the biological processes relevant for combinations containing specific drugs in the dataset, we tested the top-ranked genes in the lists ordered by the average magnitude Shapley interaction indices18,75. Following the same procedure described above, we calculated pathway enrichments using the StringDB package in R108. We used the set of pathways from Gene Ontology (GO) Biological Process terms for enrichment tests. The enrichments were calculated by a hypergeometric test implemented in the ‘get_enrichment’ method. To ensure that pathway enrichments were robust to the threshold used for selecting the highest-ranked genes, we averaged the enrichment test results over a variety of different thresholds, ranging from 200 to 800 top genes. FDR correction was applied using the Benjamini-Hochberg procedure109.
For Venetoclax, since a large number of biological process terms were significantly enriched, and since there is substantial overlap and similarity between these gene sets, we clustered the significantly enriched pathways into modules. We defined an adjacency matrix where each gene set represented a node in a network, and the Jaccard Index (a measure of overlap) between pathways was used to define edges. We binarized the matrix for pathways with Jaccard Index greater than 0.4. We then manually annotated all connected components in the resultant graph (see Supplementary Dataset 24). To plot the network, we used the spring layout functionality in the networkx library in Python111.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Extended Data
Extended Data Fig. 1 |. Descriptive statistics of Beat AML cohort.
Histograms showing the relative density of prior treatment regimens, age, cause of death, and prior treatment types in the cohort of 285 patients in our dataset, which consisted of 12,362 samples with paired gene expression and drug synergy measurements for 133 pairs of 46 anticancer drugs.
Extended Data Fig. 2 |. Feature discovery benchmark.
For each synthetic or semi-synthetic dataset (a), we trained a variety of models (b) including neural networks, GBMs, support vector machines, and elastic net regression, as well as univariate statistics (Pearson correlation). For the machine-learning models, we then used SAGE to generate global Shapley value feature attributions (c), ranked the features according to the magnitude of their attributions (d), and compared the ranked list generated by each method to the binary ground truth importance vector (e). To measure the feature discovery quality of each method, we plotted how many “true” features are found cumulatively at each point in the ranked feature list (f), then summarized the curve generated by this procedure by measuring the AUFDC. This score is then rescaled so that a score of 0 represents random performance while a score of 1 represents perfect performance.
Extended Data Fig. 3 |. Predictive performance of models trained with synthetic datasets.
Predictive performance, as measured by the Pearson correlation of the predicted and true labels for the models trained in the benchmark presented in Fig. 2.
Extended Data Fig. 4 |. Ensembling overcomes the variability in attributions present in individual models.
To understand why ensemble models were able to attain better feature discovery performance than single models, we compared the characteristics of the attribution vectors of XGBoost models trained on bootstrap resampled versions of a correlated groups dataset with a step-function outcome. a, Heatmap of feature attributions for 20 individual XGBoost models. b, Heatmap of feature attributions for 20 ensembles of XGBoost models. c, Pairs of attribution vectors from ensembled models are more similar across bootstrap resamples of the dataset than attribution vectors from single models, as measured by cosine similarity. d, Attribution vectors from ensembled models place a larger proportion of their importance on a smaller set of features than attribution vectors from single models, as measured by the Gini coefficient of the attribution vectors, a measure of vector sparseness.
Extended Data Fig. 5 |. EXPRESS improves feature attributions of deep learning models.
Comparison of feature discovery performance between individual deep learning models (gray) and ensembles of deep learning models (red) across all 12 dataset types from the synthetic benchmark. Three separate feature attribution methods are tested for each model: DeepLift, Integrated Gradients, and SHAP (in this case implemented as global attributions using the SAGE software package).
Extended Data Fig. 6 |. EXPRESS improves feature attributions of XGBoost models.
Comparison of feature discovery performance between individual XGBoost models (gray) and ensembles of XGBoost models (red) across all 12 dataset types from the synthetic benchmark. Three separate feature attribution methods are tested for each model: a) cover, b) gain, and c) SHAP.
Extended Data Fig. 7 |. EXPRESS improves feature attributions of deep learning models on additional supplementary datasets.
Comparison of feature discovery performance between individual deep learning models (gray) and ensembles of deep learning models (red) across all 25 supplementary dataset types (see Methods section on supplementary dataset types). Three separate feature attribution methods are tested for each model: DeepLift, Integrated Gradients, and c) SHAP (in this case implemented as SAGE). We find that for 73% of comparisons, EXPRESS improves feature discovery performance (for associated statistics, see Supplementary Dataset 25).
Extended Data Fig. 8 |. EXPRESS improves feature attributions of XGBoost models on additional supplementary datasets.
Comparison of feature discovery performance between individual XGBoost models (gray) and ensembles of XGBoost models (red) across all all 25 supplementary dataset types (see methods section on supplementary dataset types). Three separate feature attribution methods are tested for each model: Cover, Gain, and SHAP. We find that for 76% of comparisons, EXPRESS improves feature discovery performance (for associated statistics, see Supplementary Dataset 26).
Extended Data Fig. 9 |. EXPRESS improves feature attributions independently of improvement in model performance.
For both XGBoost models (a, trained on the Beat AML dataset with the AND function outcome; b, trained on the Beat AML dataset with the multiplicative outcome) and deep learning models (c, trained on the Beat AML dataset with the AND function outcome; and d, trained on the Beat AML dataset with the multiplicative outcome), we see that even after controlling for the effect of model ensembles on predictive performance by stratifying models (low, intermediate, and high predictive performance), within each stratification ensemble models have significantly higher AUFDC. Significance assessed by two-sided Mann−Whitney -test, * represents p < 0.05, ** represents $p < 0.01, *** represents p < 0.001, and **** represents p < 0.0001 (full statistics in Supplementary Dataset 27). The boxes mark the quartiles (25th, 50th, and 75th percentiles) of the distribution within a given predictive performance stratification, while the whiskers extend to show the minimum and maximum of the distribution (excluding outliers).
Extended Data Fig. 10 |. Ensembling improves XGBoost attributions more than explicit regularization.
Using the synthetic datasets with real AML gene expression features, we compare the increase in AUFDC seen with explicit regularization, such as per-tree column dropout and L1 regularization, with ensembling. For the synthetic datasets with AML features and the AND true function, we see that ensembles improve AUFDC significantly more than column dropout (a, two-sided Mann−Whitney -test, , ) and L1 regularization (c, , ). For the synthetic datasets with AML features and the multiplicative true function, we see that ensembles improve AUFDC significantly more than column dropout (b, , 5.25 × 10−5) and L1 regularization (d, , ).
Supplementary Material
Acknowledgements
S.-I.L. discloses support for the research described in this study from the National Science Foundation (CAREER DBI-1552309 and DBI-1759487), the National Institutes of Health (R35 GM 128638 and R01 NIA AG 061132) and the American Cancer Society (127332-RSG-15-097-01-TBG). K.N. discloses support for the research described in this study from the National Institutes of Health (R37CA225655 and P01HL142494).
Footnotes
Competing interests
The authors declare no competing interests.
Code availability
Code necessary to reproduce our experimental findings can be found in Zenodo at https://doi.org/10.5281/zenodo.7689076.
Additional information
Extended data is available for this paper at https://doi.org/10.1038/s41551-023-01034-0.
Supplementary information The online version contains supplementary material available at https://doi.org/10.1038/s41551-023-01034-0.
Peer review information Nature Biomedical Engineering thanks María Rodríguez Martínez and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Reprints and permissions information is available at www.nature.com/reprints.
Data availability
The results of this study are in part based on data generated by the Cancer Target Discovery and Development (CTD2) Network (https://ocg.cancer.gov/programs/ctd2/data-portal), established by the National Cancer Institute’s Office of Cancer Genomics. Sequencing data are available in the GDC data portal under dbGaP Study Accession phs001657. The Beat AML patient sample data used in this study were done under an early access agreement, before final accrual, harmonization and public release of the full dataset. As such, the subset of samples included in this study may differ in sample representation, quality-control thresholds and data normalizations from those found in GDC and in the final study describing the full dataset.
The analysis of the haematopoietic signatures in an external dataset used data from the Cancer Dependency Map project (DepMap); specifically, the Genetic Dependency CRISPR assays (DepMap 21Q4 Public+Score, Chronos, ‘CRISPR_gene_effect.csv’) and the expression data (21Q4 Public, ‘CCLE_expression.csv’), as well as the metadata in the Cell Line Sample Info file (‘sample_info.csv’), all accessible from the DepMap portal (https://depmap.org/portal). Source data are provided with this paper.
References
- 1.Khwaja A. et al. Acute myeloid leukaemia. Nat. Rev. Dis. Prim 2, Article 16010 (2016). [DOI] [PubMed] [Google Scholar]
- 2.Kurtz SE et al. Molecularly targeted drug combinations demonstrate selective effectiveness for myeloid- and lymphoid-derived hematologic malignancies. Proc. Natl Acad. Sci. USA 10.1073/pnas.1703094114 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Day D. & Siu LL Approaches to modernize the combination drug development paradigm. Genome Med. 8, 115 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.O’Neil J. et al. An unbiased oncology compound screen to identify novel combination strategies. Mol. Cancer Ther 15, 1155–1162 (2016). [DOI] [PubMed] [Google Scholar]
- 5.Jia J. et al. Mechanisms of drug combinations: interaction and network perspectives. Nat. Rev. Drug Discov 8, 111–128 (2009). [DOI] [PubMed] [Google Scholar]
- 6.Nair R, Salinas-Illarena A. & Baldauf H-M New strategies to treat AML: novel insights into AML survival pathways and combination therapies. Leukemia 35, 299–311 (2021). [DOI] [PubMed] [Google Scholar]
- 7.Tyner JW & Others A. Functional genomic landscape of acute myeloid leukaemia. Nature 562, 526–531 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Schenone M, Dančík V, Wagner BK & Clemons PA Target identification and mechanism of action in chemical biology and drug discovery. Nat. Chem. Biol 9, 232–240 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hopkins AL Network pharmacology: the next paradigm in drug discovery. Nat. Chem. Biol 4, 682–690 (2008). [DOI] [PubMed] [Google Scholar]
- 10.Calzolari D. et al. Search algorithms as a framework for the optimization of drug combinations. PLoS Comput. Biol 4, e1000249 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Feala JD et al. Systems approaches and algorithms for discovery of combinatorial therapies. Wiley Interdiscip. Rev. Syst. Biol. Med 2, 181–193 (2010). [DOI] [PubMed] [Google Scholar]
- 12.Wong PK et al. Closed-loop control of cellular functions using combinatory drugs guided by a stochastic search algorithm. Proc. Natl Acad. Sci. USA 105, 5105–5110 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Menden MP et al. Community assessment to advance computational prediction of cancer drug combinations in a pharmacogenomic screen. Nat. Commun 10, 2674 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Preuer K. et al. DeepSynergy: predicting anti-cancer drug synergy with Deep Learning. Bioinformatics 34, 1538–1546 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Garnett MJ et al. Systematic identification of genomic markers of drug sensitivity in cancer cells. Nature 483, 570–575 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Barretina J. et al. The Cancer Cell Line Encyclopedia enables predictive modelling of anticancer drug sensitivity. Nature 483, 603–607 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lundberg SM & Lee S-I in Advances in Neural Information Processing Systems (eds Guyon I, Von Luxburg U, Bengio S, Wallach H, Fergus R, Vishwanathan S, & Garnett R) 4765–4774 (Curran Associates, Inc., 2017). [Google Scholar]
- 18.Lundberg SM et al. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell 2, 56–67 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Shrikumar A, Greenside P. & Kundaje A. Learning important features through propagating activation differences. In Proc. 34th International Conference on Machine Learning (eds Precup D. & Teh YW) 3145–3153 (PMLR, 2017). [Google Scholar]
- 20.Sundararajan M, Taly A. & Yan Q. Axiomatic attribution for deep networks. In Proc. 34th International Conference on Machine Learning, PMLR; (eds Precup D. & Teh YW) 3319–3328 (JMLR.org, 2017). [Google Scholar]
- 21.Shapley LS A value for n-person games. Class. game theory 69 (1997). [Google Scholar]
- 22.Aas K, Jullum M. & Løland A. Explaining individual predictions when features are dependent: more accurate approximations to Shapley values. Artif. Intell 298, 103502 (2021). [Google Scholar]
- 23.Koo PK & Ploenzke M. Improving representations of genomic sequence motifs in convolutional networks with exponential activations. Nat. Mach. Intell 3, 258–266 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Schreiber J. & Singh R. Machine learning for profile prediction in genomics. Curr. Opin. Chem. Biol 65, 35–41 (2021). [DOI] [PubMed] [Google Scholar]
- 25.Covert I, Lundberg S. & Lee S-I Explaining by removing: a unified framework for model explanation. J. Mach. Learn. Res 22, 1–90 (2021). [Google Scholar]
- 26.Kim N. et al. Prediction of the sequence-specific cleavage activity of Cas9 variants. Nat. Biotechnol 38, 1328–1336 (2020). [DOI] [PubMed] [Google Scholar]
- 27.Kim HK et al. Predicting the efficiency of prime editing guide RNAs in human cells. Nat. Biotechnol 39, 198–206 (2021). [DOI] [PubMed] [Google Scholar]
- 28.Schultebraucks K. et al. A validated predictive algorithm of post-traumatic stress course following emergency department admission after a traumatic stressor. Nat. Med 26, 1084–1088 (2020). [DOI] [PubMed] [Google Scholar]
- 29.Hyland SL et al. Early prediction of circulatory failure in the intensive care unit using machine learning. Nat. Med 26, 364–373 (2020). [DOI] [PubMed] [Google Scholar]
- 30.Meier F. et al. Deep learning the collisional cross sections of the peptide universe from a million experimental values. Nat. Commun 12, Article 1185 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bar N. et al. A reference map of potential determinants for the human serum metabolome. Nature 588, 135–140 (2020). [DOI] [PubMed] [Google Scholar]
- 32.Rodriguez-Perez R. & Bajorath J. Interpretation of compound activity predictions from complex machine learning models using local approximations and shapley values. J. Med. Chem 63, 8761–8777 (2019). [DOI] [PubMed] [Google Scholar]
- 33.Rodriguez-Perez R. & Bajorath J. Interpretation of machine learning models using shapley values: application to compound potency and multi-target activity predictions. J. Comput. Aided Mol. Des 34, 1013–1026 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Tang Y-C & Gottlieb A. Explainable drug sensitivity prediction through cancer pathway enrichment. Sci. Rep 11, Article 3128 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Braithwaite B. et al. Detection of medications associated with Alzheimer’s disease using ensemble methods and cooperative game theory. Int. J. Med. Inform 141, 104142 (2020). [DOI] [PubMed] [Google Scholar]
- 36.Breiman L. Statistical modeling: the two cultures (with comments and a rejoinder by the author). Stat. Sci 16, 199–231 (2001). [Google Scholar]
- 37.Dong J. & Rudin C. Variable importance clouds: a way to explore variable importance for the set of good models. Preprint at 10.48550/arXiv.1901.03209 (2019). [DOI] [Google Scholar]
- 38.Hooker S, Erhan D, Kindermans P-J & Kim B. A benchmark for interpretability methods in deep neural networks. In 33rd Conference on Neural Information Processing Systems (eds Wallach H, Larochelle H, Beygelzimer A, d’Alché-Buc F, Fox E. & Garnett R) (Curran Associates, Inc., 2019). [Google Scholar]
- 39.Song L, Bedo J, Borgwardt KM, Gretton A. & Smola A. Gene selection via the BAHSIC family of algorithms. Bioinformatics 23, i490–i498 (2007). [DOI] [PubMed] [Google Scholar]
- 40.Zou H. & Hastie T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. B 67, 301–320 (2005). [Google Scholar]
- 41.Guyon I, Weston J, Barnhill S. & Vapnik V. Gene selection for cancer classification using support vector machines. Mach. Learn 46, 389–422 (2002). [Google Scholar]
- 42.Avsec Ž et al. Base-resolution models of transcription-factor binding reveal soft motif syntax. Nat. Genet 53, 354–366 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Maslova A. et al. Deep learning of immune cell differentiation. Proc. Natl Acad. Sci. USA 117, 25655–25666 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Farzaneh N, Williamson CA, Gryak J. & Najarian K. A hierarchical expert-guided machine learning framework for clinical decision support systems: an application to traumatic brain injury prognostication. npj Digit. Med 4, 78 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Breiman L. Random forests. Mach. Learn 45, 5–32 (2001). [Google Scholar]
- 46.Chen T. & Guestrin C. XGBoost: a scalable tree boosting system. In Proc. 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining 785–794 (ACM, 2016). [Google Scholar]
- 47.King RD, Orhobor OI & Taylor CC Cross-validation is safe to use. Nat. Mach. Intell 3, 276 (2021). [Google Scholar]
- 48.Shwartz-Ziv R. & Armon A. Tabular data: deep learning is not all you need. Inf. Fusion 81, 84–90 (2022). [Google Scholar]
- 49.Gurska LM, Ames K. & Gritsman K. Signaling pathways in leukemic stem cells. Adv. Exp. Med. Biol 1143, 1–39 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Kumar AR, Sarver AL, Wu B. & Kersey JH Meis1 maintains stemness signature in MLL-AF9 leukemia. Blood 115, 3642–3643 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Liu J. et al. Meis1 is critical to the maintenance of human acute myeloid leukemia cells independent of MLL rearrangements. Ann. Hematol 96, 567–574 (2017). [DOI] [PubMed] [Google Scholar]
- 52.Pei S. et al. Monocytic subclones confer resistance to venetoclax-based therapy in patients with acute myeloid leukemia. Cancer Discov. 10, 536–551 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Takam Kamga P. et al. Prognostic impact of notch signaling in acute myeloid leukemia (AML). Blood 132, 5242 (2018). [Google Scholar]
- 54.Kranc KR et al. Cited2 is an essential regulator of adult hematopoietic stem cells. Cell Stem Cell 5, 659–665 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Korthuis PM et al. CITED2-mediated human hematopoietic stem cell maintenance is critical for acute myeloid leukemia. Leukemia 29, 625–635 (2015). [DOI] [PubMed] [Google Scholar]
- 56.Tanaka M. et al. Targeted disruption of oncostatin M receptor results in altered hematopoiesis. Blood 102, 3154–3162 (2003). [DOI] [PubMed] [Google Scholar]
- 57.Zhao X, Li Y. & Wu H. A novel scoring system for acute myeloid leukemia risk assessment based on the expression levels of six genes. Int. J. Mol. Med 42, 1495–1507 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Zhang N, Chen Y, Lou S, Shen Y. & Deng J. A six-gene-based prognostic model predicts complete remission and overall survival in childhood acute myeloid leukemia. Onco. Targets Ther 12, 6591–6604 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Lin W. et al. SLC7A11/xCT in cancer: biological functions and therapeutic implications. Am. J. Cancer Res 10, 3106–3126 (2020). [PMC free article] [PubMed] [Google Scholar]
- 60.Kornblau SM et al. Recurrent expression signatures of cytokines and chemokines are present and are independently prognostic in acute myelogenous leukemia and myelodysplasia. Blood 116, 4251–4261 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Goenka S. & Kaplan MH Transcriptional regulation by STAT6. Immunol. Res 50, 87–96 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Peña-Martínez P. et al. Interleukin 4 induces apoptosis of acute myeloid leukemia cells in a Stat6-dependent manner. Leukemia 32, 588–596 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Bunting KD et al. Increased numbers of committed myeloid progenitors but not primitive hematopoietic stem/progenitors in mice lacking STAT6 expression. J. Leukoc. Biol 76, 484–490 (2004). [DOI] [PubMed] [Google Scholar]
- 64.Li MJ et al. GWASdb: a database for human genetic variants identified by genome-wide association studies. Nucleic Acids Res. 40, D1047–D1054 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Churpek JE et al. Genomic analysis of germ line and somatic variants in familial myelodysplasia/acute myeloid leukemia. Blood 126, 2484–2490 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Lo F-Y et al. Metabolic alterations may contribute to cabozantinib resistance in acute myeloid leukemia cells with FLT3-ITD. Blood 132, 2785 (2018). [Google Scholar]
- 67.Gal H. et al. Gene expression profiles of AML derived stem cells; similarity to hematopoietic stem cells. Leukemia 20, 2147–2154 (2006). [DOI] [PubMed] [Google Scholar]
- 68.Gentles AJ, Plevritis SK, Majeti R. & Alizadeh AA Association of a leukemic stem cell gene expression signature with clinical outcomes in acute myeloid leukemia. JAMA 304, 2706–2715 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Pollyea DA et al. Venetoclax with azacitidine disrupts energy metabolism and targets leukemia stem cells in patients with acute myeloid leukemia. Nat. Med 24, 1859–1866 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Kuusanmäki H. et al. Phenotype-based drug screening reveals association between venetoclax response and differentiation stage in acute myeloid leukemia. Haematologica 105, 708–720 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Jones CL et al. Cysteine depletion targets leukemia stem cells through inhibition of electron transport complex II. Blood 134, 389–394 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Stevens BM et al. Fatty acid metabolism underlies venetoclax resistance in acute myeloid leukemia stem cells. Nat. Cancer 1, 1176–1187 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Corces MR et al. Lineage-specific and single-cell chromatin accessibility charts human hematopoiesis and leukemia evolution. Nat. Genet 48, 1193–1203 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Kurtz SE et al. Dual inhibition of JAK1/2 kinases and BCL2: a promising therapeutic strategy for acute myeloid leukemia. Leukemia 32, 2025–2028 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Grabisch M. & Roubens M. An axiomatic approach to the concept of interaction among players in cooperative games. Int. J. Game Theory 28, 547–565 (1999). [Google Scholar]
- 76.Pollyea DA, Amaya M, Strati P. & Konopleva MY Venetoclax for AML: changing the treatment paradigm. Blood Adv. 3, 4326–4335 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Karjalainen R. et al. Elevated expression of S100A8 and S100A9 correlates with resistance to the BCL-2 inhibitor venetoclax in AML. Leukemia 33, 2548–2553 (2019). [DOI] [PubMed] [Google Scholar]
- 78.Lannert H. et al. Expression of S100 proteins in normal human hematopoietic stem cells and in AML. J. Clin. Oncol 26, 7072 (2008). [Google Scholar]
- 79.Han L. et al. Concomitant targeting of BCL2 with venetoclax and MAPK signaling with cobimetinib in acute myeloid leukemia models. Haematologica 105, 697–707 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Bock FJ, Cloix C, Zerbst D. & Tait SWG Apoptosis-induced FGF signalling promotes non-cell autonomous resistance to cell death. bioRxiv (2020). [Google Scholar]
- 81.Lamba JK Genetic factors influencing cytarabine therapy. Pharmacogenomics 10, 1657–1674 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.DeGrave AJ, Janizek JD & Lee S-I AI for radiographic COVID-19 detection selects shortcuts over signal. Nat. Mach. Intell 3, 610–619 (2021). [Google Scholar]
- 83.Geirhos R. et al. Shortcut learning in deep neural networks. Nat. Mach. Intell 2, 665–673 (2020). [Google Scholar]
- 84.Kundu S. AI in medicine must be explainable. Nat. Med 27, 1328 (2021). [DOI] [PubMed] [Google Scholar]
- 85.Bzdok D, Engemann D. & Thirion B. Inference and prediction diverge in biomedicine. Patterns 1, 100119 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Efron B. Prediction, estimation, and attribution. J. Am. Stat. Assoc 115, 636–655 (2020). [Google Scholar]
- 87.Lee S-I et al. A machine learning approach to integrate big data for precision medicine in acute myeloid leukemia. Nat. Commun 9, 42 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Erion G, Janizek JD, Sturmfels P, Lundberg S. & Lee S-I Learning explainable models using attribution priors. Preprint at arXiv1906.10670v1 (2019). [Google Scholar]
- 89.Weinberger E, Janizek J. & Lee S-I Learning deep attribution priors based on prior knowledge. Preprint at 10.48550/arXiv.1912.10065 (2019). [DOI] [Google Scholar]
- 90.Kuenzi BM et al. Predicting drug response and synergy using a deep learning model of human cancer cells. Cancer Cell 38, 672–684 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Gut G, Stark SG, Rätsch G. & Davidson NR PmVAE: learning interpretable single-cell representations with pathway modules. Preprint at bioRxiv 10.1101/2021.01.28.428664 (2021). [DOI] [Google Scholar]
- 92.Lopez R, Regier J, Cole MB, Jordan MI & Yosef N. Deep generative modeling for single-cell transcriptomics. Nat. Methods 15, 1053–1058 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Dincer AB, Celik S, Hiranuma N. & Lee S-I DeepProfile: deep learning of cancer molecular profiles for precision medicine. Preprint at bioRxiv 10.1101/278739 (2018). [DOI] [Google Scholar]
- 94.Štrumbelj E. & Kononenko I. Explaining prediction models and individual predictions with feature contributions. Knowl. Inf. Syst 41, 647–665 (2014). [Google Scholar]
- 95.Chen H, Janizek JD, Lundberg S. & Lee S-I True to the model or true to the data? Preprint at 10.48550/arXiv.2006.16234 (2020). [DOI] [Google Scholar]
- 96.Kokhlikyan N. et al. Captum: a unified and generic model interpretability library for PyTorch. Preprint at 10.48550/arXiv.2009.07896 (2020). [DOI] [Google Scholar]
- 97.Ribeiro MT, Singh S. & Guestrin C. Why should I trust you?: Explaining the predictions of any classifier. In Proc. 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 1135–1144 (ACM, 2016). [Google Scholar]
- 98.Paszke A. et al. PyTorch: an imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst 32, 8026–8037 (2019). [Google Scholar]
- 99.Pedregosa F. et al. Scikit-learn: machine learning in Python. J. Mach. Learn. Res 12, 2825–2830 (2011). [Google Scholar]
- 100.Nguyen G, Kim D. & Nguyen A. The effectiveness of feature attribution methods and its correlation with automatic evaluation scores. Adv. Neural Inf. Process. Syst 34, 26422–26436 (2021). [Google Scholar]
- 101.Covert I, Lundberg SM & Lee S-I Understanding global feature contributions with additive importance measures. Adv. Neural Inf. Process. Syst 33, 17212–17223 (2020). [Google Scholar]
- 102.Adebayo J, Muelly M, Liccardi I. & Kim B. Debugging tests for model explanations. Adv. Neural Inf. Process. Syst 33, 700–712 (2020). [Google Scholar]
- 103.Breiman L. Bagging predictors. Mach. Learn 24, 123–140 (1996). [Google Scholar]
- 104.Leek JT, Johnson WE, Parker HS, Jaffe AE & Storey JD The sva package for removing batch effects and other unwanted variation in high-throughput experiments. Bioinformatics 28, 882–883 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Edgar R. Gene Expression Omnibus: NCBI gene expression and hybridization array data repository. Nucleic Acids Res. 30, 207–210 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Chou T-C Drug combination studies and their synergy quantification using the Chou-Talalay Method. Cancer Res. 70, 440–446 (2010). [DOI] [PubMed] [Google Scholar]
- 107.Narahari Y. Game Theory and Mechanism Design Vol. 4 (World Scientific, 2014). [Google Scholar]
- 108.Szklarczyk D. et al. STRING v11: protein–protein association networks with increased coverage, supporting functional discovery in genome-wide experimental datasets. Nucleic Acids Res. 47, D607–D613 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Benjamini Y. & Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Stat. Soc. B 57, 289–300 (1995). [Google Scholar]
- 110.Love MI, Huber W. & Anders S. Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2. Genome Biol. 15, 550 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Hagberg A, Swart P. & S Chult D. Exploring Network Structure, Dynamics, and Function Using NetworkX (US Department of Energy, 2008). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The results of this study are in part based on data generated by the Cancer Target Discovery and Development (CTD2) Network (https://ocg.cancer.gov/programs/ctd2/data-portal), established by the National Cancer Institute’s Office of Cancer Genomics. Sequencing data are available in the GDC data portal under dbGaP Study Accession phs001657. The Beat AML patient sample data used in this study were done under an early access agreement, before final accrual, harmonization and public release of the full dataset. As such, the subset of samples included in this study may differ in sample representation, quality-control thresholds and data normalizations from those found in GDC and in the final study describing the full dataset.
The analysis of the haematopoietic signatures in an external dataset used data from the Cancer Dependency Map project (DepMap); specifically, the Genetic Dependency CRISPR assays (DepMap 21Q4 Public+Score, Chronos, ‘CRISPR_gene_effect.csv’) and the expression data (21Q4 Public, ‘CCLE_expression.csv’), as well as the metadata in the Cell Line Sample Info file (‘sample_info.csv’), all accessible from the DepMap portal (https://depmap.org/portal). Source data are provided with this paper.