Interplay between morphology and competition in two-dimensional colony expansion

Abstract

In growing populations, the fate of mutations depends on their competitive ability against the ancestor and their ability to colonize new territory. Here we present a theory that integrates both aspects of mutant fitness by coupling the classic description of one-dimensional competition (Fisher equation) to the minimal model of front shape (KPZ equation). We solved these equations and found three regimes, which are controlled solely by the expansion rates, solely by the competitive abilities, or by both. Collectively, our results provide a simple framework to study spatial competition.

Propagating fronts are a ubiquitous feature of spatially extended systems. Examples include the spread of an invasive species in an ecosystem [1], the spread of a ferromagnetic phase across a magnet [2], the spread of a high fitness allele through a population [3], or even the propagation of a flame front [4]. These and other applications have stimulated a sustained effort to construct and analyze coarse-grained models of traveling reaction-diffusion waves [1, 5–8]. By now, we have a general understanding of one-dimensional waves, but two and higher dimensions pose numerous challenges because of the interplay between the dynamics along the wave front and the shape of the wave front itself.

Growing microbial colonies provide an excellent experimental system to study the two-way coupling between the shape of the colony edge and the spatial distribution of different genotypes in the population [9–11]. At the same time, microbial colonies also serve as useful model systems for tumor growth and geographic expansions of plants and animals [12]. Hence, the spatial competition between two different genotypes has garnered much recent attention [13, 14].

Although many approaches have been put forward to describe how microbes colonize surfaces, we are still lacking a simple, but general framework to describe competition during colony growth. Most computational studies rely on numerical simulations of complex microscopic models, and therefore can draw few general conclusions about possible outcomes of spatial competition [15–17]. To a certain extent, this challenge has been recently addressed by theoretical studies using either field-theory [18] or geometric-optics [11, 13, 19] approaches to describe morphologies of colonies with two competing species. These theoretical models, however, are agnostic to the mechanism of competition and assume the knowledge of emergent properties, such as the invasion velocity of the mutant. In consequence, their utility is rather limited because they cannot, for example, predict the winner of the competition given the microscopic qualities of the mutant and the ancestor. Thus, there is a need for a tractable model that can integrate the microscopic dynamics with the changes in the colony shape during spatial competition.

To construct such a model, we focused on growth on rich solid media so that one can neglect nutrient diffusion [20] and complex hydrodynamics [21, 22]. Under these assumptions, the state of the colony is well-described by two quantities: the spatial extent or “height” of the colony $h(x,t)$ and mutant fraction $f(x,t)$, which change along the colony front ($x$-coordinate) and with time [18]. For simplicity, we consider only planar fronts, where $h$ is simply the distance by which the colony expanded from the inoculation site. Thus, we treat the colony edge as a thin interface. This is a reasonable approximation because the growth region extends only a few cell widths into the colony, and any successful mutant has to emerge near the colony edge; otherwise it is crowded out of the growth zone and remains trapped in the colony bulk [23].

The dynamical equations for $h(x,t)$, and $f(x,t)$ emerge naturally as generalization the well-studied limits of the Fisher-Kolmogorov-Petrovsky-Piskunov (FKPP) equation [3, 7] for one dimensional competition (no variation in $h$) and the Kardar-Parisi-Zhang (KPZ) equation [24] for interface growth (no variation in $f$).

The KPZ equation is a continuum limit of the classic Eden model of colony growth [25]. It has been quite successful at describing both deterministic and stochastic patterns in microbial colonies [26] including those observed during two-species competition [23]. The KPZ equation can also be viewed as a phenomenological model based on gradient expansion similar to its justification for surface growth phenomena [24, 26]. The dynamical equation for $h(x,t)$ reads

$$\frac{\partial h}{\partial t}=v_0+\frac{v_0}{2}{\left(\frac{\partial h}{\partial x}\right)}^2+D_h\frac{{\partial }^{2}h}{\partial x^2}+\alpha f,$$ (1)

where the first two terms express the isotropic expansion of the colony with velocity $v_0$ along the local normal to the front, the third term encodes curvature relaxation, and the fourth term accounts for the difference in the expansion velocities of the mutant and the ancestor [18]. We used a linear interpolation between the two velocities because most of our result are obtained “to the first order” in the differences between the two competitors. Higher order terms (such as $\alpha f(\partial h/\partial x{)}^2$) are similarly ignored.

Assuming that the mutant has a selective advantage $s\left(f\right)$, the dynamics of the mutant fraction $f$ is described a modified FKPP equation [3, 7]:

$$\frac{\partial f}{\partial t}=s\left(f\right)f\left(1-f\right)+D_f\frac{{\partial }^{2}f}{\partial x^2}+v_0\frac{\partial h}{\partial x}\frac{\partial f}{\partial x},$$ (2)

where the first term accounts for differences in local reproduction rates, the second accounts for spatial rearrangements due to motility or population fluxes generated by the expansion dynamics, and the third is our addition to describe “passive” changes in $f$ due to the motion of a tilted interface [18, 27, 28]. Indeed, a tilted front advances along its normal, so it moves both vertically and horizontally. The horizontal velocity $-v_0\partial h/\partial x$ advects $f(t,x)$, which manifests in the term proportional to $\partial f/\partial x$ in the equation above; see Fig. 2 in the SI [29] for an illustration.

Without the coupling to $h$, the FKPP equation is the classic model of spatial competition between two genotypes in one dimension. Its asymptotic solutions are known as traveling waves because they have the form $f(x,t)=f(x-ut)$, where $u$ is the invasion velocity of the mutant. In the following, we determine how the coupling between $h$ and $f$ affects $u$ by solving Eqs. (1) and (2) numerically using MATLAB’s pdepe (for codes, please visit [38]). We then develop an analytical theory that not only quantitatively matches the simulations, but also provides deep insights into the existence of three distinct regimes of spatial competition.

The solutions of the FKPP equation are broadly classified into so-called “pulled” and “pushed” waves depending on how the selective advantage $s$ depends on mutant frequency $f$. Pulled waves are dominated by the dynamics at leading edge, and the invasion velocity can be obtained by linearizing the FKPP equation for small $f$; the resulting ‘Fisher velocity’ is given by $u_{\mathrm{F}}=2\sqrt{D_{f}s\left(0\right)}$ (see Refs. [1, 3, 7, 8]). In contrast, the velocity of pushed waves depends on the values of $s$ at all $f$, and cannot be, in general, computed analytically except for some exactly solvable models such as with $s\left(f\right)=s_1\left(f-f_0\right)$ [30, 31]. For this model, pushed waves occur for $f_0\in (-0.5,0.5)$ with $u=\sqrt{D_f{s}_1/2}\left(1-2f_0\right)$; the waves are pulled for $f_0<-0.5$. Behavior for $f_0>0.5$ is analyzed by changing variables from $f$ to $1-f$.

We assume that the mutant has a local fitness advantage $s\left(f\right)>0$, and first consider pulled waves with $s\left(f\right)=s_0>0$. The emergence of a traveling wave of $f(x,t)$ is apparent in Fig. 1(a). The corresponding $h(x,t)$, however, is not a simple traveling wave (Fig. 1(b)). The colony front is composed of a curved portion dominated by the ‘mutant’ and a flat front dominated by the ‘ancestor’. While the transition point between these two regimes advances with the same velocity $u$, the overall shape of the curved portion depends on both time and the co-moving coordinate $(x-ut)$ because the growth dynamics encoded by $\alpha$ persist even after the mutant displaces the ancestor.

FIG. 1:

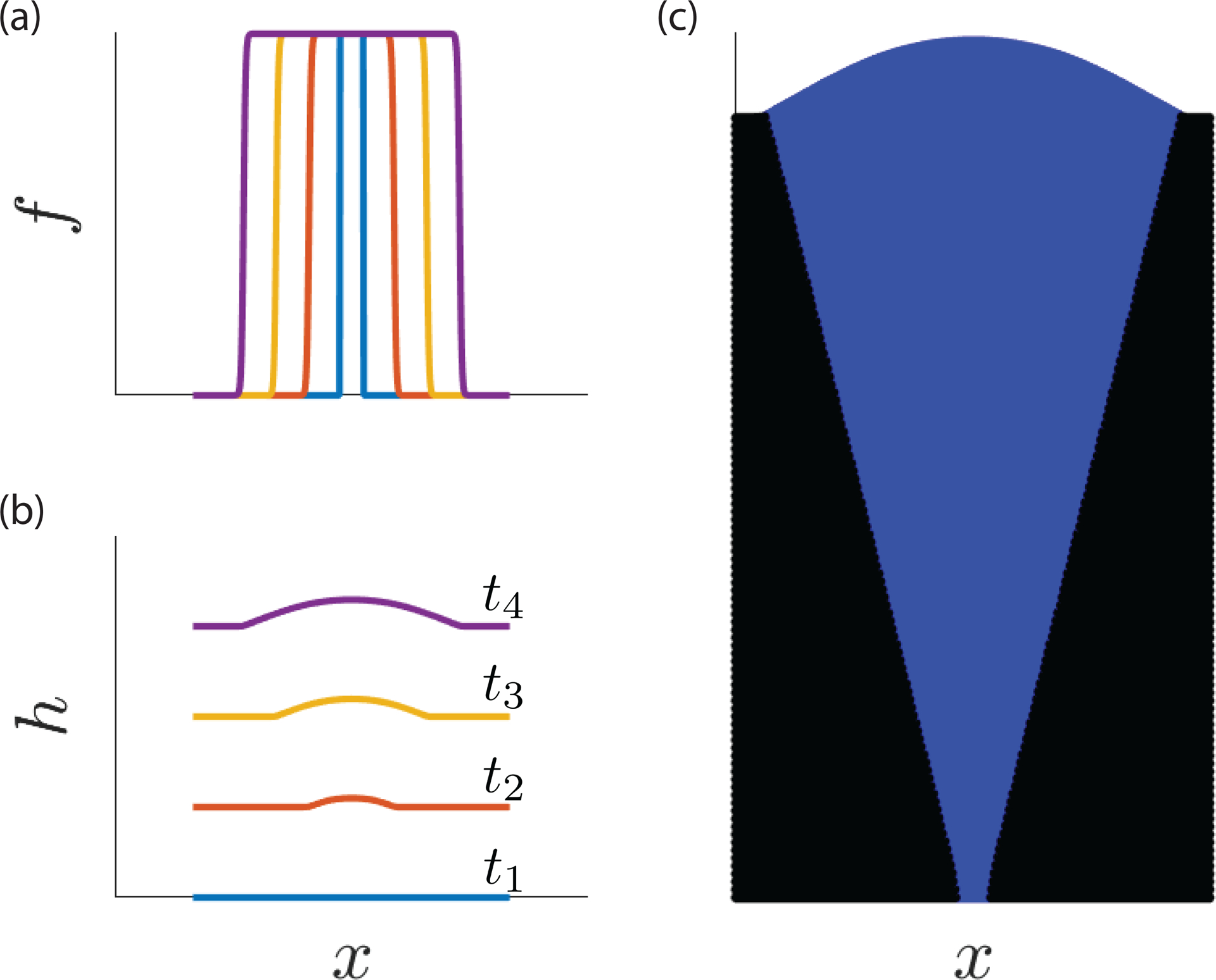
Sample simulation results generated by solving Eqs. (1) and (2) numerically in the pulled wave regime $s\left(f\right)=s_0$. (a) Profiles of mutant frequency $f(x,t)$ at five equally-spaced time slices labeled by color. (b) Height profiles $h(x,t)$ taken at the same five time points as in panel (a) with the same color convention. Starting from a flat initial condition, the height field develops a nontrivial morphology through a dependence of the growth rate of $h$ on the mutant frequency $f$. (c) The spatial distribution of the two competitors is visualized by plotting successive solutions of the height field $h$ and coloring each point according to the value of $f$ at the corresponding $x$ and $t$.

To understand how the invasion velocity $u$ is affected by the coupling to height, we computed it numerically at different values of $\alpha$. For $\alpha =0$, the equations are effectively decoupled because genetic variation along the front does not create any disturbances in the front shape, which remains $h=v_{0}t$ for all $x$. Mutant is faster than the ancestor when $\alpha >0$ and slower otherwise. While the latter case may seem paradoxical, it has actually been observed experimentally [19].

Simulation results are shown in Fig. 2, with different markers denoting different values of $s_0$. We immediately observe that the data falls into two regimes: For small $\alpha$, the invasion velocity is a constant, which depends on $s_0$. For large $\alpha$, the situation is reversed: the velocity depends on $\alpha$, but not on $s_0$. Thus, there appears to be two distinct regimes: one mediated by local competition described by the FKKP equation, and one mediated by the expansion rates in the KPZ equation.

FIG. 2:

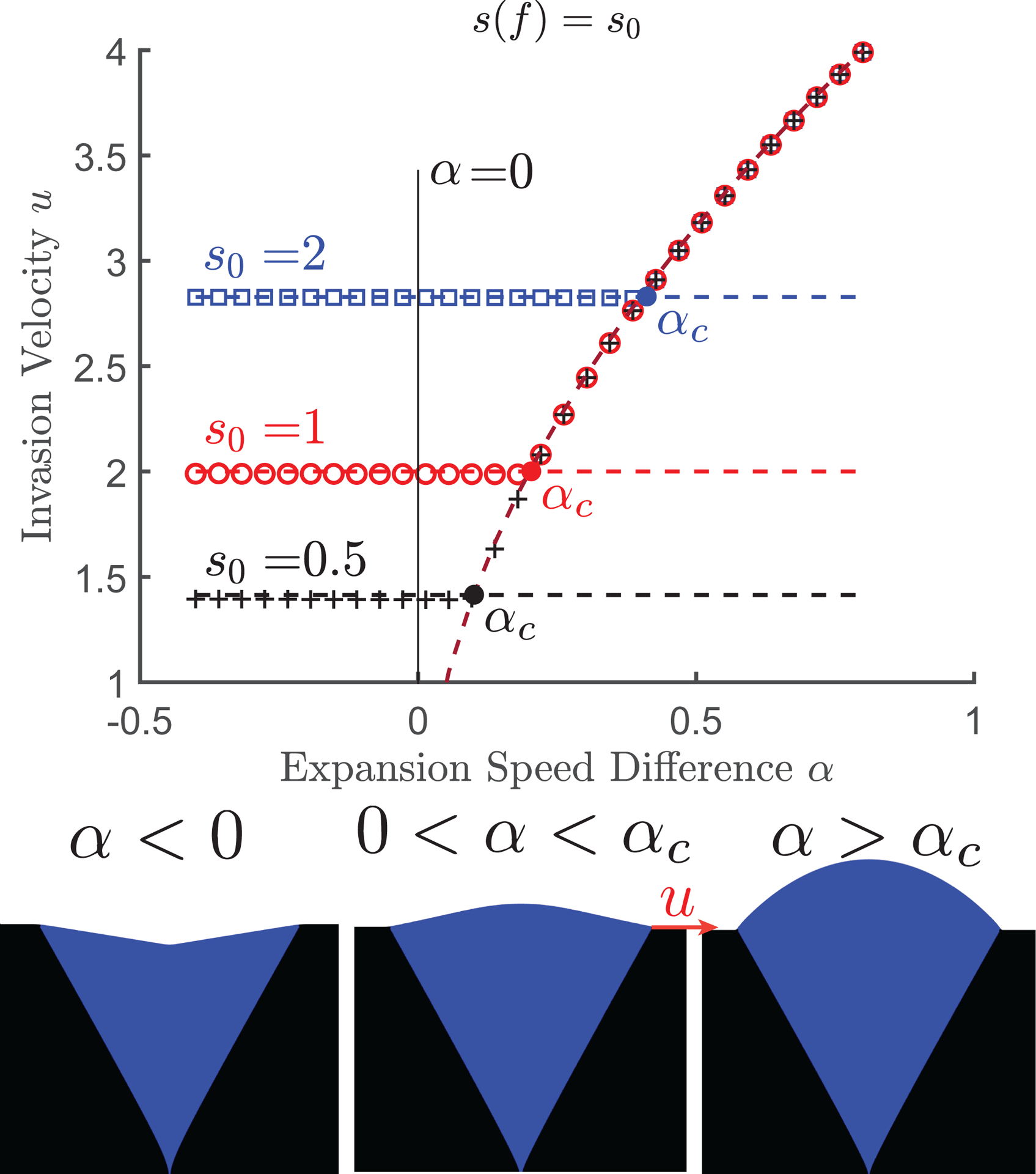
Invasion dynamics in pulled waves. (Top): Invasion velocity shows two regimes with dependence on either $\alpha$ or $s$. The horizontal dashed lines are the predicted ‘Fisher velocities’. The curved dashed line is $u=\sqrt{2\alpha v_0}$, as predicted by Eq. (3). For each value of $s_0$ the filled in circle shows the location of the transition point ${\alpha }_c$ between the composite and circular arc morphologies. (Bottom): Depending on $\alpha$, there are three distinct colony morphologies. When $\alpha <0$ the front shape is a V-shaped dent. When $0<\alpha <{\alpha }_c$ the morphology is a composite bulge consisting of a central circular arc transitioning to a constant slope at the bulge edges. When $\alpha >{\alpha }_c$ the front is entirely a circular arc. The red arrow shows the invasion velocity $u$, which is the speed of the mutant-wildtype boundary along the horizontal axis. Parameters used are $v_0=10,D_f=D_h=1$.

We tested this hypothesis by comparing solutions of the uncoupled FKKP and KPZ equations to the results in Fig. 2. For small $\alpha$, there is perfect agreement between the observed values of $u$ and the expected Fisher velocity $u_{\mathrm{F}}=2\sqrt{D_f{s}_0}$. In hindsight, this may not be too surprising since pulled waves are controlled by the dynamics at the leading edge, where $h$ is flat and the coupling term is the FKPP equation vanishes. However, the influence of growth velocity differences manifests dramatically in the shape of the front, which changes from a V-shaped dent at negative $\alpha$ to a composite bulge for positive $\alpha$; see Fig. 2.

For large $\alpha$, the simulations match

$$u=\sqrt{2\alpha \left(v_0+\alpha \right)}\approx \sqrt{2\alpha v_0,}$$ (3)

which can be obtained from the KPZ equation by analogy with the equal-time argument in Ref. [11] and the geometric theory in Ref. [19]. In this regime, the mutant forms a circular bulge [39] of radius $\left(v_0+\alpha \right)t$, while the ancestor has a flat front at height $v_{0}t$. These two curves intersect at point whose $x$-coordinate moves with velocity $u=\sqrt{2\alpha \left(v_0+\alpha \right)}\approx \sqrt{2\alpha v_0}$. The transition between the $s_0$–dependent and $\alpha$–dependent invasion velocities occurs at a critical value of ${\alpha }_c=2s_0{D}_f/v_0$ when the velocity of the circular bulge exceeds the Fisher velocity. This agrees with the general observation that a faster moving solution typically controls the behavior of a traveling wave [8].

The above results for pulled waves are surprising from both mathematical and biological perspectives. Mathematically, it is surprising that the invasion velocity $u$ is controlled by only one of the equations, i.e. there is no two-way coupling. Biologically, it seems counter-intuitive that, no amount of disadvantage in the expansion velocity $(\alpha <0)$ can overcome the competitive advantage $\left(s_0\right)$. To see whether these conclusion hold more generally, we carried out equivalent simulations for pushed waves with $s\left(f\right)=s_1\left(f-f_0\right)$. The results are shown in Fig. 3.

FIG. 3:

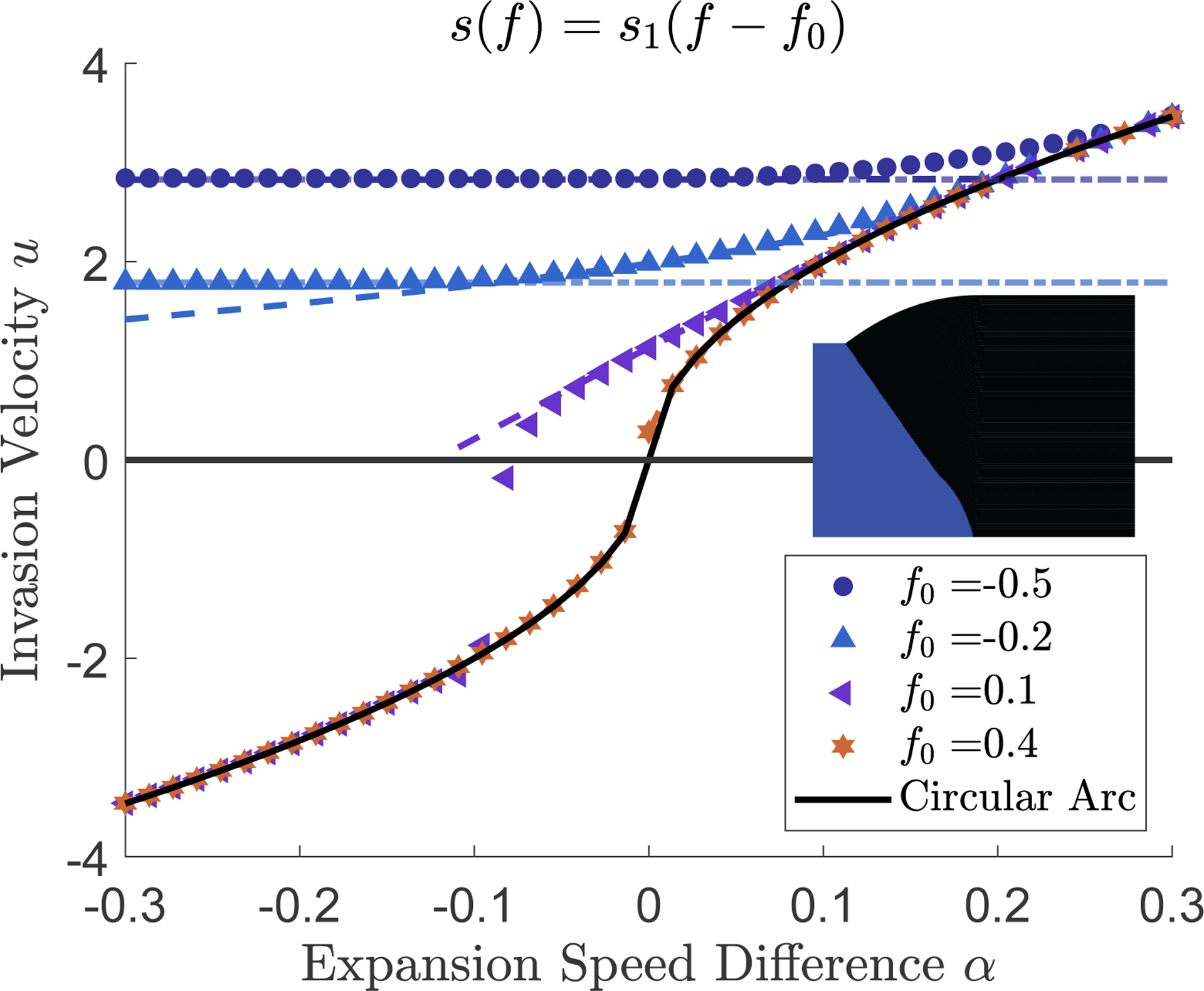
Invasion dynamics in pushed waves. Symbols show the measured invasion velocity from simulations as a function of the expansion velocity difference $\alpha$. The dashed curves show the result of the perturbation theory discussed in the text, and the horizontal dashed-dotted lines are the invasion velocity predicted from simple linearization of Eq. (2). When $\alpha$ is large and positive, all invasion velocities match the solid black line, the speed of the invading circular arc. The behavior for $\alpha$ sufficiently negative (corresponding to a mutant growing much slower than the wildtype), depends on the sign of $f_0$. When $f_0<0$, the invasion speed approaches a value predicted by the linearized equations $u=2\sqrt{-s_1{f}_0{D}_f}$. For $f_0>0$, the invasion velocity changes sign at large negative $\alpha$, reversing the competitive outcome. The negative invasion speed is that of a leftward-moving circular arc $\left(u=-\sqrt{2\left|\alpha \right|v_0}\right)$ which is depicted by the solid black line. Inset in the figure is a sample morphology which arises when the mutant is invaded by the wildtype $(u<0)$. The simulation shown is initialized as a half-space where the left half is occupied by mutant and the right by wildtype. Parameters are $v_0=20,s_1=4,D_f=D_h=1$.

Compared to pulled waves, there are three regimes. One regime occurs for large $\alpha$ and corresponds to a mutant assuming a circular bulge morphology invading at $u=\sqrt{2\alpha v_0}$. This regime is completely analogous to what we described for pulled waves above.

In addition, there are two new regimes at $\alpha$ near zero and at large negative $\alpha$. The dynamics in the latter regime depends on whether Eq. (2) describes propagation into an unstable state ($s\left(0\right)<0$, the mutant has a competitive advantage at any $f$) or into a metastable state ($s\left(0\right)>0$, the mutant needs a critical density to out-compete the ancestor).

For $s\left(0\right)<0$ ($f_0>0,f=0$ is stable), the invasion speed $u$ changes sign when $\alpha$ becomes sufficiently negative. In this case, the ancestor invades a more competitive mutant $\left(s_1>0\right)$ because it has a much larger expansion velocity. The invasion proceeds with a circular bulge of the ancestor which must advance with velocity $u=-\sqrt{2\left|\alpha \right|v_0}$.

When $s\left(0\right)>0$ ($f_0<0,f=0$ is unstable), the invasion velocity remains positive for all values of $\alpha$, and eventually becomes constant. The value of this limiting velocity matches $2\sqrt{D_{f}s\left(0\right)}=2\sqrt{-D_f{s}_1{f}_0}$, which is the velocity that one would obtain by linearizing Eq. (2). This behavior is identical to what we found for pulled waves, in Fig. 2, so, in effect, the slower expansion rate of the mutant converted its invasion of the ancestor from pushed to pulled.

The other new regime occurs for $\alpha$ near zero. In contrast to pulled waves, the invasion velocity $u$ exhibits a dependence on both $s_1$ and $\alpha$. We will now analyze this new dynamics using perturbation theory.

To find how $u$ depends on both $s\left(f\right)$ and $\alpha$, we will treat the coupling between the dynamics of $f$ and $h$, i.e. the term $v_0{\partial }_{x}h{\partial }_{x}f$ in Eq. (2), using an approach detailed in Refs. [32–35]. The scale of the perturbation is thus set by the maximal front slope which we denote $\sigma$.

The perturbative scheme proceeds as follows: In the absence of coupling, the invasion profile of a mutant fraction ($f(z=x-ut)$ is $f^{\left(0\right)}\left(z\right)$) is the solution of the standard one-dimensional Fisher equation, which are known exactly for certain $s\left(f\right)$. We can use the solution of the standard one-dimensional invasion problem to obtain the correction to $u$ due to nontrivial morphological changes associated with mutant sectors. Substituting $f^{\left(0\right)}\left(z\right)$ into Eq. (1) leads to a non-linear differential equation whose solution provides the first order profile $h^{\left(1\right)}(z=x-ut)$. As described in the SI [29] the non-linear equation can be solved exactly via a Cole-Hopf transformation, resulting in a complicated form for $h^{\left(1\right)}(z=x)$ that depends on $v_0,D_h$ and $\alpha$. Qualitatively, this height profile is a sigmoidal curve that changes from $v_{0}t$ in the region $f\to 0\left(h^{\prime }\to 0\right)$, to $v_{0}t+\sigma z$ as $f\to 1\left(h^{\prime }\to \sigma \right)$. The limiting slope can be obtained from Eq. (1) by setting $f=1$ (see [29] for details).

$$-u\sigma =\alpha +v_0{\sigma }^2/2.$$ (4)

After substituting $h^{\prime \left(1\right)}\left(z\right)$ into Eq. (2), the methodology described in Refs. [32–36] can be used to compute the first order correction to the invasion velocity, leading to the correction

$$u=u_0-\kappa v_0\sigma +O\left(v_0^2{\sigma }^2\right),$$ (5)

where $u_0$ is the unperturbed velocity for $\alpha =0$.

To coefficient $\kappa$ in Eq. (5) is a ratio of integrals that depend on the function $h^{\left(1\right)}\left(z\right)$ (see SI [29]). In general, the solution is complex, but it can be simplified in two limiting cases.

By setting $D_h=0$, equation for $h^{\left(1\right)}(z=x)$ becomes first order, and its solution simplifies the evaluation of all downstream integrals. This limit corresponds to the geometric description in which the profile simply advances along the local normal without further relaxation, yielding ${\kappa }_{\text{geom.}}=\frac{1}{4}\left(1+2f_0\right)$. The $D_h=0$ case captures the qualitative changes in $\kappa$ including the transition to pulled waves at $f_0=-0.5$, where $\kappa$ must vanish. Thus, our theory recapitulates the finding that the invasion speed becomes insensitive to the morphology when the wave becomes pulled.

The insensivity of pulled waves to morphology is a general finding of our perturbative approach. To demonstrate this, consider the dynamics of the tail of any pulled wave (with arbitrary $s\left(f\right)$), which follows a linearized Eq. (2) about $f=0$ in the co-moving frame:

$$-u{f}^{\prime }\approx s\left(0\right)f+D_f{f}^{″}+v_0{f}^{\prime }{h}^{\prime }.$$ (6)

The zeroth order solution travels at a speed $u_0=2\sqrt{s\left(0\right)D_f}$ and the profile has a tail which is asymptotic to $e^{-\sqrt{s\left(0\right)/D_f}z}$ as $z\to \mathrm{\infty }$. The correction to the invasion velocity (see SI) is a ratio of integrals, with the denominator being ${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }} {\left(f^{\left(0\right)\prime }\right)}^2{e}^{u_{0}z/D_f}dz$. Substitution of the asymptotic profile shape immediately shows that this integral diverges, and thus the correction to the invasion speed vanishes for any pulled wave.

Another useful approximation is obtained by neglecting the nonlinear term in Eq. (1), which is justified for small $\alpha$ because $\partial h/\partial x\propto \alpha$. In this case, we have to evaluate the downstream integrals numerically, but obtain a perfect agreement with the simulations at least when $\alpha$ is small; see Fig. 4. Our perturbation theory, as well as the model described in this work, rests on the assumption of small slopes in the height field $(\sigma \ll 1)$ allowing a gradient expansion description of the colony expansion. In terms of our three velocities, this requires $\alpha \ll u_0\ll v_0$

FIG. 4:

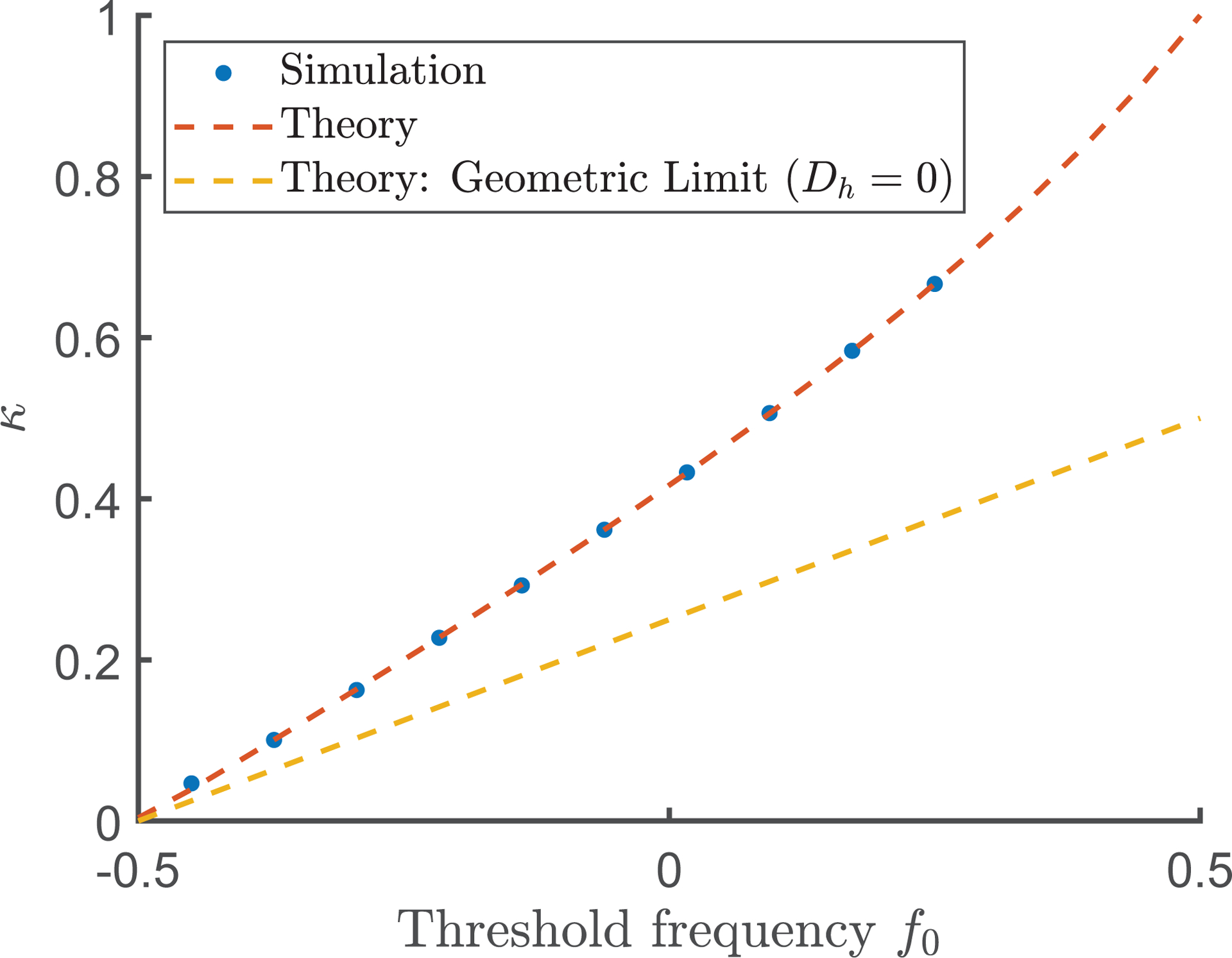
Numerical results showing the dependence of the coefficient $\kappa$ as defined in Eq. (5) on $f_0$. The numerical values of $\kappa$ were obtained by fitting measured invasion velocities as functions of $\alpha$ in the limit $\alpha \to 0$. The best-fit slope is then used to obtain $\kappa$ in Eq. (5). The red dashed line is the theoretical prediction of our perturbative analysis for the value of $D_h$ used in simulation at small $\alpha$. The yellow dashed line is the theoretical value of $\kappa$ when $D_h=0$. Parameters are $v_0=10,D_h=D_f=1,s_1=2$.

We can use perturbation theory to estimate the location of the transition from a right-moving wave (mutant taking over) to the left-moving wave (ancestor taking over). This occurs when $u=0$, i.e for $\alpha =-u_0^2/\left(2v_0{\kappa }^2\right)$. Beyond this point, simulations show that $u$ jumps discontinuously (when $f_0>0$) from $u=0$ to the value corresponding to a left-moving circular arc as discussed above.

Although we have not studied stochastic versions of Eqs. (1) and (2), we anticipate no major qualitative changes due to noise. Our focus is largely on sector morphologies formed by selective forces between strains, which have characteristic lengths scaling linearly with time, overshadowing noise-induced, sublinearly scaling fluctuations. As such, long-term ballistic sector motion should render noise corrections irrelevant, though it may cause minor quantitative alterations to invasion velocity values [36, 37]. For pulled waves, noise might also induce qualitative changes, such as a non-zero $\kappa$ reflecting noise strength.

Microbes, cancer cells, and invasive species often spread across space forming a continuous two-dimensional populations. Here, we couple a model of surface growth (KPZ equation) to a model of competition (generalized FKPP equation). The combined model faithfully describes recent observations of nontrivial colony morphologies near emerging mutants [11, 19]. Moreover, it elucidates how colonization rate and local competitive strength affects the fate of the mutation. We find that mutant takeover relies on whether the FKPP equation allows for pulled waves, driven by growth dynamics at low mutant densities, or pushed waves, influenced by growth dynamics across the entire mutant-ancestor interface.

For pulled invasions, we found that the mutant with a positive selective advantage $s\left(0\right)>0$ always wins regardless of the value of $\alpha$. For small $\alpha$, the invasion velocity depends only on $s\left(0\right)$, while for large $\alpha$, it is given by the geometric theory and depends on $\alpha$ only. For pushed waves propagating into an unstable state $s\left(0\right)>0$, the mutant always wins as well, but its invasion velocity could depend on both $s\left(f\right)$ and $\alpha$. The competitive outcome, however, could be different for pushed waves propagating into a metastable state. If $s\left(0\right)<0$, the mutant that would invade in a strictly one-dimensional population, i.e. without coupling to morphology, could lose during colony expansion. Specifically, a large negative $\alpha$ reverses the direction of invasion. Simulations with a different selection coefficient $\left(s\left(f\right)=s_3\left(f^3-f_0\right)\right)$ further suggest invasion reversal is only possible when $f=0$ is an unstable fixed point - see SI [29].

These intricate interplay between local competition and global expansion rates are supported by numerical simulations and analytical perturbation theory. Taken together our results not only elucidate many subtleties associated with mutant establishment, but also pave the way for a more parsimonious and universal description of evolutionary and ecological processes in growing populations that is also very amenable to theoretical analyses.