Continuum of quantum fluctuations in a three-dimensional S = 1 Heisenberg magnet

Abstract

Conventional crystalline magnets are characterized by symmetry breaking and normal modes of excitation called magnons, with quantized angular momentum ℏ. Neutron scattering correspondingly features extra magnetic Bragg diffraction at low temperatures and dispersive inelastic scattering associated with single magnon creation and annihilation. Exceptions are anticipated in so-called quantum spin liquids, as exemplified by the one-dimensional spin-1/2 chain, which has no magnetic order and where magnons accordingly fractionalize into spinons with angular momentum ℏ/2. This is spectacularly revealed by a continuum of inelastic neutron scattering associated with two-spinon processes. Here, we report evidence for these key features of a quantum spin liquid in the three-dimensional antiferromagnet NaCaNi₂F₇. We show that despite the complication of random Na¹⁺–Ca²⁺ charge disorder, NaCaNi₂F₇ is an almost ideal realization of the spin-1 antiferromagnetic Heisenberg model on a pyrochlore lattice. Magnetic Bragg diffraction is absent and 90% of the neutron spectral weight forms a continuum of magnetic scattering with low-energy pinch points, indicating NaCaNi₂F₇ is in a Coulomb-like phase. Our results demonstrate that disorder can act to freeze only the lowest-energy magnetic degrees of freedom; at higher energies, a magnetic excitation continuum characteristic of fractionalized excitations persists.

The existence of a spin liquid for isotropically interacting classical spins on the pyrochlore lattice was first proposed by Jacques Villain nearly 40 years ago¹. Since then, it has been established that the classical $(S\to \mathrm{\infty })$ Heisenberg antiferromagnet does not undergo any magnetic ordering transition^2–6. The magnetic interaction energy is minimized by all spin configurations with vanishing magnetization on every tetrahedron, and the ensemble of these configurations forms a macroscopically degenerate, but highly correlated, ground-state manifold. Such a collective state is termed a Coulomb phase because coarse-grained spin configurations within the manifold form a divergence-free vector field, implying dipolar correlations^7–9. Experiments probing magnetic correlations, and hence the solenoidal field, should include sharp pinch point features, as in related classical spin-ice materials, where ferromagnetic Ising interactions dominate¹⁰. Both classical spin ice and the classical Heisenberg antiferromagnet may be classified as Coulomb phases but, whereas there is much activity and progress in exploring quantum spin ice, less is understood about the quantum limit of the antiferromagnetic Heisenberg model. There is theoretical evidence that pinch point correlations survive^2,3,11–13, but the specific character of the ground state and of the magnetic excitations is unknown.

The experimental challenge lies in realizing the pyrochlore Heisenberg model in a material. The highly degenerate manifold of the Coulomb phase is susceptible to small perturbations² and lattice instabilities¹⁴ such that at low temperatures the spin liquid phase is more often than not supplanted by a broken-symmetry phase. So far, the closest realizations of a Heisenberg antiferromagnet on a pyrochlore lattice have been found in the cubic spinels. Many of these materials exhibit considerable exchange interactions extending to the second- and third-nearest neighbours¹⁵. Magnetic frustration is manifest through self-organized independent hexagonal clusters^16–19, but a magneto-structural transition severely impacts almost half of the magnetic bandwidth.

Extrinsic disorder, in the form of impurity ions, or variations in magnetic exchange interactions caused by chemical disorder may also disrupt the spin liquid. Generally, these perturbations result in a spin-freezing transition at low temperatures^20–22. For example, in the Heisenberg pyrochlore Y₂Mo₂O₇, weak disorder results in a fully frozen state with isotropic short-range spin correlations^23,24. Here, we demonstrate that disorder is not necessarily fatal to the search for quantum spin liquids, as it can act to freeze only the lowest energy magnetic degrees of freedom. At higher energies a magnetic excitation continuum characteristic of fractionalized excitations persists.

NaCaNi₂F₇ is one member of a family of recently discovered transition metal pyrochlore fluorides where charge balance in the neutral chemical structure requires an equal mixture of Na¹⁺ and Ca²⁺ (refs ^25–27). Diffraction measurements probing the average crystal structure indicate that Na¹⁺ and Ca²⁺ are uniformly and randomly distributed on the A-site of the pyrochlore lattice. Magnetic susceptibility measurements reveal Curie–Weiss behaviour, with an effective moment of $p_{\text{eff}}=3.7\left(1\right){\mu }_{\mathrm{B}}$ (where ${\mu }_{\mathrm{B}}$ is the Bohr magneton), consistent with $S=1$, and a Curie–Weiss temperature of ${\theta }_{\mathrm{C}\mathrm{W}}=129\left(1\right)\mathrm{K}$ (ref. ²⁶). A spin-glass-like freezing transition is observed at $T_{\mathrm{f}}=3.6\mathrm{K}$ in d.c. and a.c. magnetic susceptibility measurements²⁶. This freezing may result from the ${\mathrm{N}\mathrm{a}}^{1+}/{\mathrm{C}\mathrm{a}}^{2+}$ charge disorder, which is expected to generate a random variation in the magnetic exchange interactions. For the Heisenberg pyrochlore antiferromagnet described by the Hamiltonian $\mathscr{H}=1/2{\sum }_{ij}{J}_{ij}{\mathbf{S}}_i\cdot {\mathbf{S}}_j$ the freezing temperature provides an estimate²¹ of the strength of the bond disorder $\delta J=\sqrt{3/8}{k}_{\mathrm{B}}{T}_{\mathrm{f}}=0.19\mathrm{m}\mathrm{e}\mathrm{V}$ for $S=1$. Despite this disorder, for temperatures ($T$) and energies E beyond 2% of the magnetic bandwidth, we show that NaCaNi₂F₇ is an excellent approximation to a nearest-neighbour Heisenberg antiferromagnet on the pyrochlore lattice, and exhibits key characteristics of a quantum spin liquid (QSL): an excitation continuum and a finite energy maximum in the momentum-resolved spectrum of scattering at an energy transfer of the order of the nearest-neighbour exchange constant.

We start by determining the spin Hamiltonian for NaCaNi₂F₇. The elegant method employed for other frustrated magnets^28,29 is not feasible here because the magnetic energy scale is too large to reach the forced ferromagnetic state in a neutron scattering experiment. Instead we focus on the equal-time spin correlation function, which can be measured with inelastic neutron scattering and calculated for a given spin Hamiltonian in the paramagnetic state through the self-consistent Gaussian approximation (SCGA)¹⁵. Fig. 1a shows the measured equal-time structure factor $𝒮\left(q\right)$ for NaCaNi₂F₇ obtained from the energy-integrated magnetic neutron scattering intensity. More detailed information is provided by polarized neutron scattering in the $(h,h,\ell )$ plane, which is sensitive to spin components perpendicular to $\mathbf{q}$ within the $(h,h,\ell )$ reciprocal lattice plane for the spin-flip (SF) channel, and along (1,−1,0) for the non-spin-flip channel (NSF). Without further analysis, the similarity of SF and NSF magnetic neutron intensities in Fig. 1a is evidence of a near spin-space isotropic system. Weak anisotropic interactions are revealed by two features of the polarized intensity. First, the SF scattering exhibits a pronounced asymmetry of the lobes of intensity centred on (± 0.6, ± 0.5,2) positions about the dashed line parallel to (1,1,0) and passing though (0, 0, 2), as indicated in Fig. 1b. Second, the NSF intensity is diminished around the (0, 0, 2) pinch point positions.

Fig. 1 |. Equal-time structure factor in NaCaNi₂F₇.

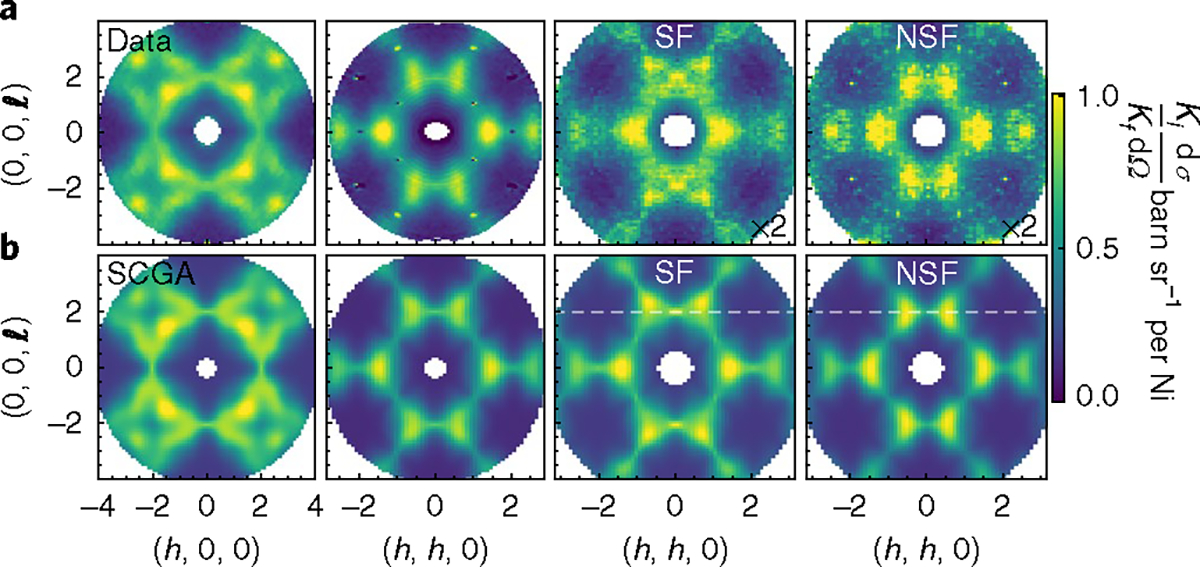
a, Measured neutron cross-section integrated over the range $0<E<14\mathrm{m}\mathrm{e}\mathrm{V}$ at $T=1.8\left(2\right)\mathrm{K}$. Polarized neutron measurements are labelled by NSF, which measures components of the dynamic spin correlation function that are perpendicular to the $(h,h,\ell )$ scattering plane, and SF, which measures the component of the dynamics spin correlation function polarized within the $(h,h,\ell )$ scattering plane and perpendicular to momentum transfer. Before integration, the data were symmetrized by folding about the lines $h=0$ and $\ell =0$ for data in the $(h,0,\ell )$ scattering plane and the lines $hh=0$ and $\ell =0$ for data in the $(h,h,\ell )$ scattering plane. No smoothing or interpolation was applied to the data. b, Energy-integrated neutron cross-section calculated using the self-consistent Gaussian approximation (SCGA) and exchange parameters $J_1=J_2=3.2\left(1\right)\mathrm{m}\mathrm{e}\mathrm{V},J_3=0.019\left(3\right)\mathrm{m}\mathrm{e}\mathrm{V}{J}_4=-0.070\left(4\right)\mathrm{m}\mathrm{e}\mathrm{V}$ and $J_{\mathrm{N}\mathrm{N}\mathrm{N}}=-0.025\left(5\right)\mathrm{m}\mathrm{e}\mathrm{V}$. Dashed lines delineate the plane of asymmetry in the SF scattering. The dipole approximation for the Ni²⁺ magnetic form factor⁴³ was used when converting the calculated $𝒮\left(\mathrm{q}\right)$ to a neutron cross-section.

The full symmetry-allowed nearest-neighbour bilinear exchange Hamiltonian takes the form $\mathscr{H}=1/2{\sum }_{ij}{J}_{ij}^{\mu \nu }{S}_i^{\mu }{S}_j^{\nu }$, where the 3 × 3 interaction matrix $J^{\mu \nu }$ is parameterized by four independent terms: the diagonal components $J_1$ and $J_2$, and off-diagonal components $J_3$ and $J_4$ (ref. ²⁹). For the next-nearest-neighbour interactions $J_{\mathrm{N}\mathrm{N}\mathrm{N}}$ we retain only the isotropic part. We find the best global fit of the measured equal-time structure factor with the SCGA using the exchange parameters: $J_1=J_2=3.2\left(1\right)\mathrm{m}\mathrm{e}\mathrm{V},J_3=0.019\left(3\right)\mathrm{m}\mathrm{e}\mathrm{V},J_4=-0.070\left(4\right)\mathrm{m}\mathrm{e}\mathrm{V}$ and $J_{\mathrm{N}\mathrm{N}\mathrm{N}}=-0.025\left(5\right)\mathrm{m}\mathrm{e}\mathrm{V}$. Details of the neutron measurements, fitting procedure and the goodness of fit diagnostics are provided in the Methods and Supplementary Information. The resulting calculated neutron intensity is shown in Fig. 1b. Although the SCGA is an approximate procedure, we find exceptional agreement between the model and data, and we shall later see that a classical Monte Carlo calculation of the specific heat based on the inferred spin Hamiltonian is consistent with our measurements. Although the effective moment of 3.7(1) μ_B implies an orbital contribution to the magnetism²⁶, we find that the effect of spin-orbit coupling on the exchange Hamiltonian is very small. We conclude that the spin Hamiltonian for NaCaNi₂F₇ closely approximates the $S=1$ Heisenberg antiferromagnet on the pyrochlore lattice, perturbed only at the percent level by symmetric and antisymmetric exchange anisotropies, next-nearest-neighbour interactions and exchange disorder.

Having established its frustrated quantum spin Hamiltonian, we now explore the corresponding magnetic excitations in NaCaNi₂F₇. Figure 2 shows the $\mathbf{q}$-dependence of the inelastic magnetic scattering through a series of constant-energy transfer slices covering the $(h,h,\ell )$ and $(h,0,\ell )$ reciprocal lattice planes. At low energy transfer, the dynamic structure factor forms a bow-tie pattern with pinch points characteristic of dipolar spin correlations. The scattering closely resembles predictions for the classical Heisenberg antiferromagnet on the pyrochlore lattice^7,8,15, but with important deviations, including a slight momentum broadening and reduction of intensity around the pinch points. For E = 8 meV the magnetic scattering extends through more of momentum space with subtle modulations in intensity, particularly near (−2, −2, 0) in the $(h,h,\ell )$ zone, where a double-ridge structure resembles highly damped dispersing spin waves in a one-dimensional magnet. Sharper features around (−2, −2, 2) and at high q arise from phonon scattering. Finally, at E = 11 meV magnetic scattering is uniformly distributed through momentum space, except for exclusion zones centred around the Γ point, where scattering is precluded for a Heisenberg model³⁰.

Fig. 2 |. Inelastic neutron scattering showing dynamic magnetic correlations in NaCaNi₂F₇.

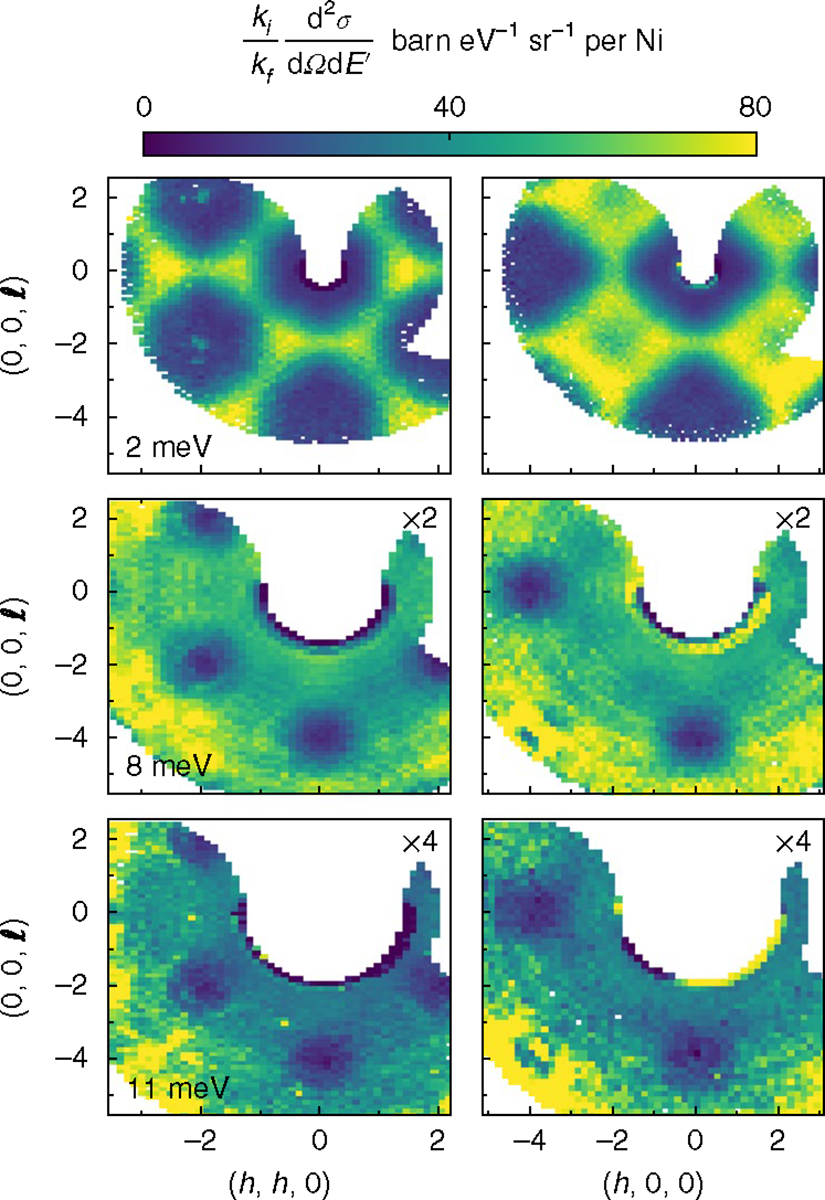
Momentum and energy dependence of inelastic magnetic scattering in NaCaNi₂F₇ for the $(h,h,\ell )$ and $(h,k,0)$ scattering planes at $=1.8\mathrm{K}$. Each slice was integrated over an energy transfer range of ± 0.25 meV. No smoothing or symmetrization was applied to the data. Above energy transfers of 0.5 meV, the dynamic magnetic correlations form a ‘bow-tie’ pattern in momentum space. The sharp pinch-point-like features around (2, 0, 0) and (2, 2, 0) positions indicate that the net magnetization per tetrahedron vanishes in the Coulomb-like phase realized in NaCaNi₂F₇. Above energies of 5 meV, the scattering forms a broad continuum with no intensity around the $\mathrm{\Gamma }$ points.

In Fig. 3 we present the momentum- and energy-resolved spin-flip neutron scattering cross-section. For our experiment this cross-section is sensitive only to magnetic scattering and nuclear incoherent scattering; thus data in Fig. 3 are representative of the dynamic structure factor uncontaminated by coherent non-magnetic scattering. The magnetic excitations form a continuum that extends over an energy bandwidth of ~12.5 meV ~4J S₁. Along the (h, h, 2) direction and pinch point ridge, the inelastic neutron intensity is relatively featureless. However, along the (2, 2, ℓ) direction, which traverses the pinch point ridge, the magnetic scattering is more structured, becoming doubly peaked above 5 meV. This precludes factorization of the dynamic structure factor: $𝒮(\mathbf{q},E)\ne 𝒮\left(\mathbf{q}\right)f\left(E\right)$, which distinguishes NaCaNi₂F₇ from the classical limit of the Heisenberg model on the pyrochlore lattice³¹. In the constant-momentum and constant-energy transfer cuts plotted in Fig. 3b,c very broad dispersive ridges are observed. Whereas the spectrum is gapless down to the 0.17 meV scale set by our finest energy resolution measurements, the dynamic structure factor is peaked at finite energy transfers and can be fitted with the spectral form of an over-damped harmonic oscillator. The characteristic energy scale disperses from $E_q=4.8\mathrm{m}\mathrm{e}\mathrm{V}~J_1$ at the pinch point $\mathbf{q}=(2,2,0)$, to $E_q=7.8\mathrm{m}\mathrm{e}\mathrm{V}$ at the nodal point $\mathbf{q}=(2,2,1)$. This spectrum distinguishes NaCaNi₂F₇ from recent theoretical treatments of the semiclassical Heisenberg model, which find a purely diffusive response that is peaked at zero energy¹³. The absence of inelastic scattering at the $\mathrm{\Gamma }$ point and our polarized neutron measurements rule out any sizeable single-ion anisotropies that could explain the peak in spectral weight at non-zero energy transfers. The only energy scale large enough to account for the resonance is the nearest-neighbour antiferromagnetic exchange interaction $J_1$.

Fig. 3 |. Momentum- and energy-resolved inelastic neutron scattering probing magnetic excitations in NaCaNi₂F₇.

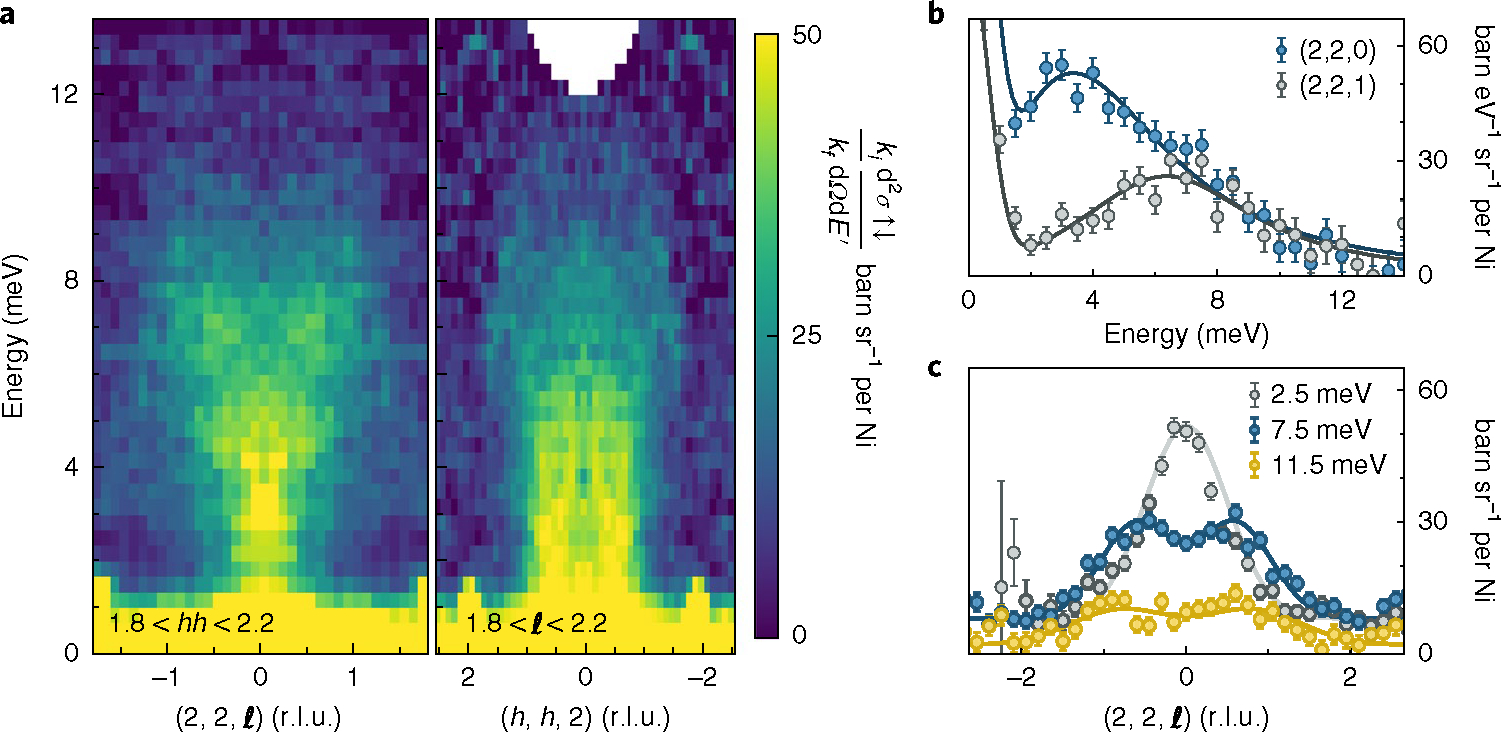
a, Energy-momentum slices through the spin-flip portion of the polarized neutron scattering cross-section at $=1.8\mathrm{K}$. The data were symmetrized by folding about the line along $(0,0,\ell )$ for the $(2,2,\ell )$-energy slice and the line along $(h,h,0)$ for the $(h,h,2)$-energy slice. No smoothing or interpolation was applied to the data. b, Constant-momentum cuts of the spin-flip cross-section through a pinch point at $\mathbf{q}=(2,2,0)$ and nodal point at (2, 2, 1) integrated over $\ell \pm 0.2$. Solid lines are a fit to the sum of a Lorentzian function centred on the elastic line and a damped oscillator form $S(E)=\frac{(n+1)2\Gamma E}{{\left(E^2-E_q^2\right)}^2+(2\Gamma E{)}^2}$, where $n$ is the thermal population factor, $\mathrm{\Gamma }$ a relaxation rate and $E_q$ the characteristic energy scale. c, Constant-energy transfer cuts, integrated over $E\pm 0.25\mathrm{m}\mathrm{e}\mathrm{V}$, showing the energy evolution of momentum-dependent scattering, which becomes doubly peaked above 5 meV. Error bars represent one standard deviation.

A conservative interpretation is that the dispersing modes are overdamped spin waves of an underlying classical magnetic order, disrupted in NaCaNi₂F₇ by exchange disorder. Since the frozen spin configurations feature non-collinear interacting spins, single-particle S = 1 magnon excitations can decay from interactions with multimagnon states to form a continuum of scattering³². Such a scenario may be appropriate for the related pyrochlore XY antiferromagnet NaCaCo₂F₇²⁵. Elastic magnetic neutron scattering from NaCaCo₂F₇ resembles that of an ordered antiferromagnet, consistent with the non-collinear magnetic structure favoured by an order-by-disorder mechanism³³. This order develops at a temperature coincident with a broad peak in the magnetic specific heat, which constitutes the total magnetic entropy of the J = 1/2 magnetic moments formed by Co ions. The fraction of elastic magnetic neutron intensity for NaCaCo₂F₇ is 0.3(1)³³, almost exactly as expected for an ordered S = 1/2 magnet (S²/S(S + 1) = 1/3). Thus, it appears that in NaCaCo₂F₇, exchange disorder truncates the magnetic correlations of the classical antiferromagnetic order favoured by the underlying Hamiltonian.

In contrast, for NaCaNi₂F₇, by comparing the spectral weight for elastic (E < 0.7 meV) and inelastic scattering (0.7 < E < 14 meV) we find ~90% of the magnetic scattering is inelastic in the low-T limit. This greatly exceeds the 50% mark for a semi-classical ground state based on $S=1$ Ni ions, and is direct evidence of a spin system dominated by quantum fluctuations. Integrating the data for the dynamic spin correlation function $𝒮(\mathbf{q},E)$ over momentum and energy, including the elastic diffuse magnetic scattering, we recover the total spectral weight of 3 $\int S(\mathbf{q},E)\mathrm{d}E{\mathrm{d}}^{3}q=13\left(1\right)$, which is consistent with the ${\left(3.7{\mu }_{\mathrm{B}}\right)}^2=13.7{\mu }_{\mathrm{B}}^2$ effective moment extracted from the high- $T$ magnetic susceptibility data²⁶.

The magnetic specific heat $C_{\mathrm{m}}\left(T\right)$ (Fig. 4a) provides an excellent overview of three distinct regimes of magnetism in NaCaNi₂F₇. For $>18\mathrm{K},C_{\mathrm{m}}\left(T\right)$ follows the form expected for the classical spin liquid (Villain’s cooperative paramagnet) phase of the Heisenberg antiferromagnet on a pyrochlore lattice. The dashed line in Fig. 4a shows that a classical Monte Carlo simulation of the Heisenberg model with the exchange parameters extracted from neutron scattering provides an excellent account of the data.

Fig. 4 |. Specific heat and elastic neutron scattering revealing spin freezing in NaCaNi₂F₇.

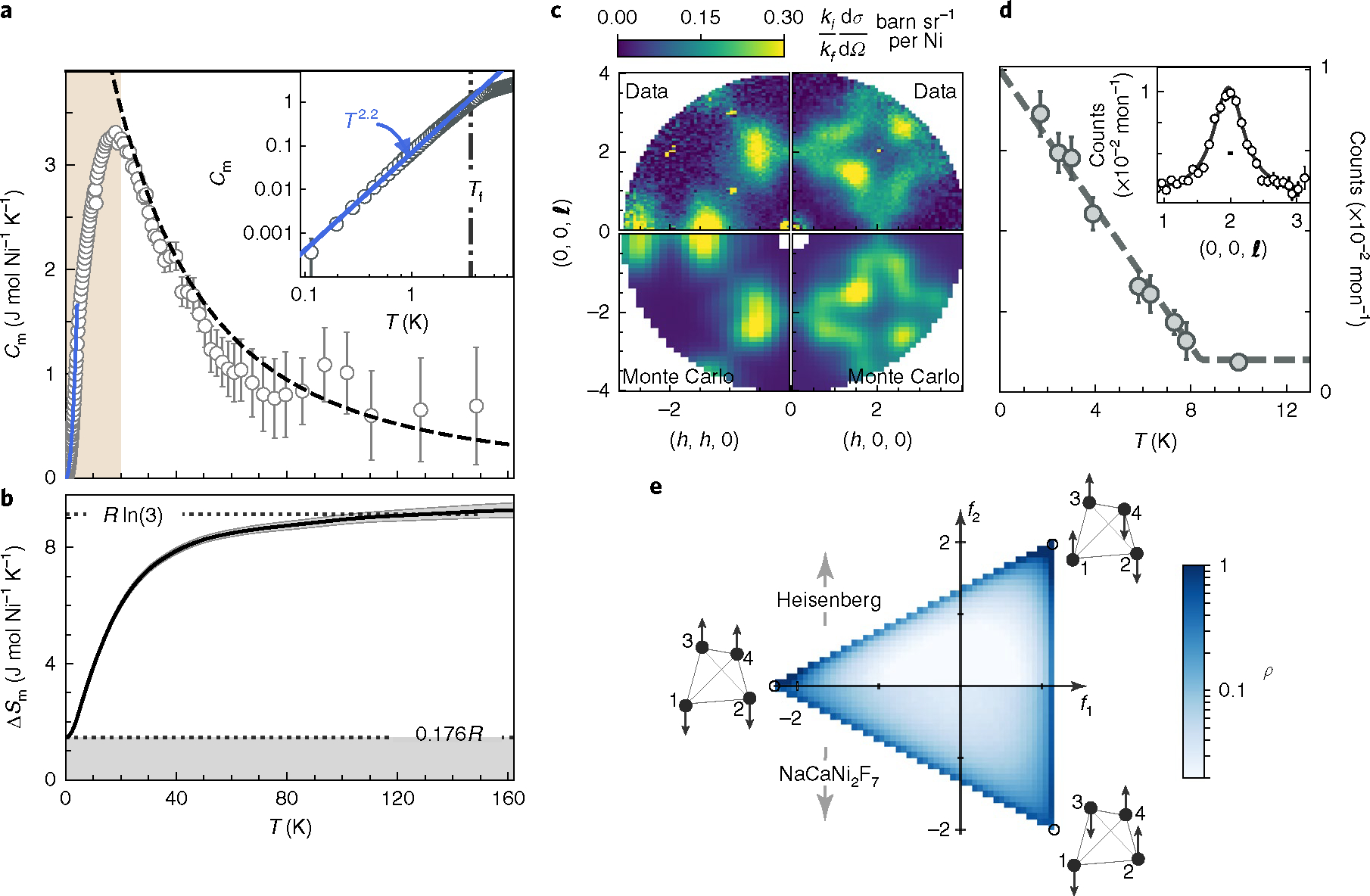
a, Magnetic specific heat. Dashed line is a classical Monte Carlo simulation and solid line is a fit to $C_{\mathrm{m}}\left(T\right)=A{T}^{\alpha }$, with $A=0.07\left(1\right)$ and $\alpha =2.2\left(1\right)$. Light shading indicates the classical to quantum crossover regime. Inset shows the low-temperature region. b, Magnetic entropy obtained by integration of $C/T$ between $T=150\mathrm{K}$ and 100 mK, corresponding to 84% of $R\mathrm{l}\mathrm{n}\left(3\right)$. c, Diffuse elastic ( $E=0$ ) magnetic scattering, integrated over the resolution window of ±0.37 meV and obtained by subtracting $T=40\mathrm{K}$ data from that at 1.8 K. Lower quadrants display disorder and configuration-averaged ground state Monte Carlo structure factors. d, Temperature-dependent intensity of the diffuse elastic scattering around $\mathbf{q}=(0,0,2)$, dashed line is ${\left(1-T/T_{\mathrm{f}}\right)}^{2\beta }$, with $T_{\mathrm{f}}=8.2\mathrm{K}$ and $\beta =0.5$. Inset shows the $T=1.8\mathrm{K}$ line shape across the pinch point, integrated over $-0.1<(h,h,0)<0.1$, the horizontal dash denotes the instrumental resolution. Error bars represent one standard deviation. e, Histogram of bond vector order parameter components $\left(f_1,f_2\right)$ from classical Monte Carlo simulations for the Heisenberg and exchange models relevant to NaCaNi₂F₇ including exchange disorder. Extremal spin configurations corresponding to collinear spin arrangements are shown.

In the second regime, where $T~J_1$, as indicated by light shading in Fig. 4a, $C_{\mathrm{m}}\left(T\right)$ falls below the classical model. The corresponding broad maximum at 18 K thus marks the crossover from classical to quantum spin liquid. Finally, for $<T_{\mathrm{f}}=3.6\mathrm{K}$, a discontinuity in ${\mathrm{d}}_{\mathrm{m}}\left(T\right)/\mathrm{d}T$ (inset of Fig. 4a) indicates spin freezing²⁶. A fit to $C_{\mathrm{m}}\left(T\right)\propto T^{\alpha }$ for $T<T_{\mathrm{f}}$ yields $\alpha =2.2\left(1\right)$. $C_{\mathrm{m}}\propto T^2$ has been found for $T<T_{\mathrm{f}}$ in a number of frustrated magnets with spin-disordered ground states^24,34,35. This form can arise from linearly dispersing bosonic quasi-particles in two dimensions. Although this might seem out of place for cubic NaCaNi₂F₇, frustration can produce soft ‘nodal’ lines which effectively reduce dimensionality to two³⁶. The lack of translational symmetry in NaCaNi₂F₇ implies the corresponding quasi-particles cannot manifest as coherent modes in neutron scattering, yet $C_{\mathrm{m}}\left(T\right)$ reflects their density of states^37,38.

In Fig. 4b we show the magnetic entropy recovered between 100 mK and 150 K that saturates at 84% of the available $R\mathrm{l}\mathrm{n}\left(3\right)$ for $S=1$. We interpret the $0.176R$ per spin residual entropy at 100 mK as indicating broken ergodicity for $T<T_{\mathrm{f}}$. Specifically, we propose that below $T_{\mathfrak{f}}$ a metastable spin configuration within the Coulomb phase manifold is kinetically arrested by the disorder potential so the material no longer explores all states of a given energy. Correspondingly, we expect spin correlations for $E<k_{\mathrm{B}}{T}_{\mathrm{f}}$ to reflect a disorder-dominated regime. Figure 4d shows the onset of elastic neutron scattering for $<8\mathrm{K}$. In a continuation of the trend in a.c.-susceptibility data²⁶, the apparent freezing temperature increases with the measurement frequency, which here is the energy resolution of $\mathrm{\Delta }E=0.37\mathrm{m}\mathrm{e}\mathrm{V}$. The momentum width of the elastic signal is independent of $T$, indicating the sample averaged spatial correlations are unaffected by the freezing transition. Figure 4c shows the elastic magnetic neutron scattering in two high-symmetry reciprocal lattice planes of the cubic lattice. The signal is dominated by extended diffuse intensity arising from short-range correlated spin configurations that are static within the 10 ps time window of our measurement. Neutron intensity is concentrated in lobes centred near $\mathbf{q}=(2n\pm 0.6,2n\pm 0.6,0)$ positions, where $n$ is an integer. Near (002) and (220), where sharp pinch point features representing long-range dipolar correlations of the pure Heisenberg model are expected, the momentum distribution of the scattering is broader than the experimental resolution. The inverse momentum width corresponds to a real-space correlation length of $\xi =6\text{Å}$, or just two nearest-neighbour lattice spacings.

By averaging the elastic $(E=0)$ intensity over the accessible parts of the Brillouin zone we find the frozen moment accounts for only $|⟨\mathbf{S}⟩|/S=44\mathrm{\%}$ of the saturation magnetization for Ni²⁺. The small fraction of frozen magnetization is similar to that of the spin- 3/2 kagome lattice KCr₃(OD)₆(SO₄)₂ (ref. ³⁹). To gain insight into the nature of this unconventional frozen low-temperature state, we have carried out classical Monte Carlo simulations of the Heisenberg Hamiltonian relevant to NaCaNi₂F₇. Random bond disorder was included by sampling from a box distribution, with a half-width of $\delta J=0.19\mathrm{m}\mathrm{e}\mathrm{V}$ and exchange parameters extracted from an independent analysis of inelastic neutron scattering data. In Fig. 4c we compare the measured elastic scattering with the corresponding numerically modelled signal. The overall qualitative agreement gives confidence in our optimized magnetic Hamiltonian and numerical simulations.

A number of theoretical investigations^2,15,40–42 have shown that small perturbations in the classical Heisenberg model, J′, in the form of exchange anisotropies or further-neighbour interactions, result in a magnetically ordered phase below temperatures of the order of J′ S². In NaCaNi₂F₇ these perturbations are significantly smaller than the freezing temperature. Correspondingly, our Monte Carlo simulations for the anisotropic Hamiltonian relevant to NaCaNi₂F₇, but without exchange disorder, find no classical magnetic order above T = 500 mK. So even if the disorder free spin-Hamiltonian for NaCaNi₂F₇ ultimately has long-range magnetic order, it is preempted by exchange-disorder-induced spin freezing.

The spin configurations generated through Monte Carlo simulation offer a unique real-space view of frozen magnetism in NaCaNi₂F₇. In the absence of disorder, the energy of the classical Heisenberg Hamiltonian is minimized by all states with zero total spin per tetrahedra, ${\mathbf{S}}_{\text{tot}}={\sum }_{i=1}^4{\mathbf{S}}_i=0$. We find the lowest energy states for the bond-disordered Heisenberg Hamiltonian with small anisotropic exchanges relevant to NaCaNi₂F₇ also fall approximately within the ${\mathbf{S}}_{\text{tot}}=0$ manifold (see Supplementary Information). This manifold is parameterized by the order parameters $f_1=\left[\left({\mathbf{S}}_1+{\mathbf{S}}_2\right)\cdot \left({\mathbf{S}}_3+{\mathbf{S}}_4\right)-2{\mathbf{S}}_1\cdot {\mathbf{S}}_2-2{\mathbf{S}}_3\cdot {\mathbf{S}}_4\right]/\sqrt{12}$ and $f_2=\left({\mathbf{S}}_1\cdot \right.\left.{\mathbf{S}}_3+{\mathbf{S}}_2\cdot {\mathbf{S}}_4-{\mathbf{S}}_2\cdot {\mathbf{S}}_3-{\mathbf{S}}_1\cdot {\mathbf{S}}_4\right)/2$ refs ^14,42). The statistical distribution of $f_1$ and $f_2$ over a Monte Carlo ensemble of tetrahedra provides a local characterization of the particular frozen ${\mathit{S}}_{\text{tot}}=0$ spin configuration. Such histograms of $\left(f_1,f_2\right)$ extracted from our Monte Carlo simulations are shown in Fig. 4e, where possible values span an equilateral triangle in the $\left(f_1,f_2\right)$ plane. Tetrahedra with pairs of antiparallel spins lie along the triangular edges and collinear spin configurations are at the vertices. The classical Heisenberg (only) model with weak bond disorder is glassy²¹, with a tendency to form locally collinear states; this is confirmed by the results in the top half of Fig. 4e (ref. ²⁰) The enhanced density along the boundaries, and away from the corners, of the lower part of the triangle in Fig. 4e indicates a tendency to form configurations of pairwise collinear spins when the small anisotropic interactions specific to NaCaNi₂F₇ are added.

Let us now discuss the fundamental challenges presented by our results on NaCaNi₂F₇. We have shown this three-dimensional spin-1 system forms a nearly spin-space-isotropic Coulomb-like phase, with vanishing net spin on each of the corner-sharing tetrahedra and a broad gapless continuum of spin-flip excitations. Because we are dealing with a crystalline solid at low temperatures, this implies the absence of propagating magnons and a spin system that either has no quasi-particles or where the quasi-particles are inaccessible to neutron scattering.

Whereas conventional spin wave theory is built upon a spin-ordered ground state, NaCaNi₂F₇ has a low-energy manifold distinguished by local constraints that do not impose a unique ordered state. There is weak exchange disorder and a non-ergodic aperiodic frozen component, but these features cannot have major impacts at high energies because of the discrepancy in energy scales $(\delta J/J\approx 6\mathrm{\%})$. More detrimental to a spin wave picture are the local soft modes that characterize corner-sharing simplexes such as the kagome, and here the pyrochlore lattice. These present scattering centres for putative magnons, which correspondingly become overdamped and lose their quasi-particle status. The broad dispersing ridges that we do observe in the $\mathbf{q}-E$ dependence of the magnetic neutron scattering cross-section (Fig. 3) might loosely be associated with such incoherent magnons.

The efficacy of a semi-classical spin wave expansion to describe quantum spin systems with incoherent magnons is, however, questionable. Specifically, quantum tunnelling may be important in describing local soft modes for $S=1$, and this could impact both the spectrum of excitations and the nature of the ground state. Considering, furthermore, that 90% of the magnetic spectral weight for NaCaNi₂F₇ lies in the inelastic channel, a description of its magnetism in terms of a quantum spin liquid may be more appropriate. For energies above $k_{\mathrm{B}}{T}_{\mathrm{f}}$, the continuous spectrum is consistent with the fractionalization of a spin-flip excitation into weakly interacting multiparticle excitations. The non-ergodic regime for energies below $k_{\mathrm{B}}{T}_{\mathrm{f}}$ might be associated with the pinning of these fractionalized excitations by exchange disorder. A quantitative measure of the frozen subspace is provided by the fraction of the total entropy that is residual $(\mathrm{\Delta }S/R\mathrm{l}\mathrm{n}(3)=16(4\left)\mathrm{\%}\right)$ which is within error bars of the fraction of the total spectral weight contained in elastic scattering $({⟨m_{\text{elastic}}⟩}^2/\left(g^{2}S(S+1)\right)=10(2)\mathrm{\%})$.

Our experiments on NaCaNi₂F₇ show frustration and weak disorder can completely suppress conventional spin order in three dimensions, leaving behind strong spin-1 quantum fluctuations at low temperatures. The quantitative spin Hamiltonian that we have developed, and the distinct collective properties that we have documented, establish NaCaNi₂F₇ as an ideal model system for what would appear to be a new state of matter.

Methods

The identification of any commercial product or trade name does not imply endorsement or recommendation by the National Institute of Standards and Technology.

Specific heat.

Heat capacity measurements were conducted using a Quantum Design PPMS with a dilution insert for temperatures between 100 mK and 4 K, and standard insert for temperatures between 2 K and 270 K. All measurements were carried out on the same 5 mg single crystal using the adiabatic pulse method. The non-magnetic contribution over the full measured temperature range was determined by scaling the measured specific heat of the iso-structural compound NaCaZn₂F₇ by the relative Debye temperatures.

Neutron scattering.

All neutron scattering measurements were performed on the same 3 g single crystal, grown as described elsewhere²⁶. Unpolarized neutron scattering measurements were performed on the MACS spectrometer⁴⁴ at the NIST Center for Neutron Research. Neutron momentum transfer is indexed in the cubic lattice with $a^{\mathrm{*}}=2\mathrm{\pi }/a=0.61{\text{Å}}^{-1}$. Measurements were performed with the sample oriented in both the $(h,h,\ell )$ and $(h,k,0)$ scattering planes. For elastic $(E=0)$ measurements the monochromator was configured in a vertical focusing configuration for a neutron energy of 5 meV. Two configurations were used for inelastic measurements, both with the monochromator in double-focusing mode. For energy transfers below 1.4 meV, MACS was operated with a fixed final energy of 3.7 meV and with Be and BeO filters before and after the sample, respectively. For energy transfers above 1.4 meV we used a fixed final energy of 5 meV with a Be filter after the sample and no incident beam filter. Data for energy transfers above 1.4 meV were corrected for the effects of contamination from high-order harmonics in the incident beam neutron monitor.

Polarized neutron scattering measurements were carried out on the HYSPEC spectrometer⁴⁵ at the Spallation Neutron Source at Oak Ridge National Lab. An incident neutron energy of 17 meV was selected using a Fermi chopper rotating at 240 Hz, resulting in an energy resolution of δE = 1.4 meV for the elastic line. The incident neutron beam polarization was defined using a vertically focusing Heusler monochromator, while the outgoing beam polarization was selected using a radially collimating supermirror array. All polarized measurements were performed with the guide field applied perpendicular to the (h, h, l) scattering plane, along the (1, −1,0) direction. In this configuration, SF scattering measures the component of magnetic cross-section that is polarized within the scattering plane and perpendicular to q, whereas NSF measures the out-of-plane component, here along the (1, −1,0) direction. The flipping ratio measured on a (4, 4, 0) nuclear Bragg peak was 16. All data reduction and analysis was carried out using the Mantid software suite⁴⁶.

Quantitative measurement of the energy- and momentum-resolved magnetic neutron cross-section in NaCaNi₂F₇ was essential for a detailed comparison of neutron scattering and specific heat data. To accurately distinguish magnetic scattering intensity, both unpolarized and polarized measurements were performed. Measured neutron count rates from both instruments were converted into absolute units of the neutron scattering cross-section using incoherent elastic scattering from the sample as a reference scattering cross-section. The scale factor for conversion to absolute units was additionally cross-checked against measurements from a vanadium standard.

Numerical methods.

We fit the static structure factor from the neutron scattering data to the corresponding prediction of the self-consistent Gaussian approximation (SCGA) at 1.8 K, to obtain the magnetic interaction parameters in the main text. Details of the method, including the cost function and error analysis, are discussed in the Supplementary Information. The results of the SCGA are complemented by classical Monte Carlo calculations, from which we extract both the specific heat and the magnetic structure factor. Monte Carlo simulations used single spin updates for continuous spin on pyrochlore lattices (with 16-site cubic unit cells) of size $N=16L^3$ for $L=3$ to $L=10$. To determine the classical ground state of the fitted spin Hamiltonian, parallel tempering Monte Carlo⁴⁷ was carried out with $T_{\mathrm{m}\mathrm{i}\mathrm{n}}=0.01\mathrm{K}$ and $T_{\mathrm{m}\mathrm{a}\mathrm{x}}=1\mathrm{K}$ with the number of replicas $N_r=\sqrt{N}\mathrm{l}\mathrm{n}\left(T_{\mathrm{m}\mathrm{a}\mathrm{x}}/T_{\mathrm{m}\mathrm{i}\mathrm{n}}\right)$ (approximately 100 for $L=3$ and 400 for $L=8$, the two sizes studied extensively, see Supplementary Information for more analyses) and the simulation carried out for a total of 10⁸ steps. With the lowest-energy configurations encountered in this finite Monte Carlo run, further iterative minimization was performed to accelerate the approach to the classical ground state. For these optimized spin configurations (many of which are local minima), two-component local order parameters ($f_1$ and $f_2$) are calculated on all $N/4$ tetrahedra of a fixed orientation (‘up’). This was repeated for 50–100 bond-disorder realizations and the combined data set, including all tetrahedra and disorder realizations, was used to obtain the two-dimensional histogram in Fig. 4. The static structure factor from these low-energy, zero-temperature configurations, for $L=8$, was averaged to obtain an estimate of the elastic neutron cross-section. Further details of all methods and algorithms employed are provided in the Supplementary Information.

Data availability

The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.