Statistics notes Variables and parameters

Like all specialist areas, statistics has developed its own language. As we have noted before,¹ much confusion may arise when a word in common use is also given a technical meaning. Statistics abounds in such terms, including normal, random, variance, significant, etc. Two commonly confused terms are variable and parameter; here we explain and contrast them.

Information recorded about a sample of individuals (often patients) comprises measurements such as blood pressure, age, or weight and attributes such as blood group, stage of disease, and diabetes. Values of these will vary among the subjects; in this context blood pressure, weight, blood group and so on are variables. Variables are quantities which vary from individual to individual.

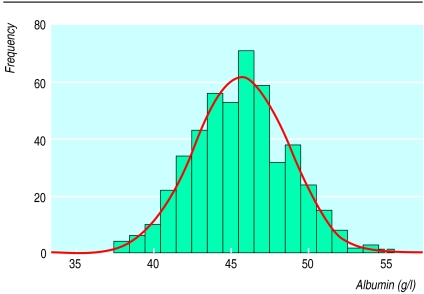
By contrast, parameters do not relate to actual measurements or attributes but to quantities defining a theoretical model. The figure shows the distribution of measurements of serum albumin in 481 white men aged over 20 with mean 46.14 and standard deviation 3.08 g/l. For the empirical data the mean and SD are called sample estimates. They are properties of the collection of individuals. Also shown is the normal¹ distribution which fits the data most closely. It too has mean 46.14 and SD 3.08 g/l. For the theoretical distribution the mean and SD are called parameters. There is not one normal distribution but many, called a family of distributions. Each member of the family is defined by its mean and SD, the parameters¹ which specify the particular theoretical normal distribution with which we are dealing. In this case, they give the best estimate of the population distribution of serum albumin if we can assume that in the population serum albumin has a normal distribution.

Most statistical methods, such as t tests, are called parametric because they estimate parameters of some underlying theoretical distribution. Non-parametric methods, such as the Mann-Whitney U test and the log rank test for survival data, do not assume any particular family for the distribution of the data and so do not estimate any parameters for such a distribution.

Another use of the word parameter relates to its original mathematical meaning as the value(s) defining one of a family of curves. If we fit a regression model, such as that describing the relation between lung function and height, the slope and intercept of this line (more generally known as regression coefficients) are the parameters defining the model. They have no meaning for individuals, although they can be used to predict an individual’s lung function from their height.

In some contexts parameters are values that can be altered to see what happens to the performance of some system. For example, the performance of a screening programme (such as positive predictive value or cost effectiveness) will depend on aspects such as the sensitivity and specificity of the screening test. If we look to see how the performance would change if, say, sensitivity and specificity were improved, then we are treating these as parameters rather than using the values observed in a real set of data.

Parameter is a technical term which has only recently found its way into general use, unfortunately without keeping its correct meaning. It is common in medical journals to find variables incorrectly called parameters (but not in the BMJ we hope²). Another common misuse of parameter is as a limit or boundary, as in “within certain parameters.” This misuse seems to have arisen from confusion between parameter and perimeter.

Misuse of medical terms is rightly deprecated. Like other language errors it leads to confusion and the loss of valuable distinction. Misuse of non-medical terms should be viewed likewise.

Figure.

Measurements of serum albumin in 481 white men aged over 20 (data from Dr W G Miller)