Significance
While nuclear fusion and quantum computing are high-profile research areas, very few concrete intersections have been identified. We draw a connection through a class of quantum dynamics simulations relevant to inertial confinement fusion microphysics modeling that enjoy a computational advantage using a quantum computer. To go beyond arguing a quantum simulation advantage based on asymptotic scaling, we describe the complete quantum algorithm necessary to compute a material’s stopping power, quantify the constant factors associated with this computation, and describe resources needed for systems relevant to current inertial confinement fusion experiments. These calculations highlight the prospective applicability of large fault-tolerant quantum computers to a high-value simulation target with classical computing investments in the hundreds of millions of CPU hours annually.
Keywords: quantum computing, fusion, algorithms, stopping-power, fault-tolerance
Abstract
Stopping power is the rate at which a material absorbs the kinetic energy of a charged particle passing through it—one of many properties needed over a wide range of thermodynamic conditions in modeling inertial fusion implosions. First-principles stopping calculations are classically challenging because they involve the dynamics of large electronic systems far from equilibrium, with accuracies that are particularly difficult to constrain and assess in the warm-dense conditions preceding ignition. Here, we describe a protocol for using a fault-tolerant quantum computer to calculate stopping power from a first-quantized representation of the electrons and projectile. Our approach builds upon the electronic structure block encodings of Su et al. [PRX Quant. 2, 040332 (2021)], adapting and optimizing those algorithms to estimate observables of interest from the non-Born–Oppenheimer dynamics of multiple particle species at finite temperature. We also work out the constant factors associated with an implementation of a high-order Trotter approach to simulating a grid representation of these systems. Ultimately, we report logical qubit requirements and leading-order Toffoli costs for computing the stopping power of various projectile/target combinations relevant to interpreting and designing inertial fusion experiments. We estimate that scientifically interesting and classically intractable stopping power calculations can be quantum simulated with roughly the same number of logical qubits and about one hundred times more Toffoli gates than is required for state-of-the-art quantum simulations of industrially relevant molecules such as FeMoco or P450.
As investment in quantum computing grows, so too does the need to assess potential computational advantages for specific scientific challenge problems. As such, going beyond asymptotic analysis to understand constant factor resource requirements clarifies the degree of such advantages, whether these advantages would be useful for problems of commercial or scientific value, the broader quantum/classical simulation frontier, and opportunities for further optimizations. Over the last decade, the problem of sampling from the eigenspectrum of the electronic structure Hamiltonian in the Born–Oppenheimer approximation has been a proving ground for constant factor analyses that quantify the magnitude of quantum speedups (1–4). But ground states can benefit from properties like area-law entanglement that might make many instances relevant to chemical and materials science efficient to accurately simulate in some contexts — even with classical algorithms (5). This leads us to search for scientific challenge problems beyond ground states, for which classical algorithms might have less structure to exploit and quantum algorithms are naturally poised to excel. Simulating quantum dynamics is arguably the most natural application for quantum computers. Just as in the case of sampling from the eigenbasis of the electronic structure Hamiltonian, here we quantify the constant factor resource estimates of dynamics calculations in order to frame the performance of current quantum algorithms with respect to classical strategies. We focus on the problem of computing the stopping power of materials in the warm dense matter (WDM) regime, for which both experimental measurements and benchmark-quality theoretical calculations are expensive and sparse. Even for mean-field levels of accuracy, high-performance-computing campaigns requiring at least hundreds of millions of CPU hours are invested annually in first-principles stopping power calculations in WDM.*
Stopping power is the average force exerted by a medium (target) on an incident charged particle (projectile) (6, 7). This force depends on the material composition and conditions of the target and the charge and velocity of the projectile. Generically, stopping power is decomposed into nuclear, electronic, and radiative contributions, but for the conditions considered in this manuscript the total stopping power will be dominated by the electronic contribution and we will implicitly identify stopping power with electronic stopping power.† Stopping powers are crucial in contexts including radiation damage in space environments (8), materials degradation in nuclear reactors (9), certain cancer therapies (10–12), electron- (13) and ion-beam (14, 15) microscopies, and the fabrication and characterization of qubits based on color centers (16) or nuclear spins (17, 18). Understanding the impact of stopping power on these applications is facilitated by the relative ease of conducting experiments, and decades of effort have produced tables of experimentally measured stopping powers for targets in ambient conditions (19–21). Such measurements require colocating uniform samples of the target with a well-characterized, narrow bandwidth source of high-energy projectiles and a spectrometer with sufficient resolution to discern small relative energy losses. This experimental setup is comparatively straightforward for a stable target, but it becomes incredibly challenging for a target at extreme pressure or temperature.
WDM (22, 23) is one such extreme regime, typified by strong Coulomb coupling and the simultaneous influence of thermal and degeneracy effects. It arises in contexts ranging from astrophysical objects (24–26) and planetary interiors (27–29) to inertial confinement fusion (ICF) targets on the way to ignition (30–33). Creating WDM conditions requires access to specialized experimental facilities (34–38) that produce short-lived and nonuniform samples with low repetition rates relative to experiments at ambient conditions. These challenges are compounded by the difficulty of simultaneously characterizing the target’s thermodynamic conditions and the projectile’s energy loss, as well as systematic errors attendant to measuring aggregate energy losses in lieu of energy loss rates. Despite outstanding recent advances in measurements of stopping power in WDM (39–41), theoretical calculations will likely remain disproportionately impactful due to the great cost of obtaining comprehensive datasets purely through experiment. Each campaign typically probes stopping powers over a narrow range of velocities for a narrow range of thermodynamic conditions that might themselves be difficult to constrain or subject to large systematic uncertainties and inhomogeneities.
The importance of stopping power in WDM, in particular, is highlighted by its significance to ICF (42). The transport of the high-energy alpha particles that are created in fusion reactions forms an important contribution to the self-heating processes that govern ignition (43–45). WDM conditions are necessarily traversed in ICF implosions – in fact, depending on the target and driver, large fractions of the target can spend most of their time in this regime. This intermediate state also plays a central role in the fuel/ablator mixing that leads to hydrodynamic instabilities limiting performance (46–48). Fast-ignition fusion concepts also rely on charged particle stopping within their separate ion or electron beam heating mechanism (49–51). Thus accurate stopping powers are one among many important elements of the microphysics modeling that informs ICF target design and experimental interpretation. However, due to the great cost of experimentally constraining stopping models in the warm dense regime, the stopping models that are used in the ICF community are often instead validated against other models with varying degrees of accuracy and efficiency.
Broadly, the stopping power models that are applied in the WDM regime fall into four categories: 1) highly detailed multiatom first-principles models (52–56), 2) highly efficient average-atom models (40, 56, 57), 3) models based on variants of the uniform electron gas (58–63), and 4) classical or semiclassical models (64–68). Type-(2), (3), and (4) models can be efficient enough to tabulate results across the wide range of thermodynamic conditions required by radiation-hydrodynamic codes that support ICF development, or even evaluated inline (69). Certain type-(3) models are used to generate high-quality reference data and as a proving ground for method development, but their lack of explicit electron-ion interaction limits their ability to capture some important phenomenology in WDM. Therefore, type-(1) models are most often used to benchmark and calibrate more approximate type-(2) and (4) models (56, 70). Given that there are precious few experiments to validate models in the WDM regime, type-(1) models are particularly valuable for quantifying the influence of details that more approximate models lack. However, type-(1) models incur large computational costs that are aggravated by the large basis sets and supercells that are required to achieve highly converged results (71).
Thus, the state-of-the-art in algorithms for type-(1) models are mean-field methods based on time-dependent density functional theory (TDDFT) (72), including Kohn–Sham (52) and orbital-free formulations (54). These methods directly evolve the electronic and nuclear dynamics on the same timescale, going beyond the Born–Oppenheimer (BO) approximation but still typically relying on a classical description of the nuclei. Even treating the electronic dynamics at a mean-field level, the computing campaigns that use type-(1) models to generate benchmark data for other stopping power models in the WDM regime can require hundreds of millions of CPU hours on some of the world’s largest supercomputers. Opportunities to constrain the accuracy of these models are limited by not only the scarcity of experimental data, but also by the notorious difficulty of developing systematically improvable approximations, particularly for the real-time electron dynamics far from equilibrium that are the central focus of type-(1) stopping power calculations.
However, quantum simulation algorithms executed on fault-tolerant quantum computers provide one potential pathway to realizing systematically improvable stopping power calculations, both in the WDM regime and in general. In this work, we propose a protocol for implementing such a calculation and analyze its resource requirements to establish a baseline estimate for the cost of outperforming classical computers in accuracy. Recently, a number of other works have examined the quantum resource requirements for simulating materials represented in first or second quantization (3, 73–77). While it is now possible to efficiently block encode periodic systems in second quantization (3, 77) and discretizations based on localized orbitals are sometimes used in modeling stopping power (78–80), they are especially poorly suited to WDM because of the unusual atomic configurations typical to extremes of pressure and temperature. Plane-wave representations that are used in first-quantized simulations of materials (75, 76) provide an efficient representation in which the number of qubits scales logarithmically with the total number of plane waves, and nuclei can be treated on the same footing as electronic degrees of freedom. Furthermore, plane-wave calculations can be more directly compared to state-of-the-art classical stopping power calculations based on plane-wave TDDFT. Thus, to assess and quantify the prospect of realizing quantum advantages in these simulations, we provide constant factor resource estimates of stopping power calculations in first quantization where the projectile is treated quantum mechanically.
There are a variety of ways to compute stopping power in the first-quantized plane-wave representation. We focus on sampling the projectile kinetic energy as a function of distance traveled and argue that within the desired accuracy range that naive Monte Carlo sampling at a number of points along the projectile trajectory is more efficient than alternative mean-estimation algorithms that enjoy Heisenberg scaling (81). After fully accounting for sampling costs, two types of time-evolution protocols, and observable accuracy requirements, we report that full ab-initio modeling of stopping power for an alpha-particle projectile in deuterium would require to Toffoli gates, depending on the time-evolution algorithm used, and logical qubits at system sizes that are converged to the thermodynamic limit. Relaxing the convergence restriction would lower these costs quadratically in the particle number and potentially serve as a WDM benchmark system. While there have been a number of works that quantify quantum resource estimates for ground state preparation and sampling from the Hamiltonian eigenbasis (1–4), this work specifically considers a dynamics problem of real world significance and scale. While the reported resource estimates are high, there are a number of avenues for reducing these.
Stopping Power from First Principles.
While there are many different methods for calculating stopping powers, the most direct method involves time evolving the target and projectile from an initial condition in which the target is stationary and the projectile has some imposed velocity , rest mass , and charge . The stopping power is related to the average rate of energy transfer between the target and projectile over the course of this evolution. Exemplary results for a classical algorithm that implements this method using Kohn–Sham TDDFT are illustrated in Fig. 1.
Fig. 1.
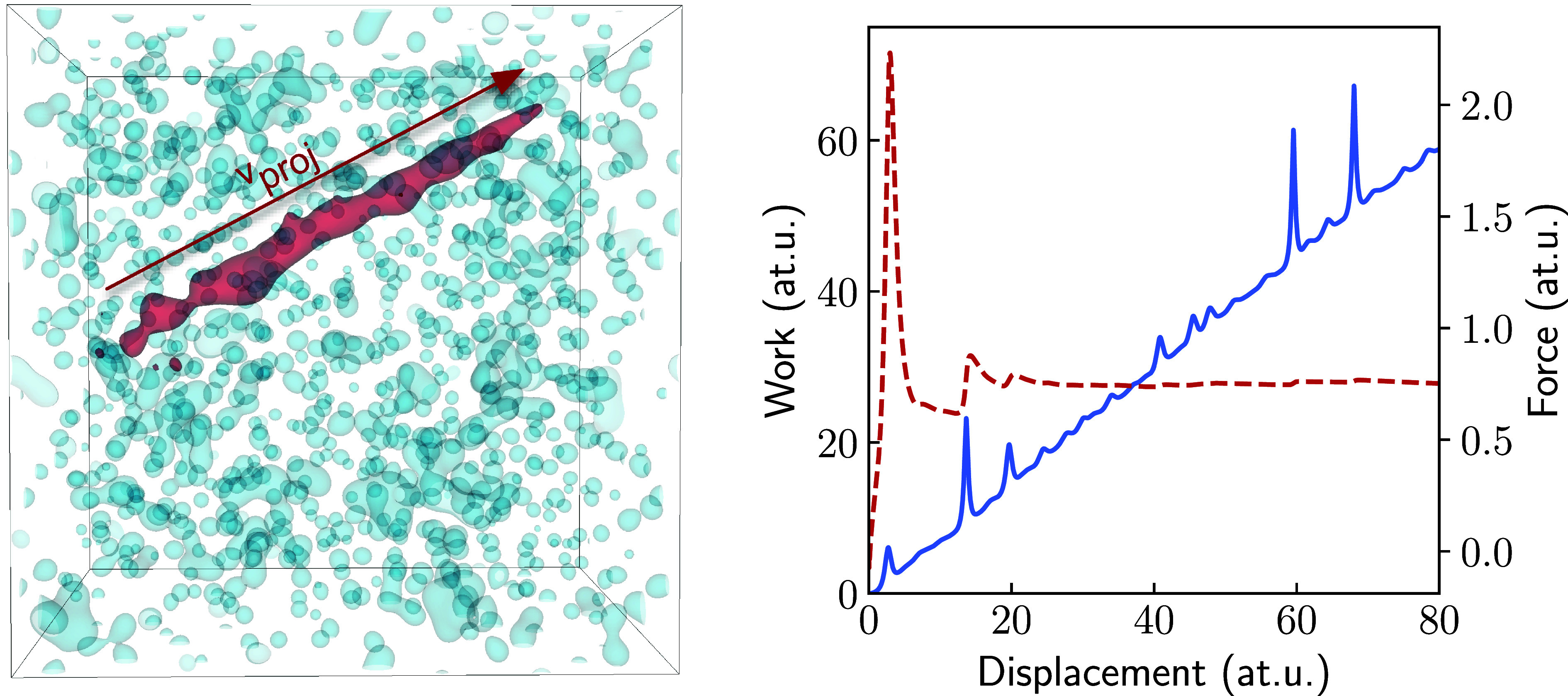
(Left) First-principles stopping power calculations involve time evolving a projectile (red) passing through a target medium (blue) while monitoring observables related to energy transfer between them. The initial velocity, , is chosen to mitigate trajectory sampling and finite-size error using techniques from ref. 71. The coupled electron-projectile dynamics are time evolved subject to this initial condition and the work or average force on the projectile is calculated throughout the trajectory. (Right) The stopping power is related to the slope of the work that the target does on the projectile as a function of its displacement from its original position (solid). A moving average for this slope (dashed) illustrates the rate at which the stopping power estimate converges. Close collisions involve large impulses in the work that are essential to capture on average. However, if these relatively rare events are included in the sample, they can dominate the variance for sample-efficient estimates.
The information required to compute a stopping power can be extracted from a number of different observables: the force that the projectile applies to the target, the force that the target applies to the projectile, the work done by the projectile on the target, and the work done by the target on the projectile. In classical first-principles calculations, the differences among the computational costs of evaluating any of these observables are negligible relative to the overall cost of time evolving the system. Thus there is no reason to prefer any particular observable, and it is even straightforward to verify the consistency among these quantities (i.e., Newton’s third law and the relationship between force and work). However, the costs of estimating these observables using a quantum algorithm differ significantly. For shot-noise limited estimation the overall cost will scale with the variance of the observable, whereas Heisenberg-scaling estimation can have costs that scale, in some cases, with the norm of the observable of interest. Thus, we should prefer low-weight observables (i.e., those supported on the projectile quantum register rather than the target) with well-behaved spectra [i.e., energies rather than forces, which exhibit pathologies when estimated naively (82, 83)].
Another distinction between classical and quantum algorithms for computing stopping powers is the relative cost of time-dependent Hamiltonian simulation. In classical stopping calculations that use Ehrenfest dynamics with TDDFT, it is common practice to explicitly break energy conservation by maintaining a fixed definite projectile velocity over the course of the evolution. While energy-conserving calculations in which the projectile is allowed to slow down under the influence of the target will produce equivalent stopping powers, minor technical advantages related to ease of implementation make the fixed velocity approach preferable in practice. The computational cost of either of these approaches is practically the same for classical simulations, but not for quantum algorithms. In fact, we will show that within the energy-conserving approach, promoting the projectile to a dynamical and quantum degree of freedom incurs relatively little overhead while facilitating the use of much simpler time-independent quantum simulation algorithms.
1. Quantum Algorithmic Protocol for Stopping Power
To circumvent the need for time-dependent Hamiltonian simulation, our protocol identifies the dynamical degrees of freedom as the electrons and the single projectile nucleus evolving in the fixed Coulomb field of the remaining nuclei comprising a representative supercell of the target material. For the projectile velocities at which electronic stopping is most relevant (on the order of 1 atomic unit) ignoring the motion of the target nuclei is justifiable unless their thermal velocities are comparable to the projectile velocity, at temperatures beyond the WDM regime. Similarly, nuclear quantum effects (e.g., zero-point energy and tunneling) can be neglected for the target nuclei, as they occur on energy scales that are many orders of magnitude smaller than those relevant to electronic stopping. These could be accounted for in our protocol at the cost of including the target nuclei as explicit quantum degrees of freedom, but they would only contribute to changes to the stopping power at levels of accuracy higher than would be relevant to ICF applications.
We consider a system composed of electrons, a quantum projectile with mass and charge , and classical nuclei with charges and positions in a cubic supercell of volume . In a plane-wave basis, the associated first-quantized BO Hamiltonian is
| [1] |
| [2] |
| [3] |
| [4] |
| [5] |
| [6] |
| [7] |
where represents a plane-wave vector with and . Each coefficient for the kinetic and potential operators are determined as integrals of the Laplacian and Coulomb operator using the plane wave basis in the standard Galerkin discretization (74, 84). is the size of the plane-wave basis, and we assume a cubic simulation cell of volume . Additionally, the set
is the set of possible differences in momentum (note the range is twice that of the range in each direction). The sets and are defined analogously for the set of plane-wave momenta available to the projectile, taken relative to its initial mean momentum with for compatibility with the supercell’s periodicity.
In the quantum algorithm, the state of the electrons are represented as three signed integers requiring qubits each. The electronic degrees of freedom require a total of qubits to represent. Representing a localized projectile with a sharply peaked momentum distribution in a plane-wave basis requires a large energy cutoff, depending on the variance of the wave packet. Given a number of plane waves for the projectile , the number of qubits needed to represent each of the -coordinates is as a set of signed integers, similar to the electronic degrees of freedom. Thus the total number of qubits to represent the non-BO system is . In SI Appendix, section III we numerically justify that for the target/projectile combinations explored in this work.
Our protocol consists of four steps: initial state preparation, time evolution, measurement, and postprocessing. The initial state of the electronic subsystem is drawn from a thermal distribution modeled as a fermionic Gaussian state, while the initial state of the projectile is a Gaussian wave packet in momentum space with a mean velocity corresponding to the projectile velocity and a variance chosen to balance accuracy and efficiency (SI Appendix, sections I and II). From that initial state, the coupled electronic-projectile system is time evolved under using qubitization (Section 1.1) or Trotterization (Section 1.2). Analysis and attendant constant-factor resource estimates are presented for both types of time-evolution algorithms. The measurement step consists of estimating the kinetic energy of the projectile via direct measurement of the kinetic energy operator on the projectile register. Since we are free to choose a relatively small variance in the nuclear wave packet, we show that shot-noise limited estimation is more efficient than Heisenberg-scaling approaches (81) unless high accuracy is required (Section 1.3). From estimates of the instantaneous projectile kinetic energy at a series of distinct times, we can estimate the stopping power using classical postprocessing similar to Fig. 1. While it is possible to directly mirror the TDDFT strategy on a fault-tolerant quantum computer—estimating the projectile energy loss at each of the thousands of time steps along its trajectory—to ensure a resource-optimal protocol, we propose a postprocessing strategy that requires many fewer samples than are typically used in postprocessing TDDFT data (Section 1.3). Finally, we estimate resource requirements for implementing this protocol to calculate electronic stopping powers for projectile/target pairings relevant to ICF applications in the WDM regime (Section 2).
1.1. Time evolution using qubitization.
The first protocol for time-evolution that we consider is using quantum signal processing (QSP) to synthesize the time-independent Hamiltonian propagator (85), which relies on qubitization (86). The qubitization walk operator is defined as
| [8] |
where (PREPARE) and (SELECT) are defined as
| [9] |
and we express as a linear combination of unitaries (LCU)
| [10] |
While many works use directly as a phase estimation target it was originally shown by Low et al. (85) that one can realize the propagator for with error for duration with
| [11] |
queries to . Specifically, the query costs are approximately
| [12] |
where the expression in the large parentheses is for the polynomial order of the function approximation for . This cost is determined by bounding the error in the Jacobi-Anger expansion and using the improved generalized QSP (87, 88).
An alternative strategy for constructing the propagator discussed in refs. 76 and 89 is simulation based on the interaction-picture algorithm. As a proxy for which strategy will be more efficient, we can refer to the “parameter region of advantage” plot in Fig. 2 of ref. 76. This plot quantifies for fixed grid spacing and particle number which algorithm is more efficient for performing phase estimation. The interaction picture results in lower Toffoli counts for very high-resolution simulations with . The qubitization approach outperforms the interaction-picture approach for moderate grid resolutions () with 10 or more electrons. In this work, we consider moderate grid resolutions with a large number of electrons and thus consider the quantum resources necessary to implement QSP.
Fig. 2.
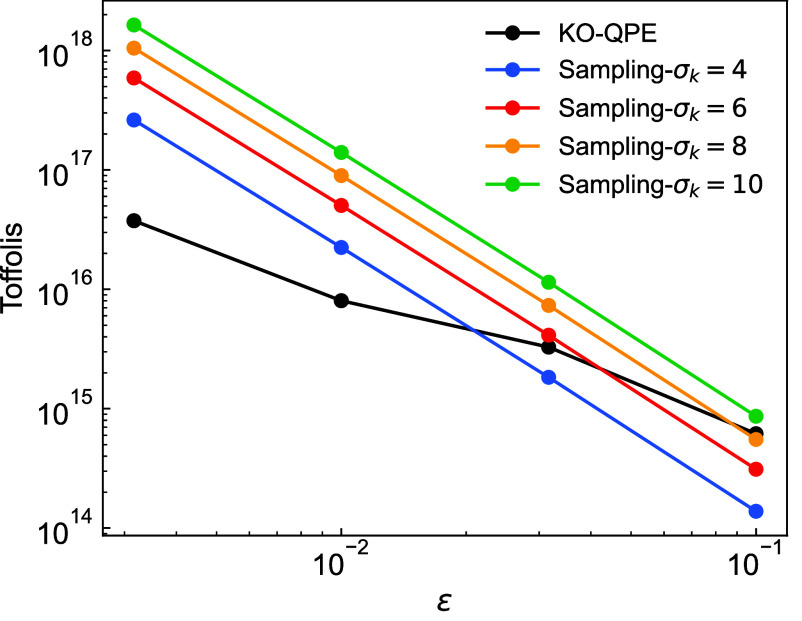
The Toffoli cost of estimating the projectile kinetic energy with traditional Monte Carlo sampling and the mean estimation algorithm from Kothari and O’Donnell (81) (KO). Both techniques have SE that linearly depends on the square root of the variance of the observable. The number of samples required for fixed SE in Standard Monte Carlo mean estimation scales as while the KO algorithm scales as but with larger constant factors originating from code (circuit) for the random variable and quantum phase estimation on the Grover like iterate used in the algorithm. More details of the algorithm’s main subroutines are provided in SI Appendix, section VI.
1.1.1. Block encoding modifications.
Here, we detail the block encoding modifications necessary to account for the non-BO projectile. A full detailed accounting of the Hamiltonian term derivations and encoding is provided in SI Appendix, section IV. In order to block encode the projectile Hamiltonian we must define , PREPUproj, PREPVproj, SELTproj, SELUproj, SELVproj such that
| [13] |
| [14] |
| [15] |
The similarity of the Hamiltonian operators for the projectile and the electrons means that much of the same infrastructure for block encoding the electronic Hamiltonian can be used for the electron-projectile Hamiltonian. The computation of for each term is thus also identical to that in ref. 76, except with replaced with and corresponds to the total charge of all nuclei treated classically. The values associated with each additional term are
| [16] |
| [17] |
| [18] |
| [19] |
| [20] |
where the corresponds to the cross term obtained from simulating the nuclear kinetic energy in the central momentum frame (Eq. 16 in SI Appendix, section IV) and corresponds to the LCU 1-norm for the projectile kinetic energy without a shift. A full justification for the projectile values (including the electronic values) can be found in SI Appendix, section IV. While these terms are substantial we find them orders of magnitude lower than the electronic kinetic energy and electronic potential values.
A considerable difference in the method for block encoding the Hamiltonian for the projectile is in how we account for the success probability of state preparation associated with the potential terms. In the case without the projectile, the state preparation is ideally split into preparation for the kinetic energy component of the Hamiltonian () and the potential components of the Hamiltonian () as
| [21] |
Here, the ancilla qubit is used to select between the kinetic and potential terms. The expression for state preparation in (Eq. 21) is not quite what is implemented, due to the fact that the most computationally efficient methods of implementing give a normalization factor of approximately . The factor of approximately corresponds to the probability of success in the state preparation, so the actual state preparation is
| [22] |
The ancilla qubit flags successful state preparation (on the state) for potential terms. The actual amplitude (which needs to be squared for the probability) is not exactly . The expression to determine the probability of success, , is given in equation 106 of ref. 76. To account for the imperfect probability of success, the choice of whether to apply the kinetic or potential term is based on both the ancilla and the success flag . A further subtlety is that we test in the block encoding of , with a further failure in the case where (representing self-interaction). The total electronic was thus defined
| [23] |
where the factor of accounts for testing .
We also previously considered the case where amplitude amplification is performed for the state preparation over . Typically, the value of is slightly smaller than , so a single step of amplitude amplification can be used to give a new probability of success (see equation 117 of ref. 76)
| [24] |
This probability will be slightly less than 1. A further step of amplitude amplification could be performed, but the extra cost would more than outweigh any advantage from the boosted success probability. With this boosted success probability one can otherwise take exactly the same approach, so (Eq. 23) would be changed to
| [25] |
The only amendment is in the probability.
For the current application where we simulate the electrons and the projectile, we now have three kinetic energy terms (, , and ) along with four potential terms (, , , and ). Of the additional two potential terms, the term requires a new state preparation over while is incorporated into the original state preparation from with slightly different logic for SELelec (discussed more in more detail in SI Appendix, section IV. Just as before we consider the tradeoffs in costs for state-preparation of the potential terms and adjusting the success probabilities for imperfect preparations. Because the number of qubits required to represent the projectile is expected to be larger than the electrons (see SI Appendix, section III for more details) the respective superpositions can be prepared on the same register with additional controls accounting for the fact that . The new value accounting for preparing the total state over both electronic and projectile degrees of freedom is thus
| [26] |
When using amplitude amplification has an identical expression except and are exchanged for and where superscript corresponds to the probability of success when performing amplitude amplification for the respective state preparations.
In the electronic-only case, additional registers for selecting between and along with kinetic and potential terms were needed. With the additional terms, we need additional registers to control the application of each operator. The adjustment of the probabilities is detailed in SI Appendix, section I. We now provide a summary accounting of the block encoding costs and relegate the detailed derivation to SI Appendix, section IV. For consistency with ref. 76, we consider the costs of each line in SI Appendix, Table S2 of that work and provide detailed cost updates for each subroutine in SI Appendix, section IV.D.
The complexity of the block encoding is still dominated by the controlled swaps (subroutine C4 in SI Appendix, section IV.D). In all cases, we find that the block encoding cost multiplied by computed with boosting the success probability of the potential using amplitude amplification is smaller than without.
1.2. Time Evolution Costs using Product Formulas.
The second method we investigate for implementing time evolution uses product formulas to implement the electron-projectile propagator. In this section, we consider a real-space grid Hamiltonian model of the electronic structure instead of the full electron-projectile system. We justify this consideration based on the fact that the electronic degrees of freedom are the dominant simulation costs. In order to simulate the time evolution using a product formula, there are three main parts.
Computing the potential energy in the position basis and applying a phase according to that energy.
Computing the kinetic energy in the momentum basis and applying the corresponding phase.
Performing a QFT between the two bases.
The product formula simulation is performed by alternating steps 1 and 2, using the QFT to switch the basis. The complexity is expected to be largest for step 1, because this requires computing the potential energy between pairs of electrons, whereas the kinetic energy just requires summing momenta squared.
The main difficulty in calculating the potential energy is in computing the approximation of the inverse square root. This was addressed in ref. 90, where it was stated that the function could be approximated to within 32 bits within five iterations, given a suitably chosen starting value for the iteration. We have numerically tested this approach and found that it is only accurate if the starting value is not too far from the correct inverse square root of the argument. Accuracy of one part in is only obtained over a range of less than a factor of 5 for the argument.
To improve on that computation, we consider a hybrid approach combining the QROM function interpolation of ref. 91 with the Newton–Raphson iteration of ref. 90. There are a number of variations that one could consider, depending on how the function interpolation is performed and how many steps of Newton–Raphson iteration are used. We find that excellent performance is obtained by using a single step of QROM interpolation with a cubic polynomial, followed by a single step of Newton–Raphson iteration. A further optimization targeting high-order product formulae is that the Newton–Raphson iteration is generalized to find instead of which saves complexity by avoiding multiplying the potential by the product formulae coefficient. There is also a choice of how many points are used in the interpolation, and we find that using two points within each factor of 2 of the argument gives relative error within about one part in . This is almost as high precision as that claimed in ref. 90 and works over the full range of input argument. In SI Appendix, section V, we provide a detailed accounting of the cost and error analysis for the QROM function interpolation followed by a single step of Newton–Raphson. Including these costs in the three multiplication and two subtractions of Newton–Raphson results in a total of
| [27] |
Toffoli cost for bits.
In SI Appendix, section V.B we estimate the number of Trotter steps using norm bounds from ref. 92. According to Theorem 4 of ref. 92, for a real-space grid Hamiltonian defined for orbital indices and spin indices of the form
| [28] |
the spectral norm error in a fixed particle manifold for an order- product formula can be estimated as
| [29] |
If the constant of proportionality is , then breaking longer evolution time into intervals gives error
| [30] |
In order to provide a simulation to within error , the number of time steps is then
| [31] |
In order to determine the constant in (Eq. 30), we numerically determine the spectral norm of (Eq. 29) for a variety of product formulas for a variety of systems scaling in and . To avoid building an exponentially large matrix, we adapt the power method to determine the spectral norm of as the square root of the maximal eigenvalue of . Using the FQE (93), we can target a particular particle number sector, projected spin sector, and use fast time evolution routines based on the structure of the Hamiltonian. Our numerics involved systems as large as 64 orbital (128 qubit) systems involving 2 to 4 particles. We determined by explicitly calculating the spectral norm of the difference between the exact unitary and a bespoke 8th-order product formula described in SI Appendix, section V.B. For we estimate a .
For the -order product formula, each step requires 17 exponentials. Each exponential has a complexity on the order of 2,395. Combining the constant factors, norm computation, and number of Toffolis required per exponential allowed us to calculate the Toffoli and qubit complexities for time evolution via product formula. We provide comparative costs to QSP in Section 2.
1.3. Projectile Kinetic Energy Estimation.
Our protocol estimates the stopping power from a time series for the projectile kinetic energy loss over the course of the electron-projectile evolution. Here, we analyze the sampling overheads for two approaches to estimating the projectile kinetic energy, one at the standard quantum limit and the other with Heisenberg scaling. This allows us to estimate the number of circuit repetitions required to achieve stopping power estimates with a target accuracy, and thus the aggregate Toffoli count for the entire protocol. For either approach, an estimate of the total number of samples needs to account for both the thermal distribution of the electrons in the initial state, the variance of the kinetic energy operator, and the effect of time evolution on both of these. Short of implementation and empirical assessment, there is no clean way to precisely bound the number of samples required to compute the stopping power while taking into account all of these factors and we rely on a few simplifying assumptions to facilitate analysis.
Our estimate of the sampling overhead for the first approach (at the standard quantum limit; see SI Appendix, Fig. S1) is based on classical Monte Carlo sampling of the projectile’s kinetic energy, given in SI Appendix, Eq. 8 in section III, using the from a plane-wave TDDFT calculation with classical nuclei and set according to the discussion in SI Appendix, section II. The variation in will be negligible over the timescale associated with electronic stopping, which is short relative to the timescale over which such a wave packet would diffuse thanks to the large difference between the electron and projectile masses. We estimate the stopping power by computing the slope of the kinetic energy change of the projectile as a function of time. We take 10 points within the simulated time interval and extract the slope and its error through least-squares regression. In SI Appendix, Fig. S1, we compare the number of samples required to resolve the stopping power to within 0.1 eV/Å a.u. We find that between and samples are required depending on the desired accuracy in the stopping power, with the sample cost growing with the velocity of the projectile. In practice, we expect to require only samples for accuracy relevant to applications in WDM. As shown in SI Appendix, section III, this corresponds to a precision (SE) in the individual kinetic energy points of approximately 0.1 Ha. If the desired accuracy in the stopping power is lowered from 0.1 to 0.5 eV/Å (corresponding to the green shaded region in SI Appendix, Fig. S1) then the number of samples required drops by a factor of 10.
However, this estimate does not directly account for the sampling overhead associated with capturing the thermal distribution of the electrons. Because the projectile and medium are far from equilibrium and will remain so over the timescale of our simulation, we do not expect that variance of the wave packet to depend on the electronic temperature and these two sources of randomness are independent. A complete assessment of the associated sampling overhead would require evaluating an ensemble of full quantum dynamics simulations in which the initial states are thermally distributed, thus, we leave this to future work. However, we expect the sampling overhead associated with capturing the thermal distribution of the electrons to already be accounted for in the overhead associated with sampling the final observable, provided we measure a low variance observable like the kinetic energy of the projectile. We note that we have tested another related strategy to estimate the sampling overhead, involving Monte Carlo estimation of the increase in energy of the electronic system. It was found to have a substantially larger variance and required an order of magnitude more samples to obtain comparable precision in the stopping power.
The second method we consider is a Heisenberg-scaling kinetic energy estimate based on an algorithm by Kothari and O’Donnell (81) (later referred to as KO). This mean-estimation algorithm has scaling of the time-evolution oracle, a quadratic advantage over Monte Carlo sampling, but requires coherent evolution of a Grover-like iterate constructed from the time-evolution unitary and a phase-oracle constructed from the projectile kinetic energy cost function—i.e. the projectile kinetic energy SELECT. To compare this strategy to expectation value estimation by Monte Carlo sampling we estimate the Toffoli complexity of time-evolution based on QSP and determine the constant factors associated with constructing the Grover-like iterate. Details on the phase-oracle construction are described in SI Appendix, section VI. The reflection oracle requires two calls to the time-evolution circuit and is also described in SI Appendix, section VI. Ref. 81 describes a decision problem associated with the mean-estimation task which can be lifted to full expectation value estimation through a series of classical reductions. Using the assumption that we have a fairly accurate estimate of the kinetic energy (valid for an almost classical projectile) the number of calls to the core decision problem is expected to be a small integer multiple. Thus our cost estimates focus on Toffoli counts associated with the core decision problem (Theorem 1.3 of ref. 81) assuming a projectile wavepacket variance of one.
To facilitate resource estimation, we have built a model of the entire protocol using the Cirq-FT software package (94), which allows us to quantify the cost of each subroutine. In Fig. 2, we plot this estimate (in black) along with estimates for standard Monte Carlo estimates based on the variance of the Gaussian wave packet representing the projectile which assumes no spreading of the particle. In the low-precision regime needed for the stopping power calculations standard sampling has a computational advantage due to the lower overhead (smaller prefactors). Coincidentally, the crossover is just beyond the necessary for the kinetic energy observable precision. In applications where higher precision is necessary (e.g., stopping at/below the Bragg peak or other dynamics problems entirely) the KO algorithm likely provides a computational advantage over sampling despite the classical reduction and phase estimation overheads.
2. Resource Estimates for ICF-Relevant Systems
We present resource estimates for stopping power calculations in three systems relevant to ongoing efforts aimed at characterizing errors in transport property calculations used in the design and interpretation of ICF and general high-energy density physics experiments (70). This allows us to explore how costs vary with the projectile and target conditions over the relevant phase space. The first system is an alpha-particle projectile in a hydrogen target at a density of 1 g/cm3. The second system is a proton projectile in a deuterium target at a density of 10 g/cm3. The third is a proton projectile in a high-density carbon target at 10 g/cm3. Details of associated Ehrenfest TDDFT calculations of the latter two can be found in ref. 56. Each system’s relevant classical parameters are defined in Table 1.
Table 1.
Summary of ICF-relevant systems considered in this work and associated classical simulation parameters
| Projectile + Target | Volume | η [electrons] | Wigner–Seitz radius [a0] | Ecut [eV] (Ha) | N 1/3 | Δ [a0] | np |
|---|---|---|---|---|---|---|---|
| Alpha + Hydrogen | 2419.68282 | 218 | 1.383 | 2,000 (73.49864) | 53 | 0.25330 | 6 |
| Proton + Deuterium | 3894.81126 | 1,729 | 0.813 | 2,000 (73.49864) | 63 | 0.24974 | 6 |
| Proton + Carbon | 861.328194 | 391 | 0.807 | 1,000 (36.74932) | 27 | 0.35239 | 5 |
a0 is the atomic Bohr radius, Ecut is the cutoff energy used in classical TDDFT calculations to model thev system, which corresponds to a grid spacing in one direction of N1/3 using a spherical cutoff, Δ is the grid spacing of the TDDFT calculations, and np is the number of qubits needed to achieve a similar resolution along one grid dimension. The reference classical calculations used different convergence criteria and merely represent a sample of systems commonly encountered when performing stopping power calculations.
For each of the systems, we consider a stopping power calculation with a projectile kinetic energy of 4 a.u. and a projectile wave packet variance of a.u. This allows us to determine the number of bits of precision needed to represent the projectile wavepacket. Considering the costs in the previous section we tabulate the block encoding costs , , and number of logical qubits, for each system in Table 2. For all systems, it was considerably cheaper to amplitude amplify the state preparation cost instead of reweighting the kinetic and potential terms.
Table 2.
Summary of quantum algorithmic parameters and costs associated with the systems listed in Table 1
| Projectile + Target | Mproj/Mproj,H | nn | kproj @ 4 a.u. | CB.E. [Toffolis] | Num. Qubits | λ |
|---|---|---|---|---|---|---|
| Alpha + Hydrogen | 3.9726 | 8 | 29,376 | 5,650 | 1744784.42 | |
| Proton + Deuterium | 1 | 8 | 7,344 | 33,038 | 88202784.59 | |
| Proton + Carbon | 1 | 8 | 7,344 | 8,841 | 7727607.07 |
Each column of the table is as follows: system description in terms of the projectile and target type, mass of the projectile relative to the proton mass , the number of bits for the projectile, , for projectile wave packet variance of a.u., the cost of block encoding the system, the required number of logical qubits, and total system .
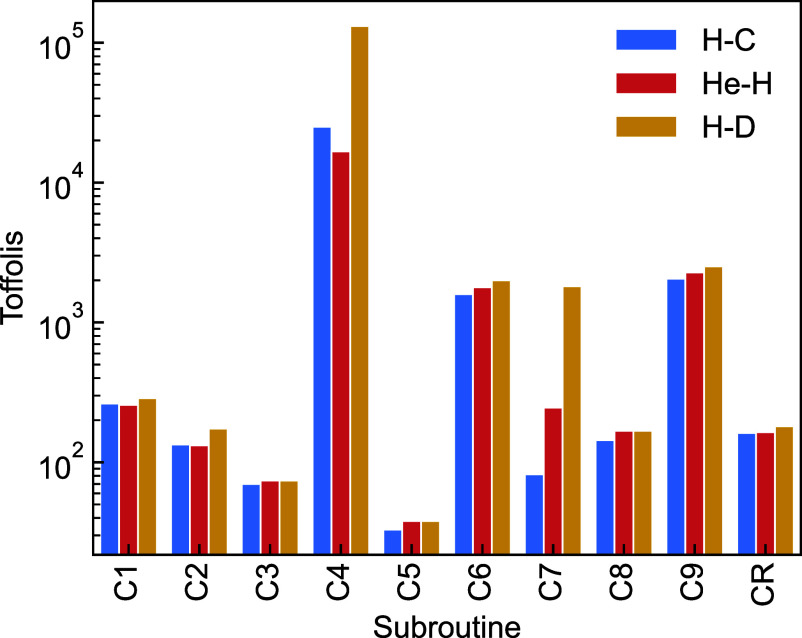
To further analyze the cost breakdown and to demonstrate the expected block encoding complexity we plot the Toffoli requirements for each subroutine outlined in the subroutine protocols of SI Appendix, section IV.D in Fig. 3. As expected controlled swaps of each electron into the working register for performing SELECT (C4) dominates the costs by an order of magnitude or more for each system. It is unlikely that this step can be further improved within this simulation protocol and representation.
Fig. 3.
Subroutine costs for each component of implementing the block-encoding. The labels C correspond to the costs enumerated in protocol SI Appendix, section IV.D. CR is the reflection cost which given the additional register and augmented is where , with being the target precision of time evolution, and .
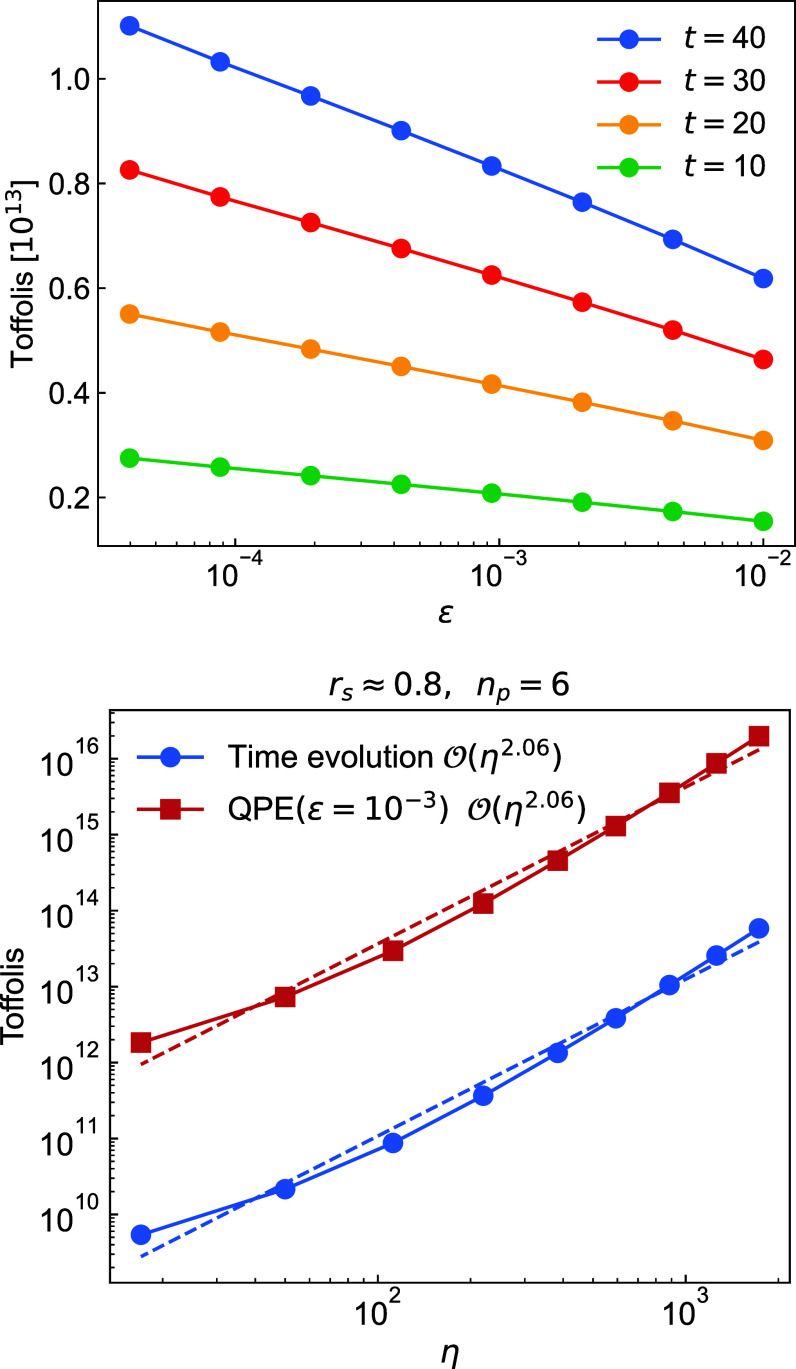
Finally, we can estimate the total Toffoli costs for performing time evolution on the electron-projectile system. In Fig. 4A, we plot the total Toffoli counts for evolving the Alpha Hydrogen system for times in units of a.u. for various infidelities . As the Toffoli complexity scales logarithmically in there is little change in the total Toffoli complexity with infidelity. Time linearly scales the query complexity which is already linearly proportional to . Given the values in Table 2 and the block encoding costs, the Toffoli gates for small constant values is not unexpected. While this is the price of one state preparation at time it has already been discussed in Section 1.3 that an additional to 100 samples for points are needed to reach the desired accuracy of the stopping power estimate. To probe costs for smaller systems, we examine the cost of systematically shrinking the unit cell at a fixed Wigner–Seitz radius. Given the scaling of qubitization, , fixing the number of planewaves and shrinking the unit cell at fixed particle density corresponds to increasing the grid resolution . Expressing the total complexity in terms of , the Toffoli complexity is expected to scale somewhere between and depending on which term is dominant in the qubitization costs. This value is plotted in blue in Fig. 4B with a slope of approximately . For reference, we provide the QPE scaling costs assuming the QPE precision in demonstrating that time-evolution with sampling can be substantially cheaper than eigenvalue estimation. While decreasing the system size while maintaining fixed grid resolution is possible we are only able to decrease the number of gridpoints by powers of two. Shrinking the system by powers of two quickly leads to nonphysically realistic system sizes, and thus, we focus on shrinking the system with increasing grid resolution which leads to a quadratic decrease in complexity with the number of particles at fixed Wigner–Seitz radius.
Fig. 4.
(Left) Toffoli complexity to synthesize the system propagator of the Alpha + Hydrogen system for time (in atomic units) for a range of fidelities. Using the lowest sample complexity considered to 100 and total times to estimate the slope the Toffoli complexity is 200 times the Toffoli costs shown. (Right) Toffoli scaling with respect to particle number at fixed and a fixed number of planewaves (increasing grid resolution). Time evolution cost is expected to scale as somewhere in between and using quantum signal processing. In blue the time evolution cost for is shown demonstrating the expected scaling along with constant factors. Constant factors associated with QPE are shown in red for which is should proportionally increase the cost. The displayed constant factor resources are in line with what is demonstrated in ref. 76 for constant .
We now make a comparison of the total Toffoli and logical qubit costs to estimate the stopping power. This requires ten kinetic energy estimations at times from to . Each time evolution is constructed with infidelity . A comparison between building the propagator with QSP and the 8th-order product formula is shown in Table 3 which includes a factor of accounting for the sampling overhead at each of the 10 time points. The product formula numerics use a prefactor of and the analytical values for the and norms.
Table 3.
Comparison of the total Toffoli cost for time-evolution using QSP or product formulas for 10 uniformly spaced times starting from and going to with infidelity including samples to measure the kinetic energy of the projectile
| Projectile + Target | QSP Toffoli | Product Formula Toffoli | QSP Qubits | Product Formula Qubits | |
|---|---|---|---|---|---|
| Alpha + Hydrogen (50%) | 28 | 1,749 | 2,666 | ||
| Alpha + Hydrogen (75%) | 92 | 3,309 | 3,902 | ||
| Alpha + Hydrogen | 218 | 5,650 | 6,170 | ||
| Proton + Carbon | 391 | 8,841 | 9,284 | ||
| Proton + Deuterium | 1729 | 33,038 | 33,368 |
The smallest Alpha + Hydrogen system used while all other systems used . For all systems, the projectile kinetic energy register used bits. The number of qubits for the product formula is estimated based on the system size plus an upper bound to the number of ancilla needed for performing the polynomial interpolation multiplications and Newton–Raphson step floating point arithmetic.
3. Discussion
We have described a quantum protocol for estimating stopping power and derived constant factor resource estimates for systems relevant to ICF. This study provides an analysis of a practically relevant quantum time dynamics simulation. It is also a specific proposal for how fault-tolerant quantum computers can contribute to the development of inertial fusion energy platforms. While the overall resource estimates are high, we expect that the product formula estimates are loose and further algorithmic innovations are possible. Supporting this optimism are the orders-of-magnitude improvements in constant factors for second-quantized chemistry simulation seen over the last five years (1–4).
We estimated that fully converged (in system size and basis-set size, with respect to TDDFT) calculations for an alpha particle projectile stopping in a hydrogen target would require Toffoli gates using QSP as the time-evolution routine. If 8th-order product formulas are used to build the electron-projectile propagator then we estimate that approximately Toffoli gates would be required. Both strategies require logical qubits to represent the system and a modest number of additional ancilla required for QROM and implementing product formulas. This estimate is for a system that is substantial in size (219 quantum particles) and corresponds to a calculation that has only been classically tractable using mean-field-like methods like TDDFT or more approximate models. Scaling down the system to a benchmark scale (29 quantum particles) would require substantially fewer resources ( Toffoli gates) and could be used to quantify the accuracy of TDDFT calculations and other approximate dynamics strategies.
In order to determine the constant factors, we compiled all time-evolution subroutines that contribute to the leading-order complexity. To implement time-evolution, we considered two methods to construct the electron-projectile propagator: QSP with qubitization and high-order product formulae. For QSP, we extended the block encoding construction of ref. 76 to account for the non-Born–Oppenheimer treatment of the projectile and analyzed the trade-off for constructing the block encoding with and without amplitude amplification for the potential state preparation. Specifically, this required modifications to the potential state preparation, additional kinetic energy preparation analysis, and new LCU -norm values. We expect that these modifications can serve as the basis for other mixed non-BO simulations in first quantization. For the product formula analysis, we introduced an optimized eighth-order formula based on the numerical protocol described in ref. 95 and greatly improved the algorithmic implementation for computing the inverse square root, the most expensive step of the propagator construction. Here we have improved this step by using QROM function approximation from ref. 91 followed by a single step of Newton–Raphson iteration. In order to analyze the overall effect of these subroutine improvements, we derived the total number of product formula steps required for fixed precision and analyzed constant factors by numerically computing the spectral norm of the difference between the product formula and the exact unitary through an adapted power-iteration algorithm. This worst-case bound indicated two orders of magnitude reduction in the Toffoli complexity for time evolution.
To complete our cost estimates for the stopping power we explored two different projectile kinetic energy estimation strategies. One involved sampling the kinetic energy of the projectile via Monte Carlo mean estimation and the second involved a Heisenberg scaling algorithm, developed in ref. 81, with a quadratic improvement over generic sampling. For the Monte Carlo sampling strategy, we utilized classical TDDFT to numerically determine an error bound, and required number of samples, for low-Z projectiles. In the KO-algorithm case, we provided a constant factor analysis of the algorithm’s core primitives leveraging Cirq-FT’s (94) resource estimation functionality. While stopping power for ICF targets turns out to only require standard limit Monte Carlo mean estimation there are a number of other settings where stopping power estimation with different accuracy parameters can be useful. In those cases, additional constant factor analysis would be required to analyze the additional classical reduction and state preparation overheads.
This work adds to the body of literature seeking to articulate specific real-world problems of high value where quantum computing might have a large impact and to quantify the magnitude of advantages offered by fault-tolerant quantum computers. As previous work in this area has shown, it is not always straightforward to identify scientific problems amenable to large quantum speedups (3). However, recent work suggests that when one is interested in exact electron dynamics—perhaps the most natural simulation problem for quantum computers—asymptotic speedups are possible over even computationally efficient mean-field classical strategies (96). These speedups are even more pronounced at finite temperature. Thus, materials properties in the preignition phase of ICF and other applications in the WDM regime are examples from a particularly rich area for exploration. Adding to this argument is the considerable difficulty in simulating flagship scale problems classically. For WDM there are no efficient, systematically improvable classical methods for first-principles electron dynamics. This work has shown that while quantum dynamics on quantum computers are a promising area, large constant factors for systems of practical interest continue to encourage further investigation into problem representation, observable estimation, classical benchmarking, and classical determination of scaling factors.
Supplementary Material
Appendix 01 (PDF)
Acknowledgments
We thank Bill Huggins, Lev Ioffe, Lucas Kocia, Robin Kothari, Alicia Magann, Jarrod McClean, Tom O’Brien, Shivesh Pathak, Antonio Russo, Stefan Seritan, Rolando Somma, and Andrew Zhao for helpful discussions. We thank Alexandra Olmstead for providing some of the atomic configurations taken from ref. 56. D.W.B. worked on this project under a sponsored research agreement with Google Quantum AI. D.W.B. is also supported by Australian Research Council Discovery Project DP210101367. A.K. and A.D.B. were partially supported by Sandia National Laboratories’ Laboratory Directed Research and Development Program (Project No. 222396) and the National Nuclear Security Administration’s Advanced Simulation and Computing Program. A.K., J.L., and A.D.B. were also partially supported by the Department of Energy (DOE) Office of Fusion Energy Sciences “Foundations for quantum simulation of warm dense matter” project. This article has been coauthored by employees of National Technology & Engineering Solutions of Sandia, LLC under Contract No. DE-NA0003525 with the U.S. DOE. The authors own all right, title, and interest in and to the article and are solely responsible for its contents. The United States Government retains and the publisher, by accepting the article for publication, acknowledges that the United States Government retains a nonexclusive, paid-up, irrevocable, world-wide license to publish or reproduce the published form of this article or allow others to do so, for United States Government purposes. The DOE will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan https://www.energy.gov/downloads/doe-public-access-plan. Some of the discussions and collaboration for this project occurred while using facilities at the Kavli Institute for Theoretical Physics, supported in part by the NSF under Grant No. NSF PHY-1748958.
Author contributions
N.C.R., D.W.B., H.N., R.B., and A.D.B. designed research; N.C.R., D.W.B., A.K., F.D.M., T.K., A.W., R.B., and A.D.B. performed research; A.K., F.D.M., T.K., A.W., and A.D.B. contributed new reagents/analytic tools; N.C.R., D.W.B., A.K., F.D.M., T.K., A.W., J.L., and A.D.B. analyzed data; and N.C.R., D.W.B., A.K., R.B., and A.D.B. wrote the paper.
Competing interests
N.C.R., F.D.M., T.K., H.N., and R.B. own Google stock.
Footnotes
This article is a PNAS Direct Submission. V.S.B. is a guest editor invited by the Editorial Board.
*Two of the coauthors (A.K. and A.D.B.) have maintained allocations on capability-class supercomputers to do stopping power calculations for nearly a decade. In their last year of allocations, this has involved 14 d of CPU time on a machine with approximately 300,000 processors.
†Specifically, we consider stopping of low-Z ionic projectiles at velocities on the order of 1 a.u. in targets near solid density. Nuclear and radiative contributions will be at least an order of magnitude smaller than our target precision, but they could be separately estimated if necessary. This style of partitioning is commonly used in classical stopping power models.
Data, Materials, and Software Availability
All study data are included in the article and/or SI Appendix. Additional software can be found in the following github repository https://github.com/ncrubin/mec-sandia (97).
Supporting Information
References
- 1.Lee J., et al. , Even more efficient quantum computations of chemistry through tensor hypercontraction. PRX Quant. 2, 030305 (2021). [Google Scholar]
- 2.von Burg V., et al. , Quantum computing enhanced computational catalysis. Phys. Rev. Res. 3, 033055–033071 (2021). [Google Scholar]
- 3.Rubin N. C., et al. , Fault-tolerant quantum simulation of materials using Bloch orbitals. PRX Quant. 4, 040303 (2023). [Google Scholar]
- 4.Berry D. W., Gidney C., Motta M., McClean J., Babbush R., Qubitization of arbitrary basis quantum chemistry leveraging sparsity and low rank factorization. Quantum 3, 208 (2019). [Google Scholar]
- 5.Lee S., et al. , Evaluating the evidence for exponential quantum advantage in ground-state quantum chemistry. Nat. Commun. 14, 1952 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bragg W. H., Kleeman R., XXXIX. On the particles of radium, and their loss of range in passing through various atoms and molecules. London, Edinburgh, Dublin Philos. Mag. J. Sci. 10, 318–340 (1905). [Google Scholar]
- 7.Bohr N. II, On the theory of the decrease of velocity of moving electrified particles on passing through matter. London, Edinburgh, Dublin Philos. Mag. J. Sci. 25, 10–31 (1913). [Google Scholar]
- 8.Fan W. C., Drumm C. R., Roeske S. B., Scrivner G. J., Shielding considerations for satellite microelectronics. IEEE Trans. Nucl. Sci. 43, 2790–2796 (1996). [Google Scholar]
- 9.Sand A. E., Ullah R., Correa A. A., Heavy ion ranges from first-principles electron dynamics. npj Comput. Mater. 5, 43 (2019). [Google Scholar]
- 10.Schardt D., Elsässer T., Schulz-Ertner D., Heavy-ion tumor therapy: Physical and radiobiological benefits. Rev. Mod. Phys. 82, 383 (2010). [Google Scholar]
- 11.Newhauser W. D., Zhang R., The physics of proton therapy. Phys. Med. Biol. 60, R155 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Shepard C., Yost D. C., Kanai Y., Electronic excitation response of DNA to high-energy proton radiation in water. Phys. Rev. Lett. 130, 118401 (2023). [DOI] [PubMed] [Google Scholar]
- 13.Joy D. C., Joy C. S., Low voltage scanning electron microscopy. Micron 27, 247–263 (1996). [Google Scholar]
- 14.Kononov A., Schleife A., Anomalous stopping and charge transfer in proton-irradiated graphene. Nano Lett. 21, 4816–4822 (2021). [DOI] [PubMed] [Google Scholar]
- 15.Kononov A., Olmstead A., Baczewski A. D., Schleife A., First-principles simulation of light-ion microscopy of graphene. 2D Mater. 9, 045023 (2022). [Google Scholar]
- 16.Wan N. H., et al. , Large-scale integration of artificial atoms in hybrid photonic circuits. Nature 583, 226–231 (2020). [DOI] [PubMed] [Google Scholar]
- 17.Asaad S., et al. , Coherent electrical control of a single high-spin nucleus in silicon. Nature 579, 205–209 (2020). [DOI] [PubMed] [Google Scholar]
- 18.Jakob A. M., et al. , Deterministic shallow dopant implantation in silicon with detection confidence upper-bound to 99.85% by ion–solid interactions. Adv. Mater. 34, 2103235 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.M. Berger, J. Coursey, M. Zucker, Estar, pstar, and astar: Computer programs for calculating stopping-power and range tables for electrons, protons, and helium ions (version 1.21) (1999). Accessed 23 August 2023.
- 20.Ziegler J. F., Ziegler M. D., Biersack J. P., SRIM—The stopping and range of ions in matter. Nucl. Inst. Methods Phys. Res. Sec. B, Beam Interact. Mater. Atoms 268, 1818–1823 (2010). [Google Scholar]
- 21.Montanari C. C., Dimitriou P., The IAEA stopping power database, following the trends in stopping power of ions in matter. Nucl. Inst. Methods Phys. Res. Sec. B, Beam Interact. Mater. Atoms 408, 50–55 (2017). [Google Scholar]
- 22.Graziani F., Desjarlais M. P., Redmer R., Trickey S. B., Frontiers and Challenges in Warm Dense Matter (Springer Science & Business, 2014), vol. 96. [Google Scholar]
- 23.Dornheim T., Groth S., Bonitz M., The uniform electron gas at warm dense matter conditions. Phys. Rep. 744, 1–86 (2018). [DOI] [PubMed] [Google Scholar]
- 24.Booth N., et al. , Laboratory measurements of resistivity in warm dense plasmas relevant to the microphysics of brown dwarfs. Nat. Commun. 6, 8742 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kritcher A., et al. , Design of inertial fusion implosions reaching the burning plasma regime. Nat. Phys. 18, 251–258 (2022). [Google Scholar]
- 26.Lütgert J., et al. , Platform for probing radiation transport properties of hydrogen at conditions found in the deep interiors of red dwarfs. Phys. Plasmas 29, 083301 (2022). [Google Scholar]
- 27.Saumon D., Guillot T., Shock compression of deuterium and the interiors of Jupiter and Saturn. Astrophys. J. 609, 1170 (2004). [Google Scholar]
- 28.Nettelmann N., et al. , Ab initio equation of state data for hydrogen, helium, and water and the internal structure of Jupiter. Astrophys. J. 683, 1217 (2008). [Google Scholar]
- 29.Benuzzi-Mounaix A., et al. , Progress in warm dense matter study with applications to planetology. Phys. Scr. 2014, 014060 (2014). [Google Scholar]
- 30.Hu S., et al. , Impact of first-principles properties of deuterium–tritium on inertial confinement fusion target designs. Phys. Plasmas 22, 056304 (2015). [Google Scholar]
- 31.Yager-Elorriaga D. A., et al. , An overview of magneto-inertial fusion on the Z machine at Sandia National Laboratories. Nucl. Fusion 62, 042015 (2022). [Google Scholar]
- 32.Abu-Shawareb H., et al. , Lawson criterion for ignition exceeded in an inertial fusion experiment. Phys. Rev. Lett. 129, 075001 (2022). [DOI] [PubMed] [Google Scholar]
- 33.Hurricane O., et al. , Physics principles of inertial confinement fusion and US program overview. Rev. Mod. Phys. 95, 025005 (2023). [Google Scholar]
- 34.Soures J., et al. , Direct-drive laser-fusion experiments with the OMEGA, 60-beam, 40 kJ, ultraviolet laser system. Phys. Plasmas 3, 2108–2112 (1996). [Google Scholar]
- 35.Nagler B., et al. , The matter in extreme conditions instrument at the Linac coherent light source. J. Synchrotron Radiat. 22, 520–525 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Falk K., Experimental methods for warm dense matter research. High Power Laser Sci. Eng. 6, e59 (2018). [Google Scholar]
- 37.Sinars D., et al. , Review of pulsed power-driven high energy density physics research on Z at Sandia. Phys. Plasmas 27, 070501 (2020). [Google Scholar]
- 38.MacDonald M., et al. , The colliding planar shocks platform to study warm dense matter at the National Ignition Facility. Phys. Plasmas 30, 062701 (2023). [Google Scholar]
- 39.Frenje J., et al. , Measurements of ion stopping around the Bragg peak in high-energy-density plasmas. Phys. Rev. Lett. 115, 205001 (2015). [DOI] [PubMed] [Google Scholar]
- 40.Zylstra A., et al. , Measurement of charged-particle stopping in warm dense plasma. Phys. Rev. Lett. 114, 215002 (2015). [DOI] [PubMed] [Google Scholar]
- 41.Malko S., et al. , Proton stopping measurements at low velocity in warm dense carbon. Nat. Commun. 13, 2893 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Zylstra A., et al. , Burning plasma achieved in inertial fusion. Nature 601, 542–548 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Singleton R. L., Charged particle stopping power effects on ignition: Some results from an exact calculation. Phys. Plasmas 15, 056302 (2008). [Google Scholar]
- 44.Temporal M., Canaud B., Cayzac W., Ramis R., Singleton R. L., Effects of alpha stopping power modelling on the ignition threshold in a directly-driven inertial confinement fusion capsule. Eur. Phys. J. D 71, 1–5 (2017). [Google Scholar]
- 45.Zylstra A., Hurricane O., On alpha-particle transport in inertial fusion. Phys. Plasmas 26, 062701 (2019). [Google Scholar]
- 46.Smalyuk V., et al. , Review of hydrodynamic instability experiments in inertially confined fusion implosions on National Ignition Facility. Plasma Phys. Controlled Fusion 62, 014007 (2019). [Google Scholar]
- 47.Zhou Y., et al. , Turbulent mixing and transition criteria of flows induced by hydrodynamic instabilities. Phys. Plasmas 26, 080901 (2019). [Google Scholar]
- 48.Gomez M., et al. , Performance scaling in magnetized liner inertial fusion experiments. Phys. Rev. Lett. 125, 155002 (2020). [DOI] [PubMed] [Google Scholar]
- 49.Roth M., et al. , Fast ignition by intense laser-accelerated proton beams. Phys. Rev. Lett. 86, 436 (2001). [DOI] [PubMed] [Google Scholar]
- 50.Atzeni S., Schiavi A., Davies J., Stopping and scattering of relativistic electron beams in dense plasmas and requirements for fast ignition. Plasma Phys. Controlled Fusion 51, 015016 (2008). [Google Scholar]
- 51.Solodov A., Betti R., Stopping power and range of energetic electrons in dense plasmas of fast-ignition fusion targets. Phys. Plasmas 15, 042707 (2008). [Google Scholar]
- 52.Magyar R. J., Shulenburger L., Baczewski A. D., Stopping of deuterium in warm dense deuterium from Ehrenfest time-dependent density functional theory. Contrib. Plasma Phys. 56, 459–466 (2016). [Google Scholar]
- 53.Ding Y., White A. J., Hu S., Certik O., Collins L. A., Ab initio studies on the stopping power of warm dense matter with time-dependent orbital-free density functional theory. Phys. Rev. Lett. 121, 145001 (2018). [DOI] [PubMed] [Google Scholar]
- 54.White A. J., Certik O., Ding Y., Hu S., Collins L. A., Time-dependent orbital-free density functional theory for electronic stopping power: Comparison to the Mermin–Kohn–Sham theory at high temperatures. Phys. Rev. B 98, 144302 (2018). [Google Scholar]
- 55.White A. J., Collins L. A., Nichols K., Hu S., Mixed stochastic-deterministic time-dependent density functional theory: Application to stopping power of warm dense carbon. J. Phys.: Condens. Matter 34, 174001 (2022). [DOI] [PubMed] [Google Scholar]
- 56.Hentschel T. W., et al. , Improving dynamic collision frequencies: Impacts on dynamic structure factors and stopping powers in warm dense matter. Phys. Plasmas 30, 062703 (2023). [Google Scholar]
- 57.Faussurier G., Blancard C., Cossé P., Renaudin P., Equation of state, transport coefficients, and stopping power of dense plasmas from the average-atom model self-consistent approach for astrophysical and laboratory plasmas. Phys. Plasmas 17, 052707 (2010). [Google Scholar]
- 58.Maynard G., Deutsch C., Energy loss and straggling of ions with any velocity in dense plasmas at any temperature. Phys. Rev. A 26, 665 (1982). [Google Scholar]
- 59.Maynard G., Deutsch C., Born random phase approximation for ion stopping in an arbitrarily degenerate electron fluid. J. Phys. 46, 1113–1122 (1985). [Google Scholar]
- 60.Moldabekov Z., Ludwig P., Bonitz M., Ramazanov T., Ion potential in warm dense matter: Wake effects due to streaming degenerate electrons. Phys. Rev. E 91, 023102 (2015). [DOI] [PubMed] [Google Scholar]
- 61.Moldabekov Z. A., Dornheim T., Bonitz M., Ramazanov T., Ion energy-loss characteristics and friction in a free-electron gas at warm dense matter and nonideal dense plasma conditions. Phys. Rev. E 101, 053203 (2020). [DOI] [PubMed] [Google Scholar]
- 62.Makait C., Fajardo F. B., Bonitz M., Time-dependent charged particle stopping in quantum plasmas: Testing the G1–G2 scheme for quasi-one-dimensional systems. Contrib. Plasma Phys. 63, e202300008 (2023). [Google Scholar]
- 63.G. Zimmerman, “Recent developments in Monte Carlo techniques” in 1990 Nuclear Explosives Code Developers’ Conference, Monterey, CA, 6–9 November 1990 (Lawrence Livermore National Lab, Livermore, CA, 1990).
- 64.Li C. K., Petrasso R. D., Charged-particle stopping powers in inertial confinement fusion plasmas. Phys. Rev. Lett. 70, 3059 (1993). [DOI] [PubMed] [Google Scholar]
- 65.Li C. K., Petrasso R., Stopping of directed energetic electrons in high-temperature hydrogenic plasmas. Phys. Rev. E 70, 067401 (2004). [DOI] [PubMed] [Google Scholar]
- 66.Brown L. S., Preston D. L., Singleton R. L. Jr., Charged particle motion in a highly ionized plasma. Phys. Rep. 410, 237–333 (2005). [Google Scholar]
- 67.Grabowski P. E., Surh M. P., Richards D. F., Graziani F. R., Murillo M. S., Molecular dynamics simulations of classical stopping power. Phys. Rev. Lett. 111, 215002 (2013). [DOI] [PubMed] [Google Scholar]
- 68.Graziani F. R., et al. , Large-scale molecular dynamics simulations of dense plasmas: The Cimarron project. High Energy Density Phys. 8, 105–131 (2012). [Google Scholar]
- 69.G. Zimmerman, D. Kershaw, D. Bailey, J. Harte, Lasnex code for inertial confinement fusion (Tech. Rep., California University, 1977).
- 70.Grabowski P., et al. , Review of the first charged-particle transport coefficient comparison workshop. High Energy Den. Phys. 37, 100905 (2020). [Google Scholar]
- 71.A. Kononov, T. Hentschel, S. B. Hansen, A. D. Baczewski, Trajectory sampling and finite-size effects in first-principles stopping power calculations. arXiv [Preprint] (2023). 10.48550/arXiv.2307.03213 (Accessed 23 August 2023). [DOI]
- 72.Correa A. A., Calculating electronic stopping power in materials from first principles. Comput. Mater. Sci. 150, 291–303 (2018). [Google Scholar]
- 73.Babbush R., et al. , Encoding electronic spectra in quantum circuits with linear T complexity. Phys. Rev. X 8, 041015 (2018). [Google Scholar]
- 74.Babbush R., et al. , Low-depth quantum simulation of materials. Phys. Rev. X 8, 011044 (2018). [Google Scholar]
- 75.Babbush R., Berry D. W., McClean J. R., Neven H., Quantum simulation of chemistry with sublinear scaling in basis size. npj Quant. Inf. 5, 92 (2019). [Google Scholar]
- 76.Su Y., Berry D., Wiebe N., Rubin N., Babbush R., Fault-tolerant quantum simulations of chemistry in first quantization. PRX Quant. 4, 040332 (2021). [Google Scholar]
- 77.Ivanov A. V., et al. , Quantum computation for periodic solids in second quantization. Phys. Rev. Res. 5, 013200 (2023). [Google Scholar]
- 78.Pruneda J., Sánchez-Portal D., Arnau A., Juaristi J., Artacho E., Electronic stopping power in LiF from first principles. Phys. Rev. Lett. 99, 235501 (2007). [DOI] [PubMed] [Google Scholar]
- 79.Zeb M. A., et al. , Electronic stopping power in gold: The role of d electrons and the H/He anomaly. Phys. Rev. Lett. 108, 225504 (2012). [DOI] [PubMed] [Google Scholar]
- 80.Maliyov I., Crocombette J. P., Bruneval F., Quantitative electronic stopping power from localized basis set. Phys. Rev. 101, 035136 (2020). [Google Scholar]
- 81.R. Kothari, R. O’Donnell, “Mean estimation when you have the source code; or, quantum Monte Carlo methods” in Proceedings of the 2023 Annual ACM-SIAM Symposium on Discrete Algorithms (SODA) (SIAM, 2023), pp. 1186–1215.
- 82.Assaraf R., Caffarel M., Computing forces with quantum Monte Carlo. J. Chem. Phys. 113, 4028–4034 (2000). [Google Scholar]
- 83.Chiesa S., Ceperley D., Zhang S., Accurate, efficient, and simple forces computed with quantum Monte Carlo methods. Phys. Rev. Lett. 94, 036404 (2005). [DOI] [PubMed] [Google Scholar]
- 84.Martin R., Electronic Structure: Basic Theory and Practical Methods (Cambridge University Press, 2004). [Google Scholar]
- 85.Low G. H., Chuang I. L., Optimal Hamiltonian simulation by quantum signal processing. Phys. Rev. Lett. 118, 010501 (2017). [DOI] [PubMed] [Google Scholar]
- 86.Low G. H., Chuang I. L., Hamiltonian simulation by qubitization. Quantum 3, 163 (2019). [Google Scholar]
- 87.Babbush R., Berry D. W., Neven H., Quantum simulation of the Sachdev-Ye-Kitaev model by asymmetric qubitization. Phys. Rev. A 99, 040301 (2019). [Google Scholar]
- 88.D. W. Berry, D. Motlagh, G. Pantaleoni, N. Wiebe, Doubling efficiency of Hamiltonian simulation via generalized quantum signal processing. arXiv [Preprint] (2024). 10.48550/arXiv.2401.10321 (Accessed 23 August 2023). [DOI]
- 89.G. H. Low, N. Wiebe, Hamiltonian Simulation in the interaction picture. arXiv [Preprint] (2018). 10.48550/arXiv.1805.00675 (Accessed 23 August 2023). [DOI]
- 90.Jones N. C., et al. , Faster quantum chemistry simulation on fault-tolerant quantum computers. New J. Phys. 14, 115023 (2012). [Google Scholar]
- 91.Sanders Y. R., et al. , Compilation of fault-tolerant quantum heuristics for combinatorial optimization. PRX Quant. 1, 020312–020382 (2020). [Google Scholar]
- 92.G. H. Low, Y. Su, Y. Tong, M. C. Tran, On the complexity of implementing Trotter steps. arXiv [Preprint] (2022). 10.48550/arXiv.2211.09133 (Accessed 23 August 2023). [DOI]
- 93.Rubin N. C., et al. , The fermionic quantum emulator. Quantum 5, 568 (2021). [Google Scholar]
- 94.T. Khattar et al., Cirq-FT: Cirq for fault-tolerant quantum algorithms (2023). https://github.com/quantumlib/Cirq/graphs/contributors. Accessed 23 August 2023.
- 95.M. E. S. Morales, P. Costa, D. K. Burgarth, Y. R. Sanders, D. W. Berry, Greatly improved higher-order product formulae for quantum simulation. arXiv [Preprint] (2022). 10.48550/arXiv.2210.15817 (Accessed 23 August 2023). [DOI]
- 96.Babbush R., et al. , Quantum simulation of exact electron dynamics can be more efficient than classical mean-field methods. Nat. Commun. 14, 4058 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.C. Nicholas et al., Data and code for: Quantum computation of stopping power for inertial fusion target design. Github. https://github.com/ncrubin/mec-sandia. Accessed 12 May 2024. [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix 01 (PDF)
Data Availability Statement
All study data are included in the article and/or SI Appendix. Additional software can be found in the following github repository https://github.com/ncrubin/mec-sandia (97).