ABSTRACT
The Escherichia coli whole-cell modeling project seeks to create the most detailed computational model of an E. coli cell in order to better understand and predict the behavior of this model organism. Details about the approach, framework, and current version of the model are discussed. Currently, the model includes the functions of 43% of characterized genes, with ongoing efforts to include additional data and mechanisms. As additional information is incorporated in the model, its utility and predictive power will continue to increase, which means that discovery efforts can be accelerated by community involvement in the generation and inclusion of data. This project will be an invaluable resource to the E. coli community that could be used to verify expected physiological behavior, to predict new outcomes and testable hypotheses for more efficient experimental design iterations, and to evaluate heterogeneous data sets in the context of each other through deep curation.
KEYWORDS: computational modeling, microbiology, whole-cell modeling
The challenge of fully characterizing the dynamics of all molecules within a living organism has been identified by many as a pressing problem. Over 4 decades ago, Francis Crick called for a coordinated worldwide scientific effort to determine a “complete solution” of Escherichia coli (1). He envisioned a central laboratory to coordinate work, standardize biological reagents and materials, and produce vast libraries. Although such an approach was never adopted, the scientific community has published millions of measurements to characterize E. coli. Even still, a complete solution, in the form of a simulation that can replicate the behaviors of living cells, remains elusive. A more modern take on Crick’s vision calls whole-cell simulation a “grand challenge of the 21st century,” since “complex behavior of the cell cannot be determined or predicted unless a computer model of the cell is constructed and computer simulation is undertaken” (2).
Many groups have created models of various scales to capture the behavior of cells in mathematical frameworks (3–6). Building off this pioneering work is the approach of whole-cell modeling, creating a mathematical representation of all of the known biological functionality of a cell that is used to update the state of the cell as it grows in silico. The concept and application of whole-cell modeling was first demonstrated in the simple organism Mycoplasma genitalium (7). The model was able to track all of the molecules and interactions within a life cycle of a bacterium, offering a detailed look into the behavior and function of the cell. Capturing all of the known gene functionalities and interactions provided new insights and novel predictions, which were then validated with experiments.
Since then, the whole-cell modeling approach has been extended to E. coli (8), allowing researchers to tap into the extensive data and knowledge that have resulted from decades of research into this model organism. Development efforts to include submodels capturing all known gene functionality are still ongoing, with 43% of known genes currently functionally incorporated. Although not yet complete, this initial work represents a significant advance in whole-cell modeling technology compared to the original M. genitalium model. In the E. coli model, all model parameters are derived from measurements made with E. coli, whereas the M. genitalium model borrowed many parameters derived from other microbes. The E. coli model can also perform simulations in multiple environments and proceed from parent to daughter cells over many division events, both of which were not possible with the M. genitalium model. E. coli is also a more complicated organism, with over 8 times as many genes as M. genitalium, many of which are regulated in response to changing environments. These advancements allow us to use the whole-cell model of E. coli as an assessment of how well we can predict complex behavior of this model organism given the currently available data sets.
In addition to serving as a model organism in scientific endeavors, E. coli has also served a prominent role in the biomanufacturing industry, where engineered strains of E. coli are often used to produce various chemical products. Despite recent advancements in simulation-assisted design in other engineering fields, metabolic engineering is still in need of an effective “digital twin” that can faithfully replicate the behavior of its physical counterpart, the engineered organism itself (9). The development of a whole-cell model of E. coli that can be used to optimize titers, rates, and yields of chemical products would revolutionize the biomanufacturing industry by immensely cutting down the costs associated with exploring new strains and environments.
In this review, we aim to highlight aspects of the E. coli whole-cell modeling project that may be of interest to the broader community of E. coli researchers. The “Approach” section will discuss the underlying concepts of whole-cell modeling, the computational framework of the E. coli model, and the needed considerations in the selection of data to be used in the model. The “Current model snapshot” section will explain how the model can be accessed and run, give an overview of which cellular functionalities are currently included, and discuss the simulation outputs and how the outputs are validated. The “Model-driven discovery” section will present potential applications of the whole-cell model as a discovery tool. Lastly, the “Discussion” section will discuss possible future directions that we are planning to take our project.
We hope that the development of a whole-cell model of E. coli will prove to be an invaluable tool to the E. coli research community. Similar to the community efforts in parameter estimation, analysis, and applications seen after the M. genitalium model (10–13), we expect the E. coli whole-cell modeling project to integrate even more with the much larger E. coli research community. Extending the whole-cell model with additional data sets and mechanistic relationships will only enhance the benefit of having a model that can integrate and assess the diverse heterogeneous data sets that continue to be generated for this organism. Much as the generation of data, characterization of genes, and identifying biological interactions, which lead to a better understanding of E. coli, are community efforts, the development of a whole-cell model could also benefit from community contributions from a wide range of researchers, from computational and experimental biologists to computer scientists and software engineers.
APPROACH
Whole-cell modeling concepts.
Whole-cell modeling seeks to link heterogeneous data sets to each other through known and inferred mechanistic interactions at the scale of the entire E. coli cell. In the current realm of computational models for biological systems, there is often a trade-off between models that are mechanistic (and, thus, biologically interpretable) and models that can capture behavior at the genome scale. Many mechanistic modeling approaches focus on a subset of the cellular processes and use a single type of mathematical representation (e.g., linear programming for flux balance analysis [FBA] [14] or ordinary differential equations [ODEs] for time evolution of small networks, including transport dynamics, growth rate control, and metabolic reaction rates [4, 15–17]) to represent the biological processes. Often, mechanistic models are difficult to build at the genome scale due to the challenge of parameterization (18, 19). In contrast to mechanistic models, machine learning or probabilistic models can be more easily extended to the genome level by using black-box models, which infer all biological interactions by integrating large omics data sets instead of using experimentally confirmed mechanisms and interactions (20–22). These models, however, inherently provide less mechanistic insight and often use parameters that are difficult to interpret in a biologically meaningful way. Some machine learning approaches seek more interpretability with a “white-box” approach (23, 24) or ensemble models where combinations with other models are used to interpret mechanisms from the results (25, 26), but it is often difficult to include this mechanistic information a priori with these approaches. Whole-cell modeling promises to bring us the best of both worlds by providing the ability to model at the genome scale while still maintaining mechanistic interactions.
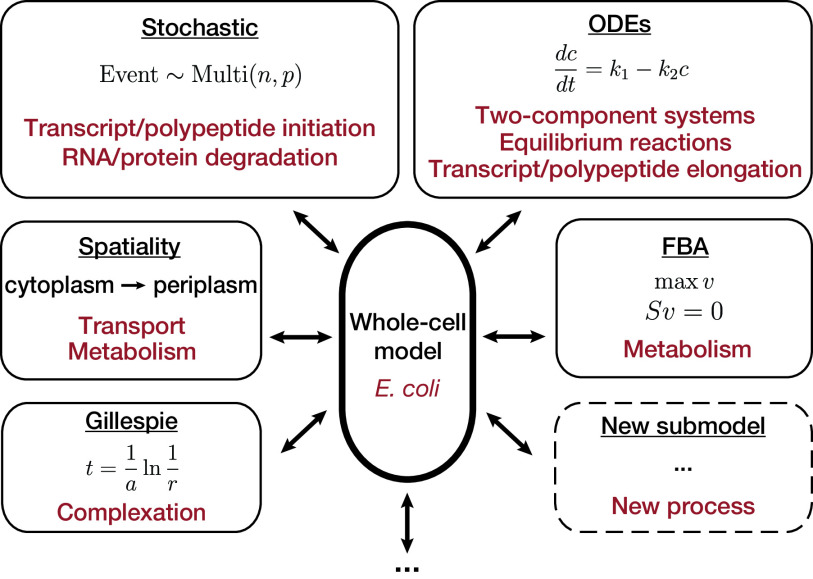
The major benefit of whole-cell modeling is that different mechanistic approaches can be integrated to take advantage of the benefits of each approach while still capturing mechanistic details of other components of the cell. For example, FBA approaches rely on an abstraction of biomass production in a cell, such as the polymerization of protein and nucleic acids, by including a biomass reaction that converts metabolites into these biomass components in a fixed proportion. Whole-cell modeling allows for the inclusion of metabolic reactions like FBA while explicitly modeling the rate of biomass formation through separate transcription and translation processes, which capture RNA and protein dynamics on a single-molecule level. Some examples of the mathematical frameworks used for different cellular processes in the current whole-cell model are shown in Fig. 1.
FIG 1.
Whole-cell modeling can integrate different types of models to meet the scale of an entire organism while including mechanistic interactions. This modular approach allows for easy expansion to include new biological features and models. Note that the Gillespie implementation will appear in a newer version of the model, not the current release.
In order to link submodels together, whole-cell modeling must assume that the individual submodels are independent over short time periods. This separation allows for the inclusion of different mathematical representations of cellular processes that are most appropriate for each aspect of cellular physiology to be modeled and can be tailored to the overall knowledge level and characterization of that physiological system. Although submodels are assumed to be independent within a time step, over longer time scales, the submodels still interact with each other through updates to the state of the cell. After each time step, consumption or production of molecules in one process will affect other processes at the next time step. Thus, these state updates tie together the separate submodels into a cohesive model of the whole cell and capture dynamic interactions between submodels.
By integrating multiple submodels, whole-cell models can expand both the scope and the accuracy of model predictions compared to the predictions that can be independently made by each submodel. The M. genitalium whole-cell model, for example, was able to accurately predict the kinetic parameters of certain enzymes in the metabolic network by simulating the growth of single-gene disruption strains (27). This prediction required a full integration of the metabolic network submodel with the transcription and translation submodels that calculate enzyme abundance and, thus, would not have been possible with a standalone FBA model for metabolism or the transcription/translation submodel.
Another benefit of whole-cell modeling is that each process can be modeled in a modular way. This allows different submodels of cell physiology to easily be swapped in or out of the whole-cell model. Performing simulations with one submodel and comparing to results with another submodel can be a way to assess the understanding of each system and lead to discovery. These comparisons can also provide evidence in support of a hypothesis about how the living cell works or test the accuracy of methods of data generation.
Whole-cell modeling framework.
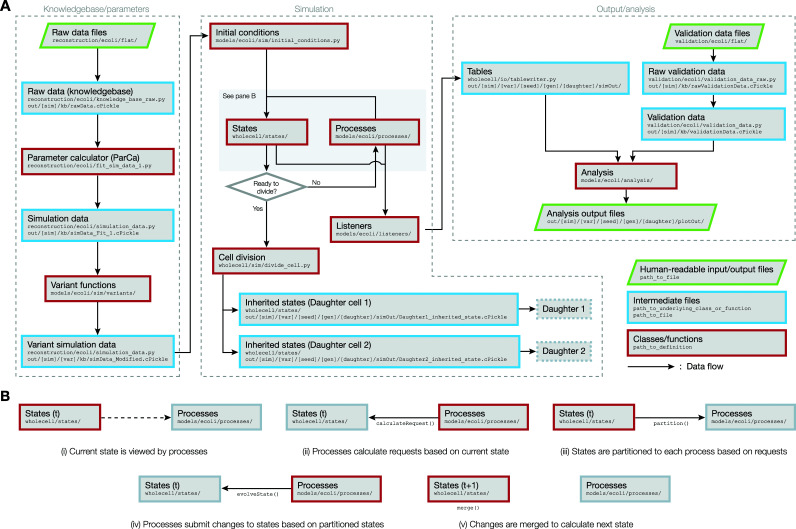
The computational framework of the E. coli whole-cell model largely consists of three sequential modules (Fig. 2A): (i) the knowledgebase/parameters module, where data are compiled to calculate simulation parameters, (ii) the simulation module, where a whole-cell simulation is executed, and (iii) the output/analysis module, where the outputs from the simulation are analyzed. Depending on the needs of the researcher, the three modules can be run individually or linked such that each module is sequentially run once the preceding modules have finished running. Details on each of these modules are presented in the sections below.
FIG 2.
(A) Flowchart that describes the flow of data between different components of the E. coli whole-cell model. The dashed boxes represent the three modules that constitute the entire workflow. File paths are given according to how the files are organized in the WholeCellEcoliRelease GitHub repository. (B) A detailed sequence of data flows that occur between States and Processes, while the simulation moves forward by a single time step from time t to t + 1.
Knowledgebase/parameters.
In the first module (Fig. 2A, knowledgebase/parameters), raw data are used to calculate the parameters that are used inside the simulation. In the first step of this module, the primary data files are tied together into a single Python object called raw data, which simply contains all unprocessed data from these files, organized by the names of each file. The raw data object is given as an input to the parameter calculator (ParCa), which converts the raw data into parameters that are directly used by the simulation itself. This conversion is necessary because many of the parameters that are required to initialize and run the current whole-cell model cannot be sourced directly from raw data and need to be derived or estimated using these raw parameters (an example of this conversion is given in “Current model snapshot,” below). The resulting parameters are packaged into the simulation data object, which serves the role of a global reference that the simulation refers to for any parameter value. In the case where a variant simulation (e.g., growth under different medium conditions and with gene knockouts) is needed, the simulation data object is modified by a variant function that changes the value of a specific parameter based on the nature of the variant. For instance, for the gene knockout variant, the variant function will set the transcription probability of the knocked-out gene to zero, such that the gene is never transcribed throughout the lifetime of the simulation. Variant functions will output a variant simulation data object, which serves the role of simulation data objects for variant simulations.
Simulation.
The second module (Fig. 2A, simulation) uses the parameters calculated from the first module to perform a whole-cell simulation. The simulation begins with the initial conditions function using the parameters given in simulation data to approximate the initial state of the simulation.
The state is a Python object that embodies the current status of all molecules within the simulation, including the counts, locations, and attributes of the molecules. The object consists of the external state object, which describes the environment that the simulation is growing in, and the internal state object, which describes the properties of all molecules within the boundaries of the cell. The internal state object uses two different representations for the status of each molecular species, depending on the level of detail required to describe the molecule (Table 1). The BulkMolecule representation is used when the only property needed to describe the molecule is the total number of counts of the species within a given compartment. ATP in the cytosol, for instance, is described using a BulkMolecule representation with the label ATP[c], since two ATP molecules in the cytosol ([c]) are assumed to be indistinguishable from each other. The UniqueMolecule representation is used when it is possible for the individual molecules to have unique attributes such that they are functionally different from each other. Active RNA polymerases, for example, are represented as such, since the individual RNA polymerases can be transcribing different genes at distinct locations on the chromosome.
TABLE 1.
Sample snapshot of the internal_state object during a whole-cell simulationa
| Type | Molecule ID | Data |
|---|---|---|
| BulkMolecules | WATER[c] | Total count: 18,512,198,212 |
| ATP[c] | Total count: 1,192,909 | |
| APORNAP-CPLX[c] | Total count: 3,151 | |
| UniqueMolecules | activeRnaPoly | Molecule 1: {“rnaIndex”: 152, “transcriptLength”: 189} |
| Molecule 2: {“rnaIndex”: 819, “transcriptLength”: 619} | ||
| activeRibosome | Molecule 1: {“proteinIndex”: 2912, “peptideLength”: 38} | |
| Molecule 2: {“proteinIndex”: 919, “peptideLength”: 91} |
Molecules constituting the internal_state can be divided into two types, BulkMolecules and UniqueMolecules, depending on whether the individual molecules can be distinguished from one another based on their unique attributes. For molecules represented as BulkMolecules, the simulation keeps track of only the total counts of the molecular species in each compartment (differentiated by a location tag, such as [c], which would indicate a molecule in the cytoplasm). For molecules represented as UniqueMolecules, the simulation keeps track of the individual attributes of each molecule.
The whole-cell simulation progresses in discrete time steps. At each time step, the interplay between the current state and the process objects determines the next state of the simulation. Each process object is designed to represent the molecular ramifications of one particular aspect of a cell’s function. In the released version of the whole-cell model, there are a total of 13 process objects, some of which are listed in Table 2. Because processes are separate from each other, each process can use the mathematical representation that is most appropriate for its underlying biology, each with the accuracy, dynamics, or constraints that are required or desired by a researcher (Fig. 1). Since the processes are assumed to be independent over the short length of a single time step, the updates to the state are made in steps described in Fig. 2B to prevent the processes from making conflicting updates. At the start of a time step, each process views the current state, and the calculateRequest method of each process is used to determine the number of molecules that are anticipated to be needed from each process. Based on the requests submitted by each of the processes, the state is partitioned such that each process has exclusive access to delete or modify the attributes of requested bulk and unique molecules. Using the pool of molecules allocated to the process, the evolveState method of each process calculates the changes that should be made to the state. These changes are then merged together to update the state, which advances the simulation by a single time step. Specific descriptions of calculations that are performed by some of the process methods can be found in Table 2.
TABLE 2.
Examples of processes implemented in the E. coli whole-cell model and a brief description of their functionalitiesa
| Process name | Function(s) |
|---|---|
| TranscriptInitiation | |
| calculateRequest | Determine the no. of transcription initiation events expected to happen |
| Request and withhold from other processes the required no. of inactive RNA polymerases | |
| evolveState | Remove allocated no. of inactive RNA polymerases |
| Initialize new active RNA polymerase molecules | |
| ChromosomeReplication | |
| calculateRequest | Determine the no. of deoxynucleoside triphosphate (dNTP) subunits needed to replicate DNA in this time step |
| Request and withhold from other processes the required no. of dNTP subunits | |
| evolveState | Remove polymerized dNTP subunits |
| Update positions of replication forks | |
| RnaDegradation | |
| calculateRequest | Determine the no. of each RNA species that should be degraded |
| Request and withhold from other processes the RNA molecules that should be degraded | |
| evolveState | Remove degraded RNA molecules |
| Add NTP subunits produced from degraded RNAs |
The implementation of two methods, namely, calculateRequest and evolveState, determines the functionality of each process. The calculateRequest method calculates the number of molecules that are expected to be used up by the process at a given time step and sends a request to the State to have the required number of molecules allocated to the process. The evolveState method uses the allocated molecules to make updates to the State.
At the end of each time step, the simulation evaluates whether the current state satisfies the conditions for a cell division event. The model currently supports a couple of options for the division criteria, reaching a certain critical mass or waiting a fixed length of time (D period) after a round of chromosome replication is finished (28), and could be expanded in the future to capture a more biophysical and mechanistic representation of the division event. If the conditions are not met, the cycle continues, and the simulation moves through another time step. If the conditions are satisfied, the cell division function divides the current state into two separate states for two daughter cells, and the simulation for the current cell is terminated. In the current version of the model, we assume that cell division occurs symmetrically, where each molecule has an equal chance of being allocated to each of the daughter cells. For simulations that extend for many generations, we often drop one of the daughter cells from the simulation to avoid an exponential increase in the number of cells to simulate.
Throughout all time steps of the simulation, objects named listeners act as loggers that record certain values of interest calculated by the states and processes. At the end of the simulation, the data logged by each of the listeners are written into binary files called tables, which are used by the downstream module to perform analyses and generate plots.
Through multiple improvements to the software implementation of the whole-cell modeling framework, we were able to cut down the computation time of simulating a single cell cycle from the roughly 24 h it took for the M. genitalium model to under 10 min for the E. coli model. This reduction in time enables us to repeat the simulation module as many times as desired depending on the purpose of the simulation. If multiple generations of cells need to be simulated, the output files that encode the inherited states of each daughter cell after division can be used to initialize the next generation of cells. The inclusion of the “adder” model of cell size homeostasis (29, 30) was a key modeling decision that made it possible for the E. coli model to maintain steady growth for multiple generations. The simulation can also be repeated with different random seeds given as inputs (due to the existence of stochastic processes within the model, each simulation output will be different), and the resulting batch of outputs can be used to evaluate the degree of heterogeneity that can arise from stochastic processes between otherwise identical cells. Lastly, the module can be run for different variants of simulation parameters, and the outputs from these individual simulations can be compared to discover how the varied parameters affect the outcome of the simulations.
Output/analysis.
The last module (Fig. 2A, output/analysis) uses the tables written by the simulations to perform analyses that help interpret the results of the simulation. Each analysis file produces plots or tables that pertain to a particular aspect of the simulation, including balanced growth, transcription rates, and concentrations of important molecules, such as RNA polymerases or ribosomes. Some analysis scripts optionally make use of the validation data object that consists of data taken from literature that was not included in the simulation data and, thus, was not taken into account during the simulation. In the E. coli model, a specific set of validation data was used as a benchmark to validate the model’s outputs. Details on how the validation was performed are presented in the following sections.
Data considerations.
With the framework to allow integration of submodels into a cohesive whole in place, the incorporation of data used to parameterize and assess the model is the next important aspect of the project to consider. Including large amounts of heterogeneous data in a whole-cell model is made easier by the fact that each physiological process can be modeled in a way best suited to the biology and data available. These data can come from many different sources, from low-throughput, highly specific measurements (e.g., single kcat and Km values for metabolic reaction kinetics) to high-throughput, omics-scale measurements with many data points (e.g., RNA sequencing counts of all RNA transcripts). For low-throughput measurements, these data points typically need to be aggregated from many different sources to include genome-wide parameters appropriate for modeling a whole cell (e.g., in the current model, metabolic reaction parameters for 431 reactions were assembled from 301 different sources). On the other hand, for high-throughput data, care must be taken for measurement bias if including and comparing many data sets (e.g., applying normalization techniques for differential expression in RNA sequencing and microarray data [31, 32]).
Another important consideration is the temporal and spatial resolution of data sets. Despite major improvements in single-cell technologies in recent years, many measurements still come from population-level experiments at fixed time points with no spatial resolution. In contrast, whole-cell modeling inherently focuses on single cells, allows for short time steps (on the order of a second), and contains compartmental separation (e.g., cytoplasm versus periplasm). This means that fine-grained temporal and spatial information needed to build whole-cell models often has to be inferred from average measurements across many cells, each of which can be at a different point in the cell cycle. Including dynamic and space-resolved single-cell data will improve the accuracy and predictive power of whole-cell models, allowing them to better capture dynamics that lead to heterogeneous cell populations.
Sometimes measurements from different data sets are not consistent with each other. For example, omics-level data (transcriptomics, degradation rates, and translation efficiencies) used to determine the number of ribosomes and RNA polymerases in an E. coli cell did not lead to enough complexes to support doubling of the cell or match more specific measurements of the number of those complexes in cells (8). These discrepancies can arise from the fact that many measurements are reported as point values, but in reality, these measurements represent some uncertainty about the underlying physical system, which will lead to uncertainty in the derived parameters (11). More details on how these inconsistencies can be addressed and how we can learn through this reconciliation are discussed in “Deep curation,” below.
As with any model, it is also imperative to include validation (and possibly test) data to assess the model output. These data should be orthogonal to the data used to parameterize the model (e.g., a proteomics data set when model protein counts are determined from transcriptomics, degradation rates, and translation efficiencies) instead of being a biological replicate of the data used for parameterization (e.g., a transcriptomics data set from a different laboratory than the transcriptomics data set used to parameterize the model). Although the model itself can provide some implicit validation that the mechanism and data are accurate by looking at high-level behavior (e.g., the cell components double and all cell components can be produced), it is not possible to truly assess the validity of the data and biological representation described by the model without validation data.
Current model snapshot
The E. coli whole-cell modeling project is an ongoing endeavor, with new features and components being continuously added to the model. In this section, we provide a description for a snapshot of the E. coli model that was most recently released to the scientific community.
Accessibility.
The most recent release of the E. coli whole-cell model can be freely accessed through the WholeCellEcoli Release GitHub repository (https://github.com/CovertLab/WholeCellEcoliRelease). As of August 2020, this repository contains a snapshot of the model that was used in our original description of this work (8). The unreleased version of the model that is actively being developed by our team is maintained in a private GitHub repository. As this repository is frequently changing and contains preliminary work at various stages of integration, access to this repository will be granted for researchers who would like to directly collaborate on or contribute to the project. We expect to release updated versions of the model in the future with corresponding publications that describe the results and changes of the new version.
Running the model.
The instructions on how to set up the E. coli whole-cell model are explained in detail in the docs directory of the WholeCellEcoliRelease GitHub repository. In short, we support two different ways to set up the environment to properly run the model. The first option is to run the model within a Docker container. A Docker image is hosted in the GitHub repository for users to pull, or a user can build their own Docker image from Dockerfiles included in the repository. Running a Docker container from either image will provide the same Python environment that the whole-cell model was developed in. The environment includes the correct version of Python (2.7.16) and all the binary libraries and Python packages that the model depends on. This method eliminates the need for users to set up the runtime environment on their own and is ideal for anyone who wants to quickly run the model and analyze its outputs. Alternatively, one can also set up the required Python virtual environment directly on one’s local machine and run the model inside the environment. Setting up the Python environment locally requires many steps that are highly dependent on the user’s computing environment and, thus, is only recommended for users who wish to participate in the active development of the model.
Any technical issues encountered while setting up and running the whole-cell model are welcome to be submitted to the Issues tab of the WholeCellEcoliRelease repository.
Included functionality.
A “complete” whole-cell model should account for all of the functionality of a living cell. Because not all genes and biological interactions in E. coli have been experimentally characterized, a more realistic goal is to incorporate the functionality of all known genes to which the E. coli whole-cell model is progressing. Table 3 shows how many instances of each type of modeled biological function are currently implemented in the whole-cell model, including functional genes, metabolites, and viable environmental conditions. Some of the major functionality includes transcription, translation, DNA replication, signaling (including zero-, one-, and two-component systems), transcription regulation, metabolism (including transport), and cell division. Current simulations exhibit stable growth and division over many generations and can respond to certain environmental changes to grow at different growth rates.
TABLE 3.
Implemented functionality in the current whole-cell model version, including physiological and modeling functions
| Category | Function | No. included |
|---|---|---|
| Gene expression | Functional gene products | 1,214 |
| RNAs | 4,558 | |
| Proteins | 4,353 | |
| Metabolism | Metabolite concentrations | 140 |
| Total metabolites | 1,176 | |
| Metabolic reactions | 1,839 | |
| Enzymes | 962 | |
| Regulation | Signaling reactions | 57 |
| Transcription factors | 22 | |
| TF-gene interactions | 438 | |
| Other | Complexation reactions | 1,023 |
| Cell compartments | 9 | |
| Environments | 3 | |
| Modeling | Processes | 13 |
| States | 3 | |
| Analysis plots | 142 | |
| Variants (experimental comparisons) | 17 |
Table 4 shows the numbers of parameters and their sources that are used to simulate each included functionality of the whole-cell model. For each functionality, we can count both the number of simulation parameters (parameters packaged into simulation data; see “Whole-cell modeling framework,” above, for details), which are parameters that are used by the simulation itself, and the number of curated parameters (parameters packaged into raw data), which are raw data points that are directly associated with an experimental measurement. Note that for some of the data, the number of simulation parameters does not match the number of curated parameters; this is because some of the simulation parameters are not direct copies of the curated parameters but rather values that are calculated or estimated from one or more of the curated parameters through the Parameter Calculator (ParCa) module of the whole-cell model (Fig. 2). For instance, to model RNA degradation, each of the 4,558 RNA species that are included in the whole-cell model needs to be associated with a parameter (Km) that quantifies its affinity with endoRNases. Since there were no identified literature sources that directly report these parameters, we use the measured half-lives of 3,876 RNA species (33) to derive the 3,876 Km values, assuming that the degradation reactions follow Michaelis-Menten kinetics. For the 682 RNA species that do not have a reported half life, we chose a representative value (the average reported half-lives of mRNAs) to calculate their Km values.
TABLE 4.
Numbers of simulation parameters, curated parameters, and data sources included in the whole-cell model grouped by physiological processa
| Process | Data type | No. of simulation parameters (simulation data) | No. of curated parameters (raw data) | No. of sources |
|---|---|---|---|---|
| Metabolism | k cat | 431 | 431 | 301 |
| Km | 208 | 208 | 155 | |
| Small-molecule concentrations | 140 | 140 | 4 | |
| Maintenance energy requirements | 2 | 2 | 1 | |
| External exchange flux presence | 54 | 54 | 1 | |
| Transcription | EndoRNase-RNA affinities | 4,558 | 3,876 (RNA half lives) | 1 |
| RNase rates | 2 | 3,876 (RNA half lives) | 1 | |
| Basal RNA expression | 4,558 | 4,288 (RNA expression) | 1 | |
| Regulated RNA expression | 438 | 900 (expression fold changes) | 36 | |
| Translation | Protein half-lives | 4,353 | 9 | 2 |
| Protein translation efficiencies | 4,353 | 2,387 | 1 | |
| Signaling | Dissociation constants (ligand-TF binding) | 56 | 28 | 1 |
| Reaction rates for two-component systems | 29 | 8 | 1 | |
| Cell properties | Growth related | 12 | 25 | 1 |
| Division timing | 3 | 3 | 2 | |
| Elongation rates | 5 | 5 | 1 | |
| Cell density | 1 | 1 | 1 |
Simulation parameters are parameters that are directly used in the simulation and can be found in the simulation data object. Each simulation parameter can be calculated from single or multiple curated parameters. Curated parameters are the raw data points that are each directly tied to an experimental measurement and are found in the raw data object. The number of sources column represents the number of individual literature sources from which the curated parameters were gathered.
Although progress is continually being made to make the whole-cell model gene complete, there are certain hurdles that prevent including all functionality. One of the major reasons is a lack of knowledge, both in terms of the available data to parameterize a submodel and the mechanisms by which molecules interact with each other to give rise to the observed behavior of actual cells. Measurement techniques are improving, which allows for greater throughput and higher accuracy, but most available data still require some level of manual curation to ensure only high-quality data are used in the model, which is why not all data that we had initially reviewed were included in this model. In general, omics-scale measurements allow more functionality to be incorporated in the easiest way by enabling the inclusion of data in bulk instead of curating thousands of papers or developing models of individual interactions. Despite recent advances in utilizing natural language processing (NLP) algorithms to automatically curate large numbers of papers (34), a more fine-grained and manual characterization of pathways and interactions is still needed in most other cases.
Output and validation.
Output from whole-cell models allows researchers to see a fine-grained representation of cell physiology that is difficult to measure in vivo. Although single-cell techniques for measuring the state of cells have progressed, a comprehensive measurement of cell composition is impossible over time due to the destructive nature of measurement techniques, such as mass spectrometry or RNA sequencing. Whole-cell modeling allows for detailed insights into cell behavior over time by effectively interpolating between fixed time point or bulk population measurements, which are often used to parameterize the model. The dynamics of all molecules in a cell are tracked over time in the simulation, so the simulation outputs can include these detailed temporal dynamics as well as other values that are even more difficult to measure experimentally. Specific cellular dynamics that the model can track and generate outputs for include, among many others, counts of all molecules, fluxes of metabolic reactions, probabilities of transcription initiation for each gene, total mass of all small metabolites, locations of replication forks, effective DNA polymerase, RNA polymerase and ribosome elongation rates, number of RNAs degraded, and fraction of active RNA polymerases and ribosomes. An example of an output plot that can be generated from the model is shown in Fig. 3. The plots follow the dynamics of events that happen around the genes rpoA, rpoB, and rpoC, which encode subunits of the core RNA polymerase enzyme.
FIG 3.
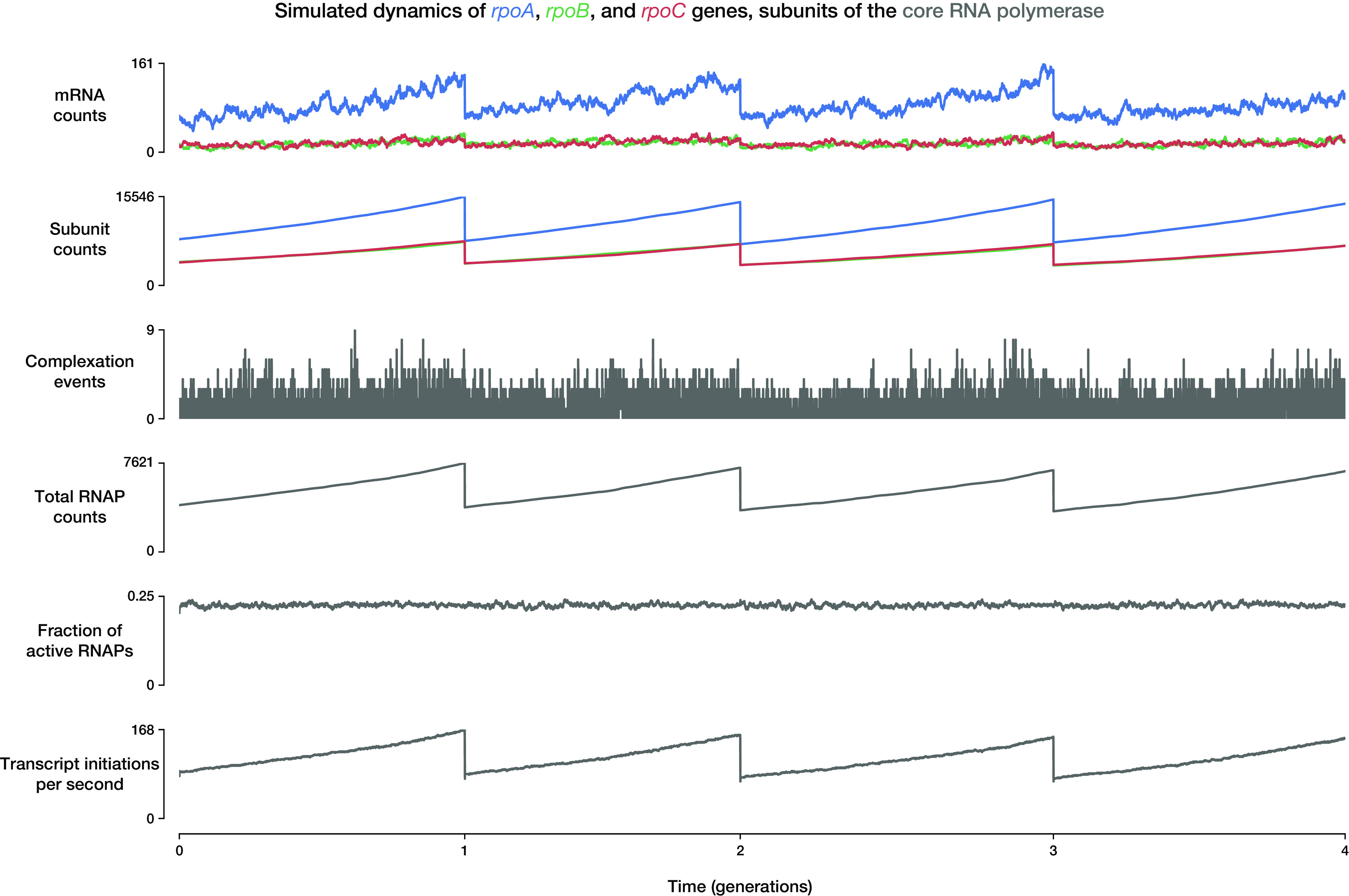
Example output plot that can be generated from the E. coli whole-cell model. The plots follow the dynamics of cellular events that happen around the genes rpoA (blue), rpoB (green), and rpoC (red), the products of which eventually become subunits of the core RNA polymerase (RNAP; gray) for the duration of 4 cell cycles. From top to bottom, the values plotted are the mRNA counts of each gene, the protein subunit counts (including those complexed into RNAPs), the number of complexation events per time step, total RNA polymerase counts, fraction of RNA polymerases that are active, and the total number of transcript initiation events that happen per second. Note that the discontinuities in some of the plots are the direct consequences of cell division events, at which the molecule counts of the mother cell are split into the two daughter cells. After a cell division event, the plots follow the dynamics of only one of the two daughter cells.
As with any model, validation of the output using previously withheld data gives more confidence in the results drawn from the model. The large numbers of data sets available in E. coli make it easier to use data sets that are preexisting and orthogonal to those used to parameterize the model in order to verify the output. However, there are still limitations in finding validation data sets that include a large number of outputs of interest (transcripts, proteins, reactions, etc.) and provide measurements made under appropriate conditions that are comparable to the conditions that can be simulated by the whole-cell model. The orthogonal data sets currently used to validate the E. coli model are proteomics, fluxomics, and gene essentiality data, as shown in Table 5. Using these data, we could verify that the protein counts and the fluxes of metabolic reactions predicted by the model align with relevant experimental values, with R2 values of 0.61 and 0.71, respectively (8).
TABLE 5.
Validation data set aside for comparison with whole-cell model output, grouped by physiological processa
| Process | Data type | No. of validation data points | No. of sources |
|---|---|---|---|
| Metabolism | Fluxomics | 23 | 1 |
| Translation | Proteomics | 4,480 | 2 |
| Cell properties | RNAP and ribosome counts | 2 | 1 |
| Gene essentiality | 4,558 | 1 |
Validation data points are experimental measurements that are not used during model construction or simulation but can be compared to model outputs. The number of sources column shows the number of individual literature sources from which the validation data points were gathered.
Second, deeper and more exciting validation is performed with follow-on validation experiments driven by model predictions. As described previously (7, 8), integrating data into whole-cell models can be used to make predictions that can be confirmed in vivo. In the E. coli model, we could make predictions on the degradation rates of certain proteins based on the predicted discrepancies between the production and degradation rates of each protein (8). More details on how the model can be used as a prediction tool to design validation experiments are discussed in “Model-driven discovery,” below.
Model-driven discovery
Building a whole-cell model is just a start to the assessment of our biological understanding of an organism. Additional benefits come from applying the model to generate new knowledge or analyze existing data and, thus, confirm or update current understanding. Several examples of applying the integrated model are highlighted below, with more applications discussed previously (35).
High-throughput discovery.
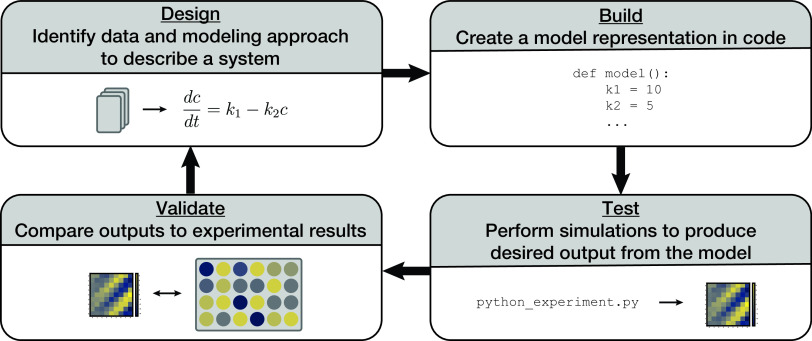
Building a comprehensive whole-cell model allows researchers to take advantage of a design-build-test-validate cycle for hypothesis testing and validation (Fig. 4). This approach can be completed much more quickly than relying solely on in vivo experimentation and can lead to high-throughput discovery. The “design” stage of this cycle requires data curation and an assessment of the most appropriate modeling approach, as discussed above. In the “build” stage, a computational model is created that uses the curated data, generates required model parameters, and solves for updates to the simulated state of the cell. In the “test” stage, in silico experiments are performed to produce output from the whole-cell model, which includes the newly added data and model. Finally, in the “validate” stage, these outputs can be validated by comparing to newly generated or already existing (and withheld from construction of the model) in vivo data. The benefit to this approach is that once a hypothesis is developed or tested in silico, it can narrow the in vivo experimental scope instead of performing a much larger and time-consuming search in vivo. Since each simulation cell cycle takes about 10 min to complete and parallel computing can be used for independent simulation cell lineages, an in silico experiment with a large number of perturbations can be queued up and run in an afternoon. This can be compared to the several weeks it takes to clone a small set of constructs and cell lines to perform an experiment in vivo. Assuming the model already contains a submodel for the hypothesis in question, iteration and new discovery can occur quite rapidly.
FIG 4.
E. coli whole-cell model can allow for a design-build-test-validate cycle that allows for high-throughput discovery. Design requires curating data and representing a system mathematically. The new model is then built in code. Executing the code allows for experimentation and produces results with the possibility of many experiments running from the model. The model results can be compared with experimental results to inform further model design.
In the “test” stage of the cycle described above, the constructed model can be leveraged for objective optimization, which can lead to new discoveries. Objective optimization can be used to determine metaparameters to use in the model based on an objective to capture a given data set or to identify parameters (like gene expression levels) to achieve a certain cellular behavior in the model. For example, if the user desired information about how to increase the growth rate, then maximizing the growth rate could be set as the objective, and input parameters that relate to gene expression, degradation rates, reaction rates, or other desired perturbations could be modified while recording the resulting growth rate (objective). Describing a target objective clearly identifies what the desired output should be and allows for the application of many common approaches to solve for parameters that will best achieve the objective. Performing a grid search can be appropriate when the number of parameters is small. For a larger search space that is smooth and convex, applying optimization techniques like gradient descent could lead to an optimal solution. However, nonconvex heuristics (e.g., simultaneous perturbation stochastic approximation or genetic algorithms) will likely need to be used due to the highly nonlinear nature of biology and stochasticity of simulations. Some examples of how objective optimization can be used to drive discovery are discussed more in the “Model predictions,” below.
In addition to targeted objective optimization, a whole-cell model can provide a means of performing a high-throughput screen. Large, genome-scale perturbations can be performed to determine the impact on a wide range of model outputs. For example, simulating gene knockouts and comparing predicted growth rates to measured values can identify discrepancies to investigate. This approach had been applied with the M. genitalium whole-cell model and led to kinetic parameter predictions that were later validated through in vivo experiments. Importantly, these newly predicted values led to more accurate simulations once included in the model (27), thereby completing the cycle and opening up the possibility of another iteration of the cycle with an improved model.
Another example of how model discovery can lead to improvements was shown with protein half-life predictions in the E. coli whole-cell model (8). By including multiple data sets and mechanisms linking RNA expression to protein levels (“design” and “build” stages), we could predict a protein degradation rate for every protein in the genome (“test” stage). For a select group of proteins where these values were significantly different from the half-life predicted by the N-end rule hypothesis (36), follow-up experiments were performed in vitro to confirm these predictions for seven proteins (“validate” stage) (8). This targeted subset of protein half-life measurements was confirmed to be different from the N-end rule and then incorporated in the whole-cell model to improve its predictive ability.
High-throughput discovery techniques are often meant to narrow the space of experiments that need to be performed in vivo, leading to faster iteration. Confirmation experiments can be used to validate the output of the model, lead to an expansion of the community knowledge of E. coli, and be used to further refine the whole-cell model. In this way, collaborations between computational groups and experimental groups can greatly improve the overall knowledgebase of this model organism.
Model predictions.
The whole-cell model is most useful and has the most potential as a tool to identify emergent properties arising from a large number of factors and interactions due to the scale of the whole-cell modeling approach and the integration of biological mechanisms that happens inside the model. The interactions between different genes are known to play a significant role in physiology and usually lead to nonlinear responses (37), which can be captured by a whole-cell model. Often, it is desirable to determine which parameters or genes work in a synergistic way to lead to a desired outcome. If the number of parameters is small enough, using a design-of-experiments approach can identify the strongest interactions between parameters (38). With a design-of-experiments approach, researchers can use either a full factorial design (every combination of parameter perturbations is included) to characterize all of the parameter interactions or a fractional factorial design (a limited subset of combined perturbations is included) to identify main parameter effects and a subset of interaction effects. A full factorial approach can quickly become computationally intractable with a large number of parameters, in which case a fractional factorial design can still be used to elucidate many of the important interactions.
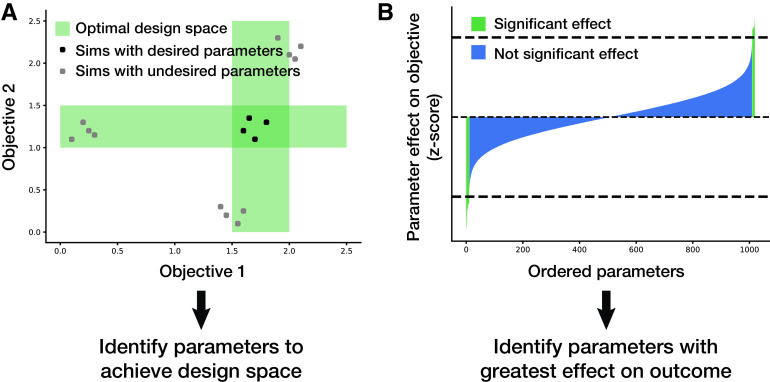
High-throughput studies can also identify parameters of interest. As shown in Fig. 5A, for a desired design space, parameters can be varied and selected based on a range of optimalities (as indicated by the green regions). Thousands of parameters in the model (e.g., RNA expression, protein degradation, etc.) can be varied to identify which ones have the most significant effect on an objective value (e.g., the growth rate of the cell, a flux through a pathway, or any other metric that can be described in the whole-cell model framework). Perturbing many parameters at once and running a large number of simulations can provide the average effect that each parameter has on the output. Using multiple-hypothesis adjustment, significant parameters can be identified as those being outside a z-score cutoff, as shown in Fig. 5B. This method has been demonstrated to be successful in identifying parameters that contribute most to increasing or decreasing the growth rate of the simulation (8).
FIG 5.
(A) Applying the model to identify parameters of interest that meet a desired design space. (B) Applying the model to identify parameters that cause a significant effect on an objective of interest.
Whole-cell models can even be used to make entirely novel predictions that fall outside the scope of prior knowledge included in the model. This was demonstrated with the original M. genitalium whole-cell model where novel enzyme functionality was predicted based on a knockout study that was not consistent with experimental data (7).
Deep curation.
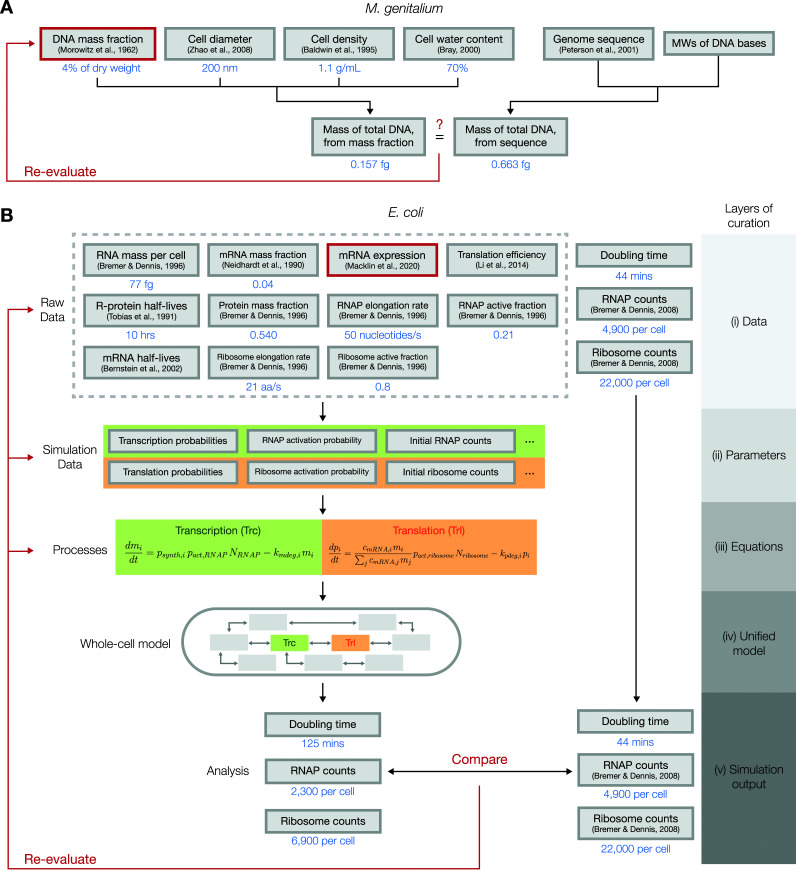
When heterogeneous, independent measurements are made on the properties of a biological system of interest, a natural assumption to make is that the measurements are consistent with each other. Although in many cases this assumption holds true, whole-cell models can highlight instances of incoherence between the measurements. In the process of building the M. genitalium whole-cell model (7), for example, it was noted that the total mass of DNA within the cell could be estimated in two different ways: one was to use the measured mass fraction of DNA (39) and the dry cell mass, which in turn can be derived from the cell diameter (40), the cell density (41), and the water content of the cell (42); the other was to use the genome sequence (43) and the molecular weights (MWs) of DNA bases (Fig. 6A).
FIG 6.
Diagrams of how deep curation could be used to evaluate the cross-consistency of heterogenous data sets. (A) In the building of the M. genitalium whole-cell model, it was noted that the mass of the total DNA could be calculated using two different methods, one from the measured mass fraction of DNA and the other from the genome sequence, and was significantly different from each other. This led to a suggestion that the measurement for the mass fraction of DNA contained errors. (B) In the E. coli whole-cell model, raw data from various sources were tied together into a unified, mechanistic model, using multiple layers of curation. Certain outputs from the resulting model, however, were inconsistent with reported experimental values, which led us to reevaluate the data sources, parameters, and equations used in the model to identify the source of the discrepancy. Using a set of criteria, including the reproducibility of results reported in the literature, we concluded that the mRNA expression data underestimated the expression of genes that encode RNA polymerase and ribosomal subunits.
If these independently measured parameters are consistent with each other, we can be more confident that the parameters are accurate and, thus, add more value to hypotheses derived from these parameters. Any inconsistencies between the parameters can prompt us to make investigations on the source of the discrepancy. In the case of the mass of DNA in M. genitalium, the mass calculated from the mass fraction was less than one-third of the mass calculated from the genome sequence. This discrepancy could have arisen from errors made in one or more of the original measurements/parameters that were used to calculate the DNA mass. In this case, it was unlikely that the large discrepancy arises from errors in the cell diameter, density, water content, genome sequencing, or molecular masses of DNA bases, as the experimental techniques used to measure these values are very straightforward and not prone to large errors. Thus, the conclusion was that the direct measurement of the DNA mass fraction in the cell presumably underestimated the actual value.
The same approach of cross-evaluating heterogeneous data sets against each other was applied to the E. coli whole-cell model, albeit in a much “deeper” sense than what had been done with the DNA mass fraction of M. genitalium (Fig. 6B). Accordingly, we chose to name this approach “deep curation” to reflect the multiple layers of curation that are involved in the cross-evaluation: (i) the data layer, where raw data are first gathered; (ii) the parameter layer, where parameters are calculated from raw data; (iii) the equation layer, where parameters are plugged into equations that describe the dynamics of the biological system; (iv) the unified model layer, where equations are tied together to form a unified model of the cell; and (v) the output layer, where the model’s outputs are compared with validation data. Details on each of these layers of curation are explained in the paragraphs below, with a special focus on data regarding transcription and translation.
In the building of the E. coli model, we started by gathering raw data from numerous sources that quantitatively measured properties of E. coli cells. Among the raw data, several sources represented in the first layer of Fig. 6B (the “data” layer) were used in constructing the transcription and translation processes, two key processes in the model that determine the rate of protein production and, in turn, the rate of cellular growth. The data used here included the measured RNA mass per cell (44), mass fraction of mRNAs (45) and proteins (44), mRNA expression (8), translation efficiencies (46), half-lives of ribosomal proteins (36), elongation rates and active fractions of RNA polymerases and ribosomes (44), and mRNA half-lives (33).
As described in “Whole-cell modeling framework,” above, the first step in running a whole-cell simulation involves the conversion of the raw data into parameters that are directly used by the simulation (the “parameters” layer). For transcription and translation, the key parameters calculated in this step include the transcription/translation probabilities of each gene/mRNA, the activation probabilities of RNA polymerases and ribosomes, and the initial counts of RNA polymerases and ribosomes. In calculating these parameters, existing literature or general knowledge on the cellular process in question can be used to make certain assumptions, which could become a source of discrepancies between data sets if the assumptions turn out to be incorrect. For instance, to calculate the transcription probabilities of each gene, we assumed that the transcription rate and the degradation rate of each mRNA must be balanced, such that the counts of each mRNA species are at steady state under short timescales.
Next, the parameters calculated in this layer are plugged into the equations that describe the dynamics of the cellular processes (the “equations” layer). In transcription, for instance, the transcription probability, the activation probability of RNA polymerases, and the current counts of RNA polymerases determine the current transcription rate of an RNA species. As in the case with the parameters layer, these equations themselves are also curated from existing literature or general knowledge on the underlying biochemistry of the cellular process, which makes these equations valid targets of reevaluation should any inconsistencies appear in later steps.
In the next layer, these equations are tied together to form a unified model. In our case, this was the complete E. coli whole-cell model, which consisted of 13 different processes, five of which were directly associated with the transcription and translation equations in the previous layer. This “unified model” layer can be used to generate the final “simulation outputs” layer, which consists of all simulated outcomes that can be generated from the unified model. The outputs in this layer can be directly compared to experimentally measured values; a significant discrepancy here would suggest that the heterogeneous data sets gathered to construct the model, including the experimentally measured value that the simulation outcomes were compared to, are inconsistent.
Upon our initial run of the E. coli whole-cell model, we immediately noticed that the simulated cell grew significantly slower (doubling time of 125 min) than actual E. coli cells growing in culture (doubling time of 44 min). Moreover, the average counts of RNA polymerases and ribosomes, the key molecules that drive transcription and translation, were also significantly lower than what has been observed experimentally (47). This led us to suspect that one or more elements in the layers of curation we performed to build the model contained significant errors, which includes the raw data that we gathered from various sources, the parameters we calculated from the raw data, the equations that we used to build the related processes in our model, or the validation data we used to compare with the simulation outputs.
We chose to reassess the elements that were deemed potential sources of this inconsistency using three criteria to evaluate the likeliness that each of these data sources may be the culprit. First, we looked at whether alternate measurements of the parameter in question exist and whether these alternate values are significantly different from the original values we had used for the model. Second, we used the whole-cell model to determine whether adjusting the parameter in question would enable the model to produce the correct outputs, in this case, the growth rate of the cell. Lastly, we checked if the adjusted values we used to produce the correct growth rate also corrected the counts of RNA polymerases and ribosomes. The only candidate that satisfied all three criteria was the mRNA expression measurement. Alternative data sets for mRNA expression showed us that the expression levels of key genes can be highly variable between independent measurements, which suggested that individual measurements of this data type are vulnerable to large errors. Through iterative parameter fitting, we could adjust the expression levels of 58 RNA polymerase and ribosomal subunits to be, on average, 61% higher, which successfully led to simulations with correct doubling times and RNA polymerase/ribosome counts (8). Thus, our conclusion was that the mRNA expression data that we had originally used as a raw data source underestimated the true expression levels of most genes that encode subunits of RNA polymerases and ribosomes.
Under ideal circumstances, each submodel of the whole-cell model should be integrated into the larger model in its original form without the need to make any changes to its parameters or assumptions. As demonstrated above, however, there are cases where certain submodels are incompatible with each other in a way that is evident through the outputs of the whole-cell model. Because each of these submodels are parameterized from experimentally measured data, any inconsistency between them points toward a possible avenue of discovery. In some cases, noise or general inaccuracy in the raw data measurements (the first layer of deep curation) could be the culprit. In other cases, an error or a missing piece of knowledge in the underlying equations that are used to calculate model parameters or build submodels (the second and third layers of deep curation) may be the reason for the discrepancies.
In either case, resolving these inconsistencies must start with a deep dive into how the measurements were originally made and how the model parameters and equations were derived in order to identify any potential sources of errors or missed assumptions. We then can assess whether addressing these errors in curated data will sufficiently rectify the incompatibilities observed in the whole-cell model, using criteria described in the example described above. In the case where an alternative measurement or equation exists that successfully fixes the model, we can simply replace the existing component with the newly found alternative. In cases where an appropriate alternative is not available, we need to determine a compatible set of parameters through optimization techniques or determine a proper modeling approach to best describe the underlying data while reconciling the submodels. In the case of transcription and translation submodels described above, we reverse-calculated the required expression levels of RNA polymerases and ribosomal proteins using the known doubling times of E. coli and used these values instead of the experimentally measured expression levels.
The E. coli whole-cell model and the concept of deep curation provide us with a platform to link heterogeneous data via a mechanistic model and automatically evaluate the cross-consistency of the integrated data through the outputs of the simulation. Deep curation will offer an unprecedented opportunity to automatically evaluate the validity of data generated for this model organism, especially as we expand the model further to include additional functionality. By identifying areas where the data seem inconsistent, we can guide future curation efforts by suggesting lines of research that could resolve the discrepancies and even make predictions for the correct values of certain parameters.
DISCUSSION
The E. coli whole-cell model introduced in this review represents a launching point for integrating the large amount of data that is continually generated for E. coli by the scientific community. Whole-cell models aim to maintain mechanistic representations of biological interactions while scaling the model up to the genome scale, which is a key feature that enables these models to make useful predictions and generate enhanced knowledge of an organism. Using the E. coli whole-cell model, we could identify discrepancies between previous measurements made on this microbe, make predictions on certain parameters and verify them experimentally, and gain novel insights on the physiology of this key model organism.
Although the current version of the model does not yet cover all known functionalities of genes, the whole-cell modeling project will continue to work toward achieving a complete whole-cell model of E. coli. There is an ongoing effort to curate new data to generate more model parameters and to represent additional biological interactions through mechanistically linked processes. Although many types of data will be useful for expanding the model, some of the most valuable data we see at the moment are kinetic parameters of protein complexation and metabolic reactions, interaction of proteins with the genome, more transcriptomics and quantitative metabolomics data under different environments, and long-read sequencing of transcripts for better transcription unit structure. As a step toward making the whole-cell model more accessible to the research community, we recently began a collaboration with EcoCyc, a curated database of the genome and biochemical components of E. coli (48), to more closely integrate the whole-cell model with the existing knowledge for E. coli generated to date. Combined with the deep curation approach, this integration will enable a rapid cross-validation of various heterogeneous data sets that have been or will be curated by EcoCyc. The knowledge gained by this integration will also be shared to the E. coli community through EcoCyc, enabling the entire research community to use the whole-cell model to generate new hypotheses, confirm understanding of this well-studied organism, and create useful predictions to speed up discovery. We are also developing visualization tools for the E. coli model that will help a broader audience engage with the inner workings of the whole-cell model.
We hope that the initial release of the E. coli whole-cell model brings us a step closer to the “complete solution of E. coli” proposed by Francis Crick. Building such a model was made possible only by the extensive amounts of data generated by the entire research community throughout history. Likewise, further improvements to the model will be heavily dependent on the contributions from researchers across all spectra of experience and expertise.
ACKNOWLEDGMENTS
We would like to thank members of the Covert lab for helpful discussions. This work was supported by the Paul G. Allen Frontiers Group through the Allen Discovery Center at Stanford and a Graduate Student Fellowship from the Kwanjeong Educational Foundation to G.S.
We declare no conflicts of interest.
Contributor Information
Markus W. Covert, Email: mcovert@stanford.edu.
Peter D. Karp, SRI International, Menlo Park, California, USA
REFERENCES
- 1.Crick FHC, Project K. 1973. The complete solution of E. coli. Perspect Biol Med 17:67–70. doi: 10.1353/pbm.1973.0061. [DOI] [Google Scholar]
- 2.Tomita M. 2001. Whole-cell simulation: a grand challenge of the 21st century. Trends Biotechnol 19:205–210. doi: 10.1016/S0167-7799(01)01636-5. [DOI] [PubMed] [Google Scholar]
- 3.Shuler ML, Leung S, Dick CC. 1979. A mathematical model for the growth of a single bacterial cell. Ann N Y Acad Sci 326:35–52. doi: 10.1111/j.1749-6632.1979.tb14150.x. [DOI] [Google Scholar]
- 4.Domach MM, Leung SK, Cahn RE, Cocks GG, Shuler ML. 1984. Computer model for glucose-limited growth of a single cell of Escherichia coli B/r-A. Biotechnol Bioeng 26:1140. doi: 10.1002/bit.260260925. [DOI] [PubMed] [Google Scholar]
- 5.Varma A, Palsson BO. 1994. Stoichiometric flux balance models quantitatively predict growth and metabolic by-product secretion in wild-type Escherichia coli W3110. Appl Environ Microbiol 60:3724–3731. doi: 10.1128/aem.60.10.3724-3731.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Tomita M, Hashimoto K, Takahashi K, Shimizu T, Matsuzaki Y, Miyoshi F, Saito K, Tanida S, Yugi K, Venter J, Hutchison C. 1999. E-CELL: software environment for whole-cell simulation. Bioinformatics 15:72–84. doi: 10.1093/bioinformatics/15.1.72. [DOI] [PubMed] [Google Scholar]
- 7.Karr JR, Sanghvi JC, Macklin DN, Gutschow MV, Jacobs JM, Bolival B, Jr, Assad-Garcia N, Glass JI, Covert MW. 2012. A whole-cell computational model predicts phenotype from genotype. Cell 150:389–401. doi: 10.1016/j.cell.2012.05.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Macklin DN, Ahn-Horst TA, Choi H, Ruggero NA, Carrera J, Mason JC, Sun G, Agmon E, DeFelice MM, Maayan I, Lane K, Spangler RK, Gillies TE, Paull ML, Akhter S, Bray SR, Weaver DS, Keseler IM, Karp PD, Morrison JH, Covert MW. 2020. Simultaneous cross-evaluation of heterogeneous E. coli datasets via mechanistic simulation. Science 369:eaav3751. doi: 10.1126/science.aav3751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Grieves MW. 2019. Virtually intelligent product systems: digital and physical twins. Complex Syst Eng Theory Pract 2019:175–200. [Google Scholar]
- 10.Karr JR, Williams AH, Zucker JD, Raue A, Steiert B, Timmer J, Kreutz C, Wilkinson S, Allgood BA, Bot BM, Hoff BR, Kellen MR, Covert MW, Stolovitzky GA, Meyer P, DREAM8 Parameter Estimation Challenge Consortium. 2015. Summary of the DREAM8 parameter estimation challenge: toward parameter identification for whole-cell models. PLoS Comput Biol 11:e1004096. doi: 10.1371/journal.pcbi.1004096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Babtie AC, Stumpf MP. 2017. How to deal with parameters for whole-cell modelling. J R Soc Interface 14:20170237. doi: 10.1098/rsif.2017.0237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Rees-Garbutt J, Chalkley O, Landon S, Purcell O, Marucci L, Grierson C. 2020. Designing minimal genomes using whole-cell models. Nat Commun 11:1–12. doi: 10.1038/s41467-020-14545-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Burke PEP, de Claudia BL, Costa LDF, Quiles MG. 2020. A biochemical network modeling of a whole-cell. Sci Rep 10:1–14. doi: 10.1038/s41598-020-70145-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Orth JD, Thiele I, Palsson BØ. 2010. What is flux balance analysis? Nat Biotechnol 28:245–248. doi: 10.1038/nbt.1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Shu J, Shuler ML. 1991. Prediction of effects of amino acid supplementation on growth of E. coli B/r. Biotechnol Bioeng 37:708–715. doi: 10.1002/bit.260370804. [DOI] [PubMed] [Google Scholar]
- 16.Bosdriesz E, Molenaar D, Teusink B, Bruggeman FJ. 2015. How fast-growing bacteria robustly tune their ribosome concentration to approximate growth-rate maximization. FEBS J 282:2029–2044. doi: 10.1111/febs.13258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Khodayari A, Maranas CD. 2016. A genome-scale Escherichia coli kinetic metabolic model k-ecoli457 satisfying flux data for multiple mutant strains. Nat Commun 7:13806–13812. doi: 10.1038/ncomms13806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Fröhlich F, Kaltenbacher B, Theis FJ, Hasenauer J. 2017. Scalable parameter estimation for genome-scale biochemical reaction networks. PLoS Comput Biol 13:e1005331. doi: 10.1371/journal.pcbi.1005331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.St John PC, Strutz J, Broadbelt LJ, Tyo KE, Bomble YJ. 2019. Bayesian inference of metabolic kinetics from genome-scale multiomics data. PLoS Comput Biol 15:e1007424. doi: 10.1371/journal.pcbi.1007424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Costello Z, Martin HG. 2018. A machine learning approach to predict metabolic pathway dynamics from time-series multiomics data. NPJ Syst Biol Appl 4:1–14. doi: 10.1038/s41540-018-0054-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Camacho DM, Collins KM, Powers RK, Costello JC, Collins JJ. 2018. Next-generation machine learning for biological networks. Cell 173:1581–1592. doi: 10.1016/j.cell.2018.05.015. [DOI] [PubMed] [Google Scholar]
- 22.Zampieri G, Vijayakumar S, Yaneske E, Angione C. 2019. Machine and deep learning meet genome-scale metabolic modeling. PLoS Comput Biol 15:e1007084. doi: 10.1371/journal.pcbi.1007084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Yang JH, Wright SN, Hamblin M, McCloskey D, Alcantar MA, Schrübbers L, Lopatkin AJ, Satish S, Nili A, Palsson BO, Walker GC, Collins JJ. 2019. A white-box machine learning approach for revealing antibiotic mechanisms of action. Cell 177:1649–1661. doi: 10.1016/j.cell.2019.04.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ma J, Yu MK, Fong S, Ono K, Sage E, Demchak B, Sharan R, Ideker T. 2018. Using deep learning to model the hierarchical structure and function of a cell. Nat Methods 15:290–298. doi: 10.1038/nmeth.4627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Brunk E, George KW, Alonso-Gutierrez J, Thompson M, Baidoo E, Wang G, Petzold CJ, McCloskey D, Monk J, Yang L, O'Brien EJ, Batth TS, Martin HG, Feist A, Adams PD, Keasling JD, Palsson BO, Lee TS. 2016. Characterizing strain variation in engineered E. coli using a multi-omics-based workflow. Cell Syst 2:335–346. doi: 10.1016/j.cels.2016.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Medlock GL, Papin JA. 2020. Guiding the refinement of biochemical knowledgebases with ensembles of metabolic networks and machine learning. Cell Syst 10:109–119. doi: 10.1016/j.cels.2019.11.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sanghvi JC, Regot S, Carrasco S, Karr JR, Gutschow MV, Bolival B, Covert MW. 2013. Accelerated discovery via a whole-cell model. Nat Methods 10:1192–1195. doi: 10.1038/nmeth.2724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wallden M, Fange D, Lundius EG, Baltekin Ö, Elf J. 2016. The synchronization of replication and division cycles in individual E. coli cells. Cell 166:729–739. doi: 10.1016/j.cell.2016.06.052. [DOI] [PubMed] [Google Scholar]
- 29.Tanouchi Y, Pai A, Park H, Huang S, Stamatov R, Buchler NE, You L. 2015. A noisy linear map underlies oscillations in cell size and gene expression in bacteria. Nature 523:357–360. doi: 10.1038/nature14562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Sauls JT, Li D, Jun S. 2016. Adder and a coarse-grained approach to cell size homeostasis in bacteria. Curr Opin Cell Biol 38:38–44. doi: 10.1016/j.ceb.2016.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bolstad BM, Irizarry RA, Strand MÅ, Speed TP. 2003. A comparison of normalization methods for high density oligonucleotide array data based on variance and bias. Bioinformatics 19:185–193. doi: 10.1093/bioinformatics/19.2.185. [DOI] [PubMed] [Google Scholar]
- 32.Li S, Łabaj PP, Zumbo P, Sykacek P, Shi W, Shi L, Phan J, Wu P-Y, Wang M, Wang C, Thierry-Mieg D, Thierry-Mieg J, Kreil DP, Mason CE. 2014. Detecting and correcting systematic variation in large-scale RNA sequencing data. Nat Biotechnol 32:888–895. doi: 10.1038/nbt.3000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Bernstein JA, Khodursky AB, Lin PH, Lin-Chao S, Cohen SN. 2002. Global analysis of mRNA decay and abundance in Escherichia coli at single-gene resolution using two-color fluorescent DNA microarrays. Proc Natl Acad Sci U S A 99:9697–9702. doi: 10.1073/pnas.112318199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Garten Y, Coulet A, Altman RB. 2010. Recent progress in automatically extracting information from the pharmacogenomic literature. Pharmacogenomics 11:1467–1489. doi: 10.2217/pgs.10.136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Carrera J, Covert MW. 2015. Why build whole-cell models? Trends Cell Biol 25:719–722. doi: 10.1016/j.tcb.2015.09.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Tobias J, Shrader T, Rocap G, Varshavsky A. 1991. The N-end rule in bacteria. Science 254:1374–1377. doi: 10.1126/science.1962196. [DOI] [PubMed] [Google Scholar]
- 37.Kim KH, Qian H, Sauro HM. 2013. Nonlinear biochemical signal processing via noise propagation. J Chem Phys 139:144108. doi: 10.1063/1.4822103. [DOI] [PubMed] [Google Scholar]
- 38.Fisher RA, et al. 1960. The design of experiments, 7th ed. Hafner Publishing Company, Ireland. [Google Scholar]
- 39.Morowitz HJ, Tourtellotte ME, Guild WR, Castro E, Woese C, Cleverdon RC. 1962. The chemical composition and submicroscopic morphology of Mycoplasma gallisepticum, avian PPLO 5969. J Mol Biol 4:93–IN5. doi: 10.1016/S0022-2836(62)80041-2. [DOI] [PubMed] [Google Scholar]
- 40.Zhao H, Dreses-Werringloer U, Davies P, Marambaud P. 2008. Amyloid-beta peptide degradation in cell cultures by mycoplasma contaminants. BMC Res Notes 1:38. doi: 10.1186/1756-0500-1-38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Baldwin WW, Myer R, Powell N, Anderson E, Koch AL. 1995. Buoyant density of Escherichia coli is determined solely by the osmolarity of the culture medium. Arch Microbiol 164:155–157. doi: 10.1007/s002030050248. [DOI] [PubMed] [Google Scholar]
- 42.Bray D. 2000. Cell movements: from molecules to motility. Garland Science, Oxford, United Kingdom. [Google Scholar]
- 43.Peterson JD, Umayam LA, Dickinson T, Hickey EK, White O. 2001. The Comprehensive Microbial Resource. Nucleic Acids Res 29:123–125. doi: 10.1093/nar/29.1.123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Bremer H, Dennis PP. 1996. Modulation of chemical composition and other parameters of the cell by growth rate. EcoSal Plus 2:1553–1569. [DOI] [PubMed] [Google Scholar]
- 45.Neidhardt FC, Ingraham JL, Schaechter M. 1990. Physiology of the bacterial cell: a molecular approach. Sinauer Associates, Sunderland, MA. [Google Scholar]
- 46.Li G-W, Burkhardt D, Gross C, Weissman JS. 2014. Quantifying absolute protein synthesis rates reveals principles underlying allocation of cellular resources. Cell 157:624–635. doi: 10.1016/j.cell.2014.02.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Bremer H, Dennis PP. 2008. Modulation of chemical composition and other parameters of the cell at different exponential growth rates. EcoSal Plus 3. doi: 10.1128/ecosal.5.2.3. [DOI] [PubMed] [Google Scholar]
- 48.Karp PD, Ong WK, Paley S, Billington R, Caspi R, Fulcher C, Kothari A, Krummenacker M, Latendresse M, Midford PE, Subhraveti P, Gama-Castro S, Muñiz-Rascado L, Bonavides-Martinez C, Santos-Zavaleta A, Mackie A, Collado-Vides J, Keseler IM, Paulsen I. 2018. The EcoCyc database. EcoSal Plus 8. doi: 10.1128/ecosalplus.ESP-0006-2018. [DOI] [PMC free article] [PubMed] [Google Scholar]