Abstract
Autism is traditionally diagnosed behaviorally but has a strong genetic basis. A genetics-first approach could transform understanding and treatment of autism. However, isolating the gene-brain-behavior relationship from confounding sources of variability is a challenge. We demonstrate a novel technique, 3D transport-based morphometry (TBM), to extract the structural brain changes linked to genetic copy number variation (CNV) at the 16p11.2 region. We identified two distinct endophenotypes. In data from the Simons Variation in Individuals Project, detection of these endophenotypes enabled 89 to 95% test accuracy in predicting 16p11.2 CNV from brain images alone. Then, TBM enabled direct visualization of the endophenotypes driving accurate prediction, revealing dose-dependent brain changes among deletion and duplication carriers. These endophenotypes are sensitive to articulation disorders and explain a portion of the intelligence quotient variability. Genetic stratification combined with TBM could reveal new brain endophenotypes in many neurodevelopmental disorders, accelerating precision medicine, and understanding of human neurodiversity.
Identifying brain changes associated with common autism genes could be a step toward personalized medicine.
INTRODUCTION
Autism is a complex condition, resulting from a combination of genetic and environmental factors (1). It is characterized by impairments in social interaction, communication, and repetitive behaviors (2). Today, autism is diagnosed behaviorally (1, 3), which underscores our current understanding and informs treatment. However, autism also has a strong genetic basis, with recent heritability estimates of up to 90% (4). A genetics-first approach may help better subtype patients, understand autism’s origins, and develop targeted treatments. However, today, less than half of patients with autism undergo genetic testing (5).
Recently, many new genes linked to autism have been identified, with copy number variations (CNVs) conferring a substantial relative risk (6). More than 200 CNVs have been linked to autism (7). These CNVs primarily arise as de novo mutations during maternal meiosis, with a proportion representing inherited germline mutations (8). An important CNV is 16p11.2 (BP4-BP5). This region underwent positive selection during human evolution from nonhuman primates, leading to concomitant changes in brain size and shape (9). 16p11.2 deletions increase the risk of autism or developmental delay by 38.7-fold, while duplications increase the risk by 20.7-fold (10). Yet, the exact in vivo influence of this region on the brain remains a mystery (9). Given that the 16p11.2 region is one of the most prevalent single genetic contributors to autism (10, 11), we focus on this region as a model to develop approaches to investigate gene-brain-behavior relationships.
How CNVs affect behavioral phenotypes is often poorly understood (3). To bridge the gap between genetics and behaviors, we study the concept of endophenotypes. Endophenotypes are intermediate traits that can be objectively defined and follow distinct developmental trajectories (12). However, structural brain imaging in autism is often normal (13). Recent papers have used functional magnetic resonance imaging (14) and electrophysiology (15) to further subtype individuals with autism, but these modalities are not widely available outside of specialized research settings. Disentangling the effects of CNV on brain structure from other confounding sources of variability represents an ongoing challenge (7). Existing brain morphometric techniques have enabled population-level comparisons among CNV cohorts (10, 16) but are not sensitive enough to differentiate the CNV-specific effects from other causes of variation. These studies used regional volumes (10), brain surface–based analysis (10, 17), and voxel-based methods (17). Furthermore, most of these studies examined a finite set of numerical indicators. Even if it were possible to detect specific statistical differences among them, they have no direct biological or physical meaning unless the corresponding model is invertible (18). However, if possible, then the ability to connect CNVs to structural changes in the brain and subsequent behavior would represent a major advance in precision medicine (3).
New machine learning techniques have the potential to expand upon the results of existing morphometric techniques and overcome their limitations (7, 19). While discriminative learning approaches have aimed to explain a given dataset, generative approaches could enhance explainability in traditionally opaque models (19–21) by enabling the model to be interrogated to visualize new instances of data. Specifically, generative physics-based models have helped visualize disease pathways or targets in several studies (22–25). This approach offers the potential to identify more disease-relevant targets compared to conventional machine learning (25).
This paper demonstrates a generative machine learning approach based on modeling how brain mass is distributed and changes. This approach is called three-dimensional (3D) transport-based morphometry (TBM) (19, 21) and is based on the mathematics of optimal mass transport (26). We choose to assess brain mass distribution, as disorders of neuronal migration, organization, and differentiation would modify brain mass distribution. Unlike most data-driven approaches, mass transport can be described by closed-form equations with theoretical guarantees (27). We leverage these equations in conjunction with supervised machine learning to directly probe underlying biological mechanisms (19). Prior work has demonstrated that this approach can automatically discover and visualize patterns hidden to detection by existing approaches (19, 22, 28, 29). This study investigates the potential of this approach in the study of neurodevelopmental disorders.
Here, we hypothesized that CNV-specific brain structural patterns could be reliably isolated from background variations, even in images that do not show obvious abnormalities. First, we extracted the CNV-specific structural pattern from Simons Variation in Individuals Project (VIP) data using TBM. We assessed whether the presence of this pattern could enable accurate prediction of 16p11.2 CNV in unseen brain images, comparing with traditional morphometry methods (see the Supplementary Materials). Next, we directly visualized the specific brain pattern driving accurate CNV detection, a key advance as TBM is generative. Last, we correlated the discovered brain pattern to behavior, investigating the proportion of behavioral variation that can be explained directly by the CNV-specific brain pattern. We demonstrate that there are distinct brain endophenotypes in autism that may be driven by genetic CNV existing on a spectrum of severity. This work may have the potential to uncover new gene-brain-behavior relationships in CNVs beyond 16p11.2, which could facilitate a genetics-first precision medicine approach to autism. Last, the technique we contribute is broadly applicable across many neurological disorders and could reveal new therapeutic targets.
RESULTS
Subject demographics
Subject demographics are summarized in Table 1. The duplication and deletion carriers had a range of diagnoses, summarized in Table 2, with multiple diagnoses per individual being most common. A one-way analysis of variance (ANOVA) demonstrates that brain tissue volume differs significantly among duplication carriers, deletion carriers, and controls. However, we report in later sections that brain tissue volume alone is not sufficient to distinguish the genetic cohorts.
Table 1. Subject demographics.
IQ scores were missing for one subject; social responsiveness score was missing for 20 subjects.
| Cohort (N = 206) | Deletion carriers (N = 48) | Duplication carriers (N = 40) | Controls (N = 118) | P value |
|---|---|---|---|---|
| Age (years) | 15 ± 12 | 27 ± 16 | 25 ± 14 | <0.001 |
| Male:Female ratio | 27:21 | 26:14 | 66:52 | 0.59 |
| Original brain tissue volume (liters) | 1.35 ± 0.15 | 1.15 ± 0.12 | 1.25 ± 0.12 | <0.001 |
| Full-scale IQ | 88 ± 14 | 93 ± 18 | 106 ± 15 | <0.001 |
| Verbal IQ | 86 ± 17 | 95 ± 17 | 106 ± 16 | <0.001 |
| Nonverbal IQ | 91 ± 13 | 92 ± 19 | 104 ± 13 | <0.001 |
| Social responsiveness score | 69 ± 37 | 54 ± 41 | 19 ± 12 | <0.001 |
Table 2. Duplication and deletion carriers had a range of diagnoses.
Diagnoses were missing for 10 participants. ADHD, attention deficit hyperactivity disorder; OCD, obsessive-compulsive disorder; ASD, autism spectrum disorder.
| Diagnoses | Number with diagnosis (%) |
|---|---|
| ADHD | 13 (14.8%) |
| Anxiety, OCD, phobia | 15 (17.1%) |
| Articulation disorder | 25 (28.4%) |
| Behavioral disorder | 7 (8.0%) |
| ASD | 11 (12.5%) |
| Coordination disorder | 20 (22.7%) |
| Tic disorder or Tourette syndrome | 5 (5.7%) |
| Enuresis | 8 (9.1%) |
| Language disorder | 14 (15.9%) |
| Learning disorder | 5 (5.7%) |
| Mood disorder | 8 (9.1%) |
| Intellectual disability | 17 (19.3%) |
| Stereotypic movement disorder | 1 (1.1%) |
| Mean number of diagnoses per subject | 1.9 ± 1.5 |
In our study, deletion carriers were generally younger than both duplication carriers and controls. This age difference could be due to ascertainment bias. A possible explanation is that deletion carriers may come to medical attention at a younger age, leading to their inclusion in the study. Despite best efforts to age-match the cohorts, this difference in age could not be completely eliminated.
CNV classification using demographic data
Age and gender alone did not differentiate 16p11.2 CNV with accuracy above chance. Including brain parenchymal volume to age and gender did not substantially improve classification accuracy, as demonstrated in Table 3. Here, accuracy and confidence intervals are reported on the test data.
Table 3. Classification performance using pLDA.
| Features | Test accuracy | Sensitivity (deletion/control/duplication) | Specificity (deletion/control/duplication) | Cohen’s kappa |
|---|---|---|---|---|
| Age and gender only | 34.1 [31.1, 37.0]% | 83.4 [81.1, 85.7]%/8.2 [6.5, 9.9]%/51.2 [48.1, 54.3]% | 51.2 [48.1, 54.3]%/96.1 [94.9, 97.3]%/66.7 [63.8, 69.6]% | 0.13 [0.11, 0.15] |
| Age, gender, and parenchymal volume | 44.2 [41.2, 47.3]% | 59.1 [56.1, 62.2]%/27.8 [25.0, 30.6]%/74.9 [72.2, 77.6]% | 70.6 [67.8, 73.4]%/78.8 [76.3, 81.3]%/70.0 [67.2, 72.9]% | 0.20 [0.17, 0.23] |
| White matter TBM | 94.6 [93.2, 96.0]% | 96.8 [95.7, 97.9]%/96.0 [94.7, 97.2]%/87.9 [85.8, 89.9]% | 98.6 [97.8, 99.3]%/92.7 [91.1, 94.3]%/98.5 [97.7, 99.3]% | 0.91 [0.89, 0.92] |
| Gray matter TBM | 88.5 [86.5, 90.5]% | 92.5 [90.9, 94.2]%/90.5 [88.6, 92.3]%/78.0 [75.4, 80.5]% | 96.4 [95.3, 97.6]%/85.9 [83.8, 88.1]%/96.6 [95.5, 97.7]% | 0.80 [0.78, 0.83] |
Data acquisition and preprocessing
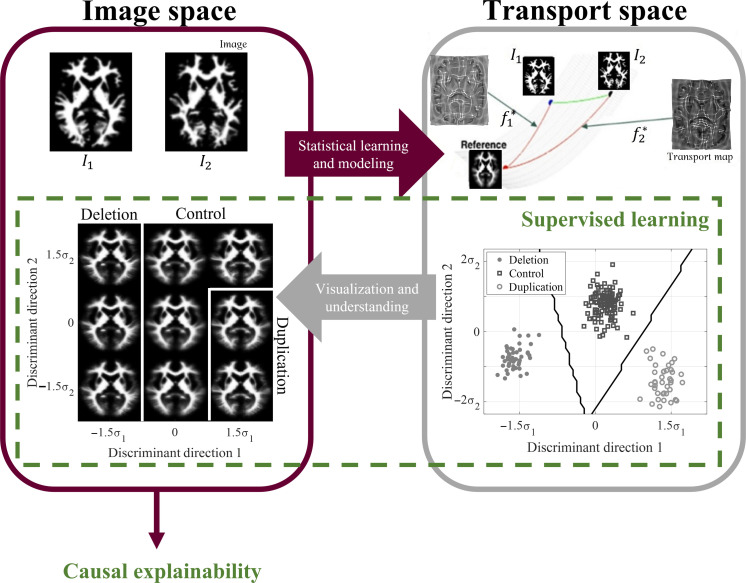
In our study, we used T1-weighted magnetization-prepared gradient-echo images (n = 206) from the Simons VIP dataset. To account for gross orientational and size differences, these images were coregistered using affine registration and segmented into gray and white matter tissues using the Statistical Parametric Mapping software. The rationale behind this separation is elaborated upon in the “Canonical correlation between gray matter and white matter variation” section. After normalizing tissue mass across all images, we used TBM (19) to transform each image into the transport domain with respect to a reference image, as depicted in Fig. 1. This transformation generated a transport map for each image, a vector field characterizing the optimal mass preserving mapping. To facilitate further analysis, we concatenated the set of transport maps into a data matrix for subsequent transport-domain analysis.
Fig. 1. 3D TBM system diagram.
Images that are not easily separable in the image domain are transformed to the transport domain, where they are represented as points on a high-dimensional Riemannian manifold. Supervised learning is performed in the transport space. The classifier decision boundaries are inverted to visualize the discriminant patterns causally driving classification as computer-generated images in the image domain. 3D TBM is performed on volumetric images, although a single white matter axial slice is shown here for illustration purposes.
Principal component variations
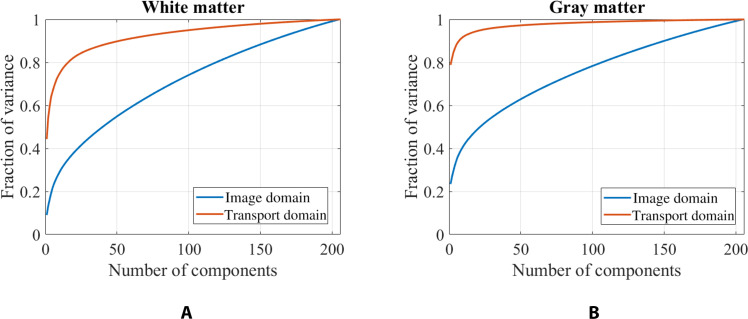
TBM enables a more efficient representation of the data in the transport domain, requiring fewer components to capture the same level of variance. Furthermore, as TBM is a bijective transformation (Fig. 1), it ensures no information loss. As demonstrated in Fig. 2, the transport domain better represents the underlying structure of both white matter and gray matter compared to the image domain. In the transport space, 96% of the white matter variance is captured with only 132 components, compared to 184 components in the image space. Similarly, 96% of the gray matter variance is captured with 46 components in the transport domain, compared to 182 components in the image domain. Furthermore, the transport domain has considerable modeling advantages over conventional deformation-based techniques, as shown in section S7.
Fig. 2. Principal components.
The (A) white matter and (B) gray matter structure are better captured using fewer components in the transport domain than the image domain.
Canonical correlation between gray matter and white matter variation
When canonical correlation is performed, a statistically significant relationship between the distribution of gray and white matter is observed (Pearson correlation coefficient = 0.56, P < 0.01), with 31% variance explained on unseen data. Thus, structural variations between white and gray matter cannot be mutually explained fully, motivating separate analyses on gray and white matter. Additional details are in section S2.
Correlation between brain parenchymal volume and structural variation
There was no statistically significant correlation between brain parenchymal volume and tissue distribution for either gray matter (Pearson correlation coefficient = 0.12, P = 0.20) or white matter (Pearson correlation coefficient = 0.21, P = 0.29) after correcting for covariates of age, gender, gene cohort, and full-scale intelligence quotient (IQ). Therefore, brain parenchymal volume did not predict the underlying variations in brain tissue distribution. The regression plots are included in fig. S1 in the Supplementary Materials.
3D TBM
Classification
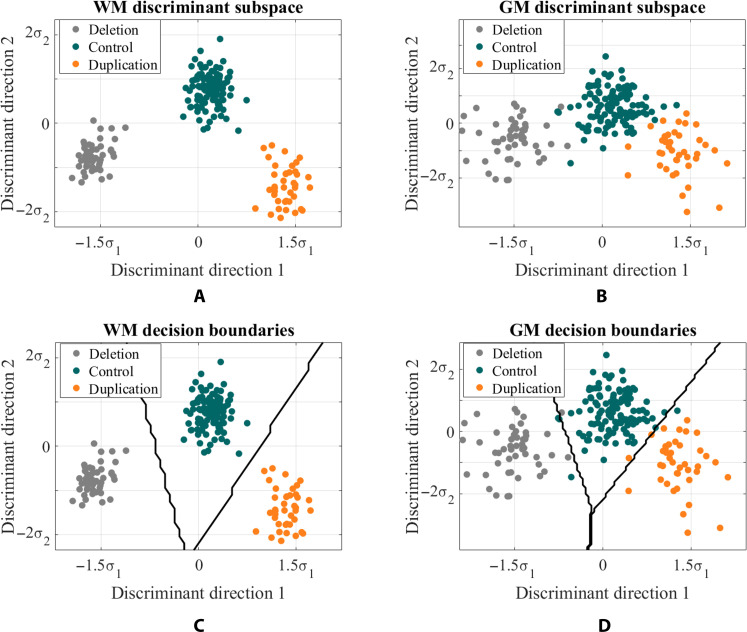
Although duplication carriers, deletion carriers, and controls were not easily separable in the image domain, they were highly separable in the transport domain in the training set. This is shown in Fig. 3 (A and B) when the subject data are projected onto the most discriminating subspace computed by penalized linear discriminant analysis (pLDA) (21, 30) for white matter and gray matter, respectively. Here, one point belongs to each individual. Furthermore, Fig. 3 (C and D) displays the average decision boundaries that separate the three classes in the training set, based on the nearest centroid distance in the transport domain.
Fig. 3. 3D TBM discriminant subspace.
Each subject in the study is represented by a point on the scatterplot. Subject data is projected onto the most discriminant subspace computed by pLDA for (A) white matter (WM) and (B) gray matter (GM). Boundaries between the classes computed based on nearest centroid classification for (C) white matter and (D) gray matter.
We observe that genetic cohorts are more separable based on white matter distribution than gray matter distribution in both the training and testing sets. Furthermore, discriminant direction 1 indicates a dose-dependent influence of 16p11.2 CNV on brain structural variation for both gray matter and white matter. Along direction 1, controls are centered at mean, whereas duplication and deletion carriers are centered reciprocally at +1.5σ1 or −1.5σ1 from the mean, where σ1 represents the SD from the mean. Discriminant direction 2 plays a role in distinguishing controls from both duplication and deletion carriers.
The classification performance in Table 3 was computed on the test set using a 10-fold cross-validation approach. To maintain original class distributions, stratified cross-validation was used. The process was repeated 1000 times with random fold partitions, and the mean final accuracy, sensitivity, specificity, and Cohen’s kappa are reported across all 1000 iterations along with 95% confidence intervals across these iterations. In each iteration, the test data were projected onto the discriminant subspace calculated from the training set, and class assignments were determined on the basis of the nearest centroid distance.
Table 3 shows that white matter structural variations can predict 16p11.2 CNV with 94.6% accuracy on test set, and gray matter architecture can predict CNV with 88.5% accuracy on test set, with robust classification even after correcting for covariates of age and gender (section S5). Combining white and gray matter did not improve discrimination ability, possibly due to collinearity, which is further elaborated in section S6. The kappa statistic indicates a near-perfect association between CNV and the architecture of white matter and gray matter (31). Furthermore, the classification performance of 3D TBM is superior to that using existing brain morphometry techniques, as described in section S10.
Visualizing brain tissue variations defining 16p11.2 CNV discrimination
3D TBM is a generative machine learning technique that enables direct visualization of the characteristic brain endophenotypes driving the ability to classify 16p11.2 CNV. In Fig. 3, brain endophenotypes can be visualized through inverse TBM transformation (19) by sampling along discriminant directions 1 and 2 for both gray and white matter. Furthermore, figs. S4 to S7 showcase TBM-generated images that illustrate the physical shifts at the interface between genetic cohorts.
Global brain structure variations
The pattern of perturbations observed indicates that the vulnerability of brain regions is diffuse rather than localized. First, as previously noted, CNV at the 16p11.2 locus is inversely associated with total brain parenchymal volume in a dose-dependent manner, as shown in Table 1.
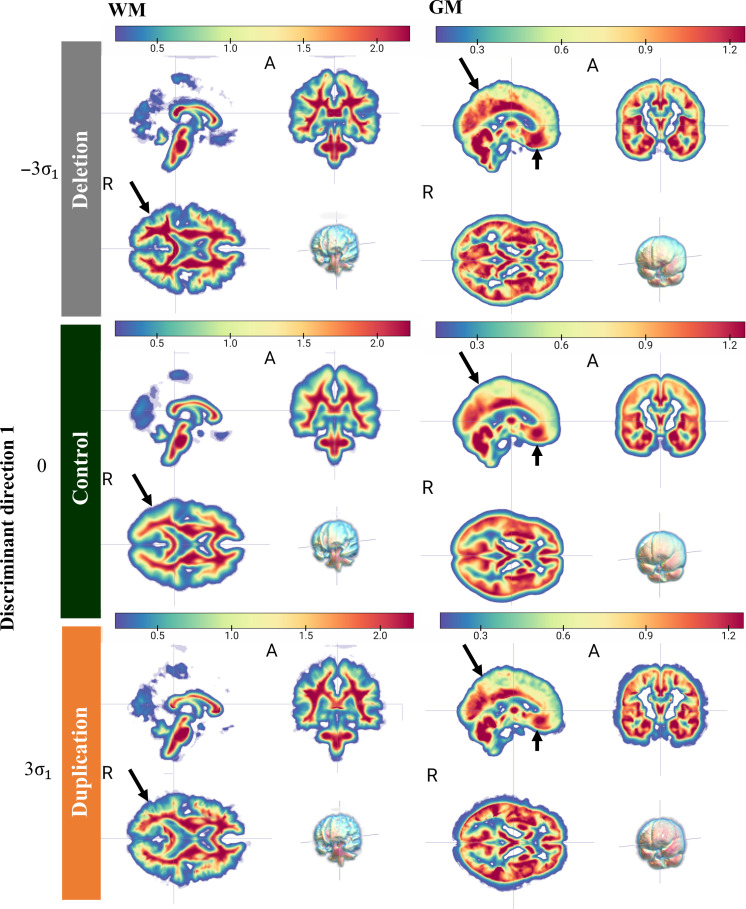
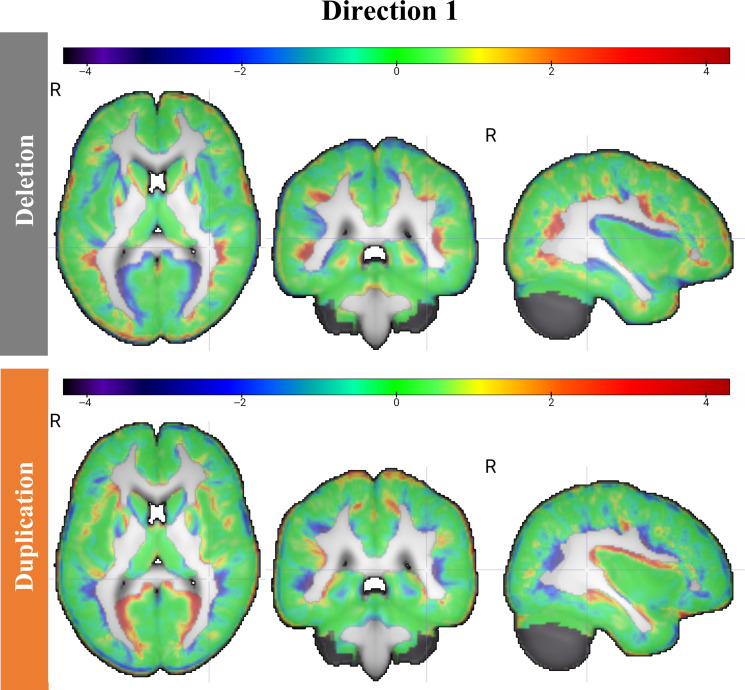
Second, even after correcting for the influence of volume before TBM analysis, the variations among duplication and deletion carriers are spatially diffuse. This is evident when visualizing the characteristic tissue shifts along direction 1 in Fig. 4, where the density of nearly every region undergoes change.
Fig. 4. TBM generated images showing spatially diffuse changes associated with 16p11.2 CNV.
The resulting 3D TBM-generated images, obtained by sampling the discriminant subspace in Fig. 2 along discriminant direction 1, depict the physical changes in white (WM) and gray matter (GM) tissue density. Red indicates relative increase in tissue density, while blue represents relative decrease. Our findings reveal diffuse tissue overgrowth in deletion carriers and tissue undergrowth in duplication carriers compared to controls, as highlighted by the black arrows in selected regions.
Third, the diffuse pattern of changes is further supported by a reciprocal pattern of local tissue expansion/contraction among duplication and deletion carriers, with opposite regions undergoing volume expansion or contraction with gene dosage. This is captured by the determinant of the Jacobian computed from the transport maps obtained from the TBM procedure, which shows a strong negative correlation with Pearson’s correlation coefficients of −0.96, (P < 0.001) for gray matter and −0.97 (P < 0.001) for white matter, for deletion and duplication carriers located −3σ1 and +3σ1 from the mean, respectively.
Fourth, deletion tends to result in gross overgrowth of gray matter tissue compared to controls, while duplication tends to result in gross undergrowth of gray matter in a dose-dependent manner. This can be measured by the fraction of the image volume occupied by brain tissue, which decreases with increasing gene dosage. For example, among deletion carriers, −3σ1 away from the mean, 39.9% of the image volume is occupied by gray matter. This decreases to 39.7% at −1.5σ1. At the mean, this fraction is 38.9%, and at +1.5σ1, it is 37.7%. At +3σ, it is 36.5%. When examining the white matter, this pattern is not as evident (Fig. 4).
Regional brain structure variations
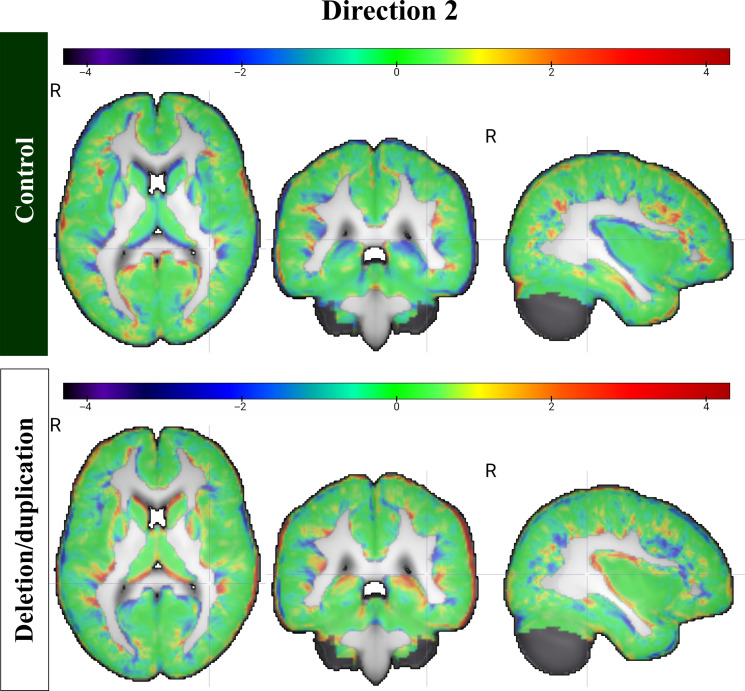
To assess the regional macrostructural variations, the images were registered to the Harvard-Oxford atlas (32), a probabilistic atlas segmenting 48 cortical and 21 subcortical regions. The relative local volume contraction and expansion at ±3 SDs from the mean displacement were calculated via Jacobian maps in the transport domain along direction 1 and direction 2. Then, voxelwise z-scores were assigned to the Jacobian maps calculated along directions 1 and 2, which are illustrated in Figs. 5 and 6, respectively.
Fig. 5. Reciprocal changes along direction 1.
Z-score maps demonstrating reciprocal changes among deletion and duplication carriers. These were derived from the determinant of the Jacobian of the transport maps.
Fig. 6. Changes along direction 2.
Z-score maps demonstrating the changes among controls and deletion/duplication carriers. These were derived from the determinant of the Jacobian of the transport maps.
Table 4 shows the top cortical regions with the largest relative volume expansion and contraction, respectively, along direction 1. Notably, the regions undergoing the most relative local volume expansion and contraction are opposite for deletion and duplication carriers. In addition, the pattern of relative expansion and contraction among the top three and bottom three subcortical regions exhibits lateralization. On the basis of the combined gray and white matter maps, the right thalamus, right cerebral cortex, and right lateral ventricle undergo the greatest relative volume expansion in duplication carriers, while the left caudate, left putamen, and left accumbens undergo the greatest relative volume contraction.
Table 4. Direction 1.
| Deletion | Duplication | ||
|---|---|---|---|
| Region | Z-score | Region | Z-score |
| Inferior frontal gyrus | 0.47 | Intracalcarine cortex | 1.02 |
| Cingulate gyrus | 0.40 | Parietal operculum | 0.96 |
| Angular gyrus | 0.35 | Central opercular cortex | 0.89 |
| Central opercular cortex | −0.85 | Angular gyrus | −0.32 |
| Intracalcarine cortex | −0.85 | Cingulate gyrus | −0.39 |
| Parietal operculum | −0.88 | Inferior frontal gyrus | −0.50 |
Table 5 summarizes the top cortical areas with the largest relative local volume expansion and contraction along direction 2. Among subcortical regions, the lateral ventricles undergo the greatest relative expansion in controls. The right caudate and pallidum and the left hippocampus undergo the most relative volume contraction. Section S11 describes the regional changes in more detail, which are summarized in tables S6 to S9.
Table 5. Direction 2.
| Controls | Deletion/duplication | ||
|---|---|---|---|
| Region | Z-score | Region | Z-score |
| Superior temporal gyrus | 0.62 | Frontal orbital cortex | 0.61 |
| Middle temporal gyrus | 0.38 | Supramarginal gyrus | 0.50 |
| Temporal pole | 0.36 | Inferior temporal gyrus | 0.43 |
| Inferior temporal gyrus | −0.41 | Temporal pole | −0.35 |
| Supramarginal gyrus | −0.49 | Middle temporal gyrus | −0.37 |
| Frontal orbital cortex | −0.60 | Superior temporal gyrus | −0.58 |
16p11.2 brain endophenotypes and behavior
The relationship between the distinct brain endophenotypes, as captured along directions 1 and 2, and behavior was investigated in the population space. Our a priori hypothesis was that articulation disorders would be associated with CNV because it was the most CNV-related disorder (Table 2).
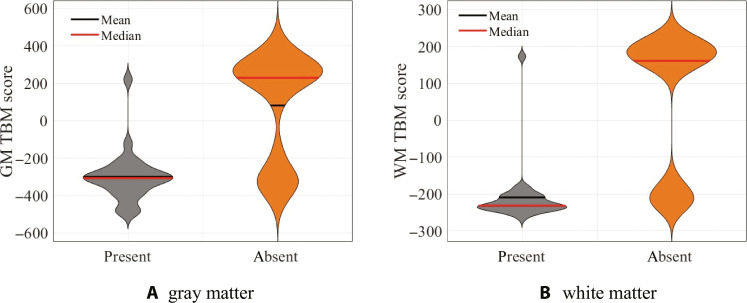
Results showed that TBM scores along discriminant direction 1 were significantly associated with articulation disorders for both gray matter (P < 0.0001) and white matter (P = 0.0002). Articulation disorders were much more common among deletion carriers, comprising 96.0% of the total individuals with the disorder, whereas duplication carriers comprised only 4.0%. These findings are depicted in Fig. 7 (A and B), which demonstrate that having a negative TBM score for either gray matter or white matter among duplication/deletion carriers was 96% sensitive and 62.9% specific for having an articulation disorder. These associations remained significant even after applying the Bonferroni correction for multiple comparisons.
Fig. 7. Articulation disorder.
The presence of articulation disorder among deletion and duplication carriers is highly associated with projection scores along discriminant direction 1 for both (A) gray matter (GM) (P < 0.0001) and (B) white matter (WM) (P = 0.0002). Among duplication/deletion carriers, having a negative TBM score for either gray matter or white matter was 96% sensitive and 62.9% specific for having an articulation disorder using logistic regression.
TBM scores along direction 2 showed a significant association with IQ scores, as revealed by multiple linear regression in the pLDA discriminant subspace computed in the transport domain. Direction 2 exhibited a stronger relationship with IQ than direction 1 for both gray and white matter. In the combined gray matter and white matter model, the weight placed on white matter direction 2 was disproportionately higher. The findings of the multiple linear regression analysis, summarized in Table 6, remain significant even after correcting for multiple comparisons using the Bonferroni correction.
Table 6. IQ variance explained by TBM projection scores.
IQ scores were missing for one subject.
| IQ | Gray matter | White matter | Combined | |||
|---|---|---|---|---|---|---|
| R 2 | P | R 2 | P | R 2 | P | |
| Full-scale IQ | 0.13 | <0.001 | 0.18 | <0.001 | 0.20 | <0.001 |
| Verbal IQ | 0.14 | <0.001 | 0.18 | <0.001 | 0.20 | <0.001 |
| Nonverbal IQ | 0.11 | <0.001 | 0.15 | <0.001 | 0.17 | <0.001 |
DISCUSSION
This research reveals new details regarding brain structural patterns linked to genetic CNV in autism. These patterns are specific enough that their presence accurately predicts the CNV from brain images alone in new, unseen individuals. Furthermore, the discovered patterns are sensitive to articulation disorders and explain a fraction of the variability in IQ. The results in this paper were enabled by 3D TBM, a generative machine learning approach that can directly probe biological mechanisms perturbing brain mass distribution. By revealing structural networks underpinning CNV-related endophenotypes in detail, this research helps advance our understanding of autism’s biological basis.
Although autism is primarily diagnosed and treated behaviorally, it is highly heritable, with recent heritability estimates of up to 90% (4). However, less than half of patients with autism now undergo genetic screening (5). In the future, findings from this preclinical study could be validated in clinical studies in several ways. First, as patients present with initial symptoms, routine brain imaging is often performed. TBM could help automatically screen these images to detect potential CNVs early and refer patients for genetic testing. Second, as we had found that brain endophenotypes exist on a spectrum quantifiable by TBM, the prognostic value of TBM scores can be investigated in the future. As new therapies emerge, new therapeutic biomarkers are needed to confirm treatment effect. In this regard, this research demonstrates that brain endophenotypes on imaging could facilitate autism screening and personalize treatment in the future. Larger cohort studies and prospective trials are needed to explore these possibilities. However, these efforts must proceed in tandem with the curation of genetically stratified datasets in autism research.
We focused on one of the most prevalent genetic causes of autism, 16p11.2 as a case study. The function of this genetic locus is largely unknown (9). We found that 16p11.2 CNVs were nearly 100% penetrant with regard to brain structural variations, enabling sensitive detection of CNV status (deletion, duplication, and control) based on brain imaging alone. We directly visualized the CNV-specific endophenotypes driving accurate discrimination, discovering a diffuse process with regional localization. Deletion carriers exhibit tissue overgrowth, while duplication carriers show undergrowth, with effects observed in even controls, on a spectrum of severity. Regionally, the areas most affected were those related to emotional processing, visuospatial ability, multisensory integration, and language, consistent with the behavioral phenotypes of autism. Furthermore, we observe lateralization in certain changes between right and left hemispheres, evolutionarily dedicated to visuospatial ability (right) and language ability (left). Furthermore, these structural variations were significantly predictive of articulation disorders, the inability to produce normal speech sounds, which comprise errors of substitution, omission, distortion, and addition (33). CNV-specific brain endophenotypes also explained a small fraction of IQ variability. The results confirm that 16p11.2 CNV, commonly occurring de novo in patients presenting with autism and other neurodevelopmental disorders (34), affect higher-order cognitive processing functions. As other CNVs also demonstrate the mirror brain phenotype, such as 22q112.2 and 15q11.2, in the future, this approach could be used to study many of the >200 CNVs linked to autism (7). CNVs are a major source of variability between individuals (35), and TBM could help further our understanding of human neurodiversity (36).
Prior studies have observed gene dosage–related effects on brain size (10) and widespread changes in axial diffusivity (37) and fractional anisotropy (FA) (38) in diffusion tensor imaging studies of deletion carriers. Another prior study reported more prevalent cortical anomalies in both 16p11.2 duplications and deletions (39), with abnormally increased or decreased cortical thickness in the deletion or duplication groups, respectively. In contrast to prior studies, a key capability of TBM is that it is generative, providing the ability to link statistical changes to potential biological mechanisms. We directly visualized the physical changes in gray and white matter within CNV-specific networks. In the near future, TBM could be used to investigate new therapies targeting neuronal migration, organization, and differentiation. For example, Ras homolog gene family member A (RhoA) inhibition and CD47 pathway modulation may help regulate the activity of 16p11.2 deletion neurons and neuronal pruning (40, 41). N-methyl-d-aspartate receptor modulators (34) and transcription factors are other potential therapies. Targeting 16p11.2 CNVs via gene therapy or transcriptional methods is a promising area of preclinical research. The pleiotropic effects of the 16p11.2 genetic locus need further exploration in the future.
Despite the heterogeneity of autism phenotype, articulation disorders and IQ could partially be explained by CNV-specific endophenotypes. The finding that 16p11.2 CNVs are significantly associated with language impairments is consistent with studies in the very recent emerging literature (42), although our findings correlate how brain macrostructure relates to behavior in a dose-depending manner. At the same time, we cannot draw conclusions about the causality of the relationship. Variable expressivity of behavior may arise from genes with multiple functions, expanding the number of cognitive functions without a proportional increase in gene count during human evolution (43). In addition, behavioral heterogeneity in individuals with 16p11.2 CNV can be influenced by both nongenetic and genetic factors (8).
The regions exhibiting the most prominent expansion/contraction due to CNV identified in this study overlap with those regions that experienced substantial changes during human evolution, including the frontal regions, parietal regions, and temporal poles (36). The networks served by direction 1 involve multisensory integration, visuospatial ability, sensation on one end and on the other, those related to reading and writing function, semantic processing, language production, and emotional regulation, consistent with observed symptoms of 16p11.2 CNV–related autism and related disorders. There appears to be lateralization, with right-sided structures serving visuospatial ability and left-sided structures serving language networks. In direction 2, in controls, the areas related to speech perception, language comprehension, familiar face recognition, emotional and social behavior, semantic processing, and socioemotional processing expand, while in deletions/duplications, areas related to decision-making, somatosensory association, interpreting tactile sensory data, phonological processing, language, semantic memory, visual processing, and sensory integration contract. Direction 2 subcortical areas exhibit less lateralization than direction 1, with a mix of visuospatial (right) and episodic verbal memory (left). These results are consistent with 16p11.2 CNV being at the crossroads of both human evolutionary history and the source of de novo mutations vitally associated with risk of autism and other neurodevelopmental disorders.
White matter structural differences enabled better differentiation of genetic cohorts compared to gray matter. The volume of long axons in white matter increases more rapidly than gray matter volumes containing dendrites and axons according to a power law (44), so that distant areas of the cortex can be better connected. Structural white matter injury outperformed gray matter functional centrality in predicting cognitive impairment after focal brain lesions in Reber et al. (45). Furthermore, white matter has less intraclass variance than gray matter, suggesting that it is more discriminatory and may have a stronger effect on brain structure related to CNV. Including gray matter features slightly increases the class variance from white matter, as shown in the Supplementary Materials. In the future, TBM on diffusion imaging can identify the specific white matter tracts affected by 16p11.2 CNV.
Several pathologic mechanisms may corroborate the findings in this study. In deletion carriers, these include increased soma size/dendrite length (34), increased synaptic marker expression, and hyperactivity, overexpression of CD47 (41). In duplication carriers, these include deficits in neuronal differentiation, reduced synaptic marker expression (40), and reduced soma size/dendrite length (34). Furthermore, myelin and myelin lipids may play a role in white matter aberrations (46). Also, dysregulation of transcription and cortical maldevelopment (34) may also play a role. Mouse models suggest synaptic dysfunction, with certain genes at the 16p11.2 locus resulting in abnormal cortical development (34), changes in synaptic function at GABAergic and glutamatergic synapses (34), disrupted corticostriatal circuitry in deletion carriers, thickening of corpus callosum in deletion carriers, and thinning in duplication carriers (34). Our findings support that duplications have reduced cortical thickness and enlarged ventricles. Changes are mostly seen in insula, calcarine cortex, accumbens, pallidum, transverse temporal gyrus, caudate, and putamen and thalamus. We also demonstrate that regional effects are independent of global effects (47). The 16p11.2 gene may also be involved in utero iron homeostasis (9). This study suggests that synaptogenesis and cortical development in utero may be involved, although further studies are needed to characterize the in vivo mechanisms.
There are several limitations in this study. The first is ascertainment bias as the population of autism seen in a clinic may reflect other factors than solely CNV (47, 48). Healthier counterparts may exist in the population, and more severe illness is not captured in these datasets as those patients may be too ill to participate in a clinical trial. A second limitation is that while the study investigated the influence of a single genetic locus, it did not directly assess the complex interaction of this gene with other genes (3, 8). Third, this paper examined pediatric through adult patients. Multiple studies have suggested that neuroimaging abnormalities do not seem to be influenced by age through adolescence and young adulthood (47), suggesting stable phenotype with changes already present in early age. As these changes are seen throughout age, but present early, early childhood may be the best time to intervene. A fourth limitation is that the causality of the gene-brain-behavior relationships cannot be established based on our results alone but may be studied further in in vivo animal models. Last, because of our genetically stratified cohort, it may not be possible to disentangle the independent effect of brain structural variations on articulation disorder from the influence of CNV. Investigating this relationship in a broader, nongenetically stratified autism population could provide valuable insights and is warranted for future research.
This preclinical study serves as a proof of concept, demonstrating that distinct brain endophenotypes linked to CNV are present and are behaviorally relevant. CNVs are increasingly recognized as valuable genetic models for exploring brain-behavior relationships (4, 49). Future research could extend this approach to study other CNVs linked to autism. Distinguishing between autism-related brain variability and variability not related to autism is an ongoing challenge (7). The large anatomic variations linked to 16p11.2 CNV (50, 51) aids discrimination of CNV-related variation from other sources of variability. In the future, tailored approaches may be necessary to detect the potentially more subtle effects of other CNVs. As genetic stratification is supported by several studies (3, 48, 52), future applications of our technique could help accelerate a genetics-first strategy in autism and other neurodevelopmental disorders to unlock new frontiers in precision medicine.
MATERIALS AND METHODS
Study population
Subjects were recruited as part of the Simons VIP (http://SimonsVIPconnect.org). This research was reviewed by the Johns Hopkins Institutional Review Board and acknowledged as exempt as the subjects were deidentified and from a preexisting database. Participants were referred by clinical genetic centers or testing laboratories, web-based networks, and self-referral of families who learned about Simons VIP (48). Subjects underwent an initial screening and review of medical records by Geisinger and Emory University (10). Peripheral blood samples were used to test for 16p11.2 CNV using fluorescent in situ hybridization (48). Inclusion criteria were those who had recurrent breakpoints at BP4-BP5 of 16p11.2 but no other pathogenic CNVs, neurogenetic diagnoses, or syndromes unrelated to 16p11.2 (48). Exclusion criteria were history of environmental insults with a potential influence on neurocognitive status (such as fetal alcohol syndrome), severe birth asphyxia, severe prematurity, and lack of fluency in English (10). The advantage of defining the inclusion criteria based on genotype was that, in contrast to behavioral diagnoses, the inclusion criteria did not change over time.
Behavioral testing included the Autism Diagnostic Observation Schedule, Autism Diagnostic Interview, and broad screening measures of social impairment such as the Social Responsiveness Scale. The core sites for phenotyping were University of Washington Medical Center, Baylor University Medical Center, and Boston Children’s Hospital. The diagnoses were based on DSM-IV-TR (Diagnostic and Statistical Manual of Mental Disorders, fourth edition, text revision) criteria (53). The developmentally appropriate cognitive measure was applied to measure the full-scale IQ among the Mullen Scales of Early Learning (54), Differential Abilities Scale second edition (55), Wechsler Intelligence Scales, or Wechsler Abbrebiated Scales of Intelligence (56). High-resolution structural brain imaging was performed at University of California (UC) and Children’s Hospital of Philadelphia (CHOP).
The control cohort consisted of subjects recruited locally near the core imaging sites (UC-San Francisco, UC-Berkeley, and CHOP) from the general population and were matched for age, sex, handedness, and nonverbal IQ. Exclusion criteria included major DSM-IV diagnoses based on clinical psychologist review or immediate family history of ASD, other developmental disorders, dysmorphic features, or genetic abnormalities. Control subjects also had a chromosome microarray, neurologic exam, a clinical psychologist interview, and a photograph evaluation for dysmorphology.
Subjects in the cohort were chosen with the aim of matching age and gender as closely as possible within each subgroup. This study cohort consisted of high-resolution structural brain images from 206 individuals belonging to control (N = 118), deletion (N = 48), and duplication (N = 40) cohorts.
Image acquisition
T1-weighted magnetization-prepared gradient-echo image (MPRAGE) images were collected. The same structural brain imaging protocol was used across sites; the clinical scanners were cross-calibrated. 3T TIM Trio magnetic resonance imaging scanners (Siemens) were used to image subjects using a 32-channel phased-array radiofrequency head coils. In the sagittal plane, 3D multi-echo MPRAGE sequences were obtained with the parameters: TR = 2530 ms, TI = 1200 ms, TE = 1.64 ms, FA = 7°, 1 mm × 1 mm × 1 mm isotropic voxels, with a field of view = 256 mm (10). Images were assessed for quality control, and the subjects with artifacts were discarded such as ringing/striping/blurring, inhomogeneities, poor head coverage, ghosting, or susceptibility artifacts.
Image preprocessing
The images were first preprocessed to exclude the skull and cerebrospinal fluid. After segmentation into gray and white matter, the affine coregistration step normalized the brains to correct for total brain size. Next, the images were normalized to have equal mass. The gray matter and white matter tissues were segmented separately. To enhance computational efficiency, the images were downsampled by a factor of two. Preprocessing was performed using the VBM8 toolbox as part of the Statistical Parametric Mapping software (SPM12).
3D transport-based learning
The 3D TBM technique is a nonlinear image transformation framework originally described by Kundu et al. (19). The premise is that patterns that may be imperceptible in the original image domain (Fig. 8) may be more readily extracted in the transform domain when applying the optimal transport (OT) metric (19). In contrast to existing approaches, 3D TBM is fully automated and does not require a priori features such as volume to discover discriminating patterns. A key contribution of 3D TBM is that it is generative. Unlike existing approaches, inverse transformation enables direct physical interpretation of the discovered discriminating patterns (19, 22, 28, 29). This paper makes modifications and extensions to the 3D TBM framework. By combining supervised machine learning classification with 3D TBM, this paper enables automated discovery and visualization of gray matter and white matter patterns sensitive to 16p11.2 CNV discrimination.
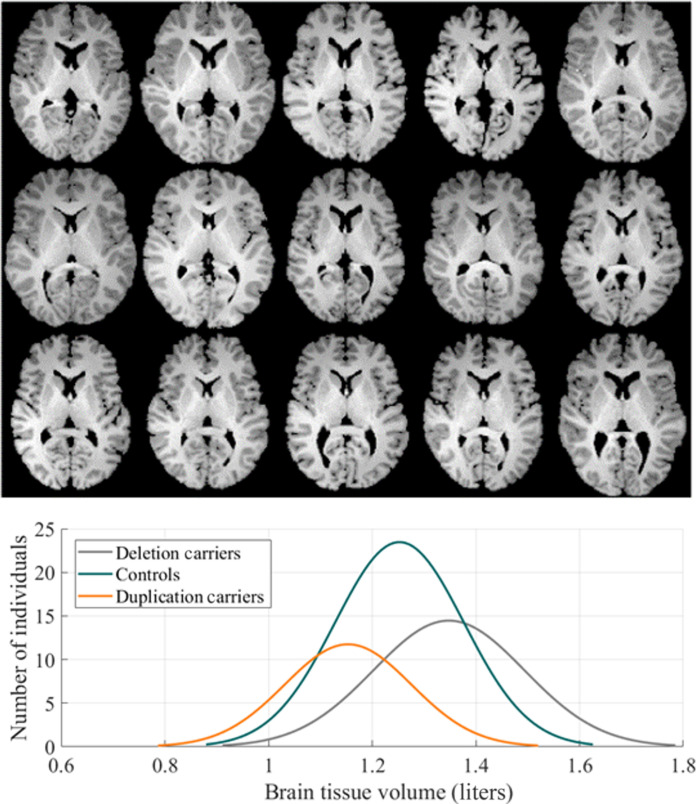
Fig. 8. Sample images.
The brains of 15 different subjects are shown (five control, five duplication, and five deletion carriers). Parenchymal tissue has been segmented, and the same axial slice is shown for each individual. Visual inspection does not reveal a pattern that differentiates the three cohorts. Furthermore, histograms of the brain tissue volumes across all three genetic cohorts demonstrate that although there is a statistically significant difference among the groups (P < 0.001), volume alone is insufficient to differentiate CNV.
Overview
As magnetic resonance imaging measures signal from water protons, the motivation of our transport-based approach is to directly quantify the shift in the tissue water distribution from one image to another. The latter is measured by the OT distance (27). The OT distance between two images measures the amount of “effort” (as quantified by amount of mass over distance moved) to morph one tissue distribution into another. The distance is optimal in terms of mass transport. The 3D TBM approach is based on applying the OT distance to discriminate images.
By contrast, existing approaches have predominantly relied on numerical statistics such as total brain volume and voxelwise statistics, without directly quantifying the physical shifts in tissue distribution (10, 57). In this sense, 3D TBM provides a unique advantage as it offers a direct physical interpretation. Figure 1 illustrates the system diagram for transport-based learning.
Discovering discriminating tissue patterns
The 3D TBM technique was used to transform gray matter and white matter images to the transport domain. For each individual image, the variations in both shape and texture with respect to a common reference are characterized in a unique transport map for each image. The transport map morphs each source image to match the common reference. The common reference image for each gray matter and white matter tissues was computed by taking the Euclidean mean of the study cohort. The OT map is the one that minimizes the amount of mass over distance moved. While the space of potential transport maps is infinite, the OT map is unique. In contrast to methods using deformation fields [i.e., deformation-based morphometry (58), voxel-based morphometry (59), and tensor-based morphometry (60)], transport maps capture variations in both shape and texture (19) and have been demonstrated to be superior in enabling physical interpretation (19) through a transport model of tissue distribution.
In mathematical terms, by treating magnetic resonance images as smooth density functions, the similarity in tissue spatial distribution between two images can be quantified based on the L2-Wasserstein distance (20). Given the set of magnetic resonance images I1, …, IN : Ω ⟶ ℝ+, corresponding to experimental subjects i = 1, …, N, where Ω = [0,1]3, the images are first intensity normalized produce densities according to Eq. 1.
| (1) |
Here, x is a 3D voxel coordinate in the original image domain. After normalizing mass across the images, the analysis equation that transforms an image in the original image domain to its corresponding representation in the transport domain can be written based on Eq. 2.
| (2) |
Here, D denotes the Jacobian matrix, and the MP is the family of all mass-preserving mappings from I0 to I1. Here, fi : Ω ⟶ Ω is a mass preserving mapping from I0 to Ii. The OT mapping is calculated from the reference image I0. The problem in Eq. 2 is well-posed, and the existence of a unique optimal solution to the above minimization was shown by Brenier (26). Thus, the transformation is bijective.
Using a common reference image reduces the number of pairwise computations from N(N − 1)/2 to N. However, the choice of reference image was found to have no significant impact on the performance of pattern recognition (20, 24), as confirmed in section S8.
OT-based learning
Formally, the metric space defined by the OT metric is a Riemannian manifold (20). The shortest distance between two images on this Riemannian manifold corresponds to a geodesic on this manifold. However, we calculate a modified (linearized) version of the transport metric (i.e., generalized geodesic) (20). Therefore, Euclidean distances in the transform space correspond to the modified geodesic distances using the transport metric. The latter means that complex, nonlinear changes in the image domain captured by the OT geodesic correspond to Euclidean distances the transform domain (19). Therefore, 3D TBM enhances separability of classes (19) and, in the 1D case, was proven to transform nonconvex sets in the original image space to convex and disjoint sets in the transform space (61). A separating hyperplane always exists for two convex and disjoint sets, thus enabling linear separability of the sets (61).
As a result of the linearized geodesic, experimental work in TBM has demonstrated that simple linear classifiers and regression models in the transform space capture complex, spatially diffuse, nonlinear shifts in tissue distribution in the image domain (19) in three dimensions as well.
Mathematically, the transport maps are vector fields that define the direction and quantity of mass transport needed to match Ii(x) to I0(x). Then, it can be shown that provides an isometric linear embedding for image Ii with respect to the linearized OT metric (20, 30). The linear embedding is generative; thus, any geometric analysis in the transform domain can be directly visualized in the image domain (19, 20, 30).
Visualizing discovered shifts in brain tissue distribution
A key contribution of this work is that 3D TBM is generative. A benefit of combining a generative technique with a physics-based model is that TBM facilitates direct visualization of physical tissue changes. The learned decision boundary can be sampled and inverted to visualize the variations driving class discrimination. The latter enables causal explainability of the classification decisions. Moreover, generative techniques such as TBM address the limitation highlighted by Friston and Ashburner (18) by providing an invertible generative model, thereby assigning direct physical meaning to statistical parameters.
Mathematically, the unique image corresponding to a given linear embedding can be recovered and visualized according to the synthesis equation in Eq. 3.
| (3) |
Here, I(x) is a physically plausible brain image generated from the mapping of an arbitrary point f(x) in the transport space to the image domain. Furthermore, this transformation is unique. Additional details are in section S10. The MRIcroGL software was used to render the TBM-generated brain images (https://nitrc.org/projects/mricrogl).
Principal component variations
After transformation to the transport domain, the standard principal components analysis (PCA) technique was applied to denoise the data in the transport domain. The dimensions of data contributing little to the overall variance in the dataset were removed. The principal components corresponding to the top 96% of the variance were retained.
Mathematically, the covariance matrix in Eq. 4 was computed.
| (4) |
Here, . The principal components are given by the eigenvectors of ST and can be used to explain the main modes of variability in the dataset (19, 24). The factorization in Eq. 5 gives both the principal components and eigenvalues, where the diagonal components of Σ represent the variance for each principal component.
| (5) |
Supervised machine learning
As previously described, nonlinear distances in the image domain can be represented in terms of Euclidean distances in the transport domain. Therefore, a linear classifier in the transport domain was designed to characterize shifts in tissue morphology (19). The pLDA technique was used to compute a subspace in the transport space that maximally separated the classes when the data were projected onto this subspace. To evaluate the performance of our machine learning classifier, we randomly partitioned the data into distinct training and test sets. We then trained the classifier by computing a discriminant subspace on the training set and tested its ability to accurately assign cohorts on the corresponding test set through a 10-fold stratified cross-validation procedure, iterated many times. Further details on the cross-validation scheme can be found in another section.
Within each training iteration, the pLDA method was used to classify individual samples after dimensionality reduction. Given the mth TBM-transformed image fm, let us refer to the vectorized version of the transport map fm as xm. A C-1 dimensional subspace in the transport space is sought using the pLDA method such that the projections of the C = 3 classes (duplication, deletion, and control) are maximally separated. The pLDA directions are given by the solution to the optimization problem in Eq. 6.
| (6) |
The matrices ST and SW are defined as in Eqs. 4 and 7.
| (7) |
where C = 3 and represents the number of classes. The pLDA technique estimates each conditional class density as a multivariate normal distribution N(μj, Σ), where the j = 1, …, C. The penalty weight α represents the tradeoff between the traditional LDA direction and the PCA directions. The parameter α is set to be 1.
In the testing phase, after the discriminant subspace is first computed based on training samples, the test data are assigned to classes. On the basis of training sample estimates, the quantities and that indicate the class mean (i.e., class centroids) and prior probability of each class j, respectively. The quantities are defined according to Eqs. 8 and 9.
| (8) |
| (9) |
In the above, xi indicates transformed images, and yi indicates their class labels for i ∈ 1, …, n, where n is the total number of samples. To classify a test sample, the class centroids are projected onto the discriminant subspace to give the transformed centroids , and the sample is assigned to the class j according to the nearest centroid, based on the following minimization rule in Eq. 10.
| (10) |
Here, refers to the assigned class label of the test sample. Test subjects were assigned to cohorts based on nearest centroid classification, correcting for the a priori proportion of subjects in each class. Sensitivity and specificity were reported using a one-against-all approach to compute the class sensitivity and specificity.
Repeated cross-validation
Stratified 10-fold cross-validation was performed during classification. For each fold, the PCA technique was performed in the training set, and the training data were projected onto the principal components capturing the top 96% of the variance. The test data were centered and projected onto the same principal components following the same procedure as in the training set. After this dimensionality reduction step, supervised machine learning was performed as described above. Stratified 10-fold cross-validation was iterated 1000 times, each with random and nonrepeated partitions of the dataset into 10 folds.
Accuracy, sensitivity, and specificity, as well as 95% confidence intervals, were determined by using the normal approximation of a binomial distribution for error estimation. The test accuracy obtained using white and gray matter distribution was compared to that based on age, gender, and brain parenchymal volume alone using the same classification scheme and reported in Table 3.
Visualizing discriminating differences
The discriminant subspace computed in the transport domain over each iteration of stratified 10-fold cross-validation was averaged to yield a single direction across each discriminant direction. The discriminant subspace computed in the training phase by the classification scheme was sampled along the maximally correlated direction. A vector field corresponding to the magnitude and direction by which brain tissue changes due to the discriminant direction is calculated. Then, inverse TBM transformation is used to visualize the interface between cohort boundaries using Eq. 3 as brain images.
Correlation with an independent variable
The influence of a clinical variable such as brain parenchymal volume on brain tissue distribution can be investigated in the transport domain. Suppose the variable of interest is ν ∈ ℝN×1. The direction in the transport domain wcorr can be computed that maximizes the covariation with the variable of interest ν according to Eq. 12.
| (11) |
Here, the direction is a vector field. The direction in the transport domain is a map characterizing tissue redistribution due to the independent variable. Here, η represents the decrement along the direction maximizing covariance. The images corresponding to the direction maximizing covariance in the transport domain can be visualized through inverse 3D TBM transformation.
Regression in the transport space
After computing the discriminant subspace in the transport domain using pLDA, the relationship between the brain macrostructural variations across each discriminant direction and behavior scores were calculated. As linear distances in the transport domain can capture complex, nonlinear variations in the image domain, linear regression was performed.
For continuous behavioral variables y (i.e., IQ), multiple linear regression was performed according to Eq. 12. Here, x1 represents the data when projected along direction 1, and x2 represents the data when projected along direction 2.
| (12) |
R2, the fraction of variance captured, was examined, and statistical significance was determined by permutation testing with 1000 iterations. For ordinal behavioral variables y (i.e., behavioral diagnoses), binary logistic regression was performed according to Eq. 13
| (13) |
Violin plots were generated according to (62).
Acknowledgments
We thank the Simons VIP foundation for access to the datasets enabling this work. We are grateful to all of the families at the participating Simons VIP sites, as well as the Simons VIP Consortium. We appreciate obtaining access to phenotypic data on SFARI Base. Approved researchers can obtain the Simons VIP population dataset described in this study by applying at https://base.sfari.org. This research was initiated while S.K. and G.K.R. were at Carnegie Mellon University. We also thank H. Huang for assistance with brain atlas coregistration and M. Shifat-E-Rabbi for discussions regarding computations.
Funding: The dataset used was collected via funding from the Simons Variation in Individuals Foundation (SFARI A118077). This work was supported in part by National Institutes of Health (grants R01GM130825 and R01NS058721), Radiological Society of North America (grant RR2126), and the Advanced Research Computing at Hopkins core facility (https://www.arch.jhu.edu), which is supported by the National Science Foundation (grant OAC 1920103).
Author contributions: S.K. and P.M. conceived and designed the study. S.K. performed the experiments. S.K., P.M., E.H.S., H.S., and G.K.R. analyzed the data. S.K. wrote the manuscript. P.M., H.S., G.K.R., and E.H.S. provided critical revisions. All authors reviewed and approved the final version of the manuscript.
Competing interests: The authors declare that they have no competing interests.
Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Code for data analysis and figure generation is provided on GitHub at https://github.com/codeshinjini/Gene-brain-behavior-link and Zenodo at https://zenodo.org/records/10982959 under GNU General Public License v2.0. TBM-generated images are provided on NeuroVault at https://neurovault.org/collections/YDTGRWGE/.
Supplementary Materials
This PDF file includes:
Supplementary Text
Figs. S1 to S15
Tables S1 to S9
References
REFERENCES AND NOTES
- 1.Geschwind D. H., Genetics of autism spectrum disorders. Trends Cogn. Sci. 15, 409–416 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.American Psychiatric Association, What is autism spectrum disorder?, https://psychiatry.org/patients-families/autism/what-is-autism-spectrum-disorder (2023). [accessed 18 November 2023].
- 3.Binder E. B., Genotype-phenotype predictions in autism: Are we there yet? Am. J. Psychiatry 178, 11–12 (2021). [DOI] [PubMed] [Google Scholar]
- 4.Sandin S., Lichtenstein P., Kuja-Halkola R., Hultman C., Larsson H., Reichenberg A., The heritability of autism spectrum disorder. JAMA 318, 1182–1184 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.A. Speaks, Should I or we have genetic testing for autism? Expert Opinion (2023).
- 6.Fu J. M., Satterstrom F. K., Peng M., Brand H., Collins R. L., Dong S., Wamsley B., Klei L., Wang L., Hao S. P., Stevens C. R., Cusick C., Babadi M., Banks E., Collins B., Dodge S., Gabriel S. B., Gauthier L., Lee S. K., Liang L., Ljungdahl A., Mahjani B., Sloofman L., Smirnov A. N., Barbosa M., Betancur C., Brusco A., Chung B. H. Y., Cook E. H., Cuccaro M. L., Domenici E., Ferrero G. B., Gargus J. J., Herman G. E., Hertz-Picciotto I., Maciel P., Manoach D. S., Passos-Bueno M. R., Persico A. M., Renieri A., Sutcliffe J. S., Tassone F., Trabetti E., Campos G., Cardaropoli S., Carli D., Chan M. C. Y., Fallerini C., Giorgio E., Girardi A. C., Hansen-Kiss E., Lee S. L., Lintas C., Ludena Y., Nguyen R., Pavinato L., Pericak-Vance M., Pessah I. N., Schmidt R. J., Smith M., Costa C. I. S., Trajkova S., Wang J. Y. T., Yu M. H. C.; The Autism Sequencing Consortium (ASC), Aleksic B., Artomov M., Benetti E., Biscaldi-Schafer M., Børglum A. D., Carracedo A., Chiocchetti A. G., Coon H., Doan R. N., Fernández-Prieto M., Freitag C. M., Gerges S., Guter S., Hougaard D. M., Hultman C. M., Jacob S., Kaartinen M., Kolevzon A., Kushima I., Lehtimäki T., Rizzo C. L., Maltman N., Manara M., Meiri G., Menashe I., Miller J., Minshew N., Mosconi M., Ozaki N., Palotie A., Parellada M., Puura K., Reichenberg A., Sandin S., Scherer S. W., Schlitt S., Schmitt L., Schneider-Momm K., Siper P. M., Suren P., Sweeney J. A., Teufel K., del Pilar Trelles M., Weiss L. A., Yuen R.; Broad Institute Center for Common Disease Genomics (Broad-CCDG); iPSYCH-BROAD Consortium, Cutler D. J., de Rubeis S., Buxbaum J. D., Daly M. J., Devlin B., Roeder K., Sanders S. J., Talkowski M. E., Rare coding variation provides insight into the genetic architecture and phenotypic context of autism. Nat. Genet. 54, 1320–1331 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Aglinskas A., Hartshorne J. K., Anzellotti S., Contrastive machine learning reveals the structure of neuroanatomical variation within autism. Science 376, 1070–1074 (2022). [DOI] [PubMed] [Google Scholar]
- 8.Duyzend M. H., Nuttle X., Coe B. P., Baker C., Nickerson D. A., Bernier R., Eichler E. E., Maternal modifiers and parent-of-origin bias of the autism-associated 16p11.2 cnv. Am. J. Hum. Genet. 98, 45–57 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Nuttle X., Giannuzzi G., Duyzend M. H., Schraiber J. G., Narvaiza I., Sudmant P. H., Penn O., Chiatante G., Malig M., Huddleston J., Benner C., Camponeschi F., Ciofi-Baffoni S., Stessman H. A. F., Marchetto M. C. N., Denman L., Harshman L., Baker C., Raja A., Penewit K., Janke N., Tang W. J., Ventura M., Banci L., Antonacci F., Akey J. M., Amemiya C. T., Gage F. H., Reymond A., Eichler E. E., Emergence of a homo sapiens-specific gene family and chromosome 16p11.2 cnv susceptibility. Nature 536, 205–209 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Qureshi A. Y., Mueller S., Snyder A. Z., Mukherjee P., Berman J. I., Roberts T. P., Nagarajan S. S., Spiro J. E., Chung W. K., Sherr E. H., Buckner R. L.; Simons VIP Consortium , Opposing brain differences in 16p11.2 deletion and duplication carriers. J. Neurosci. 34, 11199–11211 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Weiss L. A., Shen Y., Korn J. M., Arking D. E., Miller D. T., Fossdal R., Saemundsen E., Stefansson H., Ferreira M. A., Green T., Platt O. S., Ruderfer D. M., Walsh C. A., Altshuler D., Chakravarti A., Tanzi R. E., Stefansson K., Santangelo S. L., Gusella J. F., Sklar P., Wu B. L., Daly M. J.; Autism Consortium , Association between microdeletion and microduplication at 16p11.2 and autism. N. Engl. J. Med. 358, 667–675 (2008). [DOI] [PubMed] [Google Scholar]
- 12.A. M. Persico, R. Sacco, Endophenotypes in autism spectrum disorders. In: V. Patel, V. Preedy, C. Martin, Eds. Comprehensive Guide to Autism. (Springer, 2014), pp. 77–95. [Google Scholar]
- 13.Haar S., Berman S., Behrmann M., Dinstein I., Anatomical abnormalities in autism? Cereb. Cortex 26, 1440–1452 (2016). [DOI] [PubMed] [Google Scholar]
- 14.Lombardo M. V., Pramparo T., Gazestani V., Warrier V., Bethlehem R. A. I., Carter Barnes C., Lopez L., Lewis N. E., Eyler L., Pierce K., Courchesne E., Large-scale associations between the leukocyte transcriptome and BOLD responses to speech differ in autism early language outcome subtypes. Nat. Neurosci. 21, 1680–1688 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Mason L., Moessnang C., Chatham C., Ham L., Tillmann J., Dumas G., Ellis C., Leblond C. S., Cliquet F., Bourgeron T., Beckmann C., Charman T., Oakley B., Banaschewski T., Meyer-Lindenberg A., Baron-Cohen S., Bölte S., Buitelaar J. K., Durston S., Loth E., Oranje B., Persico A., Dell’Acqua F., Ecker C., Johnson M. H., Murphy D., Jones E. J. H., Stratifying the autistic phenotype using electrophysiological indices of social perception. Sci. Transl. Med. 14, eabf8987 (2022). [DOI] [PubMed] [Google Scholar]
- 16.Horev G., Ellegood J., Lerch J. P., Son Y.-E. E., Muthuswamy L., Vogel H., Krieger A. M., Buja A., Henkelman R. M., Wigler M., Mills A. A., Dosage-dependent phenotypes in models of 16p11.2 lesions found in autism. Proc. Natl. Acad. Sci. U.S.A. 108, 17076–17081 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Martin-Brevet S., Rodríguez-Herreros B., Nielsen J. A., Moreau C., Modenato C., Maillard A. M., Pain A., Richetin S., Jønch A. E., Qureshi A. Y., Zürcher N. R., Conus P.; 16p11.2 European Consortium; Simons Variation in Individuals Project (VIP) Consortium, Chung W. K., Sherr E. H., Spiro J. E., Kherif F., Beckmann J. S., Hadjikhani N., Reymond A., Buckner R. L., Draganski B., Jacquemont S., Quantifying the effects of 16p11.2 copy number variants on brain structure: A multisite genetic-first study. Biol. Psychiatry 84, 253–264 (2018). [DOI] [PubMed] [Google Scholar]
- 18.Friston K. J., Ashburner J., Generative and recognition models for neuroanatomy. Neuroimage 23, 21–24 (2004). [DOI] [PubMed] [Google Scholar]
- 19.Kundu S., Kolouri S., Erickson K. I., Kramer A. F., McAuley E., Rohde G. K., Discovery and visualization of structural biomarkers from mri using transport-based morphometry. Neuroimage 167, 256–275 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kolouri S., Tosun A. B., Ozolek J. A., Rohde G. K., A continuous linear optimal transport approach for pattern analysis in image datasets. Pattern Recognit. 51, 453–462 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wang W., Slepcev D., Basu S., Ozolek J. A., Rohde G. K., A linear optimal transportation framework for quantifying and visualizing variations in sets of images. Int. J. Comput. Vis. 101, 254–269 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kundu S., Huang H., Erickson K. I., McAuley E., Kramer A. F., Rohde G. K., Investigating impact of cardiorespiratory fitness in reducing brain tissue loss caused by ageing. Brain Commun. 3, fcab228 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ozolek J. A., Tosun A. B., Wang W., Chen C., Kolouri S., Basu S., Huang H., Rohde G. K., Accurate diagnosis of thyroid follicular lesions from nuclear morphology using supervised learning. Med. Image Anal. 18, 772–780 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Basu S., Kolouri S., Rohde G. K., Detecting and visualizing cell phenotype differences from microscopy images using transport-based morphometry. Proc. Natl. Acad. Sci. U.S.A. 111, 3448–3453 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kundu S., Ai in medicine must be explainable. Nat. Med. 27, 1328–1328 (2021). [DOI] [PubMed] [Google Scholar]
- 26.Brenier Y., Polar factorization and monotone rearrangement of vector-valued functions. Commun. Pure Appl. Math. 44, 375–417 (1991). [Google Scholar]
- 27.C. Villani, Optimal Transport: Old and New (Springer, 2008). [Google Scholar]
- 28.Kundu S., Ghodadra A., Fakhran S., Alhilali L., Rohde G., Assessing postconcussive reaction time using transport-based morphometry of diffusion tensor images. Am. J. Neuroradiol. 40, 1117–1123 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kundu S., Ashinsky B. G., Bouhrara M., Dam E. B., Demehri S., Shifat-E-Rabbi M., Spencer R. G., Urish K. L., Rohde G. K., Enabling early detection of osteoarthritis from presymptomatic cartilage texture maps via transport-based learning. Proc. Natl. Acad. Sci. U.S.A. 117, 24709–24719 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Wang W., Mo Y., Ozolek J. A., Rohde G. K., Penalized fisher discriminant analysis and its application to image-based morphometry. Pattern Recogn. Lett. 32, 2128–2135 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.McHugh M. L., Interrater reliability: The kappa statistic. Biochem. Med. 22, 276–282 (2012). [PMC free article] [PubMed] [Google Scholar]
- 32.Harvard-Oxford atlas.
- 33.D. Krishna B, L. Mary, A. George, Automatic Severity Evaluation of Articulation Disorder in Speech using Dynamic Time Warping. 2021 Fourth International Conference on Microelectronics, Signals & Systems (ICMSS), Kollam, India. (IEEE, 2021), pp. 1–6. [Google Scholar]
- 34.Rein B., Yan Z., 16p11.2 copy number variations and neurodevelopmental disorders. Trends Neurosci. 43, 886–901 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Shishido E., Aleksic B., Ozaki N., Copy-number variation in the pathogenesis of autism spectrum disorder. Psychiatry Clin. Neurosci. 68, 85–95 (2014). [DOI] [PubMed] [Google Scholar]
- 36.Neubauer S., Hublin J.-J., Gunz P., The evolution of modern human brain shape. Sci. Adv. 4, eaao5961 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Owen J. P., Chang Y. S., Pojman N. J., Bukshpun P., Wakahiro M. L., Marco E. J., Berman J. I., Spiro J. E., Chung W. K., Buckner R. L., Roberts T. P., Nagarajan S. S., Sherr E. H., Mukherjee P.; Simons VIP Consortium , Aberrant white matter microstructure in children with 16p11.2 deletions. J. Neurosci. 34, 6214–6223 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Chang Y. S., Owen J. P., Pojman N. J., Thieu T., Bukshpun P., Wakahiro M. L., Marco E. J., Berman J. I., Spiro J. E., Chung W. K., Buckner R. L., Roberts T. P. L., Nagarajan S. S., Sherr E. H., Mukherjee P., Reciprocal white matter alterations due to 16p11.2 chromosomal deletions versus duplications. Hum. Brain Mapp. 37, 2833–2848 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Blackmon K., Thesen T., Green S., Ben-Avi E., Wang X., Fuchs B., Kuzniecky R., Devinsky O., Focal cortical anomalies and language impairment in 16p11.2 deletion and duplication syndrome. Cereb. Cortex 28, 2422–2430 (2018). [DOI] [PubMed] [Google Scholar]
- 40.Sundberg M., Pinson H., Smith R. S., Winden K. D., Venugopal P., Tai D. J., Gusella J. F., Talkowski M. E., Walsh C. A., Tegmark M., Sahin M., 16p11.2 deletion is associated with hyperactivation of human ipsc-derived dopaminergic neuron networks and is rescued by rhoa inhibition in vitro. Nat. Commun. 12, 2897 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Li J., Brickler T., Banuelos A., Marjon K., Shcherbina A., Banerjee S., Bian J., Narayanan C., Weissman I. L., Chetty S., Overexpression of cd47 is associated with brain overgrowth and 16p11.2 deletion syndrome. Proc. Natl. Acad. Sci. U.S.A. 118, e2005483118 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Jimenez-Romero M. S., Fernandez-Urquiza M., Benıtez-Burraco A., Language and communication deficits in chromosome 16p11.2 deletion syndrome. J. Speech Lang. Hear. Res. 65, 4724–4740 (2022). [DOI] [PubMed] [Google Scholar]
- 43.Irie K., Doi M., Usui N., Shimada S., Evolution of the human brain can help determine pathophysiology of neurodevelopmental disorders. Front. Neurosci. 16, 871979 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Zhang K., Sejnowski T. J., A universal scaling law between gray matter and white matter of cerebral cortex. Proc. Natl. Acad. Sci. U.S.A. 97, 5621–5626 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Reber J., Hwang K., Bowren M., Bruss J., Mukherjee P., Tranel D., Boes A. D., Cognitive impairment after focal brain lesions is better predicted by damage to structural than functional network hubs. Proc. Natl. Acad. Sci. U.S.A. 118, e2018784118 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Ju J., Yang X., Jiang J., Wang D., Zhang Y., Zhao X., Fang X., Liao H., Zheng L., Li S., Hou S.-T., Liang L., Pan Y., Li H., Li N., Structural and lipidomic alterations of striatal myelin in 16p11.2 deletion mouse model of autism spectrum disorder. Front. Cell. Neurosci. 15, 718720 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Modenato C., Martin-Brevet S., Moreau C. A., Rodriguez-Herreros B., Kumar K., Draganski B., Sønderby I. E., Jacquemont S., Lessons learned from neuroimaging studies of copy number variants: A systematic review. Biol. Psychiatry 90, 596–610 (2021). [DOI] [PubMed] [Google Scholar]
- 48.Simons Vip Consortium , Simons variation in individuals project (Simons VIP): A genetics first approach to studying autism spectrum and related neurodevelopmental disorders. Neuron 73, 1063–1067 (2012). [DOI] [PubMed] [Google Scholar]
- 49.Sønderby I. E., Ching C. R. K., Thomopoulos S. I., van der Meer D., Sun D., Villalon-Reina J. E., Agartz I., Amunts K., Arango C., Armstrong N. J., Ayesa-Arriola R., Bakker G., Bassett A. S., Boomsma D. I., Bülow R., Butcher N. J., Calhoun V. D., Caspers S., Chow E. W. C., Cichon S., Ciufolini S., Craig M. C., Crespo-Facorro B., Cunningham A. C., Dale A. M., Dazzan P., de Zubicaray G. I., Djurovic S., Doherty J. L., Donohoe G., Draganski B., Durdle C. A., Ehrlich S., Emanuel B. S., Espeseth T., Fisher S. E., Ge T., Glahn D. C., Grabe H. J., Gur R. E., Gutman B. A., Haavik J., Håberg A. K., Hansen L. A., Hashimoto R., Hibar D. P., Holmes A. J., Hottenga J.-J., Hulshoff Pol H. E., Jalbrzikowski M., Knowles E. E. M., Kushan L., Linden D. E. J., Liu J., Lundervold A. J., Martin-Brevet S., Martínez K., Mather K. A., Mathias S. R., Mc Donald-Mc Ginn D. M., Mc Rae A. F., Medland S. E., Moberget T., Modenato C., Sánchez J. M., Moreau C. A., Mühleisen T. W., Paus T., Pausova Z., Prieto C., Ragothaman A., Reinbold C. S., Marques T. R., Repetto G. M., Reymond A., Roalf D. R., Rodriguez-Herreros B., Rucker J. J., Sachdev P. S., Schmitt J. E., Schofield P. R., Silva A. I., Stefansson H., Stein D. J., Tamnes C. K., Tordesillas-Gutiérrez D., Ulfarsson M. O., Vajdi A., Ent D., van den Bree M. B. M., Vassos E., Vázquez-Bourgon J., Vila-Rodriguez F., Walters G. B., Wen W., Westlye L. T., Wittfeld K., Zackai E. H., Stefánsson K., Jacquemont S., Thompson P. M., Bearden C. E.; ENIGMA-CNV Working Group; ENIGMA 22q11.2 Deletion Syndrome Working Group , Effects of copy number variations on brain structure and risk for psychiatric illness: Large-scale studies from the enigma working groups on cnvs. Hum. Brain Mapp. 43, 300–328 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Moreau C. A., Ching C. R., Kumar K., Jacquemont S., Bearden C. E., Structural and functional brain alterations revealed by neuroimaging in cnv carriers. Curr. Opin. Genet. Dev. 68, 88–98 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Owen J. P., Bukshpun P., Pojman N., Thieu T., Chen Q., Lee J., D’Angelo D., Glenn O. A., Hunter J. V., Berman J. I., Roberts T. P., Buckner R., Nagarajan S. S., Mukherjee P., Sherr E. H., Brain MR imaging findings and associated outcomes in carriers of the reciprocal copy number variation at 16p11.2. Radiology 286, 217–226 (2018). [DOI] [PubMed] [Google Scholar]
- 52.Kostic A., Buxbaum J. D., The promise of precision medicine in autism. Neuron 109, 2212–2215 (2021). [DOI] [PubMed] [Google Scholar]
- 53.American Psychiatric Association, DSM-IV-TR: Diagnostic and Statistical Manual of Mental Disorders, Text Revision (American Psychiatric Association, 75, 2000), pp. 78–85. [Google Scholar]
- 54.E. Mullen, Mullen Scales of Early Learning, AGS Edition: Manual and Item Administrative Books, (American Guidance Services Inc., 1995) pp. 1–92. [Google Scholar]
- 55.C. D. Elliott, J. D. Salerno, R. Dumont, J. O. Willis, The Differential Ability Scales - Second Edition. D. P. Flanagan & E. M. McDonough, Eds., Contemporary intellectual assessment: Theories, tests, and issues (4th ed., pp. 360–382). The Guilford Press (2018). [Google Scholar]
- 56.D. Wechsler, WAIS-III administration and scoring manual. The Psychological Corporation (1997).
- 57.Maillard A., Ruef A., Pizzagalli F., Migliavacca E., Hippolyte L., Adaszewski S., Dukart J., Ferrari C., Conus P., Mannik K., Zazhytska M., Siffredi V., Maeder P., Kutalik Z., Kherif F., Hadjikhani N., Beckmann J. S., Reymond A., Draganski B., Jacquemont S.; 16p11.2 European Consortium , The 16p11.2 locus modulates brain structures common to autism, schizophrenia and obesity. Mol. Psychiatry 20, 140–147 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Ashburner J., Hutton C., Frackowiak R., Johnsrude I., Price C., Friston K., Identifying global anatomical differences: Deformation-based morphometry. Hum. Brain Mapp. 6, 348–357 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Ashburner J., Friston K. J., Voxel-based morphometry—The methods. Neuroimage 11, 805–821 (2000). [DOI] [PubMed] [Google Scholar]
- 60.Ashburner J., Good C., Friston K. J., Tensor based morphometry. Neuroimage 11, S465 (2000). [DOI] [PubMed] [Google Scholar]
- 61.Park S. R., Kolouri S., Kundu S., Rohde G. K., The cumulative distribution transform and linear pattern classification. Appl. Comput. Harmon. Anal. 45, 616–641 (2018). [Google Scholar]
- 62.H. Hoffmann, Violin plot (https://www.mathworks.com/matlabcentral/fileexchange/45134-violin-plot), MATLAB Central File Exchange. Retrieved May 23, 2024.
- 63.Beg M. F., Miller M. I., Trouve A., Younes L., Computing large deformation metric mappings via geodesic flows of diffeomorphisms. Int. J. Comput. Vis. 61, 139–157 (2005). [Google Scholar]
- 64.Dale A. M., Fischl B., Sereno M. I., Cortical surface-based analysis. Neuroimage 9, 179–194 (1999). [DOI] [PubMed] [Google Scholar]
- 65.T. Hastie, R. Tibshirani, J. Friedman, The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Springer Series in Statistics (Springer, 2009). [Google Scholar]
- 66.H. Hotelling, Breakthroughs in Statistics (Springer, 1992), pp. 162–190. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Text
Figs. S1 to S15
Tables S1 to S9
References