Guided optimization of ToxPi model weights using a Semi-Automated approach

Abstract

The Toxicological Prioritization Index (ToxPi) is a visual analysis and decision support tool for dimension reduction and visualization of high throughput, multi-dimensional feature data. ToxPi was originally developed for assessing the relative toxicity of multiple chemicals or stressors by synthesizing complex toxicological data to provide a single comprehensive view of the potential health effects. It continues to be used for profiling chemicals and has since been applied to other types of “sample” entities, including geospatial (e.g. county-level Covid-19 risk and sites of historical PFAS exposure) and other profiling applications. For any set of features (data collected on a set of sample entities), ToxPi integrates the data into a set of weighted slices that provide a visual profile and a score metric for comparison. This scoring system is highly dependent on user-provided feature weights, yet users often lack knowledge of how to define these feature weights. Common methods for predicting feature weights are generally unusable due to inappropriate statistical assumptions and lack of global distributional expectation. However, users often have an inherent understanding of expected results for a small subset of samples. For example, in chemical toxicity, prior knowledge can often place subsets of chemicals into categories of low, moderate or high toxicity (reference chemicals). Ordinal regression can be used to predict weights based on these response levels that are applicable to the entire feature set, analogous to using positive and negative controls to contextualize an empirical distribution. We propose a semi-supervised method utilizing ordinal regression to predict a set of feature weights that produces the best fit for the known response (“reference”) data and subsequently fine-tunes the weights via a customized genetic algorithm. We conduct a simulation study to show when this method can improve the results of ordinal regression, allowing for accurate feature weight prediction and sample ranking in scenarios with minimal response data. To ground-truth the guided weight optimization, we test this method on published data to build a ToxPi model for comparison against expert-knowledge-driven weight assignments.

1. Introduction

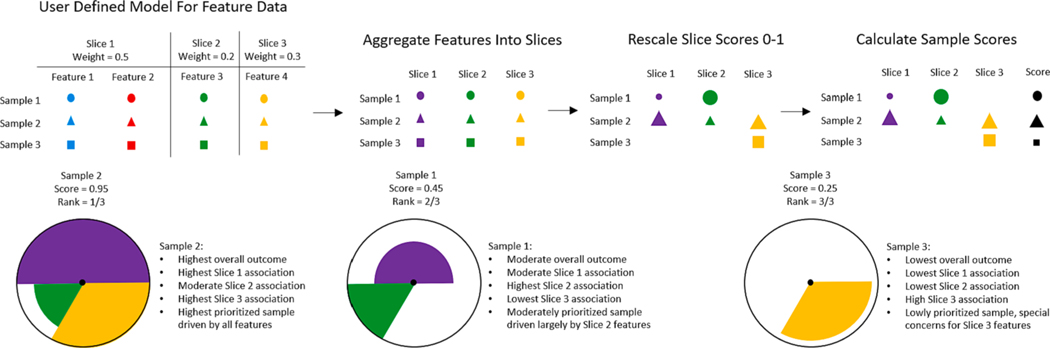
The Toxicological Prioritization Index (ToxPi) is a statistical modeling framework used to analyze feature data for predicted ranking and prioritization of samples. This framework aggregates similar features into scored ‘slices’, rescales individual slice scores to range 0–1, and then develops an overall score for each sample using a linear modeling system constrained to positive coefficients selected as user-defined slice weights, allowing for effective sample ranking. As a result of using a linear modeling system, slice weights can be interpreted as the importance of categorized features when predicting sample ranks. The resulting scores for each sample can be visualized in a ToxPi profile, displayed in Fig. 1. Slice weights are represented as the arc-width, slice scores are represented as the radius, and the overall sample scores are represented by the sum of all slice weights * radii products. These visualizations allow for quick comparison of overall feature importance, feature impacts driving a specific sample, relative impact ranking of common features between samples, and overall ranking between samples [1]. The ToxPi framework is a flexible method capable of analyzing disparate data from several different fields. It has been used to measure and compare total PFAS levels found in pine needles in North Carolina [2], to correlate phenotypic and environmental factors with lipid structures [3], to assess and rank county risk to Covid-19 across the United States [4] and to characterize climate change across the United States [5].

Fig. 1.

ToxPi framework summary, example visualizations, and example interpretations. Shapes represent samples and colors represent common features/slices. Example samples 1, 2, and 3 are ranked to show a high concern sample, a moderate concern sample, and a low concern sample. Text explanations are shown to describe how to interpret each individual profile.

Since its development, several advancements have been made, including a graphical user interface for easier analysis [6], an R package for more powerful analysis [7], and an ArcGIS Toolbox for geographic mapping and analysis [9]. These data analyses and methods showcase ToxPi’s capability for supporting decision making by categorizing risk and correlating slices to compare samples and feature importance. As coefficients for ToxPi’s linear modeling system, slice weights play an outsized role in both the prioritization of samples and the interpretation of highly ranked samples. Currently, these weights are provided by the user to represent ‘known’ feature importance, meaning that the user must have knowledge of relative feature impact in the real world. This limits studies done using the ToxPi framework, as often users may be lacking knowledge regarding the relative importance of features and are seeking a method that utilizes a form of feature weighting or selection.

Due to the wide use cases of the ToxPi framework, developing a generalized framework for feature weighting requires a method that is flexible, can be used with small amounts of known outcome data, and can predict the ranks of samples with high performance. This method must predict weights that are appropriate as coefficients for a linear model, as interpretation of these weights needs to remain simplistic to retain flexibility, consistency, and easy interpretation for decision making. Many methods currently exist for feature weighting and can be loosely categorized into unsupervised and supervised methods. Unsupervised methods, such as sparse k-means, estimate feature weights that best group similar subsets of data [10]. However, these methods do not consider prior outcome data (e.g., expert-supplied ranking information) and thus may not accurately reflect the ranking performed in ToxPi analysis. Supervised regression methods that utilize continuous response data, such as linear regression, are often used to create a weighted model that can accurately predict feature weights for linear ranking by generating the best fit line through the data [11]. As a result, continuous regression models would be a good candidate; however, generally ToxPi users do not have continuous outcomes associated with their data, causing these methods to become unusable.

Despite the lack of continuous response data, users often have a general idea of classification information regarding the relative response and can place of a few of their samples into bins (e.g., high, moderate, or low risk). For samples that are chemical entities, these bins could be delineated by reference (i.e., positive or negative control) compounds. For samples that are geographical areas, these bins could be defined by localities with demonstrably extreme high or low risk levels. With this information, a classification model can be built that predicts groupings of samples, but regression is still required to maintain the ordering of classifications. Ordinal regression is a popular classification method that utilizes regression to build a model that assigns feature weights and predicts the ordered classification responses of unknown samples [12]. For each response level, a threshold score is determined allowing unknown samples to be classified using the model, and the results are provided as an ordered classification (i.e., high, moderate, and low). However, integrating ordinal regression with the ToxPi framework presents several issues. Since ordinal regression predicts classification responses of unknown samples, it does not integrate with the ToxPi framework, as ToxPi is a linear ranking method that provides no classifications. Further, adaptation of the ToxPi framework to include classifications would result in a severe loss of ranking information, as in ordinal classification models, responses of the same level are considered to have the same outcome effect and to be the same rank. Additionally, since users generally only have prior response knowledge of a small number of samples, classifications may be inaccurate.

Herein, we propose the use of ordinal regression to obtain feature weights; however, we bypass the response thresholds for classification and directly use the weights as a linear model to predict scores, allowing for direct integration within the ToxPi framework. We explore the viability of using a classification model to predict scores that accurately rank all samples. Due to the small amount of known data many users will have, we explore the use of semi-supervised methods for the improvement of ordinal regression performance. Few semi-supervised methods have been developed that use ordinal regression, with the main setback being developing a method that can effectively integrate unknown data and can accurately assign the response level thresholds for classifying data. Gaussian and deep learning methods have been used to incorporate unknown data into ordinal regression with a tendency for low predictive classification accuracy due to incorrect placement of response level thresholds when using small amounts of known data [13,14]. To combat these issues, we propose and explore a semi-supervised approach that uses a custom genetic algorithm to incorporate unknown data and fine tune ordinal regression results.

Genetic algorithms (GAs) have been widely utilized for feature weight prediction in a variety of fields. Genetic algorithms are methods used for solving optimization problems based on natural selection properties. For the problem of optimizing feature weights, these algorithms work by taking a starting parent population of weight sets and breeding them using various properties of inheritance and evolution to produce a new child population of weight sets. This process is then repeated using the new generation of weight sets, with the idea that after several generations the population will evolve and converge to a weight set via natural selection. To model natural selection, the user provides a function based on the original problem that can be used to represent the fitness of a weight set, such that after several generations the weight sets will become optimized for the provided function. The result is a weight set that can be used as an accurate prediction for the original feature weighting problem. They have been utilized to reduce feature dimensionality in the identification of favorable water-binding sites on protein surfaces [15], to predict weights of base learners for ensemble based piRNA prediction [16], and to estimate attribute importance for customer churn prediction in the telecom sector [17], showcasing their versatility and flexibility.

We propose a method that utilizes headless chicken crossover [18] and hill climbing selection [19], in concert with a fitness function that utilizes percentage of data expected in each classification bin, to improve the performance results of ordinal regression for predicting feature weights. The headless chicken algorithm acts as a method for choosing breeding candidates for each generation, in which one of the breeding partners is randomly simulated from outside the population for each breed instead of both partners coming from within the population. This approach can help prevent the algorithm from becoming stuck in a local optimum by adding variability to the population. The hill climbing approach acts as a method for representing natural selection. Using this approach, a weight set only survives and gets passed on to the next generation if it shows an increase in fitness over that of the parent generation, ensuring that the final generation will have an improved fitness over that of the initial generation. Then, we bypass the need of predicting a threshold score for classification by using the predicted weights as ToxPi slice weights, which are then used to score and rank samples. We show that the use of known priority classifications for a small number of known samples with this method can achieve high performance results as a ranking system. The pipeline for this methodology is displayed in Fig. 2.

Fig. 2.

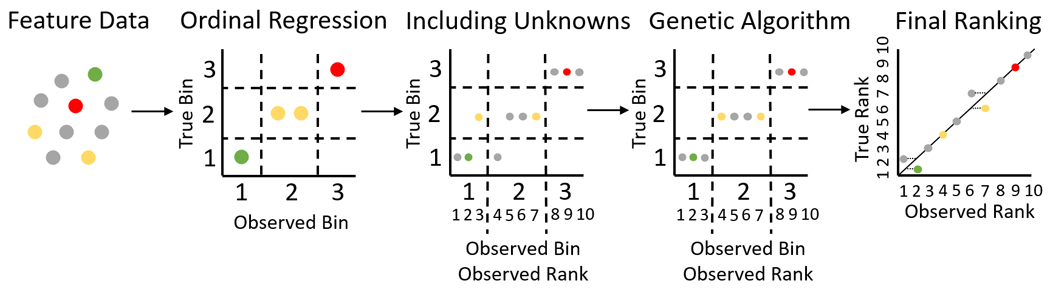
Pipeline for estimating weights and ranking samples using ordinal regression and a GA. Pipeline consists of collecting feature data with labeled classification categories of a few known samples, estimating weights using ordinal logistic regression, including unknown data via ranking and percent bin sizes as discriminants, genetic algorithm for fine-tuning the weights, and then ranking the samples using the ToxPi framework with slice weights.

We explore the viability of this method of feature weight prediction for sample ranking first using several simulated datasets that represent common use cases for the ToxPi framework, and then on a real dataset consisting of several petroleum substances that are representative of UVCBs (unknown or variable composition, complex reaction products and biological materials) that have previously been obtained, analyzed, and ranked for bioactivity levels using the ToxPi framework [20]. In the previous study, the authors conducted extensive in vitro cell assay studies on each UVCB, performed quality control measures to select high-confidence in vitro data, aggregated phenotypic results for each cell type into a slice, and used the results to build a ToxPi model representative of bioactivity level. After the analysis, they found that PAC (polycyclic aromatic compound) data was highly correlated with their ToxPi results and hypothesized that this data could be a cheaper alternative for grouping and ranking UVCBs. In this paper, we expand on their hypothesis by utilizing our feature weighting method to estimate slice weights for PAC data, build a ToxPi model to rank the UVCBs in their paper, and compare our ranking results to their results in order to show both the viability of our feature weighting method and the viability of using PAC data as a representative of bioactivity levels.

2. Methods

2.1. Overview

We provide two methods for the prediction of slice weights for the Toxicological Prioritization Index. Ordinal regression is provided and explored as a baseline method for predicting weights and testing performance on ranking, and a custom genetic algorithm was developed and provided to explore methods for improving ordinal regression performance. This performance testing was done on several simulated datasets and one real dataset and results were provided as a benchmark study for error assessment. ToxPi analysis and graphics were created using the toxpiR [7] and ggplot2 [21] packages in R version 4.2.1 [8]. Documentation and code supporting the methods described here are available at https://github.com/ToxPi/ToxPi-Weight-Optimization.

2.2. Simulating feature Data

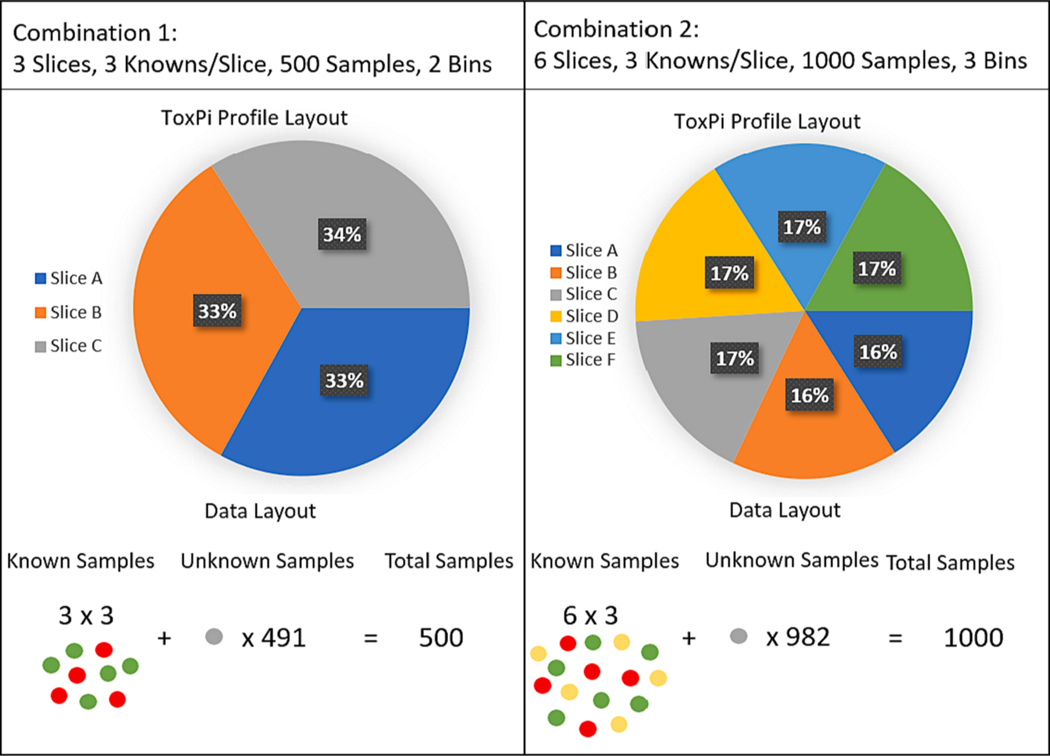
Feature data was randomly generated to simulate common use cases for the ToxPi framework. Four different datasets were generated with slice distributions of normal, gamma, uniform, and mixed. Each distribution was simulated for total slices = {3,6,9,12,15}, total ordered response levels = {2,3,4}, ratio of known samples per slice = {3,6,9,12,15}, and total samples = {500,100,5000,10000}. Known samples were randomly selected proportionally from each response level and repeated 1,000 times per simulated dataset. The true ranks of samples for each simulated dataset were determined assuming a fixed, equivalent weight set. Estimated slice weights were obtained and ranking performance results were tested and compared to the true ranks separately for each simulation. An example of parameter combinations between two simulations is shown visually in Fig. 3.

Fig. 3.

Visual comparison of two different simulations showing interpretation of all scenario parameters. The left example simulation shown represents a 3 slice model with 3 knowns per slice, 500 total samples, and 2 response levels shown by circle color. The right simulation represents a 6 slice model with 3 knowns per slice, 1000 total samples, and 3 response levels. The total number of simulation combinations tested was 1200, with testing being done for every combination of the following sets: slice number {3,6,9,12,15}, known/slice ratio {3,6,9,12,15}, total samples {500,1000,5000,10000}, response levels {2,3,4}, and data distributions {normal, gamma, beta, mixed}.

2.3. Ordinal regression for predicting slice Weights

Ordinal logistic regression was performed on the known test data to generate a probable slice weight set that properly classifies the known data into their response levels. Regression was performed using the ordinalNet package (version 2.12) in R (version 4.2.1). All slices were used simultaneously in the model as explanatory variables. Each slice coefficient was constrained to be non-negative, and slice weights were obtained directly as the variable coefficients. It is important to note that ordinal regression assumes proportional odds, meaning the coefficients of any explanatory variables are consistent when switching across the different thresholds. All slices were retained in the model regardless of significance, as ToxPi users provide slices that they want to retain in the model prior to model building. This method also assumes ToxPi users have combined highly correlated slices to minimize the error in feature weight prediction for regression. No standardization was needed prior to model building, as the ToxPi framework rescales the data within each slice between 0 and 1, allowing for direct comparison of the coefficient magnitudes. Afterwards the weight results were rescaled to sum to 100 for integration with the ToxPi framework and for consistent user interpretation of slice impact.

2.4. Genetic algorithm for predicting slice Weights

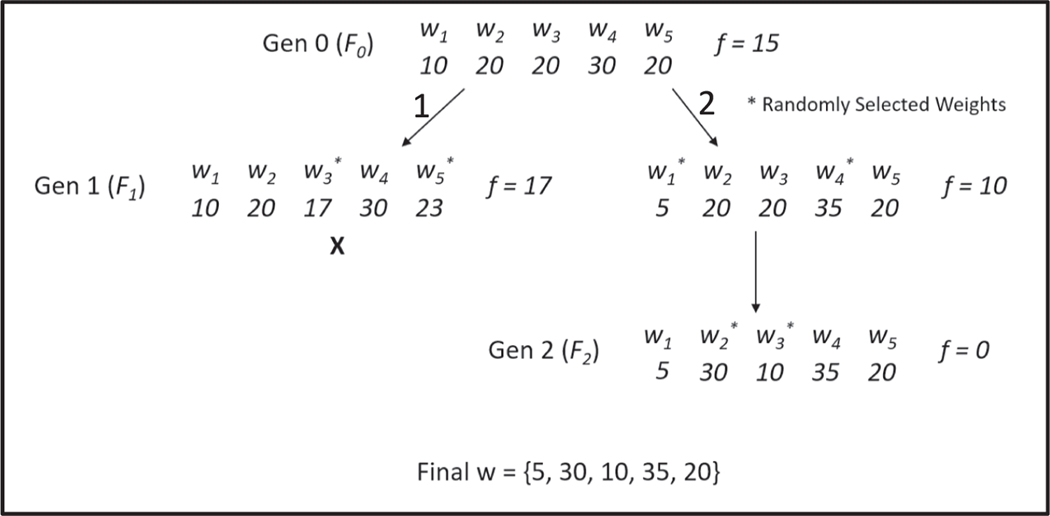
A custom genetic algorithm was developed to incorporate unknown data into weight prediction and explore the capabilities of improving ordinal regression results. The genetic algorithm uses a customization of the headless chicken algorithm combined with the hill-climbing methodology. The initial population consists of one parent weight set initialized using the ordinal regression weights. This initialization was done to reduce the search space among weight sets to make the problem more tractable while still ensuring a probable weight set is found. The crossover rate for the algorithm is set to 1 less than the number of slices such that only 2 slices are changed in the parent generation, as the use of ordinal regression results in a weight set that is already close to convergence in the fitness function and thus requires small changes. Similarly to the headless chicken algorithm, the weight set is bred with other randomly generated weight sets from outside the population. These weight sets were generated as 2 weights obtained from a gamma distribution with shape 1, as this distribution has been shown to model the Dirichlet distribution which can be used to uniformly simulate sets of data that sum to a desired number, in this case the sum of the weights was not retained in the parent weight set after crossover. These two slices are scaled such that the total sum of weights still equals 100 in the offspring, ensuring only 2 slice weights are changed and retaining consistency in weight interpretation. Under the hill-climbing methodology, the weight set is bred until the fitness function improves, such that each generation shows an improvement in fitness. The convergence criterion defaults to 500 iterations or a fitness score of 0, meaning that the algorithm will continue to breed a new weight set generation until a generation has 500 failures to decrease the fitness score or the fitness score reaches 0, representing a perfect classification of the known samples after inclusion of all the data. This convergence criterion was tested for 50, 100, 500, and 1000 iterations. An example diagram of the algorithm and fitness function is shown in Fig. 4.

Fig. 4.

Example methodology for the genetic algorithm. Generation 0 (F₀) weights (w) are obtained from ordinal regression. In the first breed (Arrow 1) weights 3 and 5 are selected to be randomly generated from outside the population. Using the new weights, a worse fitness (f) is seen and the branch ends (x). In the second breed (Arrow 2) weights 1 and 4 are selected to be randomly generated, which results in an increase in fitness. This weight set is retained, and a new generation is bred from it. This new generation results in a fitness of 0, so the genetic algorithm converges.

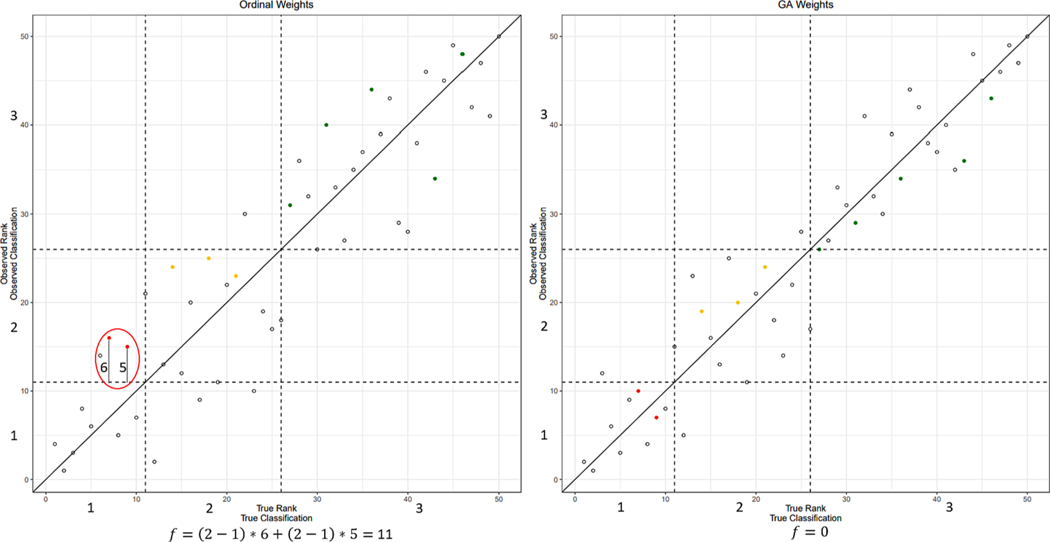
A customized fitness function was used that incorporates the unknown data into the analysis using estimated percent response level sizes provided by the user, such as the user expects 10 % of the data to be in response level 1. This function takes the weight set to be tested and determines the ToxPi score for each sample under the linear model used by the ToxPi framework. These samples are then ranked, and the response level threshold is defined as the percentages provided by the user. The fitness function then checks to see if any of the known samples have shifted to the wrong response level(percentage of data) after the inclusion of the unknown data, with a fitness score defined in Equation (1), where $y$ denotes the fitness score, $i$ denotes the $i^{th}$ sample, $n$ denotes the number of samples, $C_i^o$ denotes the true response level, $C_i$ denotes the observed response level, $D_i$ denotes the true response level threshold as a rank, and $R_i$ denotes the observed rank. This fitness function uses the response level difference as a multiplier to prioritize the proper classification of known samples and uses the rank distance from the proper threshold rank to break ties when two weight sets result in the same number of misclassifications. This results in new weight sets that improve classification accuracy while still ensuring that the desired ranking of the samples is preserved. An example visualization of the fitness function is shown in Fig. 5.

Fig. 5.

Example visualization of convergence for the genetic algorithm. The GA works by finding reference samples that ordinal regression places into the wrong percentage data threshold (e.g., the two red samples do not fall in the main diagonal), and fine tuning the weight set until these reference samples are relocated into their proper response level. Once all reference samples are in their correct response level, a fitness score of 0 is achieved denoting a perfect convergence. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

$$y={\sum }_{i=1}^n\left(\left|C_i^o-C_i\right|\right)\left(\left|D_i-R_i\right|\right)$$

2.5. Measuring Performance

A benchmark study was done to measure performance of ordinal regression and the genetic algorithm across all simulated scenarios such that users could determine the estimated ranking error based on the methodology and dataset they are using. For each dataset, known data was randomly selected 1,000 times and both the ordinal regression and genetic algorithm weight set were determined for each selection. The samples were then scored based on the ToxPi linear model for each estimated weight set and ordered by rank. The empirical distribution consisting of 1,000 mean-absolute error as a percent of total dataset size for true rank vs observed rank were measured for both ordinal regression obtained weights and GA obtained weights to estimate the performance results of using known classifications as a linear ranking system for each simulated dataset. This error can be interpreted as what percentage of the data the true rank was from the observed rank on average.

2.6. UVCB data Analysis

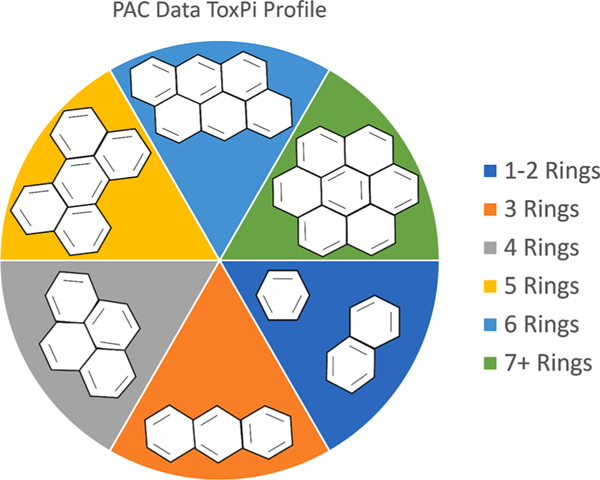
UVCB data with corresponding PAC data from the [20] paper was obtained, consisting of 141 petroleum substances previously analyzed for ToxPi scores and ranking based on in vitro cell assay data. PAC data consisted of the weight percentages of polycyclic aromatic compounds separated based on the number of aromatic rings in its structure found to be present in the petroleum substances tested. Based on the House et al Spearman rank correlation results for PAC content and ToxPi-ranked cell bioactivity, percentage weight PAC data consisting of 1–2 aromatic ring structures were combined into one slice, and 3–7 + ring structures were left as individual slices for a total of 6 slices. Using this data, a ToxPi model was built for the prediction of bioactivity levels, displayed in Fig. 6. To estimate the weights for the model, both ordinal regression and the genetic algorithm proposed were used and compared. To obtain “known” samples with response levels based on bioactivity for the weight prediction, the ToxPi ranking from the [20] paper obtained using cell assay data was split into 3 categories, with the bottom 50 % scores being assigned to low bioactivity, the top 20 % scores being assigned to high bioactivity, and the remaining 30 % in the middle being assigned to moderate bioactivity. Next, 36 known samples were randomly selected proportionally from the 3 response levels as a small set of representative samples that ToxPi users would generally have prior knowledge on. The UVCB dataset contained several samples that had no measurable PAC data, and thus provided no information regarding bioactivity response. These samples were avoided for selection as knowns and are discussed later. Using both ordinal regression and genetic algorithm obtained feature weights for the 36 known substances, separate ToxPi models were built to rank the petroleum substances based on bioactivity levels. The results were compared to the ranking of the [20] model using the correlation between the two models and the mean-absolute error as a percent of total dataset size.

Fig. 6.

ToxPi Model layout using polycyclic aromatic compounds data as slice measurements. Each slice represents the weight percentage of structures made up of specific numbers of aromatic rings.

3. Results and discussion

3.1. Fitness function Viability

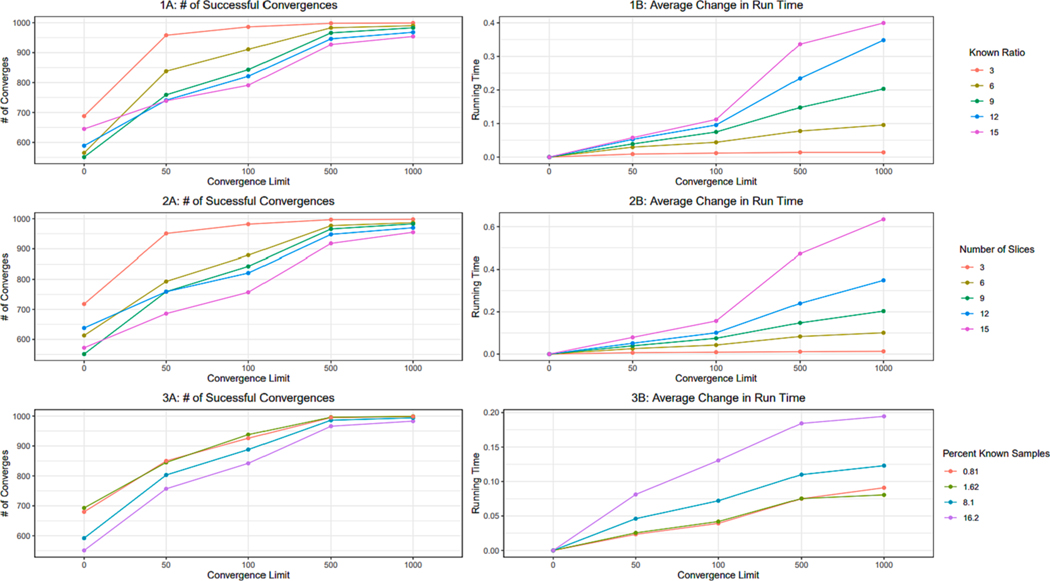
The results of changing convergence criterion for varying known ratios, number of slices, and number of samples for 1,000 trials are shown in Fig. 7.1, 7.2, and 7.3 respectively. Columns A and B respectively show the number of successful convergences and the average increase in running time of the GA over ordinal regression. A convergence criterion of 500 iterations was selected as a user default for the algorithm as it was found to significantly decrease failed convergences while maintaining a reasonable running time. The fitness function successfully converged to a fitness of zero more often for scenarios with small numbers of slices, small known/slice ratios, and larger sample sizes (i.e., smaller percentages of known data out of all data). As these factors changed from their optimum, the convergence to 0 of the fitness function decreased and the running time of the algorithm increased consistently. The decrease in efficiency as the number of slices and known ratio increase, and the total number of samples decreases, is likely due to the method of crossover used and the convergence criterion that was set. As both the number of slices and the number of known samples increases, and the total number of samples decreases towards the number of known samples, an optimal solution becomes harder to find, and changing a fixed 2 weights per breed might not be an appropriate crossover rate for optimal convergence. Furthermore, under the hill- climbing approach, 500 iterations might not be long enough to find a weight set of increased fitness within one generation as the complexity of the problem increases. To expand this method to more complex problems, a more flexible crossover rate that is variable might need to be adapted into this method. Alternatively, a more flexible convergence criterion could be implemented that either scales as problem complexity scales or avoids the hill-climbing approach altogether. The drawbacks of these adaptations would be a potentially drastic increase in running time for the method, as the convergence becomes more variable and the population increases, and no guarantee exists that the fitness will improve between generations. It is also important to note that the fitness function already converges to zero for a majority of the 1,000 trials when using the ordinal regression results, or convergence limit of 0 on the x-axis of Fig. 7. Thus, the GA has a large impact on error for a minority of trials that aren’t already converged, but it shows a lesser impact when looking at the overall distribution of the errors.

Fig. 7.

Results of the GA and fitness function based on changing convergence criteria for a scenario consisting of 3 response levels and an underlying data distribution of normal. Plots columns from left to right show the capability of the fitness function to converge to 0 out of 1,000 trials, and the average difference in running time between ordinal regression and the ga. Row 1: Results consistently using 9 slices and 500 samples but changing the known samples per slice. Row 2: Results consistently using 9 known samples per slice and 500 samples but varying number of slices. Row 3: Results consistently using 9 known samples per slice and 9 slices but varying the number of total samples to change the percentage of known samples.

3.2. Benchmark study - factors affecting ranking and GA Performance

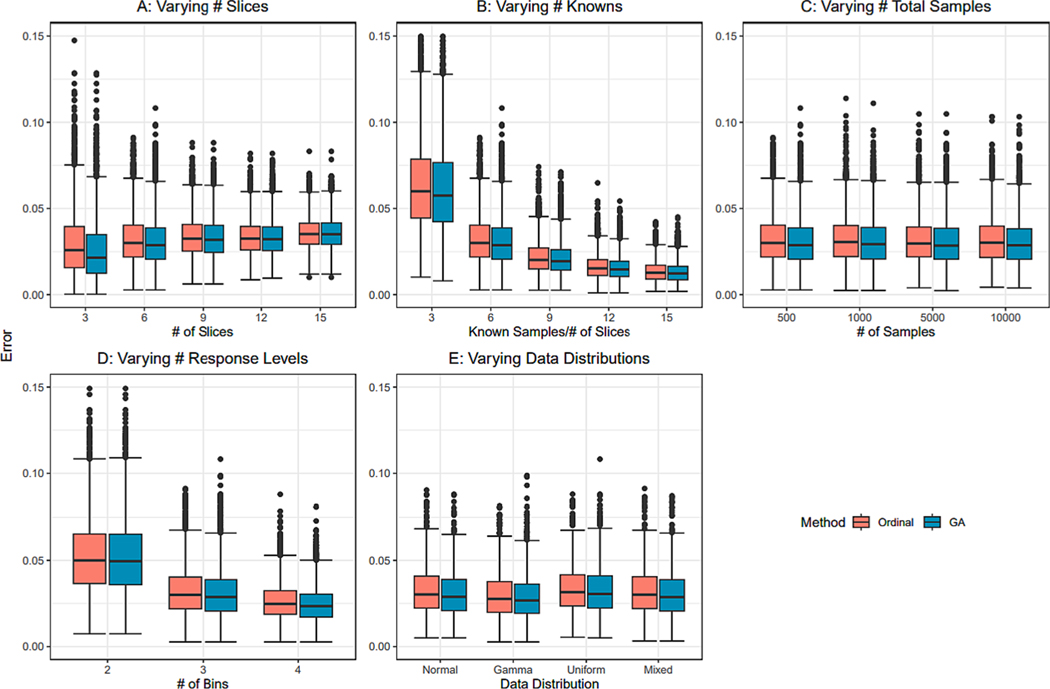
Fig. 8 shows each individual factor’s impact on the distribution of empirical error, allowing for visualization of expected error for users and exploration of how model complexity impacts ranking performance. Fig. 9 shows each individual factor’s impact on the distribution of difference in error between ordinal regression and GA ranking results, allowing for exploration of when the GA provides a benefit over ordinal regression. Factors in each figure are kept constant at 6 slices, 6 known samples/slice, 500 total samples, 3 response levels, and an aggregation of all 4 data distributions tested unless otherwise stated, and each factor is discussed below. Distributions for all factor combinations tested in the simulation study can be found in the Supplemental Figures.

Fig. 8.

Empirical distributions of MAE as a proportion of total data size affected by changing scenarios. Unless otherwise stated, error distributions are shown for 6 slices, 6 known samples per slice, 500 samples, 3 response levels, and an aggregation of all 4 data distributions tested. A: Results for varying number of slices. B: Results for varying known per slice ratios. C: Results for varying number of total samples. D: Results for varying number of response levels. E: Results for varying underlying data distributions.

Fig. 9.

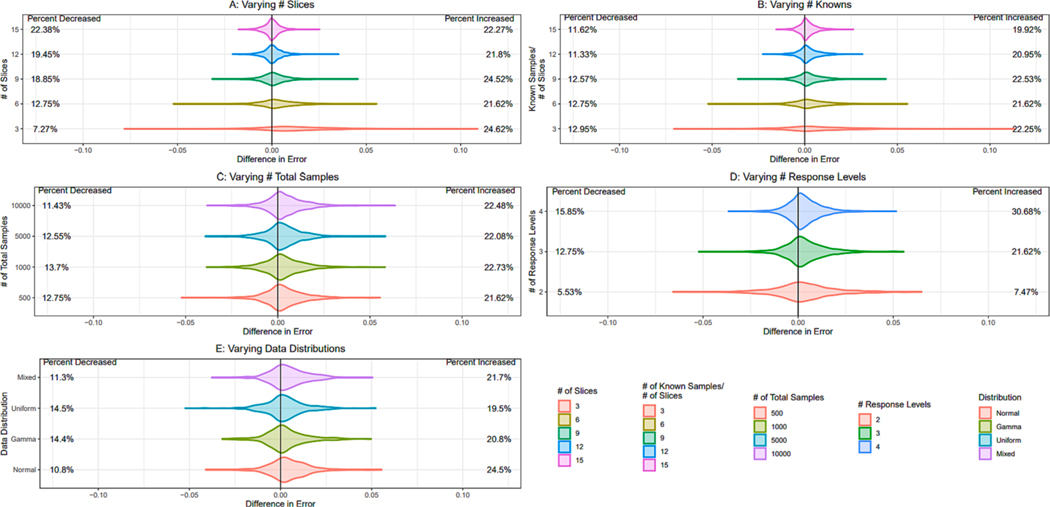
Empirical densities of difference in error for two methods (ordinal MAE - GA MAE) as a proportion of total data size affected by changing scenarios. A positive value denotes an improvement in performance by the GA. Unless otherwise stated, error difference distributions are shown for 6 slices, 6 known samples per slice, 500 samples, 3 response levels, and an aggregation of all 4 data distributions tested. Each density consists of 4,000 trials, except for densities in part E which consists of 1,000 trials per density. Percent increased and decreased respectively represent the percentage of trials showing an increase or decrease in performance by using the GA. The remaining percentage not shown can be accounted for by the number of samples that saw no change in error, all of which were removed from the density plots to allow for the closer visualization of effect when change occurs.

3.2.1. Slice number impact on performance

The percentage MAE empirical distributions for changing number of slices tested across the remaining parameter constants discussed above are shown in Fig. 8A. Total number of slices had little impact on the empirically obtained median MAE when keeping the other tested scenarios constant, with only a small increasing trend in median MAE as the number of slices increased. Although the median was only slightly impacted, the distribution of MAE saw a large change. As the number of slices increased, the variance in the distribution decreased. This effect was lessened as the known/slice ratio increased. Although the median slice impact was not greatly changed as the total number of slices increased, it is important to note that this was for a constant known/slice ratio. Thus, as a user’s number of slices increases, their total number of known samples must increase proportionally to obtain this effect on variability.

The discussed error difference distributions for changing number of slices are displayed in Fig. 9A. As the number of slices increased, the ability of the genetic algorithm to improve ordinal regression weights decreased. 3 slice models for the constant factors stated above had a right shifted distribution in error improvement, with up to an 11 % increase and 8 % decrease in percentage MAE, 25 % of trials showing improved performance, and only 7 % showing worsened performance. This right shift decreased as the model complexity increased, and the variance of error change decreased. Once a 15 slice model was reached, the error change distribution was symmetric about 0 with a small variance, suggesting little impact for the GA to change ordinal regression results.

3.2.2. Known/Slice ratio impact on Performance

The percentage MAE empirical distributions for changing known/slice ratios tested across the above discussed constant remaining parameter combination are shown in Fig. 8B. Known/Slice ratio greatly impacted the empirically obtained MAE. Both the variance of the distribution and the median MAE decreased asymptotically as the ratio increased. The largest drop was from 3x to 6x ratios, with the error changing by approximately 5 % of the dataset size. Once the ratio reached 9, the error distribution was consistently below 5 %, suggesting 9 and above as a good threshold for performing ranking analysis using this method with 6 slice models.

The discussed error difference distributions for changing known/slice ratios are displayed in Fig. 9B. As the ratio of known samples increased, the ability of the genetic algorithm to improve ordinal regression weights stayed consistent, but the variance of the difference distribution decreased. All ratios for the above discussed constant factors had a slightly right shifted distribution, showing a small improvement over ordinal regression results. As the ratio increased, the distribution showed changes of lesser magnitude, depicting a decrease in the capability to change the performance but more consistency. This, along with the MAE distributions, suggests that while the GA results will outperform ordinal regression results consistently, both the GA and ordinal regression produce high performance results for ranking and are viable options when prior knowledge on data is not lacking.

3.2.3. Sample number impact on Performance

The percentage MAE empirical distributions for changing total number of samples tested across a constant remaining parameter combination are shown in Fig. 8C. Total number of samples did not impact the empirically obtained MAE as a percentage. Both the variance of the distribution and the median MAE remained the same as the number of samples increased. It is important to note that the MAE reported is scaled for percentage of total dataset size. Since the percent does not change, this means the MAE linearly increases as total dataset size increases.

The discussed error difference distributions for changing total sample numbers are displayed in Fig. 9C. As the total number of samples increased, the ability of the genetic algorithm to improve ordinal regression weights did not change. Both the shift, variance, and percentage change of the difference distribution stayed consistent across all sample sizes.

3.2.4. Bin number impact on Performance

The percentage MAE empirical distributions for changing number of response levels tested across a constant remaining parameter combination are shown in Fig. 8D. Total number of response levels greatly impacted the empirically obtained MAE. Both the variance of the distribution and the median MAE decreased as the number of samples increased. This decrease in error was large when comparing 2–3 response levels but was much smaller when comparing 3–4 response levels. This suggests that using response levels as a method for predicting weights for direct sample ranking should use a minimum of 3 response levels when classifying results, unless a large ratio of known samples is available compared to the number of slices, which can be explored further in the Supplementary Figures.

The discussed error difference distributions for changing number of response levels are displayed in Fig. 9D. Notably, the magnitude of error changes slightly decreased across increasing number of response levels, but the likelihood of showing improvement increased greatly. Models with the above discussed constant parameters and 2 response levels showed 7.5 % of trials improving and 5.5 % of trials worsening, whereas 4 response level models showed 31 % of trials improving and 16 % worsening. This improvement in performance as number of response levels increased was expected, as the GA utilizes the response levels as a major part of the fitness function. As known samples can be accurately classified into an increasing number of response levels, both ordinal regression and the GA will see a large increase in ranking performance. Although four or more response levels will result in increasing performance for the GA, this requires prior knowledge on the amount of total data expected in each response level after analysis. As the number of response levels increases, this information becomes harder to provide and the GA could become less viable if inaccurate information is provided. For users without this information, or with an increasing number of response levels, ordinal regression is still an accurate method when prior knowledge is not lacking and is provided in the ToxPi weight estimation methodology such that users can avoid providing inaccurate information regarding response level sizes to the algorithm to ensure accurate ranking.

3.2.5. Distribution impact on performance

Distribution was not found to greatly impact performance of ordinal regression results or GA results. Example results are shown in Fig. 8E and 9E, and plots containing all four distributions are provided for each scenario in the Supplementl Figures.

3.2.6. Benchmark study conclusion

The two most important factors found to impact error for ToxPi ranking were the ratio of known samples to slices and the number of response levels used for classifying samples, both of which saw a decrease in error as they increased. Using 2 response levels or a ratio of 3 for known samples to slices saw a large peak in error, with a rapid decrease as those factors increased. Because of this, it is suggested to use this method for ranking with a minimum of 3 response levels and a ratio of 6 known samples per slice, with the preferred ratio being 9 or greater, as its error was consistently under 5 %. As the number of slices in the model increased, the error saw a small increase in its median, but a drastic decrease in its variance. The total number of samples and the underlying distribution of the data did not affect the ranking MAE percentage. The GA was found to outperform ordinal regression for less complex models containing small numbers of slices, but as model complexity increased this improvement diminished. This suggests that the GA can help to improve performance for simpler models where ordinal regression struggles, but that either method is viable as model complexity increases. A complete version of the benchmark study across all scenario combinations is provided in the supplemental methods such that users can compare error based on their model if more specific information is needed.

For usage context, these benchmark studies were designed to reflect the most common ToxPi application scenarios, which tend toward models with relatively low slice counts. As slice number increases, ToxPi visualizations become harder to assess as slice widths become exceedingly narrow. While the models are still valid, the core visualization approaches a “starburst plot”, where slice weights are not apparent. In contrast to slice number, the sample numbers appearing in ToxPi models have broad ranges, from just a few samples to over 70,000 samples. Even in these cases, the amount of known information tends to be minimal, with only a few samples acting as “reference” samples for assessment. Thus, common assessment scenarios involve splitting results into bins akin to those probed in our simulations. For ToxPi models having parameters outside those test here, our results show clear trends that could reasonably be extrapolated as a starting point for weight estimation analysis.

3.3. UVCB data analysis

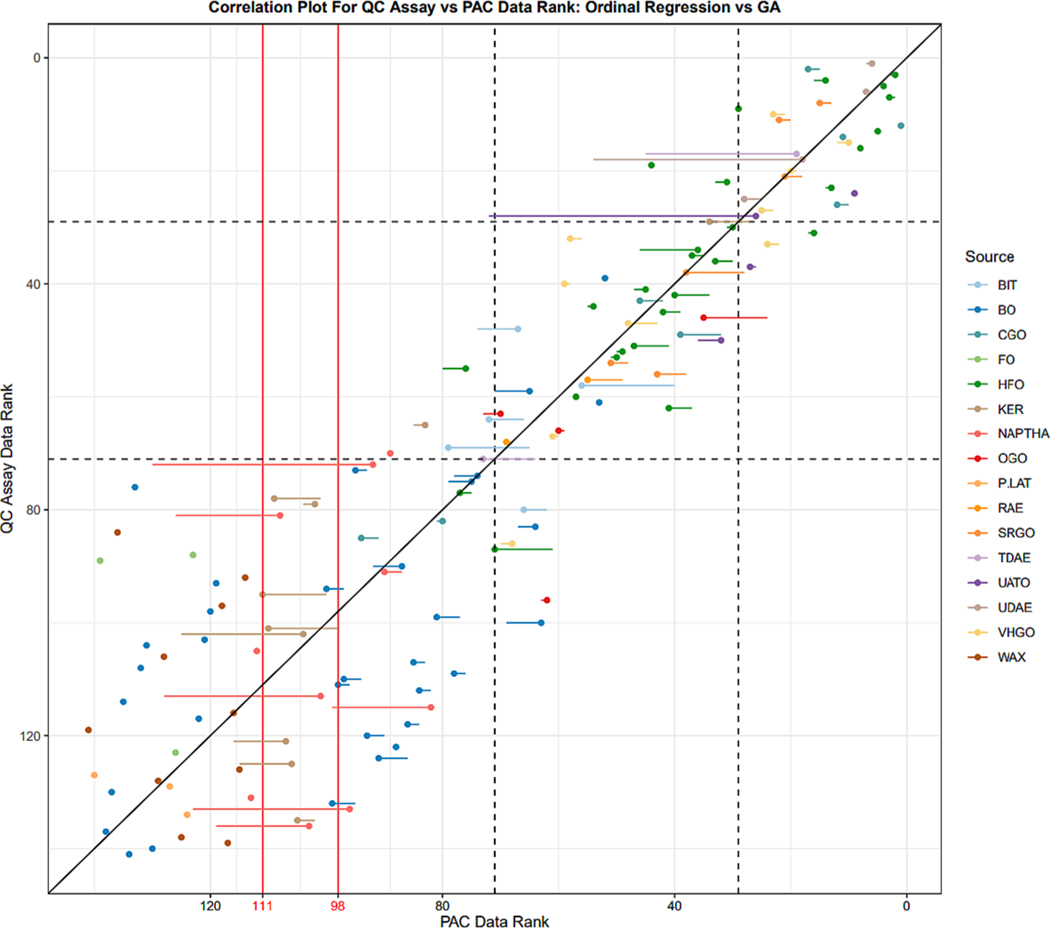
Correlation results of sample ranking for the [20] ToxPi model achieved using QC cell assay data compared to the PAC data ToxPi models with estimated weights are shown in Fig. 10. Points shown represent GA estimated ranking, whereas the start of movement lines attached to points denote ordinal regression estimated ranking, allowing for the visualization of how sample ranking changed between ordinal regression and GA weight estimation. Using ordinal regression, a weight set w = {0, 0.873, 0, 0, 0.127, 0} was estimated for 2–7 aromatic ring structures respectively, and the Pearson correlation between sample ranks was 0.89. Fine tuning this weight set using the genetic algorithm resulted in a new weight set, w = {0.007, 0.754, 0.0003, 0.206, 0.032, 0.0002}, and the Pearson correlation between sample ranks was 0.91, showing that the GA successfully improved the ranking of samples over ordinal regression. Furthermore, this high correlation validates both the use of PAC data for estimating bioactivity and the viability of ordinal regression and the genetic algorithm to accurately predict ranking results for ToxPi models.

Fig. 10.

Results for estimating petroleum substance bioactivity using PAC data. Plot shows correlation between cell assay sample ranking and PAC data sample ranking. Points denote correlation using the GA estimated weights, whereas the start of movement lines attached to points denote correlation using ordinal regression estimated weights. To the left of the red lines denote the number of samples that contained no bioactivity information using the proposed method. Using PAC data, the best-case scenario was 111 samples that provided some differentiable level in bioactivity ranking. Ordinal regression only differentiated 98 samples, whereas the GA was able to differentiate all 111 possible samples. The dashed lines represent the user defined response level thresholds, presented to help show the functioning of the generic algorithm to improve ordinal regression results. The source coloration represents the manufacturing process of the substance. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Although PAC data models had high correlation, using this method resulted in the inability to differentiate low ranking samples. 30 of the 141 samples in the dataset contained no measurable PAC data and thus always received a ToxPi score of 0 no matter the weight set. These samples consisted of petrolatums, waxes, foot oils, and base oils. Additionally, since several ordinal regression slice weights were estimated to be 0 causing the model to be reduced, another 13 samples received scores of 0 and could not be differentiated for bioactivity levels. These extra samples consisted of kerosenes and naphthas. The genetic algorithm fixed this ordinal regression error, keeping all slices present in the model and allowing for ranking differentiation for the 111 samples that contained PAC data.

The samples that received scores of zero using PAC data and thus could not be differentiated for ranking are to the left of the vertical red lines in Fig. 10, with the line labeled 98 referencing the ordinal regression differentiation threshold and the line labeled 111 referencing the GA differentiation threshold. The samples in these regions were ranked randomly for PAC data based on their order of appearance in the data, and thus show no meaningful correlation with cell assay data. Outside of this region, both ordinal regression and GA methods had high correlation with cell assay results. The improvement of the GA over ordinal regression can be largely seen near the user assigned thresholds, denoted by the dashed lines, where the GA pulls samples that are misplaced towards their proper response level. Notably, due to the complexity of the dataset and the small number of total samples, the GA failed to converge all samples into their proper threshold. The GA convergence criterion was increased to 2,000 for this dataset, at which point the fitness function stopped improving, leaving several samples just outside their desired response level threshold. Although the fitness function did not converge to 0, it was still able to greatly improve the results of ordinal regression. The MAE as a percent of the dataset size for ordinal regression was 10.5 % and for the GA 9.4 %. Although this error is larger than the simulation study distribution with 6 slices and 6 known samples per slice shown in Fig. 8, this was to be expected since PAC data is not a direct measurement of cell assay bioactivity and thus may result in excess error on top of the error from using response level machine learning models to predict rank.

With regards to time, the overall runtime using ordinal regression was 0.13 s, whereas the overall runtime using the genetic algorithm was 13.56 s. Although the change in runtime was well above that seen in the simulation studies when using the default convergence criterion of 500 iterations, this was to be expected as the convergence criterion was increased to 2000 iterations for the UVCB dataset. This shows that some datasets, largely those in which the number of known samples is closer to the total number of samples, might benefit in predictive performance from a larger convergence criterion at the cost of running time (see also Fig. 7).

4. Conclusions

Here, we propose methodology to guide optimization of ToxPi model weights. Our approach to the semi-supervised estimation of slice weights uses both ordinal regression and a custom genetic algorithm. We conduct a simulation study to explore the distributions of error for ranking samples using these methods across common user scenarios. We show that this methodology can be highly effective at ranking samples, even when only a small subset of samples can be named as guiding reference samples. We also show that the genetic algorithm has the capability to greatly improve the ranking results of ordinal regression for less complex models with smaller slice numbers. We then use this method to build a high performance ToxPi model that can predict petroleum substance bioactivity using available PAC data, confirming both the viability of the proposed ranking methodology and the use of PAC data to rank bioactivity. Overall, results showed that both ordinal regression and the custom genetic algorithm were accurate methods for predicting ToxPi rankings across a vast array of common use case scenarios, suggesting that ordinal responses can provide enough information to retain the continuous nature of individual ToxPi ranking results. Documentation and code to implement the guided weight optimization described here are available at https://github.com/ToxPi/ToxPi-Weight-Optimization, and these methods will be incorporated into future distributions of ToxPi software.

Abbreviations:

ToxPi

Toxicological prioritization index

GA

Genetic algorithm

PAC

Polycyclic aromatic compound

UVCB

Unknown or variable composition, Complex reaction products and Biological materials

MAE

Mean absolute error

QC

Quality control

Data availability

Data and methods are available at the dedicated ToxPi Github referenced in the paper