Abstract
Accurate estimation of the dispersal velocity or speed of evolving organisms is no mean feat. In fact, existing probabilistic models in phylogeography or spatial population genetics generally do not provide an adequate framework to define velocity in a relevant manner. For instance, the very concept of instantaneous speed simply does not exist under one of the most popular approaches that models the evolution of spatial coordinates as Brownian trajectories running along a phylogeny (Lemey et al., 2010). Here, we introduce a new family of models – the so-called “Phylogenetic Integrated Velocity” (PIV) models – that use Gaussian processes to explicitly model the velocity of evolving lineages instead of focusing on the fluctuation of spatial coordinates over time. We describe the properties of these models and show an increased accuracy of velocity estimates compared to previous approaches. Analyses of West Nile virus data in the U.S.A. indicate that PIV models provide sensible predictions of the dispersal of evolving pathogens at a one-year time horizon. These results demonstrate the feasibility and relevance of predictive phylogeography in monitoring epidemics in time and space.
Keywords: phylogeography, integrated velocity models, West Nile virus, PhyREX, BEAST
Introduction
Evaluating the pace at which organisms move in space during the course of evolution is an important endeavor in biology. When considering deep evolutionary time scales, understanding past dispersal events is key to explaining the spatial diversity of contemporaneous species. Over shorter time frames, making sense of the migration patterns of closely related organisms is crucial in building a detailed picture of a population’s demographic past, present and future dynamics. Tracking the spatial dynamics of pathogens during a pandemic, in particular, is of utmost interest as it conveys useful information about the means and the rapidity at which a disease is spreading in a population. Epidemiological data generally consists in records of incidence of the disease at various points in time and space. Yet, estimating the speed at which an organism spreads at the onset of an epidemic from count data is challenging (van den Bosch et al., 1992; Tisseuil et al., 2016). Similarly, characterizing the migration process from occurrence data in cases where the organism under scrutiny is already well-established in a region is not feasible. These difficulties mainly stem from the fact that count or occurrence data do not convey information about the non-independence between observations due to their shared evolutionary paths.
Genomes carry useful information about the relationships between pathogens. Observed differences between homologous genetic sequences is at the core of phylogenetic and population genetics approaches which provide a sound framework to account for the non-independence between data points in downstream analyses. This framework also accommodates for situations where nucleotide (or protein) sequences are sampled at various points in time (Drummond et al., 2003). Heterochronous samples combined with the molecular clock hypothesis (Zuckerkandl and Pauling, 1965) may then serve as a basis to infer the rate at which substitutions accumulate and to reconstruct the time scale of past demographic trajectories of the population under scrutiny (see e.g., (Ho and Shapiro, 2011) for a review).
Designing models for the joint analysis of genetic sequences and their locations of collection was initiated in the middle of the last century by Wright and Malécot who brought forward the isolation by distance model (Wright, 1943; Malécot, 1948). The rise of statistical phylogeography over the last decade proposed alternatives that are less mechanistic but still aim at capturing the main features of the spatial diffusion process. These approaches are also well suited to deal with heterochronous data and handle cases where the population of interest is scattered along a spatial continuum rather than structured into discrete demes. Lemey et al. (Lemey et al., 2010), in particular, described a hierarchical model whereby spatial coordinates evolve along a phylogenetic tree according to a Brownian diffusion process with branch-specific diffusion rates. The so-called Relaxed Random Walk (RRW) model has since then been used to characterize the spatial dynamics of several pathogens of high public health, societal and agricultural impacts, including Ebola (Dellicour et al., 2018b) and the rice yellow mottle (Issaka et al., 2021) viruses for instance.
One of the key objectives of the RRW model is to infer the rate at which organisms disperse. Pybus et al. (Pybus et al., 2012) suggested using a diffusion coefficient which derives from the ratio of the estimated squared displacement between the start and the end of a branch and the corresponding elapsed time. The branch-level ratios are then averaged over the edges in the phylogeny. Pybus et al. (Pybus et al., 2012) and then Dellicour et al. (Dellicour et al., 2017) later introduced wavefront-through-time plots, deriving from the displacement between the estimated root location and the most distant tip locations at various points in time. Trovao et al. (Trovão et al., 2015) considered instead dispersal rates which are defined as ratios of estimated displacements (using great-circle distances) by the elapsed time.
These statistics generally provide a rough characterization of the dispersal process. The limitations of the dispersal statistics mainly stem from the very nature of the RRW model: because Brownian trajectories are nowhere differentiable, the concept of instantaneous speed is simply not defined under that family of models. Also, the sum of displacements deriving from the observation of a Brownian particle at various points in time grows with the square root of the number of (equally spaced in time) observations, making the estimation of an average speed sampling inconsistent. Finally, the analysis of spatial data simulated under the Brownian motion model along birth-death trees shows that the standard dispersal statistics often fail to provide accurate estimates of speed (Dellicour et al., 2024).
The present study tackles the issue of dispersal velocity and speed estimation by introducing a new approach that models the instantaneous velocity of lineages explicitly. Under these models, the spatial coordinates of lineages derive from integrating their velocities so that we refer to “Phylogenetic Integrated Velocity” (PIV) models throughout this article. To our knowledge, this study is the first to use the integrated velocity models in a phylogenetic context. Integrated processes are common however in a variety of applications, ranging from population biology (Cumberland and Rohde, 1977) to financial economics (Barndorff-Nielsen and Shephard, 2003). In virology, longitudinal studies measuring CD4 T-cell numbers in cohorts of patients with AIDS have used them to test the hypothesis of “derivative tracking”, in which an individual’s measurements over time tend to maintain the same trajectory (Taylor et al., 1994). Closer to phylogeography, integrated processes are instrumental in the field of animal movement ecology (Johnson et al., 2008; Hooten and Johnson, 2017). Unlike simple random walks, these processes are not Markovian as the entire track provides information about the next step through the integration. They are thus relevant for accounting for directional persistence. Furthermore, the integrated processes are related to physical models of particles moving on a potential surface (Preisler et al., 2013; Russell et al., 2018), therefore permitting fine-grained modeling of animal movement telemetry data. One of the goals of the present work is to explore the potential of such approaches in the context of phylogeography, starting with the two simplest and most common models, namely the integrated Brownian and Ornstein-Uhlenbeck processes.
Although velocity is not directly observable from heterochronous and geo-referenced genetic sequences, our results indicate that this quantity can be estimated reliably. Using simulations under realistic spatial population genetics models, we show that the velocity inferred with the new models are more accurate than those deriving from the RRW approach. Velocities estimated from the analysis of multiple West Nile virus data sets were also used to predict the spatial distribution of the pathogen over a one-year time horizon in the U.S.A. Comparison of these predictions to incidence data at the county-level suggests that important features of the spatial dynamics are indeed amenable to reasonably accurate predictions.
Our ability to efficiently monitor and anticipate the spread of emerging epidemics depends on the accuracy with which the pace of dispersal can be quantified. The family of new models introduced in this study provides a relevant tool to achieve this objective. While important aspects of viral evolution may escape prediction indefinitely (Holmes, 2013) and predicting the time and/or location of the next virus outbreak remains out of reach (Wille et al., 2021; Holmes et al., 2018), the present study shows how predictive phylogeography may complement classical approaches in epidemiology.
Results
PIV models: rationale
The main attributes of models that belong to the PIV family are presented first. We focus on the process of interest along a given time interval , corresponding to the length (in calendar time units) of a given branch in the phylogeny of a sample of the organism of interest. Let be the random variable representing the location (i.e., the coordinates) of a lineage at time is its velocity, i.e., the vector that is made of the instantaneous rate at which a lineage changes its position along each dimension of the habitat at time . In all the following, we reserve the term velocity for the vector, and speed for its scalar norm. Both and are typically vectors of length two, corresponding to latitude and longitude. The location at the end of the branch may then be expressed as follows:
| (1) |
where , the location at the time of origin, is fixed. The Brownian Motion (BM) and the RRW models focus on , i.e., the process describing the evolution of the location during a time interval. While, in one dimension, BM models have a single dispersal parameter that applies to all edges in the phylogeny, the RRW model has branch-specific dispersal parameters, in a manner similar to the relaxed clock model (Drummond et al., 2006) used in molecular dating.
Instead of modeling the fluctuation of coordinates, PIV models deal with , i.e., the process describing the variation of velocity in that interval. The dynamics of spatial coordinates then derive from the integration over the velocity as stated in (1) above, hence the name “phylogenetic integrated velocity”. In the following, we introduce two stochastic processes for and characterize the corresponding distributions of . In order to simplify the presentation, we provide formulas for univariate processes only in the main text. Formulas for bi-variate (and, more generally, multivariate) processes are given in SI (sections C and D).
Behavior of PIV models
Velocities
The Integrated Brownian Motion (IBM) model relies on a Wiener process with shift and scale parameters and respectively to model . That process is Gaussian and we have (Gardiner, 2009):
| (2) |
| (3) |
The Integrated Ornstein-Uhlenbeck (IOU) model uses instead a Ornstein-Uhlenbeck (OU) process to describe the evolution of velocity. The mean and variance of velocity at time are given below (Gardiner, 2009):
| (4) |
| (5) |
The parameter in the OU model governs the strength with which is pulled towards the trend .
Spatial coordinates
We now examine the evolution of spatial coordinates under the PIV models. Characterizing the process governing the evolution of spatial coordinates will shed light on the biological relevance of the proposed approach and exhibit the main difference in behavior in comparison with the BM and, by extension, the RRW models. The stochastic processes modeling the fluctuation of velocity being Gaussian, the coordinates also follow a Gaussian process (Cumberland and Rohde, 1977). We give below the mean and variance of the distribution of given and , the coordinates and velocity at time 0.
When velocity follows a Brownian process (IBM process), we have:
| (6) |
| (7) |
A linear increase of the spatial coordinates is thus expected with a direction that is determined by the initial velocity ((6)). Because of the inertia deriving from their velocity, spatial coordinates of lineages evolving under IBM thus tend to resist changes in their direction of motion, i.e., they exhibit directional persistence (Johnson et al., 2008). This mean drift is similar to the directional random walk, used e.g. in (Gill et al., 2016) to model the spatial spread of HIV-1. The BM model has a distinct behavior as it authorizes sudden changes of direction. The RRW can even lead to large discontinuous “jumps” from one place to another (Bastide and Didier, 2023). In contrast, the IBM is smoother (differentiable) by design, and well suited to model auto-correlated movements. Moreover, as suggested by (7) above, the variance of coordinates grows cubically in time, thereby allowing the IBM model to accommodate for dispersal events over long distances in short periods of time. This process is thus able to handle fast spatial range expansion, yet with continuous and differentiable trajectories.
The corresponding expectation and variance for the IOU model are given in SI (section A). Here again, the average coordinates at the end of the branch of focus are determined by the coordinates at the start of that branch plus the expected displacement along that same edge. In this simple IOU model, the velocity of the process converges to the central value , leading to trajectories with a clear directional trend that are well suited for dispersal along an established spatial gradient. While for small values of the IOU has a behavior that is similar to the IBM, for larger values of that parameter, its variance grows linearly in time and the process behaves like a directional BM (Gill et al., 2016). The auto-correlation (or strength) parameter is thus interpreted as the amount of directional persistence present in the data (Johnson et al., 2008), with small values indicating more dependence to the trajectory path for future moves.
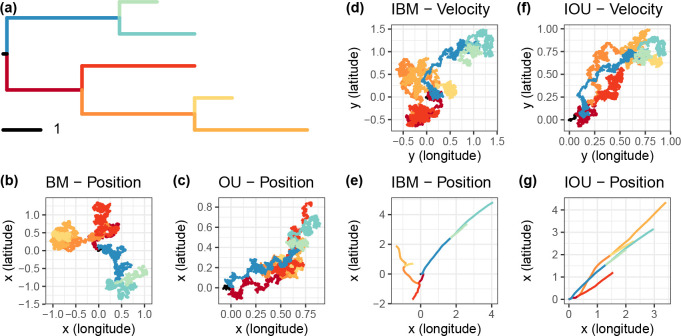
Figure 1 illustrates the behavior of the classical random walk and integrated models along a 5-tip tree. Trajectories of coordinates generated with the BM and Ornstein-Uhlenbeck (OU) versions of the random walk model are intricate, showing abrupt changes of directions in the movements (Fig. 1b, c). The same behavior is displayed by the velocity trajectories under the IBM and IOU models (Fig. 1d, f) as the models are here identical to that used for the BM and OU models indeed. Yet, integrating over these rugged paths gives smooth (differentiable) trajectories of coordinates under the corresponding models (Fig. 1e, g), with particles moving swiftly away from their initial points, illustrating the cubic variance pointed above. The IOU model presented here converges to a (1,1) velocity so that the coordinates of the five lineages show a clear directionality, stronger than that obtained with the OU model (Fig. 1g vs. c).
Figure 1: Simulated trajectories of classical random walk and PIV models on a simple tree.
Each process was simulated on the tree (a), with branches of matching colors. Movements along the latitude and longitude axes were simulated independently. (b) Random walk using Brownian motion (BM) with variance , and starting point . (c) Ornstein-Uhlenbeck process (OU) with stationary variance of , strength , starting at , and converging to its central value . (d) and (e) Velocity and position of an Integrated Brownian Motion (IBM) with variance , starting point , and starting velocity . (f) and (g) Velocity and position of an Integrated Ornstein-Uhlenbeck (IOU) with stationary variance , strength , central trend of , starting point , and starting velocity .
Accuracy of speed estimation
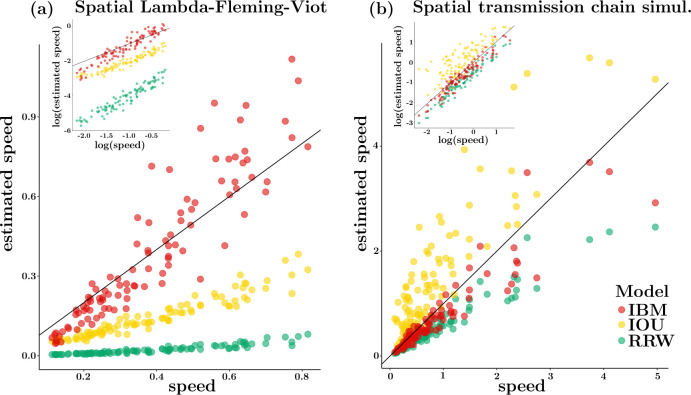
Data sets were simulated under the spatial Lambda-Fleming-Viot (SLFV) model (Etheridge, 2008; Barton et al., 2010) and an agent-based spatially explicit transmission chain simulator which aimed at mimicking outbreaks of the Ebola virus in West Africa (Lequime et al., 2020). 100 data sets were analyzed for each of these two simulation settings. As traditional speed statistics are typically computed over the whole tree (Dellicour et al., 2020a), we assessed the ability of PIV models to estimate tree-level speed by averaging node-level velocities across the tree. The classical “weighted lineage dispersal velocity” (WLDV) (Dellicour et al., 2016) was used instead for all analyses performed under the RRW model. As shown recently (Dellicour et al., 2024), we expect the WLDV statistic on RRW models to perform poorly, and would like to asses the ability of PIV models to provide more accurate speed estimates.
Examination of the estimated vs. true speed relationship (Fig. 2) indicates that the RRW model systematically underestimates speed and the bias worsens with increasing speed. This bias is strong with data simulated under the SLFV (Fig. 2a) and milder with the Ebola data sets (Fig. 2b), which is expected since the transmission trees generated in the latter case are sampled in time and not ultrametric, making the temporal signal to estimate speed stronger. Nonetheless, true speed values are, on average, 1.6 times larger than those estimated with the RRW for the Ebola data and 22 times larger for the SLFV data (the ratios for IBM are 1.2 for both simulation settings). The SLFV model assumes a finite-size habitat (a square here) and boundary effects, which occur for large and small dispersal values, are expected to impact the estimation of speed under models that ignore this constraint. Yet, the IBM model is largely immune to this issue. While the IOU model underestimates speed for the SLFV data sets, its estimates are less biased than those deriving from the RRW model. The IOU model also tends to overestimate speed on the Ebola data sets. Further examination of these results shows a clear influence of the prior distribution on the strength parameter in the IOU model, a phenomenon already observed in (Cornuault, 2022).
Figure 2: Accuracy of speed estimation under the RRW and PIV models.
True (x-axis) vs. estimated (y-axis) speed. Estimates were obtained under the IBM, IOU and RRW models. (a) 100 data sets were simulated using the spatial Lambda-Fleming-Viot process on a 10 by 10 square. (b) 100 data sets were simulated under a random walk model inspired by the Ebola epidemic in West Africa (see main text). The insets give the log-log scatterplots of the estimated vs. true speeds. The line is shown in black on each plot.
Dispersal dynamics of the West Nile virus in the U.S.A
The phylogeography of the WNV in the U.S.A. has been studied extensively (see, e.g., (Dellicour et al., 2020a)). The origin of this epidemic took place in New York City during the summer 1999 (Lanciotti et al., 1999; Campbell et al., 2002). By 2004, human infections, veterinary disease cases or infections in mosquitoes, birds, or sentinel animals had been reported to the Centers for Disease Control and Prevention (CDC) in most counties.
We fitted the PIV and RRW models to several subsets of the 801 geo-referenced sequence data set analyzed in (Dellicour et al., 2020a). PIV models are less flexible than the RRW approach as they do not authorize sudden changes of direction, as noted earlier (and see SI, section B). Therefore, ensuring that both approaches nonetheless provide comparable fit to the data is a prerequisite to further analyses. We then used the IBM model to predict the dispersal patterns and evaluate these predictions through the comparison with incidence data for the 2000–2007 time period.
Model comparison
We compared the fit of the RRW and PIV models to the WNV data using cross-validation of location information. Cross-validation is a powerful model comparison technique in the context of phylogenetic factor analysis (Hassler et al., 2022). Using a subset of 150 data points chosen uniformly at random among the 801 available observations, a leave-one-out procedure was applied to the sample coordinates. Each tip location was first hidden and its posterior density was estimated using MCMC from the remaining 149 locations and all 150 sequences (see SI, section G).
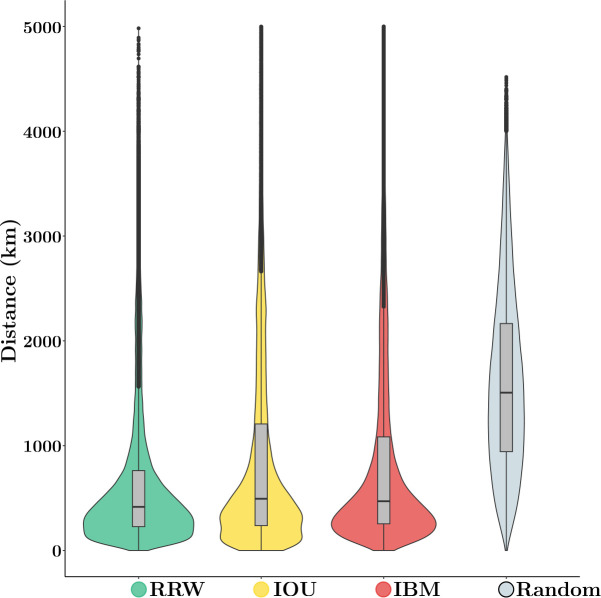
Figure 3 shows the distributions of the great circle distances between the observed and reconstructed tip locations as inferred under the PIV and the RRW models, along with that of uniform at random predictions. The three phylogeographic models have similar behavior overall with a majority of distances between true and reconstructed tip locations ranging between 238 km (25% quantile of distribution from MCMC output pooled across models) and 950 km (75% quantile) with a median of 450 km. In contrast, if inferred locations are uniform at random within the U.S.A. (excluding Alaska and Hawaii), the median distance is 1,564 km, i.e., more than three times that estimated with the phylogenetic models. This result demonstrates the ability of these models to extract meaningful signal from the data, even though these approaches do not account for habitat borders (while the uniform predictor does so). Examination of the posterior distribution deriving from each model taken separately indicates that the median distances obtained under the IBM, IOU and RRW models are 474, 496 and 416 km respectively. While the fit of the RRW model is superior to that of the PIV models, the performance of the three models are nonetheless qualitatively similar.
Figure 3: Distribution of the distance between true and estimated tip coordinates under the PIV, the RRW models and uniform at random predictions, WNV data.
Cross validation was used to predict the locations of held-one-out tip lineages under the RRW and PIV models. ‘Random’ gives the distance between two locations selected uniformly at random within the U.S.A. The y axis gives the great circle distance between coordinates (in km).
Predicting dispersal using PIV models
PIV models enable the estimation of dispersal velocity of each sampled lineage. These velocities may then serve as a basis to predict the spatial distribution of the underlying population in the near future. Here, we tested the ability of the IBM model to anticipate the dynamics of dispersal of the WNV in the early and later stages of the epidemic.
Sequences collected earlier than December of year were randomly subsampled from the complete data set with exponentially increasing weights given to recent samples. Data sets with 150 sequences were obtained except for years 2000–2002 where smaller sample sizes were considered due to a lack of observations in this time period. Estimated posterior distributions of velocities at the tips of the obtained phylogeny under the IBM model were then used as predictors of the spatial distribution of the virus in year (see section “Predictive phylogeography” in “Material and Methods”). The predicted occurrences were compared to yearly incidence data collected at the county level.
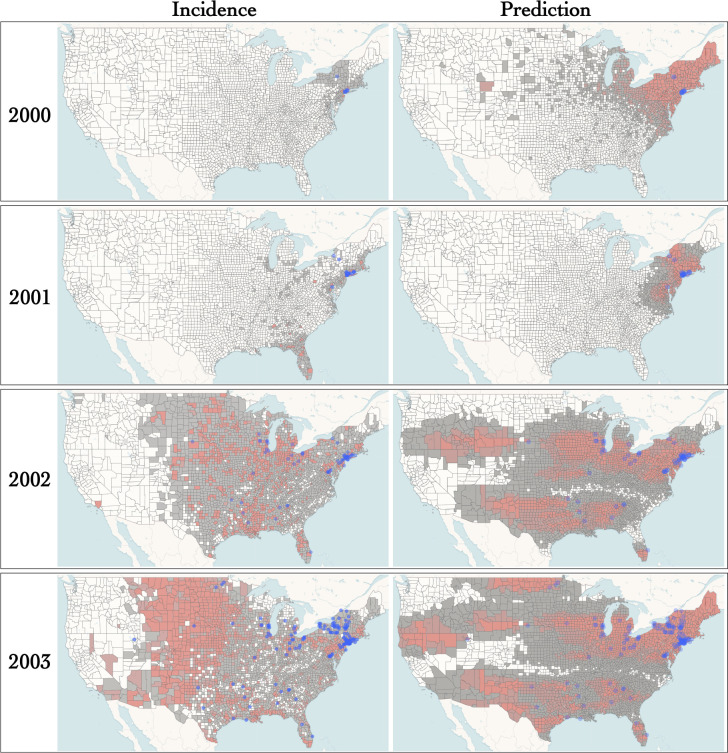
Figure 4 shows the incidence and the predicted occurrence of the WNV in the early stages in the epidemic. Samples for years 2000, 2001 and 2002 included only 7, 19 and 68 geo-referenced sequences, thereby making any prediction inherently challenging. For instance, predictions for year 2000 are overly dispersed and sensitive to priors (see SI, section H). Also, while the virus had reached Florida by 2001, our model failed to predict its presence south of North Carolina. Predictions for subsequent years rely on larger numbers of observations and demonstrate the relevance of our approach. Indeed, the PIV model successfully predicted the arrival of the pathogen along the west coast of the U.S.A. by the end of 2002. It also correctly predicted that the north west corner of the country would remain largely virus-free until the end of 2003. Predictions deriving from the RRW show qualitatively distinct patterns with a widespread presence of the virus for years 2003 and 2004 that contrasts with incidence data (see SI, section H). Overall, the RRW shows a higher sensitivity (average of 0.89 over all years for the RRW, vs. 0.72 for the IBM), but a lower specificity (average of 0.36 for the RRW, vs. 0.56 for the IBM), consistent with wider and rather vague predicted regions.
Figure 4: Incidence and predicted occurrence of WNV in the early phase of the epidemic (model for prediction: IBM).
Purple dots correspond to sampled locations. Incidence data (left) for each year and each county was obtained from the CDC. For year , predicted occurrence of the WNV (right) was inferred using data collected earlier than the end of December of year . The maps were generated with EvoLaps2 (Chevenet et al., 2024)
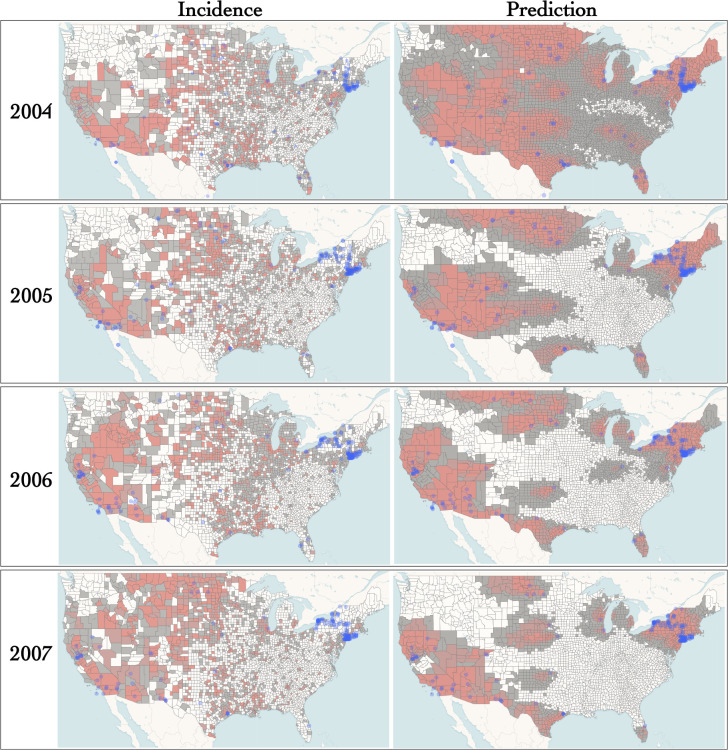
By 2004 the virus reached an endemic state and the spatial dynamics of the epidemic diverged from that of the early stages. Figure 5 shows the results for the 2004–2007 time period. Prediction at local spatial scales has limited accuracy. For instance, a high probability of occurrence was systematically estimated for the states in the North East corner of the country and the south of Texas while incidence was generally mild in these areas. Note that the difference between predicted and observed occurrence could reflect a relatively lower ecological suitability of these regions to host local WNV circulation, thereby serving a useful purpose. Moreover, the IBM model correctly predicts the expansion of the epidemic north of California and Nevada between 2005 and 2006. Also, according to our predictions, the pathogen covered limited distances in the 2004–2007 period compared to the early stages of the epidemic. This quasi stasis is confirmed by the largely similar distributions of yearly incidences. Hence, here again, our approach manages to capture changes in the spatial dynamics of the pandemic that are central in the context of pathogen surveillance.
Figure 5: Incidence and predicted occurrence of WNV in an endemic regime (model for prediction: IBM).
See caption of Fig. 4.
Discussion
The present study addresses shortcomings in the estimation of the velocity of lineages using popular models in phylogeography. These approaches rest on the probabilistic modeling of the coordinates of lineages along their phylogeny. Yet, the central concept of instantaneous speed does not exist under the most popular Relaxed Random Walk (RRW) model. As a consequence, measuring speed as a ratio between a displacement and the corresponding elapsed time leads to difficulties. In order to circumvent these limitations, we introduce Phylogenetic Integrated Velocity (PIV) models. The originality of this family of models lies in their modeling of the velocity of evolving lineages instead of their coordinates. This approach enables a proper definition of instantaneous speed, which can be inferred anywhere along the tree, including at its tips.
Data sets were simulated under two models of spatial evolution that are distinct from that underlying the PIV and RRW approaches. Results show that speed estimates obtained with PIV models are generally more accurate than those deriving from the RRW approach, especially in cases where the pace of dispersal is high. Also, unlike RRW, PIV models produce velocity vector estimates at each node of the tree. We assessed the accuracy of these estimates at tip nodes in the IBM case, and found that the velocity vectors were well estimated, with highest posterior density intervals having good coverage (see SI, section I). Yet, PIV models are less flexible than RRW in their description of the movement of lineages during the course of evolution. In particular, sudden changes in the direction of dispersal are not well accounted for by PIV models. These changes would indeed require “breaks” in the trajectory of velocities, which the underlying Gaussian processes do not allow. However, our analysis of West Nile virus data in the U.S.A. indicates that the movements of lineages display here enough inertia so that rapid changes in the spatial trajectories are seldom observed. Cross-validation suggests in fact that the two PIV models tested here provide a fit to the data similar to that obtained with the RRW. Moreover, the analytical expressions of the variance of coordinates under the IBM model grows with time in a superlinear manner, thereby allowing large displacements in short amounts of time.
Estimates of tip velocities can serve as a basis to model future dispersal events. Here, we evaluate the accuracy of predicted movements through the analysis of subsets of a large data set of West Nile virus geo-referenced sequences and county-level yearly incidence data in the U.S.A. Our predictions focus on deciding whether the pathogen will occupy (or be absent from) a given county at a given time interval in the future, i.e., a modest, yet challenging and critical endeavor compared to predicting future incidence. The proposed approach accurately predicted the arrival of the virus along the west coast of the USA in 2002 from the analysis of data collected before the end of December 2001. Furthermore, the predictions clearly point to a change of dispersal dynamics around 2004–2005 with a transition from an expansion phase to an endemic regime whereby rapid east-to-west dispersal events are replaced with short-distance migrations. While the proposed predictions have limited accuracy in the early stages of the pandemic where data is scarce and sampling likely to be biased, the PIV models successfully anticipate dispersal events in many instances. Altogether, our results indicate that the predictive phylogeography approach put forward in the present study could indeed serve a useful purpose in real time forecasting of the spread of an epidemic. Future work could aim at incorporating data on the ecological suitability of the investigated areas in order to improve predictions, in a manner similar to that used in “landscape phylogeography” (Dellicour et al., 2018a).
In addition to prediction, the PIV models are also expected to prove useful in many cases where the RRW model has been applied to quantify and compare dispersal velocity. These applications range from animal and human viruses to plant viruses. For instance, lower rates of dengue virus dispersal in urban as opposed to rural settings has implicated a major role for mosquito-mediated dispersal (Raghwani et al., 2011). Also, dispersal velocity has often been estimated for rabies lineages with dogs as the main host species, resulting in hypotheses of their spread being impacted by human activities (Talbi et al., 2010). More recently, a slow dispersal has been estimated for Lassa virus in its rodent reservoir, which could in part explain the restricted distributions of the virus (Klitting et al., 2022). Finally, increasing dispersal rates of the rice yellow mottle virus in Africa has led to the suggestion that intensification of rice cultivation could have enhanced the spread of that virus (Rakotomalala et al., 2019). Applications of the PIV models could increase the credibility of these and many more hypotheses of viral spread.
The proposed new models and predictions have limitations however. In a manner similar to that of the classical RRW framework, PIV models assume that (i) the geographical position does not impact the fitness or the molecular evolution of the pathogen, (ii) all the lineages are independent from one another, excluding any competition effect and (iii) the geographical spread of the pathogen is independent from its current position. While limiting, these assumptions permit efficient computations and provided a sound methodological framework for important phylodynamics studies (see e.g. (Baele et al., 2018) for a review). In some specific contexts such as discrete phylogeography, some of these assumptions were relaxed, see e.g. (FitzJohn, 2010; Müller et al., 2017) and references therein for (i), (Drury et al., 2016; Manceau et al., 2017; Bartoszek et al., 2017) for (ii), and (Lemey et al., 2014) for (iii). Similar extensions to the PIV framework proposed here should be considered. In particular, models of animal movement also rely on integrated processes, with an additional potential function that links the dynamics of velocity evolution of an individual to its position at each point in time (Preisler et al., 2013; Russell et al., 2018). Such a potential function could be extended to include prior knowledge on the environmental layers impacting the spread of pathogens, including natural barriers such as coastline, or could be used to test the impact of specific environmental variables on the dispersion (Dellicour et al., 2020b). However, the pruning algorithm used here (see “Material and Methods”) would not apply to these kinds of models, which are thus likely to be highly computationally intensive.
Furthermore, sampling is likely to impact the results in case it is driven by practical aspects (e.g., the distribution of genomic surveillance facilities is not uniform throughout the habitat) and does not reflect the underlying spatial distribution of the population under scrutiny (Kalkauskas et al., 2021). Recent work (Guindon and De Maio, 2021) shows how different sampling strategies can be incorporated in the RRW model. A similar framework could apply to PIV models and mitigate the impact of sampling. Additionally, when available, incidence data conveys information about the demographic dynamics of an epidemic. Hence, increased accuracy of the predictions may be achievable through the incorporation of past incidence data in the new models presented in this work.
Material and Methods
Likelihood calculation and Bayesian inference
Let and correspond to random variables denoting the vectors of positions at the tips and the internal nodes respectively. and are realizations of the corresponding random variables, where is the number of tips and is the index of the rootnode. and are the vectors of velocities at tip and ancestral nodes respectively. Here, we describe two different approaches for the Bayesian inference of PIV model parameters.
Data augmentation: sampling velocities
The first method, implemented in PhyREX (Guindon and De Maio, 2021), relies on data augmentation. It starts with the computation of , i.e., the joint density of all (i.e., ancestral and tip) locations and velocities. This density is also conditioned on the phylogeny, i.e., a rooted tree topology with node heights, which is not included in the formula below for the sake of conciseness. Given the locations and velocities at all nodes in the tree, the evolutionary process taking place along every branch is independent from that happening along the other edges. The likelihood is then evaluated as follows:
| (8) |
where the subscript corresponds to the direct parent of node . Also, is the velocity and location density at the root node. In the present work, we use a normal density for the corresponding distribution. Since is normally distributed, we can use the pruning algorithm as described in (Pybus et al., 2012) to integrate over , giving the following likelihood:
| (9) |
where is obtained through a post-order tree traversal, assuming the movements along both spatial axes are independent from one another and using the means and variances for either the IBM or the IOU model (see SI, section B). The calculation just described relies on augmented data since velocities at all nodes in the tree are considered as known. Uncertainty around these latent variables is non-negligible. Samples from the joint posterior distribution of all model parameters, including ancestral and contemporaneous velocities, were obtained through Markov Chain Monte Carlo integration.
Direct likelihood computation with the pruning algorithm
The second method for evaluating the likelihood of PIV models is implemented in BEAST (Suchard et al., 2018). It relies on the direct computation of , the likelihood of the observed positions at the tips conditionally on the tree. It uses the fact that the stochastic process that describes the joint evolution of both the velocity and position is a multivariate Markov process, that can be framed as linear Gaussian as in (Mitov et al., 2020; Bastide et al., 2021). Indeed, as shown in SI (section C), for any node with parent , the joint velocity-position vector can be written conditionally on the vector at the parent node , as: , with a Gaussian random variable with variance that is independent from , and and , two matrices and a vector of dimension 4 that only depend on the tree and the parameters of the PIV process considered. In this approach, all the velocities at the tips are considered as missing: we only observe the last two entries of vector corresponding to the position, but the velocities are unknown. In (Bastide et al., 2021), a general pruning algorithm is described to deal with this kind of process (with missing values), that provides not only the likelihood (one post-order traversal) but also the conditional distribution of non-observed traits conditioned on observed traits at the tips (one additional pre-order traversal). This algorithm hence readily gives the posterior distribution of velocities without the need to sample from them using MCMC. Moreover, it does not need to assume that movements along the spatial axes are independent from one another.
Phylogeographic Bayesian inference
In both approaches, standard operators were used to update the topology of the phylogenetic tree, the node ages along with the parameters of a HKY (Hasegawa et al., 1985a) nucleotide substitution model. The diffusion parameters of the Brownian process were also updated using standard Metropolis-Hastings steps. Most results in this study were derived with PhyREX even though BEAST outperformed PhyREX in terms of speed of parameter inference (see SI, section E). The two independent implementations of Bayesian samplers under the same models provide a robust validation of most results presented in this study.
Simulations
Spatial Lambda-Fleming-Viot model
Genealogies and the accompanying spatial coordinates were first generated according to the “individual-based” spatial Lambda-Fleming-Viot (SLFV) model (Etheridge, 2008; Barton et al., 2010). In this model, individuals give birth to descendants which locations are normally distributed. Death events are also governed by the same kernel so that the spatial density of the population is constant, on average, during the course of evolution. The normal kernel is truncated, allowing the SLFV model to accommodate habitats of finite size, as opposed to most continuous phylogeographic models. We selected the SLFV model as it describes the evolution of a population of related individuals along a spatial continuum as opposed to discrete demes. It is not subject to the shortcomings that hinder other popular spatial population genetics models such as sampling inconsistency (Barton et al., 2013) or Felsenstein’s infamous “pain in the torus” (Felsenstein, 1975). Finally and most importantly, because lineages’ coordinates evolve here according to a jump process, the exact spatial coordinates of each lineage at each point in time can be monitored. This information may then serve as a basis to evaluate the total distance covered by all lineages in the genealogy. The ratio of this distance by the corresponding elapsed time gives an (average) speed that genuinely reflects the dispersal ability of the organisms under scrutiny.
50 individuals were sampled on a 10 by 10 square defining the habitat of the corresponding population. The rate of events where lineages die and/or give birth to descendants (the so-called REX events in (Guindon et al., 2016)) was set to 103 events per unit of time per unit area and the variance of the normal density that defines the radius parameter in the SLFV model was chosen uniformly at random in [0.1, 0.3]. These parameter values are such that lineage jumps are short and frequent, thereby mimicking the behavior of a Brownian process (Wirtz and Guindon, 2023).
Ebola-like simulations
Here, we used the agent-based spatially explicit simulator implemented in the R package nosoi (Lequime et al., 2020). Parameters were chosen so as to mimic the Ebola epidemic in West Africa over a time period of 365 days, starting from a single infected host in Guéckédou (Guinea). <mono_space> nosoi </mono_space> is a discrete time, continuous space simulator that explicitly models within-host dynamics and between-host transmissions. It can exploit a geographic raster to simulate a full transmission tree where the geographic position of each infected host is tracked at all time. We simulated datasets using the same parameters as in (Lequime et al., 2020) which are informed by the literature describing human infections by Ebola. Spatial demographic data from WorldPop (www.worldpop.org) was also taken into account for these simulations.
Each host had a probability of 20% to move every day. These migrations were governed by a bivariate Gaussian distribution centered at the location of the lineage under scrutiny, with diagonal covariance matrix and equal standard deviations for longitude and latitude. The standard deviation was set constant for each simulation, and drawn from a log-normal distribution with mean and standard deviation equal to approximately 15 km in each direction. We used a raster of the entire West Africa, ensuring that no epidemic reached the border of the map within the time frame of the simulation.
As previously, we sampled 50 infected individuals randomly from the transmission tree, and extracted the sampled genealogy as well as the realized speed, that exploits the simulated position at each time of the chain. Note that the genealogies produced by these simulations are sampled through time and not ultrametric, making the estimation of speed easier.
Sequence simulation
In both simulation settings, edges in the obtained genealogy were rescaled so that the average length of an edge after scaling was 0.05 nucleotide substitutions per site. Nucleotide sequences were then generated under a strict clock model according to the HKY model of evolution (Hasegawa et al., 1985a) with transition/transversion ratio set to 4.0. 100 genealogies along with the corresponding spatial coordinates and homologous nucleotide sequences were generated this way for the SLFV and Ebola simulations.
Statistical inference
Each simulated data set was processed using the RRW, IBM and IOU models with independent coordinates. When considering their spatial components only, these models have have 3, 2 and 6 parameters respectively. The RRW model used a log-normal distribution of branch-specific dispersal rates, which is the standard parametrization for that model. The nucleotide substitution rate was set to its simulated value by taking the ratio of the tree length as expressed in molecular and calendar units. The tree-generating process was assumed to be Kingman’s coalescent (Kingman, 1982) with constant effective population size and a flat (improper) prior distribution on that parameter. Although sequences evolved according to a strict clock model, we used an uncorrelated relaxed clock model (Drummond et al., 2006) with a log-normal distribution of edge-specific substitution rate multipliers. An exponential prior with rate set to 100 was used for the variance of this log-normal density.
For each data set, the true average speed was taken as the actual euclidean (SLFV) and great-circle (Ebola) distance covered by every lineage divided by the tree length in calendar time unit. For RRW, distances between the (observed or estimated) coordinates at each end of every branch in the tree were used to derive the dispersal rate through the “weighted lineage dispersal velocity” statistic (Dellicour et al., 2016). The posterior median of that statistic was used as our speed estimate. For PIV models, speed at the tree-level was obtained by averaging the speed estimated at each node, the latter deriving from the corresponding velocities. Here again, we obtained the posterior distribution of the tree-level speed and use the median as our estimate. Note that none of the processes used for inference is the “true” process used for simulation, but simplified versions of it.
Predictive phylogeography
The PIV models provide an adequate framework to estimate velocities at the tips of the inferred phylogenies. It thus makes sense to apply them to predicting dispersal patterns. Here, we designed a prediction technique which goal is to assess whether the organism under scrutiny may be found in a given region at a given point in time after the most recent sample was collected. Our approach utilizes the posterior distribution of the velocities estimates at each tip of the phylogeny to build a predictor. The latter is obtained by linear extrapolation of the estimated velocity at each tip in the tree that assumes a constant speed of lineages after their sampling. Survival of these linear trajectories is taken into account so that older samples are less likely than recent ones to survive to a given time point in the future. This approach therefore puts more weight on recent samples to predict dispersal patterns (see SI, section F). Incidence data used for comparison was extracted from https://www.cdc.gov/west-nile-virus/data-maps/historic-data.html.
Supplementary Material
Acknowledgements
SG thanks the Institut Français de Bioinformatique for computational resources. The research leading to these results has received funding from the European Research Council under the European Union’s Horizon 2020 research and innovation programme (grant agreement no. 725422 - ReservoirDOCS) and the US National Institutes of Health (R01 AI153044, F31 AI154824). PR’s internship at the University of Montpellier was founded by the I-SITE MUSE through the Key Initiative “Data and Life Sciences”. PB thanks Pierre Gloaguen for useful discussions on the integrated models. SD acknowledges support from the Fonds National de la Recherche Scientifique (F.R.S.-FNRS, Belgium; grant n°F.4515.22) and the Research Foundation — Flanders (Fonds voor Wetenschappelijk Onderzoek — Vlaanderen, FWO, Belgium; grant n°G098321N). PL acknowledges support by the Research Foundation – Flanders (Fonds voor Wetenschappelijk Onderzoek – Vlaanderen, G051322N and G005323N).
Data and code availability
The data and code to reproduce all analyses and figures displayed in this study are available at https://github.com/pbastide/integrated_phylogenetic_models. The PhyREX and BEAST programs are open source and freely available from https://github.com/stephaneguindon/phyml and https://github.com/beast-dev/beast-mcmc respectively.
References
- Ayres D., Darling A., Zwickl D., Beerli P., Holder M., Lewis P., Huelsenbeck J., Ronquist F., Swofford D., Cummings M., et al. 2012. BEAGLE: an application programming interface and high-performance computing library for statistical phylogenetics. Systematic Biology, 61: 170–173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baele G., Dellicour S., Suchard M., Lemey P., and Vrancken B. 2018. Recent advances in computational phylodynamics. Current Opinion in Virology, 31: 24–32. [DOI] [PubMed] [Google Scholar]
- Barndorff-Nielsen O. and Shephard N. 2003. Integrated OU processes and non-Gaussian OU-based stochastic volatility models. Scandinavian Journal of Statistics, 30: 277–295. [Google Scholar]
- Barton N., Etheridge A., and Véber A. 2010. A new model for evolution in a spatial continuum. Electronic Journal of Probability, 15: 162–216. [Google Scholar]
- Barton N., Etheridge A., and Véber A. 2013. Modelling evolution in a spatial continuum. Journal of Statistical Mechanics: Theory and Experiment, 2013: P01002. [Google Scholar]
- Bartoszek K., Glémin S., Kaj I., and Lascoux M. 2017. Using the Ornstein–Uhlenbeck process to model the evolution of interacting populations. Journal of Theoretical Biology, 429: 35–45. [DOI] [PubMed] [Google Scholar]
- Bastide P. and Didier G. 2023. The Cauchy process on phylogenies: A tractable model for pulsed evolution. Systematic Biology, 72: 1296–1315. [DOI] [PubMed] [Google Scholar]
- Bastide P., Ho L. S. T., Baele G., Lemey P., and Suchard M. 2021. Efficient Bayesian inference of general Gaussian models on large phylogenetic trees. The Annals of Applied Statistics, 15: 971–997. [Google Scholar]
- Bilderbeek R. and Etienne R. 2018. babette: Beauti 2, beast2 and tracer for r. Methods in Ecology and Evolution, 9(9): 2034–2040. [Google Scholar]
- Campbell G., Marfin A., Lanciotti R., and Gubler D. 2002. West Nile virus. The Lancet Infectious Diseases, 2: 519–529. [DOI] [PubMed] [Google Scholar]
- Chevenet F., Fargette D., Bastide P., Vitré T., and Guindon S. 2024. EvoLaps 2: Advanced phylogeographic visualization. Virus Evolution, 10: vead078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clavel J., Escarguel G., and Merceron G. 2015. mvmorph : an R package for fitting multivariate evolutionary models to morphometric data. Methods in Ecology and Evolution, 6: 1311–1319. [Google Scholar]
- Cornuault J. 2022. Bayesian analyses of comparative data with the Ornstein–Uhlenbeck model: potential pitfalls. Systematic Biology, 71: 1524–1540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cumberland W. and Rohde C. 1977. A multivariate model for growth of populations. Theoretical Population Biology, 11: 127–139. [DOI] [PubMed] [Google Scholar]
- Dellicour S., Rose R., Faria N. R., Lemey P., and Pybus O. G. 2016. SERAPHIM: studying environmental rasters and phylogenetically informed movements. Bioinformatics, 32(20): 3204–3206. [DOI] [PubMed] [Google Scholar]
- Dellicour S., Rose R., Faria N., Vieira L., Bourhy H., Gilbert M., Lemey P., and Pybus O. 2017. Using viral gene sequences to compare and explain the heterogeneous spatial dynamics of virus epidemics. Molecular Biology and Evolution, 34: 2563–2571. [DOI] [PubMed] [Google Scholar]
- Dellicour S., Vrancken B., Trovão N., Fargette D., and Lemey P. 2018a. On the importance of negative controls in viral landscape phylogeography. Virus Evolution, 4: vey023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dellicour S., Baele G., Dudas G., Faria N., Pybus O., Suchard M., Rambaut A., and Lemey P. 2018b. Phylodynamic assessment of intervention strategies for the West African Ebola virus outbreak. Nature Communications, 9: 1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dellicour S., Lequime S., Vrancken B., Gill M., Bastide P., Gangavarapu K., Matteson N., Tan Y., Du Plessis L., Fisher A., et al. 2020a. Epidemiological hypothesis testing using a phylogeographic and phylodynamic framework. Nature Communications, 11: 5620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dellicour S., Lemey P., Artois J., Lam T., Fusaro A., Monne I., Cattoli G., Kuznetsov D., Xenarios I., Dauphin G., et al. 2020b. Incorporating heterogeneous sampling probabilities in continuous phylogeographic inference—application to H5N1 spread in the Mekong region. Bioinformatics, 36(7): 2098–2104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dellicour S., Bastide P., Rocu P., Fargette D., Hardy O., Suchard M., Guindon S., and Lemey P. 2024. How fast are viruses spreading in the wild? bioRxiv. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drummond A., Pybus O., Rambaut A., Forsberg R., and Rodrigo A. 2003. Measurably evolving populations. Trends in Ecology and Evolution, 18: 481–488. [Google Scholar]
- Drummond A., Ho S., Phillips M., and Rambaut A. 2006. Relaxed phylogenetics and dating with confidence. PLoS Biology, 4: e88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drury J., Clavel J., Manceau M., and Morlon H. 2016. Estimating the effect of competition on trait evolution using maximum likelihood inference. Systematic Biology, 65: 700–710. [DOI] [PubMed] [Google Scholar]
- Etheridge A. 2008. Drift, draft and structure: some mathematical models of evolution. Banach center publications, 80: 121–144. [Google Scholar]
- Felsenstein J. 1973. Maximum-likelihood estimation of evolutionary trees from continuous characters. The American Journal of Human Genetics, 25: 471–492. [PMC free article] [PubMed] [Google Scholar]
- Felsenstein J. 1975. A pain in the torus: some difficulties with models of isolation by distance. American Naturalist, 109: 359–368. [Google Scholar]
- FitzJohn R. 2010. Quantitative traits and diversification. Systematic Biology, 59: 619–633. [DOI] [PubMed] [Google Scholar]
- Gardiner C. 2009. Stochastic Methods. Springer Berlin, Heidelberg, 4th edition. [Google Scholar]
- Gill M., Tung H. L. S., Baele G., Lemey P., and Suchard M. 2016. A relaxed directional random walk model for phylogenetic trait evolution. Systematic Biology, 66: 299–319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guindon S. and De Maio N. 2021. Accounting for spatial sampling patterns in Bayesian phylogeography. Proceedings of the National Academy of Sciences, 118: e2105273118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guindon S., Guo H., and Welch D. 2016. Demographic inference under the coalescent in a spatial continuum. Theoretical Population Biology, 111: 43–50. [DOI] [PubMed] [Google Scholar]
- Hasegawa M., Kishino H., and Yano T. 1985a. Dating of the Human-Ape splitting by a molecular clock of mitochondrial-DNA. Journal of Molecular Evolution, 22: 160–174. [DOI] [PubMed] [Google Scholar]
- Hasegawa M., Kishino H., and Yano T. 1985b. Dating of the Human-Ape splitting by a molecular clock of mitochondrial-DNA. Journal of Molecular Evolution, 22: 160–174. [DOI] [PubMed] [Google Scholar]
- Hassler G., Gallone B., Aristide L., Allen W., Tolkoff M., Holbrook A., Baele G., Lemey P., and Suchard M. 2022. Principled, practical, flexible, fast: A new approach to phylogenetic factor analysis. Methods in Ecology and Evolution, 13: 2181–2197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ho S. and Shapiro B. 2011. Skyline-plot methods for estimating demographic history from nucleotide sequences. Molecular Ecology Resources, 11: 423–434. [DOI] [PubMed] [Google Scholar]
- Holmes E. 2013. What can we predict about viral evolution and emergence? Current Opinion in Virology, 3: 180–184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holmes E. C., Rambaut A., and Andersen K. G. 2018. Pandemics: spend on surveillance, not prediction. Nature, 558(7709): 180–182. [DOI] [PubMed] [Google Scholar]
- Hooten M. and Johnson D. 2017. Basis function models for animal movement. Journal of the American Statistical Association, 112: 578–589. [Google Scholar]
- Issaka S., Traoré O., Longué R. D. S., Pinel-Galzi A., Gill M., Dellicour S., Bastide P., Guindon S., Hébrard E., Dugué M.-J., et al. 2021. Rivers and landscape ecology of a plant virus, Rice yellow mottle virus along the Niger Valley. Virus Evolution, 7: veab072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson D., London J., Lea M.-A., and Durban J. 2008. Continuous-time correlated random walk model for animal telemetry data. Ecology, 89: 1208–1215. [DOI] [PubMed] [Google Scholar]
- Kalkauskas A., Perron U., Sun Y., Goldman N., Baele G., Guindon S., and De Maio N. 2021. Sampling bias and model choice in continuous phylogeography: getting lost on a random walk. PLOS Computational Biology, 17(1): e1008561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kingman J. 1982. The coalescent. Stochastic Processes and their Applications, 13: 235–248. [Google Scholar]
- Klitting R., Kafetzopoulou L., Thiery W., Dudas G., Gryseels S., Kotamarthi A., Vrancken B., Gangavarapu K., Momoh M., Sandi J., et al. 2022. Predicting the evolution of the Lassa virus endemic area and population at risk over the next decades. Nature Communications, 13: 5596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lanciotti R., Roehrig J., Deubel V., Smith J., Parker M., Steele K., Crise B., Volpe K., Crabtree M., Scherret J., et al. 1999. Origin of the West Nile virus responsible for an outbreak of encephalitis in the northeastern United States. Science, 286(5448): 2333–2337. [DOI] [PubMed] [Google Scholar]
- Lemey P., Rambaut A., Welch J., and Suchard M. 2010. Phylogeography takes a relaxed random walk in continuous space and time. Molecular Biology and Evolution, 27: 1877–1885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemey P., Rambaut A., Bedford T., Faria N., Bielejec F., Baele G., Russell C., Smith D., Pybus O., Brockmann D., and Suchard M. 2014. Unifying viral genetics and human transportation data to predict the global transmission dynamics of Human Influenza H3N2. PLoS Pathogens, 10(2): e1003932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lequime S., Bastide P., Dellicour S., Lemey P., and Baele G. 2020. nosoi: A stochastic agent-based transmission chain simulation framework in R. Methods in Ecology and Evolution, 11: 1002–1007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malécot G. 1948. Mathematics of heredity. Paris: Masson et Cie. [Google Scholar]
- Manceau M., Lambert A., and Morlon H. 2017. A unifying comparative phylogenetic framework including traits coevolving across interacting lineages. Systematic Biology, 66: 551–568. [DOI] [PubMed] [Google Scholar]
- Mitov V., Bartoszek K., Asimomitis G., and Stadler T. 2020. Fast likelihood calculation for multivariate Gaussian phylogenetic models with shifts. Theoretical Population Biology, 131: 66–78. [DOI] [PubMed] [Google Scholar]
- Mooers A., Gascuel O., Stadler T., Li H., and Steel M. 2012. Branch lengths on birth–death trees and the expected loss of phylogenetic diversity. Systematic Biology, 61: 195–203. [DOI] [PubMed] [Google Scholar]
- Müller N., Rasmussen D., and Stadler T. 2017. The structured coalescent and its approximations. Molecular Biology and Evolution, 34: 2970–2981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Müller K. 2020. here: A simpler way to find your files. R package version 1.0.1. [Google Scholar]
- Neal R. 2011. MCMC using Hamiltonian dynamics. In Brooks S., Gelman A., Jones G. L., and Meng X. L., editors, Handbook of Markov Chain Monte Carlo, pages 113–162. CRC Press, New York, NY. [Google Scholar]
- Papież L. and Sandison G. 1990. A diffusion model with loss of particles. Advances in Applied Probability, 22: 533–547. [Google Scholar]
- Paradis E. and Schliep K. 2019. ape 5.0: an environment for modern phylogenetics and evolutionary analyses in R. Bioinformatics, 35: 526–528. [DOI] [PubMed] [Google Scholar]
- Preisler H., Ager A., and Wisdom M. 2013. Analyzing animal movement patterns using potential functions. Ecosphere, 4: 1–13. [Google Scholar]
- Pybus O., Suchard M., Lemey P., Bernardin F., Rambaut A., Crawford F., Gray R., Arinaminpathy N., Stramer S., Busch M., et al. 2012. Unifying the spatial epidemiology and molecular evolution of emerging epidemics. Proceedings of the National Academy of Sciences, U.S.A., 109: 15066–15071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team 2024. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. [Google Scholar]
- Raghwani J., Rambaut A., Holmes E., Hang V. T., Hien T. T., Farrar J., Wills B., Lennon N., Birren B., Henn M., et al. 2011. Endemic dengue associated with the co-circulation of multiple viral lineages and localized density-dependent transmission. PLoS Pathogens, 7: e1002064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rakotomalala M., Vrancken B., Pinel-Galzi A., Ramavovololona P., Hebrard E., Randrianangaly J., Dellicour S., Lemey P., and Fargette D. 2019. Comparing patterns and scales of plant virus phylogeography: Rice yellow mottle virus in Madagascar and in continental Africa. Virus Evolution, 5: vez023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russell J., Hanks E., Haran M., and Hughes D. 2018. A spatially varying stochastic differential equation model for animal movement. The Annals of Applied Statistics, 12: 1312–1331. [Google Scholar]
- Sing T., Sander O., Beerenwinkel N., and Lengauer T. 2005. Rocr: visualizing classifier performance in r. Bioinformatics, 21(20): 7881. [DOI] [PubMed] [Google Scholar]
- Suchard M., Lemey P., Baele G., Ayres D. L., Drummond A., and Rambaut A. 2018. Bayesian phylogenetic and phylodynamic data integration using BEAST 1.10. Virus Evolution, 4: vey016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Talbi C., Lemey P., Suchard M., Abdelatif E., Elharrak M., Jalal N., Faouzi A., Echevarría J., S. V., Rambaut A., et al. 2010. Phylodynamics and human-mediated dispersal of a zoonotic virus. PLoS pathogens, 6: e1001166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor J., Cumberland W., and Sy J. 1994. A stochastic model for analysis of longitudinal AIDS data. Journal of the American Statistical Association, 89: 727–736. [Google Scholar]
- Tisseuil C., Gryspeirt A., Lancelot R., Pioz M., Liebhold A., and Gilbert M. 2016. Evaluating methods to quantify spatial variation in the velocity of biological invasions. Ecography, 39: 409–418. [Google Scholar]
- Trovão N., Baele G., Vrancken B., Bielejec F., Suchard M., Fargette D., and Lemey P. 2015. Host ecology determines the dispersal patterns of a plant virus. Virus evolution, 1: vev016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Bosch F., Hengeveld R., and Metz J. 1992. Analysing the velocity of animal range expansion. Journal of Biogeography, 19: 135–150. [Google Scholar]
- Wang L.-G., Lam T. T.-Y., Xu S., Dai Z., Zhou L., Feng T., Guo P., Dunn C., Jones B., Bradley T., Zhu H., Guan Y., Jiang Y., and Yu G. 2019. Treeio: An R package for phylogenetic tree input and output with richly annotated and associated data. Molecular Biology and Evolution, 37: 599–603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wickham H. 2016. ggplot2: Elegant Graphics for Data Analysis. Springer-Verlag; New York. [Google Scholar]
- Wilke C. 2024. cowplot: Streamlined plot theme and plot annotations for ‘ggplot2’. R package version 1.1.3. [Google Scholar]
- Wille M., Geoghegan J., and Holmes E. 2021. How accurately can we assess zoonotic risk? PLoS Biology, 19: e3001135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wirtz J. and Guindon S. 2023. On the connections between the spatial Lambda-Fleming-Viot model and other processes for analysing geo-referenced genetic data. Theoretical Population Biology, 158: 139–149. [DOI] [PubMed] [Google Scholar]
- Wright S. 1943. Isolation by distance. Genetics, 28: 114–138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu H. 2024. kableExtra: Construct Complex Table with ‘kable’ and Pipe Syntax. R package version 1.4.0. [Google Scholar]
- Zuckerkandl E. and Pauling L. 1965. Molecules as documents of evolutionary history. Journal of Theoretical Biology, 8: 357–366. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data and code to reproduce all analyses and figures displayed in this study are available at https://github.com/pbastide/integrated_phylogenetic_models. The PhyREX and BEAST programs are open source and freely available from https://github.com/stephaneguindon/phyml and https://github.com/beast-dev/beast-mcmc respectively.