SUMMARY
Brain states are frequently represented using a unidimensional scale measuring the richness of subjective experience (level of consciousness). This description assumes a mapping between the high-dimensional space of whole-brain configurations and the trajectories of brain states associated with changes in consciousness, yet this mapping and its properties remain unclear. We combine whole-brain modeling, data augmentation, and deep learning for dimensionality reduction to determine a mapping representing states of consciousness in a low-dimensional space, where distances parallel similarities between states. An orderly trajectory from wakefulness to patients with brain injury is revealed in a latent space whose coordinates represent metrics related to functional modularity and structure-function coupling, increasing alongside loss of consciousness. Finally, we investigate the effects of model perturbations, providing geometrical interpretation for the stability and reversibility of states. We conclude that conscious awareness depends on functional patterns encoded as a low-dimensional trajectory within the vast space of brain configurations.
In brief
Despite the microscale complexity, the brain self-organizes into a discrete number of global brain states characterized by specific behavioral patterns. Perl et al. use whole-brain models and deep learning algorithms to obtain a low-dimensional representation not only in terms of behavioral data but based on objective quantification of neuroimaging data.
Graphical Abstract
INTRODUCTION
The collective behavior of the human brain emerges from the non-linear interactions of billions of neurons interacting at trillions of time-dependent and highly specific synaptic connections.1,2 The emergent neural activity displays convergent signatures of complex behavior, including an ample repertoire of transitory states, long-range correlations in time and space, and a rapid re-organization upon perturbations, indicative of flexible and efficient information processing.3,4 Even though there is a vast number of degrees of freedom available to brain activity, the computations underlying cognitive function likely require this activity to be integrated, resulting in a lower effective number of relevant configurations.5,6 Nevertheless, it is considered that brain activity should also be highly differentiated to account for the large repertoire of possible mental states, either subjectively experienced or influencing behavior beyond the scope of conscious awareness.5
Despite the microscale complexity of the brain, integration contributes to the spontaneous self-organization of brain activity into a discrete number of global brain states characterized by specific behavioral patterns, capacity for cognitive processing, and reports of subjective experiences.7 Examples of these global states include everyday wakefulness and sleep, general anesthesia, and pathological conditions resulting from brain injury, such as coma or unresponsive wakefulness syndrome. These states are difficult to define in terms of the specific contents of first-person experience; instead, they involve overall reductions in the capacity to sustain consciousness, possibly to the point of becoming utterly devoid of subjective experiences. When assessed in terms of the accompanying behavior, it is important to note that global brain states can be characterized using the total score of unidimensional scales, with prominent examples given by the sleep staging criteria of the American Academy of Sleep Medicine (AASM),8 the coma recovery scale (CRS-R)9 for disorders of consciousness (DOCs), and the Ramsay scale for sedation and anesthesia.10 The level of arousal is frequently introduced as an additional dimension necessary to characterize global and temporally extended states of consciousness. For instance, deep sleep is generally considered a state of unconsciousness and low arousal, while high arousal can co-exist with reduced consciousness in certain patients with brain injury.11
As described above, the level of consciousness usually refers to a scalar index determined by observations of behavior but, at the same time, is used to characterize brain states with their distinct neurobiology and capacity to sustain subjective experience. Brain activity underlying different levels of consciousness (defined in this way) is multi-dimensional and ever-changing and thus seemingly incompatible with a unidimensional parametrization, resulting in an apparent mismatch between neurobiological and behavioral characterizations. The mapping from neural activity to behavioral metrics and to the intensity of reported subjective experience is inconclusive; for instance, the average local properties of single-cell dynamics (e.g., firing rates) sometime fail to correlate with the level of consciousness,12 suggesting that this mapping is based on more complex properties of collective neural behavior. We hypothesize that brain activity implicated in the capacity to sustain conscious experiences is integrated in a way that reduces the effective number of degrees of freedom and allows a low-dimensional representation not only in terms of behavioral data and subjective reports but also based on objective quantification of neuroimaging data. Thus, as individuals transition from wakefulness into a state of reduced consciousness, a significant part of the variance in their brain activity fluctuations is organized alongside a low-dimensional trajectory encoding the level of consciousness. Moreover, we hypothesize that external perturbations are capable of reversing this trajectory, which constitutes a potential mechanism underlying the reversibility of certain states of unconsciousness.
To assess these hypotheses, we first turned to the problem of obtaining a low-dimensional latent space capable of spanning whole-brain functional connectivity patterns indicative of multiple states of consciousness, including wakefulness, three stages of non-rapid eye movement (REM) sleep (N1, N2, and N3 sleep; REM sleep data were not included due to technical constraints in measuring it), two doses of the general anesthetic propofol (sedation [S] and loss of consciousness [LOC]), and two groups of patients with brain injury diagnosed with DOCs of different severity (minimally conscious state [MCS] and unresponsive wakefulness syndrome [UWS]). Note that we introduced phenomenological whole-brain models as a generative mechanism for data augmentation,13 considering the large amount of data required to successfully perform non-linear dimensionality reduction with deep variational autoencoders.14 To avoid overfitting during the data-driven discovery of this latent space, we examined whether only part of this data (i.e., wakefulness, N3 sleep, and patients in UWS) contained sufficient regularities for the adequate representation of all other brain states. We examined the relationship between the latent space encoding and previously introduced signatures of consciousness, such as metrics of functional integration15,16 and structure-function coupling.17,18 Finally, we addressed the stability of the latent space representation in terms of external perturbations,19 mainly in the context of known differences in the reversibility of unconscious states (for instance, sleep or S vs. patients in UWS).
RESULTS
Methodological overview
The procedure followed in this work is showcased in Figure 1. First, we implemented a whole-brain model with local dynamics given by the normal form of a Hopf bifurcation.20 Depending on the bifurcation parameter (a), the dynamics present two qualitatively different behaviors: fixed-point dynamics (a < 0) and oscillations around a limit cycle (a > 0). When noise is added to the model, dynamics close to the bifurcation (a ≈ 0) change stochastically between both regimes, giving rise to oscillations with complex amplitude modulations.20 Regional dynamics were coupled by the structural connectivity (SC) matrix obtained from diffusion tensor imaging (DTI) measurements. The model was used to directly simulate narrow band (0.04–0.07 Hz) fMRI time series; hence, the dominant oscillatory frequency of the model was inferred from the data.21 The whole-brain model has different bifurcation parameters in each region of the parcellation, which are constrained by the spatial maps of anatomical priors given by resting state networks (RSNs); thus, each RSN can add its own contribution to the regional bifurcation parameter.22 Following Ipina et al., these contributions are free parameters that were optimized using a genetic algorithm, with the functional connectivity (FC) matrix being the optimization target.22 Different FC matrices were considered, one for each of the following states of consciousness: wakefulness; N1, N2, and N3 sleep; anesthesia (S and LOC); and patients with DOCs (MCS and UWS). Afterward, we used the inferred parameters to simulate surrogate FC matrices that were encoded into a two-dimensional space using a deep learning architecture known as variational autoencoder (VAE). VAEs are autoencoders trained to map inputs to probability distributions in latent space, which can be regularized to produce meaningful outputs after the decoding step We characterized the latent space in terms of different FC metrics and then explored the effects of external perturbation given by wave stimulation (periodic perturbation delivered at the natural nodal frequency).19 After systematically applying the perturbations to all pairs of homotopic nodes and encoding the resulting FC matrices, we obtained low-dimensional perturbational landscapes consisting of trajectories in latent space parametrized by the stimulation intensity. In turn, these trajectories can be classified by geometrical metrics in latent space such as how closely they bring the dynamics to a predefined target state (in this case, conscious wakefulness).
Figure 1. Methodological overview.
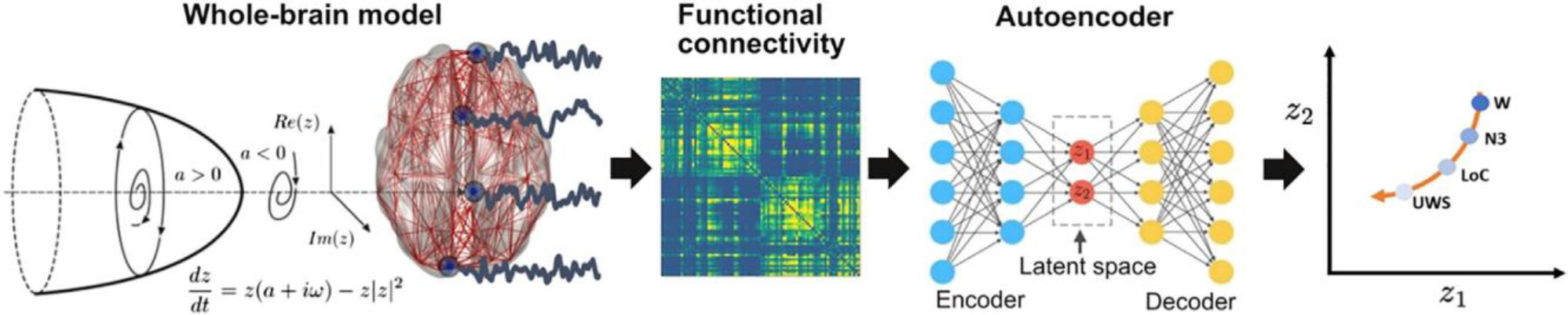
A whole-brain model with local dynamics given by Hopf bifurcations was implemented at nodes defined by the AAL parcellation, coupled with the anatomical connectome. We included spatial heterogeneity based on RSN in the model parameters. The model was tuned to reproduce the empirical FC for each condition, and the resulting parameters were used to generate a surrogate database of simulated FC matrices that were represented in a latent space using a VAE. Finally, perturbations were introduced in the model as an external periodic force, resulting in a set of trajectories in latent space (one per pair of homotopic AAL regions) parameterized accordingly the amplitude of the forcing parameter.
Latent space representation of brain states
Using the optimized whole-brain model, we generated 15,000 FC matrices for each brain state; next, we trained the VAE using an 80/20 split for training/testing (see STAR Methods for details on model training and evaluation). Note that since our goal is to determine how the different states of consciousness are organized in a low-dimensional space, we constructed such representation following a process that consisted of training a VAE with FC belonging to a reduced set of brain states representing the most extreme cases in term of consciousness (wakefulness [W] and UWS) plus one intermediate state (N3). In this way, we can avoid overfitting the VAE to all states of consciousness, which would result in a trivial result without any meaningful generalization between states. We then investigated how the latent space represented the complete set of intermediate states (which were not used as inputs to the VAE). Importantly, the inclusion of N3 as an intermediate state arises due to its similarity with LOC, S, and MCS in terms of several metrics, as found in previous work.19 After training, we encoded 300 FC matrices per state used for training, finding the results shown in Figure 2A (left). We then applied the trained autoencoder to simulated FC corresponding to all the remaining stages. This procedure generated separate clusters into the two-dimensional space organized according to the reduction of the level of consciousness (Figure 2A, middle). Advancing alongside the trajectory represented by a dashed line resulted in FC matrices associated with reduced consciousness.
Figure 2. Latent space encoding of whole-brain FC reflects loss of consciousness alongside a low-dimensional trajectory.
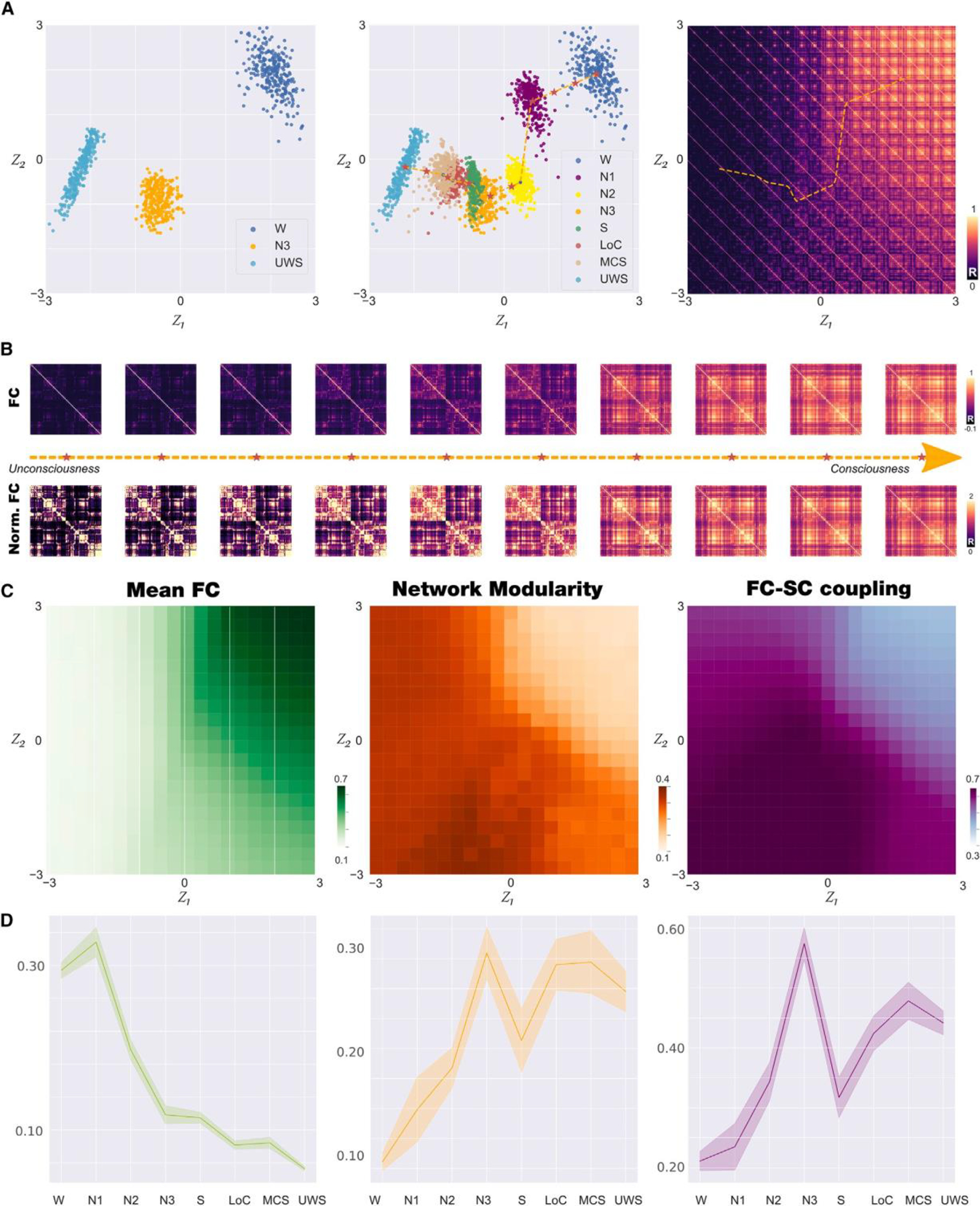
(A) We trained the VAE using simulated FC matrices corresponding to states W, N3, and UWS (left panel). We then applied the trained autoencoder to FC matrices corresponding to all other brain states, obtaining clusters of points organized alongside a low-dimensional trajectory (dashed line) representing progressive loss (legend continued on next page) of consciousness (middle panel). Applying the decoder to the latent space coordinates, we illustrate the FC matrices corresponding to each part of the latent space, including those included in the trajectory (right panel).
(B) FC matrices sampled homogeneously along the trajectory identified in (A), middle (indicated with red stars), both for matrices with (up) and without (bottom) normalization.
(C) Characterization of the latent space in terms of mean FC (left panel), network modularity (middle panel), and SC-FC coupling (right panel).
(D) Mean FC (left panel), network modularity (middle panel), and SC-FC coupling (right panel) for the 300 encoded FC matrices corresponding to each brain state(mean ± SD) (W, wakefulness; N1, N2, and N3, stages from light to deep sleep; S, sedation; LOC, loss of consciousness; MCS, minimally conscious state; UWS, unresponsive wakefulness syndrome).
We investigated the optimality of the two-dimensional representation by quantifying how this representation distinguishes the states compared with the original high-dimensional space of whole-brain FC, as well as with reduced spaces with dimensions higher than two. To do so, we trained a support vector machine (SVM) with polynomial kernel as implemented in the MATLAB function fitcecoc with the objective of distinguishing between eight class labels (each representing a state of consciousness). We subdivided the 300 samples used for each state into training (90%) and validation (10%) sets and assessed model performance using a 10 k-fold scheme with four different sets of features: (1) the lower triangular part of the FC matrix in the original data dimension; (2) z1, standing for the encoding of the 300 matrices in one-dimensional latent space; (3) the z1,z2 pair representing the encoding of the FC matrices in the two-dimensional latent space; and (4) three dimensions representing the encoding of the FC matrices in the three-dimensional latent space. For each case, we repeated this procedure 100 times, and we assessed the statistical significance of each classifier by comparing it with the same SVM but trained using data with scrambled class labels as a null model. We then constructed an empirical p value by counting how many times the accuracy of the classifier with scrambled class labels was greater than that the original classifier, and we found p < 0.001 for the four cases. In terms of accuracy of the classifiers, we obtained the following values: 0.75 ± 0.01 (full data); 0.77 ± 0.01 using one-dimensional latent dimension; 0.89 ± 0.01 using two-dimensional latent dimension; and 0.91 ± 0.01 using three-dimensional latent dimension (Figure S1). Thus, we established that latent space representations have better classification performance compared with the original high-dimensional data and that the classification performance increases with the dimension of the latent space representation. We also noted that the improvement in the performance is considerably higher when the latent space dimension changes from one to two than when the dimension increases from two to three, which is comparatively very small and close to ceiling performance. Given that two dimensions resulted in an acceptable reproduction of the data and that the improvement in accuracy from two to three dimensions was relatively marginal, we decided on a bidimensional representation, which also allows straightforward visualization.
Characterization of FC decoded from the latent space
Applying a decoder network to all latent space coordinates in (z1, z2) visualizes the FC matrices that correspond to different regions of this space, in particular those that were visited when advancing in the trajectory that interpolates the encoded brain states (Figure 2A, right). A sequence of matrices obtained in this way is shown in Figure 2B, both with (bottom) and without (top) normalization (i.e., all matrix entries add up to a fixed value). From the non-normalized matrices, it is clear that reductions in consciousness are paralleled by an overall decrease in FC values. The normalized matrices show that this decrease is not homogeneous but tends to be concentrated in certain pairs of off-diagonal entries corresponding to inter-modular connections. Based on previous work, we hypothesized that LOC would increase the FC-SC similarity17,18 Figure 2C shows how the decoded latent space coordinates are characterized in terms of the mean FC (left panel), the network modularity (middle panel), and the coupling between FC and SC (right panel). These plots converge in the presence of a gradient from the top left to the bottom right in the values of all metrics, which parallels the trajectory interpolating the encoded brain states. Finally, Figure 2D summarizes the value of these metrics for the 300 FC matrices encoded for each brain state, corroborating that LOC is associated with decreased mean FC (left), increased network modularity (middle), and increased FC-SC coupling (right). Moreover, these plots are monotonous with the exception of jumps in S (for modularity) and N3 (for FC-SC coupling). To further investigate the relationship between the latent variables and the dimensions of consciousness, we decoded all (z1, z2) pairs from the latent space within a 5 × 5 grid to generate FC matrices. We then computed the mean across rows to obtain the nodal projection of the FC, i.e., the node connectivity strength, for each decoded FC matrix. We rendered the obtained functional networks for each pair into a brain surface (Figure S2). We noted that z1 latent space coordinate could be related to the W dimension, with unspecific increasing of all the functional connections (this is observed as a flattening of the node strength in the brain renders). While the interpretation of the other dimension, z2, seems to be more subtle, it represents a reconfiguration of the functional networks that could be related to the functional changes associated with LOC independent of the overall level of activation or arousal.
Perturbational analysis of the latent space trajectory of brain states
We investigated how each state of consciousness responded to an external perturbation modeled by the inclusion of a periodic forcing at the natural frequency of each node. Following previous work,19 we applied this perturbation at different pairs of homotopic brain regions, and we parametrized it by the strength of the forcing (F0). As a result, we obtained a sequence of FC matrices per region pair, which we encoded in the latent space to visualize the behavior of the system under the perturbation. Figure 3A (left panel) illustrates the outcome of increasing the forcing for the stimulation applied to a single region pair, while Figure 3A (middle panel) represents one trajectory per choice of homotopic brain regions. In both cases, it is clear that the distance in latent space reaches an asymptotic value as the forcing keeps increasing. Averaging these terminal points across all region pairs, we estimate the mean displacements shown as arrows in Figure 3A (right panel). We note that all arrows point toward the top left corner of the latent space, which was associated with conscious W; thus, overall, the net result of the forcing is to displace the system toward this state.
Figure 3. Perturbational analysis of stability and reversibility of brain states.
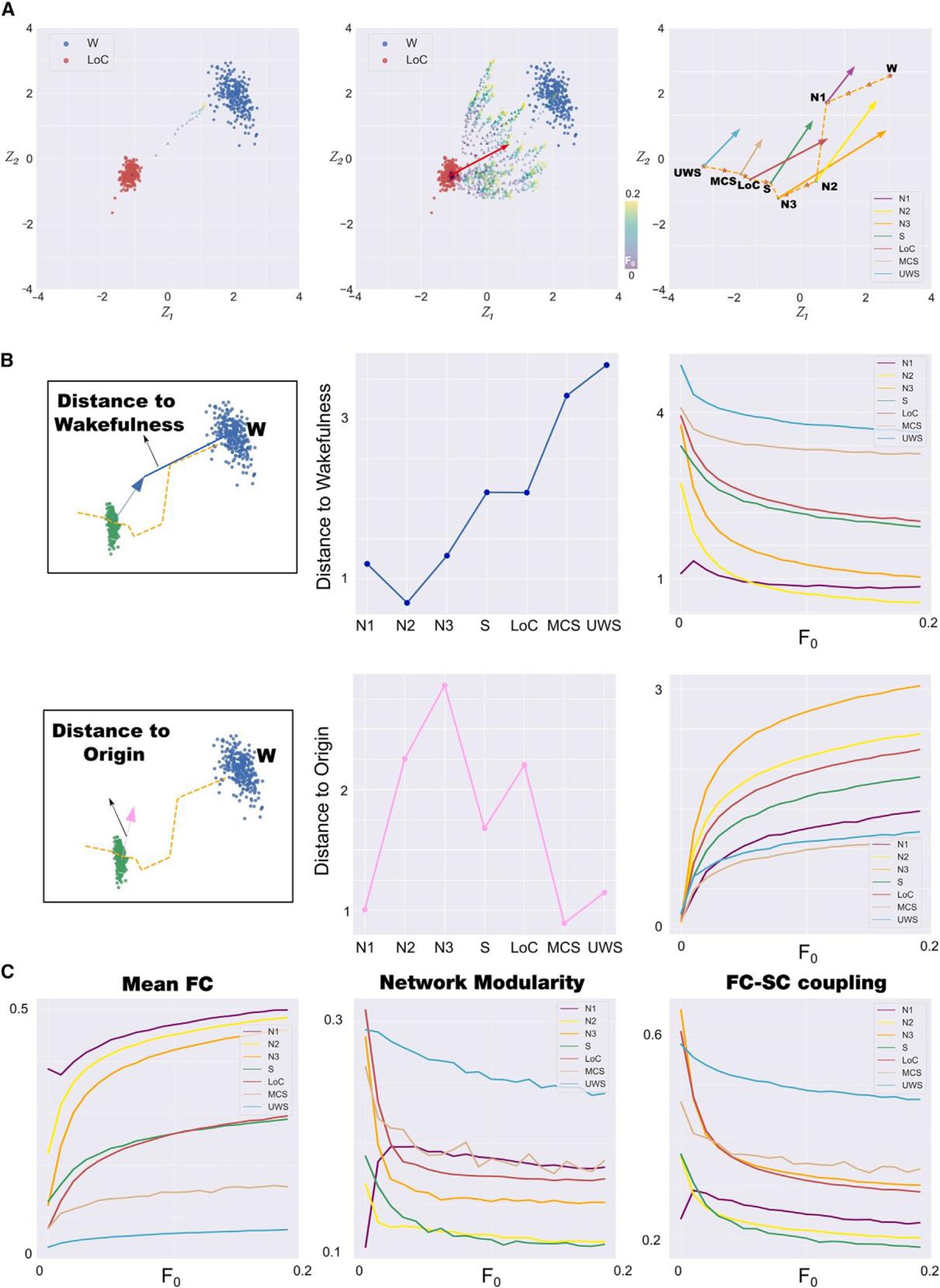
(A) Left panel: example trajectory obtained by encoding in latent space the outcome of introducing periodic forcing in the model at a single pair of homotopic regions. Middle panel: same as in the left panel but showing trajectories corresponding to all pairs of homotopic regions. Right panel: average maximal displacements for all brain states represented in the latent space.
(B) Left panel: geometric definitions of distance to wakefulness and distance to origin. Middle panel: the two metrics defined in the left panel for all brain states.
Right panel: parametric behavior of these metrics per brain state as a function of the forcing amplitude.
(C) Mean FC (left panel), modularity (middle panel), and SC-FC coupling (right panel) for each state as a function of the perturbation strength (W, wakefulness; N1,N2, and N3, stages from light to deep sleep; S, sedation; LOC, loss of consciousness; MCS, minimally conscious state; UWS, unresponsive wakefulness syndrome).
To summarize the effect of the perturbation on the latent space geometry, we introduced the metrics shown in the left panel of Figure 3B. The distance to W measures the separation between the terminal state obtained for large forcing and the centroid of the W cluster (represented with blue circles in Figure 2A), while the distance to the origin measures the separation between the terminal state and the centroid of the brain state that is being stimulated. Note that to compute these metrics, we considered the latent space of VAEs to be Euclidean, which is the most parsimonious conjecture, following Kingma et al.23 (the Euclidian assumption of the latent space could be guaranteed by including an extension of VAE proposed by Chen and colleagues24). The right panel of Figure 3B shows that the stimulation fails to bridge the gap between pharmacological and pathological unconscious states and W. Also, it highlights that the least stable states (i.e., those with the largest distance to origin values) comprise intermediate sleep stages. As expected, patients with DOCs presented highly stable states. The asymptotic behavior of these two metrics vs. the forcing is shown in the two rightmost panels of Figure 3B. It is important to note that the 2D localization of perturbations in the latent space and its proximity to W provides more information than one-dimensional metrics such as the goodness of fit (GOF) between the perturbed FCs and the FC of W, including the trajectory of the perturbation (Figure S3). Finally, to further characterize the perturbative landscape, we leveraged the results obtained in Figure 2C, where we endowed the latent space with measures obtained from the decoded FC. Figure 3C confirms the observation that stimulation tends to displace the latent space encoding toward the region associated with conscious W, with mean FC increasing vs. the forcing amplitude and with modularity and SC-FC coupling decreasing vs. forcing amplitude. Overall, the metrics introduced in Figure 3B allow us to characterize brain states in terms of intuitive geometrical observations, which indicate the sensitivity to external perturbations and the directionality of this perturbed state.
Neuroanatomical representation of the response to external stimulation
Applying the stimulation to each pair of homotopic regions results in latent space trajectories, which can be characterized by the value of different metrics computed using the terminal FC matrix. Figure 4 represents the effect of stimulation applied to states of consciousness investigated in this study. In Figure 4A, we show that the top 20% regions, when perturbed, move the initial state closer to W, quantified as the geometrical measure called distance to W. Note that we displayed the difference between the maximum across regions and the single regional value to obtain a metric that higher values mean a better transition toward W. The radar plot shows the mean value across the top 20% regions for each state. Stimulation at regions located in posterior nodes of the default mode network (DMN) (i.e., precuneus) for all brain states (except S and early sleep) was more prone to generate trajectories closer to W. Frontal regions were also featured for all brain states, also encompassing anterior midline DMN nodes (e.g., orbito-frontal cortex). We then extend the stimulation behavior assessment adding the following metrics: distance to origin, mean FC, modularity, and SC-FC coupling (in all panels, darker values indicate larger changes in the corresponding metric) (Figure 4B). Accordingly, similar regions were found for modularity and SC-FC coupling. In terms of mean FC and distance to origin, the maps were more diffuse, without clearly outlined regions that preferentially displace the dynamics toward W. The matrix in Figure S4 summarizes the similarity between the patterns rendered in Figure 4. Diagonal blocks indicate consistent results when stimulation was applied to a specific brain state, while off-diagonal blocks show that similar patterns can be obtained even when the stimulation is applied to different states of consciousness.
Figure 4. Neuroanatomical representation of the response to external stimulation.
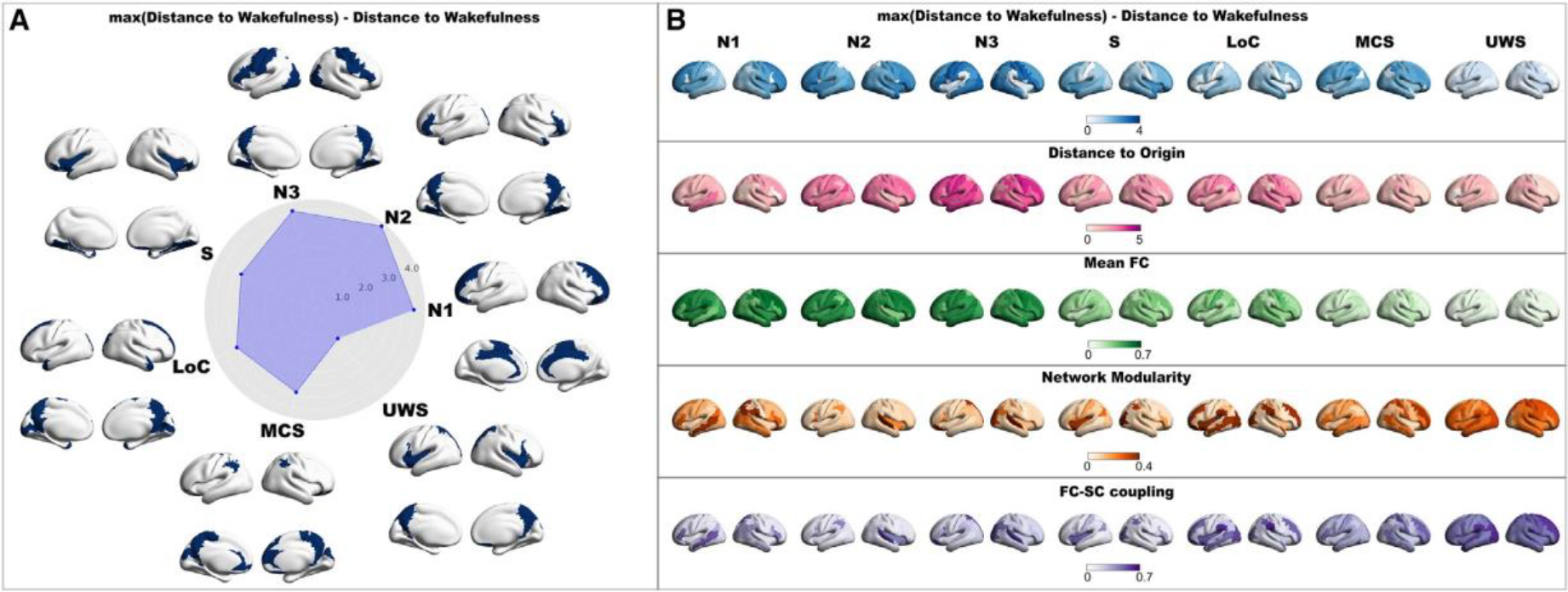
(A) The top 20% in terms of distance to wakefulness are rendered in brains for each investigated state of consciousness. The mean values across the top 20% are represented in the radar plot. Importantly, we represent the maximum value across brain regions minus the single value region to obtain a metric that increases when the transition toward wakefulness is better.
(B) We extend the analysis to the other proposed metrics in latent space. Each row corresponds to a different metric. Columns contain three-dimensional renderings where the regions are colored depending on how the corresponding metric behaves asymptotically with the perturbation strength when applied to that region pair (W, wakefulness; N1, N2, and N3, stages from light to deep sleep; S, sedation; LOC, loss of consciousness; MCS, minimally conscious state; UWS, unresponsive wakefulness syndrome).
DISCUSSION
Subjective experiences encompass a vast range of contents, yet the global and qualitative modifications of consciousness are usually described using few parameters. We demonstrated that several states of consciousness—from W to DOCs—can be meaningfully represented in a low-dimensional space where the gradual progression toward deep unconsciousness is manifest in a purely data-driven manner. We quantified the goodness of this representation by assessing the performance of SVM classifiers trained with full FC matrices and also with one-, two-, and three-dimensional FC matrices reconstructed from the corresponding latent space representations. We found that the two-dimensional latent space representation was optimal in terms of the balance between the discrimination accuracy of states of consciousness and the criterion of adopting the simplest model that adequately captures these states. By finding this representation, we lend support to the clinical practice of ordering these states along a unidimensional continuum based on behavioral assessments. This also suggests that non-linear compression via VAEs could represent an interesting method to infer scalar signatures of consciousness from neuroimaging data. Accordingly, other methods for dimensionality reduction have revealed consistent results when applied to neural activity measured during sleep and anesthesia.25–27
While previous computational efforts addressed the outcome of simulated perturbations in terms of the global state of the brain,14,19,22,28–32 our work provides a series of distinct insights. We demonstrated that the overall effect of stimulating the cortex of unconscious individuals is to displace the state toward conscious W, as clearly visualized by the arrows in the latent space of Figure 3A. Despite this, the dissimilarity of certain states of deep unconsciousness with respect to W prevented the full recovery of a conscious global brain state as a result of the stimulation. In dynamical terms, this could be explained by the saturation of the displacement trajectories as a function of the stimulation amplitude, F0. As expected, the states that could be displaced the largest distance from their original position in latent space included the intermediate sleep stages, N2 and N3, where awakenings are likely to occur due to external sensory input.8,19 Finally, the application of VAEs to the simulated dynamics allowed us to interpret the complex outcome of external perturbations by means of the latent space geometry. This development was fundamental for the heuristic assessment of the simulated perturbations, which otherwise result in multi-dimensional trajectories of difficult visualization.
We highlight that several of our results were consistent with the previous literature, regardless of the phenomenological nature of the Hopf bifurcation model.25–27 It also worthwhile to point out that SC-FC similarity as a metric biases the results to Gaussian approximation of data cloud, pushing the model into the linear regime around a local minimum. Depth of unconsciousness correlated with decreased FC, increased modularity,15,16 and similarity between SC and FC.17,18 The relationship between these variables and the depth of unconsciousness was clear except for propofol-induced S, which should perhaps be re-assessed and placed closer to early/intermediate sleep. Also, the predicted regions that should be targeted to restore a state of awareness in the participants was consistent with previous reports, including highly connected hubs within posterior regions of the DMN as well as in midline frontal and prefrontal regions.19 Moreover, these spatial profiles were consistent between conditions, suggesting the presence of a universal dynamical mechanism underlying the restoration of W upon properly targeted external perturbations.
The notion of levels of consciousness is ubiquitous in clinical and translational neuroscience, yet it is also at odds with certain theoretical accounts and first-person reports. Experimental evidence suggests that conscious perception is determined as the outcome of an all-or-none bifurcation, which questions whether consciousness can be graded in terms of intensity.33 When it comes to subjective experience, even though the information conveyed by a certain percept can be graded, high-level perception itself appears to be binary.34 Accordingly, Bayne and colleagues have argued that consciousness should not be described in terms of “levels” that determine the degree or intensity of perception; instead, multiple dimensions are likely required to adequately express the changes in the nature of subjective experience across states of consciousness.35 We note that our finding does not contradict these observations: even though we were capable of finding a low-dimensional representation where the brain states are ordered within a unidimensional trajectory, this trajectory does not necessarily reflect the intensity of the contents of consciousness. Instead, it likely reflects a combination of multiple variables that is capable of explaining most of the variance in the characterization of progressively impaired consciousness. While our analysis conveyed a characterization of latent space variables in terms of metrics that have been implicated in the trajectory from W to unconsciousness (e.g., modularity), a more precise interpretation of these variables in terms of the phenomenology of conscious experience across brain states should be the target of a future investigation, likely requiring more complex experimental paradigms beyond the measurement of spontaneous brain activity.
It is also important to mention that variables related to consciousness are not necessarily behind the latent space organization reported in this study. While it is reasonable to expect that this is indeed the case, based on the proximity of states usually regarded as similar in terms of level of consciousness, other confounding factors could be behind this proximity. For example, states induced by propofol could be more similar (regardless of the level of consciousness) due to neurochemical changes associated with the drug that are independent of its modulation of conscious awareness.36 Similar considerations could apply to sleep and to patients with DOCs. This problem is difficult to avoid insofar as states of consciousness involve non-specific modulations of brain activity that encompass neural correlates of consciousness but are not limited to them. We also characterized the latent space variables by exploring the functional networks changes that occur in the decoded FC matrices as a function of latent space coordinate pairs. We found that z1 could be related to the level of W, while z2 was related to a more complex reconfiguration of the networks, possibly related to the functional changes implicated with LOC. Nevertheless, the decoded FC matrices present a complex non-linear behavior as a function of the latent space coordinates, and a linear transformation between this space and a more biologically interpretable set of dimensions might not be possible.
The description of global brain states by means of a low-dimensional latent space using generative algorithms presents some interesting advantages. One example is the possibility of extrapolating the results in different directions of the latent space, for example generating FC matrices that would correspond to states of deeper unconsciousness than patients in UWS. Another is the possibility of interpolating between the represented states, yielding intermediate FC matrices that would correspond to intermediate levels of consciousness and thus be interpretable as the transition between the associated brain states. This is complemented by the computation of different metrics of interest per pair of latent state coordinates, which enables a simple visualization of how regions in such space relate to putative signatures of consciousness. Finally, the encoding of states obtained after simulated external perturbations can provide a simplified geometric interpretation of the outcome of complex collective changes in the brain state with clinical and translational implications.
The clinical perspective of our work is aligned with the current efforts of the scientific community to develop treatments for pathological states of reduced or absent consciousness. Several works have empirically demonstrated that external brain stimulation modulates the behavioral responsiveness in patients suffering from DOCs due to brain injury. Specifically, these works pursue the goal of finding possible interventions that allow or accelerate the recovery of consciousness as a therapeutic alternative in these patients. Invasive electrical stimulation, such as the deep brain stimulation (DBS) technique, has provided encouraging results, improving behavioral measures in patients with DOCs (i.e., CRS-S score37,38). Also, non-invasive electrical stimulation, such as transcranial direct current stimulation (tDCS), has been investigated as a potential method to improve the state of patients with DOCs.39–42 A recent publication suggests a causal effect of tDCS intervention in electroencephalography (EEG) biomarkers proposed as a signature of consciousness in a large cohort of patients with DOCs.43 Also, brain stimulation in anesthetized non-human primates has proven effective to accelerate the recovery of consciousness.44 In parallel to these experimental results, in the last years, progress in computational neuroscience has allowed us to robustly define brain states and to study transitions between them in silico. While this has been used to provide insights into the diagnosis, prognosis, and potential treatment of pathological states, the empirical validation of these models remains to be systematically addressed.45 One successful example in this direction is the application of semi-empirical models to the diagnostics and treatment of other neurologic conditions, such as epilepsy, which has received significant attention from clinical translational neuroscience.46 Our work points toward the same direction but from a broader perspective that is not focused on a particular disorder; instead, we focused on the more general concept of conscious states, thus providing potential tools to understand these states and to study the transitions between them. Nevertheless, to generate testable hypotheses and to increase the sensitivity of the method to different pathologies, which could strengthen the translational impact of the approach, an individual-level perspective should be considered. One avenue to reach this objective is to include individualized sources of information such as individual SC, disease-specific maps of gray and white matter atrophy, maps of receptor density, and transcriptomic data, among others. At the same time, to extend this approach to different pathologies, a pathology-based latent dimension determination should be considered as a way to guarantee their meaningful representation.
Obtaining a latent state representation using VAE requires a large amount of data from training, which is difficult to obtain considering the typically small sample size of fMRI experiments.47 We explored this using whole-brain computational models as a potential method for data augmentation, with encouraging results that prompt further research.13 We can also hypothesize that model-based training the VAE was more successful than using real data because model parameters could be more informative than direct fMRI observables. As an example, all regional parameters can be interpreted in terms of their influence in FC but also in relation to the (un)stability of regional dynamics, which highlights the mechanistic dimension of these features.48
We acknowledge that our results are based on the a priori selection of the phenomenological Hopf whole-brain model, which fits observables derived directly from fMRI recordings. The rationale behind the selection of the Hopf whole-brain model is based on the fact that it has been shown that emergent collective macroscopic behavior of brain models depends weakly on individual neuron behavior.49 Over the years, many different whole-brain models with varying degrees of biophysical realism have been used, ranging from spiking networks to mean-field models to oscillatory Hopf models.20,50–54 The Hopf model represents a compromise between the correct reproduction of fMRI observables without the need to fine-tune parameters related to biophysical variables.20 Moreover, the Hopf model easily captures the oscillatory nature of band-pass-filtered fMRI signals, whereas spiking and mean-field models are asynchronous, and therefore the representation of oscillatory couplings is not straightforward. Still, it is possible to include oscillations in mean-field models, as we have done in recent work.55 The results show that the best fit for this oscillatory mean-field model is exactly at the Hopf bifurcation, highlighting that the use of a more complex model does not provide an obvious advantage while resulting in drawbacks related to higher computational demands. Nevertheless, future work should explore other detailed biophysical models, which might be necessary to test hypotheses related to specific biological interpretations of model parameters and their neurophysiological implications. For instance, future research could explore mean-field models, such as the dynamical mean field (DMF) model,51 which allows us to simulate pharmacological interventions by modeling the neuromodulator effect of the specific drugs.56 At the same time, it is natural to ask how this framework could be extended to other neuroimaging modalities, such as EEG, which is clinically the gold standard for identifying the level of consciousness in clinical settings and is also cheaper than fMRI and thus has the potential to generate massive amounts of data. In this sense, we can identify a set of limitations related to building whole-brain models to fit EEG data, such as the accuracy of source space localization and its relation to the SC obtained using a different methodology and that the whole-brain models generate brain signals of each region with a specific frequency to match the empirical frequency of the fMRI data, yet EEG data present a heterogeneous power spectrum with multiple relevant frequency bands. However, an interesting future direction could be to adapt the framework to include EEG data by leveraging large amounts of recordings to train deep learning neural networks directly with empirical data.
In summary, we introduced computational methodologies to show that global brain states of impaired consciousness can be represented in a low-dimensional space, where distances parallel the known similarities between these states. All simulated perturbations displaced the encoded brain state toward W, but due to their original distance in latent space, some states (e.g., MCS, UWS) failed to approach conscious W. Our results highlight the presence of sufficient regularities across brain states to endow them with a low-dimensional and data-driven characterization paralleling the level of consciousness, an informative and practical construct that should be the target of future investigations.
Limitations of the study
On the other hand, the technical caveats of this work can be based on the fact that we use anatomical connectivity estimated in a group of healthy participants to model patient data. However, considering that patients with brain injury may present heterogeneous lesion locations, the average healthy connectivity constitutes a reasonable first estimate. Finally, we opted to simulate the stimulation of homotopic regions only and with an external periodical forcing. This restriction ensures that the stimulation protocols explored in the model are experimentally possible. Future extensions of our work could include the development of multi-regional stimulation with different protocols.
STAR★METHODS
RESOURCE AVAILABILITY
Lead contact
Further information and requests for resources should be directed to and will be fulfilled by the lead contact: Yonatan Sanz Perl (yonatan.sanz@upf.edu).
Materials availability
This study did not generate new material.
Data and code availability
Sleep dataset is publicly available since the data of publication. The DOI is listed in the key resources table. Data of disorders of Consciousness and anesthesia cannot be shared publicly because contains data and information from a clinical population of patients, and are not publicly available due to constraints imposed by the currently approved ethics protocol, but are available upon request to Comitéd’É thique Hospitalo-Facultaire Universitaire de Liège (https://www.chuliege.be/jcms/c2_16986309/fr/comite-d-ethique-hospitalo-facultaire-universitaire-de-liege/accueil): ethique@chuliege.be.
All original code has been deposited at Zenodo and is publicly available as of the date of publication. DOIs are listed in the key resources table.The software dependencies are MATLAB (2018b); Python (3.6) and Keras.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE.
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
|
| ||
| Deposited data | ||
|
| ||
| Processed fMRI data | University of Liege and University of Kiel | https://doi.org/10.5281/zenodo.7806006 |
|
| ||
| Software and algorithms | ||
|
| ||
| Whole-brain modeling & Variational Autoencoder | Custom software | https://doi.org/10.5281/zenodo.7806006 |
| MATLAB 2020b | MathWorks | https://www.mathworks.com |
| SPM | Wellcome Department of Cognitive Neurology, London, UK | https://www.fil.ion.ucl.ac.uk/spm/ |
| FSL | FMRIB Software Library | https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/ |
| Connectome Workbench | Marcus et al.57 | https://www.humanconnectome.org/software/connectome-workbench |
| Python 3.10.3 | Python | https://www.python.org/ |
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Ethic statement
Sleep data: written informed consent and the experimental protocol was approved by the local ethics committee “Ethik-Kommission des Fachbereichs Medizin der Goethe-Universität Frankfurt am Main, Germany” with the ethics application title “Visualisierung von Gehirnzuständen in Schlaf und Wachheit zum Verständnis der Abnormitäten bei Epilepsie und Narkolepsie” and the assigned number: 305/07 in Frankfurt (Germany). Propofol sedation and anesthesia dataset: written informed consent, approval by the Ethics Committee of the Medical School of the University of Liège. DoC dataset: written informed consent to participate in the study was obtained directly from healthy control participants and the legal surrogates of the patients, approval by the Ethics Committee of the Medical School of the University of Liège.
Experimental data
We analyzed fMRI recordings from 81 participants identified by their scanning site and experimental condition: Frankfurt (15 subjects during wakefulness and sleep) and Liège (14 healthy subjects during wakefulness and under propofol sedation and anesthesia, 16 patients diagnosed as MCS, 15 patients diagnosed as UWS, and 21 healthy and awake controls).
Sleep dataset
Simultaneous fMRI and EEG was measured for a total of 73 subjects and a subgroup of 55 was considering (by excluding subjects who did not fall asleep) (36 females, mean ± SD age of 23.4 ± 3.3 years). EEG via a cap (modified BrainCapMR, Easycap, Herrsching, Germany) was recorded continuously during fMRI acquisition (1505 volumes of T2*-weighted echo planar images, TR/TE = 2080 m/30 m, matrix 64 × 64, voxel size 3 × 3 × 2 mm3, distance factor 50%; FOV 192 mm2) with a 3 T S Trio (Erlangen, Germany). EEG measurements allow the classification of sleep into 4 stages (wakefulness, N1, N2 and N3 sleep) according to the American Academy of Sleep Medicine (AASM) rules. To facilitate the sleep scoring during the fMRI acquisition, pulse oximetry and respiration were recorded via sensors from the Trio [sampling rate 50 Hz]) and MR scanner compatible devices (BrainAmp MR+, BrainAmpExG; Brain Products, Gilching, Germany). We selected 15 subjects who reached stage N3 sleep (deep sleep) and contiguous time series of least 200 volumes for all sleep stages. Written informed consent and the experimental protocol was approved by the local ethics committee “Ethik-Kommission des Fachbereichs Medizin der Goethe-Universität Frankfurt am Main, Germany” with the ethics application title “Visualisierung von Gehirnzuständen in Schlaf und Wachheit zum Verständnis der Abnormitäten bei Epilepsie und Narkolepsie” and the assigned number: 305/07 in Frankfurt (Germany). Previous publications based on this dataset can be consulted for further details.58
Propofol sedation and anesthesia
Resting-state fMRI of three different states following propofol injection: wakefulness, sedation and unconsciousness were acquired from 18 healthy right-handed volunteers (4 men and 14 women; age range, 18–31 years; mean age ±SD, 23.7 ± 3.7 years). Data acquisition was performed in Liège (Belgium). Subjects fasted for at least 6 h from solids and 2 h from liquids before sedation. During the study and the recovery period, electrocardiogram, blood pressure, pulse oximetry (SpO2), and breathing frequency were continuously monitored (Magnitude 3150M; Invivo Research, Inc., Orlando, FL). The clinical evaluation of the level of consciousness was performed considering the scale used in. The investigator considered if the subject is fully awake if the response to verbal command (“squeeze my hand”) was clear and strong (Ramsay 2), as sedated if the response to verbal command was clear but slow (Ramsay 3), and as unconscious, if there was no response to verbal command (Ramsay 5–6). This procedure was repeated twice for each consciousness level assessment. Functional MRI acquisition consisted of resting-state functional MRI volumes repeated in the three states: normal wakefulness (Ramsay 2), sedation (Ramsay 3), unconsciousness (Ramsay 5). The typical scan duration was half an hour for each condition, and the number of scans per session (200 functional volumes) was matched across subjects to obtain a similar number of scans in all states. Functional images were acquired on a 3 T S Allegra scanner (Siemens AG, Munich, Germany; Echo Planar Imaging sequence using 32 slices; repetition time = 2460 ms, echo time = 40 ms, field of view = 220 mm, voxel size = 3.45 × 3.45 × 3 mm3, and matrix size = 64 × 64×32). Written informed consent, approval by the Ethics Committee of the Medical School of the University of Liège. For further details on acquisition of this dataset see previous publication.59
Disorders of consciousness
The cohort included 21 healthy controls (8 females; mean age, 45 ± 17 years), and 43 unsedated patients presenting DoC (25 in MCS and 18 in UWS; 12 females; mean age, 47 ± 18 years). Patients in UWS show signs of preserved vigilance, but do not exhibit non-reflex voluntary movements, and are incapable of establishing functional communication. Patients in MCS show more complex behavior indicative of awareness, such as visual pursuit, orientation response to pain, and non-systematic command following; nevertheless, these signs are consistent but may be manifested sporadically. The inclusion criteria for patients were brain damage at least 7 days after the acute brain insult and behavioral diagnosis of MCS or UWS performed through the best of at least five Coma Recovery Scale–Revised (CRS-R) behavioral assessments. The ethic committee of the University Hospital of Liège (Belgium) approved the study, where all data were collected. Written informed consents were obtained from all healthy subjects and the legal representative for DOC patients in accordance with the Declaration of Helsinki. 3T Siemens TIM Trio MRI scanner (Siemens Medical Solutions, Erlangen, Germany) was used to acquire the data: 300 T2*-weighted images were acquired with a gradient-echo echoplanar imaging (EPI) sequence using axial slice orientation and covering the whole brain (32 slices; slice thickness, 3 mm; repetition time, 2000 ms; echo time, 30 ms; voxel size, 3 × 3 × 3 mm; flip angle, 78°; field of view, 192 mm by 192 mm). A structural T1 magnetization-prepared rapid gradient echo (MPRAGE) sequence (120 slices; repetition time, 2300 ms; echo time, 2.47 ms; voxel size, 1.0 × 1.0 × 1.2 mm; flip angle, 9°).60
METHOD DETAILS
fMRI pre-processing
We used FSL tools to extract and average the BOLD signals from all voxels for each participant in each brain state. The FSL pre-processing included a 5 mm spatial smoothing (FWHM), bandpass filtering between 0.01 and 0.1 Hz, and brain extraction (BET), followed by a transformation to a standard space (2 mm MNI brain) and down sampling for a final representation to a 2 mm voxel space.
The next steps were implemented in MATLAB, using in house developed scripts. First, we corrected the data by performing regressions between the displacement parameters, the average signals extracted from the white matter and ventricles, their first derivatives, and the voxel-wise BOLD signals, retaining the residuals for further analysis. In the second step, we applied volume censoring (scrubbing) and discarded subjects who presented significant relative head displacements in more than 20% of the recorded frames, with a criterion for movement significance set as a displacement between consecutive frames exceeding 0.5 mm.61 Finally, we averaged all voxels within each ROI defined in the automated anatomical labeling (AAL) atlas, considering only the 90 cortical and subcortical non-cerebellar brain regions to obtain one BOLD signal per ROIs.62 During pre-processing, 4 subjects were removed from the anesthesia dataset, as well as 9 patients in MCS and 3 patients in UWS.
Structural connectivity
Diffusion tensor imaging (DTI) to diffusion weighted imaging (DWI) recordings from 16 healthy right-handed participants (11 men and 5 women; mean age: 24.75 ± 2.54 years) recruited online at Aarhus University, (Denmark) were considered for the computation of the structural connectome. We used FSL diffusion toodbox (Fdt) with the default parameters to perform the data pre-processing. We used the probtrackx tool in Fdt to provide automatic estimation of crossing fibers within each voxel, which has been shown to significantly improve the tracking sensitivity of non-dominant fiber populations in the human brain. The proportion of fibers passing through voxel that reached voxel (sampling of 5000 streamlines per voxel63) defines the connectivity probability from a seed voxel to another voxel . The connectivity probability from region to region was calculated as the number of sampled fibers in region that connected the two regions normalized by the number of streamlines per voxel (5000) times the amount of voxel in the region . All the voxels in each AAL parcel were seeded (i.e. gray and white matter voxels were considered). The resulting SC matrices were computed as the average across voxels within each ROI in the AAL thresholded at 0.1% (i.e. a minimum of five streamlines) and normalized by the number of voxels in each ROI. Finally, the data were averaged across participants.
QUANTIFICATION AND STATISTICAL ANALYSIS
Computational model
Whole-brain models have been widely used to describe the most important features of empirical brain dynamics. These models are based on the assumption that macroscopic collective brain behavior is an emergent behavior of millions of interacting units, and that this emergent behavior can be modeled and analyzed regardless of the microscale details. One example behavior consists of the transition between asynchronous noisy fluctuations to synchronous oscillations. The simplest dynamical system capable to present both behaviors is the described by a Stuart Landau non-linear oscillator, which is mathematically described by the normal form of a supercritical Hopf bifurcation20:
| (Equation 1) |
where is a complex-valued variable , is the intrinsic frequency of the oscillator. The bifurcation parameter a changes qualitatively the nature of the solutions of the system: if a>0 the system engages in a limit cycle and thus presents self-sustained oscillations (oscillating or supercritical regime), and when a<0 the dynamics decay to a stable fixed point (noisy or subcritical regime).64
The collective dynamics of resting state activity can be modeled by introducing coupling between oscillators. Several previous studies have demonstrated that whole-brain models based on Stuart Landau oscillators ruling the local dynamical behavior coupled by the anatomical structural connectivity are useful to describe static and dynamic features of brain dynamics captured by neuroimaging recordings.20,22,47 The dynamics of region (node i) in the coupled whole-brain system is described in cartesian coordinates as follows:
| (Equation 2) |
Where is an additive Gaussian noise with standard deviation and is a factor that scales the strength of the coupling equally for all the nodes. This whole-brain model has been shown to reproduce important features of brain dynamics observed in different neuroimaging recordings65
Grand average FC fitting procedure
We fitted this whole-brain model to the grand average functional connectivity of each state of consciousness. To this end we applied the same signal processing to all fMRI recordings. The signals were detrended and demeaned before band-pass filtering in the 0.04–0.07 Hz range. This frequency range was chosen because when mapped to the gray matter, this band was shown to contain more reliable and functionally relevant information.21,66 After that, we transformed the filtered time series to z-scores and computed the FC matrix as the matrix of Pearson correlations between the fMRI signals of all pairs of regions of interest (ROIs) in the AAL template. Fisher’s R-to-z transform was applied to the correlation values before averaging over participants within each state of consciousness.
We then computed the Goodness of Fit (GoF) of the fitting between the empirical and simulated grand average FC using the structure similarity index22,67 (SSIM), a metric that balances sensitivity to absolute and relative differences between the FC matrices. Thus, the SSIM can be considered a trade-off between the Euclidean and correlation distances, which are two of the most common metrics used to compare simulated and empirical FC.
We proposed to reduce the complexity of the model by grouping brain regions into well-studied functional networks, known as resting state networks (RSNs).22 We encoded the 90 bifurcation parameters () into six parameters representing the contribution of each RSN to the local dynamics by the following linear combination:
| (Equation 3) |
Where the grouping matrix is 1 in its , entry if the region is in group and zero otherwise (note that groups could be overlapping). Each RSN contributes an independent coefficient to the bifurcation parameter of region , given by . Following our previous studies, we fixed the coupling strength parameters at and optimized the to minimized 1-GoF implementing a genetic algorithm inspired in biological evolution.
The algorithm starts with a generation of 20 sets of parameters (“individuals”) chosen randomly with values close to zero, to then generate a population of outputs with their corresponding GoF. Afterward, a group of individuals is chosen based on this score and is transmitted to the next generation based on three operations: 1) elite selection occurs when an individual of a generation shows an extraordinarily high GoF in comparison to the other individuals, thus this solution is replicated without changes in the next generation; 2) the crossover operator consists of combining two selected parents to obtain a new individual that carries information from each parent to the next generation; 3) the mutation operator changes one selected parent to induce a random alteration in an individual of the next generation. In our implementation, 20% of the new generation was created by elite selection, 60% by crossover of the parents and 20% by mutation. A new population is thus generated (“offspring”) that is used iteratively as the next generation until at least one of the following halting criteria is met: 1) 200 generations are reached (i.e. limit of iterations), 2) the best solution of the population remains constant for 50 generations, 3) the average GoF across the last 50 generation is less than 10 6. Finally, the output of the genetic algorithm contains the simulated FC with the highest GoF, and the optimal coefficients .
In silico perturbation
We simulated a stimulation protocol to induce transitions between reduced states of consciousness toward wakefulness and delineate the perturbational landscape in the latent space. As in previous work,19 all stimulations were systematically applied to pairs of homotopic nodes exploring different strength forcing amplitude. The stimulation corresponds to an additive periodic forcing term incorporated to the equation of the nodes, given by , where is the forcing amplitude and the natural frequency of the nodes. We then varied the forcing amplitude F0 from 0 to 0.2 in order to parametrize the perturbation as a function of the forcing.
Variational autoencoder (VAE) training
We implemented a VAE to encode the FC matrices in a low-dimensional representation. VAE map inputs to probability distributions in latent space, which can be regularized during the training process to produce meaningful outputs after the decoding step, allowing to decode latent space coordinates. The architecture of the implemented VAE (shown in Figure 1) consisted of three parts: the encoder network, the middle variational layer, and the decoder network. The encoder is a deep neural network with rectified linear units (ReLu) as activation functions and two dense layers. This part of the network bottlenecks into the two-dimensional variational layer, with units z1 and z2 spanning the latent space. The encoder network applies a nonlinear transformation to map the FC into Gaussian probability distributions in latent space, and the decoder network mirrors the encoder architecture to produce reconstructed matrices from samples of these distributions.14
Network training consists of error backpropagation via gradient descent to minimize a loss function composed of two terms: a standard reconstruction error term (computed from the units in the output layer of the decoder), and a regularization term computed as the Kullback-Leibler divergence between the distribution in latent space and a standard Gaussian distribution. This last term ensures continuity and completeness in the latent space, i.e. that similar values are decoded into similar outputs, and that those outputs represent meaningful combinations of the encoded inputs.
We generated 15000 FC matrices corresponding to controls, W, N3 and UWS, using the model optimized as described in the previous subsection. We then created 80/20 random splits into training and test sets, using the training set to optimize the VAE parameters. The training procedure consisted of batches with 128 samples and 50 training epochs using an Adam optimizer and the loss function described in the previous paragraph.
STATISTICAL ANALYSES
We applied the Wilcoxon rank-sum method to test the significance on Supplementary material analyses and additionally, we applied the False Discovery Rate (FDR) at the 0.05 level of significance to correct multiple comparisons.68
Supplementary Material
Highlights.
The brain spontaneously self-organizes into a discrete number of global brain states
Level of consciousness refers to a scalar index determined by the behavior of those states
Whole-brain model and deep learning allow algorithmic dimension reduction of brain states
Low-dimensional space reveals an orderly organization of brain states and its transitions
ACKNOWLEDGMENTS
The authors thank participants and their families for their invaluable time and commitment to our study. The authors thank the whole staff from the Radiodiagnostic and Nuclear Medicine departments, University Hospital of Liege, especially Roland Hustinx, Claire Bernard, Jean-Flory Tshibanda, and Nathalie Maquet. Y.S.P. is supported by the European Union’s Horizon 2020 research and innovation program under the Marie Sklodowska-Curie grant 896354. E.T. is supported by PICT-2019–02294 (Agencia I+D+i, Argentina) and ANID/FONDECYT Regular 1220995 (Chile). A.I. is supported by grants from Takeda CW2680521; CONICET; FONCYT- PICT (2017–1818, 2017–1820); ANID/FONDECYT Regular (1210195, 1210176, and 1220995); ANID/FONDAP (15150012); ANID/PIA/ANILLOS ACT210096; and the Multi-Partner Consortium to Expand Dementia Research in Latin America (ReDLat), funded by the National Institutes of Aging of the National Institutes of Health under award number R01AG057234, an Alzheimer’s Association grant (SG-20–725707-ReDLat), the Rainwater Foundation, and the Global Brain Health Institute (GBHI). R.P. is post-doctoral fellow, O.G. is research associate, and S.L. is research director at FRS-FNRS. The study was further supported by the University and University Hospital of Liège; the Belgian National Funds for Scientific Research (FRS-FNRS); the European Union’s Horizon 2020 Framework Programme for Research and Innovation under the Specific Grant Agreement No. 945539 (Human Brain Project SGA3); the FNRS PDR project (T.0134.21); the ERA-Net FLAG-ERA JTC2021 project ModelDXConsciousness (Human Brain Project Partnering Project); the fund Generet; the King Baudouin Foundation; the Télé vie Foundation; the European Space Agency (ESA); and the Belgian Federal Science Policy Office (BELSPO) in the framework of the PRODEX Programme, the Public Utility Foundation “Université Européenne du Travail,” “Fondazione Europea Ricerca Biomedica,” the Bial Foundation, the Mind Science Foundation, the European Commission, the Fondation Léon Fredericq, the Mind-Care foundation, the DOCMA project (EU-H2020-MSCA–RISE–778234), the National Natural Science Foundation of China (Joint Research Project 81471100), and the European Foundation of Biomedical Research FERB Onlus. J.D.S. and E.T. are funded by a grant from STIC-AmSud (project SILIDOC - 21-STIC-11), ECOS-Sud A20M02, and ECOS-Sud U20S01. J.D.S. and G.D. are supported by the ModelDXConsciousness in the framework of the FLAG-ERA JTC 2021—HBP—2021 programme. E.T. is supported by PICT-2019–02294 (Agencia I+D+i, Argentina) and ANID/FONDECYT Regular 1220995 (Chile). The content of the article is solely the responsibility of the authors and does not represent the official views of these institutions.
INCLUSION AND DIVERSITY
We support inclusive, diverse, and equitable conduct of research.
Footnotes
DECLARATION OF INTERESTS
The authors declare no competing interests.
SUPPLEMENTAL INFORMATION
Supplemental information can be found online at https://doi.org/10.1016/j.celrep.2023.112491.
REFERENCES
- 1.Sporns O (2011). The human connectome: a complex network. Ann. N. Y. Acad. Sci. 1224, 109–125. [DOI] [PubMed] [Google Scholar]
- 2.Cole MW, Bassett DS, Power JD, Braver TS, and Petersen SE (2014). Intrinsic and task-evoked network architectures of the human brain. Neuron 83, 238–251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Chialvo DR (2010). Emergent complex neural dynamics. Nat. Phys. 6, 744–750. [Google Scholar]
- 4.Shew WL, and Plenz D (2013). The functional benefits of criticality in the cortex. Neuroscientist 19, 88–100. [DOI] [PubMed] [Google Scholar]
- 5.Tononi G, Edelman GM, and Sporns O (1998). Complexity and coherency: integrating information in the brain. Trends Cogn. Sci. 2, 474–484. [DOI] [PubMed] [Google Scholar]
- 6.Shine JM, Bissett PG, Bell PT, Koyejo O, Balsters JH, Gorgolewski KJ, Moodie CA, and Poldrack RA (2016). The dynamics of functional brain networks: integrated network states during cognitive task performance. Neuron 92, 544–554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Tassi P, and Muzet A (2001). Defining the states of consciousness. Neurosci. Biobehav. Rev. 25, 175–191. [DOI] [PubMed] [Google Scholar]
- 8.Berry RB, Brooks R, Gamaldo CE, Harding SM, Lloyd RM, Marcus CL, and Vaughn BV (2015). AASM | scoring manual version 2.2 the AASM manual for the scoring of sleep and associated events. Rules, terminology and technical specifications. Am. Acad. Sleep Med. 176, 16–31. [Google Scholar]
- 9.Kalmar K, and Giacino JT (2005). The JFK coma recovery scale - revised. Neuropsychol. Rehabil. 15, 454–460. [DOI] [PubMed] [Google Scholar]
- 10.Dawson R, von Fintel N, and Nairn S (2010). Sedation assessment using the Ramsay scale. Emerg. Nurse 18, 18–20. [DOI] [PubMed] [Google Scholar]
- 11.Laureys S (2005). Science and society: death, unconsciousness and the brain. Nat. Rev. Neurosci. 6, 899–909. [DOI] [PubMed] [Google Scholar]
- 12.Steriade M, Timofeev I, and Grenier F (2001). Natural waking and sleep states: a view from inside neocortical neurons. J. Neurophysiol. 85, 1969–1985. [DOI] [PubMed] [Google Scholar]
- 13.Perl YS, Pallavicini C, Ipiña IP, Kringelbach M, Deco G, Laufs H, and Tagliazucchi E (2020). Data augmentation based on dynamical systems for the classification of brain states. Chaos Solit. Fractals 139, 110069. [Google Scholar]
- 14.Perl YS, Bocaccio H, Pérez-Ipiña I, Zamberlán F, Piccinini J, Laufs H, Kringelbach M, Deco G, and Tagliazucchi E (2020). Generative embeddings of brain collective dynamics using variational autoencoders. Phys. Rev. Lett. 125, 238101. [DOI] [PubMed] [Google Scholar]
- 15.Tagliazucchi E, von Wegner F, Morzelewski A, Brodbeck V, Borisov S, Jahnke K, and Laufs H (2013). Large-scale brain functional modularity is reflected in slow electroencephalographic rhythms across the human non-rapid eye movement sleep cycle. Neuroimage 70, 327–339. [DOI] [PubMed] [Google Scholar]
- 16.Boly M, Perlbarg V, Marrelec G, Schabus M, Laureys S, Doyon J, Pélégrini-Issac M, Maquet P, and Benali H (2012). Hierarchical clustering of brain activity during human nonrapid eye movement sleep. Proc. Natl. Acad. Sci. USA 109, 5856–5861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Barttfeld P, Uhrig L, Sitt JD, Sigman M, Jarraya B, and Dehaene S (2015). Signature of consciousness in the dynamics of resting-state brain activity. Proc. Natl. Acad. Sci. USA 112, 887–892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tagliazucchi E, Crossley N, Bullmore ET, and Laufs H (2016). Deep sleep divides the cortex into opposite modes of anatomical–functional coupling. Brain Struct. Funct. 221, 4221–4234. [DOI] [PubMed] [Google Scholar]
- 19.Sanz Perl Y, Pallavicini C, Pérez Ipiña I, Demertzi A, Bonhomme V, Martial C, Panda R, Annen J, Ibañez A, Kringelbach M, et al. (2021). Perturbations in dynamical models of whole-brain activity dissociate between the level and stability of consciousness. PLoS Comput. Biol. 17, e1009139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Deco G, Kringelbach ML, Jirsa VK, and Ritter P (2017). The dynamics of resting fluctuations in the brain: metastability and its dynamical cortical core. Sci. Rep. 7, 3095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Cordes D, Haughton VM, Arfanakis K, Carew JD, Turski PA, Moritz CH, Quigley MA, and Meyerand ME (2001). Frequencies contributing to functional connectivity in the cerebral cortex in “resting-state” data. Am. J. Neuroradiol. 22, 1326–1333. [PMC free article] [PubMed] [Google Scholar]
- 22.Ipiña IP, Kehoe PD, Kringelbach M, Laufs H, Ibañez A, Deco G, Perl YS, and Tagliazucchi E (2020). Modeling regional changes in dynamic stability during sleep and wakefulness. Neuroimage 215, 116833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kingma DP, Salimans T, Jozefowicz R, Chen X, Sutskever I, and Welling M (2016). Improved variational inference with inverse autoregressive flow. Adv. Neural Inf. Process. Syst. 29. [Google Scholar]
- 24.Chen N, Klushyn A, Ferroni F, Bayer J, and van der Smagt P (2020). Learning flat latent manifolds with VAEs. Preprint at arXiv. 10.48550/arXiv.2002.04881. [DOI] [Google Scholar]
- 25.Stevner ABA, Vidaurre D, Cabral J, Rapuano K, Nielsen SFV, Tagliazucchi E, Laufs H, Vuust P, Deco G, Woolrich MW, et al. (2019). Discovery of key whole-brain transitions and dynamics during human wakefulness and non-REM sleep. Nat. Commun. 10, 11035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Rué-Queralt J, Stevner A, Tagliazucchi E, Laufs H, Kringelbach ML, Deco G, and Atasoy S (2021). Decoding brain states on the intrinsic manifold of human brain dynamics across wakefulness and sleep. Commun. Biol. 4, 854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Varley TF, Denny V, Sporns O, and Patania A (2021). Topological analysis of differential effects of ketamine and propofol anaesthesia on brain dynamics. R. Soc. Open Sci. 8, 201971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Sergent C, Corazzol M, Labouret G, Stockart F, Wexler M, King JR, Meyniel F, and Pressnitzer D (2021). Bifurcation in brain dynamics reveals a signature of conscious processing independent of report. Nat. Commun. 12, 11149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Windey B, and Cleeremans A (2015). Consciousness as a graded and an all-or-none phenomenon: a conceptual analysis. Conscious. Cogn. 35, 185–191. [DOI] [PubMed] [Google Scholar]
- 30.Bayne T, and Carter O (2018). Dimensions of consciousness and the psychedelic state. Neurosci. Conscious. 2018, niy008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Barttfeld P, Bekinschtein TA, Salles A, Stamatakis EA, Adapa R, Menon DK, and Sigman M (2015). Factoring the brain signatures of anesthesia concentration and level of arousal across individuals. Neuro-image. Clin. 9, 385–391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Deco G, and Kringelbach ML (2014). Great expectations: using whole-brain computational connectomics for understanding neuropsychiatric disorders. Neuron 84, 892–905. [DOI] [PubMed] [Google Scholar]
- 33.Kringelbach ML, Cruzat J, Cabral J, Knudsen GM, Carhart-Harris R, Whybrow PC, Logothetis NK, and Deco G (2020). Dynamic coupling of whole-brain neuronal and neurotransmitter systems. Proc. Natl. Acad. Sci. USA 117, 9566–9576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Deco G, Cruzat J, Cabral J, Tagliazucchi E, Laufs H, Logothetis NK, and Kringelbach ML (2019). Awakening: predicting external stimulation to force transitions between different brain states. Proc. Natl. Acad. Sci. USA 116, 18088–18097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Murray JD, Demirtasx M, and Anticevic A (2018). Biophysical modeling of large-scale brain dynamics and applications for computational psychiatry. Biol. Psychiatry Cogn. Neurosci. Neuroimaging 3, 777–787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Gollo LL, Roberts JA, and Cocchi L (2017). Mapping how local perturbations influence systems-level brain dynamics. Neuroimage 160, 97–112. [DOI] [PubMed] [Google Scholar]
- 37.Schiff ND, Giacino JT, Kalmar K, Victor JD, Baker K, Gerber M, Fritz B, Eisenberg B, Biondi T, O’Connor J, et al. (2007). Behavioural improvements with thalamic stimulation after severe traumatic brain injury. Nature 448, 600–603. [DOI] [PubMed] [Google Scholar]
- 38.Lemaire JJ, Sontheimer A, Pereira B, Coste J, Rosenberg S, Sarret C, Coll G, Gabrillargues J, Jean B, Gillart T, et al. (2018). Deep brain stimulation in five patients with severe disorders of consciousness. Ann. Clin. Transl. Neurol. 5, 1372–1384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Angelakis E, Liouta E, Andreadis N, Korfias S, Ktonas P, Stranjalis G, and Sakas DE (2014). Transcranial direct current stimulation effects in disorders of consciousness. Arch. Phys. Med. Rehabil. 95, 283–289. [DOI] [PubMed] [Google Scholar]
- 40.Thibaut A, Bruno MA, Ledoux D, Demertzi A, and Laureys S (2014). tDCS in patients with disorders of consciousness. Neurology 82, 1112–1118. [DOI] [PubMed] [Google Scholar]
- 41.Wu M, Yu Y, Luo L, Wu Y, Gao J, Ye X, and Luo B (2019). Efficiency of repetitive transcranial direct current stimulation of the dorsolateral prefrontal cortex in disorders of consciousness: a randomized sham-controlled study. Neural Plast. 2019, 7089543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Zhang Y, Song W, Du J, Huo S, Shan G, and Li R (2017). Transcranial direct current stimulation in patients with prolonged disorders of consciousness: combined behavioral and event-related potential evidence. Front. Neurol. 8, 620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Hermann B, Raimondo F, Hirsch L, Huang Y, Denis-Valente M, Pérez P, Engemann D, Faugeras F, Weiss N, Demeret S, et al. (2020). Combined behavioral and electrophysiological evidence for a direct cortical effect of prefrontal tDCS on disorders of consciousness. Sci. Rep. 10, 14323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Tasserie J Uhrig L, Sitt JD, Manasova D, Dupont M, Dehaene S, Jarraya B Deep brain stimulation of the thalamus restores signatures of consciousness in a non-human primate model. Accept. (Sci. Adv.).8 eabl5547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Kringelbach ML, and Deco G (2020). Brain states and transitions: insights from computational neuroscience. Cell Rep. 32, 108128. [DOI] [PubMed] [Google Scholar]
- 46.Jirsa VK, Proix T, Perdikis D, Woodman MM, Wang H, Gonzalez-Martinez J, Bernard C, Bénar C, Guye M, Chauvel P, and Bartolomei F (2017). The Virtual Epileptic Patient: individualized whole-brain models of epilepsy spread. Neuroimage 145, 377–388. [DOI] [PubMed] [Google Scholar]
- 47.Jobst BM, Hindriks R, Laufs H, Tagliazucchi E, Hahn G, Ponce-Alvarez A, Stevner ABA, Kringelbach ML, and Deco G (2017). Increased stability and breakdown of brain effective connectivity during slow-wave sleep: mechanistic insights from whole-brain computational modelling. Sci. Rep. 7, 14634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Wang Y, Hutchings F, and Kaiser M (2015). Computational modeling of neurostimulation in brain diseases. Prog. Brain Res. 222, 191–228. [DOI] [PubMed] [Google Scholar]
- 49.Breakspear M, Jirsa V, and Deco G (2010). Computational models of the brain: from structure to function. Neuroimage 52, 727–730. [DOI] [PubMed] [Google Scholar]
- 50.Deco G, and Jirsa VK (2012). Ongoing cortical activity at rest: criticality, multistability, and ghost attractors. J. Neurosci. 32, 3366–3375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Deco G, Ponce-Alvarez A, Hagmann P, Romani GL, Mantini D, and Corbetta M (2014). How local excitation–inhibition ratio impacts the whole brain dynamics. J. Neurosci. 34, 7886–7898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Freyer F, Roberts JA, Ritter P, and Breakspear M (2012). A canonical model of multistability and scale-invariance in biological systems. PLoS Comput. Biol. 8, e1002634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Honey CJ, Kötter R, Breakspear M, and Sporns O (2007). Network structure of cerebral cortex shapes functional connectivity on multiple time scales. Proc. Natl. Acad. Sci. USA 104, 10240–10245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Ghosh A, Rho Y, McIntosh AR, Kötter R, and Jirsa VK (2008). Cortical network dynamics with time delays reveals functional connectivity in the resting brain. Cogn. Neurodyn. 2, 115–120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Sanz Perl Y, Escrichs A, Tagliazucchi E, Kringelbach ML, and Deco G (2022). Strength-dependent perturbation of whole-brain model working in different regimes reveals the role of fluctuations in brain dynamics. PLoS Comput. Biol. 18, e1010662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Deco G, Cruzat J, Cabral J, Knudsen GM, Carhart-Harris RL, Whybrow PC, Logothetis NK, and Kringelbach ML (2018). Whole-brain multimodal neuroimaging model using serotonin receptor maps explains non-linear functional effects of LSD. Curr. Biol. 28, 3065–3074.e6. [DOI] [PubMed] [Google Scholar]
- 57.Marcus DS, Harwell J, Olsen T, Hodge M, Glasser MF, Prior F, Jenkinson M, Laumann T, Curtiss SW, and Van Essen DC (2011). Informatics and data mining tools and strategies for the human connectome project. Front. Neuroinform. 5, 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Tagliazucchi E, and Laufs H (2014). Decoding wakefulness levels from typical fMRI resting-state data reveals reliable drifts between wakefulness and sleep. Neuron 82, 695–708. [DOI] [PubMed] [Google Scholar]
- 59.Boveroux P, Vanhaudenhuyse A, Bruno MA, Noirhomme Q, Lauwick S, Luxen A, Degueldre C, Plenevaux A, Schnakers C, Phillips C, et al. (2010). Breakdown of within- and between-network resting state functional magnetic resonance imaging connectivity during propofol-induced loss of consciousness. Anesthesiology 113, 1038–1053. [DOI] [PubMed] [Google Scholar]
- 60.Laureys S, Celesia GG, Cohadon F, Lavrijsen J, León-Carrión J, Sannita WG, Sazbon L, Schmutzhard E, von Wild KR, Zeman A, et al. (2010). Unresponsive wakefulness syndrome: a new name for the vegetative state or apallic syndrome. BMC Med. 8, 68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Power JD, Mitra A, Laumann TO, Snyder AZ, Schlaggar BL, and Petersen SE (2014). Methods to detect, characterize, and remove motion artifact in resting state fMRI. Neuroimage 84, 320–341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Tzourio-Mazoyer N, Landeau B, Papathanassiou D, Crivello F, Etard O, Delcroix N, Mazoyer B, and Joliot M (2002). Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage 15, 273–289. [DOI] [PubMed] [Google Scholar]
- 63.Behrens TEJ, Woolrich MW, Jenkinson M, Johansen-Berg H, Nunes RG, Clare S, Matthews PM, Brady JM, and Smith SM (2003). Characterization and propagation of uncertainty in diffusion-weighted MR imaging. Magn. Reson. Med. 50, 1077–1088. [DOI] [PubMed] [Google Scholar]
- 64.Hansen JY, Shafiei G, Markello RD, Smart K, Cox SML, Nørgaard M, Beliveau V, Wu Y, Gallezot JD, Aumont É, et al. (2022). Mapping neurotransmitter systems to the structural and functional organization of the human neocortex. Nat. Neurosci. 25, 1569–1581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Piccinini J, Ipiñna IP, Laufs H, Kringelbach M, Deco G, Sanz Perl Y, and Tagliazucchi E (2021). Noise-driven multistability vs deterministic chaos in phenomenological semi-empirical models of whole-brain activity. Chaos 31, 023127. [DOI] [PubMed] [Google Scholar]
- 66.Achard S, Salvador R, Whitcher B, Suckling J, and Bullmore E (2006). A resilient, low-frequency, small-world human brain functional network with highly connected association cortical hubs. J. Neurosci. 26, 63–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Wang Z, Bovik AC, Sheikh HR, and Simoncelli EP (2004). Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 13, 600–612. [DOI] [PubMed] [Google Scholar]
- 68.Hochberg Y, and Benjamini Y (1990). More powerful procedures for multiple significance testing. Stat. Med. 9, 811–818. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Sleep dataset is publicly available since the data of publication. The DOI is listed in the key resources table. Data of disorders of Consciousness and anesthesia cannot be shared publicly because contains data and information from a clinical population of patients, and are not publicly available due to constraints imposed by the currently approved ethics protocol, but are available upon request to Comitéd’É thique Hospitalo-Facultaire Universitaire de Liège (https://www.chuliege.be/jcms/c2_16986309/fr/comite-d-ethique-hospitalo-facultaire-universitaire-de-liege/accueil): ethique@chuliege.be.
All original code has been deposited at Zenodo and is publicly available as of the date of publication. DOIs are listed in the key resources table.The software dependencies are MATLAB (2018b); Python (3.6) and Keras.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE.
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
|
| ||
| Deposited data | ||
|
| ||
| Processed fMRI data | University of Liege and University of Kiel | https://doi.org/10.5281/zenodo.7806006 |
|
| ||
| Software and algorithms | ||
|
| ||
| Whole-brain modeling & Variational Autoencoder | Custom software | https://doi.org/10.5281/zenodo.7806006 |
| MATLAB 2020b | MathWorks | https://www.mathworks.com |
| SPM | Wellcome Department of Cognitive Neurology, London, UK | https://www.fil.ion.ucl.ac.uk/spm/ |
| FSL | FMRIB Software Library | https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/ |
| Connectome Workbench | Marcus et al.57 | https://www.humanconnectome.org/software/connectome-workbench |
| Python 3.10.3 | Python | https://www.python.org/ |


