Oscillating neural circuits: Phase, amplitude, and the complex normal distribution

Abstract

Multiple oscillating time series are typically analyzed in the frequency domain, where coherence is usually said to represent the magnitude of the correlation between two signals at a particular frequency. The correlation being referenced is complex-valued and is similar to the real-valued Pearson correlation in some ways but not others. We discuss the dependence among oscillating series in the context of the multivariate complex normal distribution, which plays a role for vectors of complex random variables analogous to the usual multivariate normal distribution for vectors of real-valued random variables. We emphasize special cases that are valuable for the neural data we are interested in and provide new variations on existing results. We then introduce a complex latent variable model for narrowly band-pass-filtered signals at some frequency, and show that the resulting maximum likelihood estimate produces a latent coherence that is equivalent to the magnitude of the complex canonical correlation at the given frequency. We also derive an equivalence between partial coherence and the magnitude of complex partial correlation, at a given frequency. Our theoretical framework leads to interpretable results for an interesting multivariate dataset from the Allen Institute for Brain Science.

1. INTRODUCTION

Oscillations in neural circuits have been observed under a variety of circumstances and have provoked much speculation about their physiological function (Buzsaki & Draguhn, 2004; Fries, 2005). In the past 15 years, the role of oscillations at particular frequencies has been the subject of considerable experimental investigation, including causal manipulation (Cardin etal.,2009).Of particular interest is the intriguing possibility that oscillations facilitate purposeful communication across distinct parts of the brain, such as when an organism must retrieve and hold items from memory or direct its visual attention to a particular location (Miller, Lundqvist & Bastos, 2018; Schmidt et al., 2019). This has led to the idea that alterations of circuit oscillations could indicate brain dysfunction (Mathalon & Sohal, 2015).

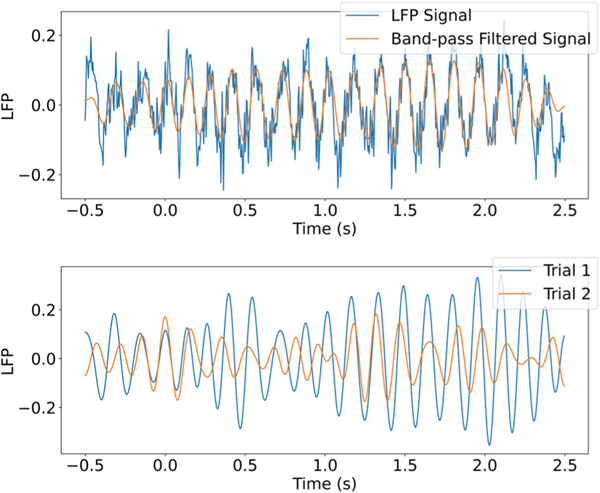
From a statistical perspective, regardless of their mechanistic function, neural oscillations can be considered useful indicators of coordinated activity across brain regions. A short snippet of data, typical of those we have analyzed, is shown in the top panel of Figure 1 together with a band-pass-filtered version. In the bottom panel are band-pass-filtered series for two trials, where at many points in time the amplitudes, phases, or both are different. When series from two electrodes (in different parts of the brain) are considered, the two phases may tend to shift forward or backward together across trials, which indicates coordinated activity. Similarly, there may be trial-to-trial correlation between the amplitudes.

Figure 1:

Three seconds of local field potential (LFP) data filtered at 6.5Hz with a window from 6 to 7Hz. In the top figure, we plot both the raw LFP signal, which consists of a noisy oscillation around 6.5Hz, and the filtered signal, which removes the noise. In the bottom figure, we plot filtered data from the same electrode across two trials. At many points in time, the two trials have different phases or amplitudes.

To quantify this form of association, an obvious question is whether it might be advantageous to consider phase and amplitude together, as defining complex numbers, and model association using multivariate complex distributions. In addition, data such as those in Figure 1 often come from many recordings in each brain region that somehow must be combined. We investigate the properties of the multivariate complex normal distribution with the goal of analyzing interactions among multiple groups of oscillating time series.

A related conceptual concern comes from the standard interpretation of coherence, which is the starting point for much frequency-based analysis of co-dependence. Under the Cramér (or Cramér–Khintchine) representation of a bivariate stationary time series, coherence is usually said to be the magnitude of the time series correlation at a particular frequency (e.g., Shumway & Stoffer, 2017, Section 4.6). The difficulty with this interpretation is that “correlation” here refers to the complex correlation for complex random variables, which is analogous to the Pearson correlation for real-valued variables in certain respects, but not others.

This article reviews and reformulates ideas drawn from the literature and then provides several new results, including a summary of interacting groups of oscillating multivariate time series using a time-domain rendering of latent coherence, which turns out to be the magnitude of a complex-valued canonical correlation. Although we have been motivated by the analysis of neural data, we believe this article will be of general statistical interest as it concerns a basic topic in time series analysis. We also hope it represents a suitable tribute to Nancy Reid, whose work has often aimed to advance statistics through conceptual clarification and consolidation.

2. BACKGROUND AND SUMMARY

We are interested in the covariation of both phase and amplitude in two or more time series. The data we analyze in Section 6 come from experiments during which animals are shown a visual stimulus repeatedly, across many trials, while neural activity is recorded from electrodes inserted into the brain. Repeated measurements across many trials is typical of neurophysiological data, and these repetitions are helpful in dealing with the striking nonstationarity present in neural recordings (see, e.g., Kass et al., 2018). In addition, neurophysiological experiments often collect data from multiple electrodes embedded in multiple brain regions.

From oscillating series such as those in the top panel of Figure 1, the band-pass-filtered version can be obtained by Fourier analytic methods (though it can also be obtained using wavelets). As long as the band in the filtering is sufficiently narrow (surrounding some particular frequency), at any point in time the phase and amplitude of the real-valued, filtered time series can be recovered using the Hilbert transform (see the Appendix) under an assumption of local stationarity (Ombao & Van Bellegem, 2008). A phase and an amplitude define a complex number, and the Hilbert transform converts a real-valued signal into the corresponding complex-valued signal. For a pair of repeatedly observed complex-valued variables, correlation is more complicated than in the real case: covariance becomes complex-valued and there are two forms of linear covariation, called covariance and pseudo-covariance. Complex covariance is defined for two complex-valued random variables $X_1$ and $X_2$ as

$$\mathrm{cov}\left(X_1,X_2\right)=\text{E}\left\{\left(X_1-\text{E}{X}_1\right)\left(\overline{X_2-\text{E}{X}_2}\right)\right\},$$

where $\overline{x}$ is the conjugate of a complex number $x$. Note that $\mathrm{cov}\left(X_1,X_2\right)$ is a complex number. Complex pseudo-covariance is defined as

$$\text{pcov}\left(X_1,X_2\right)=\text{E}\left\{\left(X_1-\text{E}{X}_1\right)\left(X_2-\text{E}{X}_2\right)\right\}.$$

The variance–covariance and pseudo-variance–covariance matrices for a complex random vector $X$ are defined analogously to the case of complex random variables, using the Hermitian and transpose operators, respectively:

$$\mathrm{var}(X)=\text{E}\left\{(X-\text{E}X){(X-\text{E}X)}^H\right\}\text{and}\text{pvar}(X)=\text{E}\left\{(X-\text{E}X){(X-\text{E}X)}^{\top }\right\},$$

where ${(X-\text{E}X)}^H={(\overline{X-\text{E}X})}^{\top }$. When the pseudo-covariance is zero, a complex random vector is called proper.

In addition to complex correlation, dependence between phase angles can be measured through phase-locking value (PLV) (Lachaux et al., 1999) which, as we show in Section 3.2.2, can be viewed as an analogue of correlation for angular random variables. For more than two phases, a recently developed class of models called torus graphs provides a thorough rendering of multivariate phase dependence (Klein et al., 2020). A torus graph is any member of the full exponential family with means and cross-products (interaction terms) on a multidimensional torus, which is the natural home for multivariate circular data because the product of circles is a torus. Thus, torus graphs are probabilistic graphical models and represent an analogue to Gaussian graphical models for circular (angular) data.

Phase coupling is also analyzed using coherence, the magnitude of coherency, which is a frequency-domain measure that has a form resembling correlation in terms of spectral densities and cross-spectral densities. One way to understand how coherence becomes complex correlation at a particular frequency is to consider the result of filtering signals with a complex band-pass filter in a band $\left({\omega }_0-\delta ,{\omega }_0+\delta \right)$ for some small $\delta$. Ombao & Van Bellegem (2008) noted that the resulting narrow-band coherence, which they called “band coherence,” is the correlation between the filtered signals. We can effectively pass to the limit as $\delta \to 0$ to get the infinitesimal version that appears in the Cramér–Khintchine representation, displayed in Section 4.1. In a similar vein, in Section 4.1 we also note that a single-frequency bivariate process with stochastic amplitudes and phases yields coherence as the magnitude of complex correlation.

Coherence has been used to understand conditional dependence relationships between time series. Dahlhaus (2000) studied so-called coherence graphs for real-valued time series and showed how conditional dependence may be inferred from the partial coherence between these signals. Partial coherence arises by inverting and rescaling a matrix of coherency values for $d$ time series, and represents a form of conditional dependence between signals (Ombao & Pinto, 2022). Tugnait (2019a,b) analyzed conditional dependence between signals with arbitrary spectra by observing that the limiting distribution of a certain class of transformations of real-valued time series takes the form of a complex normal distribution.

Our setting, in which we observe multiple signals oscillating at the same frequency, differs from those previously studied in Dahlhaus (2000) and Tugnait (2019a,b) because our signals are oscillating only at a single frequency. In Section 4, we provide a comprehensive overview of how, for our setting, complex correlation and coherency are equivalent when we assume complex normality. Similarly, we show that complex partial correlation and partial coherency are equivalent, and we discuss how these concepts are directly tied to the conditional dependence between the observed oscillating time series. Thus, by modelling band-pass-filtered data with the complex normal distribution, we obtain simple interpretations of estimated correlation and partial correlation matrices in terms of coherence and partial coherence.

Our interest is in recordings from multiple electrodes embedded in several brain regions. To take advantage of the multiple sources of activity observed from each region, we developed a novel complex normal latent variable model in which each of several latent variables represents activity in one of the regions (at a particular point in time). Our goal is to estimate the dependence among these latent variables. We specify the model in Section 5 and apply it to data in Section 6. The data we analyze are local field potentials (LFPs), which are voltage recordings from electrodes inserted into the brain; they are low-pass-filtered (smoothed) and typically down-sampled to 1kHz so that each second of data has 1000 observations. LFPs represent bulk activity near the electrode (roughly within 150–200 μm) involving large numbers of neurons (Buzsáki, Anastassiou & Koch, 2012; Einevoll et al., 2013; Pesaran et al., 2018). Our theoretical results enable us to obtain a simple interpretation of data from the Allen Institute for Brain Science, Seattle, WA. We examined three recordings in each of six regions of the visual cortex in response to a visual stimulus and estimated latent correlation and partial correlation matrices after band-pass-filtering at 6.5Hz to isolate the theta rhythm. There are many large latent correlations of the theta rhythm oscillations between regions (which, as we show, may be considered large values of latent coherence). However, the unique associations, that is, the latent partial correlations, between these regions are modest in size with the exception of the unique associations between AM and PM, as well as between DG and CA1, which exhibit latent partial correlations (latent partial coherence) close to 1.

Although some of the theorems in this article may be unsurprising to experts on the complex normal distribution and frequency-based analysis, they all represent at least novel extensions and reformulations, and several results are entirely new. In Section 3.3.3, we discuss the conditional distribution of the angles given the amplitudes in the polar coordinate representation of the complex normal distribution. Navarro, Frellsen & Turner (2017) showed that the multivariate generalized von Mises (mGvM) distribution can be viewed as a conditional distribution of the 2$d$-dimensional, real-valued multivariate normal distribution when all the amplitudes are equal to 1. Here, we change the setting of this result to the complex normal distribution, generalize the result to arbitrary amplitudes, and show how the conditional distribution changes when certain relevant restrictions are made on the parameters of the complex normal distribution. These results (appearing in Theorems 2 and 3 and Corollary 4) form new characterizations of torus graphs. In Section 4 we provide a general treatment of partial correlation, conditional correlation, and conditional dependence for the complex normal distribution. These results consolidate and reformulate what was previously available in the literature (see Section 4 for specific citations). The new results in Corollary 13 and Theorem 12 show that maximum likelihood estimation in our latent variable model produces estimates that are equivalent to complex-valued versions of canonical correlation. The proofs of the theorems and corollaries we show are provided in the Supplementary Material Section S1.

3. DEPENDENCE OF COMPLEX-VALUED RANDOM VARIABLES

In this section, we first present the data-generating setting we are attempting to model. We observe complex-valued random vectors, and our goal is to measure associations between their entries. After introducing this setting, we mostly ignore the fact that we are dealing with oscillating signals, but we will return to this important point in Section 4 when we study the relationship between coherence, complex correlation, and the complex normal distribution. This important correspondence is the basis for the analysis presented in this paper.

We first review various measures of pairwise association between complex-valued random variables, including complex correlation, PLV, and amplitude correlation. We then discuss two multivariate models for association between complex-valued random vectors: the complex normal distribution, which is based on the linear association between complex random vectors, and the torus graph distribution, which is a multivariate model for phase. In Section 3.3.3, we show some new results that describe how the torus graph distribution arises by conditioning angles on amplitudes in the complex normal distribution.

3.1. Setting: Repeated Observations of Oscillating Signals

In this article, we assume we observe $d$ time series that are oscillating at some frequency ${\omega }_0$ on each of many repeated trials. We can model the data as a $d$-dimensional random vector $\mathbf{Y}(t)$, and assume these vectors are i.i.d. across trials. Throughout most of this article, we omit the trial number from our notation. We can first apply a local band-pass filter to the raw vector $\mathbf{Y}(t)$ around the frequency ${\omega }_0$ at time $t$, and then apply the Hilbert transform to obtain a complex-valued random vector $\mathbf{X}(t)$ having components that are functions of the phases and amplitudes of the oscillations: $X_i(t)=R_i(t)\exp \left\{\iota {\text{Θ}}_i(t)\right\}$ for $R_i(t)\in (0,\infty )$ and ${\text{Θ}}_i(t)\in [-\pi ,\pi )$ for components $i\in [d]$. Here and everywhere else in the article, $[d]=\{i\in \mathbb{N}:1\le i\le d\}$, where $𝜄$ represents the imaginary unit.

3.2. Pairwise Association Between Complex-Valued Random Variables

3.2.1. Complex Correlation

Linear association between complex-valued random variables is measured by complex correlation. We defined both covariance and pseudo-covariance between complex random variables and random vectors in Section 2. The corresponding complex correlations are

$$\text{corr}\left(X_1,X_2\right)=\frac{\mathrm{cov}\left(X_1,X_2\right)}{\sqrt{\mathrm{var}\left(X_1\right)\mathrm{var}\left(X_2\right)}}\text{and}\text{pcorr}\left(X_1,X_2\right)=\frac{\text{pcov}\left(X_1,X_2\right)}{\sqrt{\mathrm{var}\left(X_1\right)\mathrm{var}\left(X_2\right)}}.$$

3.2.2. Angular Association: Phase-Locking Value

We can study the association between two phases by considering their representations as unit-length complex random variables $X_1=e^{i{\text{Θ}}_1}$ and $X_2=e^{ı{\text{Θ}}_2}$. The set of such pairs is the product of two circles, a two-dimensional torus.

The strength of the association between two angular random variables ${\text{Θ}}_1$, ${\text{Θ}}_2$ can be measured using PLV (Lachaux et al., 1999). When we have repeated observations ${\theta }_1^n$, ${\theta }_2^n$ across $N$ trials of angular observations, then we can define

$$\text{PLV}=\frac{1}{N}\left|\sum _{n=1}^N\exp \left\{l\left({\theta }_i^n-{\theta }_j^n\right)\right\}\right|,$$

which is widely used to measure the angular dependence between oscillating signals (Lepage & Vijayan, 2017).

To better understand PLV, we provide a theoretical analysis of the components of phase-based association. Suppose that $c_i=\text{E}\left\{\cos \left({\text{Θ}}_i\right)\right\}$ and $s_i=\text{E}\left\{\sin \left({\text{Θ}}_i\right)\right\}$ for $i\in \{1,2\}$. The first moment of $X_i$ is

$$\text{E}\left(X_i\right)=\text{E}\left\{\cos \left({\text{Θ}}_i\right)\right\}+ı\text{E}\left\{\sin \left({\text{Θ}}_i\right)\right\}=c_i+ıs_i=r_i{e}^{ı{\theta }_i},$$

where $r_i={\left(c_i^2+s_i^2\right)}^{1/2}$ and ${\theta }_i$ is the angle of the vector ($c_i$, $s_i$) relative to (1,0) for $i\in \{1,2\}$. The complex covariance of $X_1$ and $X_2$ is

$$\mathrm{cov}\left(X_1,X_2\right)=\text{E}\left(X_1{\overline{X}}_2\right)-\text{E}\left(X_1\right)\text{E}\left({\overline{X}}_2\right)=\text{E}\left\{e^{ı\left({\text{Θ}}_1-{\text{Θ}}_2\right)}\right\}-r_1{r}_2{e}^{ı\left({\theta }_1-{\theta }_2\right)},$$

where the pseudo-covariance of $X_1$ and $X_2$ is

$$\text{pcov}\left(X_1,X_2\right)=\text{E}\left(X_1{X}_2\right)-\text{E}\left(X_1\right)\text{E}\left(X_2\right)=\text{E}\left\{e^{ı\left({\text{Θ}}_1-{\text{Θ}}_2\right)}\right\}-r_1{r}_2{e}^{ı\left({\theta }_1+{\theta }_2\right)}.$$

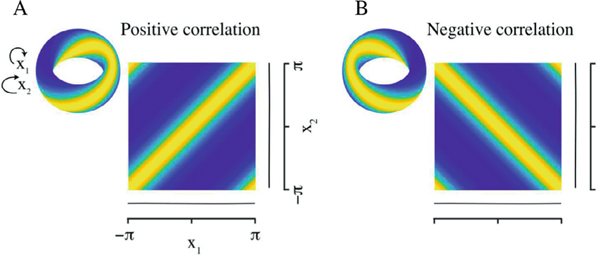
Covariance and pseudo-covariance, respectively, represent rotational and reflectional association between $X_1$ and $X_2$. Rotational covariance measures clockwise–clockwise association, and reflectional covariance measures clockwise–anticlockwise association. Both types of association are shown in Figure 2. The amplitude of the rotational covariance controls the width of the yellow high-probability band, and the phase of this complex number specifies the shift of this band, which is seen along the diagonal of the Cartesian plane; the band shifts in direction from bottom-right toward top-left (Figure 2a). The same notion applies to the reflectional covariance magnitude, but the band is positioned on the other diagonal (Figure 2b). The presence of both types of covariation is possible and can lead to concentrated marginals. However, in our experience with phases extracted from LFP neural data, we have almost always observed exclusively rotational dependence. In addition, the marginals are close to uniform. If $r_1=r_2=0$ (e.g., if the ${\text{Θ}}_i$ are uniform), then

$$\mathrm{cov}\left(X_1,X_2\right)=\text{E}\left\{e^{l\left({\text{Θ}}_1-{\text{Θ}}_2\right)}\right\}\text{and}\text{corr}\left(X_1,X_2\right)=\text{E}\left\{e^{l\left({\text{Θ}}_1-{\text{Θ}}_2\right)}\right\}.$$

The quantity $E\left\{e^{l\left({\text{Θ}}_1-{\text{Θ}}_2\right)}\right\}$ is the theoretical counterpart of PLV. Thus, in the absence of reflectional covariation, if $r_1=r_2=0$, then $E\left\{e^{l\left({\text{Θ}}_1-{\text{Θ}}_2\right)}\right\}$ is the analogue of Pearson correlation for angular random variables.

Figure 2:

The torus is the natural domain for a pair of circular random variables. Illustration of both types of circular covariance in a torus graph bivariate density, with uniform marginal densities, plotted side by side on a two-dimensional torus and a Cartesian plane. (a) Positive rotational dependence. (b) Negative reflectional dependence. The figure has been adapted from a figure in Klein et al. (2020).

3.2.3. Amplitude Correlation

For two amplitudes $R_i$, $R_j\in (0,\infty )$, the simplest way to characterize amplitude correlation is through the ordinary Pearson correlation of real-valued random variables $\text{corr}\left(R_i,R_j\right)$. Other approaches involve calculating the correlation between the log of the amplitudes or between the square of the amplitudes (Nolte et al., 2020).

3.3. Multivariate Models

3.3.1. The Complex Normal Distribution

A complex random vector $X\in {ℂ}^d$ is said to be complex normal (CN) if its real and imaginary parts are jointly multivariate normal (Andersen et al., 1995). Suppose that $(\Re \mathfrak{e}X,\Im \mathfrak{m}X)\sim 𝓝(\mu ,\text{Σ})$, where

$$\mu =\left(\begin{array}{c}{\mu }_1\\ {\mu }_2\end{array}\right)\text{and}\text{Σ}=\left(\begin{array}{cc}{\text{Σ}}_{11}& {\text{Σ}}_{12}\\ {\text{Σ}}_{12}^{\top }& {\text{Σ}}_{22}\end{array}\right),$$

so that ${\mu }_1=\text{E}(\Re \mathfrak{e}X)$, ${\mu }_2=\text{E}(\Im \mathfrak{m}X)$, ${\text{Σ}}_{11}=\mathrm{var}(\Re \mathfrak{e}X)$, ${\text{Σ}}_{22}=\mathrm{var}(\Im \mathfrak{m}X)$, and ${\text{Σ}}_{12}=\mathrm{cov}(\Re \mathfrak{e}X,\Im \mathfrak{m}X)$. Then

$$m={\mu }_1+ı{\mu }_2,\text{Γ}=\left({\text{Σ}}_{11}+{\text{Σ}}_{22}\right)+ı\left({\text{Σ}}_{12}-{\text{Σ}}_{12}^{\top }\right),\text{and}C=\left({\text{Σ}}_{11}-{\text{Σ}}_{22}\right)+ı\left({\text{Σ}}_{12}+{\text{Σ}}_{12}^{\top }\right),$$

giving a bijection between ($m$, $\text{Γ}$, $C$) and ($\mu$, $\text{Σ}$). Thus, the complex normal distribution is well defined by the parameter set ($m$, $\text{Γ}$, $C$). We denote the distribution by $X\sim 𝓒𝓝(m,\text{Γ},C)$. Recall that the distribution of $X$ is said to be proper if the pseudo-covariance matrix $C$ is zero. Further, $X$ is circularly symmetric, meaning component-wise circularly symmetric so that its pdf satisfies $p(X)=p\left(e^{l\alpha }X\right)$ for all $\alpha \in ℝ$ if and only if $X$ is proper and has mean zero (Adali, Schreier & Scharf, 2011).

Circularly symmetric, proper, and restriction-less CN distributions form full regular exponential families. This ensures that the maximum likelihood estimator, which involves firstand second-order moment statistics, is sufficient. In addition, these families form probabilistic graphical models so that conditional independence is easily characterized. We return to this in Theorem 8 and Corollary 9. We provide an abbreviated version of this theorem here; for full details, see the Supplementary Material Section S1.

Theorem 1.

Each of the following families forms a full and regular exponential family: (i) the family of CN distributions represented by $𝓒𝓝(\mu ,\text{Γ},C)$; (ii) the family of proper CN distributions $𝓒𝓝(\mu ,\text{Γ},0)$; and (iii) the family of circularly symmetric CN distributions $𝓒𝓝(0,\text{Γ},0)$.

3.3.2. Torus Graphs

Multivariate models for angular random variables are most naturally defined on the torus rather than on Euclidean space. Such a model is given in Klein et al. (2020). Here, we briefly review its construction.

To define an exponential family on a torus with a given mean and covariance structure, first- and second-order sufficient statistics are needed. Using two-dimensional rectangular coordinates (involving cosines and sines), the first-order sufficient statistics are $U_1=\left(\cos {\text{Θ}}_1,\sin {\text{Θ}}_1\right)$ and $U_2=\left(\cos {\text{Θ}}_2,\sin {\text{Θ}}_2\right)$. Second-order behaviour is summarized by

$$U_1{U}_2^{\top }=\left(\begin{array}{cc}\cos {\text{Θ}}_1\cos {\text{Θ}}_2& \cos {\text{Θ}}_1\sin {\text{Θ}}_2\\ \sin {\text{Θ}}_1\cos {\text{Θ}}_2& \sin {\text{Θ}}_1\sin {\text{Θ}}_2\end{array}\right).$$

We can then write a natural exponential family density for $\theta =\left({\theta }_1,{\theta }_2\right)$ with a canonical parameter $\eta$ consisting of ${\eta }_i\in {ℝ}^2$ and ${\eta }_{ij}\in {ℝ}^4$ for $i$, $j\in \{1,2\}$ as

$$p(\theta ;\eta )\propto \exp \left\{{\eta }_1^{\top }\left(\begin{array}{c}\cos {\theta }_1\\ \sin {\theta }_1\end{array}\right)+{\eta }_2^{\top }\left(\begin{array}{c}\cos {\theta }_2\\ \sin {\theta }_2\end{array}\right)+{\eta }_{12}^{\top }\left(\begin{array}{c}\cos {\theta }_1\cos {\theta }_2\\ \cos {\theta }_1\sin {\theta }_2\\ \sin {\theta }_1\cos {\theta }_2\\ \sin {\theta }_1\sin {\theta }_2\end{array}\right)\right\},0\le {\theta }_1,{\theta }_2\le 2\pi .$$ (1)

For $\theta =\left({\theta }_1,\dots ,{\theta }_d\right)$, (1) extends to an exponential family on a $d$-dimensional torus as

$$p(\theta ;\eta )\propto \exp \left\{\sum _{j=1}^d{\eta }_j^{\top }\left(\begin{array}{c}\cos {\theta }_j\\ \sin {\theta }_j\end{array}\right)+\sum _{i<j}{\eta }_{ij}^{\top }\left(\begin{array}{c}\cos {\theta }_i\cos {\theta }_j\\ \cos {\theta }_i\sin {\theta }_j\\ \sin {\theta }_i\cos {\theta }_j\\ \sin {\theta }_i\sin {\theta }_j\end{array}\right)\right\},0\le {\theta }_i\le 2\pi .$$ (2)

Based on simple trigonometric identities, Klein et al. (2020) reparameterized this family into a more interpretable form

$$p(\theta ;\eta (\varphi ))\propto \exp \left\{\sum _{i=1}^d{\varphi }_i^{\top }\left(\begin{array}{c}\cos {\theta }_i\\ \sin {\theta }_i\end{array}\right)+\sum _{i<j}{\varphi }_{ij}^{\top }\left(\begin{array}{c}\cos \left({\theta }_i-{\theta }_j\right)\\ \sin \left({\theta }_i-{\theta }_j\right)\\ \cos \left({\theta }_i+{\theta }_j\right)\\ \sin \left({\theta }_i+{\theta }_j\right)\end{array}\right)\right\},$$ (3)

which uses the first- and second-order statistics seen in the definitions of complex covariance. Klein et al. (2020) then defined a $d$-dimensional torus graph (TG) to be any member of the family of distributions specified by (2) or (3). If $\text{Θ}$ is distributed according to $p(\theta ;\eta )$, then we say that $\text{Θ}\sim 𝓣𝓖(\eta )$; likewise, if $\text{Θ}$ is distributed according to $p(\theta ;\eta (\varphi ))$, then we say that $\text{Θ}\sim 𝓣𝓖(\eta (\varphi ))$.

Because torus graphs form exponential families, a pair of random variables $X_i$ and $X_j$ will be conditionally independent given all other variables if and only if the four elements in the pairwise interaction parameter ${\varphi }_{ij}$ are zero. Thus, torus graphs define probabilistic graphical models.

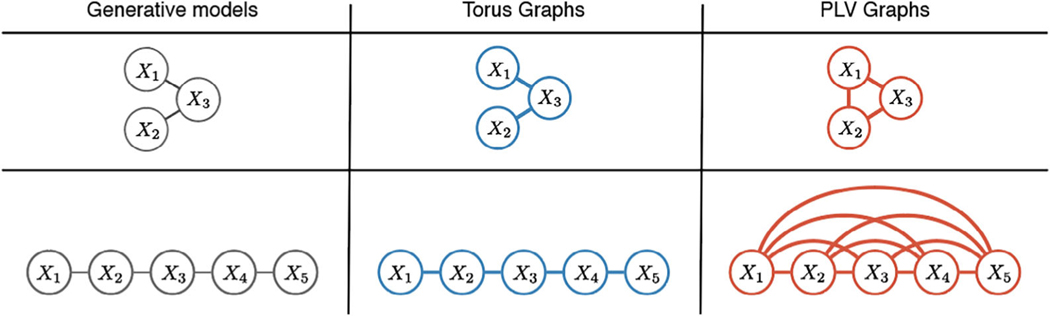
Torus graphs can uncover conditional dependence relationships, meaning pairwise dependence edges that are still present after conditioning on the rest of the random variables in the model. Conditional dependence is obscured with simple correlation-type measures such as PLV because for each edge, they consider only two random variables (see Figure 3, which displays a conditional independence graph from Klein et al. (2020)).

Figure 3:

Torus graphs can recover conditional dependence graphs when PLV fails in simulated data; see Klein et al. (2020) for details. The figure has been adapted from one in Klein et al. (2020).

There are three parameter groups in (3): marginal concentrations, rotational covariance, and reflectional covariance. Klein et al. (2020) showed that the submodel with only rotational covariance parameters (which corresponds to a proper distribution when the statistics $U_1$ and $U_2$ are considered to be complex variables) does a good job of fitting phase angles extracted from neural LFP data. In addition, they described how several alternative families of distributions can be seen as special cases of torus graphs. They then applied their torus graph model to characterize a network graph of interactions among recordings from four brain regions during a memory task.

Although torus graphs provide interesting exponential families that could have been defined long ago, they would have been irrelevant to data analysis before recent practical developments used by Klein et al. (2020) to estimate the parameters of the model.

3.3.3. Characterization of Torus Graphs Using the Complex Normal Distribution

We consider the polar coordinate representation of a random vector with a complex normal distribution and prove that the conditional distribution of the phases, given the amplitudes, form a torus graph. We provide a general statement and then offer additional theorems in the proper and circularly symmetric cases.

Suppose that $R_i\in [0,\infty )$ and ${\text{Θ}}_i\in [-\pi ,\pi )$ are the amplitude and phase of $X_i$ for $i\in [d]$. In other words, ($R_i$, ${\text{Θ}}_i$) is the polar coordinate representation of $X_i$. We consider the conditional distribution of the phases given the amplitudes. Under certain parameter restrictions on a complex normal distribution, this conditional distribution forms a torus graph.

Theorem 2.

Let $X\in {ℂ}^d$ be a complex normal random vector such that $(\Re \mathfrak{e}X,\Im \mathfrak{m}X)\sim 𝓝(\mu ,\text{Σ})$. Let $\text{Ω}={\text{Σ}}^{-1}$ be the inverse covariance matrix. If ${\text{Ω}}_{ii}={\text{Ω}}_{i+d,i+d}$ and ${\text{Ω}}_{i,i+d}=0$ for $i\in [d]$, then $\text{Θ}\mid \{R=r\}\sim 𝓣𝓖(\eta )$, where ${\eta }_i=r_i\left({(\text{Ω}\mu )}_i,{(\text{Ω}\mu )}_{i+d}\right)$ and ${\eta }_{ij}=-r_i{r}_j({\text{Ω}}_{i,j},{\text{Ω}}_{i,j+d},{\text{Ω}}_{i+d,j},{\text{Ω}}_{i+d,j+d})/2$ for $i$, $j\in [d]$.

In Theorem 2, the components of the conditioning vector $r$ appear as multipliers in the natural parameters but the graph is the same for every vector $r$.

There exists another distribution in the literature, known as the mGvM distribution, which is a more general version of the TG distribution that includes all second-moment terms (Navarro, Frellsen & Turner, 2017). Navarro et al. showed that, given a $2d$-dimensional normal distribution analogous to the complex normal distribution, $\text{Θ}\mid \{R=1\}$ is a mGvM distribution without requiring any restrictions on the parameters of the original normal distribution. In| the Supplementary Material Section S1, we generalize this result for any conditional distribution $\text{Θ}\mid \{R=r\}$ and then leverage it to prove Theorem 2 (see the Supplementary Material Section S1.2).

We can obtain a more precise characterization of the conditional distribution under the parameter restrictions $C=0$ and $m=0$.

Theorem 3.

If $X\sim 𝓒𝓝(m,\text{Γ},0)$, so that the complex normal distribution of $X$ is proper, then $\text{Θ}\mid \{R=r\}\sim 𝓣C(\eta (\varphi ))$ as in (3), where ${\varphi }_{ij,3}={\varphi }_{ij,4}=0$ and ${\varphi }_{ij,k}$ denotes the $k\text{th}$ component of ${\varphi }_{ij}$.

Corollary 4.

If $X\sim 𝓒𝓝(0,\text{Γ},0)$, so that the complex normal distribution of $X$ is circularly symmetric, then $\text{Θ}\mid \{R=r\}\sim 𝓣𝓖(\eta (\varphi ))$ with the same restrictions as in Theorem 3 and with the additional restriction that ${\varphi }_i=0$ for all $i\in [d]$.

These theorems say that when the complex normal distribution is proper, the resulting torus graph family has only rotational dependence. The absence of reflectional dependence is intuitive from the definition in Section 3.3.2 of reflectional covariance as pseudo-covariance. Under circular symmetry, because ${\varphi }_i=0$, the conditional distribution ${\text{Θ}}_i\mid \{R=r\}$ is uniform over $[0,2\pi )$ and, additionally, ${\text{Θ}}_i$ is marginally uniform. We repeat that the combination of uniformity and| only rotational dependence is a particularly important special case, partly because this is the case in which PLV becomes a circular analogue to Pearson correlation. From a theoretical perspective, according to an argument given by Picinbono (1994), stationary band-pass-filtered signals with sufficiently narrow bands are proper. In the context of the particular neural data application reported here, we provide empirical evidence for circularity in Figure S2, which shows that the sample covariance matrix has much larger entries than the sample pseudo-covariance matrix.

4. COHERENCY AND THE COMPLEX NORMAL DISTRIBUTION

Assume we have a $d$-dimensional time series for which every dimension contains an oscillation at a given frequency. As discussed previously, these oscillations can be extracted by band-pass-filtering. Spectral dependence and coherency were analyzed using the complex normal distribution by Tugnait (2019a,b), who considered a more general setting in which the spectrum of the signals may be distributed across numerous frequencies. However, when band-pass-filtered signals all oscillate at the same frequency, we get simpler and more interpretable results, which we leverage using our latent variable model in Section 5.

The key to our approach is a well-known result that coherency is a form of complex correlation for stationary signals oscillating at a particular frequency (Ombao & Van Bellegem, 2008). For single-frequency signals, it further turns out that partial coherency, which is used to study conditional dependence among time series, is equivalent to partial correlation (Dahlhaus, 2000; Ombao & Pinto, 2022). For the complex normal distribution, we provide a systematic study of complex conditional correlation, complex partial correlation, and conditional independence. We also review the relationship between complex correlation and other measures of pairwise dependence.

4.1. Coherency and Pairwise Complex Correlation

Suppose we have stationary signals $X_1(t)$ and $X_2(t)$ on $t\in [0,1]$, which may be complex-valued. Assume they have auto-covariance functions ${\text{Σ}}_{ii}(t)=\mathrm{cov}\left\{X_i\left(t_0+t\right),X_i\left(t_0\right)\right\}$ for $i\in \{1,2\}$, and a cross-covariance function ${\text{Σ}}_{12}(t)=\mathrm{cov}\left\{X_1\left(t_0+t\right),X_2(t)\right\}$. These definitions do not depend on $t_0$ because of stationarity. For $\omega \in [-0.5,0.5]$, the spectrum and cross-spectrum of the signals are

$$f_{ii}(\omega )={\int }_0^1{\text{Σ}}_{ii}(t)e^{-12\pi \omega t}dt\text{and}{f}_{12}(\omega )={\int }_0^1{\text{Σ}}_{12}(t)e^{-l2\pi \omega t}dt,$$

and the coherency is

$${\tau }_{12}(\omega )=\frac{f_{12}(\omega )}{\sqrt{f_{11}(\omega )f_{22}(\omega )}}.$$

The coherency is complex-valued. Coherence is the magnitude of the coherency. The Cramér–Khintchine decomposition (see Ch. 3 of Brémaud, 2014) is

$$\left(\begin{array}{c}{X}_1(t)\\ X_2(t)\end{array}\right)={\int }_{-0.5}^{0.5}\exp (ı2\pi \omega t)d\left(\begin{array}{c}{Y}_1(\omega )\\ Y_2(\omega )\end{array}\right),$$

where ${\left(Y_1(\omega ),Y_2(\omega )\right)}^{\top }$ is a bivariate orthogonal-increment random process. In this case, the coherency between $X_1$ and $X_2$ at the frequency ${\omega }_0$ is often considered as the complex-valued correlation coefficient between the infinitesimal increments of $Y_1$ and $Y_2$ at ${\omega }_0$, which is to say

$${\tau }_{12}\left({\omega }_0\right)=\text{corr}\left\{d{Y}_1\left({\omega }_0\right),d{Y}_2\left({\omega }_0\right)\right\}.$$

A quick way to see that this characterization makes sense is to consider two time series oscillating at a single frequency ${\omega }_0$, i.e.,

$$X_1(t)=R_1\exp \left\{\iota \left({\text{Θ}}_1+2\pi {\omega }_{0}t\right)\right\}\text{and}{X}_2(t)=R_2\exp \left\{l\left({\text{Θ}}_2+2\pi {\omega }_{0}t\right)\right\},$$

where $R_i\in [0,\infty )$ and ${\text{Θ}}_i\in [-\pi ,\pi )$ are random variables, which we think of as representing the trial-specific amplitude and phase of $X_i$, respectively, for $i\in \{1,2\}$. Then the auto-covariance and cross-covariance kernels are ${\text{Σ}}_{ii}(t)=\mathrm{var}\left(R_i{e}^{\iota {\text{Θ}}_i}\right)e^{ı2\pi {\omega }_{0}t}$ and ${\text{Σ}}_{12}(t)=\mathrm{cov}\left(R_1{e}^{\iota {\text{Θ}}_1},R_2{e}^{\iota {\text{Θ}}_2}\right)e^{\iota 2\pi {\omega }_{0}t}$. The spectrum and cross-spectrum at the frequency ${\omega }_0$ are

$$f_{kk}\left({\omega }_0\right)={\int }_0^1\mathrm{var}\left(R_i{e}^{\ell {\text{Θ}}_i}\right)e^{ı2\pi {\omega }_{0}t}{e}^{-12\pi {\omega }_{0}t}dt=\mathrm{var}\left(R_i{e}^{ı{\text{Θ}}_i}\right),k\in \{1,2\}$$ (4)

and

$$f_{12}\left({\omega }_0\right)={\int }_0^1\mathrm{cov}\left(R_1{e}^{\iota {\text{Θ}}_1},R_2{e}^{\iota {\text{Θ}}_2}\right)e^{ı2\pi {\omega }_{0}t}{e}^{-l2\pi {\omega }_{0}t}dt=\mathrm{cov}\left(R_1{e}^{\iota {\text{Θ}}_1},R_2{e}^{\iota {\text{Θ}}_2}\right),$$ (5)

respectively. In this case, the coherency is the complex-valued correlation between $X_1(t)$ and $X_2(t)$ for every $t$:

$${\tau }_{12}\left({\omega }_0\right)=\frac{f_{12}\left({\omega }_0\right)}{\sqrt{f_{11}\left({\omega }_0\right)f_{22}\left({\omega }_0\right)}}=\text{corr}\left(R_1{e}^{\iota {\text{Θ}}_1},R_2{e}^{\iota {\text{Θ}}_2}\right)=\text{corr}\left\{X_1(t),X_2(t)\right\}.$$

As a generalization of the single-frequency case, if a pair of signals are band-pass-filtered over a small frequency band, it is possible to define “band coherency” over a narrow band of frequencies. In this case, the band coherency of the filtered signals is equal to the complex correlation of the filtered signals (Ombao & Van Bellegem, 2008).

4.2. Partial Correlation, Conditional Correlation, and Conditional Independence in the Complex Normal Distribution

In the case of real-valued random variables, conditional correlation and partial correlation have been studied extensively (Baba, Shibata & Sibuya, 2004). For such real-valued random variables, conditional correlation and partial correlation are distinct quantities, and conditional dependence between random variables need not imply that either quantity is nonzero. However, real random variables that are jointly normal have the following special properties: (i) conditional correlation and partial correlation are equal, and (ii) zero conditional correlation (or partial correlation) is equivalent to conditional independence.

In the complex case, the relationship between these quantities has been partially studied in Tugnait (2019a,b) and Andersen et al. (1995). Andersen et al. (1995) define conditional covariance for the proper complex normal distribution and show how it is related to various entries in the complex precision matrix. They further relate conditional dependence to conditional covariation for the proper complex normal distribution. Tugnait (2019a,b) discusses how to assess conditional dependence for proper and improper complex normal distributions.

In this section, we define partial correlation for complex random vectors in a manner analogous to the real case. We describe the differences between partial correlation and conditional correlation for complex random variables, and we provide results relating partial correlation and conditional independence, even in the improper complex normal case.

In what follows, assume we have some complex-valued random vector $X\in {ℂ}^d$ with finite first and second moments. For any subset $𝓘\subset [d]$, let $X_{𝓘}$ denote the random vector given by the elements of $X$ whose indices are in $𝓘$ (in order). Let ${\tilde{X}}_{𝓘}\in {ℂ}^{2|𝓘|}$ be the concatenation of $X_{𝓘}$ and its conjugate, i.e., ${\tilde{X}}_{𝓘}=\left(X_{𝓘},{\overline{X}}_{𝓘}\right)$. Let $𝓛\left({\tilde{X}}_{𝓘}\right)=\left\{\alpha +{\beta }^H{\tilde{X}}_{𝓘}:\alpha \in ℂ,\beta \in {ℂ}^{2|𝓘|}\right\}$ be the linear space spanned by ${\tilde{X}}_{𝓘}$ and, for every $i\in [d]$, let ${\text{proj}}_{𝓛\left({\tilde{X}}_{𝓘}\right)}\left(X_i\right)={\text{argmin}}_{Y\in 𝓛\left({\tilde{X}}_{𝓘}\right)}\text{E}\{{\left(Y-X_i\right)}^H(Y-X_i)\}$ be the projection of $X_i$ onto that space.

Definition 5.

For $i$, $j\in [d]$, the partial correlation between $X_i$ and $X_j$ is

$$\rho \left(X_i,X_j\mid X_{[d]\setminus \{i,j\}}\right)=\text{corr}\left\{X_i-{\text{proj}}_{𝓛\left({\tilde{X}}_{[d]\setminus i,j\}}\right)}\left(X_i\right),X_j-{\text{proj}}_{𝓛({\tilde{X}}_{[d]\setminus \{i,j\}}}\left(X_j\right)\right\}$$

and the partial pseudo-correlation between $X_i$ and $X_j$ is

$$\overline{\rho }\left(X_i,X_j\mid X_{[d]\setminus \{i,j\}}\right)=\text{pcorr}\left\{X_i-{\text{proj}}_{𝓛\left({\tilde{X}}_{[d\setminus i,j)}\right)}\left(X_i\right),X_j-{\text{proj}}_{𝓛({\tilde{X}}_{[d\setminus i,j)}}\left(X_j\right)\right\}.$$

The conditional correlation is

$$\text{corr}\left(X_i,X_j\mid X_{[d]\setminus \{i,j\}}\right)=\frac{\mathrm{cov}\left(X_i,X_j\mid X_{[d]\setminus \{i,j\}}\right)}{\sqrt{\mathrm{var}\left(X_i\mid X_{[d]\setminus \{i,j\}}\right)\mathrm{var}\left(X_j\mid X_{[d]\setminus \{i,j\}}\right)}}.$$

The conditional pseudo-correlation is defined analogously by replacing cov with pcov.

We start by stating a correspondence between partial correlation and entries in a transformed precision matrix. The results in this section are proven in the Supplementary Material Section S1.

Theorem 6.

For any complex-valued random vector $X$, let $\widetilde{\text{Γ}}=\mathrm{var}(\tilde{X})$. Denote by diag($A$) the diagonal matrix, with diagonal entries the same as $A$. Let

$$P=\text{diag}{\left({\widetilde{\text{Γ}}}^{-1}\right)}^{-1/2}{\widetilde{\text{Γ}}}^{-1}\text{diag}{\left({\widetilde{\text{Γ}}}^{-1}\right)}^{-1/2}.$$

Then $\rho \left(X_i,X_j\mid X_{[d]\setminus \{i,j\}}\right)=P_{i,j}$ and $\overline{\rho }\left(X_i,X_j\mid X_{[d]\setminus \{i,j\}}\right)=P_{i,j+d}$.

Although conditional correlation and partial correlation may be different in general (Baba, Shibata & Sibuya, 2004), they coincide in the complex normal case.

Theorem 7.

If $X\sim 𝓒𝓝(m,\text{Γ},C)$, then, for $i$, $j\in [d]$

$$\rho \left(X_i,X_j\mid X_{[d]\setminus \{i,j\}}\right)=\text{corr}\left(X_i,X_j\mid X_{[d]\setminus \{i,j\}}\right)$$

and

$$\overline{\rho }\left(X_i,X_j\mid X_{[d]\setminus \{i,j\}}\right)=\text{pcorr}\left(X_i,X_j\mid X_{[d]\setminus \{i,j\}}\right).$$

In the real-valued case, if the partial correlation is zero for jointly complex normal random variables, then the two variables are conditionally independent. Because in the complex case we have to consider both types of second-order association, we must consider both partial correlation and pseudo-partial correlation. For the following theorems, given random variables $A$, $B$, and $C$, we write $A⫫B\mid C$ if the conditional distributions $A\mid C$ and $B\mid C$ are independent.

Theorem 8.

If $X\sim 𝓒𝓝(m,\text{Γ},C)$, then, $\rho \left(X_i,X_j\mid X_{[d]\setminus \{i,j\}}\right)=0$ and $\overline{\rho }\left(X_i,X_j\mid X_{[d]\setminus \{i,j\}}\right)=0$ if and only if $X_i⫫X_j\mid X_{[d]\setminus \{i,j\}}$.

A corollary of this theorem allows us to drop the reliance on the pseudo-correlation in the proper complex normal case since such a correlation must be zero.

Corollary 9.

If $X\sim 𝓒𝓝(m,\text{Γ},0)$, then $\rho \left(X_i,X_j\mid X_{[d]\setminus \{i,j\}}\right)=0$ if and only if $X_i⫫X_j\mid X_{[d]\setminus \{i,j\}}$.

By applying Theorems 6 and 8, we get the following corollary:

Corollary 10.

If $X\sim 𝓒𝓝(m,\text{Γ},C)$, then $X_i⫫X_j\mid X_{[d]\setminus \{i,j\}}$ if and only if ${\widetilde{\text{Γ}}}_{ij}^{-1}=0$ and ${\widetilde{\text{Γ}}}_{i,j+d}^{-1}=0$. In addition, if $C=0$, then $X_i$, $X_j$ are conditionally independent if and only if ${\text{Γ}}_{ij}^{-1}=0$ for $\text{Γ}=\mathrm{var}(X)$.

4.3. Partial Coherency and Partial Correlation

We now leverage the results from Section 4.2 to show a correspondence between partial coherency, a modification of coherency to account for conditional dependence, and partial correlation. Partial coherency was developed to better differentiate unique pairwise associations from associations that are shared with one or more other observed variables (Ombao & Pinto, 2022). Assume we have $d$ signals $X_1(t),\dots ,X_d(t)$ on $t\in [0,1]$. Let ${\text{Σ}}_{ij}(t)=\mathrm{cov}\left\{X_i\left(t+t_0\right),X_j\left(t_0\right)\right\}$, and define $f_{ij}(\omega )$ as in Section 4.1. Consider the matrix $\mathbf{f}(\omega )$ formed by assembling the entries of $f_{ij}(\omega )$. Let $\text{diag}\{\mathbf{f}(\omega )\}$ be the matrix containing the diagonal elements of $\mathbf{f}(\omega )$ and zero on the off-diagonals. Let

$$\mathbf{g}(\omega )=\text{diag}{\left[{\{\mathbf{f}(\omega )\}}^{-1}\right]}^{-1/2}{\{\mathbf{f}(\omega )\}}^{-1}\text{diag}{\left[{\{\mathbf{f}(\omega )\}}^{-1}\right]}^{-1/2}.$$

We call $\mathbf{g}{(\omega )}_{ij}$ the partial coherency between signals $i$ and $j$. If $X_1(t),\dots ,X_d(t)$ are all oscillating signals at some frequency ${\omega }_0$, we obtain the following theorem.

Theorem 11.

If $X_k(t)=R_k\exp \left\{\iota \left({\text{Θ}}_k+2\pi {\omega }_{0}t\right)\right\}$ for all $k\in [d]$ and $\text{pcorr}\left\{X_i(0),X_j(0)\right\}=0$, then

$$\mathbf{g}{\left({\omega }_0\right)}_{ij}=\rho \left\{X_i(0),X_j(0)\mid X_{[d]\setminus \{i,j\}}(0)\right\}.$$

This theorem follows from observing that, by our results in Section 4.1, ${\text{Σ}}_{ij}(0)=\mathbf{f}{\left({\omega }_0\right)}_{ij}$ for such signals. We can then apply Theorem 6 and, observing that the upper-right block of $\widetilde{\text{Γ}}=\mathrm{cov}(\tilde{X})$ is zero because $\text{pcorr}\left\{X_i(0),X_j(0)\right\}=0$, we obtain the desired result.

Researchers have previously studied partial coherency as a way to construct conditional independence graphs for time series (Dahlhaus, 2000). For instance, Tugnait (2019a,b) estimates conditional independence between time series by first constructing a sufficient statistic that accounts for the oscillations in a time series at all observable frequencies and then, after observing that the limiting distribution of this statistic is a complex normal random variable, deriving conditional independence tests based on this limiting distribution. As we have seen, because we are dealing with signals oscillating at a single frequency, we can estimate partial coherency simply by computing the partial correlation between the observed variables. We will use this to interpret our latent-variable model. The Supplementary Material Section S2 details various simple examples in which PLV, amplitude correlation, and coherence are compared.

4.4. Alternative Measures of Pairwise Association Between Oscillating Signals

Thus far, we have focused on coherence as a measure of association for oscillating signals. As described in Section 3, other measures exist for studying the dependence between oscillating signals. In particular, we described PLV, which many investigators use as an alternative to coherence. Since PLV was first introduced, questions have arisen over whether to use PLV, coherence, or amplitude correlation to measure connectivity between oscillatory neural signals (e.g., Lachaux et al., 1999; Srinath & Ray, 2014; Lowet et al., 2016; Lepage & Vijayan, 2017). Our intention here is to review briefly some of these arguments to understand how coherence is situated among these other possible measures of association.

Clearly, coherence depends on both the phase and amplitude of oscillatory signals. Dependence on amplitude, however, has invited criticism of coherence as a pure representation of the degree of synchrony among the phases of oscillatory signals. PLV was introduced in part to overcome the perceived limitations of this dependence (Lachaux et al., 1999). Later work showed that, particularly in nonstationary settings, estimators of coherence are not well behaved and can fail to accurately represent synchrony (Lowet et al., 2016). Other authors have criticized coherence on the grounds that it can be biased by amplitude correlation (Srinath & Ray, 2014). However, some investigators have responded to these criticisms by pointing out that coherence may up-weight trials with larger amplitude oscillations, where information about phase is likely to be stronger (Lepage & Vijayan, 2017). Thus, the inclusion of amplitude information may be beneficial.

Further, some researchers have analyzed the relationship between PLV, amplitude correlation, and coherence when particular parametric models are assumed for data. For instance, Aydore, Pantazis & Leahy (2013) found that when data are distributed according to the complex normal distribution, PLV can be written as a function of coherence, which indicates that coherence provides all the information that PLV does. Further, Aydore, Pantazis & Leahy (2013) found that both the von Mises distribution and Gaussian models are effective for studying phase associations in LFP data, and argued that PLV and cross-correlation capture the same information. More generally, Nolte et al. (2020) made the remark that, because cross-correlation provides all possible information about the second-order statistical properties of circularly symmetric, bivariate, complex normal random variables, any pairwise measure of association can be written as a function of cross-correlation (and thus coherency). Nolte et al. found that PLV and related phase-based coupling statistics, as well as amplitude–amplitude correlational statistics, can be written as functions of coherence for complex normal random variables.

Thus, if the data are assumed to be proper and complex-normal, then complex correlation, and thus coherence, provides the most detailed measure of association available. For the oscillating neural signals that are the focus of this work, the complex normal model appears to be a reasonable approximation of the data, and so we focus on coherence as our measure of pairwise association since coherence may provide much of the information contained within other measures of association.

5. A COMPLEX-NORMAL, LATENT-VARIABLE MODEL

5.1. Model

We assume that we have recordings from $K$ brain regions, and that the activity of each brain region is recorded by $d_k$ electrodes $(1\le k\le K)$ over $N$ repeated experimental trials. We assume that each electrode records an oscillating signal at some frequency, and we band-pass-filter the data to extract this oscillating signal as a preprocessing step to obtain a complex number that represents the phase and amplitude of the oscillation. For each trial $n\in [N]$, the observation $X_k^n$ from brain region $d_k$ is a $d_k$-dimensional complex-valued variable. We further assume that each $X_k^n$ is driven by a univariate latent factor $Z_k^n$, which is also complex-variate, for the model

$$X_k^n={\beta }_k{Z}_k^n+{ϵ}_k^n,{ϵ}_k^n\sim 𝓒𝓝\left(0,{\text{Φ}}_k,0\right),$$ (6)

$$Z^n=\left(Z_1^n,\dots ,Z_k^n\right)\sim 𝓒𝓝(0,\text{Γ},0),$$ (7)

where ${\beta }_k\in {ℂ}^{d_k}$ is a complex-valued factor loading, $\text{Γ}\in {ℂ}^{K\times K}$ is the latent covariance matrix, which is assumed to be positive definite, and ${ϵ}_k^n\in {ℂ}^{d_k}$ is a region-specific noise with the covariance parameter ${\text{Φ}}_k\in {ℂ}^{d_k\times d_k}$, which also is assumed to be positive definite.

Using basic properties of the complex normal distribution, the marginal distribution of the vector $X^n=\left(X_1^n,\dots ,X_K^n\right)$ of all the observed signals is

$$X^n\sim 𝓒𝓝\left(0,\left(\begin{array}{cccc}{\beta }_1{\beta }_1^H{\text{Γ}}_{11}+{\text{Φ}}_1& {\beta }_1{\beta }_2^H{\text{Γ}}_{12}& {\beta }_1{\beta }_3^H{\text{Γ}}_{13}& \dots \\ {\beta }_2{\beta }_1^H{\text{Γ}}_{21}& {\beta }_2{\beta }_2^H{\text{Γ}}_{22}+{\text{Φ}}_2& {\beta }_2{\beta }_3^H{\text{Γ}}_{23}& \cdots \\ {\beta }_3{\beta }_1^H{\text{Γ}}_{31}& {\beta }_3{\beta }_2^H{\text{Γ}}_{32}& {\beta }_3{\beta }_3^H{\text{Γ}}_{33}+{\text{Φ}}_3& \dots \\ \dots & \cdots & \dots & \dots \end{array}\right),0\right).$$ (8)

This representation shows that the model is nonidentifiable without adding additional constraints. In particular, ${\beta }_k$ can be scaled by an arbitrary complex number, and corresponding entries in $\text{Γ}$ scaled by the inverse conjugate of that number, with no change to the marginal distribution. Additionally, given an arbitrary real value $a\in ℝ$, we have that ${\beta }_k{\beta }_k^H\left({\text{Γ}}_{kk}+a\right)+\left({\text{Φ}}_k-a{\beta }_k{\beta }_k^H\right)={\beta }_k{\beta }_k^H{\text{Γ}}_{kk}+{\text{Φ}}_k$, which indicates that, while ${\text{Φ}}_k-a{\beta }_k{\beta }_k^H$ is positive semidefinite (PSD), we can add to the diagonal of ${\text{Γ}}_{kk}$ and subtract $a{\beta }_k{\beta }_k^H$ from ${\text{Φ}}_k$ and retain the same marginal distribution.

Thus, to ensure the identifiability of the parameters, we require that

1. ${\beta }_k^H{\beta }_k=1$ and $\Im \mathfrak{m}{\beta }_{k,1}=0$, where ${\beta }_{k,1}$ is the first component of ${\beta }_k$, and

2. $\sup \left\{a\ge 0:{\text{Φ}}_k-a{\beta }_k{\beta }_k^H\ge 0\right\}=0$.

To better understand the model, we show how it can produce maximum likelihood estimates that are related to the solutions for a complex extension of canonical correlation analysis (CCA; Hotelling, 1936). Bong et al. (2023) found that a real-valued, latent-variable model, which bears some similarity to the complex-valued, latent-variable model described here, could be viewed as a form of probabilistic CCA, first described in Bach & Jordan (2005). Because CCA has a distribution-free definition, the correspondence we show below with an analogue of CCA for complex-valued random vectors provides a similar distribution-free motivation for the estimation procedure we derive here.

If we observe a pair of real random vectors $Y_1\in {ℝ}^{d_1}$ and $Y_2\in {ℝ}^{d_2}$, CCA finds weights $w_1$, $w_2$ (where $w_1\in {ℝ}^{d_1}$, $w_2\in {ℝ}^{d_2}$) that maximize $\left|\text{corr}\left(w_1^{\top }{Y}_1,w_2^{\top }{Y}_2\right)\right|$. Kettenring (1971) extended CCA to multiple vector observations. For $\left(Y_1\in {ℝ}^{d_1},\dots ,Y_K\in {ℝ}^{d_K}\right)$, this so-called “multiset CCA” finds weights $w_1\in {ℝ}^{d_1},\dots ,w_K\in {ℝ}^{d_K}$ maximizing a notion of the cross-correlation among $\left(w_1^{\top }{Y}_1,\dots ,w_K^{\top }{Y}_K\right)$. Multiset CCA easily extends to complex-valued random vectors, $X_1\in {ℂ}^{d_1}\dots ,X_K\in {ℂ}^{d_K}$. In particular, we can write the optimization problem solved by complex multiset CCA as

$$\arg \underset{w_k\in {ℂ}^{d}k:k\in [K],\mathrm{var}\left(w_k^H{X}_k\right)=1}{\min }\det \left\{\mathrm{var}\left(w_1^H{X}_1,\dots ,w_K^H{X}_K\right)\right\}.$$ (9)

The solution weights $\left\{w_{k,cc}:k\in [K]\right\}$ that achieve the optimum of (9) are called canonical weights, and the resulting correlation matrix $P_{cc}=\text{corr}\left(w_{1,cc}^H{X}_1,\dots ,w_{K,cc}^H{X}_K\right)$ is called a canonical correlation matrix. The sample estimates ${\widehat{w}}_{k,cc}$ and ${\widehat{P}}_{cc}$ are obtained by replacing corr in (9) with the sample version $\widehat{\text{corr}}$ based on the observed signals $\left(X_1^n,\dots ,X_K^n\right)$ during experimental trials $n\in [N]$. We now state a theorem describing the equivalence between the canonical weights, the canonical correlation matrix, and the maximum likelihood estimator of the parameters in the model given in (6) and (7) under the given identifiability constraints. A proof is given in the Appendix.

Theorem 12.

Suppose that ${\widehat{\beta }}_k$, $k\in [K]$, and $\widehat{\text{Γ}}$ are the maximum likelihood estimators of the parameters in (6) and (7) under the given identifiability constraints, labelled as 1 and 2 following (8), based on $N$ observed tuples $\left(X_1^n,\dots X_K^n\right)$. We have the following equivalence between the maximum likelihood estimators, the canonical weights, and the canonical correlation matrix:

$${\widehat{\beta }}_k=\frac{\widehat{\mathrm{var}}\left(X_k\right){\widehat{w}}_{k,cc}}{{\Vert \widehat{\mathrm{var}}\left(X_k\right){\widehat{w}}_{k,cc}\Vert }_2}\mathit{\text{and diag}}\left({\widehat{\text{Γ}}}_{kk}^{-1/2}\right)\widehat{\text{Γ}}\mathit{\text{diag}}\left({\widehat{\text{Γ}}}_{kk}^{-1/2}\right)={\widehat{P}}_{cc}$$

for $k\in [K]$, where $\text{diag}\left({\widehat{\text{Γ}}}_{kk}^{-1/2}\right)$ is the diagonal matrix with entries ${\widehat{\text{Γ}}}_{kk}^{-1/2}$.

As a corollary of the theorem, if $K=2$, then our model is equivalent to the pairwise CCA for two complex random vectors $X_1\in {ℂ}^{d_1}$ and $X_2\in {ℂ}^{d_2}$. To demonstrate this equivalence, let us write

$$w_{1,cc},w_{2,cc}=\arg \underset{w_1\in {ℂ}^{d_1},w_2\in {ℂ}^{d_2}}{\max }\left|\text{corr}\left(w_1^{\top }{X}_1,w_2^{\top }{X}_2\right)\right|,$$

let ${\rho }_{cc}$ be the resulting canonical correlation coefficient, and let ${\widehat{w}}_{1,cc}$ and ${\widehat{\rho }}_{cc}$ be the corresponding sample estimators. We can then state the following corollary.

Corollary 13.

If ${\widehat{\beta }}_1$, ${\widehat{\beta }}_2$, and $\widehat{\text{Γ}}$ are the maximum likelihood estimators of (6) and (7) under the given identifiability constraints, then they are related to the weights and canonical correlation values through

$${\widehat{\beta }}_1=\frac{\widehat{\mathrm{var}}\left(X_1\right){\widehat{w}}_{1,cc}}{{\Vert \widehat{\mathrm{var}}\left(X_1\right){\widehat{w}}_{1,cc}\Vert }_2},{\widehat{\beta }}_1=\frac{\widehat{\mathrm{var}}\left(X_2\right){\widehat{w}}_{2,cc}}{{\Vert \widehat{\mathrm{var}}\left(X_2\right){\widehat{w}}_{2,cc}\Vert }_2},\mathit{\text{and}}\frac{{\widehat{\text{Γ}}}_{12}}{\sqrt{{\widehat{\text{Γ}}}_{11}{\widehat{\text{Γ}}}_{22}}}={\widehat{\rho }}_{cc}.$$

In the general case with more than two latent factors, fitting the marginal likelihood directly is an intractable optimization problem. Instead, we fit the model using the expectation maximization (EM) algorithm; we describe our fitting procedure in the Appendix. In Figure S1, we provide evidence that, for simulated datasets similar to the real dataset we analyze in Section 6, the estimates provided by the EM fitting procedure converge to the true parameters as the size of the dataset increases. Code for performing inference and analysis with our model is available at https://github.com/urbkn7/latent_cn.

In applying Theorem 12 to the data in Section 6, we first band-pass-filter the data so that the magnitude of the complex correlation becomes the coherence (as discussed in Section 4.1). We also decompose the covariance matrix to get partial coherence (Section 4.3).

5.2. Inference

We study the strength of the associations among the estimated latent factors in our model. To do so, we develop a parametric bootstrap procedure to test for conditional dependence between brain areas. Recall from Section 4 that for vectors distributed according to the complex normal distribution, zero entries in the latent precision matrix correspond to conditional independence relationships between the associated dimensions of the random vector. Therefore, for two regions with indices $r_1$, $r_2\in [R]$, we want to test the null hypothesis ${𝓗}_0:{\text{Γ}}_{r_1,r_2}^{-1}=0$ against the alternative hypothesis ${𝓗}_a:{\text{Γ}}_{r_1,r_2}^{-1}\ne 0$.

To employ the parametric bootstrap, we first estimate the parameters of the model on the original dataset. Let $\text{Θ}=\left\{\left\{{\beta }_k:k\in [K]\right\},\left\{{\text{Φ}}_k:k\in [K]\right\},\text{Γ}\right\}$, and let $𝓛(\text{Θ};𝓓)$ denote the likelihood of the parameters under the model given by (8) for the dataset $𝓓=\left\{X^n:n\in [N]\right\}$. We first estimate $\text{Θ}$ with the EM algorithm to obtain $\widehat{\text{Θ}}(𝓓)$, our approximation of the maximum likelihood estimator for the dataset $𝓓$. Then, we optimize the likelihood with a modified EM algorithm under the additional constraint that ${\text{Γ}}_{r_1,r_2}^{-1}=0$ (see the Appendix for details on how we solve this optimization problem) to obtain ${\widehat{\text{Θ}}}_0(𝓓)$. We then simulate datasets ${𝓓}^{(b)}\sim P_{{\widehat{\text{Θ}}}_0}$, where $1\le b\le B$ and $B$ is the total number of bootstrap datasets. Let

$$\lambda (𝓓)=\frac{𝓛\left\{{\widehat{\text{Θ}}}_0(𝓓);𝓓\right\}}{𝓛\{\widehat{\text{Θ}}(𝓓);𝓓\}}.$$

We can observe the quantile of the likelihood ratio statistic for the original data, $\lambda (𝓓)$, relative to the set of likelihood ratio statistics for the bootstrapped datasets $\left\{\lambda \left({𝓓}^{(b)}\right):b\in [B]\right\}$ to obtain a $p$-value. We can also obtain confidence intervals for parameters of interest by employing the ordinary nonparametric bootstrap. The parameters we are most interested in are contained in the latent correlation and conditional correlation matrices. We have the latent correlation matrix $S=\text{diag}{(\text{Γ})}^{-1/2}\text{Γdiag}{(\text{Γ})}^{-1/2}$ and the conditional correlation matrix $D=\text{diag}{\left({\text{Γ}}^{-1}\right)}^{-1/2}{\text{Γ}}^{-1}\text{diag}{\left({\text{Γ}}^{-1}\right)}^{-1/2}$.

6. DATA ANALYSIS

We apply the techniques we have discussed so far to a dataset of LFP data from the Allen Institute (Siegle et al., 2021). In the experiment, six electrode probes were simultaneously inserted into the mouse brain, with each probe targeting some area of the visual cortex but also recording other regions. During the experiment, the mice were presented with a variety of visual stimuli; here, we focus on presentations of drifting grating stimuli, which appear as bars moving across a screen in the mouse’s field of view. In the interest of utilizing as much data as possible, we ignore differences in the direction and size of the stimuli presented. This gives us 630 trials.

The experimenters marked every electrode with the anatomical brain area in which it resided during the experiment. We observed an oscillation at 6.5Hz in many of these areas. Therefore, we band-pass-filtered the LFP signal and then used the Hilbert transform to recover the analytic signal. We selected a single time point, 2 s into the trial, which occurs well after the stimulus disappears from the screen. Selecting this time point removes the influence of trial-locked changes in brain activity. In addition, we used five electrodes from each of the six regions for which we have data to form the set of time series we analyze.

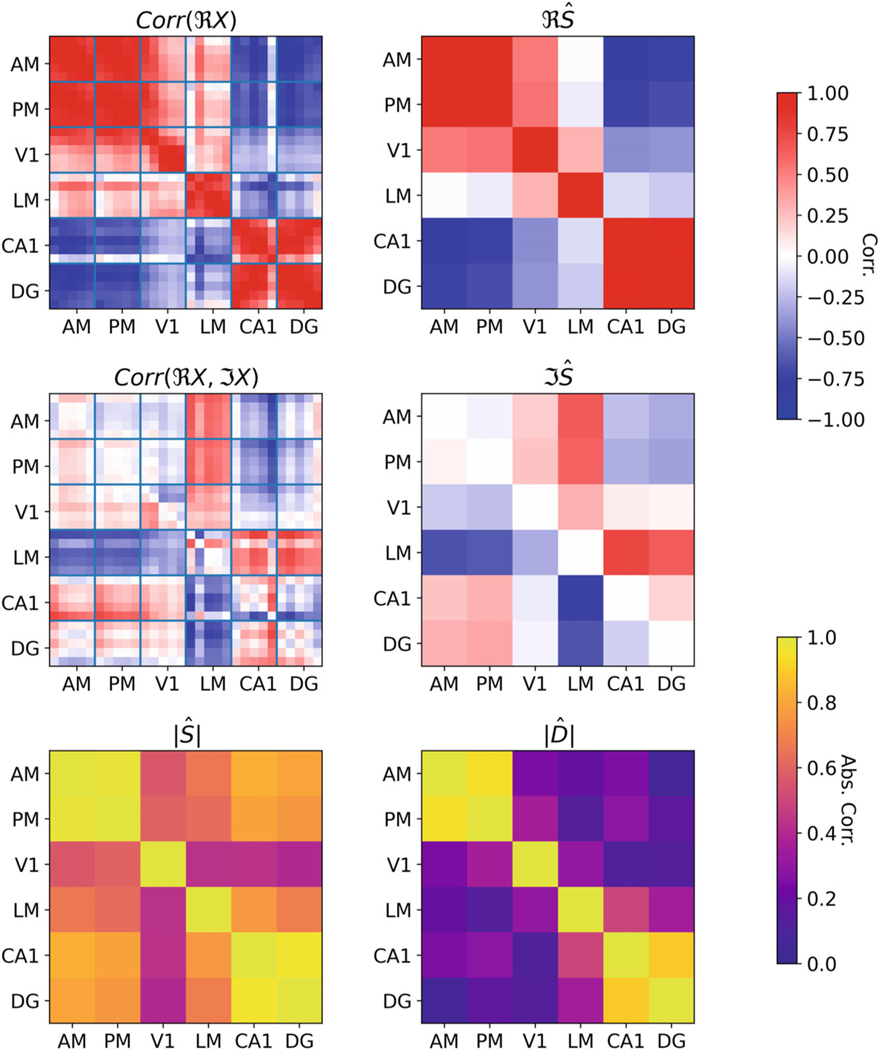
We then applied the latent variable model to this dataset. For all analyses, we used one latent variable per brain area analyzed. Each brain area has multiple electrodes embedded, which record the LFP signals; we select five electrodes from each region, and the signals from these electrodes are the observed variables in our model. In Figure 4, we show data from a single probe passing through four visual regions (AM, PM, V1, and LM) and two hippocampal regions (CA1 and DG). We display the empirical correlation matrices of the observed data as well as the latent correlation matrices and partial correlation matrices estimated using our model. These matrices of latent correlation and partial correlations are of interest since, as discussed in Section 4, in our setting they are equivalent to the coherency and partial coherency between regions. While the estimated latent marginal correlations are relatively large between many areas, the estimated partial correlations (the $\left|{\widehat{D}}_{ij}\right|\text{s}$) are strongest between two pairs of areas: between AM and PM as well as between CA1 and DG.

Figure 4:

An example of an application of the latent variable model to LFP data from the Allen Institute. The entries in the correlation matrices are arranged consecutively according to their vertical position in the inserted probe. The sample correlation for the real part of the data and the sample correlation between the real and imaginary parts of the data are denoted by $\text{corr}\left(\Re X\right)$ and $\text{corr}\left(\Re X,\Im X\right)$. The estimated latent correlation matrix is denoted by $\widehat{S}$, and the estimated latent partial correlation matrix is denoted by $\widehat{D}$. The notations $\widehat{S}$ and $\widehat{D}$ denote the absolute value of each entry in the corresponding matrices. Electrodes are labelled by the anatomical region in which they resided during the experiment. We observe that while the estimated latent correlation matrix $\widehat{S}$ has large values between many regions, the estimated latent partial correlation primarily has large values between two pairs of regions: between DG and CA1 as well as between AM and PM.

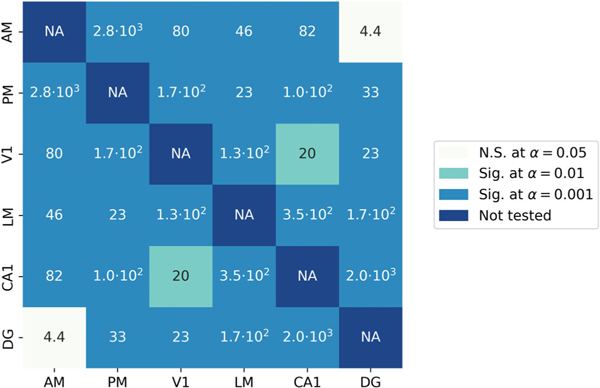
We perform the parametric bootstrap test discussed in Section 5.2 to study the significance of the entries in the latent partial correlation matrix. In Figure 5, we plot the results of this analysis. We observe significant correlations between the majority of pairs of areas for the 6.5Hz frequency.

Figure 5:

Results of parametric bootstrap test performed on all pairs of regions to test if a significant conditional correlation exists between each pair of areas. Numbers inside the boxes are likelihood ratio statistics testing the hypothesis that $\left|D_{ij}\right|>0$. The colour of each box represents the results of significance tests for three values of $\alpha$, the false-positive rate, where each significance test is done with a Bonferroni correction for multiple comparisons. The level $\alpha =0.001$ is the smallest we are able to test given our simulation settings. The likelihood ratio values indicate that some pairs would be significant at much smaller values of $\alpha$. There are significant partial correlations between most pairs of areas at $\alpha =0.001$, except between DG and AM as well as between V1 and CA1.

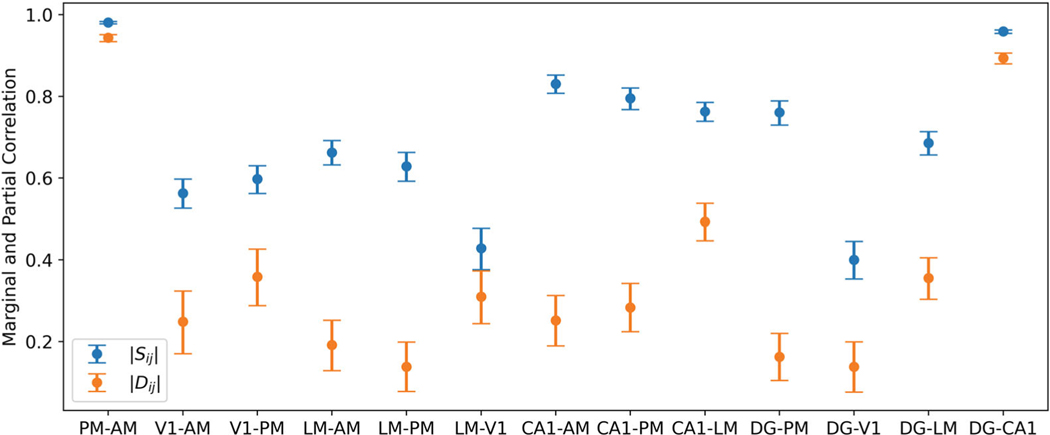
To further understand how strong the correlations between these areas are, we report bootstrap confidence intervals for the significantly nonzero parameters of the correlation and partial correlation matrices in Figure 6. For nearly all pairs of regions, the partial correlations are of modest size and are substantially smaller than the corresponding marginal correlations. However, the pairs PM–AM and DG–CA1 have large partial correlations close to 1. Also of interest are the patterns of association for the LM area. Note that the strength of the correlation between the LM and the CA1 areas is larger than that between LM and any other visual region, suggesting that LM has stronger oscillatory associations at 6.5Hz frequency with hippocampal regions than with other visual regions, despite LM itself being a visual region.

Figure 6:

Point estimates and confidence intervals of correlations (blue) and partial correlations (orange) for all pairs of regions with significantly nonzero latent partial correlations. All confidence intervals have 95% coverage. The partial correlations are smaller than the corresponding marginal correlations, with the exception of the large partial correlations between PM and AM and between DG and CA1.

7. DISCUSSION

We began with two separate goals, and ended by merging them. On the one hand, we wanted to see whether the multivariate complex normal distribution might be useful in analyzing dependence among groups of oscillating time series. On the other hand, we wished to better understand complex correlation. Our investigation, built on existing literature concerning dependence among complex random variables and complex normal variables in particular, uncovered several interesting relationships that were either not known previously or not spelled out clearly. For complex random vectors, we reviewed the distinction between partial correlation and conditional correlation(Baba,Shibata&Sibuya,2004), which are equivalent for real, normal random vectors, and we showed that the complex partial correlation and conditional correlation also coincide under complex normality. We phrased many of our theorems in terms of the general form of complex normality, including both covariance and pseudo-covariance, and then specialized to the proper case where pseudo-covariances vanish. We showed that in the proper case, pairwise conditional independence coincides with zero partial correlation, as it does for real multivariate normal distributions, and that partial coherency may be considered a partial complex correlation at a given frequency. These facts are important for analytic interpretation, as we demonstrated in our real data example.

The scientific backdrop for our work on the analysis of neural data is one of the most pressing problems in the application of statistics to neurophysiology. Specifically, the problem lies in identifying coordinated activity across two or more regions of the brain based on recordings of multiple time series that are highly nonstationary but are repeated across experimental trials. When there are many repetitions of multiple recorded values in two regions at a single time point, CCA provides a solution to the problem of determining their dependence. In the two-region case, we showed that maximum likelihood estimation for our latent variable model produces a form of latent coherence which is equivalent to the magnitude of the complex canonical correlation. In the multi-region case, maximum likelihood estimation for our model produces a generalized canonical correlation.

The latent coherencies and partial coherencies from our latent-variable model are not computed in the frequency domain but are obtained instead in the time domain with band-pass-filtering in a narrow band. For this we leaned on a key observation by Ombao & Van Bellegem (2008) that “band coherence” (a version of coherence written in terms of integrals over the band) could be interpreted as the magnitude of complex correlation of two signals. We used our results for the complex normal distribution to interpret the complex correlations and partial correlations we found in the data.

Part of understanding coherence requires a comparison to PLV, which can be generalized to the multivariate setting with torus graphs. The original motivation for PLV was discomfort with the dependence of coherence on amplitude (Lachaux et al., 1999). Like PLV, torus graphs ignore amplitude variation and any possible cross-covariation between amplitudes and phases. Thus, torus graphs might be considered models of covariation among phases after marginalizing over amplitudes. The complex normal results characterizing torus graphs as conditional distributions after conditioning on amplitudes show that even though the graphical structure (the conditional independence structure) of torus graphs does not depend on amplitude, calibration of the magnitude of interaction effects apparently depends on the amplitudes. When the amplitudes are roughly constant, coherence and PLV provide essentially equivalent results (see the Supplementary Material Section S2 and Lepage & Vijayan, 2017).

The results we found in the data are striking and intriguing. There are large partial coherences in two pairs of areas, one involving higher visual areas (AM and PM, the anterior and posterior parts of the medial visual area, which are further downstream than primary visual cortex, V1) and the other involving the hippocampus (CA1, a sub-region of the cornu ammonis and DG, the dentate gyrus). Both pairs involve areas that are contiguous, but that alone does not explain their interaction because all of these areas share anatomical boundaries with some other areas. In the case of CA1 and DG, these are the only hippocampal areas in the data. The coherence between the AM and PM areas could indicate close collaboration in neural processing and may be worth further investigation. In addition, we observed stronger coherences between LM and hippocampal regions than between LM and other visual regions, which could also be a subject of further investigation.

Often, there are dozens of time series in each region, and latent-variable models are attractive ways to reduce dimensionality for examining cross-region interactions. In an unpublished work (Orellana & Kass, 2023), a hierarchical model based on torus graphs has been used to describe large numbers of phase measurements made in each of several brain areas. This hierarchical structure has the advantage of reducing the total number of parameters, which results in better statistical inference when the amount of data is small relative to its dimensionality. To assess time-varying amplitude interaction, Bong et al. (2023) developed a time-series generalization of a factor analysis model with one latent factor for each region. They allowed for nonstationarity and included all relevant time-lagged cross-correlations. They first showed how the model leads to a time-series generalization of probabilistic CCA, based on multiset CCA (analogous to Theorem 12 here). Because of nonstationarity, each combination of a time point in one region and a time point in another region could have a unique correlation across trials, which made the covariance matrix have a large number of free parameters. The authors adapted sparse estimation methods to solve the high-dimensional inference problem and showed how it produced interpretable and interesting results when applied to their data. Closely related work can be found in Bong et al. (2020).

It would be straightforward to apply the approach here at many time points, but modelling time lags, as is done in Bong et al. (2023), would require additional work. It would also be possible to estimate partial coherence, even at a single point, using a latent, multivariate time series model, but this would require either a very high dimensional formulation along the lines of Bong et al. (2023) or a specific time series model, both of which present their own challenges.

To simplify interpretation, it was important for us to assume that the complex normal distributions were proper. In our data, this seemed to be a reasonable assumption, and in all the data we have examined using torus graphs, reflectional dependence is, similarly, either absent or difficult to detect. Perhaps future uses of the complex normal distribution, along the lines outlined here, will reveal situations in which pseudo-covariance needs to be considered. The substantial additional complication of such cases would likely present new challenges, but we hope the framework we have summarized here would provide a useful starting point.

APPENDIX

A NOTE ON THE HILBERT TRANSFORM

Here we provide an overview of the Hilbert transform, which is commonly used to recover phase and amplitude from oscillating signals (Cohen, 2014). Let $X(t)=\Re \mathfrak{e}X(t)+ı\mathfrak{J}\mathfrak{m}X(t)$ be the output of a complex signal that has been filtered in a band $\left({\omega }_0-\delta ,{\omega }_0+\delta \right)$.

We only observe $\Re \mathfrak{e}X(t)$, and the problem is to recover $X(t)$, which is possible when $\delta$ is sufficiently small. The Hilbert transform operates on $\Re \mathfrak{e}X(t)$ to produce $\Im \mathfrak{m}X(t)$ according to

$$\Im \mathfrak{m}X(t)=\text{p. v.}\int \frac{\Re \mathfrak{e}X(s)}{\pi (t-s)}ds,$$ (A1)

where the integral is over the domain of $t$. The notation $\text{p. v.}\int f(t)dt$ denotes the Cauchy principal value; this formula is given in numerous sources (e.g., Pandey, 2011), but because we have not seen a concise derivation, we provide one here.

Let us write the Fourier transforms of $X(t)$ and its complex conjugate $\overline{X}(t)$ as $𝓕(X)$ and $𝓕(\overline{X})$, and the evaluation of such transforms at a frequency $\omega$ by $𝓕(X)(\omega )$, etc. From the general relations

$$\Re \mathfrak{e}X(t)=\frac{1}{2}\{X(t)+\overline{X}(t)\}\text{and}\Im \mathfrak{m}X(t)=-\frac{l}{2}\{X(t)-\overline{X}(t)\},$$

we have the Fourier transform

$$𝓕(\Re \text{e}X)=\frac{1}{2}\{𝓕(X)+𝓕(\overline{X})\}\text{and}𝓕(\Im \mathfrak{m}X)=-\frac{l}{2}\{𝓕(X)-𝓕(\overline{X})\}.$$

Note that $𝓕(X)(\omega )$ is, from the band-pass filtering, concentrated around ${\omega }_0$, and $𝓕(\overline{X})(\omega )$ is concentrated around $-{\omega }_0$. Therefore, when $\omega >0$ the formula above gives $𝓕(\Re \mathfrak{e}X)(\omega )=𝓕(X)(\omega )/2$ and, similarly, when $\omega <0$, $𝓕(\Re \mathfrak{e}X)(\omega )=𝓕(\overline{X})(\omega )/2$. Thus, using $\mathrm{sgn}(\omega )$ to denote the sign of $\omega$, when we multiply $𝓕(\mathfrak{R}\mathfrak{e}X)(\omega )$ by $-\iota \mathrm{sgn}(\omega )$, we get

$$\{-\iota \mathrm{sgn}(\omega )\}𝓕(\Re \mathfrak{\text{e}}X)(\omega )=𝓕(\mathfrak{J}\mathfrak{m}X)(\omega ).$$

As a result, the convolution $\Re \mathfrak{e}X(t)\ast {𝓕}^{-1}\left\{-\iota \mathrm{sgn}\left({\omega }_0\right)\right\}$ satisfies

$$\Re \mathfrak{e}X(t)\ast {𝓕}^{-1}\{-ı\mathrm{sgn}(\omega )\}=\Im \mathfrak{m}X(t).$$

Inserting the formula for ${𝓕}^{-1}\left\{-\iota \mathrm{sgn}\left({\omega }_0\right)\right\}$ into the definition of convolution produces (A1), giving the Hilbert transform of $\Re \mathfrak{e}X(t)$. The resulting $X(t)$ is called the analytic signal.

FITTING PROCEDURE FOR THE LATENT FACTOR MODEL IN SECTION 5

In this section, we discuss the procedure for fitting the latent factor model (Eqs. 6 and 7) in Section 5 to the data ${\left\{X_1^n,\dots ,X_K^n\right\}}_{n=1,\dots ,N}$ from $N$ independent repeated observations. The procedure provides estimates of the model parameters $\text{Γ}$, ${\beta }_k$, and ${\text{Φ}}_k$ using the EM algorithm (Dempster, Laird & Rubin, 1977). The EM algorithm starts with initial estimates for the parameters, denoted by ${\text{Γ}}^{(0)}$, ${\beta }_k^{(0)}$, and ${\text{Φ}}_k^{(0)}$, and iteratively updates the estimates to optimize the likelihood through alternating E-steps and M-steps, which we will describe next. We denote the estimates after the $r\text{th}$ update by ${\text{Γ}}^{(r)}$, ${\beta }_k^{(r)}$, and ${\text{Φ}}_k^{(r)}$.

At the $(r+1)\text{th}$ iteration, the E-step calculates the sufficient statistics of the latent factors $\left\{Z_1^n,\dots Z_K^n\right\}$ conditional on the observed data $\left\{X_1^n,\dots ,X_K^n\right\}$ and the parameter estimates ${\text{Γ}}^{(r)}$, ${\beta }_k^{(r)}$, and ${\text{Ψ}}_k^{(r)}$ after the $r\text{th}$ iteration. The full joint probability density of the observed data and the latent factors, given the $r\text{th}$ parameter estimates, is

$$\begin{gathered} p\left(X,Z;{\text{Γ}}^{(r)},{\beta }_k^{(r)},{\text{Φ}}_k^{(r)}\right)\propto \frac{1}{\det \left({\text{Γ}}^{(r)}\right)}\exp \left(-Z^H{\left\{{\text{Γ}}^{(r)}\right\}}^{-1}Z\right) \\ \times \prod _{k=1}^K\left(\frac{1}{\det \left({\text{Φ}}_k^{(r)}\right)}\exp \left\{-{\left(X_k-{\beta }_k^{(r)}{Z}_k\right)}^H{\left\{{\text{Φ}}_k^{(r)}\right\}}^{-1}\left(X_k^n-{\beta }_k^{(r)}{Z}_k\right)\right\}\right), \end{gathered}$$

where $Z=\left(Z_1,\dots ,Z_K\right)$ is the concatenation of the latent factors. Further,

$$\text{E}\left(Z\mid X,{\text{Γ}}^{(r)},{\beta }_k^{(r)},{\text{Φ}}_k^{(r)}\right)={\left({\left\{{\text{Γ}}^{(r)}\right\}}^{-1}+D^{(r)}\right)}^{-1}{V}^{(r)},$$

$$\mathrm{var}\left(Z\mid X,{\text{Γ}}^{(r)},{\beta }_k^{(r)},{\text{Φ}}_k^{(r)}\right)={\left({\left\{{\text{Γ}}^{(r)}\right\}}^{-1}+D^{(r)}\right)}^{-1},\text{and}$$

$$\text{pvar}\left(Z\mid X,{\text{Γ}}^{(r)},{\beta }_k^{(r)},{\text{Φ}}_k^{(r)}\right)=O_K,$$

where $D^{(r)}$ is a diagonal matrix with entries $D_{kk}^{(r)}={\beta }_k^{(r)H}{\left\{{\text{Φ}}_k^{(r)}\right\}}^{-1}{\beta }_k^{(r)}$, $V^{(r)}$ is a vector of elements $V_k^{(r)}={\beta }_k^{(r)H}{\left\{{\text{Φ}}_k^{(r)}\right\}}^{-1}{X}_k$, and $O_K$ is the $K\times K$ zero matrix. For brevity, we denote $\text{E}\left(Z^n\mid X^n,{\text{Γ}}^{(r)},{\beta }_k^{(r)},{\text{Φ}}_k^{(r)}\right)$ and $\mathrm{var}\left(Z^n\mid X^n,{\text{Γ}}^{(r)},{\beta }_k^{(r)},{\text{Φ}}_k^{(r)}\right)$ by ${\text{E}}^{n(r)}$ and ${\mathrm{var}}^{(r)}$. (We note that ${\mathrm{var}}^{(r)}$ is invariant over $n\in [N]$.)

In the M-step, we find the parameters maximizing the expectation of the full log-likelihood function with respect to both ${\left\{X^n\right\}}_n$ and ${\left\{Z^n\right\}}_n$ conditional on ${\left\{X_1^n,\dots ,X_K^n\right\}}_n$, ${\text{Γ}}^{(r)}$, ${\varphi }_k^{(r)}$, and ${\beta }_k^{(r)}$. The conditional expectation of the full log-likelihood function for the model is

$$\begin{gathered} \text{E}\left(\ell \left(\text{Γ},{\beta }_k,{\text{Φ}}_k;{\left\{X^n,Z^n\right\}}_n\right)\mid X,{\text{Γ}}^{(r)},{\beta }_k^{(r)},{\text{Φ}}_k^{(r)}\right) \\ \stackrel{+C}{=}\sum _{n=1}^N[-\text{ln det}(\text{Γ})-\text{tr}\left\{{\text{Γ}}^{-1}\left({\mathrm{var}}^{(r)}+{\text{E}}^{n(r)}{\text{E}}^{n(r)H}\right)\right\} \\ +\sum _{k=1}^K\{-\text{ln det}\left({\text{Φ}}_k\right)-{\left(X_k^n\right)}^H{\text{Φ}}_k^{-1}{X}_k^n+{\overline{E}}_k^{n(r)}{\beta }_k^H{\text{Φ}}_k^{-1}{X}_k^n+{\left(X_k^n\right)}^H{\text{Φ}}_k^{-1}{\beta }_k{E}_k^{n(r)} \\ -{\beta }_k^H{\text{Φ}}_k^{-1}{\beta }_k\left({\mathrm{var}}_{kk}^{(r)}+E_k^{n(r)}{\overline{E}}_k^{n(r)}\right)\}]. \end{gathered}$$

The parameters are complex-valued, so we use Wirtinger calculus to take derivatives. Using formulas from Adali, Schreier & Scharf (2011), we take derivatives and set them equal to zero to achieve the update steps

$${\text{Γ}}^{(r+1)}={\mathrm{var}}^{(r)}+\frac{1}{N}\sum _{n=1}^N{\text{E}}^{n(r)}{\text{E}}^{n(r)H},$$

$${\beta }_k^{(r+1)}=\frac{\sum _n{X}_k^n{\overline{\text{E}}}_k^{n(r)}}{\sum _n\left({\mathrm{var}}_{kk}^{(r)}+{\text{E}}_k^{n(r)}{\overline{\text{E}}}_k^{n(r)}\right)},\text{and}$$

$${\text{Φ}}_k^{(r+1)}={\mathrm{var}}_{kk}^{(r)}{\beta }_k^{(r+1)}{\left({\beta }_k^{(r+1)}\right)}^H+\frac{1}{N}\sum _{n=1}^N\left(X_k^n-{\beta }_k^{(r+1)}{\text{E}}_k^{n(r)}\right){\left(X_k^n-{\beta }_k^{(r+1)}{\text{E}}_k^{n(r)}\right)}^H.$$

We also have the identifiability constraints ${\beta }_k^H{\beta }_k=1$, $\mathfrak{J}\mathfrak{m}{\beta }_k(1)=0$, and $\sup \{a\ge 0:{\varphi }_k-a{\beta }_k{\beta }_k^H⪰0\}=0$. To produce estimates that satisfy these constraints, we utilize the following procedure. First, we adjust the elements of $\widehat{\text{Γ}}$ and ${\widehat{\beta }}_k$ so that ${\beta }_k^H{\beta }_k=1$, and $\Im \mathfrak{m}{\beta }_k(1)=0$; this can be accomplished by multiplying the rows and columns in $\widehat{\text{Γ}}$ and the ${\widehat{\beta }}_k$ vectors by a complex-valued scalar. To ensure that $\sup \left\{a\ge 0:{\varphi }_k-a{\beta }_k{\beta }_k^H⪰0\right\}=0$, we solve a convex optimization problem by maximizing $\alpha$ under the constraint that ${\varphi }_k-a{\beta }_k{\beta }_k^H⪰0$. We then subtract $a{\widehat{\beta }}_k{\widehat{\beta }}_k^H$ from ${\widehat{\varphi }}_k$ and add $\alpha$ to ${\text{Γ}}_{kk}$.

We use a procedure based on the method of moments to obtain starting values for the EM algorithm, a strategy that has been shown theoretically to often result in near-optimal parameter estimates (Balakrishnan, Wainwright & Yu, 2017). To do so, we start by computing the sample covariance matrix over the data. Then, we estimate the parameter vectors ${\beta }_k$ by examining the submatrices given by $\widehat{\mathrm{cov}}\left(X_k^n,X_i^n\right)$. In particular, because under the correct model specification, we have that $\mathrm{cov}\left(X_k^n,X_i^n\right)={\text{Γ}}_{ki}{\beta }_k{\beta }_i^H$, we can take any column of $\widehat{\mathrm{cov}}\left(X_k^n,X_i^n\right)$ and normalize it according to the identifiability constraints to obtain an estimate of ${\beta }_k$. We do this and average over all the corresponding columns to get an overall estimate of ${\beta }_k$. Once ${\beta }_i$ and ${\beta }_j$ have been estimated, it is then straightforward to obtain estimates of ${\text{Γ}}_{ij}$ by dividing the entries in $\widehat{\mathrm{cov}}\left(X_i^n,X_j^n\right)$ by those in ${\beta }_i{\beta }_j^H$.

Now we briefly address our strategy for parameter estimation under a null hypothesis, as is done in the inference method we introduce. Under the null hypothesis, we are assuming that some entry of the latent precision matrix, ${\text{Γ}}_{ij}^{-1}$, is zero. To satisfy this assumption, we need to modify our estimation procedure. Observe that the conditional expectation of the log-likelihood depends on $\text{Γ}$ through

$$-\text{ln det Γ}-\text{tr}\left\{{\text{Γ}}^{-1}({\text{var}}^{(r)}+E^{n(r)}{E}^{n(r)H})\right\}.$$

Thus, we need to optimize this expression over $\text{Γ}$ under the constraints that ${\text{Γ}}_{ij}^{-1}=0$ while ensuring that $\text{Γ}$ remains a Hermitian PSD matrix. Fortunately, this is a convex optimization problem, and while there is no explicit expression for the optimal $\text{Γ}$ under these constraints, we can solve this problem numerically using a convex optimization package. Then, we can estimate the remaining variables using the explicit formulas given above.

PROOF OF THEOREM 12

Let $u_k=S_{kk}^{-1/2}{\beta }_k{\text{Γ}}_{kk}^{1/2}$ and ${\text{Ψ}}_k=S_{kk}^{-1/2}{\text{Φ}}_k{S}_{kk}^{-1/2}$, where $S_{k\ell }={\beta }_k{\text{Γ}}_{k\ell }{\beta }_{\ell }^H+{\text{Φ}}_k{\delta }_{k\ell }$ is a submatrix of the marginal covariance matrix $S$ of $\left(X_1,\dots ,X_K\right)$ and ${\delta }_{k\ell }=1$ if $k=\ell$ and ${\delta }_{k\ell }=0$ otherwise, for $k$, $\ell \in [K]$. Then the second identifiability constraint can be rewritten as $u_k^H{u}_k={\beta }_k^H{S}_{kk}^{-1}{\beta }_k{\text{Γ}}_{kk}=1$ and

$$\begin{gathered} u_k^H{\text{Ψ}}_{kk}{u}_k={\text{Γ}}_{kk}^{1/2}{\beta }_k^H{S}_{kk}^{-1}{\text{Φ}}_k{S}_{kk}^{-1}{\beta }_k{\text{Γ}}_{kk}^{1/2} \\ ={\text{Γ}}_{kk}^{1/2}{\beta }_k^H{S}_{kk}^{-1}\left(S_{kk}-{\beta }_k{\text{Γ}}_{kk}{\beta }_k^H\right)S_{kk}^{-1}{\beta }_k{\text{Γ}}_{kk}^{1/2} \\ ={\beta }_k^H{S}_{kk}^{-1}{\beta }_k{\text{Γ}}_{kk}-{\left({\beta }_k^H{S}_{kk}^{-1}{\beta }_k{\text{Γ}}_{kk}\right)}^2 \\ =1-1^2=0,k\in [K]. \end{gathered}$$

That is, $u_k$ is orthogonal to ${\text{Ψ}}_{kk}$. Denoting the block diagonal matrix of $\left\{S_{kk}:k\in [K]\right\}$ by $V$, we have that $R=V^{-1/2}S{V}^{-1/2}$ has submatrices

$$R_{k\ell }=S_{kk}^{-1/2}{S}_{k\ell }{S}_{\ell \ell }^{-1/2}=u_k{\text{Γ}}_{kk}^{-1/2}{\text{Γ}}_{k\ell }{\text{Γ}}_{kk}^{-1/2}{u}_{\ell }^H+{\text{Ψ}}_k{\delta }_{k\ell }.$$

Because of the orthogonality between $u_k$ and ${\text{Ψ}}_k$, the calculation of $\det (R)$ and $R^{-1}$ is straightforward: $\det (R)=\det (\text{Ω})/\prod _k\text{pdet}\left({\text{Ψ}}_k\right)$ and $Q=R^{-1}$ consists of submatrices

$$Q_{kl}=u_k{\text{Ω}}_{kl}{u}_{\ell }^H+{\text{Ψ}}_k^{+}{\delta }_{k\ell },$$

where $\text{Ω}=\text{diag}\left({\text{Γ}}_{kk}^{1/2}\right){\text{Γ}}^{-1}\text{diag}\left({\text{Γ}}_{kk}^{1/2}\right)$ is the inverse correlation matrix and $\text{pdet}(A)$ and $A^{+}$ are the pseudo determinant and Moore–Penrose pseudo-inverse of a PSD matrix $A$. Notice that ${\text{Ψ}}_k=I-u_k{u}_k^H={\text{Ψ}}_k^{+}$ and hence $\text{pdet}\left({\text{Ψ}}_k\right)=1$. In turn, the negative log-likelihood under the model (Eqs. 6 and 7) of the parameter set $\left\{\text{Γ}\right\}\cup \left\{{\beta }_k,{\text{Φ}}_k:k\in [K]\right\}$ with respect to the observed time series ${\left\{X_1^n,\dots ,X_K^n\right\}}_{n=1,\dots ,N}$ is

$$\begin{gathered} \text{nll}\left(\text{Γ},{\beta }_k,{\text{Φ}}_k;{\left\{X_1^n,\dots ,X_K^n\right\}}_{n=1,\dots ,N}\right) \\ =\text{ln det}(S)+\text{tr}\left(S^{-1}\widehat{S}\right) \\ =-\text{ln det}(\text{Ω})+\sum _k\ln \text{pdet}\left({\text{Ψ}}_k\right)+\sum _k\text{ln det}\left(S_{kk}\right)+\text{tr}(\text{Ω}\widehat{P})+\sum _{k}tr\left({\text{Ψ}}_k^{+}{S}_{kk}^{-1/2}{\widehat{S}}_{kk}{S}_{kk}^{-1/2}\right) \\ =-\text{ln det}(\text{Ω})+\text{tr}(\text{Ω}\widehat{P})+\sum _k\left[\text{ln det}\left(S_{kk}\right)+\text{tr}\left\{\right(S_{kk}^{-1}-w_k{w}_k^H\}{\widehat{S}}_{kk}\text{)}\right], \end{gathered}$$

where

$$\widehat{P}=\widehat{\mathrm{var}}\left[\left(w_k^H{X}_k:k\in [K]\right)\right],{\widehat{S}}_{kl}=\widehat{\mathrm{cov}}\left[X_k,X_l\right],w_k=S_{kk}^{-1/2}{u}_k,$$

and $\widehat{\text{var}}$ and $\widehat{\text{cor}}$ indicate the sample variance and covariance operators, for $k$, $\ell \in [K]$. The maximum likelihood estimator minimizes $\text{nll}\left(\theta ;{\left\{X_1^n,\dots ,X_K^n\right\}}_{n=1,\dots ,N}\right)$ with respect to $S_{kk}^{-1}:w_k^H{S}_{kk}{w}_k=1$. That is,

$${\nabla }_{S_{kk}^{-1}}\text{nll}=S_{kk}-{\widehat{S}}_{kk}=S_{kk}{w}_k{\lambda }_k{w}_k^H{S}_{kk},$$

for some ${\lambda }_k\in ℝ$ and for all $k\in [K]$. Because $w_k^H{S}_{kk}{w}_k=1$,

$$1-w_k^H{\widehat{S}}_{kk}{w}_k=w_k^H{S}_{kk}{w}_k-w_k^H{\widehat{S}}_{kk}{w}_k=w_k^H{S}_{kk}{w}_k{\lambda }_k{w}_k^H{S}_{kk}{w}_k={\lambda }_k.$$

Therefore, the two terms $\text{ln det}\left(S_{kk}\right)$ and $\text{tr}\left(\left(S_{kk}^{-1}-w_k{w}_k^H\right){\widehat{S}}_{kk}\right)$ may be rewritten as

$$\text{ln det}\left(S_{kk}\right)=-\text{ln}\left(1-{\lambda }_k\right)+\text{ln det}\left({\widehat{S}}_{kk}\right)$$

and

$$\text{tr}\left(\left(S_{kk}^{-1}-w_k{w}_k^H\right){\widehat{S}}_{kk}\right)=\text{tr}\left(\left(S_{kk}^{-1}-w_k{w}_k^H\right)\left(S_{kk}-S_{kk}{w}_k{\lambda }_k{w}_k^H{S}_{kk}\right)\right)=d_k-1.$$

The maximum likelihood estimation problem then reduces to minimizing

$$\text{nll}\left(\text{Ω},w_k,{\lambda }_k;{\left\{X_1^n,\dots ,X_K^n\right\}}_{n=1,\dots ,N}\right)=-\text{ln det}(\text{Ω})-\sum _k\ln \left(1-{\lambda }_k\right)+\text{tr}(\text{Ω}\widehat{P}).$$

with the restriction that $\text{diag}\left({\text{Ω}}^{-1}\right)=1$. Let $w_k^{\prime }=w_k/\sqrt{1-{\lambda }_k}$, ${\text{Ω}}^{\prime }=\text{diag}\left(\sqrt{1-{\lambda }_k}\right)\text{Ω}\text{diag}\left(\sqrt{1-{\lambda }_k}\right)$, and ${\widehat{P}}^{\prime }=\widehat{\mathrm{var}}\left[\left(w_k^{\prime H}{X}_k:k\in [K]\right)\right]$. The likelihood can be rewritten as

$$\text{nll}\left({\text{Ω}}^{\prime },w_k^{\prime };{\left\{X_1^n,\dots ,X_K^n\right\}}_{n=1,\dots ,N}\right)=-\text{ln det}\left({\text{Ω}}^{\prime }\right)+\text{tr}\left({\text{Ω}}^{\prime }{\widehat{P}}^{\prime }\right),$$

which is maximized when ${\text{Ω}}^{\prime }={\widehat{P}}^{\prime -1}$, given that $w_k^{\prime }$ is fixed for $k\in [K]$. Thus, maximum likelihood estimation is equivalent to finding $w_k^{\prime }$ minimizing $\text{ln det}\left({\widehat{P}}^{\prime }\right)$ under ${w_k^{\prime }}^H{\widehat{S}}_{kk}{w}_k^{\prime }=1$ for $k\in [K]$, which is the GENVAR procedure of Kettenring (1971).