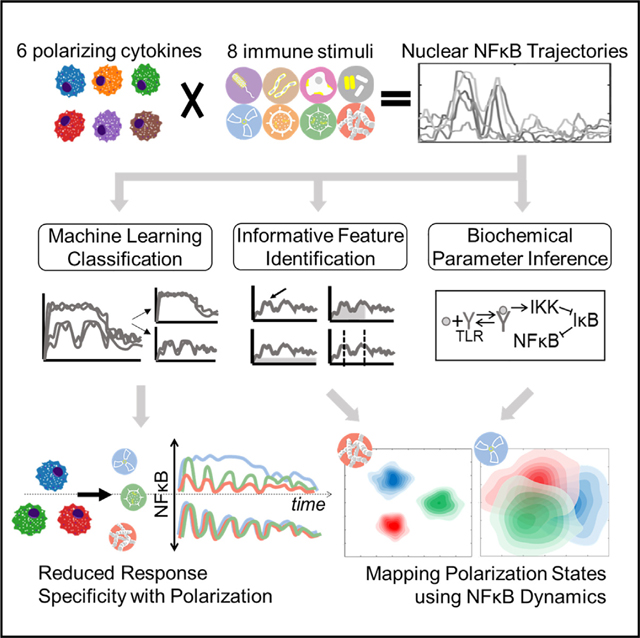
SUMMARY
The functional state of cells is dependent on their microenvironmental context. Prior studies described how polarizing cytokines alter macrophage transcriptomes and epigenomes. Here, we characterized the functional responses of 6 differentially polarized macrophage populations by measuring the dynamics of transcription factor nuclear factor κB (NF-κB) in response to 8 stimuli. The resulting dataset of single-cell NF-κB trajectories was analyzed by three approaches: (1) machine learning on time-series data revealed losses of stimulus distinguishability with polarization, reflecting canalized effector functions. (2) Informative trajectory features driving stimulus distinguishability (“signaling codons”) were identified and used for mapping a cell state landscape that could then locate macrophages conditioned by an unrelated condition. (3) Kinetic parameters, inferred using a mechanistic NF-κB network model, provided an alternative mapping of cell states and correctly predicted biochemical findings. Together, this work demonstrates that a single analyte’s dynamic trajectories may distinguish the functional states of single cells and molecular network states underlying them. A record of this paper’s transparent peer review process is included in the supplemental information.
In brief
Cellular functions are modulated by their microenvironment but are typically characterized by static molecular profiles. We quantified how macrophage dynamic signaling responses to 8 immune stimuli are affected by 6 polarizing cytokines. Measuring the dynamics of a single analyte revealed distinct stimulus-discrimination patterns and informed new maps of functional cell states.
Graphical Abstract
INTRODUCTION
Powerful new experimental single-cell measurement modalities have motivated the development of a number of analytical approaches for data-driven cell state characterization. In particular, single-cell RNA sequencing (scRNA-seq), which provides thousands of data points for each cell, prompted the development of dimensionality reduction and visualization workflows that reveal the heterogeneity of cell types and cell states within a given sample.1 However, functional cell states may involve kinetic information that is not captured by scRNA-seq measurements of mRNA abundances at a single time point. Using live-cell imaging, pioneering work examined the response dynamics of calcium signaling to ATP exposure and showed different cellular states within a heterogeneous population of epithelial cells.2 Similarly, differences in extracellular signalregulated kinase (ERK) signaling dynamics in the mitogen-activated protein kinase (MAPK) pathway reflected spatial variability in the tumor microenvironment.3 Thus, high-throughput measurements of single-cell signaling dynamics may offer a more complete or at least alternative means for characterizing the states of cells in a population. However, given the complexity of signaling dynamics data, it remains unclear what strategies are best suited for revealing and visualizing heterogeneous cell states and rendering insights about how cells differ from their dynamic signaling responses to stimuli. Here, we addressed these questions using macrophages as a model system. Macrophages not only need to detect different pathogen or host stimuli but also need to mount a response that is appropriate to the stimulus encountered.4,5 The signaling system that controls macrophage responses to pathogens, tissue injury, or cytokines activates a handful of effectors, including the central immune response transcription factor, nuclear factor κB (NF-κB). NF-κB activation shows stimulus-specific activation dynamics6–8 that can control the expression of immune response genes9–13 and reprogram the epigenome.14 A recent set of single-cell studies in primary macrophages characterized a temporal signaling code that consists of 6 dynamical features, termed “signaling codons,” that are deployed stimulus-specifically.15 Upon recognition of an activating stimulus, macrophages perform a wide range of tasks from the phagocytosis of pathogen components and cellular debris, antigen presentation, recruitment of other immune cells to sites of infection, and activation of system-wide immune responses.16 The functional responses elicited depend not only on the identity of the activating stimulus but also on the microenvironmental context of the macrophage.17 More specifically, the microenvironmental cytokine milieu polarizes macrophages into different biological functional states to accentuate specific functional stimulus-specific responses over others.18
Macrophage polarization was first described in terms of a M1 versus M2 dichotomy.19 M1 macrophages found in inflamed microenvironments defined by the presence of interferon (IFN)γ play critical roles in defending the host from pathogens, such as in bacterial, viral, and fungal infections. M2 macrophages have anti-inflammatory function and regulate wound healing and repair functions.20,21 However, it is now recognized that these M1 and M2 states are representative of a larger spectrum of macrophage states in vivo.22–26 Many previous studies have characterized differences in polarization states based on transcriptomic,27–29 epigenomic,30,31 or proteomic32,33 profiling, with recent advances in single-cell technologies revealing heterogeneity within these states.34–37 However, such snap-shot measurements of molecular abundances (that may or may not be at steady-state) merely provide markers for the actual functional states of macrophages. A quantitative characterization of macrophages in different polarization states based on their functional responses at single-cell resolution has not yet been reported.
Many studies have described molecular mechanisms by which polarizing cytokines affect NF-κB activation.38–42 Here, we examined how macrophage polarization affects the stimulus-specific dynamics of NF-κB activity and developed computational workflows to utilize these complex temporal trajectories to characterize the functional signaling cell states induced by microenvironmental cytokines. We leveraged a live microscopy workflow to generate a large dataset of single-cell nuclear NF-κB time course trajectories in response to 8 stimuli and 6 polarization conditions. We applied machine learning (ML) approaches to quantitatively compare NF-κB response specificity across polarization states and decompose NF-κB responses into informative dynamic trajectory features (signaling codons). Applying machine-learning classifiers either directly to the time-series data or the derived signaling codons, we found that stimulus-response specificity was diminished with polarization. However, which specific stimulus responses were less distinct and which signaling codons were driving these losses in distinction varied with polarization state. Given the observed differential effects of polarization on NF-κB response dynamics, we used the single-cell signaling trajectories to generate mappings of macrophage polarization states. The first mapping was based on a dimensionality reduction via functional principal-component analysis (PCA). The second mapping was based on decomposing trajectories into signaling codons and was used to predict the cell states of macrophages conditioned by an unrelated fatty acid. The third mapping was based on biochemical parameters inferredfrom an established mechanistic mathematical model of the NF-κB signaling network. These inferred biochemical parameters constituted an alternative dimensionality reduction of the trajectory data and give insight about the state of the molecular network.
RESULTS
An experimental pipeline for studying NF-κB dynamics in polarized macrophages
To study how polarization of macrophages by microenvironmental cytokines may affect NF-κB signaling responses to various pro-inflammatory stimuli, we generated a large dataset with mVenus-RelA knockin macrophages that were polarized in 6 different conditions and then stimulated with 8 different pro-inflammatory stimulation ligands. Generating this large dataset with 48 experimental conditions was made possible by producing macrophages from a HoxB4-transduced myeloid precursor line43 derived from the mVenus-RelA knockin mouse strain. Macrophages produced in this manner showed responses that were close to indistinguishable from those observed in bone marrow-derived macrophages in terms of NF-κB signaling dynamics and endotoxin-induced gene expression in contrast to the often-used Raw264.7 cell line (Figures S1A–S1C). Importantly, cell cultures initiated with the myeloid precursor line may be more reproducible than when bone marrow is used, as the latter contains macrophage precursor cells at different stages of maturity and in variable relative abundances. In addition, control experiments were performed to ensure that Hoechst as nuclear marker did not cause signaling artifacts (Figure S1D) and that potential photobleaching did not affect the time course measurement of nuclear mVenus-RelA fluorescence (Figures S1E and S1F).
Within our experimental workflow, differentiated macrophages were exposed to interferons, IFNβ or IFNγ, to polarize toward M1, interleukin (IL)-10, IL-13, or IL-4 for M2 polarization, or unexposed for naive (M0) polarization for 24 h, and then stimulated with agonists for different toll-like receptors such as R848 (Toll-like receptor [TLR]8), poly(I:C) (TLR3), Pam3CSK (TLR1/2), CpG (TLR9), Flagellin (TLR5), FSL1 (TLR2/6), or lipopolysaccharide (LPS) (TLR4) as well as the pro-inflammatory cytokine tumor necrosis factor (TNF) (Figure 1A). The resulting single-cell nuclear NF-κB trajectories were captured by an established live-cell microscopy workflow and quantified by a robust image analysis pipeline15 (Figure S2A). For each experimental condition, we obtained two biological replicates, with hundreds of single-cell NF-κB trajectories that passed quality control metrics (see STAR Methods) in each dataset (Table S1). This dataset encompasses a total of 68,056 cells, each characterized by a trajectory derived from 98 microscopy images.
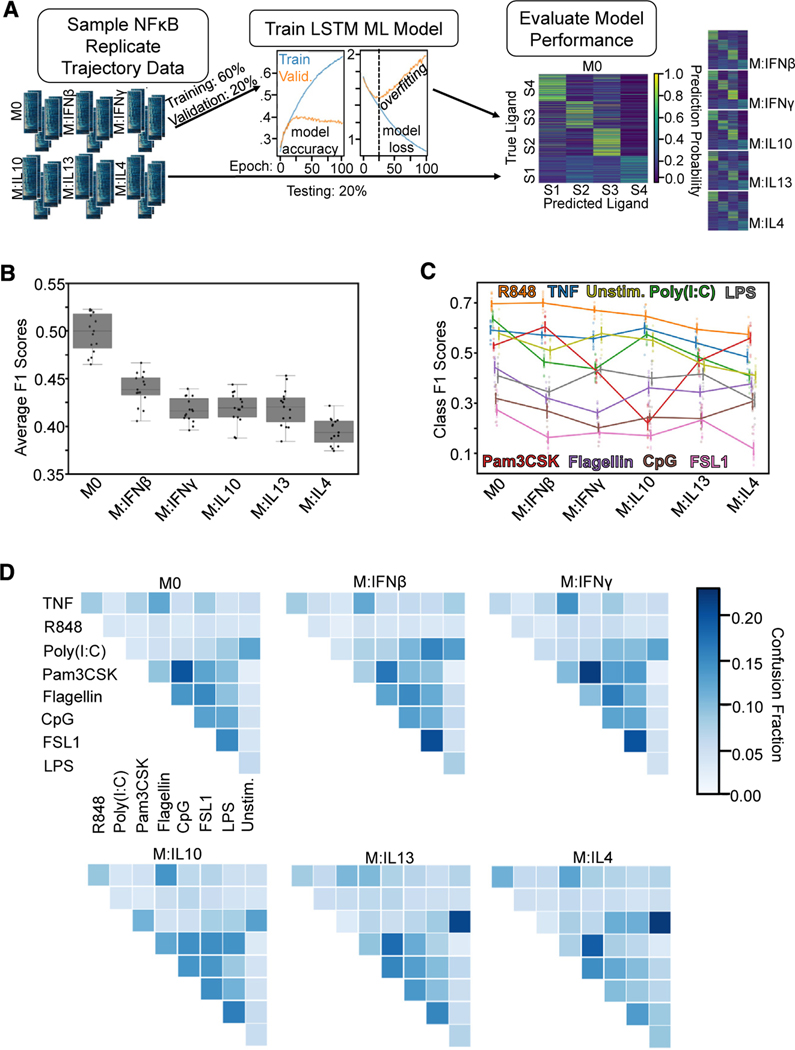
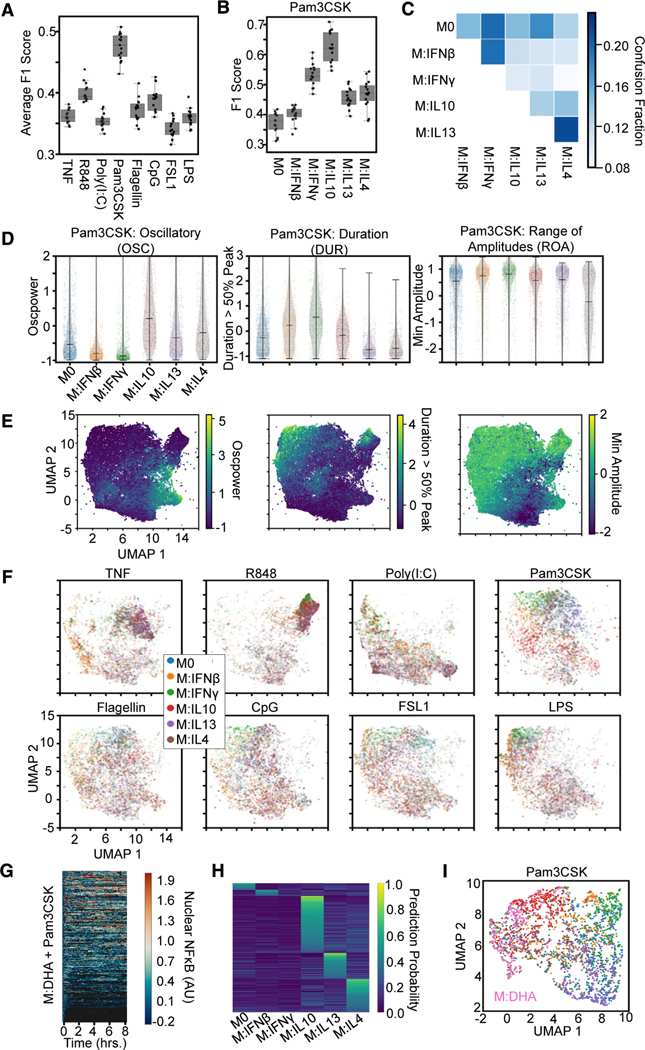
Figure 1. Single-cell NF-κB trajectories across 6 polarization states following 8 different stimulations.
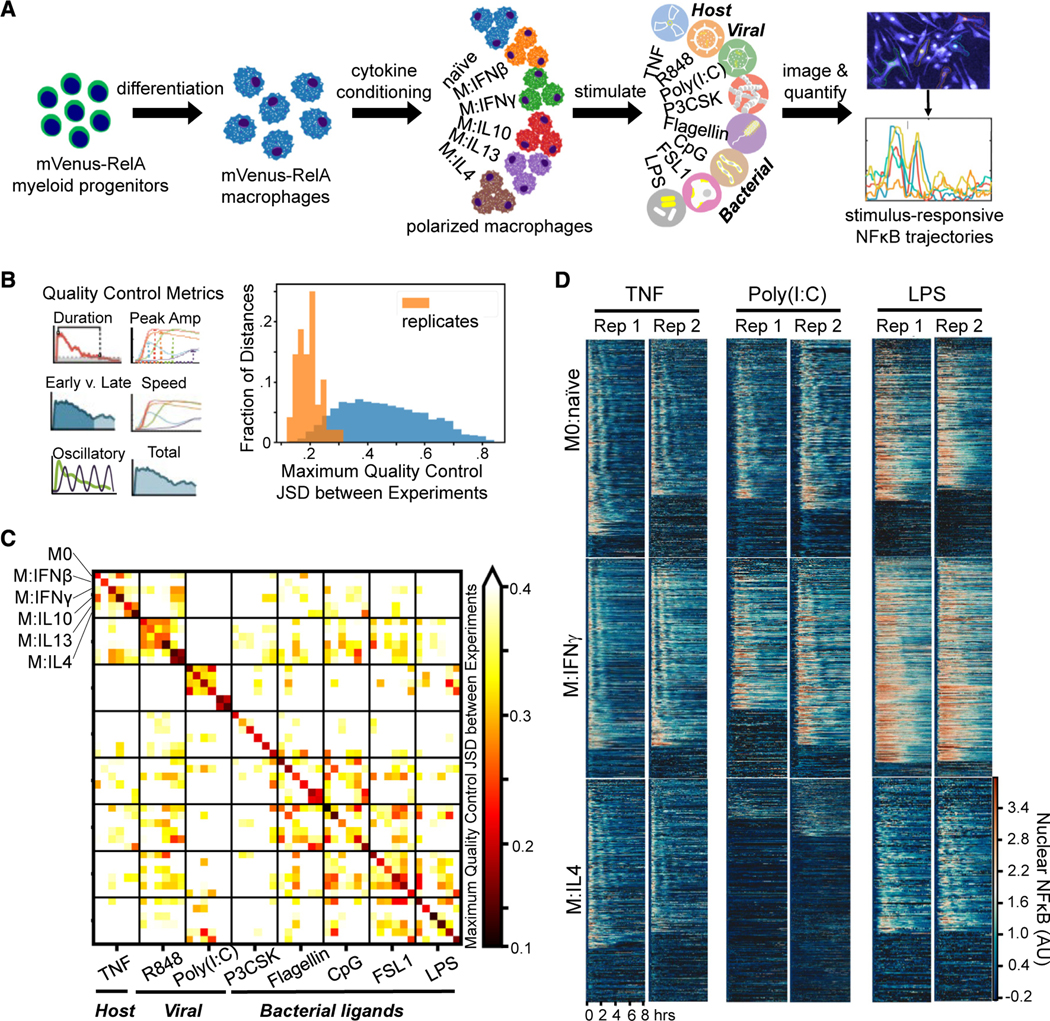
(A) Experimental pipeline for obtaining single-cell NF-κB responses in different polarization and stimulation conditions to study the effect of polarization on stimulus responses.
(B) Histogram of maximum Jensen-Shannon distance (JSD) between distributions of quality control (QC) metrics from experiments, with distances between replicate experiments in orange and distances between different experimental conditions in blue.
(C) Along the diagonal of the distance matrix are the maximum QC JSD between replicates for each experimental condition. Experimental conditions are ordered by stimuli and further sub-ordered by polarization state. The off-diagonal elements are the maximum QC JSD between replicates of different experimental conditions. Maximum of color bar set to 0.4 to focus on smaller distances.
(D) Example replicate NF-κB trajectory datasets in M0, M:IFNγ, and M:IL-4 polarization states with TNF, poly(I:C), and LPS stimulation. Each row in a heatmap corresponds to a single macrophage in the experiment, and the color corresponds to the amount of nuclear (active) NF-κB.
We examined the replicates by focusing on previously identified informative trajectory features, termed signaling codons,15 for quality control (Table S2; Figure 1B). Using the Jensen-Shannon distance (JSD) of these quality control metrics between each population of cells as a measure of dissimilarity, we found that the maximum JSD between replicates was in general much smaller than between cells stimulated in different conditions. This assured us that the biological differences of interest are larger than the technical variability associated with the experimental and image analysis workflow. We used the JSD as a measure of dissimilarity between distributions since it is a distance metric and observes properties such as symmetry and the triangle inequality. A more detailed analysis revealed that some polarization and stimulus combinations to be more similar than most (Figure 1C), such as responses to R848 in cells polarized with IL-13 and IL-4 or responses to Flagellin and CpG in cells polarized with IFNβ. Visual inspection of heatmaps that depict the actual time course measurements (Figure 1D), as well as visualizations of the trajectories in aggregate44–46 (Figure S2B), confirmed that stimulus-specific signaling characteristics are preserved in each replicate, while the precise fraction of seemingly non-responding cells varied between some replicates.
These preliminary visualizations demonstrate differences in NF-κB activation dynamics under different polarizing cytokine treatments. Given the importance of NF-κB for orchestrating immune responses, these differences in activation likely underlie functional differences between polarization states rather than being simply indirect effects of polarization. Indeed, building a linear model from our measurements of total NF-κB activity to predict gene expression data from polarized human macrophages following stimulation47 (see STAR Methods), we find for a majority of stimulus-responsive genes that better model fits are achieved with the original versus permuted data (Figure S3A), indicating NF-κB signaling dynamics can carry information about differences in gene expression related to polarization state. These predictions perhaps unsurprisingly can be improved if measurements of baseline chromatin accessibility for each polarization state are also included (see STAR Methods; Figure S3B), suggesting chromatin accessibility can add information to NF-κB signaling dynamics to better inform differences in gene expression related to polarization state. Considering this functional relevance of NF-κB activation, we then turned to computational data analysis methods that respect the single-cell nature of the data to characterize the effect of polarization on the stimulus-response NF-κB signaling dynamics.
An ML classifier characterizes stimulus-response specificity
Given that polarization appears to alter NF-κB stimulus responses, we asked whether polarization may affect the degree of stimulus-response specificity in NF-κB dynamics. To quantify stimulus distinguishability based on NF-κB trajectories, we first implemented a long short-term memory (LSTM)-based ML classifier.48 LSTM is a recurrent neural network (RNN) architecture developed to handle the vanishing/exploding gradient problem frequently encountered when training RNN’s. LSTM networks are well suited to perform classification or prediction tasks on time-series data because of their ability to learn long-term dependencies in input sequences.49 This motivated our choice to leverage an LSTM-based model, as we could reasonably utilize the time-series data directly as input without needing to find an appropriate transformation of the data into features first.
The classifier was trained on different ligand identification tasks using 80% of the stimulus-response trajectories from all polarization states as input data (Figure 2A; see STAR Methods). By comparing the output model’s classification performance on the remaining 20% of the data, which was unseen during training, we were able to quantify how stimulus distinguishability was affected by polarization (Figure 2A). For each classification task, the data were resampled, and the training procedure was repeated 15 times to estimate uncertainty in the obtained performance metrics. To quantify classification performance, two metrics were used. First, the F1 score, the harmonic mean of the accuracy and precision for each class, is a measure of classification performance and hence stimulus distinguishability. Second, the confusion fraction, the mean incorrect prediction probability between pairs of classes, quantifies the convergence of the NF-κB trajectories associated with two stimuli. We observed that the LSTM-based classifier achieved better performance than a random forest classifier and a simple feedforward network classifier using the time-series data across all polarization states as input (Figure S4A).
Figure 2. An LSTM-based ML classifier reveals decreased stimulus-response specificity with macrophage polarization.
(A) For each classification task, data were sampled from all polarization states to train and test the LSTM ML model. Input data were split into training (60%), validation (20%), and testing sets (20%), where validation loss was used to monitor model overfitting.
(B) Macro-averaged class F1 score for the task of classifying each ligand (including unstimulated) across polarization states demonstrates loss of stimulus-response specificity with polarization.
(C) Class F1 scores across polarization states from the same model as in (B).
(D) Confusion fractions across polarization states for different ligand stimulations reveal polarization-dependent patterns in stimulus-response specificity. Error bars in (C) correspond to 95% confidence intervals with n = 15.
We first applied the LSTM-based classifier to the tasks of discriminating individual ligands. We found that macrophages showed higher macro-averaged F1 scores in unpolarized naive conditions than any of the five polarization conditions, suggesting naive macrophages have greater stimulus-response specificity than their polarized counterparts (Figure 2B). This remained true even when using different classifier models and when separate models were trained for each polarization state (Figures S4B and S4C). We then considered ligand source classes: we combined NF-κB trajectories from poly(I:C) and R848 under the “viral” label, Pam3CSK, Flagellin, CpG, FSL1, and LPS under the “bacterial” label, and considered TNF as “host.” Naive macrophages still showed the greatest macro-averaged F1 score for the task of classifying ligand sources as well (Figures S4D–S4F), confirming the loss of stimulus-specificity with polarization.
Examining the performance of each ligand individually, however, we found that the decrease to stimulus-response specificity with polarization was caused by different ligand identifiability losses depending on the state (Figure 2C). For example, the ability to distinguish host cytokine TNF was maintained across polarization states, whereas other pathogen-associated molecular pattern (PAMP) distinguishability like Pam3CSK dropped with IL-10 polarization and Flagellin dropped with IFN polarization. We then asked what caused the diminished identifiability by inspecting the confusion fractions between ligands (Figure 2D). Confusion with unstimulated cells (0.21 ± 0.01, 0.22 ± 0.01) suggested the most diminished responses to poly(I:C) with IL-13 and IL-4 polarization. Confusion among bacterial ligands was common across polarization states; however, pairs such as FSL1 and LPS (0.2 ± 0.01) were particularly elevated with IFN conditioning. Overall, the ML analysis revealed losses in the stimulus-specificity of NF-κB signaling with all polarizers, but each polarization condition affected different ligand responses differentially.
Specific dynamical trajectory features are informative for distinguishing stimuli
While the LSTM-based ML classifier revealed that the distinguishability of stimulus-response NF-κB trajectories was affected by polarization, we next wanted to describe how alterations in NF-κB response trajectories induced by polarization drove these changes in stimulus identifiability. Hence, we sought to first identify trajectory features that are important for stimulus-response specificity. Refining a previously established strategy,15 we generated a library of 190 trajectory features derived from the NF-κB time-series data, which was further reduced to 71 features after filtering for highly correlated features (Table S3; see STAR Methods). These 71 features were then used as input for an XGBoost ML classifier (Figure 3A), a model comprised of an ensemble of decision trees built in an additive manner through boosting.50,51 The XGBoost model had similar performance to the LSTM-based model and recapitulated the loss in performance with polarization when tasked with discriminating the individual ligands across the polarization states (Figure 3B).
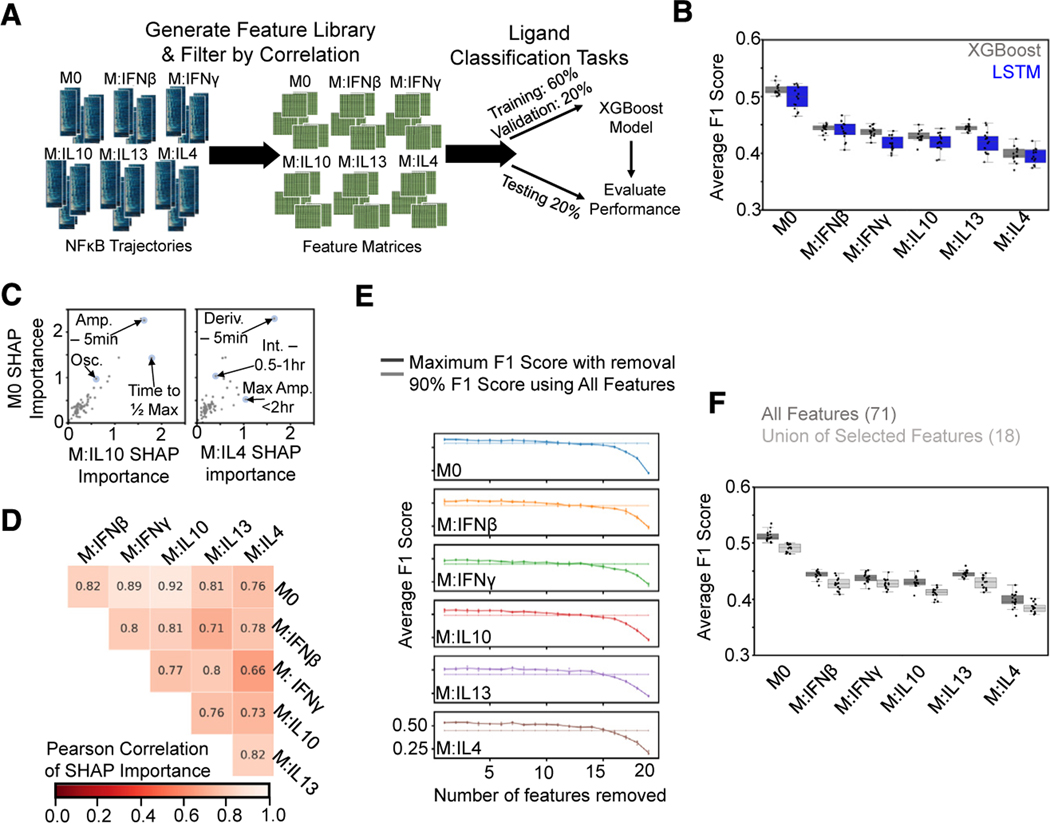
Figure 3. A feature-based ML classifier recapitulates LSTM results and reveals features informative for specificity.
(A) A set of features was derived from the NF-κB trajectories, and the resulting feature library was used to train and test XGBoost classifiers on ligand discrimination tasks.
(B) Comparison of macro-averaged class F1 scores for the task of classifying ligands across polarization states for XGBoost and LSTM models reveals similar drop in performance with polarization.
(C) Comparison of mean absolute SHAP values summed over classes for M0 model versus IL-10 and IL-4 models from XGBoost models trained independently for each polarization state on the task of classifying ligands (Amp., amplitude; Deriv., derivative; Int., integral; Osc., oscillatory).
(D) Pearson correlation of mean absolute SHAP values summed over classes between different polarization models.
(E) Maximum macro-averaged F1 score obtained as features are removed from the set of top 20 features returned by the SHAP analysis for each polarization state. Model performance deteriorates once 14–15 features are removed; hence, 6–7 features are retained. Solid line with increased transparency displays threshold of 90% macro-averaged F1 score using all features for training.
(F) Comparison of XGBoost model macro-averaged F1 score when trained across all polarization states using all features (same model as in B) versus union of the selected features. Error bars in (E) correspond to 95% confidence intervals with n = 15.
To identify trajectory features informative for response specificity, we then trained an XGBoost model for each polarization state separately. We utilized the Shapley additive explanations (SHAP) method52 that was developed to provide interpretability to ML models to assess feature importance (see STAR Methods). Comparing the SHAP-derived feature importance values between polarization states did reveal some differences; for example, “time to ½ max” and “max amplitude < 2 h” were more important for classification of IL-10 and IL-4 responses, respectively, compared with M0 responses (Figure 3C). Overall, however, comparisons across polarization states demonstrated similar utilization of trajectory features in model predictions (Figure 3D; Table S4).
To define a minimal subset of informative features to utilize in subsequent analyses, we started with the top 20 most important features identified through the SHAP method for each polarization state (Table S4) and then iteratively removed features from this set until model performance declined (see STAR Methods). The average F1 scores of the resulting models did not greatly deteriorate until 14–15 features had been removed from the original set of 20, resulting in 6 or 7 features retained for each polarization state (Figure 3E). Using the union of the selected feature subsets (18 features total) for training a model across the polarization states resulted in performance not much less than that of using all features (Figure 3F). The selected features (Table S5) describe early, peak, and late activation speeds (EAS, PAS, and LAS), range of amplitudes (ROA), early phase activity (EPA), duration (DUR), and oscillations (OSC). As they convey information about extra-cellular stimuli to the nucleus, these seven features have been dubbed signaling codons.15
To further reduce the dimensionality of these informative features, we used linear discriminant analysis (LDA) to find a linear combination of a representative subset of signaling codons that attempts to discriminate all TNF from all PAMP responses in our dataset (Figure 4A). Prior work has suggested that the level of immune threat a macrophage encounters (host cytokine versus PAMP) is encoded by responsive NF-κB signaling dynamics,53 and we wondered how this may be achieved via signaling codons. Examining the coefficients of the LDA model, we found increased immune threat was associated with reduced EAS, PAS, and OSC but increased ROA, EPA, and DUR (Figure 4B). The analysis provided a ranking of experimental conditions by relative immune threat, where, for example, maximal macrophage activation is elicited by LPS plus IFNγ8,15,39 (Figure 4C). Overall, M2 polarizers were associated with lower immune threat values and M1 polarizers with higher values; however, examining each stimulation condition separately, the relative ordering of individual polarization conditions varied (Figure 4D).
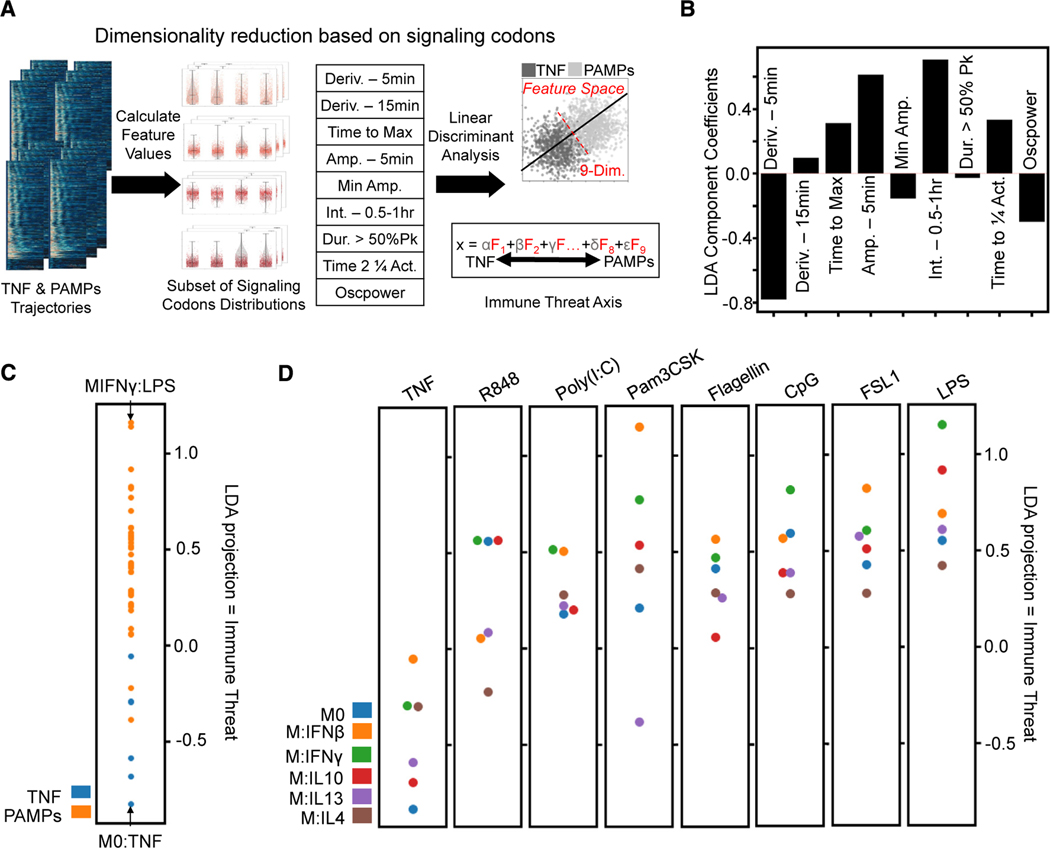
Figure 4. Characterization of informative features by immune threat.
(A) The subset of signaling codons is calculated from the single-cell NF-κB trajectories, and then LDA finds a linear combination that best distinguishes threat level (host TNF versus PAMP responses). Upsampling the smaller host TNF class to balance the classes gave an overall accuracy of approximately 68% for this binary classifier (Deriv., derivative; Amp., amplitude; Int., integral; Act., activity).
(B) Coefficient applied to each informative feature to obtain the LDA projection, hence characterizing immune threat: decreased 5-min derivative, increased time to max, increased 5-min amplitude, increased 2nd half-hour integral, increased time to quarter total activity, and decreased oscillations.
(C) Comparing mean LDA projection of host TNF versus pathogen (PAMPs) responses; this axis quantifies immune threat as pathogen responses are more positive along it.
(D) Comparing mean LDA projection of different polarizer responses for each stimulation condition shows more M1-polarized responses with positive LDA values and more M2 polarized responses with negative LDA values.
Polarizing cytokines have distinct effects on NF-κB stimulus-response specificities
We could now investigate how polarization affects the stimulus-specific deployment of signaling codons and how these changes drive losses in stimulus-response specificity. We first examined the increased confusion of host cytokine TNF with polarization. For IL-4 polarization, which had the lowest discrimination of TNF (Figure 2C), increased confusion was evident with R848, poly(I:C), CpG, and LPS (Figure 5A). IL-4 polarization caused R848 deployment of signaling codons, such as EPA and DUR to become more TNF-like (Figures 5B and 5C). In other polarization states, we found that confusion of PAMPs with TNF was partially driven by a reduction of the EAS and OSC of TNF responses, rendering them more “pathogen-like” (Figures S5A–S5F).
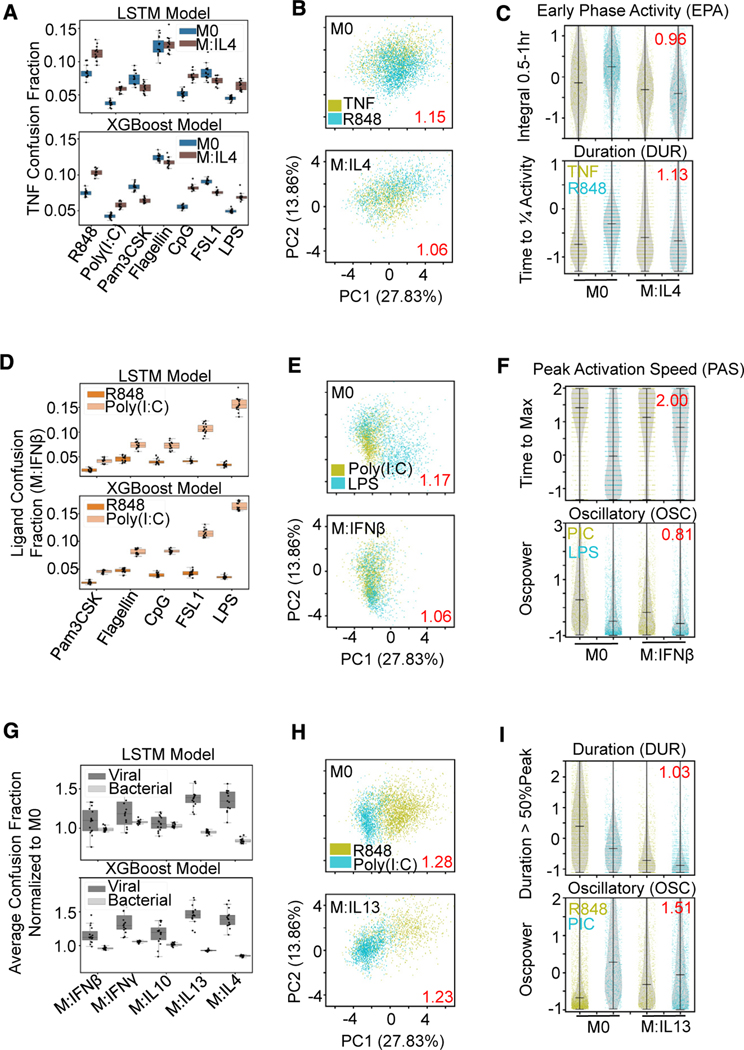
Figure 5. Macrophage polarization affects ligand distinguishability uniquely.
(A) Confusion fraction derived from both the LSTM and XGBoost models between the host ligand (TNF) and the pathogen ligands (R848, poly(I:C), Pam3CSK, Flagellin, CpG, FSL1, and LPS) in the IL-4 and M0 polarization states shows larger increase with R848, poly(I:C), CpG, and LPS stimulation.
(B) PCA projection of the 18 signaling codons from the single-cell responses to TNF and R848 with M0 and IL-4 polarization; dispersion measure in red (average pairwise distance between classes divided by average pairwise distance within classes) illustrates convergence of stimulus responses with IL-4 polarization.
(C) Decreased early phase activity and duration feature distributions of R848 responses with IL-4 polarization contribute to convergence; log2 fold reduction in Jensen-Shannon distance between ligand responses with polarization in red.
(D) Confusion fraction derived from both the LSTM and XGBoost models between the viral ligands (R848, poly(I:C)) and the bacterial ligands (Pam3CSK, Flagellin, CpG, FSL1, and LPS) in the IFNβ polarization state; illustrates greatest confusion between poly(I:C) and LPS.
(E) PCA projection of the single-cell responses to poly(I:C) and LPS with M0 and IFNβ polarization illustrates convergence with IFNβ polarization.
(F) Decreased peak activation speed of LPS and decreased oscillations of poly(I:C) (PIC) contribute to convergence of stimulus responses with polarization.
(G) Average confusion fraction within viral and bacterial ligands normalized to M0 performance from the same LSTM and XGBoost models shows greater relative viral ligand confusion with polarization compared with bacterial.
(H) PCA projection of the single-cell responses to R848 and poly(I:C) with M0 and IL-13 polarization illustrates convergence of stimulus responses with IL-13 polarization.
(I) Decreased duration and increased oscillations of R848 responses contribute to convergence of stimulus responses with polarization.
Next, we further investigated the convergence of distinct pathogen response signals with polarization. Confusion between viral and bacterial ligands was elevated across all polarization states, particularly IFNβ (Figure S4F). We found that poly(I:C) and LPS deployment of signaling codons became more similar with IFNβ polarization (Figure 5D), with the convergence driven most by decreased PAS upon LPS stimulation and decreased OSC upon poly(I:C) stimulation (Figures 5E and 5F), corresponding to an increase in immune threat for both ligands. Inspecting EPA and OSC in other polarization states (Figures S5G–S5L) supported the notion that IFNβ or IFNγ polarization converged responses to diverse PAMPs into a more monolithic or stereotyped pathogen-like response, whereas IL-10 and IL-13 polarization diminished these pathogen-like features.
We then examined the ability of macrophages to distinguish particular PAMPs within a pathogen class. We examined the confusion fraction between the two viral ligands and the average confusion fraction between all pairs of bacterial ligands across all polarization conditions. Confusion fractions normalized to the naive condition scores revealed polarization had a greater effect on viral PAMPs distinguishability compared with bacterial, particularly with IL-13 and IL-4 polarization (Figure 5G). A large decrease in the response DUR for R848 and poly(I:C) responses with IL-13 polarization, as well as increase in OSC for R848, drive the convergence of these two viral PAMPs with polarization (Figures 5H and 5I).
NF-κB stimulus-response dynamics can map macrophage polarization states
The fact that NF-κB stimulus-response dynamics are affected by polarization suggests that, conversely, polarization states may be identifiable by the dynamical NF-κB response to a specific stimulus. To investigate this, we trained an XGBoost model using the library of 71 features to identify the polarizing cytokines across stimulation conditions (Figure 6A) and identified the ten features most important for this model’s predictions, using the SHAP values (Table S6). We found that the classifier had the greatest macro-averaged F1 score with Pam3CSK stimulation, suggesting this stimulation condition best separates the polarization states. In particular, responses to Pam3CSK stimulation provided greater discrimination of IFNγ and IL-10 polarization (Figures 6B and 6C). To independently corroborate the discrimination of polarization states, we trained an LSTM classifier that also had a greater macro-averaged F1 score with Pam3CSK stimulation (Figure S6A).
Figure 6. Mapping macrophage polarization states with NF-κB signaling response dynamics.
(A) Macro-averaged class F1 scores from an XGBoost model trained (using the library of 71 features) for the task of classifying each polarizer across stimulation conditions provide a quantification of polarizer distinguishability for each stimulus.
(B) F1 scores for Pam3CSK stimulation responses reveal identification of IFNγ and IL-10 drive distinguishability.
(C) Confusion fractions highlights distinguishability of IL-10.
(D) Distributions for top 3 informative feature from the single-cell responses to Pam3CSK across all polarization conditions. Oscillatory values separate IL-10 from other M2 polarizers and M1 polarizers from the other states. Duration values separate IL-13 and IL-4 from other states and slightly separate IFNβ from IFNγ. Minimum amplitude separates IL-13 from IL-4.
(E) Uniform manifold approximation and projection (UMAP) of all NF-κB responses (sampled such that number of cells per condition is equivalent, 1,338) using the top 10 features identified by SHAP analysis colored by feature values.
(F) UMAP of the NF-κB responses (same as in E) split by each stimulus colored by polarization state.
(G) Single-cell nuclear NF-κB trajectories from hMPDMs pretreated with docosahexaenoic acid (DHA) and stimulated with Pam3CSK.
(H) Single-cell classification probabilities for DHA-pretreated Pam3CSK-stimulated macrophages from XGBoost model trained on polarized Pam3CSK responses defined by the top ten features identified in the polarization classification task.
(I) UMAP of Pam3CSK-stimulated response colored by polarization states (colors same as F) or pretreated with DHA.
Examining the top 3 identified trajectory features revealed how polarizers differentially alter NF-κB dynamics in response to Pam3CSK, particularly among M1 and M2 type polarizers, thereby permitting distinguishability of cell states. IL-10-polarized responses to Pam3CSK differ from those polarized with IL-13 and IL-4 due to their increased OSC, and IFNγ-polarized responses differ from those polarized with IFNβ due to their increased DUR (Figure 6D). Finally, we used the top ten important features for uniform manifold approximation and projection (UMAP) to display the 6 polarization states. To provide some orientation, we first examined how the values of the trajectory features varied over this map (Figure 6E), which revealed distinct regions of increased OSC and DUR and decreased ROA. Visual inspection of the UMAP colored by polarization states indicated Pam3CSK stimulation did indeed best separate the six polarization states compared with other stimulation conditions (Figure 6F). In parallel, we also used functional principal-component analysis (PCA)54 to directly dimensionality-reduce the single-cell NF-κB trajectories and used the top ten principal components for UMAP visualization (Figures S6B and S6C); these revealed similar discrimination patterns but do not identify signaling features that are responsible.
To explore the utility of characterizing macrophage polarization states with NF-κB signaling dynamics, we employed our analysis to characterize an additional cell state. Deficiency of docosahexaenoic acid (DHA) has been associated with several diseases, and studies have reported health benefits of dietary supplementation.55,56 These effects might be partially explained by DHA promoting an anti-inflammatory response, and indeed, DHA has been described in recent studies as being able to induce a M2-like macrophage polarization state.57,58 Given Pam3CSK stimulation demonstrated the greatest identifiable distinction between polarization conditions, macrophages pretreated with DHA were stimulated with Pam3CSK, resulting in 350 single-cell NF-κB trajectories (Figure 6G). The top ten features identified from the polarization distinguishability task were then used to train an XGBoost model on the Pam3CSK-stimulated trajectories and then predict the polarization states of the DHA-pretreated cells. A majority of the DHA pretreated cells had the highest prediction probability for an M2 polarization state, with very little prediction probability for naive or M1 polarization states (Figure 6H). Finally, UMAP visualization of the Pam3CSK-stimulated responses across the polarization states plus pretreatment with DHA reveals IL-10 and IL-4 polarization states in closer proximity to the DHA pretreatment (Figure 6I).
Inferred biochemical parameters distinguish polarizers, similar to signaling dynamics
Differential NF-κB signaling responses to stimulation among polarization states are due to differential kinetic rate constants that control the dynamics of NF-κB signaling. Such biochemical parameters define the molecular network state that underlies what is phenomenologically described as “cell state.” We therefore asked whether we could use an established mathematical model of the NF-κB signaling network to derive biochemical parameter distributions for each polarization condition based on the single-cell NF-κB trajectory data and thereby characterize the cell state not merely based on phenomenological features but molecular network features. We leveraged a mechanistic ordinary differential equation (ODE) model that connects upstream ligand-receptor interactions to downstream NF-κB nuclear translocation via IκB kinase (IKK) activation and negative feedback via inhibitor of NF-κB alpha (IκBα) production.15
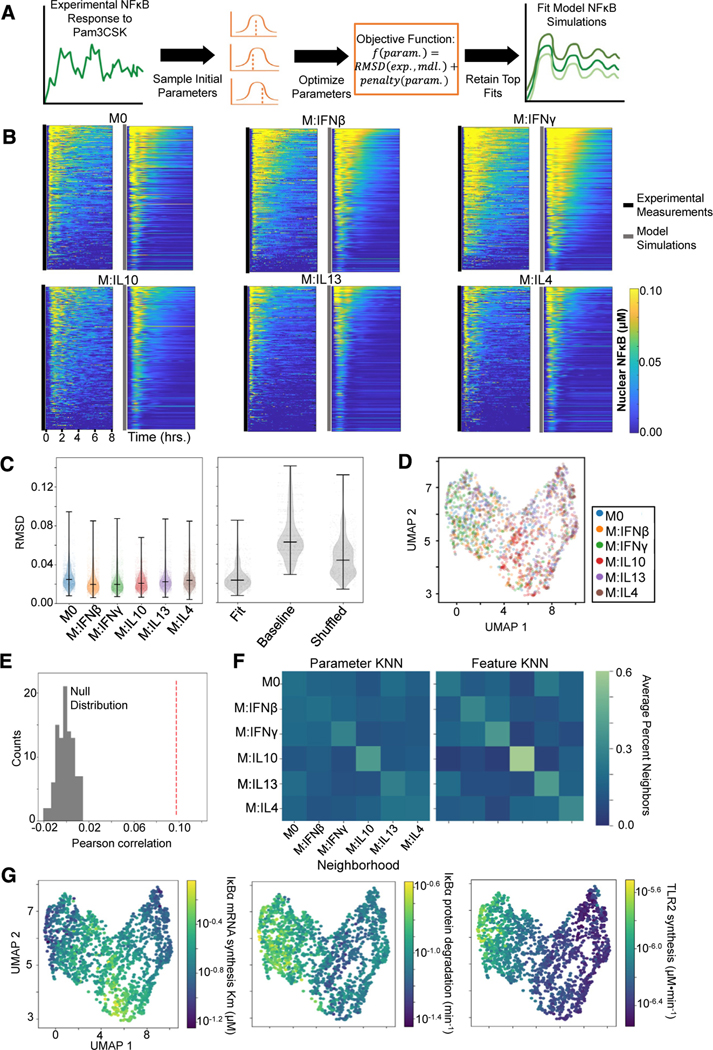
We focused on NF-κB activation following Pam3CSK stimulation since these data demonstrated the greatest distinction among polarization states and hence utilized only the upstream TLR1/2 module of the mechanistic model (Figure S7A). We selected a subset of biochemical parameters from this model to optimize that spanned across the topology and demonstrated greater sensitivity when varied (Figure S7B). From each polarization state, 300 single cells were randomly sampled, and parameter fits for each cell were obtained. Briefly, for each cell, a local optimization procedure was repeated 100 times, each time initialized at a different set of biochemical parameter values. This optimization procedure aimed to minimize the deviation between the experimental and model NF-κB trajectories and the deviation of the optimized parameter values from the published parameter values. The top ten parameter fits among the 100 iterations based on this objective were retained for downstream analysis (Figure 7A; see STAR Methods).
Figure 7. Characterizing macrophage polarization states with inferred biochemical parameters.
(A) General pipeline for obtaining model parameter fits for a single-cell NF-κB response to Pam3CSK consists of randomly initializing the optimization procedure 100 times and retaining the ten fits with the minimum objective value. This objective function is composed of a root-mean-square deviation (RMSD) term that captures the discrepancy between the experimental (exp.) and model (mdl.) NF-κB trajectory and a penalty term that captures deviation of the parameters (param.) from the published baseline values.
(B) Experimental NF-κB trajectories of 300 sampled cells per polarization state alongside the model simulations corresponding to their best parameter fits.
(C) RMSD between the model simulations resulting from the top 10 parameter fits and the corresponding experimental trajectory across the polarization states (left) and the RMSD between the experimental trajectories and the best-fit parameter model simulations, the baseline published parameter model simulation, and shuffled fit parameter model simulations (right).
(D) UMAP visualization based on biochemical parameter fits of sampled single cells colored by polarization states.
(E) Pearson correlation between cell-cell parameter dissimilarities and feature distances (red dashed line) compared with null distribution of Pearson correlation values computed from permuting the data 100 times.
(F) Average neighborhood composition for each polarization state based off the parameter dissimilarities (left) and feature distances (right). The 15 nearest neighbors were chosen to define the neighborhood for each cell (equivalent to UMAP).
(G) UMAP visualization (as in D) with cells colored with average parameter value across the top ten fits.
Visualizing the model simulations corresponding to the top parameter fit alongside the experimental trajectories demonstrates good agreement (Figure 7B). Quantifying the root-mean-square deviation (RMSD) between the top 10 model fits and the corresponding experimental trajectory for all cells sampled within each polarization state reveals average RMSD values below 0.03 across all states. For comparison, the average RMSD between the model simulation using the published baseline parameter values and the experimental trajectories was greater than 0.06, and randomly shuffling the parameter fits across the experimental trajectories gave an average RMSD greater than 0.04 (Figure 7C), highlighting the improvements obtained by the optimization procedure.
Examining the distribution of fit biochemical parameters demonstrates differences in values across polarization states (Figure S7C). Utilizing a cell-cell dissimilarity measure based on the average JSD between the retained parameter fits (see STAR Methods), we generated a UMAP visualization of the sampled Pam3CSK-stimulated cells (Figure 7D). Similar to the prior analysis of Pam3CSK responses based on NF-κB trajectory features, distinguishability of polarizers appears to be driven by IL-10-polarized cells separating from other M2 polarized cells and IFNγ cells separating from other M1-polarized cells. For a more quantitative assessment, we compared the pairwise cell dissimilarity matrix based on the fit parameter values and the pairwise cell distance matrix based on the previously identified top 10 informative trajectory features. We found a significant positive Pearson correlation between corresponding cell-cell parameter dissimilarity and feature distance values (Figure 7E; see STAR Methods). Finally, we utilized these matrices to define the k-nearest neighbors (KNN) for each cell. These KNN graphs are the input ultimately visualized in the UMAP illustrations. For each polarization state, we report the average composition of their neighborhoods, revealing similarities between the parameter and feature KNN (Figure 7F). We found with both the parameter and feature KNN, IL-10-polarized cells have on average the greatest proportion of their own polarization state in their neighborhoods, followed by IFNγ cells, which have a greater proportion of their neighborhoods occupied by IFNβ cells.
Finally, we asked what biochemical parameter perturbations might be associated with specific polarization treatments. For IL-10 polarization, we observed an increased predicted Km for NF-κB-induced transcription of IκBα (Figure 7G), suggesting a potential reduced sensitivity of IκBα transcription in response to NF-κB activity. A Kolmogorov-Smirnov test performed between the IL-10 and naive parameter distribution found a statistically significant difference (p = 1.32e–71). The model-inferred free IκBα degradation rate was increased among IFNγ polarized cells (IFNγ versus M0 p = 3.40e–16), which is consistent with prior experimental observations of IFNγ induction of proteasome activators, which accelerate IκBα degradation.39 We also observed increased TLR2 synthesis rates predicted for M1 type polarizers and decreased synthesis rates predicted for M2 type polarizers, especially IL-13 and IL-4 (IL-4 versus IFNγ p = 3.71e–148). This finding is consistent with recent scRNA-seq measurements of polarized hMPDMs,59 which demonstrates reduced expression of TLR2 with IL-4 polarization (Figure S7D). These studies demonstrate the feasibility of using phenomenological stimulus-response data to infer kinetic biochemical parameters that may provide a molecular-mechanistic characterization of distinct functional cell states.
DISCUSSION
The “cell states” of macrophages induced by polarizing cytokines have been profiled via steady-state measurements of the transcriptome or epigenome. However, these snap-shot profiles may not fully describe the dynamic functions of macrophages. One functionally important indicator of the dynamic response of macrophages is the transcription factor NF-κB, for which we recently developed a fluorescent reporter mouse that allows tracking of its nuclear activity in single cells by live-cell imaging. Here, we explored the ability to utilize NF-κB stimulus-responsive activation dynamics to characterize the functional states of macrophages exposed to different polarizing cytokines. We first generated an unprecedented dataset of single-cell NF-κB response trajectories associated with a wide array of polarizing cytokines and stimulating ligands and then developed analytical workflows for interpreting these complex datasets. Our analyses revealed polarization-specific effects on the dynamics and specificity of NF-κB signaling that could be traced to specific stimuli and specific trajectory features. Thus, our results revealed that, for a given stimulus, NF-κB dynamics contain information about the polarization state of the macrophage. This allowed us to use stimulus-response NF-κB dynamics to map distinct macrophage functional states onto a multi-dimensional landscape and infer alterations to the molecular signaling network underlying these states.
Given the unprecedented quantity and quality of dynamic single-cell signaling data, appropriate considerations for trajectory data were essential for their analysis. First, simply treating a n-time point trajectory as a n-dimensional vector disregards the relationship between time points. For example, quantifying the distinction between trajectories as the Euclidean distance between time points can fail to capture differences of highly dynamic or oscillatory trajectories appropriately. Two single-cell trajectories with similar dynamical patterns but slightly displaced in time could be computed to be highly distinct.60 Secondly, although summary statistics of time-series data are easy to compute, they are often insufficient. For example, taking the time point by time point mean of single-cell trajectories can obscure asynchronous oscillatory dynamics observed at the single-cell level.61 Average behavior descriptions furthermore mask the heterogeneity of single-cell responses and the overlap between distributions from distinct conditions.62 Employing measures of spread or shape that are used to characterize distributions is also not fully informative if taken from time series because they also do not recognize the inter-time point correlations and so risk overestimating the dispersion.
We addressed these challenges using two approaches. The first is applying an ML approach that allowed for trajectory distinguishability to be explored in a feature-free manner. Indeed, the LSTM classifier performed with higher accuracy than alternative classifiers trained on the time-series data. The LSTM architecture allows direct analysis of time-series data as its underlying RNN-type architecture treats time points in a sequence rather than as discrete features by considering the output of previous time points in calculating the output of the current time point.63 Furthermore, ML classification permits an interrogation of distinguishability at a single-cell resolution as it samples distinct single cells in its training, and unique classification predictions can be made for each cell in testing. We used the LSTM-based ML classifier for a quantitative assessment of stimulus-response specificity. We found that classifier performance dropped for the polarized responses, suggesting broadly a loss of response specificity with polarization. Examining the confusion fractions across the polarization states revealed however that different stimulus responses contributed to the losses in specificity for each polarization state.
Our second approach to address the challenges of time-series data analysis was to reduce these data into informative trajectory features. These signaling codons,15 sufficiently describe the stimulus-specific dynamical NF-κB trajectories, and their values are more robust to the temporal shifts previously discussed. In essence, signaling codons constitute a lower dimensional representation of the data, thereby expanding the range of analysis tools that can be used and provide greater interpretability. Although our previous study presented a method based on maximizing mutual information to select dynamical features that correlate with the stimulus, this approach is computationally impractical as more features are to be considered because of the combinatorial explosion. Here, we explored an ML approach for this purpose. Classifiers based on the XGBoost architecture have been shown to outperform other ML methods64 and SHAP analysis on these trained models provides a way of quantifying feature importance that accounts for feature interactions. After training an XGBoost ML classifier on the stimulus-response data from each polarization state and SHAP analysis to give an initial feature ranking, we used a recursive feature elimination approach to select a subset of 6–7 informative features per polarization state, totaling a combined set of 18 dynamical features. Using these selected dynamical features, or signaling codons, for classification resulted in models nearly as accurate as models trained on all 71 features. Further analysis of these features associated them with elevated or reduced immune threat, and comparison of these features across polarization states revealed that convergence of several stimulus responses in M1 polarization states was facilitated by a gain in pathogen-like features, whereas in M2 polarization states the opposite was observed.
These findings emphasized that NF-κB trajectories not only contain information about the stimulus but also about the microenvironmental context of the cell. Thus, we explored methods to extract that context-specific information from NF-κB response trajectories that result from a particular stimulus. We used the aforementioned ML approaches to identify with which stimulation condition the greatest distinction among polarization states could be achieved. We then utilized two methods to map the polarization states, which consistently demonstrated Pam3CSK as the stimuli that could best distinguish them. Functional PCA, which uses a basis of trajectories for decomposition, allowed for dimensionality reduction of the time-series data directly. However, using a set of informative trajectory features as input for a UMAP visualization allowed for greater interpretability of differences between polarization states. Ultimately, we can leverage these data and analyses to characterize macrophages exposed to novel polarizing substances, and here, we demonstrated our ability to predict DHA pretreatment as an M2-like polarizer, consistent with recent findings.57
Stimulus-response NF-κB dynamics ultimately reflect the expression levels and kinetic reaction rates of signaling mediators within that network, such as rates of synthesis, degradation, complex association and dissociation, and catalysis. Leveraging an established mechanistic model of the NF-κB signaling network, we inferred how polarization modifies these biochemical parameters. Focusing on Pam3CSK single-cell responses, we determined the distribution of biochemical parameters for each polarization state. The resulting biochemical parameters represent in effect a dimensionality reduction of the complex dynamic trajectories based on known molecular mechanisms. That mapping revealed similar discrimination patterns among polarizers as the mapping based on trajectory features. However, this analysis additionally suggests potential biochemical alterations to the NF-κB signaling network state that underlie the observed phenotypic changes in signaling dynamics. For example, NF-κB activation dynamics in IFNγ polarized macrophages separate from other states likely due to increased degradation of free IκBα and synthesis of TLR2, in line with prior biochemical analyses.39,65
Mapping cells onto a multi-dimensional cell state landscape using dynamic measurements of a single analyte is remarkable. Snap-shot measurements of multiple cell surface makers are often used to distinguish one cell type from another.66,67 scRNA-seq and multiplexed single-molecule fluorescence in situ hybridization (FISH) allow for an even larger number of analytes to be measured achieving finer, or unbiased mapping of cell types or cell states.68,69 NF-κB RelA expression is ubiquitous and not cell-type-specific. Instead, it is NF-κB’s nuclear translocation dynamics that reflect the state of the signaling network when stimulated with a specific ligand that allow for discrimination of cell states. Signaling network dynamics may also capture information not contained in mRNA abundance measurements at steady-state.70 Importantly, the biological functions of macrophages are their dynamic immune responses, and these are only deployed in response to stimulus. Future studies will undoubtedly explore the relationship between alternative cell state mapping strategies. This study demonstrates that mapping cell states based on dynamical responses to a perturbation is possible and provides workflows that may be transferrable to other cells, analytes, and perturbations.
STAR★METHODS
RESOURCE AVAILABILITY
Lead contact
Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Alexander Hoffmann (ahoffmann@ucla.edu).
Materials availability
All resources generated in this study are available from the lead contact.
Data and code availability
RNA-seq data have been deposited at SRA under BioProject: PRJNA819468 and GEO: GSE246566 and are publicly available as of the date of publication. Accession numbers are listed in the key resources table. Trajectory data generated from microscopy experiments have been deposited at Mendeley Data: https://doi.org/10.17632/gkxzb5hcmk.1 and are publicly available as of the date of publication. Available on GitHub is software used for image analysis (https://github.com/brookstaylorjr/MACKtrack), code to calculate trajectory features (https://github.com/signalingsystemslab/polarized_macs_NFκB_response_dynamics), and code for mathematical modeling and inferred parameter fits (https://github.com/michaeliter/nfκB_param_fitting). Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
|
| ||
| Chemicals, peptides, and recombinant proteins | ||
|
| ||
| lipopolysaccharide (LPS) | Sigma Aldrich, B5:055 | L2880 |
| Murine TNF | Roche | 11271156001 |
| Pam3CSK4 | InvivoGen | tlrl-pms |
| polyinosine-polycytidylic acid (Poly(I:C)) | InvivoGen | tlrl-picw |
| Synthetic CpG ODN 1668 | InvivoGen | tlrl-1668 |
| Recombinant flagellin (FLA) | InvivoGen | tlrl-flic |
| FSL1 | InvivoGen | tlrl-fsl |
| R848 | InvivoGen | tlrl-r848 |
| Recombinant Mouse-IFNβ | PBL Assay Science | 12401–1 |
| Recombinant-Murine-IFNg | PeproTech | 315–05 |
| Recombinant-Murine -IL10 | PeproTech | 210–10 |
| Recombinant-Murine-IL13 | PeproTech | 210–13 |
| Recombinant-Murine-IL4 | PeproTech | 214–14 |
| Docosahexaenoic acid | Sigma-Aldrich | D-2534 |
| TRIzol reagent | Invitrogen | 15596018 |
| Hoechst 33342 dye | Thermo Fisher | 62249 |
|
| ||
| Critical commercial assays | ||
|
| ||
| Direct-zol RNA isolation kit | Zymo Research | R2060 |
| KAPA Stranded RNA-Seq Kit | KAPA Biosystems | KK8421 |
|
| ||
| Deposited data | ||
|
| ||
| Single cell NFκB signaling dynamics | This paper | Mendeley Data: https://doi.org/10.17632/gkxzb5hcmk.1 |
| RNA-seq data of hMPDM, BMDM, and RAW 264.7 cells stimulated with LPS | This paper | GEO: GSE246566 |
|
| ||
| Experimental models: Cell lines | ||
|
| ||
| RelA-mVenus hMPs | This paper | hMPs |
| RAW 264.7 | ATCC | TIB-71 |
|
| ||
| Experimental models: Organisms/strains | ||
|
| ||
| RelAmVenus/mVenus (C57BL/6) | Adelaja et al.15 | JAX stock 38987 |
|
| ||
| Software and algorithms | ||
|
| ||
| MACKtrack - Image Analysis (single cell tracking and measurement) | Adelaja et al.15 | https://github.com/brookstaylorjr/MACKtrack |
| NFκB trajectory feature calculations | This paper | https://github.com/signalingsystemslab/polarized_macs_NFkB_response_dynamics https://doi.org/10.5281/zenodo.11099125 |
| NFκB math model and parameter inference | This paper | https://github.com/michaeliter/nfkb_param_fitting https://doi.org/10.5281/zenodo.11099470 |
| Cutadapt | Martin71 | https://github.com/marcelm/cutadapt |
| PRINSEQ | Schmieder and Edwards72 | https://sourceforge.net/projects/prinseq/files/ |
| STAR | Dobin et al.73 | https://github.com/alexdobin/STAR |
| Samtools | Danecek et al.74 | https://github.com/samtools/samtools |
| featureCounts | Liao et al.75 | https://subread.sourceforge.net/ |
| DESeq2 | Love et al.76 | https://github.com/thelovelab/DESeq2 https://doi.org/10.18129/B9.bioc.DESeq2 |
| edgeR | Robinson et al.77 | https://bioinf.wehi.edu.au/edgeR/https://doi.org/10.18129/B9.bioc.edgeR |
| stats-package (R4.1.1) | R Core Team78 | https://www.r-project.org/ |
| Tslearn | Tavenard et al.46 | https://github.com/tslearn-team/tslearn/ |
| TensorFlow 2 | Abadi et al.79 | https://github.com/tensorflow/tensorflow https://doi.org/10.5281/zenodo.4724125 |
| Keras API | Chollet80 | https://github.com/keras-team/keras |
| scikit-learn | Pedregosa et al.81 | https://scikit-learn.org/stable/ |
| Google Colaboratory | https://colab.google/ | |
| XGboost | Chen and Guestrin51 | https://github.com/dmlc/xgboost |
| SHAP (SHapley Additive exPlanations) | Lundberg et al.82 | https://github.com/shap/shap |
| scikit-fda | Suárez et al.83 | https://github.com/GAA-UAM/scikit-fda |
| Uniform Manifold Approximation & Projection (UMAP) | McInnes et al.84 | https://github.com/lmcinnes/umap |
| MATLAB ODE simulation & optimization | The MathWorks Inc.85 | https://www.mathworks.com/ |
EXPERIMENTAL MODEL AND STUDY PARTICIPANT DETAILS
Macrophage Cell Culture and Stimulation
Myeloid precursor cells were prepared from RelA-mVenus mouse strain15 by HoxB4-mediated transduction (hMP).43 hMP-Derived Macrophages (hMPDMs) were prepared by culturing hMPs in L929-conditioned medium using standard Bone-Marrow Derived Macrophage (BMDM) culture method.15 hMPDMs were re-plated in imaging dishes on day 6 at 20,000 cells/well in an 8-well ibidi SlideTek chamber, for imaging at an appropriate density on day 10 or day 11. hMPDMs were treated with polarization reagents (IL4 (10 ng/mL) (PeproTech), IL13 (50 ng/mL) (PeproTech), IL10 (20 ng/ML) (PeproTech), IFNγ (10 ng/mL) (PeproTech), IFNβ (100 U/ML) (PBL Assay Science)) or left untreated (M0) 24 hours before stimulation. Stimulation was done with the toll-like receptor (TLR) 4 agonist, lipopolysaccharide (LPS) (10 ng/mL) (Sigma Aldrich), TLR3 agonist, polyinosine-polycytidylic acid (Poly(I:C) (50 μg/mL) (InvivoGen), TLR9 agonist, CpG B ODN (100 nM) (InvivoGen); TLR2 agonists, Pam3CSK4 (100 ng/mL) (InvivoGen) and FSL1 (3 ng/mL) (InvivoGen), TLR8 agonist, R848 (1 μg/mL) (InvivoGen), TLR5 agonist, Flagellin (10 ng/mL) (InvivoGen), or cytokine TNF (1 ng/mL) (R&D Systems) without media replacement. Doses were selected to give maximal response. For the experiment with DHA pretreatment (docosahexaenoic acid, 200 μM (Sigma Aldrich)) and Pam3CSK stimulation, replating was performed on day 5 and imaging performed on day 10.
METHOD DETAILS
RNA Isolation and Sequencing
Bone-Marrow Derived Macrophages (BMDMs) were cultured with standard methods, L929-conditioned medium.15 Raw 264.7 cells were cultured in DMEM 10 % FBS media. After stimulation, cells were harvested at desired time points. For PolyA+ RNA, cells were harvested in TRIzol reagent (Life Technologies, Carlsbad, CA). Then, DNA-free RNA was extracted from cell using DIRECTzol kit (Zymo Research, Irvine, CA) according to manufacturer’s instructions. After RNA extraction, libraries for polyA+ RNA were prepared using KAPA Stranded RNA-Seq Kit for Illumina Platforms (KAPA Biosystems, Wilmington, MA) according to the manufacturer’s instructions. Resulting cDNA libraries were single-end sequenced with a length of 50bp on an Illumina HiSeq 2000 (Illumina, San Diego, CA).
Analysis of RNA-seq data
After adapter trimming with cutadapt,71 sequences were preprocessed with PRINSEQ72 using the “dust” method to filter low complexity sequences with the maximum allowed score set to 7 and sequences with more than 10% ambiguous bases were removed. Single-end reads were mapped to reference mouse genome (mm10) using STAR73 with the following options: –outFilterMultimapNmax 20–alignS JoverhangMin 8 –alignSJDBoverhangMin 1 –outFilterMismatchNmax 999 –outFilterMismatchNoverLmax 0.04 –alignIntronMin 20 –alignIntronMax 1000000 –alignMatesGapMax 1000000 –seedSearchStartLmax 30. Only primary mapped reads with alignment score (MAPQ)>30 were then selected by Samtools.74 Ribosomal RNA was filtered out using the intersect function in bedtools with a minimal overlap fraction of 0.1 and finally reads mapped to the Y chromosome or mitochondria were removed for downstream analysis. Transcript abundance was quantified based on GENECODE M4 annotation using featureCounts75 using option ‘-t exon -g gene_id. For analysis, genes with no counts across all experiments were filtered out. An average pseudocount of 2 was added to the raw counts, where the exact value added to each library was proportional to the library size. The counts were then normalized for differences in library size by calculating the counts per million (CPM) and then the base 2 log fold changes were calculated from those values. Genes induced by LPS were determined to be those that had a log2 Fold Change greater than or equal to 1 after 3 hours post LPS stimulation in two replicate experiments of BMDM’s.
Live-cell imaging
Macrophages were stained with nuclear staining dye, Hoechst 33342 (5 ng/mL) two hours prior to imaging within ibidi chambers. Cells were imaged at 5-minute intervals on a Zeiss AxioObserver platform with live-cell incubation, using epifluorescent excitation from a Sutter Lambda XL light source. The first three images collected (pre-stimulation) were used to determine the baseline activity of NFκB for each cell. After 15 minutes of the start of imaging, conditioned culture media containing stimulus was injected into the respective well of ibidi chamber in situ. Images were recorded on a Hamamatsu Orca Flash 2.0 CCD camera for 12.5 hours.
Image processing and quality control
Microscopy time-lapse images were exported for single-cell tracking and measurement in MATLAB R2018a,used in earlier work.15 Briefly, cells were identified using DIC images, then segmented, guided by nuclear staining from the Hoechst image. Segmented cells were linked into trajectories across successive images, then nuclear and cytoplasmic boundaries were defined and used for measurement in fluorescent channel for mVenus-NFκB. Nuclear NFκB levels were quantified on a per-cell basis, normalized to image background levels, then were baseline-subtracted. The first three images collected (pre-stimulation) were used to determine the baseline activity of NFκB for each cell. The mean fluorescence value from these three frames was subtracted from the complete trajectory to normalize each cell. For downstream analysis and visualization, the third timepoint corresponds to time = 0 and 97 timepoints after that were included (~ 8 hour trajectories). Mitotic cells, as well as cells that drifted out of the field of view, were excluded from analysis. The code (MACKtrack) used for this analysis are publicly available at GitHub (https://github.com/brookstaylorjr/MACKtrack).
To quantify the 6 quality control (QC) metrics, 11 features were obtained from the NFκB trajectories (Table S2). For quality control metrics formed by more than one trajectory feature, the trajectory features were z-scored and the mean of the z-scores was taken to get the QC metric value. During quality control analysis to determine biological replicates, z-scoring was performed over cells in the experimental condition of interest. Additionally, for the quality control analysis, the trajectory features from only “responding” cells were considered. A cell was deemed a responder if its trajectory exceeded three times the standard deviation of the baseline for at least 5 consecutive time points. Experiments were finally deemed biological replicates if the Jensen-Shannon distance (JSD) between each of their quality control metric distributions were below a pre-specified threshold, 0.3. This threshold was selected based off a set of pilot experiments containing replicates for several conditions and visual inspection of the trajectories. For the visualizations presented in Figure 1, z-scoring was performed over all cells in all experimental conditions listed in Figure S3A to calculate quality control metrics.
To calculate the Jensen-Shannon distances (JSD) between quality control metric distributions, the Freedman-Diaconis rule86 was first used to select a bin width for each quality control metric. Using this bin width and the extremum quality control metric values, a histogram that approximates the probability density function for each experiment can be constructed and used to calculate the JSD (the square root of the Jensen Shannon Divergence using the base 2 logarithm).
QUANTIFICATION AND STATISTICAL ANALYSIS
Relating NF-κB dynamics to Gene Expression in polarized macrophages
RNAseq and ATACseq data was obtained from a prior study of human macrophages.47 Briefly this study conditioned human macrophages 64 hours prior to stimulation with either 10 ng/ml IFNγ, 200 U/ml INFβ, or left untreated (naïve condition). Macrophages were stimulated with 100 ng/ml Lipid A, 5 ng/ml TNFα, 100 ng/ml Pam3CSK, 20 μg/ml poly(I:C), or 200 U/ml IFNβ. ATACseq was performed on the conditioned macrophages prior to stimulation and RNAseq was performed on both unstimulated and stimulated macrophages (1.5, 3, 5.5, and 10 hours). Genes with less than 4 RPKM across all samples were eliminated from the RNAseq dataset76 and genes with significant upregulation (adjusted (BH) pVal <= 0.05, log2FC >= 2) upon stimulation at any time-point from any precondition-stimulation treatment were detected with edgeR77 (2299 genes) and retained for downstream analysis. For each condition, the total gene expression over the time course (integral of normalized CPM values76 with unstimulated value deducted) was calculated for each replicate. NFκB trajectory data was utilized from the naïve, IFNβ, and IFNγ polarized hMPDMs treated with LPS (paired with Lipid A RNAseq data), TNF, Pam3CSK4, and Poly(I:C). For each condition, the total activity (integral of baseline deducted values) was averaged over the single cells of each replicate.
First a linear model (stats package in R4.1.178) was constructed to predict gene expression activity from the NFκB total activity averaged over replicates. More specifically the formula GE ~ LPS_NA + TNF_NA + P3K_NA + PIC_NA was used, where GE is the average gene expression activity for the gene of interest and NA are the average NFκB total activity with the stimulations specified. Each stimulation condition has a separate variable as genes respond to multiple transcription factors and stimuli activate these transcription factors differently. NA values are only nonzero for data where that stimulation was used. For each gene model, 12 data points were fit (3 polarization conditions x 4 stimulation conditions). Next the linear models were constructed after permuting the gene expression activity across polarization states. NFκB signaling dynamics can carry information about the polarization-induced changes in gene expression if the model fits on the original data outperform those on the permuted data. In the next analysis, peaks overlapping with the region ± 1 kilobase of the transcription start site of each upregulated gene were identified from the ATACseq dataset. 947 genes had at least one peak and these were retained for downstream analysis. Now the linear model to predict gene expression activity used both NFκB total activity and the ATAC peak values (normalized by size factors76) averaged over the replicates. Genes containing more than one peak within the promoter region had these ATAC values summed. The formula GE ~ LPS_NA + TNF_NA + P3K_NA + PIC_NA + LPS_CA + TNF_CA + P3K_CA + PIC_CA was used, where CA are the average chromatin accessibility. These data do not vary with stimulation condition, however their effect on gene expression might. CA values are only nonzero for data where that stimulation was used. The Akaike Information Criterion (AIC) was used to compare the models constructed from only NFκB signaling dynamics to the models constructed with additional chromatin accessibility information.
LSTM-based ML Classifier
The LSTM-based Machine Learning (ML) Classifier was implemented in TensorFlow 2 79 using the Keras API.80 The classifier utilized the trajectories from time = 0 to 8.083 hours for a total of 98 timepoints. Trajectories with missing (nan) values were excluded from this analysis. For each classification task described, the data was split 60% for training, 20% for validation, and 20% for testing. The trajectories were sampled such that for each combination of ligand stimulation and polarization state the number of trajectories were equivalent. More specifically, for each combination of ligand stimulation and polarization state the trajectories were either downsampled or resampled to reach the mean number of trajectories across the ligand stimulation and polarization state combinations (1329 cells per condition with tasks with unstimulated cells, 1338 without). A standard scaling, fit from the training data, was additionally applied across each time point. For each classification task, the data was shuffled and resplit 15 times to estimate uncertainty in output performance metrics. The confidence intervals reported were two-sided and used a T-distribution with degrees of freedom one less than the sample size (n-1).
The architecture of the machine learning classifier consisted of a LSTM layer with the dimensionality of the output set to the number of timepoints, 98, followed by a fully connected layer with the dimensionality of the output set to the number of classes. A softmax activation function was finally applied to the output of the fully connected layer. The weights of the classifier were optimized by minimizing the categorical cross-entropy loss objective function with the Adam algorithm using the following default parameters: learning rate=0.001, beta 1=0.9, beta 2=0.99, epsilon = 1e-08, batch size=32. With increasing number of training epochs, the value of the loss function over the training data will continue to decrease whereas eventually the value of the loss function over the validation data (data unseen during optimization) will begin to increase. This signals overfitting, as the trained model loses generalizability of its performance on new data. We employed a simple early stopping technique to address this. For each classification task, the validation loss was monitored during training and the epoch number corresponding approximately to the start of the rise in validation loss was determined. Training was then terminated just prior to this epoch.
The testing data held out during training was finally used to evaluate the performance of the trained model. The output of the classifier is the probability that a trajectory belongs to each class. To assign the trajectory to a class, the class with the highest prediction probability for each trajectory gave the assignment. These output prediction probabilities and class assignments from the testing data were then used to calculate the performance metrics as described.
A random forest classifier and feedforward neural network classifier were also trained and tested in the same manner for comparison. The random forest model was implemented using the scikit-learn Python package81 with default parameters (n_estimators=100, criterion=‘gini’, max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features= sqrt(n_features), max_leaf_nodes=None, min_impurity_decrease=0.0, bootstrap=True, max_samples= X.shape[0]). The feedforward network model was implemented identically to the LSTM network model, except the LSTM layer was replaced with a Dense layer with output set to the number of timepoints, 98, and a ReLU activation function. All machine learning models were run in the Google Colaboratory environment.87
Feature Library and XGBoost ML Classifier
An initial library of 190 trajectory features was further reduced to a size of 71, eliminating features that contributed to high pairwise correlations based off of Kendall’s Tau (maximum pairwise correlation reduced to 0.76 from 0.91, Table S3). The code to calculate these features are provided on the GitHub site. The XGBoost model was implemented using the XGboost Python Package51 (version 0.90). Once again, trajectories with missing (nan) timeseries values were excluded from this analysis. For each classification task, the data was sampled as previously described for the LSTM-based models and similarly the training was repeated 15 times to estimate uncertainty in output performance. A standard scaling, fit from the training data, was also applied to each feature.
All XGBoost models used a ‘multi:softmax’ objective and up to 1000 estimators. An early stopping criterion was applied to prevent overfitting, where if the multiclass log loss (cross-entropy) value did not improve after 10 rounds, training was terminated. All other parameters were set to the package defaults (max_depth = 6, max_leaves = 0, grow_policy = depthwise, eta(learning_rate) = 0.3, tree_method = auto, gamma = 0, min_child_weight = 1, max_delta_step = 0, subsample = 1, sampling_method = uniform, colsample_bytree = 1, colsample_bylevel = 1, colsample_bynode = 1, reg_alpha = 0, reg_lambda = 1, scale_pos_weight = 1).
To assess feature importance in model predictions, the SHAP package (version 0.41.0) was used.82 The function TreeExplainer was run on the trained models and the resulting “shap_values” were saved. An importance score for each feature was then obtained by taking the absolute value of the “shap_values”, averaging them across all instances, and then summing them over all classes. Uncertainty in these importance scores was once again obtained by repeating this measure for the 15 trained models. To further select features from the top 20 features identified as most important for each polarization state, a recursive feature elimination procedure was pursued. Starting with the original 20 features, each feature was trialed for removal (i.e. a model was trained using the 19 remaining features and the resulting performance was recorded, taking the average over three samplings to account for variability). The feature whose removal resulted in the best model performance (hence this feature was the least essential for maintaining performance) was removed from the set and the process began again with this set of 19 features. The procedure was repeated until only one feature remained in the set. Best model performance was monitored as features were removed to identify at what point feature removal resulted in a substantial loss in performance and the features remaining beyond this point defined the selected minimal set.
For LDA and PCA calculations using the trajectory features, the scikit-learn Python package81 (version 1.0.2) was used, cells with missing values were excluded, and the standard scaler was applied. The confidence intervals reported were two-sided and used a normal distribution with associated z-scores.
Functional Principal Component Analysis
Functional principal component analysis of the NFκB response trajectories across all stimulation and polarization conditions was performed using scikit-fda83 (version 0.7.1). An equal number of samples from each experimental condition was used. This analysis operated directly on the centered raw data (discretized FPCA) without first converting the data using a basis representation. The first ten principal components were then utilized to create a UMAP projection of the data using the Uniform Manifold Approximation & Projection package84 (version 0.5.3) with default parameters.
Mathematical Modeling of NFκB Signaling
The NFκB signaling network and ordinary differential equation (ODE) mechanistic model was adapted from prior work.15 Biochemical parameters relevant to Pam3CSK stimulation were selected from the model topology (Figure S7A). To evaluate their sensitivity, each parameter was varied across a constraint region centered around their published values (Figure S7B). Seven sensitive parameters were chosen for optimization: IκBα protein degradation rate, IκBα mRNA synthesis Km, IκBα transcriptional delay, NFκB initial abundance, TLR2 synthesis rate, ligand-receptor complex degradation rate, and TAK1 inactivation rate. The constraint region utilized was 0.1x-10x the baseline value for IκBα protein degradation rate, IκBα mRNA synthesis Km, TLR2 synthesis rate, ligand-receptor complex degradation rate, and TAK1 inactivation rate. The IκBα transcriptional delay parameter was constrained between 0.5x-2x the baseline value and NFκB initial abundance was constrained between 0.04 to 0.3 μM.
Experimental nuclear NFκB trajectories (A.U.) were converted to μM to permit comparison with model simulations. A scaling factor of 0.0313 was applied that was previously derived by considering the experimentally measured macrophage volume and expected range of NFκB nuclear concentration following maximum stimulation with LPS. From each of the six polarization states, 300 single cells were sampled from the Pam3CSK responses. For each cell, the optimization process was repeated 100 times. Each time, the optimization process was initialized at a different biochemical parameter set from a collection of 100 randomly sampled parameter sets. The MATLAB (version R2020b)85 function, fminsearch, was utilized for optimization. This function implements the Nelder-Mead simplex method, a gradient-free local optimization algorithm which excels at quickly optimizing complex multi-dimensional functions.88 The parameter ‘MaxIter’ was set to 100 with all other parameters set to default values. This MATLAB implementation of the Nelder-Mead simplex method does not natively support lower and upper bound constraints on optimization variables, so the biochemical parameter constraint regions were enforced by utilizing transformations to map between each biochemical parameter constraint region and the real line. More specifically, the following function was applied to the optimization variables to project them into the constraint region of the corresponding parameter during each iteration of the optimization procedure. Here, and are the lower and upper bounds of parameter , and is the corresponding optimization variable:
The objective function that was minimized by this optimization process has two main components: trajectory RMSD and parameter distance penalty. The trajectory RMSD value refers to the root-mean-square deviation between a cell’s experimental and model-simulated nuclear NFκB time series. Due to the increased biological relevance of capturing the first few peaks of these trajectories, the first four hours of the time series are weighted two times more in the RMSD calculation. The parameter distance penalty refers to the root-mean-square (RMS) value of the ratio between the altered parameters and their published values in log space. The base of the logarithm applied depended on the constraint region for each parameter. For example, the penalty for parameters with a 0.1x-10x constraint would be base 10. This penalty value was scaled by 0.1 to weigh it equally against the trajectory RMSD in the objective function. For every cell, the optimized parameter sets associated with the 10 lowest objective function values were retained for subsequent analyses. The objective function () can be summarized as follows:
After completion of the parameter fitting pipeline, the difference between parameter distributions across polarization states was evaluated using the two-sample Kolmogorov-Smirnov test (kstest2, ‘unequal’ alternative hypothesis) in MATLAB.85 Next, the pairwise cell dissimilarities were computed using the parameter distributions composed of the top 10 model fits. For each pair of cells, the Jenson-Shannon distance (JSD) was calculated for each set of parameter distributions. The parameter distribution JSD values were then averaged to produce the calculated dissimilarity measure between two cells. This dissimilarity calculation can be summarized as follows, where is the parameter distribution for parameter in cell :
These distances formed the parameter-based dissimilarity matrix that was utilized in the UMAP visualizations. In the subsequent correlation analyses, the parameter-based dissimilarity matrix was compared to a feature-based distance matrix, which was obtained by calculating the Euclidean distance between the 10 trajectory features for each pair of cells. The Pearson correlation coefficient was calculated by flattening the upper triangles of each matrix into a 1D vector.
Supplementary Material
Highlights.
Polarization of macrophages affects stimulus-response NF-κB dynamics
Signaling codons reveal how NF-κB dynamics are changed by polarizers
NF-κB stimulus-response dynamics define a landscape of macrophage functional states
Model-inferred biochemical parameters define underlying molecular network states
ACKNOWLEDGMENTS
The authors acknowledge lab members for discussions, Eric Deeds (UCLA) for critical reading of the manuscript, and Roberto Spreafico for helping to establish the hMPDM experimental system. A.S. was supported by NIH T32GM008185 and T32GM008042. Funding was provided by NIH R01AI127864, R01AI32835, and R01AI127867 to A.H.
Footnotes
DECLARATION OF INTERESTS
The authors declare no competing interests.
SUPPLEMENTAL INFORMATION
Supplemental information can be found online at https://doi.org/10.1016/j.cels.2024.05.002.
REFERENCES
- 1.Andrews TS, and Hemberg M. (2018). Identifying cell populations with scRNASeq. Mol. Aspects Med 59, 114–122. 10.1016/j.mam.2017.07.002. [DOI] [PubMed] [Google Scholar]
- 2.Yao J, Pilko A, and Wollman R. (2016). Distinct cellular states determine calcium signaling response. Mol. Syst. Biol 12, 894. 10.15252/msb.20167137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Davies AE, Pargett M, Siebert S, Gillies TE, Choi Y, Tobin SJ, Ram AR, Murthy V, Juliano C, Quon G, et al. (2020). Systems-Level Properties of EGFR-RAS-ERK Signaling Amplify Local Signals to Generate Dynamic Gene Expression Heterogeneity. Cell Syst. 11, 161–175.e5. 10.1016/j.cels.2020.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sheu KM, Luecke S, and Hoffmann A. (2019). Stimulus-specificity in the responses of immune sentinel cells. Curr. Opin. Syst. Biol 18, 53–61. 10.1016/j.coisb.2019.10.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Luecke S, Sheu KM, and Hoffmann A. (2021). Stimulus-specific responses in innate immunity: Multilayered regulatory circuits. Immunity 54, 1915–1932. 10.1016/j.immuni.2021.08.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hoffmann A, Levchenko A, Scott ML, and Baltimore D. (2002). The IκB-NF-κB Signaling Module: Temporal Control and Selective Gene Activation. Science 298, 1241–1245. 10.1126/science.1071914. [DOI] [PubMed] [Google Scholar]
- 7.Werner SL, Barken D, and Hoffmann A. (2005). Stimulus Specificity of Gene Expression Programs Determined by Temporal Control of IKK Activity. Science 309, 1857–1861. 10.1126/science.1113319. [DOI] [PubMed] [Google Scholar]
- 8.Covert MW, Leung TH, Gaston JE, and Baltimore D. (2005). Achieving Stability of Lipopolysaccharide-Induced NF-κB Activation. Science 309, 1854–1857. 10.1126/science.1112304. [DOI] [PubMed] [Google Scholar]
- 9.Nelson DE, Ihekwaba AEC, Elliott M, Johnson JR, Gibney CA, Foreman BE, Nelson G, See V, Horton CA, Spiller DG, et al. (2004). Oscillations in NF-κB Signaling Control the Dynamics of Gene Expression. Science 306, 704–708. 10.1126/science.1099962. [DOI] [PubMed] [Google Scholar]
- 10.Ashall L, Horton CA, Nelson DE, Paszek P, Harper CV, Sillitoe K, Ryan S, Spiller DG, Unitt JF, Broomhead DS, et al. (2009). Pulsatile Stimulation Determines Timing and Specificity of NF-κB-Dependent Transcription. Science 324, 242–246. 10.1126/science.1164860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tay S, Hughey JJ, Lee TK, Lipniacki T, Quake SR, and Covert MW (2010). Single-cell NF-κB dynamics reveal digital activation and analogue information processing. Nature 466, 267–271. 10.1038/nature09145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lee REC, Walker SR, Savery K, Frank DA, and Gaudet S. (2014). Fold change of nuclear NF-κB determines TNF-induced transcription in single cells. Mol. Cell 53, 867–879. 10.1016/j.molcel.2014.01.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sen S, Cheng Z, Sheu KM, Chen YH, and Hoffmann A. (2020). Gene Regulatory Strategies that Decode the Duration of NFκB Dynamics Contribute to LPS-versus TNF-Specific Gene Expression. Cell Syst. 10, 169–182.e5. 10.1016/j.cels.2019.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cheng QJ, Ohta S, Sheu KM, Spreafico R, Adelaja A, Taylor B, and Hoffmann A. (2021). NF-κB dynamics determine the stimulus specificity of epigenomic reprogramming in macrophages. Science 372, 1349–1353. 10.1126/science.abc0269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Adelaja A, Taylor B, Sheu KM, Liu Y, Luecke S, and Hoffmann A. (2021). Six distinct NFκB signaling codons convey discrete information to distinguish stimuli and enable appropriate macrophage responses. Immunity 54, 916–930.e7. 10.1016/j.immuni.2021.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Rivera A, Siracusa MC, Yap GS, and Gause WC (2016). Innate cell communication kick-starts pathogen-specific immunity. Nat. Immunol 17, 356–363. 10.1038/ni.3375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Murray PJ, and Wynn TA (2011). Protective and pathogenic functions of macrophage subsets. Nat. Rev. Immunol 11, 723–737. 10.1038/nri3073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Murray PJ (2017). Macrophage Polarization. Annu. Rev. Physiol 79, 541–566. 10.1146/annurev-physiol-022516-034339. [DOI] [PubMed] [Google Scholar]
- 19.Mills CD, Kincaid K, Alt JM, Heilman MJ, and Hill AM (2000). M-1/M-2 macrophages and the Th1/Th2 paradigm. J. Immunol 164, 6166–6173. 10.4049/jimmunol.164.12.6166. [DOI] [PubMed] [Google Scholar]
- 20.Mantovani A, Sica A, and Locati M. (2005). Macrophage polarization Comes of Age. Immunity 23, 344–346. 10.1016/j.immuni.2005.10.001. [DOI] [PubMed] [Google Scholar]
- 21.Wynn TA, Chawla A, and Pollard JW (2013). Macrophage biology in development, homeostasis and disease. Nature 496, 445–455. 10.1038/nature12034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Sica A, and Mantovani A. (2012). Macrophage plasticity and polarization: in vivo veritas. J. Clin. Invest 122, 787–795. 10.1172/JCI59643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Murray PJ, Allen JE, Biswas SK, Fisher EA, Gilroy DW, Goerdt S, Gordon S, Hamilton JA, Ivashkiv LB, Lawrence T, et al. (2014). Macrophage activation and polarization: nomenclature and experimental guidelines. Immunity 41, 14–20. 10.1016/j.immuni.2014.06.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ginhoux F, Schultze JL, Murray PJ, Ochando J, and Biswas SK (2016). New insights into the multidimensional concept of macrophage ontogeny, activation and function. Nat. Immunol 17, 34–40. 10.1038/ni.3324. [DOI] [PubMed] [Google Scholar]
- 25.Atri C, Guerfali FZ, and Laouini D. (2018). Role of Human Macrophage Polarization in Inflammation during Infectious Diseases. Int. J. Mol. Sci 19, 1801. 10.3390/ijms19061801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Blériot C, Chakarov S, and Ginhoux F. (2020). Determinants of Resident Tissue Macrophage Identity and Function. Immunity 52, 957–970. 10.1016/j.immuni.2020.05.014. [DOI] [PubMed] [Google Scholar]
- 27.Beyer M, Mallmann MR, Xue J, Staratschek-Jox A, Vorholt D, Krebs W, Sommer D, Sander J, Mertens C, Nino-Castro A, et al. (2012). High-Resolution Transcriptome of Human Macrophages. PLoS One 7, e45466. 10.1371/journal.pone.0045466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Xue J, Schmidt SV, Sander J, Draffehn A, Krebs W, Quester I, De Nardo D, Gohel TD, Emde M, Schmidleithner L, et al. (2014). Transcriptome-Based Network Analysis Reveals a Spectrum Model of Human Macrophage Activation. Immunity 40, 274–288. 10.1016/j.immuni.2014.01.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Spiller KL, Wrona EA, Romero-Torres S, Pallotta I, Graney PL, Witherel CE, Panicker LM, Feldman RA, Urbanska AM, Santambrogio L, et al. (2016). Differential gene expression in human, murine, and cell line-derived macrophages upon polarization. Exp. Cell Res 347, 1–13. 10.1016/j.yexcr.2015.10.017. [DOI] [PubMed] [Google Scholar]
- 30.Denisenko E, Guler R, Mhlanga MM, Suzuki H, Brombacher F, and Schmeier S. (2017). Genome-wide profiling of transcribed enhancers during macrophage activation. Epigenetics Chromatin 10, 50. 10.1186/s13072-017-0158-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gerrick KY, Gerrick ER, Gupta A, Wheelan SJ, Yegnasubramanian S, and Jaffee EM (2018). Transcriptional profiling identifies novel regulators of macrophage polarization. PLoS One 13, e0208602. 10.1371/journal.pone.0208602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Huang C, Lewis C, Borg NA, Canals M, Diep H, Drummond GR, Goode RJ, Schittenhelm RB, Vinh A, Zhu M, et al. (2018). Proteomic Identification of Interferon-Induced Proteins with Tetratricopeptide Repeats as Markers of M1 Macrophage Polarization. J. Proteome Res 17, 1485–1499. 10.1021/acs.jproteome.7b00828. [DOI] [PubMed] [Google Scholar]
- 33.Li P, Hao Z, Wu J, Ma C, Xu Y, Li J, Lan R, Zhu B, Ren P, Fan D, et al. (2021). Comparative Proteomic Analysis of Polarized Human THP-1 and Mouse RAW264.7 Macrophages. Front. Immunol 12, 700009. 10.3389/fimmu.2021.700009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Liu SX, Gustafson HH, Jackson DL, Pun SH, and Trapnell C. (2020). Trajectory analysis quantifies transcriptional plasticity during macrophage polarization. Sci. Rep 10, 12273. 10.1038/s41598-020-68766-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Muñoz-Rojas AR, Kelsey I, Pappalardo JL, Chen M, and Miller-Jensen K. (2021). Co-stimulation with opposing macrophage polarization cues leads to orthogonal secretion programs in individual cells. Nat. Commun 12, 301. 10.1038/s41467-020-20540-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Mulder K, Patel AA, Kong WT, Piot C, Halitzki E, Dunsmore G, Khalilnezhad S, Irac SE, Dubuisson A, Chevrier M, et al. (2021). Cross-tissue single-cell landscape of human monocytes and macrophages in health and disease. Immunity 54, 1883–1900.e5. 10.1016/j.immuni.2021.07.007. [DOI] [PubMed] [Google Scholar]
- 37.Dichtl S, Sanin DE, Koss CK, Willenborg S, Petzold A, Tanzer MC, Dahl A, Kabat AM, Lindenthal L, Zeitler L, et al. (2022). Gene-selective transcription promotes the inhibition of tissue reparative macrophages by TNF. Life Sci. Alliance 5, e202101315. 10.26508/lsa.202101315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Yang CH, Murti A, Pfeffer SR, Basu L, Kim JG, and Pfeffer LM (2000). IFNα/β promotes cell survival by activating NF-κB. Proc. Natl. Acad. Sci. USA 97, 13631–13636. 10.1073/pnas.250477397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Mitchell S, Mercado EL, Adelaja A, Ho JQ, Cheng QJ, Ghosh G, and Hoffmann A. (2019). An NFκB Activity Calculator to Delineate Signaling Crosstalk: Type I and II Interferons Enhance NFκB via Distinct Mechanisms. Front. Immunol 10, 1425. 10.3389/fimmu.2019.01425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.O’Neill LA, Sheedy FJ, and McCoy CE (2011). MicroRNAs: the fine-tuners of Toll-like receptor signalling. Nat. Rev. Immunol 11, 163–175. 10.1038/nri2957. [DOI] [PubMed] [Google Scholar]
- 41.Curtale G, Mirolo M, Renzi TA, Rossato M, Bazzoni F, and Locati M. (2013). Negative regulation of Toll-like receptor 4 signaling by IL-10–dependent microRNA-146b. Proc. Natl. Acad. Sci. USA 110, 11499–11504. 10.1073/pnas.1219852110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Xu J, Zhou L, Ji L, Chen F, Fortmann K, Zhang K, Liu Q, Li K, Wang W, Wang H, et al. (2016). The REGγ-proteasome forms a regulatory circuit with IκBy IL-10–dependent microRNA-146bs E. Nat. Commun 7, 10761. 10.1038/ncomms10761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Ruedl C, Khameneh HJ, and Karjalainen K. (2008). Manipulation of immune system via immortal bone marrow stem cells. Int. Immunol 20, 1211–1218. 10.1093/intimm/dxn079. [DOI] [PubMed] [Google Scholar]
- 44.Sakoe H, and Chiba S. (1978). Dynamic programming algorithm optimization for spoken word recognition. IEEE Trans. Acoust. Speech Signal Process 26, 43–49. 10.1109/TASSP.1978.1163055. [DOI] [Google Scholar]
- 45.Cuturi M, and Blondel M. (2017). Soft-DTW: a differentiable loss function for time-series. In Proceedings of the 34th International Conference on Machine Learning, ICML’17, 70 (JMLR.org), pp. 894–903. [Google Scholar]
- 46.Tavenard R, Faouzi J, Vandewiele G, Divo F, Androz G, Holtz C, Payne M, Yurchak R, Rußwurm M, Kolar K, et al. (2020). Tslearn, A Machine Learning Toolkit for Time Series Data. J. Mach. Learn. Res 21, 1–6.34305477 [Google Scholar]
- 47.Cheng Q, Behzadi F, Sen S, Ohta S, Spreafico R, Teles R, Modlin RL, and Hoffmann A. (2019). Sequential conditioning-stimulation reveals distinct gene- and stimulus-specific effects of Type I and II IFN on human macrophage functions. Sci. Rep 9, 5288. 10.1038/s41598-019-40503-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Hochreiter S, and Schmidhuber J. (1997). Long Short-Term Memory. Neural Comput. 9, 1735–1780. 10.1162/neco.1997.9.8.1735. [DOI] [PubMed] [Google Scholar]
- 49.Van Houdt G, Mosquera C, and Nápoles G. (2020). A review on the long short-term memory model. Artif. Intell. Rev 53, 5929–5955. 10.1007/s10462-020-09838-1. [DOI] [Google Scholar]
- 50.Friedman JH (2001). Greedy function approximation: A gradient boosting machine. Ann. Statist 29, 1189–1232. 10.1214/aos/1013203451. [DOI] [Google Scholar]
- 51.Chen T, and Guestrin C. (2016). XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 785–794. 10.1145/2939672.2939785. [DOI] [Google Scholar]
- 52.Lundberg SM, and Lee S-I (2017). A Unified Approach to Interpreting Model Predictions. In Advances in Neural Information Processing Systems (Curran Associates, Inc.). [Google Scholar]
- 53.Lane K, Andres-Terre M, Kudo T, Monack DM, and Covert MW (2019). Escalating Threat Levels of Bacterial Infection Can Be Discriminated by Distinct MAPK and NF-κB Signaling Dynamics in Single Host Cells. Cell Syst. 8, 183–196.e4. Cells, host. 10.1016/j.cels.2019.02.008. [DOI] [PubMed] [Google Scholar]
- 54.Ramsay JO, and Silverman BW (2005). Functional Data Analysis, Second Edition (Springer; ). [Google Scholar]
- 55.Holub BJ (2009). Docosahexaenoic acid (DHA) and cardiovascular disease risk factors. Prostaglandins Leukot. Essent. Fatty Acids 81, 199–204. 10.1016/j.plefa.2009.05.016. [DOI] [PubMed] [Google Scholar]
- 56.Sun GY, Simonyi A, Fritsche KL, Chuang DY, Hannink M, Gu Z, Greenlief CM, Yao JK, Lee JC, and Beversdorf DQ (2018). Docosahexaenoic acid (DHA): An essential nutrient and a nutraceutical for brain health and diseases. Prostaglandins Leukot. Essent. Fatty Acids 136, 3–13. 10.1016/j.plefa.2017.03.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Chang HY, Lee H-N, Kim W, and Surh Y-J (2015). Docosahexaenoic acid induces M2 macrophage polarization through peroxisome proliferator-activated receptor γ activation. Life Sci. 120, 39–47. 10.1016/j.lfs.2014.10.014. [DOI] [PubMed] [Google Scholar]
- 58.Kawano A, Ariyoshi W, Yoshioka Y, Hikiji H, Nishihara T, and Okinaga T. (2019). Docosahexaenoic acid enhances M2 macrophage polarization via the p38 signaling pathway and autophagy. J. Cell. Biochem 120, 12604–12617. 10.1002/jcb.28527. [DOI] [PubMed] [Google Scholar]
- 59.Sheu KM, Guru AA, and Hoffmann A. (2023). Quantifying stimulus-response specificity to probe the functional state of macrophages. Cell Syst. 14, 180–195.e5. 10.1016/j.cels.2022.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Kinnunen PC, Luker KE, Luker GD, and Linderman JJ (2021). Computational methods for characterizing and learning from heterogeneous cell signaling data. Curr. Opin. Syst. Biol 26, 98–108. 10.1016/j.coisb.2021.04.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Singh A, Marcoline FV, Veshaguri S, Kao AW, Bruchez M, Mindell JA, Stamou D, and Grabe M. (2019). Protons in small spaces: discrete simulations of vesicle acidification. PLoS Comput. Biol 15, e1007539. 10.1371/journal.pcbi.1007539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Altschuler SJ, and Wu LF (2010). Cellular Heterogeneity: Do Differences Make a Difference? Cell 141, 559–563. 10.1016/j.cell.2010.04.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Yu Y, Si X, Hu C, and Zhang J. (2019). A Review of Recurrent Neural Networks: LSTM Cells and Network Architectures. Neural Comput. 31, 1235–1270. 10.1162/neco_a_01199. [DOI] [PubMed] [Google Scholar]
- 64.Wu J, Li Y, and Ma Y. (2021). Comparison of XGBoost and the Neural Network model on the class-balanced datasets. In 2021 IEEE 3rd International Conference on Frontiers Technology of Information and Computer (ICFTIC) (IEEE), pp. 457–461. 10.1109/ICFTIC54370.2021.9647373. [DOI] [Google Scholar]
- 65.Matsuguchi T, Musikacharoen T, Ogawa T, and Yoshikai Y. (2000). Gene Expressions of Toll-Like Receptor 2, But Not Toll-Like Receptor 4, Is Induced by LPS and Inflammatory Cytokines in Mouse Macrophages1. J. Immunol 165, 5767–5772. 10.4049/jimmunol.165.10.5767. [DOI] [PubMed] [Google Scholar]
- 66.Gonzalez-Juarrero M, Shim TS, Kipnis A, Junqueira-Kipnis AP, and Orme IM (2003). Dynamics of Macrophage Cell Populations During Murine Pulmonary. J. Immunol 171, 3128–3135. 10.4049/jimmunol.171.6.3128. [DOI] [PubMed] [Google Scholar]
- 67.Roussel M, Bartkowiak T, and Irish JM (2019). Picturing polarized myeloid phagocytes and regulatory cells by mass cytometry. Methods Mol. Biol 1989, 217–226. 10.1007/978-1-4939-9454-0_14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Cochain C, Vafadarnejad E, Arampatzi P, Pelisek J, Winkels H, Ley K, Wolf D, Saliba A-E, and Zernecke A. (2018). Single-Cell RNA-Seq Reveals the Transcriptional Landscape and Heterogeneity of Aortic Macrophages in Murine Atherosclerosis. Circ. Res 122, 1661–1674. 10.1161/CIRCRESAHA.117.312509. [DOI] [PubMed] [Google Scholar]
- 69.Liao M, Liu Y, Yuan J, Wen Y, Xu G, Zhao J, Cheng L, Li J, Wang X, Wang F, et al. (2020). Single-cell landscape of bronchoalveolar immune cells in patients with COVID-19. Nat. Med 26, 842–844. 10.1038/s41591-020-0901-9. [DOI] [PubMed] [Google Scholar]
- 70.Maltz E, and Wollman R. (2022). Quantifying the phenotypic information in mRNA abundance. Mol. Syst. Biol 18, e11001. 10.15252/msb.202211001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Martin M. (2011). Cutadapt removes adapter sequences from high-throughput sequencing reads. EMBnet.journal 17, 10–12. 10.14806/ej.17.1.200. [DOI] [Google Scholar]
- 72.Schmieder R, and Edwards R. (2011). Quality control and preprocessing of metagenomic datasets. Bioinformatics 27, 863–864. 10.1093/bioinformatics/btr026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Dobin A, Davis CA, Schlesinger F, Drenkow J, Zaleski C, Jha S, Batut P, Chaisson M, and Gingeras TR (2013). STAR: ultrafast universal RNA-seq aligner. Bioinformatics 29, 15–21. 10.1093/bioinformatics/bts635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Danecek P, Bonfield JK, Liddle J, Marshall J, Ohan V, Pollard MO, Whitwham A, Keane T, McCarthy SA, Davies RM, et al. (2021). Twelve years of SAMtools and BCFtools. GigaScience 10, giab008. 10.1093/gigascience/giab008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Liao Y, Smyth GK, and Shi W. (2014). featureCounts: an efficient general purpose program for assigning sequence reads to genomic features. Bioinformatics 30, 923–930. 10.1093/bioinformatics/btt656. [DOI] [PubMed] [Google Scholar]
- 76.Lov MI., Hube W., and Ander S. (2014). Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2. Genome Biol. 15, 550. 10.1186/s13059-014-0550-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Robinson MD, McCarthy DJ, and Smyth GK (2010). edgeR: a Bioconductor package for differential expression analysis of digital gene expression data. Bioinformatics 26, 139–140. 10.1093/bioinformatics/btp616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.R Core Team (2021). R: A Language and Environment for Statistical Computing (R Foundation for Statistical Computing). [Google Scholar]
- 79.Abadi M, Barham P, Chen J, Chen Z, Davis A, Dean J, Devin M, Ghemawat S, Irving G, Isard M, et al. (2016). TensorFlow: A System for Large-Scale Machine Learning. Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI ‘16), 265–283. [Google Scholar]
- 80.Chollet F. (2015). Keras (GitHub). https://github.com/keras-team/keras. [Google Scholar]
- 81.Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, et al. (2011). Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res 12, 2825–2830. [Google Scholar]
- 82.Lundberg SM, Erion G, Chen H, DeGrave A, Prutkin JM, Nair B, Katz R, Himmelfarb J, Bansal N, and Lee S-I (2020). From Local Explanations to Global Understanding with Explainable AI for Trees. Nat. Mach. Intell 2, 56–67. 10.1038/s42256-019-0138-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Suárez A, Torrecilla JL, Berrocal MC, Carreño CR, Manchón PM, Bernabé AH, Manso PP, Hong Y, Fernandez DG, Eyriès PMR-P, et al. (2019). scikit-fda (Grupo de Aprendizaje Automático – Universidad Autónoma de Madrid). [Google Scholar]
- 84.McInnes L, Healy J, and Melville J. (2020). UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction. Preprint at arXiv. [Google Scholar]
- 85.The MathWorks Inc. (2020). MATLAB Version: 9.9.0.2037887 (R2020b) (The MathWorks Incorp.) [Google Scholar]
- 86.Freedman D, and Diaconis P. (1981). On the histogram as a density estimator:L2 theory. Z. Wahrscheinlichkeitstheorie verw Gebiete 57, 453–476. 10.1007/BF01025868. [DOI] [Google Scholar]
- 87.Bisong E. (2019). Google Colaboratory. In Building Machine Learning and Deep Learning Models on Google Cloud Platform: A Comprehensive Guide for Beginners, Bisong E, ed. (Apress; ), pp. 59–64. 10.1007/978-1-4842-4470-8_7. [DOI] [Google Scholar]
- 88.Nelder JA, and Mead R. (1965). A Simplex Method for Function Minimization. Comput. J 7, 308–313. 10.1093/comjnl/7.4.308. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
RNA-seq data have been deposited at SRA under BioProject: PRJNA819468 and GEO: GSE246566 and are publicly available as of the date of publication. Accession numbers are listed in the key resources table. Trajectory data generated from microscopy experiments have been deposited at Mendeley Data: https://doi.org/10.17632/gkxzb5hcmk.1 and are publicly available as of the date of publication. Available on GitHub is software used for image analysis (https://github.com/brookstaylorjr/MACKtrack), code to calculate trajectory features (https://github.com/signalingsystemslab/polarized_macs_NFκB_response_dynamics), and code for mathematical modeling and inferred parameter fits (https://github.com/michaeliter/nfκB_param_fitting). Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
|
| ||
| Chemicals, peptides, and recombinant proteins | ||
|
| ||
| lipopolysaccharide (LPS) | Sigma Aldrich, B5:055 | L2880 |
| Murine TNF | Roche | 11271156001 |
| Pam3CSK4 | InvivoGen | tlrl-pms |
| polyinosine-polycytidylic acid (Poly(I:C)) | InvivoGen | tlrl-picw |
| Synthetic CpG ODN 1668 | InvivoGen | tlrl-1668 |
| Recombinant flagellin (FLA) | InvivoGen | tlrl-flic |
| FSL1 | InvivoGen | tlrl-fsl |
| R848 | InvivoGen | tlrl-r848 |
| Recombinant Mouse-IFNβ | PBL Assay Science | 12401–1 |
| Recombinant-Murine-IFNg | PeproTech | 315–05 |
| Recombinant-Murine -IL10 | PeproTech | 210–10 |
| Recombinant-Murine-IL13 | PeproTech | 210–13 |
| Recombinant-Murine-IL4 | PeproTech | 214–14 |
| Docosahexaenoic acid | Sigma-Aldrich | D-2534 |
| TRIzol reagent | Invitrogen | 15596018 |
| Hoechst 33342 dye | Thermo Fisher | 62249 |
|
| ||
| Critical commercial assays | ||
|
| ||
| Direct-zol RNA isolation kit | Zymo Research | R2060 |
| KAPA Stranded RNA-Seq Kit | KAPA Biosystems | KK8421 |
|
| ||
| Deposited data | ||
|
| ||
| Single cell NFκB signaling dynamics | This paper | Mendeley Data: https://doi.org/10.17632/gkxzb5hcmk.1 |
| RNA-seq data of hMPDM, BMDM, and RAW 264.7 cells stimulated with LPS | This paper | GEO: GSE246566 |
|
| ||
| Experimental models: Cell lines | ||
|
| ||
| RelA-mVenus hMPs | This paper | hMPs |
| RAW 264.7 | ATCC | TIB-71 |
|
| ||
| Experimental models: Organisms/strains | ||
|
| ||
| RelAmVenus/mVenus (C57BL/6) | Adelaja et al.15 | JAX stock 38987 |
|
| ||
| Software and algorithms | ||
|
| ||
| MACKtrack - Image Analysis (single cell tracking and measurement) | Adelaja et al.15 | https://github.com/brookstaylorjr/MACKtrack |
| NFκB trajectory feature calculations | This paper | https://github.com/signalingsystemslab/polarized_macs_NFkB_response_dynamics https://doi.org/10.5281/zenodo.11099125 |
| NFκB math model and parameter inference | This paper | https://github.com/michaeliter/nfkb_param_fitting https://doi.org/10.5281/zenodo.11099470 |
| Cutadapt | Martin71 | https://github.com/marcelm/cutadapt |
| PRINSEQ | Schmieder and Edwards72 | https://sourceforge.net/projects/prinseq/files/ |
| STAR | Dobin et al.73 | https://github.com/alexdobin/STAR |
| Samtools | Danecek et al.74 | https://github.com/samtools/samtools |
| featureCounts | Liao et al.75 | https://subread.sourceforge.net/ |
| DESeq2 | Love et al.76 | https://github.com/thelovelab/DESeq2 https://doi.org/10.18129/B9.bioc.DESeq2 |
| edgeR | Robinson et al.77 | https://bioinf.wehi.edu.au/edgeR/https://doi.org/10.18129/B9.bioc.edgeR |
| stats-package (R4.1.1) | R Core Team78 | https://www.r-project.org/ |
| Tslearn | Tavenard et al.46 | https://github.com/tslearn-team/tslearn/ |
| TensorFlow 2 | Abadi et al.79 | https://github.com/tensorflow/tensorflow https://doi.org/10.5281/zenodo.4724125 |
| Keras API | Chollet80 | https://github.com/keras-team/keras |
| scikit-learn | Pedregosa et al.81 | https://scikit-learn.org/stable/ |
| Google Colaboratory | https://colab.google/ | |
| XGboost | Chen and Guestrin51 | https://github.com/dmlc/xgboost |
| SHAP (SHapley Additive exPlanations) | Lundberg et al.82 | https://github.com/shap/shap |
| scikit-fda | Suárez et al.83 | https://github.com/GAA-UAM/scikit-fda |
| Uniform Manifold Approximation & Projection (UMAP) | McInnes et al.84 | https://github.com/lmcinnes/umap |
| MATLAB ODE simulation & optimization | The MathWorks Inc.85 | https://www.mathworks.com/ |