Deriving Automated Device Metadata From Intracranial Pressure Waveforms: A Transforming Research and Clinical Knowledge in Traumatic Brain Injury ICU Physiology Cohort Analysis

Abstract

IMPORTANCE:

Treatment for intracranial pressure (ICP) has been increasingly informed by machine learning (ML)-derived ICP waveform characteristics. There are gaps, however, in understanding how ICP monitor type may bias waveform characteristics used for these predictive tools since differences between external ventricular drain (EVD) and intraparenchymal monitor (IPM)-derived waveforms have not been well accounted for.

OBJECTIVES:

We sought to develop a proof-of-concept ML model differentiating ICP waveforms originating from an EVD or IPM.

DESIGN, SETTING, AND PARTICIPANTS:

We examined raw ICP waveform data from the ICU physiology cohort within the prospective Transforming Research and Clinical Knowledge in Traumatic Brain Injury multicenter study.

MAIN OUTCOMES AND MEASURES:

Nested patient-wise five-fold cross-validation and group analysis with bagged decision trees (BDT) and linear discriminant analysis were used for feature selection and fair evaluation. Nine patients were kept as unseen hold-outs for further evaluation.

RESULTS:

ICP waveform data totaling 14,110 hours were included from 82 patients (EVD, 47; IPM, 26; both, 9). Mean age, Glasgow Coma Scale (GCS) total, and GCS motor score upon admission, as well as the presence and amount of midline shift, were similar between groups. The model mean area under the receiver operating characteristic curve (AU-ROC) exceeded 0.874 across all folds. In additional rigorous cluster-based subgroup analysis, targeted at testing the resilience of models to cross-validation with smaller subsets constructed to develop models in one confounder set and test them in another subset, AU-ROC exceeded 0.811. In a similar analysis using propensity score-based rather than cluster-based subgroup analysis, the mean AU-ROC exceeded 0.827. Of 842 extracted ICP features, 62 were invariant within every analysis, representing the most accurate and robust differences between ICP monitor types. For the nine patient hold-outs, an AU-ROC of 0.826 was obtained using BDT.

CONCLUSIONS AND RELEVANCE:

The developed proof-of-concept ML model identified differences in EVD- and IPM-derived ICP signals, which can provide missing contextual data for large-scale retrospective datasets, prevent bias in computational models that ingest ICP data indiscriminately, and control for confounding using our model’s output as a propensity score by to adjust for the monitoring method that was clinically indicated. Furthermore, the invariant features may be leveraged as ICP features for anomaly detection.

KEY POINTS

Question: What is the effect of intracranial pressure (ICP) monitor type on ICP waveform features, and can a machine learning model be developed to identify the source of the ICP waveform and aid efforts in using waveform data for clinical decision support?

Findings: Sixty-two robust and top-performing ICP features were identified to differentiate external ventricular drain (EVD) from intraparenchymal monitor (IPM) recordings. The developed proof-of-concept model can accurately and robustly classify ICP waveforms originating from EVD or IPM.

Meanings: This tool can impute metadata from large-scale retrospective datasets lacking data for monitor type, summarize confounding by indication for placing one monitor type versus another, and the invariant features may be leveraged as ICP features for anomaly detection.

Intracranial pressure (ICP) monitoring is used for guiding the management of acute brain injury (ABI) in patients at risk for elevated ICP or hydrocephalus (1, 2). Although mean ICP has been widely integrated into treatment standards (3), ICP waveforms capture continuous, high-resolution data on the trajectory of ICP, providing valuable information about cerebral perfusion pressure (CPP), cerebral compensatory reserve, and regulation of cerebral blood flow and volume (4, 5). ICP-derived features have provided significant additional information and have been increasingly implemented in recent years, such as pulse amplitude index, the correlation between cerebral CPP, and pulse amplitude (RAC) (6, 7).

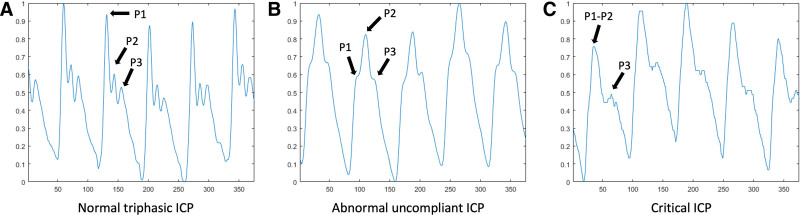
Machine learning (ML) approaches are powerful tools to further analyze and interpret ICP waveform data, which offer the promise to expand our ability to detect and predict intracranial hypertension or clinical deterioration (8–12). Quantitative characteristics have been used to enhance ICP signal quality and recognize nonartifactual ICP pulses (7), identify clamping of external ventricular drain (EVD)-derived ICP waveforms (13), and quantify the P1, P2, and P3 peaks within ICP pulse (which reflect the routine cycle of ICP in the brain, containing valuable continuous information on dynamic cerebrospinal pathophysiology, rather than the overall mean value) (14) (Fig. 1).

Figure 1.

Example intracranial pressure (ICP) waveform data from this cohort. A, Normal triphasic ICP. B, Abnormal, uncompliant ICP. C, Critical ICP.

Although ML-derived ICP waveform characteristics have increasingly informed treatment, there are gaps in understanding how ICP monitor type may bias waveform characteristics used for these predictive tools. Differences between EVD- and intraparenchymal monitor (IPM)-derived waveforms have not been well accounted for, which may be critical to prevent bias in computational models that ingest ICP data indiscriminately, particularly as these contextual data are missing in many large-scale retrospective datasets.

The decision to place an EVD versus an IPM may relate to the need for cerebrospinal fluid (CSF) drainage to manage intracranial hypertension (1, 3, 15–17). Accordingly, tools that use waveform data may be confounded by clinical indication, predicting outcomes based on patient characteristics associated with EVD placement, rather than signal features that encode the physiologic underpinnings of future risk. For example, EVD waveforms are altered during continuous or intermittent CSF drainage (1, 18, 19), may be dampened by catheter malpositioning or partial occlusion (1, 20), and may be inaccurate after patient movement until releveling (1, 20). IPMs may also have inaccuracies related to varying degrees of zero drift over time, which influence the ICP waveform (1, 3, 16, 21). We, therefore, hypothesized that there are differences in the ICP waveform features between EVDs and IPMs. However, in many clinical datasets, ICP monitor-type data are unavailable; the information is not encoded in physiologic monitor outputs and can be missed or expensive to obtain (22). If predictive models developed without this contextual information are to be robust and reliable in guiding clinical management without confounding by monitor indication, learning the provenance of ICP data will likely be necessary to ensure models are accurate and generalizable. For example, this type of device information is essential when seeking Food and Drug Administration approval for software algorithms, given the need to define a “context of use” for algorithms using clinical data. We, therefore, sought to understand the effect of ICP monitor type on ICP waveform features and to develop a tool identifying the source of an ICP waveform that can aid efforts to use ICP waveform data for clinical decision support (8, 14, 23–25).

In this proof-of-concept framework, we examined the multicenter Transforming Research and Clinical Knowledge in Traumatic Brain Injury (TRACK-TBI) ICU physiology cohort. We aimed to identify the distinctive waveform characteristics associated with each type of ICP monitor and to develop an ML framework for classifying ICP waveform data as originating from an EVD or an IPM.

MATERIALS AND METHODS

Population and Inclusion Criteria

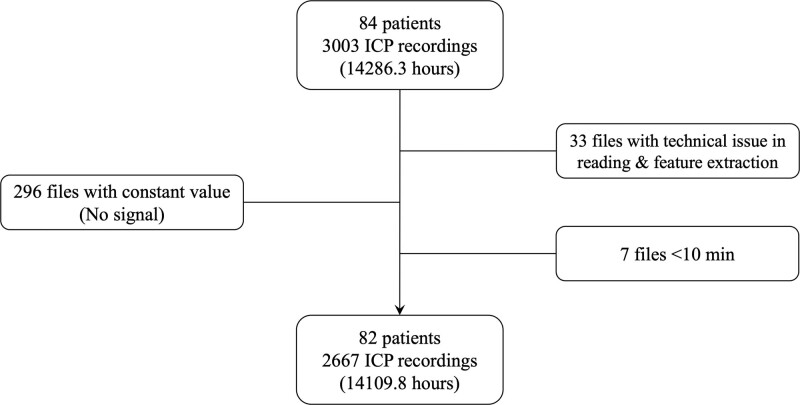
The TRACK-TBI study was approved by the institutional review board (IRB) of each site, and written informed consent was obtained from all subjects (see Supplementary Materials for IRB details, http://links.lww.com/CCX/B362). Procedures were followed in accordance with the ethical standards of IRB and with the Helsinki Declaration as revised in 2013. Inclusion and exclusion criteria for the TRACK-TBI study (ClinicalTrials.gov; No. NCT02119182) have been previously described (26–28). Inclusion criteria for this study were age greater than or equal to 18 years, enrollment from hospitals with the capability to record and extract bedside telemetry, available ICP waveform recordings with ground-truth labeling of ICP source, and undergoing ICP monitoring. Exclusion criteria for ICP epochs were corrupted files, flat signal with no physiologic content, or duration less than 10 minutes (precluding appropriate windowing for feature extraction; Fig. 2). The term “ICP epochs” here refers to the division of ICP recordings into separate files or segments. Each epoch typically corresponds to a distinct time period within the recordings. The Kruskal-Wallis one-way analysis of variance test for nonparametric data was used to investigate if there were clinical differences between groups with EVD, IPM, and both monitor types (Table S1, http://links.lww.com/CCX/B362).

Figure 2.

Consolidated Standards of Reporting Trials diagram of included data. ICP = intracranial pressure.

ICP Data Preprocessing

To ensure consistency in our analysis, we resampled the ICP waveforms to a common sampling frequency using a finite impulse response antialiasing low pass filter on the raw signal (29). This low pass filter attenuates the frequency components above a specific cutoff frequency, downsampling the bandwidth of a signal. Given that most waveforms were recorded at a sampling frequency of 125 Hz and that this was the lowest frequency present in our study population, we selected this as our desired sampling frequency and subsequently down-sampled the remaining waveforms to align with it. Furthermore, a straightforward outlier detection protocol was implemented based on the probability of occurrence of each sample value within each waveform. This protocol identifies outliers as samples with a probability equal to or less than 0.01, which was empirically obtained. These outliers were replaced with the median value of the respective waveform to ensure that artifacts with high absolute amplitude do not impact our features. In post hoc experiments to evaluate whether the care environment or the innate monitor signal was imprinting information in the waveform, we extended our analysis by removing to ensure that our model performance was representative of true elements of the ICP signals, rather than the influence of environmental factors such as adjustment of EVD height. In the Supplementary Materials (http://links.lww.com/CCX/B362), we have conducted comparative analyses to demonstrate that the added value of such artifacts to our model did not significantly improve its performance.

Feature Extraction

The necessity to extract features from various domains (including time, frequency, time-frequency, and nonlinear) in physiologic waveform analysis stems from the multidimensional nature of such data. Each domain captures distinct aspects of the data, facilitating a comprehensive understanding of the underlying patterns and dynamics. Time series data often contain noise or irrelevant information that can obscure the underlying signal. Transforming the data into different domains through techniques such as Fourier or wavelet transforms facilitates the separation of the signal from the noise, enhancing the ability to identify meaningful features and patterns within the data.

Thus, in this study, a comprehensive and established set of features from various domains was extracted and can be classified into four distinct categories: 1) general features, capturing the overall characteristics of the entire ICP waveform, 2) beat-to-beat features, capturing the characteristics of each ICP beat, defined as the period between each P1 (percussion wave), 3) beat variability features, capturing the fluctuations of time between ICP beats caused by the cardiac pulsation cycle, and 4) window-based features, capturing the ICP features within rolling windows with a length of 5 minutes and no overlap. The selection of features was based on previous literature in the field of time series analysis. These included, but were not limited to, autocorrelation, energy in short-time Fourier transform domain, power spectral density features, approximate and Shannon entropy, Hurst exponent, Higuchi fractal dimension, and polynomial curve fitting, calculated as previously described (6, 30–35). To account for the varying size of the ICP waveforms and incorporate temporal information, we extracted a secondary set of features that included the maximum, median, sd, 1st, 25th, 75th, and 99th percentiles, as well as the mean and sd of first and second differences (lags) of beat-to-beat, beat variability, and window-based features. Lag features incorporate historical data into a time series analysis or forecasting model and can help capture important patterns and trends in the data. The first difference is created by taking the difference between a value in a time series and a previous value. The second difference is the first difference of the first difference feature. This approach allowed us to create a fixed input feature vector despite the variability in waveform length. In total, we extracted 842 features (Table 1).

TABLE 1.

List of Extracted Features

Feature Category	Description	Features	Secondary Features
General	Captures the overall characteristics of the entire ICP waveform	Autocorrelation Hurst exponent (Torres-García et al [33]) Kolmogorov Complexity (Kaspar and Schuster, 1987) Approximation entropy Higuchi fractal dimension (Kesić and Spasić [30]) Katz fractal dimension (Wijayanto et al, 2019) Energy at different frequency bands in the short-time Fourier transform domain Spectral centroid (Kulkarni and Bairagi [31]) Spectral spread Spectral entropy Spectral rolloff (Tobore et al [32]) Mean and median frequency (Phinyomark et al, 2012) Occupied and power bandwidth (Mert, 2016) Energy in different frequency bands in power spectral density Shannon entropy (Liang et al, 2015) Periodogram slope (Lendner et al, 2020)	None
Beat-to-beat	Captures the characteristics of each ICP beat, defined as the period between each P1 (percussion wave)	Autocorrelation Energy in different frequency bands in power spectral density Polynomial curve fitting over ICP’s beat with degree 4	Mean Maximum Minimum Median sd 1st, 25th, 75th, and 99th percentiles Mean (diff1) sd (diff1) Mean (diff2) sd (diff2)
Beat variability	Captures the characteristics of the fluctuations of time between ICP beats	Root mean square of successive differences Probability of intervals > 50 ms or < –50 ms Average beats interval in 1 min Mean of the first lag of beats’ intervals Histogram-based features from beat intervals (Oster et al, 2013)	Mean Maximum Minimum Median sd 1st, 25th, 75th, and 99th percentiles Mean (diff1) sd (diff1) Mean (diff2) sd (diff2)
Window-based	Captures the inherent ICP features using a rolling window with a length of 5 min and no overlap	Hurst exponent (Torres-García et al) (33) Energy in different frequency bands in power spectral density Petrosian fractal dimension (Chyzhyk et al [33], Zabihi et al [34]) Shannon entropy Higuchi fractal dimension (Kesić and Spasić [30]) Spectral centroid (Kulkarni and Bairagi [31]) Spectral spread Spectral entropy Spectral rolloff (Tobore et al [32]) Mean and median frequency (Phinyomark et al, 2012) Occupied and power bandwidth Energy in different frequency bands in spectral power density Shannon entropy (Liang et al, 2015) Periodogram slope (Lendner et al, 2020)	Mean Maximum Minimum Median sd 1st, 25th, 75th, and 99th percentiles Mean (diff1) sd (diff1) Mean (diff2) sd (diff2)
		Eigenvalues of phase space (Zabihi et al [34]) Phase space nullcline (Zabihi et al [34])

diff₁ = first difference, diff₂ = second difference, ICP = intracranial pressure, .

Feature Selection and Classification

For feature selection and classification tasks, we used a nested five-fold patient-wise cross-validation scheme. The outer loop partitioned the data into five folds, with four of these folds comprising 80% of the data being used for feature selection and model training, whereas the remaining 20% was used for evaluating the model performance (Fig. S1, http://links.lww.com/CCX/B362). This process was repeated until each fold had served as the test set. The inner loop applied another five-fold cross-validation procedure to the training set to select the most significant features and repeated this process 10 times with different random seeds. In each fold of the inner loop, the top features were selected based on the out-of-bag feature importance (36, 37). We defined a threshold, referred to as k1, as the top 600 features. The threshold for selecting top features is a trade-off between choosing only the most significant features and ensuring, we have a sufficiently large set for analysis (i.e., identifying jointly selected features) within our nested cross-validation framework. Our choice of threshold is purely data-driven and was determined through various trials and iterations only on the training data to strike the right balance. The inner five-fold cross-validation loop was repeated 10 times, resulting in 50 sets of k1 features. These k1 features were then ranked by selection frequency, and based on a threshold, referred to as k2, the 75th percentile, the most frequent ones were chosen as the final selected feature set.

For each outer loop iteration, our model was trained to differentiate waveform data from an EVD from an IPM, using the features selected in the inner loop by using 150 bootstrap-aggregated decision trees. Subsequently, the model was evaluated on the hold-out test set. To conduct a comparative analysis, we also used linear discriminant analysis (LDA) for classification in the outer loop. As a more simple classifier, LDA allowed us to evaluate the robustness of the model and ensure performance was not a result of overfitted decision trees (36–38). Additionally, for a fair evaluation, as an extra step, we retained the nine patients with both monitoring types as unseen held-out data and used them solely for evaluation purposes.

Evaluation Metrics

We used a comprehensive set of seven metrics to evaluate the model’s performance. These included the area under the receiver operating characteristic curve (AU-ROC), sensitivity, specificity, precision, false-positive rate, accuracy, and F1 score, where EVDs were classified as the positive class and IPMs as the negative class.

Subgroup Analysis

To ensure the reliability of our model, we analyzed its robustness and extracted features by assessing them across various patient subgroups. These subgroups were created using 24 potential clinical confounding variables (Tables S1 and S2, http://links.lww.com/CCX/B362). Two different strategies were used: clustering and propensity score-based confound-isolating cross-validation schemes, as illustrated in Figure S2 (http://links.lww.com/CCX/B362). These methods allowed us to assess the extent to which our model and features remained robust in the presence of patient variability and potential confounding factors.

Unlike conventional cross-validation, which randomly partitions data into training and testing sets, confound-isolating cross-validation uses various techniques to stratify the data into a series of strata or folds (35, 38). These methods isolate one or a specific combination of confounding variables within each fold, allowing for a more thorough evaluation of the model’s robustness. During the training and testing phases, the model is tested on a fold with a distinct confounding distribution than the training folds, decreasing the probability of spurious correlations influencing the evaluation.

First, we adopted a cluster-based approach in which we used the k-medoids clustering algorithm (39) and iteratively partitioned the data into three, five, and eight clusters with unique clinical phenotypes. Testing on a distinct cluster from those used for training enabled us to assess the model’s performance or features when accounting for the confounding variable.

Additionally, we used a propensity score-based approach to stratify the data based on a calculated propensity score, representing the likelihood of an ICP waveform belonging to the EVD class given the patient’s clinical characteristics. We partitioned the data by propensity score quantile, forming four distinct subgroups used within the confound-isolating cross-validation process (Fig. S2, http://links.lww.com/CCX/B362).

RESULTS

Patient Characteristics

Of 84 patients meeting inclusion criteria, 82 patients with 2667 ICP epochs, totaling 14,109.8 hours of signal available, met the criteria for analysis (Fig. 2). Forty-seven patients were monitored with an EVD, 26 with an IPM, and 9 with both (Table S1, http://links.lww.com/CCX/B362). As mentioned in Figure S1 (http://links.lww.com/CCX/B362), we used the random downsampling approach to balance the number of EVD and IPM samples before training the model. Mean age, Glasgow Coma Scale (GCS) total, GCS motor score upon admission, presence and amount of midline shift, decompressive hemicraniectomy, and traumatic brain pathology were similar between groups. Monitor type was significantly associated with institutions due to differing local practices regarding monitor choice at the contributing institutions despite otherwise similar clinical presentation among their patients. Additionally, IPM was used more frequently in patients with unilateral sluggish or nonreactive pupils with the right pupil reactivity, yielding a statistically significant difference between the EVD and IPM groups. Other nonsignificant univariate differences between patients with an EVD or IPM can be found in Table S1(http://links.lww.com/CCX/B362).

Model Performance

In patient-wise five-fold cross-validation in the unseen test data using bagged decision trees (BDT) and LDA classifiers, sensitivity, specificity, F1, and AU-ROC exceeded 0.81 (BDT: 0.944 ± 0.038, LDA: 0.883 ± 0.051), 0.704 (BDT: 0.869 ± 0.097, LDA: 0.817 ± 0.064), 0.828 (BDT: 0.922 ± 0.032, LDA: 0.876 ± 0.032), and 0.866 (BDT: 0.932 ± 0.043, LDA: 0.900 ± 0.016) across all folds, respectively (Tables S3 and S4, http://links.lww.com/CCX/B362).

Adding 11 features based solely on artifactual segments did not meaningfully alter model performance, with no changes in any evaluation metric larger than 0.005 for BDT (Table S10, http://links.lww.com/CCX/B362) and 0.015 for LDA (Table S11, http://links.lww.com/CCX/B362).

Furthermore, using the BDT (our primary classifier), we obtained a sensitivity of 0.848, specificity of 0.747, F1 score of 0.805, and AU-ROC of 0.826, based on nine patients with both monitoring types as unseen held-out data (Table S12, http://links.lww.com/CCX/B362).

Subgroup Analyses for Rigor and Robustness

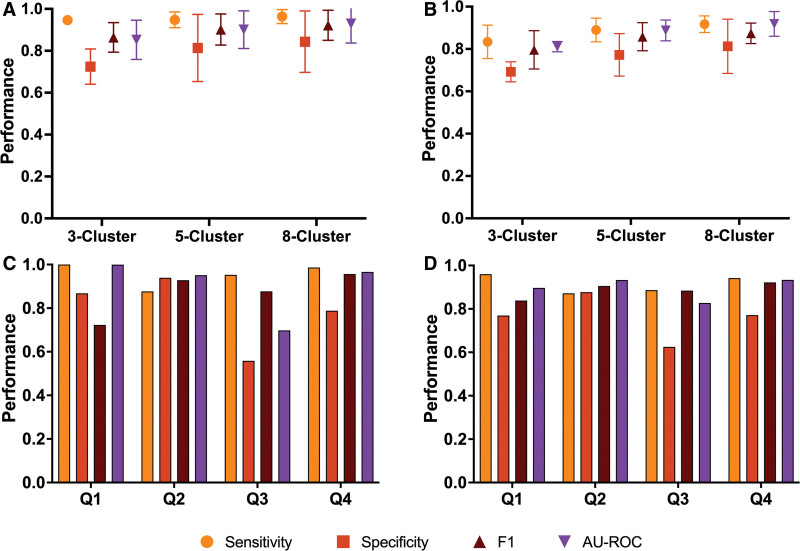
In cluster-based confound isolation cross-validation, we observed an average sensitivity above 0.947 when classifying with BDT (cluster 3, 0.947 ± 0.017; cluster 5, 0.948 ± 0.038, cluster 8, 0.963 ± 0.033; Fig. 3A; Table S6, http://links.lww.com/CCX/B362) and 0.834 when classifying with LDA (cluster 3, 0.834 ± 0.079; cluster 5, 0.890 ± 0.056; cluster 8, 0.917 ± 0.039; Fig. 3B; Table S7, http://links.lww.com/CCX/B362). Average specificity was above 0.724 with BDT (cluster 3, 0.724 ± 0.084; cluster 5, 0.813 ± 0.160; cluster 8, 0.844 ± 0.146; Fig. 3A; Table S6, http://links.lww.com/CCX/B362) and 0.692 with LDA (cluster 3, 0.692 ± 0.047; cluster 5, 0.772 ± 0.010; cluster 8, 0.813 ± 0.128; Fig. 3B; Table S7, http://links.lww.com/CCX/B362). F1 scores were above 0.864 for BDT (cluster 3, 0.864 ± 0.071; cluster 5, 0.902 ± 0.074; cluster 8, 0.922 ± 0.072; Fig. 3A; Table S6, http://links.lww.com/CCX/B362) and 0.796 for LDA (cluster 3, 0.796 ± 0.091; cluster 5, 0.858 ± 0.066; cluster 8, 0.874 ± 0.048; Fig. 3B; Table S7, http://links.lww.com/CCX/B362). Lastly, AU-ROC was greater than 0.852 for BDT (cluster 3, 0.852 ± 0.094; cluster 5, 0.901 ± 0.090; cluster 8, 0.929 ± 0.092; Fig. 3A; Table S6, http://links.lww.com/CCX/B362) and 0.811 for LDA (cluster 3, 0.811 ± 0.024; cluster 5, 0.888 ± 0.049; cluster 8, 0.919 ± 0.058; Fig. 3B; Table S7, http://links.lww.com/CCX/B362). Across all metrics, performance increased as the number of clusters increased. Detailed reporting and further metrics are available in the Supplementary Materials (http://links.lww.com/CCX/B362).

Figure 3.

Model performance of confounder-isolating cross-validation for subgroup analysis. A, Evaluation metrics from cluster-based approach to confounder-isolation with bagged decision tree classifier. B, Evaluation metrics from cluster-based approach to confounder-isolation with linear discriminant analysis. C, Evaluation metrics from propensity score-based approach to confounder-isolation with bagged decision tree classifier (fold 1: 0–0.478, fold 2: 0.478–0.691, fold 3: 0.691–0.835, fold 4: 0.835–1). D, Evaluation metrics from propensity score-based approach to confounder-isolation with linear discriminant analysis (fold 1: 0–0.228, fold 2: 0.228–0.582, fold 3: 0.582–0.927, fold 4: 0.927–1).

The worst groups in our cluster analyses, defined as those with sensitivity or specificity below 70%, were significantly less severe in pupil reactivity, total GCS score, and midline shift. The cluster 3 analysis contained one worst group (vs. remaining patients: L pupil, p = 0.023; R pupil, p = 0.039; GCS, p < 0.001; midline shift, p = 0.003; Table 2). There were two worst groups in the cluster 5 (vs. remaining patients: L pupil, p = 0.001 and p = 0.063; R pupil, p = 0.004 and p = 0.072; GCS, p = 0.016 and p < 0.001; midline shift, p = 0.004 and p = 0.011) and cluster 8 analyses (vs. remaining patients: L pupil, p = 0.095 and p = 0.086; R pupil, p = 0.111 and p = 0.097; GCS, p = 0.800 and p < 0.001; midline shift, p = 0.004 and p = 0.022; Table 2).

TABLE 2.

Comparison of Four Potential Confounding Factors Between the Worst-Group Patients Against the Remaining Patients in Two Subgroup Analyses (p values)

Confounder Subgroup Strategy	Worst Group vs. Resta	Left Pupil Reactivityb	Right Pupil Reactivityb	Total Glasgow Coma Scale Score	Midline Shift
Confounder cluster strata	Cluster 3	0.033	0.039	< 0.001	0.003
	Cluster 5	0.001	0.004	0.016	0.004
	Cluster 5	0.063	0.072	< 0.001	0.011
	Cluster 8	0.095	0.111	0.800	0.004
	Cluster 8	0.086	0.097	< 0.001	0.022
Propensity score strata	Bagged decision trees	0.905	0.788	0.593	0.649
	Linear discriminant analysis	0.572	0.447	0.384	0.741

^aWorst-group patients were defined as any of those with either sensitivity or specificity below 70%.

^bAt admission.

Cluster 5 and cluster 8, both contained the worst-group patients.

Using propensity score-based cross-validation, we found a mean sensitivity of 0.954 ± 0.048, mean specificity of 0.788 ± 0.143, mean F1 score of 0.871 ± 0.090, and mean AU-ROC of 0.904 ± 0.120 when classifying with BDT (Fig. 3C). When using LDA, mean sensitivity was 0.915 ± 0.037, mean specificity was 0.761 ± 0.090, mean F1 score was 0.887 ± 0.032, and mean AU-ROC was 0.898 ± 0.043 (Fig. 3D). A complete list of results for the subgroup analysis can be found in the Supplementary Materials (Tables S6–S9, http://links.lww.com/CCX/B362).

Feature Selection

Examining standard, cluster-based, and propensity score-based cross-validation schemes, feature selection converged on 62 features jointly selected by both BDT and LDA methods across all evaluated cross-validation schemes. Figure S4 (http://links.lww.com/CCX/B362) articulates observed differences between EVDs and IPMs in boxplots and kernel density plots for a sample of the selected features, which demonstrate greater complexity and volatility in EVDs versus consistency and stability in IPMs as key differentiators. Features selected were Higuchi fractal dimension short-time-frequency energy band (11–16 Hz), spectral centroid, summation of power spectral density in 20–40 Hz, autocorrelation, coefficients of polynomial fit on ICP beat, Hurst exponent, eigenvalues of phase space (34) (Fig. S4, A and B, http://links.lww.com/CCX/B362), coefficients of an autoregressive model with order 4 (Fig. S4, C and D, http://links.lww.com/CCX/B362), Petrosian fractal dimension, Shannon entropy, singular values of phase space, spectral entropy, spectral rolloff, mean normalized frequency of the power spectrum, spectral slope, and phase space nullcline (34) (Fig. S4, http://links.lww.com/CCX/B362). For a complete list of features, including their definitions, we refer to Table S2 (http://links.lww.com/CCX/B362).

DISCUSSION

This proof-of-concept study developed an ML model to accurately and robustly classify ICP waveform features distinct to ICP monitor type and generate automated metadata designating the ICP monitor as originating from an EVD or IPM. Our model was able to achieve an average F1 score of 0.922 (± 0.032) and 0.876 (± 0.032) using BDT and LDA, respectively, in a patient-wise five-fold cross-validation. This demonstrates the promise of our approach, which is further reflected in all computed evaluation metrics and confusion matrices. These results indicate that there are meaningful differences in ICP waveforms from EVDs and IPMs and that the data source should be carefully considered and accounted for as a potential source of bias in future ICP waveform analysis. Additionally, where this contextual metadata is unavailable, our model may be trusted to generate it through analysis of ICP waveform characteristics with further validation on broader datasets.

To our knowledge, this is the first effort to detect the source of ICP waveforms, that is, EVDs versus IPMs, from signatures of their recordings. As we have demonstrated, meaningful differences in ICP waveforms from EVDs and IPMs indicate that the ICP monitor type should be carefully considered and accounted for in future ICP waveform analyses, as it may cause bias and influence clinical decision-making. The developed framework illustrates that features of ICP monitor types are identifiable, and such features can be potentially informative for various analyses of ICP waveforms.

Lessons Learned From ICP Features

We identified 62 distinct characteristics of ICP that consistently emerged as the most significant features, regardless of the classifier, cross-validation scheme, or subgroup analysis used. These invariant features exhibit promising potential for other ICP analyses. Notably, of these 62 features, 44 are window-based. In contrast, only 15 and 4 are chosen from beat-to-beat and general features, respectively. This observation implies that the type of monitor significantly influences trends within the ICP waveform over time, as opposed to each cycle of the ICP pulse or the overall ICP signal. Additionally, the most frequently selected secondary features (24/62) were lag (first and second differences) features, which supports this conclusion and underscores the efficacy of lag features in ICP analysis. As adding features based on artifacts did not meaningfully alter model performance, we conclude that our data preprocessing did not eliminate important information for accurate classification.

We observed a trend of higher complexity levels in EVDsversus IPMs. Differences in the eigenvalues of the covariance matrix of reconstructed phase space of the ICP waveform (Fig. S4, A and B, http://links.lww.com/CCX/B362) indicate unique underlying dynamics and patterns present in the time series data, especially in such cases of complex and nonlinear systems (40). We speculate that this increased complexity in EVD signals arises from either the use of a fluid column to generate the signal and resulting debris or transmitted vibrations, lack of discretization at an intermediate ICP monitor breakout box before being relayed to the patient’s physiologic monitor, or alternatively the complex milieu of the ventricular system, in which CSF pulsations in the lateral ventricles have phasic coupling between adjacent compartments such as fourth ventricle or circle of Willis arterial signals (41).

EVDs exhibit a higher sd of autoregressive parameters (Fig. S4, C and D, http://links.lww.com/CCX/B362), which capture the temporal patterns and dependencies within the time series (42), that is, how consistent or uniform the signal is. This suggests that EVDs have more significant fluctuations and vary widely from one window to another than IPMs, which demonstrate more stability and consistency in the model parameters. This indicates greater complexity or nonlinearity in the underlying process generating EVDs compared with IPMs. Similarly, the distances among the intersected nullclines in the phase space (Fig. S4, E and F, http://links.lww.com/CCX/B362), representing cluster 3 exhibiting distinct characteristics within each ICP monitor type (34), are greater in EVDs compared with IPMs, suggesting more volatility. This may arise from various factors, including abrupt shifts in underlying ICP patterns, outliers, or alterations in the system’s dynamics, all of which could be attributed to clamping and drainage of the EVD. Unfortunately, due to the historical nature of this dataset, details on EVD probes and institutional clamping protocols were not available to include in this analysis.

Lessons Learned From Subgroup Analysis

To ensure the reliability of our model, we have used subgroup analysis using clustering and propensity scores. In our cluster analysis, we found that increasing the number of clusters led to improved performance across all evaluation metrics. This improvement can be attributed to providing more clusters for training, allowing the model to learn more efficiently. This observation was held for BDT and LDA models (7.7% and 10.8% improvement in AU-ROC of BDT and LDA, respectively; Tables S6 and S7, http://links.lww.com/CCX/B362). However, we also found that certain patients consistently performed relatively poorly (the worst group, defined as those with either sensitivity or specificity below 70%) in the unseen test fold, regardless of the chosen model or number of clusters. Upon closer inspection, we discovered that these patients had significantly less severe total GCS scores, pupil reactivity upon admission, and the amount of midline shift in most clustering configurations (Table 2). This may suggest that our identifiable ICP features are more apparent when ICP is abnormal and that our model may be limited in application to less severe patients, although no significant changes were identified between the potential confounders of the worst-group patients and other patients in the propensity score-based analysis (Table 2). Importantly, our model performance was strongest for the most critical populations compared with the marginally weaker performance in clusters of less severe patients, allowing for reasonable applicability of our findings in the clinical areas of greatest need. However, future studies should examine this finding in a larger cohort, including other diagnoses of ABI beyond TBI, to increase the generalizability of this proof-of-concept study.

Sample Size to the Number of Features Ratio

In this study, the number of extracted features is relatively larger than that of the sample (patients). In classical statistics, this implies overfitting. However, we would like to provide the following perspectives: 1) tree-based ensembles are highly adaptive to “large p, small n” problems: the robustness of tree-based ensembles (our primary choice for classifier) has been proved empirically when the number of samples is lower than the features (43). Such scenarios are common in studies focused on genomic data analysis, where the number of features (genes) often exceeds the number of samples (patients). 2) Proper evaluation matters: to ensure our findings’ validity and avoid overfitting, we not only used nested cross-validation but also used confound-isolating cross-validation to detect potential biases, albeit at the expense of reducing our performance. 3) A naive classifier shows the true discriminant power of features: in addition to using BDT, we repeated all the analyses by using a simple classifier, that is, LDA. This choice was made to underscore the discriminative capabilities of features rather than relying solely on advanced ML techniques. Thus, our proof-of-concept framework provides a robust performance despite the lower number of features.

Limitations

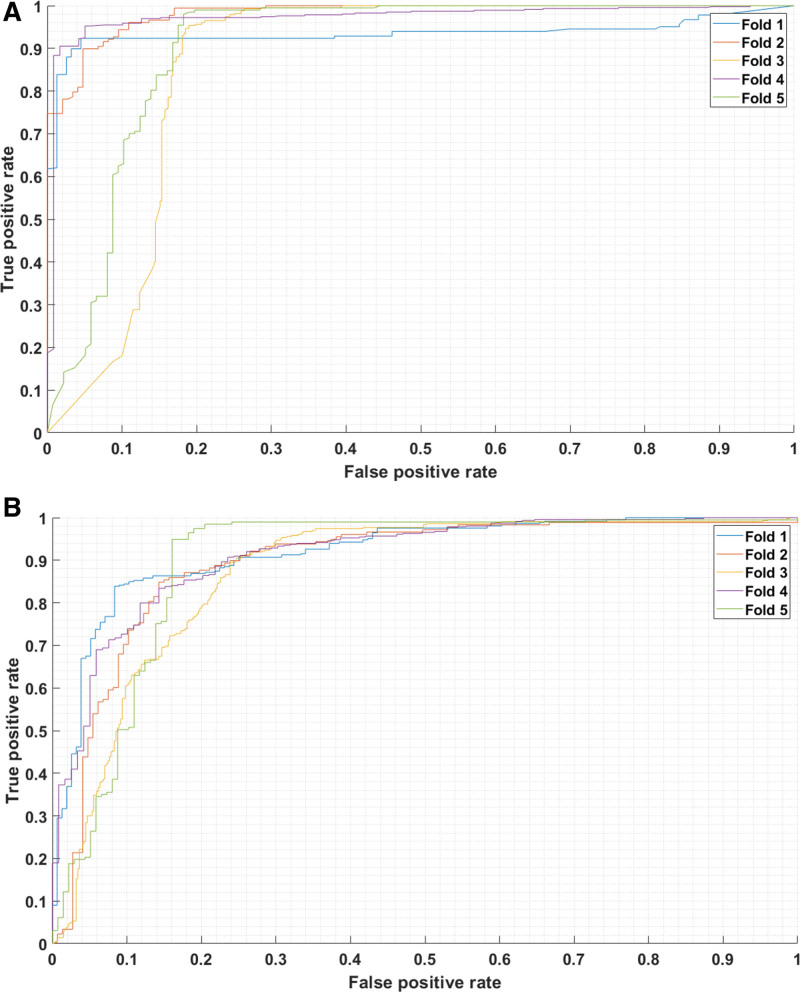
Our analysis confirms that decision tree-based models have demonstrated their considerable power and superiority in various applications (44, 45). We also used a simple LDA classifier to showcase the discriminating ability of our features. Although LDA exhibited relatively lower performance than BDT, it still yielded promising results on average (0.9 AU-ROC and F1 score 0.876) and showed smaller decreases in performance in subgroup analyses (5.6% reduction in specificity and 0.2% decrease in AU-ROC vs. 8.1% and 2.8% for BDT). Further, in the worst-performing group, LDA significantly outperformed BDT in terms of specificity and AU-ROC (Fig. 4, C and D). These results demonstrate that BDT is prone to overfitting despite being more sophisticated than LDA, suggesting that bias may contribute to the model performance and highlighting the necessity of conducting further subgroup analyses with external datasets to robustly evaluate the model’s performance.

Figure 4.

Model performance of intracranial pressure (ICP) waveform-derived features. A, Area under the receiver operating characteristic curve (AU-ROC) with bootstrap-aggregated decision trees used for classification. B, AU-ROC curve with the linear discriminant analysis (LDA) used for classification. Note that the LDA method demonstrated better consistency of the AU-ROC across all folds (better worst-fold performance).

In addition, the developed ML model in this study is based solely on patients with TBI. Further research is necessary to investigate if the developed framework can also be used in patients with diagnoses beyond TBI.

CONCLUSIONS

The developed proof-of-concept ML framework accurately and robustly identified features of ICP derived from an EVD or IPM and was able to generate automated metadata designating the provenance of an ICP monitor based on monitor type. Accuracy was evident across procedures designed to ensure robustness through confound-isolating cross-validation. The developed framework can impute metadata from retrospective ICP datasets lacking data for monitor type, enabling future waveform analysis controlling for the bias introduced by the monitor type. This is especially critical for multicenter collaboration across datasets in which labels have not been harmonized or remain unknown due to the lack of metadata during data collection. Our model can also consequently summarize confounding by indication for placing one monitor type versus another, which may itself account for differences in treatment response or outcomes. The invariant ICP features may additionally be leveraged in future strategies implementing ML for classification and prediction.

ACKNOWLEDGMENTS

The authors thank Jason K. Barber, a biostatistician from the Department of Biostatistics at the University of Washington, Seattle, for his help in data collection, as well as the Transforming Research and Clinical Knowledge in Traumatic Brain Injury Investigators: Shankar Gopinath, MD, Baylor College of Medicine; Ramesh Grandhi, MD MS, University of Utah; Christopher Madden, MD, UT Southwestern; Michael McCrea, PhD, Medical College of Wisconsin; Randall Merchant, PhD, Virginia Commonwealth University; Laura Ngwenya, MD PhD, University of Cincinnati; Claudia Robertson, MD, Baylor College of Medicine; David Schnyer, PhD, UT Austin; John K. Yue, MD, University of California, San Francisco.