Abstract
Despite recent experimental progress in characterizing cell migration mechanics, our understanding of the mechanisms governing rapid cell movement remains limited. To effectively limit tumor growth, antitumoral T cells need to rapidly migrate to find and kill cancer cells. To investigate the upper limits of cell speed, we developed a new hybrid stochastic-mean field model of bleb-based cell motility. We first examined the potential for adhesion-free bleb-based migration and show that cells migrate inefficiently in the absence of adhesion-based forces, i.e., cell swimming. While no cortical contractility oscillations are needed for cells to swim in viscoelastic media, high-to-low cortical contractility oscillations are necessary for cell swimming in viscous media. This involves a high cortical contractility phase with multiple bleb nucleation events, followed by an intracellular pressure buildup recovery phase at low cortical tensions, resulting in modest net cell motion. However, our model suggests that cells can employ a hybrid bleb- and adhesion-based migration mechanism for rapid cell motility and identifies conditions for optimality. The model provides a momentum-conserving mechanism underlying rapid single-cell migration and identifies factors as design criteria for engineering T cell therapies to improve movement in mechanically complex environments.
Keywords: PHYSICAL SCIENCES, Biophysics and Computational Biology, Cell migration, biophysical model, amoeboid, bleb, actomyosin contractility
Cell migration is a complex multistep process that is critical for in vivo processes such as, morphogenesis1, maintaining tissue health and homeostasis2, and driving diseases such as cancer, including cancer cell dissemination during metastasis3 and immune cell migration within tumors4. Single cells migrating in three-dimensional environments use two dominant modes of migration: amoeboid and mesenchymal5. The amoeboid phenotype is characterized by a rounded cellular morphology, high cortical contractility, low cell-matrix adhesions and narrow/tight extracellular spaces, and it is commonly associated with the formation of blebs6-13, which are pressure driven spherical cellular membrane protrusions that are initiated by either a local membrane-cortex detachment or a local cortex rupture14-16. This amoeboid blebby phenotype has been reported under some conditions for transformed cells (e.g. melanoma, breast and squamous carcinoma cells in vivo;17-20), and is frequently utilized by T cells21-23. The mesenchymal-like phenotype, which is frequently displayed by fibroblasts and multiple cancer types, including carcinomas, fibrosarcomas and glioblastoma24,25. It is characterized by an elongated morphology, strong cell-matrix adhesion, available space in the extracellular environment and the formation of actin-rich leading-edge structures such as spike-like filopodia or broad flattened lamellipodia10,12,24,26. In their lifetime, cells navigate through extremely complex microenvironments, such as tight porous viscoelastic tissues or narrow vascular pores. As a result, many cancer cells5,12,17,27-31 and immune cells, including T cells21, can extend both types of cellular protrusions, and adapt to different mechanical and chemical microenvironments by transitioning between mesenchymal and amoeboid migration phenotypes.
T cell-based cancer therapies offer a promising approach in the fight against cancer32. However, successful T cell-based therapies have been limited mainly to hematologic cancers. Solid tumors create a highly immunosuppressive and fibrotic microenvironment that hinders the physical infiltration and activity of cytotoxic T cells, thus enabling tumor growth and metastasis33,34. Despite the significant progress in understanding bleb formation in recent years21,35,36, it remains largely unknown how bleb-producing T cells exchange momentum with their surroundings to navigate through challenging mechanical and chemical microenvironments such as tumors. Hence, a combination of biophysical modeling and cutting-edge experimental approaches is needed to elucidate T cell migration mechanisms and establish design criteria for next-generation immune engineering strategies to enhance T cell infiltration, migration, and sampling within the tumor mass.
Adhesion-dependent migration, described and mathematically modeled using a motor-clutch framework25, has long been thought to be required for cell motility37, but some recent findings have challenged this view11,26,38–51. Following the seminal paper by Lämmermann et al.38, which demonstrated that leukocyte migration in vitro and in vivo is independent of various integrin heterodimers, there has been an ongoing debate about the extent to which the rapid migration of immune cells, particularly those exhibiting an amoeboid phenotype, is dependent on adhesion-based forces40,44,48,51. The question of whether immune cells can swim through tissues autonomously or if they depend on other adhesion molecules (e.g. CD44) for migration remains unresolved. We investigate a possible adhesion-independent migration mechanism in this paper, specifically bleb-based cell swimming. Our initial focus on cell swimming is motivated by these studies and by the persistent question of how T cells navigate through distinct microenvironments, ranging from lymph nodes to extracellular spaces of varying densities.
Most animal cells have a dense, thin actomyosin layer that lies underneath the plasma membrane that produces cortical tension mediated forces that are transmitted to the membrane by membrane-cortex linker proteins, such as Ezrin, Radixin and Moesin proteins52,53. Upon a local membrane-cortex cohesion loss, cortical forces no longer get transmitted to the plasma membrane and a bleb nucleates and undergoes fast expansion reaching bleb sizes of order . At the bleb nucleation site, the local hydrostatic pressure presumably drops, and cytoplasmic material flows from the center of the cell to the low-pressure bleb site54,55. The bleb cycle ends by the self-assembly of new cortex underneath the bleb membrane, which drives bleb retraction14,56. Yet, it is not obvious whether this form of cell motility requires cell-matrix adhesion interactions, nonspecific cell-matrix friction interactions or if the cell can achieve a net displacement after each bleb cycle in adhesion-independent conditions.
Bleb nucleation57-62 and bleb growth55,63–65 have been studied theoretically using coarse-grained mechanistic models. In addition, a handful of amoeboid/bleb-based motility biophysical models have also been recently developed, where the intracellular and extracellular spaces were assumed to behave as viscous fluids49,50,66-78. Most of these cell migration models assume that plasma membrane and cortex are a single composite material. Two of these studies, however. account for the mechanical interactions between the intracellular viscous fluid, the actin cortex and the cell membrane66,67. However, the model by Lim et al.66 does not satisfy conservation of momentum, since it does not account for the forces exerted by the cortex on the cytoplasm as it moves through the crowded intracellular medium. Likewise, the model of Copos and Strychalski67 introduces a cortical viscoelastic force that depends on a reference cortical configuration, as well as a steric interaction force with the walls. Although the enforced no-penetration fluid flow condition at the boundaries ensures conservation of linear momentum in the fluid, the inclusion of these two forces does not guarantee that the total force exerted by the cell on the medium vanishes. To address this gap, in the present study, we first develop a momentum-conserving mechanistic model of bleb-based cell swimming in a viscoelastic medium to assess whether bleb-producing cells such as T cells can mechanically swim in the absence of adhesions, identify the key cellular components that regulate the motile capabilities of swimming cells, and quantify the theoretical maximum speed that a cell can achieve using this migration mechanism. We determine that bleb-based cell swimming is theoretically possible but so inefficient that it is not a plausible in vivo fast migration mechanism. Rather, our analysis suggests an alternative hybrid model where blebbing mediates rapid protrusion extension and subsequent adhesion, even when weak, effectively captures the newly gained cell position. The biophysical model provides key insights to mechanically control and potentially maximize migration of blebby cells such as T cells that can contribute to the design of tumor stroma-targeting and cell-specific engineering strategies to enhance the intratumoral migration capabilities of antitumor immune cells.
RESULTS
Biophysical model of bleb-based cell swimming
We first aim to investigate the cell migration capabilities of bleb-producing cells in an unbounded viscoelastic medium through the development of a two-dimensional biophysical mechanistic model (see Supplemental Material for a detailed description of the model). The cell is composed of two distinct structures: a cellular membrane and an actomyosin cortex (Fig. 1A). Both are considered Lagrangian structures defined by a set of nodes that are connected to each other and the associated fluids as described below and in more detail in the supplement. As the cell migrates through the environment, both membrane and cortex structures transmit forces on the surrounding medium, generating viscoelastic stresses. At the continuum level, conservation of mass and momentum on the incompressible viscoelastic fluid reads
| (1) |
| (2) |
| (3) |
where is the fluid velocity, is the total stress, is the total force density on the fluid and equal to the sum of the membrane force density and cortical force density generated in the intracellular medium. The total stress is the sum of two contributions: a purely viscous stress and a viscoelastic stress :
| (4) |
| (5) |
where we have chosen the FENE-P constitutive relation for the stress to model the viscoelastic nature of the intracellular and extracellular spaces79. Here, p is the hydrostatic pressure, and are, respectively, the fluid viscosity and polymer viscosity, is the polymer stress relaxation time, is the conformation stress tensor and is the polymer extensibility parameter, a measure of the maximum polymeric deformation. The time evolution of the conformation stress tensor reads
| (6) |
The first term on the right-hand side (RHS) of Eq. (6) captures stress relaxation kinetics, the second term captures polymer advection, and the last two terms capture rotation and deformation of the polymeric material.
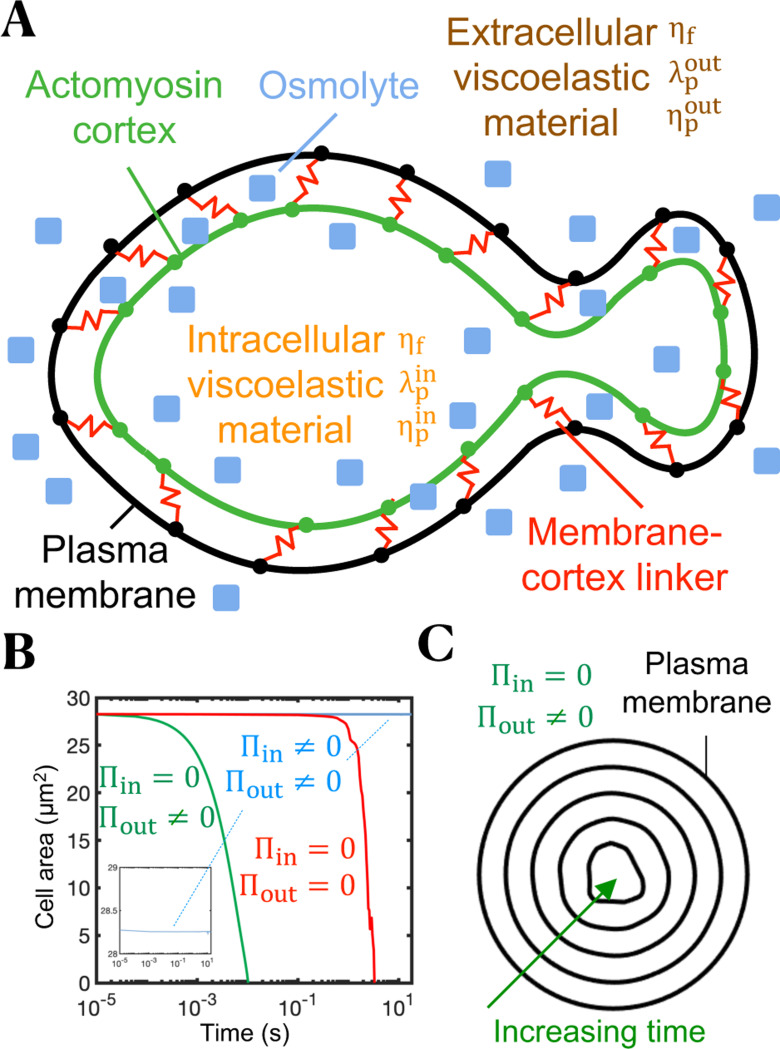
Figure 1.
Intracellular osmotic pressure sets cell size and prevents cell shrinkage fostered by extracellular osmotic pressure and cortical tension. (A) Sketch of the bleb-based cell swimming model. Plasma membrane and actomyosin cortex are mechanically linked by reversible Hookean elastic linkers that stochastically associate and dissociate in a force-independent and -dependent manner, respectively. Intracellular and extracellular spaces are viscoelastic materials with associated fluid viscosity , polymer viscosity and polymer stress relaxation time . Osmotic effects are included. (B) Time-evolution of cell area for three different osmotic conditions. Intracellular osmotic pressure: , extracellular osmotic pressure: . (C) Cell shrinkage due to a reverse osmotic shock (). Thus, inclusion of intracellular osmolytes is necessary to prevent cell collapse due to inward cortical tension and extracellular osmotic forces that tend to force water out of the cell.
The cell membrane is an elastic structure subjected to tension, bending and membrane-cortex adhesion forces, and the cortex is considered an actomyosin poroelastic structure that generates myosin-mediated forces that obey a linear force-velocity relationship and create tension in the cortical network60,80-82. The actin cortex experiences drag forces as cytoplasmic material flows through the porous actomyosin network. Mass conservation of membrane-cortex linkers, and actin and myosin in the cortex follows simple stochastic association and dissociation kinetics. No-slip between the plasma membrane and viscoelastic fluids is enforced. Furthermore, the model accounts for osmotic effects, which we found was essential for maintenance of cell volume. The intracellular osmotic pressure resists cortex and extracellular osmotic inward forces, all forces combined set cell size and shape. A hypothetical complete depletion of intracellular osmolyte would cause a sudden cell shrinkage within a few milliseconds as the cortex would otherwise squeeze out all the intracellular water (Fig. 1B). The model equations are solved using an immersed boundary method83. The specific model parameter values used are summarized in Table S2, unless stated otherwise in the text/figure captions, and the code used for the T cell migration biophysical model is available in reference84. Additional details can be found in the Supplemental Information.
Single bleb formation, expansion and retraction allows cells to swim in viscoelastic environments
Using the above framework, we proceed to study cell dynamics during a single bleb cycle by enforcing local membrane-cortex detachment. Membrane-cortex uncoupling is followed by a drop in local intracellular hydrostatic pressure and cytoplasmic viscoelastic fluid material flows through the detached actomyosin meshwork from the center of the cell to the low-pressure region, mediating bleb expansion (Figs. 2A, B, and movie S1). The poroelastic permeable cortex does not sustain pressure forces and moves retrogradely towards the cell center85,86, with actomyosin contractile inward forces balanced by cytoplasm-mediated drag forces, which arise as cytoplasmic material flows through the porous actomyosin network (see Eq. S16). Notice that, in the extreme case where the cortex-cytoplasm drag coefficient is extremely high, the actin meshwork moves along with the cytoplasm, preventing the cytoplasm from filling up the bleb. Eventually, cortex components that detach from the membrane disappear via turnover kinetics (i.e. first-order disassembly without concomitant assembly; see Eqs. S20-21). The bleb cycle ends by recruitment of new cortex constituents underneath the bleb membrane, which nucleates new actin filaments that recruit myosin motors that transmit inward forces to the plasma membrane driving bleb retraction and cytoplasm from the bleb region to the center of the cell in a low intracellular hydrostatic pressure gradient phase (Figs. 2A, 2B and S4). We observe that the bleb area at the end of the cycle is primarily limited due to the increase in the local hydrostatic pressure from cortex reformation rather than membrane tension (Fig. S4). We observe that the plasma membrane follows similar trajectories during bleb expansion and bleb retraction. A forward movement of cytoplasmic material translocates the center of mass of the cell forward in the direction of the bleb during bleb growth, and a rearward movement of cytoplasmic material translocates the center of mass of the cell in the opposite direction during bleb retraction. Cell shape-based swimming of microscale biological cells in a Newtonian fluid (i.e. at low Reynolds number) requires non-reciprocal body deformations to generate locomotion87. Accordingly, we observe that net cell displacements at the end of the bleb cycle are minimal in Newtonian environments (Fig. S4). This result is in contrast with the model by Lim et al., which shows that individual blebbing events lead to significant net cell displacements. This discrepancy likely arises from a violation of momentum conservation in their model. However, reciprocal motion can lead to net cell motion in viscoelastic environments, as observed in single-hinge reciprocal microswimmers experiments moving through shear-thickening and shear-thinning fluids88. For physiologically relevant model parameters, cell displacements are larger during bleb expansion compared to those during bleb retraction due to the rapid and slow rates of bleb expansion and retraction phases, respectively. The cell shears its environment at distinct rates during both phases, resulting in significant net cell displacements () during a single bleb cycle of ~2.5 seconds (Figs. 2C-E), for a mean speed of . We can estimate the 3D effective cell motility coefficient as 89, where cells run at an effective velocity given by during an effective runtime . Given that reported blebbing frequencies are on the order of ~4s−185, we assume that the time needed for the cell to translocate during each bleb cycle is the limiting factor in each cell run; thus (Figs. 6A, B). Under these assumptions, . This value is an order of magnitude smaller than the in-vivo motility coefficient of bleb-producing cells (), suggesting that the adhesion-free bleb-based cell migration mechanism is unlikely to be the mode of migration for T cells navigating through tissues. For non-physiological fast cortex turnover times, the timescales of bleb expansion and retraction are similar, preventing cells from achieving net cell motion during a single bleb cycle (Fig. S3). Overall, our results indicate that net cell displacements can be achieved by bleb-based cell swimming in viscoelastic environments, but only at rates insufficient to explain rapid T cell motility in vivo.
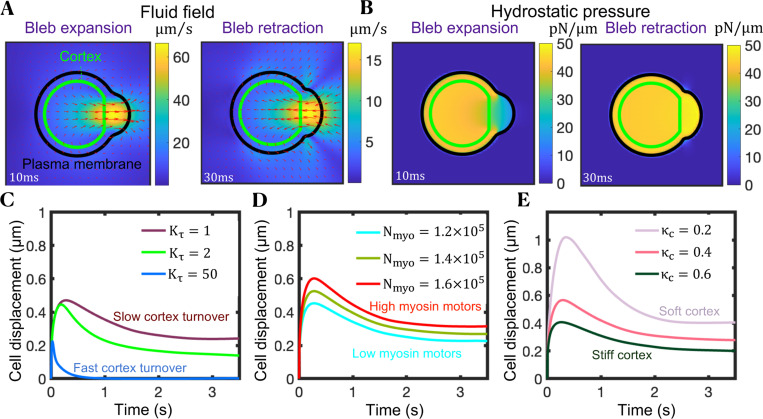
Figure 2.
Cells can achieve moderate net cell displacements during a single bleb cycle in viscoelastic environments without adhesion-based forces, thanks to the differential shear rates associated with bleb growth and retraction phases. (A,B) Snapshots of the magnitude of the fluid velocity and velocity vectors (A), and hydrostatic pressure (B) acquired at two time-points during early bleb expansion and early retraction. for panels (A) and (B). (C−E) Time-evolution of the cell centroid for three different values of the cortex turnover parameter (C), for three different values of the number of myosin molecules inside the cell (D) and three different values of the cortical stiffness per unit of actin parameter (E). Greater cell displacements are achieved for slower cortical turnover kinetics, and a more contractile and softer cortex. In all panels, membrane-cortex linkers are broken by hand locally in a small region at time t = 0, mimicking a local downregulation of membrane-cortex linkers due to a chemical signal or force. Polymeric model parameter values: .
Figure 6.
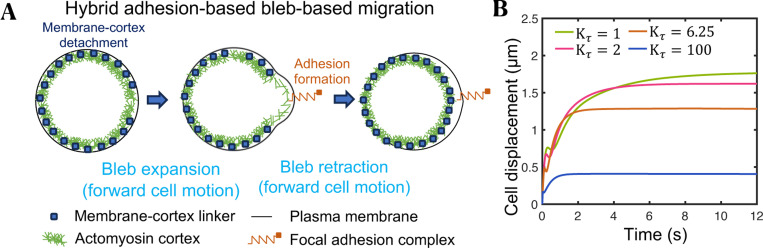
Cell-extracellular matrix adhesion is required for optimal bleb-based cell motility. (A) Visual representation of one complete cell migration cycle in the hybrid adhesion-based bleb-based mode of migration. (B) Time-evolution of the cell centroid for four different values of the cortex turnover factor . Larger cell displacements are achieved for slow cortex turnover times. Physiological cortex turnover times correspond to (see Table S1).
High intracellular hydrostatic pressure gradients and a softer cortex favor larger cell displacements during a bleb cycle
Next, we employed the model to define how different cellular conditions influence cell displacements during an individual bleb cycle. For a given membrane-cortex detachment size, more contractile and/or softer actomyosin cortices favor larger cell displacements during bleb expansion (Figs. 2D and 2E), resulting in greater overall cell displacements at the end of the bleb cycle. High cortical squeezing, mediated by a higher number of myosin motors in the cell, causes larger intracellular hydrostatic pressure gradients after membrane-cortex dissociation. This drives stronger cytoplasmic flows and results in larger bleb sizes and cell displacements during an individual bleb cycle (Fig. 2D). A softer cortex gives rise to stronger intracellular flows (Fig. S1A), and delays both intracellular hydrostatic pressure equilibration (Fig. S1B) and the end of bleb expansion (Fig. 2E). During this expansion phase, active stresses are concentrated at the cell’s rear and center, away from the actomyosin-free bleb region. The cortex, being a highly crosslinked actin network, allows these active stresses to propagate throughout the cell90. As new cortex is recruited beneath the plasma membrane bleb, it experiences retrograde pulling forces from the highly contractile regions away from the bleb, transmitting these forces to the plasma membrane at the leading edge. In cells with a softer cortex, this stress propagation is diminished, resulting in delayed bleb retraction and larger cell displacements at the end of a bleb cycle (Fig. 2E). Interestingly, bleb expansion rates obtained from Fig. 2 () are at least an order of magnitude higher than diffusion-limited polymerization rates of monomeric G-actin into F-actin 91-93, which drive filopodial and lamellipodial extension, suggesting that maximal cell migration speeds might involve bleb expansion dynamics rather than F-actin self-assembly-driven protrusions.
The cell produces viscoelastic stresses on its surroundings as blebs expand/retract. The spatial structure of these stresses is examined in Figs. S3A (inset) and S3D, where high polymer stresses concentrate at the front of the cell, providing an additional resistance to pressure-driven bleb expansion. This results in lower cell displacements at the end of the bleb cycle for extracellular materials with a low stress relaxation time . Cell displacements at the end of the bleb cycle are greater in low density extracellular spaces (Fig. S2A) and are nearly insensitive to extracellular stress relaxation times (Fig. S2B). Low plasma membrane tension also causes maximal cell displacements in an individual bleb cycle (Fig. S2C), as membrane tension builds up at the cell front during bleb growth thus opposing further expansion (Fig. S3D) and a softer membrane provides less elastic resistance to forward plasma membrane motion. Overall, our model results show that larger cell displacements during a single bleb migration cycle are favored by low-density extracellular spaces, providing novel insights into the mechanisms used by phenotypically amoeboid cells when navigating complex porous networks. Likewise, our model demonstrates that soft actomyosin cortices, high myosin motor levels, and softer plasma membranes also favor cell displacement, identifying intracellular factors that may be perturbed to engineer cells that move better in mechanically heterogeneous complex environments.
Sustained adhesion-free bleb-based cell swimming in Newtonian environments requires cortical contractility oscillations
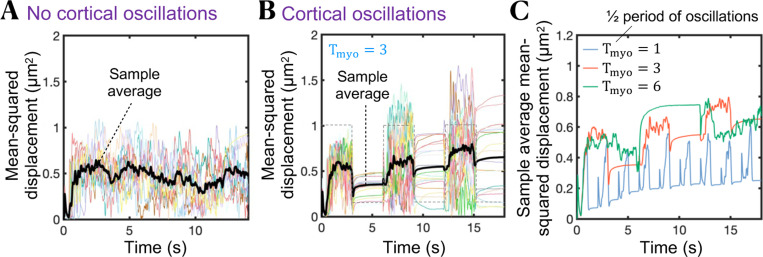
Since a single cycle of bleb extension-retraction results in minimal net cell displacement, we next explored whether bleb-producing cells can swim in adhesion-free conditions by producing bleb-based cell shape changes. To embrace more complex variations in the dynamics of cortex component amounts we introduce stochasticity in the kinetics of membrane-cortex linkers, actin and myosin, where membrane-cortex linkers stochastically associate in a force-independent manner and unbind by force with an effective dissociation rate that increases exponentially with force according to Bell’s law94 (see Supplemental Material for additional details). Hereinafter, we consider intracellular and extracellular spaces to be viscous fluids. We find that bleb-producing cells that maintain a consistently high contractility level cannot effectively migrate, as shown by the plateau reached by the sample average mean-squared displacement-time curve after a few bleb nucleation events (Fig. 3A and movie S2). The significant cell displacement achieved by the cells during the first bleb cycles suggests that cells could potentially migrate starting from a healed cortex with a fully pressurized intracellular cytoplasm. Therefore, we introduced a cortical contractility oscillator signal into the model, to mimic cortical contractility oscillations95,96, and allow the cortex to recover and “heal” before stochastically initiating the next bleb cycle. We find that cells are capable of modest swimming by producing high-to-low cortical contractility oscillations, where a high cortical tension phase characterized by multiple bleb nucleation events is followed by an intracellular pressure buildup recovery phase at low cortical contractility, resulting in mean-squared cell displacements that increase over time (Fig. 3B). Intermediate frequencies of the cortical oscillation signal seem to maximize cell swimming migratory capabilities (Fig. 3C). Overall, these results show that adhesion-free bleb-based cell shape changes combined with high-to-low cortical tensions are a possible strategy by which cells could move through biological tissues or fluids via a stochastic swimming behavior of repeated cycles of bleb-based protrusions driven by oscillations in cortical contractility. That is, our model predicts that amoeboid carcinoma and immune cell swimming is theoretically possible in Newtonian environments but is too slow to explain experimentally observed speeds of rapid T cell migration (46,97,98).
Figure 3.
Cortical contractility oscillations are required for effective bleb-based cell swimming. (A,B) Time-evolution of mean squared displacement of 20 cells in the absence of cortical oscillations (A), and in the presence of cortical oscillations (B). The sample average over all cells (black line) increases over time for cells that produce cortical tension oscillations. Cells that do not produce cortical contractility oscillations are incapable of migrating effectively after the first bleb nucleation/expansion event. The gray dashed line in (B) indicates the waveform of the temporal oscillatory signal . (C) Sample average mean squared displacement over time for three different periods (in seconds) of the cortical contractility oscillation signal. Intracellular and extracellular spaces are assumed to be Newtonian.
Maximal bleb-based migratory potential achieved for high myosin motors and a soft cortex
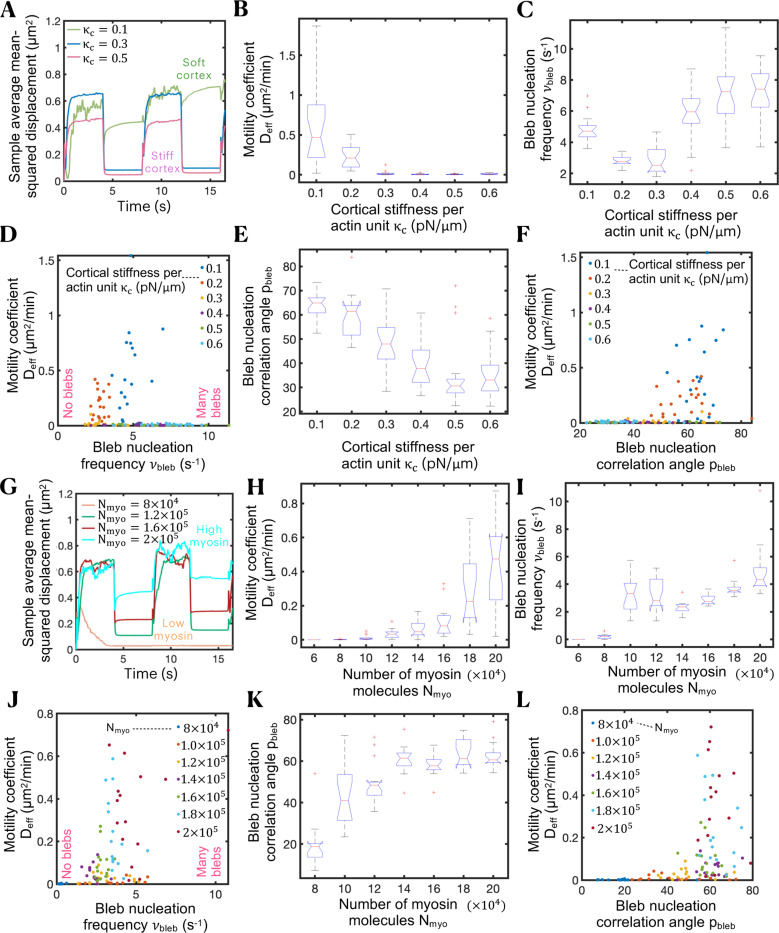
To explore the optimum cellular conditions for maximal cell motility via the oscillatory bleb-based swimming mechanism identified above, we identify two important model parameters that strongly modulate cell motility: cortical stiffness and cortical tension. We find that a soft cortex is essential for cell motility (Figs. 4A and 4B). Cortical stiffnesses per unit of actin, , higher than give rise to extremely low random cell motility coefficients, as shown in Fig. 4B. For an estimated number of actin units at each cortical node of (see Supplemental Information), our model predicts that a cell with a cortical stiffness greater than 4000 pN/μm cannot swim effectively. Quantitative analysis shows a biphasic behavior of bleb nucleation frequency as a function of cortical stiffness. When cortical stiffness is high, the cortex is unable to rapidly adjust to deformations in the plasma membrane. This frequently places membrane-cortex linkers under high tension, leading to frequent membrane-cortex linker ruptures and increased bleb nucleation frequencies. In the limit of low cortical stiffness, in-plane cortical motion caused by contractility gradients can also often subject membrane-cortex linkers to a high tensional state causing frequent bleb nucleation events as well. Consequently, a minimum nucleation frequency is found at intermediate cortical stiffnesses, as depicted in Figs. 4C and 4D. Intermediate bleb nucleation frequencies correlate with maximal cell random motility coefficients (Fig. 4D). Whereas cells cannot swim under low-frequency conditions, since effectively cells nucleate a sequence of isolated bleb cycles, leading to no swimming, high-frequency blebbing cells are not capable of successfully pressurizing their cytoplasm between consecutive bleb events, causing a decrease in their swimming propulsion efficiency. Intermediate blebbing frequencies are therefore ideal conditions for swimming, where the synchronized nucleation of multiple blebs indeed allows cells to break time-reversibility and migrate with modest effectiveness () in the absence of adhesion-based forces. Interestingly, metastatic potential of prostate cancer cells have been reported to correlate with reduced F-actin and high blebbing frequency99. The polar angle between consecutive bleb nucleation events (see Supplemental Material for further details), here referred to as bleb nucleation correlation angle , monotonically decreases with cortex stiffness, as shown in Fig. 4E, with soft-cortex cells and stiff-cortex cells nucleating blebs at and , respectively, as depicted in Fig. 4F.
Figure 4.
Swimming capabilities of bleb-producing cells can be modulated by cortical contractility and cortical stiffness. (A) Time-evolution of sample average mean squared displacement for four different values of the cortical stiffness per unit of actin parameter . (B,C) Effective random motility coefficient (B) and bleb nucleation frequency (C) as a function of . Cells swim more efficiently for lower cortex stiffnesses. The effective diffusion coefficient is extracted from the data by fitting a line constrained to go through the origin in the mean-squared-displacement-time plots over 16 seconds. (D) Scatter plot showing the relationship between and for different values of . Intermediate bleb nucleation frequencies correlate with maximal random motility coefficients. (E) Polar angle between consecutive bleb nucleation events as a function of . (F) Scatter plot showing the relationship between and for different values of . Maximal random motility coefficients are observed for polar angles of ~60°–70°. (G) Time-evolution of sample average mean squared displacement for number of myosin motors . (H,I) Effective random motility coefficient (H) and bleb nucleation frequency (I) as a function of . Cells swim more efficiently for high number of motors. (J) Scatter plot showing the relationship between and for different values of . (K) Polar angle between consecutive bleb nucleation events as a function of . (L) Scatter plot showing the relationship between and for different values of . Maximal random motility coefficients are observed for polar angles of ~60°. Intracellular and extracellular spaces are assumed to be Newtonian.
We additionally find that high cortical contractility is essential for bleb-based cell motility, with high-myosin-motor cells possessing a higher motility coefficient than low-myosin-motor cells, as depicted by the mean-squared displacement curves, effective random motility coefficients and wind rose migratory cell track (Figs. 4G, H and S4, respectively. Higher number of myosin motors increases blebbing frequency and bleb nucleation correlation angle (Figs. 4I-L). Maximal cell motility coefficients not only correlate with intermediate blebbing frequencies (as already discussed) but also with intermediate bleb-to-bleb polar angles, as shown in the scatter plots in Figs. 4J and 4L. Maximal cell motility coefficients correlate with bleb nucleation frequencies of and bleb-to-bleb polar angles of pbleb~60°. Cells that nucleate sequential blebs with low correlation angles (), i.e. blebs on top of blebs, approach geometrical reciprocal motion resulting in vanishing cell motility coefficients, whereas cells that nucleate sequential blebs too separated from each other spatially () lose directionality/cell polarization, do not create effective non-reciprocal plasma membrane deformations and their migratory potential is penalized, as Fig. 4L shows. Whereas slow turnover time of cortex components, low fluid viscosity and low membrane tension favor bleb-based cell spreading, we have not observed any statistically significant difference in migration capabilities for the different values explored of cortex porosity, as depicted in Fig. S7. We hypothesize that the actomyosin cortical meshwork hinders cytoplasmic flows during both bleb expansion and bleb retraction, and so the slowing of cytoplasmic flows during both phases cancels out and its effect on bleb-based cell motility becomes insignificant. Overall, our model results show that cells with a soft cortex and elevated cortical tension exhibit more efficient motility by extending large bleb protrusions and the precise spatiotemporal nucleation of blebs, suggesting that engineering therapeutic T cells to possess increased cortical tension and/or a softer cortex would favor bleb-based T cell movement in complex environments. Notably, our cortical tension result is consistent with recent experimental findings, where high contractility pushed adhesive T cells into a faster amoeboid phenotype21.
Blebs nucleate in regions of high cortical tension, low membrane-cortex linker density and high intracellular osmotic pressure.
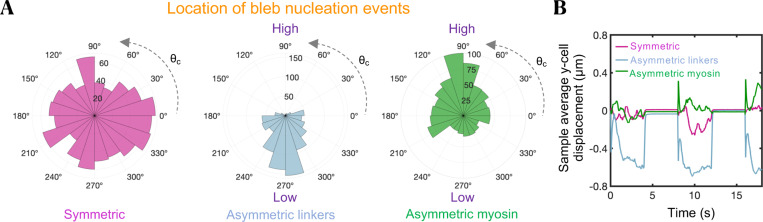
We next investigated the role of spatial variations in mechanical factors that potentially control the location of bleb nucleation sites, and thus bleb-based cell directionality. Bleb nucleation events are initiated by a local decrease in membrane-cortex cohesion. We explore three different scenarios: spatially dependent cortical myosin recruitment, spatially dependent membrane-cortex linker recruitment, and asymmetric distribution of ion pumps within the plasma membrane. Blebs preferentially form in regions of high cortical contractility (high myosin) and low membrane-cortex linker levels, as shown in Fig. 5A, and in agreement with experimental observations22,100,101. Linkers preferentially reach a high tensional state in areas of myosin enrichment, as they are subjected to higher cortical inward forces that eventually cause them to dissociate by force in a runaway process, giving rise to local membrane-cortex detachment and bleb formation. As the bleb enlarges, the membrane-cortex detachment size keeps increasing due to the ongoing rupture of membrane-cortex linkers, while a new cortex forms beneath the plasma membrane. Concurrently, the expansion of the bleb shifts the cortical force at its neck from inward to outward, reducing the tensional state of linkers, and effectively preventing further detachment of the membrane from the cortex. In a similar way, linkers located in low linker density regions are overpowered by high cortical loads making them more susceptible to failure. The highly polarized orientational distribution of blebbing events forces cells to extend protrusions along one axis, restricting their motion to only one degree of freedom, and in turn impeding their migration as shown in Fig. 5B and consistent with the scallop theorem87. Therefore, enforcing the formation of blebs in a small subregion of the cell turns out to be a poor cell shape change-based swimming strategy. Linker failure is also exacerbated in high intracellular osmotic pressure regions (Fig. S8). The highly porous cortex does not sustain net osmotic forces, therefore an increase in local intracellular osmotic pressure causes membrane outward motion, straining linkers which eventuates in a cascade of linker failures and bleb formation. This finding is consistent with the study by Yoshida & Soldati102, which show that low osmolarity media triggers blebbing, highlighting the importance of osmotic stresses in blebbing. Overall, our model results show that a competition between membrane-cortex adhesion and a combination of osmotic and myosin-driven cortical forces control the location of bleb formation sites, again identifying potential cell engineering strategies to alter and control cell protrusion dynamics to enhance motility.
Figure 5.
Blebs nucleate in regions of high myosin and low membrane-cortex linker levels. (A) Polar distribution of bleb nucleation events for three different conditions: uniform association of membrane-cortex linkers and myosin: (red violet), asymmetric kinetic association rate constant of membrane-cortex linkers: (blue) and asymmetric kinetic association rate constant of myosin: (green). Here, is the polar angle associated to each cortical node. (B) Time-evolution of sample average vertical cell displacements for the three different conditions. For the chosen parameter values, larger blebs are formed in the asymmetric linker configuration, resulting in larger displacements during the high cortical contractility phase. Intracellular and extracellular spaces are assumed to be Newtonian.
Rapid cell migration is potentially enabled by a hybrid bleb- and adhesion-based mode of migration for optimum cell motility
In order to analyze whether bleb-based swimming is a feasible mechanism that explains observed T cell motility in vitro and in vivo, we explore if blebbing alone can mediate efficient cell migration in the absence of adhesion-based forces, or if it requires adhesion interactions with the environment for optimal motility. We find that bleb-based coordinated cell-scale deformations are inefficient and lead to maximal migration motility coefficients of (Fig. 4), an order of magnitude lower than reported in vivo cell motility coefficients of bleb-producing cells such as T cells (), which display much faster speeds than those achieved by mesenchymal cells ( for U251 glioma cells103), suggesting that swimming is not the primary T cell movement mechanism.
To address this discrepancy between maximum swimming speed and well documented T cell motility coefficients in vitro and in vivo, we investigate the effect of cell-environment adhesion interactions on the migration capabilities of bleb-producing adherent cells by constructing a simple hybrid adhesion-based, bleb-based cell migration biophysical model (Fig. 6A, see Supplemental Material for a detailed description of the model). Our findings indicate that adhesion interactions with the environment significantly increase cell migration speeds, with cells being capable of translocating approximately up to during an isolated bleb cycle of 9 seconds (Fig. 6B), for a mean speed of . In this mode of migration, we observe that blebbing allows cells to push their cell front forward at a very fast rate (), much faster than F-actin polymerization rates and consistent with experimental observations85, followed by formation of focal adhesions at the cell front, which prevents cell rearward motion during bleb retraction and mediates subsequent traction force generation and fast forward cell translocation. Our model shows that bleb producing adherent cells migrate more effectively for slow cortex turnover times (Fig. 6B) and under high cortical tension conditions (Fig. S9A). Interestingly, while a softer cortex favors greater cell displacements during bleb expansion, a stiffer cortex causes larger cell displacements during bleb retraction, with the highest net cell displacements occurring at intermediate cortical stiffnesses (Fig. S9B). Repeated cycles of adhesion-based blebbing dynamics can lead to diffusive cell behavior, assuming that bleb nucleation sites are independent of the location of previous bleb nucleation events. We can again estimate the 3D effective cell motility coefficient associated with this hybrid migration mechanism as . This value is comparable to the in-vivo motility coefficient of bleb-producing cells, suggesting that the hybrid cell migration mechanism is likely the mode of migration for T cells navigating through tissues. Remarkably, our model predicts that in cells employing a hybrid adhesion-bleb-based migration strategy, cell displacements remain unaffected by the stiffness of the substrate, as shown in Fig. S9C. This finding aligns with experimental observations from T cells on quasi-3D elastic platforms21. In these experiments, cells treated with Nocodazole, a microtubule destabilizer, exhibited high contractility and an amoeboid-like morphology. These cells showed a migration potential that was independent of the rigidity of the nanotexture (see Fig. 2C in reference21), potentially suggesting that Nocodazole-treated high contractile T cells might use a bleb-adhesion-based migration mode. The observed insensitivity of cell migration speed on substrate rigidity among these cells starkly differs from the behavior observed in the adhesion-based motor-clutch migration mode, where migration of highly contractile cells is sensitive to the stiffness of the substrate25. Crucially, the effectiveness of the hybrid adhesion-bleb migration mode hinges on the predominant formation of cell-matrix adhesions at the leading edge of the cell (Fig. S9D). If cell-matrix adhesions are largely formed at the rear of the cell, cell movement is predicted to be significantly reduced (Fig. S8D). We also note that enhanced traction forces mediated by actin polymerization forces have not been considered in this analysis, but it is predicted that they would enhance significantly the cell migratory potential of adherent blebby cells. However, how cells coordinate the spatiotemporal assembly and disassembly of focal adhesions, actin polymerization and traction forces with blebbing remains to be determined.
In summary, our findings uncover potential mechanisms that are unlikely (i.e. swimming model) or possible (i.e. hybrid bleb-adhesion model) to mediate the remarkable ability of T cells to rapidly navigate through tissues. Our analysis does not support an adhesion-free swimming strategy based on changes in their cell shape, specifically through the formation of protruding blebs; however. this mechanism allows them to slowly explore/sample the surrounding microenvironments prior to robust directed movement. Moreover, our analysis suggests that fast migration requires the presence of cell-environment adhesion interactions. Synergy between fast forward plasma membrane motion driven by bleb expansion followed by cell-matrix adhesion formation and subsequent traction force production potentially maximizes the migration potential of T cells. Indeed, our model predicts that adherent blebby cells can enhance their hybrid migration capabilities by increasing cortical contractility and optimizing their cortical stiffness to an intermediate value and identifies a viable cell engineering strategy to enhance T cell movement.
DISCUSSION
We have introduced a mechanistic model of adhesion-free bleb-based cell motility to elucidate the physical principles and potential molecular components that modulate bleb-based cell swimming (i.e. adhesion-free motility) capabilities and identify how these molecular regulators can be perturbed to modulate their swimming potential. The amoeboid cellular phenotype has been associated with immune cell migration21,22,104 as well as with multiple cancer cells displaying epithelial to amoeboid transitions with enhanced cell invasion, immunosuppression, stem cell potential and metastatic capabilities105-109. Although the developed model is aimed at providing insights to effectively engineer therapeutic T cells with enhanced migration capabilities, the model’s applicability extends broadly to all bleb-producing cells, including amoeboid cancer cells, with a major goal being to induce fast amoeboid T cell migration and target/inhibit amoeboid cancer cell migration. While our model addresses crucial aspects relevant to this research area by elucidating the most plausible mechanisms of fast T cell migration, consistent with experimental data, and within the constraints of current modeling capabilities and knowledge, it does not capture every complex detail inherent in real cells. Integrating every molecular constituent and biological aspect into our biophysical model is beyond practical reach. Missing explicit intracellular and extracellular factors include microtubules, septins, aquaporins and cytokines, which are known to influence cortex behavior, the functionality of cell adhesion molecules, and the overall migration of T cells21,110-112. According to Tabdanov et al.21, microtubules play a more significant role in regulating GTPase RhoA signaling than serving as direct mechanical elements. GEF-H1 associates. with polymerized microtubules, and upon depolymerization, GEF-H1 is released, increasing its guanosine exchange activity. This leads to higher RhoA activation and increased cortical contractility21,95. Our model indirectly incorporates the effect of microtubules on T cell migration by simulating this global/local effect on actomyosin contraction. Microtubule instability led to increased cortical contractility, promoting T cell migration (Tabdanov et al., Nat Comm 2021). This finding aligns with our modeling results, where we observe that high cortical contractility induces rapid migration of both adhesion-independent and adhesion-dependent blebbing cells, as shown in Figs. 2D and S9A, respectively. Additionally, our model does not account for the role of the nucleus, which acts as a physical barrier and completely arrests T cell migration through interstitial pores smaller than 7 μm2 when matrix metalloproteinase-independent pathways are involved113.
Our model results indicate that sustained adhesion-free bleb-based cell motility requires oscillatory cortical forces in Newtonian environments, where cells alternate between a high-contractility motility phase and a low-contractility pressure buildup phase. These pulsatile actomyosin forces, which can arise from different mechanochemical sources, including calcium signal fluctuations96,114, myosin phosphorylation-based biochemical oscillators115,116, and ERK-based mechanochemical signaling, among others, do not seem to be essential in bleb-based cell swimming only, but also in other biological contexts including adhesion-based cell migration95, compaction117, cell intercalations96 and tissue integrity116 during morphogenesis, and temporal regulation of actin polymerization and vesicle exocytosis114. Repeated sequences of a single bleb nucleation event, bleb expansion, cortex recruitment and bleb retraction do not cause sustained cell swimming in Newtonian fluids, since the plasma membrane follows similar paths during bleb expansion and retraction. However, we show that individual blebs in viscoelastic environments or spatiotemporal synchronization of multiple bleb nucleation events in Newtonian environments allows cells to break time-reversibility and effectively migrate in the absence of adhesion-based forces, albeit at rates well below those exhibited by T cells. Additionally, our results indicate that coordinated cell-scale deformations driven by blebs are inefficient and result in maximal motility coefficients of , an order of magnitude lower than those reported by bleb-producing cells in vivo (21). In such poor swimming conditions, interstitial flows would dominate in certain tissues over the inherent swimming motion of cells rendering cell swimming less relevant to cell translocation118,119. Our analysis gives a new physical perspective of the mechanism underlying potential swimming of bleb-producing cells and provides a strategy to modulate cell swimming potential by targeting the cortex, plasma membrane and extracellular environment.
Other possible adhesion-free cell swimming mechanisms rely on peristaltic waves120, osmotic pressure gradients121, Marangoni stresses49,50 or slippage between plasma membrane and surrounding fluid122 possibly caused by mechanical coupling of transmembrane proteins, powered by F-actin retrograde flows, with the surrounding fluid40,48. Reversat et al.44 proposed an alternative mechanism for adhesion-free migration, suggesting that T cells can navigate through serrated microfluidic channels without relying on adhesion or friction-based forces. Their theory posits that cell migration is driven by intracellular pressure gradients generated by retrograde flows and the curvature of actin flows caused by the channel wall topography. While their experimental results show an intriguing dependence of cell migration speed on wall topography, their proposed migration model contradicts established physical laws. The authors claim that the local force exerted by intracellular hydrostatic pressure directly gets transmitted to the channel walls. According to their theory, this pressure force, acting perpendicular to the walls, and summed across the cell’s surface, generates a net hydrostatic force, serving as a propulsion mechanism that drives the cell in the direction opposite to the actin flows. Their interpretation overlooks critical physical aspects of plasma membranes. Disregarding viscous stresses, water molecules can only exert a net force on the plasma membrane, and therefore on the channel walls, by crossing the plasma membrane via water-lipid drag interactions123. A local increase in intracellular hydrostatic pressure will induce an efflux of water, drawing the plasma membrane inwards, away from the channel walls, thus not transmitting any hydrostatic force to the walls, as the authors claim. It is unclear whether T cells migrated through these microchannels in the absence of adhesion/friction forces, as the authors claim, due to the technical challenge of completely blocking nonspecific adhesions. A plausible interpretation of their experimental findings, consistent with our model results, is that the magnitude of the adhesion/friction-based forces with the cellular environment (i.e. channel walls) may depend on its topographical features. We note that weak adhesions that last only a few seconds are sufficient in our model to enable fast migration in the hybrid mode.
Although cell signaling might play an important role in the coordination of multiple blebbing events, cells can orchestrate blebbing and control bleb frequency and bleb-to-bleb distance by temporal modulation of cortical tension and stiffness, where high tension and soft cortex favor optimum conditions. This is consistent with experiments, where high cortical contractility is associated with fast amoeboid-like cell motility5,24,124. Motor activity levels can be modulated by the internal cellular state as well as by environmental cellular conditions. As an example, nuclear deformation mediated by enhanced cellular confinement can activate mechanotransduction pathways125,126 that enhance actomyosin contractility and therefore would be predicted to increase cell swimming potential. Whereas low contractile cells nucleate blebs at low frequencies and in regions near recent bleb nucleation sites, high contractile cells nucleate blebs at ~4Hz and cause membrane-cortex detachment at bleb-to-bleb separation polar angles of ~60°. These blebbing frequencies and bleb-to-bleb separation distances correlate with maximal cell motility coefficients. In addition, our model shows that blebbing events are expected to be favored in cell regions of high cortical forces, low membrane-cortex adhesion and local intracellular osmotic pressure. This is consistent with experimental data, where blebbing was less frequent in the ezrin/radixin/moesin-rich uropod-like structure of cells28,127-129 and favored in calcium-dependent high myosin contraction regions at the leading edge of cells13. Chemoattractants, which have also been associated with bleb polarization130–132, potentially modulate some of the three driving factors mentioned above. Interestingly, we find that unidirectional bleb-based cell swimming is not possible via highly polarized bleb nucleation events, strongly suggesting that persistent directional cell migration, observed in different confined systems11,26,43,133 might require the presence of cellular frictional/adhesive forces with the environment39,44.
We show that cells might employ a hybrid migration mechanism that combines blebbing and the formation of cell-matrix adhesions for optimal cell motility. Unlike in bleb-based cell swimming, the cell advances in the same direction during both bleb expansion and retraction phases in this proposed hybrid mode of migration, achieving speeds that are comparable to physiological T cell migration speeds. Our results indicate that adherent blebby T cells can exhibit a highly migratory phenotype by increasing their contractility and fine-tuning their cortical stiffness to intermediate values. This mode of migration is consistent with a recent study that shows that T cells push and pull on the extracellular matrix and require adhesion-based forces to migrate through in vitro systems134. Recent experimental observations additionally support this hybrid mode of migration. For instance, melanoma cells exhibit blebbing while moving through soft collagen matrices, pushing collagen aside at the leading edge during bleb expansion, and pulling it in during bleb retraction via adhesions135, as in our hybrid model. Similarly, rapid β1 integrin-dependent bleb-based migration of breast cancer cells involved extracellular matrix reorganization at membrane blebs136 with integrin clustering occurring at these sites. These findings align with the fast hybrid adhesion-based bleb-based migration mechanism, which relies on the predominant formation of cell-matrix adhesions at the cell’s leading edge. It is also consistent with another cell migration study, where recruitment of the branched actin nucleator Arp2/3 frequently follows membrane-cortex detachment, depletion of the ERM membrane-cortex linker ezrin and protrusion expansion101. In some instances, however, cell-extracellular matrix adhesion formation and blebbing events anticorrelate in space, potentially suggesting the presence of F-actin assembly-driven protrusions or pressure-only-driven protrusions137. Recent modeling results also suggest that cortical squeezing at the cell rear combined with focal adhesion formation at the cell front is a fast and robust cell migration strategy138. It is unclear though how blebbing, actin polymerization forces, traction forces, and spatial dynamics of focal adhesion assembly and disassembly integrate all together in this model.
Although friction has been associated to the major factor explaining cell migration in passivated microfluidic devices11,133, it remains uncertain whether cellular interactions with the extracellular matrix in healthy or transformed tissues exhibit more elastic-like or friction-like characteristics over long time scales. Notice that, while our model assumes that the mechanical interactions with the extracellular environment are elastic in nature, it can, in effect, account for friction-like interactions with the environment. This is supported by the fact that cell-matrix elastic interactions are effectively equivalent to friction-like cell-matrix interactions under conditions of high dissociation rates of cell-matrix adhesion bonds139,140. Therefore, this bleb-based friction-based migration regime can be achieved by cells embedded in extracellular matrix within in vitro or in vivo environments and falls under the broader bleb- and adhesion-based hybrid framework.
Overall, our work provides a new physical perspective of the possible mechanisms underlying the migration of blebby cells such as T cells and some cancer cells. The developed model provides not only strategies to enhance exploratory bleb-based T cell swimming but also suggested that pushing cells into a hybrid bleb- and adhesion-based mode of migration is a promising engineering strategy to increase T cell migration in tumors. Additional studies are needed to investigate to what extent this hybrid mode of migration can be adopted by T cells in vivo, which presents an exciting avenue for prospective theoretical and experimental research. To achieve this, advanced imaging, cell engineering and quantitative analysis combined with biophysical modeling will be indispensable in uncovering cell-specific and context-specific migration mechanisms. Ultimately, a faithful model can be used to define optimal states for maximal T cell migration and maximally effective immune cell therapies, and thereby guide the development of genetically engineered T cells optimized to migrate through mechanically challenging tumor microenvironments.
Supplementary Material
ACKNOWLEDGEMENTS
Research reported in this publication was supported by grants from the National Institutes of Health U54CA210190, P01CA254849 and U54CA268069, and from the National Science Foundation, grant number 2222434. We thank members of the Provenzano and Odde labs for helpful conversations throughout the course of this work. The content of this work is solely the responsibility of the authors and does not necessarily represent the official views of the NIH or NSF.
References
- 1.Friedl P. & Gilmour D. Collective cell migration in morphogenesis, regeneration and cancer. Nat Rev Mol Cell Biol 10, 445–457 (2009). 10.1038/nrm2720 [DOI] [PubMed] [Google Scholar]
- 2.Karamanos N. K., Theocharis A. D., Neill T. & Iozzo R. V. Matrix modeling and remodeling: A biological interplay regulating tissue homeostasis and diseases. Matrix Biol 75–76, 1–11 (2019). 10.1016/j.matbio.2018.08.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Yamaguchi H., Wyckoff J. & Condeelis J. Cell migration in tumors. Curr Opin Cell Biol 17, 559–564 (2005). 10.1016/j.ceb.2005.08.002 [DOI] [PubMed] [Google Scholar]
- 4.Nicolas-Boluda A. & Donnadieu E. Obstacles to T cell migration in the tumor microenvironment. Comp Immunol Microbiol Infect Dis 63, 22–30 (2019). 10.1016/j.cimid.2018.12.006 [DOI] [PubMed] [Google Scholar]
- 5.Panková K., Rösel D., Novotný M. & Brábek J. The molecular mechanisms of transition between mesenchymal and amoeboid invasiveness in tumor cells. Cell Mol Life Sci 67, 63–71 (2010). 10.1007/s00018-009-0132-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Goudarzi M. et al. Identification and regulation of a molecular module for bleb-based cell motility. Dev Cell 23, 210–218 (2012). 10.1016/j.devcel.2012.05.007 [DOI] [PubMed] [Google Scholar]
- 7.Sanz-Moreno V. & Marshall C. J. The plasticity of cytoskeletal dynamics underlying neoplastic cell migration. Curr Opin Cell Biol 22, 690–696 (2010). 10.1016/j.ceb.2010.08.020 [DOI] [PubMed] [Google Scholar]
- 8.Ibo M., Srivastava V., Robinson D. N. & Gagnon Z. R. Cell Blebbing in Confined Microfluidic Environments. PLoS One 11, e0163866 (2016). 10.1371/journal.pone.0163866 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Logue J. S. et al. Erk regulation of actin capping and bundling by Eps8 promotes cortex tension and leader bleb-based migration. Elife 4, e08314 (2015). 10.7554/eLife.08314 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Patel S. et al. Myosin II and Arp2/3 cross-talk governs intracellular hydraulic pressure and lamellipodia formation. Mol Biol Cell 32, 579–589 (2021). 10.1091/mbc.E20-04-0227 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ruprecht V. et al. Cortical contractility triggers a stochastic switch to fast amoeboid cell motility. Cell 160, 673–685 (2015). 10.1016/j.cell.2015.01.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bergert M., Chandradoss S. D., Desai R. A. & Paluch E. Cell mechanics control rapid transitions between blebs and lamellipodia during migration. Proc Natl Acad Sci U S A 109, 14434–14439 (2012). 10.1073/pnas.1207968109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Blaser H. et al. Migration of zebrafish primordial germ cells: a role for myosin contraction and cytoplasmic flow. Dev Cell 11, 613–627 (2006). 10.1016/j.devcel.2006.09.023 [DOI] [PubMed] [Google Scholar]
- 14.Charras G. T., Hu C. K., Coughlin M. & Mitchison T. J. Reassembly of contractile actin cortex in cell blebs. J Cell Biol 175, 477–490 (2006). 10.1083/jcb.200602085 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Paluch E. K. & Raz E. The role and regulation of blebs in cell migration. Curr Opin Cell Biol 25, 582–590 (2013). 10.1016/j.ceb.2013.05.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Charras G. & Paluch E. Blebs lead the way: how to migrate without lamellipodia. Nat Rev Mol Cell Biol 9, 730–736 (2008). 10.1038/nrm2453 [DOI] [PubMed] [Google Scholar]
- 17.Tozluoğlu M. et al. Matrix geometry determines optimal cancer cell migration strategy and modulates response to interventions. Nat Cell Biol 15, 751–762 (2013). 10.1038/ncb2775 [DOI] [PubMed] [Google Scholar]
- 18.Sahai E. & Marshall C. J. Differing modes of tumour cell invasion have distinct requirements for Rho/ROCK signalling and extracellular proteolysis. Nat Cell Biol 5, 711–719 (2003). 10.1038/ncb1019 [DOI] [PubMed] [Google Scholar]
- 19.Wolf K. et al. Compensation mechanism in tumor cell migration: mesenchymal-amoeboid transition after blocking of pericellular proteolysis. J Cell Biol 160, 267–277 (2003). 10.1083/jcb.200209006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Rösel D. et al. Up-regulation of Rho/ROCK signaling in sarcoma cells drives invasion and increased generation of protrusive forces. Mol Cancer Res 6, 1410–1420 (2008). 10.1158/1541-7786.MCR-07-2174 [DOI] [PubMed] [Google Scholar]
- 21.Tabdanov E. D. et al. Engineering T cells to enhance 3D migration through structurally and mechanically complex tumor microenvironments. Nat Commun 12, 2815 (2021). 10.1038/s41467-021-22985-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Takesono A., Heasman S. J., Wojciak-Stothard B., Garg R. & Ridley A. J. Microtubules regulate migratory polarity through Rho/ROCK signaling in T cells. PLoS One 5, e8774 (2010). 10.1371/journal.pone.0008774 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Obeidy P. et al. Partial loss of actin nucleator actin-related protein 2/3 activity triggers blebbing in primary T lymphocytes. Immunol Cell Biol 98, 93–113 (2020). 10.1111/imcb.12304 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Friedl P. Prespecification and plasticity: shifting mechanisms of cell migration. Curr Opin Cell Biol 16, 14–23 (2004). 10.1016/j.ceb.2003.11.001 [DOI] [PubMed] [Google Scholar]
- 25.Bangasser B. L. et al. Shifting the optimal stiffness for cell migration. Nat Commun 8, 15313 (2017). 10.1038/ncomms15313 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Liu Y. J. et al. Confinement and low adhesion induce fast amoeboid migration of slow mesenchymal cells. Cell 160, 659–672 (2015). 10.1016/j.cell.2015.01.007 [DOI] [PubMed] [Google Scholar]
- 27.Sanz-Moreno V. et al. Rac activation and inactivation control plasticity of tumor cell movement. Cell 135, 510–523 (2008). 10.1016/j.cell.2008.09.043 [DOI] [PubMed] [Google Scholar]
- 28.Lorentzen A., Bamber J., Sadok A., Elson-Schwab I. & Marshall C. J. An ezrin-rich, rigid uropod-like structure directs movement of amoeboid blebbing cells. J Cell Sci 124, 1256–1267 (2011). 10.1242/jcs.074849 [DOI] [PubMed] [Google Scholar]
- 29.Friedl P. & Wolf K. Tumour-cell invasion and migration: diversity and escape mechanisms. Nat Rev Cancer 3, 362–374 (2003). 10.1038/nrc1075 [DOI] [PubMed] [Google Scholar]
- 30.Taddei M. L., Giannoni E., Comito G. & Chiarugi P. Microenvironment and tumor cell plasticity: an easy way out. Cancer Lett 341, 80–96 (2013). 10.1016/j.canlet.2013.01.042 [DOI] [PubMed] [Google Scholar]
- 31.Saito K., Ozawa Y., Hibino K. & Ohta Y. FilGAP, a Rho/Rho-associated protein kinase-regulated GTPase-activating protein for Rac, controls tumor cell migration. Mol Biol Cell 23, 4739–4750 (2012). 10.1091/mbc.E12-04-0310 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Leen A. M., Rooney C. M. & Foster A. E. Improving T cell therapy for cancer. Annu Rev Immunol 25, 243–265 (2007). 10.1146/annurev.immunol.25.022106.141527 [DOI] [PubMed] [Google Scholar]
- 33.Lanitis E., Dangaj D., Irving M. & Coukos G. Mechanisms regulating T-cell infiltration and activity in solid tumors. Ann Oncol 28, xii18–xii32 (2017). 10.1093/annonc/mdx238 [DOI] [PubMed] [Google Scholar]
- 34.Slaney C. Y., Kershaw M. H. & Darcy P. K. Trafficking of T cells into tumors. Cancer Res 74, 7168–7174 (2014). 10.1158/0008-5472.CAN-14-2458 [DOI] [PubMed] [Google Scholar]
- 35.Krummel M. F., Bartumeus F. & Gérard A. T cell migration, search strategies and mechanisms. Nat Rev Immunol 16, 193–201 (2016). 10.1038/nri.2015.16 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Nordenfelt P., Elliott H. L. & Springer T. A. Coordinated integrin activation by actin-dependent force during T-cell migration. Nat Commun 7, 13119 (2016). 10.1038/ncomms13119 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Jacquemet G., Hamidi H. & Ivaska J. Filopodia in cell adhesion, 3D migration and cancer cell invasion. Curr Opin Cell Biol 36, 23–31 (2015). 10.1016/j.ceb.2015.06.007 [DOI] [PubMed] [Google Scholar]
- 38.Lämmermann T. et al. Rapid leukocyte migration by integrin-independent flowing and squeezing. Nature 453, 51–55 (2008). 10.1038/nature06887 [DOI] [PubMed] [Google Scholar]
- 39.Bergert M. et al. Force transmission during adhesion-independent migration. Nat Cell Biol 17, 524–529 (2015). 10.1038/ncb3134 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.O’Neill P. R. et al. Membrane Flow Drives an Adhesion-Independent Amoeboid Cell Migration Mode. Dev Cell 46, 9–22.e24 (2018). 10.1016/j.devcel.2018.05.029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Malawista S. E. & de Boisfleury Chevance A. Random locomotion and chemotaxis of human blood polymorphonuclear leukocytes (PMN) in the presence of EDTA: PMN in close quarters require neither leukocyte integrins nor external divalent cations. Proc Natl Acad Sci U S A 94, 11577–11582 (1997). 10.1073/pnas.94.21.11577 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Renkawitz J. et al. Adaptive force transmission in amoeboid cell migration. Nat Cell Biol 11, 1438–1443 (2009). 10.1038/ncb1992 [DOI] [PubMed] [Google Scholar]
- 43.Yip A. K., Chiam K. H. & Matsudaira P. Traction stress analysis and modeling reveal that amoeboid migration in confined spaces is accompanied by expansive forces and requires the structural integrity of the membrane-cortex interactions. Integr Biol (Camb) 7, 1196–1211 (2015). 10.1039/c4ib00245h [DOI] [PubMed] [Google Scholar]
- 44.Reversat A. et al. Cellular locomotion using environmental topography. Nature 582, 582–585 (2020). 10.1038/s41586-020-2283-z [DOI] [PubMed] [Google Scholar]
- 45.Woolf E. et al. Lymph node chemokines promote sustained T lymphocyte motility without triggering stable integrin adhesiveness in the absence of shear forces. Nat Immunol 8, 1076–1085 (2007). 10.1038/ni1499 [DOI] [PubMed] [Google Scholar]
- 46.Hons M. et al. Chemokines and integrins independently tune actin flow and substrate friction during intranodal migration of T cells. Nat Immunol 19, 606–616 (2018). 10.1038/s41590-018-0109-z [DOI] [PubMed] [Google Scholar]
- 47.Barry N. P. & Bretscher M. S. Dictyostelium amoebae and neutrophils can swim. Proc Natl Acad Sci U S A 107, 11376–11380 (2010). 10.1073/pnas.1006327107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Aoun L. et al. Amoeboid Swimming Is Propelled by Molecular Paddling in Lymphocytes. Biophys J 119, 1157–1177 (2020). 10.1016/j.bpj.2020.07.033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Wu H., de León M. A. P. & Othmer H. G. Getting in shape and swimming: the role of cortical forces and membrane heterogeneity in eukaryotic cells. J Math Biol 77, 595–626 (2018). 10.1007/s00285-018-1223-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Wang Q. & Othmer H. G. Computational analysis of amoeboid swimming at low Reynolds number. J Math Biol 72, 1893–1926 (2016). 10.1007/s00285-015-0925-9 [DOI] [PubMed] [Google Scholar]
- 51.Paluch E. K., Aspalter I. M. & Sixt M. Focal Adhesion-Independent Cell Migration. Annu Rev Cell Dev Biol 32, 469–490 (2016). 10.1146/annurev-cellbio-111315-125341 [DOI] [PubMed] [Google Scholar]
- 52.Fehon R. G., McClatchey A. I. & Bretscher A. Organizing the cell cortex: the role of ERM proteins. Nat Rev Mol Cell Biol 11, 276–287 (2010). 10.1038/nrm2866 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Nambiar R., McConnell R. E. & Tyska M. J. Control of cell membrane tension by myosin-I. Proc Natl Acad Sci U S A 106, 11972–11977 (2009). 10.1073/pnas.0901641106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Goudarzi M., Boquet-Pujadas A., Olivo-Marin J. C. & Raz E. Fluid dynamics during bleb formation in migrating cells in vivo. PLoS One 14, e0212699 (2019). 10.1371/journal.pone.0212699 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Strychalski W. & Guy R. D. Intracellular Pressure Dynamics in Blebbing Cells. Biophys J 110, 1168–1179 (2016). 10.1016/j.bpj.2016.01.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Taneja N. & Burnette D. T. Myosin IIA drives membrane bleb retraction. Mol Biol Cell 30, 1051–1059 (2019). 10.1091/mbc.E18-11-0752 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Fang C., Hui T. H., Wei X., Shao X. & Lin Y. A combined experimental and theoretical investigation on cellular blebbing. Sci Rep 7, 16666 (2017). 10.1038/s41598-017-16825-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Alert R. & Casademunt J. Bleb Nucleation through Membrane Peeling. Phys Rev Lett 116, 068101 (2016). 10.1103/PhysRevLett.116.068101 [DOI] [PubMed] [Google Scholar]
- 59.Boulbitch A. et al. Shape instability of a biomembrane driven by a local softening of the underlying actin cortex. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics 62, 3974–3985 (2000). 10.1103/physreve.62.3974 [DOI] [PubMed] [Google Scholar]
- 60.Tinevez J. Y. et al. Role of cortical tension in bleb growth. Proc Natl Acad Sci U S A 106, 18581–18586 (2009). 10.1073/pnas.0903353106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Lim F. Y., Chiam K. H. & Mahadevan L. The size, shape, and dynamics of cellular blebs. Europhysics Letters 100 (2012). [Google Scholar]
- 62.Brugués J. et al. Dynamical organization of the cytoskeletal cortex probed by micropipette aspiration. Proc Natl Acad Sci U S A 107, 15415–15420 (2010). 10.1073/pnas.0913669107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Woolley T. E. et al. Cellular blebs: pressure-driven, axisymmetric, membrane protrusions. Biomech Model Mechanobiol 13, 463–476 (2014). 10.1007/s10237-013-0509-9 [DOI] [PubMed] [Google Scholar]
- 64.Strychalski W. & Guy R. D. A computational model of bleb formation. Math Med Biol 30, 115–130 (2013). 10.1093/imammb/dqr030 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Young J. & Mitran S. A numerical model of cellular blebbing: a volume-conserving, fluid-structure interaction model of the entire cell. J Biomech 43, 210–220 (2010). 10.1016/j.jbiomech.2009.09.025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Lim F. Y., Koon Y. L. & Chiam K. H. A computational model of amoeboid cell migration. Comput Methods Biomech Biomed Engin 16, 1085–1095 (2013). 10.1080/10255842.2012.757598 [DOI] [PubMed] [Google Scholar]
- 67.Copos C. & Strychalski W. Actin Turnover Required for Adhesion-Independent Bleb Migration. Fluids 7 (2022). [Google Scholar]
- 68.Bottino D. C. & Fauci L. J. A computational model of ameboid deformation and locomotion. Eur Biophys J 27, 532–539 (1998). 10.1007/s002490050163 [DOI] [PubMed] [Google Scholar]
- 69.Campbell E. J. & Bagchi P. A computational model of amoeboid cell motility in the presence of obstacles. Soft Matter 14, 5741–5763 (2018). 10.1039/c8sm00457a [DOI] [PubMed] [Google Scholar]
- 70.Campbell E. J. & Bagchi P. A computational study of amoeboid motility in 3D: the role of extracellular matrix geometry, cell deformability, and cell-matrix adhesion. Biomech Model Mechanobiol 20, 167–191 (2021). 10.1007/s10237-020-01376-7 [DOI] [PubMed] [Google Scholar]
- 71.Dalal S., Farutin A. & Misbah C. Amoeboid swimming in a compliant channel. Soft Matter 16, 1599–1613 (2020). 10.1039/c9sm01689a [DOI] [PubMed] [Google Scholar]
- 72.Farutin A. et al. Amoeboid swimming: a generic self-propulsion of cells in fluids by means of membrane deformations. Phys Rev Lett 111, 228102 (2013). 10.1103/PhysRevLett.111.228102 [DOI] [PubMed] [Google Scholar]
- 73.Moure A. & Gomez H. Computational model for amoeboid motion: Coupling membrane and cytosol dynamics. Phys Rev E 94, 042423 (2016). 10.1103/PhysRevE.94.042423 [DOI] [PubMed] [Google Scholar]
- 74.Wu H. et al. Amoeboid motion in confined geometry. Phys Rev E Stat Nonlin Soft Matter Phys 92, 050701 (2015). 10.1103/PhysRevE.92.050701 [DOI] [PubMed] [Google Scholar]
- 75.Wu H. et al. Amoeboid swimming in a channel. Soft Matter 12, 7470–7484 (2016). 10.1039/c6sm00934d [DOI] [PubMed] [Google Scholar]
- 76.Binagia J. P., Guido C. J. & Shaqfeh E. S. G. Three-dimensional simulations of undulatory and amoeboid swimmers in viscoelastic fluids. Soft Matter 15, 4836–4855 (2019). 10.1039/c8sm02518e [DOI] [PubMed] [Google Scholar]
- 77.Woolley T. E., Gaffney E. A. & Goriely A. Random blebbing motion: A simple model linking cell structural properties to migration characteristics. Phys Rev E 96, 012409 (2017). 10.1103/PhysRevE.96.012409 [DOI] [PubMed] [Google Scholar]
- 78.Munoz-Lopez M. J., Kim H. & Mori Y. A reduced 1D stochastic model of bleb-driven cell migration. Biophys J 121, 1881–1896 (2022). 10.1016/j.bpj.2022.04.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Housiadas K. D. & Beris A. N. Polymer-induced drag reduction: Effects of the variations in elasticity and inertia in turbulent viscoelastic channel flow. Physics of Fluids 15, 2369–2384 (2003). [Google Scholar]
- 80.Chugh P. et al. Actin cortex architecture regulates cell surface tension. Nat Cell Biol 19, 689–697 (2017). 10.1038/ncb3525 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Chugh P. & Paluch E. K. The actin cortex at a glance. J Cell Sci 131 (2018). 10.1242/jcs.186254 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Svitkina T. M. Actin Cell Cortex: Structure and Molecular Organization. Trends Cell Biol 30, 556–565 (2020). 10.1016/j.tcb.2020.03.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Peskin C. S. The immersed boundary method. Acta Numerica 11, 479–517 (2002). [Google Scholar]
- 84.Alonso-Matilla R., Provenzano P. P. & Odde D. J. T cell migration software, <https://drive.google.com/drive/folders/1K3l7wPINGG-CZvQ7VTzwMqQzB1TOjqMF?usp=drive_link> (2024).
- 85.Maugis B. et al. Dynamic instability of the intracellular pressure drives bleb-based motility. J Cell Sci 123, 3884–3892 (2010). 10.1242/jcs.06run2 [DOI] [PubMed] [Google Scholar]
- 86.Grebecki A. Dynamics of the contractile system in the pseudopodial tips of normally locomoting amoebae, demonstrated in vivo by video-enhancement. Protoplasma 154, 98–111 (1990). [Google Scholar]
- 87.Purcell E. M. Life at low Reynolds number. American Journal of Physics 45, 3–11 (1977). [Google Scholar]
- 88.Qiu T. et al. Swimming by reciprocal motion at low Reynolds number. Nat Commun 5, 5119 (2014). 10.1038/ncomms6119 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Berg H. C. Random walks in biology. (Princeton University Press, 1993). [Google Scholar]
- 90.Saha A. et al. Determining Physical Properties of the Cell Cortex. Biophys J 110, 1421–1429 (2016). 10.1016/j.bpj.2016.02.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Pollard T. D. Rate constants for the reactions of ATP- and ADP-actin with the ends of actin filaments. J Cell Biol 103, 2747–2754 (1986). 10.1083/jcb.103.6.2747 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Yu M. et al. mDia1 senses both force and torque during F-actin filament polymerization. Nat Commun 8, 1650 (2017). 10.1038/s41467-017-01745-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Kuhn J. R. & Pollard T. D. Real-time measurements of actin filament polymerization by total internal reflection fluorescence microscopy. Biophys J 88, 1387–1402 (2005). 10.1529/biophysj.104.047399 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Bell G. I. Models for the specific adhesion of cells to cells. Science 200, 618–627 (1978). 10.1126/science.347575 [DOI] [PubMed] [Google Scholar]
- 95.Lee S. H. et al. A molecular clock controls periodically driven cell migration in confined spaces. Cell Syst 13, 514–529.e510 (2022). 10.1016/j.cels.2022.05.005 [DOI] [PubMed] [Google Scholar]
- 96.Tao H. et al. Oscillatory cortical forces promote three dimensional cell intercalations that shape the murine mandibular arch. Nat Commun 10, 1703 (2019). 10.1038/s41467-019-09540-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Jerison E. R. & Quake S. R. Heterogeneous T cell motility behaviors emerge from a coupling between speed and turning in vivo. Elife 9 (2020). 10.7554/eLife.53933 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Miller M. J., Wei S. H., Cahalan M. D. & Parker I. Autonomous T cell trafficking examined in vivo with intravital two-photon microscopy. Proc Natl Acad Sci U S A 100, 2604–2609 (2003). 10.1073/pnas.2628040100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Khan Z. S., Santos J. M., Vaz N. G. & Hussain F. Enhanced blebbing as a marker for metastatic prostate cancer. Biomicrofluidics 13, 034110 (2019). 10.1063/1.5085346 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Asante-Asamani E. et al. A role for myosin II clusters and membrane energy in cortex rupture for Dictyostelium discoideum. PLoS One 17, e0265380 (2022). 10.1371/journal.pone.0265380 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Welf E. S. et al. Actin-Membrane Release Initiates Cell Protrusions. Dev Cell 55, 723–736.e728 (2020). 10.1016/j.devcel.2020.11.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Yoshida K. & Soldati T. Dissection of amoeboid movement into two mechanically distinct modes. J Cell Sci 119, 3833–3844 (2006). 10.1242/jcs.03152 [DOI] [PubMed] [Google Scholar]
- 103.Liu C. J., Shamsan G. A., Akkin T. & Odde D. J. Glioma Cell Migration Dynamics in Brain Tissue Assessed by Multimodal Optical Imaging. Biophys J 117, 1179–1188 (2019). 10.1016/j.bpj.2019.08.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Friedl P. & Weigelin B. Interstitial leukocyte migration and immune function. Nat Immunol 9, 960–969 (2008). 10.1038/ni.f.212 [DOI] [PubMed] [Google Scholar]
- 105.Graziani V., Rodriguez-Hernandez I., Maiques O. & Sanz-Moreno V. The amoeboid state as part of the epithelial-to-mesenchymal transition programme. Trends Cell Biol (2021). 10.1016/j.tcb.2021.10.004 [DOI] [PubMed]
- 106.Emad A. et al. Superior breast cancer metastasis risk stratification using an epithelial-mesenchymal-amoeboid transition gene signature. Breast Cancer Res 22, 74 (2020). 10.1186/s13058-020-01304-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Crosas-Molist E. et al. The NADPH oxidase NOX4 represses epithelial to amoeboid transition and efficient tumour dissemination. Oncogene 36, 3002–3014 (2017). 10.1038/onc.2016.454 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Gao Y. et al. Loss of ERα induces amoeboid-like migration of breast cancer cells by downregulating vinculin. Nat Commun 8, 14483 (2017). 10.1038/ncomms14483 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Giannoni E. et al. EphA2-mediated mesenchymal-amoeboid transition induced by endothelial progenitor cells enhances metastatic spread due to cancer-associated fibroblasts. J Mol Med (Berl) 91, 103–115 (2013). 10.1007/s00109-012-0941-9 [DOI] [PubMed] [Google Scholar]
- 110.Zhovmer A. S. et al. Septins provide microenvironment sensing and cortical actomyosin partitioning in motile amoeboid T lymphocytes. Sci Adv 10, eadi1788 (2024). 10.1126/sciadv.adi1788 [DOI] [PubMed] [Google Scholar]
- 111.Hara-Chikuma M. et al. Chemokine-dependent T cell migration requires aquaporin-3-mediated hydrogen peroxide uptake. J Exp Med 209, 1743–1752 (2012). 10.1084/jem.20112398 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Tanaka Y. et al. T-cell adhesion induced by proteoglycan-immobilized cytokine MIP-1 beta. Nature 361, 79–82 (1993). 10.1038/361079a0 [DOI] [PubMed] [Google Scholar]
- 113.Wolf K. et al. Physical limits of cell migration: control by ECM space and nuclear deformation and tuning by proteolysis and traction force. J Cell Biol 201, 1069–1084 (2013). 10.1083/jcb.201210152 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Takeshita N. et al. Pulses of Ca2+ coordinate actin assembly and exocytosis for stepwise cell extension. Proc Natl Acad Sci U S A 114, 5701–5706 (2017). 10.1073/pnas.1700204114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Qin X. et al. A biochemical network controlling basal myosin oscillation. Nat Commun 9, 1210 (2018). 10.1038/s41467-018-03574-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Vasquez C. G., Tworoger M. & Martin A. C. Dynamic myosin phosphorylation regulates contractile pulses and tissue integrity during epithelial morphogenesis. J Cell Biol 206, 435–450 (2014). 10.1083/jcb.201402004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Maître J. L., Niwayama R., Turlier H., Nédélec F. & Hiiragi T. Pulsatile cell-autonomous contractility drives compaction in the mouse embryo. Nat Cell Biol 17, 849–855 (2015). 10.1038/ncb3185 [DOI] [PubMed] [Google Scholar]
- 118.Kingsmore K. M. et al. MRI analysis to map interstitial flow in the brain tumor microenvironment. APL Bioeng 2 (2018). 10.1063/1.5023503 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Curley C. T. et al. Augmentation of brain tumor interstitial flow via focused ultrasound promotes brain-penetrating nanoparticle dispersion and transfection. Sci Adv 6, eaay1344 (2020). 10.1126/sciadv.aay1344 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Franz A., Wood W. & Martin P. Fat Body Cells Are Motile and Actively Migrate to Wounds to Drive Repair and Prevent Infection. Dev Cell 44, 460–470.e463 (2018). 10.1016/j.devcel.2018.01.026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121.Stroka K. M. et al. Water permeation drives tumor cell migration in confined microenvironments. Cell 157, 611–623 (2014). 10.1016/j.cell.2014.02.052 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Stone H. A. & Samuel A. D. Propulsion of Microorganisms by Surface Distortions. Phys Rev Lett 77, 4102–4104 (1996). 10.1103/PhysRevLett.77.4102 [DOI] [PubMed] [Google Scholar]
- 123.Guell D. C. B. H. Physical Mechanism of Membrane Osmotic Phenomena. Ind Eng Chem Res 35, 3004–3014 (1996). [Google Scholar]
- 124.Lämmermann T. & Sixt M. Mechanical modes of ‘amoeboid’ cell migration. Curr Opin Cell Biol 21, 636–644 (2009). 10.1016/j.ceb.2009.05.003 [DOI] [PubMed] [Google Scholar]
- 125.Lomakin A. J. et al. The nucleus acts as a ruler tailoring cell responses to spatial constraints. Science 370 (2020). 10.1126/science.aba2894 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126.Venturini V. et al. The nucleus measures shape changes for cellular proprioception to control dynamic cell behavior. Science 370 (2020). 10.1126/science.aba2644 [DOI] [PubMed] [Google Scholar]
- 127.Martinelli S. et al. Ezrin/Radixin/Moesin proteins and flotillins cooperate to promote uropod formation in T cells. Front Immunol 4, 84 (2013). 10.3389/fimmu.2013.00084 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128.Rossy J., Gutjahr M. C., Blaser N., Schlicht D. & Niggli V. Ezrin/moesin in motile Walker 256 carcinosarcoma cells: signal-dependent relocalization and role in migration. Exp Cell Res 313, 1106–1120 (2007). 10.1016/j.yexcr.2006.12.023 [DOI] [PubMed] [Google Scholar]
- 129.Niggli V. & Rossy J. Ezrin/radixin/moesin: versatile controllers of signaling molecules and of the cortical cytoskeleton. Int J Biochem Cell Biol 40, 344–349 (2008). 10.1016/j.biocel.2007.02.012 [DOI] [PubMed] [Google Scholar]
- 130.Langridge P. D. & Kay R. R. Blebbing of Dictyostelium cells in response to chemoattractant. Exp Cell Res 312, 2009–2017 (2006). 10.1016/j.yexcr.2006.03.007 [DOI] [PubMed] [Google Scholar]
- 131.Doitsidou M. et al. Guidance of primordial germ cell migration by the chemokine SDF-1. Cell 111, 647–659 (2002). 10.1016/s0092-8674(02)01135-2 [DOI] [PubMed] [Google Scholar]
- 132.Zatulovskiy E. & Kay R. R. Chemotactic Blebbing in Dictyostelium Cells. Methods Mol Biol 1407, 97–105 (2016). 10.1007/978-1-4939-3480-5_7 [DOI] [PubMed] [Google Scholar]
- 133.Maiuri P. et al. Actin flows mediate a universal coupling between cell speed and cell persistence. Cell 161, 374–386 (2015). 10.1016/j.cell.2015.01.056 [DOI] [PubMed] [Google Scholar]
- 134.Caillier A., Oleksyn D., Fowell D. J., Miller J. & Oakes P. W. T cells use focal adhesions to pull themselves through confined environments. J Cell Biol 223 (2024). 10.1083/jcb.202310067 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135.Driscoll M. K. et al. Proteolysis-free amoeboid migration of melanoma cells through crowded environments via bleb-driven worrying. Dev Cell (2024). 10.1016/j.devcel.2024.05.024 [DOI] [PMC free article] [PubMed]
- 136.Guzman A., Avard R. C., Devanny A. J., Kweon O. S. & Kaufman L. J. Delineating the role of membrane blebs in a hybrid mode of cancer cell invasion in three-dimensional environments. J Cell Sci 133 (2020). 10.1242/jcs.236778 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137.Beckham Y. et al. Arp2/3 inhibition induces amoeboid-like protrusions in MCF10A epithelial cells by reduced cytoskeletal-membrane coupling and focal adhesion assembly. PLoS One 9, e100943 (2014). 10.1371/journal.pone.0100943 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 138.Maxian O., Mogilner A. & Strychalski W. Computational estimates of mechanical constraints on cell migration through the extracellular matrix. PLoS Comput Biol 16, e1008160 (2020). 10.1371/journal.pcbi.1008160 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 139.Tawada K. & Sekimoto K. Protein friction exerted by motor enzymes through a weak-binding interaction. J Theor Biol 150, 193–200 (1991). 10.1016/s0022-5193(05)80331-5 [DOI] [PubMed] [Google Scholar]
- 140.Howard J. Mechanics of Motor Proteins and the Cytoskeleton. (Oxford University Press, 2018). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.