Abstract
The specific activity of enzymes can be altered over long timescales in cells by synonymous mutations that alter a messenger RNA molecule’s sequence but not the encoded protein’s primary structure. How this happens at the molecular level is unknown. Here, we use multiscale modelling of three Escherichia coli enzymes (type III chloramphenicol acetyltransferase, d-alanine–d-alanine ligase B and dihydrofolate reductase) to understand experimentally measured changes in specific activity due to synonymous mutations. The modelling involves coarse-grained simulations of protein synthesis and post-translational behaviour, all-atom simulations to test robustness and quantum mechanics/molecular mechanics calculations to characterize enzymatic function. We show that changes in codon translation rates induced by synonymous mutations cause shifts in co-translational and post-translational folding pathways that kinetically partition molecules into subpopulations that very slowly interconvert to the native, functional state. Structurally, these states resemble the native state, with localized misfolding near the active sites of the enzymes. These long-lived states exhibit reduced catalytic activity, as shown by their increased activation energies for the reactions they catalyse.
A protein enzyme’s specific activity (that is, the catalytic turnover per unit of time per unit of mass of soluble protein) can change depending on the codons used to encode the protein1–6 both in vitro and in vivo. The specific activity of the Escherichia coli enzyme type III chloramphenicol acetyltransferase (CAT-III), for example, decreases by approximately 20% for more than 20 min when fast-translating synonymous mutations are introduced into its transcript1,6. This change in activity is long lived as it is comparable to the E. coli cell doubling time (~20 min). Synonymous mutations change the sequence of nucleotides composing a messenger RNA (mRNA) molecule, which in turn changes the speed at which translation elongation occurs7 but not the protein’s primary structure. Specific activity measurements control for differences in protein expression and the formation of insoluble aggregates through centrifugation or gel separation1–3,8. For enzymes that do not require post-translational modifications, these observed changes in specific activity indicate that, inside cells, newly expressed proteins can populate long-lived conformational states that are not native, have reduced functionality, somehow bypass the chaperone and degradation machinery and do not aggregate. Furthermore, these observations indicate that the distribution of these kinetically trapped states is sensitive to changes in the translation elongation speed.
This alternative state of soluble proteins is distinct from the three typical states9 of a protein, being either (1) folded and functional, (2) misfolded and aggregated or (3) degraded. The structural, kinetic and energetic properties of this alternative state of proteins is a fundamental, unanswered question in biochemistry and molecular biology. Soluble, nonfunctional states do not just occur for enzymes; other protein functions can also be altered. The hormone-transporting protein transthyretin, for example, can have 20% of its soluble fraction in a nonfunctional state10. There are hints in the literature of some of the structural properties of this state. NMR-derived structures of β/γ-crystallin produced from two synonymous mRNA variants showed that it populates two soluble conformations differing in the formation of a disulfide bond11. Disulfide bonds represent an energetically strong constraint on folding topologies and are uncommon: only 5 and 20%, respectively, of E. coli and human cytoplasmic proteins contain disulfide bonds12. Furthermore, many enzymes that exhibit specific activity changes due to synonymous mutations do not contain disulfide bonds1–3,5. Thus, the nature of these structurally altered subpopulations has not yet been resolved, although experimental data rule out misfolding involving quaternary structures. For example, gel separation and chromatography experiments rule out the formation of off-pathway dimers and higher-order oligomers for many enzymes that normally function in a monomeric state1,2,4,8.
Here, we use a novel multiscale approach across the dimensions of time, space and energy to simulate the synthesis, post-translational behaviour and function of enzymes under different translation rate schedules that arise from synonymous codons. We establish that our modelling approach can predict the experimentally measured changes in specific activity for CAT-III, d-alanine–d-alanine ligase B (DDLB) and dihydrofolate reductase (DHFR). Dissecting the structures and kinetics of co- and post-translational folding that occur in our simulations, we show that synonymous mutations shift the folding pathways and populations of near-native non-covalent lasso entanglements, each of which has its own intrinsic activity (as measured by the reaction rate constant kcat) and leads to long-term changes in the enzymatic specific activity.
Results
Recapitulating experimental trends of CAT-III
First, we applied our modelling protocol to the E. coli enzyme CAT-III to test whether the method correctly predicts the influence of synonymous mutations on specific activity. CAT-III has been shown to have a 20% decrease in specific activity when faster-translating codons are introduced through synonymous mutations1. We created both fast- and slow-translating synonymous mRNA sequences (denoted, respectively, CAT-IIIfast and CAT-IIIslow) by replacing each wild-type codon with its fastest or slowest synonymous variant (Fig. 1b; mRNA sequences are reported in Supplementary Methods Section 22). The resulting slow mRNA variant takes twice as long to translate than the fast variant (Fig. 1f). We simulated the synthesis and post-translational behaviour of CAT-III resulting from the fast and slow mRNA variants and calculated their respective specific activities (equation (4)) at the end of the post-translational simulations. In our model, CAT-IIIfast exhibited 83.6% (95% confidence interval (CI) = 72.0–96.5% from bootstrapping; P = 0.0067 (random permutation test); 106 permutations) of the specific activity of CAT-IIIslow (Fig. 1g). This comparison, known as the relative specific activity (equation (5)), is common in biochemical studies1,3. Thus, our modelling approach qualitatively recapitulates experimentally observed changes in CAT-III’s enzyme activity due to synonymous mutations.
Fig. 1 |. A multiscale approach for understanding the influence of synonymous codons on the structure and function of enzymes.
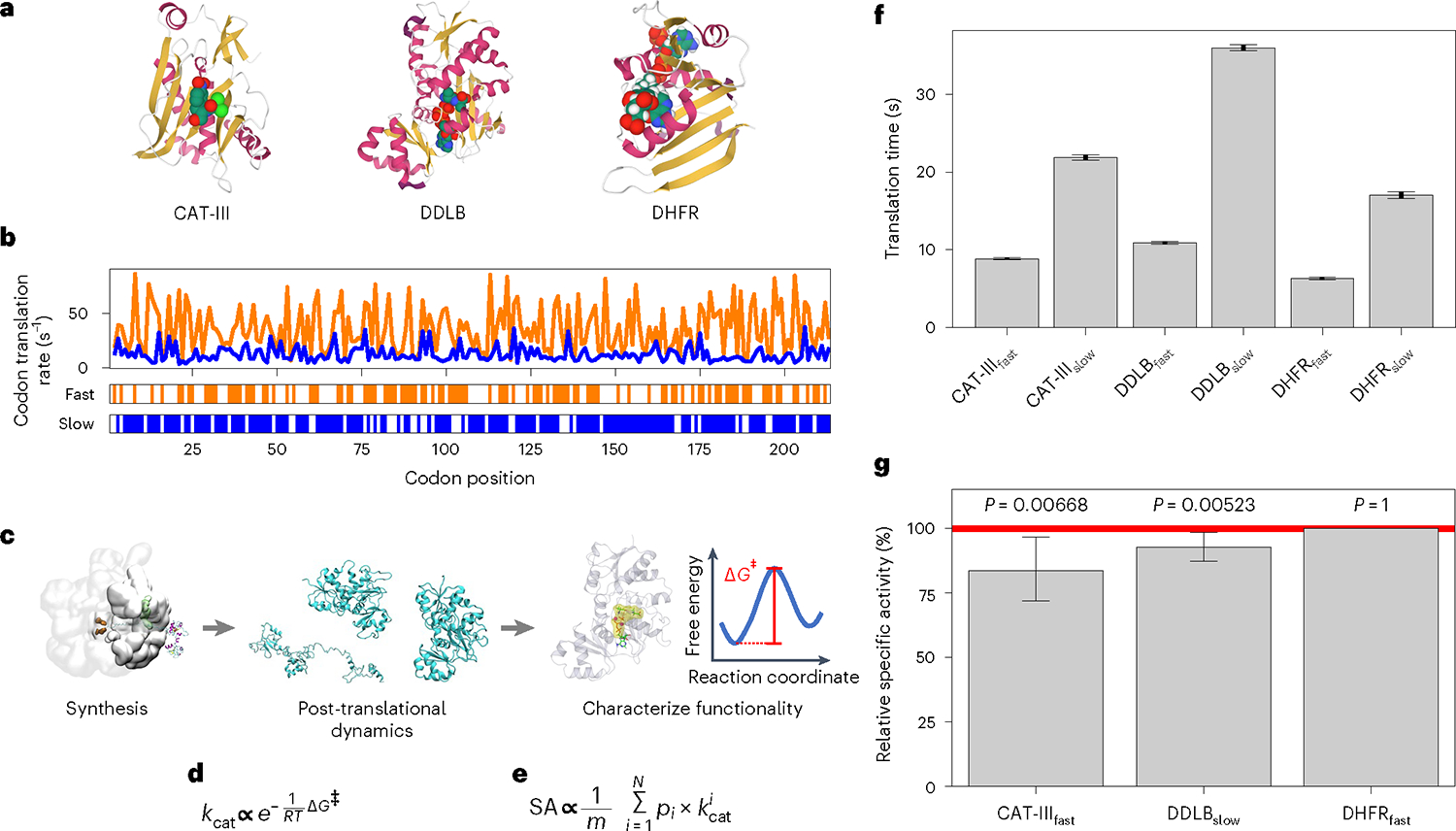
a, Crystal structures of the three enzymes investigated in this study, with secondary structure elements highlighted and substrates presented. b, Codon translation rates of CAT-III fast and slow synonymous mRNA variants, with the mutation sites presented on the bottom bars. c, Schematic of the multiscale approach, including the coarse-grained protein synthesis and post-translational dynamics, and the all-atom characterization of enzymatic functionality. d, Enzymatic reaction rate kcat estimated from the activation free energy ΔG‡. e, Enzyme specific activity (SA) estimated as the ensemble average of reaction rates, kcat (see equation (4)). f, Comparison of the translation times for the fast and slow synonymous mRNA variants. g, Relative specific activities for CAT-III, DDLB and DHFR. The specific activity values are normalized to the higher specific activity value found in fast and slow mRNA variants. The error bars in f and g represent 95% CIs about the mean, as estimated using bootstrapping over all simulation trajectories (sample sizes, n = 100 trajectories for CAT-III and DDLB and n = 50 trajectories for DHFR in f and n = 1,000 trajectories for CAT-III and DDLB and n = 500 trajectories for DHFR in g). P values characterize the statistical significance of the difference in specific activities between the proteins produced from the fast and slow variants. They were calculated using a one-tailed permutation test. The specific activities of CAT-III and DDLB are sensitive to translation speed changes, whereas that of DHFR is not.
Other enzymes that are sensitive to translation speed changes
Using a virtual screening strategy (see Supplementary Results), we identified a protein that was likely to be sensitive to changes in translation speed (that is, DDLB) and an insensitive protein (that is, DHFR). We simulated the synthesis and post-translational dynamics of DDLB and DHFR from their fast- and slow-translating mRNA variants (the sequences are presented in Supplementary Methods Section 22) using the same simulation protocol as that applied to CAT-III. The slow variants of DDLB and DHFR translated, respectively, three and two times slower than their fast variants (Fig. 1f). We found that the specific activity of was 92.7% (95% CI = 87.3–98.3%) that of (P = 0.0052) 60 s after synthesis was completed. exhibited a specific activity that was 100% (95% CI = 100–100%) that of (P = 1; that is, not statistically significant). Therefore, our model describes enzymes whose specific activity is either sensitive (DDLB) or insensitive (DHFR) to changes in translation speed over long timescales.
Accurate prediction of trends in specific activity
To experimentally test whether has a reduced enzymatic activity compared with we recombinantly expressed the fast and slow DDLB variants in E. coli using the same mRNA sequences as in the simulations. We then purified the enzyme and assayed the reaction kinetics (see Supplementary Methods Section 19). We observed that the fast variant had a higher level of protein expression 5 h after induction than the slow variant, consistent with the fast mRNA variant translating faster (Supplementary Fig. 11). The reaction rate constant was measured across five biological replicates of the fast and slow variants (Supplementary Table 11). We found that the specific activity of was, on average, 88% (; 95% CI = 81.3–94.8%) that of (P = 0.0186; one-tailed -test for ). In contrast, we performed the same experiments to measure the of fast and slow DHFR variants (see Supplementary Methods Section 20). Consistent with our model prediction, the specific activity of was indistinguishable from that of ; 95% CI = 68–115%; P = 0.5323; two-tailed t-test for ; see Supplementary Table 12). Thus, our modelling approach also successfully predicts the trends in changes in activity for DDLB and DHFR, indicating that the model is realistic.
Near-native, lasso-like entangled structures
Next, we identified in our simulations the structures, catalytic properties and folding pathways that cause these activity changes. First, we examined the structural distributions of CAT-III, DDLB and DHFR in the post-translational simulations using a clustering algorithm that employs both structural information and temporal interconversion rates between metastable states. Specifically, after numerous tests of different metrics, we performed structural clustering on the basis of the fraction of native contacts formed in the enzyme’s substrate-binding regions (denoted as Qact; equation (3)) and the fraction of native contacts that exhibited non-native topological entanglements (denoted as G; equation (2); see Methods). The resulting metastable states are shown in Fig. 2a,b for CAT-III, Fig. 3a,b for DDLB and Fig. 4a,b for DHFR.
Fig. 2 |. Fast translation partitions more CAT-III into post-translational kinetically trapped entangled states.
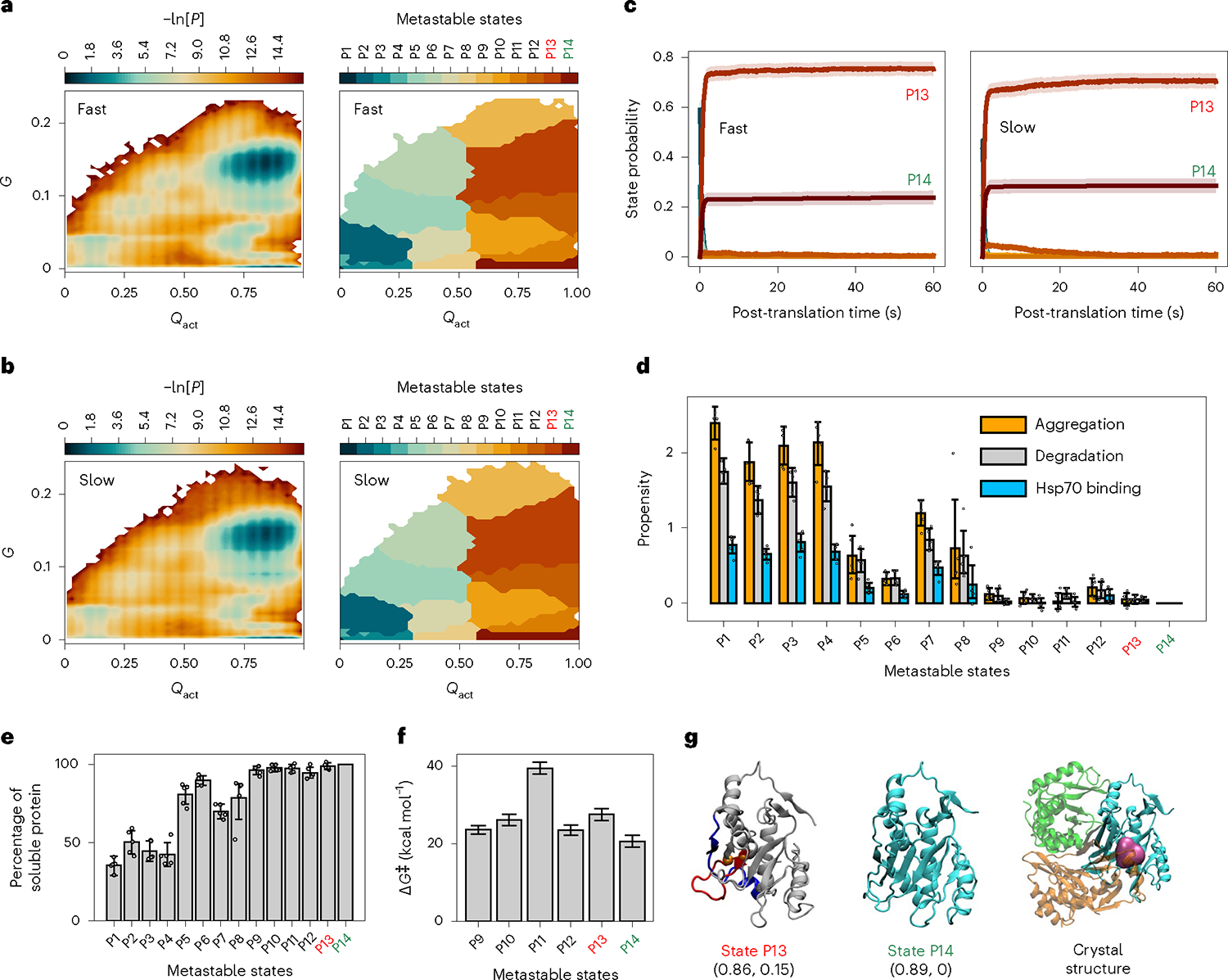
a,b, Log probability surfaces (−ln[P], where P is the probability of sampling particular Qact and G values) for the post-translational folding of fast-translating (a) and slow-translating (b) mRNA variants as a function of the order parameters Qact and G (left) and the regions corresponding to different metastable states (right). The native state is located in the bottom right-hand corner of these plots. c, Time courses of gross state probabilities (soluble + insoluble; same colours as the metastable states in a and b) with error bars shown as transparent stripes for fast (left) and slow (right) variants. d, Aggregation, degradation and Hsp70 binding propensities of each metastable state, calculated using Supplementary Equation (19). e, Percentage of soluble protein in each metastable state, calculated using Supplementary Equation (17). f, Median transition state barrier heights (ΔG‡) for the native and near-native metastable states calculated from the QM/MM simulations. g, From left to right: representative structures of the near-native kinetically trapped state P13 (the closed loop and threading segment of the entangled region are coloured in red and blue, respectively), the native state P14 and the trimer crystal structure (3CLA), with the substrate shown in magenta and three monomers shown in green, orange and cyan. The Qact and G values of the most probable cluster (microstate) for each state are reported below the structure in the format (Qact value, G value). In a–g, kinetically trapped entangled states are labelled in red, the native state (that is, state P14) is labelled in green and the others are labelled in black. All error bars represent 95% CIs of the statistics calculated by bootstrapping over all simulation trajectories/representative structures (sample sizes, n = 1,000 trajectories in c, n = 5 representative structures in d and e and n = 1,000 frames in f). Each of the bar charts in d and e is overlaid with the data points of the five representative structures. The structure of P13 can be explored interactively at https://obrien-lab.github.io/visualize_entanglements/.
Fig. 3 |. Slow translation partitions more DDLB into post-translational kinetically trapped entangled states.
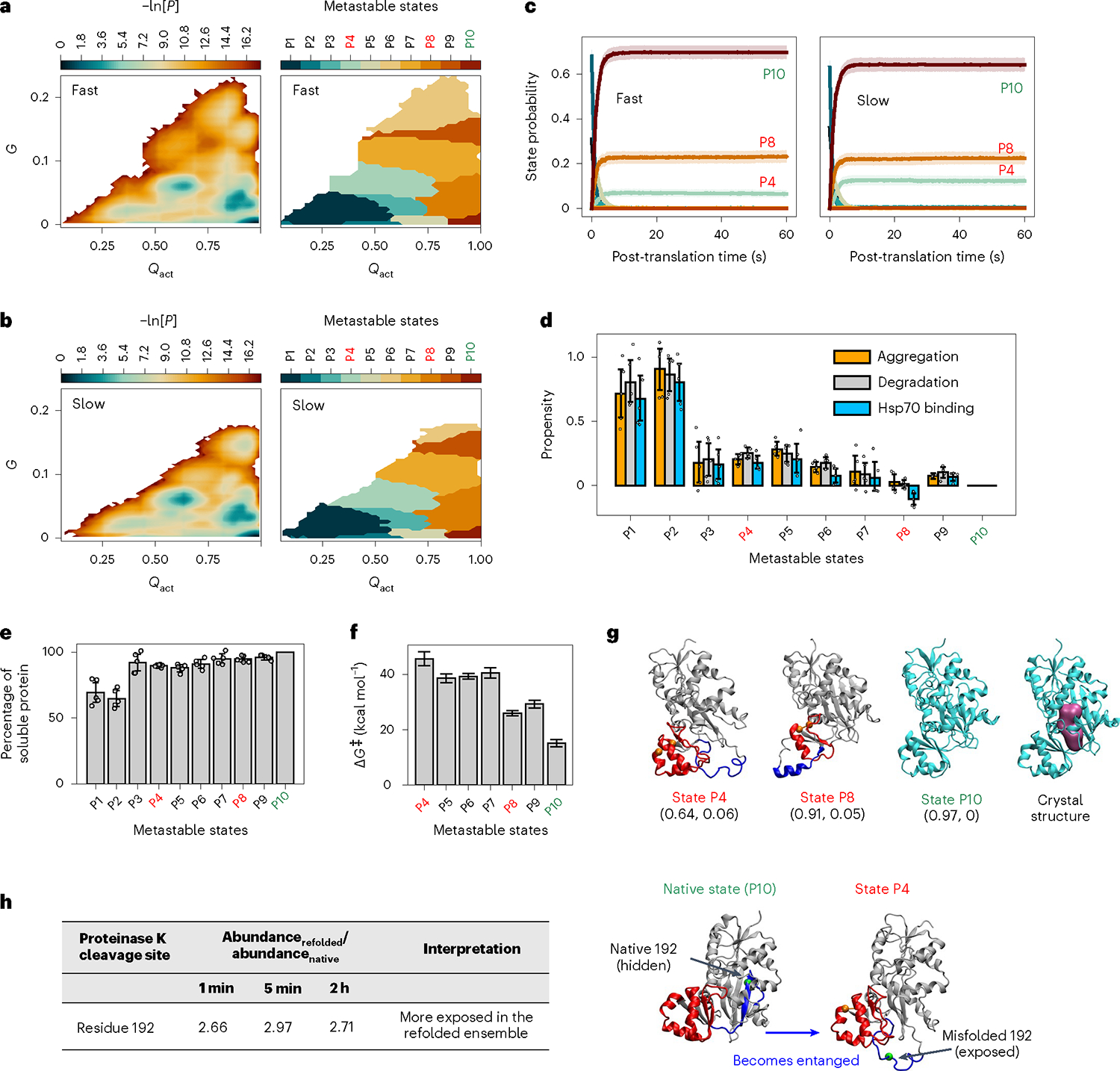
a,b, Log probability surfaces (−ln[P], where P is the probability of sampling particular Qact and G values) for the post-translational folding of fast-translating (a) and slow-translating (b) mRNA variants as a function of the order parameters Qact and G (left) and the regions corresponding to different metastable states (right). The native state is located in the bottom right-hand corner of these plots. c, Time courses of gross state probabilities (soluble + insoluble; same colours as the metastable states in a and b) with error bars shown as transparent stripes for fast (left) and slow (right) variants. d, Aggregation, degradation and Hsp70 binding propensities of each metastable state, calculated using Supplementary Equation (19). e, Percentage of soluble protein in each metastable state, calculated using Supplementary Equation (17). f, Median transition state barrier heights (ΔG‡) for the near-native metastable states calculated from the QM/MM simulations. g, From left to right: representative structures of the near-native kinetically trapped states P4 and P8 (the closed loops and threading segments of the entangled regions are coloured in red and blue, respectively), the native state P10 and the crystal structure (4C5C), with the substrate shown in magenta. The Qact and G values of the most probable cluster (microstate) for each state are reported below the structure in the format (Qact value, G value). h, Left, LiP-MS results for refolded DDLB. Only the peptides showing significantly different abundance (the abundance must have at least a twofold difference and the P value must be <0.01) from the refolded protein through all three time points are presented. Right, representative structures of the native state and the entangled state P4. The entanglement in state P4 is represented in the same way as in g. The native conformation corresponding to the entanglement is highlighted in the native state structure. The proteinase K site residue 192 is shown as a green ball. It is significantly more exposed to solvent in the entangled state P4. In a–h, kinetically trapped entangled states are labelled in red, the native state (that is, state P10) is labelled in green and the others are labelled in black. All error bars represent 95% CIs of the statistics calculated by bootstrapping over all simulation trajectories/representative structures (sample sizes, n = 1,000 trajectories in c, n = 5 representative structures in d and e and n = 1,000 frames in f). Each of the bar charts in d and e is overlaid with the data points of the five representative structures. The structures of P4 and P8 can be explored interactively at https://obrien-lab.github.io/visualize_entanglements/.
Fig. 4 |. No kinetically trapped states arise in synonymous variants of DHFR.

a,b, Log probability surfaces (−ln[P], where P is the probability of sampling particular Qact and G values) for the post-translational folding of fast (a) and slow (b) mRNA variants as a function of the order parameters Qact and G (left) and the regions corresponding to different metastable states (right). The native state is located in the bottom right-hand corner of these plots. c, Time courses of gross state probabilities (soluble + insoluble; same colours as the metastable states in a and b) with error bars shown as transparent stripes for fast (left) and slow (right) variants. d, Aggregation, degradation and Hsp70 binding propensities of each metastable state, calculated using Supplementary Equation (19). e, Percentage of soluble protein in each metastable state, calculated using Supplementary Equation (17). f, Median transition state barrier heights (ΔG‡) for the near-native metastable states calculated from the QM/MM simulations. g, From left to right: representative structures of the shallow-entangled state P2 (the closed loop and threading segment of the entangled region are coloured in red and blue, respectively), the native state P3 and the crystal structure (4KJK), with the substrate shown in magenta. The Qact and G values of the most probable cluster (microstate) for each state are reported below the structure in the format (Qact value, G value). In a–g, the native state (that is, state P3) is labelled in green and the others are labelled in black. All error bars represent 95% CIs of the statistics calculated by bootstrapping over all simulation trajectories/representative structures (sample sizes, n = 500 trajectories in c, n = 5 representative structures in d and e and n = 1,000 frames in f). Each of the bar charts in d and e is overlaid with the data points of the five representative structures. The structure of P2 can be explored interactively at https://obrien-lab.github.io/visualize_entanglements/.
Across the metastable states, we observed diverse misfolded structures for CAT-III and DDLB (Supplementary Figs. 5 and 6). Most of the misfolded structures exhibited topological entanglements, and many of these entangled structures were near native, having >60% of native contacts formed (Qact ≥ 0.6 and G ≥ 0.02; interactive visualization is provided at https://obrien-lab.github.io/visualize_entanglements/). Misfolded, metastable states P9, P10, P11, P12 and P13 of CAT-III exhibited Qact and G values, respectively, of 0.66 and 0.18, 0.72 and 0.04, 0.80 and 0.02, 0.84 and 0.09 and 0.86 and 0.15, while the native state (P14) had values of 0.89 and 0 (Fig. 2g and Supplementary Fig. 5). The DDLB misfolded states P4, P6, P7, P8 and P9 exhibited values of 0.64 and 0.06, 0.83 and 0.19, 0.85 and 0.09, 0.91 and 0.05 and 0.92 and 0.15, respectively, while the native state (P10) had values of 0.97 and 0 (Fig. 3g and Supplementary Fig. 6). In contrast, DHFR exhibited fewer misfolded states and only one entangled, misfolded state, with Qact and G values of 0.73 and 0.05 compared with the values 0.93 and 0 for its native state (Fig. 4g and Supplementary Fig. 7). All of the topological entanglements that we observed had a non-covalent lasso topology13–17, where native contacts within a certain folded region established a closed loop along the protein backbone and another segment in the same chain threaded through this loop to become entangled (Fig. 5). None of them were topologically knotted, as identified by a knot detection algorithm18, meaning that pulling on their termini would result in a fully extended conformation. Thus, all three enzymes sampled near-native, entangled structures during folding.
Fig. 5 |. Illustration of the G metric and non-covalent lasso topology.

Bottom left, contact map of native contacts, where the top and bottom triangular regions represent the native contacts within the native crystal structure of CAT-III (top left) and one of the misfolded structures in state P13 (bottom right), respectively. The native contacts in the misfolded structure are coloured based on the linking number g, calculated using Supplementary Equation (16). Top right, topology diagram of the non-covalent lasso entanglement formed by the native contact of residues 167 and 183, as an instance, where the closed loop is shown in red and the threading segment is shown in blue. As described in equation (2), the G metric of this misfolded structure, G = 0.12, was calculated by counting the number of native contacts within the misfolded structure, whose g value is different from that of the same native contact within the crystal structure (that is, the number of native contacts covered by the black circles in the lower triangular region of the contact map, which is 55), and normalizing them to the total number of native contacts in the crystal structure (that is, G = 55/442 = 0.12).
Some entangled structures are long-lived kinetic traps
To disentangle a misfolded structure, it is often necessary to unfold some portion of the properly folded segments to attain the native state. This can be energetically costly. Therefore, we hypothesized that these near-native, entangled structures are long-lived kinetic traps. To test this hypothesis, we calculated the post-translational probability of being in each metastable state as a function of time. These results are reported in Figs. 2c, 3c and 4c. For CAT-III and DDLB, entangled states (P13 for CAT-III and P4 and P8 for DDLB) persisted with appreciable populations (>10%) until 60 s after nascent protein release from the ribosome. For DHFR, the single entangled state (P2) populated only 0.2% of the trajectories and disentangled by 10 s. As a further test, we examined whether any post-translational trajectory of CAT-III or DDLB that reached an entangled state ever converted to an unentangled state. For CAT-III and DDLB, we found that 92.7 and 100% of trajectories sampled an entangled state and, of these, 78.6 and 10.4% did not convert to a state that was not entangled by the end of the simulations. Thus, we conclude that many of these entangled structures represent long-lived kinetic traps that convert to the native state slowly.
Entangled structures have altered catalytic properties
The non-covalent lasso entanglement intermediates we observed are a form of misfolding, as they represent ordered structures that are not native. Therefore, we hypothesized that some of these entangled structures have catalytic properties different from those of the native ensemble. To test this hypothesis, we calculated the transition state barrier height of the enzyme reaction of each metastable state that formed a native or near-native active site (Qact ≥ 0.6) using a back-mapping procedure to an all-atom representation and subsequent quantum mechanics/molecular mechanics (QM/MM) umbrella sampling simulations of the catalytic reaction (see the potential of mean force plots in Supplementary Figs. 8–10). Thus, for each metastable state, we obtained the median activation free energy barrier ΔG‡ going from reactants to products. For all three proteins, the native state had the lowest activation energy (Figs. 2f, 3f and 4f) and the other metastable states had higher barriers. Thus, these misfolded and entangled intermediates contribute to changes in specific activity. Coupled with the observation that entangled structures tend to be long-lived kinetic traps, we also conclude that these specific metastable states lead to reduced specific activity over long timescales.
Deep entanglements are usually long lived
Not all entangled structures are long-lived kinetic traps; otherwise, the entangled structure of DHFR (state P2 in Fig. 4g and Supplementary Fig. 7) would persist. Sliding a small number of residues out of the closed loop (Fig. 5; see also Supplementary Methods Section 11) tends to be easier than sliding a large number of residues. In addition, unfolding a small number of residues during disentanglement also tends to be easier than unfolding a large number of residues. Therefore, we hypothesized that the minimum number of residues involved in the threading segment, whose reptation can cause disentanglement, and the minimum number of residues needed to unfold during the disentanglement process should correlate with the ability of entangled metastable states to interconvert to unentangled states. To test this hypothesis, we analysed the representative structures from each metastable state. The entanglement of DHFR involved only, on average, five residues in the threading segment, and sliding these segments through the loop should not cause any portion of the protein to unfold. For CAT-III and DDLB, entangled states that never disentangled in the simulations involved, on average, 35 and eight residues, respectively, in the threading segment and had 31 and 53 residues that needed to unfold during disentanglement (see https://obrien-lab.github.io/visualize_entanglements/). These results are consistent with our hypothesis and suggest that because DHFR’s entanglement is shallow (that is, it involves a few residues and does not need to unfold to disentangle), thermal fluctuations can easily disentangle this structure, while thermal energy is not sufficient to quickly disentangle the CAT-III and DDLB deep entanglements.
To examine how long it will take to disentangle deep and shallow entanglements in a higher-resolution model, we back-mapped two deep-entangled conformations (one from CAT-III state P13 and the other from DDLB state P4) and one shallow-entangled conformation (from DHFR state P2) to an all-atom representation (see Supplementary Methods Section 13). We then carried out temperature jump simulations to estimate the disentangling times (Supplementary Figs. 12a, 13a and 14a,b). To account for force field biases affecting the kinetics, we also simulated and calculated the unfolding time of native DHFR at these temperatures and compared it with its experimentally measured unfolding rate (, extrapolated to 0 M urea at 298 K)19,20. (Among these three enzymes, only DHFR has experimentally reported refolding kinetics.) From these simulations, the disentangling rates () and unfolding rates () were extrapolated to 298 K. We found that the all-atom force field accelerated the unfolding of DHFR by 144-fold at 298 K. By correcting for this force field bias using this acceleration factor (that is, ), we estimated that for the deep entanglements in CAT-III and DDLB, the values of are 6.2 × 103 s (95% CI = 29 s–1 × 106 s) and 1.3 × 104 s (95% CI = 28 s–4 × 106 s), respectively. The shallow entanglement of DHFR becomes disentangled with a timescale of 71 s (95% CI = 4 × 10−3–2 × 106 s), which is two orders of magnitude faster than the deep entanglements. These results suggest that the deep-entangled metastable states we have identified are likely to be long-lived kinetic traps, persisting for hours.
Native-like entangled states are likely to remain soluble
The proteostasis machinery in cells has the potential to catalyse the folding (repair) or degradation (clearance) of these entangled structures. The entangled structures could also potentially aggregate and be removed from the pool of soluble enzymes. We accounted for the effects of these processes by estimating the aggregation, degradation and Hsp70 binding propensities of the different metastable states (see Supplementary Methods Section 14.2 and Supplementary Equation (19)). We observed, as expected, that the less structured metastable states have a higher propensity to aggregate, be degraded or interact with chaperones. For example, relative to the native state, states P1–P8 of CAT-III (see structures in Supplementary f. 5) are much more likely to experience one of these processes, as indicated by the larger magnitude of the bar plots in Fig. 2d. However, states P9–P13 exhibit similar propensities to the native state (P14) to aggregate, be degraded or become chaperone substrates. Similar results were observed for DDLB (Fig. 3d) and DHFR (Fig. 4d). Thus, our model indicates that some of these entangled structures do not interact with the proteostasis machinery any more than the native state does. Therefore, the altered specific activity we observe is likely to persist inside cells over long timescales. This prediction was confirmed by our enzyme kinetics assays (see the section ‘Accurate prediction of trends in specific activity’), since the fast and slow variants of DDLB were expressed in E. coli cells possessing the full complement of the proteostasis machinery (see Supplementary Methods Section 19).
We estimated the percentage of proteins in each metastable state that are likely to remain soluble by accounting for the aggregation, degradation and Hsp70 binding propensities within each metastable state (see Supplementary Methods Section 14.2 and Supplementary Equation (17)). We found that for both CAT-III and DDLB, many of the near-native entangled structures remained soluble. At least 97% of the proteins in entangled states P10, P11, P12 and P13 for CAT-III were estimated to remain soluble (Fig. 2e), while at least 89% of the proteins in entangled states P4, P6, P7, P8 and P9 of DDLB were expected to remain soluble (Fig. 3e). Thus, many of the long-lived, near-native entangled states are likely to remain soluble and free from aggregation, degradation and catalysed folding by chaperones.
The reason for this is that these near-native structures sequester the residues and sequence motifs21 that promote these processes to an extent similar to that in the native state. For example, state P13 of CAT-III exposes a similar amount of hydrophobic surface area as the native state ensemble (36.2 versus 34.7 nm2), so too with the exposed surface areas of residues that promote aggregation (21.6 versus 18.9 nm2) and interactions with the chaperone Hsp70 (40.0 versus 38.6 nm2).
Consistency with limited proteolysis mass spectrometry experiments
To experimentally test whether these entangled states exist, we carried out limited proteolysis mass spectrometry22 (LiP-MS) in which E. coli lysates were globally unfolded through incubation in 6 M guanidinium chloride, then refolded by dilution, and the conformations of the resulting refolded proteins were assessed by their susceptibility to proteolysis with proteinase K. With liquid chromatography tandem mass spectrometry, tens of thousands of fragments were identified and quantified21, of which a number were from DDLB and DHFR, enabling an assessment of whether or not their refolded conformations were similar to their native forms. In these experiments, proteins were allowed to refold for 1 min, 5 min or 2 h following dilution from denaturant, then pulse proteolysis was conducted, providing a snapshot of their structural ensemble at distinct timescales. Peptide fragments that contained a cleavage site arising from proteinase K were interpreted as demarcating sites within a protein that were solvent exposed or unstructured; hence, if such a fragment was present in greater abundance in the refolded samples (relative to untreated, native samples), it implied that a population of the protein failed to form the native-like structure at that site. Additional details can be found in Supplementary Methods Section 21. For DDLB, we found one statistically significant peptide fragment (abundance ratio greater than twofold; P < 0.01 by Welch’s t-test), with a proteinase K cleavage site at residue 192, whose abundance was at least 2.6 times greater in the refolded samples at all three time points (Fig. 3h; the full dataset is provided in Supplementary Table 13), indicating that residue 192 is more exposed to solvent than in the native state. Cross-referencing this site against the long-lived metastable states in our simulations (Fig. 3g), we found that state P4 contains an entanglement in which residue 192 is part of the threading segment and more exposed to solvent (Fig. 3h). This misfolding results in a 12-fold increase in the solvent-accessible surface area for residue 192 compared with the native state, in which it is part of a β sheet. In addition, states P4 and P8 were sampled by DDLB when refolding was commenced from a thermally denatured state in our model (Supplementary Fig. 15), indicating that many of the same misfolded states populated during synthesis are also populated through refolding in the absence of the ribosome. Thus, comparison of the LiP-MS data to co- and post-translational folding is reasonable. Therefore, our simulations provide a molecular interpretation of LiP-MS refoldability experiments and are consistent with the existence of protein entangled states.
In contrast, we predicted that DHFR does not exhibit long-lived misfolded states. Indeed, in the LiP-MS data there was a peptide that exhibited a significant abundance difference in the refolded samples after 5 min of refolding time; however, it was not present at the 1 min and 2 h time points (Supplementary Table 14), indicating that the refolded protein is indistinguishable from its native conformation on long timescales. Thus, any structural distortions in DHFR during refolding were short lived. The single significant peptide indicates that a region spanned by residues 77–98 is more exposed to solvent in the misfolded state than in the native state. Indeed, in the short-lived entangled state, P2, we found that this region had a 5% larger solvent-accessible surface area than in the native state (a 1.05-fold increase with a 99% CI of 1.02–1.07; two-tailed t-test, P = 6 × 10−6). Therefore, this negative control provides further evidence of the accuracy of our model’s predictions.
Synonymous mutations alter the entangled state populations
Next, we examined how translation speed changes affected the post-translational populations of entangled structures. We observed that for CAT-III, 60 s after translation termination, 76.3% (95% CI = 73.6–78.9%) of the structures were entangled when synthesis was fast, while 71.6% (95% CI = 68.8–74.3%) were entangled when synthesis was slow. Likewise, the entangled population of DDLB accounted for 35.7% (95% CI = 32.7–38.7%) and 30.2% (95% CI = 27.3–33.0%) of the total under slow and fast translation, respectively. In contrast, the population of entangled structures for DHFR remained zero regardless of the translation speed 10 s post-termination. Thus, synonymous mutations can alter the population distributions of entangled states over long timescales for deep entanglements.
Synonymous mutations cause a divergence of folding pathways
We hypothesized that the changes in translation speed alter the co-translational folding pathways of the protein. First, we assessed how different the nascent chain structural distributions were under fast and slow translation by applying the Jensen–Shannon divergence metric (Supplementary Equation (21)) to the population of microstates identified as part of our Markov state modelling. A Jensen–Shannon value of 0 means that there is no difference between the distributions, while a value of ln2 means the distributions are completely different. We found that for all three proteins, the structural divergence induced by synonymous mutations was small at short nascent chain lengths and tended to increase as the nascent chain length increased (Fig. 6b,e,h). The maximum divergence occurred at or near the longest nascent chain length before the nascent chain was released from the ribosome. For DHFR, the structural ensembles arising from fast and slow synthesis started to diverge at approximately 110 residues in length, while for CAT-III and DDLB, the two distributions started to diverge at 190 and 210 residues, respectively. Thus, the fast and slow translation rates altered the co-translational distributions of conformations for all three enzymes.
Fig. 6 |. Co- and post-translational folding pathways of CAT-III, DDLB and DHFR.

a,d,g, The most probable folding pathways of CAT-III (a), DDLB (d) and DHFR (g) are presented as a directed graph where the nodes represent metastable states, with representative structures shown in the boxes. The edges represent the transitions in the 80% most likely pathways. The nodes corresponding to the native state and the kinetically trapped states are framed in green and red, respectively. The transitions (arrows) that are observed in only the fast or slow variants are marked in orange and blue, respectively. b,e,h, Jensen–Shannon divergence of the co-translational microstate distributions (left; Supplementary Equation (21)) and post-translational metastable state distributions (right; Supplementary Equation (22)) of CAT-III (b), DDLB (e) and DHFR (h), comparing fast and slow variants, with a red line indicating zero divergence. aa, amino acids. c,f,i, Co-translational pathway probabilities (* → end state C*) and post-translational pathway probabilities from the co-translational end states to the native state (C* → native state) for CAT-III (c), DDLB (f) and DHFR (i). The pathway probabilities whose changes were >5% are highlighted in yellow. The post-translational pathway probabilities are normalized by the corresponding co-translational pathway probabilities that involve the particular co-translational end state.
The post-translational (metastable state) structural distributions (Supplementary Equation (22)) for DHFR, which were initially different between fast and slow synthesis, rapidly converged to the same distribution (that is, they had Jensen–Shannon values equal to zero; Fig. 6h). For CAT-III and DDLB, the two distributions did not reconverge 60 s after synthesis (0.02 for CAT-III and 0.27 for DDLB; see Fig. 6b,e). Thus, the changes in conformation caused by synonymous mutations are quickly forgotten by DHFR due to its rapid equilibration, while CAT-III and DDLB retain a memory of those co-translational differences due to kinetic trapping.
To characterize changes in co- and post-translational folding pathways, we calculated the populations and pathway probabilities of transitions between metastable states occurring co- and post-translationally under the different translation schedules (see Supplementary Methods Section 17). As shown in Fig. 6, black arrows between metastable states indicate that a transition was observed between those states in both translation schedules in the top 80% of populated pathways, blue arrows indicate that the transition was seen only in the slow translation schedule and orange arrows indicate that the transition was seen only in the fast translation schedule.
We identified nine co- and three post-translational metastable states for DHFR (representative structures shown in Fig. 6g). The co- and post-translational folding pathways were very similar, as most of the transitions were seen in both translation schedules (black arrows in Fig. 6g). There were some differences though. Transitions from state C7 to C9 and from C9 to C8 were observed only for the slow schedule. The pathway probabilities, however, demonstrated that even though the initial post-translational structural distribution differed, all states converted to the native state by the end of the post-translational simulations (Fig. 6i). For example, the pathway probabilities of C8→P3 and C9→P3 were 100% for both fast and slow translation. An exception was the transition probability of C6→P3 that occurs in the fast variant but not in the slow variant, because in the slow variant state C6 is never populated. However, because C6 quickly converts to the native state P3, the effect on the time-dependent native state population is negligible. Thus, the co-translational folding of DHFR was slightly affected by differences in translation speed; however, these differences quickly disappeared due to rapid folding from all post-translational metastable states.
In contrast, CAT-III exhibited a co- and post-translational folding network (Fig. 6a) and pathway probabilities that were sensitive to translation speed changes and whose resulting differences persisted post-translationally. Nine co-translational and 14 post-translational metastable states were identified for CAT-III (Fig. 6a). Seven of these post-translational metastable states (P5, P6, P9, P10, P11, P12 and P13) exhibited entangled structures, while no co-translational states exhibited entanglement. Thus, entanglement is a post-translational process for CAT-III (see Supplementary Videos 1 and 2 visualizing, respectively, the process of entanglement versus correct folding). Very different co-translational folding pathways were observed starting at a nascent chain length of approximately 195 residues, where the divergence metric exhibited a large increase (Fig. 6b), and transitions into and out of co-translational metastable state C9 started to differ between the fast and slow translation schedules (as indicated by the blue and orange arrows in Fig. 6a). For example, only in the slow schedule could C9 transition to C6, while only in the fast schedule could C5 transition to P1. These differences in allowed transitions persisted post-translationally as well, with state P13 being an effective sink during the post-translational simulations (that is, allowing no direct or indirect transitions to the native state (P14) once it was reached). This sink had deep-entangled structures, consistent with our earlier observation that the deep-entangled states tend to be kinetic traps (as indicated by the red border around metastable state P13 in Fig. 6a). Finer-grained consideration of the folding pathways showed that post-translationally, CAT-IIIfast partitioned 5.0% (95% CI = 1.1–8.9%) more protein into sink P13, while CAT-IIIslow partitioned 4.7% (95% CI = 0.8–8.6%) more protein into native state P14. The transitions towards the native state P14 were enhanced for CAT-IIIslow, whereas the transitions towards the kinetic trap P13 were enhanced for CAT-IIIfast. This is also indicated by the pathway probabilities shown in Fig. 6c. Synonymous mutations also led to smaller changes in other states, including the entangled states P6, P10 and P12. Thus, the change in translation speed causes differences in the CAT-III co-translational folding pathways once at least 195 residues have been synthesized, and these differences lead to changes in the populations of post-translationally entangled states, thereby altering the transition state barrier for the reaction this enzyme carries out (Fig. 2f) and affecting the specific activity of CAT-III over long timescales (Fig. 1g).
Similar to CAT-III, DDLB also exhibited co- and post-translational folding pathways that were sensitive to changes in translation speed across its 11 co- and ten post-translational metastable states. However, unlike CAT-III, DDLB co-translationally formed entangled structures (states C8 and C9) that persisted to form entangled post-translational states (states P1, P3, P4 and P8). In CAT-III, the divergence in co-translational folding pathways between fast and slow translation schedules monotonically increased with increasing chain length (Fig. 6b). However, the co-translational folding pathways of DDLB diverged starting at a nascent chain length 110 residues but reconverged around 190 residues, diverging again starting at 210 residues (Fig. 6e). The first divergence involved a transition to state C4 with the fast schedule that did not occur with the slow schedule (orange arrow in Fig. 6d). This state ultimately interconverted to state C3, which is an obligatory intermediate in both schedules. The second divergence started at state C7, in which 6% more nascent chains went to entangled state C8 with the slow schedule than with the fast schedule, and the rest went to state C10. Parallel co- and post-translational folding pathways then arose. In one pathway, transitions were observed from C10→C11→P2, while the other transitions from C8→C9→P1 involved entangled structures in all states (Fig. 6d; see also Supplementary Videos 3 and 4 illustrating the processes of entanglement and folding). The increased probability of this entangled pathway during slow translation decreased the probability that DDLB would post-translationally reach the native state P10 (3.9 versus 11.7% in slow versus fast translation; Fig. 6f), while DDLBslow partitioned 5.8% (95% CI = 3.2–8.3%) more protein (gross amount; that is, soluble plus insoluble) into the near-native kinetic trap P4 after post-translation. Thus, we again see that entangled states act as sinks with altered transition state barriers for the enzyme’s reaction (Fig. 3f). These population shifts among these states and the folding pathways they take part in lead to long-lived changes in specific activity.
Discussion
A detailed understanding of the molecular mechanisms giving rise to the coupling of enzyme activity to synonymous mutations would provide biochemists, molecular biologists, evolutionary biologists and biomedical researchers with a framework with which to interpret experiments on the influence of codon usage on protein structure and function, cellular phenotype, disease and some of the selection pressures shaping mRNA sequence evolution. In this study, we developed a novel multiscale model that qualitatively recapitulates the experimental observations for the specific activity of CAT-III variants1 and correctly predicts the trends in specific activity changes of DDLB and DHFR variants, giving us confidence that the model is realistic. This provided us with the opportunity to study the structures, pathways and kinetics that give rise to this phenomenon.
Our key findings are: (1) changes in elongation kinetics induced by synonymous mutations can alter co-translational nascent chain structural ensembles and folding pathways; (2) for some enzymes, such as CAT-III and DDLB, these changes in the structural ensemble can persist long after the nascent chain has been released from the ribosome; (3) this persistence arises from conformational states that are long-lived kinetic traps; (4) these kinetic traps arise at the molecular level from deep entanglements that slowly disentangle because they require the unfolding of already folded protein segments; (5) these entanglements are non-covalent lasso topologies in which a closed loop is formed by a backbone segment connecting two residues that form a non-covalent native contact, and another segment threads through this loop; (6) many of these entangled structures have decreased catalytic efficiencies due to structural perturbation of their active sites; (7) some entangled structures are very similar to the native state, exposing similar extents of hydrophobic surface area and chaperone binding motifs; and (8) because of their near-native conformations, these entangled structures can bypass the chaperone and degradation machinery of the cell and do not exhibit an increased propensity to aggregate. This situation results in a soluble fraction of enzymes with decreased specific activities that can persist for long time periods in cells.
Two concepts central to our explanation—intramolecular entanglement and subpopulations of kinetically trapped states—are not without precedent. The material properties of entangled synthetic polymers have long been studied and modelled23,24 in the field of polymer physics. Also, there has been a large amount of research focused on knotted proteins that often contain disulfide bonds or topologies in which when the protein’s ends are pulled in opposite directions the protein does not fully extend14,25–27. These characteristics, however, were not present in our entanglements. The entanglements we observed formed a closed loop due to a non-covalent native contact, and if both ends of the protein were pulled, disentanglement would occur. Recently, this type of entanglement has been detected in almost one-third of the protein structures deposited in the Protein Data Bank15. Thus, the potential for protein segments to form non-native, non-covalent lassos is plausible. Kinetically trapped states of proteins have been observed in single-molecule experiments probing the functioning of flavoenzymes28,29. In one study, heterogeneous populations of the protein cholesterol oxidase were observed to stochastically switch very slowly between active and nonactive states28. However, in that study, the influence of protein synthesis on the distribution of conformational states was not probed. Thus, a novel aspect of our discovery is that it combines the phenomena of entanglement and kinetic trapping as essential to the mechanism by which synonymous mutations affect co- and post-translational protein structure and function.
In contrast with CAT-III and DDLB, the changes in DHFR’s co-translational structures and folding pathways did not persist post-translationally. This is consistent with previous studies showing that DHFR has fast folding kinetics and an absence of off-pathway intermediates30 and kinetic traps31. Two reasons for this are that DHFR only negligibly populates an entangled conformation and that the entanglement it forms is shallow; its disentanglement requires only five residues to slide out of the closed loop and there is no requirement to unfold any other portions of the protein to do so. Thus, this shallow entanglement is rapidly disentangled without large structural rearrangements. In contrast, CAT-III and DDLB entanglements involve many more residues, requiring large structural rearrangements to become disentangled, leading to longer-lived entangled structures. Thus, the presence of entanglement is not sufficient to guarantee a kinetic trap. The nature of the entanglement and the native structure surrounding it is critical.
Long-lived entangled states have the potential to be probed using a variety of experimental techniques. Ensemble-level experiments, such as NMR and X-ray crystallography, often require appreciable populations to detect a substrate, which might make entanglement detection difficult. Many biophysical techniques used in protein folding (such as fluorescence resonance energy transfer, tryptophan fluorescence and circular dichroism) are sensitive to subpopulations, but tend to have low structural resolution, which would limit their capacity to distinguish near-native conformations. Therefore, hydrogen–deuterium exchange mass spectrometry and LiP-MS, which can localize conformational differences within a protein, combined with molecular modelling, seem promising in detecting signatures of entanglements. Cryogenic electron microscopy, with its ability to build structural classes from heterogeneous populations, might also be effective for systems of suitable size and resolution, although the increased flexibility of entangled regions may prove a challenge.
It is reasonable to expect that the enzymatic activity of initially misfolded proteins should increase with time as the protein relaxes to its native state. Based on the disentangling timescale of 104 s (see the section ‘Deep entanglements are usually long lived’), we estimate that it would take more than 3 h for the specific activities between fast and slow variants to converge. This is consistent with what was found for CAT-III, where the specific activity of synonymous mutant CAT-III did not converge to that of the wild type within 20 min1. For DDLB, because the LiP-MS results confirmed that the misfolded states can persist for longer than 2 h, it is reasonable to anticipate that the specific activities between fast and slow DDLB variants will take more than 2 h to converge, which is also consistent with our prediction. Further experiments, such as a time-dependent activity assay coupled with pulse–chase protein expression and production, could be applied to measure such timescales.
This study provides a plausible explanation of how synonymous mutations can alter enzyme activity in cells. Synonymous mutations alter translation elongation speeds and change the population of nascent chain conformations in entangled states that are near native but have lower catalytic efficiencies than that of the native state. Hence, the specific activity—a quantity averaged over the populations of proteins in different conformational states—can increase or decrease due to synonymous mutations. The experimental search for these entangled structures and their roles in influencing protein structure, function and phenotypes in cells is likely to be a fruitful area of research in the future.
Online content
Any methods, additional references, Nature Portfolio reporting summaries, source data, extended data, supplementary information, acknowledgements, peer review information; details of author contributions and competing interests; and statements of data and code availability are available at https://doi.org/10.1038/s41557-022-01091-z.
Methods
Coarse-grained simulation model
To model transitions between the native state and the unfolded state, we utilized a Gō-based coarse-grained model33–37 for all of the proteins studied. Briefly, this coarse-grained model represents each residue as a single interaction site centred on the Cα position and uses a structure-based potential energy function (see Supplementary Equation (1)). The force field parameters were optimized by training the parameters to reproduce the folding stability free energies of 18 small single-domain proteins38, followed by assignment of the minimum values that can reproduce the structural stability for a given protein. To map the simulation timescale to an experimental timescale, we used the scaling factor , which is the ratio of bulk experimental folding times to simulated folding times (see Supplementary Table 4). The high-resolution crystal structure PDB 4V9D39 was used to coarse-grain the E. coli ribosome, with the A- and P-site transfer RNA (tRNA) molecules modelled based on the PDB structure 5JTE40. The entire 50S subunit, including the A- and P-site tRNAs, was coarse-grained using the three-/four-point model of ribosomal RNA33 and the Cα model for ribosomal protein33 and then truncated to include only those coarse-grained interaction sites within 30 Å of the centre line of the exit tunnel and within 20 Å of the peptidyl transferase centre (identified as A2602 in the 23S ribosomal RNA of the E. coli ribosome), as well as the interaction sites at the ribosome surface near the exit tunnel opening. This resulted in 4,577 interaction sites for the cropped coarse-grained E. coli ribosome.
Protein synthesis on the ribosome was modelled using a continuous synthesis protocol that describes A-site tRNA binding, peptidyl transfer, tRNA translocation and ribosome trafficking41 at each nascent chain length using codon translation rates obtained from the model of Fluitt at al.42 (see Supplementary Equations (11) and (13)). Post-translational dynamics were modelled by simulating the nascent protein in the absence of the ribosome. Simulations for both co- and post-translational folding were performed via Langevin dynamics with a collision frequency of 0.05 ps−1 and a time step of 15 fs using OpenMM43. Details of the model setup can be found in Supplementary Methods Sections 1–8.
Virtual screening for enzymes that exhibit kinetic traps
To identify candidate enzymes that may have kinetic traps, we created a dataset of well-characterized monomeric E. coli enzymes by searching the relevant databases EzCatDB44,45, UniProt46 and RCSB PDB47. The wild-type enzymes were then parameterized and their synthesis and post-translational dynamics were simulated with a 14-d wall time. The candidates were selected using the scoring function
| (1) |
where is the mean post-translational folding time calculated using the double-pathway kinetics scheme of Supplementary Equation (6) with no delay time (that is, ) and is an indicator of whether (equals 1) or not (equals 0) misfolding occurs at or near the substrate-binding site and persists to the end of the simulation. We assigned equal weights for these two terms because they are considered equally important in identifying long-lived kinetic traps that have perturbed enzymatic functions. A higher score indicates a higher possibility for the enzyme to have long-lived kinetic traps that have misfolding in the substrate-binding pocket during its post-translational folding dynamics. Further details of the screening can be found in Supplementary Methods Section 9.
Characterizing post-translational misfolded structures
The misfolded structures of the post-translational folding process were characterized using the metrics and is an order parameter that measures the extent to which there is a change of entanglement in a given structure compared with the native structure and is calculated as
| (2) |
where is one of the native contacts in the native crystal structure, nc is the set of native contacts formed in the current structure, and are, respectively, the total linking number of the native contact in the current and native structures estimated using Supplementary Equation (16) (see Supplementary Methods Section 11 for details), is the total number of native contacts within the native structure, and the selection function equals 1 when the condition is true and 0 when it is false. The larger is, the larger the number of residues that have changed their entanglement status relative to the native state. That is, reports on the presence of non-native entanglements in structures.
is the fraction of native contacts that have formed in the enzyme substrate-binding pocket. Residues composing the substrate-binding pocket were identified as those residues within 8 Å of any atoms of the relevant ligands present in the crystal structure. The values were calculated for all of the native contacts between one atom within the substrate-binding pocket and any other atom, as shown below:
| (3) |
where and are the residue indices and satisfy is the intersection set of residues within secondary structure elements (α helical or β strands) and the substrate-binding pocket, is the set of all residues within secondary structure elements and and are step functions that equal 1 when residues and have native contact and 0 when and do not have native contact in the current structure and native structure, respectively. Native contacts are considered formed when the distance between the Cα atoms of residues and does not exceed 1.2 times their native distance and the native distance does not exceed 8 Å. In the case of CAT-III, residue set also includes native contacts in the trimer interface region (residues 25–33 and 150–157) to monitor the folding of the trimer interface as well. Note that the native contacts used in calculating are restricted to those within secondary structure elements, while the entire set of native contacts is used to calculate . Details of the assessment procedure can be found in Supplementary Methods Section 12.
Specific activity estimation
For each metastable state , identified using the Markov state modelling procedure reported in Supplementary Methods Section 12, we randomly selected five conformations from all of the microstates (based on the probability distribution of the microstates within the metastable state) and back-mapped them to all-atom structures (see Supplementary Methods Section 13). We then used QM/MM simulations (see Supplementary Methods Section 14) to calculate the transition state barrier for each of the five conformations, and from these, we determined the median activation barrier height . Only the metastable states that formed a near-native active site (), as well as the native state, were taken to estimate , while the others were considered to have an infinite barrier height (zero reaction rate). Assuming the rate constants of each metastable state have similar pre-exponential factors that can be treated as a constant, the specific activity for a protein can be estimated using the probability distribution of metastable states (state probability ) and the activation free energy barrier height of each state as
| (4) |
where is the molecular weight of the enzyme, is the pre-exponential factor allowing us to convert to the reaction rate constant, is the total number of metastable states, is the gas constant and is the temperature. In many codon usage studies1,3,8, the relative specific activity is often used to compare the enzymatic activities of a protein produced by synonymous mRNA variants. In this study, the maximum specific activity among the fast and slow synonymous mRNA variants of an enzyme was used for normalization:
| (5) |
where is the relative specific activity under saturating conditions. Note that the pre-exponential factor and the molecular weight cancel out when the specific activity is normalized; therefore, they do not need to be estimated. The details of estimating the state probability (accounting for the soluble fraction only) and the activation free energy barrier height () are presented in Supplementary Methods Section 14. The materials and experimental methods for measuring the specific activities of the DDLB and DHFR variants are presented in Supplementary Methods Sections 19 and 20, respectively.
Supplementary Material
Acknowledgements
S.D.F. acknowledges support from the National Institutes of Health (NIH) Director’s New Innovator Award (DP2GM140926) and National Science Foundation (MCB-2045844). S.J.B. acknowledges support from the NIH (GM-122595), Eberly Family Distinguished Chair in Science and Howard Hughes Medical Institute. E.P.O. acknowledges support from the National Science Foundation (MCB-1553291) and NIH (R35-GM124818). Computations in this work were carried out on the Extreme Science and Engineering Discovery Environment supercomputer32 (which is supported by MCB-160069) and the Pennsylvania State University’s Institute for Computational and Data Sciences’ Roar supercomputer. The CLS Behring Fermentation Facility and Huck Institutes of the Life Sciences at the Pennsylvania State University provided equipment and training to grow and purify DHFR biological replicates. We thank T. Berek and P. Kashyap for help with growing and purifying the DHFR biological replicates.
Footnotes
Competing interests
The authors declare no competing interests.
Additional information
Supplementary information The online version contains supplementary material available at https://doi.org/10.1038/s41557-022-01091-z.
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Code availability
All of the computer code developed in this work is available in the GitHub repositories https://github.com/obrien-lab/cg_simtk_protein_folding and https://github.com/obrien-lab/Activation-Energy-Estimation-Workflow under the MIT License. Detailed instructions on code usage, basic theory and examples of the input/output are available in the wiki pages of the above repositories.
Data availability
Data supporting the main findings of this study are available within the Article and its Supplementary Information and source data files. We cannot feasibly provide all ~5.3 TB of molecular dynamics trajectory data, but we provide the input data that were used to perform the simulations in this study in the repository subdirectory https://github.com/obrien-lab/cg_simtk_protein_folding/blob/master/example/input_data.tar.xz. All of the data that support the findings of this study, as well as the biological materials that were used to test the enzymatic activity of the DDLB and DHFR variants and for the LiP-MS experiments, are available from the corresponding author upon reasonable request. The raw mass spectrometry data for DDLB and DHFR have been deposited to the ProteomeXchange Consortium via the PRIDE partner repository with the dataset identifier PXD031425. A website (https://obrien-lab.github.io/visualize_entanglements/) was created to provide interactive visualization of the key misfolded, entangled structures predicted in this study. Source data are provided with this paper.
References
- 1.Komar AA, Lesnik T & Reiss C Synonymous codon substitutions affect ribosome traffic and protein folding during in vitro translation. FEBS Lett. 462, 387–391 (1999). [DOI] [PubMed] [Google Scholar]
- 2.Zhao F, Yu C-H & Liu Y Codon usage regulates protein structure and function by affecting translation elongation speed in Drosophila cells. Nucleic Acids Res. 45, 8484–8492 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Spencer PS, Siller E, Anderson JF & Barral JM Silent substitutions predictably alter translation elongation rates and protein folding efficiencies. J. Mol. Biol. 422, 328–335 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hunt R et al. A single synonymous variant (c.354G>A [p.P118P]) in ADAMTS13 confers enhanced specific activity. Int. J. Mol. Sci. 20, 5734 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Crombie T, Boyle JP, Coggins JR & Brown AJ The folding of the bifunctional TRP3 protein in yeast is influenced by a translational pause which lies in a region of structural divergence with Escherichia coli indoleglycerol-phosphate synthase. Eur. J. Biochem. 226, 657–664 (1994). [DOI] [PubMed] [Google Scholar]
- 6.Walsh IM Testing the Effects of Synonymous Codon Usage on Co-Translational Protein Folding Using Novel Experimental and Computational Techniques. PhD thesis, Univ. Notre Dame (2019). [Google Scholar]
- 7.Yu C-H et al. Codon usage influences the local rate of translation elongation to regulate co-translational protein folding. Mol. Cell 59, 744–754 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Walsh IM, Bowman MA, Santarriaga IFS, Rodriguez A & Clark PL Synonymous codon substitutions perturb cotranslational protein folding in vivo and impair cell fitness. Proc. Natl Acad. Sci. USA 117, 3528–3534 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sala AJ, Bott LC & Morimoto RI Shaping proteostasis at the cellular, tissue, and organismal level. J. Cell Biol. 216, 1231–1241 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Liu Y et al. Small molecule probes to quantify the functional fraction of a specific protein in a cell with minimal folding equilibrium shifts. Proc. Natl Acad. Sci. USA 111, 4449–4454 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Buhr F et al. Synonymous codons direct cotranslational folding toward different protein conformations. Mol. Cell 61, 341–351 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Martelli PL, Fariselli P & Casadio R Prediction of disulfide-bonded cysteines in proteomes with a hidden neural network. Proteomics 4, 1665–1671 (2004). [DOI] [PubMed] [Google Scholar]
- 13.Niemyska W et al. Complex lasso: new entangled motifs in proteins. Sci. Rep. 6, 36895 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Sulkowska JI On folding of entangled proteins: knots, lassos, links and θ-curves. Curr. Opin. Struct. Biol. 60, 131–141 (2020). [DOI] [PubMed] [Google Scholar]
- 15.Baiesi M, Orlandini E, Seno F & Trovato A Sequence and structural patterns detected in entangled proteins reveal the importance of co-translational folding. Sci. Rep. 9, 8426 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Baiesi M, Orlandini E, Seno F & Trovato A Exploring the correlation between the folding rates of proteins and the entanglement of their native states. J. Phys. A: Math. Theor. 50, 504001 (2017). [Google Scholar]
- 17.Connolly ML, Kuntz I & Crippen GM Linked and threaded loops in proteins. Biopolymers 19, 1167–1182 (1980). [DOI] [PubMed] [Google Scholar]
- 18.Jarmolinska AI, Gambin A & Sulkowska JI Knot_pull—python package for biopolymer smoothing and knot detection. Bioinformatics 36, 953–955 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Jennings PA, Finn BE, Jones BE & Matthews CR A reexamination of the folding mechanism of dihydrofolate reductase from Escherichia coli: verification and refinement of a four-channel model. Biochemistry 32, 3783–3789 (1993). [DOI] [PubMed] [Google Scholar]
- 20.Garbuzynskiy SO, Ivankov DN, Bogatyreva NS & Finkelstein AV Golden triangle for folding rates of globular proteins. Proc. Natl Acad. Sci. USA 110, 147–150 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Nissley DA et al. Universal protein misfolding intermediates can bypass the proteostasis network and remain soluble and less functional. Nat. Commun. 13, 3081 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Feng Y et al. Global analysis of protein structural changes in complex proteomes. Nat. Biotechnol. 32, 1036–1044 (2014). [DOI] [PubMed] [Google Scholar]
- 23.Kröger M Developments in polymer theory and simulation. Polymers (Basel) 12, 30 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Pawlak A The entanglements of macromolecules and their influence on the properties of polymers. Macromol. Chem. Phys. 220, 1900043 (2019). [Google Scholar]
- 25.Sułkowska JI, Sułkowski P & Onuchic J Dodging the crisis of folding proteins with knots. Proc. Natl Acad. Sci. USA 106, 3119–3124 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Haglund E et al. Pierced lasso bundles are a new class of knot-like motifs. PLoS Comput. Biol. 10, e1003613 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Haglund E et al. The unique cysteine knot regulates the pleotropic hormone leptin. PLoS ONE 7, e45654 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lu HP, Xun L & Xie XS Single-molecule enzymatic dynamics. Science 282, 1877–1882 (1998). [DOI] [PubMed] [Google Scholar]
- 29.Yang H et al. Protein conformational dynamics probed by single-molecule electron transfer. Science 302, 262–266 (2003). [DOI] [PubMed] [Google Scholar]
- 30.Heidary DK, O’Neill JC, Roy M & Jennings PA An essential intermediate in the folding of dihydrofolate reductase. Proc. Natl Acad. Sci. USA 97, 5866–5870 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bitran A, Jacobs WM, Zhai X & Shakhnovich E Cotranslational folding allows misfolding-prone proteins to circumvent deep kinetic traps. Proc. Natl Acad. Sci. USA 117, 1485–1495 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Towns J et al. XSEDE: accelerating scientific discovery. Comput. Sci. Eng. 16, 62–74 (2014). [Google Scholar]
- 33.O’Brien EP, Christodoulou J, Vendruscolo M & Dobson CM Trigger factor slows co-translational folding through kinetic trapping while sterically protecting the nascent chain from aberrant cytosolic interactions. J. Am. Chem. Soc. 134, 10920–10932 (2012). [DOI] [PubMed] [Google Scholar]
- 34.Sharma AK, Bukau B & O’Brien EP Physical origins of codon positions that strongly influence cotranslational folding: a framework for controlling nascent-protein folding. J. Am. Chem. Soc. 138, 1180–1195 (2016). [DOI] [PubMed] [Google Scholar]
- 35.Fritch B et al. Origins of the mechanochemical coupling of peptide bond formation to protein synthesis. J. Am. Chem. Soc. 140, 5077–5087 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Nissley DA & O’Brien EP Structural origins of FRET-observed nascent chain compaction on the ribosome. J. Phys. Chem. B 122, 9927–9937 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Leininger SE, Trovato F, Nissley DA & O’Brien EP Domain topology, stability, and translation speed determine mechanical force generation on the ribosome. Proc. Natl Acad. Sci. USA 116, 5523–5532 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Nissley DA et al. Electrostatic interactions govern extreme nascent protein ejection times from ribosomes and can delay ribosome recycling. J. Am. Chem. Soc. 142, 6103–6110 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Dunkle JA et al. Structures of the bacterial ribosome in classical and hybrid states of tRNA binding. Science 332, 981–984 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Arenz S et al. A combined cryo-EM and molecular dynamics approach reveals the mechanism of ErmBL-mediated translation arrest. Nat. Commun. 7, 12026 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Sharma AK et al. A chemical kinetic basis for measuring translation initiation and elongation rates from ribosome profiling data. PLoS Comput. Biol. 15, e1007070 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Fluitt A, Pienaar E & Viljoen H Ribosome kinetics and aa–tRNA competition determine rate and fidelity of peptide synthesis. Comput. Biol. Chem. 31, 335–346 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Eastman P et al. OpenMM 7: rapid development of high performance algorithms for molecular dynamics. PLoS Comput. Biol. 13, e1005659 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Nagano N EzCatDB: the enzyme catalytic-mechanism database. Nucleic Acids Res. 33, D407–D412 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Nagano N et al. EzCatDB: the enzyme reaction database, 2015 update. Nucleic Acids Res. 43, D453–D458 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.The UniProt Consortium. UniProt: the universal protein knowledgebase. Nucleic Acids Res. 46, 2699 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Berman HM et al. The Protein Data Bank. Nucleic Acids Res. 28, 235–242 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data supporting the main findings of this study are available within the Article and its Supplementary Information and source data files. We cannot feasibly provide all ~5.3 TB of molecular dynamics trajectory data, but we provide the input data that were used to perform the simulations in this study in the repository subdirectory https://github.com/obrien-lab/cg_simtk_protein_folding/blob/master/example/input_data.tar.xz. All of the data that support the findings of this study, as well as the biological materials that were used to test the enzymatic activity of the DDLB and DHFR variants and for the LiP-MS experiments, are available from the corresponding author upon reasonable request. The raw mass spectrometry data for DDLB and DHFR have been deposited to the ProteomeXchange Consortium via the PRIDE partner repository with the dataset identifier PXD031425. A website (https://obrien-lab.github.io/visualize_entanglements/) was created to provide interactive visualization of the key misfolded, entangled structures predicted in this study. Source data are provided with this paper.


