A log rank test for clustered data with informative within-cluster group size

Abstract

The log rank test is a popular nonparametric test for comparing survival distributions among groups. When data are organized in clusters of potentially correlated observations, adjustments can be made to account for within-cluster dependencies among observations, eg, tests derived from frailty models. Tests for clustered data can be further biased when the number of observations within each cluster and the distribution of groups within cluster are correlated with survival times, phenomena known as informative cluster size and informative within-cluster group size. In this manuscript, we develop a log rank test for clustered data that adjusts for the potentially biasing effect of informative cluster size and within-cluster group size. We provide the results of a simulation study demonstrating that our proposed test remains unbiased under cluster-based informativeness, while other candidate tests not accounting for the clustering structure do not properly maintain size. Furthermore, our test exhibits power advantages under scenarios in which traditional tests are appropriate. We demonstrate an application of our test by comparing time to functional progression between groups defined initial functional status in a spinal cord injury data set.

1 ∣. INTRODUCTION

In many applications in survival analysis, data are organized in clusters within which survival times may be correlated. For example, an analyst may examine the time to the onset of tooth decay for individuals in a certain population. Time to onset is measured for multiple teeth within each individual, and in the context of clustered data, the individuals form the clusters and the teeth the potentially dependent observations within clusters. If there is interest in comparing the survival distribution among groups, say, upper and lower teeth in our hypothetical example, clearly traditional i.i.d. methods such as the popular log rank test are invalidated. The dependence among observations can be handled by stratification by cluster or by including cluster or frailty terms in a proportional hazards regression model, corresponding to a generalized estimating equations (GEEs) and mixed effects approach to handling within-cluster correlation, respectively. In such marginal analyses, the clusters form the primary units of analysis, for example, patients, and the observations within cluster are generally replicate measurements of the outcome in question.

An additional problem can present when the number of observations per cluster, termed the cluster size, is nonconstant across clusters. In some applications, cluster size can be associated with the random variable of interest, a phenomenon referred to as informative cluster size. For example, individuals with poor dental health are more likely to experience tooth decay and tooth loss. Such individuals are thus more likely to experience shorter times to the onset of tooth decay and have fewer teeth available to be measured. A marginal analysis of the time to onset of tooth decay may be able to account for dependencies among teeth within individuals but can give positively biased estimates of the survival distribution of the time to onset of tooth decay, since individuals tending to have shorter onset times may also have fewer teeth and thus contribute fewer observations to the overall data set.

Hoffman et al¹ introduced a Monte Carlo method known as within-cluster resampling (WCR) that is resistant to the biasing effects of informative cluster size in the marginal analysis of clustered data. WCR operates by randomly selecting single observations from each cluster with equal probability to form resampled data sets, which are i.i.d. under the assumption of independent clusters. Traditional i.i.d. methods, like the log rank test, can be applied to the resampled data set, and the process repeated many times to produce a WCR test statistic averaged over all Monte Carlo runs. Hoffman et al¹ demonstrated that this approach was resistant to the biasing effects of informative cluster size. Williamson et al² developed an approach asymptotically equivalent to WCR that does not require Monte Carlo resampling, referred to as cluster-weighted averaging. In this approach, the traditional i.i.d. methods applied to the resampled data sets are weighted by the inverse of the cluster size and applied to the entire data set. This approach has since been used to develop clustered data analogs of the proportional hazards models for survival data,^3,4 one- and two-sample Wilcoxon tests,^5,6 and estimators of correlation coefficients^7,8 among others.

Huang and Leroux⁹ detailed another type of informativeness for clustered data in which the within-cluster distribution of an explanatory covariate, particularly a categorical factor indicating group membership, is correlated with the outcome of interest. Such informativeness potentially biases not only traditional methods for clustered data, like GEE, but also methods adjusting for informative cluster size like WCR and within-cluster averaging. Huang and Leroux⁹ suggested a modified WCR procedure in which first a group defined by the categorical factor is randomly selected with equal probability from among all possible groups in a given cluster. Then, an observation is randomly selected with equal probability from the set of observations corresponding to the group selected in the first step. The resampled data set is built in this fashion and the WCR procedure continues as before. The authors also introduced asymptotically equivalent doubly weighted GEEs for estimation under this type of informativeness that eliminated the need for Monte Carlo resampling. In the context of hypothesis testing for comparing groups, we term informativeness of this type informative within-cluster group size. Dutta and Datta¹⁰ referred to it as “informative intra-cluster group size” and developed multisample rank sum tests for clustered data resistant to it.

In this paper, we develop a weighted log rank test for right-censored, clustered survival data that remains unbiased under informative cluster size and within-cluster group size. In the Section 2, we introduce our notation, define and comment upon the hypothesis to be tested, detail the adapted WCR approach to testing the appropriate null hypothesis, and derive our weighted log rank test. In the Section 3, we provide the results of a simulation study to evaluate our proposed test and compare its performance to the traditional, stratified, cluster-weighted, and frailty approaches to testing. We also apply our test statistic to compare time to functional progression in a data set of spinal cord injured individuals. We offer concluding remarks in the Section 4.

2 ∣. METHODS

We develop our proposed log rank test statistic for clustered data under informative within-cluster group size. For simplicity, we develop our test statistic for comparing two groups. The extension to more than two groups is straightforward, details of which are provided in the Appendix.

Let $M$ be the number of clusters. The $j\text{th}$ survival and censoring times in cluster $i$ are $T_{ij}$ and $C_{ij}$. We observe $(X_{ij},{\delta }_{ij})$, where $X_{ij}=\text{min}\{T_{ij},C_{ij}\}$ and ${\delta }_{ij}=I[T_{ij}\le C_{ij}]$ is the event indicator. Denote the two groups to be compared as Group 0 and Group 1, and let $G_{ij}$ be an indicator variable for membership in Group 1. The size of cluster $i$ is denoted by $n_i$, and let $n_{i0}$, and $n_{i1}$ denote the number of Group 0 and Group 1 observations in cluster $i$, respectively. The data for cluster $i$ are denoted as ${\mathbf{V}}_i=\{n_i,X_{ij},{\delta }_{ij},G_{ij},1\le i\le n_i\}$. We note that, under this structure, the cluster sizes, group indicators, and, by extension, within-cluster group sizes are considered to be random, potentially associated with the survival times, $T_{ij}$. We assume that the clusters are independent.

We will test the null hypothesis that the marginal survival functions in the two groups are equal

$$H_0:S_0(t)=S_1(t)(=S(t)\text{say})\text{for all}t,$$ (1)

where $S_k(t)=P[T_{ij}>t\mid G_{ij}=k]$. Dutta and Datta¹⁰ provide a thorough discussion of different ways in which the common distribution defined by the null hypothesis ($S(t)$ in our case) can be empirically estimated, and how these different constructions imply comparisons of different marginal quantities. In brief, the common survival function of $H_0$ can be defined as (1) that of a typical observation in the population of all observations, (2) that of a typical observation from a typical cluster, where “typical” is defined by the observed within-cluster group size, and (3) that of a typical observations from a typical cluster where “typical” is defined by assuming equal representation of groups within each cluster. In many settings, these three marginal distributions coincide and the null hypotheses are equivalent. Notably, when cluster size and/or the within-cluster group size are informative, the null hypotheses do not coincide. In what follows, we focus on the third of the aforementioned marginal survival distributions.

Initially, we will consider only clusters with complete within-cluster group structure but will extend the statistic to account for incomplete structures. We begin by considering the modified WCR scheme of Dutta and Datta.¹⁰ From cluster $i$, we randomly select one of the two groups (0 or 1) with equal probability 1/2 and denote this resampled group indicator $G_i^{\ast }$. Then, from the observations in cluster $i$ belonging to group $G_i^{\ast }$, we randomly select a survival time and its event indicator and denote this pair $(X_i^{\ast },{\delta }_i^{\ast })$. We do this for each cluster to create a resampled data set $(X_i^{\ast },{\delta }_i^{\ast },G_i^{\ast }),1\le i\le M$. Since clusters are assumed to be independent, this resampled data set is i.i.d. Furthermore, any informativeness in the within-cluster group size for survival times is marginalized by the selection of groups within-cluster with equal probability. The traditional log rank test can then be applied to the resampled data set. Let the counting process for observed failures in group $k=0,1$ in the resampled data set be $N_k^{\ast }(t)={\sum }_{i=1}^{M}I[X_i^{\ast }\le t,{\delta }_i^{\ast }=1,G_i^{\ast }=k]$, and let the at risk process from group $k$ be $Y_k^{\ast }(t)={\sum }_{i=1}^{M}I[X_i^{\ast }\ge t,G_i^{\ast }=k]$. Define the aggregated failure and at risk processes as $N^{\ast }(t)=N_0^{\ast }(t)+N_1^{\ast }(t)$ and $Y^{\ast }(t)=Y_0^{\ast }(t)+Y_1^{\ast }(t)$. The log rank test statistic for the resampled data is then

$$Z_1^{\ast }(t)=\underset{0}{\overset{t}{\int }}\mathrm{d}{N}_1^{\ast }(s)-\frac{Y_1^{\ast }(s)}{Y^{\ast }(s)}\mathrm{d}{N}^{\ast }(s).$$ (2)

The estimated variance of $Z_1^{\ast }(t)$ denoted ${\widehat{\sigma }}^{{\ast }^2}(t)$, can be calculated in the usual way (see, for example, the work of Andersen et al¹¹). $H_0$ is rejected if $Z_1^{\ast }{(t)}^2∕{\sigma }^{{\ast }^2}(t)$ is greater that ${\chi }_{1,1-\alpha }^2$. However, this procedure makes inefficient use of the data, using only one observation from each cluster, so the WCR approach repeats the resampling procedure many times, averages the test statistics $Z_1^{\ast }(t)$ over the replicate resampled data sets, calculates a variance expression for the averaged test statistic developed by Hoffman et al,¹ and then compares to the chi-square distribution to accept or reject $H_0$.

To avoid the computational expense and randomness of WCR, we can employ an asymptotically equivalent conditional expectation calculation first introduced by Williamson et al² and adapted by Huang and Leroux⁹ and Dutta and Datta¹⁰ for informative within-cluster group sizes. In particular, we calculate the conditional expectation of the counting and at risk processes for the resampled data, given the original data

$$\begin{gathered} {\widehat{N}}_k(t)=E\left[N_k^{\ast }(t)\mid \{{\mathbf{V}}_1,\dots ,{\mathbf{V}}_M\}\right] \\ =\sum _{i=1}^M\sum _{j=1}^{n_i}\frac{1}{2n_{ik}}I[X_{ij}\le t,{\delta }_{ij},G_{ij}=k] \\ =\sum _{i=1}^M\sum _{j=1}^{n_i}{\omega }_{ik}I[X_{ij}\le t,{\delta }_{ij},G_{ij}=k] \\ {\widehat{Y}}_k(t)=E\left[Y_k^{\ast }(t)\mid \{{\mathbf{V}}_1,\dots ,{\mathbf{V}}_M\}\right] \\ =\sum _{i=1}^M\sum _{j=1}^{n_i}\frac{1}{2n_{ik}}I[X_{ij}\ge t,G_{ij}=k] \\ =\sum _{i=1}^M\sum _{j=1}^{n_i}{\omega }_{ik}I[X_{ij}\ge t,G_{ij}=k], \end{gathered}$$

where, for convenience, we have defined the weights ${\omega }_{ik}={(2n_{ik})}^{-1}$. These equalities are informally verified by considering the WCR procedure. Within each cluster, groups are selected with uniform probability 1/2, and then observations are selected with uniform probability $1∕n_{ik}$, with $k$ representing the group having been selected. We apply the WCR procedure to each of the counting and at risk processes, rather than the test statistic itself although the two are asymptotically equivalent. Define the aggregated counting processes $\widehat{N}(t)={\widehat{N}}_0(t)+{\widehat{N}}_1(t)$ and $\widehat{Y}(t)={\widehat{Y}}_0(t)+{\widehat{Y}}_1(t)$. We define our log rank test statistic for clustered data to be

$${\widehat{Z}}_1(t)=\underset{0}{\overset{t}{\int }}\mathrm{d}{\widehat{N}}_1(s)-\frac{{\widehat{Y}}_1(s)}{\widehat{Y}(s)}\mathrm{d}\widehat{N}(s).$$ (3)

The variance of ${\widehat{Z}}_1(t)$ can be estimated by jackknife. Let ${\widehat{Z}}_{1(-i)}$ be the value of ${\widehat{Z}}_1$ calculated with data from cluster $i$ removed. Let ${\widehat{Z}}_{1(i)}^d={\widehat{Z}}_1-{\widehat{Z}}_{1(-i)}$ and ${\widehat{Z}}_1^d=M^{-1}{\sum }_{i-1}^M{\widehat{Z}}_{1(i)}^d$. We estimate the variance of ${\widehat{Z}}_1(t)$ by

$${\widehat{\sigma }}^2(t)=\text{Var}\left({\widehat{Z}}_1(t)\right)=\frac{M}{M-1}\sum _{i=1}^M{\left({\widehat{Z}}_{1(i)}^d-{\widehat{Z}}_1^d\right)}^2.$$ (4)

Under appropriate conditions, we expect ${\widehat{Z}}_1{(t)}^2∕{\widehat{\sigma }}^2(t)$ to follow a ${\chi }_1^2$ distribution that can be used in the usual way to accept or reject $H_0$.

For data with incomplete within-cluster group structure, we utilize the modified WCR procedure and conditional expectation calculation described by Dutta and Datta.¹⁰ When both groups are represented in a given cluster, resampling for that cluster proceeds as before. If only 1 of the 2 groups is represented, that group is “selected” with probability 1, and a single observation from that particular group is selected with uniform probability. Under this resampling procedure, the conditional expectations of the resampled data counting processes $N_k^{\ast }(t)$ and $Y_k^{\ast }(t)$, and thus, the weights ${\omega }_{ik}$ assigned to observations in ${\widehat{N}}_k(t)$ and ${\widehat{Y}}_k(t)$ change. It is not difficult to see, that under this modified resampling scheme,

$${\omega }_{ik}=\{\begin{array}{cc}{(2n_{ik})}^{-1},\hfill & \text{if}{n}_{i0}>0,n_{i1}>0\hfill \\ n_{ik}^{-1},\hfill & \text{if}{n}_{i{k}^{\prime }}=0,k^{\prime }\ne k\hfill \\ 0,\hfill & \text{if}{n}_{ik}=0.\hfill \end{array}\phantom{\}}$$ (5)

Essentially, observations are weighted by one-half of the inverse of the within-cluster group sizes when both clusters are represented, the inverse of the within-cluster group size when only the group being counted is represented, and 0 when the group being counted is not represented. The test statistics can be constructed according to formula (3) and variance calculated by the same jackknife procedure described above. We evaluate our test statistic via simulation in the next section.

3 ∣. RESULTS

We evaluated the performance of our cluster-weighted log rank test by conducting a simulation study and applying the test to a SCI data set featuring clustering. The results of each are detailed in the following sections.

3.1 ∣. Simulation study

Our simulation study included two designs, one with complete within-cluster group structure and one with incomplete within-cluster group structure. In each design, both the distribution of groups within each cluster and the survival times were a function of some latent factor, inducing informativeness in the within-cluster group size. We compared the size and power of five candidate tests: (1) the log rank test, (2) the log rank test stratified by cluster, (3) an inverse cluster size weighted log rank test, (4) the inverse within-cluster group size weighted test statistic developed above, and (5) the test of the group indicator coefficient from a Cox model with gamma frailty parameter. We note that the inverse cluster size weighted log rank test statistic for group $k$ can be defined as

$${\overline{Z}}_1(t)=\underset{0}{\overset{t}{\int }}\mathrm{d}{\overline{N}}_1(s)-\frac{{\overline{Y}}_1(s)}{\overline{Y}(s)}\mathrm{d}\overline{N}(s),$$

where the counting processes ${\overline{N}}_k(t)$ and ${\overline{Y}}_k(t)$ are defined analogously to ${\widehat{N}}_k(t)$ and ${\widehat{Y}}_k(t)$ from Section 2, but with weights ${\omega }_{ik}=n_i^{-1}$. In both designs, we evaluated the performance of these test statistics in comparing two groups for $M=30,50$, and 100 clusters. We calculated the size and power of each test as the proportion of rejections of the null hypothesis over 3000 Monte Carlo iterations.

In the first design, we adapted a simulation design featuring informative cluster size for survival data³ to additionally feature an informative within-cluster group size. Survival times were generated according to a frailty model parameterized as $\lambda (t\mid G_{ij},w_i)={\lambda }_0(t)w_i\text{exp}(\beta G_{ij})$, where ${\lambda }_0(t)$ represents the baseline hazard, $G_{ij}$ represents the Group 1 indicator, $w_i$ represents the frailty parameter for cluster $i$, and $\beta$ represents the regression parameter. For each cluster, we simulated a frailty parameter, $w_i$, according to the positive stable distribution¹² with correlation parameter 0.5, inducing moderate correlation among within-cluster survival times. The size of each cluster, $n_i$, was defined to be $c_1$ if $w_i>\text{Med}(w_1,\dots ,w_n)$ and $c_2$ otherwise. The pair $(c_1,c_2)$ was chosen in different simulations to be (10, 10), (15, 5), and (5, 15), reflecting no association, negative association, and positive association between cluster size and survival times, respectively. Group membership (0 or 1) within each cluster was simulated from the $\text{BIN}(1,p)$ distribution, where $p$ was chosen in different simulations to be $0.5$, $1-(\text{rank}(w_i)-0.5)∕M$, and $(\text{rank}(w_i)-0.5)∕M$. Under $p=0.5$, there was no informativeness of the within-cluster group size. For $p=1-(\text{rank}(w_i)-0.5)∕M$, clusters with longer survival times tended to have more observations from Group 1. For $p=(\text{rank}(w_i)-0.5)∕M$, clusters with shorter survival times tended to have more observations from Group 1. In clusters having membership from only 1 of the two groups, we switched the group status of one randomly selected observation to ensure a complete intra-cluster group structure. Survival times were then generated as $t_{ij}=\frac{-\text{ln}(u)}{{\lambda }_0(t)w_i\text{exp}(\beta G_{ij})}$, where ${\lambda }_0=0.25$, and $\beta$ ranged over 0, 0.2, 0.4, 0.6, and 0.8. Censoring times $c_{ij}$ were generated in each configuration from the $\text{UNIF}(0,D)$ distribution, with $D$ selected so that approximately 25% and 50% of observations were censored in each combination of simulation parameters.

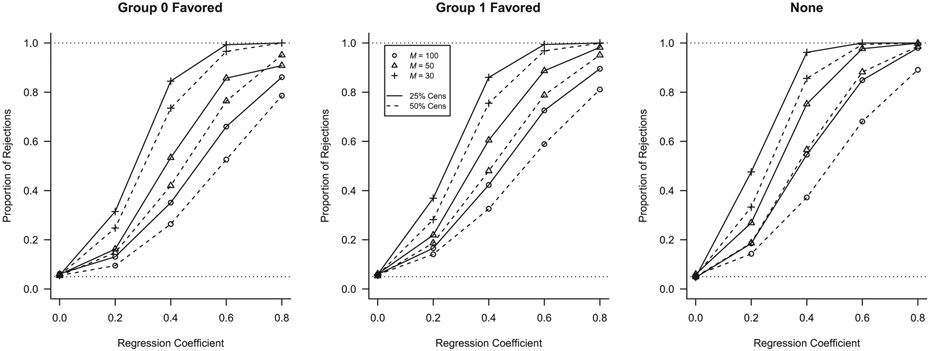
Table 1 provides the results of several of the parameter configurations for a small number of clusters $(M=30)$ and heavy censoring (50%). Both the traditional and cluster-weighted log rank tests were heavily biased when the within-cluster group size was informative, rejecting the null hypothesis in nearly all iterations in which the null hypothesis was true. Furthermore, these tests exhibited counterintuitive behavior with regard to regression parameter $\beta$, as power actually decreased for both tests as $\beta$ increased. The frailty model test was biased under cluster- and group-size informativeness, but to a far lesser degree than the log rank and cluster-weighted log rank tests. We briefly note that other distributions commonly used for frailty parameter failed to correct for informativeness as well (results not shown). The stratified log rank test and our group-weighted log rank test exhibited appropriate size under all settings and appropriate behavior with respect to $\beta$. All tests were approximately unbiased when the within-cluster group size was not informative. The stratified log rank test and frailty model test exhibited power advantages over other tests under no informativeness, and the stratified test was more powerful than our test under all configurations. Figure 1 illustrates that our new log rank test exhibited appropriate behavior with respect to the number of clusters and the censoring rate. Additional tables and figures containing results for this simulation design can be found in the online supplementary material for this manuscript.

TABLE 1.

Estimates of size and power for three log rank tests under simulation design 1 with $M=30$ clusters and heavy (50%) censoring. Positive/Negative cluster size informativeness indicates that larger/smaller clusters tended to have longer survival times. Group size informativeness indicates which group tended to be over-represented in clusters with longer survival times. LR = log rank, SLR = stratified log rank, CWLR = cluster size-weighted log rank, GWLR = group size-weighted log rank, and Frailty = frailty model

Informativeness			Power
Group Size	Cluster Size	Test	Size	$\beta =0.2$	$\beta =0.4$	$\beta =0.6$	$\beta =0.8$
None	None	LR	0.054	0.10	0.22	0.44	0.67
		SLR	0.048	0.16	0.49	0.83	0.97
		CWLR	0.061	0.11	0.22	0.42	0.64
		GWLR	0.055	0.14	0.37	0.68	0.89
		Frailty	0.045	0.17	0.50	0.84	0.98
	Positive	LR	0.044	0.09	0.23	0.45	0.67
		SLR	0.051	0.17	0.50	0.85	0.97
		CWLR	0.057	0.08	0.17	0.30	0.47
		GWLR	0.055	0.11	0.24	0.47	0.70
		Frailty	0.042	0.17	0.51	0.86	0.98
	Negative	LR	0.043	0.11	0.33	0.62	0.84
		SLR	0.050	0.16	0.48	0.81	0.96
		CWLR	0.055	0.10	0.26	0.48	0.69
		GWLR	0.055	0.16	0.47	0.78	0.95
		Frailty	0.057	0.16	0.50	0.84	0.97
Group 0	None	LR	1.000	1.00	1.00	1.00	1.00
		SLR	0.058	0.13	0.36	0.70	0.90
		CWLR	1.000	1.00	1.00	1.00	1.00
		GWLR	0.055	0.10	0.26	0.53	0.79
		Frailty	0.095	0.29	0.61	0.89	0.97
	Positive	LR	1.000	1.00	1.00	1.00	1.00
		SLR	0.052	0.11	0.35	0.63	0.85
		CWLR	0.994	1.00	1.00	1.00	1.00
		GWLR	0.057	0.08	0.20	0.37	0.60
		Frailty	0.074	0.23	0.53	0.79	0.95
	Negative	LR	1.000	1.00	1.00	1.00	1.00
		SLR	0.045	0.14	0.41	0.75	0.93
		CWLR	1.000	1.00	1.00	1.00	1.00
		GWLR	0.053	0.11	0.33	0.59	0.85
		Frailty	0.097	0.32	0.68	0.91	0.98
Group 1	None	LR	1.000	1.00	1.00	0.99	0.97
		SLR	0.051	0.13	0.37	0.70	0.91
		CWLR	1.000	1.00	0.98	0.94	0.83
		GWLR	0.058	0.14	0.33	0.59	0.81
		Frailty	0.090	0.07	0.22	0.54	0.81
	Positive	LR	1.000	1.00	0.98	0.95	0.86
		SLR	0.053	0.15	0.38	0.67	0.89
		CWLR	1.000	0.98	0.94	0.87	0.72
		GWLR	0.052	0.12	0.25	0.46	0.63
		Frailty	0.075	0.08	0.25	0.52	0.78
	Negative	LR	1.000	1.00	0.97	0.86	0.64
		SLR	0.048	0.14	0.43	0.73	0.94
		CWLR	1.000	1.00	0.98	0.89	0.72
		GWLR	0.066	0.16	0.40	0.67	0.88
		Frailty	0.093	0.07	0.25	0.57	0.85

FIGURE 1.

Power corves for the proposed within-cluster group size weighted log rank test at different sample sizes and censoring rates under noninformative cluster size. Clusters with longer survival times had over-representation from Group 0 (left panel), over-representation from Group 1 (center), or equal group representation (right)

In the second design, we adapted a simulation design utilized to evaluate a nonparametric rank sum test under informative within-cluster group size.¹⁰ Briefly, we simulated bivariate random effects, $(a_{i0},a_{i1})$, for each cluster from a bivariate normal distribution with mean zero, standard deviation equal to 0.25, and correlation equal to 0. Within-cluster group sizes were then generated as $n_{i0}\sim \text{POI}(10+{5a}_{i0}^2)$ and $n_{i1}\sim \text{POI}(10+5a_{i1})$, and $n_i=n_{i0}+n_{i1}$. The group indicator $G_{ij}$ was defined in each cluster so that $n_{i0}$ observations were in Group 0 and $n_{i1}$ in Group 1. We note that clusters with incomplete group structure were permitted under this design. We then simulated survival times $T_{ij}=\text{exp}\left(0.5+\delta \ast G_{ij}+a_{i{G}_{ij}}+{ϵ}_{ij}\right)$, where the effect size parameter $\delta$ took values 0, 0.05, 0.10, and 0.15 and the ${ϵ}_{ij}$ were i.i.d. $N(0,{0.3}^2)$. Censoring times were again generated from the $\text{UNIF}(0,D)$ distribution, with $D$ selected under each configuration of simulation parameters so that approximately 25% and 50% of observations were censored.

Table 2 provides the results for this simulation design. Our group-weighted log rank test continued to maintain size fairly well and to exhibit appropriate behavior with regard to censoring rates and the number of clusters. The size of the cluster-weighted test was different than the nominal size, while the traditional, stratified, and frailty model tests exhibited sizes that were substantially different from the targeted size of 0.05.

TABLE 2.

Estimates of size and power for three log rank tests under simulation design 2. LR = log rank, SLR = stratified log rank, CWLR = cluster size-weighted log rank, GWLR = group size-weighted log rank, and Frailty = frailty model

$\mathit{N}$	Censoring	Test	Size	Power
				$\delta =0.05$	$\delta =0.10$	$\delta =0.15$
30	Light	LR	0.318	0.470	0.716	0.865
		SLR	0.307	0.435	0.684	0.854
		CWLR	0.076	0.148	0.337	0.567
		GWLR	0.058	0.110	0.281	0.509
		Frailty	0.349	0.494	0.743	0.892
	Heavy	LR	0.370	0.534	0.745	0.900
		SLR	0.337	0.495	0.720	0.887
		CWLR	0.082	0.167	0.354	0.576
		GWLR	0.057	0.140	0.297	0.532
		Frailty	0.381	0.542	0.774	0.922
50	Light	LR	0.390	0.653	0.879	0.974
		SLR	0.349	0.602	0.853	0.973
		CWLR	0.064	0.209	0.514	0.794
		GWLR	0.053	0.151	0.436	0.741
		Frailty	0.396	0.656	0.899	0.983
	Heavy	LR	0.339	0.609	0.846	0.961
		SLR	0.326	0.540	0.818	0.951
		CWLR	0.066	0.206	0.499	0.768
		GWLR	0.049	0.148	0.428	0.711
		Frailty	0.369	0.614	0.865	0.969
100	Light	LR	0.251	0.962	1.000	1.000
		SLR	0.044	0.819	1.000	1.000
		CWLR	1	1	1	1
		GWLR	1	1	1	1
		Frailty	0.076	0.898	1.000	1.000
	Heavy	LR	0.237	0.919	1.000	1.000
		SLR	0.052	0.702	0.999	1.000
		CWLR	1	1	1	1
		GWLR	1	1	1	1
		Frailty	0.074	0.821	1.000	1.000

3.2 ∣. Application

We applied our weighted log rank test to a spinal cord injury (SCI) data set featuring clustering of observations. The data are from participants in the Christopher and Dana Reeve Foundation’s NeuroRecovery Network (NRN), a network of treatment centers providing activity-based therapy to individuals with SCI.¹³ NRN participants receive regular sessions of standardized activity-based therapy and undergo comprehensive functional evaluations after approximately every 20 treatment sessions. One of the functional measurements taken at the periodic comprehensive functional evaluation is the Neuromuscular Recovery Scale (NRS), developed by NRN researchers to measure functional recovery without compensation.¹⁴ The NRS is administered by therapists and requires individuals with SCI to perform 14 functional tasks including postural changes, sitting, standing, and walking (Table 3). The therapist provides an ordinal rating called the phase of recovery for each task after observing the participant attempt to complete it. Phase 1 represents the lowest measure of capability and Phase 4 represents a return to pre-injury functional capacity. The NRS has been show to possess good reliability, validity, and responsiveness.^15-18

TABLE 3.

Functional tasks of the Neuromuscular Recovery Scale (NRS) administered to NeuroRecovery Network (NRN) patients, and enrollment distribution of phase classifications. Each item is measured on an ordinal scale referred to as the phase of recovery, which ranges from Phase 1 (most impaired) to Phase 4 (full recovery). NA = Not analyzed here

Category	NRS Tasks
Treadmill training	Stand adaptability Stand retraining (NA) Step adaptability Step retraining
Trunk control	Reverse sit up Trunk extension while sitting Sit upright Sit up
Lower extremity	Sit to stand Stand upright Walk
Upper extremity	Reach and grasp item (NA) Reach overhead (NA) Open door (NA)
Tasks Rated Phase 1	Tasks Rated Phase 2	Enrollment Frequency (%)
0	10	1 (1%)
1	9	3 (2%)
2	8	6 (3%)
3	7	8 (5%)
4	6	13 (7%)
5	5	20 (12%)
6	4	31 (18%)
7	3	36 (20%)
8	2	31 (18%)
9	1	23 (13%)
10	0	0 (0%)

Progression from one phase of recovery to the next is an important marker of functional recovery, so the time to progression to the next NRS Phase is an outcome of interest to clinicians. Our specific interest was in determining if the time to progression was different between tasks rated as NRS Phase 1 at enrollment (representing tasks with the most severe functional deficit) and tasks rated as Phase 2 at enrollment. In a marginal comparison as described above, our interest was in testing $H_0:S_1(t)=S_2(t)$, where $S_k(t)$ represents the survival function for NRS tasks measured to be Phase $k$ at enrollment.

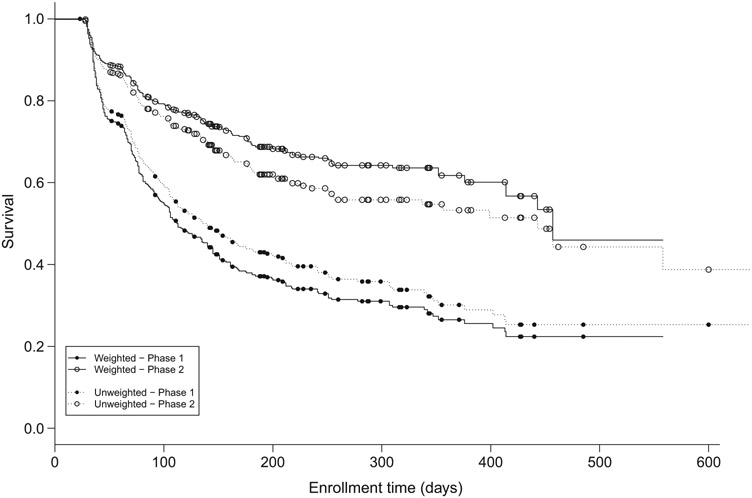
We considered 10 of the 14 NRS tasks (three upper extremity tasks were added to and one treadmill task removed from the NRS during data collection) for 172 NRN participants. In the context of clustered data, the 172 NRN participants defined the clusters and the times to progression for the 10 NRN tasks the observations within each cluster. Clearly, cluster size was fixed and thus noninformative, but the within-cluster group size, defined by the phase of recovery for each task at enrollment (1 or 2), was variable and thus potentially informative. Most of the 172 patients had five or more items initially rated in Phase 1 of recovery (141 (82%), Table 3), and one patient had an incomplete group structure with all items rated in Phase 2 at enrollment. Of the 1720 overall times to progression, 679 were observed to occur and 1041 were right censored. The maximum observed time to progression was 558 days and the maximum censored time 1191 days. Figure 2 plots Kaplan-Meier estimates of the survival functions for the time to progression to the next NRS phase for the two groups. The weighted estimators, which correspond to our weighted log rank test, were calculated as ${\widehat{S}}_k(t)={\prod }_{s\le t}(1-d{\widehat{N}}_k(s)∕{\widehat{Y}}_k(s))$ with ${\widehat{N}}_k(s)$ and ${\widehat{Y}}_k(s)$ defined as above. There were notable differences between our weighted estimated survival functions and the traditional Kaplan-Meier estimates in both groups.

FIGURE 2.

Estimated survival functions for time to time to progression to the next Neuromuscular Recovery Scale phase of recovery for spinal cord injured NeuroRecovery Network participants. The traditional Kaplan-Meier estimator is plotted as dotted lines and the weighted estimator as solid lines. The plot is truncated at 600 days; the last observed progression time was 585 days and the last censored time 1191 days

We calculated our weighted log rank test statistic for comparing these two groups to be $X^2=94.3$. Compared against the critical value of ${\chi }_1^2(.95)=3.84$, this indicated a substantial difference in time to progression between groups. Figure 2 makes clear that progression from Phase 1 to Phase 2 occurred much more rapidly than progression from Phase 2 to Phase 3. A possible clinical explanation for this is that the functional gains required for progression from Phase 1 to Phase 2 may be less difficult to achieve for SCI individuals than those for progression from Phase 2 to Phase 3.

The unweighted log rank statistic for these data was $X^2=51.5$, while the stratified log rank test produced $X^2=112.0$. The test of the group coefficient from a gamma frailty Cox model was $X^2=94.1$. Although all tests rejected $H_0$, the weighted, stratified, and frailty test statistics were notably larger. Figure 2 illustrates that this was potentially due to some informativeness in the within-cluster covariate distribution. The traditional Kaplan-Meier estimator overestimated survival for NRS items initially scored as Phase 1 relative to the weighted Kaplan-Meier estimator and underestimated survival for items initially scored as Phase 2, giving the appearance that the survival curves were closer together (although still significantly different).

4 ∣. DISCUSSION

When conducting a marginal analysis of clustered data, it is important not only to gage potential cluster-based informativeness but also to clarify the marginal analysis of interest. We explain in the context of our analysis of the SCI data in Section 3. Our marginal analysis showed that the time to progression from Phase 1 to Phase 2 was shorter than the time to progression from Phase 2 to Phase 3. Recall that the clusters in this marginal analysis were individuals with SCI and the observations within cluster were individual tasks on the NRS. Thus, we conclude that a typical NRS task initially measured as Phase 1 from a typical individual with SCI will progress to Phase 2 more quickly than a typical NRS task initially measured as Phase 2 from a typical individual with SCI will progress to Phase 3. As previously noted, our analysis implicitly assumes “typical” to mean equitable representation of tasks initially measured as Phase 1 and Phase 2. Furthermore, it is important to keep in mind that in these marginal analyses, the cluster, ie, the patient in many applications, forms the primary unit of analysis and the observations within cluster are replicate measurements. Because of this and since our test statistic is asymptotically normal, it is important to note that the reliability of the test hinges in part on having a sufficient number of clusters, rather than observations. Our simulations indicate that the test performs reasonably well for samples with as few as 30 clusters.

Of course, other marginal analyses for this and other clustered survival data are possible. Two alternatives also noted in Section 2 define different marginal analysis based on different conceptions of a “typical” observation. One alternative considers the marginal survival distribution of typical observations in the population of all observations, corresponding to a GEE approach. Another alternative also considers typical observations from typical clusters but defines typical to correspond to the observed within-cluster distribution of groups or other potentially explanatory covariates. As previously noted,^8-10,19 these marginal analyses often coincide, particularly when there are no concerns of informativeness. Our simulation results suggest that our weighted log rank test performs better than the traditional log rank test or a clustered averaged log rank test when cluster size and within-cluster group size are noninformative but may be less powerful than stratified and frailty model-based approaches. However, the traditional, cluster-weighted, and frailty model-based tests were biased under our first simulation design when cluster and/or within-cluster group size was informative. The log rank test stratified by cluster remained unbiased under all configurations of our first simulation design and exhibited a clear power advantage over all tests, including our within-cluster group size weighted test. However, under our second simulation design, the stratified log rank test and all other competitor tests were biased, while our test remained approximately unbiased. We briefly note that the informative cluster-averaged log rank test evaluated in Section 3 can be obtained from the cluster-weighted proportional hazards methodology developed by Cong et al,³ but as demonstrated here, this test would fail to maintain the targeted nominal size under informative within-cluster group size.

Other approaches to this particular data set and clustered survival data in general are possible. One may be interested in estimating the multivariate survival distribution of the 10 NRS tasks among groups defined by an external covariate. Given that the NRS tasks measure different aspects of patient function and recovery, one may be interested in the specific NRS tasks themselves and perhaps comparing univariate survival distributions for specific tasks among groups. A competing risks analysis would be a reasonable approach if one were interested in examining the time to first progression and identifying NRS tasks typically showing first progression. It should be noted that this is not a true competing risks setup because time to progression for other NRS tasks remains observable even after observation of the first progression on an NRS task. Nevertheless, it remains that there are many approaches to analyzing clustered survival data, and analysts should be clear on the purpose of their analyses and implications of their results.

Seaman et al¹⁹ provide a thorough discussion of the nuances involved in the analysis of clustered data and clarify the relationship between informativeness in cluster size and missingness of observations. Furthermore, they outline conditions of informativeness and missingness under which different marginal analyses of clustered data coincide, and when they differ, with particular focus on weighted versions of GEE models and modified random effects models. The paper provides a number of technical results and an example analysis of a clustered data set for illustration. The authors conclude that their is an inherent danger of misinterpreting results from marginal analyses of clustered data and recommend careful thought be given to the marginal analysis of interest and the selection of the method appropriate for the analysis of interest.

Standard software routines implementing the Cox proportional hazards model can be use to obtain an approximate version of our proposed test. For example, in the survival library^20,21 of the R software environment,²² a Cox proportional hazards model can be specified with a single group-membership covariate, a clustering term to identify clusters of correlated observations and induce a robust sandwich variance estimate (which closely approximates the jackknife variance estimate suggested above) and case weights equal to the appropriate ${\omega }_{ik}$ defined above. The resulting test of the estimated coefficient for the group membership covariate approximates our proposed testing procedure detailed above and provides a more computationally efficient way of estimating variance.