Topography Driven Surface Renewal

Abstract

Natural surfaces excel in self-renewal and preventing bio-fouling, while synthetic materials placed in contact with complex fluids quickly foul [1, 3]. We present a novel biophysics inspired mechanism [4, 5] for surface renewal using actuating surface topography, generated by wrinkling. We calculate a critical surface curvature, given by an intrinsic characteristic length scale of the fouling layer that accounts for its effective flexural or bending stiffness and adhesion energy, beyond which surface renewal occurs. The effective bending stiffness includes the elasticity and thickness of the fouling patch, but also the boundary layer depth of the imposed wrinkled topography. The analytical scaling laws are validated using finite element simulations and physical experiments. Our data span over five orders of magnitude in critical curvatures and are well normalized by the analytically calculated scaling. Moreover, our numerics suggests an energy release mechanism whereby stored elastic energy in the fouling layer drives surface renewal. The strategy is broadly applicable to any surface with tunable topography and fouling layers with elastic response.

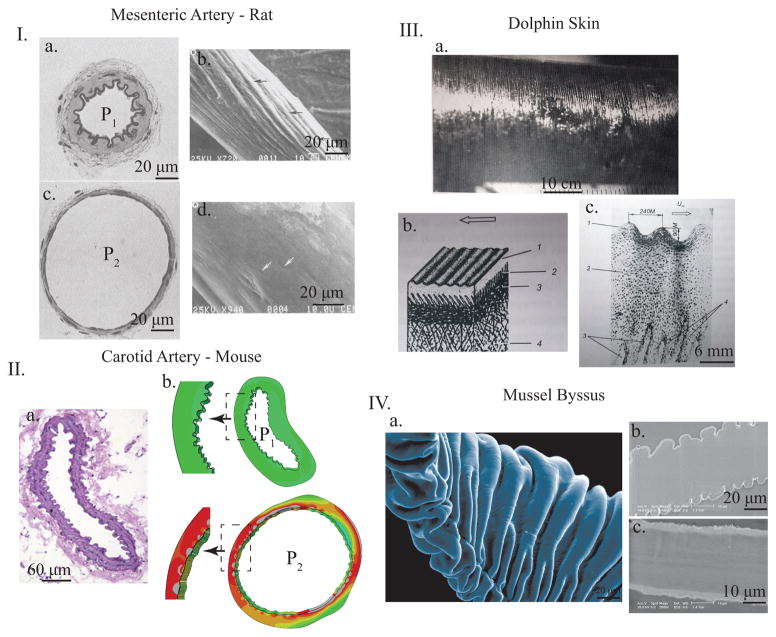
Natural surfaces, such as the inner lining of arteries, are far superior at resisting unwanted fouling as compared to artificial surfaces [1, 2]. For decades material scientists have attacked the problem of fouling through chemical surface modification to reduce interfacial energy, however these strategies are not sufficiently general to create a sustainably non-fouling surface [2, 3]. Nature solves the problem of surface self-renewal by using a multi-scale approach [1, 3]. Inherently ‘living’ and molecular aspects of natural surfaces include a biochemical powerhouse of specialized interfacial cells such as the endothelium lining of blood vessels or epithelial cells on skin and hollow viscus organs [3]. On a more macroscopic level, many natural surfaces are endowed with non-flat surface texture or topography [4, 5]. Wrinkling, a continuous and smooth surface amplitude undulation [6–9], is one of the most ubiquitous topographic patterns observed in nature: arteries [5, 10, 11] (see figure 1I. and II.), lung surfactant [8], ureter [12], skin (see figure 1III.) [4, 13, 14], mussel byssus (see figure 1IV.) [5], intestines [15], and the brain [16]. Many of these wrinkling interfaces are also under constant threat of biofouling such as platelet/thrombus adhesion in arteries [10] or bacteria in the lung/ureter/skin and on marine surfaces [17, 18]. Furthermore, these natural surface topographies often change or actuate as a function of driving forces in the environment, such as the wrinkling and un-wrinkling of arteries with pulse pressure (see figure 1I. and II.) [11].

FIG. 1.

Representative images of wrinkling surfaces in various biologic systems. I. Muscular artery from rat mesentery. a. and c. show the fixed histology at low (P₁) and high (P₂) blood pressures while b. and d. show SEM images of silicone casts of similar non-fixed arteries at equivalent pressures to the histology slides. In both sets of images, it is apparent that wrinkle and fold patterns appear on the inside of the artery at lower pressures and disappear as the artery distends with higher pressure (adapted with permission from [11]). II a. Histology of mouse carotid artery with luminal (inner) wrinkling. b. and c. show numerical simulations where this exact artery geometry is pressurized, showing the smoothing out of luminal wrinkles with increasing luminal pressure, showing the generality of the mechanism. III. Dolphin skin with periodic macroscopic wrinkles (a.) and the representative histology (b.) and (c.), adapted with permission from [13]. IV. Mussel byssus showing the intricate external wrinkles with SEM (a.) and the two states of the byssus under different conditions wrinkles (b.) and flat (c.), adapted from [5].

Such surface topography can greatly improve antifouling characteristics and functionality [1, 2, 18–26]. In this paper, building upon the rich literature of non-linear surface elastic instabilities [27–30], we explore a new mechanism of antifouling in which actuation from a smooth to a wrinkled surface induces topography-driven delamination of films adhered to the surface. The surface remains undamaged during the entire process and hence repeated actuation yields a “self-renewing” surface that can prevent continued build-up of foulant. A combination of theory, simulations, and experiments show that surface curvature κ (which quantifies the local topography) couples to surface renewal through a general relationship κ_c ~ 1/ℓ_ec, where the intrinsic length scale ℓ_ec, calculated explicitly, depends on interfacial adhesion energy and the effective elastic bending response of an adhered layer, and κ_c is the threshold curvature to detach the fouling layer.

In general, a bilayer with a thin stiff membrane adhered to a thicker soft substrate under an applied strain ε wrinkles with two characteristic length scales, wavelength λ ~ h×(E_m/E_s)^1/3 and amplitude $A~\lambda \sqrt{\epsilon }$, where E_m is the membrane modulus, h is membrane thickness, and E_s the substrate modulus [6, 7]. The second relationship is the well known inextensibility condition [4, 8, 31]. Suppose now that to the flat or weakly wrinkled bilayer is adhered a softer patch of material with a modulus E_p and thickness t representing a bacterial film or platelet aggregate forming the nidus of a blood clot on an arterial surface. The foulant patch being softer than the membrane layer (E_m ≫ E_s ≳ E_p) means that the patch does not influence the mechanics of wrinkling set by the substrate and membrane (see Supplementary Information: SI 1.1-Wrinkled Topography and videos 1–5). The interfacial stability is initially dominated by the chemical interaction between the surface and the patch, defined through the adhesion energy γ [27–30]. As the bilayer begins to wrinkle, the topography, characterized by surface curvature defined as κ = A/λ², grows as amplitude increases with bilayer compression. At some critical amplitude A_c or, equivalently, critical curvature κ_c = A_c/λ², the adhered patch begins to delaminate from the wrinkled surface forming discrete blisters of length l and amplitude A_l that co-exist with still attached material (see figure 2). Moreover, once deadhesion nucleates, interfacial cracks spread beyond the initial failure zone inducing delamination of the entire patch (see SI videos 1–5). Since the wrinkling mechanics of the bilayer are preserved during this deadhesion process, one may stretch the surface back to its the original clean state, hence the term ‘a mechanically-renewing’ surface.

FIG. 2.

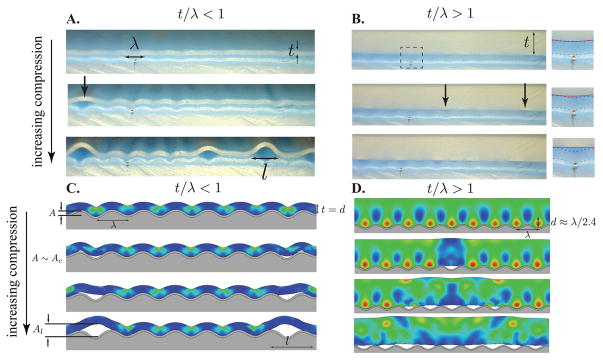
Representative images near A ~ A_c for thin-patch limit (A/C, t/λ = 0.25) and thick-patch limit (B/D t/λ = 1.25), for experimental soft silicone patches on wrinkling surfaces (top) and finite element simulations (bottom), see SI for details (SI 1.2-Silicone Patch Experiment, 1.3-FEA Simulation Methods, and 1.4-Elastic Energy Color Map). In the thin-patch limit, the patch conformally follows the wrinkling surface with strain energy distributed throughout its thickness. As A_c is approached, strain energy release through rotation off the surface into a less curved shape drives delamination (see SI videos 1 and 3). In the thick-patch limit, a boundary layer of increased strain energy exists near the wrinkled interface with a penetration length d ~ λ. As A_c is reached, the stored boundary layer energy is released driving patch detachment without much global rotation (see SI videos 2, 4, and 5). Inset in B shows zoom of patch/membrane interface: patch bottom (red line) and membrane top (blue line).

Using finite element analysis (FEA) and silicone patch experiments, we study the dependence of A_c on γ and the ratio of patch thickness to surface wavelength (t/λ), the dominant dimensionless parameter in the problem. Quasi-static simulations are performed using the ABAQUS dynamic explicit solver (Simulia, Dessault System, RI) (see SI 1.3-FEA Simulation Methods for simulation details). The patch (foulant), membrane, and substrate are modeled as hyperelastic materials under plainstrain conditions. Working within the general contact formulation of the explicit solver, a cohesive zone model (CZM) is used for the patch/membrane interface. The interfacial cohesive stress σ_coh is related to the adhesion energy density $\gamma ={\sigma }_{\text{coh}}{\delta }_{\text{coh}}=k_c{\delta }_{\text{coh}}^2$, where δ_coh is the interface thickness (initially δ_coh = 0 with a stress free interface and interfacial failure occurs when δ_coh = δ_critical) and k_c is the cohesive stiffness parameter [32]. Here we use γ×area as the interfacial adhesion energy between two materials. Physical experiments are carried out using silicone membranes, 250–3000 μm in thickness, adhered to initially flat bilayers, that upon compression wrinkle with a well defined wavelength λ = 1.5 mm (see figure 2A/B and SI 1.2-Silicone Patch Physical Experiments).

The measured critical amplitudes spread over five decades, with a general trend toward increasing critical amplitude with increasing adhesion energy, and decreasing critical amplitude with increasing ratio t/λ (see figure 3). Both trends are non-linear and follow a power law behavior. Moreover, the simulations and physical experiments show a strong cross-over behavior between ‘thin’ and ‘thick’ patches. For thin patches, those with t/λ < 1 (see figures 2A/C and red data in figure 3), the patch conformally follows the surface topography leading to build up of strain energy throughout the thickness of the patch. As patch thickness increases and becomes greater than the wrinkle wavelength, t/λ > 1 (see figures 2B/D and black data in figure 3), the strain energy is strongly concentrated in a near-interface boundary layer with the patch free surface remaining nearly undeformed and seemingly unaffected by the interfacial deformation field. In both cases, the simulations point toward an energy release mechanism whereby elastic energy stored in the patch drives interfacial crack propagation. As figure 2C/D and SI videos 3 and 4 show, interfacial failure is accompanied by a simultaneous decrease in local strain energy within the length of patch above the failed interface, l.

FIG. 3.

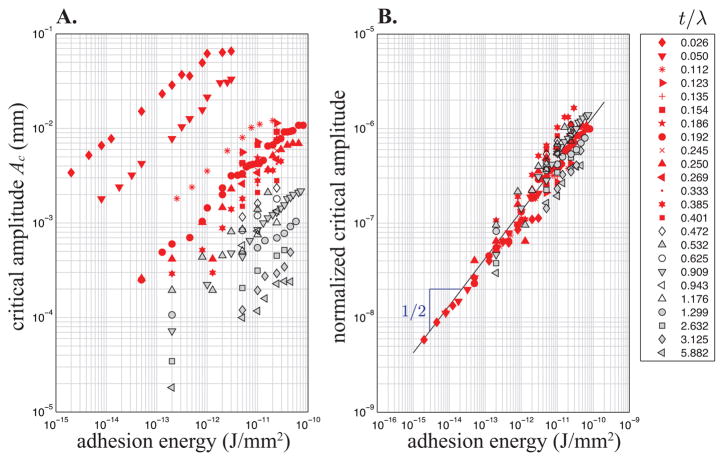
A. Log-log plot of A_c versus adhesion energy over a range of t/λ ratios, for E_p ≈ 30 kPa and ν_p ≈ 1/2 (E_m ≈ 1.23 GPa, E_s ≈ 15.8 MPa, ν_m ≈ ν_s ≈ 1/2). B. The over five decades of critical amplitudes are collapsed onto a master curve by normalization with the calculated theoretical scaling law $\sqrt{B_d}{A}_c/{\lambda }^2$ (see Eq. 1). Here the solid line represents the relation $c\times \sqrt{\gamma }$ where c ≈ 0.134 is obtained by fitting the thin patch data. In A and B open and gray symbols correspond to the thick limit t > λ/p with p ≈ 2.4.

In the theoretical analysis, we study the energetics of the patch and interface as the bilayer surface wrinkles. The effect of the wrinkling is imposed via a boundary condition along the interface (see SI 1.1-Wrinkled Topography). Assuming the deformation occurs quasi-statically, in the thin patch limit, bending energy dominates patch elasticity and is estimated as U_B = (B_p/2) ∫_S κ² dS ~ (B_p/2)(A/λ²)²S, where S = bL, L is system length, b its width, and $B_p=E_p{t}^3/12(1-{\nu }_p^2)$ is patch bending stiffness. Here ν_p is the Poisson ratio of the adhered material. As part of the patch (length l < L) de-adheres, the elastic energy gains two new contributions: the new bending energy of the detached region with smaller curvature $U_B^{\prime }~(B_p/2){(A_l/l^2)}^2{S}_l$ and the elastic energy dissipated during the transition: $U_B^{″}~(B_p/2){(A/{\lambda }^2)}^2{S}_l$, where S_l = bl is the area of detached interface. Thus, the available elastic energy in the system is $U_E~U_B+U_B^{\prime }-U_B^{″}$.

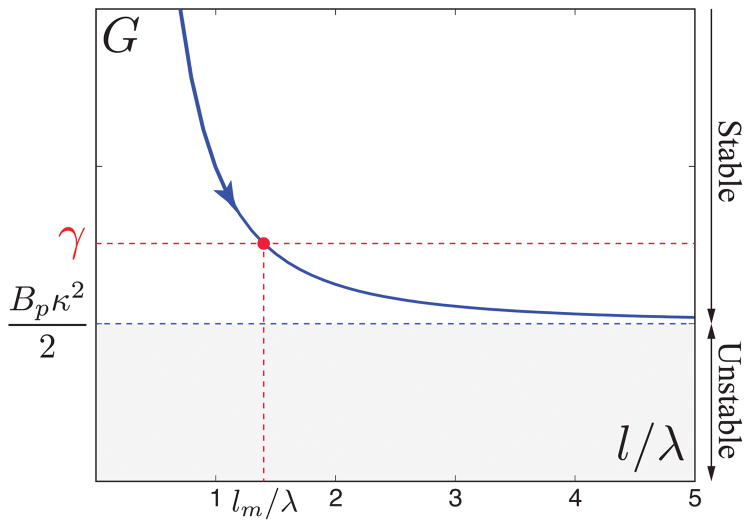
Since new surfaces are created during interfacial failure, the important function to study is the total energy U_E +γS_l. The possibility of having an equilibrium state requires the analysis of the condition ∂_lU_E +γb = 0 that can be studied by introducing the energy release rate G ≡ –∂_lU_E/b [33]. We obtain G ~ (B_pκ²/2)(1 + λ²/l²) a monotonically decreasing function of l (see figure 4). Note that the scaling analysis does not capture the exact form of the energy release function G for l/λ < 1, which must be bounded for small defects as it is observed in the simulations (see SI figure S3) [33].

FIG. 4.

Energy release rate as a function of the dimensionless fracture length l/λ. A patch with an initial detached length l increases its length to the equilibrium length l_m if B_pκ²/2 < γ (or $\kappa {\ell }_{ec}<\sqrt{2}$). For B_pκ²/2 ≥ γ (or $\kappa {\ell }_{ec}\ge \sqrt{2}$), G is always larger than the interfacial adhesion energy (gray region) and then the fracture propagates without arrest.

There is interfacial fracture while G > γ until the detached region grows to reach the condition G = γ and the equilibrium length $l_m/\lambda =1/\sqrt{2/{(\kappa {\ell }_{ec})}^2-1}$. Here ℓ_ec = (B_p/γ)^1/2 is an intrinsic length scale (see below), similar to an elastocapillary length, whose value depends on the particular physics dominating the elastic response of the adhered layer. Figure 4 shows that an equilibrium solution exists for B_pκ²/2 < γ (or $\kappa {\ell }_{ec}<\sqrt{2}$), but the system is unstable for any initial value of l if B_pκ²/2 ≥ γ (or $\kappa {\ell }_{ec}\ge \sqrt{2}$) when there is always available energy to produce fracture. Thus, the threshold condition for complete detachment corresponds to ${\kappa }_c{\ell }_{ec}=(A_c/{\lambda }^2){\ell }_{ec}=\sqrt{2}$. It defines the critical amplitude for patch deadhesion as $A_c~{(2\gamma /B_p)}^{1/2}{\lambda }^2=\sqrt{2}{\lambda }^2/{B_p}^{1/2}\times {\gamma }^{1/2}$. In figure 3B, we plot the critical simulation amplitudes normalized by λ²/B_p ^1/2; the red data points all collapse onto a single master curve given by c×γ^1/2, in agreement with the theoretical scaling analysis.

In the thick limit t ≫ λ, the increased thickness of the patch prevents energy release by pure rotation or bending. The simulations and experiments point toward a near-interface mechanism whereby only the strains near the bound interface are released (see figure 2B/D and SI videos 4 and 5). The elastic strain energy of a thick free slab is U₀ ~ E_pε²tS/2 where ε is the strain imposed and tS is the volume. However, near the wrinkled interface, the local strain energy is increased because of the extra surface deformation field which is proportional to ε_p ~ ∂_yu_x ~ A/λ. Similarly, the layer deformed by the wrinkled substrate has a volume d × S where d is a penetration length estimated as d ~ λ. Hence, the strain energy in the attached thick patch is $U_S~U_0+E_p{\epsilon }_p^2\lambda S/2$. Since the patch is thick, once a subset of length l detaches, it initially lacks sufficient freedom to bend and release the compressive strain by rotating, therefore it keeps its initial strain energy U₀. The new elastic energy is $~U_S-E_p{\epsilon }_p^2{S}_l\lambda /2$, where the last term gives the release of elastic energy because of fracture. We obtain for the energy release function $G=E_p{\epsilon }_p^2\lambda /2$ and the critical amplitude in the thick patch limit: A_c ~ λ²/(E_pλ³)^1/2 × γ^1/2.

The thin and thick scalings suggest that the critical amplitude can be written in general as $A_c={\lambda }^2/B_d^{1/2}\times c{\gamma }^{1/2}$, where c is the fit constant for the thin limit, $B_d=E_p{d}^3/12(1-{\nu }_p^2)$ is an effective bending stiffness, and d is a penetration length that accounts for the depth of the deformation in the patch. We expect d = t in the thin limit and d = λ/p in the thick limit where p is a free parameter. Because of continuity in the definition of the penetration length, d = t for t < λ/p and d = λ/p for t > λ/p, hence the parameter p captures the position of the crossover.

In figure 3B, we optimize the parameter p by using the least square method and obtain p ≈ 2.4 (see SI 1.5-Thin and Thick Limit Crossover Analysis). Thus, the criterion for topography driven deadhesion then becomes

$${\kappa }_c=A_c/{\lambda }^2=c{(\gamma /B_d)}^{1/2}$$ (1)

A generalization of the definition for the elastocapillary length to ℓ_ec = (B_d/γ)^1/2 gives the condition κ_c ~ 1/ℓ_ec for deadhesion. Interestingly, for a configuration with a prescribed wavelength, the maximum curvature is achieved for $A~\sqrt{\epsilon }\lambda ~\lambda$, or κ ~ 1/λ, showing that a given topography has the potential to detach patches with elastocapillary lengths larger or similar to λ.

Nature inspired topography induced surface renewal introduces a new mechanism for mechanically coupled interfacial failure adding to the existing literature dominated by edge and wrinkle delamination mechanisms [18–21, 27–30, 33]. To compare the different mechanisms, we re-write the given formulations in terms of critical strains for interfacial failure. For our topography mechanism, the critical nominal compressive strain ε_c at which delamination nucleates is related to the critical amplitude as $A_c=(\sqrt{2}/\pi )\sqrt{{\epsilon }_c-{\epsilon }_0}\lambda$, where we have included the numerical prefactors computed in [8, 31] and the strain ε₀ that accounts for the initial strain that is necessary to start the wrinkling configuration. Equation 1 shows that the critical strain can be predicted to be

$${\epsilon }_c=\frac{{(\pi c)}^2}{2}\frac{{\lambda }^2\gamma }{B_d}+{\epsilon }_0$$ (2)

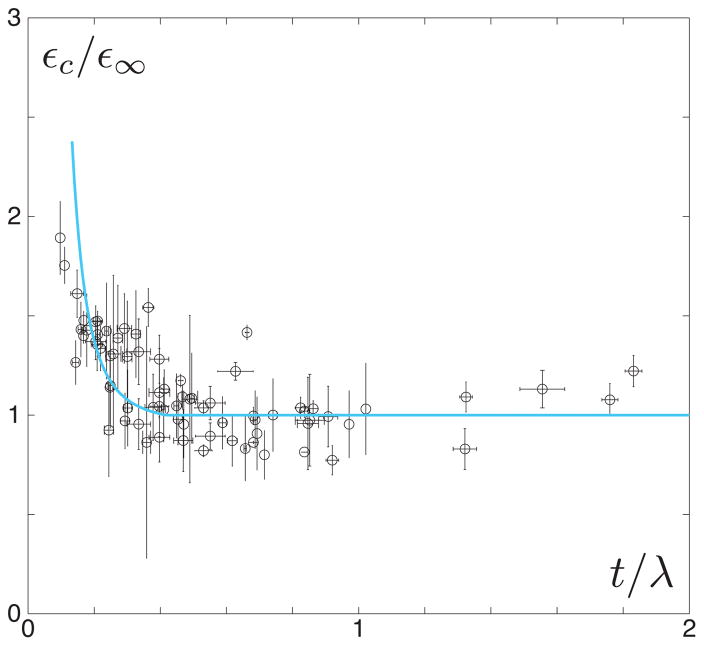
It is noteworthy that ε_c ~ t⁻³ in the thin limit t/λ ≪ 1 and ${\epsilon }_c\to {\epsilon }_{\infty }=6{(\pi c)}^2(1-{\nu }_p^2)p^3\gamma /\lambda +{\epsilon }_0$ in the thick limit t/λ ≫ 1. To check this relation, we carried out a set of experiments where patches with varying thicknesses were placed on top of a bilayer surface and measured the critical strain for deadhesion. Figure 5 compares the normalized critical strain obtained from experiments with the predicted values.

FIG. 5.

Pieces of soft silicone are placed onto initially flat bilayer surfaces. The support bilayer (E_m ≈ 3MPa, E_s ≈ 30 kPa, ν_m ≈ ν_s ≈ 1/2) is compressed and wrinkles appear (λ ≈ 1500μm) growing in amplitude as a function of nominal strain according to the inextensibility relation $A=(\sqrt{2}/\pi )\sqrt{\epsilon -{\epsilon }_0}\lambda$. Multiple patch thicknesses are tested from 250 to 2750 μm, giving a range of t/λ values both within the thin (see figure 2A) and thick (see figure 2B) regimes. The qualitative mechanism of deadhesion observed in these physical experiments is nearly identical to that seen with simulations (compare to experimental and numerical images in figure 2). Here we plot the cumulative critical strains for different experimental surfaces with identical wavelength. The open circles and error bars correspond to the average of three experiments done with each patch on an individual surface and the standard deviations, respectively. To control for variability in adhesion energy, which is sensitive to small changes in sample preparation, the critical strain for deadhesion ε_c is normalized in each data set by the smallest critical strain ε_∞, which usually corresponds to the thickest patch. The solid curve represents ε_c/ε_∞ predicted by Eq. 2, where E_p ≈ 30 kPa, γ ≈ 0.02 J/mm², ν_p ≈ 1/2, and ε₀ ≈ 0.1 for this particular system. The data clearly fall into two regimes: a thickness dependent and thickness independent regime. This is in agreement with our simulations and analytical predictions, whereby in the thin-patch limit ε_c ~ 1/t³ while in the thick-patch limit there is no dependence on t.

In general, for a topography with a given wavelength, the energy release rate is G ~ (B_d/2)κ² ~ B_dε/λ² in the large failed interface limit l → ∞. It increases as patch thickness becomes larger showing that thick patches are easier to detach than thin patches as seen in figure 3A. This is simple to understand, thin patches can easily follow the topography and the available energy is low. Thus, different mechanisms for delamination must be compared in the thin patch limit when patches are harder to detach. Conversely, for a given patch thickness, the energy release rate decays for small (G ~ λ) and large (G ~ 1/λ²) wavelengths, showing that G has a peak and delamination is optimized for an imposed wavelength λ ~ t.

A key feature of the proposed mechanism is to generate fracture propagation without arrest, therefore leading to the complete detachment of the patch. Other mechanisms [28, 33] for film delamination are comparable to our thin regime analysis and produce a similar effect. The basic element is to have a continuous supply of elastic energy for the fracture process that gives a constant value for the energy release rate in the limit of a large failed interface, l → ∞. This is the case for edge delamination [18, 21, 28, 33] where the elastic energy and energy release rate for a patch de-adhered a length l are U_E ≈ E_ptε²b(L – l)/2 and G = E_ptε²/2 ~ ε². However, G ~ B_pε/λ² ~ ε in the proposed topographic mechanism (thin limit) showing that for small strains more energy is available for fracture in the form of wrinkles.

Another competing mechanism is when the adhered patch itself is sufficiently stiff to wrinkle without necessity of a given topography (there is no membrane)[27, 29, 30]. This possibility is constrained to patches with large mismatch E_p/E_s ≫ 1, since the critical strain for wrinkling is ${\epsilon }_c^w\approx {(E_p/E_s)}^{-2/3}$ [4, 6, 7, 9]. In the large mismatch limit the elastic energy of the system can be computed as $U_E\approx B_p(\epsilon /{\lambda }_w^2)b(L-l)$ where λ_w ≈ (B_p/E_s)^1/3 gives the classical relation for wrinkles [6, 7]. The corresponding energy release rate is $G=B_p\epsilon /{\lambda }_w^2$, that is similar to the expression for an imposed topography in the thin patch limit because the available energy for fracture is stored in wrinkles in both cases. However, wavelength is imposed as a boundary condition for the topographic mechanism making it an independent control parameter while λ_w is an emergent length scale dictated by material properties.

Interfaces abound in nature and are often at risk for fouling. As figure 1 shows, many natural interfaces from inside of arteries to the skin of marine animals are wrinkled. These wrinkling patterns are not static and undergo dynamic changes in amplitude. No study to date has explored the potential role of such dynamic structures at complex interfaces. In this paper, we define a physical mechanism whereby dynamic wrinkling leads to surface renewal when the response of the adhered fouling layer is elastic. Many biological fouling layers (biofilms), including thrombus, show complex viscoelastic constitutive responses [3, 20, 22, 23, 25, 34]. Such materials are elastic on short time scales T < Λ, where Λ is an intrinsic elastic relaxation time of the given material, and have a more dissipative viscous response at T > Λ. Recent work [34] showed that Λ approaches a universal value of 1100 seconds for a wide variety of biologic biofilm like materials. From the perspective of our current mechanism of fouling layer disruption, this means that topographic surface renewal in biologic systems with biofilm-like fouling, including fouling on arterial surfaces dominated by platelet adhesion, could occur if actuation frequencies are equal to or greater than Λ⁻¹ ~ 0.001 s⁻¹, since at these frequencies the material response of the biofilm approaches that of an elastic solid.

In this Letter, we show that dynamic surface topography can be more effective at generating interfacial fracture than traditional mechanisms (edge and wrinkle delamination). By calculating ε_c for a given system, topographic surface renewal provides a novel bio-mimetic and tailorable strategy for designing self-cleaning surfaces in a variety of biomedical and industrial applications as well as controllable adhesion in fields such as soft robotics.