Skip to main content
PMC home page
ACS Physical Chemistry Au logoLink to ACS Physical Chemistry Au
. 2024 May 20;4(4):400–407. doi: 10.1021/acsphyschemau.4c00011

Measuring Vesicle Loading with Holographic Microscopy and Bulk Light Scattering

Lan Hai Anh Tran †, Lauren A Lowe †,‡, Yaam Deckel †,‡, Matthew Turner †,§, James Luong †,∥, Omar Abdullah A Khamis †, Megan L Amos †,‡, Anna Wang †,‡,⊥,#,*
PMCID: PMC11274288  PMID: 39069977

Abstract

graphic file with name pg4c00011_0008.jpg

We report efforts to quantify the loading of cell-sized lipid vesicles using in-line digital holographic microscopy. This method does not require fluorescent reporters, fluorescent tracers, or radioactive tracers. A single-color LED light source takes the place of conventional illumination to generate holograms rather than bright field images. By modeling the vesicle’s scattering in a microscope with a Lorenz–Mie light scattering model and comparing the results to data holograms, we are able to measure the vesicle’s refractive index and thus loading. Performing the same comparison for bulk light scattering measurements enables the retrieval of vesicle loading for nanoscale vesicles.

Keywords: vesicles, holography, encapsulation, lipid bilayer, GUVs

1. Introduction

The semipermeable lipid bilayer membrane is a core feature of all life on Earth.1 As a result, entire fields of research are dedicated to lipid bilayer assemblies: they are used as models for plasma membranes,2−5 biomimicking artificial cells,6−9 and vessels for drug delivery.10−12 In order to understand their key function as a biological container, it is critical to have methods of quantifying their loading (i.e., the amount of material they encapsulate) and how that changes as a function of time.

Current techniques such as radiolabeling13−17 and fluorescent labeling15−18 are commonly used for monitoring encapsulated solutes but can be expensive. Moreover, the hydrophobic moieties in fluorescent tags can often interact with the hydrophobic membrane19 or have undesired interactions with other encapsulated components.20 A label-free technique is thus preferable.

In previous work, we demonstrated that a core–shell light scattering model could be used to measure the thickness of lipid bilayer membranes to within the accuracy of cryogenic electron microscopy measurements.21 This approach required preprocessing the vesicle samples with extrusion through nanometer-sized pores to create a sample of a narrow size distribution and defined (uni)-lamellarity.

In this work, we demonstrate a method to determine the loading of single vesicles using light scattering on a minimally modified microscope. In this technique, known as in-line digital holographic microscopy, a white light source is replaced by a coherent light source, such that the diffraction pattern of the object has more detail in the fringes. Instead of objects becoming blurred when moving out of focus, the hologram arising from interference between undiffracted and diffracted light changes and provides information about the object’s axial position, which is usually quantified by measuring the object’s distance z from the focal plane of the objective (Figure 1). The information contained in the fringes enables objects to be tracked in three dimensions and for the refractive index and radius to be measured.22

Figure 1.

Figure 1

Open in a new tab

(A) Phase contrast and (B) holographic images of vesicles encapsulating sucrose (nominal concentration: 0.5 M) diluted into an isotonic glucose solution. Under coherent illumination, changing the focal plane of the microscope results in changes in the diffraction pattern of the vesicle. When in focus, the vesicle (inside the white dotted circle) is barely visible in holographic mode.

We then fit a generative model for how the objects scatter light to the holograms using an implementation of Lorenz–Mie scattering within the Python package HoloPy.23 While this technique has been used to track biological scatterers such as E. coli in 3D,24 distinguish between populations of scatterers in complex mixtures,25 and measure the size and refractive indices of colloidal objects,26 its utility for extracting the refractive index of vesicles has not yet been demonstrated.

We find that the solute loading of individual cell-sized vesicles (giant unilamellar vesicles, GUVs) can be quantified from the digital holograms and used to monitor content leakage. From data and modeled holograms, we determine that this technique is optimal for characterizing vesicles that have a radius greater than 1 μm and a position between 6 and 15 μm from the focal plane. This method works well when the solute loading is high enough to achieve a sufficient refractive index contrast with the medium such that the scattered signal is well above the fringe intensities from neighboring vesicles. For weaker scatterers such as vesicles with lower solute loading and much smaller vesicles, we demonstrate that bulk light scattering measurements may be more appropriate.

2. Results and Discussion

2.1. Modeling

To extract the refractive index of colloidal objects from holograms, a light scattering model for the assumed geometry of the object/scatterer was used to generate holograms that are iteratively fit to the data hologram. The reasons for using a simple model to fit the hologram are two-fold. First, while a 160 × 160 pixel hologram of a spherical scatterer takes less than a minute to fit on a typical processor,27 the time taken to fit holograms scales with the square of the number of fitting parameters.28 Second, some fitting parameters are strongly correlated, and the fitting landscape potentially contains multiple local minima as parameters are adjusted to compensate for each other.29,30 Thus, reducing the number of fitting parameters can aid fit convergence. We therefore first sought to verify that holograms of vesicles could be fitted effectively with the simplest model–a homogeneous sphere.

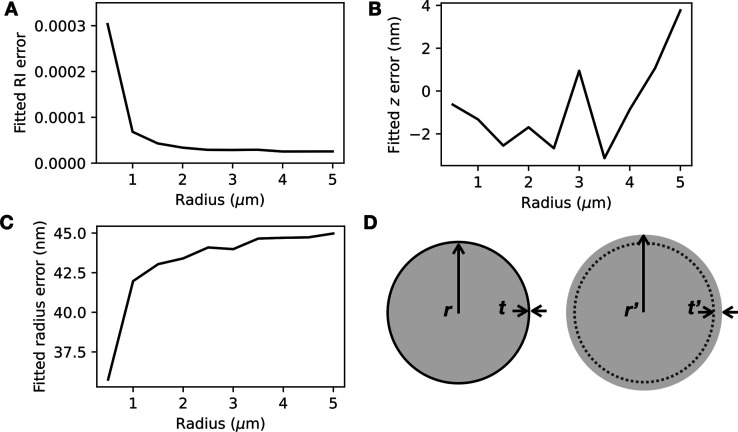
Although vesicles are core–shell structures, with a lipid bilayer corresponding to the shell and the aqueous interior of the vesicle corresponding to the core, the shell is very thin (approximately 3–5 nm thick21) compared to the typical diameter of vesicles (∼μm). Consequently, the shell is expected to contribute far less to the scattering, and it may be possible to ignore the presence of the shell in the hologram analysis routine. To test this hypothesis, we used an exact core–shell model for Mie scatterers to model holograms of loaded vesicles (see Experimental Section) and a homogeneous sphere model to extract parameters from the holograms. We found that the simple homogeneous sphere model is sufficient for retrieving refractive index information about the vesicle’s internal contents: the discrepancy between the fitted refractive index of the vesicle contents and the value used for the core–shell calculation was below 0.0001 refractive index unit (RIU) for vesicles larger than 1 μm in radius (Figure 2A). The error in the fitted z coordinate was less than 5 nm for all vesicle sizes tested (Figure 2B). The same trends were seen for vesicles that are bilamellar (Figure S1). While the z error appears to increase with vesicle radius, we found that this could be reduced by increasing the analyzed hologram’s size (Figure S2) to enable more fringes to be analyzed.

Figure 2.

Figure 2

Open in a new tab

Light scattering model for a homogeneous sphere can be used to extract the refractive index of the contents of a vesicle (a core–shell scatterer with a very thin shell). (A) The fitted error in the refractive index n becomes negligible for vesicles larger than 1 μm in radius. (B) The fitted error in z remains below 5 nm and fluctuates with vesicle size. (C) The fitted error in r remains approximately 40 nm for all vesicle sizes. (D) Schematic showing a core–shell scatterer with inner radius r and shell thickness t (left) and a homogeneous sphere with radius r′ = r + t′ (right).

With the refractive index (n) measurement and z localization performing extremely well, the sphere model appeared to compensate for the absence of the shell by fitting to a larger radius r′ = r + t′, with an error of approximately 42.5 nm (Figure 2C,D). We suspect that this is because an additional “layer” of vesicle contents could have a similar optical path length to a lipid shell. The optical path length of the additional layer (thickness t′ = 42.5 nm, see Figure 2D) can be calculated by multiplying t′ with the layer’s refractive index contrast with the medium (Δn ∼ 0.0077), giving t′Δn ∼ 0.3279 nm. The optical path length of the lipid shell can be found by multiplying the thickness t = 3 nm with the refractive index contrast with the medium for the lipid, Δnlipid ∼ 0.1191, which gives tΔnlipid ∼ 0.3574 nm. The sphere model thus appears to extract n and z information from vesicle holograms well by modeling a slightly larger sphere with a homogeneous refractive index. This is yet another example of the “effective sphere” model working well for inhomogeneous scatterers.26,31,32

One surprising finding was that, given the optimization algorithm used (Levenberg–Marquardt), the homogeneous sphere model appeared to be more robust to poor initial guesses than the core–shell models, even when tight constraints were placed on the refractive index nlipid and the thickness of the shell t (Figure S3). Another key advantage of using this effective sphere model is that it enables the retrieval of vesicle loading even when the refractive index of the lipid is unknown. Indeed, there are few reports33,34 of lipid refractive index, especially as a function of wavelength.

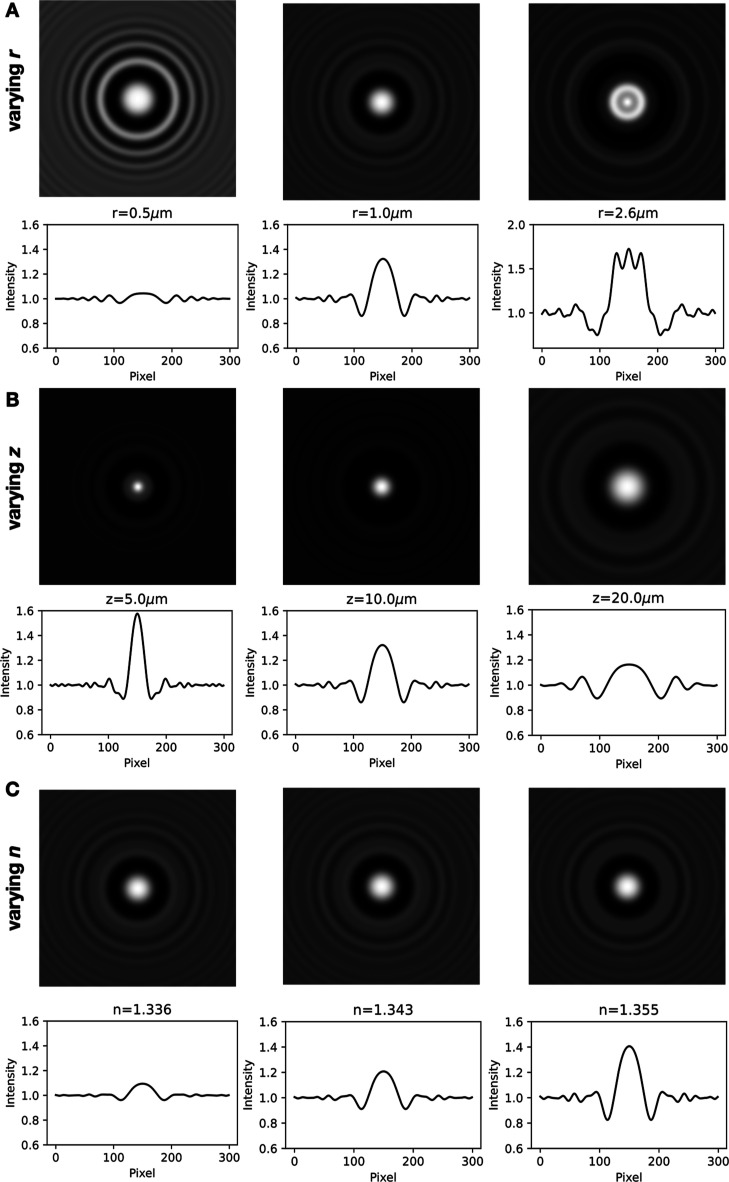
We also sought to determine how vesicles of varying sizes, positions, and refractive indices scatter light to gain further insight into the limitations of the technique. As with all Mie scatterers, the fringe pattern and scattering intensity vary nonmonotonically with the object’s refractive index and size. We found that the holograms contain more features when they are of larger vesicles (Figure 3A) and vesicles that are closer to the focal plane of the objective (Figure 3B). Two adjustments to image acquisition could therefore improve information retention: a camera with sufficiently small pixel sizes could help capture the detailed fringe information, and larger image sizes could be used to capture sufficient numbers of fringes. Finally, the refractive index variation is captured in the contrast of the fringes (Figure 3C) rather than the fringe pattern or spacing.

Figure 3.

Figure 3

Open in a new tab

Holograms and the intensity values across the center of the hologram were calculated for vesicles with varying (A) r, (B) z, and (C) refractive index n. Varying r and z changes the hologram fringe pattern and contrast, whereas varying n only changes the fringe contrast. See also Videos S1–S3. Parameters used in (A): z = 10 μm, the internal refractive index n = 1.35, the lipid refractive index nlipid = 1.47, and the lipid shell thickness t = 3 nm; (B): r = 1 μm, n = 1.35, nlipid = 1.47, and t = 3 nm; and (C): r = 1 μm, z = 10 μm, nlipid = 1.47, and t = 3 nm.

To analyze the impact of noise on refractive index retrieval, we simulated holograms with different content loadings and different types of noise (Figure S4). Random Gaussian noise did not impact refractive index retrieval by more than 0.0002 RIU (corresponding to <5 mM sucrose), even for the weakest-scattering vesicles. Because the information in holograms of spherical objects is radially symmetric, there is a lot of redundant information in holograms, and even a small random subset of pixels should contain enough information for retrievals.27 Noise taken from experimental holograms, which contain random noise as well as slowly varying background variations, resulted in errors of no more than 0.0004 RIU (corresponding to <10 mM sucrose). The presence of additional fringes from a nearby vesicle impacted the refractive index retrieval more, leading to errors of 0.0008 RIU (corresponding to <20 mM sucrose). Very crowded samples thus present the largest challenge for refractive index retrieval, especially for samples that have low solute loading compared to the concentration of solute in the medium. This is because they have poor hologram fringe contrast and are more easily impacted by the presence of fringes from neighboring vesicles.

2.2. Experimental Validation

We opted to use a self-assembly method to encapsulate a model solute, sucrose. This is because methods commonly used to make GUVs that encapsulate a known concentration of solute often require the presence of oil, which can remain as a contaminant in the bilayer.35 While researchers have found that the oil often does not impact the bilayer’s mechanical properties, such as rigidity and fluidity, its presence will significantly alter the optical properties.36 Furthermore, emulsion-transfer methods can lead to vesicles catastrophically rupturing and thus losing their contents. To avoid these complications for this validation study, we followed the protocol for making oleic acid GUVs from micelles as described in detail in Kindt et al. and Lowe et al.1,37 in the presence of 500 mM sucrose. This method has been previously used to encapsulate a range of solutes including small-molecule dyes and even colloidal particles.1,38 We then diluted the samples 1 part in 10 into an isotonic solution containing glucose, resulting in vesicles that encapsulated sucrose and maintained a sucrose gradient.

The vesicles with encapsulated sucrose appear dark under phase contrast imaging, as shown in Figure 1A, because the external glucose solution has a lower refractive index. Holograms of the same vesicle sample are shown in Figure 1B. When in focus, the vesicles are almost invisible owing to their low refractive index contrast with the medium. As the focus is shifted, interference fringes appear, revealing information about the contents of the vesicles.

We then fit22 the holograms to a Lorenz–Mie model for how spheres scatter light that takes the objective lens into account.39 The input parameters for the model are the vesicle’s refractive index n, radius r, and centroid location x, y, z. Examples of best-fit results returned by the Levenberg–Marquardt algorithm are shown in Figure S5.

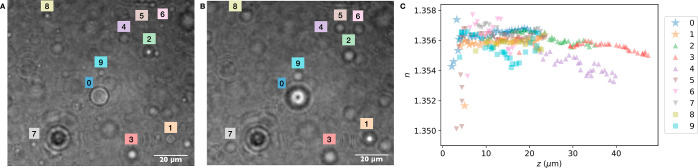
Because the detail in the fringes increases with the vesicle’s proximity to the focal plane (Figure 3B), we sought to determine whether the distance from the focal plane impacted the measured refractive index. Analyzing holograms of the same vesicles, but at different focal planes (while allowing r to freely vary during fitting), reveals that spherical aberration significantly decreases the measured refractive indices for vesicles within z < 6 μm of the focal plane, in agreement with the conclusions found by Martin and co-workers40 (Figure 4, see also Video S4). The measured refractive index also decreases with z > 15 μm, potentially due to poor fringe contrast and interference from nearby objects at these larger distances (see also Figure S4). For vesicles 4 and 9 in Figure 4, there are fringes from neighboring vesicles visible throughout the hologram series, and the degradation in refractive index retrieval is particularly pronounced (see also Figure S6). We therefore recommend taking holograms of vesicles with an axial position of 6 μm < z < 15 μm.

Figure 4.

Figure 4

Open in a new tab

(A,B) Holograms of vesicles are captured at several different focal planes. (C) The vesicles labeled in (A,B) were analyzed at different z distances to retrieve their refractive index n as a function of z. See also Video S4.

2.2.1. Measuring Vesicle Loading

The most basic use case is to measure the encapsulation of solutes inside vesicles. To correlate a refractive index measurement with vesicle loading, we needed to know the refractive index of sucrose as a function of concentration. We used an Abbe refractometer to measure standard curves for sucrose and glucose solutions in the presence of 100 mM bicine buffer at the sodium line (λ = 589 nm; Figure S7).

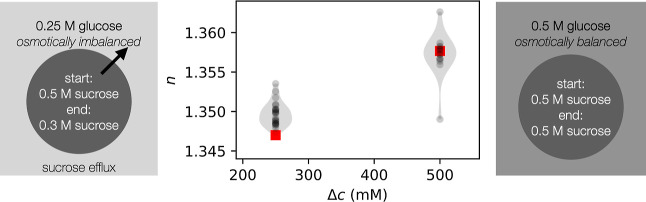
The measured refractive indices reveal that vesicles diluted into an isotonic solution did not exhibit content loss, whereas vesicles diluted into a hypotonic solution did have content loss (Figure 5). This is in line with expectations of the membrane being semipermeable; the permeability of water vastly exceeds that of glucose or sucrose, leading to water influx when vesicles are immersed into a hypotonic solution. The strain on the membrane results in rupture, which leads to content loss, membrane resealing, and further cycles of rupture and reseal41 until the osmotic stress no longer leads to membrane rupture.

Figure 5.

Figure 5

Open in a new tab

Vesicles encapsulating 500 mM sucrose were diluted into buffers containing either 250 mM glucose (resulting in an osmotic imbalance; number of vesicles N = 23) or 500 mM glucose (N = 14). The refractive indices of individual vesicles were measured with holography. For the vesicles exposed to a hypotonic solution, there was a content loss of approximately 200 mM sucrose. Refractive indices of 250 and 500 mM encapsulated sucrose are shown as red squares. The vesicles analyzed were between 1 and 2 μm in radius.

2.2.2. Measuring Vesicle Leakage

Another use case is to measure the leakage of an encapsulated solute over time. We diluted vesicles self-assembled in the presence of sucrose 1 part in 10 into an isotonic solution containing glucose, resulting in vesicles that encapsulate sucrose in the lumen. Because there is both a sucrose and glucose gradient across the membrane, the two sugars are expected to slowly exchange over time, limited by the less permeable solute (sucrose).

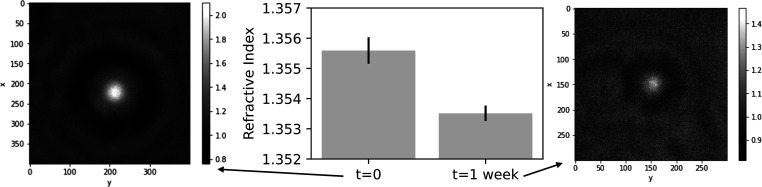
We found that a sample which initially measured n = 1.3556 ± 0.0004 corresponds to an encapsulated sucrose concentration of 380 mM (Figure 6). Over 1 week, the same sample had vesicles measuring n = 1.3535 ± 0.0003, corresponding to the encapsulation of 260 mM sucrose and 120 mM glucose. Given the time scale of a week and the average flux across the membrane, this corresponds to a sucrose permeability of 2 × 10–11 cm/s. This value compares well against the measured permeability of glucose across the same membrane (7 × 10–11 cm/s from Sacerdote and Szostak42), which is expected to be faster because of its smaller molecular weight.

Figure 6.

Figure 6

Open in a new tab

Refractive indices of vesicles encapsulating sucrose in a glucose bath were tracked over 1 week to determine sucrose/glucose exchange over time (N = 8). Representative holograms are shown, with dimensions in pixels. Error bars represent the standard deviation from the mean.

2.3. Bulk Light Scattering Measurements

The scattering of a single vesicle is challenging to analyze when the refractive index contrast with the medium is sufficiently low or when the vesicle is sufficiently small. For these cases, we recommend that bulk light scattering measurements (turbidometry) be used to quantify the average vesicle loading in the sample. We previously showed that a core–shell sphere model can be fitted to turbidity measurements of fatty acid and phospholipid vesicle samples to determine vesicle membrane thickness.21

In Figure 7, we show the extinction owing to the scattering (“Absorbance”) of a sample of vesicles encapsulating sucrose, as measured on a UV–visible spectrophotometer. As the concentration difference Δc between the internal contents and external medium increases, the modeled and experimental absorbances increase.

Figure 7.

Figure 7

Open in a new tab

Experimental absorbance spectra (red) of POPC vesicles diluted into isotonic or hypotonic buffers. The modeled absorbance (gray) has no fitting parameters and was determined using the expected sucrose concentration difference (Δc) between the interior and exterior of the vesicles. Taking the vesicle size distribution measured using DLS (black, dotted) into account makes little difference to the modeled absorbance.

This approach, while providing information on smaller vesicles compared to holography, requires that all parameters other than the refractive index of the vesicle’s contents n be known and constrained. The most typical method to control vesicle size involves extruding vesicles through pores to generate nanoscale vesicles. At these smaller length scales, the exact refractive index and thickness of the membrane all play a large role in the vesicle’s scattering relative to the aqueous core.21 However, the refractive index and thickness of most lipid bilayer compositions are unknown. The presence of bilamellar vesicles is also expected to impact the scattering significantly, given the large surface area-to-volume ratio of these scatterers.21 Vesicles prepared via slightly different methods have slightly different distributions in lamellarity, leading to different amounts of sample scattering (Figure S8). Turbidometry must therefore be approached with caution, with complementary methods such as cryogenic electron microscopy to constrain the lamellarity, dynamic light scattering (DLS) to measure the size, and a good estimate for the refractive index and thickness of the lipid, before the turbidity data can be used to extract the refractive index of the vesicles’ contents.

3. Conclusions

In summary, we have shown that holographic images of vesicles can be analyzed against a Lorenz–Mie light scattering model to quantify the refractive index of the vesicles. The measurement is noninvasive and requires only microliters of sample. The lipid thickness and refractive index do not need to be known if the vesicles are unilamellar. Retrieval of the refractive index n from holograms appears to be robust within 0.0005 RIU, even in the presence of noise. The main limiting factors for successful n retrieval are the presence of nearby vesicles and the vesicles being too small. For vesicles smaller than 1 μm in radius, we demonstrate that bulk light scattering may be more promising under some circumstances. In future work, this can be expanded to analyzing different solutes and the effects of pores and toxins on the ability of lipid membranes to retain solutes.

4. Experimental Section

4.1. Chemicals

Oleic acid (≥99%), bicine (≥99%), 2-oleoyl-1-palmitoyl-sn-glycero-3-phosphocholine (POPC) (≥99.0%), and chloroform (≥99.8%) were purchased from Sigma-Aldrich. Sucrose was purchased from Ajax Finechem and d(+)-glucose monohydrate from Calbiochem. Five M NaOH solution and 10x phosphate-buffered saline (PBS) (1.37 M NaCl, 0.027 M KCl, 0.0147 M KH2PO4, 0.081 M Na2HPO4) were purchased from Lowy Solutions. All water used was Millipore (18.2 MΩ·cm). All chemicals were used as received.

4.2. Vesicle Preparation

Vesicles were prepared by the self-assembly method.1 In brief, 5 mM oleic acid vesicles were prepared in a buffer that contained 100 mM Na-bicine (pH 8.3) and up to 500 mM sucrose by adding the appropriate amount of oleate micelles. The microcentrifuge tube was then agitated for 1 week on an orbital shaker at 100 rpm (PSU-10i Grant Bio, UK).

To make 0.1 M oleate micelle stock, 5 M NaOH (30 μL) and oleic acid (31.5 μL) were added to Milli-Q water (970 μL) in a microcentrifuge tube before being placed on an orbital shaker at 100 rpm (PSU-10i Grant Bio, UK) for 1 h until clear. One M bicine stock solution was adjusted to pH 8.3 by the addition of NaOH.

The vesicle suspensions were then diluted ten-to-one hundred-fold into a buffer containing 100 mM Na-bicine (pH 8.3) and up to 500 mM glucose. Three μL of the diluted vesicle sample was then sealed between a 22 × 22 mm coverslip and a 25 × 75 mm glass slide using silicone vacuum grease (Dow Corning, USA).

4.3. Imaging

Vesicles were imaged by phase contrast or holographic modalities using a 1.3 NA 100× objective (Nikon, Japan) on a TE-2000 inverted microscope (Nikon, Japan). Diascopic illumination was provided by a pT-100 LED (CoolLED, UK). Holographic illumination was provided by a 660 nm mounted LED (Thorlabs, M660 L4, 940 mW, 12 mA, λ = 660 nm; Thorlabs, USA) following the setup described by Giuliano and co-workers.43 Images were captured with a pco.edge 4.2 (PCO Imaging, Germany) using a 10 ms exposure time.

4.4. Bulk Light Scattering Measurements

POPC nanoscale vesicles for bulk light scattering measurements were prepared by thin film hydration. 100 μL of a 100 mM solution of POPC in chloroform was added to a 4 mL glass vial. The sample was heated on a hot plate to remove the solvent and yield a film of POPC. The film was hydrated with 1 mL of 500 mM sucrose in 1x PBS (pH 7.4) and vortexed vigorously for approximately 5 min. Samples were sonicated for 1 h in ice water before being passed 21 times through a polycarbonate filter with pores 100 nm in diameter using a mini-extruder (Avanti Polar Lipids, USA). The sample was left to agitate on an orbital shaker (PSU-10i Grant Bio, UK) for at least 1 h at 100 rpm before being diluted 1 in 10 into a dilution buffer. Dilution buffers were composed of 1x PBS with varying concentrations of sucrose (500 mM, 375 mM, 250 mM, or 125 mM) (pH 7.4).

The turbidity of extruded vesicle samples was measured using a V-730 UV–visible spectrophotometer (JASCO, Japan) and semimicro UV cuvettes (BRAND, Germany), with the dilution buffer used as the blank. Vesicle size was measured with DLS using a Malvern Zetasizer Nano ZS and 12 mm square polystyrene cuvettes (DTS0012) (Malvern Panalytical, UK), with the number averages input into the core–shell sphere model.

Bulk scattering calculations were performed using HoloPy as described in Wang et al.,21 with the inclusion of the concentration of sucrose externally as a known parameter and the internal concentration of sucrose as a fitting parameter. The additional required parameters were set as follows: radii r as measured using DLS, the lipid refractive index nlipid ∼ 1.4744 with the wavelength dependence as outlined previously,21 area per lipid a = 0.627 nm2,45 and lipid shell thickness t = 4.5 nm for POPC.

4.5. Hologram Calculations and Analysis

Core–shell modeling of vesicle holograms was performed by using the core–shell module in the package HoloPy.23 The parameters were set as follows: radii r varying from 0.1 to 5 μm, z varying from 0 to 20 μm, and the internal refractive index n varying from 1.3311 to 1.3577. The lipid refractive index was set to nlipid = 1.47, and the lipid shell thickness was set to t = 3 nm.

The holograms were analyzed by iterative comparison to a Lorenz–Mie model for scattering from a homogeneous sphere using HoloPy. As described by Martin and co-workers,26 this procedure can be used to quantify the location, refractive index, and size of the scatterers. In brief, the Lorenz–Mie model is used to calculate the scattered electric field from a vesicle using values for its refractive index, size, and three-dimensional location. This field is then interfered with a plane wave to generate a modeled hologram. The modeled hologram is compared pixel-by-pixel to the data hologram, and the sum of the squared residuals is recorded as the cost function. By continually generating new holograms, a Levenberg–Marquardt algorithm then finds the best-fit values for refractive index, size, and three-dimensional location: the values that minimize the sum of the squared residuals.

The medium index after diluting sucrose-laden vesicles into a glucose medium contained both sucrose and glucose. The refractive index values used for the medium at 589 nm were estimated by linear combinations of the sucrose and glucose values shown in Figure S7. For hologram fitting, the refractive index of the medium was adjusted to 660 nm by assuming that the dispersion of the aqueous medium was dominated by that of water nwater(λ) = 1.313242 + 15.7834/λ – 4382/λ2 + 1.1455 × 106/λ3.46,47 The values were then adjusted back to 589 nm for comparison with the measurements from the Abbe refractometer.

For any vesicles with fitted distances closer than zcritical = 6 μm, the spherical aberration was accounted for by adjusting the fitted refractive index values by 0.0009 RIU/Δμm, where Δμm is the difference between the fitted z distance and zcritical. This slope was determined from fitting the data points with z < 6 μm in Figure 4C to a straight line.

Acknowledgments

L.A.L. thanks the support of an Australian Government Research Training Program Scholarship. A.W. thanks the support of an Australian Research Council Discovery Early Career Award (DE210100291), the Human Frontier Science Program (RGP0029/2020), and support from the Alfred P. Sloan Foundation and Gordon and Betty Moore Foundation.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsphyschemau.4c00011.

  • Change in hologram intensity valueswith varying radius (AVI)

  • Change in hologram intensity values with varying z (AVI)

  • Change in hologram intensity values with varying internal refractive index (AVI)

  • Data holograms for the vesicle sample corresponding to Figure 4 (AVI)

  • Fitted errors, model comparisons, noise analysis, data holograms and best-fit holograms, holograms of vesicles 4 and 9 from Figure 4, average measured refractive indices, and additional absorbance spectra (PDF)

Author Contributions

L.H.A.T. and L.A.L. contributed equally. CRediT: Lan Hai Anh Tran formal analysis, investigation, visualization, writing-review & editing; Lauren A Lowe conceptualization, formal analysis, investigation, methodology, supervision, writing-original draft, writing-review & editing; Yaam Deckel investigation, methodology; Matthew Turner investigation, methodology, validation; James Hien Luong validation; Omar Abdullah A Khamis conceptualization, investigation, validation; Megan L. Amos investigation; Anna Wang conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing-original draft, writing-review & editing.

The authors declare no competing financial interest.

Supplementary Material

pg4c00011_si_001.avi (288.1KB, avi)
pg4c00011_si_002.avi (603.4KB, avi)
pg4c00011_si_003.avi (293.4KB, avi)
pg4c00011_si_004.avi (17.2MB, avi)
pg4c00011_si_005.pdf (9.4MB, pdf)

References

  1. Kindt J. T.; Szostak J. W.; Wang A. Bulk Self-Assembly of Giant, Unilamellar Vesicles. ACS Nano 2020, 14, 14627–14634. 10.1021/acsnano.0c03125. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Sarkis J.; Vié V. Biomimetic Models to Investigate Membrane Biophysics Affecting Lipid–Protein Interaction. Front. Bioeng. Biotechnol. 2020, 8, 270. 10.3389/fbioe.2020.00270. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Luchini A.; Vitiello G. Mimicking the Mammalian Plasma Membrane: An Overview of Lipid Membrane Models for Biophysical Studies. Biomimetics 2021, 6, 3. 10.3390/biomimetics6010003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Scott H. L.; Kennison K. B.; Enoki T. A.; Doktorova M.; Kinnun J. J.; Heberle F. A.; Katsaras J. Model Membrane Systems Used to Study Plasma Membrane Lipid Asymmetry. Symmetry 2021, 13, 1356. 10.3390/sym13081356. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Simons K.; Vaz W. L. C. Model Systems, Lipid Rafts, and Cell Membranes. Annu. Rev. Biophys. 2004, 33, 269–295. 10.1146/annurev.biophys.32.110601.141803. [DOI] [PubMed] [Google Scholar]
  6. Xu C.; Hu S.; Chen X. Artificial cells: from basic science to applications. Mater. Today 2016, 19, 516–532. 10.1016/j.mattod.2016.02.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Siontorou C. G.; Nikoleli G.-P.; Nikolelis D. P.; Karapetis S. K. Artificial Lipid Membranes: Past, Present, and Future. Membranes 2017, 7, 38. 10.3390/membranes7030038. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Rothschild L. J.; Averesch N. J. H.; Strychalski E. A.; Moser F.; Glass J. I.; Cruz Perez R.; Yekinni I. O.; Rothschild-Mancinelli B.; Roberts Kingman G. A.; Wu F.; et al. Building Synthetic Cells—From the Technology Infrastructure to Cellular Entities. ACS Synth. Biol. 2024, 13, 974–997. 10.1021/acssynbio.3c00724. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Lu Y.; Allegri G.; Huskens J. Vesicle-based artificial cells: materials, construction methods and applications. Mater. Horiz. 2022, 9, 892–907. 10.1039/D1MH01431E. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Liu P.; Chen G.; Zhang J. A Review of Liposomes as a Drug Delivery System: Current Status of Approved Products, Regulatory Environments, and Future Perspectives. Molecules 2022, 27, 1372. 10.3390/molecules27041372. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Bozzuto G.; Molinari A. Liposomes as nanomedical devices. Int. J. Nanomed. 2015, 10, 975–999. 10.2147/IJN.S68861. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Lakshmi V. S.; Manohar R. D.; Mathan S.; Dharan S. S. Ufasomes: A Potential Vesicular Carrier System. J. Pharmaceut. Sci. Res. 2020, 12, 1332–1335. [Google Scholar]
  13. Mui B. L.; Cullis P. R.; Evans E. A.; Madden T. D. Osmotic properties of large unilamellar vesicles prepared by extrusion. Biophys. J. 1993, 64, 443–453. 10.1016/S0006-3495(93)81385-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Anderson M.; Omri A. The Effect of Different Lipid Components on the In Vitro Stability and Release Kinetics of Liposome Formulations. Drug Delivery 2004, 11, 33–39. 10.1080/10717540490265243. [DOI] [PubMed] [Google Scholar]
  15. Mansy S. S.; Szostak J. W. Thermostability of model protocell membranes. Proc. Natl. Acad. Sci. U.S.A. 2008, 105, 13351–13355. 10.1073/pnas.0805086105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Jin L.; Kamat N.; Jena S.; Szostak J. Fatty Acid/Phospholipid Blended Membranes: A Potential Intermediate State in Protocellular Evolution. Small (Weinheim an der Bergstrasse, Germany) 2018, 14, e1704077 10.1002/smll.201704077. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Chen I. A.; Salehi-Ashtiani K.; Szostak J. W. RNA catalysis in model protocell vesicles. J. Am. Chem. Soc. 2005, 127, 13213–13219. 10.1021/ja051784p. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Emami S.; Su W.-C.; Purushothaman S.; Ngassam V. N.; Parikh A. N. Permeability and Line-Tension-Dependent Response of Polyunsaturated Membranes to Osmotic Stresses. Biophys. J. 2018, 115, 1942–1955. 10.1016/j.bpj.2018.09.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Hughes L. D.; Rawle R. J.; Boxer S. G. Choose Your Label Wisely: Water-Soluble Fluorophores Often Interact with Lipid Bilayers. PLoS One 2014, 9, e87649 10.1371/journal.pone.0087649. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Quinn M. K.; Gnan N.; James S.; Ninarello A.; Sciortino F.; Zaccarelli E.; McManus J. J. How fluorescent labelling alters the solution behaviour of proteins. Phys. Chem. Chem. Phys. 2015, 17, 31177–31187. 10.1039/C5CP04463D. [DOI] [PubMed] [Google Scholar]
  21. Wang A.; Chan Miller C.; Szostak J. W. Core-Shell Modeling of Light Scattering by Vesicles: Effect of Size, Contents, and Lamellarity. Biophys. J. 2019, 116, 659–669. 10.1016/j.bpj.2019.01.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Lee S. H.; Roichman Y.; Yi G. R.; Kim S. H.; Yang S. M.; Blaaderen A. v.; Oostrum P. v.; Grier D. G. Characterizing and tracking single colloidal particles with video holographic microscopy. Opt. Express 2007, 15, 18275–18282. 10.1364/oe.15.018275. [DOI] [PubMed] [Google Scholar]
  23. Barkley S.; Dimiduk T. G.; Fung J.; Kaz D. M.; Manoharan V. N.; McGorty R.; Perry R. W.; Wang A. Holographic Microscopy With Python and HoloPy. Comput. Sci. Eng. 2020, 22, 72–82. 10.1109/MCSE.2019.2923974. [DOI] [Google Scholar]
  24. Wang A.; Garmann R.; Manoharan V. Tracking E. coli runs and tumbles with scattering solutions and digital holographic microscopy. Opt. Express 2016, 24, 23719–23725. 10.1364/OE.24.023719. [DOI] [PubMed] [Google Scholar]
  25. Winters A.; Cheong F. C.; Odete M. A.; Lumer J.; Ruffner D. B.; Mishra K. I.; Grier D. G.; Philips L. A. Quantitative Differentiation of Protein Aggregates From Other Subvisible Particles in Viscous Mixtures Through Holographic Characterization. J. Pharm. Sci. 2020, 109, 2405–2412. 10.1016/j.xphs.2020.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Martin C.; Altman L. E.; Rawat S.; Wang A.; Grier D. G.; Manoharan V. N. In-line holographic microscopy with model-based analysis. Nat. Rev. Methods Primers 2022, 2, 83. 10.1038/s43586-022-00165-z. [DOI] [Google Scholar]
  27. Dimiduk T. G.; Perry R. W.; Fung J.; Manoharan V. N. Random-subset fitting of digital holograms for fast three-dimensional particle tracking [Invited]. Appl. Opt. 2014, 53, G177–G183. 10.1364/AO.53.00G177. [DOI] [PubMed] [Google Scholar]
  28. Fung J.; Perry R. W.; Dimiduk T. G.; Manoharan V. N. Imaging multiple colloidal particles by fitting electromagnetic scattering solutions to digital holograms. J. Quant. Spectrosc. Radiat. Transf. 2012, 113, 2482–2489. 10.1016/j.jqsrt.2012.06.007. [DOI] [Google Scholar]
  29. Ruffner D. B.; Cheong F. C.; Blusewicz J. M.; Philips L. A. Lifting degeneracy in holographic characterization of colloidal particles using multi-color imaging. Opt. Express 2018, 26, 13239. 10.1364/OE.26.013239. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Dimiduk T. G.; Manoharan V. N. Bayesian approach to analyzing holograms of colloidal particles. Opt. Express 2016, 24, 24045–24060. 10.1364/OE.24.024045. [DOI] [PubMed] [Google Scholar]
  31. Altman L. E.; Quddus R.; Cheong F. C.; Grier D. G. Holographic characterization and tracking of colloidal dimers in the effective-sphere approximation. Soft Matter 2021, 17, 2695–2703. 10.1039/D0SM02262D. [DOI] [PubMed] [Google Scholar]
  32. Fung J.; Hoang S. Computational assessment of an effective-sphere model for characterizing colloidal fractal aggregates with holographic microscopy. J. Quant. Spectrosc. Radiat. Transf. 2019, 236, 106591. 10.1016/j.jqsrt.2019.106591. [DOI] [Google Scholar]
  33. Khlebtsov N. G.; Kovler L. A.; Zagirova S. V.; Khlebtsov B. N.; Bogatyrev V. A. Spectroturbidimetry of Liposome Suspensions. Colloid J. 2001, 63, 491–498. 10.1023/A:1016718324830. [DOI] [Google Scholar]
  34. Jones S. H.; King M. D.; Ward A. D. Atmospherically relevant core–shell aerosol studied using optical trapping and Mie scattering. Chem. Commun. 2015, 51, 4914–4917. 10.1039/C4CC09835H. [DOI] [PubMed] [Google Scholar]
  35. Kirchner S. R.; Ohlinger A.; Pfeiffer T.; Urban A. S.; Stefani F. D.; Deak A.; Lutich A. A.; Feldmann J. Membrane composition of jetted lipid vesicles: a Raman spectroscopy study. J. Biophot. 2012, 5, 40–46. 10.1002/jbio.201100058. [DOI] [PubMed] [Google Scholar]
  36. Schaich M.; Sobota D.; Sleath H.; Cama J.; Keyser U. F. Characterization of lipid composition and diffusivity in OLA generated vesicles. Biochim. Biophys. Acta Biomembr. 2020, 1862, 183359. 10.1016/j.bbamem.2020.183359. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Lowe L. A.; Loo D. W. K.; Wang A.. Membrane Lipids: Methods and Protocols; Cranfield C. G., Ed.; Methods in Molecular Biology; Springer US: New York, NY, 2022; pp 1–12. [Google Scholar]
  38. Deckel Y.; Lowe L. A.; Rawat S.; Turner M.; Luong J.; Wang A. Using Holographic Microscopy To Measure the Effect of Confinement on Crowding Agents in Lipid Vesicles. ChemBioChem 2023, 24, e202300069 10.1002/cbic.202300069. [DOI] [PubMed] [Google Scholar]
  39. Leahy B.; Alexander R.; Barkley S.; Martin C.; Manoharan V. N. Large depth-of-field tracking of colloidal spheres in holographic microscopy by modeling the objective lens. Opt. Express 2020, 28, 1061–1075. 10.1364/oe.382159. [DOI] [PubMed] [Google Scholar]
  40. Martin C.; Leahy B.; Manoharan V. N. Improving holographic particle characterization by modeling spherical aberration. Opt. Express 2021, 29, 18212–18223. 10.1364/OE.424043. [DOI] [PubMed] [Google Scholar]
  41. Koslov M. M.; Markin V. S. A theory of osmotic lysis of lipid vesicles. J. Theor. Biol. 1984, 109, 17–39. 10.1016/S0022-5193(84)80108-3. [DOI] [PubMed] [Google Scholar]
  42. Sacerdote M. G.; Szostak J. W. Semipermeable lipid bilayers exhibit diastereoselectivity favoring ribose. Proc. Natl. Acad. Sci. U.S.A. 2005, 102, 6004–6008. 10.1073/pnas.0408440102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Giuliano C. B.; Zhang R.; Wilson L. G. Digital Inline Holographic Microscopy (DIHM) of Weakly-scattering Subjects. J. Vis. Exp. 2014, (84), e50488 10.3791/50488-v. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Khlebtsov B. N.; Kovler L. A.; Bogatyrev V. A.; Khlebtsov N. G.; Shchyogolev S. Y. Studies of phosphatidylcholine vesicles by spectroturbidimetric and dynamic light scattering methods. J. Quant. Spectrosc. Radiat. Transf. 2003, 79–80, 825–838. 10.1016/S0022-4073(02)00322-9. [DOI] [Google Scholar]
  45. Kučerka N.; Nieh M.-P.; Katsaras J. Fluid phase lipid areas and bilayer thicknesses of commonly used phosphatidylcholines as a function of temperature. Biochim. Biophys. Acta Biomembr. 2011, 1808, 2761–2771. 10.1016/j.bbamem.2011.07.022. [DOI] [PubMed] [Google Scholar]
  46. Quan X.; Fry E. S. Empirical equation for the index of refraction of seawater. Appl. Opt. 1995, 34, 3477. 10.1364/AO.34.003477. [DOI] [PubMed] [Google Scholar]
  47. Van Engen A. G.; Diddams S. A.; Clement T. S. Dispersion measurements of water with white-light interferometry. Appl. Opt. 1998, 37, 5679. 10.1364/AO.37.005679. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

pg4c00011_si_001.avi (288.1KB, avi)
pg4c00011_si_002.avi (603.4KB, avi)
pg4c00011_si_003.avi (293.4KB, avi)
pg4c00011_si_004.avi (17.2MB, avi)
pg4c00011_si_005.pdf (9.4MB, pdf)

Articles from ACS Physical Chemistry Au are provided here courtesy of American Chemical Society

RESOURCES