Local synaptic inhibition mediates cerebellar granule cell pattern separation and enables learned sensorimotor associations

Abstract

The cerebellar cortex plays a key role in generating predictive sensorimotor associations. To do so, the granule cell layer is thought to establish unique sensorimotor representations for learning. However, how this is achieved and how granule cell population responses contribute to behavior have remained unclear. To address these questions, we have used in vivo calcium imaging and granule cell-specific pharmacological manipulation of synaptic inhibition in awake, behaving mice. These experiments indicate that inhibition sparsens and thresholds sensory responses, limiting overlap between sensory ensembles and preventing spiking in many granule cells that receive excitatory input. Moreover, inhibition can be recruited in a stimulus-specific manner to powerfully decorrelate multisensory ensembles. Consistent with these results, granule cell inhibition is required for accurate cerebellum-dependent sensorimotor behavior. These data thus reveal key mechanisms for granule cell layer pattern separation beyond those envisioned by classical models.

Introduction

Associative learning is an essential process linking sensation and action, providing a key mechanism to modify behavior. The cerebellum plays a central role in associative sensorimotor learning, both for generating coordinated movements and cognitive processes^{1, 2}. To do so, the cerebellum receives excitatory mossy fiber input from diverse sources³ that transmit sensory, motor, and cognitive information to granule cells in the granule cell layer⁴. Granule cells must integrate and relay these signals to Purkinje cells, the output neurons of the cerebellar cortex, in a manner that establishes unique sensorimotor representations necessary for associative learning and the expression of learned cerebellum-dependent behaviors.

Classical models speculate that unique granule cell representations are generated through a process of “pattern separation”^{5, 6}. Expansion recoding is one mechanism thought to enable pattern separation, because mossy fiber inputs are distributed onto a population of granule cells that is ~100-fold larger than the number of mossy fiber inputs⁶. Because each granule cell receives ~4 inputs that can transmit the same or different modalities^7–10, random mixing is also thought to facilitate pattern separation. Another key mechanism proposed by classical theories is the thresholding of granule cell activity by local inhibitory interneurons in the granule cell layer called Golgi cells. Golgi cells exhibit spontaneous pacemaker activity, releasing GABA that acts continuously on granule cells to produce a tonic inhibitory current^{11, 12}. This tonic inhibition regulates the spike threshold¹³ and gain of granule cell responses¹⁴. In addition, Golgi cells receive feedforward excitation from mossy fibers and feedback excitation from granule cells, thus allowing them to respond dynamically to the inputs and outputs of the granule cell layer. Together, this tonic and phasic Golgi cell inhibition has long been hypothesized as necessary for creating sparse, non-overlapping granule cell population codes.

In contrast with predictions of classical theories, modern calcium imaging approaches have shown that granule cell responses can be dense and redundant in some conditions^15–18. These studies have indicated that complex behaviors requiring task engagement, learning, and compound body movements likely to involve sensory, motor, cognitive, and efference copy signals can result in relatively widespread granule cell activity. In such cases, where there are many complex granule cell representations evolving across time, it has been challenging to disentangle discrete sensory representations and how they combine to form complex multisensory codes that remain dissociable for learning and behavior. Moreover, it has been difficult to test what mechanisms shape these sensory representations, as there has been a lack of tools for acute, cell type-specific manipulations of granule cell GABAergic inhibition. Thus, how the granule cell layer encodes discrete sensory input at the population level, how local synaptic inhibition contributes to such representations, and what role granule cell inhibition plays in cerebellum-dependent behavior have remained unclear.

To address these long-standing questions, we have used an approach that allows in vivo measurement of cerebellar granule cell population responses while acutely blocking synaptic inhibition in a cell–type-specific manner. Specifically, we have used multiphoton population imaging and in combination with the DART system^{19, 20} (Drugs Acutely Restricted by Tethering) to acutely block synaptic inhibition onto granule cells. In response to discrete sensory input, we find that granule cell population activity is sparse, and can be variable in terms of response probability, neural ensemble identity, and response timing across trials. In contrast, acutely blocking synaptic inhibition dramatically enhances stimulus-evoked responses, revealing a large population of previously inactive cells, suggesting that thresholding is a key mechanism for sparsifying granule cell population ensembles. In addition, thresholding establishes separable granule cell populations that can only respond to combined multisensory inputs, a property that would not be possible if ensemble sparsity were determined by inputs alone. Surprisingly, we also find that inhibition can be recruited in a stimulus-specific manner, further enhancing pattern separation by removing cells from multisensory ensembles that are part of unisensory ensembles. In support of our finding that synaptic inhibition plays a central role in granule cell layer pattern identity and pattern separation, we find that blocking inhibition onto granule cells impairs the expression of a learned, cerebellum-dependent sensorimotor behavior. Together, these data reveal multiple distinct computations mediated by GABAergic inhibition onto granule cells that support sensory encoding, pattern separation, and behavior in ways that extend classical models.

Results

Inhibition sparsens population-level sensory representations

To measure sensory-evoked activity in populations of cerebellar granule cells, we performed two-photon calcium imaging of GCaMP6f, which has been shown to report spiking in granule cells in vitro¹⁶ (Fig. 1a-b). By crossing Ai148²¹ and BACα6Cre-A transgenic mice²², we observed dense labeling of granule cells, with only rare off-target labeling of Purkinje cells, which were excluded from imaging analysis (Methods, Supplementary Fig. 1). Crus I of the lateral cerebellum is a major target of both auditory and somatosensory pathways²³, and granule cells in this lobule are robustly driven by both auditory and somatosensory stimuli^{9, 24, 25}. Thus, we imaged activity in Crus 1 in response to auditory stimuli (Fig. 1c-g, pure tones: 1, 5 and 10 kHz at 68 and 72 dB; Supplementary Fig. 2) and somatosensory stimuli (Fig. 1h-l. gentle orofacial air puffs: 10, 15 and 20 PSI; Supplementary Fig. 3).

Figure 1. Local synaptic inhibition sparsens and thresholds cerebellar granule cell sensory responses.

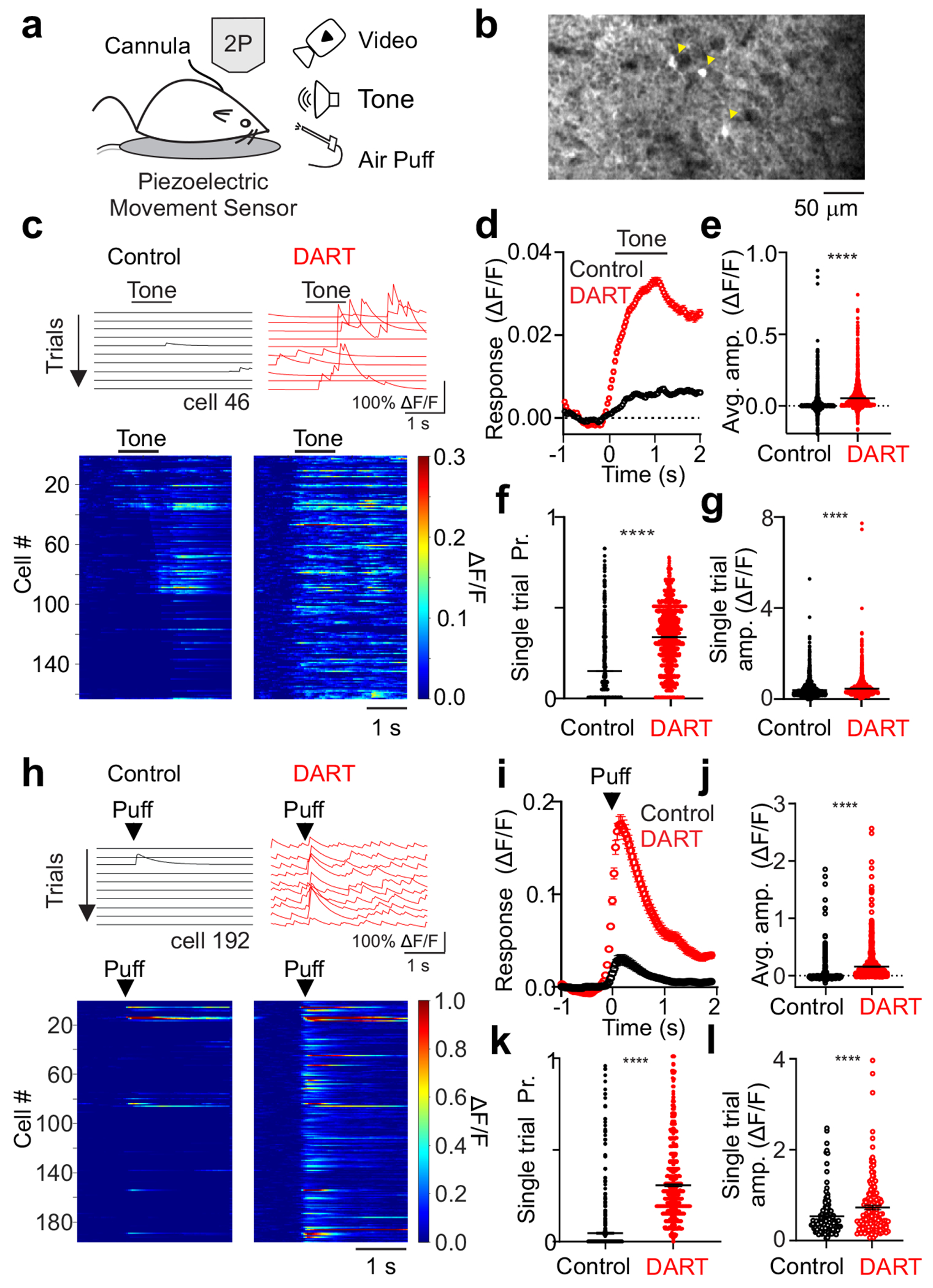
a. Schematic of experimental approach. b. Example average field of view across trials of granule cells expressing GCaMP6f during presentation of a somatosensory stimulus in the absence of whole-body movement. Yellow arrows designate significantly responsive cells. c. Top, example calcium traces (ΔF/F) from a granule cell on sequential tone presentation trials before (black) and after (red) gabazine.1^DART.2 infusion (“DART”, 1 μM). Bottom, mean responses of all cells with significant responses to a tone before (left) and after DART application (right) in an example mouse with granule cell HTP expression. Example cell above is cell 46. d. Mean time course of responses during tone presentation before (black,) and after (red) DART infusion (n = 3360 cells). Error is SEM across cells from 6 mice. e. Mean response amplitudes for individual cells before (black) and after (red) DART infusion. Black lines are mean ± SEM across cells. f. Same as e, for response probability. g. Same as e, for mean responses on all trials with significant responses (n = 1942 cells). h-l. Same as c-g, for responses to somatosensory stimuli from 6 mice (i-k, n = 815 cells, l, n = 315 cells). Example cell in h is cell 192 in the heatmap. ****p<0.0001, paired t-test (e-g, j-l).

Our goal was to measure how discrete sensory inputs are encoded in the granule cell layer and could be used as an initial substrate for associative learning. While movement has been shown to enhance associative learning in one cerebellum-dependent behavior, it is not necessary for learning per se²⁶. Thus, because Crus I receives input related to whisking and likely other movements^27–31 that could confound our measures of sensory ensembles, we took multiple steps to isolate sensory-related granule cell activity (see Methods). First, animals were habituated to orofacial airpuffs, such that they produced reflexive whisker movements on only a minority of trials. Second, high-speed video was used to detect whisker and facial movements between trials and isolate responses related to these movements³² (Supplementary Fig. 4). Third, we controlled for spontaneous and reactive body movements using a sensitive piezo vibration sensor^{33, 34} (Fig. 1a, Supplementary Fig. 5). Together, these methods enabled us to discard trials with body movement and demonstrate that whisking-related activity does not significantly contaminate sensory responses (Supplementary Figs. 4, 5; Methods).

In control conditions, combining data across stimulus frequencies and intensities reveals that both auditory and somatosensory stimuli recruit population level granule cell activity in Crus I (Fig. 1). All stimuli evoke granule cell responses that begin near the time of stimulus onset (Fig 1c,d,h,i). For auditory stimuli, which could be delivered for a longer duration (1 s) than somatosensory stimuli, individual granule cells respond at times across the duration of the stimulus window (Fig. 1c, 6a), and many granule cells respond preferentially at the offset of the stimulus (Fig. 1c). Overall, granule cells in control conditions produce modest responses (Fig. 1d,e,i,j) occurring with a low probability (Figure 1f,k; auditory: 0.14 ± 0.00, n = 3360 cells; somatosensory: 0.06 ± 0.00, n = 815 cells) and small single trial amplitude (Fig. 1 g, l; auditory: 0.41 ± 0.01 ΔF/F, n = 1942 cells; somatosensory: 0.53 ± 0.04, n = 118 cells). These properties are consistent for all individual auditory and somatosensory stimuli tested (Supplementary Fig. 2,3).

Figure 6. Cerebellar granule cells respond with temporal variability to auditory stimuli.

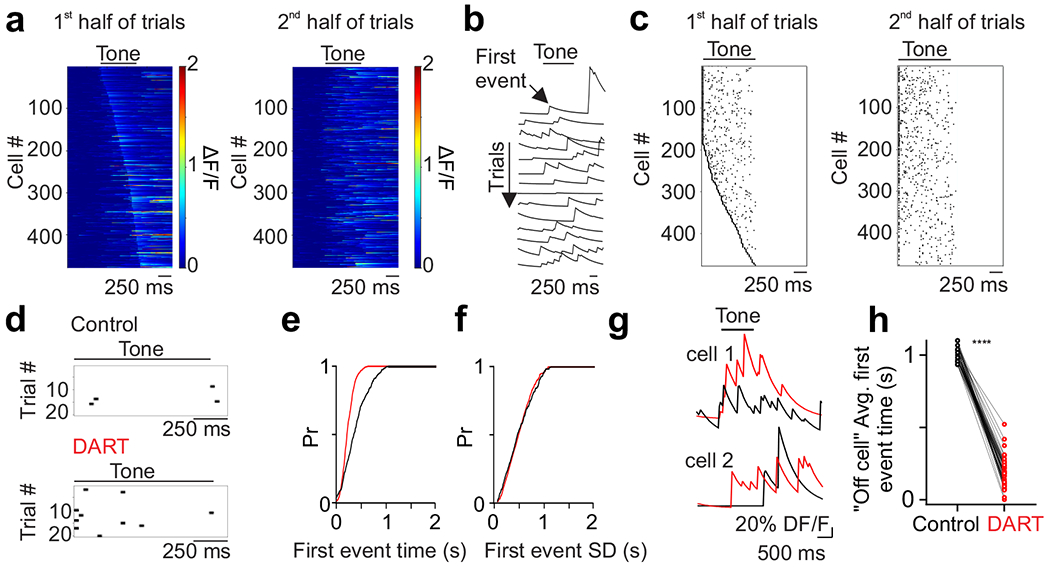
a. Left, mean tone-evoked responses on the first half of trials for all cells ordered by peak response time (n = 478 cells, n = 3 mice). Right, same as on left for the second half of trials, ordered according to peak responses during the first half. b. Example calcium traces (ΔF/F) from a granule cell during sequential tone presentation trials. Arrow notes first event following tone onset. c. Left, first event times for all cells during the first half of trials ordered by timing of earliest first event. Right, first event times during the second half of trials ordered the same as on left. d. First event times for significant trials of an example cell in control (top) and after DART infusion (bottom). e. Cumulative distribution of mean first event times for all cells in control (black; n = 1631) and after DART infusion (red; n = 3718; Kolmogorov-Smirnov p<0.0001). f. Same as e, for mean standard deviation of first event times (Kolmogorov-Smirnov p = 0.9859). g. Example traces in control (black) and after DART infusion (red) for two example cells. Note the cell on the top has an increase in peak activity without a change in onset, while the cell on the bottom responds to tone offset in control but tone onset in DART. h. Mean response time in control (black) and after DART (red) for cells with a mean first peak time at or after tone offset in control conditions (n=47; paired t-test p<0.0001).

Both classical models^{5, 6} and in vivo whole-cell recordings¹³ have suggested that inhibition restricts granule cell sensory responses due to spike thresholding. Therefore, local inhibition could explain the low probability and amplitude of individual granule cell trial-by-trial responses. To test how local synaptic inhibition regulates sensory-evoked granule cell responses, we used the DART system¹⁹ to selectively block GABA_A receptors on granule cells (Fig. 1, Supplementary Fig. 1,6-8). Here, we expressed a GPI-anchored HaloTag Protein (HTP_GPI) in granule cells to acutely and specifically antagonize GABA_A receptors upon infusion of gabazine.1^DART.2 (Fig. 1, “DART”). This manipulation dramatically altered responses to all sensory stimuli tested (Fig. 1, Supplementary Figs. 2,3), producing significantly larger mean population responses (Fig. 1d-e,i-j), increased response probability (Fig. 1f,k; auditory: 0.38 ± 0.00, n = 3360 cells, p<0.0001, paired t-test; somatosensory: 0.31 ± 0.01, n = 815 cells, p<0.0001, paired t-test), and increased amplitude of single trial responses (Fig. 1g,l; auditory: 0.60 ± 0.02 ΔF/F, n = 1942 cells, p<0.0001, paired t-test; somatosensory: 0.88 ± 0.07, n = 315 cells, p<0.0001, paired t-test). These changes in single trial response probability and amplitude were observed across all individual variations of auditory and somatosensory stimuli tested (Supplementary Figs. 2-3).

In addition to changes in sensory evoked responses, we also observed a significant enhancement of spontaneous activity when inhibition was blocked (Fig. 1c,h, control F: 0.000 ± 0.000, DART F: 0.004 ± 0.001, n = 1616 cells, p<0.0001, paired t-test). This effect is consistent with previous data revealing that a non-specific block of GABAergic inhibition in the cerebellar cortex increases spontaneous granule cell spiking and can degrade the signal-to-noise ratio of sensory evoked responses³⁵.

To test the selectively of these effects, we used a variation of gabazine.1^DART.2 that cannot bind HTP (non-binding gabazine.1^nbDART, “nbDART”) and a variation of HTP that cannot bind ligand (^ddHTP). Neither nbDART infused into animals expressing HTP, nor DART infused into animals expressing ^ddHTP significantly changed auditory or somatosensory responses (Supplementary Figs. 6,7). Together, these results are consistent with a central role of GABAergic inhibition in enforcing granule spike thresholds to restrict population activity, maintaining sparsity of spiking both within and across trials.

Importantly, many granule cells that are silent in control conditions become responsive after blocking synaptic inhibition, resulting in a dramatic increase in the number of granule cells responsive to both auditory and somatosensory stimulation (Fig. 1c,h, Fig. 2a). We therefore compared the number of responsive cells to a conservative estimate of the total cells present in our field of view (based on the size of ROIs detected with our analysis, see Methods). This allowed us to estimate that, under baseline conditions, approximately 5.2 ± 0.5% of granule cells in our field of view responded to any individual auditory stimulus and 1.1 ± 0.2% of granule cells responded to any individual somatosensory stimulus (Fig. 2b). Following block of synaptic inhibition, there was a large expansion in the fraction of granule cells responsive to both auditory (13.1 ± 1.3%, p<0.0001, n = 26 stimulus conditions, paired t-test) and somatosensory (7.7 ± 2.1%, p<0.01, n = 12 stimulus conditions, paired t-test) stimuli (Fig. 2b). Two points merit emphasis: First, these results indicate that the fluorescent granule cell responses we have measured are unlikely to reflect subthreshold activity, as the majority of granule cells were not responsive until inhibition was blocked. These cells necessarily received excitatory input in control conditions that was not reported by GCaMP activity. Second, the sparsity of granule cell population responses we have measured is due to local synaptic inhibition, not a sparsity of incoming mossy fiber input.

Figure 2. Synaptic inhibition restricts the number of granule cells recruited by sensory input.

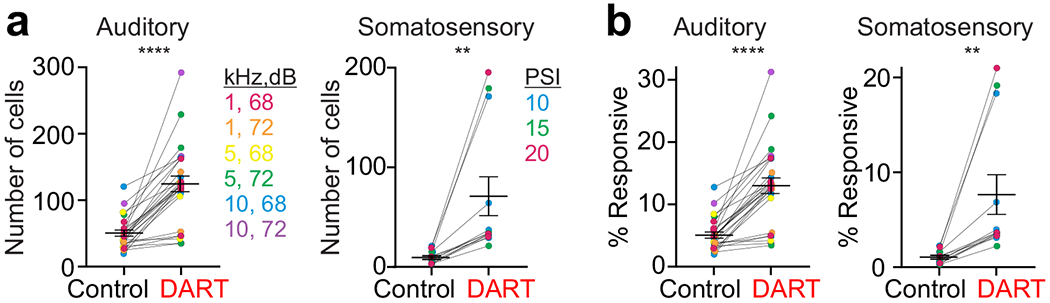
a. Number of responsive cells in each mouse before and after DART for each auditory (left, n = 6 mice) and somatosensory (right, n = 6 mice) stimulus. Colors represent specific stimulus conditions; note that not all stimulus conditions were tested in each mouse. Error is SEM across conditions. b. Same as a, for fraction of total responsive cells. **p<0.01, ****p<0.0001, paired t-test (a-b).

Inhibition establishes discrete unisensory ensembles

Given that each stimulus evokes sparse granule cell activity under control conditions, we next asked whether individual granule cells respond selectively to distinct stimuli. We find that granule cells prefer individual stimulus features, such that cells with robust responses to auditory stimuli of a given frequency respond more weakly to other frequencies (Fig. 3a-g; n = 3 mice; all comparisons to preferred stimulus: p<0.0001, one-way ANOVA). Similarly, neurons that respond to a given somatosensory (Fig. 3i, Supplementary Fig. 10; all comparisons to preferred stimulus: p<0.05, one-way ANOVA) or auditory (Supplementary Figs. 9,10; all comparisons to preferred stimulus: p<0.0001, one-way ANOVA) stimulus intensity respond less strongly to other intensities. Notably, these stimulus preferences were graded, and across the population there was considerable variability in the responsivity to nonpreferred stimuli (Fig. 3b-d, Supplementary Fig. 10).

Figure 3. Cerebellar granule cells exhibit stimulus feature preferences that are not abolished by blocking synaptic inhibition.

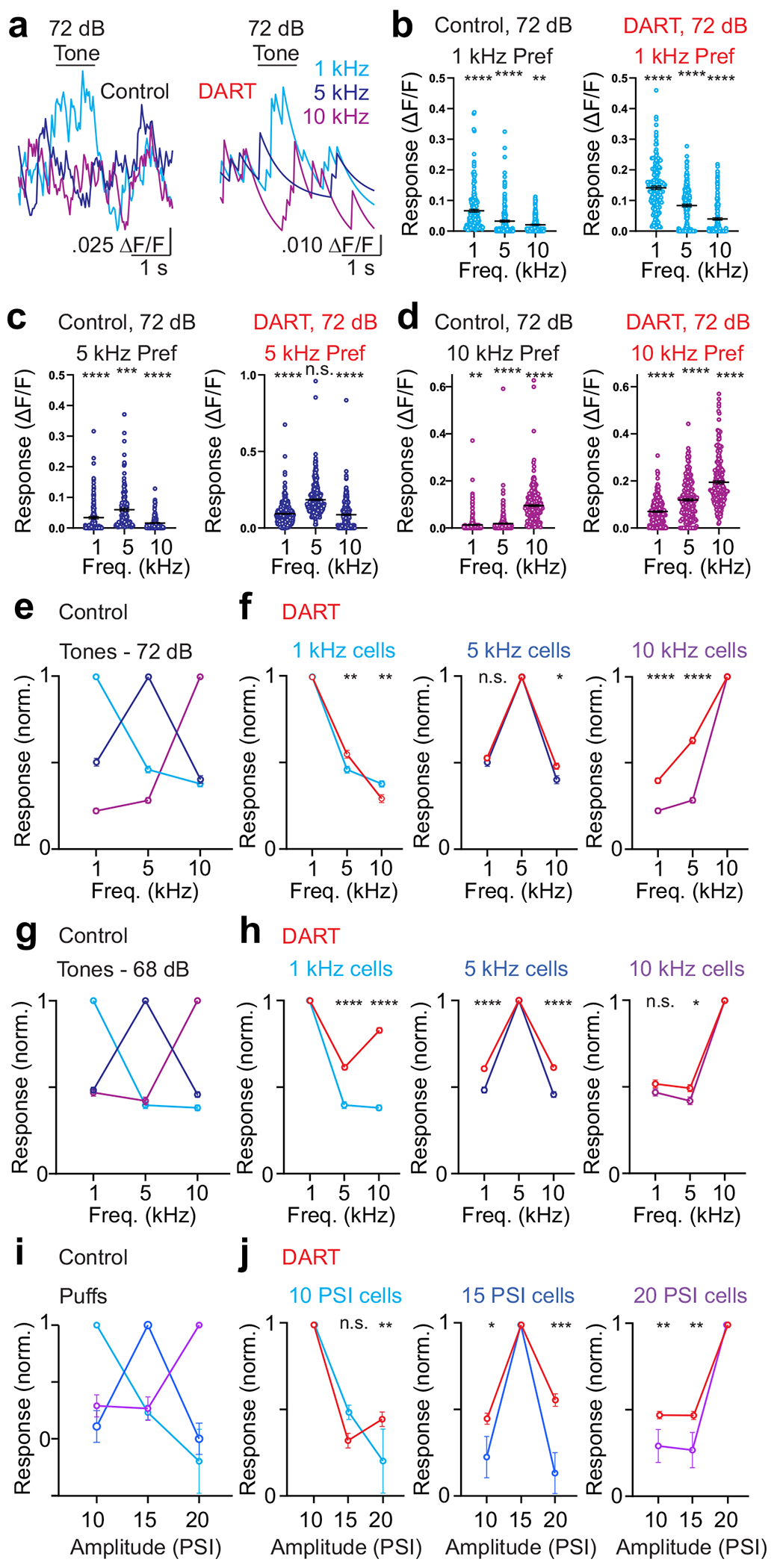
a. Average change in fluorescence (ΔF/F) for an example cell in response to pure tones at 1 kHz (light blue), 5 kHz (dark blue), and 10 kHz (magenta). Note that the cell responds preferentially to a 1 kHz tone before (left) and after (right) DART infusion. b. Maximum responses for cells significantly responsive to 72 dB tones that prefer 1 kHz. Error is SEM across cells (control: n = 184 cells, DART: n = 170 cells; n = 3 mice). c. Same as b, for cells preferring 5 kHz (control: n = 141 cells, DART = 331 cells). d. Same as b, for cells preferring 10 kHz (control: n = 313, DART: n = 224). e. Normalized responses in control conditions for all granule cells responsive to 72 dB tones, grouped according to the frequency that drove the maximum response: 1 kHz: n = 184 cells; 5 kHz: n = 141 cells; 10 kHz: n = 313 cells; n = 3 mice. Error is SEM across cells. f. Same as e, for tone-responsive granule cells before and after DART infusion (red): 1 kHz: n = 170 cells; 5 kHz: n = 331 cells; 10 kHz: n = 224 cells. g. Same as e, for granule cells responsive to 68 dB tones preferring: 1 kHz: n = 227 cells; 5 kHz: n = 211 cells; 10 kHz: n = 166 cells; n = 3 mice. h. Same as e, for tone-responsive granule cells before and after DART infusion (red): 1 kHz: n = 250 cells; 5 kHz: n = 297 cells; 10 kHz: n = 169 cells. i. Same as e, for all puff responsive cells preferring: 10 PSI: n = 45 cells; 15 PSI: n = 47 cells; 20 PSI: n = 74 cells; n = 3 mice. j. Same as i, for puff responsive cells before and after DART infusion (red): 10 PSI: n = 100 cells; 15 PSI: n = 69 cells; 20 PSI: n = 202 cells). *p<0.05, **p<0.01, ***p<0.001, ***p<0.0001, one-way ANOVA.

We next tested how GABAergic inhibition regulates stimulus preferences in granule cells. In neocortical cells, there is evidence that sensory tuning can by sharpened by local synaptic inhibition in some conditions³⁶. For granule cells matched between control and after DART infusion (i.e. those responsive in both conditions), we find that removal of synaptic inhibition partially alters stimulus preferences (Fig. 3f,h,j), though mean population preferences remained significant when inhibition was blocked (Supplementary Fig. 10; auditory: all comparisons to preferred stimulus: p<0.0001, one-way ANOVA; somatosensory: all comparisons to preferred stimulus: p<0.0001, one-way ANOVA). Consistent with enhanced response probabilities in DART, which led to an increased fraction of cells responding to more than one stimulus (Supplementary Fig. 11), stimulus tuning was broadened modestly by blocking inhibition. Overall, however, these data suggest that granule cell stimulus preferences are largely inherited from presynaptic mossy fiber input, consistent with the small number of mossy fibers that impinge on individual granule cells and the lack of recurrent processing among granule cells.

To test how these stimulus preferences establish discrete population responses, we first measured the overlap across activated populations. We find that granule cells that respond to each stimulus feature establish ensembles with partial overlap (Fig. 4a,b; auditory fraction overlap: 0.53 ± 0.02, n = 6 stimulus conditions; somatosensory fraction overlap: 0.06 ± 0.01, n = 3 stimulus conditions).

Figure 4. Synaptic inhibition facilitates pattern separation for auditory and somatosensory responsive granule cell ensembles.

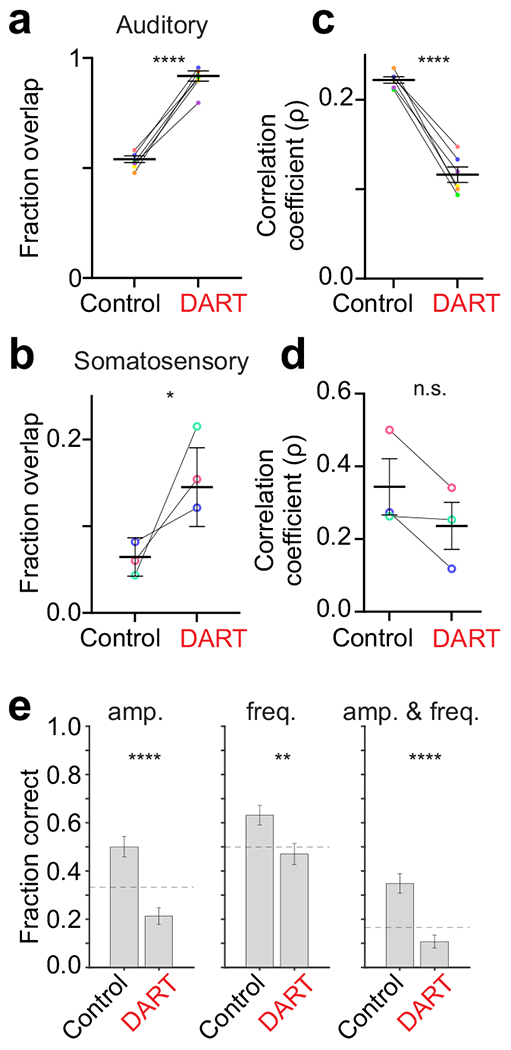
a-b. Fraction of overlap for each stimulus condition (colors) and across all conditions (black) before and after DART for auditory (a; n = 6 stimulus conditions, each in 3 mice) and somatosensory (b; n = 3 stimulus conditions, each in 3 mice) stimuli. Error is SEM across conditions. c-d. Same as a-b for the Pearson correlation of neuronal identity across trials. *p<0.05, ****p<0.0001, n.s.; p = 0.35, paired t-tests (a-d). e. Classification performance for an example mouse under control (328 cells, 23x6 trials) and gabazine.1^DART.2 (319 cells, 22x6 trials) conditions for correctly identifying the sound amplitude only (left; p = 4.14x10⁻⁷), frequency only (middle; p = 0.0039), and amplitude and frequency (right; p = 1.17x10⁻⁶). Dashed lines indicate chance performance. Error bars are SEM estimated using the Wald method for binomial distributions. p-values calculated from the Wald Test (one-sided). **p<0.001, ***p<0.001.

On average, auditory ensembles contained 83.7 ± 14.7 cells, whereas somatosensory ensembles contained only 29.4 ± 6.5 cells. Therefore, the average overlap for auditory ensembles was 44.3 ± 0.2 cells, but only 1.8 ± 0.1 cells for somatosensory ensembles. This was partly due to the smaller size of somatosensory ensembles and fewer stimulus conditions for this modality, but may also be partly due to their greater stability (Fig. 4c,d).

In the DART condition, where there is a large number of responsive cells that were unresponsive in control conditions, we find significantly more overlap between the ensembles that are responsive to each individual stimulus (Fig. 4a,b; auditory: 0.90 ± 0.02, n = 6 mice, p<0.0001, paired t-test; somatosensory: 0.16 ± 0.03, n = 3 mice, p = 0.03, paired t-test). Thus, blocking synaptic inhibition decreases the separability of the average population response to different sensory stimuli.

Sensory discrimination can also be influenced by trial-over-trial variability. Despite representing different stimuli with discrete ensembles, there was significant variability across trials within each ensemble of cells responding to any given stimulus feature (Fig. 4c,d). On average, each ensemble of responsive granule cells was only weakly correlated across trials (Pearson correlation, auditory: ρ = 0.22 ± 0.00; somatosensory: ρ = 0.34 ± 0.08). Thus, while the sparse population response allows for discrete granule cell ensembles to represent individual stimulus features on average, the ensembles can be somewhat stochastic across trials, a feature that may contribute to the relatively slow time course cerebellar learning as compared with some other forms of associative learning^{37, 38}. Notably, despite the smaller ensemble sizes, we observed a higher correlation across trials within somatosensory ensembles.

Importantly, the large number of newly active cells in DART also added variability to ensemble identities, as ensembles became even less correlated across trials when inhibition was blocked (Fig. 4c,d; auditory: 0.12 ± 0.01, 21.9 ± 0.8 trials/ensemble, 6 mice, p<0.0001, paired t-test; somatosensory: 0.24 ± 0.06, 16.7 ± 2.9 trials/ensemble, 3 mice, p = 0.35, paired t-test). These results suggest that the higher mean response probability in DART (Fig. 1) is not sufficient to counter the variability introduced by the large number of additional responsive cells when inhibition is blocked. Together, these results indicate that inhibition serves to segregate granule cell ensembles representing discrete stimulus features largely by thresholding population activity.

By limiting population overlap, we expect that inhibition increases granule cell pattern separation and thereby improves discriminability of sensory inputs. To determine whether inhibition in fact serves to increase the discriminability of sensory ensembles, we used the mouse with the largest number of trials per stimulus conditions to train a decoder to identify presented stimuli (Methods). Under control conditions, using a population of 321 granule cells, single trial auditory responses could be correctly categorized above chance according to their amplitude, their frequency, or the combination of amplitude and frequency (Fig. 4e, amplitude p = 0.008, frequency p = 0.003, amplitude and frequency p = 6.26x10⁻⁵, Student’s t-test). When synaptic inhibition was blocked with DART, however, categorization was significantly impaired for all stimulus conditions (Fig. 4e, control vs DART; amplitude p = 4.14x10⁻⁷, frequency p = 0.004, amplitude and frequency p = 1.17x10⁻⁶, paired t-test), falling below chance performance. For somatosensory responses, the smaller ensemble sizes prevented robust decoding, but the same trends remained comparing control and DART conditions (Control: 51.1 ± 12.9% correct DART: 42.2 ± 12.8% correct (chance = 33% correct), p = 0.2). Thus, while a dataset with more trials per stimulus condition is needed for a quantitative understanding for how the loss of inhibition alters the decoding of granule cell population responses, these results support a key role for granule cell synaptic inhibition in maintaining sensory pattern separation.

Multiple inhibitory computations shape multisensory ensembles

Our data indicate that excitatory inputs from mossy fibers and local synaptic inhibition can establish ensembles of granule cells that encode individual sensory stimuli. However, it has also been demonstrated anatomically and physiologically that some granule cells receive mossy fiber input from more than one source^7–9, and it is thought that integration of these inputs can enhance the diversity of granule cell encoding^5–7. Therefore, we next tested the principles that govern this integration by examining population responses to overlapping stimuli of two different modalities (Fig. 5).

Figure 5. Coincident stimuli create unique granule cell ensembles.

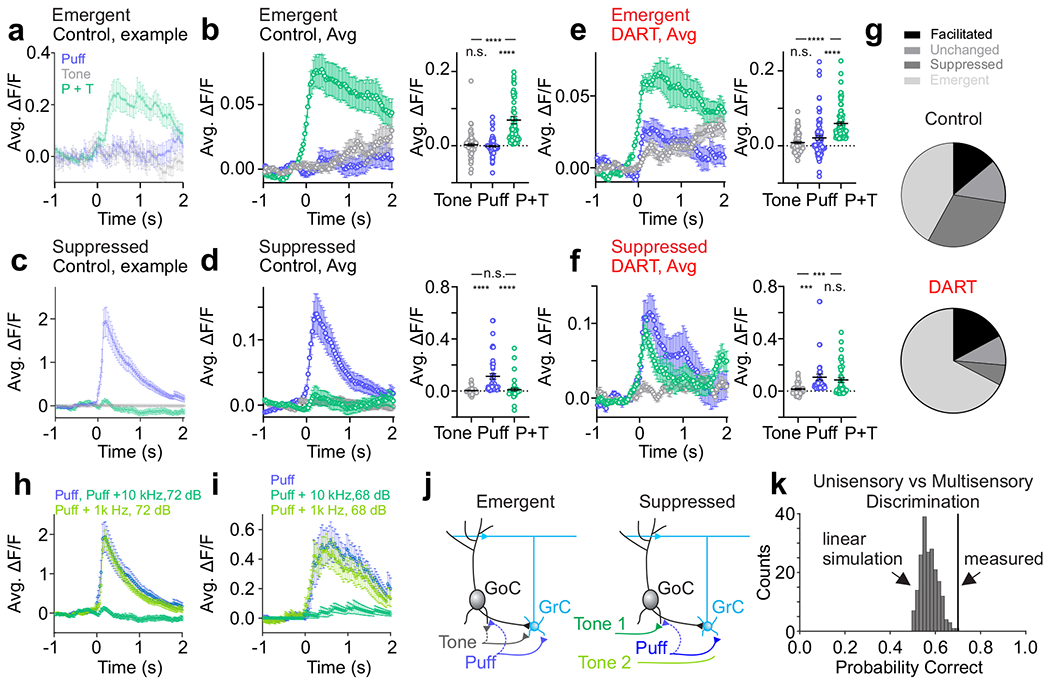
a. Time course of responses to uni- (tone: gray; puff: blue) and multisensory (tone + puff: green) stimuli for an example emergent cell (puff n = 17 trials, tone n = 13 trials, tone+puff n = 24 trials). Error is SEM across trials. b. Left, same as a, for all emergent cells (n = 79 cells, subset matched to DART condition, n = 3 mice). Right, amplitude of responses to tone, puff and tone + puff for all matched emergent cells. Error is SEM across cells. c-d. Same as a-b, for matched suppressed cells (n = 43 cells, n = 3 mice). e-f. Same as b and d, for matched cells after DART infusion. g. Pie charts illustrating relative prevalence of each response category before (top; facilitated: n = 161, unchanged: n = 158, suppressed: n = 355, emergent: n = 488) and after (bottom; facilitated: n = 172, unchanged: n = 93, suppressed: n = 63, emergent: n = 676) DART infusion. h-i. Example cells illustrating stimulus-specific suppression. Both cells respond robustly to the puff alone (blue), but each is suppressed in response to a specific combination of puff and tone of a given frequency and amplitude (dark green), but not a different frequency and amplitude (light green) (h, puff n=17 trials, puff+1kHz 72dB n = 24 trials, puff+10kHz 72dB n = 24 trials; i, puff n = 17 trials, puff+1kHz 68 dB n = 24 trials, puff+10kHz 68dB n = 24 trials). Error is SEM across trials. j. Granule cell layer circuit motif that would produce emergent responses (left) and stimulus-specific suppression (right). GrC- granule cell; GoC- Golgi cell. k. Black line indicates uni- vs. multisensory discrimination performance from granule cell population responses. Distribution shows discrimination performance for 200 sets of simulated multisensory responses generated by linearly combining random draws from two unimodal responses (one auditory and one somatosensory). The classification performance indicated by the black line has a z-score of 3.21, corresponding to p = 0.0023. ***p<0.001, ****p<0.0001, RM ANOVA with Tukey’s multiple comparisons (b,d,e,f).

Consistent with previous single cell recordings showing enhanced spiking in response to convergent multisensory mossy fiber input^{7, 9}, we find that some cells exhibit larger responses to combined auditory and somatosensory input than to somatosensory input alone (Supplementary Fig. 12, “facilitated”, n = 161 cells, p<0.01, RM ANOVA with Tukey’s multiple comparisons). Thus, part of the population code representing multisensory stimulus combinations is reflected by increased activity within the same cells that respond to each stimulus in isolation.

We also find, however, that the identity of cells that define multisensory ensembles differ with respect to the ensembles representing each stimulus in isolation in two important ways: First, we find that many granule cells with no significant responses to either stimulus alone became active in response to combined auditory and somatosensory stimulation (Fig. 5a,b,g and Supplementary Fig. 19, “emergent”, n = 488 cells, tone or puff vs. tone + puff: p<0.0001, RM ANOVA with Tukey’s multiple comparisons). These data suggest that integration of both stimulus modalities is necessary to drive these granule cells above spike threshold. These ‘emergent’ cells thus generate a novel multisensory ensemble by adding new cells that are not present in the ensembles representing each stimulus in isolation.

Second, we also observed a large population of granule cells that are suppressed in response to combined somatosensory and auditory stimulation (Fig. 5c,d,g and Supplementary Fig. 19, “suppressed”, n = 355 cells, puff vs. tone + puff: p<0.0001, RM ANOVA with Tukey’s multiple comparisons). Many of these cells are completely silenced, thus subtracting them from the ensembles representing individual stimuli in isolation. This effect therefore further separates the new, multisensory ensemble from the unisensory ensembles. Together, the emergent and suppressed populations of granule cells represent the vast majority of total granule cells in our measurements (Fig. 5g), suggesting that whatever mechanism is responsible for these computations is critical for the encoding of complex multisensory stimuli in the granule cell layer.

To test whether local synaptic inhibition provides the necessary mechanism to establish suppressed and emergent populations, we again utilized the DART system to acutely block inhibition. An analysis of matched cells between control and DART conditions revealed that inhibition powerfully shapes both the emergent and suppressed granule cell populations (Fig. 5e,f,g). Specifically, though emergent cells had no significant response to either stimulus alone in control conditions, we find that blocking synaptic inhibition revealed responses to each individual stimulus (Fig. 5e, tone = 0.8 ± 2.9% ΔF/F, puff = 2.1 ± 0.6% ΔF/F, n = 79 cells, p<0.0001, paired t-test), again consistent with a spike thresholding effect. These data also contextualize the strategy of utilizing widespread subthreshold input instead of sparse, high-fidelity suprathreshold input, as it would not be possible to generate these unique emergent multisensory ensembles with the latter strategy.

We also find that the suppressed population was dependent on synaptic inhibition, as suppression was abolished in the presence of DART (Fig. 5f, n = 43 cells, puff vs. tone + puff: p = 0.38, RM ANOVA with Tukey’s multiple comparisons). These data indicate that inhibition can be recruited in a stimulus-specific manner, where in this case, auditory input can recruit inhibition that suppresses responses to somatosensory input, but does not directly excite these granule cells even in the absence of inhibition. In this manner, local inhibition can mediate subtractive stimulus integration, operating to suppress the response of one input when another is present. Consistent with theoretical work, which has hypothesized that such a mechanism could act to diversify granule cell representations by reducing ensemble overlap during combined stimulus presentations³⁹, our data indicate that stimulus-specific suppression provides a widespread and powerful means to generate unique multisensory ensembles.

To further explore this computation, we varied the features of co-presented stimuli. We find that suppression can be specific even within the same modality during co-presentation of stimuli with different features (Fig. 5h,i and Supplementary Fig. 19). These data suggest that local synaptic inhibition is a crucial source for generating diversity in granule cell population responses during complex sensory input, segregating multisensory ensembles from each other and from those representing each stimulus in isolation (Fig. 5j).

To test this directly, we trained a decoder to categorize a stimulus as either unisensory (auditory or somatosensory), or multisensory. Stimuli were correctly categorized on 70% of trials (Fig. 5k, decoding 521 granule cell responses from 30 unisensory and 30 multisensory trials, 3 mice). To determine how stimulus-specific inhibition and thresholding of emergent cells contribute to discrimination of multisensory ensembles, we synthesized multisensory population responses that consisted exclusively of the linear summation of measured unisensory responses (see Methods). We find that these synthetic multisensory responses are significantly less discriminable from the unisensory responses as compared to measured multisensory responses (Fig. 5k, p = 0.0023). This reveals that the population diversity generated by the novel multisensory interactions identified here (stimulus-specific suppression and emergent responses) serve to significantly enhance pattern separation in the granule cell layer.

Sensory responses can exhibit temporal variability

In addition to population identity, the timing of granule cell activity has been hypothesized to play an important role in behavior and learning^{4, 40, 41}. Therefore, we also tested how granule cells represent the timing of sensory input and how this depends on local synaptic inhibition. We find that the average responses of individual granule cells during a 1-second auditory stimulus forms a population response that tiles the duration of the stimulus (Fig. 6a)⁴². Surprisingly, however, we find that many granule cells do not respond with reproduceable timing across trials (Fig. 6a). Because the peak of mean ΔF/F responses can be biased by a small number of trials with large responses, we also computed response timing according to the onset of fluorescent responses during the stimulus window on individual trials (Fig. 6b,c). This measure again supports the conclusion that the timing of most granule cell responses is not reproduceable across trials (Fig. 6c). To quantify this variability, we measured the jitter in response onset across trials (Fig. 6d). While a subset of granule cells (17.6%) responded with relatively low jitter, exhibiting a S.D. less than 100 ms across trials, we found that most granule cells have an onset time that varies by hundreds of milliseconds across trials (Fig. 6f; control onset S.D. = 0.77 ± 0.02). These results suggest that a large fraction of granule cells do not exhibit a high degree of across-trial consistency during a 1-second stimulus, which is on the longer range for stimuli that drive robust cerebellar learning. Notably, however, we did find that earlier responding granule cells exhibited higher response probabilities and less jitter on average (Supplementary Fig. 13), supporting the hypothesis that they may receive stronger inputs. In line with this idea, earlier responding cells were also less sensitive to blocking inhibition (Supplementary Fig. 13). Together, these results may support the idea that reduced across-trial consistency of granule cell responses at longer intervals could degrade learning for prolonged stimuli⁴³.

We find that blocking synaptic inhibition shifts the distribution of response onset times earlier (Fig. 6d,e and Supplementary Fig. 14-15; first event times: control, n = 1631 cells, DART, n = 3718 cells; Kolmogorov-Smirnov p<0.0001). Surprisingly, however, we do not observe a corresponding reduction in response jitter (Fig. 6f, Kolmogorov-Smirnov p = 0.9859). This was due to the higher response probability across trials in the DART condition, where there were many more total trials with significant stimulus responses (Fig. 6d). As a result, while there were more trials with earlier response times when inhibition was blocked, there were also more trials with late responses, preventing an overall change in mean response jitter (Fig. 6d,f). These data are consistent with previous results suggesting that response timing in granule cells is not exclusively regulated by synaptic inhibition⁴⁴ and must, therefore, also reflect parameters such as variability in input timing, and cellular properties such as short-term plasticity of mossy fiber input⁷ and the intrinsic membrane properties of granule cells⁴⁵.

In control conditions, we also find that many granule cells respond at or near the offset of the auditory stimulus (Fig. 1c, 6a,g). These ‘off’ cells represented 5.4% of the responsive population. When inhibition was blocked, these cells responded much earlier during the auditory stimulus (Fig. 6g-h; n = 47 cells, p<0.0001, paired t-test). This indicates that, under control conditions, recruitment of inhibition during the sensory stimulus prevents these cells from responding immediately, even though they receive sufficient excitation during the stimulus to drive spiking if inhibition is removed. Together, these data suggest that inhibition serves to diversify the temporal responses of granule cells by both limiting the number of early responses during a stimulus presentation and establishing a population of cells that selectively represents the late component of sensory input.

Inhibition is required for cerebellum-dependent behavior

Our data reveal that synaptic inhibition powerfully restricts the population of granule cells recruited by sensory input and shapes many features of the population ensembles that encode sensory stimuli. In principle, these effects may support the predictions of classical and recent computational models^{5, 6, 46} proposing that granule cell inhibition acts to segregate the population codes necessary for both learning and the expression of learned behaviors. To test this hypothesis directly, we utilized the cerebellum-dependent task delay eyelid conditioning. For this task, mice were trained on a freely moving treadmill⁴⁷ to associate a brief corneal air puff (unconditioned stimulus, “US”) with a co-terminating neutral auditory tone (5 kHz, 250 ms; conditioned stimulus, “CS+”; Fig. 7a-d). We first trained mice until the probability of conditioned responses (“CR”) in each session had plateaued (0.80 ± 0.06, n = 8 mice; Fig. 7d). In a subset of mice, infusion of muscimol into the eyelid conditioning region of the cerebellar cortex at the floor of the primary fissure, which spread into the anterior interpositus⁴⁷, abolished conditioned responses, confirming cerebellar dependence (n = 3 mice; Fig. 7c and Supplementary Fig. 16). Notably, this is a different area than we used for our imaging experiments since it is too deep for optical access. We expect, however, that the principles by which synaptic inhibition influences sensory integration are conserved, given the stereotyped circuitry of granule cell layer.

Figure 7. Local synaptic inhibition is necessary for expression of a sensorimotor association.

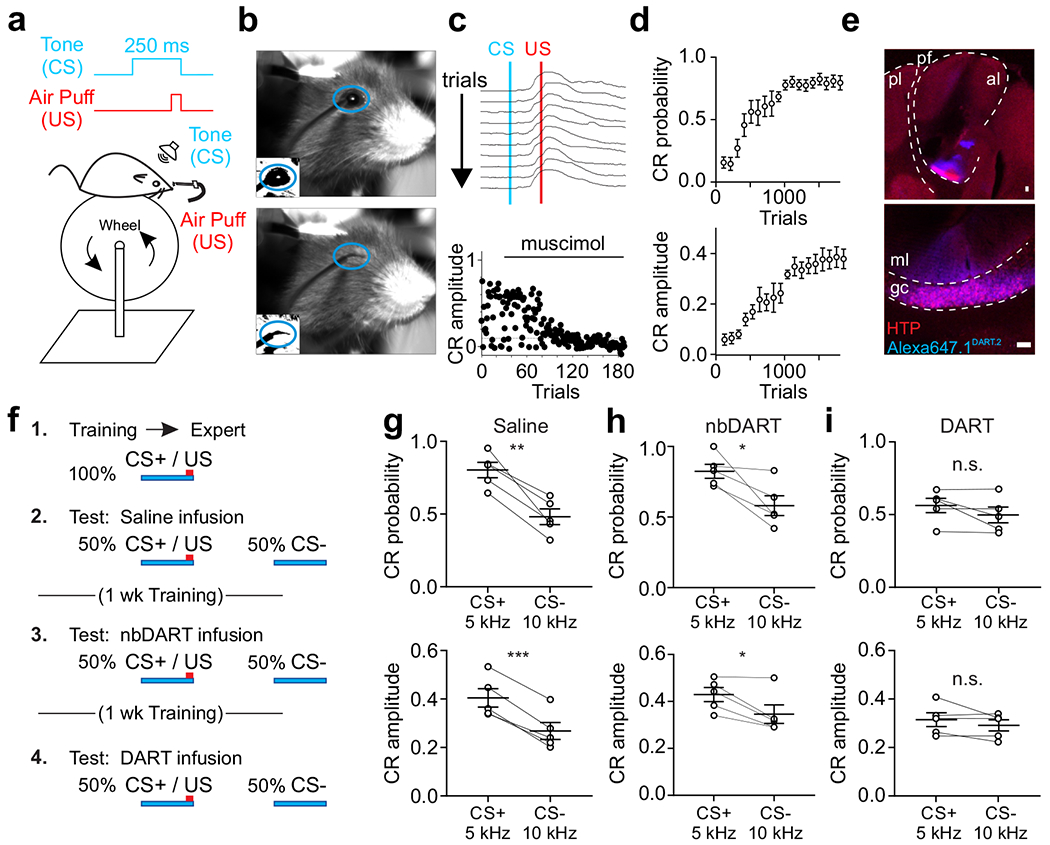
a. Schematic of experimental design. CS: conditioned stimulus (tone); US: unconditioned stimulus (corneal air puff). b. Sample frames before (top) and after (bottom) air puff delivery. Blue oval indicates ROI analyzed to evaluate conditioned responses. Insets show thresholded binary image used for calculating fractional eyelid closure. c. Top, example consecutive eyelid traces from a trained mouse. Blue line marks onset of tone (CS). Red line marks onset of US. Note the eyelid begins to close before the US. Bottom, time course of conditioned response (CR) amplitude for a trained mouse on trials before and after local infusion of muscimol (1 mM). d. Average CR probability (top) and amplitude (bottom) during training (n=8 mice). Error is SEM across mice. e. Example confocal images (scale 50 μm) of a representative mouse expressing HTP (red) in granule cells in the eyelid conditioning region with bound Alexa647.1^DART.2 (cyan). Top, pl: posterior lobe; al: anterior lobe; pf: primary fissure. Bottom, ml: molecular layer; gc: granule cell layer. f. Experimental time course. CS+: tone frequency paired with air puff (5 kHz); CS−: unpaired tone frequency (10 kHz); nbDART: non-binding gabazine.1^nbDART. g. Average CR probability (top) and amplitude (bottom) for individual mice during presentation of CS+ and CS− trials after saline infusion (n = 5 mice). h. Same as g, after infusion of gabazine.1^nbDART (1 μM). i. Same as g, after infusion of gabazine.1^DART.2 (1 μM). *p<0.05, **p<0.01 ***p<0.001, paired t-test (g-i). Error bars are SEM.

To test whether mice could discriminate between the learned CS+ and similar auditory stimuli that had not been paired with a US during learning (CS−), we next measured responses in a cohort of mice for which two different CS− tones (1 and 10 kHz) and the CS+ tone were presented on randomly interleaved trials. In these experiments, consistent with previous work in rabbits^{48, 49} and mice⁵⁰, we find that the response probability and amplitude of CRs were significantly and equivalently reduced for both CS− tones as compared to the CS+ tone (Supplementary Fig.17; n = 4 mice; CR probability: CS+ vs. CS− (1 kHz or 10 kHz): p<0.005; RM ANOVA with Dunnett’s multiple comparisons; CR amplitude: CS+ vs. CS− (1 kHz or 10 kHz): p<0.05). Because we obtained the same result for two different CS− tones, we moved forward in testing a single CS− for DART experiments to maximize trial numbers.

To test whether granule cell inhibition is critical for sensory integration in this cerebellum-dependent task, we again utilized the DART system to block GABA_ARs. In a well-trained cohort expressing HTP in granule cells in the eyelid conditioning region of the cerebellar cortex (Fig. 7e), mice were subjected to 3 test sessions, each one week apart with daily CS+ only training in between (Fig. 7f). Test sessions with control infusions of saline or nbDART into the eyelid conditioning region revealed that trained mice effectively distinguished the CS+ from a single tone with a different frequency (10 kHz, 250 ms; “CS−”) (Fig. 7g-h; n = 5 mice; CS+ vs CS− in saline: CR probability: p<0.005, paired t-test; CR amplitude: p<0.0005; CS+ vs CS− in nbDART:, CR probability: p = 0.03, paired t-test, CR amplitude: p = 0.03, paired t-test). However, blocking synaptic inhibition to granule cells in the eyelid conditioning region with functional DART reduced conditioned response probability and amplitude during CS+ trials such that behavior was indistinguishable from CS− trials (Fig. 7i; n = 5 mice; CS+ vs CS− in DART: CR probability: p = 0.19, paired t-test; CR amplitude: p = 0.25). DART infusion did not significantly impact responses to the CS− (saline vs DART: CR probability: p = 0.89, paired t-test; CR amplitude: p = 0.69). Interestingly, we did not observe an effect on the trajectory of CRs when granule cell inhibition was blocked (Supplementary Fig. 18), suggesting that response kinematics may be largely shaped downstream, perhaps by inhibition and excitation onto Purkinje cells or elsewhere in the circuit. Together, these data indicate that granule cell inhibition is necessary for accurate cerebellum-dependent sensorimotor responses by shaping the contextual representations that are harnessed for behavior.

Discussion

By imaging granule cell responses to discrete sensory input while manipulating local synaptic inhibition, we have revealed multiple key computations that extend classical Marr-Albus models of granule cell layer processing. First, we find that local synaptic inhibition can enforce sparse granule cell population activity in terms of both response probability and cell number. Moreover, consistent with its role as a pattern separation layer, we find that granule cells represent sensory stimuli as discrete ensembles that also depend on inhibition to limit overlap. For multisensory ensembles, inhibition defines population codes by establishing multisensory-only cells and suppressing responses of unisensory cells in a stimulus-specific manner. In these ways, which extend the predictions of classical models, inhibition can generate novel multisensory granule cell ensembles that enhance pattern separation. Finally, in agreement with our imaging data suggesting that inhibition serves a central role in establishing discrete sensory representations, we find that granule cell inhibition is required for accurate sensorimotor behavior in a cerebellum-dependent task.

Recent work has shown that, during complex behaviors, granule cell activity can be denser than was predicted by classical Marr-Albus models^15–18. In contrast, our goal was to isolate discrete sensory responses, independent of motor-related signals and contextual modulation²⁶. With this experimental design, population responses were relatively sparse for auditory and somatosensory stimuli. It is possible that when combined with motor inputs, these stimuli would activate denser sensory representations as seen during complex behavior. However, the cells recruited during whisking were largely distinct from those activated by tones and orofacial puffs. This supports an alternative interpretation, where the density of responses observed during complex behaviors may represent the joint activity of different motor and sensory ensembles.

The sparsity of sensory ensembles depended on synaptic inhibition. For unisensory stimuli, inhibition acted primarily via spike thresholding, as blocking inhibition dramatically increased the responsive population, producing large scale overlap across ensembles. Spike thresholding also played a key role in generating multisensory ensembles by establishing cells that only respond to specific input combinations. Notably, this would not be possible with sparse mossy fiber input that instead drove high fidelity granule cell spiking. Thus, we speculate that it may be more appropriate to consider thresholding inhibition as a mechanism to enhance combinatorial diversity of granule cell responses than to enforce population sparsity per se.

While the thresholding effects of calcium indicators might artificially sparsen representations and enhance the effects of blocking inhibition, the stimulus-specific inhibition we observe is not sensitive to this caveat. This subtractive mechanism regulated a large fraction of cells in our multisensory experiments, representing a powerful additional means of pattern separation. Such lateral inhibition may explain early measurements showing that inhibition can vary according to the specific combination of vestibular nerve stimulation⁵¹, and is supported by in vitro measurements suggesting that Golgi cells can be recruited in a pathway specific manner⁵². Moreover, recent experiments have revealed that, while many Golgi cells are coordinated during behavior, a large fraction can also display diverse activity patterns that may reflect stimulus specific drive⁵³. Indeed, our measurements reveal that stimulus-specific recruitment of inhibition is a widespread mechanism that shapes multisensory population activity in vivo. Notably, this mechanism is in direct opposition to the concept of Golgi cell inhibition of granule cells acting exclusively as a broad, general feedback system proposed by classical Marr-Albus theories.

Together, these findings suggest that inhibition can provide the granule cell layer with an even greater capacity for pattern separation than was described by classical Marr-Albus models. Based on these properties, we speculate that inhibition may serve to counteract the intrinsic limitations on combinatorial diversity that are imposed by the anatomical architecture of mossy fiber input to granule cells⁵⁴. Our simple decoders argue that inhibition is important for pattern separation. However, future work is needed to test whether inhibition shapes higher dimensional activity structures⁵⁵, for instance by decorrelating sensory representations^{56, 57}. Together, these computations have the potential to support effective pattern separation even if granule cell activity exceeds the levels proposed in classical models during behaviors involving diverse cerebellar input.

Typically, models of cerebellar learning assume consistency of individual granule cell timing across trials, at least for stimulus durations that are appropriate for learning⁴³. Here, we find that a minority of granule cells (~20%) exhibited low temporal jitter across trials, with the remainder exhibiting higher temporal variability. While previous measurements have shown that the timing of mossy fiber input can be highly reproduceable across trials⁵⁸, this may not translate into a consistency of granule cell spike timing due to pre- or post-synaptic regulation^{44, 45, 59, 60}. The reliability of inputs may also be modality specific⁶¹, as different mossy fibers can have different strengths and short-term plasticity, and likely have different temporal consistency depending on source. Our data support this possibility, as somatosensory ensembles exhibited less variability than auditory ensembles, despite their smaller size. Moreover, we found that earlier responding granule cells exhibited less temporal variability, perhaps related to the inverse relationship between cerebellar learning and stimulus duration⁶².

We find that the variability in granule cell spike timing was not dramatically altered when inhibition was blocked. While feedforward inhibition can play a powerful role in establishing spike timing in some circuits⁶³, the mossy fiber recruitment of Golgi cell inhibition onto granule cells is relatively weak and inconsistent⁶⁴. Moreover, inhibitory postsynaptic currents onto granule cells often occur before the arrival of excitatory input in vivo⁶⁵. Such inhibition evoked before or during excitation likely serves primarily to increase granule cell spike thresholds^{13, 35, 66} rather than as a timing mechanism, consistent with our current observations. As such, refinement of spike timing may not be a primary function of synaptic inhibition in the granule cell layer.

In addition to temporal variability, we observe variability in the identity of granule cell ensembles representing sensory stimuli across trials, an effect primarily due to the relatively low probability of responses on single trials. This low response probability may provide part of the explanation for why cerebellar learning can be slow to accumulate across trials, at least as compared to the requirements for induction of synaptic plasticity in the cerebellum when inputs are highly reproduceable⁶⁷. Behavioral states that accelerate the acquisition of cerebellar learning, such as locomotion, may therefore act by increasing the reliability of granule cell responses. Investigating how granule cell sensory responses are modulated by behavioral state is thus an important future direction.

While our measurements support mechanisms of pattern separation, most analogous learning circuits are also thought to involve a secondary process called pattern completion that stabilizes representations. Notably, our observations have been made in the absence of learning, and we speculate that a pattern completion processes in the cerebellum could serve to stabilize representations in space and time during learning. Indeed, the cerebellar cortex includes sites of plasticity at almost every node in the circuit, as well as a feedback pathway that provides the type of recurrent structure necessary for pattern completion circuits^{68, 69}. Future measurements will be necessary to test how granule cell representations are altered across learning.

We have also demonstrated that sensorimotor behavior in a cerebellum-dependent eyelid conditioning task relies on granule cell inhibition. Specifically, conditioned responses to a CS+ and CS− become indistinguishable when inhibition is blocked. If this change were simply due to mice equally associating the CS+ and CS−, one might expect an increase in the probability of conditioned responses to the CS−. Instead, we observed only a decrease in the response probability to the CS+. This result is consistent with several observations from our imaging data.

First, granule cell tuning was only partly reduced when inhibition was blocked, suggesting that the impairment of sensory discrimination is not solely due to a loss of tuning of the ‘learned’ granule cell population. However, our data also show that blocking inhibition greatly increases the number of responsive cells (Figure 1). Because these emergent cells were not active during conditioning, they were not part of the circuit pathway modified during learning. In addition, spontaneous activity is greatly enhanced when inhibition is blocked, degrading the signal-to-noise ratio of granule cell sensory encoding³⁵. We therefore speculate that the enhanced spontaneous activity and the emergent, unlearned CS+ responding cells act to bombard downstream Purkinje cells with non-specific signals that dilute those from the pathways modified during learning. Such results are consistent with a model in which the cerebellum implements a probabilistic binary choice to recognize learned patterns⁷⁰, producing fewer CRs as the learned pattern becomes less discernable. Such a decreased discriminability of the new CS+ ensemble from the learned CS+ ensemble is consistent with the observation that the behavior does not revert to the unlearned condition (i.e. where there is no CR), but instead becomes more similar to the CS− response. Loss of synaptic inhibition therefore leads to both a degraded CS+ representation and a decrease in discriminability with the CS−, both of which likely contribute to the behavioral effect.

Our inferences about the circuit responses that mediate behavior rely on recordings from a nearby part of the cerebellum to the one necessary for this behavior^{47, 71}. Given the highly conserved anatomical and physiological properties of the cerebellum, we expect that the function of inhibition will also be conserved. Nonetheless, new tools will be needed to investigate the activity of large populations of granule cells in the region of the cerebellum required for eyelid conditioning, and to track their activity across learning.

Together, our results reveal several mechanisms of cerebellar granule cell layer sensory encoding that depend on local synaptic inhibition. In addition, we find that behavior associated with these patterns is highly dependent on inhibitory tone, consistent with findings that chronic hyperexcitability of granule cells can lead to diverse behavioral changes^72–74. These findings thus significantly extend long-standing predictions of classical Marr-Albus models for how the cerebellar cortex establishes and utilizes discrete sensory representations to guide behavior.

Methods:

Mice

All experimental procedures using animals were performed with approval of the Duke University Animal Care and Use Committee. Experiments were conducted during the light cycle with both male and female adult mice (>P60). All mice were housed in an animal facility with standardized temperature and humidity, with 12 h light/dark cycles with food and water ad libitum. Imaging experiments were performed with Ai148 (TIT2L-GC6f-ICL-tTA2)-D (Jackson Labs 030328) mice crossed with BACα6Cre-A²² (n = 21, female n = 12, male n = 9). Eyelid conditioning experiments used BACα6Cre-A mice (n = 5, female n = 3, male n = 2). C57/B6J (Jackson Labs 000664) was the primary background for all mice, with up to 50% CBA/CaJ (Jackson Labs 000654) for eyelid conditioning experiments.

Surgical procedures

Animals received dexamethasone (3 mg/kg) 3–4 h before surgery. All surgeries were performed under anesthesia, using an initial dose of ketamine/xylazine (50 mg/kg and 5 mg/kg) 5 min before, and 1.0-2.0% isoflurane throughout surgery. Breathing rate and toe pinch responsivity were continuously monitored during surgeries. A heating pad (TC-111 CWE) was used to maintain body temperature. For imaging and eyelid conditioning mice, titanium headplates (HE Parmer) were attached to the skull with Metabond (Parkell). Animals received buprenex (0.05 mg/kg) and cefazolin (50 mg/kg) twice daily for 2 d after surgeries.

For imaging experiments, adult mice (P50–60) were given a 3-mm diameter craniotomy over Crus I at approximately 3.0 mm lateral and 4.3 mm posterior to lambda. Crus I was injected (WPI UMP3) with 150 nL of either AAV7m8-X0117-CAG-DIO-[⁺HTP-GGSGG₈-GPI-2A-dTomato]-WPRE-pA (HTP_GPI) (1 × 10¹²; Duke Viral Vector Core) or AAV7m8-6360D-CAG-DIO-[^ddHTP-GGSGG₈-GPI-2A-dTomato]-WPRE-pA (^ddHTP) (1 × 10¹²; Duke Viral Vector Core) at a rate of 30 nL/min and a depth of 350 μm at 2–3 sites. Glass windows consisting of two 3-mm coverslips bonded to a 5-mm coverslip (Warner Instruments No. 1) with index matched adhesive (Norland No. 1) were installed in the craniotomy using Metabond. Imaging mice receiving saline and drug infusions received a plastic cannula (Plastics One; C315GS/PK length 0.5 mm) positioned immediately rostral to the imaging window and attached with Metabond. All mice were given 8 weeks to allow viral expression, including 1-2 weeks of habituation to head restraint.

For eyelid conditioning experiments, adult mice (P50–60) were given 0.3-mm diameter craniotomies at approximately 1.8 mm lateral and 5.85 mm posterior to bregma. Three equidistant 80 nL injections of either AAV-DIO-⁺HTP_GPI (1 × 10¹²) or AAV-DIO-^ddHTP_GPI (1 × 10¹²) were performed at a rate of 30 nL/min and a depth of 4.0 mm. Mice receiving saline and drug infusions were implanted with a plastic cannula (Plastics One; C315GS/PK length 3.0 mm) over the injection site that was secured with Metabond. A subset of wild type mice (n = 3) received cannulas but no virus injection at the same location. Mice were given 8 weeks to allow viral expression, including a minimum of 2 weeks for recovery before habituation to head restraints and training.

Calcium imaging

Two-photon imaging was performed with a resonant scanning microscope (Neurolabware) using a 16X water immersion objective (Nikon CFI175 LWD 16xW 0.8NA). A polymer (MakingCosmetics, 0.4% Carbomer 940) was used to stabilize the immersion solution during imaging. For GCaMP and TdTomato imaging, a Ti:Sapphire laser tuned to 920 nm (Spectra Physics, Mai Tai eHP DeepSee) was raster scanned via a resonant galvanometer (8 kHz, Cambridge Technology) onto the cerebellum at a frame rate of 30 Hz and a field of view of 278 μm × 117 μm (796 × 264 pixels) (Supplemetary Video 1). Scanbox software (Neurolabware) was used to collect data through a green filter (510 ± 42 nm band filter (SEMrock)) onto GaAsP photomultipliers (H10770B-40, Hamamatsu).

Behavior

During imaging, animals were head-fixed in a custom sled atop a piezoelectric sensor (C.B. Gitty, 41 mm ‘jumbo’ piezo) read from and triggered through a multifunction data acquisition device (90 Hz, USB X, National Instruments) to measure animal movement^{33, 34}. In a subset of experiments, whole-body motion was simultaneously recorded from a CMOS camera (60 Hz, Genie Nano M640 NIR, Teledyne Dalsa) with a fixed focal length lens (6 mm f/2.8, Edmund optics). During imaging, frame-by-frame whisker and facial movements were monitored with the aid of IR LEDs (Swann) from a CMOS camera (60 Hz, Genie Nano M640 NIR, Teledyne Dalsa) with a fixed focal length lens (6 mm f/2.8, Edmund optics) positioned 13 cm above the animal’s head. Piezoelectric and video data were acquired and aligned to imaging data using Scanbox software (Neurolabware) and custom code written in MATLAB (Mathworks). For imaging experiments, sensory stimuli were delivered in pseudorandomized 167 s blocks with randomized inter-trial intervals (ITI) using Mworks (http://mworks-project.org). For somatosensory stimulation, low intensity air puffs (10, 15, or 20 psi, a range of intensities found to produce little or no behavioral response after habituation, delivered block-wise) were delivered from a metal tube 5 cm from the center of the vibrissae (5630–10200 ms ITI; 18–29 trials/block). Pure tones of either 68 or 72 dB with frequencies of 1, 5, or 10 kHz were delivered individually block-wise or in randomized pairs for single auditory stimulation (3800–15000 ms ITI; 9–23 trials/block). While we did not detect audible responses from somatosensory air puffs or reliable movements such as inspiration during stimulation, we cannot rule out possible contributions of these or other such effects in our measured granule cell responses. Imaging sessions lasted between 1.25–2.25 hours.

For eyelid conditioning, the behavioral setup was constructed according to Heiney et al. (2014). Prior to experiments, all mice were habituated to head restraint on the same wheel used for training for 30–60 min/day until they calmly entered head restraints and walked comfortably on the wheel (5–10 d). Stimulus delivery and frame acquisition for video monitoring were triggered with an Arduino Uno microcontroller board (Arduino) controlled with modified Arduino and Matlab code written for Neuroblinks software (Medina lab). Mice were trained during daily sessions of 100–300 trials in which a 50-ms air puff (30 psi) was delivered 3 mm from the mouse’s cornea (unconditioned stimulus, US) and paired with a co-terminating 250-ms, 5 kHz, 70 dB tone (conditioned stimulus, CS). Each session contained one randomly delivered CS only test trial and one US only test trial. Trials were only initiated if the eyelid was open >70–80% for at least 200 ms and at a minimum of 10 s apart⁴⁷.

In vivo pharmacological infusions

Saline and drugs were infused into awake, head-fixed mice using an automated pump (WPI UMP3), a Hamilton syringe (10 μl Gastight model 1701 RN) and a plastic internal cannula (Plastics One, C315IS) threaded into the guide cannula. All infusions had a total volume of 1 μl delivered at a rate of 1 μl/min. To estimate the spread of pharmacological agents under the imaging window, 10 mM fluorescein dye (Sigma-Aldrich #F6377) dissolved in sterile artificial cerebrospinal fluid (aCSF; 150 nM NaCl, 4 mM KCl, 2 mM MgCl2, 2 mM CaCl2, 10 mM HEPES, 10 mM glucose, pH 7.4) was infused through the cannula rostral to the imaging window, followed by a 1 h rest and perfusion. For all other imaging and behavior experiments, aCSF only or either 1 μM non-binding gabazine.1^nbDART or 1 μM gabazine.1^nbDART.2 was dissolved in sterile aCSF and applied, followed by a 20-min rest. Infusions were delivered at least 1 d apart for each animal. At least one day after gabazine.1^nbDART administration, 1 μM Alexa647.1^DART.2 was dissolved in sterile aCSF and infused, followed by 1 h rest and perfusion. In a subset of eyelid conditioning experiments, fluorescent muscimol (1 mM; BODIPY TMR-X muscimol conjugate; Invitrogen) was infused in wild type mice, followed by a 3-min rest period.

Histology

Mice were anaesthetized with an IP injection of ketamine/xylazine (200 mg/kg and 30 mg/kg, respectively) prior to perfusion with PBS and 4% paraformaldehyde. 50 μm sagittal sections were cut using a vibrotome (Pelco 102). Slices were mounted using Southern Biotech DAPI-Fluoromount G or Vectashield Vibrance (Vector labs) then imaged using an upright confocal microscope (Leica SP8).

Slice Electrophysiology

Acute brain slices and associated whole-cell electrophysiological recordings (pClamp v10.3) of synaptic inhibition were performed as described previouslyⁱ⁴⁰. Synaptic inhibition was measured at the reversal potential for excitation (0 mV).

Data Analysis

Multi-photon imaging:

All acquired two-photon images were processed using the opensource Python toolbox for large scale calcium imaging data analysis CaImAn⁷⁵. First, images were corrected for motion over 60 × 60-pixel patches using a piecewise rigid motion correction algorithm (NoRMCorre⁷⁶). All videos were manually screened to ensure adequate motion correction. Whole experiments that could not be made to produce a stable averaged image were excluded from further analysis. Images collected before and after drug infusions, without displacing the objective, were motion registered and segmented together to enable reliable comparison between conditions. Then, source separation was performed using constrained non-negative matrix factorization (CNMF⁷⁷). This algorithm includes exclusion of fluorescence changes originating in the neuropil. Regions of interest (ROI) identified by CNMF were then sorted according to spatial stability, transient signal-to-noise ratio, and performance in a CNN based classifier⁷⁵ (Supplementary Fig. 20). ROIs were then excluded based on their proximity to the edge of the FOV and overlap with non-specifically labelled structures (i.e., anything other than putative granule cells) in motion-registered, averaged images using custom MATLAB code. Remaining raw Ca2+ time courses computed by CNMF were screened for periods in which the signal exceeded 6 standard deviations from the mean of either the first or last 20,000 imaging frames for >2 s, as such changes were noted to occur in cells that become bright and swell over the course of an experiment and were presumed to be unhealthy/dying. ROIs with this fluorescence signature and a bright, swollen appearance in motion-registered, averaged images were excluded from further analysis. Additionally, raw Ca2+ time courses lacking stability by 1) slowly drifting in magnitude or 2) transiently or permanently losing all signal were excluded from further analysis to allow reliable comparison of responses throughout each experiment. Fluorescence changes (ΔF) were normalized to a 1-s window of baseline fluorescence prior to stimulus onset for each trial. Individual cell responses were considered significant if they surpassed 2 standard deviations (SD) from the baseline period between 90–180 ms after stimulus onset (somatosensory stimulation), or if any sliding window beginning at stimulus onset and ending 0.1 s after stimulus offset surpassed 2 SD of any equal-length window during the baseline period (auditory stimulation). Even though we do not make any corrections for multiple comparisons, this 2 SD threshold puts our false positive rate below 5%. Some cells with significant responses in the control condition no longer achieved significance after DART infusions due to high levels of activity in the baseline period, despite having activity during the stimulus windows. Because this reduced signal-to-noise impaired accurate measurement of sensory responses, cells that lost significance in DART were not included for condition-matched analyses (Fig. 3,5, Supplementary Figs., 9-13). The fraction of responsive granule cells (% responsive) for each condition was estimated by calculating the number of granule cell sized ROIs (~14.7 pixel diameter) that would tile the FOV (796 x 264 pixels) without overlap. First and peak event times and amplitudes during individual trials were calculated using trapezoidal numerical integration, identifying peaks ≥120 ms. ‘Off’ cells were defined as cells having a mean first peak time at or after stimulus offset. Response probability was calculated as the fraction of trials that a cell was significantly responsive to the sensory stimulus. Fraction overlap quantifies the proportion of responsive cells that respond to multiple stimulus conditions.

Unisensory stimulus classification

To classify auditory stimuli, calcium signals from populations of granule cells were used. First, noise was removed in two steps. 1) Smoothing: calcium signals were first smoothed by a 3-frame boxcar filter. 2) Threshold: after smoothing, baseline noise was estimated from 25 frames (30 Hz sampling) preceding the stimulus. Events that exceeded 2-SD above the baseline noise were retained, signals below this threshold were set to zero. A granule cell response was defined as the peak calcium signal (between the initiation of the sound and 5 frames after it ended) on each trial after smoothing and thresholding. A population response was defined by accumulating this peak calcium signal across all granule cells for a given trial. This created a matrix of responses that was [cells x trials]. Given a limited number of trials in many experiments (~20) and a large population response (~300 cells), response classification was performed using a non-parametric nearest-neighbor approach⁷⁸. This approach computed the distance of a test trial to all training trials. While the correlation structure of the data was preserved in this analysis, the decoder assumes no trial-by-trial correlations, and therefore is insensitive to this structure. The test trial was classified according to the stimulus condition that produced the nearest response among the training trials. Test-trials were selected from a ‘hold-one-out’ approach and the remainder of the data was used for training. Three classification tasks were run: identify the frequency of the stimulus (three categories, Fig. 4e left); identify the amplitude of the stimulus (two categories, Fig. 4e middle); and identify the amplitude and frequency of the stimulus (six categories, Fig. 4e right). Classification was performed across all trials. For stimulus classification under control conditions, responses from 328 granule cells were used with 23 trials for each condition. For the gabazine.1^DART.2 discrimination, 319 granule cells were used with 22 trials for each condition.

Several control analyses were run to ensure the discrimination results were not overly sensitive to changes in the procedure described above. First, half the number of cells were tested in each condition, to make sure the results were relatively insensitive to this parameter. The results in Figure 4 were qualitatively similar; none of the trends or statistically significant differences changed. Second, we defined responses in several different ways. In addition to using the peak amplitude (described above), we also used: 1) the time of the peak response; 2) the time and amplitude of the peak response; 3) the time the response initially crossed 2-SD above baseline; 4) the time and amplitude the response initially crossed baseline; 5) the integrated calcium signal between frame 30 (when tone was initiated) and 65 (five frames after it ceased); 6) the integrated calcium signal from ‘5)’ and the initial time it crossed the significance threshold. The results in Figure 4 were qualitatively similar; none of the trends changed, but under some response definitions, some differences failed to clearly reject the null hypothesis (p-values were > 0.05). In Figure 4, error bars represent SEM and were computed by using the Wald method of confidence interval estimation for binomial distributions.

The same procedures were used to classify puff stimuli. Responses were classified using a population of 275 granule cells with 15 trials for each stimulus amplitude under control and DART conditions. Decoding was performed on the peak response between frames 27 and 37 on each trial.

Unisensory versus multisensory response discrimination

Actual multisensory (sound and puff) responses were not the linear combination of unisensory (sound or puff) responses. To examine the consequences of this deviation from linear signal summation on stimulus discrimination (multi- versus unisensory), we simulated linear multisensory responses by summing unisensory responses sampled from responses to either auditory stimulus with responses to the puff stimulus for each cell. Discrimination performance (correctly discriminating between unisensory and multisensory responses) was then measured using multisensory responses or the simulated linear multisensory responses (Fig. 5). Response classification was performed using a non-parametric nearest-neighbor approach⁷⁸. Responses were derived from 521 granule cells and 30 multisensory and 30 unisensory trials (10 auditory trials at two frequencies and 10 puff). Calcium signals were smoothed and thresholded as described in the previous subsection. Responses were defined as the integrated calcium signal starting at the time the signal crossed threshold after the initiation of the auditory stimulus until 5 frames (30 Hz sampling) after the termination of the auditory stimulus. Qualitative results and significance tests were robust to halving the number of cells and/or using other definitions of ‘response,’ such as the amplitude of the peak response and the time-of-peak response. Notably, our resampling approach for simulating multisensory responses has the added consequence of disrupting the correlation structure. Thus, it could be either the loss of non-linear interactions or the correlation structure that impairs discrimination. However, given that the nearest-neighbor decoder has limited knowledge of the correlation structure, it is more likely that the impaired decoding is due to the decrease in sparsity of responses in DART.

Behavior Analysis:

For imaging experiments, a machine-learning-based algorithm (DeepLabCut³²) was used to automatically track components of the face, whiskers, and head in accompanying high-speed videos. Tracked features were initially labeled manually in a small portion of frames (30) to train the algorithm, then x and y locations of each feature were automatically determined for all remaining frames. Motion was evaluated as cumulative displacement of these coordinates during aligned calcium imaging frames.

To validate the effectiveness of the piezo sensor at detecting motion, the same sensory stimuli used in imaging experiments were delivered while collecting high-speed video of each mouse’s head and limbs. Machine learning-based motion tracking with DeepLabCut³² revealed that the sensor reliably detects limb motion and other movements such as grooming (Supplementary Fig. 5). Specifically, limb and facial movements were aligned with piezo traces, revealing that piezo measurements reliably reflect movements of all four limbs, as well as fine movements of the ears and face. Video detected motion and piezo recordings do not have a one-to-one relationship, however, and some changes in piezo voltage do not correspond with any visible movement detected by video. We interpret these changes in piezo voltage as likely to reflect muscle tension as the mouse prepares to move, as they generally occur immediately preceding video detected movements. However, nearly all video-detected movements are less than 5 frames away from piezo deflections that are >1 standard deviation from the mean, so this threshold was used to segregate imaging frames recording during movement. Trials were excluded from analysis if movement occurred anytime between the second before stimulus onset and 300 ms after stimulus offset.

In addition to removing signals related to movement, piezo voltage traces identify frames in which significant animal movement causes failures of imaging motion correction. Two-color imaging of both neural activity with GCaMP6f and tdTomato indicates that instances of tdTomato fluorescence fluctuations (indicating Z-motion or another motion correction failure) are also excluded from analysis using the above criteria (Supplementary Fig. 5).

Because mice whisk frequently, and granule cells in Crus I can be tuned to whisker movements^{27, 29} , we used a different approach to segregate cells that are modulated during whisking. During imaging, videos of the head and whiskers were used to align whisker movements to changes in granule cell activity. Because some granule cells can be tuned for whisker deflection angle²⁷, whisker movements were then parsed according to movement amplitude, and whisks that occurred between trials and in the absence of whole-body movement were used to identify granule cells that were modulated specifically by whisking. Whisk modulated cells overlapped very modestly with ensembles responsive to auditory or somatosensory stimulation (7.7 ± 4.5% of sensory and whisking responsive cells). Accordingly, inclusion of whisk modulated cells had no significant effect on auditory (unpaired t-test, P=0.9686) and somatosensory (unpaired t-test, P=0.4864) responses on average. (Supplementary Fig. 4).

For eyelid conditioning experiments, behavioral data were analyzed using modified Matlab code written for Neuroblinks software (Medina lab). Briefly, fraction of eyelid closure was calculated for each video frame by generating a binary image of a region of interest surrounding the eye, thresholded to provide maximal discriminability for each experiment, then summing pixel counts for each frame. Conditioned responses (CRs) were defined by eyelid closure >10%. CR probability for a given session was calculated according to all paired trials during that session. CR amplitudes were calculated as the mean closure during a 4-frame window preceding the US.

Statistics and Reproducibility

Sample sizes were similar to sample sizes used for comparable studies in the field^{15, 34}: 3 mice or more per condition were used for imaging and eyelid conditioning experiments, with the exception of only 2 mice used for ddHTP imaging experiments. Each imaging experiment included over 150 active cells. No statistical methods were used to select sample sizes. Data exclusions and rationale are indicated in relevant sections above. Data distributions were assumed to be normal but this was not formally tested. All paired and unpaired t-tests were two-sided. The students t-test in figure 4e was one-sided. Adjustments for multiple comparisons were performed for ANOVAs. Exact p-values for all tests are reported in Supplementary Table 1. All major results were replicated in multiple mice. Additionally, major results were replicated in mice with viral, rather than transgenic, calcium indicator expression and using different analytical approaches. Mice were randomly selected for experimental groups. Trial types were pseudo-randomized during imaging experiments and randomized by behavioral software for eyelid conditioning experiments. Investigators were not blinded to mouse group during experiments or analysis.

Data Availability:

Due to the large size of these datasets, data that support the findings of this study are available from the corresponding author upon request.