Abstract
Cytokinesis, the fission of a mother cell into two daughter cells, is a simple and dramatic cell shape change. Here, we examine the dynamics of cytokinesis by using a combination of microscopy, dynamic measurements, and genetic analysis. We find that cytokinesis proceeds through a single sequence of shape changes, but the kinetics of the transformation from one shape to another differs dramatically between strains. We interpret the measurements in a simple and quantitative manner by using a previously uncharacterized analytic model. From the analysis, wild-type cytokinesis appears to proceed through an active, extremely regulated process in which globally distributed proteins generate resistive forces that slow the rate of furrow ingression. Finally, we propose that, in addition to myosin II, a Laplace pressure, resulting from material properties and the geometry of the dividing cell, generates force to help drive furrow ingression late in cytokinesis.
Keywords: cell dynamics, myosin II, dynacortin, RacE, cell mechanics
How cells form diverse shapes such as extended neurons or columnar epithelium or change shape during movement is an important mystery in cell biology. Cytokinesis, the mechanical separation of a mother cell into two daughter cells, is a simple shape change that is essential for cell viability. Its failure can lead to defects in cell growth and aneuploidy, causing diseases such as cancer.
Cytokinesis is coordinated by the mitotic spindle, which delivers cues to the actin-rich cortex. These cues lead to a redistribution of a number of cytoskeletal proteins, including myosin II, to the cell's equator (1). In the classic model, myosin II constricts an equatorial actin ring, producing two daughter cells (2-6). Puzzlingly, cytokinesis in some cell types proceeds fairly normally without myosin II. Other observations suggest that both the polar/global and equatorial regions of the cell cortex have important roles in the contractile process (7-11). Thus, cytokinesis appears to be executed by a complex network, involving multiple force-generating systems and regulatory feedback loops. Consequently, many proteins may contribute important functions to cytokinesis without producing gross phenotypes when mutated (12). However, at present, we know very little about how the entire cytokinesis machinery works.
Here, we analyze the time dependency of furrow ingression of wild-type and mutant Dictyostelium cytokineses by measuring the furrow diameter and length and applying an appropriate rescaling strategy. This method reveals, in a noninvasive way, features distinctive of each strain. In all cell types, cytokinesis proceeds through essentially the same sequence of shapes. However, the kinetics of transformation between shapes differs dramatically between wild-type and mutant strains. We analyzed the role of equatorial proteins, myosin II and the actin crosslinker cortexillin I, and global proteins, RacE small GTPase and the actin crosslinker dynacortin (Fig. 1A). Each protein plays an important role in cytokinesis and cortical mechanics (7, 13-18). Each mutant strain follows a unique time-dependent trajectory of furrow ingression. By comparing the data with a quantitative model, the cylinder thinning model, we propose that myosin II-generated active radial stresses, a Laplace pressure generated from material properties and RacE/dynacortin-generated resistive stresses, govern furrow-thinning dynamics. With this combination of genetics and cell imaging and modeling, a quantitative framework in which molecular mechanisms are related to cytokinesis dynamics becomes possible.
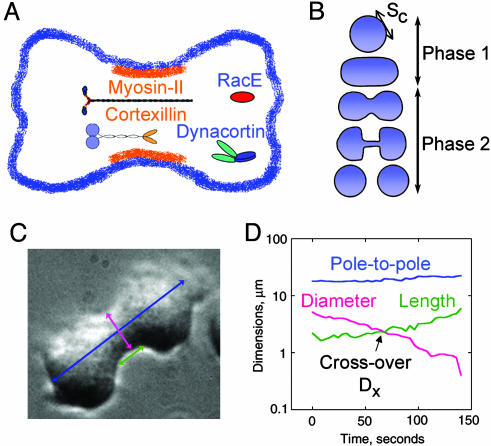
Fig. 1.
The shape changes of cytokinesis. (A) Schematic cartoon showing localizations of myosin II, RacE, dynacortin, and cortexillin I. (B) A cartoon of the shape changes of wild-type cytokinesis. The break between phase 1 and phase 2 indicate the predicted transition state of furrow ingression (18). (C) A phase micrograph of a wild-type cell in cytokinesis. The furrow diameter (pink arrow), furrow length (green arrow), and the pole-to-pole (blue arrow) were monitored with 4-s resolution for each cell. (D) An example plot from a wild-type cell showing how the dimensions changed with time. The crossover point, Dx, is indicated.
Materials and Methods
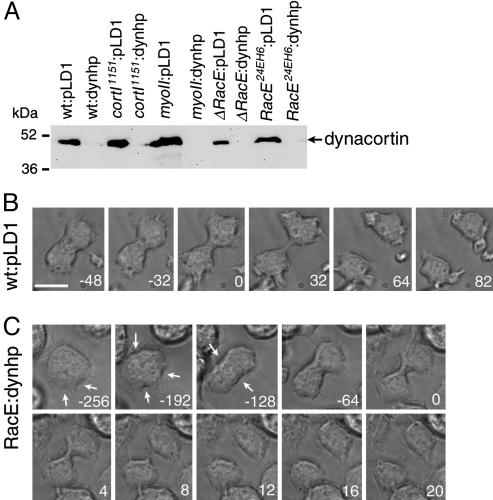
Strains. All genetic strains used in this study have been described in refs. 15 and 19-21. Wild-type cells were HS1000 cells (19). Control strains carried the parental plasmid, pLD1A15SN, which allowed all cells to be grown under identical media conditions (19). To generate the RacE/dynacortin and myosin II/dynacortin double-mutant combinations, RacE and myosin II mutant strains were transformed with a dynacortin hairpin (dynhp) construct (15). No dynacortin protein was detectable in dynhp cells by Western immunodetection by using anti-dynacortin antibodies as described and quantified in ref. 15.
Microscopy. Log-phase Dictyostelium cells were plated in imaging chambers. Because temperature can impact physical parameters such as viscosity, the imaging temperature was standardized to 22 ± 0.5°C. Cells were imaged with a ×40 oil, NA1.3 objective and a ×1.6 optivar. UV, IR, and green filters were used to eliminate phototoxicity. Frames were collected every 2 s until the intercellular bridge was severed by using the ip lab software package (Scanalytics, Billerica, MA). The time-lapse movies were analyzed by using nih image (http://rsb.info.nih.gov/nih-image/Default.html), Microsoft excel, and kaleidagraph (Synergy Software, Reading, PA).
Results
Wild-Type Furrows Constrict Exponentially. To initiate our analysis, we studied the dynamics of wild-type cytokinesis and defined two phases of shape progression (Fig. 1B; see also Movies 1 and 2, which are published as supporting information on the PNAS web site). During phase 1, the mother cell rounds up, elongates into a cylinder, and forms a cleavage furrow that links up smoothly with the daughter cells (Figs. 1B and 2B). Although the shape of the polar cortex is variable because of ruffling, the shape in the furrow region always appears taut. During phase 2, the cleavage furrow cortex constricts until a discrete bridge is formed. The cell now appears more dumbbell-shaped, and the bridge is a geometrically separate structure from the two daughter cells. The bridge thins out as a result of cytoplasmic flow from the bridge before severing. Typically, the scission point is located near one of the daughter cells instead of in the middle of the bridge. After breakup, the bridge rapidly recoils into the daughter cell to which it is connected. In short, the entire sequence of shape changes can be described as a transformation from one geometrically simple shape to another: from a single sphere to two spheres connected by a cylinder to two daughter spheres.
Fig. 2.
RacE/dynacortin double mutants show uncontrolled cell morphology. (A) Western analysis by using anti-dynacortin antibodies indicates that dynhp significantly reduces dynacortin levels in all genetic backgrounds, wild type, cortI1151, myosin II, ΔRacE, and RacE24E. (B) Time series of micrographs of a wild-type cell undergoing division. The time series was taken from Movie 1. (C) ΔRacE:dynhp cells have altered cytokinesis dynamics. The cell attempts multiple furrows (arrows) before committing to a single cleavage plane at -128 s. The furrow ingresses slowly, then a rapid decrease is observed between 0 and 8 s. Movie frames come from Movie 3. Numbers in B and C are time in seconds. Time 0 is when Dx was reached. (Scale bar: 10 μm.)
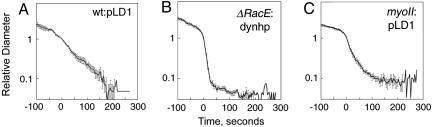
To see which aspects of the detailed cytokinesis dynamics are robust, we averaged measurements from individual cells so that the same stage of division in different cells is reliably correlated. We measured the minimum furrow diameter and furrow length as a function of time (Fig. 1 C and D). To measure the furrow length, we defined the furrow as the region where the sides of the bridge were parallel (i.e., the cylindrical portion). During late stages, typically when the furrow diameter is approximately ≤4 μm, the length is completely objective, whereas during early stages, the furrow has more curvature, making the cylindrical portion somewhat more subjective. For these early stages, we defined the length as the most cylindrical portion to the region in which the divergence angle from the long axis of the cell was approximately <25°. From the diameter and length vs. time plots, we observed that for every cell, there was a time point when the minimal furrow diameter and furrow length were equal; we defined this distance as the crossover distance, Dx. The crossover time was reset to 0, and Dx was reset to 1. The remaining furrow diameters were divided by Dx. Because Dx is a constant, the division does not affect the kinetics of furrow thinning but allows the trajectories to collapse onto a universal trajectory (Fig. 3). To verify the success of rescaling, nonaveraged data were analyzed before being averaged for curve fitting and further analysis (Fig. 3; see also Fig. 6, which is published as supporting information on the PNAS web site). The rescaling allowed the kinetics of cytokinesis for a large number of cells across a variety of genotypes to be compared. For wild type, the furrow diameters decayed nonlinearly and were best described as an exponential trajectory with k = -0.012 s-1 (Fig. 3A).
Fig. 3.
Rescaling of the furrow diameter thinning data for each genetically modified strain of Dictyostelium cells. Each strain showed a distinct trajectory, depending on genotype. Error bars at each time point are standard errors of the mean. (A) Control wild-type cells carrying the empty vector pLD1. (B) ΔRacE:dynhp. (C) Myosin II mutant lines carrying pLD1. Composite of all data is shown in Fig. 7. Apparent velocities (v), rates (k), cross-over distances (Dx), and n values are presented in Table 1. To verify the success of the rescaling, nonaveraged data for these three graphs are shown in Fig. 6.
RacE and Dynacortin Provide a Brake. To analyze how globally distributed RacE and dynacortin (19, 22, 23) control furrow ingression dynamics, we studied two RacE mutant lines (an insertional mutant, RacE24E, and a deletion line, ΔRacE; ref. 20) and dynacortin mutants generated by silencing dynacortin with a hairpin construct (dynhp; Fig. 2 A) (15). The mutant strain data were rescaled through the same scheme as for the wild type. These mutants showed a nonlinear, triphasic trajectory characterized by a slow phase, followed by a more rapid thinning phase and then a final phase where the intercellular bridge dwelled for a period before severing (Fig. 7 B, C, and G, which is published as supporting information on the PNAS web site). Dx occurs at the transition between the slow and fast phases, and the transition was especially apparent in the RacE mutants (Fig. 7 C and G). We combined the first two phases into a “prebridge phase” and considered the final bridge-dwelling phase as a separate entity.
Because wild-type, RacE, and dynacortin lines displayed fundamentally different trajectories, we created a metric for direct comparison between each strain. We defined an apparent velocity as the speed with which the furrow diameter thinned from 2·Dx to 0.1·Dx. We determined the time required to traverse 2·Dx to 0.1·Dx, then calculated an apparent velocity by dividing 1.9·Dx by the time required to traverse that distance. For wild-type cells, the apparent velocity was 0.022 μm/s. For the prebridge phase, RacE and wt:dynhp cells displayed similar apparent velocities as the wild-type cells (Fig. 7; see also Table 1, which is published as supporting information on the PNAS web site). Thus, the wild type and RacE and dynacortin mutants use different trajectories to achieve similar overall apparent velocities. The trajectories of the RacE mutant strains were rescued by the introduction of GFP-RacE (Fig. 7 D and H and Table 1).
When we silenced dynacortin in the RacE mutant backgrounds, the apparent velocity was significantly increased as compared with wild-type cells (Figs. 2 A and C, 3B, and 7 E and I, and Table 1). The ΔRacE:dynhp cells showed a single phenotypic class with a high apparent velocity (0.089 μm/s; Fig. 3B; see also Movie 3, which is published as supporting information on the PNAS web site). RacE24E:dynhp double mutants displayed two classes of phenotypes, both of which demonstrate how RacE and dynacortin synergize to control cell shape during cytokinesis. One class showed a high apparent velocity (0.096 μm/s), whereas the second class had a slower apparent velocity (0.035 μm/s) and formed membrane blebs as the furrow ingressed (Fig. 7 E and F; see also Movies 4 and 5, which are published as supporting information on the PNAS web site). Thus, a feedback mechanism may slow down furrow ingression if the plasma membrane ruptures from the cortex. Blebbing has been observed for nonadherent RacE24E cells (14). Because nonadherent Dictyostelium have less polymeric actin (14), nonadherent RacE24E and adherent RacE24E:dynhp cells may have similarly altered cortical mechanics. When we averaged the fastest velocities from the steepest part of the curves of the individual raw data sets, the velocities were 0.31 ± 0.040 μm/s (n = 16) for ΔRacE:dynhp and 0.19 ± 0.037 μm/s (n = 10) for RacE24E:dynhp with the fastest observed velocities at 0.74 μm/s and 0.44 μm/s for ΔRacE:dynhp and RacE24E:dynhp, respectively. Thus, simultaneous removal of RacE and dynacortin caused up to a 30-fold (0.74 vs. 0.022) increase in furrow thinning velocity compared with the wild type. We propose that RacE and dynacortin regulate resistive stresses that slow furrow ingression; in essence, they provide a brake. Later, we present a simple, analytical model in which these resistive stresses account for the observed thinning dynamics.
Myosin II Mutant Furrow Thinning. Next, we investigated the role of myosin II in furrow thinning dynamics. The rescaling for myosin II mutants had to be modified because the dividing myosin II cell had a long cylindrical shape so that a crossover point was not immediately detectable. However, as the minimal furrow diameter decreased, the intercellular bridge was exposed that elongated similarly as the other strains. We fit this portion of the bridge-lengthening curve, extrapolated back to find Dx, and used this result to rescale the bridge-thinning trajectories. The myosin II mutants showed a similar nonlinear trajectory (Fig. 3C; see also Movie 6, which is published as supporting information on the PNAS web site). During the prebridge phase, the myosin II mutants had a slow phase followed by a faster phase with the transition again occurring at Dx. Silencing of dynacortin in the myosin II-null cells (myoII:dynhp) accelerated the apparent velocity of the prebridge phase nearly 2-fold without changing the fundamental furrow-thinning trajectory of the myosin II-null cells (Fig. 7L and Table 1; see also Movie 7, which is published as supporting information on the PNAS web site). Thus, the residual contractile mechanism of the myosin II mutants is slowed by the presence of dynacortin, supporting a role of dynacortin as a cytokinesis brake. When GFP-myosin II was expressed in the myosin II cells, the prebridge phase was converted into an exponential trajectory, and Dx was easily detected as in wild type (Fig. 7K and Table 1; see also Movie 8, which is published as supporting information on the PNAS web site).
Global and Equatorial Actin Cross-Linking. Previously, we demonstrated that removal of either dynacortin or cortexillin-I from cells resulted in a softer cortex (15). Cortexillin-I concentrates in the cleavage furrow cortex, whereas dynacortin distributes in a complementary fashion to cortexillin-I during cytokinesis (19, 24). The carboxyl-terminal half of dynacortin (C181, sufficient for actin cross-linking) rescues the growth and cortical mechanics defects of cortexillin-I mutants (15). The cortexillin I mutant furrows thinned after a triphasic trajectory (Fig. 7M). Rescue with cortexillin I returns the thinning trajectory to an exponential (Fig. 7N). Interestingly, cortexillin I mutants rescued with dynacortin C181 showed a faster triphasic trajectory (Fig. 7O and Table 1). Although C181 rescues growth rate, furrow symmetry, crossover distance and cortical viscoelasticity, it does not rescue the furrow-thinning trajectory to an exponential (15). Thus, equatorial and global actin cross-linking proteins modulate furrow-thinning dynamics in distinct ways.
Model for Cytokinesis Dynamics. To evaluate the phase 2 furrow thinning dynamics, we compared the cell with a viscoelastic fluid. Two principal material properties that control the dynamics of viscoelastic fluids are the stretch modulus and viscosity (Supporting Appendix 1, which is published as supporting information on the PNAS web site). The stretch modulus (Sc) is the in-plane viscoelasticity of the cortex that is generated by the actin cytoskeleton and plasma membrane and is an energy cost for adding surface area to the cell. Because cells are viscoelastic fluids rather than elastic solids, the stretch modulus, similar to the surface tension of a liquid droplet, gives rise to a Laplace pressure that serves to minimize the surface area to volume ratio (25). Thus, during phase 1 of cytokinesis, the stretch modulus serves to resist the initial deformation of the cell. During phase 2, when a geometrically distinct intercellular bridge forms, the stretch modulus gives rise to a positive Laplace pressure difference (P = 2Sc/R vs. P = Sc/a) between the bridge and the daughter cells (Fig. 4A and Supporting Appendix 1). The pressure difference tends to push cytoplasm from the bridge to speed up cytokinesis. For wild-type Dictyostelium cells, the stretch modulus (Sc) has been measured to be between 0.06 and 1.5 nN/μm, depending on time scale and whether the measurements were made by laser-tracking microrheology (LTM) or micropipette aspiration (MPA) (14, 15, 26) (K. D. Girard, S. C. Kuo, and D.N.R., unpublished data). Because the stretch modulus of the echinoderm egg cleavage furrow and the bending modulus of the mammalian cleavage furrow have been observed to increase as cytokinesis proceeds (9, 27-29), the Laplace pressure difference could be even larger than predicted from a uniform stretch modulus.
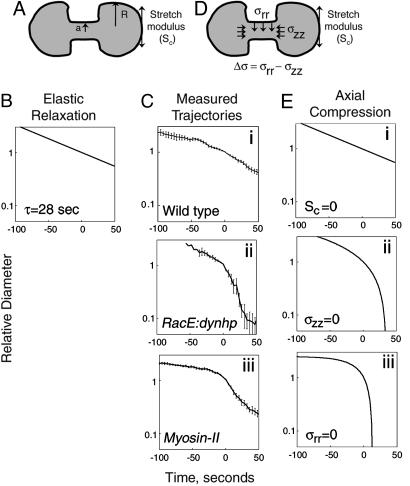
Fig. 4.
Cylinder thinning model vs. measured furrow-thinning trajectories. (A) The viscoelasticity of the cell membrane and actin-rich cortex gives rise to a stretch modulus (Sc; arrows tangent to the surface of the cell), which results in a positive Laplace pressure difference between the intercellular bridge (radius a) and daughter cells (radius R). (B) Cylinder thinning model with elastic relaxation (relaxation time τ = 28 s). (C) Measured trajectories for wild type (i) and RacE/dynacortin (ii) and myosin II (iii) mutants. (D) Cylinder thinning model with contractile stress σrr (vertical arrows) and compressive stress σzz (horizontal arrows). Δσ is the difference between σrr and σzz. (E) Furrow-thinning trajectories calculated by using the cylinder-thinning model. For all calculated trajectories, the cytoplasmic viscosity, μ, was assumed to be 0.35 nN·s/μm2. (Ei) We assume compensation of the stretch modulus so that Sc approaches 1,000-fold less than the 1.5 nN/μm measured by using MPA (14, 26) or 40-fold less than the Sc measured by using LTM (K. D. Girard, S. C. Kuo, and D.N.R., unpublished data) and Δσ = 0.025 nN/μm2 (see Fig. 9). (Eii) We assume the compressive stresses regulated by RacE and dynacortin are absent so that σzz = 0 nN/μm2, Sc = 0.02 nN/μm and Δσ = 0.015 nN/μm2. From microaspiration and LTM studies, RacE and dynacortin mutants have 20% and 50% of wild-type Sc, respectively (14, 15). The Sc value used for RacE/dynacortin is justified from our LTM studies where on the seconds time scale (0.2 rad/s), wild-type Sc is 0.06 nN/μm, wt:dynhp Sc is 0.02 nN/μm, and Sc after latrunculin treatment of wild-type cells is 0.009 nN/μm (K. D. Girard, S. C. Kuo, and D.N.R., unpublished data). Thus, these data bracket Sc for RacE:dynhp cells. Because of the rapid movements of RacE mutant cells, we cannot measure Sc for these cells by using LTM. (Eiii) We assume that radial stresses generated by myosin II are absent, so that σrr = 0, Δσ = -0.08 nN/μm2, and Sc = 0.1 nN/μm. Stretch modulus of myosin II mutant cells is based on LTM measurements (K. D. Girard, S. C. Kuo, and D.N.R., unpublished data).
Viscosity is the energy cost for fluid flow and should slow down the cell shape change. Cytoplasmic viscosities (μ) are nonlinear, and for Dictyostelium range, from 10 to 350 Pa·s, depending on the applied force (30). As large-scale shape changes are likely to be dominated by the highest viscosity, the relevant viscosity for cytokinesis is likely to be 350 Pa·s (0.35 nN·s/μm2).
If one assumes that furrow thinning and bridge recoil are driven only by the stretch modulus and the resistance is due solely to viscous drag, then a dimensional analysis suggests the process occurs with a velocity proportional to Sc/μ that depends on the geometry of the bridge (31, 32) (Supporting Appendix 1). For a cylindrical bridge, the proportionality factor is 1/3, yielding a velocity, v = Sc/3 μ. This ratio describes an entirely passive mechanism for the thinning of the cylindrical bridge and predicts that the wild-type furrow bridge ingression and bridge recoil after severing would achieve velocities in the 1.5 μm/s range by using the largest stretch modulus and viscosity. For wild-type and mutant cells, the recoil of the intercellular bridge occurred with velocities in the 1-2 μm/s range, indicating that recoil velocity, stretch modulus, and viscosity are consistent within a framework of v = Sc/3 μ (Fig. 8 and Movie 9, which are published as supporting information on the PNAS web site).
The measured apparent velocity of wild-type furrow ingression is ≈70-fold (1.5 μm/s vs. 0.022 μm/s) slower than the predicted velocity. Further, the passive mechanism predicts a linear decrease rather than the exponential decay displayed by the wild-type cells. Therefore, the wild-type thinning dynamics are not driven solely by a passive mechanism.
To analyze the measured trajectories more quantitatively, we considered a simple analytical model of furrow thinning in which the intercellular bridge is modeled as a perfect cylinder (Supporting Appendix 1). We first considered whether bulk elasticity effects of the cleavage furrow cytoskeleton could control the furrow-thinning rates. However, a long time constant for elastic relaxation (τ = 28 seconds) was required to match the measured wild-type dynamics (Fig. 4 B vs. Ci; Supporting Appendix 1, Eq. 18). Because the measured relaxation time constant for Dictyostelium is <1 s (30), slowing of furrow thinning by elastic effects seems unlikely. More importantly, bulk elasticity effects, which only allow exponential decay, do not explain the mutant trajectories.
Next, we hypothesized that compressive stresses (σzz) exist at the two ends of the intercellular bridge and, hence, slow down cytokinesis (Fig. 4D and Supporting Appendix 1, Eq. 12). In addition, radial stresses (σrr) are actively generated at the surface of the cylindrical intercellular bridge and act to thin the bridge, speeding up cytokinesis. For a cylindrical bridge, the antagonistic effect of the radial and compressive stresses is characterized simply by the stress difference (Δσ = σrr - σzz). The hypothesis of the model is that axial compression acts on the ends of the furrow to cancel the Laplace pressure, slowing the flow of cytoplasm out of the bridge so that the decay is controlled by the myosin II-driven radial stresses. Importantly, these compressive stresses do not need to be generated precisely at the ends of the furrow. Rather, they may be generated by the viscoelasticity of the daughter cell cortical cytoskeleton or cytoplasm, producing resistance vectors that sum to vectors that counteract flow from the bridge. Setting the viscosity, μ, to 0.35 nN·s/μm2, the cylinder thinning model produced furrow thinning trajectories, which are in good agreement with those observed for the mutants (Fig. 4 Cii and Ciii vs. Eii and Eiii). The parameters for Δσ and Sc (given in the Fig. 4 legend), which were used to obtain the calculated trajectories, are reasonable given available measured values (14, 15). The RacE/dynacortin mutant trajectory was best modeled by allowing the stretch modulus and a positive Δσ to drive furrow ingression, consistent with the idea that these proteins slow furrow thinning by providing a brake, which counteracts the Laplace pressure. Consistent with the idea that myosin II generates the active radial stresses, the myosin II mutant dynamics are recapitulated if we set σrr to 0 so that Δσ is negative. Thus, the major distinction between the mutants was that RacE/dynacortin mutants required a positive Δσ, whereas the myosin II mutants required a negative Δσ. Both sets of mutants had furrow-thinning trajectories that accelerated near Dx, consistent with Dx representing the point when the stretch modulus strongly favors furrow thinning.
To obtain exponential decay furrow-thinning dynamics, we propose that RacE and dynacortin-generated compressive stresses counteract the effects of the stretch modulus. This balance creates the exponential decay observed for wild-type cytokinesis when the measured rate constant k (-0.012 s-1) for wild-type thinning was used to calculate the stress difference (Δσ) between the radial and compressive stress (-k = Δσ/6 μ; Δσ = 0.025 nN/μm2) (Fig. 4 Ci vs. Ei). Clearly, changes in the viscosity can also impact the dynamics of bridge thinning; we present several calculated trajectories where stretch modulus and viscosity are varied to demonstrate how these parameters might contribute to the trajectory (Fig. 9, which is published as supporting information on the PNAS web site).
Using the values obtained from the dynamics analysis, we estimated the amount of radial stresses generated by myosin II and relate that to actual amounts of myosin II present in the cleavage furrow cortex (Supporting Appendix 2, which is published as supporting information on the PNAS web site). Using the stress difference from wild-type cells and the compressive stresses that account for the myosin II mutant furrow-thinning dynamics (Fig. 4E), the active radial stresses (σrr =Δσ + σzz) are ≈0.1 nN/μm2. The actual amounts of myosin II present in the furrow around Dx are predicted to generate radial stresses that closely agree with the observed stresses from the dynamics analysis (6). In short, wild-type thinning dynamics are exquisitely controlled by RacE and dynacortin and are largely driven by active myosin II-generated radial stresses.
Discussion
Two broadly defined mechanical models, polar relaxation and equatorial contractility, have dominated the cytokinesis field in recent decades (18). The polar relaxation model ascribes expansive forces to the polar cortex. An increase in the viscoelasticity of the cleavage furrow cortex then guides cleavage furrow ingression (9, 27-29). In the equatorial contractility model, equatorial myosin II ATPase generates the cleavage forces (2-4). Although these two classic models are invaluable for generating a framework for relating proteins to the mechanics of cytokinesis, they are inherently limited as they are unnecessarily dichotomous and are nondynamical. Our data support a model in which both global and equatorial proteins interact to control the dynamics of furrow ingression.
To create a quantitative framework for cytokinesis, we developed a simple analytical model in which the phase 2 dividing cell is compared with a simple viscoelastic fluid. The rationale for the proposed model was that the number of parameters (myosin II mechanochemistry, a Laplace pressure, resistive stresses, and viscosity) should be minimized and that the parameters should be largely experimentally verifiable. These restrictions limit the model because it is not completely molecular and does not allow the values of stretch modulus, viscosity, or active and compressive stresses to vary temporally or spatially as furrow-thinning proceeds. Although this model is clearly simplified, it is physically grounded and appropriate given current available experimental data.
From the analysis, it becomes clear that wild-type cells behave very differently from viscoelastic fluids. In contrast, myosin II and RacE/dynacortin mutant cytokineses have furrow-thinning trajectories that are much easier to reconcile from fluid mechanical considerations and the available measured physical parameters. Wild-type furrow-thinning trajectories are more difficult to reconcile, perhaps because wild-type cells have more contractile mechanisms at their disposal than the mutants have.
Two classes of stretch modulus values have emerged from MPA and LTM. MPA yields a wild-type Sc of 1.5 nN/μm, whereas LTM yields a wild-type Sc of 0.06 nN/μm (at 0.2 rad/s), producing a 25-fold (1.5 vs. 0.06) discrepancy (14, 15, 26). In contrast, measured stretch modulus values for myosin II mutants are 0.5 nN/μm from MPA (ref. 24; J. C. Effler, P. Iglesias, and D.N.R., unpublished data) and 0.1-0.2 nN/μm from LTM (K. D. Girard, S. C. Kuo, and D.N.R., unpublished data), yielding only a 3-5-fold discrepancy for this genotype and ruling out systematic differences in the two methods. These results beg the question as to what these parameters indicate about cortical mechanics. Interestingly, the LTM-derived values readily account for the furrow-thinning dynamics, whereas the MPA-derived values account for the bridge recoil. Previously, we showed that the amount of myosin II at the furrow cortex at the phase 1/2 transition is predicted by using MPA values (6), whereas the myosin II amount present at the time of Dx is predicted from the dynamics analysis by using LTM-derived values (Supporting Appendix 2). Because MPA measures long-range mechanics (several micrometer range) and LTM measures short-range mechanics (low micrometer range), phase 1 cytokinesis may be dominated by long-range mechanics and phase 2 may be controlled by short-range mechanics (25). Bridge recoil occurs over several microns, and given its high velocity, it may again be dominated by long-range mechanics. Thus, RacE- and dynacortin-created compressive stresses may only need to counteract a 40-fold difference in Laplace pressure rather than a 1,000-fold difference (compare Fig. 9 A vs. D and F vs. D).
How RacE and dynacortin generate compressive stresses to slow cytokinesis becomes a fundamental question for understanding the control of cytokinesis dynamics. These proteins may modulate the cortical and/or cytoplasmic viscoelasticity of the daughter cells. The viscoelasticity of the daughter cells may generate resistive (compressive) stresses that slow furrow thinning. A prediction from the model then is if the compressive stresses could be alleviated perhaps by micromanipulation, then furrow thinning should accelerate. Another mechanical parameter to consider is the mechanical phase angle (tan-1(viscous modulus/elastic modulus)). Myosin II increases the phase angle, making the cortex more liquid-like (viscous), whereas dynacortin reduces the phase angle, making the cortex more solid-like (elastic) (15) (K. D. Girard, S. C. Kuo, and D.N.R., unpublished data). This and other data indicate that dynacortin and myosin II have opposite effects on cortical mechanics. Because dynacortin and myosin II have complementary distributions in dividing wild-type cells, these two proteins probably control cytokinesis dynamics by modulating cortical mechanical properties in an antagonistic manner.
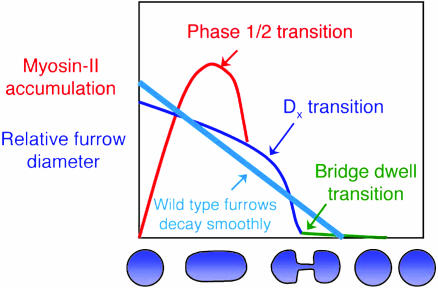
In summation, our analysis suggests a picture for cleavage furrow contractility that has three mechanical transitions (Fig. 5). The first transition occurs between phase 1 and phase 2, corresponding to the point when the maximum amount of myosin II localizes at the cleavage furrow (6). Because myosin II mutant Dictyostelium divide on surfaces, crawling forces help elongate the cell during phase 1; indeed, nonadherent myosin II mutants fail to elongate during phase 1 (7). We suggest that the Laplace pressure helps drive the myosin II mutant cleavage furrow contractility during phase 2. If crawling forces drove the entire myosin II mutant cytokinesis, then for every 10-fold decrease in furrow diameter, the pole-to-pole distance should increase 100-fold. However, the pole-to-pole distance of the myosin II mutants increases only ≈2-fold during the entire cytokinesis. A Laplace pressure is a good candidate for providing these additional forces. The second transition occurs at Dx, when the mutant bridge thinning accelerates. The third transition occurs at the formation of the final intercellular bridge, which dwells for a period before scission. We propose that cytoskeletal disassembly controls the bridge dwelling time and several cytoskeletal mutants disrupt this final stage of cytokinesis (for example, refs. 33-36 and E. M. Reichl and D.N.R., personal observation).
Fig. 5.
Three mechanical transitions of cleavage furrow contractility. Wild-type cells pass smoothly through each transition, leading to bridge severing.
Finally, cells may control furrowing dynamics and tap into their passive mechanical forces by regulating proteins similar to RacE and dynacortin. By molecularly controlling passive and active force-generating mechanisms, cells may perform error-free cytokinesis under a wide variety of mechanical environments. Other examples where excessive forces govern biological processes include Listeria motility (37) and the morphogenic movements of Drosophila embryogenesis (38). In conclusion, by combining genetics and careful quantification of cytokinesis dynamics with an analytical model, we suggest that resistive stresses generated by RacE and dynacortin work against myosin II-generated forces and material forces generated by the stretch modulus to exquisitely control cytokinesis dynamics.
Supplementary Material
Acknowledgments
We thank Janet Effler for checking our math; Kris Girard for Western analysis; Elizabeth Reichl, Runa Musib, Mary Schuler, and Jim Spudich for comments on the manuscript; and Jim Spudich and Arturo Delozanne (University of Texas, Austin) for sharing myosin II and RacE mutant cells. We thank the Burroughs-Wellcome Fund (D.N.R.), the National Institutes of Health (D.N.R.), and the National Science Foundation (W.Z.) for support.
Author contributions: W.Z. and D.R. designed research, performed research, analyzed data, and wrote the paper.
Abbreviations: LTM, laser-tracking microrheology; MPA, micropipette aspiration.
References
- 1.Rappaport, R. (1996) Cytokinesis in Animal Cells (Cambridge Univ. Press, Cambridge, U.K.).
- 2.DeLozanne, A. & Spudich, J. A. (1987) Science 236, 1086-1091. [DOI] [PubMed] [Google Scholar]
- 3.Zurek, B., Sanger, J. M., Sanger, J. W. & Jockusch, B. M. (1990) J. Cell Sci. 97, 297-306. [DOI] [PubMed] [Google Scholar]
- 4.Straight, A. F., Cheung, A., Limouze, J., Chen, I., Westwood, N. J., Sellers, J. R. & Mitchison, T. J. (2003) Science 299, 1743-1747. [DOI] [PubMed] [Google Scholar]
- 5.He, X. & Dembo, M. (1997) Exp. Cell Res. 233, 252-273. [DOI] [PubMed] [Google Scholar]
- 6.Robinson, D. N., Cavet, G., Warrick, H. M. & Spudich, J. A. (2002) BMC Cell Biology 3, 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Zang, J.-H., Cavet, G., Sabry, J. H., Wagner, P., Moores, S. L. & Spudich, J. A. (1997) Mol. Biol. Cell 8, 2617-2629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.O'Connell, C. B., Warner, A. K. & Wang, Y.-l. (2001) Curr. Biol. 11, 702-707. [DOI] [PubMed] [Google Scholar]
- 9.Matzke, R., Jacobson, K. & Radmacher, M. (2001) Nat. Cell Biol. 3, 607-610. [DOI] [PubMed] [Google Scholar]
- 10.Kurz, T., Pintard, L., Willis, J. H., Hamill, D. R., Gönczy, P., Peter, M. & Bowerman, B. (2002) Science 295, 1294-1298. [DOI] [PubMed] [Google Scholar]
- 11.Nagasaki, A., de Hostos, E. L. & Uyeda, T. Q. P. (2002) J. Cell Sci. 115, 2241-2251. [DOI] [PubMed] [Google Scholar]
- 12.Skop, A. R., Liu, H., Yates, J., Meyer, B. J. & Heald, R. (2004) Science 305, 61-66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Pasternak, C., Spudich, J. A. & Elson, E. L. (1989) Nature 341, 549-551. [DOI] [PubMed] [Google Scholar]
- 14.Gerald, N., Dai, J., Ting-Beall, H. P. & DeLozanne, A. (1998) J. Cell Biol. 141, 483-492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Girard, K. D., Chaney, C., Delannoy, M., Kuo, S. C. & Robinson, D. N. (2004) EMBO J. 23, 1536-1546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Simson, R., Wallraff, E., Faix, J., Niewöhner, J., Gerisch, G. & Sackmann, E. (1998) Biophys. J. 74, 514-522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Faix, J., Steinmetz, M., Boves, H., Kammerer, R. A., Lottspeich, F., Mintert, U., Murphy, J., Stock, A., Aebi, U. & Gerisch, G. (1996) Cell 86, 631-642. [DOI] [PubMed] [Google Scholar]
- 18.Robinson, D. N. & Spudich, J. A. (2004) Curr. Opin. Cell Biol. 16, 182-188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Robinson, D. N. & Spudich, J. A. (2000) J. Cell Biol. 150, 823-838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Larochelle, D. A., Vithalani, K. K. & DeLozanne, A. (1996) J. Cell Biol. 133, 1321-1329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ruppel, K. M., Uyeda, T. Q. P. & Spudich, J. A. (1994) J. Biol. Chem. 269, 18773-18780. [PubMed] [Google Scholar]
- 22.Robinson, D. N., Girard, K. D., Octtaviani, E. & Reichl, E. M. (2002) J. Muscle Res. Cell Motil. 23, 719-727. [DOI] [PubMed] [Google Scholar]
- 23.Larochelle, D. A., Vithalani, K. K. & DeLozanne, A. (1997) Mol. Biol. Cell 8, 935-944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Weber, I., Gerisch, G., Heizer, C., Murphy, J., Badelt, K., Stock, A., Schwartz, J.-M. & Faix, J. (1999) EMBO J. 18, 586-594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Reichl, E. M., Effler, J. C. & Robinson, D. N. (2005) Trends Cell Biol. 15, 200-206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Dai, J., Ting-Beall, H. P., Hockmuth, R. M., Sheetz, M. P. & Titus, M. A. (1999) Biophys. J. 77, 1168-1176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Hiramoto, Y. (1963) Exp. Cell Res. 32, 76-88. [DOI] [PubMed] [Google Scholar]
- 28.Hiramoto, Y. (1990) Ann. N.Y. Acad. Sci. 582, 22-30. [DOI] [PubMed] [Google Scholar]
- 29.Wolpert, L. (1966) Exp. Cell Res. 41, 385-396. [DOI] [PubMed] [Google Scholar]
- 30.Feneberg, W., Westphal, M. & Sackmann, E. (2001) Eur. Biophys. J. 30, 284-294. [DOI] [PubMed] [Google Scholar]
- 31.Kowalewski, T. A. (1996) Fluid Dyn. Res. 17, 121-145. [Google Scholar]
- 32.Entov, V. M. & Hinch, E. J. (1997) J. Non-Newtonian Fluid Mech. 72, 31-53. [Google Scholar]
- 33.Adachi, H., Takahashi, Y., Hasebe, T., Shirouzu, M., Yokoyama, S. & Sutoh, K. (1997) J. Cell Biol. 137, 891-898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Swan, K. A., Severson, A. F., Carter, J. C., Martin, P. R., Schnabel, H., Schnabel, R. & Bowerman, B. (1998) J. Cell Sci. 111, 2017-2027. [DOI] [PubMed] [Google Scholar]
- 35.Liu, T., Williams, J. G. & Clarke, M. (1992) Mol. Biol. Cell 3, 1403-1413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Nagasaki, A. & Uyeda, T. Q. (2004) Mol. Biol. Cell 15, 435-446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Giardini, P. A., Fletcher, D. A. & Theriot, J. A. (2003) Proc. Natl. Acad. Sci. USA 100, 6493-6498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hutson, M. S., Tokutake, Y., Chang, M.-S., Bloor, J. W., Yenakides, S., Kiehart, D. P. & Edwards, G. S. (2003) Science 300, 145-149. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.