Machine Learning Based Methodology to Identify Cell Shape Phenotypes Associated with Microenvironmental Cues

Abstract

Cell morphology has been identified as a potential indicator of stem cell response to biomaterials. However, determination of cell shape phenotype in biomaterials is complicated by heterogeneous cell populations, microenvironment heterogeneity, and multi-parametric definitions of cell morphology. To associate cell morphology with cell-material interactions, we developed a shape phenotyping framework based on support vector machines. A feature selection procedure was implemented to select the most significant combination of cell shape metrics to build classifiers with both accuracy and stability to identify and predict microenvironment-driven morphological differences in heterogeneous cell populations. The analysis was conducted at a multi-cell level, where a “supercell” method used average shape measurements of small groups of single cells to account for heterogeneous populations and microenvironment. A subsampling validation algorithm revealed the range of supercell sizes and sample sizes needed for classifier stability and generalization capability. As an example, the responses of human bone marrow stromal cells (hBMSCs) to fibrous vs flat microenvironments were compared on day 1. Our analysis showed that 57 cells (grouped into supercells of size 4) are the minimum needed for phenotyping. The analysis identified that a combination of minor axis length, solidity, and mean negative curvature were the strongest early shape-based indicator of hBMSCs response to fibrous microenvironment.

Introduction

The morphology of a cell is influenced by a combination of many intracellular mechanical processes, interactions with other cells and the surrounding extracellular matrix [1–7]. Thus, cell morphology reflects the integrative effect of many distinct processes and signaling pathways across different scales [4, 5] and may be a valuable descriptor of cell behaviors in differentiation [8–14], function or dysfunction [15], migration [16–18] and cancer progression [19]. For example, a recent study by Marklein et al [8] demonstrates over 90% accuracy in the prediction of day 35 mineralization of human bone-marrow derived mesenchymal stem cells (hMSCs) cultures of varying donors and passages based on day 3 cell morphology. In another recent study by Unadkat et al [10], cell morphology was also investigated as an indicator of cell genotypic and phenotypic responses. Beyond being a possible indicator, some studies have shown that either affecting cell morphology with surface topographical cues [20–23] or directly manipulating cell morphology through geometric constraints of cell adhesive regions can elicit genotypic or phenotypic alterations [5–7, 24]. Therefore, cell morphology may contribute as a descriptor, indicator or intermediate factor in characterizing cell-material interactions. High-throughput single-cell bioimaging has enabled the quantification of heterogeneous cell population with many cell shape features that are increasingly difficult to interpret. In addition, the complex biomaterial microenvironment can also contribute to the heterogeneity of cell shape response. Innovative analytical tools must be developed to identify and combine key cell shape features correlated with biological outcome while accounting for both multi-parametric complexity and biological heterogeneity.

Multi-parametric single-cell data are widely used in biomaterials studies with technologies such as bioimaging, single-cell PCR and flow cytometry. In order to associate multi-parametric single cell data with cell-material interactions, appropriate computational and statistical tools are required to quantify the informative content of data and describe differences between cell populations. Common statistical methods typically used are Student’s t-test and ANOVA analyses. These approaches describe differences of the multi-parametric data by comparing the values of each single metric across different cell populations with a statistical hypothesis test which outputs a p-value [25, 26]. This has proven valuable to determine individual metrics that may be important in characterizing cell-material interactions. However, if we intend to describe the cell phenotypes for cell populations with more comprehensive representations by combining multiple metrics, these approaches are limited as they omit correlations between metrics in describing cell population differences.

Representations of multi-parametric data can be obtained by other statistical methods, such as principal component analysis (PCA) and singular value decomposition (SVD) [8, 27, 28]. More recent methods (for instance, self-organizing maps [29] and multidimensional scaling [9]) can achieve reduced multidimensional representations of cell morphology. However, these methods bring other limitations. In particular, they are not designed to separate different classes optimally and, the achieved dimensional reduction introduces more abstract descriptions of the system in terms of linear or non-linear combinations of metrics, bringing difficulties to determine relevant features in defining the cell phenotypes. To address these limitations, we have developed an approach to overcome several of these limitations by generating multi-dimensional linear classifiers that allow simple interpretation for classification and phenotyping in reduced metric space.

In this study, we investigated the morphology of human bone marrow stromal cells (hBMSCs) in fibrous substrates compared to that of cells on flat films (Fig 1.a) in presence or absence of osteogenic differentiation media. Fibrous materials are widely used in both research and clinical applications of tissue engineering and regeneration medicine. Previous studies had demonstrated that hBMSCs cultures on fibrous substrates developed osteogenic differentiation after 50 days of culturing without any osteogenic supplement [21]. Morphological response of hBMSCs in fibrous substrates is being investigated as a possible mechanism for osteogenic differentiation observed in this microenvironment [21, 30–33]. This hypothesis is supported by several studies describing mechanistic associations between hMSCs shape and subsequent differentiation [5–7]. However, only a few individual cell shape features have been investigated for their association with differentiation, and cell morphologies vary greatly across a fibrous substrate. To address this limitation, we have developed an analysis framework for multi-parametric single-cell data based on support vector machines (SVMs) [34–36] to quantify shape differences of hBMSCs populations and associate them with different microenvironments (Fig 1.b). SVM classifiers are designed to find the optimal classification boundary that separates data points in the multidimensional shape metric space. We investigated a wide range of shape metrics to quantify global and local shape features, including cell size and aspect ratio, cytoskeletal branching, and local boundary curvature. Moreover, the resulting SVM classifiers provided a selection of reduced shape metrics to quantify hBMSCs shape phenotypes in specific microenvironments.

Fig 1.

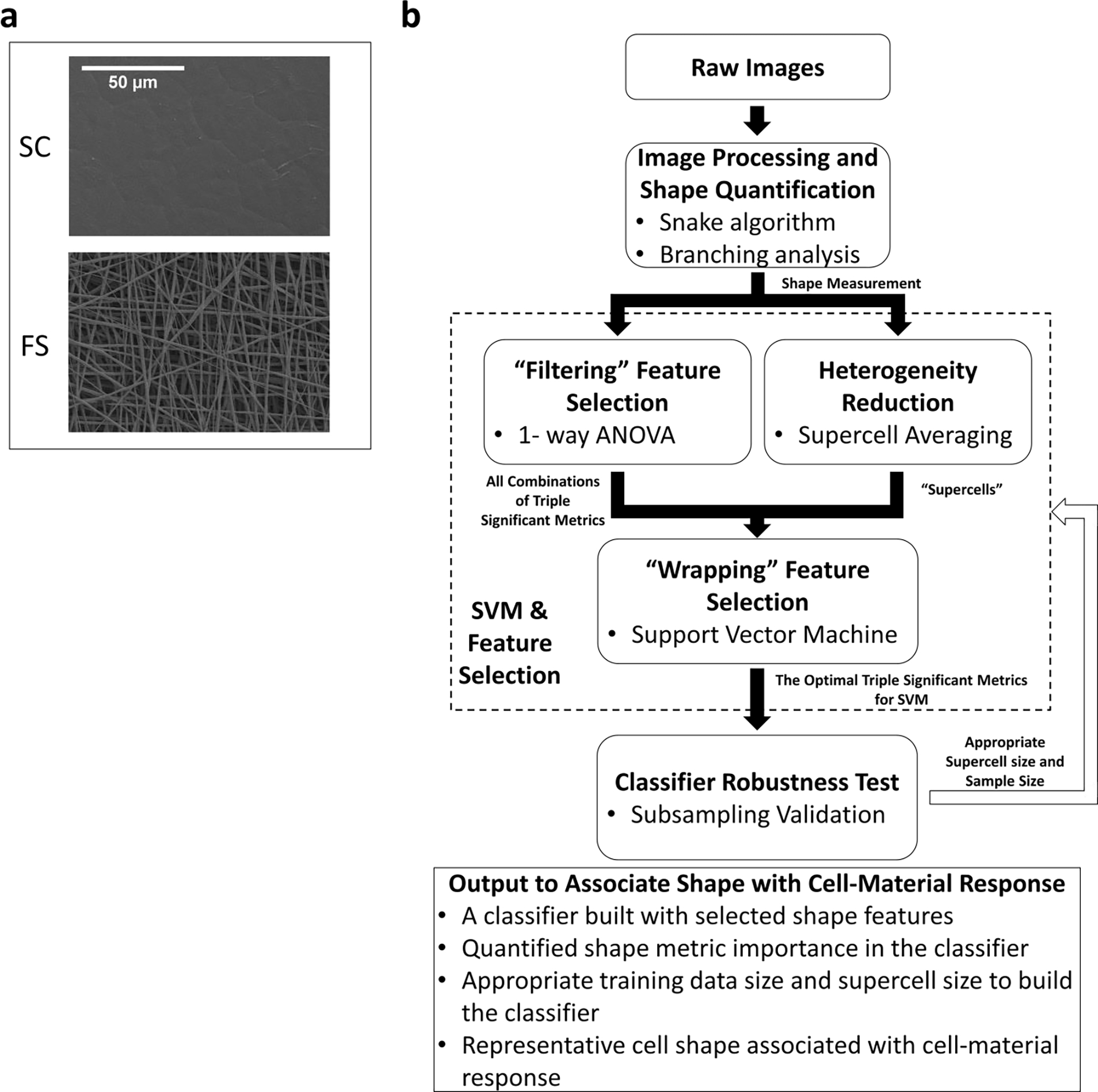
(2-column). (a) SEM images of PCL fibrous substrates and PCL spin-coated film. (b) Schematic flow chart of the analysis procedure and outcomes of the computational tools developed in this study.

However, the heterogeneous cell population and the heterogeneous microenvironment may cause variability in cell morphology, where difference between shapes of single cells within the same culture environment are observed. Within the SVM scenario, variability in cell morphology can lead to highly overlapping cell populations and, thus poorly performing classifiers on the single-cell level. In order to address single-cell heterogeneity from different sources, a method of averaging shape metrics over a small subset of randomly selected cells known as “supercell” averaging [36, 37] was implemented to improve the training and prediction accuracies of the SVM classifiers. Instead of solely focusing on phenotypes on single-cell level, the SVM/supercell paradigm allowed consideration of cell shape phenotypes associated to small groups of cells, i.e. “supercells”. The random sampling used to generate supercells can introduce uncertainty in the SVM classifier. The tradeoff between prediction accuracy, supercell averaging and uncertainty in the classifier were quantitatively determined in this study. Furthermore, by introducing a subsampling validation procedure, we studied the sample size as another important limiting factor in the construction of single-cell or supercell phenotypes and its effects on classifier prediction accuracy. By combining multiple metrics and learning at small cell group levels, the SVM/supercell paradigm quantitatively identified changes in population behavior of cell morphology for four different conditions. Building on this approach, a systematic analysis of the cell response to the physics and chemistry of their surrounding biomaterial could be carried out.

Materials and Methods

Certain commercial equipment, instruments, or materials are identified in this paper in order to specify the experimental procedure adequately. Such identification is not intended to imply recommendation or endorsement by the National Institute of Standards and Technology, nor is it intended to imply that the materials or equipment identified are necessarily the best available for the purpose.

Preparation of substrates

To fabricate poly(ε-caprolactone) fibrous substrates (FS), PCL solution (0.15 g/mL in 5: 1 volume ratio of chloroform: methanol) was dispensed by a 3 mL syringe and pump (0.5 mL/h) through a 21 gauge 1” shaft, flat tip, dispensing needle over an array of 0.95 cm² tissue-culture polystyrene (TCPS) disks arranged on a grounded aluminum foil over a 6 h period. The distance between the syringe needle and the target TCPS disk array was 20.4 cm. The needle was connected to a positive lead of 13.5 kV. To help the adhesion of PCL fibers over the target TCPS disk array, the disks were sprayed with 70 % by mass ethanol solution every 10 min to enhance fiber deposition to the disks. The diameter of fabricated PCL fibers was (589 ± 116) nm (n=151) as determined by scanning electron microscopy imaging (2.00 kV, 5000x).

PCL films (SC) were prepared by spin-coating PCL solution (0.7 mL, 0.1 g/mL in glacial acetic acid) on tissue-culture polystyrene dishes at 1100 rpm for 30 s. Films were air dried at room temperature overnight and heated above 60 °C for 4 to 5 times in order to achieve a reproducible cobblestone pattern in the films [38]. Films were punched into disks of 0.95 cm². The surface roughness of the SC is (92.76 ± 10.69) nm determined by atomic force microscopy.

FS and SC disks were placed in 48-well tissue-culture polystyrene plates. Plates were sterilized by ethylene oxide for 12 h and then purged under vacuum for 2 days. Before cell seeding, each well was fully wetted with media (α-minimum essential media from Invitrogen supplemented with 16.6 % by volume fetal bovine serum from Atlanta Biologicals, 4 mmol/L L-glutamine and penicillin-streptomycin) and incubated at 37 °C with 5 % CO₂ for 48 h [21].

Cell culture

Primary human bone marrow stromal cells (hBMSCs, donor 7038, Tulane Center for Gene Therapy) at passage 4 were cultured with media and dissociated with 0.25 % mass fraction trypsin and then re-suspended in media. Cell concentration was calculated with a hemocytometer. Cells were then diluted with regular cell culture media or media with osteogenic supplement (OS) of dexamethasone (10 nmol/L), β-glycerophosphate (20 mmol/L) and ascorbic acid (0.05 mmol/L) to the desired cell concentration (5,000 cells/mL or 2,500 cells/cm²) for both media types. 0.5 mL hBMSCs suspension was seeded to each well in four conditions (FS, SC, FS+OS and SC+OS). hBMSCs were then cultured at 37 °C with 5 % CO₂ for 24 h. The seeding density of 1,000–3,000 cells/cm² had been used for in vitro studies to investigate hBMSCs osteogenesis with different bioassays, as well as studies correlating hBMSCs’ early morphology with later differentiation fates [5, 8–12, 39, 40]. This seeding density results in many isolated cells after 24 hours. While cell-cell contact could be a factor in many contexts, affecting both cell behavior and cell shape, prior work had identified single cell shape as a possible early marker of differentiation [9, 13, 21]. Therefore, in this study, we focused on single cells morphology as a model system to validate our method.

Fixation and fluorescence staining of cells

hBMSCs were fixed with 3.7 % by volume formaldehyde in Dulbecco’s phosphate-buffered saline (PBS) and then washed with PBS for 3 times. 0.1 % by volume Triton-X in PBS was used to permeabilize hBMSCs for 10 min. Samples were washed with PBS 3 times, then soaked in blocking buffer (50 mg/mL bovine serum albumin in PBS) for 30 min. Alexa Fluor 546 phalloidin (0.33 μM in blocking buffer) was added to stain F-actin of hBMSCs for 1h at room temperature and then washed away with washing buffer (10 mg/mL bovine serum albumin in PBS). Nuclei were stained by 4’, 6-diamidino-2-phenylindole (DAPI, 0.3 μΜ) for 5 min. All samples were then rinsed with washing buffer and PBS. Stained samples were store at 4 °C in PBS protected from light before imaging.

Confocal microscopy

3-D cell morphology was imaged with confocal microscopy (Leica SP5). Samples were immersed in PBS. High-resolution 3-D z-stack images were captured by a 63x water immersion objective with the numerical aperture of 1 AU and the z-step size of 700 nm. The z depth of each stack is determined by the expansion of each cell in z direction. Alexa Fluor 546 phalloidin staining demonstrated the cell cytoskeletal boundary and DAPI staining of nucleus was used to identify single cells manually for the analysis. Cells touching the edges of field of view of each image were omitted. 121 cells of FS, 114 cells of SC, 125 cells of FS+OS and 116 cells of SC+OS were imaged and analyzed (Fig 2.a and Supplementary Fig 1).

Fig 2.

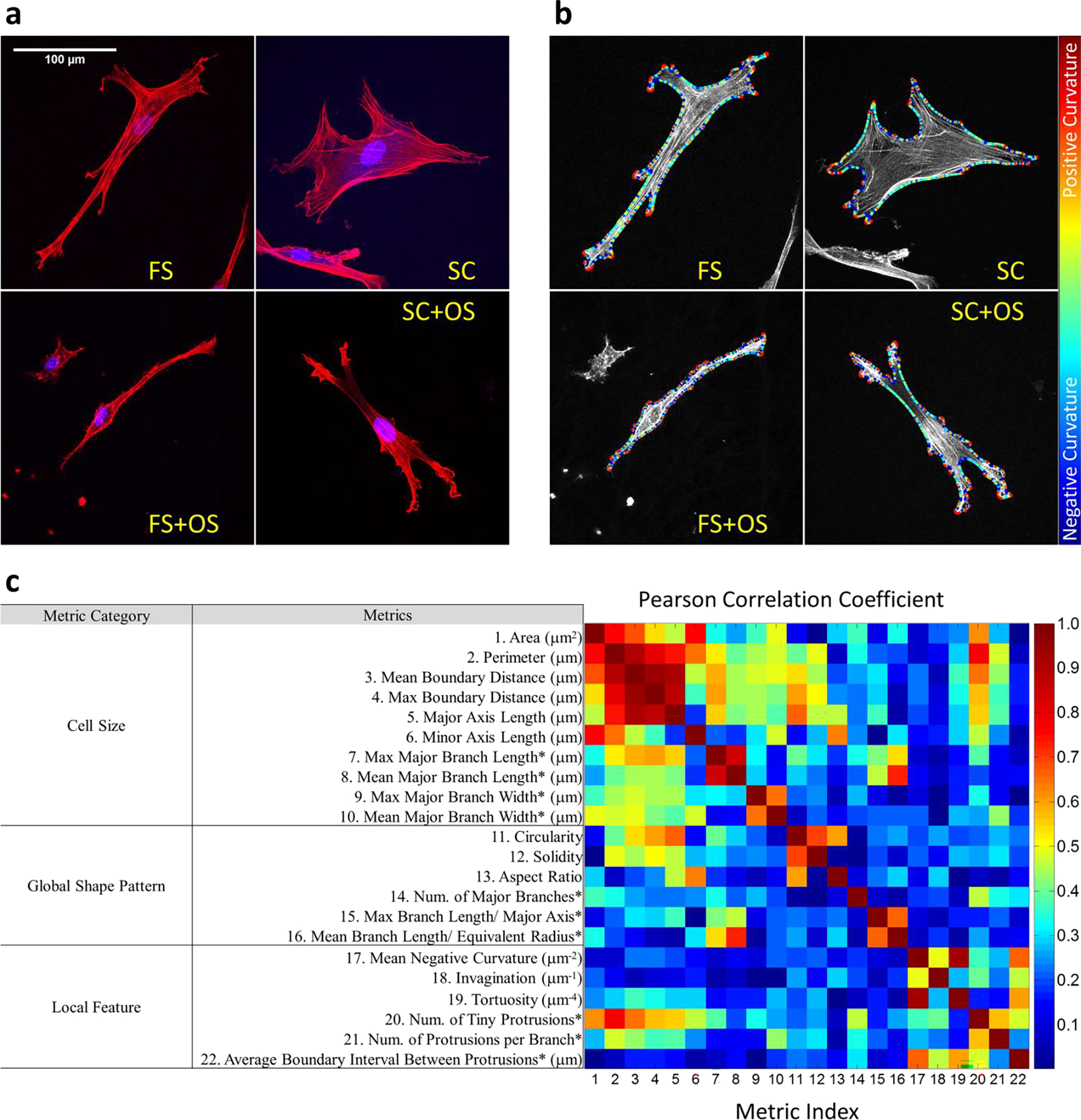
(2-column). Quantification of cell shapes in different microenvironment (FS and SC with or without OS). (a) Maximum intensity projections of the confocal z-stack images (red: actin, blue: nucleus). (b) Outlines of hBMSCs were obtained with snake algorithm which allowed calculation of local curvature. Boundary regions were colored differently according to local curvatures. (c) 22 metrics were quantified to describe hBMSCs shapes and sorted into 3 categories about different aspects of cell shape. 12 metrics were obtained with the snake outlines (without asterisks) and 10 metrics were obtained from branch analysis (with asterisks). The correlations between shape metrics were calculated with Pearson correlation coefficient.

Image processing and cell morphology measurement

On both FS and SC, the dimension of cells in the z direction is much smaller compared to their dimension in the xy plane. Therefore, as a first step, we analyze 2-D cell shapes based on projections onto the xy plane. 2-D maximum intensity projections were made and analyzed with an active contour model (snake algorithm) implemented by a custom MATLAB script based on a package created by Xu et al [41], defining cell outlines represented by positions of a set of representative points, i.e., “snakes”. Snakes were initiated with the convex hulls of the hBMSCs and converged to fit the cell boundary in an energy minimization process driven by force fields assumed according to the brightness gradient of Alex Fluor 546 phalloidin channel and mechanical properties arbitrarily defined for the snake [41]. In particular, the parameters used to identify outlines of hBMSCs were the snake elasticity parameter α (2×10⁻⁵), the snake bending rigidity β (5×10⁻⁵), the viscosity parameter γ (0.2), the external force weight (1×10⁻³), and the distance range between two consecutive representative points (2 to 3 pixels). Once snake representations of each cell were obtained, the snakes and the original images were automatically overlaid to generate new images for visual inspections. Tiny protrusions on the cell boundary were identified with a custom MATLAB script by locating local curvature regions, which were smoothed with a Gaussian filter to neglect features smaller than 1 μm. Protrusions on the cell boundary were identified as regions of positive local curvature. Branch topology of the dendritic morphology of cells was analyzed by pinching representative points of the tiny protrusions and skeletonizing the cell boundary with a custom MATLAB script implementing the level-set method [42] that kept the connectivity of all the tiny protrusions (Fig 2.b). Based on the quantified cell boundary and branch topology, hBMSCs morphologies in different microenvironments were characterized with 22 shape metrics of 2-D cell shape (Fig 2.c and Supplementary Table 1) and compared with 1-Way ANOVA and associated Tukey’s test in pairwise comparisons (Supplementary Fig 2). The Pearson’s correlations of any 2 of these metrics were also calculated and represented in Fig 2.c. The correlations between shape metrics imply that it would be redundant to use all shape metrics to analyze morphological differences. Thus, in this manuscript, we identify what combinations of shape metrics best represent morphological differences.

Cell morphology classification with Support Vector Machines (SVM)

A 22-D Cartesian coordinate system of cell morphology, in which each axis represented one shape metric, was developed for the 22 shape metrics. Within this representation, each cell was described as a 22-D shape metric vector, i.e., as a point in this multidimensional space, whose position conveyed information of that cell’s morphology. In pairwise comparisons of cell populations grown in different microenvironments (FS, SC, FS+OS and SC+OS), each shape metric was normalized to Z-scores, which ensured that the distribution of each metric had zero mean and unit variance. The Z-score transformation of a variable X is defined by

$$Z=\frac{X-\overline{X}}{\sigma \left(X\right)}$$ (1)

where $\bar{X}$ and $\sigma \left(X\right)$ are the mean and standard deviation of the distribution of X for all data points in the comparison, respectively.

After being transformed to Z-scores, multidimensional shape metric datasets from cell populations cultured in two different conditions were taken as the learning datasets on which Support Vector Machines (SVMs) were trained with the kernlab package in R language. Linear-kernel SVM is a supervised machine learning method designed to find the optimal (maximum margin) hyperplane that separates two classes of data points. Because usually the datasets are not linearly separable, the process has some degree of tolerance to data points within the margin or misclassified data points, which are defined as support vectors as they affect the position of the class boundary. The degree of tolerance is quantified with a cost function. Depending on the choice of the cost parameter, the tradeoff between margin size and training classification accuracy can be tuned in the cost function which is minimized by the SVM algorithm (see supplementary information 1) [34]. Here, we define the training classification accuracy as the percentage of cells correctly classified by the SVM hyperplane, summing all correctly classified cells from both culturing conditions. Although non-linear-kernel SVMs introduce non-linear mappings of the data to allow more flexible class boundary representations and, therefore, may improve the training classification accuracy, such added flexibility comes at the risk of incurring overfitting [43], i.e., obtaining artificial solutions that misrepresent the true boundaries between the classes. Moreover, the linear-kernel SVM allows us to obtain a straightforward interpretation of the machine-learned parameters in terms of the original shape metrics. Indeed, the components of the unit normal vector $\mathbf{n}$ of the classifier hyperplane indicate the relative importance of the different shape metrics to separate the two cell populations.

“Supercell” method to overcome single-cell heterogeneity

A challenge in the classification of biological samples is the problem of cell heterogeneity [44]. Highly overlapping cell populations lead to poorly performing and unreliable machine learning classification boundaries, since the maximum-margin optimization process becomes ill-defined. In order to improve the robustness of the classification scheme, Candia et al [36, 37] proposed the “supercell” approach as a pre-processing method that improves phenotyping under conditions of high heterogeneity at the single-cell level. In order to capture cell phenotypes in multidimensional metric space, a “supercell of size N” is defined as the average of the individual measurement vectors of a group of N randomly chosen cells. By repeatedly taking different random subsets of N cells, supercell samples can be built with the original single-cell datasets. Since the single-cell sample size, N_s, is usually small, supercell averaging is typically performed by selecting cells at random with replacement. That is, allowing the same single cell to be chosen more than once. This procedure is similar to the more commonly known method of bootstrapping [45]. By iterating this procedure, we obtain a representative sample of N_supercell supercells out of the original sample of N_s single cells.

In this work, the number of single cells measured under each condition (FS, SC, FS+OS, and SC+OS) was N_s ~120. Since the supercell averaging method was stochastic, the procedure to randomly generate a supercell sample consisting of 120 supercells was repeated 100 times with different supercell sets generated. For each of these 100 repeating procedures, SVM was used to obtain a classification boundary between two conditions. The final classifier hyperplane orientation was defined by the average normal vector $\overline{\mathbf{n}}$ over all unit normal vectors $\mathbf{n}$ of each machine learning repeat, i.e.,

$$\overline{\mathbf{n}}=\sum _{all}\mathbf{n}/\Vert \sum _{all}\mathbf{n}\Vert$$ (2)

The average training classification accuracy was calculated from averaging over all repeating machine learning procedures with different supercell sets. The classifier hyperplane stability was then measured as the average cosine function $⟨\mathrm{c}\mathrm{o}\mathrm{s}\theta ⟩$ (inner product) of the angle between the normal vector determined by each machine learning procedure and the average classifier normal vector.

$$⟨\mathrm{c}\mathrm{o}\mathrm{s}\theta ⟩=⟨\stackrel{-}{\mathbf{n}}\cdot \mathbf{n}⟩$$ (3)

And the average classifier hyperplane fluctuation is quantified by the equivalent average angular deviation ${\theta }^{\prime }$ defined as

$${\theta }^{\prime }=\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{c}\mathrm{o}\mathrm{s}(⟨\mathrm{c}\mathrm{o}\mathrm{s}\theta ⟩)$$ (4)

Selection of representative shape metrics

Bioimaging analysis approaches typically begin with computing a large number of features, although it is well known that many of these features may be redundant or irrelevant [46]. Feature selection methods are then applied to select a small set of representative features that are most relevant to characterize the objects or regions of interest [47]. The 22 shape metrics extracted here from the image of a single cell can be broadly grouped into 3 categories, namely cell size measures, global morphology pattern features and local features (Fig 2.c). As expected, some of these shape metrics are redundant and highly correlated, while others may be irrelevant to the goal of characterizing differences between different growing conditions.

In our approach, we first implemented a “filtering” step [43], in which shape metrics showing statistically significant differences (p <0.01) between microenvironments, were preselected based on 1-way ANOVA and Tukey multi-comparison test (Supplementary Fig 2). Then, a feature selection method based on the SVM/supercell paradigm was used to investigate the optimal combination of shape metrics for classification. All combinations of 3 shape metrics were used to build different metric spaces. The subsequent SVM analysis used a “wrapping” step in which features were selected according to the performance of the classifier (Fig 1.b) [43, 48, 49]. In general, the combination of 3 shape metrics with the highest training classification accuracy among those that satisfy a certain classifier hyperplane stability criterion was finally selected to represent the population morphology difference.

Subsampling Validation

With the selected shape metrics, a subsampling validation procedure was employed to decide which training data size and supercell size are appropriate to build the classifier hyperplane. In this procedure, a training subsample of a certain size was randomly picked from the original cell population and then randomly generated 120 supercells of a certain supercell size. The SVM/supercell paradigm was applied to these data sets to train a classifier hyperplane. 120 supercells of the same size were also randomly made with the remaining sample to form a test subsample. The hyperplane achieved with the training subsample was utilized to predict the test subsample. The percentage of correctly classified supercells (containing the correct classifications in both culturing conditions) in the test subsample was defined as prediction accuracy of the classifier hyperplane.

This subsampling validation procedure was repeated for multiple times (number of subsample test repeats = 200) for a certain training sample size and supercell size. For each repeat, the classifier hyperplane normal vector was calculated. The average cosine function of the angle between the instant classifier normal vector and the average classifier normal vector again was calculated as a measure of classifier hyperplane stability. Both prediction accuracy and the classifier hyperplane stability were taken into account to decide the appropriate training sample size and supercell size.

Results

The application of SVM/supercell paradigm increases the training accuracy of the classification on supercells generated from the original single-cell population and reduces the number of support vectors for SVM (Fig 3.a). It should be noted, however, that as the supercell size is increased, the classifier hyperplane stability decreases as well (Fig 3.b). For small supercell size, an increase in supercell size causes a decrease in the number of support vectors and a decrease in margin size, leading to a decrease in classifier stability. With the application of SVM/supercell paradigm, the accuracy of predicting supercells is also increased (Fig 4). Thus, the level of supercell averaging (as implied by the chosen supercell size N) determines the trade-off between training classification accuracy, prediction accuracy and the classifier hyperplane stability. As revealed by the subsampling validation, the sample size to build the classifier also affects the classifier hyperplane stability (Fig 4).

Fig 3.

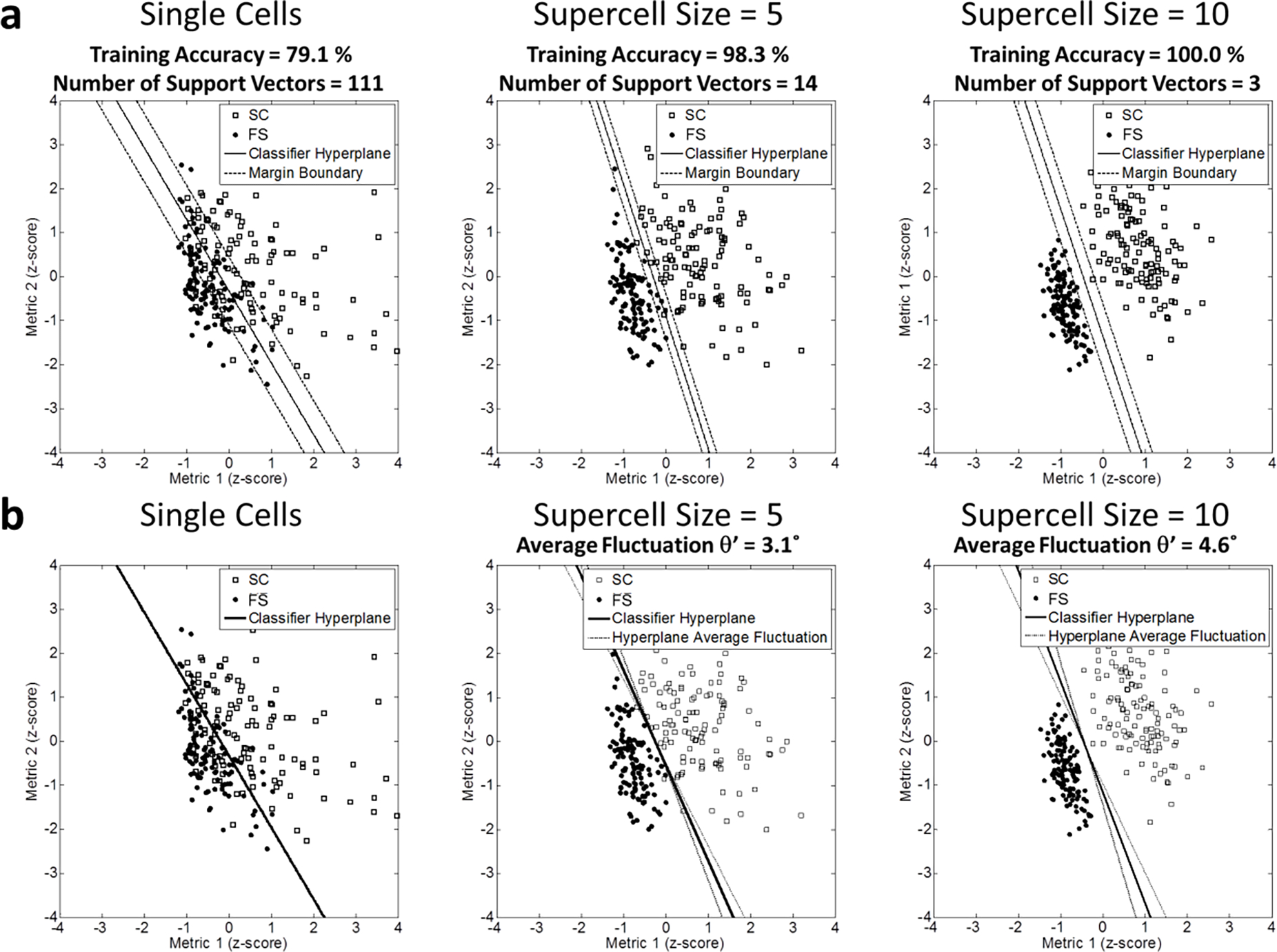
(2-column). (a) Schematic demonstration of the influence of supercells on SVM of a linear kernel in 2-D metric space. The instant classifier hyperplanes were demonstrated with the solid straight line. The margin between two classes was defined with the black dash lines. (b) Supercells populations were randomly generated from the original single cells for 100 times (only supercells of one loop is plotted). The average classifier hyperplane was demonstrated with the solid straight line. Randomness of supercell generation perturbed the classifier hyperplane. The average fluctuation of the classifier hyperplane ${\theta }^{\prime }$ was indicated with the black dash lines.

Fig 4.

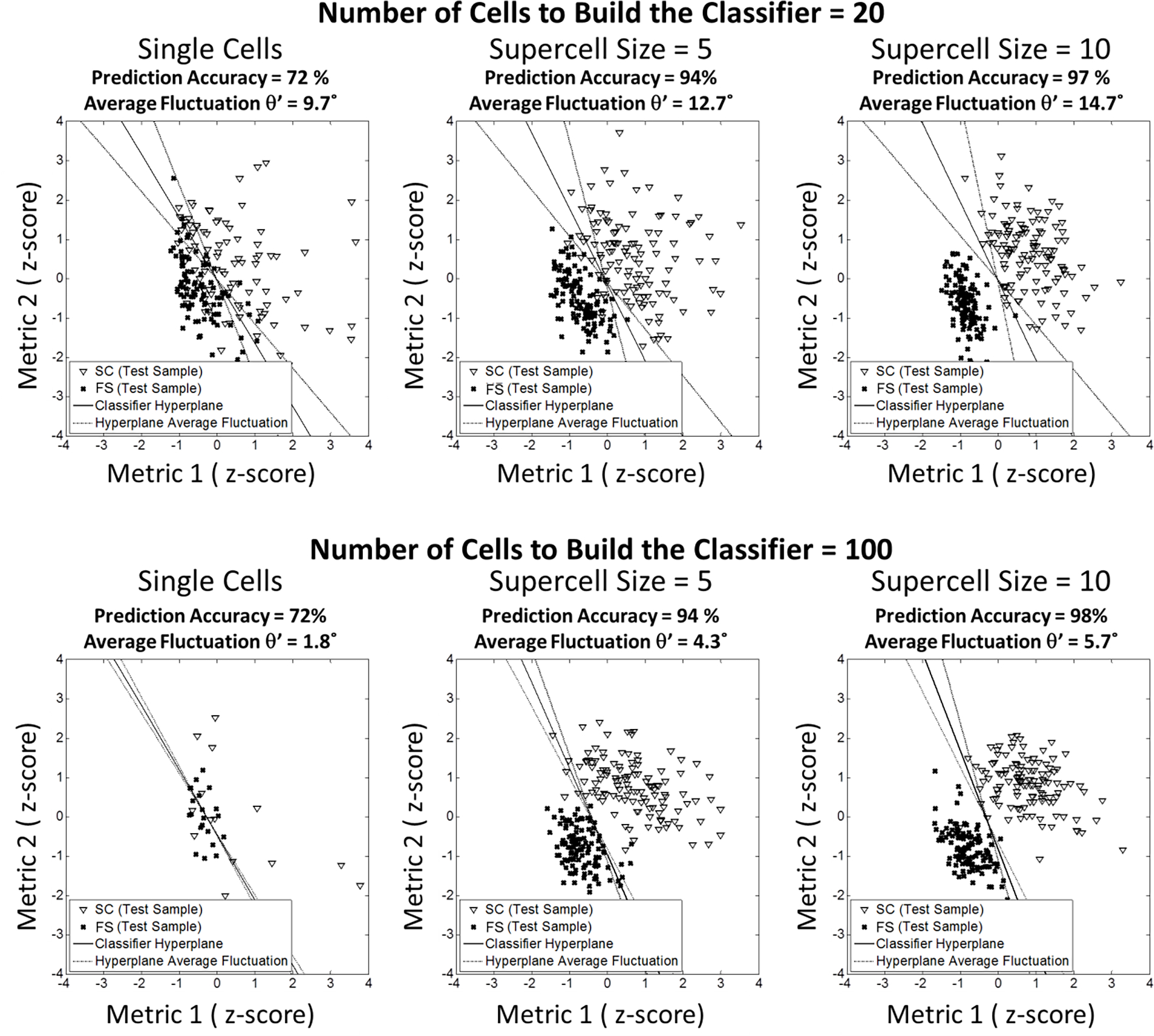
(2-column). Illustration of the subsampling procedure to test appropriate data size and supercell size to build the classifier hyperplane with stability and predictive potential. Classifiers were built with the training subsamples of the original cells. And the fluctuation of the classifier hyperplane orientation ${\theta }^{\prime }$ caused by random subsampling was measured (the scatterplots showing original cells or supercells of only 1 loop). Achieved classifier hyperplanes were then tested with the test subsamples comprised of cells in the rest of the total sample. Percentage of the accurate classification was taken as the measurement of the prediction potential.

For the comparison of FS vs. SC, increasing supercell size can affect the feature selection of the most significant 3 metrics, as demonstrated (Fig 5.a). At supercell size = 1, the selected metrics include mean major branch width, circularity, and mean negative curvature. At supercell size = 2, 3, 4, the selected metrics include area, circularity and mean negative curvature. At supercell size = 5, 6, 7, the selected metrics include minor axis length, circularity and mean negative curvature. At supercell size = 8, 9, the selected metrics include area, solidity and mean negative curvature. There is an overlap in metric combinations identified at different supercell sizes. All of the metrics identified by the SVM might be considered important. By increasing supercell size, the training classification accuracy can reach 100 %. However, there is a concurrent decrease in classifier hyperplane stability (Fig 5.b). Therefore, a balance must be drawn between accuracy and classifier hyperplane stability when selecting an appropriate supercell size for analysis. In Table 1, we report the selection of 3 representative features which satisfied a classifier hyperplane stability threshold of ${\theta }^{\prime }<{8.1}^{\circ }(⟨\mathrm{c}\mathrm{o}\mathrm{s}\theta ⟩\ge 0.99$) at supercell size of N = 5 to distinguish cell morphologies between 2 different microenvironments (differences between FS, FS+OS, SC, SC+OS, All FS, All SC, All OS, All w/o OS are described).

Fig 5.

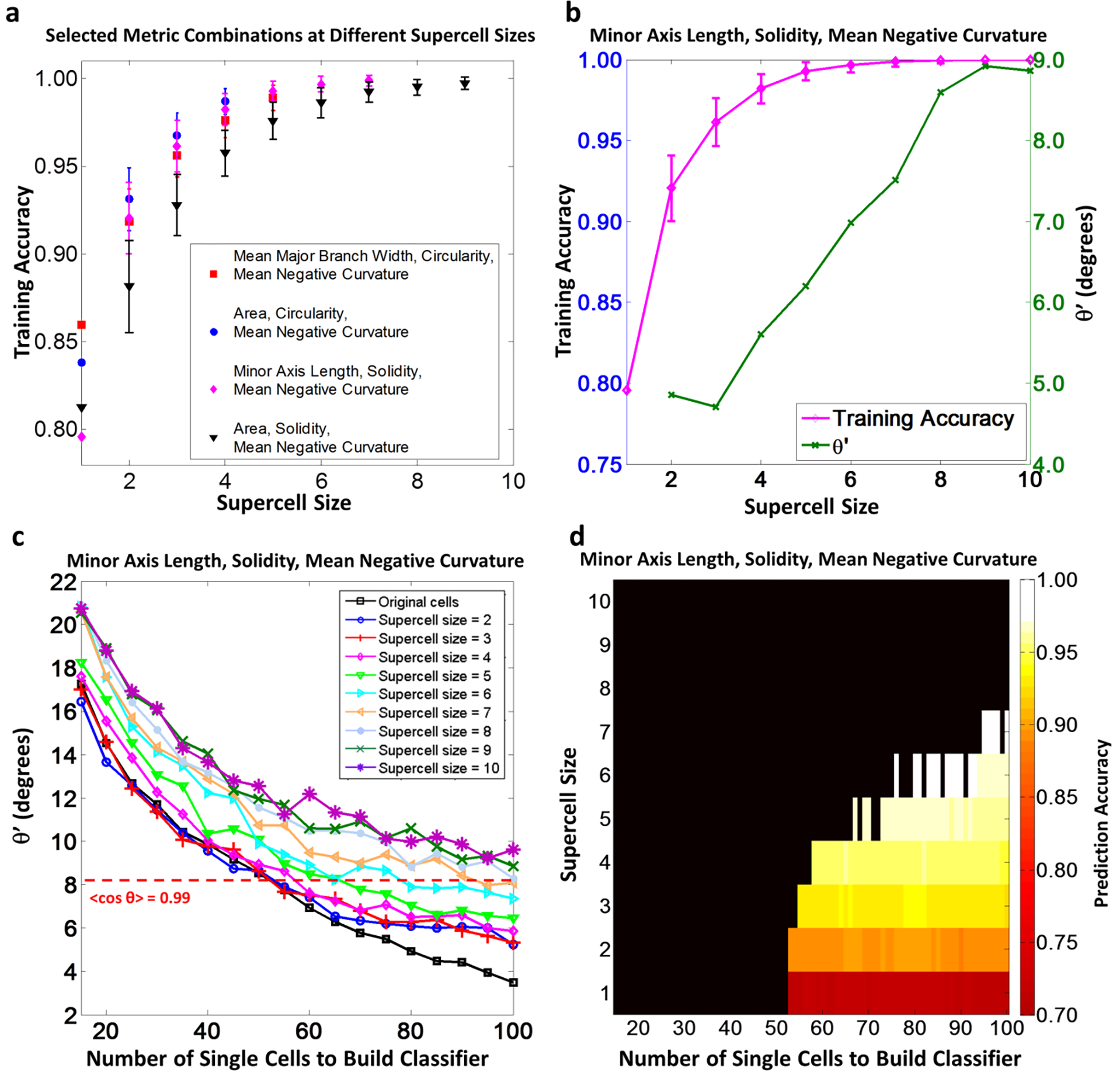
(2-column). Results of SVM analysis and associated subsampling validation of selecting 3 shape metrics to compare morphological difference of hBMSCs populations of FS and SC. (a) At different supercell sizes, Shape metric combinations of 3 shape metrics with the highest training classification accuracy were selected if the average classifier hyperplane fluctuation ${\theta }^{\prime }<{8.1}^{\circ }(⟨\mathrm{c}\mathrm{o}\mathrm{s}\theta ⟩>0.99$). The figure shows the training accuracies of SVMs built with these selected combinations for all supercell size, if ${\theta }^{\prime }<{8.1}^{\circ }(⟨\mathrm{c}\mathrm{o}\mathrm{s}\theta ⟩>0.99$). (b) Training classification accuracy and average classifier hyperplane fluctuation ${\theta }^{\prime }$ of the selected shape metric combination in SVM training with supercell implementation. (c) In subsampling validation, classifier hyperplanes were built with different random subsample sizes and supercells sizes. Average classifier hyperplane fluctuation was quantified by ${\theta }^{\prime }$. A threshold of ${\theta }^{\prime }<{8.1}^{\circ }(⟨\mathrm{c}\mathrm{o}\mathrm{s}\theta ⟩>0.99$) was chosen to define stable classifier hyperplanes (red dotted line) (d) Prediction accuracy of the classifier hyperplanes in the subsampling validation when the built classifiers were tested with the rest of the total sample at different supercell sizes. The dark region represented combinations of training data size and supercell size causing unstable classifier hyperplane. In the stable region, combinations of the training data size and supercell size were colored according to the prediction accuracy. All error bars in (a) and (b) represent standard deviation.

Table 1.

(2-column). Selected three shape metrics with the highest training classification accuracy (values are indicated with ± standard deviation). In subsampling validation part b, NA (not applicable) means there is no combination of training sample size and supercell size that yield a prediction accuracy > 95% and at the same time $\theta \text{'}<{8.1}^{\circ }$ ($〈\cos \theta 〉$> 0.99.)

Training (100 Iterations)
Comparison	FS vs. SC		FS vs. FS+OS		FS vs. SC+OS		SC vs. SC+OS		FS+OS vs. SC+OS		All FS vs. All SC		All w/o OS vs. All OS
Supercell Size	5		5		5		5		5		10		10
Selected Classifier (cos θ ≥ 0.99, Highest Training Accuracy)	Metrics	Vector	Metrics	Vector	Metrics	Vector	Metrics	Vector	Metrics	Vector	Metrics	Vector	Metrics	Vector
	Minor Axis Length	−0.86±0.04	Mean Negative Curvature	−0.96±0.03	Max Boundary Distance	−0.70±0.05	Mean Negative Curvature	−0.86±0.03	Area	−0.94±0.02	Circularity	0.72±0.03	Mean Negative Curvature	−0.93±0.03
	Solidity	−0.43±0.06	Aspect Ratio	0.2±0.1	Circularity	0.66±0.05	Circularity	−0.39±0.07	Perimeter	0.28±0.05	Mean Boundary Distance	−0.66±0.04	Perimeter	−0.33±0.06
	Mean Negative Curvature	0.24±0.08	Circularity	−0.13±0.08	Mean Major Branch Width	−0.2±0.1	Tortuosity	0.31±0.09	Mean Negative Curvature	0.20±0.05	Mean Negative Curvature	0.21±0.05	Num. of Tiny Protrusions	0.2±0.1
Training Accuracy	(99±1) %		(92±2) %		(98±1) %		(95±2) %		(98±1) %		(100±0) %		(96±1) %
Subsampling Validation (200 Iterations)
a. For Fixed Supercell Size =5, Training Sample Size = 90
Prediction Accuracy	(97±2) %		Hyperplane Not Stable		(98±4) %		Hyperplane Not Stable		(93±3) %		(97±2) %		Hyperplane Not Stable
b. For Prediction Accuracy ≥ 95 %, θ' < 8.1° (<cos θ> ≥ 0.99)
Least Supercell Size	4		NA		5		NA		6		5		11
Least Training Sample Size	57		NA		89		NA		54		58		206

To distinguish morphologies of hBMSCs in FS and SC, at supercell size = 5, the optimal combination of 3 shape metrics was identified as minor axis length, solidity and mean negative curvature. The accuracy of the classifier training is (99±1) % (Fig 5.a and b, Table 1), indicating a high correlation of the classification and the microenvironment difference. The average normal vector of the classifier hyperplane is (−0.86±0.04, −0.43±0.06, 0.24±0.08). According to the normal vector of the classifier hyperplane, hBMSCs in FS have smaller width, lower cell to convex hull area ratio and higher concavity along the boundary. The average classifier normal vector suggested that in order to distinguish hBMSCs morphologies in FS and SC with the classifier hyperplane, morphological difference in minor axis length is the most distinct shape metric followed by solidity. Mean negative curvature is the least distinct shape metric among the three selected shape metrics.

We implemented a subsampling validation procedure to test the robustness of the classifier built with the selected shape metric combination of minor axis length, solidity, and mean negative curvature in terms of classifier hyperplane stability and predictive accuracy. Here, both the training subsample size and the supercell size to build the classifier varied. We found that the classifier hyperplane stability was improved with increasing number of cells in the training set to build the classifier (Fig 5.c). The classifier stability threshold of ${\theta }^{\prime }<{8.1}^{\circ }(⟨\mathrm{c}\mathrm{o}\mathrm{s}\theta ⟩\ge 0.99$) was still assumed to define stable classifications as demonstrated with the red dash line in Fig 5.c. In Fig 5.d, classifier hyperplane stability and prediction accuracy were combined to quantify effect of data size and supercell size on the classifier for selected shape metrics. To summarize the subsampling validation, in order to maintain stability and prediction accuracy of the classifier hyperplane, morphology difference should be quantified with appropriate selections of supercell size and training data size. Selecting 95 % as desired prediction accuracy, supercell size of at least 4 is appropriate and the required minimal number of single cells in the training set is 57 (Fig 5.c and d). This supports the efficacy to train a stable classifier hyperplane with the selected shape metrics at supercell size of 5 and current data size (121 hBMSCs of FS and 114 hBMSCs of SC).

In addition to comparison of FS and SC which is associated with hBMSCs response to different material topography, we also investigated the hBMSCs morphological difference in pairwise comparisons of other microenvironment. The comparison of FS vs. FS+OS and the comparison of SC vs. SC+OS are associated with osteogenic supplement’s effect on cell-material response in different material structures. Distinguishing hBMSCs morphologies of FS+OS and SC+OS is associated with hBMSCs response to the material structure in presence of OS. It is also interesting to compare morphologies of hBMSCs of FS and SC+OS because they both induce osteogenic differentiation in later stages of cell culture through either material properties or chemical inducement[21]. We also defined cell populations by mixing cell populations in the same materials or the same chemical treatment and made pairwise comparisons. The same feature selection and subsampling test procedure based on SVM/supercell paradigm were applied to all these comparisons. Table 1 lists the results of involved metrics, average normal vector and metric importance, training classification accuracy and prediction accuracy of the optimal metric combination comprised of 3 shape metrics. This enables identification of hBMSCs’ various morphological responses to either structural difference of substrate or chemical treatment and to estimate whether structural factor or chemical induction is more efficient to determine hBMSCs morphology after 24 h of culture. The results demonstrated that after 24 hours of culturing, higher perimeter to area ratio and smaller cell size were the leading difference induced by fiber structure. On the other hand, increasing boundary concavity and roughness were identified as the most distinct morphological change induced with osteogenic supplement. In the subsampling validation, the classifiers achieved prediction accuracy of more than 96 % at supercell size = 5 and training sample size = 90 in comparison of all FS vs. all SC, however classifiers for all OS vs. all no OS failed to maintain classifier hyperplane stability. On the other hand, in order to reach ${\theta }^{\prime }<{8.1}^{\circ }(⟨\mathrm{c}\mathrm{o}\mathrm{s}\theta ⟩\ge 0.99$) and prediction accuracy of 95 %, the least supercell size and least training sample size of all FS vs. all SC were smaller than that of the comparison of all OS and all no OS (Table 1). These results suggest that morphology of hBMSCs in different environments on day 1 was more influenced by scaffold structural differences than chemical stimulus.

In order to visualize the population morphological difference of the two classes defined by the 3 selected features and associated classifier in each pairwise comparison, we selected “canonical cells” as representative cell shapes from the single cells which are always well classified by the SVM classifier trained on supercells (i.e., they are always on the correct side and outside the margin for all classifier hyperplanes trained with different supercell sets. See supplementary information 2) and represented them in Fig 6. Therefore, the morphologies of these cells reflected the typical morphological responses to different microenvironment.

Fig 6.

(2-column). Shapes of “canonical cells” representing the morphological difference between hBMSCs cultured in different microenvironments.

Discussion

SVM/supercell paradigm associates cell morphologies with microenvironment

In this study, in order to address challenges in associating hBMSCs morphology with the cell-material response, we designed an analytical approach based on a SVM/supercell paradigm to facilitate multi-parametric analysis while accounting for the high variability in cell morphology in a cell population. First, we identified combinations of 3 shape metrics (from an original set of 22 metrics) that clearly discriminate the cell population in one microenvironment from another in pairwise comparisons. With a reduced metric space, we decrease the occurrence of redundant shape metrics where redundancy can bring about not only interpretation difficulties but also noise and overfitting problems [43]. The feature selection procedure directly selects a subset of the original metrics with straightforward geometrical and biological explanations to describe the morphological difference between two classes. In contrast, other remapping methods for metric redundancy reduction, such as principal component analysis [8, 27, 28] and multidimensional scaling [9], output abstract functions of the original metrics. Additionally, simplicity of the linear kernel for SVM enables us to use a single normal vector for the class boundary to quantify the population morphology difference and obtain the shape metric importance ranking within the classifier. These properties of this analysis technique bring convenience of interpretation about cell-material morphological responses and facilitate the targeting of future studies on biological mechanisms that may be associated with particular cell morphological features.

Variability in single-cell morphology within each cell population can bring outliers and population overlaps. This reduces the training accuracy of linear SVMs, where a large portion of the training data set will perform as the support vectors (i.e., cells within the margin or misclassified cells) of SVMs [34]. A large fraction of support vectors is a sign of low training accuracy and subsequently low generalization capability of the trained classifier [50, 51]. As demonstrated on single cells in the subsampling validation procedure, the number of support vectors increases linearly with respect to the training data size (i.e., the number of cells imaged) (Fig 7). Thus, SVM training with single cells does not benefit, in terms of training and prediction accuracies on single cells, from an increase in the training data size. Upon the application of the supercell method however, the number of support vectors decreases as the supercell size increases (Fig 3.a and Fig 7) and both training and prediction accuracies of SVMs are improved.

Fig 7.

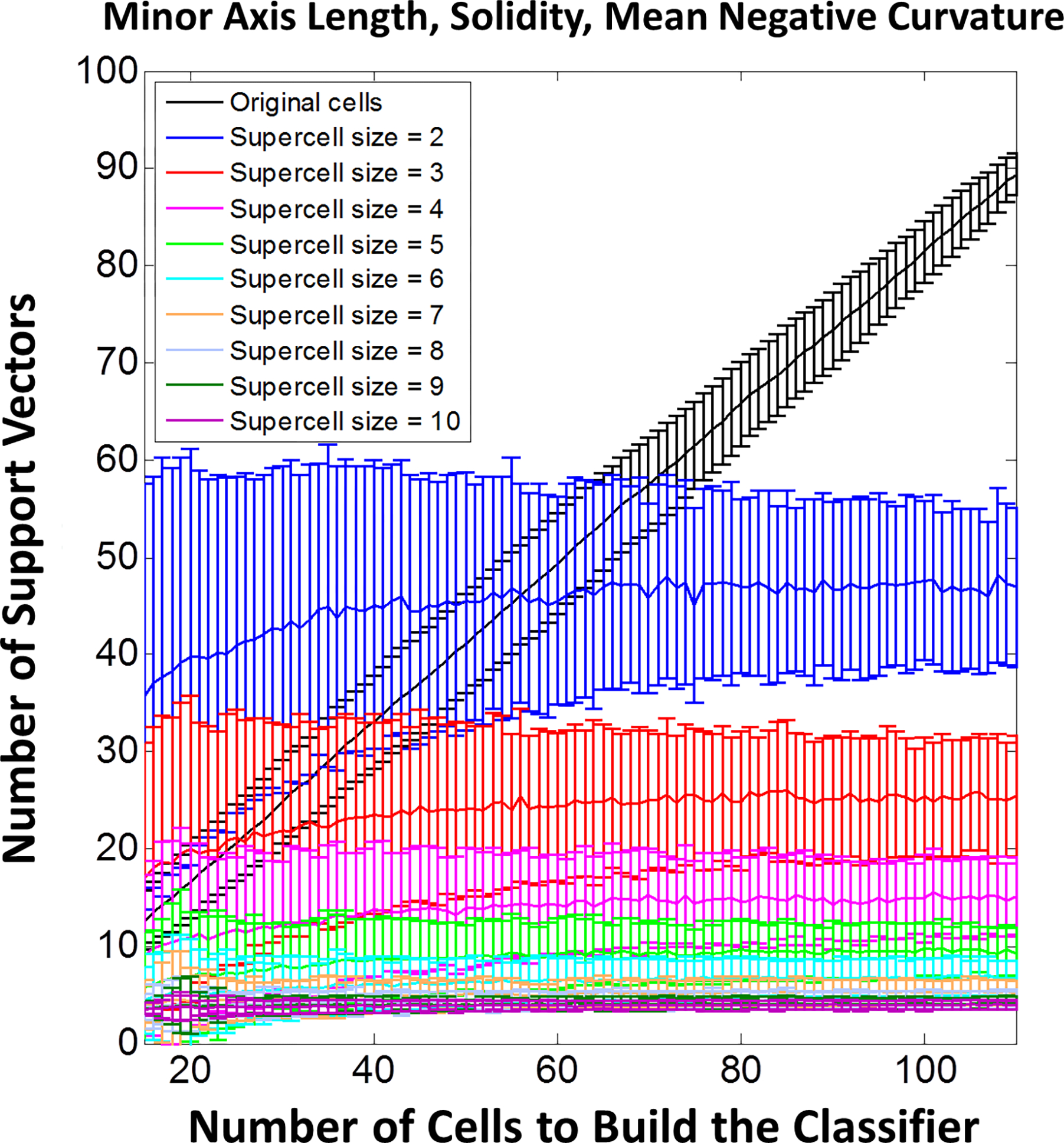
(1-column). Number of support vectors required for the SVM classifier of different sample sizes and supercell sizes in subsampling validation of selecting 3 shape metrics to compare morphological difference of hBMSCs populations on FS and SC. Error bars represent standard deviation.

In addition, the number of support vectors reaches a plateau as the training data size increases (Fig 7). This implies that given a certain population of cells, we can establish a data set of finite data size that is sufficient to generalize cell population difference and is sufficient for reliable predictions of small groups of cells (supercells). In contrast, on the single-cell level even with larger data set sizes, SVMs may not be sufficient to directly generalize information about cell population difference to predict new single cells well. Training accuracies can be improved by non-linear classifier kernels or including more metrics in the metric space in SVM. However, these approaches may suffer from higher number of support vectors that compromise generalization capability in addition to the interpretation and overfitting difficulties described previously.

In the SVM/supercell paradigm, the influence of variability in cell morphology and the number of support vectors can be reduced to generate classifiers that have higher generalization capability as evidenced by increased prediction accuracy for investigating cell population phenotype. As an example, if we attempt to train a classifier based on single cells, the highest accuracy of that classifier is 86 % and the prediction accuracy that can be achieved for each individual cell is approximately 80 % (Fig 5.a and d) across the population. However, these results cannot be significantly improved by increasing the training set size due to the increasing number of support vectors required to build the classifier (Fig 5.d and e). Alternatively, if we train a classifier on supercells, training accuracy can reach % accuracy values over 99 % (Fig 5.b and Table 1). In the application the SVM/supercell paradigm in the prediction of cell class, we can image a small number of cells from the new sample and calculate the average shape metrics across these cells (generating a supercell) then apply the classifier trained at the same supercell size, resulting in prediction accuracies that can be over 95 % (Fig 5.d and Table 1). This provides greater confidence in the prediction of biomaterial-induced cell shape population behavior.

However, in both training and subsampling validation procedures, we found that the randomness of supercell generation also introduces bias which contributes to the complexity of the represented morphologies and brings uncertainty of the classifier orientation (Fig 5.b and c). Therefore, the selected supercell size should be tested for reliable cell shape phenotyping and shape metric importance comparison. Furthermore, in the subsampling validation procedure we found that the classifier stability was improved by increase in training data size. Thus, sufficient data size is required to generalize the cell morphology complexity introduced by both single-cell heterogeneity and bias of supercells. Combined with the measure of prediction accuracy, we determined the appropriate combination of training sample data size and supercell size to assure both reproducibility of the shape metric importance information and the usefulness of the classifier in future predictions (Fig 5.d and Table 1).

Several factors can contribute to the variability of cell morphology in a sample. Since cell morphology is usually identified at a snapshot in time, cells in the same population can be in different states of attachment, migration and cell cycle [52] Due to disordered properties of the biomaterial topography, a variety of different niches may exist in a single culture and play roles in the overall functional outcome of the population [21, 22]. In addition stem cell cultures are inherently heterogeneous and may contain different subsets of cells based on their source, isolation and expansion history [53]. Since the majority of cell differentiation assays are based on global responses from the culture (i.e., RT-PCR, mineral staining, alkaline phosphatase activity, proliferation assays) and not the single-cell responses, cell morphology data obtained at the single-cell level may not be reflective for overall cell culture response because of single-cell heterogeneity. As discussed above, the proposed method successfully dealt with single-cell heterogeneity by implementing a supercell method and subsequent SVM analysis, which reduced the effect of variability in cell morphology and improved the capability of SVM classifiers to quantify and predict cell population response to different microenvironments.

Quantifying differences in cell behaviors is crucial for estimating effect of biomaterials. By combining multiple metrics and learning at supercell levels, the proposed SVM/supercell paradigm could be well suited to reveal even subtle difference in cell population behavior upon changing of the chemistry or physics of biomaterials. In the quantitative phenotyping of cell population behaviors, the selected metric combination and classifier quantify the way that cells change behaviors in response to varying conditions. The subsampling validation quantifies not only the strength of the phenotype but also sufficiency of data for phenotyping. In a systematic screen of biomaterials, our approach toward quantification and validation of the classifiers could be used for pairwise comparison of cells in all conditions, i.e. revealing a matrix of comparisons.

Cell-material interactions reflected by morphology

Cell morphology has gained attention from researchers studying several cellular functions including proliferation [24], differentiation [5–14, 21, 22] and migration [16–18]. It has been demonstrated that global cell morphology control such as control in spreading area and elongation may affect properties of the cytoskeleton and cell adhesions to regulate cell proliferation or differentiation [5, 6, 24]. Local morphological changes such as protrusions and invaginations have also been associated with the enrichment or activity of intracellular signaling [17, 54]. By identifying cell shape phenotype with multi-parametric analysis, we can better understand the role of cell morphology in directing global functional outcomes and the microenvironmental cues that may induce the regulation.

In this study, we specifically examine the cell shape phenotypes associated with fibrous substrates and osteogenic supplement. Both fibrous substrates and osteogenic supplement have been demonstrated to promote osteogenic differentiation [21]. However, the mechanisms behind these interactions are not well understood and might be varied. Previous studies also suggested that the fiber environment may promote cell morphology responses that are associated with osteogenic differentiation [21, 30–33]. With the SVM/supercell paradigm, we have identified specific cell shape metrics that distinguish cells in fibrous substrates (FS) from those on the control flat surfaces (SC films). The distinguishing metrics include minor axis length, major branch width, area, solidity, circularity, and mean negative curvature. The major morphological response of hBMSCs to fibrous substrates is identified as the narrower width of the cell [8]. Changes in solidity and circularity suggested that the cell morphology in fibrous substrates is also more dendritic. Boundaries of cells in fibrous substrates are also rougher than those on the flat substrate. These changes are visualized with the selected representative cell shapes in Fig 6.

We have also identified cell shape metrics associated with the fibrous environment regardless of chemical supplement treatment and metrics associated with chemical supplement treatment regardless of scaffold type. These comparisons identify cell shape metrics that may be most important to cellular response to either the fibrous substrates or osteogenic supplement. For example, in all FS group regardless of OS treatment conditions, circularity and mean boundary distance and mean negative curvature become important to distinguish them from those on flat control surfaces. In all OS environments regardless of the substrate types, the shape metrics related to boundary roughness such as mean negative curvature and perimeter and number of tiny protrusions were found to be more important to distinguish these cells from those without OS treatment. FS environment was found to be more influential in determination of cell morphology on day 1, according to the training accuracy and subsampling validation results of the classifiers and the visualization of the selected representative cell shapes (Table 1 and Fig 6).

Traditional shape features such as area, perimeter and cell elongation that we call “global” are measured by metrics that are not particularly sensitive to local curvature or local protrusions. Our work shows that “local” shape metrics that emphasize local curvature or protrusions are also important in describing morphological response of cells to fibrous materials. Branching features were found to be important in elucidating some differences in cell morphology. A possibly related phenomenon is that dendritic branching may have important biological significance for cell signaling where the global phosphorylation level of some messenger proteins can be enhanced by subcellular protrusions structures [54]. Another local shape feature that was prominent in distinguishing cells of different microenvironments was boundary curvature. Curvature around the cells boundary has been associated with cytoskeletal force generation and intracellular mechanotransduction [6, 55].

Interestingly, in studies where human mesenchymal stem cells (hMSCs) were forced to assume artificial geometries with shape features associated with metrics identified in the current study, differences in osteogenic potential were observed. For example, in a study by Kilian et al [6], cell elongation of cell shape and cell boundary curvature (similar to metrics of minor axis length, solidity and mean negative curvature in our study) were found to be relevant to not only cytoskeleton and focal adhesion spatial organizations but also hMSCs’ potential of osteogenesis and adipogenesis. Further analysis suggested that the c-Jun N-terminal kinase (JNK) and extracellular related kinase (ERK1/2) cascades as well as the wingless-type (Wnt) signaling and mitogen-activated protein kinase cascades (MAPK) might mediate the regulation of cell shape on hMSCs differentiation [6]. These pathways associated with RhA-ROCK pathways [4, 5] were also found to regulate expressions of Runt-related transcription factor 2 (RUNX2), peroxisome proliferator-activated receptor gamma (PPAPγ), and Sox-9 which are closely related to osteogenesis, adipogenesis and chondrogenesis [56, 57]. These studies shed light on the mechanisms with which cells could have functional changes in response to surrounding microenvironment.

In many biomaterial scaffolds, the interactions of the heterogeneous cell population and the heterogeneous microenvironment are complex and increase variability in cell morphology. Approaches to correlate cell morphology with cell function however, have utilized artificial cell shape constraints, often via micro-patterning techniques, to investigate influence of cell shape features on cell function [5, 6], and constrained geometries are not generally representative of the wide range of cell shapes found in the complex biomaterial environments (i.e., Supplementary Fig 1). Therefore, it is difficult to apply cell shape related observations from these types of studies when trying to investigate cell shape-function interactions in more complex micro-environments. By identifying cell shape phenotypes and representative cell shapes for different microenvironments we may be able to target microenvironment relevant cell shapes in micro-patterning studies. To facilitate this, we have developed an approach to identify canonical cell shapes that may represent each cell population. This allows us to gain systematic visualization for the morphological differences observed in different microenvironments (Fig 6), in spite of the variability in cell morphology from cell to cell. These cell shapes may also serve as candidate templates for the future investigation of the effects of cell shape on cell function with micro-patterning techniques.

Conclusions

We implemented an SVM/supercell based methodology to quantify morphological response of hBMSCs populations to different microenvironments with a classifier comprised of selected shape metrics. This method enables us to focus on a few representative shape metrics obtained from the automated image quantification process and compare the importance of different shape metrics in phenotyping. This method also enables us to overcome issues caused by single-cell heterogeneity in phenotyping, as the supercell averaging is implemented to reduce influence of variability in cell morphology that affects the performance of SVM classifiers. Our work introduces a subsampling validation procedure to quantify the robustness of the classifier boundary in terms of classifier hyperplane stability and predictive accuracy. We found that smaller, more elongated and more dendritic shape is the major morphological changes induced by fibrous substrates in hBMSCs on day 1. On the other hand, osteogenic supplement triggered morphological changes occur mostly in terms of cell boundary concavity and roughness. In addition to our automated classification, we also identified “representative” cells that can be used for visualization and human interpretation, as well as a starting point for cell shape templating.