Abstract
Understanding the genotype-by-environment interaction (GEI) and considering it in the selection process is a sine qua non condition for the expansion of Brazilian eucalyptus silviculture. This study’s objective is to select high-performance and stable eucalyptus clones based on a novel selection index that considers the Factor Analytic Selection Tools (FAST) and the clone’s reliability. The investigation explores the nuances interplay of GEI and extends its insights by scrutinizing the relationship between latent factors and real environmental features. The analysis, conducted across seven trials in five Brazilian states involving 78 clones, employs FAST. The clonal selection was performed using an extended FAST index weighted by the clone’s reliability. Further insights about GEI emerge from the integration of factor loadings with 25 environmental features through a principal component analysis. Ten clones, distinguished by high performance, stability, and reliability, have been selected across the target population of environments. The environmental features most closely associated with factor loadings, encompassing air temperature, radiation, and soil characteristics, emerge as pivotal drivers of GEI within this dataset. This study contributes insights to eucalyptus breeders, equipping them to enhance decision-making by harnessing a holistic understanding-from the genotypes under evaluation to the diverse environments anticipated in commercial plantations.
Keywords: Genotype-by-environment interaction, Factor analytic mixed models, tree breeding, reliability, environmental features
Subject terms: Agricultural genetics, Plant breeding
Introduction
Brazilian silviculture is continuously growing. In 2022, the production value in silviculture increased by 14.9%, setting new national records, as reported by the Brazilian Institute of Geography and Statistics (IBGE). IBGE data also revealed that the planted forests’ total area exceeds 9.5 million hectares, with a substantial 77% of this area dedicated to species from the Eucalyptus genus. Ensuring a sustainable and secure expansion of eucalyptus-planted forests necessitates the identification of clones adapted to environmental changes. These clones must be capable of withstanding various challenges posed by marginal environments, including factors such as drought, frost, poor soil quality (whether chemical or physical), and unfavourable weather conditions for optimal tree growth1,2. This crucial task is typically achieved through rigorous testing of selection candidates in multi-environment trials (MET). These trials must be strategically installed in environments that accurately represent the conditions that clones may encounter in commercial plantations. In other words, MET should properly sample the genotype-by-environment interaction (GEI), the phenomenon that dictates the differential behavior of clones in response to different environmental stimuli3.
There are two main types of GEI: Scale-type, also known as simple or non-crossover, where changes in performance do not affect genotype ranking; and Rank-type, also called complex or crossover, where the opposite is true4,5. Managing GEI is crucial, especially in situations where it is rank-type, as it requires statistical solutions that not only isolate these effects but also incorporate them into the selection process. Factor Analytic (FA) mixed models provide these solutions. This method was developed as an alternative to multivariate models and a mixed model counterpart to AMMI (Additive Main Effects and Multiplicative Interaction)6–9. The core idea is to reduce dimensionality to a certain number of latent covariates (the factors) by leveraging the covariance between environments intrinsic to these factors10. FA considers genotypic heteroscedasticity and predicts a candidate’s performance in an untested environment. For its mixed model framework, it successfully deals with unbalanced data and can leverage kinship or molecular information11. Furthermore, Factor Analytic Selection Tools (FAST)12 provide straightforward alternatives for precise decision-making in the search for high-performance and/or stable genotypes.
Factor analytic models primarily focus on understanding the “genotype” portion of GEI. However, an alternative approach to explore interaction dynamics is to examine the “environment” portion using data from environmental features. This paradigm has been evolving since the early ’70s but gained significant traction in the last decade due to improved computational resources13–17. The comprehensive approach involves integrating FA models with environmental information, bridging the “genotype” and “environment” aspects of GEI. This integration combines real environmental covariates with latent environmental covariates (the factors), offering a powerful tool for both prediction and inference2,18,19. This integrated approach has proven beneficial in various contexts, such as defining breeding zones, studying genotypic responses to climatic changes, exploring the intricate relationship between genomics and environmental data and predicting the genotypic performance to new, untested environments18,19. In the specific case of eucalyptus breeding, studies like that of Callister et al.2 used FA models integrated with genomics and environmental data to delineate breeding zones for Eucalyptus globulus Labill. Another example of usage is reported by Costa e Silva et al.20, who investigated how eucalyptus genotypes are influenced by changes in weather-related environmental features by regressing genotypic values onto climatic variables. Such integrated approaches hold promise for advancing our understanding of the complex interplay between genetics and environmental factors in tree breeding programs.
This study presents a unique application of the FAST methodology in the context of eucalyptus breeding. Notably, we extended FAST by integrating it with a candidate’s reliability. This enhancement aimed to select eucalyptus clones with high performance, stability, and high-quality information, facilitating targeted recommendations across diverse environments and decreasing the risk of a flawed decision. Additionally, we delved into the dynamics of GEI by examining the relationship between known and latent environmental covariates. To achieve this, we adapted the methodology outlined by Bakare et al.21, integrating the outcomes of the FA model with environmental features in a single partial least squares regression.
Results
Single-environment trial analyses
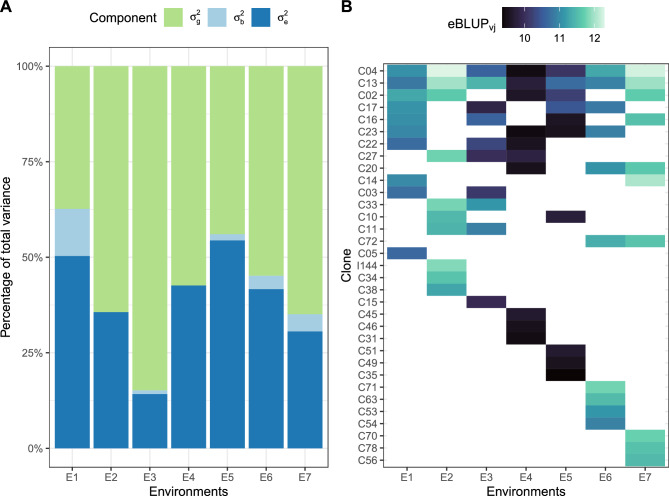
The genotypic variance constituted the major portion of the total variance in all environments but E1 and E5 (Fig. 1A). Furthermore, the genotypic effects were significant in all analysed environments. Thirty-three distinct clones were among the top ten selections in individual environments, with clones C04 and C13 being the only ones consistently chosen across all environments (Fig. 1B).
Figure 1.
Results of the individual analyses per environment: (A) percentage of each variance component attributed to the total variance; and (B) performance of the top ten clones in each environment. In (A), the genotypic variance was significant in all environments. In (B), a blank cell indicates that the clone in the y-axis was not selected in the x-environment.
FA outcomes
Model selection
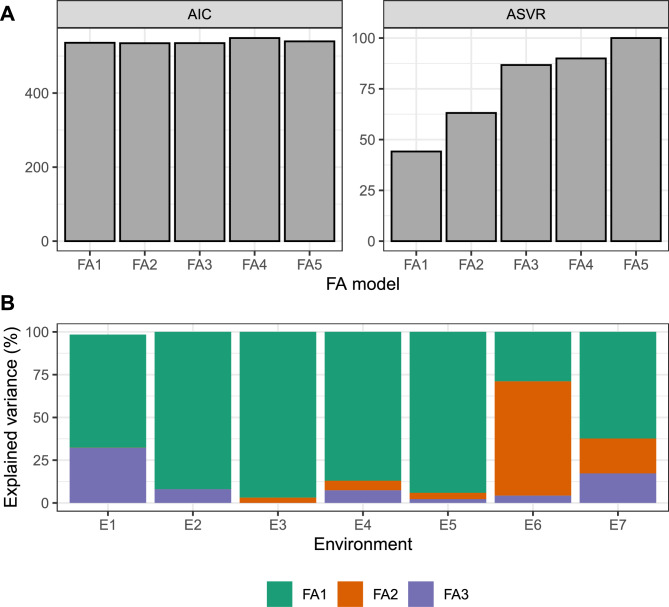
The Akaike Information Criterion (AIC) exhibits minimal changes with the number of factors. Subtle increases in explanatory power are observed from FA3 onward. FA3, with an explanatory power of 87%, was selected as the model for further analysis (Fig. 2A). In this model, the first factor predominantly explained the variance in all environments except E6, where the second factor played a more prominent role. The contribution of the third factor was minor across all environments except E1 and E7 (Fig. 2B). The factor loadings of each environment in each of the chosen model’s three factors are in the Supplementary Material (Table S1)
Figure 2.
Selection of the proper number of factors for the FA model: (A) Akaike information criterion (AIC, left plot) and average semivariances ratio (ASVR, right plot), and (B) explained variance per factor and environment of the selected model (FA3).
Heritability and pairwise genotypic correlations
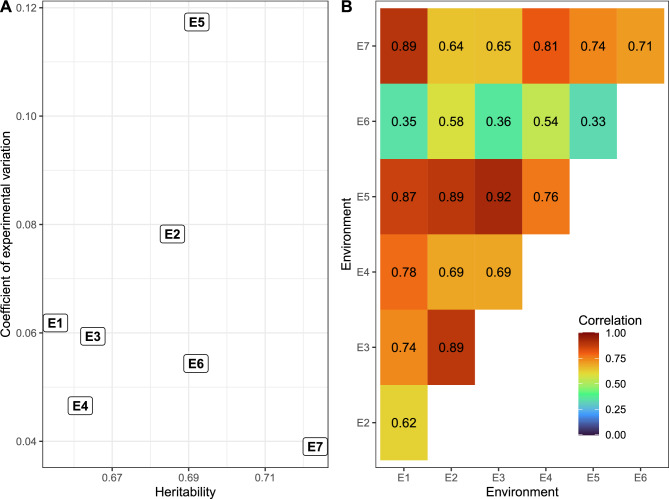
The heritability varied from 0.65 to 0.72, and the coefficient of variation (CV) ranged from 0.04 to 0.12 (Fig. 3A), indicating good experimental precision. Genotypic correlations between environments ranged from 0.33 to 0.92, with E6 showing the most significant deviation from its peers. The closest relationship was observed between E5 and E3 (Fig. 3B).
Figure 3.
(A) The biplot illustrates the heritability (x-axis) and coefficient of experimental variation (in decimal scale, y-axis) for each environment. (B) The heatmap displays the pairwise correlation between environments. In the upper triangle, genotypic correlations are presented, while the lower triangle exhibits correlations derived from the relationship between environments based solely on environmental features.
Selection
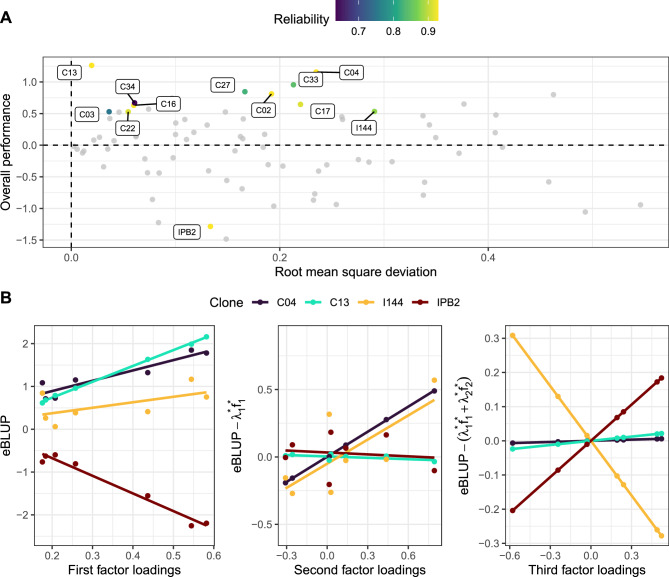
Using the selection index, we selected the top ten clones for global performance and stability across environments (Fig. 4A), namely C13, C04, C03, C34, C16, C22, C27, C02, C33, and C17. These clones meet the three criteria considered for building the index: they have high global performance, can keep it acceptably high across environments, and have trustworthy information. Note that all selected clones beat the two commercial checks. The two clones that were consistently selected in all individual analyses were also selected by the index (C13 and C04). Notably, C13 is more stable than C04, as evidenced by the lower RMSD of C13, and the steeper slope of C04 in the latent regression plots of the second and third factors (Fig. 4B). The selection of these clones will provide an expected gain of 8.30%.
Figure 4.
Overall performance vs root mean squared deviation (A), and latent regression plots comparing two top performers (C04 and C13) and two commercial checks (I144 and IPB2) (B). In (A), the higher the overall performance (or the more distant from zero in the y-axis), the better. Stable clones have low root mean squared deviation (global) (or closer to zero in the x-axis).
Environmental drivers of the GEI
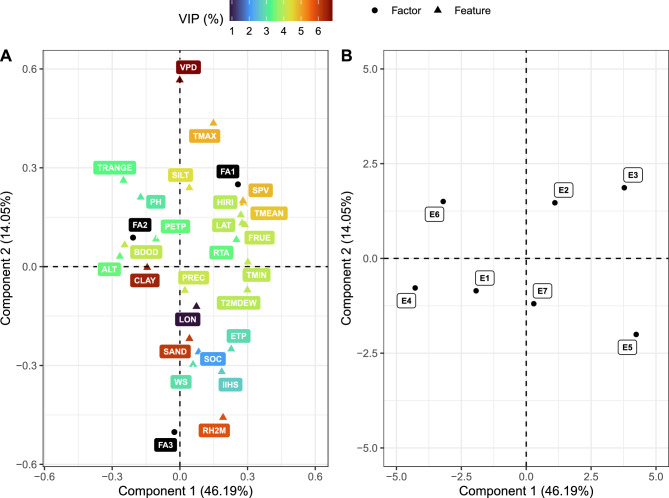
Five components were selected for the partial least squares regression (PLSR) model, which explained over 90% of the total variance. The PLSR biplot (considering the first two components) revealed that features like TMAX, TMEAN, SPV, and HIRI are highly associated with the first factor, while PH, BDOD, ALT, TRANGE and CLAY are linked to the second factor (Fig. 5A). Notably, FA3 does not show substantial influence from any specific environmental feature, despite being closer to RH2M. Among the tested features, VPD, RH2M, CLAY, SAND, SPV and temperature-related features play crucial roles in driving GEI in the dataset. The spatial arrangement of environments in Fig. 5B shows how they are related based on the GEI and the environmental features. E6 and E5 seem to be the most different environments. In fact, E5 is the most geographically distant (see Fig. 7), and E6 has a marked drought period and was the most different regarding explanation dynamics in the FA models.
Figure 5.
Results of partial least squares regression: (A) relationship between real (features) and latent (factors) environmental covariates (biplot of the predictors’ and responses’ loadings considering the first two components); and (B) relationship between environments based on both environmental features and factors (biplot of predictors’ scores considering the first two components). FA1, FA2 and FA3 are the first, second and third factors, respectively. For the environmental features’ acronyms, see Table 1. In (A), colour scale represents the variable importance in projection (VIP), in percentage, of each environmental feature.
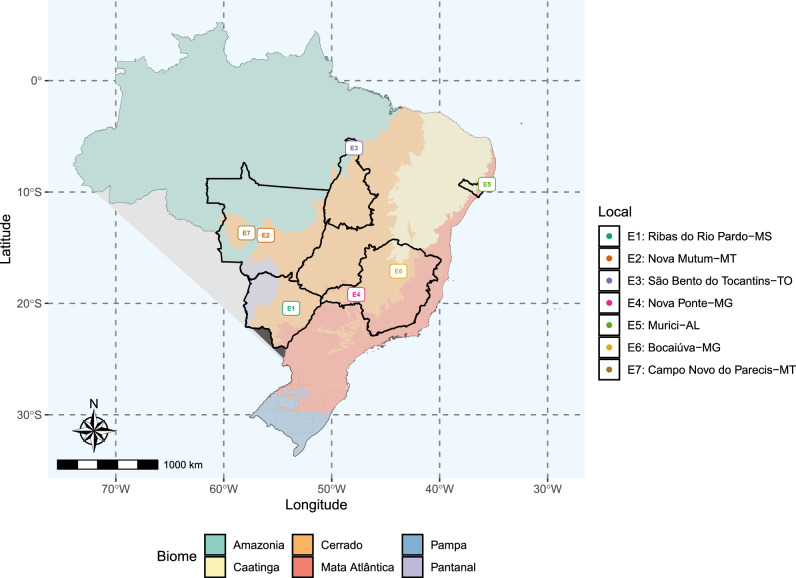
Figure 7.
The map illustrates the locations of trials across Brazil. State borders are depicted by contours, with each colour signifying a distinct Brazilian biome. On the right, the legend provides details on the corresponding municipalities for each trial, while the map labels utilize codes specific to this study. This map was generated using the ggplot2 package, v. 3.5.1 (https://ggplot2.tidyverse.org/articles/ggplot2.html), and the files publicly available at the Brazilian Institute of Geography and Statistics website.
Discussion
This study establishes the efficacy of FAST for the selection and recommendation of eucalyptus clones across diverse environments. A novel aspect of this approach is the integration of FAST with the clone’s reliability, introducing an additional criterion-information quality-in the decision-making process. Moreover, our investigation focuses on the environmental determinants of GEI by exploring the relationship between latent factors and actual environmental features, identifying the most influential factors driving differential phenotypic expression across environments.
When addressing GEI, two approaches come into play. The first entails an environment-specific strategy, focusing on recommendations to each environment based on individual analyses’ outcomes, as depicted in Fig. 1. While optimal, this approach is often impractical due to financial constraints, making it challenging to run breeding programs for each environment separately. The second option involves leveraging biometrical solutions to consider data from all environments simultaneously and incorporate GEI into the decision-making process. Here, the objective is to identify candidates with consistently high and stable performance across all trials, as illustrated in Fig. 4. Factor analytic models are a gold standard method for implementing the latter alternative7,8,22. This study outlines a recommended pipeline for eucalyptus breeders utilizing FA models: (1) initiate the process by selecting an appropriate model, determining the optimal number of factors based on explicative power (Fig. 2); (2) employ the selected model to explore experimental precision and the nature of GEI within the dataset (Fig. 3); and (3) utilize FAST for clonal selection, enabling a comprehensive assessment of high-performance and stability across diverse environments. Furthermore, breeders can compare selected clones’ behaviour across environments with commercial checks using latent regression plots (Fig. 4).
The variability observed in genotypic correlations between environments underscores the nuanced nature of GEI in the dataset. While many correlations are positive and high (), suggesting subtle changes in clonal performance in terms of genotypic value, breeders must not overlook the presence of GEI. The information provided in Fig. 1 emphasizes that the majority of selected clones differ across environments. This highlights that even subtle changes can impact clonal selection, and recommending suboptimal candidates may result in financial setbacks in eucalyptus silviculture. Selecting a low-performing clone over a promising one can have repercussions for at least seven years, the number of years to reach rotation age in commercial plantations. Environment E6 (Bocaiúva-MG) stood out as the location where clones exhibited the most divergent responses. Notably, it was the only environment in which the second factor held the highest explicative power (Fig. 2) and was somewhat poorly related to the other environments in the partial least squares regression (Fig. 5B). This specific site is characterized by a substantial temperature range and a distinct period with minimal precipitation, making it a preferred choice for testing clones for drought tolerance23,24. The unique conditions of E6 likely contribute to the distinct behaviour observed in the second factor and the heightened variability in clonal responses.
The relationship illustrated in Fig. 3B represents the manifestation of genotypic responses to environmental influences. We integrated these responses with the actual environmental features of each environment to evaluate the environmental drivers of GEI in the dataset and establish a comprehensive relationship between environments (Fig. 5). Some crucial environmental features have been extensively discussed in the literature. Queiroz et al.24 in Brazil found that temperatures between 6 C and 31 C are generally favourable for tree growth, but the optimum temperature range varies depending on the species or hybrid. For example, the most planted hybrid in Brazil, E. grandis E. urophylla, thrives in tropical conditions and requires higher temperatures for optimal growth. Mean temperature values outside this range can potentially damage eucalyptus through impacts on the photosynthetic apparatus and alterations in internal water relations, often associated with heatwaves, droughts, or frosts25–27. Temperature changes are also correlated with shifts in latitude—approaching zero latitude tends to increase mean temperatures; and altitude—higher altitudes usually have lower temperatures. In the context of climate change, Elli et al.1 identified temperature as a critical factor, projecting potential reductions in tree growth for plantations in the Brazilian Center-North region (latitudes closer to zero). Figure 5A also revealed an important role of features related to water relations (VPD and RH2M) and soil-related features. The relevance of these features evidences the susceptibility of eucalyptus forests to changes in water availability in both soil and atmosphere28–30. It justifies the ongoing efforts in breeding eucalyptus for drought tolerance. It is noteworthy that the PLSR-FA integration, although recent, has been contributing significantly to understanding the relationship between GEI and real environmental variables, as outlined in Bakare et al.21 and Araújo et al.19.
The discussion addressed in the previous paragraph alert to a concerning scenario for plant breeding. According to the last report of the Intergovernmental Panel on Climate Change, the last fifty years had the most steep increase in temperatures in the last 2000 years31. Particularly in Brazil, droughts and heat waves are becoming more frequent32,33. Given this fact, plant breeders should focus on developing genotypes that can keep performing acceptably whilst enduring extreme conditions. This is specially important for forest species, which stay in the field for several years (even decades). Breeding efforts are a must for reaching sustainable forestry. In this sense, enviromics initiatives are an important ally to appropriately address the genotype-by-environment interaction from both “genotype” and “environment” frameworks, instead of focusing only on the “genotype” as it is usually done2,19,34.
The complexities arising from genotype-environment interactions underscore the importance of selecting stable candidates to mitigate financial risks. Poor decisions can lead to substantial investments in low-performing clones, making the selection of stable, high-performing candidates crucial for forestry companies operating in diverse environments. By opting for stable candidates, the number of clones needed for clonal seedling production is reduced, streamlining nursery processes and enhancing efficiency in large-scale projects. This not only optimizes resource utilization but also facilitates a more adaptive response to climate change, a key element for sustainability and long-term success in the forestry sector. The selection process resulted in the identification of 10 high-performing clones with acceptable stability potential, outperforming both commercial checks. Notably, the clones outperformed I144, the most planted clone in Brazil, which validates their potential. With reliability exceeding 0.8 for all clones except C34, the selection was based on high-quality information.
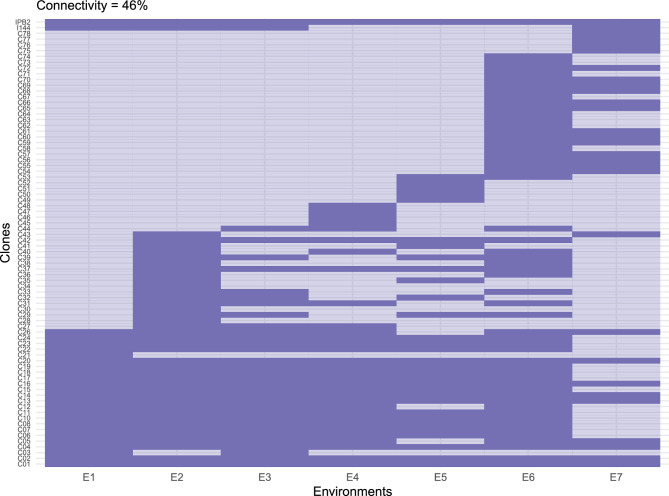
Considering reliability becomes crucial due to the varied sampling of each clone across the trial network, as illustrated in Fig. 6. For instance, consider clone C50, which was only tested in environment E5. Since we did not have kinship information, the FA model will predict the performance of this clone in environments where it was not tested based on its performance in E5 and the covariance between this environments and the others35,36. In a scenario where C50 performed exceptionally well, it would probably be selected in the FAST index. However, relying on C50 for recommendations to other environments entails risks. These environments might lack the specific factors present in E5 that contributed to C50’s superior performance. In contrast, clone C13, tested and selected in all environments, exhibited consistent performance superior to commercial checks. With high reliability, the risk of C13 performing poorly in other environments is minimized. By incorporating the clones’ reliability into the FAST index, the decision-making process is more robust, accounting for potential risks and ensuring informed selections37. Enhancing the reliability of clone per se sampling is not solely dependent on direct evaluations. Utilizing kinship matrices, whether derived from pedigree or genomics, offers an avenue to capitalize on information from related clones, thereby refining allele sampling38. Additionally, employing models that account for genetic interactions within the trial contributes to isolating a pure genotypic value, unburdened by indirect genetic effects39. It is noteworthy that various methods are available to address risk in plant breeding. For instance, the approach proposed by Dias et al.40 harnesses the probabilistic foundation of the Bayesian framework, providing a comprehensive strategy to navigate uncertainties in the breeding process.
Figure 6.
Heatmap depicting the connectivity in the dataset. Intense-coloured cells indicate the presence of the clone of the y-axis in the trial of the x-axis, and light-coloured cells, the absence. This heatmap was generated using the ggplot2 package, v. 3.5.1 (https://ggplot2.tidyverse.org/articles/ggplot2.html)..
Methods
The dataset encompasses seven advanced clonal tests conducted in five Brazilian states (see Fig. 7). The clones used in these trials originate from breeding programs of various pulp companies located in different regions of Brazil, meaning they were tested and selected for a specific environmental range. ArborGen®, the owner of the analyzed dataset, is a company that sells genetic material from both its own breeding program and partner companies. The objective of these trials was to evaluate the adaptation of tested clones to environmental conditions different from those in which they were initially tested. For confidentiality reasons, the clones’ identifications have been coded. Only the two commercial checks, IPB2 and I144, retained their original identification as they are public domain. Most of the clones were E. grandis E. urophylla hybrids, with some being pure E. grandis or E. urophylla (see Supplementary Material Table S2). The trials serve as representatives of diverse environmental conditions that clones may encounter in commercial plantations. Some environments are particularly critical: E1 and E6 are more prone to drought, while E2 is characterized by high heat and humidity. E5 uniquely represents the Northeastern region, and E3 the Northern region. Furthermore, four out of six biomes are represented in our dataset. Installed between February 2019 and February 2020, each trial was laid out in a randomized complete blocks design, featuring four repetitions and thirty-six plants per plot. Eight clones are consistent across all trials. The dataset exhibits a 46% connectivity (see Fig. 6). In this study, “trial” and “environment” are used interchangeably.
We measured the diameter at breast height (DBH) when the trees were months old. It is important to note that all trees within a specific trial were measured at the same age, although the ages varied among different trials. The DBH was measured using a diametric tape.
Environmental features
Utilizing coordinates (latitude and longitude) and information on sowing and data collection dates, we gathered data on 25 environmental features (refer to Table 1). Features pertaining to weather and climate throughout the established period (daily records) were obtained using the EnvRtype package41 in the R software environment version 4.3.242. This package serves as a user-friendly tool for retrieving features from the NASAPOWER database43. Additionally, soil-related features were acquired as rasters from SoilGrids44 and processed using the raster package in R45.
Table 1.
Environmental features considered in the analyses, and their respective minimum, 25% quartile, mean, 75% quartile and maximum values.
| Feature | Acronym | Unit | Minimum | 25% quartile | Mean | 75% quartile | Maximum |
|---|---|---|---|---|---|---|---|
| Longitude | LON | − 57.8919 | − 56.1094 | − 49.5761 | − 43.8150 | − 35.6094 | |
| Latitude | LAT | − 20.4428 | − 19.1983 | − 14.6973 | − 13.6750 | − 6.0432 | |
| Altitude | ALT | m | 102.00 | 389.00 | 511.72 | 670.00 | 993.00 |
| Mean air temperature | TMEAN | C | 9.70 | 23.27 | 24.98 | 27.01 | 34.92 |
| Maximum air temperature | TMAX | C | 14.33 | 28.26 | 30.73 | 32.95 | 42.49 |
| Minimum air temperature | TMIN | C | 3.24 | 17.91 | 20.09 | 22.88 | 28.58 |
| Dew point | T2MDEW | C | − 7.08 | 14.03 | 17.62 | 21.47 | 24.87 |
| Daily temperature range | TRANGE | C/day | 1.61 | 7.43 | 10.64 | 13.80 | 23.73 |
| Wind speed | WS | m/s | 0.18 | 0.89 | 1.84 | 2.50 | 5.91 |
| Relative humidity | RH2M | % | 17.56 | 57.44 | 68.02 | 80.81 | 94.44 |
| Precipitation | PREC | mm/day | 0.00 | 0.00 | 3.07 | 3.48 | 66.86 |
| Horizontal infrared radiation intensity | HIRI | MJ/m2/day | 255.18 | 371.52 | 388.17 | 410.41 | 453.37 |
| Insolation incidence on a horizontal surface | IIHS | MJ/m2/day | 1.97 | 16.88 | 19.51 | 22.55 | 32.21 |
| Extraterrestial radiation | RTA | MJ/m2/day | 23.74 | 30.38 | 34.85 | 39.32 | 42.27 |
| Vapour pressure deficit | VPD | kPa | 0.10 | 0.76 | 1.37 | 1.75 | 4.68 |
| Slope of saturation vapour pressure curve | SPV | kPaC | 0.08 | 0.18 | 0.20 | 0.21 | 0.31 |
| Potential evapotranspiration | ETP | mm/day | 0.87 | 7.66 | 8.94 | 10.38 | 14.79 |
| Deficit by precipitation | PETP | mm/day | − 14.79 | − 9.78 | − 5.87 | − 4.61 | 61.76 |
| Effect of temperature on radiation use efficiency | FRUE | – | 0.00 | 0.83 | 0.88 | 0.98 | 1.00 |
| Soil organic content | SOC | g/kg | 13.30 | 14.20 | 19.32 | 23.80 | 24.70 |
| Silt content | SILT | % | 14.00 | 15.00 | 21.37 | 28.00 | 36.00 |
| Sand content | SAND | % | 30.00 | 43.00 | 46.69 | 52.00 | 59.00 |
| Clay content | CLAY | % | 26.00 | 27.00 | 32.11 | 35.00 | 41.00 |
| pH | PH | – | 4.90 | 5.10 | 5.22 | 5.40 | 5.70 |
| Bulk density of the fine earth fraction | BDOD | kg/dm3 | 1.20 | 1.30 | 1.31 | 1.40 | 1.40 |
Statistical analyses
We used the mean DBH across plants within plots. In the mathematical notation below, V is the number of clones (), J is the number of environments (), R is the number of replicates (), and N is the number of phenotypic observations, with , with being the number of observations per environment. This distinction is necessary since the trials have different sizes. We performed all analyses under the linear mixed model framework, where the residual maximum likelihood46 is used to estimate the variance components. These are necessary for predicting the best linear unbiased predictions (BLUPs) using Henderson’s mixed model equation47,48. These analyses were performed in the ASReml-R package49.
Single-trial analyses
First, we fitted the following linear mixed model for single-trial analysis:
| 1 |
where is a vector of phenotypic records, is the model intercept, connected to by a vector of ones; is the vector of block random effects [], accompanied by its incidence matrix ; is the vector of random genotypic effects [], connected to by its design matrix ; and is the vector of random residual effects [].
The individual analyses were conducted to assess the significance of genotypic effects in each trial using the likelihood ratio test. Additionally, we identified the top ten clones in each environment for subsequent comparison with the FAST outcomes (described in the following section).
Factor analytic linear mixed models
The FA model is described as follows:
| 2 |
where is a vector of fixed environment effects, connected to by its incidence matrix . contains the effects due to differences in geographical location, temporal variation and tree ages. The other terms, previously described in Eq. (1), have new dimensions: is changed by N, and is substituted by V. In addition, and are nested effects, so their dimensions are and . Their incidence matrix changed accordingly. The conditional distribution of the random effects of Eq. (2) is:
| 3 |
where are identity matrices whose order is indicated by their subscripts, is the matrix of factor loadings , is the diagonal matrix of factor scores variances , is the diagonal matrix of specific variances , is the Kronecker product and is the direct sum.
In Eq. (2), the eBLUPs are obtained using the following multiple regression:
| 4 |
where is the vector of factor scores and is the vector of lack-of-fit effects, associated to .
Factors need to be rotated when . We performed the rotation process based on the singular value decomposition, described by Smith et al.22. Henceforth, the matrix of rotated loadings will be represented by , and the vector of rotated scores will be represented by . These replace and at Eqs. (4) and (3).
We selected the number of factors of the FA model based on its explicative power. Since parsimony tends to decrease as explicative power increases, we selected the model with more than 85% of explicative power that had the smaller K. For that, we used the average semivariances ratio50. As an addendum for complementing information on the models’ explicative power and parsimony, we computed the Akaike Information Criterion (AIC)51 and the percentage of explained variance per factor and per environment (), given by, respectively:
| 5 |
| 6 |
where LogL is the logarithm of the maximum point of the residual likelihood function, and t is the number of parameters.
After defining the number of factors of the FA model, we computed the pairwise genotypic correlation between environments as follows52:
| 7 |
where is a matrix of pairwise genotypic correlations and is a diagonal matrix whose elements are the inverse of the square roots of the diagonal elements of .
Using the chosen model, we also computed the generalized heritability53 and the experimental coefficient of experimental variation, given by, respectively:
| 8 |
| 9 |
where is the pairwise prediction error variance. The parameters described above are indexed by environment, for Eq. (2) provides environment-wise variances.
The extraction of outputs from the FA model was performed using a homemade function (fa.outs), available from https://github.com/saulo-chaves/May_b_useful/blob/main/fa.outs.R.
Factor analytic selection tools
To facilitate the selection process, we used the FAST12. From the premise that the first factor resumes the genotypic main effect54, we computed the overall performance of each clone as follows:
| 10 |
Using the same premise previously mentioned, one may assume that the other factors represent stability. Assuming that a stable clone is the one that can have its performance easily predicted across environments, we measured the stability of a clone using the root mean squared deviation from a fictitious latent regression, given by:
| 11 |
where e is the portion of (Eq. 4) without .
We associated these metrics with the reliability of the clone, given by:
| 12 |
where is the prediction error variance of the v genotype, and is the mean genotypic variance across environments. Reliability is useful in the context of unbalanced data, a scenario that can be applied in this study.
We used , and in an index to perform the selection50:
| 13 |
note that the FAST metrics are weighted by reliability. This additional consideration enhances confidence in the selection process, as it incorporates not only the performance itself but also the quality of the information.
After identifying the top-performing clones, we conducted a comparative analysis with the two commercial checks using latent regression plots55. The number of plots corresponds to the number of factors, which is contingent on the selected model. The initial plot illustrates the latent regression between the eBLUPs () and the first factor loadings. Subsequent plots feature on the y-axis and the kth factor loadings on the x-axis.
Linking FA to environmental features
We computed the mean of each feature for each environment and compiled them into , the matrix representing environmental features, with P denoting the number of features. Then, we performed a partial least square regression (PLSR)—using the kernel algorithm56,57—of the environmental features on the rotated factor loadings:
| 14 |
where is a matrix of coefficients and is a matrix of residuals. The PLSR was fitted using the pls package58. This analysis served the dual purpose of understanding the connection between factors and environmental features and inferring the relationship between environments using both real and latent environmental covariates. We also assessed the relative importance of each environmental feature to the underlying GEI variation in the dataset. For this purpose, we computed the variable importance in projection (VIP)59, given by:
| 15 |
where is the sum of squares explained by the a-th PLS component (, and A is defined via leave-one-out cross-validation), is the loading weight of the p-th feature in the a-th component, and is a vector of loading weights in the a-th component. We transformed the VIPs to a percentage scale using . The VIP was computed using the plsVarSel package60.
Ethical statement
The cultivated Eucalyptus spp. clones were provided by ArborGen®. We confirm that we have complied with all necessary regulations for this type of research.
Supplementary Information
Acknowledgements
We thank ArborGen® for providing the data used in this study.
Author contributions
S.F.S.C. analysed the data; S.F.S.C. and M.B.D. wrote the first draft; K.O.G.D. and L.L.B. reviewed the drafts. All authors reviewed the final version of the manuscript.
Funding
This research was supported by Fundação de Amparo a Pesquisa do Estado de Minas Gerais (FAPEMIG), Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), and Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES).
Data availability
The data and the code are available from the corresponding author upon reasonable request.
Competing interests
The authors declare no competing interests
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-024-69299-2.
References
- 1.Elli, E. F., Sentelhas, P. C. & Bender, F. D. Impacts and uncertainties of climate change projections on Eucalyptus plantations productivity across Brazil. For. Ecol. Manage.474, 118365. 10.1016/j.foreco.2020.118365 (2020). 10.1016/j.foreco.2020.118365 [DOI] [Google Scholar]
- 2.Callister, A. N. et al. Enviromic prediction enables the characterization and mapping of Eucalyptus globulus Labill breeding zones. Tree Genet. Genomes20, 3. 10.1007/s11295-023-01636-4 (2024). 10.1007/s11295-023-01636-4 [DOI] [Google Scholar]
- 3.Smith, A. B., Cullis, B. R. & Thompson, R. The analysis of crop cultivar breeding and evaluation trials: An overview of current mixed model approaches. J. Agric. Sci.143, 449–462. 10.1017/S0021859605005587 (2005). 10.1017/S0021859605005587 [DOI] [Google Scholar]
- 4.Waters, D. L., van der Werf, J. H. J., Robinson, H., Hickey, L. T. & Clark, S. A. Partitioning the forms of genotype-by-environment interaction in the reaction norm analysis of stability. Theor. Appl. Genet.136, 99. 10.1007/s00122-023-04319-9 (2023). 10.1007/s00122-023-04319-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.van Eeuwijk, F. A., Bustos-Korts, D. V. & Malosetti, M. What should students in plant breeding know about the statistical aspects of genotype × environment interactions?. Crop Sci.56, 2119–2140. 10.2135/cropsci2015.06.0375 (2016). 10.2135/cropsci2015.06.0375 [DOI] [Google Scholar]
- 6.Piepho, H.-P. Analyzing genotype-environment data by mixed models with multiplicative terms. Biometrics53, 761–766. 10.2307/2533976 (1997). 10.2307/2533976 [DOI] [Google Scholar]
- 7.Piepho, H.-P. Empirical best linear unbiased prediction in cultivar trials using factor-analytic variance-covariance structures. Theor. Appl. Genet.97, 195–201. 10.1007/s001220050885 (1998). 10.1007/s001220050885 [DOI] [Google Scholar]
- 8.Smith, A. B., Cullis, B. R. & Thompson, R. Analyzing variety by environment data using multiplicative mixed models and adjustments for spatial field trend. Biometrics57, 1138–1147. 10.1111/j.0006-341X.2001.01138.x (2001). 10.1111/j.0006-341X.2001.01138.x [DOI] [PubMed] [Google Scholar]
- 9.Burgueño, J., Crossa, J., Cornelius, P. L. & Yang, R.-C. Using factor analytic models for joining environments and genotypes without crossover genotype × environment interaction. Crop Sci.48, 1291–1305. 10.2135/cropsci2007.11.0632 (2008). 10.2135/cropsci2007.11.0632 [DOI] [Google Scholar]
- 10.Kelly, A. M., Smith, A. B., Eccleston, J. A. & Cullis, B. R. The accuracy of varietal selection using Factor Analytic Models for Multi-Environment plant breeding trials. Crop Sci.47, 1063–1070. 10.2135/cropsci2006.08.0540 (2007). 10.2135/cropsci2006.08.0540 [DOI] [Google Scholar]
- 11.Piepho, H.-P., Möhring, J., Melchinger, A. E. & Büchse, A. BLUP for phenotypic selection in plant breeding and variety testing. Euphytica161, 209–228. 10.1007/s10681-007-9449-8 (2008). 10.1007/s10681-007-9449-8 [DOI] [Google Scholar]
- 12.Smith, A. B. & Cullis, B. R. Plant breeding selection tools built on factor analytic mixed models for multi-environment trial data. Euphytica214, 143. 10.1007/s10681-018-2220-5 (2018). 10.1007/s10681-018-2220-5 [DOI] [Google Scholar]
- 13.Wood, J. T. The use of environmental variables in the interpretation of genotype-environment interaction. Heredity37, 1–7. 10.1038/hdy.1976.61 (1976). 10.1038/hdy.1976.61 [DOI] [PubMed] [Google Scholar]
- 14.Freeman, G. H. & Perkins, J. M. Environmental and genotype-environmental components of variability VIII. Relations between genotypes grown in different environments and measures of these environments. Heredity27, 15–23. 10.1038/hdy.1971.67 (1971). 10.1038/hdy.1971.67 [DOI] [Google Scholar]
- 15.Cooper, M. & Messina, C. D. Can we harness “enviromics’’ to accelerate crop improvement by integrating breeding and agronomy?. Front. Plant Sci.12, 735143. 10.3389/fpls.2021.735143 (2021). 10.3389/fpls.2021.735143 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Costa-Neto, G. M. F., Crossa, J. & Fritsche-Neto, R. Enviromic assembly increases accuracy and reduces costs of the genomic prediction for yield plasticity in maize. Front. Plant Sci.12, 717552. 10.3389/fpls.2021.717552 (2021). 10.3389/fpls.2021.717552 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Crossa, J. et al. The modern plant breeding triangle: Optimizing the use of genomics, phenomics, and enviromics data. Front. Plant Sci.12, 651480. 10.3389/fpls.2021.651480 (2021). 10.3389/fpls.2021.651480 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tolhurst, D. J., Gaynor, R. C., Gardunia, B., Hickey, J. M. & Gorjanc, G. Genomic selection using random regressions on known and latent environmental covariates. Theor. Appl. Genet.135, 3393–3415. 10.1007/s00122-022-04186-w (2022). 10.1007/s00122-022-04186-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Araújo, M. S. et al. GIS-FA: An approach to integrating thematic maps, factor-analytic, and envirotyping for cultivar targeting. Theor. Appl. Genet.137, 80. 10.1007/s00122-024-04579-z (2024). 10.1007/s00122-024-04579-z [DOI] [PubMed] [Google Scholar]
- 20.Costa e Silva, J., Potts, B. M. & Dutkowski, G. W. Genotype by environment interaction for growth of Eucalyptus globulus in Australia. Tree Genet. Genomes2, 61–75. 10.1007/s11295-005-0025-x (2006). 10.1007/s11295-005-0025-x [DOI] [Google Scholar]
- 21.Bakare, M. A. et al. Parsimonious genotype by environment interaction covariance models for cassava (Manihot esculenta). Front. Plant Sci.13, 569. 10.3389/fpls.2022.978248 (2022). 10.3389/fpls.2022.978248 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Smith, A. B., Norman, A., Kuchel, H. & Cullis, B. R. Plant variety selection using interaction classes derived from factor analytic linear mixed models: models with independent variety effects. Front. Plant Sci.12, 1857. 10.3389/fpls.2021.737462 (2021). 10.3389/fpls.2021.737462 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hubbard, R. M. et al. Contrasting water use of two Eucalyptus clones across a precipitation and temperature gradient in Brazil. For. Ecol. Manage.475, 118407. 10.1016/j.foreco.2020.118407 (2020). 10.1016/j.foreco.2020.118407 [DOI] [Google Scholar]
- 24.Queiroz, T. B. et al. Temperature thresholds for Eucalyptus genotypes growth across tropical and subtropical ranges in South America. For. Ecol. Manage.472, 118248. 10.1016/j.foreco.2020.118248 (2020). 10.1016/j.foreco.2020.118248 [DOI] [Google Scholar]
- 25.Valdés, A. E. et al. Drought tolerance acquisition in Eucalyptus globulus (Labill.): A research on plant morphology, physiology and proteomics. J. Proteomics79, 263–276. 10.1016/j.jprot.2012.12.019 (2013). 10.1016/j.jprot.2012.12.019 [DOI] [PubMed] [Google Scholar]
- 26.Mokochinski, J. B. et al. Metabolic responses of Eucalyptus species to different temperature regimes. J. Integr. Plant Biol.60, 397–411. 10.1111/jipb.12626 (2018). 10.1111/jipb.12626 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Pita-Barbosa, A. et al. Developing a roadmap to define a potential ideotype for drought tolerance in Eucalyptus. Forest Sci.69, 101–114. 10.1093/forsci/fxac044 (2023). 10.1093/forsci/fxac044 [DOI] [Google Scholar]
- 28.Piedallu, C., Gégout, J.-C., Perez, V. & Lebourgeois, F. Soil water balance performs better than climatic water variables in tree species distribution modelling. Glob. Ecol. Biogeogr.22, 470–482. 10.1111/geb.12012 (2013). 10.1111/geb.12012 [DOI] [Google Scholar]
- 29.Lim, H., Alvares, C. A., Ryan, M. G. & Binkley, D. Assessing the cross-site and within-site response of potential production to atmospheric demand for water in Eucalyptus plantations. For. Ecol. Manage.464, 118068. 10.1016/j.foreco.2020.118068 (2020). 10.1016/j.foreco.2020.118068 [DOI] [Google Scholar]
- 30.Macfarlane, C., White, D. A. & Adams, M. A. The apparent feed-forward response to vapour pressure deficit of stomata in droughted, field-grown Eucalyptus globulus Labill. Plant Cell Env.27, 1268–1280. 10.1111/j.1365-3040.2004.01234.x (2004). 10.1111/j.1365-3040.2004.01234.x [DOI] [Google Scholar]
- 31.Calvin, K. et al. IPCC, 2023: Climate change 2023: Synthesis report. In Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change (eds. Core Writing Team et al.). IPCC, Geneva, Switzerland. Tech. Rep., Intergovernmental Panel on Climate Change (IPCC) (2023). 10.59327/IPCC/AR6-9789291691647.
- 32.Geirinhas, J. L. et al. Recent increasing frequency of compound summer drought and heatwaves in Southeast Brazil. Environ. Res. Lett.16, 034036. 10.1088/1748-9326/abe0eb (2021). 10.1088/1748-9326/abe0eb [DOI] [Google Scholar]
- 33.Marengo, J. A., Torres, R. R. & Alves, L. M. Drought in Northeast Brazil–past, present, and future. Theoret. Appl. Climatol.129, 1189–1200. 10.1007/s00704-016-1840-8 (2017). 10.1007/s00704-016-1840-8 [DOI] [Google Scholar]
- 34.Resende, R. T. et al. Satellite-enabled enviromics to enhance crop improvement. Mol. Plant17, 848–866. 10.1016/j.molp.2024.04.005 (2024). 10.1016/j.molp.2024.04.005 [DOI] [PubMed] [Google Scholar]
- 35.Krause, M. D. et al. Boosting predictive ability of tropical maize hybrids via genotype-by-environment interaction under multivariate GBLUP models. Crop Sci.60, 3049–3065. 10.1002/csc2.20253 (2020). 10.1002/csc2.20253 [DOI] [Google Scholar]
-
36.Burgueño, J., Campos, G., Weigel, K. & Crossa, J. Genomic prediction of breeding values when modeling genotype
 environment interaction using pedigree and dense molecular markers. Crop Sci.52, 707–719. 10.2135/cropsci2011.06.0299 (2012). 10.2135/cropsci2011.06.0299 [DOI] [Google Scholar]
environment interaction using pedigree and dense molecular markers. Crop Sci.52, 707–719. 10.2135/cropsci2011.06.0299 (2012). 10.2135/cropsci2011.06.0299 [DOI] [Google Scholar] - 37.Yazdi, M. H., Visscher, P. M., Ducrocq, V. & Thompson, R. Heritability, reliability of genetic evaluations and response to selection in proportional hazard models. J. Dairy Sci.85, 1563–1577. 10.3168/jds.S0022-0302(02)74226-4 (2002). 10.3168/jds.S0022-0302(02)74226-4 [DOI] [PubMed] [Google Scholar]
- 38.Wientjes, Y. C. J., Veerkamp, R. F. & Calus, M. P. L. The effect of linkage disequilibrium and hamily telationships on the teliability of genomic prediction. Genetics193, 621–631. 10.1534/genetics.112.146290 (2013). 10.1534/genetics.112.146290 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ferreira, F. M. et al. A novel strategy to predict clonal composites by jointly modeling spatial variation and genetic competition. For. Ecol. Manage.548, 121393. 10.1016/j.foreco.2023.121393 (2023). 10.1016/j.foreco.2023.121393 [DOI] [Google Scholar]
- 40.Dias, K. O. G. et al. Leveraging probability concepts for cultivar recommendation in multi-environment trials. Theor. Appl. Genet.135, 1385–1399. 10.1007/s00122-022-04041-y (2022). 10.1007/s00122-022-04041-y [DOI] [PubMed] [Google Scholar]
- 41.Costa-Neto, G., Galli, G., Carvalho, H. . F., Crossa, J. & Fritsche-Neto, R. EnvRtype: A software to interplay enviromics and quantitative genomics in agriculture. G3 Genes|Genomes|Genet.11, jkab040. 10.1093/g3journal/jkab040 (2021). 10.1093/g3journal/jkab040 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.R Core Team. R: A Language and environment for statistical computing (2023). Programmers: _:n2360.
- 43.Sparks, A. H. nasapower: A NASA POWER global meteorology, surface solar energy and climatology data client for R. J. Open Sourc. Softw.3, 1035. 10.21105/joss.01035 (2018). 10.21105/joss.01035 [DOI] [Google Scholar]
- 44.Poggio, L. et al. SoilGrids 2.0: Producing soil information for the globe with quantified spatial uncertainty. SOIL7, 217–240. 10.5194/soil-7-217-2021 (2021). 10.5194/soil-7-217-2021 [DOI] [Google Scholar]
- 45.Hijmans, R. J. raster: Geographic data analysis and modeling. R package version 3.6-26 (2023).
- 46.Patterson, H. D. & Thompson, R. Recovery of inter-block information when block sizes are unequal. Biometrika58, 545–554. 10.1093/biomet/58.3.545 (1971). 10.1093/biomet/58.3.545 [DOI] [Google Scholar]
- 47.Henderson, C. R. Best Linear Unbiased Estimation and Prediction under a selection model. Biometrics31, 423. 10.2307/2529430 (1975). 10.2307/2529430 [DOI] [PubMed] [Google Scholar]
- 48.Henderson, C. R., Kempthorne, O., Searle, S. R. & von Krosigk, C. M. The estimation of environmental and genetic trends from records subject to culling. Biometrics15, 192–218. 10.2307/2527669 (1959). 10.2307/2527669 [DOI] [Google Scholar]
- 49.The VSNi Team. asreml: Fits Linear Mixed Models using REML (2023).
- 50.Chaves, S. F. S. et al. Analysis of repeated measures data through mixed models: An application in Theobroma grandiflorum breeding. Crop Sci.63, 2131–2144. 10.1002/csc2.20995 (2023). 10.1002/csc2.20995 [DOI] [Google Scholar]
- 51.Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control19, 716–723. 10.1109/TAC.1974.1100705 (1974). 10.1109/TAC.1974.1100705 [DOI] [Google Scholar]
- 52.Cullis, B. R., Smith, A. B., Beeck, C. P. & Cowling, W. A. Analysis of yield and oil from a series of canola breeding trials. Part II. Exploring variety by environment interaction using factor analysis. Genome53, 1002–1016. 10.1139/G10-080 (2010). 10.1139/G10-080 [DOI] [PubMed] [Google Scholar]
- 53.Cullis, B. R., Smith, A. B. & Coombes, N. E. On the design of early generation variety trials with correlated data. J. Agric. Biol. Environ. Stat.11, 381–393. 10.1198/108571106X154443 (2006). 10.1198/108571106X154443 [DOI] [Google Scholar]
- 54.Stefanova, K. T. & Buirchell, B. Multiplicative mixed models for genetic gain assessment in lupin breeding. Crop Sci.50, 880–891. 10.2135/cropsci2009.07.0402 (2010). 10.2135/cropsci2009.07.0402 [DOI] [Google Scholar]
- 55.Cullis, B. R., Jefferson, P., Thompson, R. & Smith, A. B. Factor analytic and reduced animal models for the investigation of additive genotype-by-environment interaction in outcrossing plant species with application to a Pinus radiata breeding programme. Theor. Appl. Genet.127, 2193–2210. 10.1007/s00122-014-2373-0 (2014). 10.1007/s00122-014-2373-0 [DOI] [PubMed] [Google Scholar]
- 56.Lindgren, F., Geladi, P. & Wold, S. The kernel algorithm for PLS. J. Chemometr.7, 45–59. 10.1002/cem.1180070104 (1993). 10.1002/cem.1180070104 [DOI] [Google Scholar]
- 57.Dayal, B. S. & MacGregor, J. F. Improved PLS algorithms. J. Chemometr.11, 73–85 (1997). [DOI] [Google Scholar]
- 58.Liland, K. H., Mevik, B.-H. & Wehrens, R. pls: Partial Least Squares and Principal Component Regression, R package version 2.8-3 (2023).
- 59.Wold, S., Sjöström, M. & Eriksson, L. PLS-regression: a basic tool of chemometrics. Chemom. Intell. Lab. Syst.58, 109–130. 10.1016/S0169-7439(01)00155-1 (2001). 10.1016/S0169-7439(01)00155-1 [DOI] [Google Scholar]
- 60.Mehmood, T., Liland, K. H., Snipen, L. & Sæbø, S. A review of variable selection methods in Partial Least Squares Regression. Chemom. Intell. Lab. Syst.118, 62–69. 10.1016/j.chemolab.2012.07.010 (2012). 10.1016/j.chemolab.2012.07.010 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data and the code are available from the corresponding author upon reasonable request.