Abstract
Single-cell assay for transposase-accessible chromatin using sequencing (scATAC-seq) is being increasingly used to study gene regulation. However, major analytical gaps limit its utility in studying gene regulatory programs in complex diseases. In response, MOCHA (Model-based single cell Open CHromatin Analysis) presents major advances over existing analysis tools, including: 1) improving identification of sample-specific open chromatin, 2) statistical modeling of technical drop-out with zero-inflated methods, 3) mitigation of false positives in single cell analysis, 4) identification of alternative transcription-starting-site regulation, and 5) modules for inferring temporal gene regulatory networks from longitudinal data. These advances, in addition to open chromatin analyses, provide a robust framework after quality control and cell labeling to study gene regulatory programs in human disease. We benchmark MOCHA with four state-of-the-art tools to demonstrate its advances. We also construct cross-sectional and longitudinal gene regulatory networks, identifying potential mechanisms of COVID-19 response. MOCHA provides researchers with a robust analytical tool for functional genomic inference from scATAC-seq data.
Subject terms: Gene regulatory networks, Data processing, Statistical methods, Software, Biotechnology
Analytical gaps limit the utility of scATAC-seq for studying gene regulatory programs in human disease. Here, authors describe MOCHA, a robust analytical tool with advanced statistical modelling that enables functional genomic inference in large cross-sectional and longitudinal human studies.
Introduction
Single-cell assay for transposase-accessible chromatin using sequencing (scATAC-seq)1–3 has become increasingly popular in recent years for studying biological and translational questions around gene regulation and cell identity and has revealed insights on diverse topics such as tumor-related T cell exhaustion4, trained immunity in monocytes in patients with COVID-195, regulators of innate immunity in COVID-196, and potentially causal variants for Alzheimer’s disease and Parkinson’s disease7. Many sophisticated software tools have been developed for analyzing scATAC-seq data8, covering functionalities such as dimensionality reduction and clustering9–11, semi-automated cell type annotation10,11, identification of open chromatin regions12–16, characterization of motif usage and enrichment17–20, and inference on gene regulatory networks11,21,22. Integrating these developments, recent end-to-end analysis pipelines streamline the analytical process from quality control and cell type annotation to accessibility and motif analysis9–12,23. Together these tools have facilitated the extraction of biological insights from scATAC-seq data.
Despite these advances, major analytical gaps in scATAC-seq data analysis limit the construction of robust and reproducible gene regulatory networks to study human disease. First, human disease studies require reliable evaluation of sample- and cell-type-specific open chromatin to capture human genetic heterogeneity and cell-type-specific regulatory regions. However, visibility into these forms of heterogeneity is compromised by existing packages10–13,15, which usually mix cells across either samples or cell types to compensate for the low coverage of scATAC-seq. Second, scATAC-seq data is intrinsically sparse. Only 5–15% of open chromatin regions are detected in individual cells9. Both single-cell and pseudo-bulk ATAC-seq data can contain an excessively high number of regions without accessibility measurements. While zero-inflated (ZI) statistical methods are widely used and often debated in analyzing single-cell ribonucleic acid sequencing (scRNA-seq) data24–28, such methods are not implemented in popular tools for scATAC-seq data analysis, likely leading to many unreliable results. Third, previous studies have shown that pseudo-replication bias (cell-interdependence) generates many false results in scRNA-seq analysis, if left unaddressed29,30. Similarly, existing scATAC-seq tools, which use the Wald, Wilcoxon, and logistic regression tests at the single-cell level10,31, do not address this issue and thus may generate many false results as well. Additionally, others have applied methods designed for bulk RNA-seq (such as DESeq)32. The few existing reviews describe the methods mentioned above, but do not benchmark them comprehensively8,31. In longitudinal studies, these challenges are exacerbated as subjects have multiple interdependent samples. To postulate robust gene regulatory networks in human disease, the research community needs a tool to address these challenges.
To this end, we developed a suite of analytical modules for robust functional genomic inference in heterogeneous human disease cohorts, in an open R package called MOCHA (Model-based single-cell Open CHromatin Analysis). First, we developed a method for evaluating sample- and cell-type-specific chromatin accessibility in low coverage scATAC-seq. Second, we implemented ZI statistical methods33–37 for differential accessibility analysis, co-accessibility analysis, and mixed effects modeling. Third, we aggregated scATAC-seq data per cell type into normalized pseudo-bulk tile-sample accessibility matrices (TSAMs) to capture donor and cell type-centric accessibility. This TSAM directly addresses the issue of cell interdependence (pseudo-replication) and enables modeling cross-sectional and longitudinal gene regulatory landscapes of human disease in large cohorts. We benchmarked MOCHA against state-of-the-art methods in identifying regions of open chromatin, differential accessibility, and co-accessibility. More importantly, we demonstrate MOCHA’s ability to construct gene regulatory networks from both cross-sectional and longitudinal analyses of scATAC-seq data on CD16 monocytes from our COVID-19 cohort38. We also demonstrate how to integrate MOCHA with existing tools11,17,33,39, contrast its functionality with other existing tools, and adapt it for custom approaches. In all, we anticipate MOCHA will accelerate the analysis and interpretation of gene regulatory networks using scATAC-seq data.
Results
MOCHA overview
We developed MOCHA based on our COVID19 dataset (Methods), which was collected on n = 91 peripheral blood mononuclear cell (PBMC) samples of either COVID+ participants (n = 18, 10 females and 8 males, 3–5 samples per participant, a total of 69 samples) or uninfected COVID- participants (n = 22, 10 females and 12 males, one sample per participant). We obtained high-quality scATAC-seq data of 1,311,638 cells from the samples. Unless specified, we mainly used a cross-sectional subset of the COVID19 dataset (denoted as COVID19X, n = 39) in MOCHA’s development, including data of the COVID- samples and the first samples of the COVID+ participants during early infection (<16 days post symptom onset (PSO), n = 17, 9 females and 8 males).
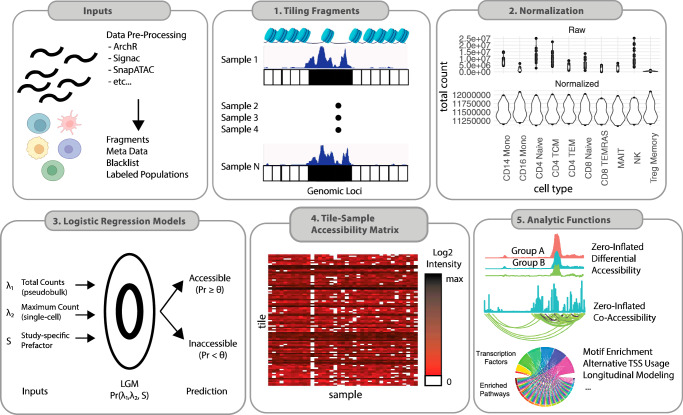
We designed MOCHA to serve as an analytical framework for sample-centric scATAC-seq data analysis, after quality control assessments (filtering duplicate fragments and low quality cells), cell type labeling, and doublet removal. MOCHA identifies sample- and cell type-specific open chromatin and provides a range of analytical functions for complex scATAC-seq data analysis (Fig. 1 and Supplementary Fig. 1):
Fig. 1. General workflow of MOCHA.
Schematic representation of the core functionalities in MOCHA, starting from scATAC input data (fragments, black list, cell type labels, and sample metadata). Using these data, MOCHA generates fragment counts for every 500 bp tiles (1), normalizes the count data (2), and leverages single-cell and pseudo-bulk information to identify open tiles in a cell type- and sample-specific manner (3). It then generates population-level open chromatin matrices for each cell type (4), which is the starting point for downstream analytical functions (5). MOCHA includes improvements to differential accessibility analysis, co-accessibility analysis, and longitudinal modeling. It also provides functions for identifying alternatively regulated transcription starting sites, motif enrichment, and dimensionality reduction. Panels were generated using Adobe Illustrator. Panel 1 also used BioRender, released under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International license.
(i) Tiling: MOCHA divides the genome into pre-defined 500 base pair (bp) tiles, which allows head-to-head comparisons on chromatin accessibility across samples and cell types and avoids complex peak-merging procedure on non-aligned summits9,11.
(ii) Normalization: Since sequencing depth may differ across samples in a large-scale scATAC-seq study (Supplementary Fig. 2a), it is essential to normalize scATAC-seq data prior to meaningful accessibility analysis. MOCHA counts the number of fragments that overlap with individual tiles in individual cells, collects the total and the maximum fragment counts for each tile from all cells of a targeted cell type per sample, and normalizes the fragment counts by the total number of fragments of the cell type per sample to reduce the effects of variations in sequencing depth and cell count (Methods). Compared with other normalization approaches, this approach resulted in the lowest coefficient of variation (CV) distribution on 2230 invariant CCCTC-binding factor (CTCF) sites on the COVID19 dataset (Supplementary Fig. 2b, n = 91). Additionally, this normalization implicitly addresses batch effects around sequencing depth and cell numbers, the effects of which may not be evident in the single cell space (Methods, Supplementary Fig. 3). As indicated by the low to moderate CV values, this approach also makes it possible to compare normalized accessibility across samples (Supplementary Fig. 2b) and cell types (Supplementary Fig. 2c).
(iii) Accessibility evaluation: MOCHA applies logistic regression models (LRMs) to evaluate whether a tile in a given cell type and sample is accessible based on three parameters (Methods): the normalized total fragment count λ(1), the normalized maximum fragment count λ(2), and a study-specific prefactor to account for differences in data quality between training and user datasets. The global prefactor, S, is needed for a broad application of MOCHA as data quality, sequencing depth, and cell count may result in a large difference in median number of fragments per cell either between different studies (e.g., 3600 to 9000 fragments per cell, Supplementary Fig. 4a, b) or across cell types in different organs (e.g., 4k − 25k fragments per cell, Supplementary Fig. 5). Since can only be evaluated on scATAC-seq data, its usage distinguishes MOCHA from peak-calling methods based on pseudo-bulk ATAC-seq data only. Using the full COVID19 dataset (n = 91), we generated pseudo-bulk ATAC-seq data from scATAC-seq data of all cells of a targeted cell type, ran MACS240 to identify all accessible regions, and used these labels as the imperfect “ground truth” to train and test the LRMs. More specifically, we used natural killer (NK) cells (n = 179,836) for training, which had 750 million total fragments, or 15x the recommended coverage for MACS241,42. On this dataset, MACS2 identified 1.15 million tiles as accessible and the remaining 4.39 million tiles having fragments were labeled as ‘inaccessible’. Using these tiles as positives and negatives, respectively, we developed cell count-specific LRMs with varying coefficient to account for variations in cell count across samples (Supplementary Fig. 6a-b). The Youden Index43 was used to balance the tradeoff between sensitivity and specificity (Supplementary Fig. 6b) and generate cell count-dependent thresholds. MOCHA applies smoothing and interpolation to find the proper coefficients and thresholds for cell counts not in the training. Once trained, all coefficients and thresholds for the LRMs are fixed for new datasets and applied to all cell types, with the exception for S which needs to be adjusted to account for difference in fragments per cell in new datasets.
The LRM model was trained exclusively on NK cells in the full COVID19 dataset and then assessed on either other cell types in the dataset (using the same S) or other human or mouse datasets (using S evaluated from the corresponding studies). We validated the LRMs (Supplementary Fig. 6c, d) using data of CD14 monocytes (n = 135,949), naive B cells (n = 60,595), CD16 monocytes (n = 28,525), NK CD56 bright cells (n = 14,692), and conventional dendritic cells (cDCs, n = 9915). We used sensitivity, specificity, area under the receiver operating characteristic (ROC) curve (AUC), and Youden’s J statistic to quantify the performance (Supplementary Fig. 6c, d). Overall MOCHA had a good performance even at low cell counts. For example, MOCHA achieved an AUC ranging from 0.693 (CD14 monocytes), 0.703 (CD16 monocytes), to 0.741 (NK CD56 bright cells) with only 50 cells.
(iv) Tile-sample accessibility matrix (TSAM): MOCHA first uses the LRMs to identify accessible tiles from cells of a targeted cell type in individual samples and then keeps only tiles that are common to at least a user-defined fraction threshold of samples. Afterwards, MOCHA generates a TSAM for the cell type with rows being the accessible tiles, columns the samples, and elements the corresponding λ(1) values. While λ(2) is informative for identifying sample-specific accessibility (Supplementary Fig. 7), λ(1) provides a more robust assessment on chromatin accessibility and was chosen for cross-sample comparisons and downstream analyses. A total of 215,649 accessible tiles were identified on CD16 monocytes with a fraction threshold of 20% (Supplementary Fig. 2d) across either COVID+ or COVID- samples in the COVID19X dataset (n = 39). About 25% elements in the obtained TSAM were zero (Supplementary Fig. 2e, f), reflecting the sparsity of scATAC-seq data even after pseudo-bulking. Statistical testing against negative binomial (NB) distributions revealed the data was ZI (Supplementary Fig. 18c), indicating the necessity of applying ZI statistical methods for downstream analysis.
(v) Differential accessibility analysis (DAA): Similar to other methods, MOCHA first filters out noisy tiles. Tiles are excluded if either 1) the median log2(λj(1) + 1) value (across all samples) is lower than a user-defined threshold or 2) their difference (between two sample groups) in percentage of zeros is less than a user-defined threshold. Unlike other methods, MOCHA includes functions to heuristically define these thresholds. For the COVID19X dataset (n = 39), we noticed that the log2(λj(1) + 1) values in the TSAM of CD16 monocytes followed a bi-modal model and thus chose a value of 12 near the higher mode as the median accessibility threshold (Supplementary Fig. 2g). Additionally, we observed a 25% difference in fragment counts between COVID+ and COVID- samples (Supplementary Fig. 2a), so we set a 50% threshold for the difference in the percentage of zeros to control for technical differences. MOCHA then applies a two-part Wilcoxon test34,35 to identify differential accessibility tiles (DATs) within the cell type between the two sample groups (Methods). DATs have either a large fold change (FC) in accessibility (Supplementary Fig. 2h) and/or large difference in percentage of zeros (Supplementary Fig. 2i). For comparison, ArchR11 uses the standard Mann-Whitney-Wilcoxon (MWW) test along with a post-test log2(FC) cutoff to identify differential regions on bias-matched cell populations, while Signac10 constructs LRMs and prioritizes differential regions based on FC.
(vi) Co-accessibility analysis (CAA): MOCHA applies the ZI Spearman correlation36 to evaluate two types of co-accessibility between tiles in TSAMs (“Methods” section). The inter-cell type co-accessibility is evaluated across cell types where data from different samples are stacked. The inter-sample co-accessibility is evaluated within a targeted cell type but across different samples. Both types are important to infer potential gene regulatory networks, one for understanding differences between cell types and the other for understanding differences between sample groups.
In addition, MOCHA has functions for dimensionality reduction, motif enrichment, analysis for alternative transcription starting site (TSS) regulation, and longitudinal modeling. TSAMs can also be passed to some existing scATAC-seq tools such as ArchR and chromVAR and other bioinformatics tools such as Monocle3 for further analysis. Furthermore, users can easily leverage information from TSAMs to conduct their own interrogations of scATAC-seq data. MOCHA’s functionalities are mostly complementary to those of PALMO44, a previously published platform by our group for analyzing longitudinal omics data (Supplementary Table 1). MOCHA can run on a standard desktop or modern laptop computer with at minimum 2GB of RAM, 1 Core CPU 2.0 GHz/core. For best performance, at least 8GB of RAM and 4 + CPU cores are recommended to take advantage of MOCHA’s parallelization.
MOCHA reliably detects sample-specific chromatin accessibility
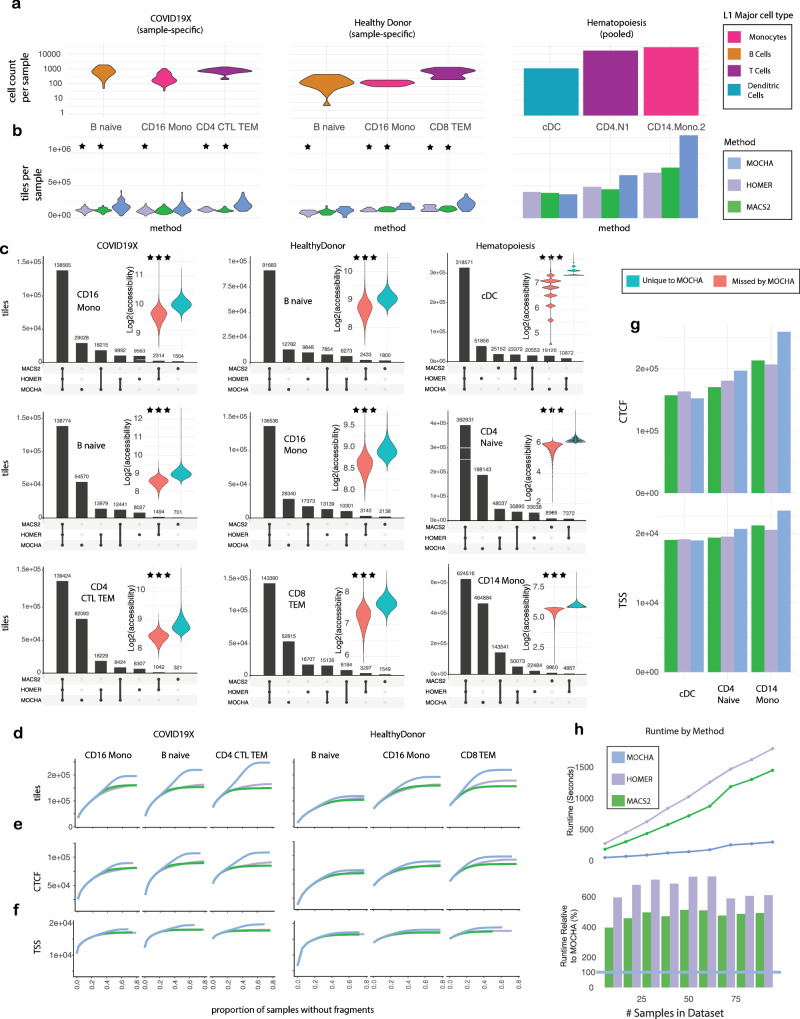
A crucial component of scATAC-seq data analysis is to reliably detect which chromatin regions are accessible. We benchmarked MOCHA against the popular tools MACS240 and HOMER45. The former is also implemented in ArchR11, Signac10, and SnapATAC9. We compared these tools using three scATAC-seq datasets with different data quality and sequencing depth (“Methods” section and Supplementary Fig. 6a): (i) COVID19X (n = 39, Fig. 2) or COVID19 (n = 91, Supplementary Fig. 6); (ii) HealthyDonor, a dataset of 18 PBMC samples of n = 4 healthy donors44; and (iii) Hematopoiesis, an assembled dataset of hematopoietic cells from 49 samples of diverse data quality11, which was treated as a single sample in this study. To ensure a fair comparison and remove artifacts due to tiling, we trimmed the broad peaks by MACS2 or HOMER and removed the tail ends of peaks that extended onto tiles with no signal (“Methods” section). Three representative cell types with moderate to high cell counts were selected from each of the three datasets for the comparison, with cell count per sample ranging from 227 to 743 (COVID19X, median), 163 to 784 (HealthyDonor, median), and 1175 to 27463 (Hematopoiesis), respectively (Fig. 2a and Supplementary Fig. 6b).
Fig. 2. Benchmarking MOCHA with MACS2 and HOMER on open chromatin identification.
a Cell counts per sample in three cell types from each of three scATAC-seq datasets. The same three cell types in the three corresponding datasets (Methods) were used, including COVID19X (n = 39), HealthyDonor (n = 18, middle), and Hematopoiesis (treated as n = 1, right). b The number of open tiles per sample from MOCHA (light blue), MACS2 (green), or HOMER (light purple). The same colors are used in d–h. b, c The two-sided MWW was used to compare results by MOCHA vs MACS2 (P-value = 4.8e-5, 0.055, 3.6e-11, 0.12, 5.8e-4, 9.9e-4) and HOMER (P-value = 1.3e-4, 3.0e-2, 1.8e-9, 2.4e-2, 1.32e-4, 3.0e-3), listed left to right. c UpSet plot showing overlaps between open tiles from MOCHA, MACS2, or HOMER. For the COVID19X and HealthyDonor datasets, tiles common to >20% of samples were kept. For the Hematopoiesis dataset, all tiles were kept. Insert: Violin plot of signal (i.e., log2(normalized fragment count+1)) from tiles missed by MOCHA (i.e., those from MACS2 and/or HOMER but not MOCHA, left l) and from those unique to MOCHA (i.e., those identified only by MOCHA, right panel). All P-values = 2.2e-16 (Wilcoxon test). d–f The cumulative number of detected tiles (d), tiles overlapping with CCCTC-binding factor (CTCF) sites (e), or tiles overlapping with transcription starting sites (TSSs, f) as a function of the maximum fraction of samples without overlapping fragments in the COVID19X (left panel) or HealthyControl (right panel) datasets. g The number of detected CTCF sites (top panel) or TSSs (bottom panel) in the Hematopoiesis dataset. h, The actual (top panel) and the relative (with respect to MOCHA, bottom panel) runtime to identify open chromatin from single cell data as a function of the number of samples. The black horizontal line in the bottom panel marks the MOCHA runtime. CD16 Mono: CD16 monocytes; B Naive: naive B cells; CD4 CTL: CD4+ cytotoxic T lymphocytes; CD4 TEM: CD4+ effector memory T cells; CD8 TEM: CD8+ effector memory T cells; cDC: conventional dendritic cells; CD4 Naive: naive CD4+ T cells; CD14 Mono: CD14 monocytes. * = 0.01 < P < 0.05, ***P < 0.001. Source data is provided in “SourceData_Figure2-1.xlsx” and “SourceData_Figure2-2.zip”. Panels were generated using Adobe Illustrator.
To benchmark performance on sample-specific accessibility, we compared the number of open regions detected in individual samples (Fig. 2b). On COVID19X, MOCHA detected a median of 129k–195k open tiles per sample, which was 19–64% higher (significantly with P < 0.05 in 5/6 cases) than the corresponding numbers by MACS2 or HOMER. Similarly on HealthyDonor, MOCHA detected a median of 117k–216k open tiles per sample, a 35–59% increase (significantly with P < 0.05 in 5/6 cases) over the corresponding numbers by MACS2 or HOMER. On Hematopoiesis, MOCHA detected 370k open tiles in cDCs, 665k in naive CD4+ T cells, and 1.28 m in CD14 monocytes, which were <7% lower, >43% higher, and >70% higher, respectively, than the corresponding numbers by MACS2 or HOMER. Thus MOCHA detected more open chromatin regions than MACS2 and HOMER in individual samples for almost all cases. Additionally, we constructed 110 simulated scATAC-seq datasets by simulating 10 fixed peaksets as the ground truth for open and closed regions. For each peakset, we sampled 11 cellular abundances (ranging from 75 to 5000 cells) to mimic cell populations in a typical scATAC-seq sample. We applied MOCHA, HOMER, and MACS2 algorithms to identify open regions in the simulated data in the same way as to real data, without changing any parameters. Across 90% of the simulations, MOCHA had a higher F1 score, and thus more accurately detected open regions vs noise (Supplementary Fig. 8a). We also conducted simulations by varying the number of fragments per cell (1k–4.5k) and the total number of open regions (150k–350k, mimicking three different cell types). The results show that MOCHA attained the highest F-1 score in 210/240 iterations (87.5%, Supplementary Fig. 8b–d).
To assess the consistency between open tiles detected by the three tools, we generated TSAMs with a fraction threshold of 20% based on tiles detected by each tool and compared the corresponding tiles in TSAMs (Fig. 2c). Most tiles were detected by all three tools. As described above, MOCHA detected more tiles than MACS2 and HOMER in almost all cases. Among all tiles detected by MACS2 and/or HOMER, 95–97% were also detected by MOCHA in COVID19X, 92–93% in HealthyDonor, and 84–97% in Hematopoiesis. Tiles detected only by MOCHA contained on average more fragments than tiles missed by MOCHA (Fig. 2c, inserts; P < 0.001). Furthermore, when we ran linkage disequilibrium score analysis46, MOCHA identified 195 enriched annotations, MACS2 190, HOMER 192, with an overlap of 188 between all three methods (Supplementary Fig. 9). Thus MOCHA not only captured the majority of tiles detected by MACS2 and HOMER but also added extra tiles of better signals of potential biological significance than those by MACS2 or HOMER.
To further elucidate differences among tiles detected by the three tools, we calculated the percentage of zeros among all samples for each tile in each TSAM and obtained the corresponding cumulant distributions (Fig. 2d). While all three tools agreed on open tiles common to most samples, MOCHA detected more sample-specific tiles than MACS2 and HOMER. To test whether these additional tiles potentially contained biological information, we generated the corresponding cumulative distributions on tiles mapped to CTCF sites or TSSs and observed similar patterns (Fig. 2e, f). This suggests that the extra tiles detected by MOCHA may carry important biological information. MOCHA also detected similar or more open CTCF sites and open TSSs in Hematopoiesis compared to MACS2 and HOMER (Fig. 2g).
Calling peaks on pooled cells of interest is a common practice in scATAC-seq data analysis9–11. To compare MOCHA, MACS2 and HOMER on this approach, we pooled cells of the three cell types in the three datasets, randomly downsampled the cells to a series of predetermined cell counts, and applied the three tools to detect accessible tiles (Supplementary Fig. 4c). MOCHA consistently detected more tiles, more CTCF sites, and more TSSs than MACS2 and HOMER in almost all cases.
To demonstrate that MOCHA is applicable beyond immune cells and human data, we benchmarked all three methods on a multi-organ mouse scATAC atlas47 (Supplementary Fig. 5). We called open tiles on 20 randomly selected and representative organ-cell type populations ranging from tens to thousands of cells (Supplementary Fig. 5a, b) and compared the number of open tiles, CTCF sites, and TSS detected per each method (Supplementary Fig. 5c–e). MOCHA identified comparable numbers of open chromatin regions, CTCF sites, and TSSs.
Finally, we benchmarked the runtime for each tool on a cloud computing environment. MOCHA was consistently faster than HOMER in all tested cases and MACS2 in all practical cases for sample- and cell-type specific analyses (Fig. 2h). Of note, individual cell populations in scATAC-seq data range primarily between tens to thousands of cells, due to technological limitations. Additionally, we estimated run times by pooling cells across samples (Supplementary Fig 4d), and demonstrated that MOCHA provided fastest runtimes in almost all cases.
MOCHA implements zero-inflated differential accessibility and co-accessibility analyses
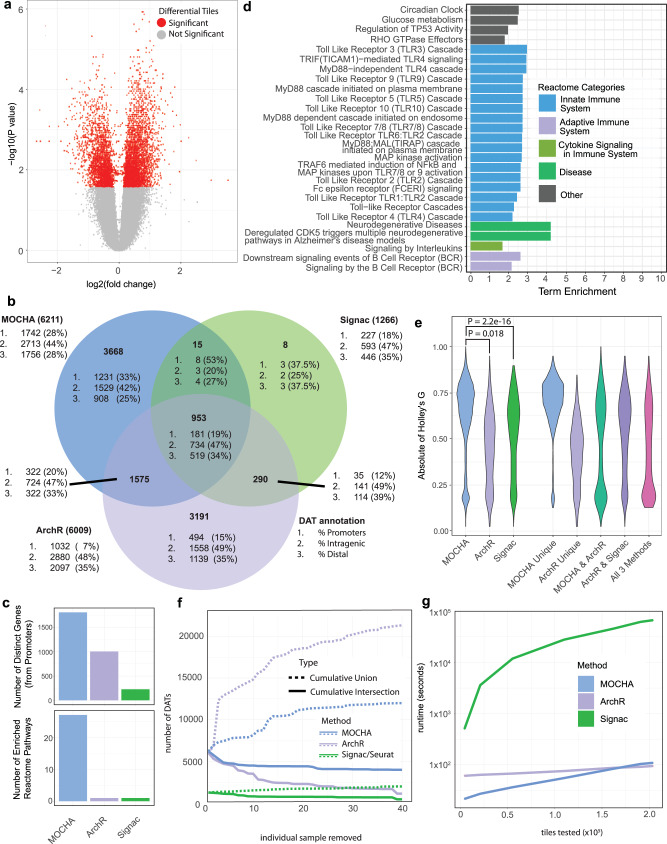
We evaluated MOCHA’s ZI modules against existing state-of-the-art tools for DAA and CAA. We first benchmarked MOCHA with ArchR and Signac on DAA. To eliminate differences in open-chromatin/peak-callling by the three tools and ensure a head-to-head comparison, we restricted the DAA benchmark to the 215,649 CD16 monocytes tiles identified by MOCHA in the COVID19X dataset (“Methods” section). We then applied each method to identify DATs between COVID+ (n = 17) and COVID- (n = 22) participants using these tiles. MOCHA identified 6211 DATs (false discovery rate (FDR) < 0.2, Fig. 3a, Supplementary Fig. 10a). In comparison, ArchR and Signac detected 6009 and 1266 DATs, respectively (Fig. 3b). While 28% of DATs by MOCHA were in gene promoter regions, the corresponding percentage was 17% for ArchR and 18% for Signac. As a result, MOCHA, ArchR, and Signac identified 1811, 1006, and 228 genes, respectively, with DATs in their promoter regions. These genes were enriched (FDR < 0.05) in 27, 1, and 1 Reactome pathways48 (Fig. 3c), respectively, illustrating a striking distinction by MOCHA. The same trend was also observed for other pathway databases (Supplementary Fig. 10b). Among the 27 Reactome pathways revealed by MOCHA (Fig. 3d), toll-like receptors (TLRs), myeloid differentiation primary response 88 (MyD88), interleukins, and nuclear factor kappa B (NF-κB) pathways all play important roles in innate immune response to viral infection49, consistent with the expected functions of CD16 monocytes. Thus DATs by MOCHA revealed more biological insights than those by ArchR or Signac.
Fig. 3. Benchmarking MOCHA with ArchR and Signac on differential accessibility analysis.
a MOCHA’s differential accessible tiles (DATs) in CD16 monocytes between COVID+ samples during early infection (n = 17) and COVID- samples (n = 22) in the COVID19X dataset. The volcano plot illustrates the log2(FC) on the x-axis against the -log10(P value) on the y-axis, where FC represents fold change in accessibility. The log2(FC) was estimated using the Hodges-Lehmann estimator110. The P value was calculated based on the two-part Wilcoxon test (two-sided, zero-inflated)35. DATs with a false discovery rate (FDR) < 0.2 were considered as significant. b Venn Diagram of MOCHA, Signac, and ArchR’s DATs. The count and percentage of 1) promoters, 2) intragenic tiles, and 3) distal tiles are shown for each method and each Venn diagram subset. c The number of (top) genes with differential promoters and (bottom) enriched Reactome pathways for each method are depicted using barplots. d Reactome Pathway enrichment results based on genes with differential promoter tiles. Pathway categories are annotated using Reactome’s pathway hierarchy. e Violin plot of Holley’s |G| from 1000 bootstrapped samples, each containing 50 randomly selected DATs from each category. Categories with <50 DATs were not tested. Two-sided Wilcoxon rank-sum test was used. f Leave-one-sample perturbation analysis to test the robustness of each method in differential accessibility analysis. New sets of DATs were calculated iteratively after removing each sample once. The robustness was assessed by the number of total (solid line) and conserved (dotted line) DATs detected across perturbations. g Each method’s runtime (in seconds) as a function of the number of tested tiles. Source data is provided in “SourceData_Figure3-S10.xlsx”. Panels were generated using Adobe Illustrator.
To quantify the DAT accuracy for each method, we evaluated its efficiency in separating COVID19+ and COVID19- samples. We randomly selected 50 DATs, performed k-means (k = 2) clustering to reflect the two-group comparison, calculated the absolute value of the G index (|G|) of agreement50, and repeated the process 1000 times. DATs by MOCHA better separate COVID19+ and COVID19- samples than those by ArchR (P < 0.001) or Signac (P < 0.001, Fig. 3e). Similar results were obtained for N = 25, 50, 75, and 100 randomly selected DATs (Supplementary Fig 12a). It should be noted that this analysis is aimed for benchmarking, not for routine biological analyses.
Biologically meaningful DATs should be robust against minor changes in the sample set. Following strategies applied in DESeq251, we assessed the stability of our DAT results across different sample subsets and benchmarked DAT differences as proxies for evaluating false positives and false negatives. Starting with DATs from the full sample set (n = 39), we iteratively removed one sample at a time and recalculated DATs from the reduced subset of samples (n = 38). We repeated this process until each sample was removed once. From there, we collected the set of conserved (e.g., cumulative intersection, proxy for evaluating false negatives) and inflated (e.g., cumulative additional, proxy for evaluating false positives) DATs across all iterations. Ultimately, 3990 (64%) of the 6211 DATs by MOCHA were conserved (Fig. 3f), which was 1.8–3.4 times higher than the corresponding rate of ArchR (1136/6009, 20%) or Signac (458/1264, 36%). MOCHA had 5782 (93%) additional DATs, which was 2.7 times lower than the corresponding rate by ArchR (15310/6009, 255%) and 1.6 times higher than that by Signac (735/1264, 58%). MOCHA was more robust than ArchR and had a split performance in comparison with Signac in detecting DATs regardless of sample set. However, MOCHA had 3990 conserved DATs, 8.7 times higher than those of Signac (458). MOCHA provided a better balance between sensitivity and robustness in detecting DATs compared to ArchR and Signac.
When benchmarking runtime, we observed that MOCHA and ArchR took 1.8 and 1.6 min, respectively, to evaluate approximately 200,000 tiles, while Signac took 18.6 h (Fig. 3g). MOCHA was 23–614x faster than Signac and 0.86–2.8x as fast as ArchR.
In addition, we benchmarked MOCHA against bulk differential methods from RNA-seq (DESeq2) and ChIP-seq (DiffChIPL). MOCHA performed significantly better at classification tests (p < 0.001, Supplementary Figs. 11 and 12), as well as in identifying enriched pathways. Additionally, we assessed false positive rates (FPRs) by shuffling the disease labels (Supplementary Fig 12b). MOCHA had a 0% FPR across all 50 random permutations. In comparison, the minimum, median, and maximum FPR for other methods were: DESeq2 (0%, 0%, 3%), DiffChipL (0%, .05%, 11.1%), Signac (0%, 0.43%, 13.5%), and ArchR (0.11%, 1.0%. 41.6%). We also assessed recalls by downsampling the number of subjects (Supplementary Fig 12c). Signac obtained higher recalls with its very conservative (thus very few) DAT calls, while the remaining 4 methods obtained similar recalls. We note that the recall evaluated in this approach was likely a lower bound due to disease/human heterogeneity and sample size reduction, a loss of > 20% of power when the sample size was reduced from n = 39 to n = 30 based on 2-sample t-test (Supplementary Fig 12d). Overall, MOCHA provided comparable performance on recall, and better performance on FPR than other methods.
Next, we compared the ZI and the standard Spearman correlations across cell types and samples in the COVID19X dataset based on log2(λ(1) + 1) in TSAMs. Guided by prior studies52,53, we leveraged published HiC interaction data to enrich for correlated regions, and used this to benchmark the two correlation methods using HiC (Methods). For the inter-cell type co-accessibility, we used known promoter-enhancer interactions in naive CD4+ and CD8+ T cells54 to define possibly interacting tile pairs (1.21 million) while randomly selecting 100k tile pairs as a negative background for comparison (Methods). Both correlation approaches largely generated similar results (Supplementary Fig. 13a, Spearman correlation = 0.687, P = 2.2 × 10−16), but disagreements were also observed (Supplementary Fig. 13b). The ZI correlation better distinguished promoter-enhancer pairs from the random pairs than the standard correlation (Kolmogorov–Smirnov (KS) test statistic = 0.26 vs. 0.13), and identified 1000x more promoter-enhancers pairs (15,988 vs. 149, FDR < 0.1, Supplementary Fig. 13c, d). For the inter-sample co-accessibility, we first collected a subset of tiles in the TSAM of CD16 monocytes that roughly located in the first million bp of chromosome 4 (chr4:121500-1130999) and then used both correlation approaches to calculate the inter-sample correlations between all pairs (about 34.5k) of these tiles. While both correlation approaches generally agreed with each other with a rank correlation of 0.69 (P < 0.001, Supplementary Fig. 13e), 9550/34,596 (28%) of the tested correlations switched sign between the two approaches and 2087/34,596 (6%) of them differed in value by >0.25 (Supplementary Fig. 13f). Thus properly accounting for ZI is essential for reliable CAA in sparse scATAC-seq data.
Networks of alternatively regulated genes in early SARS-CoV-2 infection
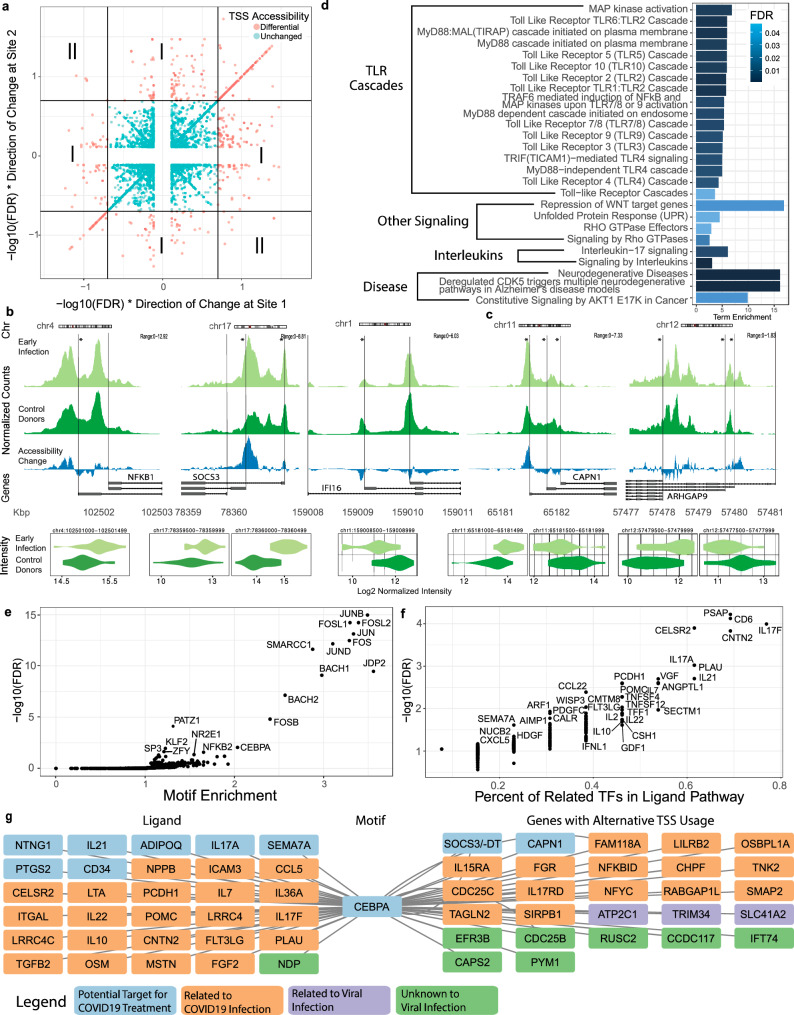
To demonstrate how improvements in MOCHA can be leveraged for constructing gene regulatory networks, we investigated possible alternative TSS regulation by CD16 monocytes during early SARS-CoV-2 infection (Methods), using the COVID19X dataset. We observed two types of alternatively regulated genes (ARGs, Fig. 4a). Type I (n = 278 genes, Fig. 4b) had at least one TSS showing differential accessibility (FDR < 0.2) between COVID19+ and COVID19- samples, while other open TSSs had no change. Type II included 5 genes with at least two differential TSSs in opposing directions (ATP1A1, UBAP2L, YWHAZ, CAPN1, and ARHGAP9; Fig. 4c). Interestingly, all Type II ARGs were previously associated with COVID-19 and two (ATP1A1 and CAPN1) have been proposed as therapeutic targets for COVID-19 (Supplementary Table 2). Pathway enrichment analysis55 on all Type I and Type II ARGs revealed that they were enriched in pathways of the innate immune response to infection, including MyD88 and TLR responses (Fig. 4d). The same analysis based on DATs from Signac and ArchR identified a total of 483 and 45 ARGS (type I and type II), respectively (Supplementary Fig. 14). However, neither of these gene sets were enriched for any immune pathways, suggesting their limited utility in such analyses.
Fig. 4. Regulatory network construction on alternative transcription starting sites in CD16 monocytes during early COVID-19 infection.
a Scatter plot of differential accessibility at potential alternative transcription starting sites (TSSs). False discovery rate (FDR) and fold change (FC) were evaluated on chromatin accessibility in CD16 monocytes between COVID+ samples during early infection (n = 17) and COVID- samples (n = 22) in the COVID19X dataset. All pairwise combinations of -log10(FDR)*sign(log2(FC)) are shown. TSS pairs were categorized as type I if only one TSS was significantly differential (FDR < 0.2), or type II if both were significantly differential but in the opposite directions. Pairs of TSSs that were significantly differential in the same direction were not considered. b, c Coverage tracks illustrating type I (b) or type II (c) alternative TSS regulation around exemplar genes (* denotes a significant differential accessibility tile (DAT), FDR < 0.2). Precise FDR values are in the source data file. d Reactome pathway enrichment for genes with alternatively regulated TSSs (both type I and II). Pathway annotation was based on Reactome’s hierarchical database. e Motif enrichment using DATs involved in alternatively regulated TSSs and their co-accessible tiles (within ±1 M bp, zero-inflated correlation >0.5). f NicheNet-based ligand-motif set enrichment analysis (LMSEA) on motifs with FDR < 0.01. g A network centered around CEBPA that was constructed using significant ligands, motifs, and genes with alternatively regulated TSS sites. Ligand-motif links represent NicheNet-based associations. Motif-gene links represent motif presence in either an alternative TSS tile, or tiles correlated to an alternative TSS. TF transcription factor; Source data is provided in “SourceData_Figure4.xlsx”. Panels were generated using Adobe Illustrator.
To understand the upstream signaling mechanisms regulating ARGs, we first applied MOCHA to identify potential, distal regulatory tiles that were co-accessible (inter-sample, within 1 Mbp) with the corresponding DATs. Motif enrichment analysis on DATs of ARGs and their co-accessible tiles identified 13 enriched motifs, including activator protein-1 (AP-1) family motifs, PATZ1, and CEBPA (FDR < 0.05, Fig. 4e). Next, we carried out ligand-motif set enrichment analysis (LMSEA, Methods) based on a priori ligand-motif (transcription factor (TF)) interactions in NicheNet56. We identified 122 significantly enriched ligands (FDR < 0.05, Fig. 4f), many of which, including IL17, IL21 and PLAU, have already been implicated in COVID-19 (Source Data Fig. 4g). Finally, we constructed a network that linked ligands, TFs, and ARGs together (Methods). Notably, the subnetwork of CEBPA is particularly interesting (Fig. 4g): CEBPA was proposed as a COVID-19 therapeutic target57 and identified as a key regulator in CD14 monocytes of hospitalized COVID-19 patients from scATAC-seq data6. Furthermore, 29/30 of its upstream ligands were either therapeutic targets or altered during SARS-CoV-2 infection, and 20/27 of its downstream ARGs were associated to COVID-19 or viral infection57–64. Two ARGs, SOCS3/SOCS3-DT and CAPN1, were potential targets for COVID-19 treatment65. Using MOCHA’s differential accessibility and co-accessibility modules, we constructed a putative upstream regulatory network that could be driving alternative TSS regulation in CD16 monocytes during early SARS-CoV-2 infection. Given that these results are largely aligned with the literature, we anticipate that this approach can be used more generally to identify potentially novel biological mechanisms.
Longitudinal analysis of chromatin accessibility during COVID-19 recovery
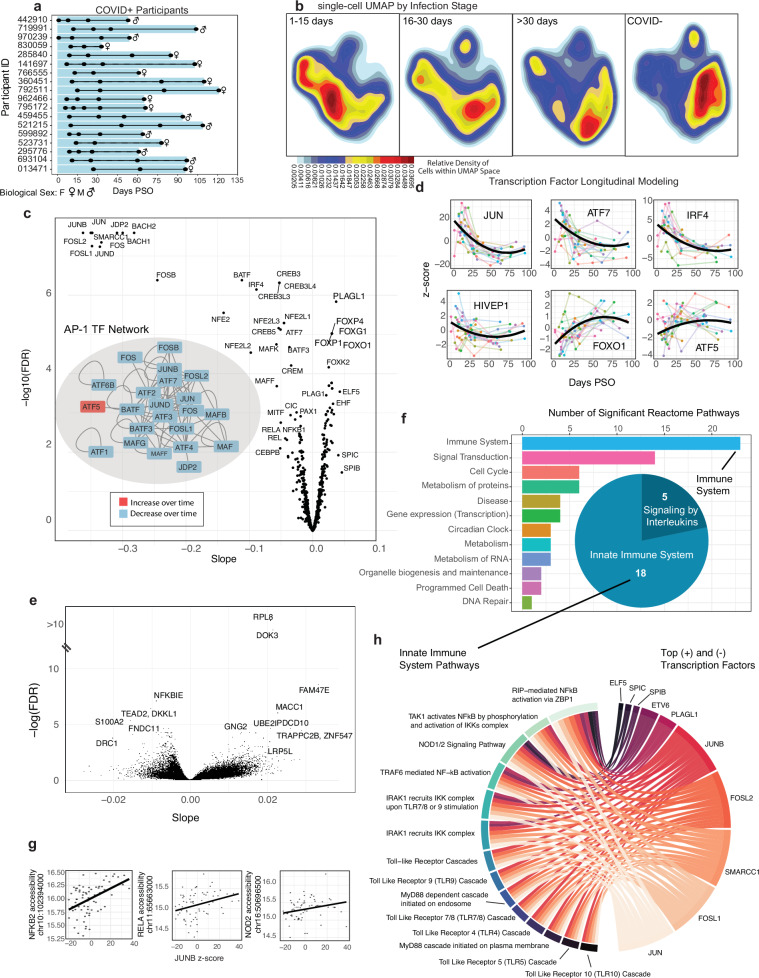
To understand chromatin regulation during COVID-19 recovery, we analyzed scATAC-seq data of CD16 monocytes from our longitudinal COVID-19 study (Fig. 5a). The dataset, denoted as COVID19L, was collected on 69 longitudinal PBMC samples from 18 COVID+ participants (10 females and 8 males) over a period of 1–121 days PSO (Methods). We integrated MOCHA with existing tools and developed customized approaches to analyze the data at both single-cell and pseudo-bulk levels.
Fig. 5. Integrative analyses to reveal longitudinal dynamics in CD16 monocytes during COVID-19 recovery.
a Longitudinal COVID19 cohort overview (n = 18). Time points indicated by black dots illustrate sample availability for each COVID+ participant. b Single-cell Density UMAPs using open regions in CD16 monocytes from MOCHA (full COVID19 dataset, n = 91 samples), showing cells from COVID+ samples during early infection (1–15 days PSO, n = 21), late infection (16–30 days PSO, n = 13), and recovery (>30 days PSO, n = 35), and COVID- samples (n = 22). c Volcano plot illustrating the −log10(FDR) vs. the slope of motif usage over time. Motif usage quantified using Z-scores from ChromVAR run on the TSAM. Insert: The network showing interacting TFs within the AP-1 family (APID database118). TFs were color-coded by the sign of their slope. d Longitudinal motif usage over time for an exemplary set of TFs. Individual participants and population trends are shown with thin lines (colored-coded by subject), and thick black lines (population trend). e Volcano plot illustrating the −log10(FDR) vs. the slope of promoter accessibility over time based on (ZI-GLMM). A subset of the top promoters are labeled with their corresponding genes. f Significant Reactome pathways (FDR < 0.1) enriched for genes with significant promoter accessibility changes. The pathways were aggregated into upper-level pathway annotations using Reactome’s database hierarchy. The barplot shows the number of pathways in each category. The pie chart breaks down the immune system pathways by Reactome’s next level categories. g Three scatter plots illustrating examples of associations between promoter accessibility (y-axis) and JUNB’s ChromVar z-score (x-axis). The thick black line shows the population trend from ZI-GLMM. h Bipartite network illustrating associations between the top 5 motifs (largest positive (+) or negative (−) slope) and 14 significant innate immune pathways. Motif-promoter associations only shown if Motif is related to >33% of significant genes in a pathway. c–h Data from CD16 monocytes in the COVID19L dataset (n = 69). PSO post symptom onset, UMAP Uniform Manifold Approximation and Projection, TSAM tile-sample accessibility matrix, FDR false discovery rate, TF transcription factor, AP-1 activator protein-1, ZI-GLMM zero-inflated generalized linear mixed model. Source data is provided in “SourceData_Figure5.xlsx”, including precise FDR values. Panels were generated using Adobe Illustrator.
First, open tiles from the TSAM of CD16 monocytes were imported into ArchR as a peakset for dimensionality reduction. The resulting Uniform Manifold Approximation and Projection66 (UMAP) plot showed a clear shift in cellular population from initial infection to 30+ days post infection, at which time the cellular population appeared similar but not identical to that of the 22 COVID- participants (Fig. 5b).
Second, days PSO were binned (Fig. 5b) and used to learn a Monocle367 trajectory, which largely followed the cellular population shift across the UMAP space (Supplementary Fig. 15a). Using ArchR, we further identified genes with GeneScore changes or tiles from the TSAM with accessibility shifts along this trajectory (Supplementary Fig. 15b). The genes with promoter accessibility shifts in CD16 monocytes were enriched in 72 immune system pathways, including 39 innate immune, 15 adaptive immune, and 18 cytokine signaling pathways (Supplementary Fig. 15c, right panel). In comparison, the corresponding pathway counts from the GeneScore analysis was only 10, 2, 4, and 4, respectively (Supplementary Fig. 15c, left panel). TSAM-based results were more informative and aligned better with the expected roles of CD16 monocytes than GeneScore-based ones.
Third, we converted the TSAM of CD16 monocytes into a chromVAR object and calculated sample-specific z-scores for TF activity (Methods). This enabled us to apply generalized linear mixed models (GLMM) to identify TFs with dynamic activities in CD16 monocytes during COVID-19 recovery, adjusting for age and sex in the models. Among the 223 TFs whose activity changed significantly in time (FDR < 0.1, Fig. 5c, d), the AP-1 family (such as ATF1-7, JUN/B/D, MAF/F/G/K, FOS/B, and BACH1-2; Fig. 5c, insert) and the NF-κB family (such as REL/A and NFKB1-2) mostly had decreased activities, in consistency with their inflammatory, infection-responsive functions. On the contrary, the forkhead box (FOX) TF family (such as FOXP1/4, FOXG1, FOXO1, and FOXK2) had increased activities, which agrees with their known roles in immune homeostasis68–70. In comparison, we also identified 86 TFs with chromVAR z-score changes along the pseudotime trajectory described above, among which only 31 were unique (Supplementary Fig. 16). Longitudinal analysis based on real time identified more TFs with dynamic activities during COVID-19 recovery than the trajectory analysis based on pseudotime.
Fourth, the TSAM of CD16 monocytes was used to examine how gene promoter accessibility shifted during COVID-19 recovery. The data had about 20% zeros, which can be associated with either technical dropouts or biological features. We applied ZI-GLMM to model both types of zeroes (Methods, Supplementary Fig. 18). Given that only 0.193% of highly accessible tiles (which are defined as having at least 80% non-zero values within any infection stage and include most promoters) had variance predominately explained by batch, we did not include batch as a covariate (Methods, Source Data File: Variance Decomposition). A total of 2,120 genes demonstrated promoter accessibility shifts over time (FDR < 0.1, adjusting for age and sex), including genes regulating immune inflammation such as NFKBIE and DOK3 (Fig. 5e and Supplementary Fig. 17a)71–73. This gene set was enriched for 71 Reactome pathways (FDR < 0.1; Fig. 5f). Interestingly, among the 23 immune system pathways, five involve signaling by interleukins and 18 are related to the innate immune system (such as TLR-, MyD88-, and IRAK1-related pathways), but none are specific to the adaptive immune system. Again, these results are consistent with the expected roles of CD16 monocytes during viral infection.
Finally, to discover possible TF-gene regulations in CD16 monocytes during COVID-19 recovery, we applied ZI-GLMM to examine whether TFs with significant activity changes were associated with genes with significant promoter accessibility changes (Methods). For example, we found that JUNB chromVAR z-score was significantly associated (P < 0.05) with the promoter accessibility of 19 genes in the TLR4 cascade pathway (Fig. 5g and Supplementary Fig. 17b). As an illustration, we selected the top five TFs having the largest positive (PLAGL1, ELF5, ETV6, SPIB, and SPIC) or negative (JUN, FOSL1, SMARRC1, FOSL2 and JUNB) slopes, respectively, against time and examined their associations with gene promoters within the 18 innate immune pathways enriched during COVID-19 recovery (Fig. 5f). Nine of the 10 TFs had high to medium expression in CD16 monocytes while the exception SPIB had a very low expression in CD16 monocytes but high expression in their progeny, macrophages, based on published datasets74–77. The five TFs having negative slopes were significantly associated (P < 0.05) with 14 pathways (Fig. 5h), consistent with the prominent roles of AP-1 TF family in innate immunity. Among the five TFs with positive slopes, PLAGL1 and ETV6 were significantly associated (p < 0.05) with five innate immune pathways, SPIB and SPIC with 2, and ELF1 with 1, respectively. Four innate immune pathways did not show significant associations with any of these top 10 TFs. While wet-lab validation is needed, such TF-gene associations generate interesting biological hypotheses regarding gene expression regulation in CD16 monocytes during COVID-19 recovery and can be expanded to include enhancers and additional regulatory elements. To the best of our knowledge, ZI mixed modeling is currently not possible in other existing scATAC-seq data analysis packages. Together, these results demonstrate MOCHA is a valuable tool in studying chromatin dynamics and gene regulatory networks based on longitudinal scATAC-seq data.
Discussion
We developed MOCHA to robustly infer active gene regulatory programs in human disease cohorts based on scATAC-seq. First, we showed that our open chromatin model significantly agreed and was able to detect more sample-specific open chromatin regions than MACS2 and HOMER. Second, we identified differential accessible regions that better distinguish between COVID+ and COVID- participants than those by ArchR and/or Signac and uniquely revealed pathways affected by SARS-CoV-2 infection. Third, we constructed ligand-TF-gene networks on potential alternative TSS regulations during SARS-CoV-2 infection using only scATAC-seq data. Fourth, using ZI mixed models, we identified motifs and promoters that were associated with COVID-19 recovery and constructed a TF-pathway network to infer which pathways were functionally important during COVID-19 recovery. MOCHA substantially increased the value of scATAC-seq in our distinct disease cohorts (including COVID19) by enabling robust modeling and visibility into the functional implications of chromatin accessibility. In addition, we illustrated how MOCHA can be integrated with existing tools such as ArchR, Monocle3, chromVAR, and NicheNet while enabling customized analysis using ZI-mixed effects models to gain unique insights from scATAC-seq data. Furthermore, we demonstrated that MOCHA can also be applied to data from a range of human and mouse tissues. The LRMs of MOCHA can be retrained if a different tile size (other than 500 bp) is preferred or when data is collected on non-diploid cells. Vignettes for analyzing patterns of dropout across cell types are also provided. Given its capabilities, we believe MOCHA is a valuable addition for analyzing scATAC-seq data, especially in biomedical research.
Constructing robust regulatory networks begins with reliable identification of patient- and cell-type-specific open chromatin. We used peaks called by MACS2 on pseudo-bulk ATAC-seq data as imperfect “ground truth” to train and validate MOCHA, and constructed LRMs to identify sample-specific accessibility using statistically informative single-cell and pseudobulk features, resulting in λ(1) and λ(2). While other features were tested, they were not statistically informative. The training data of NK cells (n = 179,836, 750 million fragments) had enough sequencing depth for reliable MACS2 performance and thus likely reliable MOCHA training. However, MACS2 might call every fragment as a peak for less abundant cell types, leading to many false positives. To mitigate such artifacts, some pipelines artificially limit the number of peaks called by MACS211. To provide a reasonable comparison, we focused our benchmarking on cell types with moderate to high cell counts. MOCHA outperformed MACS2 in calling sample-specific regions despite relying on MACS2 for training. In theory, MOCHA was not designed to call open tiles on datasets of mixed cells from multiple studies. For example, we used a global prefactor to account for differences in data quality instead of, more properly, estimating an for each of the many studies within the Hematopoiesis dataset. Nevertheless, MOCHA outperformed MACS2 and HOMER on all three datasets of varying data quality, although only slightly on the Hematopoiesis dataset. In simulation studies, we benchmarked the three methods across a broader set of conditions (cell abundance, sequencing depth, and total open regions). MOCHA outperformed MACS2 and HOMER in about 90% of all conditions. It is possible that the LRMs in MOCHA may need to be retrained if the difference in species, sample type, experimental protocol, sequencing depth, data quality, etc., becomes overwhelmingly large between our training data and user data. Due to a lack of access to GPU hardware78 and integration challenges13, we benchmarked MOCHA only with MACS2 and HOMER, which are the most widely incorporated open source peak callers. Given its strong performance against these standard algorithms, MOCHA’s robust open chromatin results provided a solid foundation for downstream analysis. We note that some biological questions (e.g., copy number variation79, causal variants80, nucleosome positioning81, and the role of pioneer factors82) may not be best answered with tools such as MOCHA calling broad peaks.
Additionally, gene regulatory networks require clear identification of accessibility changes. However, the presence of drop-out leads to many unreliable results. We notice that there has been a debate on whether scRNA-seq data is ZI27. That discussion centers around measurement vs expression models27. scATAC-seq data is even sparser than scRNA-seq data with a near binary (0 or 1) measurement of accessibility1, and a detection rate of 1– 10% on expected accessible peaks at the single-cell level (compared to 10–45% of expressed genes being detected per cell in scRNA-seq)8. The incorporation of ZI statistical methods to handle drop out is a major advantage of MOCHA over most existing tools. ZI methods provide well-documented improvements over their counterparts on ZI data83,84. While ZI methods are applied to scRNA-seq data exclusively at single-cell level, the sparsity of scATAC-seq data makes it necessary to apply ZI methods even at pseudo-bulk level in most analyses. Our analyses showed that excess zeros in pseudobulk scATAC-seq data were not fully captured by negative binomial distributions, motivating the use of ZI statistics. We applied the two-part Wilcoxon model34 for DAA, ZI correlation36 for CAA, and ZI-GLMM33 for longitudinal modeling in MOCHA and demonstrated how MOCHA led to more informative results than existing tools. While ZI-GLMM approaches model biological zeroes and technical drop-outs separately, more research is needed to fully disentangle them. No ZI method is needed for open chromatin identification since only tiles that contain fragments are evaluated and we don’t impute accessibility for empty tiles. It is noted that, while many bulk ATAC-seq or bulk RNA-seq approaches (e.g., DiffChIPL, DESeq2, EdgeR, Limma, and more)51,85–91 also utilize generalized linear models; they do not account for ZI. Recent literature has been moving towards analyzing scATAC-seq data implementing ZI approaches92–95.
While single-cell analysis provides granularity into cellular behavior, human cohort studies are usually interested in identifying patient-level behavior across cell populations. While current methods are centered at the single cell level, MOCHA aggregates scATAC-seq data into TSAMs to facilitate sample-centric analysis. To the best of our knowledge, while pseudo bulking is fairly common in analyzing scRNA-seq data and inspired our use of it in MOCHA, this rather simple approach has not been reported to analyze scATAC-seq data. The approach provides several important advantages. First, as literature in the scRNA-seq spaces has shown, the approach specifically addresses pseudo-replication bias in single-cell data and avoids computationally expensive single-cell mixed effect models, following recent advice for analyzing scRNA-seq data29,30. Second, the sample-centric approach makes it computationally feasible to analyze large, diverse human cohorts and explicitly models patient-level heterogeneity. Third, since the TSAM is constructed from standard Bioconductor data structures, its flexibility enables a broad range of scientific enquiries into gene and chromatin regulation and supports seamless integration with a variety of bioinformatics tools. For example, we applied ZI-GLMM and chromVAR to study COVID-19 recovery on our longitudinal scATAC-seq data. We believe TSAMs facilitate the extraction of genomic insights from large-scale, heterogeneous scATAC-seq data. Nevertheless, the approach is underpowered for studies of small sample size and not appropriate for comparing a handful of samples. We plan to adapt MOCHA for small-scale studies in the future.
We selected CD16 monocytes in our COVID19 dataset to showcase the utility of MOCHA in biomedical research. Our results reveal from multiple perspectives that the genomic regions associated with innate immune pathways (such as TLR, MyD88, and NF-κB) played essential roles in SARS-CoV-2 infection and patient recovery, aligning with the expected functions of CD16 monocytes during viral infection96. To the best of our knowledge, explicit longitudinal analysis on scATAC-seq data has not been reported, limiting the value of scATAC-seq in studying the regulatory landscapes of disease progression and recovery. Furthermore, despite the large number of publications on COVID-19, alternative TSS regulation during SARS-CoV-2 infection has not been reported. We consider MOCHA as a tool to generate interesting hypotheses from scATAC-seq data, which nevertheless need to be validated in follow-up studies. An in-depth, comprehensive analysis of our COVID19 cohort is beyond the scope of current work and will be presented in a follow-up paper.
In short, we present MOCHA as a tool to better infer gene regulation from scATAC-seq in biomedical and biological research. MOCHA is freely available as an R package in CRAN.
Methods
Inclusion and ethical considerations
All study activities were approved by institutional review boards at the participating institutions where required. Informed consent was obtained from all participants at the Seattle Vaccine Trials Unit to participate in the study and to publish their corresponding research data. Two participants declined to publish their raw sequencing data. All human data are anonymized, and the human cohort data used in this manuscript had either prior IRB approval or were publicly available.
Longitudinal COVID-19 cohort
We recruited in the greater Seattle area n = 18 participants (10 females and 8 males, aged 22–79 years) who tested positive (COVID+) for SARS-CoV-2 virus (Wuhan strain) and n = 23 uninfected (COVID-) participants (10 females and 13 males, aged 29–77 years) for our longitudinal COVID-19 study38, “Seattle COVID-19 Cohort Study to Evaluate Immune Responses in Persons at Risk and with SARS-CoV-2 Infection”. Due to recruitment during the pandemic, there is a bias towards first responders. All COVID+ participants had mild to moderate symptoms. Peripheral blood mononuclear cell (PBMC) and serum samples were collected from the COVID- participants at a single time point and from the COVID+ participants at 3–5 time points over a period of 1–121 days post-symptom-onset (PSO, total samples n = 70). Study data were collected and managed using REDCap electronic data capture tools hosted at Fred Hutchinson Cancer Research Center (FHCRC). The FHCRC Institutional Review Board (IRB) approved the studies and procedures. Informed consent was obtained from all participants at the Seattle Vaccine Trials Unit to participate in the study and to publish their corresponding research data. Two participants declined to publish their raw sequencing data. Sex of participants was determined based on self-reporting. Participants were not compensated for being in this study.
COVID19 single-cell ATAC-seq
PBMC isolation
Blood collected in acid citrate dextrose tubes was transferred to Leucosep tubes (Greiner Bio One). The tube was centrifuged at 800–1000x g for 15 min and the PBMC layer recovered above the frit. PBMCs were washed twice with Hanks Balanced Solution without Ca+ or Mg+ (Gibco) at 200–400 × g for 10 min, counted, and aliquoted in heat-inactivated fetal bovine serum with 10% dimethylsulfoxide (DMSO, Sigma) for cryopreservation. PBMCs were cryopreserved at −80 °C in Stratacooler (Nalgene) and transferred to liquid nitrogen for long-term storage.
FACS neutrophil depletion
To remove dead cells, debris, and neutrophils prior to scATAC-seq, PBMC samples were sorted by fluorescence-activated cell sorting (FACS) prior to cell permeabilization as described previously97. Cells were incubated with Fixable Viability Stain 510 (BD, 564406) for 15 min at room temperature and washed with AIM V medium (Gibco, 12055091) plus 25 mM HEPES before incubating with TruStain FcX (BioLegend, 422302) for 5 min on ice, followed by staining with mouse anti-human CD45 FITC (BioLegend, 304038, 1.0 uL/10e6 cells) and mouse anti-human CD15 PE (BD, 562371, 1.0 uL/10e6 cells) antibodies for 20 min on ice. Cells were washed with AIM V medium plus 25 mM HEPES and sorted on a BD FACSAria Fusion. A standard viable CD45+ cell gating scheme was employed: FSC-A x SSC-A (to exclude sub-cellular debris), two FSC-A doublet exclusion gates (FSC-W followed by FSC-H), dead cell exclusion gate (BV510 LIVE/DEAD negative), followed by CD45+ inclusion gate. Neutrophils (defined as SSC high, CD15+) were then excluded in the final sort gate. An aliquot of each post-sort population was used to collect 50,000 events to assess post-sort purity.
Sample preparation
Permeabilized-cell scATAC-seq was performed as described previously97. A 5% w/v digitonin stock was prepared by diluting powdered digitonin (MP Biomedicals, 0215948082) in DMSO (Fisher Scientific, D12345), which was stored in 20 μL aliquots at −20 °C until use. To permeabilize, 1 × 106 cells were added to a 1.5 mL low binding tube (Eppendorf, 022431021) and centrifuged (400 × g for 5 min at 4 °C) using a swinging bucket rotor (Beckman Coulter Avanti J-15RIVD with JS4.750 swinging bucket, B99516). Cells were resuspended in 100 μL cold isotonic Permeabilization Buffer (20 mM Tris-HCl pH 7.4, 150 mM NaCl, 3 mM MgCl2, 0.01% digitonin) by pipette-mixing 10 times, then incubated on ice for 5 min, after which they were diluted with 1 mL of isotonic Wash Buffer (20 mM Tris-HCl pH 7.4, 150 mM NaCl, 3 mM MgCl2) by pipette-mixing five times. Cells were centrifuged (400 × g for 5 min at 4 °C) using a swinging bucket rotor, and the supernatant was slowly removed using a vacuum aspirator pipette. Cells were resuspended in chilled TD1 buffer (Illumina, 15027866) by pipette-mixing to a target concentration of 2300–10,000 cells per μL. Cells were filtered through 35 μm Falcon Cell Strainers (Corning, 352235) before counting on a Cellometer Spectrum Cell Counter (Nexcelom) using ViaStain acridine orange/propidium iodide solution (Nexcelom, C52-0106-5).
Tagmentation and fragment capture
scATAC-seq libraries were prepared according to the Chromium Single Cell ATAC v1.1 Reagent Kits User Guide (CG000209 Rev B) with several modifications. 15,000 cells were loaded into each tagmentation reaction. Permeabilized cells were brought to a volume of 9 μl in TD1 buffer (Illumina, 15027866) and mixed with 6 μl of Illumina TDE1 Tn5 transposase (Illumina, 15027916). Transposition was performed by incubating the prepared reactions on a C1000 Touch thermal cycler with 96– Deep Well Reaction Module (Bio-Rad, 1851197) at 37 °C for 60 min, followed by a brief hold at 4 °C. A Chromium NextGEM Chip H (10x Genomics, 2000180) was placed in a Chromium Next GEM Secondary Holder (10x Genomics, 3000332) and 50% Glycerol (Teknova, G1798) was dispensed into all unused wells. A master mix composed of Barcoding Reagent B (10x Genomics, 2000194), Reducing Agent B (10x Genomics, 2000087), and Barcoding Enzyme (10x Genomics, 2000125) was then added to each sample well, pipette-mixed, and loaded into row 1 of the chip. Chromium Single Cell ATAC Gel Beads v1.1 (10x Genomics, 2000210) were vortexed for 30 s and loaded into row 2 of the chip, along with Partitioning Oil (10x Genomics, 2000190) in row 3. A 10x Gasket (10x Genomics, 370017) was placed over the chip and attached to the Secondary Holder. The chip was loaded into a Chromium Single Cell Controller instrument (10x Genomics, 120270) for GEM generation. At the completion of the run, GEMs were collected and linear amplification was performed on a C1000 Touch thermal cycler with 96–Deep Well Reaction Module: 72 °C for 5 min, 98 °C for 30 s, 12 cycles of 98 °C for 10 s, 59 °C for 30 s and 72 °C for 1 min.
Sequencing library preparation
GEMs were separated into a biphasic mixture through addition of Recovery Agent (10x Genomics, 220016); the aqueous phase was retained and removed of barcoding reagents using Dynabead MyOne SILANE (10x Genomics, 2000048) and SPRIselect reagent (Beckman Coulter, B23318) bead clean-ups. Sequencing libraries were constructed by amplifying the barcoded ATAC fragments in a sample indexing PCR consisting of SI-PCR Primer B (10x Genomics, 2000128), Amp Mix (10x Genomics, 2000047), and Chromium i7 Sample Index Plate N, Set A (10x Genomics, 3000262) as described in the 10x scATAC User Guide. Amplification was performed in a C1000 Touch thermal cycler with 96–Deep Well Reaction Module: 98 °C for 45 s, for 9 to 11 cycles of: 98 °C for 20 s, 67 °C for 30 s, 72 °C for 20 s, with a final extension of 72 °C for 1 min. Final libraries were prepared using a dual-sided SPRIselect size-selection cleanup. SPRIselect beads were mixed with completed PCR reactions at a ratio of 0.4x bead:sample and incubated at room temperature to bind large DNA fragments. Reactions were incubated on a magnet, and the supernatant was then transferred and mixed with additional SPRIselect reagent to a final ratio of 1.2x bead:sample (ratio includes first SPRI addition) and incubated at room temperature to bind ATAC fragments. Reactions were incubated on a magnet, the supernatant containing unbound PCR primers and reagents was discarded, and DNA-bound SPRI beads were washed twice with 80% v/v ethanol. SPRI beads were resuspended in Buffer EB (Qiagen, 1014609), incubated on a magnet, and the supernatant was transferred resulting in final, sequencing-ready libraries.
Quantification and sequencing
Final libraries were quantified using a Quant-iT PicoGreen dsDNA Assay Kit (Thermo Fisher Scientific, P7589) on a SpectraMax iD3 (Molecular Devices). Library quality and average fragment size were assessed using a Bioanalyzer (Agilent, G2939A) High Sensitivity DNA chip (Agilent, 5067-4626). Libraries were sequenced on the Illumina NovaSeq platform with the following read lengths: 51nt read 1, 8nt i7 index, 16nt i5 index, 51nt read 2.
Data preprocessing
scATAC-seq libraries were processed as described previously97. In brief, cellranger-atac mkfastq (10x Genomics v1.1.0) was used to demultiplex BCL files to FASTQ. FASTQ files were aligned to the human genome (10x Genomics refdata-cellranger-atac-GRCh38-1.1.0) using cellranger-atac count (10x Genomics v1.1.0) with default settings. Fragment positions were used to quantify reads overlapping a reference peak set (GSE123577_pbmc_peaks.bed.gz from GEO accession GSE12357798), which was converted from hg19 to hg38 using the liftOver package for R99, ENCODE reference accessible regions (ENCODE file ID ENCFF503GCK100), and TSS regions (TSS ± 2 kb from Ensembl v93101 for each cell barcode using a bedtools (v2.29.1102) analytical pipeline.
Quality control
Custom R scripts were used to remove cells with less than 1,000 uniquely aligned fragments, less than 20% of fragments overlapping reference peak regions, less than 20% of fragments overlapping ENCODE TSS regions, and less than 50% of peaks overlapping ENCODE reference regions. The ArchR package11 was used to assess doublets in scATAC data. Doublets were identified using the ScoreDoublets function using a filter ratio of 8, and cells with a Doublet Enrichment score exceeding 1.3 as determined by ArchR’s doublet detection algorithm11 were not considered for downstream analysis.
Dimensionality reduction and cell type labeling
We used the ArchR package to generate a count matrix for a PBMC reference peak set98. Dimensionality reduction was performed using the ArchR addIterativeLSI function (parameters varFeatures = 10,000, iterations = 2), and the addClusters function was used to identify clusters in latent semantic indexing (LSI) dimensions using the Louvain community detection algorithm. For visualization, Uniform Manifold Approximation and Projection66 (UMAP) was performed using ArchR’s addUMAP function at the default settings. The ArchR addGeneIntegrationMatrix function (parameters transferParams = list(dims = 1:10, k.weight = 20)) was used to label scATAC cells using the Seurat level 1 cell types from the Seurat v4.0 PBMC reference dataset103. To generate clusters that more closely matched label transfer results, we performed K-means clustering on the UMAP coordinates using 3 to 50 cluster centers and identified a set of clusters that each had > 80% of cells sharing a single cell type identity. Almost all such clusters contained ≥98% cells from a single major cell type (T cells, B cells, NK cells, or monocytes/DCs/other), with the exception of a single cluster with 88% purity. We used clusters of the same major cell type to subset the data into T cells, B cells, NK cells, or monocytes/DCs/other for downstream analyses. For each major cell type, we repeated the same dimensionality reduction (LSI/UMAP) process on the scATAC-seq data with the same settings. We then performed a second round of label transfer, using the ArchR addGeneIntegrationMatrix function (same parameters as described above for level 1), to reach level 2 and 3 cell labelings of the Seurat PBMC reference dataset. These labels were consolidated into 25 cell types for most analysis, except for the co-accessibility analysis where 17 cell types were used to match the published promoter-capture HiC resource54. The median cell labeling score across all cells that passed quality control was 0.74.
Three Human scATAC-seq datasets for MOCHA development and benchmarking
COVID19 dataset
Two samples (1 COVID- sample, male; 1 COVID+ sample, female, collected on day 12 PSO) from our longitudinal COVID-19 cohort were lost due to low sample volume. The scATAC-seq data of the remaining samples was denoted as the COVID19 dataset (n = 91) in this study. After removing doublets and cells of poor quality, high quality data of 1,311,638 cells were obtained. The data was split into two overlapping subsets for some analyses: 1) A cross-sectional dataset (denoted as COVID19X, n = 39) included data of COVID- samples (n = 22, 10 females and 12 males) and the first samples of COVID+ participants (n = 17, 9 females and 8 males) during early infection (<16 days PSO). 2) A longitudinal dataset (denoted as COVID19L, n = 69) included all data for the 18 COVID+ participants (10 females and 8 males). The overlap between COVID19X and COVID19L was 17, which were the first samples of COVID+ participants. The full dataset (COVID19) can be accessed at GEO under accession number GSE173590.
HealthyDonor dataset
This longitudinal scATAC-seq dataset44 was collected on 18 PBMC samples of 4 healthy donors (aged 29–39 years) over 6 weeks (1 female and 1 male, weeks 2–7; 2 males, weeks 2, 4, and 7). The donors had no diagnosis of active or chronic disease during the study. The data is publicly available at GEO under accession number GSE190992. We used the dataset as is, except we removed cells with doublet enrichment score exceeding 1.3, based on ArchR’s doublet detection algorithm11. High quality data of 145,711 cells were obtained. From this dataset, we consolidated existing annotations into 25 cell types with a published median cell labeling score of 0.78.
Hematopoiesis dataset
This dataset was downloaded from (https://www.dropbox.com/s/sijf2votfej629t/Save-Large-Heme-ArchRProject.tar.gz). It consists of ~220,000 hematopoietic cells from the hematopoiesis dataset in ArchR11. As described in their Supplementary Table 1, the dataset was assembled from 49 samples in four data sources, of different sample types (mixed, sorted, and unsorted cells; PBMCs; and bone marrow mononuclear cells), and generated using different sample processing protocols and on different technical platforms. We used ArchR to generate doublet scores and removed clusters with both high doublet scores and a mixture of disparate cell types. This doublet removal only applied to sequencing wells that were not sorted, purified cells. In the end, data of 95,599 cells were obtained. Because many of the cell types were sorted populations run on an individual well, many cell types were not available across samples. As a result, we treated all cell types as coming from a single sample for benchmarking purposes. We used previously published cell annotations, with a median labeling score of 0.70.
Mouse Pan-Organ scATAC Atlas
This dataset (GEO: GSE111586) was downloaded from https://atlas.gs.washington.edu/mouse-atac/. We performed doublet removal and then used the data for benchmarking purposes on non-human scATAC-seq datasets. The original cell type labels were used in the analysis.
Assessing dataset noise using the Altius Peakset
To assess ‘noise’ within a dataset (i.e., fragments from closed regions known as heterochromatin), we used the Altius consensus peakset100 of over 3.6 million DNase I hypersensitive sites within the human genome as an approximation of all potentially accessible sites. We calculated the overlap rate between fragments and the Altius consensus peakset for each cell type and dataset, in order to assess the quality of the data. The COVID19 dataset had an median Altius peakset overlap rate of 88.9%, while the corresponding rates for the HealthyDonor dataset and the Hematopoiesis dataset were 75.5% and 82%, respectively.
MOCHA overview
MOCHA is implemented as an open-source R package under the GPLv3 license in CRAN. All code and development versions of MOCHA are available in MOCHA’s github repository.
MOCHA is designed to run in-memory and interoperate with common Bioconductor methods and classes (e.g., RaggedExperiment, MultiAssayExperiment, and Summarized Experiment). It takes as input four objects that are commonly generated from scATAC-seq after cell labeling and the removal of doublets and cells of low quality data. These four objects are: 1) a list of GRanges or GRangesList containing per-sample ATAC fragments, 2) cell metadata with cell labels, 3) a BSGenome annotation object for the organism, and 4) a GRanges containing blacklisted regions. These inputs can be passed to MOCHA directly from an ArchR object. Alternatively, results can be extracted from Signac, SnapATAC, or ArchR, and converted to common Bioconductor data objects, which can then be imported into MOCHA. By operating on well-supported Bioconductor objects, MOCHA’s inputs and outputs are compatible with the broader R ecosystem for sequencing analyses, and are easily exportable to genomic file formats such as BED and BAM.
MOCHA’s core functionality runs as a pipeline from these inputs to perform sample-specific open tile prediction and consensus analysis, resulting in a TSAM represented as a Bioconductor RangedSummarizedExperiment. On systems with sufficient memory, MOCHA’s functions can be parallelized over samples with the ‘numCores’ parameter to decrease runtime. From the TSAM, MOCHA provides functions for ZI co-accessibility and ZI differential accessibility analysis. The format of the TSAM output enables additional downstream analyses with other R packages. For example, the TSAM RangedSummarizedExperiment can be used directly as the counts matrix input for motif deviations analysis with the chromVAR R package. Additional details on the workflow and functions on the MOCHA package are provided in Supplementary Fig. 1.
MOCHA objects
MOCHA’s workflow generates two major objects: an OpenTiles Object, and a Tile-Sample Accessibility Matrix (TSAM) object. An OpenTiles Object is created by callOpenTiles and stores tile accessibility information at the sample and cell type level, along with sample-specific metadata in a MultiAssay Experiment, which contains:
- RaggedExperiment (Bioconductor) for each cell type
-
◦Accessibility calls and normalized intensity across samples
-
◦
Sample-level metadata in the colData slot.
- Additional metadata as a list in the metaData slot.
-
◦Cell type-level metadata in a SummarizedExperiment (Bioconductor)
-
▪Cell counts, fragment number, and other relevant metadata
-
▪
-
◦Transcript and Genome database used for calling
-
◦History of the object
-
◦
From there, user-defined cutoffs are used to identify study-level open chromatin regions. These regions are used to generate tile-by-sample accessibility matrices (i.e., TSAMs) for downstream analysis. These TSAMs are saved in a SummarizedExperiment format, containing:
- Tile-Sample Accessibility Matrix for each cell type
-
◦Counts at the complete set of open regions (across all cell types)
-
◦
- Tile metadata saved in the rowRanges slot
-
◦Genomic positions for each tile
-
◦Boolean/indicator columns labeling population-level open tiles for each cell type
-
◦Columns labeling the type of region (e.g., promoter, intergenic, distal)
-
◦Columns labeling the associated genes for promoter and intergenic tiles
-
◦
Sample-level metadata in the colData slot.
- Additional metadata as a list in the metaData slot.
-
◦Cell type-level metadata in a SummarizedExperiment (Bioconductor)
-
▪Cell counts, fragment number, and other relevant metadata
-
▪
-
◦Transcript and Genome database used for calling
-
◦History of the object
-
◦
These TSAM can then be integrated with ArchR, ChromVar, and other Bioconductor-compatible R packages for downstream analyses.
Tiling the genome
MOCHA splits the genome into pre-defined, non-overlapping 500 base-pair tiles that remain invariant across samples and cell types. MOCHA annotates each tile using a user-provided transcript database (e.g., HG38 Transcript Database) as follows: Promoter regions are 2000 bp upstream and 200 bp downstream from transcriptional start sites104. Intragenic regions are tiles that fall within a gene body, but not within the promoter regions. All other regions are classified as distal.
From there, we only consider tiles that overlap with ATAC fragments. MOCHA counts the number of fragments in a tile as follows
| 1 |
| 2 |
If a fragment falls between two tiles, it is counted on both tiles.
Normalization
Normalization techniques using invariant CTCF sites
We examined three normalizing approaches: dividing the number of fragments by 1) the total number of fragments for sample i, cell type j (i.e., ); 2) the total number of fragments for sample i (i.e., ), and 3) the total number of cells in sample i, cell type j. We evaluated the above normalization methods along with the raw data based on a list of 2230 cell-type invariant CCCTC-binding factor (CTCF) sites from the ChIP Atlas database105. These loci were identified in at least 201/204 (99%) of blood cell types present in the ChIP-seq Atlas database106. Using these CTCF sites, each approach was assessed based on the corresponding distribution of coefficient of variation (CV) in peak accessibility. MOCHA normalizes data using .
Sample- and cell type-specific normalization
For each sample i, cell type j, and tile t, MOCHA calculates the following normalized features:
| 3 |
| 4 |
Since the NK population used for model training contained 750 million fragments, a scaling factor of is applied to make the raw and normalized counts on the same scale across cellular abundances, and keep normalized values greater than 1 to minimize convergence errors in downstream model training. Biologically, λ(1)i,j,t is designed to capture the total number of fragments across all cells (e.g., pseudo-bulk), normalized by the sequencing depth for that cell type and sample. Given the sparsity of scATAC-seq data and the assumption of limited number of genomic copies (2x-4x) in a typical cell, λ(2)i,j,t is designed to capture the presence of multiple fragments in a tile from any cell, which can only be evaluated on single-cell data. This approach combines single cell and pseudo-bulk information for downstream prediction. Normalizing by is used to normalize both sequencing depth and cell population variability. This approach provides both a sample- and cell-type-specific normalization scheme.
Evaluation of open chromatin accessibility
Training of logistic regression models for predicting tile accessibility
MOCHA assumes a typical ploidy per cell (two to four copies of the genome). Its pseudocode and further details are provided in Supplementary Fig. 2 in order to allow for modifications when the above assumption does not hold.
We used scATAC-seq data of 179k NK cells in the COVID19 (n = 91) dataset as the training dataset. First, we normalized the scATAC-seq data and collapsed it into pseudobulk data. Second, we applied MACS240 (‘-g hs -f BED --nolambda --shift -75 --extsize 150 --broad’, ‘--model -n’, using the parameters set in ArchR) to identify accessible peaks in the pseudobulk data. We chose these settings to match the behavior of MACS2 in a commonly-used scATAC data analysis software, modified to call broad rather than narrow peaks. The resulting peaks were then overlaid onto our pre-defined 500 bp tiles. We trim the broad peaks by 75 base pairs at each end and remove the tail ends of peaks that extend onto tiles with no signal. MACS2 identified 1.15 million tiles as ‘accessible regions’ and the remaining 4.39 million tiles with fragments were labeled as ‘inaccessible’. We labeled all other fragment-containing regions as inaccessible, and used these ‘accessible’ and ‘inaccessible’ regions for training. Third, we randomly selected NK cells at cell counts ranging from 170k to 5 at discrete intervals, generating 10 replicates for subsets <50k cells, and 5 replicates for larger subsets. In each of the subsets, we calculated λ(1)i,j,t and λ(2)i,j,t at individual tiles. Fourth, we trained a LRM for each selected subset of NK cells based on the tile labeling just described. The LRM was fitted using a logit ‘link’ function and applying the default loss function from the GLM logistic regression function in R. For each sample of cells, the LRM calculates a probability score to assess the likelihood of a tile being accessible, using the formula
| 5 |
Here is the intercept, and are coefficients for λ(1)i,j,t and λ(2)i,j,t, respectively. A tile is predicted as accessible if or inaccessible if where is the threshold value separating accessible and inaccessible tiles. Since it is not possible to balance open vs closed tiles in real-data, this leads to prevalence imbalances that need to be addressed. To account for this, we used the Youden index107 to calculate optimal in this study, using the cutpointR R package.
Fifth, we collected , , from the 10 or 5 replicated runs on n cells and then took the corresponding median coefficients, i.e., , , , and , to construct the predictive model for a sample of n cells. Finally, we used the learned coefficients and the learned thresholds to smoothen the model to interpolate the model across cellular abundances that the model was not trained on. The final model is composed of a set of smoothened coefficients , , , and smoothened thresholds from all examined .
Model evaluation metrics
To quantify a model’s performance, we counted their true positives (TPs), false positives (FPs), true negatives (TNs), and false negatives (FNs), and used these to calculate false positive rates, recall, and F1-score.
Prediction of tile accessibility on new data
To predict accessibility in a new dataset, MOCHA first accounts for differences in sequencing depth and cell count across datasets and calculates the ratio, S, of the median (across samples) number of total fragments in the training data, and the corresponding median in the new dataset. MOCHA then scales both λ(1)i,j,t and λ(2)i,j,t in the new dataset by S and calculates the likelihood of a tile being accessible as
| 6 |
where is the number of cells of the targeted cell type in the targeted sample. The normalization and scaling factors enable the same smoothened coefficients to be used on new data, regardless of cell type or tile position. As before, a tile is predicted as accessible if or inaccessible if where is the threshold value separating accessible and inaccessible tiles.
Benchmarking open regions
To benchmark MACS2, HOMER, and MOCHA, we ran each tool per sample and cell type to generate comparable accessibility measurements across three cell types in three different datasets. For MACS2, we used the following parameters to call broad peaks (‘-g hs -f BED --nolambda --shift -75 --extsize 150 --broad --nomodel -n’), in accordance with previous published scATAC-seq settings11. For HOMER, we used the findPeaks function with default parameters, and added (‘-style histone’) to call broad peaks. While HOMER and MACS2 are primarily designed around the properties of ChIP-seq and DNase-seq, they are also recommended for use with bulk ATAC-seq41.
To ensure head-to-head comparisons, we overlaid HOMER and MACS2’s peaks into MOCHA’s predefined 500 base-pair tiles to translate peak calls into open tile calls. Similar to training, we trimmed 75 bp off each end, as MACS2’s shift/extsize parameters extend fragments to improve peak calling under the -nomodel flag. By trimming, we avoid counting the tails of peaks that extend into tiles with no actual fragments. This trimming approach allows for a direct head-to-head comparison of open regions detected across methods. Additionally, all three methods are provided the same normalized pseudo-bulk intensity information to ensure comparable peak calling and prevent confounding peak calling and normalization. After translating MACS2 and HOMER peaks into open tiles, we then compared the number of open tiles per sample across all methods, cell types, and datasets.
Next, we generated a TSAM for each cell type across all three methods. The TSAM is a matrix with an array-type structure, where each cell contains the normalized λ(1)i,j intensities for a given sample i, at tile j. We kept open tiles that were called in at least 20% of samples (or all tiles in Hematopoiesis). By generating a TSAM for each method, we compared reproducible, population-level open tiles across all three methods. The 20% threshold was applied to filter out noisy data.
CTCF and TSS Sites for benchmarking
CTCF sites were drawn from the ChipSet Atlas105. In brief, we download a bed file containing CTCF peaks for all blood cell types, and then used Plyranges’s reduce_ranges108 function to collapse duplicate peak calls into one non-redundant and smaller file for detecting overlaps. This process was done for both Hg19 (n = 197,882) and Hg38 (n = 184,588). TSS sites were taken from Bioconductor database TxDb.Hsapiens.UCSC.hg19.knownGene for the Hematopoiesis dataset (which was aligned to Hg19), and TxDb.Hsapiens.UCSC.hg38.refGene for the other datasets by first extracting the transcripts for all genes. The TSS were then extracted from the transcripts using the promoters() command (Hg19, n = 62,265, Hg38, n = 88,819). We then calculated the number of tiles that overlapped with a CTCF and TSS site using the subsetByOverlaps function from the GenomicRanges104 R package.
Runtime comparison on open chromatin analysis
Using the CD14 monocyte population in our COVID19 dataset (n = 91), we produced 13 subsamples ranging from 100,000 to 10 cells and measured 10 replicates of the time it takes to conduct open chromatin analysis. Our runtime comparisons were conducted on N2 machines on the Google Cloud Platform, with 64 vCPUs and 512GB RAM. MOCHA version 0.2.0 was used. The R package tictoc was used to record elapsed time.
Downsampling comparison on open chromatin
Since pooling cells across samples before calling open tiles is a common approach, we benchmarked all three methods on the same randomly selected cell subsets ranging from 5 cells to the full set in the COVID19 dataset (n = 91). For this comparison, we utilized the same three cell types across the same three datasets. For each cell type and dataset, we used the following procedures. For MOCHA:
Generate a coverage object using predefined 500 base-pair tiles on all pooled cells (e.g., CD16 monocytes).
Predict open tiles on the pooled cells.
Count the total number of open tiles, the number of open tiles overlapping with CTCF sites, and the number of open tiles overlapping with TSSs.
Repeat (1–3) for all pre-specified downsampled cell counts.
For MACS2 and HOMER:
1. Generate a coverage file on all pooled cells (e.g., CD16 monocytes),
2. Call peaks on the pooled cells.
3. Convert the peak regions onto the pre-defined MOCHA tiles.
4. Remove tiles that extend onto empty regions.
5. Count the total number of open tiles, the number of open tiles overlapping with CTCF sites, and the number of open tiles overlapping with TSSs.
6. Repeated (1–5) for the pre-specified downsampled cell counts.
Simulating fragments and open chromatin from scATAC-seq
To benchmark HOMER, MACS2, and MOCHA, we designed a simulation study to determine the sensitivity, specificity, and accuracy of each method. The simulated scATAC-seq data is constructed in 6 steps as follows:
Step 1: Defining open and closed tiles as the ground truth. We first splitted each chromosome into 500 bp tiles. We then assigned roughly 200,000 open tiles across the genome, with the number of open tiles per chromosome being proportional to the chromosome’s length. Afterwards, we distributed the open tiles along each chromosome with a sinusoidal probability (negative values set to 0) with a periodicity of 10 tiles, to mimic periodic appearances of open regions followed by large closed regions. All other tiles were defined to be closed. We treated these open and closed tiles as the ground truth in this simulation analysis. In this step, each sampling draws a different peakset and thus mimics a cell type with its own peakset.
Step 2: Simulating the number of fragments in individual cells. Each simulated cell was randomly allocated a mean of 4k fragments, following a Poisson distribution ( = 4000). To simulate our quality control (QC) thresholds for sequencing depth, we excluded cells with fewer than 1000 fragments. The process was repeated until a target number of simulated cells was reached.
Step 3: Assigning fragments to open and closed tiles within each cell. Simulating a FRIP (fraction of reads in peaks) score of 95%, a random number of fragments were assigned to the open tiles using a Poisson distribution ( = 0.95*fragment number) while the rest fragments were randomly assigned to the closed tiles with equal weight. For the open tiles, we first simulated their relative weight using a Beta distribution (1,3) and then allocated the corresponding fragments to individual open tiles according to their relative weights. These weights were set to simulate real data of many low accessible tiles and few highly accessible ones.
Step 4: Positioning fragments in individual tiles. To determine the precise location of fragments assigned to open tiles, we first assigned the midpoint of each fragment to the center of the corresponding tile and then used a Poisson distribution (=5) to add a random offset from the center. The direction of the offset (left or right) was randomly generated with a Bernoulli distribution (p = 0.5). For fragments assigned to closed tiles, their position was randomly distributed across ‘closed’ tiles.
Step 5: Determining the length of individual fragments. We simulated the length of individual fragments following a Poisson mixture distribution so that approximately 90% of fragments have a mean length of 75 bp, and 10% with a mean length of 200 bp.
Step 6: Assembling simulated scATAC-seq data. All simulated fragments from all simulated cells were treated as a scATAC-seq sample, saved in a single fragment file, and converted into a normalized bedgraph file for peak calling.
Using the above process, we ran two sets of simulations: 1) varying the number of cells to model cell types of different abundances, and 2) varying the total number of open regions to mimic cell types of different open tiles. For the first set, we simulated samples with a range of cell counts: 75, 100, 150, 200, 250, 500, 1000, 1500, 2000, 3000, and 5000 cells. Tiles having no fragments were removed from individual samples, resulting in different ground truth tiles per sample. This process was repeated 10 times for each cell count. The pairwise overlap rate between the 10 peaksets sampled in Step 1 ranged between 8.4% to 8.6%. 110 simulated samples were generated.
For the second set of simulations, we fixed the number of cells (250) but varied the number of fragments per cell (1k, 1.5k, 2k, 2.5k, 3k, 3.5k, 4k, 4.5k) and the location and number of open regions (150k, 250k, 350k). The three peaksets sampled in Step 1 overlapped at rates between 6.3% to 14.8%. For each peakset, 10 samples were simulated at each value for fragments per cell, generating a total of 240 simulated samples. This enables the simulation of different cell types (total open regions and/or fragment variations due to ploidy variation) and technical influences from sequencing depth (fragments per cells). Based on existing vignettes and documentation, we note different tools apply different QC cutoffs to filter out low quality cells: ArchR=1k, Signac=1k, SnapATAC=3k. To cover a wide range of conditions, we simulated fragments per cell from 4.5k (our internal datasets) down to 1k, where ArchR and Signac would retain approximately 50% of cells.
We then ran all three methods (MOCHA, MACS2, & HOMER) to identify open tiles, in the following manner. For MACS2 and HOMER, we called peaks and converted the open peakset into 500 bp tiles for direct comparison across methods, and removed tiles that minimally overlap the peakset (<75 bp overlap) to avoid tiling artifacts. Finally, we compared the open tiles from each method with the ground truth using previously described model evaluation metrics.
Assessment on zero-inflation in pseudobulk scATAC-seq Data
To assess ZI in pseudobulk scATAC-seq data, we fitted a negative binomial (NB) distribution on pseudobulked accessibility λj(1) at each open tile. We then tested whether λj(1) was ZI using the DHARMa R package, which utilizes the model fits from the glmmTMB R package. More specifically, the test compared the observed number of zeros with that expected from a NB distribution: An estimate of >1 means that there are more zeros than expected by a NB model and a p < 0.05 means that the observed and the expected zeros in the data is significantly different. To be comprehensive, we ran the test using two standard parameterizations of the NB family, as implemented in the glmmTMB package: The variance grows either linearly (NB1) or quadratically (NB2) with the mean. The λj(1) was ZI if p < 0.05 and statistic > 1, or underinflated if p < 0.05 and statistic <1.
Differential accessibility analysis
MOCHA’s zero-inflated method for DAA
MOCHA identifies differential accessibility tiles (DATs) in a targeted cell type between sample groups A and B in three steps:
First, similar to others10,11, MOCHA prioritizes tiles for testing using heuristic functions to calculate two data-driven thresholds. MOCHA transforms the total fragment count {λ(1)} in the corresponding TSAM to log2(λ(1) + 1) and fits a mixture model of two normal distributions on all log2(λ(1) + 1) values in the TSAM (Supplementary Fig. 2g). This bimodal model provides a heuristic threshold to prioritize high-signal tiles. From there, we used the TSAM metadata to identify any differences in sequencing depth by comparing the median number of fragments per sample between groups. This analysis informs the ZI threshold. Given our initial observations of a 25% difference in fragment counts, we set a 50% threshold (2X the observed sequencing depth difference) to control for technical artifacts. Tiles that do not pass either threshold are assigned a DAT P value of NA, and those passing thresholds are then tested for differential accessibility.
Second, MOCHA tests for differential accessibility as follows. Denote the percentages of zeroes among samples of the two groups as ρA and ρB and the corresponding medians of non-zero log2(λj(1) + 1) values as μA and μB. MOCHA then tests whether a tile is a DAT based on the following hypothesis testing:
Null hypothesis (): ρA = ρB and μA = μB
Alternative hypothesis (): ρA ≠ ρB or μA ≠ μB.
MOCHA uses the two-part Wilcoxon (TP-W) test35 to combine results from the binomial test on ρA and ρB with results from the Wilcoxon rank-sum test on μA and μB. Since each test statistic can be transformed to follow a distribution (i.e., and ), MOCHA combines them into a single test statistic, i.e., = + , and consequently evaluates from it a single P value34. In the absence of zeros, the TP-W test mathematically reduces to the standard Wilcoxon rank-sum test.
Finally, to control for multiple testing, MOCHA calculates a modified q-value to adjust for False Discovery109 for each tile and uses a default threshold of 0.2 to identify DATs. Since the P values are inflated near 1 (see Supplementary Fig. 10a), the background is estimated from P ≤ 0.95 only.
In addition, MOCHA uses the Hodges-Lehmann estimator110 to estimate log2(fold change) on chromatin accessibility between the two sample groups. More specifically, MOCHA first calculates the difference between each sample pair (one sample each from group A or B) having non-zero log2(λ(1) + 1) values and then takes the median from all paired differences as an estimate for log2(fold change) between the two sample groups.
Benchmarking MOCHA with ArchR, Signac, DESeq2, and DiffChipL on DAA
ArchR’s, Signac’s, DESeq2’s, and DiffChipL’s DA modules were each run on a single cell count matrix generated from the same tile set (215,649 tiles) as the COVID19X CD16 monocytes TSAM. For ArchR, default settings were used, except we modified maxCells to include all cells (n = 24,744). For Signac, we lowered the minimum percent detection (pct = 0.001), and the log2FC threshold (logfc.threshold = 0.05) in order to test the full tileset, thus enabling a full head-to-head comparison. As a close analog of Signac’s tutorial, we also set latent.vars to ‘nFrags’ to adjust for sequencing depth. For DESeq2 and DiffChipL, the single cell matrix was pseudobulked by sample to generate raw counts, as required for DESeq2’s and DiffChipL’s workflow before running differentials. Default settings for normalization and differentials were used, in line with both method’s tutorials.
To assess the false positive rate (FPR, 1 - specificity) of the methods, we conducted 50 permutation tests in which labels for COVID+ and COVID- samples were randomized and significant DATs were identified as in the real data in each test. All DATs thus identified were considered as false positives (FPs) and the FPR was evaluated as the ratio of the number of FPs to the number of the original DATs from the real data.
Due to a lack of “ground truth”, it is not possible to accurately evaluate the recall (sensitivity) of the methods. Nevertheless, we estimated a lower bound of the recall by downsampling the samples from n = 39 to n = 38, 37, …, 30. More specifically, we randomly selected the targeted number of samples, identified the DATs, and estimated the recall as the ratio of the number of the new DATs to the number of the original DATs. We repeated the process 15 times for each targeted sample size. To save computing time, we limited the analysis to tiles in chromosome 4 only. Some of the false negatives may be specific to removed samples, due to disease/human heterogeneity. The loss of power due to sample size reduction also increases the number of false negatives. Thus the recall evaluated in the approach is likely a lower bound.
Power analysis when downsampling
We conducted a power analysis to illustrate the theoretical power loss when reducing the sample size from n = 39 to n = 30. We first calculated the statistical power of detecting differences with a moderate effect size (d = 0.5) under an =0.05 using a 2-sample t-test (COVID+, n = 17; COVID-, n = 22). We then downsampled from n = 39 to n = 30 and calculated the power with d = 0.5 and =0.05 while maintaining the COVID+/COVID- sample ratio as close to 17/22 as possible. Finally, we divided the statistical power at each n, with the power observed at n = 39, to calculate relative power loss due to downsampling.
Assessing discriminative power per method
We randomly subsampled 50 DATs from the output of each method, ran K-means clustering (K = 2), and generated the following confusion matrix to summarize the predictions.
| COVID+ | COVID− | ||
|---|---|---|---|
| Cluster 1 | a | b | a + b |
| Cluster 2 | c | d | c + d |
| a + c | b + d | a + b + c + d |
We then calculated Holley’s50 to assess how well the 50 randomly selected DATs in separating COVID+ and COVID- samples. We used |G| for the comparison since it is irrelevant which cluster is enriched for COVID+ samples. We repeated this process 1,000 times to obtain a distribution for each method.
DAA runtime comparison
To evaluate each method’s speed in DAA, we started by testing all 215,649 tiles in the CD16 monocytes TSAM, and gradually decreased the number of tested tiles. At each downsample, we tracked the run time required to identify DATs within those randomly selected tiles. The tictoc R package was used to calculate runtime.
Co-accessibility analysis
MOCHA’s zero-inflated method for CAA
MOCHA applies ZI Spearman correlation36,37 to evaluate the co-accessibility of two tiles (e.g., X and Y) across either cell types or samples based on the corresponding log2(λ(1) + 1) values. More specifically, the method first calculates the standard Spearman correlation on (X,Y) pairs of non-zero data (i.e., X > 0 and Y > 0), denoted as , and then adjusts it in the presence of zeroes in either tile as follows:
| 7 |
where
which quantify how zeros are distributed among the two tiles across all data points with . In the absence of zeros, the ZI-Spearman correlation reduces to the standard Spearman correlation, i.e., . MOCHA makes two modifications to an R implementation of the method28: 1) The Spearman correlation () is calculated in C language for optimal computing time and 2) undefined ZI Spearman correlations (when cannot be calculated) are assigned to NA rather than replacing them with the standard Spearman correlations with zeros treated as normal data.
Benchmarking inter-cell-type co-accessibility
We used a previously published promoter-capture HiC (pcHiC) resource54 which identified promoter-enhancer regulatory links. From there, we used the liftOver R package, version 1.22.0, and the Hg19 to Hg38 conversion file (hg19ToHg38.over.chain, https://hgdownload.soe.ucsc.edu/gbdb/hg19/liftOver/) to convert promoter/enhancer loci from HG19 to HG38. The large HiC windows for Promoters and enhancers were then tiled into 500 bp windows to generate all potential promoter-enhancer tile (PET) pairs. We only kept PET pairs when both tiles were identified as accessible by MOCHA in naive CD4+ and CD8+ T Cells and had pcHiC evidence supporting their interaction specifically in naive CD4+ and CD8+ T cells. We used this final list of 1.2 million PET pairs as a foreground set of regions that are enriched for biologically relevant interactions within these cell types. We then generated a background set of randomly selected pairs of tiles to generate an empirical null distribution. We calculated the Spearman and ZI-spearman correlations across 17 cell types to identify pairs of regions that are co-accessible in T cells vs other cell types (17 cell types include B intermediate, B memory, B naïve, CD14 Mono, CD16 Mono, CD4 Effector, CD4 Naïve, CD8 Effector, CD8 Naïve, DC, HSPC, MAIT, NK, NK Proliferating, NK_CD56bright, OtherT, and Treg). We then used the Kolmogorov–Smirnov (KS) distance to quantify how well the two correlation methods separated the PET pairs from the random pairs. We then calculated an empirical P value for each PET pair based on the foreground and the empirical null distributions, and then accounted for multiple comparisons (Benjamini-Hochberg method). A PET pair was considered as significant if FDR < 0.1.
Pathway enrichment analysis
Pathway enrichment analysis was mostly restricted to the Reactome pathway database. All genes within the database reference of TxDb.Hsapiens.UCSC.hg38.refGene from Bioconductor111 were selected as the background. Over-representation analysis was performed using WebGestaltR112. We annotated enriched pathways at the highest level within the Reactome’s database hierarchy. Lower level annotations on immune system pathways were provided to discern adaptive, innate, and general signaling pathways. Using WebGestaltR, pathway enrichment analysis was performed once on Wikipathways, Gene Ontology (Biological Processes, Non-redundant), and KEGG for illustrative purposes.
Linkage disequilibrium score regression analysis
Linkage Disequilibrium Analysis was performed using the codebase from https://github.com/bulik/ldsc and reference files from https://zenodo.org/records/8292725. GWAS summary statistics were pulled from EMBL’s GWAS catalog for studies GCST90029015113 (Autoimmune disease), GCST90038603114 (Immune Aging), and GCST90043674115 (Abnormal Immune Response). Using the LDSC scripts, munge_sumstats.py was used to generate summary statistics files for heritability analysis. Peak calls on 9 cell types (across 3 datasets) by all 3 methods (total of 27 peaksets) from Fig. 2 were split up by chromosome for computing efficiency and the make_annot.py was used to generate an annotation file for each before modeling (Source Data for Fig. 2). LDSC was then run (--l2 flag) on each bed file of peak calls using reference files from above, generating a file that could be used along with the reference baseline LD scores for heritability analysis on each GWAS summary file. Overlap between methods was then counted, when the same annotation was enriched in different method’s peaksets from the same cell type, in the same dataset, and using the same GWAS study’s results.
Identification of alternatively regulated transcription start sites
We extracted all TSSs from the Transcript database TxDb.Hsapiens.UCSC.hg38.refGene found on BioConductor111, and then expanded them upstream by 125 bp to account for TSSs falling very close to a tile boundary. We filtered out genes with only one TSS. If alternative TSSs of the same gene occurred within a user-defined neighborhood (default: 150 bp) of each other, we collapsed them into a single TSS. We then found the intersection between alternative TSSs and the 6211 DATs between COVID+ and COVID- samples in CD16 monocytes. TSSs that landed on a DAT were assigned with the FDR (q-value) of the corresponding DATs. We categorized alternatively regulated genes (ARGs) as
Type I: A gene had a subset of TSSs showing differential accessibility (FDR < 0.2) in the same direction and another subset being open but not differential.
Type II: A gene had at least two TSSs showing differential accessibility (FDR < 0.2) but in opposite directions.
Motif enrichment analysis on alternatively regulated TSSs and associated regulatory regions
Motif matching was done using the motifmatchr package and the CISBP motif database, as provided by the chromVARmotif package (https://github.com/GreenleafLab/chromVARmotifs). MOCHA uses a standard hypergeometric test to identify enriched motifs, with a user-provided foreground and background tile sets. For multi-testing corrections, the resulting p-values were converted into FDRs (Benjamini–Hochberg method). To understand the upstream signaling mechanisms regulating ARGs, we first applied MOCHA to identify tiles that were within ±1 M bp of and also co-accessible (inter-sample, ZI-Spearman correlation > 0.5) with the corresponding DATs. These DATs and their co-accessible tiles were selected as the foreground tile set. For the background tile set, we chose all tiles with TSSs and their co-accessible tiles that did not overlap with the foreground set. These foreground and background tile sets were used to calculate CISBP motif enrichment regulating ARGs.
Ligand-motif set enrichment analysis
The NicheNet56 database has identified links between upstream ligands and downstream transcription factors (TFs) that regulate gene expression56. Using the same principle as pathway enrichment analysis, we designed a Ligand-Motif Set Enrichment Analysis (LMSEA) framework to capture potential drivers of our observed motifs (i.e., ligands regulate the TFs in our dataset). Specifically, LMSEA tests whether motifs linked to a ligand of interest are significantly (using hypergeometric test) over-represented in our observed motifs relative to the ligand’s motif set within NicheNet. The Benjamini and Hochberg (BH) procedure was used to adjust P values for multiple comparisons. An FDR value < 0.05 was considered significant.
Construction of ligand-transcription factor-gene network
We constructed ligand-TF-gene networks and visualized them using Cytoscape116. The nodes were ARGs, enriched motifs (TFs), and enriched ligands. Edges were drawn as follows: a motif-gene link was created if an enriched TF was found within the TSS-containing DATs of an ARG or their co-accessible tiles, a ligand-motif link was drawn if a ligand was known to interact with a TF in NicheNet’s ligand-transcription matrix.
Longitudinal analysis of COVID-19 response at single-cell level
Grouping COVID+ samples by infection stage
COVID+ samples (n = 69) in the COVID19 dataset were grouped by the corresponding infection stage, including early infection (1–15 days PSO, n = 21), late infection (16–30 days PSO, n = 13), and recovery ( > 30 days PSO, n = 35).
Generation of density UMAP
We extracted sample-specific open tiles on CD16 monocytes for all samples in the full COVID19 dataset (n = 91). From there, we generated a TSAM by aggregating all tiles that were called in at least 20% of samples at any infection stage or uninfected. We extracted the tiles from the resulting TSAM and added them to the original ArchR project via addPeakSet. We then generated a single-cell peak matrix from this tile set, using addPeakMatrix, and used it as input for ArchR’s iterative LSI and UMAP functions. The LSI was run with default parameters, except for the number of iterations (5 instead of 2). The UMAP was run on standard ArchR settings11 on the resulting iterative LSI object. Based on the resulting single-cell UMAPs, we generated a density plot for each infection stage or uninfected.
Pseudotime trajectory analysis
We used ArchR’s standard Monocle3 pipeline to conduct a trajectory analysis. We instructed Monocle to construct a trajectory from cells belonging to samples in the order of early infection, late infection, recovery, and uninfected. The resulting trajectory was overlaid on the single-cell UMAP. Following the above trajectory, three distinct pseudotime heatmaps were generated using ArchR’s standard protocol and the following input single-cell matrices: log2-normalized GeneScores, peak (tile) accessibility, and ChromVAR z-scores. Using ArchR’s functions with default settings, we further extracted pseudotime-changing elements for each of the three matrices.
Longitudinal analysis of COVID-19 response at pseudo-bulk level
Longitudinal analysis of motif usage
We modeled longitudinal motif usage using pseudobulk ChromVar motif z-scores. We converted the TSAM of CD16 monocytes from the COVID19L dataset (n = 69) into a ChromVAR-compatible object, and then ran ChromVAR on the TSAM-derived object to generate sample-level motif z-scores. We then modeled motif usage with the following generalized linear mixed effect model (GLMM):
| 8 |
where was the centered days PSO (i.e., days PSO of individual samples minus the mean days PSO of all samples)117 and indicated that random intercepts were used for individual participants. The P values associated with the linear terms were extracted using the lmerTest package. We converted the P values to FDRs (Benjamini-Hochberg method) to control multiple testing. Motifs with a FDR < 0.1 were considered as significantly changing in time.
Transcription factor network
The activator protein-1 (AP-1) family network was obtained by subsetting the APID protein-protein interaction database118 down to just the significant AP1-family TFs. Edges between nodes were included if they were supported by at least four experiments. The nodes were color-coded using the signs of the corresponding coefficient of . The network was drawn using Cytoscape116.
Longitudinal analysis of gene promoter accessibility
We collected promoter tiles from the TSAM of CD16 monocytes in the COVID19L dataset and modeled their accessibility using either GLMMs or ZI-GLMMs with the glmmTMB package33. More specifically, for promoters with zeroes, we applied the ZI-GLMM modeling as follows
| 9 |
where was short for log2(λj(1) + 1), was days PSO, indicated that random intercepts were used for individual participants, and ZI was modeled as a function of the total cell counts in individual samples with no intercept. For promoters without zeroes, we applied the GLMM modeling as follows
| 10 |
where the ZI component was omitted. The P values associated with were extracted and converted to FDRs (Benjamini-Hochberg method) to control multiple testing. Promoters with a FDR < 0.1 were considered as significantly changing in time. For promoters attributed to multiple genes, all genes were included for pathway enrichment and downstream analyses.
Transcription factor and gene promoter associations
Linking transcription factor to gene promoters
We evaluated whether motif z-scores were statistically associated with gene promoter accessibility via ZI-GLMMs as follows
| 11 |
where was short for log2(λj(1)+1). All pairs of significantly changing TFs and significantly changing gene promoters were evaluated. We considered a TF and a gene promoter to be associated if the continuous coefficient of was statistically significant (P < 0.05) without adjusting for multiple testing.
Linking transcription factor to innate immune pathways
Using the TF-gene promoter associations, we calculated the percentage of significant genes in an innate immune pathway being associated with a TF. For visualization purposes, the network only displayed an edge between a TF and a pathway if more than 33% of significant genes in that pathway were associated with the TF.
Variance decomposition on longitudinal COVID19 dataset
To identify significant covariates for modeling accessibility, we ran variance decomposition on highly accessible tiles (defined as having at least 80% non-zero values within any infection stage). We modeled Age, Sex, time (i.e., days since symptom onset), Batch, and Donor as random effects using the following formula:
and then we used the relative variances to identify the most influential factor for each tile.
Modeling zero-inflated associations across covariates
To identify factors associated with high presence of zeroes in scATAC pseudo bulk data, we ran the following zero-inflated models
on all promoter tiles to test whether zeroes were associated with Cell Counts, Age, and Sex. We extracted the p-values from the glmmTMB and summarized the associations using the histograms of the p-values.
Statistics and reproducibility
The datasets used in this manuscript were selected for benchmarking purposes, and therefore there is no need for sample-size calculation, randomization, or blinding. No samples were excluded from the analyses. Any computational data cleaning and processing are described accordingly.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Supplementary information
Acknowledgements
We thank the study participants for their dedication to this project; the Allen Institute founder, Paul G. Allen, for his vision, encouragement, and support; Allan Jones for his support to our COVID-19 study; Qiuyu Gong for providing code for plotting single-cell density within UMAP space; Ziyuan He, Peiyao Zhang, Marla Glass, and Sandra Munro for review and helpful discussions of the manuscript draft; Leila Shiraiwa and Nina Kondza for laboratory operations support; the Human Immune System Explorer (HISE) software development team at the Allen Institute for Immunology for their support and dedication. This paper and the research behind it would not have been possible without the collaborative computational data analysis environment provided by HISE. The research reported in this publication was supported in part by COVID supplements from the National Institute of Allergy and Infectious Diseases and the Office of the Director of the National Institutes of Health under award numbers UM1AI068618-14S1 and UM1AI069481-14S1 (M.J.M.). This work was also supported by Paul G. Allen Family Foundation Award #12931 (M.J.M.); Seattle COVID-19 Cohort Study (Fred Hutchinson Cancer Research Center, M.J.M.); and the Joel D. Meyers Endowed Chair (M.J.M.). The content is solely the responsibility of the authors and does not necessarily represent the official views of the funders.
Author contributions
S.R.Z, M.P.P, and X.-j.L. conceived the study and jointly designed the development, benchmarking, and analysis. M.J.M. and T.F.B. acquired the funding. T.R.T, P.J.S., X.-j.L., M.J.M., and T.F.B. designed the COVID-19 study. J.L.C. and M.J.M. enrolled participants and collected their samples. M.W., J.R., and P.J.S. processed the samples and performed the scATAC-seq experiment. S.R.Z., M.P.P., I.M., and L.O. developed the software package. I.M. led the CRAN submission. S.R.Z, M.P.P., and X.-j.L. analyzed the data. X.-j.L. supervised and directed the project. S.R.Z, M.P.P., and X.-j.L. wrote the manuscript. All authors provided edits and comments to the manuscript.
Peer review
Peer review information
Nature Communications thanks Jing Su, Pengyuan Yang and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Data availability
All relevant data supporting the key findings of this study are available within the article and its Supplementary Information files. The HealthyDonor (GSE190992) and COVID19 (GSE173590) scATAC-seq datasets have been deposited in the Gene Expression Omnibus (GEO) database under accession numbers “GSE190992” and “GSE173590”, respectively. The corresponding raw data are available via authorized access at dbGaP under accession number phs003203.v1.p1 and phs002576.v1.p1, respectively. This mouse dataset used in this study is available in the GEO database under accession code GSE111586, and was obtained by downloading from https://atlas.gs.washington.edu/mouse-atac/. The Hematopoiesis dataset was downloaded from the ArchR Manuscript Repository. All source data files and corresponding code for all figures are provided at 10.5281/zenodo.11459041.
Code availability
MOCHA is a freely available R package in CRAN that can be easily downloaded using R or RStudio (https://cran.rstudio.com/web/packages/MOCHA/index.html). MOCHA can be cited with the 10.5281/zenodo.11459041, which includes the exact MOCHA version used for this manuscript. MOCHA can also be found at https://github.com/aifimmunology/MOCHA119. Code used to generate the figures can be found at https://github.com/aifimmunology/MOCHA_manuscript and within the above Zenodo DOI.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Samir Rachid Zaim, Mark-Phillip Pebworth.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-024-50612-6.
References
- 1.Buenrostro, J. D. et al. Single-cell chromatin accessibility reveals principles of regulatory variation. Nature523, 486–490 (2015). 10.1038/nature14590 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Cusanovich, D. A. et al. Multiplex single cell profiling of chromatin accessibility by combinatorial cellular indexing. Science348, 910–914 (2015). 10.1126/science.aab1601 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Mezger, A. et al. High-throughput chromatin accessibility profiling at single-cell resolution. Nat. Commun.9, 3647 (2018). 10.1038/s41467-018-05887-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Satpathy, A. T. et al. Massively parallel single-cell chromatin landscapes of human immune cell development and intratumoral T cell exhaustion. Nat. Biotechnol.37, 925–936 (2019). 10.1038/s41587-019-0206-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.You, M. et al. Single-cell epigenomic landscape of peripheral immune cells reveals establishment of trained immunity in individuals convalescing from COVID-19. Nat. Cell Biol.23, 620–630 (2021). 10.1038/s41556-021-00690-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Zhang, B. et al. Altered and allele-specific open chromatin landscape reveals epigenetic and genetic regulators of innate immunity in COVID-19. Cell Genom.3, 100232 (2023). 10.1016/j.xgen.2022.100232 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Corces, M. R. et al. Single-cell epigenomic analyses implicate candidate causal variants at inherited risk loci for Alzheimer’s and Parkinson’s diseases. Nat. Genet.52, 1158–1168 (2020). 10.1038/s41588-020-00721-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Chen, H. et al. Assessment of computational methods for the analysis of single-cell ATAC-seq data. Genome Biol20, 241 (2019). 10.1186/s13059-019-1854-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fang, R. et al. Comprehensive analysis of single cell ATAC-seq data with SnapATAC. Nat. Commun.12, 1337 (2021). 10.1038/s41467-021-21583-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Stuart, T., Srivastava, A., Madad, S., Lareau, C. A. & Satija, R. Single-cell chromatin state analysis with Signac. Nat. Methods18, 1333–1341 (2021). 10.1038/s41592-021-01282-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Granja, J. M. et al. ArchR is a scalable software package for integrative single-cell chromatin accessibility analysis. Nat. Genet.53, 403–411 (2021). 10.1038/s41588-021-00790-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ashuach, T., Reidenbach, D. A., Gayoso, A. & Yosef, N. PeakVI: a deep generative model for single-cell chromatin accessibility analysis. Cell Rep. Methods2, 100182 (2022). 10.1016/j.crmeth.2022.100182 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Gabitto, M. I. et al. Characterizing chromatin landscape from aggregate and single-cell genomic assays using flexible duration modeling. Nat. Commun.11, 747 (2020). 10.1038/s41467-020-14497-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Li, Z. et al. Chromatin-accessibility estimation from single-cell ATAC-seq data with scOpen. Nat. Commun.12, 6386 (2021). 10.1038/s41467-021-26530-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Xiong, L. et al. SCALE method for single-cell ATAC-seq analysis via latent feature extraction. Nat. Commun.10, 4576 (2019). 10.1038/s41467-019-12630-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Yuan, H. & Kelley, D. R. Author correction: scBasset: sequence-based modeling of single-cell ATAC-seq using convolutional neural networks. Nat. Methods20, 162 (2023). 10.1038/s41592-022-01754-2 [DOI] [PubMed] [Google Scholar]
- 17.Schep, A. N., Wu, B., Buenrostro, J. D. & Greenleaf, W. J. chromVAR: inferring transcription-factor-associated accessibility from single-cell epigenomic data. Nat. Methods14, 975–978 (2017). 10.1038/nmeth.4401 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.de Boer, C. G. & Regev, A. BROCKMAN: deciphering variance in epigenomic regulators by k-mer factorization. BMC Bioinform.19, 253 (2018). 10.1186/s12859-018-2255-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ji, Z., Zhou, W. & Ji, H. Single-cell regulome data analysis by SCRAT. Bioinformatics33, 2930–2932 (2017). 10.1093/bioinformatics/btx315 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kartha, V. K. et al. Functional inference of gene regulation using single-cell multi-omics. Cell Genom.2, 100166 (2022). [DOI] [PMC free article] [PubMed]
- 21.Pliner, H. A. et al. Cicero predicts cis-regulatory DNA interactions from single-cell chromatin accessibility data. Mol. Cell71, 858–871.e8 (2018). 10.1016/j.molcel.2018.06.044 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bravo González-Blas, C. et al. cisTopic: cis-regulatory topic modeling on single-cell ATAC-seq data. Nat. Methods16, 397–400 (2019). 10.1038/s41592-019-0367-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hu, K., Liu, H., Lawson, N. D. & Zhu, L. J. scATACpipe: a nextflow pipeline for comprehensive and reproducible analyses of single cell ATAC-seq data. Front. Cell Dev. Biol.10, 981859 (2022). 10.3389/fcell.2022.981859 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Finak, G. et al. MAST: a flexible statistical framework for assessing transcriptional changes and characterizing heterogeneity in single-cell RNA sequencing data. Genome Biol.16, 278 (2015). 10.1186/s13059-015-0844-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Jiang, R., Sun, T., Song, D. & Li, J. J. Statistics or biology: the zero-inflation controversy about scRNA-seq data. Genome Biol.23, 31 (2022). 10.1186/s13059-022-02601-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kharchenko, P. V., Silberstein, L. & Scadden, D. T. Bayesian approach to single-cell differential expression analysis. Nat. Methods11, 740–742 (2014). 10.1038/nmeth.2967 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sarkar, A. & Stephens, M. Separating measurement and expression models clarifies confusion in single-cell RNA sequencing analysis. Nat. Genet.53, 770–777 (2021). 10.1038/s41588-021-00873-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ghazanfar, S. et al. Investigating higher-order interactions in single-cell data with scHOT. Nat. Methods17, 799–806 (2020). 10.1038/s41592-020-0885-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Zimmerman, K. D., Espeland, M. A. & Langefeld, C. D. A practical solution to pseudoreplication bias in single-cell studies. Nat. Commun.12, 738 (2021). 10.1038/s41467-021-21038-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Squair, J. W. et al. Confronting false discoveries in single-cell differential expression. Nat. Commun.12, 5692 (2021). 10.1038/s41467-021-25960-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Shi, P. et al. Fundamental and practical approaches for single-cell ATAC-seq analysis. aBIOTECH3, 212–223 (2022). 10.1007/s42994-022-00082-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Nuno, K. A. et al. Convergent epigenetic evolution drives relapse in acute myeloid leukemia. bioRxiv10.1101/2023.10.10.561642 (2023). [DOI] [PMC free article] [PubMed]
- 33.Brooks, M. E. et al. glmmTMB balances speed and flexibility among packages for zero-inflated generalized linear mixed modeling. R J.9, 378–400 (2017). 10.32614/RJ-2017-066 [DOI] [Google Scholar]
- 34.Taylor, S. & Pollard, K. Hypothesis tests for point-mass mixture data with application to’omics data with many zero values. Stat. Appl. Genet. Mol. Biol.8, Article 8 (2009). 10.2202/1544-6115.1425 [DOI] [PubMed] [Google Scholar]
- 35.Lachenbruch, P.A. Analysis of Data with Clumping at Zero. Biometrische Zeitschrift18, 351–356 (1976).
- 36.Pimentel, R. S., Niewiadomska-Bugaj, M. & Wang, J.-C. Association of zero-inflated continuous variables. Stat. Probab. Lett.96, 61–67 (2015). 10.1016/j.spl.2014.09.002 [DOI] [Google Scholar]
- 37.Pimentel. Kendall’s Tau and Spearman’s Rho for Zero Inflated Data. Ph. D. dissertation. (Western Michigan University, 2009).
- 38.Talla, A. et al. Longitudinal immune dynamics of mild COVID-19 define signatures of recovery and persistence. bioRxiv10.1101/2021.05.26.442666 (2021).
- 39.Bates, D., Mächler, M., Bolker, B. & Walker, S. Fitting linear mixed-effects models using lme4. arXiv10.48550/arXiv.1406.5823 (2014).
- 40.Zhang, Y. et al. Model-based analysis of ChIP-Seq (MACS). Genome Biol.9, R137 (2008). 10.1186/gb-2008-9-9-r137 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Yan, F., Powell, D. R., Curtis, D. J. & Wong, N. C. From reads to insight: a hitchhiker’s guide to ATAC-seq data analysis. Genome Biol.21, 22 (2020). 10.1186/s13059-020-1929-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Buenrostro, J. D., Wu, B., Chang, H. Y. & Greenleaf, W. J. ATAC-seq: a method for assaying chromatin accessibility genome-wide. Curr. Protoc. Mol. Biol.109, 21.29.1–21.29.9 (2015). 10.1002/0471142727.mb2129s109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Pepe, M. S. The Statistical Evaluation of Medical Tests for Classification and Prediction (OUP Oxford, 2003).
- 44.Vasaikar, S. V. et al. A comprehensive platform for analyzing longitudinal multi-omics data. Nat. Commun.14, 1–16 (2023). 10.1038/s41467-023-37432-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Heinz, S. et al. Simple combinations of lineage-determining transcription factors prime cis-regulatory elements required for macrophage and B cell identities. Mol. Cell38, 576–589 (2010). 10.1016/j.molcel.2010.05.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Bulik-Sullivan, B. K. et al. LD Score regression distinguishes confounding from polygenicity in genome-wide association studies. Nat. Genet.47, 291–295 (2015). 10.1038/ng.3211 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Cusanovich, D. A. et al. A single-cell atlas of in vivo mammalian chromatin accessibility. Cell174, 1309–1324.e18 (2018). 10.1016/j.cell.2018.06.052 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Jassal, B. et al. The reactome pathway knowledgebase. Nucleic Acids Res.48, D498–D503 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Seth, R. B., Sun, L. & Chen, Z. J. Antiviral innate immunity pathways. Cell Res.16, 141–147 (2006). 10.1038/sj.cr.7310019 [DOI] [PubMed] [Google Scholar]
- 50.Silveira, P. S. P. & Siqueira, J. O. Better to be in agreement than in bad company: a critical analysis of many kappa-like tests assessing one-million 2x2 contingency tables. arXiv10.48550/arXiv.2203.09628 (2022). [DOI] [PMC free article] [PubMed]
- 51.Love, M. I., Huber, W. & Anders, S. Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2. Genome Biol.15, 550 (2014). 10.1186/s13059-014-0550-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Gate, R. E. et al. Genetic determinants of co-accessible chromatin regions in activated T cells across humans. Nat. Genet.50, 1140–1150 (2018). 10.1038/s41588-018-0156-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Fortin, J.-P. & Hansen, K. D. Reconstructing A/B compartments as revealed by Hi-C using long-range correlations in epigenetic data. Genome Biol.16, 180 (2015). 10.1186/s13059-015-0741-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Javierre, B. M. et al. Lineage-specific genome architecture links enhancers and non-coding disease variants to target gene promoters. Cell167, 1369–1384.e19 (2016). 10.1016/j.cell.2016.09.037 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Subramanian, A. et al. Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. Proc. Natl. Acad. Sci. USA.102, 15545–15550 (2005). 10.1073/pnas.0506580102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Browaeys, R., Saelens, W. & Saeys, Y. NicheNet: modeling intercellular communication by linking ligands to target genes. Nat. Methods17, 159–162 (2020). 10.1038/s41592-019-0667-5 [DOI] [PubMed] [Google Scholar]
- 57.Safety, tolerability, & therapeutic potential of mtl-cebpa in covid-19. Health Research Authorityhttps://www.hra.nhs.uk/planning-and-improving-research/application-summaries/research-summaries/safety-tolerability-therapeutic-potential-of-mtl-cebpa-in-covid-19/ (2020).
- 58.Karcioglu Batur, L. & Hekim, N. Correlation between interleukin gene polymorphisms and current prevalence and mortality rates due to novel coronavirus disease 2019 (COVID-2019) in 23 countries. J. Med. Virol.93, 5853–5863 (2021). 10.1002/jmv.27127 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Lin, X. et al. ORF8 contributes to cytokine storm during SARS-CoV-2 infection by activating IL-17 pathway. iScience24, 102293 (2021). 10.1016/j.isci.2021.102293 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Maione, F. et al. Interleukin-17A (IL-17A): a silent amplifier of COVID-19. Biomed. Pharmacother.142, 111980 (2021). 10.1016/j.biopha.2021.111980 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Wilz, S. W. A clinical trial of IL-15 and IL-21 combination therapy for COVID-19 is warranted. Cytokine Growth Factor Rev.58, 49–50 (2021). 10.1016/j.cytogfr.2020.10.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Hou, Y., Ding, Y., Nie, H. & Ji, H.-L. Fibrinolysis influences SARS-CoV-2 infection in ciliated cells. bioRxiv10.1101/2021.01.07.425801 (2021).
- 63.Ali, G. et al. Fibrinolytic niche is required for alveolar type 2 cell-mediated alveologenesis via a uPA-A6-CD44+-ENaC signal cascade. Signal Transduct. Target. Ther.6, 97 (2021). 10.1038/s41392-021-00511-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Liang, X. et al. Clinical characterization and therapeutic targets of vitamin A in patients with hepatocholangiocarcinoma and coronavirus disease. Aging13, 15785–15800 (2021). 10.18632/aging.203220 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Juibari, A. D., Rezadoost, M. H. & Soleimani, M. The key role of Calpain in COVID-19 as a therapeutic strategy. Inflammopharmacology30, 1479–1491 (2022). 10.1007/s10787-022-01002-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.McInnes, L., Healy, J., Saul, N. & Großberger, L. UMAP: uniform manifold approximation and projection. J. Open Source Softw.3, 861 (2018). 10.21105/joss.00861 [DOI] [Google Scholar]
- 67.Trapnell, C. et al. The dynamics and regulators of cell fate decisions are revealed by pseudotemporal ordering of single cells. Nat. Biotechnol.32, 381–386 (2014). 10.1038/nbt.2859 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Peng, S. L. Forkhead transcription factors in chronic inflammation. Int. J. Biochem. Cell Biol.42, 482–485 (2010). 10.1016/j.biocel.2009.10.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Fan, W. et al. FoxO1 regulates Tlr4 inflammatory pathway signalling in macrophages. EMBO J29, 4223–4236 (2010). 10.1038/emboj.2010.268 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.He, Z.-H. et al. The nuclear transcription factor FoxG1 affects the sensitivity of mimetic aging hair cells to inflammation by regulating autophagy pathways. Redox Biol.28, 101364 (2020). 10.1016/j.redox.2019.101364 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Modi, B. P. et al. Mutations in fetal genes involved in innate immunity and host defense against microbes increase risk of preterm premature rupture of membranes (PPROM). Mol. Genet. Genomic Med.5, 720–729 (2017). 10.1002/mgg3.330 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Thimmulappa, R. K. et al. Nrf2 is a critical regulator of the innate immune response and survival during experimental sepsis. J. Clin. Invest.116, 984–995 (2006). 10.1172/JCI25790 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Yang, Y.-Y. et al. Dok3 is involved in cisplatin-induced acute kidney injury via regulation of inflammation and apoptosis. Biochem. Biophys. Res. Commun.569, 132–138 (2021). 10.1016/j.bbrc.2021.06.097 [DOI] [PubMed] [Google Scholar]
- 74.Monaco, G. et al. RNA-seq signatures normalized by mRNA abundance allow absolute deconvolution of human immune cell types. Cell Rep.26, 1627–1640.e7 (2019). 10.1016/j.celrep.2019.01.041 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Uhlén, M. et al. Proteomics. Tissue-based map of the human proteome. Science347, 1260419 (2015). 10.1126/science.1260419 [DOI] [PubMed] [Google Scholar]
- 76.Schmiedel, B. J. et al. Impact of genetic polymorphisms on human immune cell gene expression. Cell175, 1701–1715.e16 (2018). 10.1016/j.cell.2018.10.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Lachmann, A. et al. Massive mining of publicly available RNA-seq data from human and mouse. Nat. Commun.9, 1366 (2018). 10.1038/s41467-018-03751-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Lal, A. et al. Deep learning-based enhancement of epigenomics data with AtacWorks. Nat. Commun.12, 1507 (2021). 10.1038/s41467-021-21765-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Nikolic, A. et al. Copy-scAT: deconvoluting single-cell chromatin accessibility of genetic subclones in cancer. Sci. Adv.7, eabg6045 (2021). 10.1126/sciadv.abg6045 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Yu, F. et al. Variant to function mapping at single-cell resolution through network propagation. Nat. Biotechnol.40, 1644–1653 (2022). 10.1038/s41587-022-01341-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Xu, B. et al. DeNOPA: decoding nucleosome positions sensitively with sparse ATAC-seq data. Brief. Bioinform.23, bbab469 (2022). 10.1093/bib/bbab469 [DOI] [PubMed] [Google Scholar]
- 82.Gong, W., Dsouza, N. & Garry, D. J. SeATAC: a tool for exploring the chromatin landscape and the role of pioneer factors. Genome Biol.24, 125 (2023). 10.1186/s13059-023-02954-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Gleiss, A., Dakna, M., Mischak, H. & Heinze, G. Two-group comparisons of zero-inflated intensity values: the choice of test statistic matters. Bioinformatics31, 2310–2317 (2015). 10.1093/bioinformatics/btv154 [DOI] [PubMed] [Google Scholar]
- 84.Naya, H. et al. A comparison between Poisson and zero-inflated Poisson regression models with an application to number of black spots in Corriedale sheep. Genet. Sel. Evol.40, 379–394 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Gontarz, P. et al. Comparison of differential accessibility analysis strategies for ATAC-seq data. Sci. Rep.10, 10150 (2020). 10.1038/s41598-020-66998-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Chen, Y., Chen, S. & Lei, E. P. DiffChIPL: a differential peak analysis method for high-throughput sequencing data with biological replicates based on limma. Bioinformatics38, 4062–4069 (2022). 10.1093/bioinformatics/btac498 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Stark, R., Brown, G. & Others. DiffBind: differential binding analysis of ChIP-Seq peak data. R package version100 (2011).
- 88.Faux, T. et al. Differential ATAC-seq and ChIP-seq peak detection using ROTS. NAR Genom. Bioinform.3, lqab059 (2021). 10.1093/nargab/lqab059 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Qiu, X. et al. CoBRA: containerized bioinformatics workflow for reproducible ChIP/ATAC-seq analysis. Genom. Proteom. Bioinform.19, 652–661 (2021). 10.1016/j.gpb.2020.11.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Luecken, M. D. et al. Benchmarking atlas-level data integration in single-cell genomics. Nat. Methods19, 41–50 (2022). 10.1038/s41592-021-01336-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Smyth, G. K. limma: linear Models for Microarray Data. in Bioinformatics and Computational Biology Solutions Using R and Bioconductor (eds. Gentleman, R., Carey, V. J., Huber, W., Irizarry, R. A. & Dudoit, S.) 397–420 (Springer New York, 2005).
- 92.Lan, W. et al. scIAC: clustering scATAC-seq data based on Student’s t-distribution similarity imputation and denoising autoencoder. in 2022 IEEE International Conference on Bioinformatics and Biomedicine (BIBM) 206–211 (IEEE, 2022).
- 93.Maniatis, C., Vallejos, C. A. & Sanguinetti, G. SCRaPL: a Bayesian hierarchical framework for detecting technical associates in single cell multiomics data. PLoS Comput. Biol.18, e1010163 (2022). 10.1371/journal.pcbi.1010163 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Hu, D. et al. Effective multi-modal clustering method via skip aggregation network for parallel scRNA-seq and scATAC-seq data. Brief. Bioinform. 25, bbae102 (2024). [DOI] [PMC free article] [PubMed]
- 95.Zhao, F., Ma, X., Yao, B. & Chen, L. scaDA: a novel statistical method for differential analysis of single-cell chromatin accessibility sequencing data. bioRxiv10.1101/2024.01.21.576570 (2024) [DOI] [PMC free article] [PubMed]
- 96.Kapellos, T. S. et al. Human monocyte subsets and phenotypes in major chronic inflammatory diseases. Front. Immunol.10, 2035 (2019). 10.3389/fimmu.2019.02035 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Swanson, E. et al. Simultaneous trimodal single-cell measurement of transcripts, epitopes, and chromatin accessibility using TEA-seq. Elife10, e63632 (2021). 10.7554/eLife.63632 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Lareau, C. A. et al. Droplet-based combinatorial indexing for massive-scale single-cell chromatin accessibility. Nat. Biotechnol.37, 916–924 (2019). 10.1038/s41587-019-0147-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Luu, P.-L., Ong, P.-T., Dinh, T.-P. & Clark, S. J. Benchmark study comparing liftover tools for genome conversion of epigenome sequencing data. NAR Genom. Bioinform.2, lqaa054 (2020). 10.1093/nargab/lqaa054 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Meuleman, W. et al. Index and biological spectrum of human DNase I hypersensitive sites. Nature584, 244–251 (2020). 10.1038/s41586-020-2559-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Yates, A. D. et al. Ensembl 2020. Nucleic Acids Res.48, D682–D688 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Quinlan, A. R. & Hall, I. M. BEDTools: a flexible suite of utilities for comparing genomic features. Bioinformatics26, 841–842 (2010). 10.1093/bioinformatics/btq033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Hao, Y. et al. Integrated analysis of multimodal single-cell data. Cell184, 3573–3587.e29 (2021). 10.1016/j.cell.2021.04.048 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Lawrence, M. et al. Software for computing and annotating genomic ranges. PLoS Comput. Biol.9, e1003118 (2013). 10.1371/journal.pcbi.1003118 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Zou, Z., Ohta, T., Miura, F. & Oki, S. ChIP-Atlas 2021 update: a data-mining suite for exploring epigenomic landscapes by fully integrating ChIP-seq, ATAC-seq and Bisulfite-seq data. Nucleic Acids Res.10.1093/nar/gkac199 (2022). [DOI] [PMC free article] [PubMed]
- 106.Oki, S. et al. ChIP-Atlas: a data-mining suite powered by full integration of public ChIP-seq data. EMBO Rep.19, e46255 (2018). 10.15252/embr.201846255 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Youden, W. J. Index for rating diagnostic tests. Cancer3, 32–35 (1950). [DOI] [PubMed] [Google Scholar]
- 108.Lee, S., Cook, D. & Lawrence, M. plyranges: a grammar of genomic data transformation. Genome Biol.20, 4 (2019). 10.1186/s13059-018-1597-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Storey, J. D. A direct approach to false discovery rates. J. R. Stat. Soc. Ser. B Stat. Methodol.64, 479–498 (2002). 10.1111/1467-9868.00346 [DOI] [Google Scholar]
- 110.Hodges, J. L. & Lehmann, E. L. Estimates of location based on rank tests. Ann. Math. Stat. 34, 598–611 (1963).
- 111.Huber, W. et al. Orchestrating high-throughput genomic analysis with Bioconductor. Nat. Methods12, 115–121 (2015). 10.1038/nmeth.3252 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Liao, Y., Wang, J., Jaehnig, E. J., Shi, Z. & Zhang, B. WebGestalt 2019: gene set analysis toolkit with revamped UIs and APIs. Nucleic Acids Res.47, W199–W205 (2019). 10.1093/nar/gkz401 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Loh, P.-R., Kichaev, G., Gazal, S., Schoech, A. P. & Price, A. L. Mixed-model association for biobank-scale datasets. Nat. Genet.50, 906–908 (2018). 10.1038/s41588-018-0144-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Dönertaş, H. M., Fabian, D. K., Valenzuela, M. F., Partridge, L. & Thornton, J. M. Common genetic associations between age-related diseases. Nat Aging1, 400–412 (2021). 10.1038/s43587-021-00051-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Jiang, L., Zheng, Z., Fang, H. & Yang, J. A generalized linear mixed model association tool for biobank-scale data. Nat. Genet.53, 1616–1621 (2021). 10.1038/s41588-021-00954-4 [DOI] [PubMed] [Google Scholar]
- 116.Su, G., Morris, J. H., Demchak, B. & Bader, G. D. Biological network exploration with Cytoscape 3. Curr. Protoc. Bioinform.47, 8.13.1–24 (2014). 10.1002/0471250953.bi0813s47 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Kutner, M. H., Nachtsheim, C. J., Neter, J. & Wasserman, W. Applied Linear Regression Models. vol. 4 (McGraw-Hill/Irwin New York, 2004).
- 118.Alonso-López, D. et al. APID database: redefining protein–protein interaction experimental evidences and binary interactomes. Database2019, baz005 (2019). 10.1093/database/baz005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Rachid Zaim, S. et al. A MOCHA’s advanced statistical modeling of scATAC-seq data enables functional genomic inference in large human cohorts. Zenodo10.5281/zenodo.11459041 (2024).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All relevant data supporting the key findings of this study are available within the article and its Supplementary Information files. The HealthyDonor (GSE190992) and COVID19 (GSE173590) scATAC-seq datasets have been deposited in the Gene Expression Omnibus (GEO) database under accession numbers “GSE190992” and “GSE173590”, respectively. The corresponding raw data are available via authorized access at dbGaP under accession number phs003203.v1.p1 and phs002576.v1.p1, respectively. This mouse dataset used in this study is available in the GEO database under accession code GSE111586, and was obtained by downloading from https://atlas.gs.washington.edu/mouse-atac/. The Hematopoiesis dataset was downloaded from the ArchR Manuscript Repository. All source data files and corresponding code for all figures are provided at 10.5281/zenodo.11459041.
MOCHA is a freely available R package in CRAN that can be easily downloaded using R or RStudio (https://cran.rstudio.com/web/packages/MOCHA/index.html). MOCHA can be cited with the 10.5281/zenodo.11459041, which includes the exact MOCHA version used for this manuscript. MOCHA can also be found at https://github.com/aifimmunology/MOCHA119. Code used to generate the figures can be found at https://github.com/aifimmunology/MOCHA_manuscript and within the above Zenodo DOI.