ModDotPlot—rapid and interactive visualization of tandem repeats

Abstract

Motivation

A common method for analyzing genomic repeats is to produce a sequence similarity matrix visualized via a dot plot. Innovative approaches such as StainedGlass have improved upon this classic visualization by rendering dot plots as a heatmap of sequence identity, enabling researchers to better visualize multi-megabase tandem repeat arrays within centromeres and other heterochromatic regions of the genome. However, computing the similarity estimates for heatmaps requires high computational overhead and can suffer from decreasing accuracy.

Results

In this work, we introduce ModDotPlot, an interactive and alignment-free dot plot viewer. By approximating average nucleotide identity via a k-mer-based containment index, ModDotPlot produces accurate plots orders of magnitude faster than StainedGlass. We accomplish this through the use of a hierarchical modimizer scheme that can visualize the full 128 Mb genome of Arabidopsis thaliana in under 5 min on a laptop. ModDotPlot is bundled with a graphical user interface supporting real-time interactive navigation of entire chromosomes.

Availability and implementation

ModDotPlot is available at https://github.com/marbl/ModDotPlot.

1 Introduction

Large tandemly repeating blocks of DNA, such as satellite repeats and their complex higher-order structures, are ubiquitous in many eukaryotic genomes, yet have been notoriously difficult to sequence and assemble. These motifs occur disproportionately in telomeric, centromeric, and heterochromatic regions of the genome (Logsdon and Eichler 2022), and are commonly referred to as genomic “dark matter” due to their prior absence from reference genomes (Sedlazeck et al. 2018). Recent advances in long-read sequencing and assembly tools have enabled genomics researchers to successfully assemble these complex regions, culminating in the first complete human genome (Nurk et al. 2022) as well as important model organisms such as Arabidopsis (Naish et al. 2021) and nonhuman primates (Makova et al. 2024). More broadly, with tools such as Verkko (Rautiainen et al. 2023) and hifiasm (UL) (Cheng et al. 2024) now able to automatically assemble complete “telomere-to-telomere” chromosomes, developing new methods to analyze these previously dark regions of the genome has taken on new importance.

Traditionally, dot plots have been useful visualizations to characterize the structure of complex repeats (Maizel and Lenk 1988). To generate such a plot, a sequence S is typically aligned with itself using software such as MUMmer (Marçais et al. 2018), and plotted in a 2D space. This approach results in a set of line segments from $[x,y]$ to $[x+l-1,y+l-1]$ for all matches of length l (above some minimum length threshold) beginning at positions x and y in S. This yields a single diagonal line segment, representing the sequence aligned with itself, and all off-diagonal segments representing the location of paralogous repeat copies. If based on a gapped sequence alignment, these segments may also be colored by their average sequence identity, but the internal, fine-grained structure of the repeats cannot be represented by this technique.

To overcome this limitation, recent work by Vollger et al. (2022) introduced StainedGlass, which relies on a rasterized rather than vectorized approach. In this framework, the aim is to generate a similarity matrix M_w where each cell $M_w(A_i,B_j)$ relates two genomic intervals A_i and B_j of length w beginning at positions wi and wj in S. By re-framing the problem in terms of intervals rather than single bases, a percent identity can be computed between all pairs of intervals and the matrix M_w can be rendered as a heatmap where each cell (pixel) represents the percent identity between the two substrings at the corresponding interval positions. This technique has extended the previously binary dot plot into a rich spectrum of information and proven highly effective for visualizing patterns of sequence evolution within tandem repeat arrays of both humans and plants (Wlodzimierz et al. 2023, Logsdon et al. 2024).

Although heatmaps produced by StainedGlass have been useful in practice, the workflow used to generate them has inherent limitations. First, StainedGlass uses Minimap2 (Li 2018) to determine sequence identity by computing the number of matches, mismatches, insertions, and deletions between pairs of substrings. Minimap2’s alignment heuristic is not well-suited for repetitive sequences (Sahlin et al. 2023) and leads to long runtimes, especially for short tandem repeats. For example, a single 3-Mb human centromere requires over one hour to plot when running on a high-performance compute cluster. Furthermore, StainedGlass partitions the input sequence into intervals of a fixed size. Similar substrings that are split across this boundary may fail to align, leading to inaccurate identity estimates.

To improve upon these limitations, we propose a k-mer-based approach that bypasses the computationally expensive requirement of sequence alignment. Estimating sequence identity from sets of k-length substrings (k-mers) has seen increasing use in genomics (Ondov et al. 2016). Such tools typically utilize downsampling methods, such as minhash, to reduce the size of each k-mer set before estimating sequence identity using the Jaccard index or related set similarity measure.

In this work, we introduce ModDotPlot, a novel heatmap visualization tool that rapidly estimates sequence identity using hierarchical modimizers, a form of fractional minhashing (Irber et al. 2022). Modimizers are defined as hashed k-mer values that have no remainder when divided by some number s, which we refer to as the sparsity. Here we restrict s to powers of two, $s=2^d$, which conveniently results in the set of modimizers being: (i) precisely those hash values with d zeros in their least significant bits, and (ii) a strict subset of the modimizers defined by $s=2^{d-1}$. We use this efficient membership test and hierarchical property to efficiently downsample genomic k-mers at multiple levels of sparsity. We show that the resulting modimizers can be used to accurately estimate the average nucleotide identity (ANI) of two substrings, while being resistant to segmentation artifacts and orders of magnitude faster than StainedGlass. To conclude, we demonstrate ModDotPlot’s ability to elucidate the centromeric satellite structure of both plants and animals.

2 Materials and methods

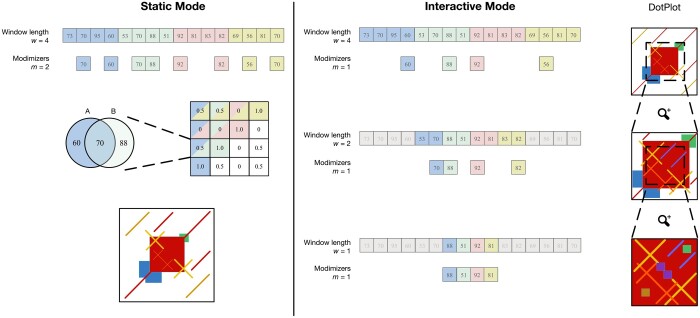
ModDotPlot takes as input a list of sequences in FASTA format and outputs a self-identity heatmap for each sequence, as well as comparative heatmaps for all pairwise combinations of sequences. In describing our methods, we assume the construction of a self-identity heatmap, but the necessary modifications for constructing comparative heatmaps is straightforward. ModDotPlot can be run one of two ways, specified at runtime: Static mode produces a static image file for each plot, while Interactive mode builds a plot hierarchy using multiple modimizer values so that the plot resolution can be adjusted in real time as the user adjusts the zoom level. We outline the workflow of both possible modes of ModDotPlot in Fig. 1.

Figure 1.

Overview of ModDotPlot’s workflow for producing a self-identity plot. Static mode: Hashed k-mers are evenly partitioned into intervals of length w. Modimizers are selected based on an estimated sketch size m within each interval. For each pairwise combination of intervals, identity is computed and stored in a matrix M_w. Finally, a heatmap is created based on the color thresholds provided. Interactive mode: Three distinct modimizer partitions are produced from a minimum interval length of $\widehat{w}$=1 up to w = 4. At launch, a heatmap is rendered for the largest window size (here, w = 4). When the field of view is zoomed by half (highlighted region), the dot plot is rendered using a submatrix created from the partition at w = 2. This process can extend until a plot produced from the minimum interval length $\widehat{w}$ is reached, with m remaining constant among all layers. While m = 1 is used here for demonstration, ModDotPlot adjusts the modimizer sparsity such that $m\approx 1000$ in practice

ModDotPlot first decomposes each sequence S of length n into a list of its constituent k-mers S_k. Each k-mer and its reverse complement are passed through a hash function $h:\Omega \to [0,H]$ for some $H\in \mathbb{R}$, with the smaller of the two values added into S_k. Once broken down into k-mers, ModDotPlot partitions S_k into evenly sized and nonoverlapping genomic intervals of size w, also referred to as the window size. We define the number of intervals as $r=\frac{n-k+1}{w}$, which we refer to as the resolution. This determines the height and width of the resulting heatmap. To reduce the runtime and space complexity of handling large sequences, ModDotPlot sketches each interval A into sets based on a modulo function, as originally proposed by Broder (1997). We formally define our algorithm for sketching S_k in Supplementary Algorithm S1. This generates the following set for each interval:

$$MO{D}_s(A)=\forall a\in \{S_k[A]\}:a\equiv 0 \text{mod} s$$ (1)

We refer to any k-mer present in the sketch $MO{D}_s(A)$ as a modimizer. We define $s\in {\mathbb{Z}}^{+}$ as the modimizer sparsity and restrict s to powers of 2. Note that the sparsity value is inversely related to the number of modimizers selected (i.e. the density), with s = 2 resulting in approximately every second k-mer being selected, s = 4 with every fourth k-mer, and so on. Given a set of k-mers sampled from a long random string, the expected number of modimizers per window is:

$$m=\mathbb{E}[|MO{D}_s(A)|]=\frac{w}{s}$$ (2)

We refer to m as the modimizer sketch size, with larger values of m increasing the accuracy of the minhash similarity estimates. Given a desired plot resolution r and target sketch size m, the corresponding window size $w=\frac{n}{r}$ and required sparsity $s=\frac{w}{m}$ can be automatically derived. Based on prior work (Ondov et al. 2016), we use m = 1000 as a good compromise between accuracy and efficiency.

In practice, if the k-mers in interval A are highly repetitive, then the true size of $MO{D}_s(A)$ can be significantly less than m. To avoid selecting too few k-mers in a window, we introduce a threshold set to half the expected number of modimizers. If the size of $MO{D}_s(A)$ is less than this threshold, modimizers are iteratively recomputed at half the sparsity until the modimizer count threshold is met or the sparsity hits one (i.e. every k-mer in A is included in the sketch).

Once the input sequence is partitioned and sketched, ModDotPlot produces a similarity matrix M_w by estimating the identity between each pairwise combination of intervals A and B, which we refer to as a cell in the matrix. We estimate the proportion of k-mers in A that are contained in B, and vice-versa, via the containment index (Broder 1997):

$${\widehat{c}}_{\mathit{mod}}(A,B)=\frac{|MO{D}_s(A)\cap MO{D}_s(B)|}{|MO{D}_s(A)|}$$ (3)

Hera et al. (2023) show that for the FracMinHash scheme, a correction factor is needed for an unbiased estimate of the containment index, to account for cases where $|MO{D}_s(A)|$ differs greatly from $|MO{D}_s(B)|$. In practice, this can occur when interval A occurs in a repetitive genomic interval while interval B does not. Since modulo hashing is a variant of fractional minhashing, the same correction applies and we include the expected value in the denominator to achieve an unbiased estimate of the containment index:

$$c_{\mathit{mod}}(A,B)=\frac{\left|MO{D}_s\right(A)\cap MO{D}_s(B\left)\right|}{\left|MO{D}_s\right(A\left)\right|(1-{(1-\frac{1}{s})}^{\left|\right\{A\left\}\right|})}$$ (4)

Furthermore, since the containment index drops exponentially with respect to the mutation rate (Koslicki and Zabeti 2019), it is useful to represent this as an estimate of percent sequence identity. As implemented in MashScreen (Ondov et al. 2019), we model the probability of mutation at each position in a k-mer with the binomial distribution to estimate the ANI as:

$$AN{I}_c(A,B)=c_{\mathit{mod}}{(A,B)}^{\frac{1}{k}}$$ (5)

For self-identity plots, ModDotPlot sets $M_w(A,B)=\max \{AN{I}_c(A,B),AN{I}_c(B,A)\}$ to ensure the resulting matrix is symmetric. We note that the containment index is not a distance metric, as it neither satisfies the symmetry property nor the triangle inequality property; however, for two equally sized intervals, we show that ANI_c correlates well with an alignment-based ANI. Furthermore, the containment index has the desirable property of not requiring a set operation in its denominator, meaning it is possible to increase the length of interval B without penalizing ANI_c. We take advantage of this property to overcome segmentation artifacts, as described later.

Once the matrix of containment indices is computed, ModDotPlot outputs an identity heatmap analogous to a genomic dot plot. The heatmap is assigned a range of color values, ranging from t (a user provided threshold identity threshold) to 100. Any cells in the matrix $<t$ are left uncolored. Use of t < 85 is not recommended, as the identity estimate rapidly loses accuracy below this value for typical values of k and m, since the higher divergence may result in very few, or zero, k-mers shared between the two intervals. Given a symmetric self-identity dot plot, the upper diagonal of the dot plot can be used to produce a triangular dot plot in addition to the standard square.

2.1 Modimizer hierarchy

Modimizers present a quick and efficient sketching approach, as given a sparsity of $s=2^d$, only the first d bits of each k-mer hash need to be checked to verify membership in MOD_s. In addition, modimizers are context-independent, providing a guarantee that any k-mer selected as a modimizer in one set will also be a modimizer in every other set, regardless of the neighboring context or genomic interval. Given these properties, it is guaranteed that any modimizer in $MO{D}_{s_1}(A)$ will also occur in $MO{D}_{s_2}(A)$ when s₁ is an integer multiple of s₂:

$$MO{D}_{s_1}(A)\subseteq MO{D}_{s_2}(A) \text{if} \frac{s_1}{s_2}\in {\mathbb{Z}}^{+}$$ (6)

Thus, for a geometric sequence of sparsity values, the smaller modimizer sets will always be subsets of the larger ones. We call this the hierarchical property of modimizers. This property distinguishes hierarchical modimizers from using a modulo function to uniformly sample k-mers (Das and Schatz 2022), and to the best of our knowledge is a novel introduction of this property. As we describe below, we leverage this property in order to reduce the memory and runtime overhead when generating dot plots at multiple zoom levels.

A hierarchical modimizer index consists of l modimizer sets with window sizes $\widehat{w},\hspace{0.17em}2\widehat{w}$, …, $2^{(l-1)}\widehat{w}$ and corresponding sparsities $\widehat{s},\hspace{0.17em}2\widehat{s}$, …, $2^{(l-1)}\widehat{s}$. Given a user-specified modimizer sketch size $\widehat{m}$ and minimum window size $\widehat{w}$, the initial sparsity is defined as $\widehat{s}=2^{\lfloor {\hspace{0.17em}\text{log}\hspace{0.17em}}_2\left(\frac{\widehat{w}}{\widehat{m}}\right)\rfloor }$. To construct progressively sparser levels of the hierarchy, let A be an interval of size 2w, and A_L and A_R be the w-sized left and right halves of A respectively. Due to the hierarchical property, the modimizers for the next sparser level can be sampled from the previous level since $MO{D}_{2s}(A)\subseteq MO{D}_s(A_L)\cup MO{D}_s(A_R)$. Repeating this process, additional levels of the hierarchy are sampled until the window size exceeds $\frac{\left|S\right|}{r}$, i.e. the resulting number of intervals would be less than the minimum resolution. For example, a 250-Mb sequence plotted with a minimum window size of 10 Kbp and a resolution of 1000 would result in 5 layers, since l = 5 is the largest l such that $2^{(l-1)}\widehat{w}\le \frac{\left|S\right|}{r}$. We formally define our algorithm for producing the modimizer hierarchy in Supplementary Algorithm S2.

The runtime and space complexity for building the initial modimizer layer is $\mathcal{O}(n)$, as this requires linear scan of the sequence of size n. The expected complexity of each successive layer is half the previous due to the sparsity increasing by powers of two, so the overall runtime and space complexity of Supplementary Algorithm S2 remains $\mathcal{O}(n)$. This approach mirrors the “multilevel winnowing” (Jain et al. 2018) or “SHIMMER” (Chin and Khalak 2019) indices, but our use of modimizers rather than minimizers allows for unbiased containment estimates. From this index, similarity matrices can be efficiently computed for any pair of genomic ranges of the input sequence, with the maximum resolution determined by the minimum window size chosen when building the hierarchy.

2.2 Offset and window expansion

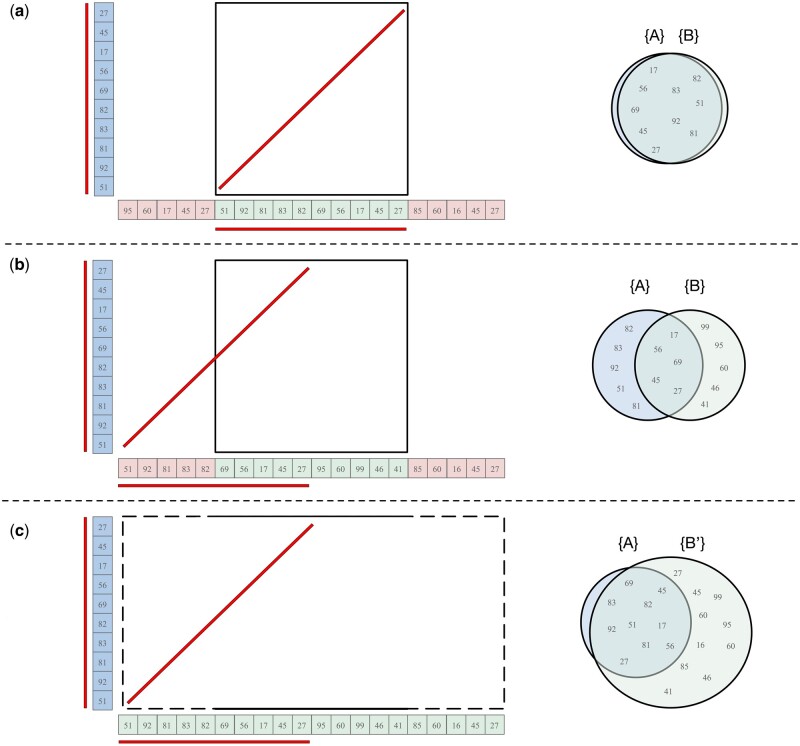
When partitioning the input sequence into discrete intervals, it’s possible that two highly similar sequences can be partitioned in different ways, resulting in an inaccurate sequence identity estimate between them (Fig. 2). This occurs whenever the two similar sequences are “out of register” and have a different offset relative to the start of the full sequence and that difference is not a multiple of the interval length. The result is that the sequences of the two intervals only partially overlap, rather than fully match. This can also occur within tandem repeats when the unit size is larger than the interval length, such as the rDNA arrays of human acrocentric chromosomes.

Figure 2.

Sample cases for different interval offsets. k-mers shared between intervals A and B are underlined. (a) In an ideal partition, the shared k-mers are perfectly captured in both intervals. (b) In a worse-case partition, only half of the shared k-mers are captured in the cell, leading to a misleading identity estimate for this region. (c) By keeping A fixed, but expanding B to $B^{\prime }$, ModDotPlot is able to better capture the similarity between two similar sequences with different offsets. The containment index of A in $B^{\prime }$ is then used to determine the score of the dot plot matrix cell $M_w(A,B)$

To overcome this offset issue, ModDotPlot extends each interval B by $\frac{w}{2}$ in each direction to form the expanded interval $B^{\prime }$. The containment index is then computed as $c_{\mathit{mod}}{(A,B^{\prime })}^{1/k}$, accounting for any sequence similarities that extend beyond the boundaries of B. We show the effect of this approach when computing the containment index in Fig. 2, as well as a practical example with human rDNA in Supplementary Fig. S1. Since B does not appear in the denominator of Equation (4), expanding the size of B does not penalize or bias the containment index. Doubling the size of B accounts for the worst-case scenario of a match diagonal beginning in the middle of the interval, and so is the default behavior, but this expansion factor can be turned off or adjusted if necessary.

2.3 Implementation and user interface

ModDotPlot is implemented in the Python programming language (version 3.7 or later). By default, ModDotPlot runs in interactive mode using Plotly with Dash (Hossain 2019), which itself uses the Flask web framework. Consequently, plots are visualized on a web browser connected to the user’s localhost. Interactive ModDotPlot can also be run remotely, e.g. on a compute cluster, via port forwarding over an ssh tunnel. In static mode, containment indices are saved into a compressed BED file, and dot plots are produced using the Plotnine plotting library (Kibirige et al. 2024). In addition to the standard rectangular plots, static mode also supports triangular plot styles.

An important parameter common to all k-mer based methods is the choice of k, as this represents a trade-off between sensitivity and specificity. Smaller k-mers are more sensitive for detecting identity within divergent intervals, but lose specificity due to chance k-mer collisions. ModDotPlot allows for flexibility in setting k, but based on prior work (Ondov et al. 2016), we set a default k = 21 to ensure accurate estimates in most cases.

k-mers are hashed using MurmurHash3 (Appleby 2016) and all similarity matrices are stored in the form of NumPy arrays (Harris et al. 2020). The size of a similarity matrix is proportional to $\mathcal{O}(r^2)$ rather than the length of the genome sequence. By default, ModDotPlot uses a resolution of r = 1000 for efficient visualizations on most standard displays. To enable a responsive interface in interactive mode, a full similarity matrix is precomputed for each level of the modimizer hierarchy. However, since the number of layers scales logarithmically with the sequence length, only a few layers are needed in practice (e.g. $l\le 5$). When zooming on the plot, the appropriate matrix is chosen such that the number of cells in the matrix is at least the number of pixels in the plot. To prevent redundant computations of similarity matrices for future exploration, NumPy matrices can be saved as binary files and loaded directly as input.

Supplementary Figure S2 shows a screenshot of ModDotPlot’s user interface in interactive mode. Hovering over the plot shows the exact genomic coordinates, along with the corresponding estimated identity of each section. This example shows a plot highlighting the repeat-rich 30-Mb Y chromosome from a siamang gibbon (Symphalangus syndactylus). Users can select a number of preset color-schemes, including high contrast schemes to aid visually impaired or color-blind users, or specify custom colors, either in hex code or RGB format. ModDotPlot also supports the creation of fully customizable static plots as PDF and PNG files.

3 Results

3.1 Plot accuracy

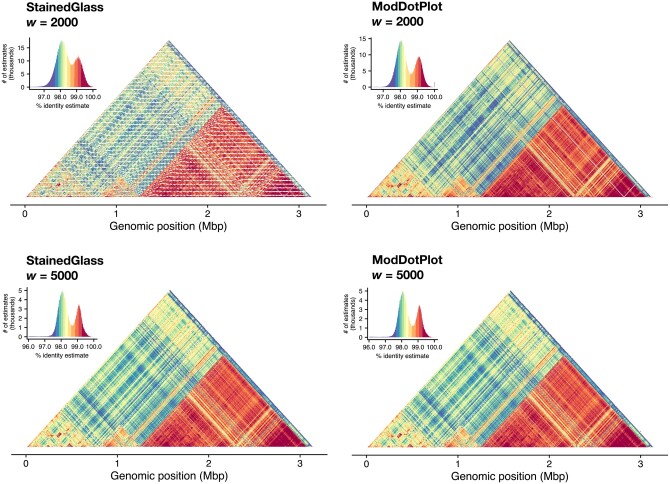
To showcase the improvements of ModDotPlot over StainedGlass, Fig. 3 shows the plots produced by both tools for the centromeric alpha satellite array of the human HG002 X chromosome. The StainedGlass default window size of 2000 produces a highly “checkered” plot containing streaks of apparently low identity within the array. However, this is not representative of any sort of centromere biology; rather, it is an artifact of partitioning the genome into windows of a fixed size. The canonical DXZ1 higher-order repeat (HOR) present in this array consists of twelve monomers totaling ∼2050 bp (Miga et al. 2014), which is slightly longer than the selected window size. Using a window size of 5000 is sufficient to contain a complete HOR and alleviate this problem, but this comes at the cost of a lower resolution plot and requires advance knowledge of the repeat structure. In contrast, ModDotPlot produces an accurate plot regardless of window length and HOR size.

Figure 3.

Plots produced by StainedGlass (column 1) and ModDotPlot (column 2), representing the upper diagonal self-identity heatmap of the HG002 DXZ1 satellite array (ChrX:57,680,000–61,000,000). Rows represent a window size of 2000 (r = 1570 in ModDotPlot) and 5000 (r = 678) respectively. ModDotPlot was run with a default m = 1000. Plotting artifacts in the StainedGlass w = 2000 example are due to interactions between the partitioning window size and tandem repeat periodicity

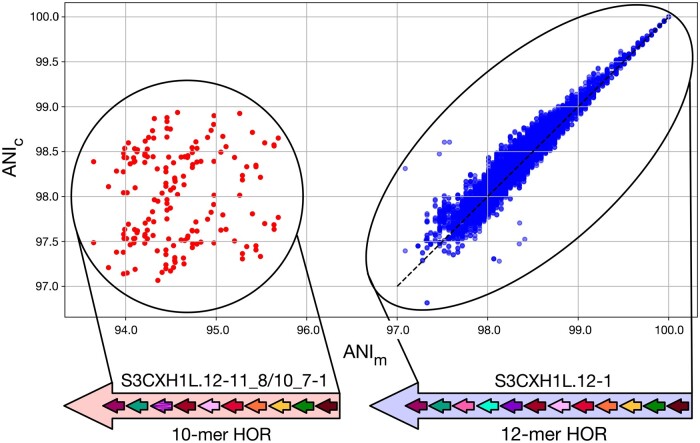
Figure 4 shows the strong correlation between ModDotPlot ANI_c values and an alignment-based ANI_m computed by MUMmer (Marçais et al. 2018), but with the accuracy of ANI_c decreasing with increasing sparsity (reduced sketch size), as expected (Supplementary Fig. S3). For each pairwise combination of HORs present in chrX:58,000,771–58,200,827, the MUMmer ANI_m was taken from the “AvgIdentity” of one-to-one alignments computed by the v4.0.1 “dnadiff” program. The vast majority of HORs, representing the canonical 12-mer structure, fall within the consensus range of 97%–100% sequence identity (Miga et al. 2014) with high concordance (r = 0.965) between ModDotPlot and MUMmer. Larger differences between the two methods arise from pairs of windows containing structural variation that confound MUMmer’s alignment-based similarity.

Figure 4.

Scatterplots showing the linear relationship between MUMmer ANI_m and ModDotPlot ANI_c, using CHM13 chrX:58 000 771–58 200 827. The outlier group labeled on the left represents a noncanonical 10-mer HOR (chrX:58 060 405–58 062 120), which is scored differently by the two methods due to the presence of a large deletion when compared to the 12-mer HOR. The dashed line represents ANI_m = ANI_c

The containment index used by ModDotPlot does not penalize k-mer copy number differences or large insertions/deletions (indels) in the same way a global alignment would. For example, within the chromosome X centromeric array we observed a small number of windows where the ANI_m and ANI_c values differed substantially. Closer investigation revealed the presence of a single noncanonical HOR, consisting of a shorter 10 monomer repeat that was scored higher by ANI_c when compared to the canonical 12 monomer repeat (Fig. 4). The difference between these two repeats is interpreted as a large indel by MUMmer, resulting in a reduced ANI_m. However, this difference is not penalized by ANI_c, as the 10 monomers present in the shorter HOR are well-contained within the canonical 12 monomer.

Thus, ANI_c is more akin to a local alignment similarity, i.e. the average similarity between the sequences that are shared, and reflects the point mutation rate between two sequences rather than the rate of larger structural variants. This is an important distinction, because in this case MUMmer ANI_m confounds these two evolutionary processes, while ANI_c isolates the point mutation rate of the individual monomers. Such differences between ANI_c and ANI_m are most pronounced within HOR satellite arrays, which are prone to unequal crossing over leading to frequent expansion and contraction of the arrays (Altemose et al. 2022). For this reason, the UniAligner (Bzikadze and Pevzner 2023) tool, which is specifically built for aligning long tandem repeats, similarly uses an indel penalty of zero during its k-mer alignment phase.

3.2 Modimizer sparsity

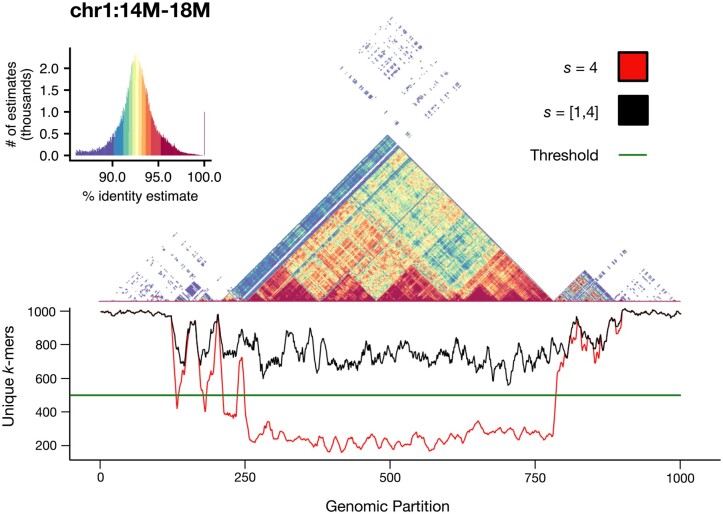
Compared to other sketching approaches, modimizers lack any sort of “window guarantee,” meaning that no lower bounds exist on the number of k-mers that will be selected for each interval. In addition, the containment index is computed on sets of k-mers, not multisets (i.e. only the presence or absence of a k-mer is considered), so highly repetitive intervals will typically result in smaller k-mer sets, which can lead to reduced accuracy when estimating the containment. Although this is partially taken into account by the error term provided in Equation (4), we demonstrate that by dynamically modifying the sparsity, as done in Supplementary Algorithm S1, the number of modimizers selected per window can be kept above acceptable levels. Figure 5 shows this on a 4-Mb centromeric region of CHM13 chromosome 1. Regions of alpha satellite repeats show a steep decline in the number of distinct k-mers; however, this can be corrected by adaptively reducing the modimizer sparsity in this region to boost the number of k-mers selected per window to at least $\frac{m}{2}$ and thus improve the containment estimates. Without this correction, we find that real similarities between low-complexity satellite arrays can go entirely undetected.

Figure 5.

Self-identity plot of the centromere of CHM13 Chromosome 1, overlaid with a smoothed unique k-mer frequency chart. Using a window size w = 4000 and a sparsity s = 4, the expected number of modimizers per window is m = 1000. When using an uncorrected sparsity value, the number of unique modimizers per window can drop to under 200. By detecting the unexpectedly small set sizes and adjusting the sparsity of these windows, the total number of modimizers in each window can be increased to at least $\frac{m}{2}$ (or, in pathological cases, all k-mers in the window)

3.3 Comparative plots

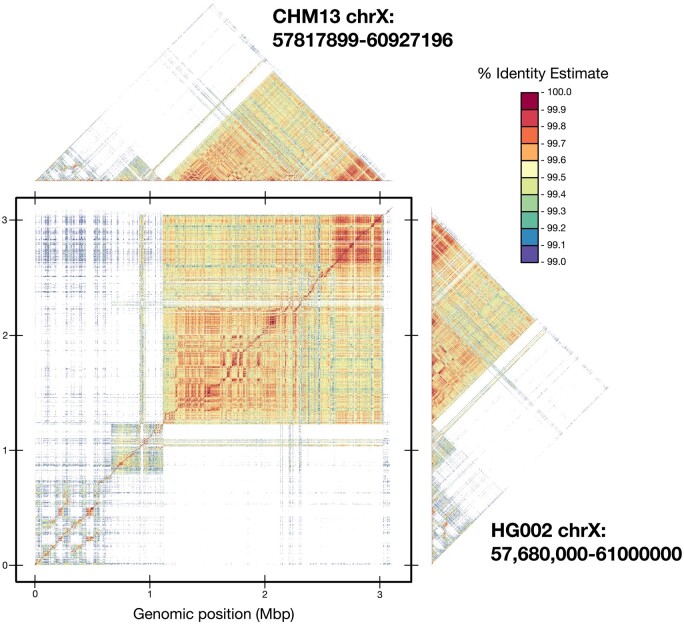
In addition to self-identity plots, ModDotPlot is also able to generate comparative plots between two different sequences. As an example, we showcase a pairwise dot plot between the DXZ1 alpha satellite arrays of two different human X chromosome centromeres, one from the HG002 genome and one from the CHM13 genome (Fig. 6). These two arrays have been previously assembled and compared (Altemose et al. 2022), but it is difficult to understand their structural differences by comparing only their self-identity plots. By plotting the two arrays against each other, their orthology relationship becomes clear. The comparative dot plot of the HG002 and CHM13 DXZ1 arrays reveals a faint diagonal representing the shared history of the two sequences, punctuated by over 300 large duplications/deletions distributed throughout the array (Bzikadze and Pevzner 2023). As noted above, centromeric satellite arrays are one of the fastest evolving regions of the human genome and accumulate many such structural variants through various recombinational mechanisms. Because of their unique evolutionary patterns, and propensity for bulk insertions/deletions, they have been one of the most difficult regions of the genome to align using traditional approaches.

Figure 6.

Comparative dot plot of chromosome X DXZ1 satellite array from the HG002 and CHM13 genomes, overlaid with self-identity plots, using a 99% identity threshold. A faint, high-identity diagonal is visible in the comparative plot, indicating the orthologous sequences between these two highly variable arrays

3.4 Runtime and memory

In Table 1, we compare the runtime and memory usage of ModDotPlot to StainedGlass across input sequences of various species and sizes. These include the HG002 X chromosome centromere (same sequence as Fig. 3), the gibbon Y chromosome (Supplementary Fig. S2), the human Y chromosome (Rhie et al. 2023), and the entire gap-free reference genomes of Arabadopsis (Naish et al. 2021) and CHM13 (Nurk et al. 2022), containing 5 and 24 chromosomes, respectively. For each input, both a static matrix and interactive matrices containing three layers were produced, based on a window size proportional to the length of the largest chromosome in the input group. Interactive StainedGlass plots were created in a similar way to ModDotPlot (i.e. a bottom-up approach based on a minimum window size), and stored in Cooler format (Abdennur and Mirny 2020).

Table 1.

Analysis of memory and runtime needed to produce the similarity matrix^a

				ModDotPlot		StainedGlass
Sequence	n (mbp)	Plot Type	w (bp)	CPU time (s)	Memory (GB)	CPU time (s)	Memory (GB)
Human CHM13 Chr1 Centromere	4.0	Static	4000	11.10	0.43	1871.31	12.95
		Interactive	1000	204.85	1.16	2812.49	13.44
Gibbon mSymSyn1 ChrY	29.9	Static	32 000	51.16	2.05	9857.57	30.13
		Interactive	8000	193.22	2.41	11 264.01	33.50
Human HG002 ChrY	62.5	Static	64 000	80.47	4.06	11 214.19	43.18
		Interactive	16 000	269.84	5.90	14 806.91	48.95
Arabadopsis Col-CEN Whole Genome	128.5 c = 5	Static	32 000	289.12	6.13	16 014.17	33.41
		Interactive	8000	1734.11	9.57	20 187.19	35.20
Human CHM13 Whole Genome	3117.3 c = 24	Static	256 000	15 238.04	40.24	—	—
		Interactive	64 000	29 101.76	44.31	—	—

^aThis does not include plot runtime, as that is the same between StainedGlass and ModDotPlot. ModDotPlot was run with a target sketch size of m = 1000 for all samples. For the whole genome assemblies of Arabadopsis and CHM13, the runtime includes the comparative matrix between each pairwise combination of chromosomes, in addition to self-identity comparisons. StainedGlass was unable to complete CHM13 whole genome within 72 h of CPU time.

In all cases, ModDotPlot exhibits orders of magnitude lower runtime and memory requirements than StainedGlass. An analysis of the Snakemake report generated by StainedGlass showed that the Minimap2 alignment dominated the runtime and memory usage and was the clear bottleneck of the pipeline. We note that despite both tools requiring the sequence identity computation of r² cells in each matrix, importantly, ModDotPlot’s runtime is independent of sequence length n. Computing ANI_c for each cell requires a set intersection operation on two sets of size m, making Equation (5)’s runtime complexity $\mathcal{O}(m)$. This can be observed in Table 1, as in interactive mode with high r, both Y chromosomes and the Human Chr1 centromere took a similar amount of CPU time, despite each sequence being vastly different in size. In contrast, StainedGlass requires each cell to run Minimap2 on an unsketched sequence of length $w=\frac{n}{r}$. The $\mathcal{O}(n)$ runtime for identity estimation hinders the ability of StainedGlass to visualize whole genomes and large sequences.

4 Discussion

Traditional dot plot methods have struggled with the complexity and abundance of genomic repeats, often leading to oversimplified or inaccurate representations. The use of heatmaps offers a substantial improvement over classic vectorized dotplots as they allow for a more natural and nuanced representation of tandem repeats, thereby capturing subtle variations and patterns that vectorized plots obscure. This is especially true for the typical use case where the genomic sequences are manyfold larger than the resolution of the display so that a single pixel intrinsically represents many kilobases of sequence (e.g. a gigabase genome plotted on a 4K display). ModDotPlot improves upon previous methods in terms of speed and computing requirements by an order of magnitude, enabling visualization of whole genomes on a laptop. At the heart of ModDotPlot’s efficiency is its use of hierarchical modimizers, which enable the interactive visualization of vertebrate-sized genomes on a typical laptop. Additionally, the use of expanded intervals combined with the containment index efficiently corrects for registration artifacts inherent to rasterized similarity heatmaps. This is especially important for centromeric and rDNA repeats that are composed of large subunits that can straddle adjacent windows.

A number of additional features could be added to further extend the utility of ModDotPlot. We note how readily satellite arrays and other repeat classes can be visually identified from the dot plots, e.g. satellite arrays appear as dense blocks of color, segmental duplications as lines, and palindromes as lines that cross the diagonal. This raises the possibility of repeat annotation and classification using automated interpretation of dot plots, possibly through machine learning techniques. Additionally, the integration of arbitrary annotation tracks alongside the dot plots would add the ability to visualize genes and other notable features in the context of structural repeats and variation, as is possible with other visualization tools such as HiGlass (Kerpedjiev et al. 2018). Lastly, ModDotPlot currently computes similarity matrices in advance of plotting, but with sufficiently fast set operations it would be possible to compute similarity matrices directly from the hierarchical modimizer index on the fly. This would enable interactive exploration of plots with essentially arbitrary resolution.

ModDotPlot highlights the power of minhashing as a fast yet accurate heuristic for sequence alignment, even within the most complex satellite repeat arrays. While our results show that using modimizers to estimate ANI_C is accurate within the recommended 85% identity threshold, alternative sketching approaches may further the utility of this approach. Minmers, for example, allow for an unbiased and accurate identity estimate, with the added advantage of having a window guarantee (Kille et al. 2023). While such methods can improve sensitivity for more diverged sequences, this comes at the expense of being slower to compute. However, the results presented here suggest that such methods may be able to guide alignments through highly repetitive and variable satellite arrays, ultimately improving our understanding of the structure, function, and evolution of these previously dark regions of the genome.

Supplementary data

Supplementary data are available at Bioinformatics online.

Conflict of interest

None declared.

Funding

This work was supported, in part, by the Intramural Research Program of the National Human Genome Research Institute, US National Institutes of Health [to A.P.S. and A.M.P.]; NSF awards [IOS-2216612, IOS-1758800 to M.C.S.]; and the Human Frontier Science Program award [RGP0025/2021 to M.C.S.]. This work utilized the computational resources of the NIH HPC Biowulf cluster (https://hpc.nih.gov).