Effects of recirculation and air change per hour on COVID-19 transmission in indoor settings: A CFD study with varying HVAC parameters

Abstract

COVID-19 has already claimed over 7 million lives and has infected over 775 million people globally [1]. SARS-CoV-2, the virus that causes Covid-19, spreads primarily through droplets from infected people's airways, rendering Heating, Ventilation, and Air Conditioning (HVAC) systems critical in controlling infection risk levels in the indoor environment. To understand the dynamics of exhaled droplets and aerosols and the percentage of particles that are inhaled, escaped, recirculated, or trapped on different surfaces for a variety of environmental settings, we have presented our findings from the Computational Fluid Dynamics (CFD) modeling to investigate the impact of changing HVAC parameters in this paper. When combined with the spatial and temporal distribution of droplets, this method can be used to assess the potential risk and strengthen resilience. This finding demonstrates the viability and usefulness of CFD for modeling the distribution and dynamics of droplets and aerosols in confined environments. Our study demonstrates that raising the Air Change per Hour (ACH) from 2 to 8 reduces the risk of particle inhalation by nearly 70 %. Additionally, limiting the amount of air recirculation or increasing the amount of fresh air helps to reduce the number of airborne particles in an indoor space. To reduce the potential for respiratory droplet-related transmission and to provide relevant recommendations to the appropriate authority, the same computational approach could be applied to a wide range of ventilated indoor environments such as public buses, restaurants, exhibitions, and theaters.

1. Introduction

According to the [1], coronavirus spreads through coughing/sneezing respiratory droplets larger than 5 μm [2,3]. These particles, when airborne and then directly inhaled or transmitted from infected surfaces, play a crucial role as the primary medium for transmitting the virus. Extensive research has been conducted to investigate the feasibility of viral transmission through smaller airborne particles [4]. From the literature, we can find growing evidence supporting the detection of SARS-CoV-2 virus RNAs in air-suspended particles, which further strengthens the hypothesis of pathogen transmission and survival in the air [5,6]. Furthermore, analysis of upper respiratory tract specimens from asymptomatic individuals infected with the COVID-19 virus has shown that the respiratory microparticles of infected individuals can significantly contribute to the airborne spread of the virus during routine activities [7,8].

When discussing floating droplet particles, the comprehension of their generation, induced by exhalation, talking, coughing, and sneezing becomes important [9,10]. Within indoor environments, some of these produced particles exit the space through ventilation, while others deposit on surfaces and may settle or re-enter the air, and the rest are inhaled by people. In indoor transmission of microorganisms, the distribution of droplets varies substantially due to the presence of flow patterns. Therefore, understanding the flow pattern and limiting the spread of droplets in indoor environments such as workplaces, conference rooms, elevators, airlines, and restaurants is a common topic of discussion, and potential solutions are frequently presented [[11], [12], [13], [14], [15]]. Prior to the COVID-19 pandemic, multiple studies were conducted by Gupta et al. [[16], [17], [18]] to explore the dispersion of human respiratory droplets under varying conditions and identified importance of strategic placement of inlet and outlet based on flow trajectories. Moreover, the role of doors and windows in the dynamics of airflow and the subsequent dissemination of particles should not be underestimated. In 2020, a study [19] on aerosol transmission in the classroom showed that opening the windows in a room reduces aerosol transmission between students by 80 %. Similarly, Z. Zhang et al. [20], identified aerosol transmission channels inside an urban bus and assessed risk-reduction strategies. Although their study highlighted the dilution of particle concentration caused by airflow recirculation through the window, the authors didn't identify the optimum percentage of recirculation that might contribute to a reduction in the particle concentration. In contrast, there have been researchers who have focused on examining the spatial risks within indoor environments. For instance Ref. [21], employed numerical modeling to assess the dispersion of cough droplets in a small conference room and found lateral-supply top-return and upper-supply top-return are more likely to infect those seated in the center. Similarly, [15] conducted a simulation study on the transmission of virus-laden droplets from sneezing at a café and concluded that face-to-face dining is extremely susceptible to direct infection.

To minimize the spread of the pathogen-containing particles, all the works presented above discussed about increasing the percentage of particles that leave the originating space, thereby reducing the percentage of particles that deposit onto surfaces and the body. These control mechanisms can be broadly classified into two categories; behavior-based and engineering-based controls. It is well acknowledged that the risk of transmission can be lowered by behavior-based controls, such as isolation, frequent hand washing, and good workplace hygiene. Similarly, in indoor settings, the spread of the SARS-CoV-2 virus can be influenced by engineering controls, such as heating, ventilation, and air conditioning system settings, as this virus is primarily transmitted through inhalation. As a part of this engineering control, many organizations have advocated for increased outside air ventilation rates, but little information regarding precise ventilation and filtration goals has been found to date. Furthermore, the literature we have reviewed seldom mentions the proportion of air recirculation needed to achieve ideal air quality. Therefore, the generation and exposure in an environment resembling an indoor environment with varied HVAC settings, particularly the combined impact of recirculation and ACH, still remain unclear.

A considerable number of studies have focused on modeling indoor spaces to analyze the risks associated with coughing and particle dispersion. Among these spaces, the classroom environment in educational institutions emerges as one of the most crucial settings to be modeled for such analyses. According to the 2020 census, approximately 73.2M students were enrolled in school, representing 23.3 % of the population aged 3 and older [22], with college students adding an additional 19.0M [23]. Thus, there is significant interest in understanding how airborne particles can spread in semi-confined, ventilated indoor environments, such as classrooms, considering the instructor or a student releases the virus in the form of droplets or aerosol. Due to the heightened interest in this problem domain, this study aims to assess the classroom type indoor transmission risk by employing the CFD technique using the Ansys Fluent solver. By conducting different ventilation parameter testing (i.e., ACH and recirculation), this study aims to aid educational institution authorities and facility managers in evaluating risks associated with inhalation-transmitted pathogens and thus facilitating the development of an enhanced resilient indoor classroom environment.

2. Methods

In this section, we will cover the methodologies and parameters used in designing the classroom, generating the mesh, establishing initial and boundary conditions for the model, and understanding the core equations that control particle transport, force balance, and turbulence.

2.1. Classroom geometry

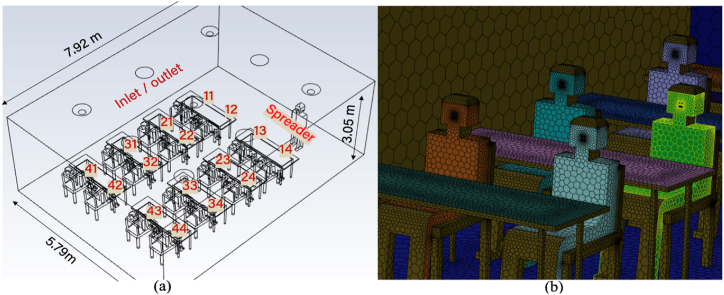
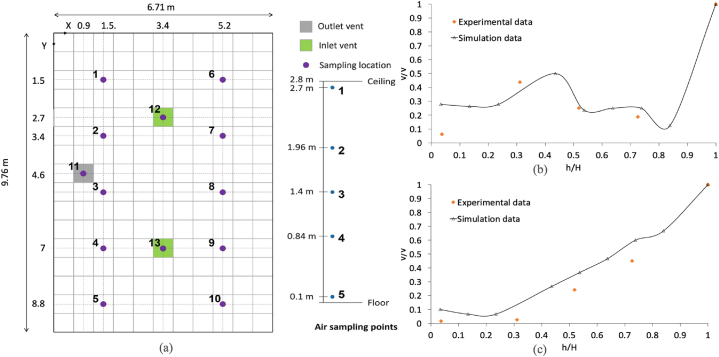
While there is a wide variety of classroom sizes, we choose to model a small, standard classroom with modest furnishing. This study considered a representative classroom of around 140 m³ in size, at The University of Arizona. Solid Works 3D modeling software was used to develop a three-dimensional model of the room using the following dimensions: 7.92 m in length, 5.79 m in width, and 3.05 m in height, and can accommodate 16 individuals (Fig. 1 (a)). Since similar-sized rooms are frequently used for conferences and meetings in the corporate world, thus the model's conclusions are applicable in a range of indoor settings. In this study, there are 16 students seated at desks (seating height of 1.30 m from the floor) and 1 instructor standing (standing height of 1.76 m) at the front of the classroom [24]; Fig. 1 depicts the geometry of the room.

Fig. 1.

Modeled (a) classroom geometry, (b) representative 3D human body geometry.

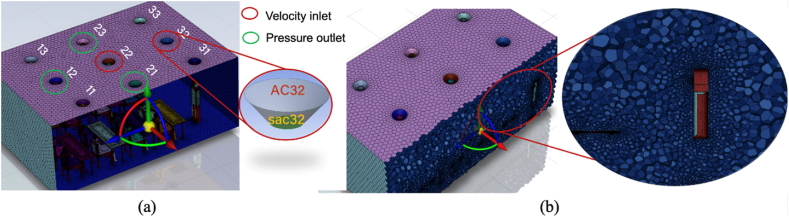
The model includes chairs and tables, and each student is represented by a model of similar stature. A human body with a rectangular head shape was modeled for each individual (Fig. 1 (b)). We considered a $3.124\times {10}^{-4}$ m² mouth opening of the human body to be the primary origin of cough injection [25]. To enhance geometrical realism and flow direction integrity, we modeled chairs and tables in the classroom. As depicted in Fig. 2 (a), we modeled 9 inlet and outlet locations for this classroom to model and evaluate the effect on recirculation and spatial distribution of inlet/outlet locations. To simulate particle recirculation, outlets were strategically configured with varying ratios of reflecting and non-reflecting surface areas. For instance, when considering 30 % recirculation, 30 % of the outlet area reflects particles back into the space, while the remaining 70 % of the outlet area allows particles to exit the computational domain as they reach the outlet. By adjusting these ratios, we were able to simulate different levels of particle recirculation within the space. For this study, we conducted tests on seven out of the nine specified locations for the inlet/outlet combination, as presented in Table 1. Each inlet and outlet were designed with two sections, namely "AC" (with a surface area of $19.63\times {10}^{-2}$ m²) and "sac" (with a surface area of $3.14\times {10}^{-2}$ m²), in order to enhance the modeling flexibility of the ACH and air recirculation percentage (Fig. 2(a)). The airflow from the inlets was assumed to be perpendicular to the inlet boundary. Depending on the modeling scenarios, our designed inlet/outlet locations and corresponding "AC" and "sac" sections were modeled as velocity inlet, pressure outlet, or wall to satisfy the ACH and air recirculation needs for that specific scenario.

Fig. 2.

(a) Surface meshing with adaptive inlet/outlet design, (b) Volume meshing.

Table 1.

Summary of simulated scenarios.

Scenario	ACH	Airflow (m3/min)	Recirculation %	Inlet	Outlet	Inlet velocity (m/s)
1	2	4.67	70 %	AC32, AC22, sac32, sac22	AC12, sac21, sac23	0.2
2	4	9.35	70 %	AC32, AC22, sac32, sac22	AC12, sac21, sac23	0.4
3	6	14.02	70 %	AC32, AC22, sac32, sac22	AC12, sac21, sac23	0.6
4	8	18.69	70 %	AC32, AC22, sac32, sac22	AC12, sac21, sac23	0.8
5	2	4.67	50 %	AC32, AC22, sac32, sac22	AC11, AC13, sac21, sac23	0.2
6	4	9.35	50 %	AC32, AC22, sac32, sac22	AC11, AC13, sac21, sac23	0.4
7	6	14.02	50 %	AC32, AC22, sac32, sac22	AC11, AC13, sac21, sac23	0.6
8	8	18.69	50 %	AC32, AC22, sac32, sac22	AC11, AC13, sac21, sac23	0.8
9	2	4.67	30 %	AC32, AC22, sac32, sac22	AC12, sac21, sac23	0.2
10	4	9.35	30 %	AC32, AC22, sac32, sac22	AC12, sac21, sac23	0.4
11	6	14.02	30 %	AC32, AC22, sac32, sac22	AC12, sac21, sac23	0.6
12	8	18.69	30 %	AC32, AC22, sac32, sac22	AC12, sac21, sac23	0.8

2.2. Mesh generation

As shown in Fig. 2, a polyhedral mesh of the classroom was developed for the purpose of this study. The mesh was generated using the meshing software ANSYS Fluent. The mesh contains 789,700 mesh cells, 4,456,383 nodes, and 5,295,323 faces with a maximum surface skewness of 0.751, orthogonal quality of (minimum = 0.18, maximum = 1, and average = 0.93), and minimum cell volume of ${1.27e}^{-10}{m}^3$. A finer mesh can capture gradients across an element more precisely. Nevertheless, because solving the model with very fine mesh sizes throughout the entire volume is computationally expensive, it is advantageous to have different mesh sizes depending on the area. To capture velocity and pressure gradients more correctly near surfaces, we used a finer mesh near the body surfaces and progressively increased it as the distance from the surface and walls increased (e.g., Fig. 2. (b) for an illustration).

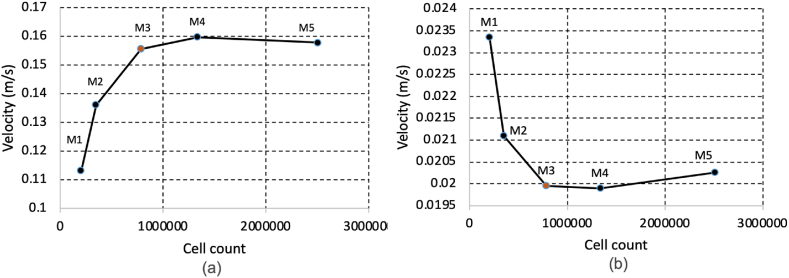
2.2.1. Mesh independence

Mesh independence analysis was conducted to determine the optimal mesh size that maintains the required precision while minimizing computational resources. An adaptive meshing approach was employed, where regions are refined or coarsened to ensure sufficient resolution in critical areas while keeping the total cell count manageable. Five different mesh sizes were tested: 201,260 cells (M1), 347,705 cells (M2), 789,700 cells (M3), 1,334,786 (M4), and 2,505,831 cells (M5). The velocity was observed at two different locations, as shown in Fig. 3(a) and (b). The results indicate that the velocity values stabilize at M3 and remain consistent when the mesh is further refined to M4 and M5. Therefore, the M3 mesh was selected for this study.

Fig. 3.

Mesh independence study showing velocity measurement at different locations.

2.3. Boundary conditions

According to ASHRAE 62.1 guidelines for indoor air quality, the minimum ACH rates permitted in a classroom breathing zone ranges from 4 to 8. Acceptable outside air rates for a classroom with nine or more students are 0.28 m³ per minute per person and 37 people per 100 m² for air class 1 [26]. As used here, "air class 1″ refers to an environment in which the air is clean, smells pleasant, and causes minimal discomfort to the senses.

According to this guideline, our model classroom must have a minimum airflow of 6.26 m³/min to accommodate 16 students and 1 instructor. This minimal 6.26 m³/min flow rate corresponds to a 2.68 ACH level. In this study, three different recirculation levels and four ACH levels were employed. The determination of the ACH and recirculation level for our model was based on the facility management report of the University of Arizona [27], which provided comprehensive data on their facilities. According to this report, among the 388 facilities on the campus, including classrooms, 50 % of them had ACH values exceeding 8, while 26 % fell within the range of 6–8 ACH. Additionally, 24 % of the facilities ranged from 2 to 4 ACH, and only 3 facilities had ACH values lower than 2. As a result, our study encompassed four distinct ACH levels: 8, 6, 4, and 2. The higher ACH values were representative of newer facilities and hospital buildings, whereas the lower ACH values potentially indicated older facilities. Moreover, according to the report the air handling units (AHUs) at the University of Arizona has a range of fresh air intake from 4 % to 100 %, or alternatively, a recirculation range from 96 % to 0 %. Furthermore, existing literature [28] suggests that an air recirculation rate of 70–80 % is considered energy-efficient for air conditioning systems. In light of this background knowledge, three distinct levels of air recirculation were selected for our study: 70 %, 50 %, and 30 %. The primary objective of this selection was to create a comprehensive range of ACH and recirculation scenarios that encompassed significant variations in airflow patterns and particle transport behavior. Furthermore, as part of this study, we considered an average wall temperature (including the floor, ceiling, and side walls) of 300 K, along with an average body heat flux of 30 W/m², representing a seated resting position for the students. The incoming air temperature was set at 298 K.

2.4. Problem description

The question addressed by this study is the exposure of students to respiratory droplets emitted by a person (the instructor) in a classroom environment with different mechanical ventilation conditions. We considered the instructor to be the emitter due to the physical orientation of the teacher and students, which offers a more appropriate vantage point for evaluating face-to-face instruction. When the emitter coughs, it releases respiratory droplets. The coughing event produces particles that range in size from one to hundreds of micrometers, are made up of saliva and mucus, and are expelled out with the exhaled air stream. Each of the instances considered in this study is a component of a matrix of hypothetical scenarios in which we assessed the ultimate fate of the particles (e.g., inhaled, trapped, recirculated, deposited on different surfaces) following the injector's coughing, for a 6-min simulation period.

2.5. Particle size distribution

It is crucial to consider precise particle form, size, and kinetics since particle characteristics significantly impact aerosol and droplet movement within a system. As there is no universal agreement on particle size or suspension time threshold, the distinction between aerosols and droplets is rather arbitrary. Droplets are suspended particles with a diameter higher than 5 μm, whereas aerosols are particles with a diameter smaller than 5 μm. This is the classic distinction between a "droplet" and an "aerosol (or droplet nuclei)" [29]. While aerosols can stay in the air for an extended period, it is thought that droplets can fall to the ground in a matter of seconds.

Researchers have observed a broad spectrum of sizes and transport properties of cough particles. According to research [30], cough aerosol contains particles with diameters ranging from 0.1 to 100 μm, with a median diameter of 8.5 μm. Using a laser aerosol particle spectrometer, the same group [31] measured a size range of 0.35–10 μm, while another group [32] assessed a mean size distribution of 0.62–15.9 μm for cough droplets. According to a review [2] that compiled data from multiple studies on the topic, the size of cough-generated particles ranged from 0.1 to 100 μm. Another study [25] conducted their experiments considering rosin rammler distribution with a range of 1–300 μm based on the observation of [33]. Based on the broad range of particle size distribution observed by the researchers, we considered rosin rammler distribution for injected cough particles with a minimum diameter of 1 μm, a maximum diameter of 300 μm, and a mean diameter of 16.7 μm. The mass fraction of droplets with a diameter greater than d is represented by the quantity Y_d, which characterizes the Rosin-Ramler diameter distribution as demonstrated by:

$$Y_d=e^{-{\left(\frac{d}{\bar{d}}\right)}^n}$$ (1)

where $\bar{d}$ is the mean droplet diameter and n is the size distribution spread parameter.

2.6. Respiration profile

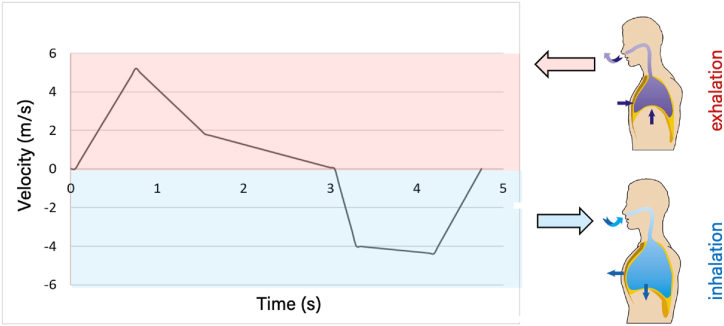
Inhalation is one of the major routes of exposure to virus particles for humans. It is possible to catch an infection simply by breathing in particles that are floating in the air. A person's exposure to airborne particles is governed by a number of factors, including the particle's size, the number of viruses it contains, and the individual's immune system's resilience. When conducting CFD analysis of the number of particles a person inhales, the individual's breathing pattern becomes a crucial aspect that can considerably alter the deposition statistics. In order to give accurate modeling and reliable deposition statistics, our model considers different breathing pattern for individual student. We used the baseline profile described in Ref. [34] as our reference point, and we initiated the profile at varying intervals over a certain period of time to add randomness into the students' respiration. The beginning of a breathing cycle is shown as a function (Fig. 4) with a period of 4.7 s, a maximum exhalation speed of 5.2 m/s, and an inhaling speed of 4.4 m/s. The average temperature of a person's breath is approximated to be 307 degrees K [35] in this model.

Fig. 4.

Respiration profile for an individual student.

2.7. Particle transport

For each scenario, the initial steady-state flow for the different air change rates (2, 6, and 8 ACH) is computed and then used as the initial condition for simulations of coupled transient flow and particle transport. Particle flow is influenced by the volume of air released during each respiratory event, which is captured by solving for flow in transient mode. In this study, we assumed a one-way coupling between flow and particle transport, with flow affecting particle transport but particle concentration being inadequate to affect flow. Studies show that kinematics and particle dispersion are both influenced by humidity. In addition, the likelihood of airborne transmission is considerably higher in dry indoor environments (i.e., 40 % RH) than in humid situations (i.e., >90 % RH) [36]. According to that study, the relative humidity of indoor environments should be between 40 and 60 %. However, based on our observations of classrooms and research labs and the University of Arizona's arid climate, we considered a relative humidity level of 25 % for this study.

This model employs Lagrangian discrete phase modeling with Euler-Lagrange as its basis. As the fluid phase is modeled by the Navier-Stokes equations as a continuum, the particles or droplets are tracked as they move through the flow. It is possible to transfer motion, mass, and energy between the dispersed and fluid phases. In the Discrete Phase Model, the equations defining physics are developed using the Lagrangian approach and then transiently solved. Individual particle or droplet trajectories are calculated at regular intervals during the fluid phase computation. The model predicts the trajectories of individual droplets as they move through the air and water vapor mixture by taking the influence of external forces, turbulent dispersion, and the nature of the flow into account. To track the particles, the model applies Newton's second equation of motion, which equates the droplets' inertia force to the external forces acting on them. This approach couples discrete with continuous phases and accounts for the effects of gravity, drag, lift, and inertia. When it comes to the dispersion of particles greater than 1 μm in size, gravity has a greater influence than Brownian motion. According to the assumption of the model, the Discrete Phase Model (DPM) particles employed in the Lagrangian droplet representation had no effect on the Eulerian phase. After a predetermined number of particle time steps, the model's flow solution is updated to reflect the particle's new location.

2.7.1. Particle force balance equations

Using a Lagrangian reference frame, the model predicts the trajectory of a discrete phase particle by integrating the force balance on the particle. This force balance, which can be represented as equation (2) [37], equates the inertia of a particle with the forces acting on it.

$$\frac{d\overrightarrow{u_p}}{dt}=F_D\left(\overrightarrow{u}-\overrightarrow{u_p}\right)+\overrightarrow{g}\frac{\left({\rho }_p-\rho \right)}{{\rho }_p}+\overrightarrow{F}$$ (2)

here, $\overrightarrow{F}$ stands for additional acceleration which is measured in terms of force per unit of particle mass and $F_D\left(\overrightarrow{u}-\overrightarrow{u_p}\right)$ represents the drag force measured in terms of per unit parcel mass. Here, $\overrightarrow{u}$ represents the velocity of the fluid or continuous phase, $\overrightarrow{u_p}$ represents the velocity of the particle or droplet, $\rho$ is the density of the fluid, ${\rho }_p$ is the droplet density.

2.7.2. Turbulence modeling

The physical phenomena known as turbulence can be described as being chaotic and multiscale. It is not a property of the fluid itself; rather, it is a state of flow. The difference between laminar and turbulent flow is that turbulent flow is asymmetric. It is typically a three-dimensional flow that is unstable and possesses diffusion and dissipation characteristics. In terms of the turbulence model, the motion of turbulence is considered nonlinear in mathematics, which makes it challenging to find a solution to the turbulence problem.

In this study, we utilized RNG-based k-ε turbulence model for turbulence modeling. RNG k-ε model is derived from the standard k-ε model and while it is identical in form, it includes certain enhancements, such as a condition that considerably improves the accuracy of the flow for a wide range of flows. In contrast to the large Reynolds number suggested by the standard k-ε model, a low Reynolds number is taken into account for RNG based model. Because of these features, RNG k-ε model is more robust and precise in fluid flow than the standard k-ε model. By employing a mathematical approach known as "renormalization group" (RNG) methods, the RNG-based k- ε turbulence model is developed from the instantaneous Navier-Stokes equations.

2.8. Model description

In this study, three different recirculation levels and four ACH levels were employed. Pressure-outlet boundary conditions were considered when modeling the inhalation/exhalation of the student manikin. Ventilation inlets are represented as velocity inlets with input velocities based on the calculation from room volume and corresponding ACH level. In addition, Table 1 presents the airflow (m³/min) value, which serves as a unit of measure for volume flow. Equation (3) can be utilized to calculate the airflow value.

$$airflow\left(\frac{m^3}{\mathit{min}}\right)=totalvolume\left(m^3\right)\times \frac{ACH}{60}$$ (3)

In consideration of Arizona's arid climate, we selected a relative humidity of 25 %. The outlet that allows air to escape is modeled as a pressure outlet with atmospheric pressure. The cough originates from the instructor, positioned on the right front side of the room. We initialized a cough as the velocity inlet boundary condition and injected the droplets with a constant velocity of 8.5 m/s [38] for 0.4 s [39]. We considered a mass flow rate of $7.225\times {10}^{-5}kg/s$, resulting in a total injected mass of $2.89{\times 10}^{-5}kg$ over a cough duration of $0.4$ second. The total injected mass resulted in a total of 2960 parcels being introduced into the simulation domain. These parcels are referred to as particles throughout this manuscript to maintain consistency. When an individual coughs, millions of aerosols are released, which poses computational challenges as it becomes impractical to track each aerosol individually using the solver. To address this challenge, Ansys combines particles with similar properties, such as velocity and position, and groups them together as parcels. This approach allows for efficient tracking and management of these parcels during the simulation. As shown in Table 1, we ran our simulation for a total of 12 scenarios for 6 min following the cough injection.

3. Results

The observed airflow behavior in the performed simulations aids in understanding the airflow patterns and the potential formation of eddies and vortices due to obstructions (e.g., manikins, tables, chairs). This understanding allows us to comprehend the particle deposition behavior throughout the space. We begin by discussing the validation study to ensure model fidelity, followed by a discussion of our results.

3.1. Validation

The experimental data on airflow velocities from the classroom was used to validate the CFD simulation presented in this study. In the classroom, the experiment was conducted in an isolated environment that, with a few exceptions, closely approximated the simulated domain. The measured volume of the room is approximately 31 % larger than the simulated volume. In addition to the existence of a column in the room's center, this area is defined by tables and chairs that are arranged differently than in the simulated domain. Also, there are two doors in the room, which were not designed in the simulated classroom. To correspond with our simulation domain, we kept the door closed; nonetheless, there could be some external influence on airflow near the floor due to the clearance between the door and the floor. Finally, to ensure geometric realism, the student body manikins were deliberately excluded from the validation model in order to closely replicate an unoccupied classroom environment, taking into account the potential influence of additional geometry on the simulation outcomes.

At thirteen locations, vertical profiles of air velocity were observed at heights of 0.1 m, 0.84 m, 1.4 m, 1.96 m, and 2.7 m. In this section, we presented data on two distinct points. The figures (Fig. 5 (b), (c)) demonstrate that the developed CFD model fairly predicted the velocity at point 9, and inlet 13. However, the experimental data for inlet 13 (Fig. 5 (c)) revealed that the actual normalized velocity was slightly lower than the simulated data. This variation may be attributed to the difference between the design of the inlet vent and the actual inlet grilles installed in the room. The designed inlet grilles feature a radial construction that regulates the incoming air both sideways and downwards, resulting in greater sustained circulation in the room's mid-height compared to the installed inlet vents, which circulate air to the room sideways and always at an angle. The increasing/decreasing pattern of airflow velocity observed at different locations in the room, as depicted by the developed model in this study, closely corresponds to the experimental data collected based on the normalized height. As a result, it can be concluded that the proposed CFD simulation represents the airflow pattern along the height, thereby enabling the effective assessment of the specified simulated scenarios.

Fig. 5.

(a) Experimental observation points for air velocity with varying heights, (b) Normalized simulated air velocity at inlet point 11 of Fig. 2(a) compared with the experimental velocity of point 9 of Fig. 5 (a), (c) Normalized simulated air velocity at inlet 12 of Fig. 2(a) compared with the experimental velocity at inlet 13 of Fig. 5 (a).

3.2. Air flow streamlines and velocity vectors

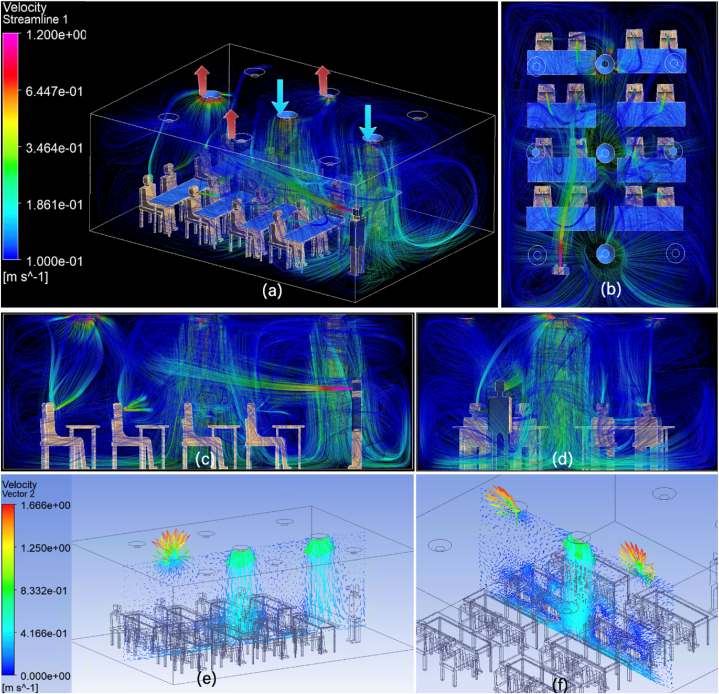
The dispersion of particles is determined by the characteristics of the surrounding flow and the forces acting on the particles. The presence of walls and other indoor impediments alters flow physics by forcing the fluid to recirculate through its surroundings. Fig. 6 depicts the airflow (a-d) and velocity vector field (e, f) within the classroom for scenario 4 (8 ACH, 30 % recirculation). The blue arrows represent the velocity inlet, indicating the incoming airflow into the room, while the red arrow represents the pressure outlet, representing the airflow exiting the room. These figures were generated using Ansys CFD post-processing tool, considering both forward and backward flow directions within the domain.

Fig. 6.

Trajectory of airflow within the room: (a) isometric view, (b) top view, (c) side view, (d) back view, and velocity vectors in (e) the center YZ plane, (f) the XY plane across the space of the classroom for scenario 4.

In buildings, airflow patterns can be categorized into two main types: displacement flow and entrainment flow. Displacement flow is characterized by air movement within a space in a piston-like motion, achieved by strategically placing inlets and outlets on opposite walls. In this type of flow, the room air remains relatively undisturbed, and there is limited mixing with the supply air. On the other hand, entrainment flow involves the mixing of supply air from ceiling-based sources with the room air. This type of flow allows for greater interaction between the supply air and the room air. In our model, we specifically considered entrainment flow for the airflow, which is why we incorporated inlets and outlets in the ceiling to facilitate this type of airflow pattern. From Fig. 6 (a) we can see that the airflow originating from the inlets descends from the ceiling to the floor and disseminates towards both sides of the room, as depicted in Fig. 6 (b) and 6 (d). This airflow pattern generates eddies on the left and right sides of the room, as well as behind the teacher, as observed in Fig. 6 (c). Conversely, Fig. 6 (b) illustrates that the airflow resulting from the teacher's cough is sufficiently strong to reach the second row, where it subsequently mixes with the surrounding air streams. Similarly, the side view presented in Fig. 6 (c) provides a clear visualization of the mixing of air streams from different parts of the room. We can see that the exhaled air of students in the last row is primarily influenced by the outlets positioned at the back and thus removed quickly, while students seated in the front and middle rows experience a mixed influence from both the inlets and outlet air streams. It is evident from these figures that when a person coughs, the airflow from their mouth interacts with the ventilation-induced flow field in the room depending on inlet and outlet's location, leading to the redistribution of particles carried by the cough airflow.

Similarly, in Fig. 6 (e), the velocity vectors are depicted in a vertical YZ cross-section through the middle of the room. As anticipated by the discussed airflow illustrated in Fig. 6 (a), air descends from the ceiling and spreads throughout the room. Due to the high inlet velocity of 0.8 m/s, the velocity vectors at the midplane have a significant influence on the entire space, as indicated by the cross-sections in Fig. 6 (a). The unobstructed pathway in the center of the room directs the airflow, resulting in the highest air velocities in that region. The formation of vortices between the instructor's back and the wall, as depicted in Fig. 6 (e), is consistent with the streamlines shown in Fig. 6 (c). Lastly, Fig. 6 (f) illustrates the formation of vertical eddies between the students' bodies and the tables, creating flow obstructions and generating vortices.

3.3. Spatio-temporal distribution of particles from a single cough

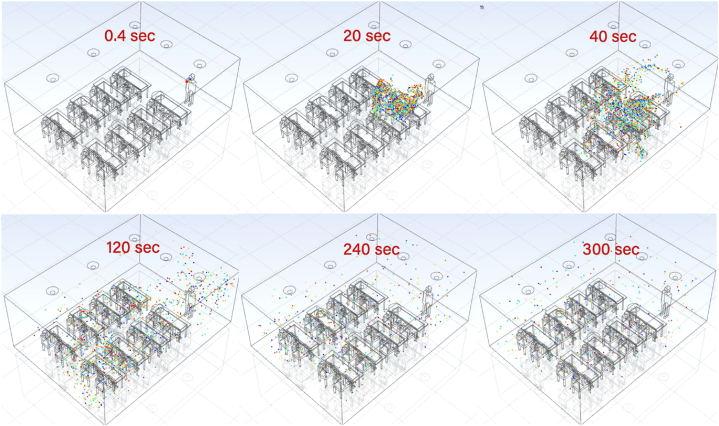
Afterward, we calculate the number of particles injected into the classroom when the instructor coughs. Here we focus on the coughed-up particles and their spatial-temporal distributions in the classroom environment as depicted in Fig. 7. In order to further demonstrate the dynamic nature of these observations, we present a snapshot of the cough distribution at six distinct timesteps: 0.4 s, 20 s, 40 s, 120 s, 240 s, and 300 s. The color gradient represents the varying residence times of particles, providing a visual representation of how long particles have been present in the domain before being deposited or leaving the room. The gradient showcases the temporal aspect of the particles, with blue representing shorter residence times and red indicating longer residence times. In Fig. 7, the first instance is shown at 0.4 s after the instructor starts to cough. We can observe the position of the particles shifts slightly to the right after 20 s, probably due to the interaction of the eddy flow shown in Fig. 6 (c). Initially, particles travel together with the primary airflow generated by the cough. In addition, the movement of particles is simultaneously influenced by the effects of gravity, drag, lift, and the surrounding flow. Larger-diameter particles have a higher tendency to settle due to the gravitational pull than smaller particles. After 40 s, the particles are observed to be scattered towards the top right quarter of the room, with a large number of particles settling on the table surfaces of the first and second rows. In this instance, the obstruction generated by the table expedites the deposition of the particle.

Fig. 7.

Spatio-temporal distribution of the particles over the classroom for scenario 4.

Due to the interaction with the recirculation flow vortex formed at the left side and rear of the instructor (Fig. 6 (b), (c)), we can observe some particles flowing to the instructor's back in durations between 80 and 120 s. As the number of particles and their mass diminish in a room, the effect of the surrounding flow increases, and the particles spread across the space. ACH, recirculation rate, inlet and outlet position, size and shape, and tables and chairs position all have an impact on the surrounding airflow. At around 240 s, we can see the emergence of a uniform distribution of particles throughout space. This observation is consistent with the findings of [17], who assumed a properly mixed flow after 3 min of simulation.

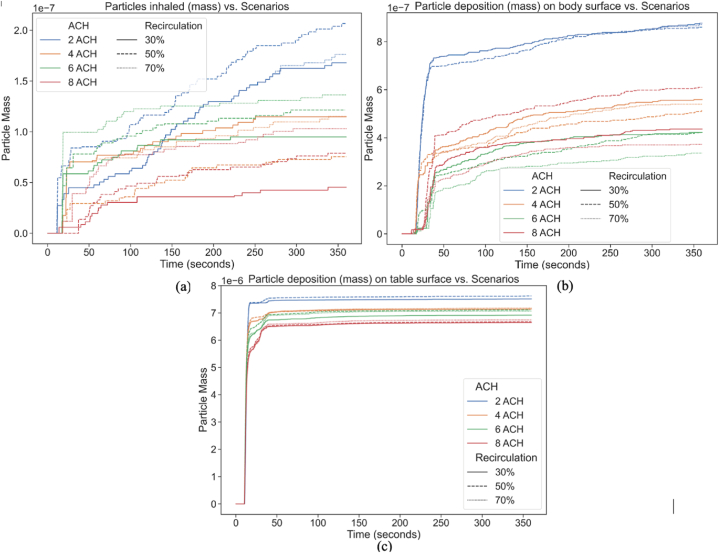
Fig. 8 is a visual representation of the quantitative information obtained from this simulation study. As shown in Table 1, we evaluated 12 distinct scenarios, each involving a combination of four distinct ACH levels (2, 4, 6, 8) and three different recirculation levels (30 %, 50 %, 70 %). Instead of displaying the total number of particles along the Y-axis, the total mass is presented in this figure. The presented measurement unit is the kilogram (kg). Such a comparison allows the study of the airborne contagion exposure of all the students in the room.

Fig. 8.

Temporal progression of particle fate (a) inhaled, (b) body, (c) table for different scenarios.

When analyzing Fig. 8 (a), it is evident that the highest particle mass breathed within the classroom happened at lowest ACH level (2 ACH), while the highest ACH level (8 ACH) resulted in the lowest particle mass. This is owing to the fact that the concentration of aerosols and droplets in the students' breathing zone is reduced when the HVAC system has a stronger airflow (a higher ACH value). It is also evident that the reduction of recirculation percentage from 50 % to 30 % has a significant effect on the reduction of inhalation levels for both 2 ACH and 8 ACH. Intuitively, an ACH level of 4 or 6 corresponds to an inhalation level that falls somewhere between 2 and 8, and the difference in the percentage of recirculated air is less pronounced. In addition, from the figures we can see that over 50 % of the particles are inhaled within the first 50 s of coughing, regardless of the scenario. This highlights the rapid dispersion and early exposure risks associated with cough-generated particles.

We gathered data on particle deposition on the upper body surfaces of the students based on the scenarios presented in Fig. 8 (b). At the end of the simulation, we were able to identify a significant difference in which, for the 2ACH scenario, body deposition is more than one hundred percent more than in the best-case scenario (8 ACH). However, the impact of recirculation level is less obvious for body deposition statistics, with the exception of 8 ACH with a 50 % recirculation level, which resulted in higher deposition than the case with 70 %. This behavior may be induced by the recirculation of cough particles with the main airflow in the room, which may cause a considerable number of particles to become entrapped in the initial few seconds after coughing.

Fig. 8. (c) displays the total mass deposited on the tabletop surfaces. Due to the fact that the teacher was stationed on the right side of the classroom, cough injection would directly cause particles to be deposited on the flat table surfaces. If the teacher had been positioned in the center of the room, however, the majority of table deposits would have drifted toward the walkway in the center of the room. The figures reveal that 2 ACH was responsible for the highest mass of table deposits, while 8 ACH was responsible for the lowest. Compared to the remaining 4 and 6 ACH scenarios, only 30 % of recirculation with 6 ACH cases exhibited any change. Coughing makes larger droplets more sensitive to gravity, resulting in their deposition on flat surfaces within seconds. Less influenced by gravity, lighter particles can be carried further by a coughed-up stream of air. In scenarios characterized by higher ACH values, the deposition of particles on surfaces is reduced due to the increased momentum of the incoming air and the stronger suction created by the outgoing airflow.

3.4. Particle deposition

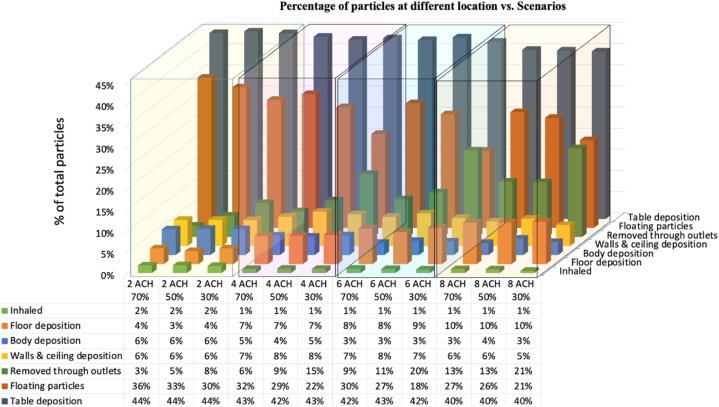
In Fig. 9 we present a summary of particle deposition data at various locations (i.e., table deposition, floating in the room, removed through outlets, walls and ceiling deposition, body deposition, floor deposition, and inhaled) for the same injection. Each color-coded cuboidal section corresponds to a distinct ACH level, and within the cube, we can observe the change in final deposition according to the recirculation percentage.

Fig. 9.

Particle deposition statistics based on location.

Regardless of the recirculation percentage, we can observe a slightly decreased tendency from left to right for table deposition. Because the HVAC airflow promotes turbulent dispersion, the droplet cloud is disrupted and its distribution within the room is enhanced, resulting in fewer particles on the table surface. Additionally, if we obtain the total number of floating particles in the room volume after 6 min of simulation, we can observe an internal declining trend for each ACH value. Globally, the number of floating particles decreases as the ACH level increases, and this trend is also evident in the recirculation percentage. Even while the increased ACH level creates increased turbulence in the room air and thus fewer particles settle on the table, the increased airflow-induced pressure outlet vents remove the floating particles from the room more quickly, resulting in less suspended particles after 6 min of coughing. This behavior can be deduced from the particle data illustrated in Fig. 9 labeled "removed thorough outlets". In the instance of 70 % recirculation for 2 ACH, only 3 % particles were removed from the space, whereas 30 % recirculation resulted in 8 % particles being removed. As the ACH level increases to 8, decreasing the recirculation rate from 70 % to 30 % results in roughly 60 % more particles being removed from the room. This suggests that, in the case of reduced air change, we can significantly improve internal air quality by decreasing air recirculation or by introducing more fresh air.

A similar pattern was seen with regard to floor deposition, where increasing ACH and recirculation percentages exhibit a positive slope in relation to floor deposition count. Nevertheless, a question may arise regarding the disparity in deposition on the table and the floor, which, although being flat surfaces, exhibit opposite tendencies. This phenomenon may be explicable by the presence of a stronger, more turbulent flow with a higher ACH. As the instructor positioned in front of the right-side tables, at lower ACH levels, the airflow within the room was less turbulent and caused less deviation of the cough trajectory, with the majority of particles settling on the tables. With a greater ACH, however, due to a stronger airflow within the room, cough particles were promptly spread across a larger area. They shifted their trajectory from the table to the remainder of the room's surface, resulting in a greater number of depositions on the floor.

The majority of particles are settled on tables and floors due to gravitational forces, as shown by the statistics presented above. In addition, we can see from Fig. 9 regardless of the recirculation percentage level, table deposition is always the highest, and the sum of the table and floor deposition equates to roughly 50 % of the particle deposition. This highlights the significance of regular cleaning of tables and floors with the proper disinfectant, which is often overlooked in common areas such as classrooms where desks are not designated to specific individuals and occupants frequently disregard personal hygiene practices. In addition, as we increase the ACH level, we observe a growing number of particles leaving the room with increased airflow, starting at 5 % and increasing to 13 % in the event of a 50 % recirculation rate. Moreover, if we add more fresh air and thus decrease the recirculation percentage from 50 % to 30 %, the percentage of particles removed through outlets increases from 11 % to 20 % for the 6 ACH case and from 13 % to 21 % for the 8 ACH case. Therefore, if we cannot afford a higher ACH value, we can ensure that more particles are removed from the room by decreasing the recirculation percentage or increasing the fresh air supply. This decision needs to be made by facility management personnel and authorities based on the availability of resources and the urgency of risk mitigation.

4. Discussion

On the basis of our findings, we can see that gravity deposits a significant fraction of the droplet/aerosol particles on the tables and floor, regardless of the ACH and recirculation level, which may be the most important source of secondary touch-based transmission. Therefore, all flat surfaces must be cleaned regularly with an adequate disinfectant, and touching should be avoided to limit the risk of virus transmission through surface contact. In addition, considering the natural death period of the virus on different surfaces, the actual risk may not be precisely equivalent to the amount of table and floor deposits and may be less in fact; however, this does not diminish the significance of routine cleaning in these facilities.

Increasing the ACH level reduces the number of particles in a room by removing more particles through the outlet vent; on average, increasing the ACH from 2 to 8 has enhanced particle extraction by approximately 300 % for high recirculation level. In addition, if we increase the amount of fresh air and reduce the recirculation level from 70 % to 30 %, the number of particles extracted from the room increases by nearly 60 %. This large decrease in airborne particles demonstrates the importance of introducing more fresh air into the room. However, due to limited resources and the need to make an informed choice based on resource availability. Facility management people can consider 6 ACH and a 30 % recirculation level, which eliminates approximately 150 % more particles than 2 ACH 30 % recirculation cases.

Finally, inhalation is a direct risk that leads to increased exposure, which accelerates disease progression and increases the likelihood of experiencing severe symptoms. It was observed that 8 ACH and 30 % recirculation scenarios resulted in the lowest risk of inhalation, whereas 2 ACH scenarios resulted in a risk of inhalation that was around 100 % more. Based on the findings, we can recommend that the room be supplied with higher ventilation (8 ACH) and more fresh air (perhaps 30 % recirculation). However, if we reduce the ACH level to 6 or 4, the number of particles inhaled exhibits a consistent pattern regardless of the recirculation level. This suggests that additional factors (particles within the room and particles removed through outlets) must be reviewed at that stage to set the recirculation level. In addition, the extraction of particles in the exit vent may be a concern for central air conditioning systems, which require routine cleaning to prevent the accumulation of particle residue in the ventilation system.

5. Conclusions

In this paper, we analyzed the influence of ventilation rate and recirculation percentage on droplet/aerosol transmission in a classroom occupied by students with varying respiratory profiles. According to the study findings, a higher ventilation rate and, consequently, a higher ACH improve the extraction of droplets through the outlet vent. In addition, decreasing the percentage of recirculation leads to fewer particles remaining inside a room.

The scenarios analyzed in this study were intended to be representative of a typical classroom setting. Nevertheless, the classroom layout influences the airflow pattern, which changes throughout the space. The configuration of the room involves choices made by the authority, such as the placement of the inlet and outlet, table, and chairs. The results of this study are limited to a single indoor setting with a stationary instructor at the front. In reality, the instructor's movement throughout the classroom may alter the distribution of particles inhaled by the students, depending on their positions. However, it is assumed that the global distribution of particles inhaled, trapped on different surfaces, and removed by outlets will be comparable, with airflow, drag, velocity, and gravity being the primary determinants. Therefore, the recommendations offered in this study are appropriate for indoor applications in general. Utilizing agent-based modeling methodology, the statistics obtained from this study could be used to develop touch-based transmission risk models for indoor environments. Based on this model, we can perform a predictive analysis of the overall airborne and touch-based transmission risk for a variety of facilities. Moreover, these study data might be employed not only for COVID-19 infectious risk research but also for a spectrum of virus-induced risk research.

In addition, this study did not determine the initial point of transmission in the classroom based on the distribution of infected individuals. As infection depends on many factors in addition to inhalation (e.g., touch and movement behavior, age, sex, race), we did not explicitly explore the infectious risk in this study but instead aimed to provide a comparative evaluation of varying ACH and recirculation levels on the distribution of particles. Future studies could use detailed spatial analysis and mapping of infected individuals to understand how different seating arrangements (e.g., traditional, collaborative) impact transmission dynamics. Future research could involve experimental or simulation studies to determine the volume of fresh air required for various classroom sizes and occupancy levels to reduce infection rates. To generalize the findings, similar studies could be conducted in environments such as public transportation, restaurants, exhibitions, and theaters to validate the applicability of the results. This study considered a closed-door simulation; however, testing different air sources in combination with regular AC vents (e.g., open doors, open windows) could provide additional understanding of the dynamics. Human behavior, such as mask-wearing, speaking, coughing, and movement, can significantly impacts transmission risk and therefore future studies should integrate these behavioral factors into the models to enhance the accuracy of predictions and recommendations. Investigating the effectiveness of advanced air purification technologies, such as HEPA filtration, in different indoor settings could also provide valuable insights. Future research should also focus on validating temperature in non-isothermal simulations, as this would further strengthen the model's validity. Conducting such validation, despite current constraints, would enhance our understanding of the interplay between airflow, temperature profiles, and particle distribution.

However, all these different analyses would require a considerable amount of computational time and power, so we need to balance our resources with the goal that we want to achieve. With recent advancements in generative AI, such as Generative Adversarial Networks (GANs) and Variational Autoencoders (VAEs), we can reduce our time and effort by augmenting our modeling with AI-driven studies. For instance, GANs and VAEs can be utilized to create or impute synthetic datasets that simulate various indoor environments, allowing researchers to explore a wider range of scenarios and reducing the need for extensive experiments [40,41]. AI-driven simulations using Deep Reinforcement Learning (DRL) can be helpful to model complex interactions between airflow, particle dynamics, and human behavior, providing more nuanced insights into transmission patterns.

Financial support and sponsorship

This study was supported by The University of Arizona.

Availability of data and materials

Data associated with the study has not been deposited into a publicly available repository. Data will be available from the author on reasonable request.

CRediT authorship contribution statement

Md Tariqul Islam: Writing – original draft, Validation, Methodology, Data curation, Conceptualization. Yijie Chen: Writing – review & editing, Methodology, Formal analysis. Dahae Seong: Writing – review & editing, Methodology, Formal analysis, Conceptualization. Marc Verhougstraete: Writing – review & editing, Supervision, Project administration, Funding acquisition, Conceptualization. Young- Jun Son: Writing – review & editing, Supervision, Project administration, Conceptualization.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.