Abstract
The kagome superconductor CsV3Sb5 hosts a variety of charge density wave (CDW) phases, which play a fundamental role in the formation of other exotic electronic instabilities. However, identifying the precise structure of these CDW phases and their intricate relationships remain the subject of intense debate, due to the lack of static probes that can distinguish the CDW phases with identical spatial periodicity. Here, we unveil the out-of-equilibrium competition between two coexisting 2 × 2 × 2 CDWs in CsV3Sb5 harnessing time-resolved X-ray diffraction. By analyzing the light-induced changes in the intensity of CDW superlattice peaks, we demonstrate the presence of both phases, each displaying a significantly different amount of melting upon excitation. The anomalous light-induced sharpening of peak width further shows that the phase that is more resistant to photo-excitation exhibits an increase in domain size at the expense of the other, thereby showcasing a hallmark of phase competition. Our results not only shed light on the interplay between the multiple CDW phases in CsV3Sb5, but also establish a non-equilibrium framework for comprehending complex phase relationships that are challenging to disentangle using static techniques.
Subject terms: Electronic properties and materials, Phase transitions and critical phenomena, Structure of solids and liquids, Materials science
The interplay between charge density wave states in emerging kagome superconductors is a topic of ongoing debate. Here, the authors unveil the out-of-equilibrium competition between two coexisting charge density waves in CsV3Sb5 by harnessing time-resolved X-ray diffraction.
Introduction
Kagome metals AV3Sb5 (A = K, Rb, Cs) possess a plethora of proximal phases stemming from the interplay between the non-trivial band topology, lattice geometric frustration, and electronic correlations1–4. Ensuing or accompanying the emergence of charge density waves (CDWs), a cascade of symmetry breaking phases including orbital flux state5–8, electronic nematicity9, and superconductivity accompanied by a pair density wave9–14 arise. Therefore, deciphering the nature of the CDW phases in this series of compounds is of paramount significance. More intriguingly, unlike the other analogs in this family, CsV3Sb5 hosts a variety of interrelated CDW phases, which exhibit different out-of-plane stacking but identical in-plane 2 × 2 lattice reconstructions composed of either star-of-David (soD) or inverse-soD patterns2,15–17. These three-dimensional CDW reconstructions comprise two types of frozen phonons at the M and L points in the momentum space. These M (L) modes comprise alternating distortions of V-V bonds that are in-phase (out-of-phase) across neighboring kagome planes (Fig. 1a, b)18. Various combinations of the M and L order parameters along the three symmetry-equivalent directions give rise to the rich CDW ecology. Notably, the 2 × 2 × 2 CDW reconstructions prevail in CsV3Sb5, which compete with the subdominant 2 × 2 × 4 and 2 × 2 × 1 stackings15–17,19 and evolve into a quasi-one-dimensional CDW upon doping or under pressure20,21.
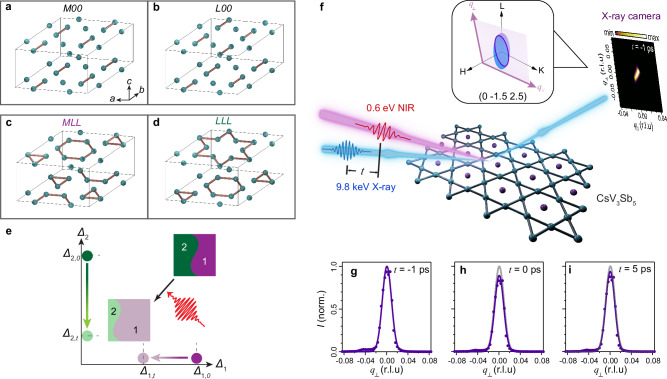
Fig. 1. Phase competition and CDW superlattice dynamics in CsV3Sb5.
a, b Lattice distortions corresponding to the instabilities of phonons at M (0.5 0 0) and L (0.5 0 0.5) points in the momentum space. M00 (L00) corresponds to the case where the in-plane unit-cell doubling is along the a-axis and no doubling is present along the other two symmetry-equivalent directions, namely the b- and (a + b)-axes. c, d Two most probable 2 × 2 × 2 CDW structures of CsV3Sb5. Note that in panels (a–d) only the contracted bonds are colored in brown and only the V atoms are represented by the green balls for clarity. e Schematic evolution of the two competing phases, Δ1 and Δ2, in the phase space. The purple (green) arrow characterizes the change in the amplitude of Δ1(2), which is suppressed less (more) by light. Two insets show that phase competition leads to a suppression in order parameter amplitude and a change in real space domain size upon light excitation. f Schematic of the near-infrared (NIR) pump and hard X-ray probe experimental setup (Methods). Time delay t between the pump and probe can be varied. The sample is rotated nearly around its surface normal to fulfill the Bragg condition for a given diffraction peak. V atoms are represented by green balls while Sb atoms are represented by purple balls. Cs atoms are neglected in the crystal structure for clarity. Raw image of the (0 -1.5 2.5) superlattice peak before pumping is shown. The inset depicts the two-dimensional X-ray camera plane in the three-dimensional momentum space when measuring the peak at (0 -1.5 2.5). The two directions, q⊥ and q//, are nearly parallel to L and K directions, respectively. This holds true for the other peaks under investigation. g–i Intensity linecuts I integrated over the q// direction normalized by its equilibrium peak value at representative time delays. Solid lines are fits to Gaussians. Gray curves in panels (h, i) are the fitting curves reproduced from panel (g) for better comparison.
Despite the intensive investigations, the real-space structure of the dominant 2 × 2 × 2 CDW ground state has not been conclusively determined. A number of CDW reconstructions with different Landau free energy functionals of the M and L order parameters have been predicted theoretically18. Different experimental probes have reported contradictory evidence of two possible superlattice configurations, namely either the “LLL” structure with alternative aligned soD and inverse soD stacking14,22–24, or the “MLL” structure with staggered inverse soD stacking (Fig. 1c, d)9,16,17,19,25–27. Although the conflicting experimental observations can be reconciled if the two CDW phases coexist, deterministic evidence demonstrating the presence of both phases has not been uncovered. Moreover, despite the potential coexistence of the two phases, it remains elusive whether they compete or cooperate with each other, hindering the understanding of the other electronic orders.
In general, it is challenging to distinguish two phases with identical reciprocal lattice vectors using static diffraction-based techniques. However, the relationship between different phases can be uncovered in an out-of-equilibrium pathway. According to a recent theoretical proposal, two competing phases that coexist inhomogeneously in real space will exhibit distinct dynamics upon light stimuli28,29. Although the amplitude of both phases, characterized by Δ1 and Δ2, will be quenched by light irradiation, the domain size of the less suppressed state will expand while the dimension of the other phase will shrink (Fig. 1e). The distinct behaviors of the two phases to light irradiation thus provide direct evidence of phase competition. This non-equilibrium protocol can serve as a smoking gun to distinguish the two charge-ordered phases in CsV3Sb5, because the disparity in their structures could influence the strength of their responses to photo-excitation.
The different responses of the two CDWs can then be uniquely substantiated by time-resolved diffraction: a decrease in CDW satellite peak intensity reflects the suppression of order parameter amplitude and phase coherence, while the alteration in peak width reveals the change in real-space domain size30. In this work, by interrogating the dynamics of CDW superlattice peak intensity employing time-resolved X-ray diffraction (tr-XRD), we first demonstrate the coexistence of MLL and LLL phases. Furthermore, the CDW peaks contributed by the less suppressed MLL phase exhibit a width decrease owing to the domain expansion, while the peaks contributed by the more suppressed LLL phase display a width increase. These observations unequivocally signify the competition between the two coexisting CDW phases out of equilibrium.
Results
We experimentally investigated three CDW superlattice peaks located at (H K L) = (0 -1.5 2.5), (-0.5 -1 2), and (0 -1.5 3), where (H K L) denotes the Miller indices. Based on the structure factor calculation results (Methods and Supplementary Note 1), we have determined that the first and second peaks are predominantly contributed by the MLL phase, while the third peak can be attributed to both the MLL and LLL phases. Therefore, the ability to observe the first two peaks already demonstrates the existence of MLL, consistent with previous static X-ray diffraction results15. The different peak width of (0 -1.5 3) from (0 -1.5 2.5) hints at its potentially different origin (Supplementary Note 9), while more deterministic insights into the potential coexistence of both phases can be provided by monitoring the dynamics of all three peaks. Moreover, for the peaks generated by the MLL phase, L = half integer peaks are exclusively caused by L distortion, whereas L = integer CDW peaks are the result of both M and L distortions. Thus, analyzing both types of peaks will enable us to reveal the dynamics of M and L modes in MLL.
We conducted tr-XRD measurements on single-crystal CsV3Sb5 in the reflection geometry (Fig. 1f and Methods). Diffraction peaks onset at Tc = 91 K in all three aforementioned positions (Supplementary Note 2), signifying the emergence of the long-range CDW12,16,17,24,31,32. To melt the CDW, we employed an ultrafast laser pulse centered around 0.6 eV as the pump, which excites the electrons around M and L points where CDW instabilities arise33. Moreover, our detection plane is nearly parallel to the (0 K L) plane and thus sensitive to changes in both in-plane (q//) and out-of-plane (q⊥) directions (Fig. 1f inset and Methods).
We first examine the temporal evolution of the L = half integer CDW peak at (0 -1.5 2.5) acquired at a temperature of 30 K with a pump fluence of F = 2.5 mJ/cm2 by varying the time delay t between the pump and the probe. To better visualize the CDW peak profile, we integrate the image along the q// direction and subtract the background (Fig. 1g). At the instant of pump impingement t = 0, a prompt decrease in the peak intensity can be observed (Fig. 1h). This drop in peak intensity signifies a reduction of MLL amplitude. The rocking curve upon light irradiation shows a uniform decrease in intensity without changing the Bragg condition (Supplementary Note 3). At t = 5 ps, the intensity drop partially recovers (Fig. 1i). A closer examination of the raw image along both q-directions reveals that the dynamics is nearly q-independent (Supplementary Note 4). Hence, we can integrate the image around the superlattice peaks to quantitatively track the temporal evolution of peak intensity I as a function of t at various F (Fig. 2a). Ensuing the rapid decrease in I within 200 fs, which indicates a nonthermal light-induced quenching of the CDW, we observe a partial recovery over several picoseconds to a quasi-equilibrium state that lasts >100 ps. A pronounced oscillation at 1.3 THz can also be resolved atop the recovery process. We tentatively attribute it to a coherent phonon strongly coupled to the CDW, as previously assigned (Supplementary Note 5)34–36. Note that despite the grazing incidence of the X-ray probe at an angle of 2.94°, a large mismatch in the penetration depth of the pump (~78 nm)33 and the probe (~564 nm) renders most of the probed region unexcited. Owing to the ~7-fold mismatch, a full melting of CDW at the topmost layer corresponds to a ~18% drop in peak intensity that integrates the entire probed region (Supplementary Note 7). Therefore, a maximal drop of 14% without saturation over F suggests an incomplete melting of MLL of the entire probed region.
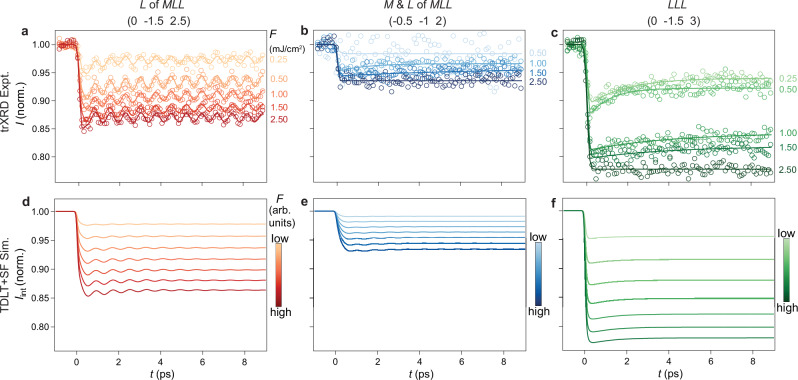
Fig. 2. Dynamics of the CDW peak intensity revealing the coexistence of CDWs.
a–c Temporal evolution of the intensity I obtained by tr-XRD measurements at T = 30 K normalized to the static value for select pump fluences F of CDW peaks at (0 -1.5 2.5), (-0.5 -1 2), and (0 -1.5 3), respectively. Solid lines in panel (a) are fits to a single damped oscillation atop a single exponential decay, while solid lines in panels (b, c) are fits to a single exponential decay (Methods). d–f Temporal evolution of the normalized integrated intensity Iint obtained by simulations based on a combination of time-dependent Landau theory (TDLT) and structural factor (SF) calculation (Methods). The disparity in penetration depths of the X-ray when measuring different peaks has been considered (Supplementary Note 13). Fluence ranges are identical for all three peaks. The order parameter governing each peak is shown at the top.
In contrast, the L = integer CDW peak at (-0.5 -1 2), which also derives from the MLL structure, exhibits a significantly smaller light-induced suppression (Fig. 2b). As mentioned before, L distortion should predominantly contribute to the (0 -1.5 2.5) peak, whereas both M and L distortions contribute to the (-0.5 -1 2) peak. The less melting of the latter peak thus suggests that compared to L mode, M mode is more resilient to optical drive, signifying a decoupling of M and L distortions out of equilibrium. This is not entirely surprising as recent X-ray diffraction measurements have uncovered their decoupling under hydrostatic pressure32. On the other hand, the L = integer CDW peak at (0 -1.5 3) shows a substantially larger quenching, which reaches 18% reduction in I at F = 1.5 mJ/cm2. Further decrease up to 22% accompanied by a dynamical slowing down of the recovery time at F = 2.5 mJ/cm2 suggests the CDW is nearly completely melted in multiple top layers (Fig. 2c and Supplementary Note 12)37. If this peak also arises from the MLL phase, a partial melting together with a nearly fluence-independent recovery as the other two peaks should otherwise be expected. This inconsistency can only be reconciled if the (0 -1.5 3) peak mainly stems from a distinct LLL phase, which is more susceptible than MLL to excitation. Our tr-XRD data thus qualitatively demonstrate the coexistence of LLL with MLL. As a reference, Bragg peaks at (0 0 1) and (0 -1 3) show no observable change in the same fluence regime within our signal-to-noise ratio (Supplementary Note 6).
To gain a quantitative understanding of the different peak dynamics and examine the coexistence of both CDW phases, we develop a time-dependent Laudau theory (TDLT)38–43 and leverage it to simulate the temporal evolution of both M and L order parameters, which determines the dynamics of different peaks originating from the MLL and LLL phases. Our dynamical theory is based on a static Landau theory with all the parameters obtained from first-principles calculations (Methods and Supplementary Note 7)18,44,45. In the time-resolved simulation, we model the light stimulus as a quenching of the quadratic term in the free energy, prone to releasing the CDW distortion and restoring a higher symmetry. However, the quenching of M and L can be different at the same fluence, representing the different susceptibility of M and L order parameters to photo-excitation. We then incorporate the dynamics of M and L modes into the structure factor of different peaks to calculate their intensity evolution. Finally, we include the pump-probe penetration depth mismatch to emulate the experimentally measured data. For the MLL phase, under the assumption that the M mode is ~3 times less responsive to photo-excitation than the L mode, we find a quantitative agreement between the simulation and the experiment of the two peaks (Fig. 2d, e). This in turn validates the assumption that M and L exhibit different quenchability and decoupling upon light excitation. The simulated intensity decrease of the (0 -1.5 3) peak, however, shows considerable disagreement with the experimental value (Supplementary Note 7). To address this problem, without adding further assumptions, we simulate the dynamics of the LLL phase and find that the fluence required to completely melt it is about 2 times smaller than that of the MLL phase. Its higher susceptibility to light excitation can quantitatively reproduce the larger intensity drop of the peak at (0 -1.5 3) (Fig. 2f). Our simulation hence confirms that the different dynamics of various peaks arise from the coexistence of the two CDW phases that exhibit different susceptibilities to light excitation.
To further investigate whether the MLL and LLL compete with each other out of equilibrium, we scrutinize the temporal evolution of the width of various superlattice peaks. To better visualize the subtle light-induced change in peak width, we first normalize the integrated linecuts by their peak values and subtract the linecut before time zero from the one after time zero. By doing so, a decrease in peak width will result in a dip-peak-dip feature, while an increase leads to a peak-dip-peak feature (Fig. 3a, e). For the peak at (0 -1.5 2.5), a dip-peak-dip feature can be clearly resolved after pumping, while the differential linecut is nearly zero before pumping (Fig. 3b). By fitting the peak profile with a Gaussian along both q// and q⊥ directions at various t, we extract the temporal evolution of the peak full width at half maximum, σ// and σ⊥. Both show a reduction followed by a slow recovery, mirroring the dynamics of the peak intensity, albeit with a delay in rise time (Fig. 3c, d and Supplementary Note 13). The temporal evolution of σ// and σ⊥ of the peak at (-0.5 -1 2) exhibit a quantitatively similar behavior, despite a considerably smaller decrease in peak intensity (Supplementary Note 8). This similarity supports that the two peaks arise from the same MLL phase whose domain size is expanded by light. This behavior is nonthermal as opposed to the peak broadening around Tc (Supplementary Note 9), and different from the conventional observation of light-induced topological defects which cause an increase in peak width30,46. On the contrary, the differential linecut, as well as the temporal evolution of σ// and σ⊥ of the peak at (0 -1.5 3), shows an increase in peak width upon pumping (Fig. 3f–h). The opposite behavior of this peak suggests its different origin compared to the other two peaks and reveals the light-induced contraction of the LLL domain. This dichotomy highlights the competition between the MLL and LLL phases, because in the absence of competition, optical quenching will decrease the coherence length of both phases and always induce peak width increase. Another critical observation is that the relative change in σ⊥ is larger than that of σ// for all the peaks, implying optical excitation is more likely to shuffle the out-of-plane stacking rather than reconstructing the in-plane 2 × 2 distortions.
Fig. 3. Dynamics of the CDW peak width revealing the competition between CDWs.
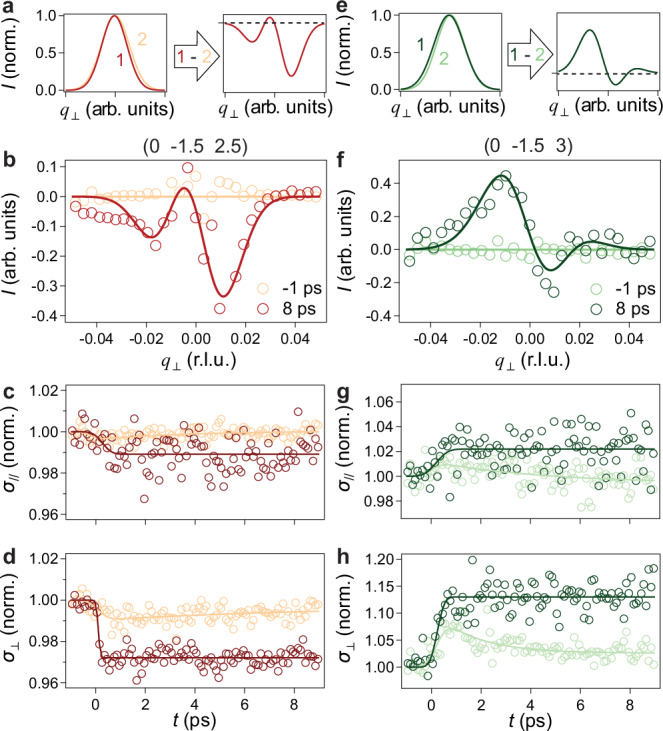
a Schematics of the differential peak-intensity-normalized linecuts along q⊥, which are obtained by subtracting a broader Gaussian from a narrower Gaussian. b Differential peak-intensity-normalized linecuts along q⊥ acquired at t = −1 and t = 8 ps of the peak at (0 -1.5 2.5). Solid lines are fits to zero constant and subtraction of two Gaussians, respectively. c, d Temporal evolution of the (0 -1.5 2.5) peak width along q// and q⊥ directions pumped at F = 0.25 (light orange) and 2.5 mJ/cm2 (dark red) normalized by their equilibrium values. Solid lines are fits to a single exponential decay. e Schematics of the differential peak-intensity-normalized linecuts along q⊥, which are obtained by subtracting a narrower Gaussian from a broader Gaussian. f–h Same plots as panels (b–d) but for the peak at (0 -1.5 3). Lighter and darker green correspond to pumping at F = 0.25 and 2.5 mJ/cm2, respectively. Errors from standard deviation of the Gaussian fitting are about 2.5% and 6.5% for σ// and σ⊥ for both peaks, respectively, which we do not show in the plots for clarity.
Note that the differential linecuts appear asymmetric, because the CDW superlattice peak width change is accompanied by a peak shift, whose amplitude and dynamics are significantly distinct from the weak thermal-expansion-induced Bragg peak shift. Similar phenomena have been observed in photo-induced enhancement of CDW in cuprates47, stemming from the light-induced change in the phase of the CDW. Using similar methodology, we find a qualitative match between the peak shift value and the peak width change in our compound (Supplementary Note 10). Nevertheless, since this displacement is very subtle (~0.0001 r.l.u.), we refrain from drawing any quantitative conclusions.
Discussion
Now we pictorially summarize the physical picture of the optical modulation in Fig. 4. Light excitation reduces the peak intensity of both phases and alters the peak width along both in-plane and out-of-plane directions in momentum space (Fig. 4a, b). This change in peak width corresponds to an expansion of the MLL domain and a contraction of the LLL domain along both in-plane and out-of-plane directions in three-dimensional real space (Fig. 4c, d). The opposing dynamics are rooted in a larger suppression of the amplitude of the LLL phase in the phase space (Fig. 4e, f).
Fig. 4. Physical picture of the CDW dynamics in the presence of phase competition.
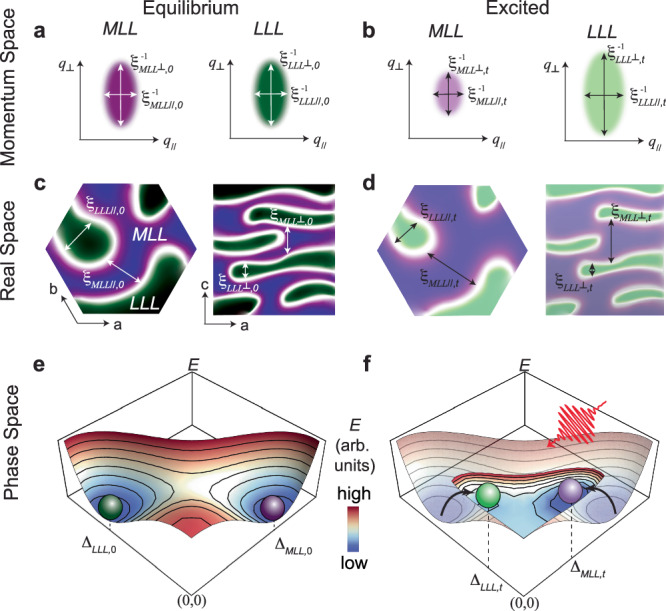
a, b Schematics of equilibrium and excited diffraction patterns of peaks arising from the MLL and LLL structures, respectively. Purple and green correspond to the MLL and LLL phases, respectively. The lighter color in the excited cases characterizes the lower peak intensity, while the change in peak dimensions characterizes the light modulation of peak width. Peak widths are inversely proportional to the correlation lengths (ξ) as denoted. ξMLL//,0 and ξMLL⊥,0 (ξLLL//,0 and ξLLL⊥,0) are the equilibrium correlation lengths of the MLL (LLL) phase in the in-plane and out-of-plane directions, respectively, while ξMLL//,t and ξMLL⊥,t (ξLLL//,t and ξLLL⊥,t) are the excited correlation lengths of the MLL (LLL) phase in the in-plane and out-of-plane directions, respectively. c, d Schematics of equilibrium and excited real-space configuration of the MLL and LLL structures in and out of the kagome plane, respectively. Color code is the same as that used in panels (a, b). Equilibrium and excited correlation lengths are denoted. The spatial inhomogeneity of light suppression, as reflected by the color gradient, suggests MLL expands the most along both in-plane and out-of-plane directions near the sample surface. e, f Schematics of free energy landscapes of the equilibrium and excited states in the phase space constructed by the MLL and LLL phases (Supplementary Note 11). Color bar indicates the energy E. ΔMLL,0 and ΔMLL,t (ΔLLL,0 and ΔLLL,t) are the equilibrium and excited values of the order parameter amplitude of the MLL (LLL) phases. Note that this figure represents the general case where LLL near the surface is incompletely melted.
The out-of-equilibrium competition between the two phases can be explained by the fact that both phases tend to open gaps around the Fermi level at similar momentum space locations. Therefore, the loss of density of states resulting from one charge gap inhibits the development of the other. However, the microscopic reasons determining the susceptibility of different CDW phases to excitation cannot be deduced from the phenomenological Landau theory. Based on a recent theory which uncovers that the interlayer coupling plays a crucial role in determining the favored CDW ground state48, we hypothesize that the different melting capabilities of the two CDW phases emerge from their distinct interlayer coupling. Since the out-of-plane distortion of M and L modes has a π-phase difference, it is intuitive that they will harbor distinct interlayer coupling. This is consistent with our experimental results where M mode is less optically amenable than L mode. Furthermore, this supports the observation that MLL is less quenchable than LLL since it contains M distortion.
Using a combination of tr-XRD measurements and TDLT simulations, we not only identify the coexistence of two 2 × 2 × 2 CDW phases in CsV3Sb5, but also illustrate their competing relationship out of equilibrium, which should persist in equilibrium. This discovery raises a wealth of opportunities for scrutinizing the relationship between other CDW reconstructions in this system, such as the 2 × 2 × 415–17,19 and 4 × 1 × 1 phases27, which both elude our current detection. Understanding the interplay between different CDWs also provides insights for comprehending the unconventional superconductivity in this material, characterized by a pair density wave that inherits the fingerprints of the CDW49–52. Moreover, this framework for decoding phase competition can be extended to a myriad of exotic electronic orders such as orbital and multipolar orders, which may be detectable by diffraction but remain silent to static external perturbations like magnetic field or pressure. We also envision our work will inspire advances in time-resolved microscopy with atomic resolution, enabling visualization of transient structure changes in three-dimensional real space.
Methods
Sample preparation
Single crystals of CsV3Sb5 were synthesized from Cs (solid, Alfa 99.98%), V (powder, Sigma 99.9%, purified with an HCl and Ethanol 9:10 mixture), and Sb (shot, Alfa 99.999%) using the self-flux method in an argon glovebox with oxygen and moisture levels <0.5 ppm. Elemental reagents were loaded into a pre-seasoned tungsten carbide vial to form a precursor flux with a composition of Cs:V:Sb = 20:15:120. Argon-sealed vials were milled for 60 min in a SPEX 8000D mill. The resulting powder was loaded into 2 mL alumina (Coorstek) crucibles and sealed inside steel tubes under argon. Samples were heated to 1000 °C at a rate of 200 °C/h, soaked at that temperature for 12 h, then cooled down to 900 °C at a rate of 5 °C/h, and finally slowly cooled to 500 °C at a rate of 1 °C/h. Single crystals were extracted mechanically and exfoliated along the [0 0 1] direction with scotch tape immediately before the experiment to obtain a fresh and smooth surface. The whole sample was then kept in a vacuum with a pressure <10−6 torr at low temperature.
Time-resolved X-ray diffraction measurements
The experiments were performed at the X-ray pump-probe (XPP) end station of the Linac Coherent Light Source (LCLS), SLAC National Accelerator Laboratory53,54. An optical parametric amplifier seeded by a Ti:Sapphire laser produces a near infrared (NIR) laser pulse centered around 0.6 eV with a duration of 50 fs, which was used as a pump. It excited the sample at an incident angle of 13° with p-polarization and with a focal spot size of 0.27 × 1.2 mm2. The fluence of the pump is tunable from 0 to 4 mJ/cm2, above which thermal damage may occur. A time-delayed X-ray pulse centered around 9.835 keV with a duration of 40 fs was employed as the probe. It was incident at a grazing angle of 2.95° with respect to the sample surface and with a focal spot size of 0.1 × 0.25 mm2. The single-shot diffraction patterns were recorded on a two-dimensional Jungfrau1M detector positioned 155 mm away from the sample. The timing jitter between the pump and probe beams was corrected on a single-shot basis using a spectroencoding diagnostic tool to achieve a time resolution of <80 fs.
During the experiment, we first scanned the rocking curve around the Bragg position of each peak at critical time delays: one before time zero (t = −2 ps) and another when the light-induced change is maximal (t = 0.5 ps). The peak intensity uniformly decreases without noticeable peak shift, indicating a predominant melting of the CDW order. Therefore, to track the intensity change, we can measure the time traces at the optimized Bragg condition—at the peak of the rocking curves—without the need to measure rocking curves at every time delay.
After acquiring the CCD images, the first step in our analysis involves subtracting the background intensity, calculated by averaging the intensity of pixels far from the diffraction peaks on the CCD, from each image. This background subtraction is performed at every time delay, ensuring that the relative intensity change ΔI/I, as shown in Fig. 2, arises exclusively from the peak intensity change. Therefore, the difference in intensity suppression among peaks is not artificially influenced by background intensity.
Structure factor simulations
We performed the structure factor (SF) calculation to simulate the peak intensity. Without considering any CDW-induced lattice distortion, SF reads
| 1 |
where H, K, L are Miller indices for a diffraction peak, xj, yj, zj are positions of the j-th atom in a unit cell, and fj is an atomic form factor depending on (H K L). Here, we only consider in-plane V-V bond distortions within the two kagome planes, because they are the leading lattice instabilities that generate the CDW as predicted by theories and demonstrated by X-ray diffraction measurements19,45. The modified SF due to the CDW formation can be easily calculated by counting all the V atoms in the expanded unit cell and substituting xj → xj + δxj and yj → yj' + δyj, where δxj and δyj correspond to the distortion induced by the V-V bond contraction. See Supplementary Note 1 for more details.
Time-dependent Landau theory simulations
The equilibrium Landau free energy functional of the MLL and LLL phases has been derived elsewhere18,45 and all the Landau parameters have been determined by density functional theory simulations. Both potentials can be expanded up to the quartic order of M and L order parameters. To account for the phonon oscillation exclusively occurring in L = half integer peaks, we include a lattice order parameter X in a harmonic potential which primarily linearly couples to L. Therefore, the total free energy is the summation of two parts (see Supplementary Note 7 for a detailed derivation):
| 2 |
| 3 |
| 4 |
and
| 5 |
where αM and αL are the coefficients of the quadratic terms with tunable temperature T and different transition temperatures TM and TL. Both of them should be negative so that the ordered phase can be realized when T < TM/L. uM, uL, λM, λL, , , and are the coefficients of the quartic terms. βM and βML are the coefficients of the trilinear coupling terms. ω is the coupled phonon frequency, and g is the electron-phonon coupling constant.
We assume M and L are electronic and thus display overdamped dynamics, while X displays an underdamped dynamics. The dynamical equations of order parameters can be expressed as (See Supplementary Note 7 for detailed explanations):
| 6 |
where γM, γM, and γX are phenomenological decay constants to account for damping of electronic and structural order parameters.
Temporal evolution of M and L are calculated by numerically solving the equations of motion. Their dynamics are then included in the structure factor calculations to simulate the dynamics of different CDW peaks.
Fitting formulas for the time traces
To fit the temporal evolution of peak intensity and peak width, we used the following expression including a single exponential decay, a single damped oscillation, and a background:
| 7 |
where t is the pump-probe time delay, t0 is time zero, tr is the rise time, A is the amplitude of the exponential decay, T is the decay time, B is the amplitude of the oscillation, τ is the oscillation decay time, ω is the oscillation angular frequency, ϕ is the phase, and C is the offset on the measured timescale. The phonon term is only included for the fitting in Fig. 2a.
Supplementary information
Acknowledgements
The authors thank Edoardo Baldini, Riccardo Comin, Pavel Dolgirev, Emre Ergeçen, Mingu Kang, Anshul Kogar, Tianchuang Luo, Zhiyuan Sun, Zhuquan Zhang, Minhui Zhu, and Alfred Zong for stimulating discussions. H.N., K.H.O, Y.S, A.v.H. and N.G. are supported by the National Science Foundation under Grant No. DMR-2226519 (data analysis and modeling) and Gordon and Betty Moore Foundation’s EPiQS Initiative grant GBMF9459 (data taking). A.v.H. gratefully acknowledges funding by the Alexandar von Humboldt foundation. S.D.W and A.C.S. gratefully acknowledge support via the UC Santa Barbara NSF Quantum Foundry funded via the Q-AMASE-i program under award DMR-1906325. Z.P is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under contract DE-AC02-76SF00515, both through the Division of Materials Sciences and Engineering and through the use of the LCLS, SLAC National Accelerator Laboratory. Q.L.N. acknowledges the Bloch Fellowship in Quantum Science and Engineering by the Stanford-SLAC Quantum Fundamentals, Architectures and Machines Initiative. T.S., M.C.H., A.W., C.M., and D.Z., as well as the use of the LCLS, SLAC National Accelerator Laboratory, are supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515.
Author contributions
H.N., K.H.O., Y.S., A.v.H., Z.P., A.C.S., Q.L.N., M.C., and T.S. performed the experiment. A.C.S. and S.D.W. synthesized, characterized, and prepared the samples for the experiment. Q.L.N., T.S., M.C.H., A.W., C.M., and D.Z. maintained the beamline and set up the accompanying optics used in the experiment. H.N. performed theoretical calculations. H.N., K.H.O., Y.S., A.v.H., Z.P., and A.C.S. analyzed the data with help from Q.L.N. and V.E. H.N., K.H.O., and Y.S. wrote the manuscript with critical input from D.Z., S.D.W., N.G, and all other authors. The work was supervised by N.G.
Peer review
Peer review information
Nature Communications thanks the anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Data availability
Source data generated in this study and data supporting the figures in the main text are available at https://zenodo.org/records/12810096. Other datasets generated in this study and the code used for simulations are available from the corresponding author upon request.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Honglie Ning, Kyoung Hun Oh, Yifan Su.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-024-51485-5.
References
- 1.Ortiz, B. R. et al. New kagome prototype materials: discovery of KV3Sb5, RbV3Sb5, and CsV3Sb5. Phys. Rev. Mater.3, 094407 (2019). 10.1103/PhysRevMaterials.3.094407 [DOI] [Google Scholar]
-
2.Ortiz, B. R. et al. CsV3Sb5: A
 topological kagome metal with a superconducting ground state. Phys. Rev. Lett.125, 247002 (2020).
10.1103/PhysRevLett.125.247002 [DOI] [PubMed] [Google Scholar]
topological kagome metal with a superconducting ground state. Phys. Rev. Lett.125, 247002 (2020).
10.1103/PhysRevLett.125.247002 [DOI] [PubMed] [Google Scholar] - 3.Kang, M. et al. Twofold van hove singularity and origin of charge order in topological kagome superconductor CsV3Sb5. Nat. Phys.18, 301–308 (2022). 10.1038/s41567-021-01451-5 [DOI] [Google Scholar]
- 4.Jiang, Y.-X. et al. Unconventional chiral charge order in kagome superconductor KV3Sb5. Nat. Mater.20, 1353–1357 (2021). 10.1038/s41563-021-01034-y [DOI] [PubMed] [Google Scholar]
- 5.Feng, X., Jiang, K., Wang, Z. & Hu, J. Chiral flux phase in the kagome superconductor AV3Sb5. Sci. Bull. 66, 1384–1388 (2021). 10.1016/j.scib.2021.04.043 [DOI] [PubMed] [Google Scholar]
- 6.Denner, M. M., Thomale, R. & Neupert, T. Analysis of charge order in the kagome metal AV3Sb5 (A = K, Rb, Cs). Phys. Rev. Lett.127, 217601 (2021). [DOI] [PubMed]
- 7.Christensen, M. H., Birol, T., Andersen, B. M. & Fernandes, R. M. Loop currents in AV3Sb5 kagome metals: Multipolar and toroidal magnetic orders. Phys. Rev. B106, 144504 (2022). 10.1103/PhysRevB.106.144504 [DOI] [Google Scholar]
- 8.Mielke, C. et al. Time-reversal symmetry-breaking charge order in a kagome superconductor. Nature602, 245–250 (2022). 10.1038/s41586-021-04327-z [DOI] [PubMed] [Google Scholar]
- 9.Nie, L. et al. Charge-density-wave-driven electronic nematicity in a kagome superconductor. Nature604, 59–64 (2022). 10.1038/s41586-022-04493-8 [DOI] [PubMed] [Google Scholar]
- 10.Lou, R. et al. Charge-density-wave-induced peak-dip-hump structure and the multiband superconductivity in a kagome superconductor CsV3Sb5. Phys. Rev. Lett.128, 036402 (2022). 10.1103/PhysRevLett.128.036402 [DOI] [PubMed] [Google Scholar]
- 11.Oey, Y. M. et al. Fermi level tuning and double-dome superconductivity in the kagome metal CsV3Sb5−xSnx. Phys. Rev. Mater.6, L041801 (2022). 10.1103/PhysRevMaterials.6.L041801 [DOI] [Google Scholar]
- 12.Chen, Q., Chen, D., Schnelle, W., Felser, C. & Gaulin, B. D. Charge density wave order and fluctuations above TCDW and below superconducting Tc in the kagome metal CsV3Sb5. Phys. Rev. Lett.129, 056401 (2022). 10.1103/PhysRevLett.129.056401 [DOI] [PubMed] [Google Scholar]
-
13.Kato, T. et al. Fermiology and origin of Tc enhancement in a kagome superconductor
 . Phys. Rev. Lett.129, 206402 (2022).
10.1103/PhysRevLett.129.206402 [DOI] [PubMed] [Google Scholar]
. Phys. Rev. Lett.129, 206402 (2022).
10.1103/PhysRevLett.129.206402 [DOI] [PubMed] [Google Scholar] - 14.Kang, M. et al. Charge order landscape and competition with superconductivity in kagome metals. Nat. Mater.22, 186–193 (2023). [DOI] [PubMed] [Google Scholar]
- 15.Ortiz, B. R. et al. Fermi surface mapping and the nature of charge-density-wave order in the kagome superconductor CsV3Sb5. Phys. Rev. X11, 041030 (2021). [Google Scholar]
- 16.Stahl, Q. et al. Temperature-driven reorganization of electronic order in CsV3Sb5. Phys. Rev. B105, 195136 (2022). 10.1103/PhysRevB.105.195136 [DOI] [Google Scholar]
- 17.Xiao, Q. et al. Coexistence of multiple stacking charge density waves in kagome superconductor CsV3Sb5. Phys. Rev. Res.5, L012032 (2023). 10.1103/PhysRevResearch.5.L012032 [DOI] [Google Scholar]
- 18.Christensen, M. H., Birol, T., Andersen, B. M. & Fernandes, R. M. Theory of the charge density wave in AV3Sb5 kagome metals. Phys. Rev. B104, 214513 (2021). 10.1103/PhysRevB.104.214513 [DOI] [Google Scholar]
- 19.Kautzsch, L. et al. Structural evolution of the kagome superconductors AV3Sb5 (A = K, Rb, and Cs) through charge density wave order. Phys. Rev. Mater.7, 024806 (2023). 10.1103/PhysRevMaterials.7.024806 [DOI] [Google Scholar]
- 20.Zheng, L. et al. Emergent charge order in pressurized kagome superconductor CsV3Sb5. Nature611, 682–687 (2022). 10.1038/s41586-022-05351-3 [DOI] [PubMed] [Google Scholar]
- 21.Kautzsch, L. et al. Incommensurate charge-stripe correlations in the kagome superconductor CsV3Sb5−xSnx. npj Quant. Mater.8, 37 (2023). 10.1038/s41535-023-00570-x [DOI] [Google Scholar]
- 22.Hu, Y. et al. Coexistence of trihexagonal and star-of-david pattern in the charge density wave of the kagome superconductor AV3Sb5. Phys. Rev. B106, L241106 (2022). 10.1103/PhysRevB.106.L241106 [DOI] [Google Scholar]
- 23.Li, C. et al. Coexistence of two intertwined charge density waves in a kagome system. Phys. Rev. Res.4, 033072 (2022). 10.1103/PhysRevResearch.4.033072 [DOI] [Google Scholar]
- 24.Subires, D. et al. Order-disorder charge density wave instability in the kagome metal (Cs,Rb)V3Sb5. Nat. Commun.14, 1015 (2023). 10.1038/s41467-023-36668-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Xu, Y. et al. Three-state nematicity and magneto-optical Kerr effect in the charge density waves in kagome superconductors. Nat. Phys.18, 1470–1475 (2022). 10.1038/s41567-022-01805-7 [DOI] [Google Scholar]
- 26.Wu, Q. et al. Simultaneous formation of two-fold rotation symmetry with charge order in the kagome superconductor CsV3Sb5 by optical polarization rotation measurement. Phys. Rev. B106, 205109 (2022). 10.1103/PhysRevB.106.205109 [DOI] [Google Scholar]
- 27.Zhao, H. et al. Cascade of correlated electron states in the kagome superconductor CsV3Sb5. Nature599, 216–221 (2021). 10.1038/s41586-021-03946-w [DOI] [PubMed] [Google Scholar]
- 28.Sun, Z. & Millis, A. J. Transient trapping into metastable states in systems with competing orders. Phys. Rev. X10, 021028 (2020). [Google Scholar]
- 29.Sun, Z. & Millis, A. J. Pump-induced motion of an interface between competing orders. Phys. Rev. B101, 224305 (2020). 10.1103/PhysRevB.101.224305 [DOI] [Google Scholar]
- 30.Zong, A. et al. Evidence for topological defects in a photoinduced phase transition. Nat. Phys.15, 27–31 (2019). 10.1038/s41567-018-0311-9 [DOI] [Google Scholar]
- 31.Li, H. et al. Observation of unconventional charge density wave without acoustic phonon anomaly in kagome superconductors AV3Sb5 (A = Rb, Cs). Phys. Rev. X11, 031050 (2021). [Google Scholar]
- 32.Li, H. et al. Discovery of conjoined charge density waves in the kagome superconductor CsV3Sb5. Nat. Commun.13, 6348 (2022). 10.1038/s41467-022-33995-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Zhou, X. et al. Origin of charge density wave in the kagome metal CsV3Sb5 as revealed by optical spectroscopy. Phys. Rev. B104, L041101 (2021). 10.1103/PhysRevB.104.L041101 [DOI] [Google Scholar]
- 34.Ratcliff, N., Hallett, L., Ortiz, B. R., Wilson, S. D. & Harter, J. W. Coherent phonon spectroscopy and interlayer modulation of charge density wave order in the kagome metal CsV3Sb5. Phys. Rev. Mater.5, L111801 (2021). 10.1103/PhysRevMaterials.5.L111801 [DOI] [Google Scholar]
- 35.Wang, Z. X. et al. Unconventional charge density wave and photoinduced lattice symmetry change in the kagome metal CsV3Sb5 probed by time-resolved spectroscopy. Phys. Rev. B104, 165110 (2021). 10.1103/PhysRevB.104.165110 [DOI] [Google Scholar]
- 36.Azoury, D. et al. Direct observation of the collective modes of the charge density wave in the kagome metal CsV3Sb5. Proc. Natl. Acad. Sci. USA120, e2308588120 (2023). 10.1073/pnas.2308588120 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Zong, A. et al. Dynamical slowing-down in an ultrafast photoinduced phase transition. Phys. Rev. Lett.123, 097601 (2019). 10.1103/PhysRevLett.123.097601 [DOI] [PubMed] [Google Scholar]
- 38.Beaud, P. et al. A time-dependent order parameter for ultrafast photoinduced phase transitions. Nat. Mater. 13, 923–927 (2014). 10.1038/nmat4046 [DOI] [PubMed] [Google Scholar]
- 39.Trigo, M. et al. Coherent order parameter dynamics in SmTe3. Phys. Rev. B99, 104111 (2019). 10.1103/PhysRevB.99.104111 [DOI] [Google Scholar]
- 40.Huber, T. et al. Coherent structural dynamics of a prototypical charge-density-wave-to-metal transition. Phys. Rev. Lett.113, 026401 (2014). 10.1103/PhysRevLett.113.026401 [DOI] [PubMed] [Google Scholar]
- 41.Gorobtsov, O. Y. et al. Femtosecond control of phonon dynamics near a magnetic order critical point. Nat. Commun.12, 2865 (2021). 10.1038/s41467-021-23059-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Zhou, F. et al. Dynamical criticality of spin-shear coupling in van der waals antiferromagnets. Nat. Commun.13, 6598 (2022). 10.1038/s41467-022-34376-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.de la Peña Muñoz, G. A. et al. Ultrafast lattice disordering can be accelerated by electronic collisional forces. Nat. Phys.19, 1489–1494 (2023).
- 44.Tan, H., Liu, Y., Wang, Z. & Yan, B. Charge density waves and electronic properties of superconducting kagome metals. Phys. Rev. Lett.127, 046401 (2021). 10.1103/PhysRevLett.127.046401 [DOI] [PubMed] [Google Scholar]
- 45.Ritz, E. T., Fernandes, R. M. & Birol, T. Impact of Sb degrees of freedom on the charge density wave phase diagram of the kagome metal CsV3Sb5. Phys. Rev. B107, 205131 (2023). 10.1103/PhysRevB.107.205131 [DOI] [Google Scholar]
- 46.Trigo, M. et al. Ultrafast formation of domain walls of a charge density wave in SmTe3. Phys. Rev. B103, 054109 (2021). 10.1103/PhysRevB.103.054109 [DOI] [Google Scholar]
- 47.Wandel, S. et al. Enhanced charge density wave coherence in a light-quenched, high-temperature superconductor. Science376, 860–864 (2022). 10.1126/science.abd7213 [DOI] [PubMed] [Google Scholar]
- 48.Li, H., Liu, X., Kim, Y. B. & Kee, H.-Y. Origin of π-shifted three-dimensional charge density waves in the kagomé metal AV3Sb5 (A = Cs, Rb, K). Phys. Rev. B108, 075102 (2023). 10.1103/PhysRevB.108.075102 [DOI] [Google Scholar]
- 49.Chen, H. et al. Roton pair density wave in a strong-coupling kagome superconductor. Nature599, 222–228 (2021). 10.1038/s41586-021-03983-5 [DOI] [PubMed] [Google Scholar]
- 50.Li, H. et al. Small fermi pockets intertwined with charge stripes and pair density wave order in a kagome superconductor. Phys. Rev. X13, 031030 (2023). [Google Scholar]
- 51.Luo, H. et al. Electronic nature of charge density wave and electron-phonon coupling in kagome superconductor KV3Sb5. Nat. Commun.13, 273 (2022). 10.1038/s41467-021-27946-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Zhong, Y. et al. Nodeless electron pairing in CsV3Sb5-derived kagome superconductors. Nature617, 488–492 (2023). 10.1038/s41586-023-05907-x [DOI] [PubMed] [Google Scholar]
- 53.Emma, P. et al. First lasing and operation of an ångstrom-wavelength free-electron laser. Nat. Photon. 4, 641–647 (2010). 10.1038/nphoton.2010.176 [DOI] [Google Scholar]
- 54.Chollet, M. et al. The X-ray pump–probe instrument at the linac coherent light source. J. Synchrotron Radiat.22, 503–507 (2015). 10.1107/S1600577515005135 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Source data generated in this study and data supporting the figures in the main text are available at https://zenodo.org/records/12810096. Other datasets generated in this study and the code used for simulations are available from the corresponding author upon request.