Skip to main content
PMC home page
BMJ Medicine logoLink to BMJ Medicine
. 2024 Aug 14;3(1):e000784. doi: 10.1136/bmjmed-2023-000784

Development and validation of a prognostic model to predict birth weight: individual participant data meta-analysis

John Allotey 1,2, Lucinda Archer 2,3, Kym I E Snell 2,3, Dyuti Coomar 1,2, Jacques Massé 4, Line Sletner 5, Hans Wolf 6, George Daskalakis 7, Shigeru Saito 8, Wessel Ganzevoort 6, Akihide Ohkuchi 9, Hema Mistry 10,11, Diane Farrar 12, Fionnuala Mone 13, Jun Zhang 14,15, Paul T Seed 16,17, Helena Teede 18, Fabricio Da Silva Costa 19, Athena P Souka 20, Melanie Smuk 21, Sergio Ferrazzani 22,23, Silvia Salvi 22,23, Federico Prefumo 24, Rinat Gabbay-Benziv 25, Chie Nagata 26, Satoru Takeda 27, Evan Sequeira 28, Olav Lapaire 29, Jose Guilherme Cecatti 30, Rachel Katherine Morris 3, Ahmet A Baschat 31, Kjell Salvesen 32,33, Luc Smits 34, Dewi Anggraini 35, Alice Rumbold 36, Marleen van Gelder 37, Arri Coomarasamy 1,2, John Kingdom 38, Seppo Heinonen 39, Asma Khalil 40,41, François Goffinet 42,43, Sadia Haqnawaz 44, Javier Zamora 1,2,45, Richard D Riley 3, Shakila Thangaratinam 1,2,46,✉; for the International Prediction of Pregnancy Complications collaborative network, Alex Kwong, Ary I Savitri, Sohinee Bhattacharya, Cuno SPM Uiterwaal, Annetine C Staff, Louise Bjoerkholt Andersen, Elisa Llurba Olive, Christopher Redman, Maureen Macleod, Baskaran Thilaganathan, Javier Arenas Ramírez, Francois Audibert, Per Minor Magnus, Anne Karen Jenum, Fionnuala M McAuliffe, Jane West, Lisa M Askie, Peter A Zimmerman, Catherine Riddell, Joris van de Post, Sebastián E Illanes, Claudia Holzman, Sander M J van Kuijk, Lionel Carbillon, Pia M Villa, Anne Eskild, Lucy Chappell, Luxmi Velauthar, Miriam van Oostwaard, Stefan Verlohren, Lucilla Poston, Enrico Ferrazzi, Christina A Vinter, Mark Brown, Karlijn C Vollebregt, Josje Langenveld, Mariana Widmer, Camilla Haavaldsen, Guillermo Carroli, Jørn Olsen, Nelly Zavaleta, Inge Eisensee, Patrizia Vergani, Pisake Lumbiganon, Maria Makrides, Fabio Facchinetti, Marleen Temmerman, Robert Gibson, Tiziana Frusca, Jane E Norman, Ernesto A Figueiró-Filho, Hannele Laivuori, Jacob A Lykke, Agustin Conde-Agudelo, Alberto Galindo, Alfred Mbah, Ana Pilar Betran, Ignacio Herraiz, Lill Trogstad, Gordon G S Smith, Eric A P Steegers, Read Salim, Tianhua Huang, Annemarijne Adank, Wendy S Meschino, Joyce L Browne, Rebecca E Allen, Kerstin Klipstein-Grobusch, Caroline A Crowther, Jan Stener Jørgensen, Jean-Claude Forest, Ben W Mol, Yves Giguère, Louise C Kenny, Anthony O Odibo, Jenny Myers, SeonAe Yeo, Lesley McCowan, Eva Pajkrt, Bassam G Haddad, Gustaaf Dekker, Emily C Kleinrouweler, Édouard LeCarpentier, Claire T Roberts, Henk Groen, Ragnhild Bergene Skråstad, Kajantie Eero, Athanasios Pilalis, Renato T Souza, Lee Ann Hawkins, Francesc Figueras, Francesca Crovetto
Editor: Linda Gough
PMCID: PMC11344865  PMID: 39184566

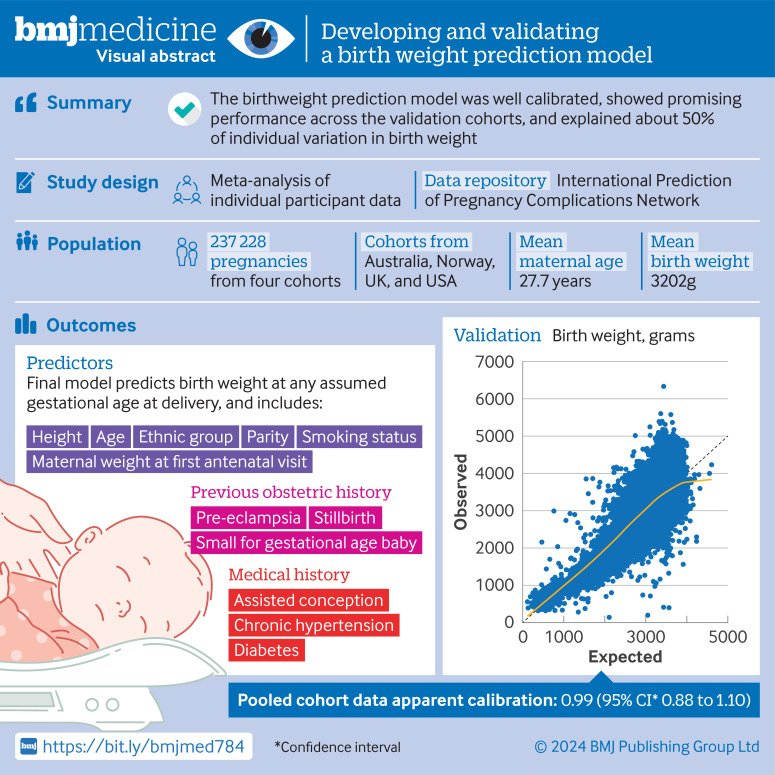
Abstract

Objective

To predict birth weight at various potential gestational ages of delivery based on data routinely available at the first antenatal visit.

Design

Individual participant data meta-analysis.

Data sources

Individual participant data of four cohorts (237 228 pregnancies) from the International Prediction of Pregnancy Complications (IPPIC) network dataset.

Eligibility criteria for selecting studies

Studies in the IPPIC network were identified by searching major databases for studies reporting risk factors for adverse pregnancy outcomes, such as pre-eclampsia, fetal growth restriction, and stillbirth, from database inception to August 2019. Data of four IPPIC cohorts (237 228 pregnancies) from the US (National Institute of Child Health and Human Development, 2018; 233 483 pregnancies), UK (Allen et al, 2017; 1045 pregnancies), Norway (STORK Groruddalen research programme, 2010; 823 pregnancies), and Australia (Rumbold et al, 2006; 1877 pregnancies) were included in the development of the model.

Results

The IPPIC birth weight model was developed with random intercept regression models with backward elimination for variable selection. Internal-external cross validation was performed to assess the study specific and pooled performance of the model, reported as calibration slope, calibration-in-the-large, and observed versus expected average birth weight ratio. Meta-analysis showed that the apparent performance of the model had good calibration (calibration slope 0.99, 95% confidence interval (CI) 0.88 to 1.10; calibration-in-the-large 44.5 g, −18.4 to 107.3) with an observed versus expected average birth weight ratio of 1.02 (95% CI 0.97 to 1.07). The proportion of variation in birth weight explained by the model (R2) was 46.9% (range 32.7-56.1% in each cohort). On internal-external cross validation, the model showed good calibration and predictive performance when validated in three cohorts with a calibration slope of 0.90 (Allen cohort), 1.04 (STORK Groruddalen cohort), and 1.07 (Rumbold cohort), calibration-in-the-large of −22.3 g (Allen cohort), −33.42 (Rumbold cohort), and 86.4 g (STORK Groruddalen cohort), and observed versus expected ratio of 0.99 (Rumbold cohort), 1.00 (Allen cohort), and 1.03 (STORK Groruddalen cohort); respective pooled estimates were 1.00 (95% CI 0.78 to 1.23; calibration slope), 9.7 g (−154.3 to 173.8; calibration-in-the-large), and 1.00 (0.94 to 1.07; observed v expected ratio). The model predictions were more accurate (smaller mean square error) in the lower end of predicted birth weight, which is important in informing clinical decision making.

Conclusions

The IPPIC birth weight model allowed birth weight predictions for a range of possible gestational ages. The model explained about 50% of individual variation in birth weights, was well calibrated (especially in babies at high risk of fetal growth restriction and its complications), and showed promising performance in four different populations included in the individual participant data meta-analysis. Further research to examine the generalisability of performance in other countries, settings, and subgroups is required.

Trial registration

PROSPERO CRD42019135045

Keywords: Obstetrics, Pregnancy complications

WHAT IS ALREADY KNOWN ON THIS TOPIC

  • Accurate and practical methods for predicting birth weight can help identify pregnancies at greater risk of adverse perinatal outcomes and provide opportunities for early intervention to improve outcomes

  • Because of their small sample size and dichotomisation of birth weight outcome, current birth weight prediction models have a high risk of bias, further limiting their power and usefulness

  • Existing prediction models show varying levels of accuracy with limited assessment of their generalisability in different populations or settings

WHAT THIS STUDY ADDS

  • A prediction model for birth weight at various potential gestational ages was developed and validated, based on data readily available at the first antenatal visit

  • The model was derived from a large, ethnically diverse dataset, with cohorts from the US, UK, Norway, and Australia, with continuous birth weight data, and showed good calibration performance on internal-external cross validation

  • The model was particularly well calibrated (smallest prediction errors) in the lower end of predicted birth weight, and explained about 50% of individual variation in birth weights

HOW THIS STUDY MIGHT AFFECT RESEARCH, PRACTICE, OR POLICY

  • The predictive ability of the model could be useful for early identification of babies at risk of abnormal growth at the time of the antenatal booking

  • The model could help inform clinical decision making in pregnancies at high risk of fetal growth restriction and its complications

  • Use of the prediction model in practice might require evaluation in cluster randomised trials and should be evaluated in other countries, settings, and subgroups

Introduction

Identifying abnormal fetal growth patterns antenatally can help reduce perinatal mortality and morbidity.1 Birth weight and estimated fetal weight for gestational age are important indicators of the health of the mother and the baby's chance of survival and future health.2,4 Babies with a birth weight below the population threshold of the 10th centile are usually classified as small for gestational age and considered to be at greater risk of adverse outcomes because of growth restriction.5 6 In these babies, the odds of stillbirth and neonatal death are substantially higher than normal weight fetuses at every week beyond the expected date of delivery.2 Also, the healthcare needs for babies born small for gestational age is higher on average than babies born at appropriate weight for their gestational age.7

Accurate and practical methods of predicting birth weight can help identify babies with an increased risk of adverse perinatal outcomes and provide opportunities for early intervention to improve their outcomes. Current methods of estimating birth weight and fetal weight rely on formulas from fetal biometry on antenatal ultrasound,8 9 an approach associated with considerable variation in precision and consistency of measurement.10 11 Global health inequity is further widened in many resource poor settings with a high burden of perinatal mortality but limited access to ultrasound machines or experienced operators, which affects effective antenatal monitoring of fetal growth.12

Developing accurate birth weight prediction models in individual studies is limited because of small sample size, selectiveness in the population used for developing the model,13 and dichotomisation of predictors or birth weight outcome.14 15 Furthermore, the predictive performances of previously published models have not been validated externally, and so none can currently be recommended for use in routine clinical practice.16 In this study, we used an individual participant data meta-analysis to overcome these limitations. We developed and validated a multivariable prediction model for birth weight at various potential gestational ages of delivery, with routinely available obstetric history and personal data collected at the first antenatal visit. Figure 1 shows the visual abstract.

Figure 1. Visual abstract.

Figure 1

Open in a new tab

Methods

Our individual participant data meta-analysis followed existing recommendations for developing and validating a prediction model,17,20 and used a prospective protocol registered with PROSPERO. We reported our findings based on the transparent reporting of a multivariable prediction model for individual prognosis or diagnosis (TRIPOD) cluster guideline for development and validation of a prediction model in clustered data (online supplemental appendix 1).21

Data sources and study population

Eligible studies were identified from the International Prediction of Pregnancy Complications (IPPIC) individual participant data network dataset.22 23 Access to the IPPIC dataset was provided after application to the IPPIC data access committee. The IPPIC dataset contains individual participant data from observational studies and cohorts nested within randomised studies reporting various maternal and perinatal outcomes.22 Women in the studies were recruited with sampling methods and inclusion criteria designed to capture a broad cross section of the target population. Studies in the network were identified by searching major databases for studies reporting risk factors for adverse pregnancy outcomes, such as pre-eclampsia, fetal growth restriction, and stillbirth, from database inception to August 2019. The quality of the individual participant data from each study was assessed with the participants, predictors, and outcomes domains of the prediction model risk-of-bias assessment (PROBAST) tool.24 Details of the search, identification, inclusion of studies, and individual participant data harmonisation for the IPPIC dataset are provided elsewhere.25 26

Candidate predictors

Clinically relevant candidate predictors were identified from the literature27 and prioritised by clinical experts with a two round Delphi process. From an initial list of 33 predictor variables, candidate predictors were: maternal weight at the first antenatal visit, maternal height, maternal age, parity, smoking status, ethnic group (white, black, South Asian, Hispanic, mixed, or other), history of chronic hypertension, history of diabetes, assisted conception, and any previous history of pre-eclampsia, stillbirth, and a baby born small for gestational age. We included gestational age at delivery as a predictor in our model to allow us to produce birth weight predictions for a range of assumed gestational ages at delivery.27 Maternal weight at the first antenatal visit was standardised in the IPPIC dataset to include weight before pregnancy and at the first trimester.

Outcome

Our primary aim was to develop a model to predict the birth weight of a baby at any potential gestational age of delivery. As a continuous measure, our outcome was not limited by arbitrary cut-off values and, if needed, the predicted birth weight could be converted into predicted centiles based on any fetal growth standard.28,30 Predicting birth weight at various gestational ages at delivery also provides information on the severity of any restricted growth and the expected timing of onset to allow planning for appropriate management.

Model development and validation cohorts

Data from four studies (237 228 pregnancies;31,34 online supplemental appendix 2) within the IPPIC individual participant data network dataset provided the best combination of candidate predictor variables while maximising the numbers of cohorts and participants for developing the model. All four studies included pregnant women from different ethnic groups. Data on obstetric history and personal characteristics were obtained by various methods, including self-reporting, routine data collected from medical records, or recorded by the research team with prespecified definitions.

The sample size for developing the model should ensure small optimism in predictor effect estimates, a small difference between the apparent and adjusted R2, precise estimation of the mean predicted birth weight (the model intercept), and precise estimation of the model's residual standard deviation.35 To calculate the minimum sample size required, we assumed a lower bound of 0.5 for the anticipated adjusted R2 of the model to be developed, and an intercept value of −0.935, with a standard error of 0.043 (on the log10 scale) based on a previously published birth weight prediction model.27 Hence a minimum sample of 618 women was required to consider up to 50 predictor parameters in a linear regression model. The sample size in the development and internal-external cross validation cohorts far exceeded these estimates.

Statistical analysis

Missing data

We used multiple imputation by chained equations, assuming a missing-at-random mechanism, to generate 100 imputed datasets for each of the included cohorts separately to retain heterogeneity between the study cohorts.36 Continuous variables were imputed with linear regression, binary variables with logistic regression, and categorical variables with predictive mean matching. The imputation model included all candidate predictors and outcome to help ensure that the missing-at-random assumption was reliable. Imputed outcomes were not included in the analysis. We did not impute when all values were missing or when >90% of values were missing. After imputation, we checked the consistency of imputations by comparing distributions of values and summary statistics for imputed datasets with the original unimputed data.

Non-linear relations between continuous candidate predictors and the outcome were considered with multivariable fractional polynomial models.37 38 Fractional polynomials were first identified in the complete case datasets, with each of the non-linear terms, and then included in the imputation model to allow us to consider this non-linearity when developing the model. Fractional polynomial terms for gestational age at delivery and maternal height were included in the final model to account for non-linear relations with birth weight (online supplemental appendix 3).

Model development

We developed the prediction model with multilevel linear regression, with a random effect on the intercept to account for clustering by cohort. We used backward elimination for variable selection where the same model (with the same candidate predictors) was fitted to all imputations, and pooled Wald tests (with Rubin's rules) were used for backward elimination, with P>0.157 (proxy for Akaike information criterion) for exclusion.39

To adjust for overfitting in the development of the model, we calculated the heuristic shrinkage factor in each imputation and pooled for all imputations with Rubin's rules to obtain the average shrinkage factor.40 41 This average shrinkage factor was then applied to each beta coefficient in the model, and subsequently the average intercept value was re-estimated (holding fixed the shrunken beta coefficients) to ensure that the final model predictions were calibrated-in-the-large.

Internal-external cross validation

We maximised our access to individual participant data from multiple studies and used an internal-external cross validation approach.42 43 With the same approach as described above, a model predicting birth weight was developed with all but one of the four cohorts, keeping one cohort for validation. The shrunken model equation was then applied to the excluded cohort to calculate the predicted birth weight at the observed gestational age at delivery. Predictive performance was then evaluated for the model in this excluded cohort, based on values for calibration-in-the-large, calibration slope, root mean squared error, mean absolute error, and R2. This process was then repeated until each cohort had been used to assess the external validation of the model. If required, we will include the largest cohort in all cycles of the internal-external cross validation approach to ensure a large sample size for developing the model in each cycle. Calibration plots were also produced for each cycle of the internal-external cross validation, plotting average observed and expected values for all imputations.

Predictive performance measures from the internal-external cross validation were summarised with a random effects meta-analysis to give a summary estimate of overall performance. The calibration slope and calibration-in-the-large were pooled on their original scales. Confidence intervals were derived with the Hartung-Knapp-Sidik-Jonkman variance correction.44 Heterogeneity in model performance for all internal-external cross validation cycles was quantified with τ2 and 95% prediction intervals.

Apparent performance of the model developed with all four cohorts was calculated for each cohort individually and for all four cohorts (without accounting for clustering). Cohort specific apparent predictive performance was summarised with a random effects meta-analysis to give a pooled estimate of overall apparent model performance. We also carried out a sensitivity analysis of the predictive performance of the model by gestational age at delivery (32-36 weeks and ≥37 weeks) to assess the differential model performance in these populations. All analyses were performed with Stata 16 software.45

Patient and public involvement

Members of the public were involved in prioritising the research question, and developing, designing, and managing the research. The study is supported by the Hildas (https://www.dhlnetwork.com/news), a dedicated patient and public involvement group in women's health. The team members were involved in the interpretation and reporting of the results. Findings will be further disseminated in workshop events with key stakeholders and in a format more suitable for patients and members of the public.

Results

Study population

The model development and validation dataset included four studies (237 228 pregnancies) from four countries, one each from the UK (Allen et al, 2017),32 Norway (STORK Groruddalen research programme 2010),33 Australia (Rumbold et al, 2006),31 and the US (National Institute of Child Health and Human Development (NICHD), 2018).34 Three studies were prospective observational studies of unselected pregnant women32,34 whereas one was a randomised trial of nulliparous pregnant women at low risk of complications of pregnancy.31 The US based study34 made up >95% of the pooled sample size. Women in the combined dataset were mostly from the white ethnic group (50%, n=118 554), followed by black (22%, n=52 691) and Hispanic (17%, n=40 422) ethnic groups. Median gestational age at delivery for the four studies was 39 weeks (interquartile range 38-40), mean maternal age was 27.7 years (standard deviation (SD) 7.4), and birth weight was 3202 g (SD 643.4) (table 1). Assessment of risk of bias of the cohorts with the PROBAST tool considered that all cohorts were at low risk of bias in the domains of participant selection, predictor, and outcome reporting.

Table 1. Characteristics of women in development and internal-external cross validation cohorts: UK (Allen et al, 2017),32 Australia (Rumbold et al, 2006),31 Norway (STORK Groruddalen research programme, 2010)33 and US (National Institute of Child Health and Human Development (NICHD), 2018)34 cohorts, and pooled data.

Characteristics Allen et al, 2017 Rumbold et al, 2006 STORK Groruddalen, 2010 NICHD, 2018 Pooled data
Values Missing values Values Missing values Values Missing values Values Missing values Values Missing values
No of pregnancies 1045 — 1877 — 823 — 233 483 — 237 228 —
Median (IQR) gestational age at delivery (weeks) 40.0 (39.3-40.6) 1 (0.1) 40.0 (39.0-41.0) — 40.0 (38.9-40.9) 22 (2.7) 39.0 (38.0-40.0) 7929 (3.4) 39.0 (38.0-40.0) 7952 (3.4)
Median (IQR) maternal weight (kg) 62.0 (55.0-69.0) 5 (0.5) 66.0 (58.5-76.0) 103 (5.5) 64.6 (56.9-72.9) 421 (51.2) 66.7 (57.6-80.3) 31 314 (13.4) 66.7 (57.6-80.0) 31 843 (13.4)
Mean (SD) maternal height (cm) 161.5 (13.3) — 165.3 (15.7) 138 (7.4) 163.6 (13.3) — 163.3 (6.6) 37 567 (16.1) 163.3 (8.0) 37 705 (15.9)
Mean (SD) maternal age (years) 29.9 (7.4) 1 (0.1) 26.4 (6.7) — 29.9 (6.7) — 27.7 (7.4) 339 (0.1) 27.7 (7.4) 340 (0.1)
Nulliparous 584 (55.9) — 1877 (100.0) — 381 (46.3) — 93 545 (40.1) — 96 387 (40.6) —
Smoked during pregnancy 38 (3.6) — 364 (19.4) 39 (2.1) 50 (6.1) — 15 547 (6.7) — 15 999 (6.7) 39 (0.2)
Ethnic group — 2 (0.2) 4 (0.2) — — — 9557 (4.1) — 9563 (4.0)
 White 398 (38.1) — 1777 (94.7) — 379 (46.1) 116 000 (49.7) — 118 554 (50.0) —
 Black 108 (10.3) — 3 (0.2) — 62 (7.5) 52 518 (22.5) — 52 691 (22.2) —
 South Asian 495 (47.4) — 1 (0.1) — 200 (24.3) 9487 (4.1) — 10 183 (4.3) —
 Hispanic — — 1 (0.1) — 12 (1.5) 40 409 (17.3) — 40 422 (17.0) —
 Mixed 12 (1.1) — 4 (0.2) — — 347 (0.1) — 363 (0.2) —
 Other 30 (2.9) — 87 (4.6) — 170 (20.7) 5165 (2.2) — 5452 (2.3) —
History of hypertension 10 (1.0) — 9 (0.5) — 13 (1.6) — 4589 (2.0) — 4621 (1.9) —
History of diabetes 11 (1.1) — 8 (0.4) — — — 4946 (2.1) 7878 (3.4) 4965 (2.1) 7878 (3.3)
Assisted conception 23 (2.2) — 50 (2.7) 39 (2.1) 13 (1.58) — 1472 (0.6) 109 799 (47.0) 3354 (1.4) 109 838 (46.3)
Any previous pre-eclampsia 17 (1.6) — — — — — 10 131 (4.3) 31 545 (13.5) 10 148 (4.3) 31 545 (13.3)
Any previous stillbirth 12 (1.1) — — — 81 — 2029 (0.9) 96 159 (41.2) 2049 (0.9) 96 159 (40.5)
Any previous baby born small for gestational age 67 (6.4) — — — 31 (3.8) — 2857 (1.2) 9640 (4.1) 2955 (1.2) 9640 (4.1)
Mean (SD) birth weight (g) 3298.3 (524.5) 4 (0.4) 3382.0 (608.9) 6 (0.3) 3418.3 (570.1) 38 (4.6) 3199.8 (644.1) 2674 (1.1) 3202.0 (643.4) 2722 (1.1)
Open in a new tab

Data are number (%) unless indicated otherwiseValues are number (percentage), unless otherwise stated. .Missing values reported as number (percentage).

Missing values are number (%).

IQRinterquartile rangeNICHDNational Institute of Child Health and Human DevelopmentSDstandard deviation

Apparent model performance

The final multivariable model included all 13 candidate predictors of assumed gestational age at delivery, maternal weight at the first antenatal visit, maternal height, maternal age, parity, smoking status, ethnic group, history of chronic hypertension, history of diabetes, assisted conception, and previous history of pre-eclampsia, stillbirth, and a baby born small for gestational age (table 2).

Table 2. Model coefficients for final birth weight model and each internal-external cross validation cycle, with study specific intercepts.

Continuous outcome model, coefficient
Pooled data Excluding Allen et al, 2017 cohort* Excluding Rumbold et al, 2006 cohort† Excluding STORK Groruddalen, 2010 cohort‡
Gestational age at delivery (weeks)
 Weeks−2 24 200 000 24 300 000 24 600 000 24 200 000
 Weeks−2 × ln weeks −9274661 −9278365 −9383827 −9256070
Maternal weight (kg) 2.708811 2.706337 2.702486 2.712717
Maternal height (cm)
 cm3 0.0000752 0.0000750 0.0000747 0.0000749
Maternal age (years) 3.138301 3.142642 3.160154 3.160331
Nulliparous −92.03335 −91.72014 −91.86725 −91.48258
Smoker −118.0368 −118.025 −119.9714 −118.4065
Ethnic group
 White Reference Reference Reference Reference
 Black −174.2521 −174.4343 −174.5623 −174.2543
 South Asian −73.23465 −71.06526 −73.76615 −72.71608
 Hispanic −9.562515 −9.582163 −10.10826 −9.50801
 Mixed −64.73106 −62.95441 −65.91944 −64.19719
 Other −60.38814 −59.96023 −60.27113 −62.70106
History of hypertension −36.27748 −36.01454 −36.19573 −36.47012
History of diabetes 149.9896 150.6165 150.6321 150.0034
Assisted conception −78.7545 −81.1364 −79.92499 −93.85787
Any previous pre-eclampsia −84.16068 −84.04261 −83.93942 −84.10901
Any previous stillbirth −13.59535 −13.11023 −13.67015 −13.1444
Any previous baby small for gestational −481.7414 −486.7372 −481.4254 −485.4757
Intercept (average for all studies) 9210.304 9212.973 9259.176 9200.492
Heuristic shrinkage factor 0.9997 0.9997 0.9998 0.9997
Open in a new tab
*

UK cohort, Allen et al, 2017.32

†

Australia cohort, Rumbold et al, 2006.31

‡

Norway cohort, STORK Groruddalen research programme, 2010.33

The apparent performance of the model showed good calibration within each cohort, with calibration slopes of 0.88 (95% confidence interval (CI) 0.89 to 0.96) for the Allen et al, 2017 cohort, 1.04 (0.99 to 1.09) for the Rumbold et al, 2006 cohort, 1.30 (0.95 to 1.11) for the STORK Groruddalen research programme, 2010 cohort, and 0.99 (0.99 to 0.99) for the NICHD 2018 cohort. Calibration-in-the-large values were near zero in each cohort: 33.1 g (95% CI 7.1 to 59.1) for the Allen cohort, 13.4 g (−6.5 to 33.3) for the Rumbold cohort, 104.7 g (75.6 to 133.8) for the STORK Groruddalen cohort, and 31.4 g (29.7 to 33.2) for the NICHD cohort. The ratio of mean observed to mean predicted birth weight in each cohort was near 1.00 (range 1.01-1.04), with confidence intervals that overlapped one (table 3).

Table 3. Overall apparent model performance and by cohort: UK (Allen et al, 2017),32 Australia (Rumbold et al, 2006),31 Norway (STORK Groruddalen research programme, 2010),33 and US (National Institute of Child Health and Human Development (NICHD), 2018)34 cohorts, and pooled data.

Pooled estimate Allen et al, 2017(n=1045) Rumbold et al, 2006 (n=1877) STORK Groruddalen, 2010 (n=823) NICHD, 2018 (n=233 483) Pooled data(n=237 228)
Calibration slope
 Point estimate 0.99 0.88 1.04 1.03 0.99 0.99
 Confidence interval 0.88 to 1.10 0.89 to 0.96 0.99 to 1.09 0.95 to 1.11 0.99 to 0.99 0.99 to 0.99
 Prediction interval 0.70 to 1.28 — — — — —
 τ2 (95% CI) 0.00 (0.00 to 0.04) — — — — —
Calibration-in-the-large (g)
 Point estimate 44.45 33.11 13.40 104.69 31.43 31.53
 Confidence interval −18.44 to 107.33 7.07 to 59.14 −6.45 to 33.26 75.62 to 133.76 29.69 to 33.17 29.81 to 33.26
 Prediction interval −136.62 to 225.51 — — — — —
 τ2 (95% CI) 1400 (257 to 13000) — — — — —
Observed to expected birth weight ratio
 Point estimate 1.02 1.01 1.01 1.04 1.01 1.01
 Confidence interval 0.97 to 1.07 0.96 to 1.06 0.94 to 1.07 0.98 to 1.09 0.92 to 1.11 0.92 to 1.11
 Prediction interval 0.95 to 1.08 — — — — —
 τ2 (95% CI) 0.00 (0.00 to 0.00) — — — — —
R2* (%)
 Median 46.9 32.7 47.8 45.7 56.1 56.0
 Range 32.3-56.3 32.3-32.9 47.5-48.1 45.1-46.3 56.0-56.3 55.9-56.1
 Interquartile range 39.0-52.1 32.6-32.8 47.8-47.9 45.6-45.9 56.1-56.2 56.0-56.1
Open in a new tab
*

Reported as median, range, and interquartile range across for imputations as because R-squared 2 cannot be summarised acrossfor all imputations using with Rubin's rules.

CIconfidence interval

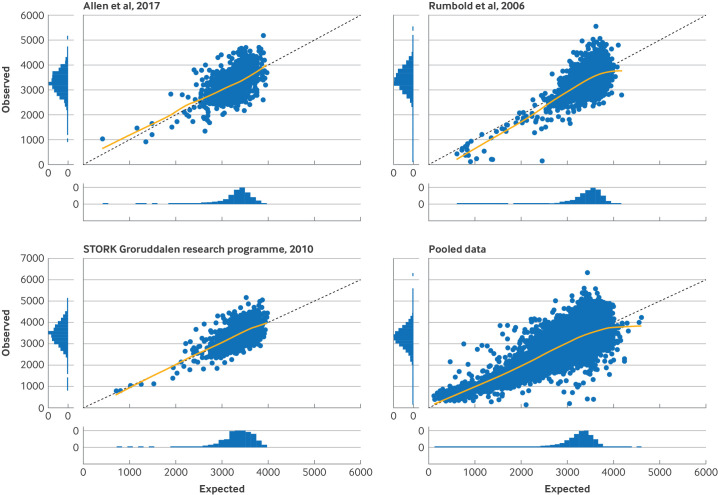
We used a meta-analysis to summarise performance for the four cohorts and found good calibration, on average, with a pooled calibration slope of 0.99 (95% CI 0.88 to 1.10) and a pooled calibration-in-the-large of 44.5 g (−18.4 to 107.3), corresponding to a pooled ratio of mean observed to mean predicted birth weight of 1.02 (0.97 to 1.07) (table 3). Calibration curves were close to the line of ideal calibration for all four cohorts.

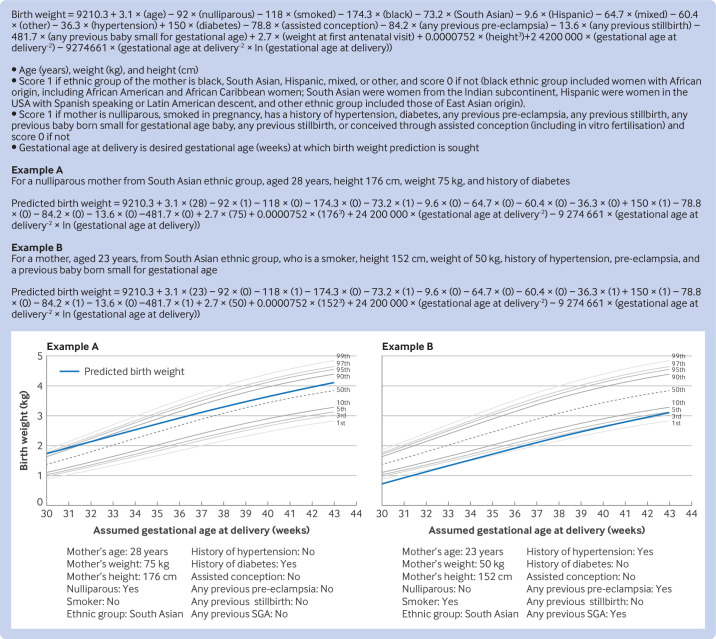
The pooled estimate for proportion of variation in birth weight explained by the birth weight model (R2) was 46.9% (range 32.7-56.1% in each cohort) (table 3). Errors in predictions varied in individuals, as shown by the range of observed versus expected birth weights in the pooled data panel of figure 2, with a root mean squared error of 427.8 g for all cohorts, ranging from a low of 427.7 g (NICHD, 2018 cohort) to 438.2 g (Rumbold et al, 2006 cohort). We found no evidence of overfitting in the development data in any cycle of the internal-external cross validation, with a heuristic shrinkage estimate of ≥0.9997 for all imputed datasets and internal-external cross validation cycles. Figure 2 shows the final prediction equation developed with all four cohorts, to calculate birth weight at any desired gestational age of delivery, with examples of how to calculate birth weight with the equation.

Figure 2. Calibration plots of observed versus expected birth weights for UK (Allen et al, 2017; 1045 pregnancies),32 Norway (STORK Groruddalen research programme, 2010; 823 pregnancies),33 and Australia (Rumbold et al, 2006; 1877 pregnancies)31cohorts, and for pooled data (237 228 pregnancies).

Figure 2

Open in a new tab

Figure 3. Final equation for prediction of birth weight at any potential gestational age of delivery with worked examples, superimposed over a GROW growth chart. SGA=baby born small for gestational age.

Figure 3

Open in a new tab

Internal-external cross validation

The internal-external cross validation analysis was done by including the largest of the four cohorts (NICHD, 2018)34 in all cycles of the internal-external cross validation, to ensure that the sample size for development of the model was always large enough to develop a reliable model, and that the validation performance calculated was representative of an external validation of the final model, which was highly influenced by this cohort. We therefore developed a model in three cohorts and applied this model within the fourth cohort, but did not include a cycle where a model was developed without the NICHD 2018 study. Estimates of calibration slope for the internal-external cross validation cycles showed minimal overfitting to the development cohort in each cycle, with estimates of 0.90 (95% CI 0.82 to 0.97) when validated in the Allen et al, 2017 cohort, 1.07 (1.02 to 1.12) when validated in the Rumbold et al, 2006 cohort, and 1.04 (0.96 to 1.12) when validated in the STORK Groruddalen research programme, 2010 cohort (table 4). The pooled calibration slope for the internal-external cross validation cycles showed excellent performance with little overfitting and negligible miscalibration (on average 1.00, 95% CI 0.78 to 1.23). Model performance by calibration-in-the-large also showed minimal miscalibration, with overestimation of birth weight, on average, by only 22.3 g and 33.4 g when validated in the Allen et al, 2017 and Rumbold et al, 2006 cohorts respectively, whereas the model underestimated birth weight by 86.4 g, on average, when validated in the STORK Groruddalen research programme, 2010 cohort (table 4). For each internal-external cross validation cycle, the ratio of mean observed to mean predicted birth weight was near perfect, ranging from 0.99 to 1.03 (table 4). The pooled calibration-in-the-large suggested an underestimation of birth weight by only 9.7 g (−154.3 to 173.8), on average, for the internal-external cross validation cycles (table 4).

Table 4. Predictive performance of developed birth weight model with average intercept in each internal-external cross validation cycle. UK (Allen et al, 2017),32 Australia (Rumbold et al, 2006),31 and Norway (STORK Groruddalen research programme, 2010)33 cohorts, and pooled estimate.

Pooled estimate Allen et al, 2017 Rumbold et al, 2006 STORK Groruddalen, 2010
No of pregnancies for model development — 236 183 235 351 236 405
No of pregnancies for external validation — 1045 1877 823
Calibration slope
 Point estimate 1.00 0.90 1.07 1.04
 Confidence interval 0.78 to 1.23 0.82 to 0.97 1.02 to 1.12 0.96 to 1.12
 Prediction interval −0.25 to 2.26 — — —
 τ2 (95% CI) 0.01 (0.00 to 0.14) — — —
Calibration-in-the-large (g)
 Point estimate 9.72 −22.32 −33.42 86.41
 Confidence interval −154.3 to 173.8 −48.36 to 3.7 −53.4 to −13.5 57.3 to 115.5
 Prediction interval −943.23 to 962.67 — — —
 τ2 (95% CI) 4200 (801 to 76000) — — —
Observed to expected birth weight ratio
 Point estimate 1.00 1.00 0.99 1.03
 Confidence interval 0.94 to 1.07 0.95 to 1.04 0.94 to 1.05 0.97 to 1.09
 Prediction interval 0.81 to 1.20 — — —
 τ2 (95% CI) 0.00 (0.00 to 0.01) — — —
R2* (%)
 Median 45.7 32.6 47.4 45.7
 Range 32.2-47.8 32.2-32.8 47.1-47.8 45.0-46.2
 interquartile range 32.7-47.4 32.5-32.7 47.4-47.5 45.5-45.8
Open in a new tab
*

Reported as median, range, and interquartile range for imputations because R2 cannot be summarised for all imputations with Rubin’s rules.

CIconfidence interval

Visual inspection of the calibration plots also showed good calibration, on average, for all three cycles of internal-external cross validation, with calibration curves close to the ideal line (figure 2). Errors in individual level predictions were still large for some, however, with a root mean squared error of 428.9 g, 441.3 g, and 424.6 g, for the models validated in the Allen et al, 2017, Rumbold et al, 2006, and STORK Groruddalen research programme, 2010 cohorts, respectively. Sensitivity analysis of predictive performance of the IPPIC birth weight model by gestational age at delivery did not show differential calibration performance for prediction of birth weight in term and late preterm babies (online supplemental appendix 4) or difference in individual level error distributions for different numbers of weeks of gestation (online supplemental appendix 5).

Discussion

Principal findings

Our IPPIC birth weight model, developed with data that are readily available at the antenatal booking, showed excellent prediction of birth weight, on average, and promising performance in four different populations included in the individual participant data meta-analysis. We used a robust Delphi process to prioritise candidate predictors, ensuring that we included clinically meaningful variables. We also used best practice prognostic model methods to develop and validate our birth weight prediction model. Our model predicted the birth weight of a baby at various potential gestational ages of delivery, based on maternal weight, height, age, parity, smoking status, ethnic group, history of chronic hypertension, history of diabetes, assisted conception, and previous history of pre-eclampsia, stillbirth, and babies born small for gestational age. We validated the model with an internal-external cross validation approach.

The model, when tested in cohorts in different countries, explained about 50% of individual level variability, and had good calibration performance in high and low risk populations. Prediction errors were smallest in individuals at the lower end of the range of predicted birth weights, which is important in informing clinical decisions in pregnancies at high risk of fetal growth restriction and related complications.

Strengths and limitations of this study

Our individual participant data meta-analysis simultaneously developed and validated a prediction model for birth weight. We developed our model with data from the harmonised IPPIC individual participant data, from cohorts from different countries,22 23 which provided us with a larger sample size than is achievable with just one study. This approach allowed us to develop a more comprehensive prediction model, applicable in different populations and settings included in these individual participant data. We evaluated clinically relevant predictors that are routinely available at the antenatal booking in both high and low resource settings, allowing the model to be easily applied in high income as well as in low income countries where perinatal mortality rates are highest.46 Although our prediction model showed promising performance after three cycles of internal-external cross validation in women from the UK, Norway, and Australia, multiple external validations with data specifically from low income settings are needed to fully evaluate if the the model can be transferred to these settings. These external validations will help verify the model's robustness and suitability for use in other countries and subgroups, strengthening its practical use in clinical practice.

Our model can be used to generate predictions of birth weight conditional on any clinically relevant gestational age at delivery. Integration of the model as part of routine growth charts has the potential to inform antenatal counselling and empower women to contribute towards shared decision making with clinicians about the frequency of monitoring in pregnancy and discussions on timing of birth, where concerns about the growth of the fetus exist. Further external validation of the model in different populations and settings, however, is required before implementation in clinical practice. Our prediction of birth weight was on the continuous scale, and therefore our model is not limited by arbitrary cut-off values used to define small or large for gestational age. This approach allows clinicians to calculate predicted birth centiles based on any fetal growth standard of their choice, such as GROW, INTERGROWTH 21st, and WHO.28,30

We used a systematic approach to develop and validate our birth weight prediction model, by first identifying and prioritising candidate predictors with a Delphi process and then using multiple imputation to deal with missing data for both predictors and outcome to avoid the loss of useful information.47 48 We used rigorous statistical methods to develop the prediction model and evaluate the predictive performance, with individual participant data from multiple cohorts to assess any potential heterogeneity in performance for the cohorts.

Our study had some limitations. Although mean birth weight was similar in all cohorts, the NICHD cohort had a higher standard deviation in birth weight, with greater variability than the other cohorts. This heterogeneity could be a result of variation in personal characteristics within the population, potentially affecting the generalisability of the model. Considering that the NICHD cohort was retained in all internal-external cross validation cycles, exploring the model's performance within this heterogenous context is important. External validation of the model in other datasets that represent different regions and populations will help confirm the model's generalisability, enhancing its practical applicability.

The average calibration performance of the model was good for all cohorts but varied in individual cohorts, with some underprediction in the smaller cohorts, mainly in those with the highest birth weight. Although overall calibration of the model was good, miscalibration for individual observations was found, particularly at the higher end of the range of predicted birth weights. This miscalibration produced a wide range of observed birth weights for a particular predicted birth weight in all cycles of the internal-external cross validation. This range was much narrower in the clinically important range for the lower predicted birth weights, however, where pregnancies have a higher risk of growth restriction and require intervention. Our model explained 47% of the variability in birth weight in the dataset, ranging from 56% (NICHD, 2018 cohort) to 33% (Allen et al, 2017 cohort). These differences in R2 estimates are partly a result of chance, but could also be because of differences in predictor effects in the various populations. Future research might explore if some variables, such as maternal weight or height, interact with country location and should be modelled differently for each location to improve variance explained.

Comparison with existing evidence

Most published models predict the risk of a baby born small for gestational age rather than birth weight.16 Dichotomisation of birth weight limits the power and usefulness of a prediction model. The use of specific cut-off values can also result in both overdiagnosis and underdiagnosis of fetal growth abnormalities, depending on the criteria used.49 These models were also usually poorly reported, with only a third being internally validated (10/28, 36%), and two (7%) were externally validated and showed limited predictive performance.50 51 Calibration measures were rarely reported in these studies, with only four (14%) reporting these performance measures. A prediction formula, rule, or score that would allow independent external validation was reported in only 16 (57%) of these models. Other published birth weight prediction models were developed for use in specific populations and have not undergone external validation to determine their generalisability to new and different populations.13 So far, no individual test is satisfactorily predictive of birth weight or small for gestational age to warrant recommendation in routine clinical use.52

We reported the development and validation of our prediction model in line with current guidelines on the transparent reporting of multivariable prediction models developed or validated with clustered data.21 Our model showed good calibration performance on internal-external cross validation, with only slight overprediction of birth weight, by 9.7 g on average. Our model also required the user to enter the assumed gestational age at delivery. Although the actual date of delivery is not known when making predictions, the option to enter various possible gestational ages for delivery allows the user to produce a plot of predictions of birth weight for various time points.

The Royal College of Obstetricians and Gynaecologists in the UK recommends, at the antenatal booking, assessing for risk factors for fetuses that are small for gestational age, to identify those who might need increased surveillance.53 The American College of Obstetricians and Gynecologists recommends screening for unspecified medical and obstetric risk factors, but does not recommend use of uterine artery Doppler or biochemical markers, citing lack of evidence on improvement of outcomes.54 The Society of Obstetricians and Gynaecologists of Canada calls for clinical risk factor based screening,55 whereas the Royal Australian and New Zealand College of Obstetricians and Gynaecologist suggests risk assessment through a combination of biomarkers, Doppler ultrasound, and major maternal clinical risk factors.56 The choice of risk factors and their combination to predict risk of small for gestational age or fetal growth restriction in any of these guidelines was not based on formal prediction modelling.

Relevance for clinical practice and research

The prediction of birth weight is an important aspect of antenatal care because it can provide valuable information to healthcare providers and expectant mothers about the growth and development of the fetus, with cost effective use of limited fetal monitoring resources. Accurate predictions of birth weight can also help identify infants who might have an increased risk of adverse outcomes, such as preterm birth or stillbirth, and allow for early interventions to improve outcomes. The development of accurate birth weight prediction models has been challenging, however, because individual studies often have limited sample sizes, variable definitions of birth weight outcome and predictors, with no external validation of any model developed.11 14 49 57 Our individual participant data meta-analysis combined data from multiple studies to develop a mathematical model, providing a more robust estimate of the association between included predictors and birth weight. Use of multiple datasets in the IPPIC data repository allowed us to carry out extensive validation of the model for different geographical regions, health systems, settings, and in populations of women with different baseline risks.

Only clinical characteristic predictors were included in the model, making it potentially applicable to both low and high resource settings. The predictors included are easy to measure and routinely available in clinical practice. Incorporating the model into practice will be simple because no additional measures are required to calculate the birth weight for potential gestational ages of delivery. Because the model includes factors that influence fetal growth and perinatal risk, its predictive ability is particularly useful for early identification of risk of abnormal growth at the antenatal booking. Thus the model can alert healthcare providers to take appropriate actions and provide necessary care in monitoring high risk pregnancies.

Our work was in direct response to calls from the National Institute for Health and Care Excellence and the Royal College of Obstetricians and Gynaecologists for predictive tests or strategies to identify women at risk of delivering a small baby, particularly growth restricted infants with complications,53 58 and the priorities of the UK Department of Health to reduce the incidence of stillbirths and neonatal deaths. Further research is needed to evaluate the ease of implementation of our birth weight model into routine clinical practice and to determine any barriers and facilitators of its use. This research should include assessment of the acceptability of the prediction model as a screening tool for pregnant women and their families, as well as healthcare providers.

The effect of using our birth weight model in clinical practice might require evaluation in cluster randomised trials to assess whether its use improves perinatal outcomes, or evaluation in an implementation study to show that it can be integrated into routine care at a population level. These studies could evaluate the use of the model to inform interventions (such as close monitoring or planned delivery) compared with routine care on perinatal mortality. Although the feasibility of these trials is challenging because of the sample size required to show an effect on perinatal mortality, proxies for perinatal mortality could be used, such as morbidity, to achieve sufficient power.59

Conclusions

We have developed a simple prediction model incorporating routinely available clinical predictors to predict birth weight at various potential gestational ages at delivery. The model explained about 50% of the variability, showed good calibration, and its use could help identify pregnancies at increased risk of adverse outcomes to allow planning of appropriate management or early intervention to improve perinatal outcomes. Further multiple external validations in different settings and populations will help confirm the generalisability of the model.

supplementary material

online supplemental file 1
bmjmed-3-1-s001.docx (23.1KB, docx)
DOI: 10.1136/bmjmed-2023-000784
online supplemental file 2
bmjmed-3-1-s002.pdf (67.9KB, pdf)
DOI: 10.1136/bmjmed-2023-000784
online supplemental file 3
bmjmed-3-1-s003.pdf (248.6KB, pdf)
DOI: 10.1136/bmjmed-2023-000784
online supplemental file 4
bmjmed-3-1-s004.pdf (62.1KB, pdf)
DOI: 10.1136/bmjmed-2023-000784
online supplemental file 5
bmjmed-3-1-s005.pdf (433.2KB, pdf)
DOI: 10.1136/bmjmed-2023-000784

Acknowledgements

The International Prediction of Pregnancy Complications (IPPIC) data repository was originally set up by funding from the National Institute for Health Research Health Technology Assessment Programme (14/158/02). We acknowledge all researchers in the IPPIC collaborator network who contributed data to this individual participant data meta-analysis, including the original teams involved in the collection of the data, and participants who took part in the research studies. The authors are solely responsible for the views expressed in this article and they do not necessarily represent the views, decisions, or policies of the institutions with which they are affiliated.

The views expressed are those of the author(s) and not necessarily those of the National Institute for Health and Care Research or the Department of Health and Social Care.

Footnotes

Funding: This project was funded by the National Institute for Health and Care Research Health Technology Assessment UK programme 17/148/07. The funder had no role in considering the study design or in the collection, analysis, interpretation of data, writing of the report, or decision to submit the article for publication.

Provenance and peer review: Not commissioned; externally peer reviewed.

Ethics approval: Not applicable.

Data availability free text: All data requests should be submitted via email to the corresponding author for consideration. Access to available anonymised data might be granted after review by the International Prediction of Pregnancy Complications data sharing committee and once appropriate agreements are in place.

Collaborators: Members of the International Prediction of Pregnancy Complications (IPPIC) collaborative network: Alex Kwong, University of Bristol; Ary I Savitri, University Medical Centre Utrecht; Sohinee Bhattacharya, University of Aberdeen; Cuno SPM Uiterwaal, University Medical Centre Utrecht; Annetine C Staff, University of Oslo; Louise Bjoerkholt Andersen, University of Southern Denmark; Elisa Llurba Olive, Hospital Universitari Vall d’Hebron; Christopher Redman, University of Oxford; Maureen Macleod, University of Dundee; Baskaran Thilaganathan, St George’s University of London; Javier Arenas Ramírez, University Hospital de Cabueñes; Francois Audibert, Université de Montréal; Per Minor Magnus, Norwegian Institute of Public Health; Anne Karen Jenum, University of Oslo; Fionnuala M McAuliffe, University College Dublin; Jane West, University of Bristol; Lisa M Askie, University of Sydney; Peter A Zimmerman, Päijät-Häme Central Hospital; Catherine Riddell, Better Outcomes Registry and Network (BORN); Joris van de Post, Academisch Medisch Centrum; Sebastián E Illanes, University of the Andes; Claudia Holzman, Michigan State University; Sander MJ van Kuijk, Maastricht University Medical Centre; Lionel Carbillon, Assistance Publique-Hôpitaux de Paris Université; Pia M Villa, University of Helsinki and Helsinki University Hospital; Anne Eskild, University of Oslo; Lucy Chappell, King’s College London; Luxmi Velauthar, Queen Mary University of London; Miriam van Oostwaard, IJsselland Hospital; Stefan Verlohren, Charité University Medicine; Lucilla Poston, King’s College London; Enrico Ferrazzi, University of Milan; Christina A Vinter, University of Southern Denmark; Mark Brown, University of New South Wales; Karlijn C Vollebregt, Academisch Medisch Centrum; Josje Langenveld, Atrium Medisch Centrum Parkstad; Mariana Widmer, World Health Organization; Camilla Haavaldsen, Akershus University Hospital; Guillermo Carroli, Centro Rosarino De Estudios Perinatales; Jørn Olsen, Aarhus University; Nelly Zavaleta, Instituto Nacional De Salud; Inge Eisensee, Aarhus University; Patrizia Vergani, University of Milano-Bicocca; Pisake Lumbiganon, Khon Kaen University; Maria Makrides, South Australian Health and Medical Research Institute; Fabio Facchinetti, Università degli Studi di Modena e Reggio Emilia; Marleen Temmerman, Aga Khan University; Robert Gibson, University of Adelaide; Tiziana Frusca, Università degli Studi di Parma; Jane E Norman, University of Edinburgh; Ernesto A Figueiró-Filho, Mount Sinai Hospital; Hannele Laivuori, University of Helsinki and Helsinki University Hospital; Jacob A Lykke, Rigshospitalet; Agustin Conde-Agudelo, Eunice Kennedy Shriver National Institute of Child Health and Human Development; Alberto Galindo, Universidad Complutense de Madrid; Alfred Mbah, University of South Florida; Ana Pilar Betran, World Health Organization; Ignacio Herraiz, Universidad Complutense de Madrid; Lill Trogstad, Norwegian Institute of Public Health; Gordon GS Smith, Cambridge University; Eric AP Steegers, University Hospital Nijmegen; Read Salim, HaEmek Medical Centre; Tianhua Huang, North York General Hospital; Annemarijne Adank, Erasmus Medical Centre; Wendy S Meschino, North York General Hospital; Joyce L Browne, University Medical Centre Utrecht; Rebecca E Allen, Queen Mary University of London; Kerstin Klipstein-Grobusch, University Medical Centre Utrecht; Caroline A Crowther, University of Adelaide; Jan Stener Jørgensen, Syddansk Universitet; Jean-Claude Forest, Centre Hospitalier Universitaire de Québec; Ben W Mol, Monash University; Yves Giguère, Laval University; Louise C Kenny, University of Liverpool; Anthony O Odibo, University of South Florida; Jenny Myers, University of Manchester; SeonAe Yeo, University of North Carolina at Chapel Hill; Lesley McCowan, University of Auckland; Eva Pajkrt, Academisch Medisch Centrum; Bassam G Haddad, Portland State University; Gustaaf Dekker, University of Adelaide; Emily C Kleinrouweler, Academisch Medisch Centrum; Édouard LeCarpentier, Centre Hospitalier Intercommunal Creteil; Claire T Roberts, University of Adelaide; Henk Groen, University Medical Centre Groningen; Ragnhild Bergene Skråstad, St Olavs Hospital; Kajantie Eero, University of Helsinki and Helsinki University Hospital; Athanasios Pilalis, University of Athens; Renato T Souza, University of Campinas; Lee Ann Hawkins, University of Calgary; Francesc Figueras, University of Barcelona; Francesca Crovetto, University of Barcelona.

Contributor Information

John Allotey, Email: j.allotey.1@bham.ac.uk.

Lucinda Archer, Email: l.a.archer@bham.ac.uk.

Kym I E Snell, Email: k.snell.2@bham.ac.uk.

Dyuti Coomar, Email: D.Coomar@bham.ac.uk.

Jacques Massé, Email: jacques.masse.med@ssss.gouv.qc.ca.

Line Sletner, Email: line.sletner@medisin.uio.no.

Hans Wolf, Email: h.wolf@amsterdamumc.nl.

George Daskalakis, Email: gdaskalakis@yahoo.com.

Shigeru Saito, Email: s30saito@med.u-toyama.ac.jp.

Wessel Ganzevoort, Email: j.w.ganzevoort@amsterdamumc.nl.

Akihide Ohkuchi, Email: okuchi@jichi.ac.jp.

Hema Mistry, Email: Hema.Mistry@warwick.ac.uk.

Diane Farrar, Email: Diane.Farrar@bthft.nhs.uk.

Fionnuala Mone, Email: F.Mone@qub.ac.uk.

Jun Zhang, Email: junjimzhang@sina.com.

Paul T Seed, Email: paul.seed@kcl.ac.uk.

Helena Teede, Email: helena.teede@monash.edu.

Fabricio Da Silva Costa, Email: Fabricio.DaSilvaCosta@health.qld.gov.au.

Athena P Souka, Email: athena.souka@googlemail.com.

Melanie Smuk, Email: m.smuk@qmul.ac.uk.

Sergio Ferrazzani, Email: Sergio.Ferrazzani@unicatt.it.

Silvia Salvi, Email: sissi.salvi@gmail.com.

Federico Prefumo, Email: federico.prefumo@gmail.com.

Rinat Gabbay-Benziv, Email: gabbayrinat@gmail.com.

Chie Nagata, Email: nagata-chi@ncchd.go.jp.

Satoru Takeda, Email: stakeda@juntendo.ac.jp.

Evan Sequeira, Email: evan.sequeira@aku.edu.

Olav Lapaire, Email: Olav.Lapaire@usb.ch.

Jose Guilherme Cecatti, Email: cecatti@unicamp.br.

Rachel Katherine Morris, Email: r.k.morris@bham.ac.uk.

Ahmet A Baschat, Email: abascha1@jhmi.edu.

Kjell Salvesen, Email: pepe.salvesen@ntnu.no.

Luc Smits, Email: luc.smits@maastrichtuniversity.nl.

Dewi Anggraini, Email: dewi.anggraini@ulm.ac.id.

Alice Rumbold, Email: Alice.Rumbold@sahmri.com.

Marleen van Gelder, Email: Marleen.vanGelder@radboudumc.nl.

Arri Coomarasamy, Email: a.coomarasamy@bham.ac.uk.

John Kingdom, Email: john.kingdom@sinaihealth.ca.

Seppo Heinonen, Email: seppo.heinonen@hus.fi.

Asma Khalil, Email: asmakhalil79@googlemail.com.

François Goffinet, Email: francois.goffinet@aphp.fr.

Sadia Haqnawaz, Email: sadianawaz@blueyonder.co.uk.

Javier Zamora, Email: javierza@gmail.com.

Richard D Riley, Email: r.d.riley@bham.ac.uk.

Shakila Thangaratinam, Email: s.thangaratinam.1@bham.ac.uk.

Linda Gough, Email: lindamgough@gmail.com.

Data availability statement

Data are available upon reasonable request.

References

  • 1.Hadlock FP, Harrist RB, Martinez-Poyer J. In utero analysis of fetal growth: a sonographic weight standard. Radiology. 1991;181:129–33. doi: 10.1148/radiology.181.1.1887021. [DOI] [PubMed] [Google Scholar]
  • 2.Agarwal U, Hugh O, Gardosi J. Prospective risk of stillbirth according to fetal size at term. J Perinat Med. 2022;50:748–52. doi: 10.1515/jpm-2022-0200. [DOI] [PubMed] [Google Scholar]
  • 3.von Beckerath A-K, Kollmann M, Rotky-Fast C, et al. Perinatal complications and long-term neurodevelopmental outcome of infants with intrauterine growth restriction. Am J Obstet Gynecol. 2013;208:130. doi: 10.1016/j.ajog.2012.11.014. [DOI] [PubMed] [Google Scholar]
  • 4.Hutcheon JA, Liauw J. Should fetal growth charts be references or standards? Epidemiology (Sunnyvale) 2021;32:14–7. doi: 10.1097/EDE.0000000000001275. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Vayssière C, Sentilhes L, Ego A, et al. Fetal growth restriction and intra-uterine growth restriction: guidelines for clinical practice from the French College of Gynaecologists and Obstetricians. Eur J Obstet Gynecol Reprod Biol. 2015;193:10–8. doi: 10.1016/j.ejogrb.2015.06.021. [DOI] [PubMed] [Google Scholar]
  • 6.Saving babies’ lives version two: a care bundle for reducing perinatal mortality. [15-Oct-2020]. https://www.england.nhs.uk/wp-content/uploads/2019/03/Saving-Babies-Lives-Care-Bundle-Version-Two-Updated-Final-Version.pdf Available. Accessed.
  • 7.Dietz PM, Rizzo JH, England LJ, et al. Health care utilization in the first year of life among small- and large- for-gestational age term infants. Matern Child Health J. 2013;17:1016–24. doi: 10.1007/s10995-012-1082-z. [DOI] [PubMed] [Google Scholar]
  • 8.Shepard MJ, Richards VA, Berkowitz RL, et al. An evaluation of two equations for predicting fetal weight by ultrasound. Am J Obstet Gynecol. 1982;142:47–54. doi: 10.1016/s0002-9378(16)32283-9. [DOI] [PubMed] [Google Scholar]
  • 9.Hadlock FP, Harrist RB, Carpenter RJ, et al. Sonographic estimation of fetal weight. The value of femur length in addition to head and abdomen measurements. Radiology. 1984;150:535–40. doi: 10.1148/radiology.150.2.6691115. [DOI] [PubMed] [Google Scholar]
  • 10.Milner J, Arezina J. The accuracy of ultrasound estimation of fetal weight in comparison to birth weight: a systematic review. Ultrasound. 2018;26:32–41. doi: 10.1177/1742271X17732807. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Möst L, Schmid M, Faschingbauer F, et al. Predicting birth weight with conditionally linear transformation models. Stat Methods Med Res. 2016;25:2781–810. doi: 10.1177/0962280214532745. [DOI] [PubMed] [Google Scholar]
  • 12.Kim ET, Singh K, Moran A, et al. Obstetric ultrasound use in low and middle income countries: a narrative review. Reprod Health. 2018;15:129. doi: 10.1186/s12978-018-0571-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Shulman Y, Shah BR, Berger H, et al. Prediction of birthweight and risk of macrosomia in pregnancies complicated by diabetes. Am J Obstet Gynecol MFM. 2023;5:101042. doi: 10.1016/j.ajogmf.2023.101042. [DOI] [PubMed] [Google Scholar]
  • 14.Li C, Peng Y, Zhang B, et al. Birth weight prediction models for the different gestational age stages in a Chinese population. Sci Rep. 2019;9:10834. doi: 10.1038/s41598-019-47056-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Kuhle S, Maguire B, Zhang H, et al. Comparison of logistic regression with machine learning methods for the prediction of fetal growth abnormalities: a retrospective cohort study. BMC Pregnancy Childbirth. 2018;18:333. doi: 10.1186/s12884-018-1971-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Kleinrouweler CE, Cheong-See FM, Collins GS, et al. Prognostic models in obstetrics: available, but far from applicable. Am J Obstet Gynecol. 2016;214:79–90. doi: 10.1016/j.ajog.2015.06.013. [DOI] [PubMed] [Google Scholar]
  • 17.Altman DG, Vergouwe Y, Royston P, et al. Prognosis and prognostic research: validating a prognostic model. BMJ. 2009;338:b605. doi: 10.1136/bmj.b605. [DOI] [PubMed] [Google Scholar]
  • 18.Moons KGM, Royston P, Vergouwe Y, et al. Prognosis and prognostic research: what, why, and how? BMJ. 2009;338:b375. doi: 10.1136/bmj.b375. [DOI] [PubMed] [Google Scholar]
  • 19.Royston P, Moons KGM, Altman DG, et al. Prognosis and prognostic research: developing a prognostic model. BMJ. 2009;338:b604. doi: 10.1136/bmj.b604. [DOI] [PubMed] [Google Scholar]
  • 20.Riley RD, van der Windt D, Croft P, et al., editors. Prognosis research in healthcare: concepts, methods and impact. Oxford, UK: Oxford University Press; 2019. [Google Scholar]
  • 21.Debray TPA, Collins GS, Riley RD, et al. Transparent reporting of multivariable prediction models developed or validated using clustered data: TRIPOD-cluster checklist. BMJ. 2023;380:e071018. doi: 10.1136/bmj-2022-071018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Allotey J, Snell KI, Smuk M, et al. Validation and development of models using clinical, biochemical and ultrasound markers for predicting pre-eclampsia: an individual participant data meta-analysis. Health Technol Assess. 2020;24:1–252. doi: 10.3310/hta24720. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Sheikh J, Allotey J, Kew T, et al. Effects of race and ethnicity on perinatal outcomes in high-income and upper-middle-income countries: an individual participant data meta-analysis of 2 198 655 pregnancies. Lancet. 2022;400:2049–62. doi: 10.1016/S0140-6736(22)01191-6. [DOI] [PubMed] [Google Scholar]
  • 24.Wolff RF, Moons KGM, Riley RD, et al. PROBAST: a tool to assess the risk of bias and applicability of prediction model studies. Ann Intern Med. 2019;170:51–8. doi: 10.7326/M18-1376. [DOI] [PubMed] [Google Scholar]
  • 25.Allotey J, Whittle R, Snell KIE, et al. External validation of prognostic models to predict stillbirth using International Prediction of Pregnancy Complications (IPPIC) network database: individual participant data meta-analysis. Ultrasound in Obstet & Gyne. 2022;59:209–19. doi: 10.1002/uog.23757. [DOI] [PubMed] [Google Scholar]
  • 26.Snell KIE, Allotey J, Smuk M, et al. External validation of prognostic models predicting pre-eclampsia: individual participant data meta-analysis. BMC Med. 2020;18:302. doi: 10.1186/s12916-020-01766-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Poon LCY, Karagiannis G, Staboulidou I, et al. Reference range of birth weight with gestation and first-trimester prediction of small-for-gestation neonates. Prenat Diagn. 2011;31:58–65. doi: 10.1002/pd.2520. [DOI] [PubMed] [Google Scholar]
  • 28.Papageorghiou AT, Ohuma EO, Altman DG, et al. International standards for fetal growth based on serial ultrasound measurements: the fetal growth longitudinal study of the INTERGROWTH-21st project. Lancet. 2014;384:869–79. doi: 10.1016/S0140-6736(14)61490-2. [DOI] [PubMed] [Google Scholar]
  • 29.de Onis M, Garza C, Victora CG, et al. The WHO multicentre growth reference study: planning, study design, and methodology. Food Nutr Bull. 2004;25:S15–26. doi: 10.1177/15648265040251S103. [DOI] [PubMed] [Google Scholar]
  • 30.Gardosi J, Francis A, Turner S, et al. Customized growth charts: rationale, validation and clinical benefits. Am J Obstet Gynecol. 2018;218:S609–18. doi: 10.1016/j.ajog.2017.12.011. [DOI] [PubMed] [Google Scholar]
  • 31.Rumbold AR, Crowther CA, Haslam RR, et al. Vitamins C and E and the risks of preeclampsia and perinatal complications. N Engl J Med. 2006;354:1796–806. doi: 10.1056/NEJMoa054186. [DOI] [PubMed] [Google Scholar]
  • 32.Allen RE, Zamora J, Arroyo-Manzano D, et al. External validation of preexisting first trimester preeclampsia prediction models. Eur J Obstet Gynecol Reprod Biol. 2017;217:119–25. doi: 10.1016/j.ejogrb.2017.08.031. [DOI] [PubMed] [Google Scholar]
  • 33.Jenum AK, Sletner L, Voldner N, et al. The STORK Groruddalen research programme: a population-based cohort study of gestational diabetes, physical activity, and obesity in pregnancy in a multiethnic population. Rationale, methods, study population, and participation rates. Scand J Public Health. 2010;38:60–70. doi: 10.1177/1403494810378921. [DOI] [PubMed] [Google Scholar]
  • 34.Eunice Kennedy Shriver National Institute of Child Health and Human Development NICHD DASH consortium of safe labor (CSL) study page. [25-Jul-2018]. https://dash.nichd.nih.gov/study/2331 Available. Accessed.
  • 35.Riley RD, Snell KIE, Ensor J, et al. Minimum sample size for developing a multivariable prediction model: part I - continuous outcomes. Stat Med. 2019;38:1262–75. doi: 10.1002/sim.7993. [DOI] [PubMed] [Google Scholar]
  • 36.Riley RD, Tierney J, Stewart LA, editors. Individual participant data meta-analysis: a handbook for healthcare research. Wiley, Chicester; 2021. [Google Scholar]
  • 37.Sauerbrei W, Royston P. Building multivariable prognostic and diagnostic models: transformation of the predictors by using fractional polynomials. J R Stat Soc Ser A Stat Soc. 1999;162:71–94. doi: 10.1111/1467-985X.00122. [DOI] [Google Scholar]
  • 38.Royston P, Altman DG. Regression using fractional polynomials of continuous covariates: parsimonious parametric modelling. Appl Stat. 1994;43:429. doi: 10.2307/2986270. [DOI] [Google Scholar]
  • 39.Jolani S, Debray TPA, Koffijberg H, et al. Imputation of systematically missing predictors in an individual participant data meta-analysis: a generalized approach using MICE. Stat Med. 2015;34:1841–63. doi: 10.1002/sim.6451. [DOI] [PubMed] [Google Scholar]
  • 40.Van Houwelingen JC, Le Cessie S. Predictive value of statistical models. Stat Med. 1990;9:1303–25. doi: 10.1002/sim.4780091109. [DOI] [PubMed] [Google Scholar]
  • 41.Little RJA, Rubin DB. Statistical analysis with missing data. New York: John Wiley; 2002. https://onlinelibrary.wiley.com/doi/book/10.1002/9781119013563 Available. [Google Scholar]
  • 42.Debray TPA, Moons KGM, Ahmed I, et al. A framework for developing, implementing, and evaluating clinical prediction models in an individual participant data meta-analysis. Stat Med. 2013;32:3158–80. doi: 10.1002/sim.5732. [DOI] [PubMed] [Google Scholar]
  • 43.Riley RD, Ensor J, Snell KIE, et al. External validation of clinical prediction models using big datasets from e-health records or IPD meta-analysis: opportunities and challenges. BMJ. 2016;353:i3140. doi: 10.1136/bmj.i3140. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 44.Röver C, Knapp G, Friede T. Hartung-Knapp-Sidik-Jonkman approach and its modification for random-effects meta-analysis with few studies. BMC Med Res Methodol. 2015;15:99. doi: 10.1186/s12874-015-0091-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 45.StataCorp . Stata statistical software: release 14. College Station, TX: StataCorp LP; 2014. [Google Scholar]
  • 46.Mortality rate, neonatal (per 1,000 live births) - low and middle income, high income estimates developed by the UN inter-agency group for child mortality estimation (UNICEF, WHO, world bank, UN DESA population division) at Childmortality.org. [29-Mar-2023]. https://data.worldbank.org/indicator/SH.DYN.NMRT?locations=XO-XD Available. Accessed.
  • 47.Rubin DB. Multiple imputation for nonresponse in surveys. New York: Wiley; 1987. https://onlinelibrary.wiley.com/doi/book/10.1002/9780470316696 Available. [Google Scholar]
  • 48.White IR, Royston P, Wood AM. Multiple imputation using chained equations: issues and guidance for practice. Stat Med. 2011;30:377–99. doi: 10.1002/sim.4067. [DOI] [PubMed] [Google Scholar]
  • 49.Wilcox AJ, Cortese M, McConnaughey DR, et al. The limits of small-for-gestational-age as a high-risk category. Eur J Epidemiol. 2021;36:985–91. doi: 10.1007/s10654-021-00810-z. [DOI] [PubMed] [Google Scholar]
  • 50.Meertens LJE, Scheepers HC, De Vries RG, et al. External validation study of first trimester obstetric prediction models (expect study I): research protocol and population characteristics. JMIR Res Protoc. 2017;6:e203. doi: 10.2196/resprot.7837. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 51.Melamed N, Baschat A, Yinon Y, et al. FIGO (International Federation of Gynecology and Obstetrics) initiative on fetal growth: best practice advice for screening, diagnosis, and management of fetal growth restriction. Int J Gynaecol Obstet. 2021;152 Suppl 1:3–57. doi: 10.1002/ijgo.13522. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 52.Morris RK. Prediction and prevention of fetal growth restriction and compromise of fetal wellbeing. Systematic reviews and meta-analyses with model based economic evaluation. A thesis submitted to the University of Birmingham for the degree of doctor of philosophy. College of Medical and Dental Sciences the University of Birmingham. 2010. [5-May-2018]. http://etheses.bham.ac.uk/1319/1/Morris11PhD.pdf Available. Accessed.
  • 53.Royal College of Obstetricians and Gynaecologists The investigation and management of the small-for-gestational-age fetus - RCOG green-top guideline No.31: 2nd edition | February 2013 | minor revisions. 2014. [29-Jun-2022]. https://www.rcog.org.uk/globalassets/documents/guidelines/gtg_31.pdf Available. Accessed.
  • 54.Fetal growth restriction: ACOG practice bulletin, number 227. Obstet Gynecol. 2021;137:e16–28. doi: 10.1097/AOG.0000000000004251. [DOI] [PubMed] [Google Scholar]
  • 55.Lausman A, Kingdom J, Gagnon R, et al. Intrauterine growth restriction: screening, diagnosis, and management. J Obstet Gynaecol Can. 2013;35:741–8. doi: 10.1016/S1701-2163(15)30865-3. [DOI] [PubMed] [Google Scholar]
  • 56.The Royal Australian and New Zealand College of Obstetricians and Gynaecologists Screening in early pregnancy for adverse perinatal outcomes. Prenatal Screening for Adverse Pregnancy Outcomes C-Obs 61. 2015 https://ranzcog.edu.au/wp-content/uploads/2022/05/Screening-in-Early-Pregnancy-for-Adverse-Perinatal-Outcomes.pdf Available. [Google Scholar]
  • 57.Tao J, Yuan Z, Sun L, et al. Fetal birthweight prediction with measured data by a temporal machine learning method. BMC Med Inform Decis Mak. 2021;21:26. doi: 10.1186/s12911-021-01388-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 58.National Institute for Health and Care Excellence (NICE) Antenatal care for uncomplicated pregnancies clinical guideline [cg62]. isbn 978-1-4731-0891-2. 2008. https://www.nice.org.uk/guidance/cg62 Available. [PubMed]
  • 59.Smith GC, Moraitis AA, Wastlund D, et al. Universal late pregnancy ultrasound screening to predict adverse outcomes in nulliparous women: a systematic review and cost-effectiveness analysis. Health Technol Assess. 2021;25:1–190. doi: 10.3310/hta25150. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

    This section collects any data citations, data availability statements, or supplementary materials included in this article.

    Supplementary Materials

    online supplemental file 1
    bmjmed-3-1-s001.docx (23.1KB, docx)
    DOI: 10.1136/bmjmed-2023-000784
    online supplemental file 2
    bmjmed-3-1-s002.pdf (67.9KB, pdf)
    DOI: 10.1136/bmjmed-2023-000784
    online supplemental file 3
    bmjmed-3-1-s003.pdf (248.6KB, pdf)
    DOI: 10.1136/bmjmed-2023-000784
    online supplemental file 4
    bmjmed-3-1-s004.pdf (62.1KB, pdf)
    DOI: 10.1136/bmjmed-2023-000784
    online supplemental file 5
    bmjmed-3-1-s005.pdf (433.2KB, pdf)
    DOI: 10.1136/bmjmed-2023-000784

    Data Availability Statement

    Data are available upon reasonable request.

    Articles from BMJ Medicine are provided here courtesy of BMJ Publishing Group

    RESOURCES