Skip to main content
PMC home page
Biochemical Journal logoLink to Biochemical Journal
. 1993 Aug 15;294(Pt 1):87–94. doi: 10.1042/bj2940087

Control analysis applied to single enzymes: can an isolated enzyme have a unique rate-limiting step?

G C Brown 1, C E Cooper 1
PMCID: PMC1134569  PMID: 8363590

Abstract

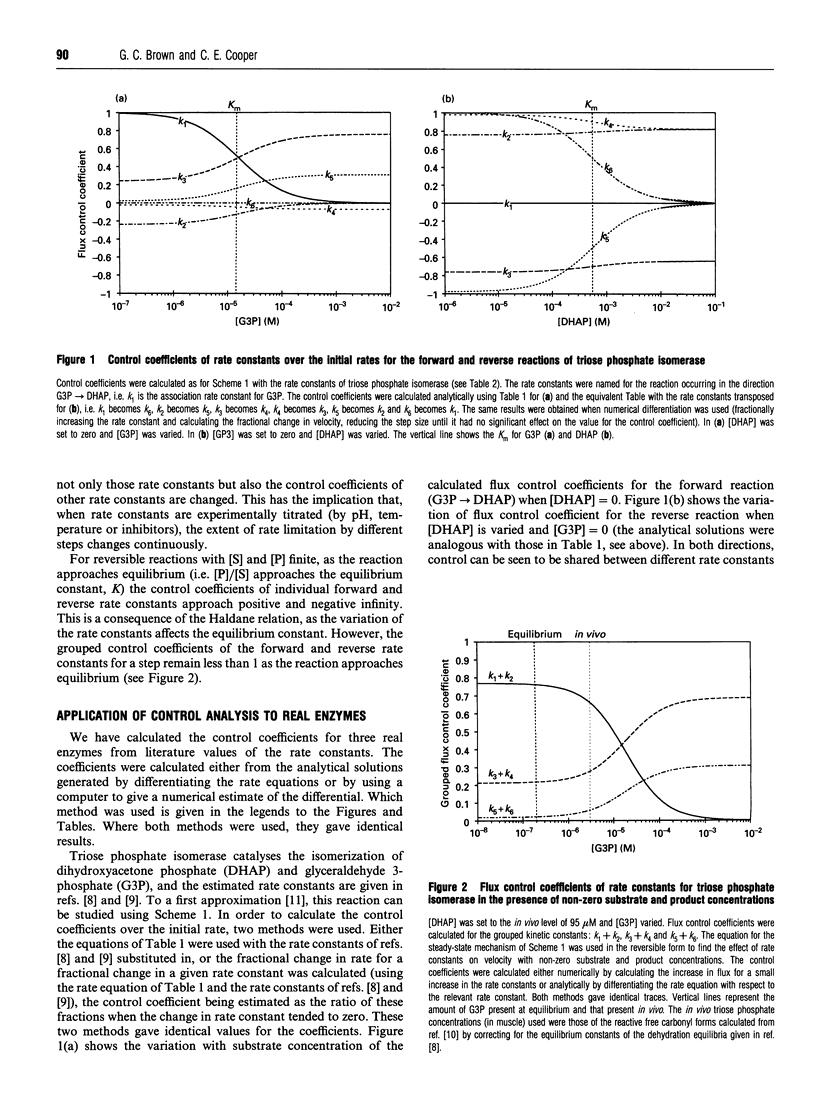
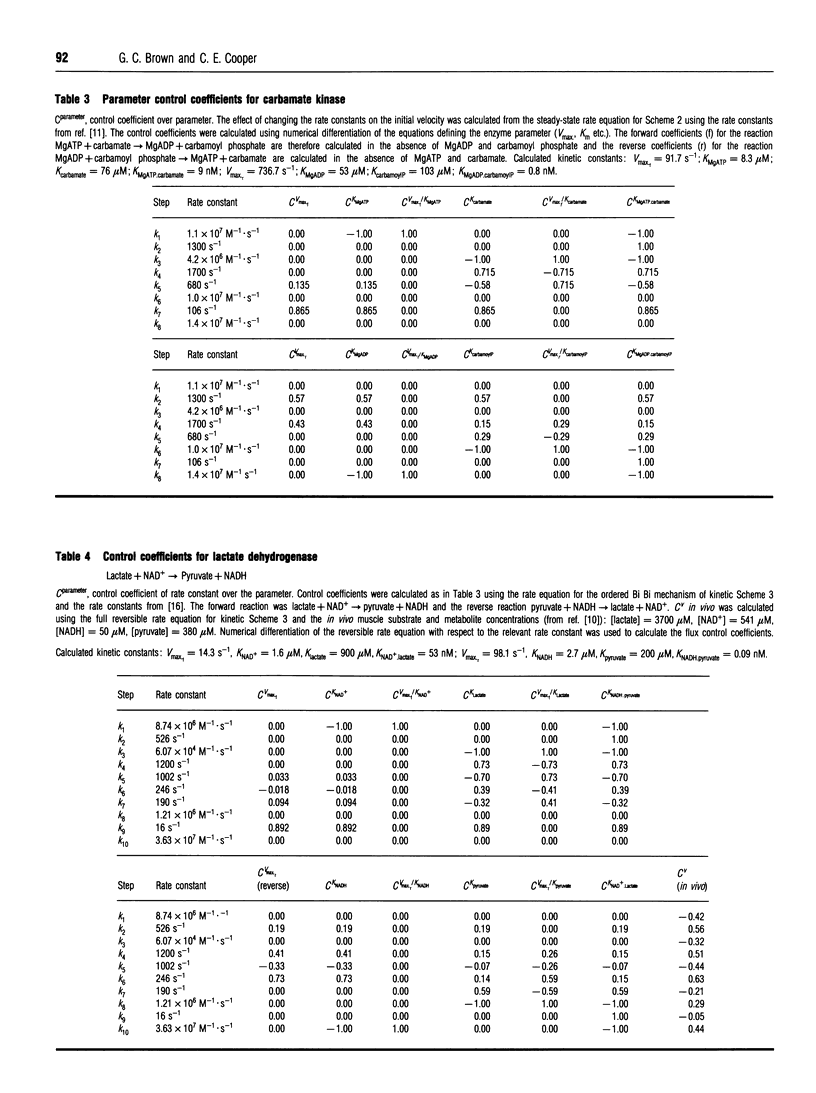
Control analysis is used to analyse and quantify the concept of a rate-limiting step within an enzyme. The extent to which each rate constant within the enzyme limits the steady-state rate of the enzyme and the levels of enzyme intermediate species are quantified as flux and concentration control coefficients. These coefficients are additive and obey summation theorems. The control coefficients of triose phosphate isomerase, carbamate kinase and lactate dehydrogenase are calculated from literature values of the rate constants. It is shown that, contrary to previous assumption, these enzymes do not have a unique rate-limiting step, but rather flux control is shared by several rate constants and varies with substrate, product and effector concentrations, and with the direction of the reaction. Thus the general assumption that an enzyme will have a unique rate-limiting step is unjustified.

Full text

PDF
87

Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Albery W. J., Knowles J. R. Evolution of enzyme function and the development of catalytic efficiency. Biochemistry. 1976 Dec 14;15(25):5631–5640. doi: 10.1021/bi00670a032. [DOI] [PubMed] [Google Scholar]
  2. Albery W. J., Knowles J. R. Free-energy profile of the reaction catalyzed by triosephosphate isomerase. Biochemistry. 1976 Dec 14;15(25):5627–5631. doi: 10.1021/bi00670a031. [DOI] [PubMed] [Google Scholar]
  3. Bernhard S. A., Srivastava D. K. Functional consequences of the direct transfer of metabolites in muscle glycolysis. Biochem Soc Trans. 1987 Oct;15(5):977–981. doi: 10.1042/bst0150977. [DOI] [PubMed] [Google Scholar]
  4. Burbaum J. J., Raines R. T., Albery W. J., Knowles J. R. Evolutionary optimization of the catalytic effectiveness of an enzyme. Biochemistry. 1989 Nov 28;28(24):9293–9305. doi: 10.1021/bi00450a009. [DOI] [PubMed] [Google Scholar]
  5. Ellington A. D., Benner S. A. Free energy differences between enzyme bound states. J Theor Biol. 1987 Aug 21;127(4):491–506. doi: 10.1016/s0022-5193(87)80145-5. [DOI] [PubMed] [Google Scholar]
  6. Fersht A. R. Catalysis, binding and enzyme-substrate complementarity. Proc R Soc Lond B Biol Sci. 1974 Nov 19;187(1089):397–407. doi: 10.1098/rspb.1974.0084. [DOI] [PubMed] [Google Scholar]
  7. Giersch C. Control analysis of metabolic networks. 1. Homogeneous functions and the summation theorems for control coefficients. Eur J Biochem. 1988 Jun 15;174(3):509–513. doi: 10.1111/j.1432-1033.1988.tb14128.x. [DOI] [PubMed] [Google Scholar]
  8. Heinrich R., Rapoport T. A. A linear steady-state treatment of enzymatic chains. General properties, control and effector strength. Eur J Biochem. 1974 Feb 15;42(1):89–95. doi: 10.1111/j.1432-1033.1974.tb03318.x. [DOI] [PubMed] [Google Scholar]
  9. Kacser H., Burns J. A. The control of flux. Symp Soc Exp Biol. 1973;27:65–104. [PubMed] [Google Scholar]
  10. Marshall M., Cohen P. P. A kinetic study of the mechanism of crystalline carbamate kinase. J Biol Chem. 1966 Sep 25;241(18):4197–4208. [PubMed] [Google Scholar]
  11. Northrop D. B. Minimal kinetic mechanism and general equation for deuterium isotope effects on enzymic reactions: uncertainty in detecting a rate-limiting step. Biochemistry. 1981 Jul 7;20(14):4056–4061. doi: 10.1021/bi00517a017. [DOI] [PubMed] [Google Scholar]
  12. Pettersson G. Effect of evolution on the kinetic properties of enzymes. Eur J Biochem. 1989 Oct 1;184(3):561–566. doi: 10.1111/j.1432-1033.1989.tb15050.x. [DOI] [PubMed] [Google Scholar]
  13. Pettersson G., Pettersson P. Ultimate limits for the reaction flux and metabolite levels that may be evolutionarily reached in a linear metabolic pathway. Eur J Biochem. 1990 Nov 26;194(1):135–139. doi: 10.1111/j.1432-1033.1990.tb19436.x. [DOI] [PubMed] [Google Scholar]
  14. Ray W. J., Jr Rate-limiting step: a quantitative definition. Application to steady-state enzymic reactions. Biochemistry. 1983 Sep 27;22(20):4625–4637. doi: 10.1021/bi00289a003. [DOI] [PubMed] [Google Scholar]
  15. Renard M., Fersht A. R. Anomalous pH dependence of kcat-KM in enzyme reactions. Rate constants for the association of chymotrypsin with substrates. Biochemistry. 1973 Nov 6;12(23):4713–4718. doi: 10.1021/bi00747a026. [DOI] [PubMed] [Google Scholar]
  16. Südi J. How to draw kinetic barrier diagrams for enzyme-catalysed reactions. Biochem J. 1991 May 15;276(Pt 1):265–268. doi: 10.1042/bj2760265. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biochemical Journal are provided here courtesy of The Biochemical Society

RESOURCES