Abstract
Background
Predicting energy requirements for older adults is compromised by the underpinning data being extrapolated from younger adults.
Objectives
To generate and validate new total energy expenditure (TEE) predictive equations specifically for older adults using readily available measures (age, weight, height) and to generate and test new physical activity level (PAL) values derived from 1) reference method of indirect calorimetry and 2) predictive equations in adults aged ≥65 y.
Methods
TEE derived from “gold standard” methods from n = 1657 (n = 1019 females, age range 65–90 y), was used to generate PAL values. PAL ranged 1.28–2.05 for males and 1.26–2.06 for females. Physical activity (PA) coefficients were also estimated and categorized (inactive to very active) from population means. Nonlinear regression was used to develop prediction equations for estimating TEE. Double cross-validation in a randomized, sex-stratified, age-matched 50:50 split, and leave one out cross-validation were performed. Comparisons were made with existing equations.
Results
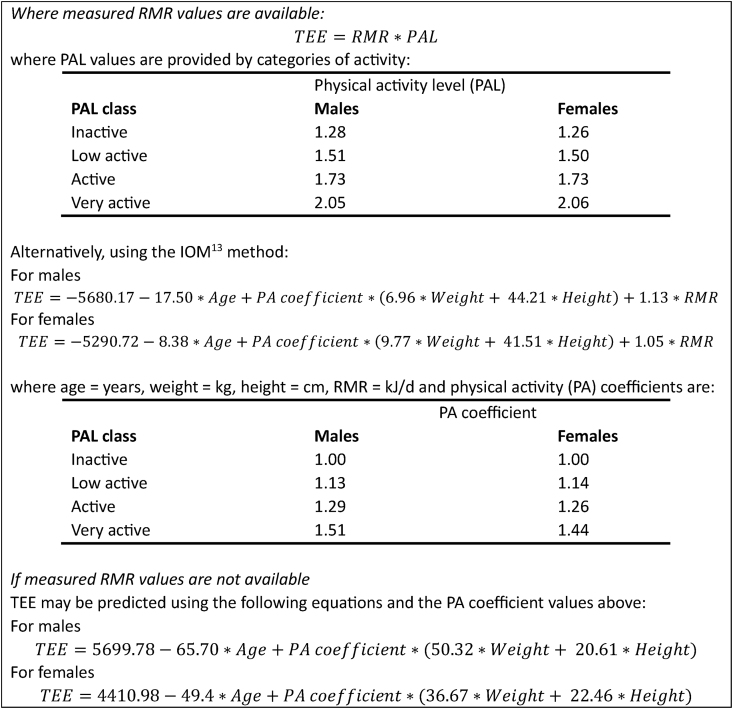
Equations predicting TEE using the Institute of Medicine method are as follows: For males, TEE = −5680.17 − 17.50 × age (years) + PA coefficient × (6.96 × weight [kilograms] + 44.21 × height [centimeters]) + 1.13 × resting metabolic rate (RMR) (kilojoule/day). For females, TEE = −5290.72 − 8.38 × age (years) + PA coefficient × (9.77 × weight [kilograms] + 41.51 × height [centimeters]) + 1.05 × RMR (kilojoule/day), where PA coefficient values range from 1 (inactive) to 1.51 (highly active) in males and 1 to 1.44 in females respectively. Predictive performance for TEE from anthropometric variables and population mean PA was moderate with limits of agreement approximately ±30%. This improved to ±20% if PA was adjusted for activity category (inactive, low active, active, and very active). Where RMR was included as a predictor variable, the performance improved further to ±10% with a median absolute prediction error of approximately 4%.
Conclusions
These new TEE prediction equations require only simple anthropometric data and are accurate and reproducible at a group level while performing better than existing equations. Substantial individual variability in PAL in older adults is the major source of variation when applied at an individual level.
Keywords: total energy expenditure, older adults, resting energy expenditure, physical activity, prediction equation
Introduction
The changing demographic of our globally aging population has implications for nutrition science and its application to human health. In 2022, 771 million people were aged ≥65 y; the proportion of this cohort is expected to increase to 16.0% or 1.6 billion by 2050 [1]. Multiple changes in body composition occur through the aging process. These changes include weight change, decreased lean mass, and increased fat mass [2], with the impact of these changes on health outcomes not fully understood [3]. However, the change in body composition and consequently the nutritional requirements for older adults are not translated at a population level, where nutrition recommendations such as dietary guidelines [4], predictive nutrient equations [5], and other anthropometric measures [2] are frequently based on data obtained from younger cohorts. Limited analyses of energy requirements in older adults have been undertaken [6], and the predictive energy equations recently released by the National Academies of Sciences, Engineering, and Medicine [7] classify older adults within the entire adult category of 19+ y. In this United Nations Decade of Healthy Ageing [8], it is timely that nutrition and exercise recommendations at population, community, and individual levels are supported by predictive energy equations that reflect the energy needs of older adults.
The “gold standard” or reference method for measuring total energy expenditure (TEE) is doubly labeled water (DLW) [9]. It is the only method that enables TEE to be measured in free-living subjects without disruption to participants and measures the total energy expended in metabolic processes (resting metabolic rate [RMR]) and energy expended in any activity. The method involves the ingestion of water labeled with 2 nonradioactive stable isotopes (deuterium [2H] and oxygen [18O]) with the elimination of the tracers (through spot urine samples) collected over 7–14 d. TEE is calculated through the difference in isotope elimination rates [10,11]. A comprehensive worldwide database of daily TEE through the lifespan has been compiled [9]. However, using DLW is expensive, time consuming, and requires sophisticated analytical facilities to determine TEE at a participant level. Alternatively, TEE may be estimated using wearable activity monitors but are of questionable accuracy [12] and again are time consuming to use, which is why predictive equations are commonly applied at both the population and individual level.
There are 2 approaches to predicting TEE: either directly from anthropometric measurements (height and weight) and age stratified for sex [13], or through equations that measure the component parts of TEE using estimates of RMR, with scaling factors applied for physical activity level (PAL), which when combined, estimate daily energy expenditure. Many of the equations utilized both for RMR and PAL were developed many years ago [9], many have not been purposively developed for the older adult population and are extrapolated from younger subjects [7]. Where inappropriate predictive equations are used, under- or overestimation of TEE will arise [6], with associated impacts on energy estimates and weight status.
Previously, our analysis of a large TEE dataset (n = 1488) in an older adult population (≥65 y) [14] determined that 3 predictive equations for RMR most closely estimated TEE: the Ikeda [15], Livingston [16], and Mifflin [17] equations, although accuracy at an individual level was relatively poor, and a high degree of proportional bias was noted as energy expenditure increased. Our more recent analysis [18] of sourced data was undertaken in an international dataset of adults aged ≥65 y (n = 1686, 38.5% male) where RMR was measured using the reference method of indirect calorimetry. We generated and validated new RMR equations specifically for older adults. The present analysis extends the prior analysis in a large dataset of DLW measurements of older adults and aimed to: 1) generate and validate new TEE predictive equations using both simple anthropometry-based predictions and with RMR-based predictions, 2) compare the performance of these new equations against the “gold standard” TEE data, and 3) generate age-appropriate PAL values for adults aged ≥65 y.
Methods
Ethical approval
This research was approved by the university Human Research Ethics Committee (27291).
Dataset formation
The dataset was composed of participant-level data contributed by research groups internationally. A systematic literature search conducted in 2016 [6,14] and updated in 2021 using the same methods [18], identified papers describing original measured TEE data using DLW in adults ≥65 y. Studies of participants with acute conditions impacting energy metabolism such as those receiving treatment in intensive care were excluded. Authors of studies were contacted by our research team requesting their data to be shared. Multiple variables were sought, including participant sex (male and female), age (in years; to the nearest whole year), body weight (in kilograms; to the nearest 0.1 kg), height (in centimeters; to the nearest 0.1 cm), reference measured RMR (measured by indirect calorimetry; in kilojoule/day, to the nearest kilojoule), and reference measured TEE (measured by DLW; in kilojoule/day, to the nearest kilojoule), with the primary outcome of interest being TEE.
The dataset comprised n = 2159 participant-level records, derived from n = 39 studies [5,[19], [20], [21], [22], [23], [24], [25], [26], [27], [28], [29], [30], [31], [32], [33], [34], [35], [36], [37], [38], [39], [40], [41], [42], [43], [44], [45], [46], [47], [48], [49], [50], [51], [52], [53], [54], [55], [56]]. Of these, n = 32 participants were removed from the analysis due to missing data (including no age, sex, weight, or height). Additional exclusions included outliers (n = 2), age <65 y (n = 15), and Tanzanian hunter-gathers (n = 4). A further 420 records were removed for not having measured RMR leaving n = 1686 (aged 65–79.9 y, n = 355; aged ≥80.0 y, n = 1331) for predictor development. On preliminary analysis, a further 29 participants were removed for having physiologically unrealistic TEE or RMR values, for example, RMR > TEE or a PAL >2.5, the upper limit set for very active persons [13] to yield a final dataset of 1657 for analysis (Figure 1).
FIGURE 1.
Flow diagram of participant records into the analysis. RMR, resting metabolic rate; TEE, total energy expenditure.
PALs and physical activity coefficients
Using the same approach as our previous analysis [14], PAL was calculated for males and females to characterize energy expenditure above the RMR of the population. PAL was calculated from measured TEE divided by measured RMR. Mean PAL values were calculated for males and females separately, for the complete dataset and separately, for those aged 65–79.9 y and those aged ≥80 y. The mean PAL values were also calculated for each of the United States Institute of Medicine (IOM) [13] recommendations for activity categories: sedentary (PAL ≥ 1.0–1.4), low active (PAL ≥ 1.4–1.6), active (PAL ≥ 1.6–1.9), and very active (PAL ≥ 1.9–2.5). Physical activity (PA) coefficients were calculated for each of these PAL categories with the PA coefficient for the sedentary category set as 1.00 and scaled for the other PAL categories according to IOM methodology. These mean values were calculated for the complete dataset and separately, for those younger and older than 80 y of age.
Prediction of TEE
Anthropometry-based prediction: TEE was predicted from age, weight, height, and physical activity category according to the IOM [13] method:
| TEE = A + B × age + PA coefficient × (D × weight + E × height) | (equation 1) |
where A is a constant, PA coefficient is calculated from mean PAL as described above and B, D, and E are coefficients determined by solving equation 1 using nonlinear regression.
PAL-based prediction: TEE was calculated from RMR, either measured or predicted from published prediction equations of Porter et al. [18] as the product:
| TEE = PAL × RMR | (equation 2) |
Combined anthropometry- and PAL-based prediction: equation 1 was adapted to include RMR as an additional predictor variable.
| TEE = A + B × age + PA coefficient × (D × weight + E × height) + F × RMR | (equation 3) |
All calculations were performed with TEE and RMR expressed in kJ/d, weight in kg, height in cm, and age in y for males and females separately. Nonlinear regression was performed using Python 3.9 with scipy.optimize.least_squares routine with the “lm” Levenberg–Marquardt method option selected (SciPy.org 1.9.3 manual. scipy.optimize import least_squares 2022 https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.least_squares.html). Goodness of fit was determined as the coefficient of determination (R2) values.
Statistical analysis
Statistical analyses were performed using MedCalc v20.2 for Windows (MedCalc Software). Results are expressed as mean ± SD and range except where otherwise indicated. Comparison of distributions of proportions of participants in each activity category were assessed using the Z test.
Predictive performance of newly generated equations was assessed using double-cross-validation in which a randomized, sex-stratified, age-matched 50:50 split (2% tolerance) of the total sample was carried out (n = 1657; Group A = 827, Group B = 830) using the allocation module of XL Toolbox (version 7.3.4, available at https://www.xltoolbox.net/). Where no significant difference was found between the 2 groups, a single equation for the completed dataset was generated with its predictive performance assessed using the leave one out cross-validation procedure (Solverstat 2019 R0; software available at https://solverstat.wordpress.com/). Predictive equations were compared using Pearson correlation, paired sample t-test, Lin’s concordance correlation, residual SD for random differences (Passing–Bablok regression) and Bland–Altman limits of agreement (LOA) analysis with ranking of multiple comparisons based on calculation of median absolute percentage error [57].
Results
Participant characteristics
The general anthropometric characteristics of this older adult dataset are presented in Table 1. Most participants were in the lower age stratum (<80.0 y) in both males and females. Mean BMI (27.0 kg/m2) was higher for adults aged 65–79.9 y, and lower in the older cohort of adults aged ≥80 y (BMI = 24.3 kg/m2 females; BMI = 25.1 kg/m2 males). Both TEE and RMR were higher in males and the younger cohort compared with the equivalent female and older cohorts.
TABLE 1.
Participant characteristics∗
| Males | Females | |||
|---|---|---|---|---|
| Age range (y) | 65–79.9 | ≥80.0 | 65–79.9 | ≥80.0 |
| Number | 512 | 126 | 801 | 218 |
| Weight (kg) | 81.5 ± 15.9 (38.0–144.0) | 72.5 ± 14.1 (42.4–108.4) | 69.4 ± 15.3 (37.8–127.6) | 58.3 ± 14.1 (29.3–101.4) |
| Height (cm) | 173.4 ± 7.9 (147.0–196.0) | 169.3 ± 7.0 (145.8–190.0) | 160.1 ± 7.1 (142.0–195.9) | 154.4 ± 8.2 (129.0–180.0) |
| BMI (kg/m2) | 27.0 ± 4.4 (16.0–42.5) | 25.1 ± 4.1 (14.6–36.2) | 27.0 ± 5.5 (15.6–47.8) | 24.3 ± 5.1 (13.6–40.9) |
| Measured TEE (kJ/d) | 10,591 ± 1935 (3605–17,430) | 8575 ± 1865 (3784–13,736) | 8447 ± 1505 (3028–15,930) | 6633 ± 1494 (3230–11,320) |
| Measured RMR (kJ/d) | 6381 ± 964 (3380–9557) | 5402 ± 1022 (3380–9627) | 5125 ± 831 (2890–8527) | 4312 ± 813 (2640–6803) |
| PAL | 1.67 ± 0.25 (1.01–2.49) | 1.58 ± 0.24 (1.04–1.58) | 1.66 ± 0.27 (1.01–2.48) | 1.55 ± 0.28 (1.05–2.37) |
BMI, body mass index; PAL, physical activity level; RMR, resting metabolic rate; TEE, total energy expenditure.
Data are reported as mean ± SD (range).
PALs
Calculated PALs and PA coefficients are presented in Table 2. The mean PAL was approximately 1.67 for males and females <80.0 y falling slightly to 1.58 and 1.55 for males and females aged ≥ 80 y, respectively. Generally, PAL distributions were very similar between males and females, with mean calculated PAL of 1.65 and 1.64, respectively. Most participants were classed as low active or active, although proportionally more of the over 80 y-old participants were in the inactive category, 22% of males and 30% of females compared with 13% and 16%, respectively, of the 65–79.9 y age group. The distribution of participants across physical activity categories did not differ significantly between males and females. The distributions of PAL values are presented graphically in Supplementary Figures 1 and 2. PA coefficients ranged from 1.0 for inactive to 1.51 for very active males.
TABLE 2.
Physical activity level and physical activity coefficients by age category∗
| Age category | Physical activity category | Males |
Females |
||||
|---|---|---|---|---|---|---|---|
| Number (%) | PAL | PA coefficient | Number (%) | PAL | PA coefficient | ||
| ≥65 y | Overall mean | 638 | 1.652 ± 0.250 (1.012–2.487) | 1.22 | 1019 | 1.639 ± 0.274 (1.015–2.481) | 1.21 |
| Inactive | 95 (15%) | 1.284 ± 0.096 (1.012–1.400) | 1.00 | 192 (19%) | 1.262 ± 0.104 (1.015–1.396) | 1.00 | |
| Low active | 182 (29%) | 1.506 ± 0.059 (1.403–1.599) | 1.13 | 281 (28%) | 1.503 ± 0.057 (1.400–1.599) | 1.14 | |
| Active | 262 (41%) | 1.732 ± 0.081 (1.601–1.897) | 1.29 | 369 (36%) | 1.735 ± 0.085 (1.601–1.899) | 1.26 | |
| Very active | 99 (16%) | 2.059 ± 0.138 (1.902–2.487) | 1.51 | 177 (17%) | 2.065 ± 0.132 (1.900–2.481) | 1.44 | |
| ≥65–79.9 y | Overall mean | 512 | 1.668 ± 0.251 (1.012–2.487) | 1.24 | 801 | 1.665 ± 0.269 (1.015–2.481) | 1.23 |
| Inactive | 67 (13%) | 1.288 ± 0.093 (1.012–1.400) | 1.00 | 128 (16%) | 1.278 ± 0.099 (1.015–1.400) | 1.00 | |
| Low active | 143 (28%) | 1.504 ± 0.059 (1.404–1.599) | 1.13 | 214 (27%) | 1.506 ± 0.057 (1.400–1.599) | 1.14 | |
| Active | 216 (42%) | 1.738 ± 0.082 (1.601–1.897) | 1.29 | 305 (38%) | 1.734 ± 0.086 (1.601–1.900) | 1.26 | |
| Very active | 86 (17%) | 2.063 ± 0.141 (1.902–2.487) | 1.51 | 154 (19%) | 2.068 ± 0.130 (1. 902–2.481) | 1.44 | |
| ≥80 y | Overall mean | 126 | 1.584 ± 0.236 (1.036–2.239) | 1.19 | 218 | 1.547 ± 0.276 (1.045–2.370) | 1.16 |
| Inactive | 28 (22%) | 1.273 ± 0.103 (1.036–1.394) | 1.00 | 66 (30%) | 1.235 ± 0.108 (1.046–1.391) | 1.00 | |
| Low active | 39 (31%) | 1.514 ± 0.061 (1.403–1.594) | 1.14 | 65 (30%) | 1.497 ± 0.056 (1.402–1.598) | 1.13 | |
| Active | 46 (37%) | 1.706 ± 0.067 (1.605–1.870) | 1.27 | 65 (30%) | 1.743 ± 0.084 (1.601–1.899) | 1.27 | |
| Very active | 13 (10%) | 2.030 ± 0.118 (1.905–2.239) | 1.49 | 22 (10%) | 2.049 ± 0.142 (1.902–2.370) | 1.43 | |
PA, physical activity; PAL, physical activity level.
Data are reported as mean ± SD (range), unless stated otherwise.
Prediction of TEE from RMR adjusted for PAL
Prediction of TEE from RMR adjusted for PAL are presented in Table 3. The commonly used approach of assuming an average PAL value performed poorly with wide LOA, at ±30% irrespective of sex and age category (≥80 or <80 y). Predicted TEE was only moderately correlated with measured TEE, rs varied from 0.61 to 0.69. A highly significant 3-fold improvement in both correlation and LOA was achieved when participants were stratified by PAL category (inactive, low active, active, and very active). Additional stratification by age group made no further improvement in predictive ability of PAL values. Comparative LOA plots for predicted TEE against measured TEE by subgroup for age and gender are shown in Supplementary Figures 3–6.
TABLE 3.
Comparison of measured total energy expenditure with predicted total energy expenditure based on resting metabolic rate multiplied by physical activity level
| Age class | PAL value used | Males (n = 638) |
Females (n =1019) |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Regression1 |
Regression1 |
||||||||||||
| rc | LOA2 |
Intercept |
Slope |
rs | MAPE |
rc | LOA2 |
Intercept |
Slope |
rs | MAPE |
||
| (%) | kJ/d | (%) | (%) | kJ/d | (%) | ||||||||
| All participants (≥65 y) | Overall mean PAL | 0.67 | 3092 (±29.7) | 1935 | 0.81 | 0.66 | 9.6 | 0.62 | 2742 (±32.8) | 1347 | 0.83 | 0.61 | 11.5 |
| Stratified by PAL category | 0.963 | 10923 (±10.4) | 5.0 | 1.0 | 0.96 | 4.1 | 0.963 | 8993 (±11.4) | −23 | 1.00 | 0.96 | 4.3 | |
| Stratified by age category and mean PAL | 0.68 | 3082 (±29.4) | 1402 | 0.86 | 0.67 | 9.7 | 0.65 | 2741 (±32.4) | 783 | 0.91 | 0.62 | 11.4 | |
| Stratified by age and PAL category | 0.963 | 10903 (±10.4) | −43 | 1.00 | 0.96 | 3.9 | 0.963 | 9043 (±11.1) | -44 | 1.01 | 0.96 | 4.2 | |
LOA, limit of agreement; MAPE, median absolute percentage error; PAL, physical activity level (see text and Table 1).
Regression = measured total energy expenditure versus predicted; rc = Lin’s concordance correlation coefficient; rs = Spearman correlation coefficient.
LOA = 1.96 SD limits of agreement.
Values significantly different (P < 0.0001) compared with values calculated using mean physical activity level.
Calculation of regression coefficients for prediction of TEE from age, weight, height, PA coefficient, and RMR
The calculated coefficients for Equations (equation 1), (equation 3) are presented in Table 4 stratified by age category. In all cases, other than females aged ≥80 y, when excluding RMR as a predictor variable, regressions of TEE on anthropometric variables and RMR were moderate to good (R2 > 0.3). Including RMR as a predictor variable markedly improved the regressions with most having R2 values greater than 0.8. Notably, the strength of the relationship was markedly better as indicated by relative magnitude of R2 when regressions were stratified by activity level compared with using the total population.
TABLE 4.
Physical activity coefficients for activity categories and regression coefficients for prediction of total energy expenditure from age, weight, height, and resting metabolic rate
| Model | Males (n = 638) |
Females (n = 1019) |
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PA coefficient | A1 (constant) | B1 (age) | D1 (weight) | E1 (height) | F1 (RMR) | R2 | PA coefficient | A1 (constant) | B1 (age) | D1 (weight) | E1 (height) | F1 (RMR) | R2 | ||
| Age class |
PAL |
Prediction based on age, weight, and height |
|||||||||||||
| A ≥65 y |
All | 1.22 | 8319.1 | −83.0 | 50.7 | 14.6 | 0.46 | 1.21 | 4621.7 | −64.5 | 38.5 | 26.4 | 0.46 | ||
| Inactive | 1.00 | −4000.3 | −11.4 | 60.4 | 48.9 | 0.70 | 1.00 | −1360.7 | −47.3 | 45.9 | 37.8 | 0.71 | |||
| Low active | 1.13 | 5366.5 | −57.0 | 58.7 | 15.1 | 0.71 | 1.14 | 1174.1 | −38.9 | 40.6 | 33.8 | 0.65 | |||
| Active | 1.29 | 7873.5 | −83.4 | 45.6 | 19.0 | 0.66 | 1.26 | 2508.8 | −42.5 | 36.2 | 29.8 | 0.56 | |||
| Very active | 1.51 | 7560.4 | −112.3 | 38.1 | 31.7 | 0.52 | 1.44 | 4418.0 | −60.8 | 25.5 | 30.6 | 0.39 | |||
| B 65–79.9 y |
All | 1.24 | 17,841.6 | −103.4 | 54.6 | 25.4 | 0.33 | 1.23 | 4906.3 | −57.5 | 36.9 | 22.6 | 0.33 | ||
| Inactive | 1.00 | −1144.1 | −25.9 | 59.7 | 38.5 | 0.75 | 1.00 | 4703.8 | −67.9 | 41.5 | 27.9 | 0.53 | |||
| Low active | 1.13 | 7671.2 | −75.8 | 56.8 | 11.1 | 0.66 | 1.14 | 447.2 | −46.2 | 41.6 | 40.2 | 0.57 | |||
| Active | 1.29 | 7782.9 | −98.8 | 43.9 | 25.0 | 0.60 | 1.26 | 2281.8 | −42.3 | 36.3 | 30.9 | 0.51 | |||
| Very active | 1.51 | 9512.1 | −134.2 | 37.0 | 30.6 | 0.45 | 1.44 | 3890.7 | −46.2 | 26.4 | 28.1 | 0.32 | |||
| C ≥80 y |
All | 1.19 | −633.5 | −34.9 | 69.5 | 30.9 | 0.54 | 1.16 | 947.4 | −40.5 | 45.5 | 34.1 | 0.47 | ||
| Inactive | 1.00 | −8470.5 | −43.1 | 64.7 | 91.0 | 0.54 | 1.00 | −2015.6 | −23.8 | 57.0 | 42.6 | 0.69 | |||
| Low active | 1.14 | −176.9 | 50.3 | 73.9 | −12.2 | 0.64 | 1.13 | −1894.6 | 13.0 | 37.5 | 26.6 | 0.58 | |||
| Active | 1.27 | 9301.6 | −42.7 | 50.2 | −5.2 | 0.50 | 1.27 | 2768.6 | −27.2 | 35.6 | 21.7 | 0.46 | |||
| Very active |
1.49 |
−5089.9 |
−50.4 |
46.2 |
57.5 |
0.79 |
1.43 |
−3686.2 |
−32.9 |
10.5 |
61.6 |
0.15 |
|||
| Prediction based on age, weight, height, and RMR |
|||||||||||||||
| D ≥65 y |
All | 1.22 | 6638.1 | −55.8 | 24.5 | 1.3 | 0.81 | 0.51 | 1.21 | 4405.1 | −53.4 | 26.7 | 14.6 | 0.53 | 0.52 |
| Inactive | 1.00 | −1026.6 | −6.9 | 11.2 | 12.9 | 1.0 | 0.90 | 1.00 | 876.5 | −22.3 | 12.9 | 11.1 | 0.9 | 0.89 | |
| Low active | 1.13 | 680.0 | −1.7 | 4.7 | −1.9 | 1.4 | 0.95 | 1.14 | 465.9 | −4.7 | 2.5 | 1.4 | 1.4 | 0.95 | |
| Active | 1.29 | 2232.3 | −15.1 | 1.4 | −1.5 | 1.6 | 0.90 | 1.26 | −985.0 | −1.3 | 3.0 | 8.3 | 1.6 | 0.90 | |
| Very active | 1.51 | 2604.5 | −24.6 | 0 | −0.5 | 1.94 | 0.82 | 1.44 | 3881.0 | −8.8 | 4.1 | −12.7 | 1.9 | 0.86 | |
| E 65–79.9 y |
All | 1.24 | 14,412.0 | −48.7 | 17.8 | −45.0 | 1.1 | 0.42 | 1.23 | 4463.5 | −44.8 | 25.9 | 11.8 | 0.5 | 0.38 |
| Inactive | 1.00 | −1034.1 | −9.2 | 15.8 | 14.1 | 1.0 | 0.89 | 1.00 | 1334.9 | −32.8 | 10.1 | 14.3 | 0.9 | 0.82 | |
| Low active | 1.13 | 1914.1 | −13.5 | 5.3 | −3.2 | 1.4 | 0.93 | 1.14 | 435.8 | −3.7 | 1.8 | 1.0 | 1.4 | 0.94 | |
| Active | 1.29 | 1914.7 | −4.3 | −3.9 | 1.6 | 1.6 | 0.89 | 1.26 | −1405.1 | −3.6 | 2.2 | 11.3 | 1.6 | 0.89 | |
| Very active | 1.51 | 3128.9 | −23.1 | −1.8 | −2.8 | 2.0 | 0.80 | 1.44 | 3726.8 | −6.4 | 5.4 | −12.6 | 1.9 | 0.84 | |
| F ≥80 y |
All | 1.19 | −1459.7 | −32.8 | 42.9 | 26.3 | 0.7 | 0.63 | 1.16 | 2065.6 | −41.7 | 30.5 | 19.3 | 0.6 | 0.53 |
| Inactive | 1.00 | 36.4 | −7.2 | −3.2 | 9.2 | 1.1 | 0.90 | 1.00 | 2149.8 | −27.3 | 20.6 | 2.2 | 1.0 | 0.91 | |
| Low active | 1.14 | −739.5 | 13.7 | 7.5 | −3.3 | −1.4 | 0.95 | 1.13 | −1209.1 | 11.9 | 5.2 | 3.8 | 1.3 | 0.96 | |
| Active | 1.27 | −669.0 | −8.7 | −3.6 | 8.8 | 1.7 | 0.90 | 1.27 | 1238.7 | 4.8 | 5.8 | −6.3 | 1.5 | 0.88 | |
| Very active | 1.49 | 5847.0 | −79.1 | −15.0 | 1.5 | 2.5 | 0.97 | 1.43 | 4929.4 | 10.8 | −16.4 | −25.2 | 2.3 | 0.80 | |
PA, physical activity; PAL, physical activity level; RMR, resting metabolic rate.
A–F = prediction regression equation coefficients (see text).
Prediction of TEE from PA, anthropometric variables, and RMR
The predictive power of the different equations (Table 4) was assessed by regression and LOA analysis and the results are presented in Table 5. Because prediction of TEE was not markedly influenced by age stratification (Table 3), this analysis was performed including all participants irrespective of age. Predictive performance for TEE from anthropometric variables and population mean PA was moderate with LOA at ±30%. This improved to ±20% if PA was adjusted for activity category (inactive, low active, active, and very active). Where RMR was included as a predictor variable, the performance improved further to ±10% with a median absolute prediction error of approximately 4%. Because this analysis compared methods using all participants who were also used to develop the PA and regression coefficients, the mean bias was essentially zero and LOA would be underestimated. In the absence of an independent validation population, a split-group cross-validation approach was used with TEE predicted using sex-adjusted activity category PA value (Table 2) and the results are presented in Table 6.
TABLE 5.
Comparison of measured total energy expenditure with predicted total energy expenditure based on physical activity coefficient prediction equations (reported in Table 4)
| Age class | Activity category | Males (n = 638) |
Females (n =1019) |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Regression1 |
Regression1 |
|||||||||||||
|
rc |
LOA2 |
Intercept |
Slope |
rs |
MAPE |
rc |
LOA2 |
Intercept |
Slope |
rs |
MAPE |
|||
| (%) | kJ/d | (%) | (%) | kJ/d | (%) | |||||||||
| All participants (≥65 y) | Prediction based on age, weight, and height |
|||||||||||||
| Overall mean PA coefficient | 0.63 | 3009 (±30.3) | 3633 | 0.64 | 0.67 | 9.7 | 0.65 | 2362 (±30.1) | 2810 | 0.66 | 0.66 | 10.1 | ||
| Stratified by PA coefficient | 0.87 | 1953 (±20.0) | 1054 | 0.89 | 0.87 | 5.8 | 0.83 | 1755 (±21.8) | 1275 | 0.85 | 0.83 | 7.1 | ||
| Stratified by age category and mean PA coefficient | 0.69 | 3019 (±30.2) | 3850 | 0.63 | 0.66 | 10.1 | 0.65 | 2354 (±29.8) | 2850 | 0.65 | 0.66 | 9.9 | ||
| Stratified by age and PA coefficient |
0.88 |
1918 (±19.5) |
992 |
0.90 |
0.87 |
5.7 |
0.84 |
1736 (±21.5) |
1226 |
0.85 |
0.83 |
6.9 |
||
| Prediction based on age, weight, height, and RMR | ||||||||||||||
| Overall mean PA coefficent | 0.68 | 2845 (±28.4.0) | 3033 | 0.70 | 0.70 | 9.1 | 0.68 | 2269 (±28.7) | 2521 | 0.69 | 0.69 | 9.8 | ||
| Stratified by PA coefficient | 0.96 | 1053 (±10.3) | 226 | 0.99 | 0.96 | 4.0 | 0.97 | 842 (±10.6) | 185 | 0.98 | 0.96 | 3.9 | ||
| Stratified by age category and mean PA coefficient | 0.68 | 2772 (±27.5) | 2938 | 0.71 | 0.71 | 9.3 | 0.69 | 2263 (±28.5) | 2577 | 0.68 | 0.69 | 9.9 | ||
| Stratified by age and PA coefficient | 0.97 | 1040 (±10.1) | 197 | 0.98 | 0.97 | 3.8 | 0.97 | 830 (±10.5) | 191 | 0.98 | 0.96 | 3.9 | ||
LOA, limit of agreement; MAPE, median absolute percentage error; PA, physical activity (see text and Table 4).
Regression = measured TEE versus predicted; rc = Lin’s concordance correlation coefficient; rs = Spearman correlation coefficient.
LOA = 1.96 SD limits of agreement.
TABLE 6.
Cross-validation of total energy expenditure predictions from age, weight, height, physical activity, and resting metabolic rate
| Model | Prediction coefficients |
Cross-validation predictions1 |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Regression2 |
||||||||||||||
| PA |
A |
B x age |
D x weight |
E x height |
F x RMR |
R2 |
rc |
Bias5 |
LOA3 |
Intercept |
Slope |
rs |
||
| (constant) | (y) | (kg) | (cm) | (kJ/d) | kJ/d (%) | kJ/d (%) | (kJ/d) | |||||||
| Group |
Sex |
Prediction based on age, weight, and height |
||||||||||||
| A | Females | .4 | 4834.5 | −53.9 | 33.1 | 23.4 | 0.69 | 0.82 | −75 (−2.3) | −1944 to 1793 (−26.5 to 22.0) | 1159 | 0.87 | 0.82 | |
| Males | .4 | 4780.3 | −58.4 | 51.9 | 21.6 | 0.77 | 0.86 | −12 (−1.3) | −1957 to 1934 (−23.2 to 20.6) | 1522 | 0.85 | 0.88 | ||
| B |
Females | .4 | 3934.7 | −44.3 | 41.5 | 21.2 | 0.72 | 0.83 | 52 (−0.8) | 1690 to 1795 (−23.9 to 22.3) | 1562 | 0.80 | 0.82 | |
| Males |
.4 |
6768.6 |
−74.2 |
48.9 |
19.2 |
0.74 |
0.85 |
29 (−1.0) |
−2090 to 2148 (−23.8 to 21.8) |
1078 |
0.89 |
0.86 |
||
| Prediction based on age, weight, height, and RMR |
||||||||||||||
| A | Females | .4 | −5541.6 | −8.9 | 6.0 | 42.5 | 1.13 | 0.89 | 0.94 | 35 (0.5) | −1100 to 1169 (−14.0 to 14.1) | 318 | 0.95 | 0.93 |
| Males | .4 | −5971.5 | −15.3 | 8.9 | 44.3 | 1.12 | 0.89 | 0.94 | −69 (−1.2) | −1405 to 1267 (−14.8 to 12.4) | 802 | 0.93 | 0.94 | |
| B | Females | .4 | −5046.3 | −7.5 | 14.4 | 40.1 | 0.96 | 0.88 | 0.93 | 4 (0.5) | −1190 to 1182 (−15.6 to 14.6 | 495 | 0.94 | 0.92 |
| Males | .4 | −5320.0 | −19.2 | 5.4 | 44.0 | 1.14 | 0.89 | 0.94 | 74 (0.04) | −1287 to 1436 (−12.6 to 13.0) | 64 | 0.99 | 0.94 | |
LOA, limit of agreement; PA, physical activity; RMR, resting metabolic rate.
TEE predicted in group A using coefficients generated in Group B and vice versa; R2= coefficient of determination.
Regression = measured TEE versus predicted; rc = Lin’s concordance correlation coefficient; rs = Spearman correlation coefficient
LOA = 1.96 SD limits of agreement.
PA values according to age group and sex (see text and Table 4).
Measured – predicted
Regression coefficients were similar for each model when compared according to sex between the 2 groups suggesting that each is modeling similar populations. Correlations between predicted and measured TEE were slightly lower than observed for the combined population analysis (Table 5). The mean population differences (biases) were small, generally approximately 1% with LOA approximately ±22% for prediction based on anthropometric variables only or ±14% when RMR was included as a predictor variable.
Prediction of TEE using predicted RMR
Measured RMR was available in the current dataset and was used in the foregoing analyses but may not always be available. Predictions of TEE using RMR predicted from published equations are compared with those using measured RMR and to the measured reference TEE and are presented in Table 7. Prediction of TEE was slightly worse using any of the 3 published equations for predicting RMR when compared with using measured RMR. LOA all increased by approximately absolute 7%, from ±14% to ±21%. Performances of each RMR-prediction equation were similar. The final prediction models are shown in Figure 2.
TABLE 7.
Comparison of predicting total energy expenditure from age, weight, height, physical activity, and resting metabolic rate either measured or predicted from published equations
| Prediction | Males (n = 638) |
Females (n = 1019) |
||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Regression1 |
Regression1 |
|||||||||||||||
| TEE |
rc | Bias2 |
LOA3 |
Intercept |
Slope |
rs | MAPE |
TEE |
rc | Bias2 |
LOA3 |
Intercept |
Slope |
rs | MAPE |
|
| kJ/d | kJ/d | kJ/d (%) | kJ/d | (%) | kJ/d | kJ/d | kJ/d (%) | kJ/d | (%) | |||||||
| Reference value | 10,192 ± 2081 | 8059 ± 1676 | ||||||||||||||
| Measured RMR | 10,128 ± 1963 | 0.94 | −64 | −1280 to 1406 (−12.9 to 13.4) | 381 | 0.96 | 0.94 | 4.5 | 8058 ± 11573 | 0.94 | −1 | −1131 to 1132 (−14.7 to 13.8) | 443 | 0.94 | 0.93 | 4.6 |
| Livingston et al. [16] | 10,235 ± 1896 | 0.86 | 43 | −2091 to 2006 (−23.0 to 20.1) | 921 | 0.92 | 0.86 | 5.8 | 7961 ± 1670 | 0.84 | 98 | −1758 to 1954 (−22.9 to 24.2) | 117 | 1.0 | 0.82 | 7.7 |
| Porter et al. [18] | 10,124 ± 1858 | 0.85 | −68 | −2067 to 2204 (−23.1 to 22.3) | 913 | 0.90 | 0.84 | 6.4 | 8052 ± 1681 | 0.83 | −7 | −1887 to 1900 (−24.7 to 23.6) | −78 | 1.01 | 0.81 | 8.2 |
| Ikeda et al. [15] | 9983 ± 1809 | 0.85 | −209 | −1874 to 2293 (−20.8 to 22.7) | 1052 | 0.88 | 0.85 | 6.7 | 8120 ± 1631 | 0.83 | 61 | −1927 to 1804 (−25.4 to 22.1) | 263 | 0.98 | 0.81 | 8.0 |
LOA, limit of agreement; MAPE, median absolute percentage error; RMR, resting metabolic rate; TEE, total energy expenditure.
Regression, measured TEE versus predicted; rs, Spearman correlation coefficient; rc , Lin’s concordance correlation coefficient.
Measured − predicted; TEE = mean ± SD.
LOA = 1.96 SD limits of agreement.
FIGURE 2.
Prediction models for the estimation of total energy expenditure (TEE) and physical activity coefficients in adults aged ≥65 y. IOM, Institute of Medicine; PA, physical activity; PAL, physical activity level; RMR, resting metabolic rate.
Discussion
Using a large international database of “gold standard” measures, this novel analysis investigated the relative performance of different methods for the prediction of TEE in older adults. Three approaches were assessed: first, prediction from RMR by simple adjustment for PAL; second, prediction based on anthropometric measures (age, height, and weight) adjusted for physical activity using the IOM approach [13]; and third, prediction again but additionally including RMR as a predictor variable. The first and third approaches assume that a measure of RMR is available so, additionally, the validity of using predicted rather than measured RMR was evaluated. Participant-level data were obtained from original research undertaken in heterogeneous populations, hence equations derived in this analysis will be broadly applicable for the majority of older adults.
Overall, all approaches provided reasonable estimates of TEE at a population level with biases of 2% or less but performed variably and less well when estimating TEE in an individual. The simplest and currently the most commonly used approach for predicting TEE is simply to multiply RMR by a factor to account for PAL. Typically, a population mean value is used, for example, 1.69 for males and 1.66 for females [14] Comparable values determined in the present study were 1.65 and 1.64, respectively. However, this provided for poor estimation of TEE with LOA for individual prediction approximating ±30%. Stratifying PAL into 4 categories (inactive, low active, active, and very active) improved prediction to within ±10% for males and ±11% for females (approximately ±14% on cross-validation). Predictive performance was similar when RMR was combined with the IOM regression approach based on anthropometric prediction. In the absence of using RMR, prediction performance was again poor with LOA approximately ±30%. Alternatively, RMR may be estimated using a well-validated prediction equation such as those of Porter et al. [18], Ikeda et al. [15], or Livingston et al. [16] and then use one of the methods listed in Figure 2.
The best-performing prediction of TEE exhibited LOA of approximately ±10%, raising the question of whether this degree of inaccuracy in an individual is clinically acceptable. There is no consensus on what magnitude of error is acceptable. The Evidence Analysis Working Group has suggested that 20% error is unacceptable when predicting RMR, although noting that prediction of RMR varies with age and ethnic group [58]. There appears to have been no attempts to date to determine a “clinically meaningful difference” [59] for TEE estimation, although this approach has suggested that differences of 10% is a useful threshold in metabolic research [60,61]. It would be prudent to heed the advice of the Evidence Analysis Working Group “The Expert Panel advises clinical judgment regarding when to accept estimated RMR using predictive equations in any given individual” and apply this similarly to prediction of TEE [58].
There remains variability in estimating TEE at the individual level, although this can be reduced by adjusting for variability in PAL. The methods described above require that physical activity is measured or estimated. However, rarely is physical activity measured directly, instead it is typically assessed by activity questionnaires, which may be subject to large interindividual variation. The International Physical Activity Questionnaire [62] is an example of a commonly used tool with established validity [63]. This tool was designed primarily for population surveillance but has been used satisfactorily in clinical settings but takes approximately 15 min to complete. The simpler 5-item Simple Physical Activity Questionnaire may be used as an alternative [64]. Gerrior et al. have provided a spreadsheet template for simplifying further calculation of PAL and PA coefficients and allocating participants to their appropriate PA category [65]. This spreadsheet could be easily modified to incorporate the prediction equations developed in this study.
The current analysis highlights the large individual variability in PAL in this age group and, in particular, the large proportion of older adults who maintain a high level of physical activity as they age. More than 50% of older adults in each age bracket were active (PAL values >1.5), and many including those ≥80 y of age were active or very active (47% males and 50% of females). This underscores the likelihood of error in predicting TEE when using a single assumed PAL value across all individuals.
The present analysis has several strengths and limitations. A notable strength is the international breadth of the database and the sole use of reference methods for TEE (DLW) and RMR (indirect calorimetry). The sample size (n = 1686) was sufficiently large to continue to provide statistically acceptable sample sizes when subdivided by sex, age stratum, and activity level. A weakness of the analysis is that no completely independent sample was available for validation of the developed predictive algorithms. Notably, although a robust cross-validation approach was adopted, physical activity categories were those determined from the PAL values for the sample population. Ideally, allocation of participants to physical activity strata would have been more appropriately performed based on the assessment of actual physical activity, for example, using questionnaires. Unfortunately, such data were unavailable, and it is an important area for future research. We acknowledge that the data used for modeling may have been baseline height in longer-term studies, which may decline through the aging process. We also acknowledge heterogeneity across the age span with confounders including medications and other treatments associated with aging, along with physical conditions of participants that may have an effect on metabolism, which may influence the utility of these equations.
This analysis has demonstrated that, at a population level, TEE can be reliably predicted from anthropometric and RMR measurements but less well in individuals. Improvement in an individual is achievable by incorporating PAL values specific to the activity level of the individual, for example, assessed by targeted questionnaires or by the use of accelerometers now readily available to many embedded in smartphones [66]. Further improvement in prediction may be possible by adjustment for FFM rather than simply using body weight as a predictor variable as for RMR [67].
Acknowledgments
We thank the National Cancer Institute (NCI) for access to NCI’s data collected by the Interactive Diet and Activity Tracking in AARP Study. The statements contained herein are solely those of the authors and do not represent or imply concurrence or endorsement by NCI. Additional acknowledgments are listed in the supplementary file.
Author contributions
The authors’ responsibilities were as follows – JP, LCW, KN, ZD, SG, HT: conceived the research; JP, KN, ZD, SG, RP, MLN, HT, LCW: acquired data; LCW, AW: analyzed the database; all authors: contributed to data interpretation; JP, LCW, HT: wrote the manuscript; and all authors: reviewed and approved the final manuscript.
Conflict of interest
LCW reports a relationship with ImpediMed Limited that includes consulting or advisory. RP reports that financial support was provided by the National Heart Lung and Blood Institute and reports a relationship with the National Heart Lung and Blood Institute that includes funding grants. MLN reports that financial support was provided by the National Cancer Institute and reports a relationship with National Cancer Institute that includes funding grants. The other authors report no conflicts of interest.
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors. The Women’s Health Initiative program is funded by the National Heart, Lung, and Blood Institute; National Institutes of Health; and United States Department of Health and Human Services through contracts 75N92021D00001, 75N92021D00002, 75N92021D00003, 75N92021D00004, and 75N92021D00005.
Data availability
Data described in the manuscript, code book, and analytic code will not be made available because of the confidentiality clauses contained in the agreements to obtain many of the datasets obtained for this analysis.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.ajcnut.2024.02.005.
Appendix A. Supplementary data
The following is the Supplementary data to this article:
References
- 1.World Population Prospects 2022 Summary of Results. [Internet]. United Nations Department of Economic and Social Affairs Population Division; New York, USA: 2022. [Google Scholar]
- 2.Lv Y., Mao C., Gao X., Ji J.S., Kraus V.B., Yin Z., et al. The obesity paradox is mostly driven by decreased noncardiovascular disease mortality in the oldest old in China: a 20-year prospective cohort study. Nat. Aging. 2022;2:389–396. doi: 10.1038/s43587-022-00201-3. [DOI] [PubMed] [Google Scholar]
- 3.Woo J. What is an optimal BMI after eighty? Nat. Aging. 2022;2:371–372. doi: 10.1038/s43587-022-00212-0. [DOI] [PubMed] [Google Scholar]
- 4.Dietary Guidelines for Americans, [Internet] 2020. 9th ed., U.S. Department of Agriculture and U.S. Department of Health and Human Services, New York, USA, 2015; pp. 2020–2025.https://www.DietaryGuidelines.gov Available from: Last updated December 2020; cited 1 July 2023. [Google Scholar]
- 5.Nguo K., Truby H., Porter J. Total energy expenditure in healthy ambulatory older adults aged ≥80 years: a doubly labelled water study. Ann. Nutr. Metab. 2023;79(2):95–105. doi: 10.1159/000528872. [DOI] [PubMed] [Google Scholar]
- 6.Porter J., Nguo K., Gibson S., Huggins C.E., Collins J., Kellow N.J., Truby H. Total energy expenditure in adults aged 65 years and over measured using doubly-labelled water: international data availability and opportunities for data sharing. Nutr. J. 2018;17:40. doi: 10.1186/s12937-018-0348-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.National Academies of Sciences . The National Academies Press; Washington, DC: 2023. Engineering, and Medicine, Dietary Reference Intakes for Energy. [PubMed] [Google Scholar]
- 8.United Nations UN Decade of Healthy Ageing – The Platform. https://www.decadeofhealthyageing.org/ Available from: Last updated 2022; Cited 1 July 2023.
- 9.Pontzer H., Yamada Y., Sagayama H., Ainslie P.N., Andersen L.F., Anderson L.J., et al. Daily energy expenditure through the human life course. Science. 2021;373:808–812. doi: 10.1126/science.abe5017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Schoeller D.A., Van Santen E. Measurement of energy expenditure in humans by doubly labeled water method. J. Appl. Physiol. Respir. Environ. Exerc. Physiol. 1982;53:955–959. doi: 10.1152/jappl.1982.53.4.955. [DOI] [PubMed] [Google Scholar]
- 11.Speakman J.R. The history and theory of the doubly labeled water technique. Am. J. Clin. Nutr. 1998;68:932S–938S. doi: 10.1093/ajcn/68.4.932S. [DOI] [PubMed] [Google Scholar]
- 12.O’Driscoll R., Turicchi J., Beaulieu K., Scott S., Matu J., Deighton K., et al. How well do activity monitors estimate energy expenditure? A systematic review and meta-analysis of the validity of current technologies. Br. J. Sports Med. 2020;54:332–340. doi: 10.1136/bjsports-2018-099643. [DOI] [PubMed] [Google Scholar]
- 13.Institute of Medicine of the National Academies . The National Academies Press; Washington DC: 2005. DRI Dietary Reference Intakes for Energy, Carbohydrate, Fiber, Fat, Fatty Acids, Cholesterol, Protein, and Amino Acids. [Google Scholar]
- 14.Porter J., Nguo K., Collins J., Kellow N., Huggins C.E., Gibson S., et al. Total energy expenditure measured using doubly labeled water compared with estimated energy requirements in older adults (≥65 y): analysis of primary data. Am. J. Clin. Nutr. 2019;110:1353–1361. doi: 10.1093/ajcn/nqz200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ikeda K., Fujimoto S., Goto M., Yamada C., Hamasaki A., Ida M., et al. A new equation to estimate basal energy expenditure of patients with diabetes. Clin. Nutr. 2013;32:777–782. doi: 10.1016/j.clnu.2012.11.017. [DOI] [PubMed] [Google Scholar]
- 16.Livingston E.H., Kohlstadt I. Simplified resting metabolic rate—predicting formulas for normal-sized and obese individuals. Obes. Res. 2005;13:1255–1262. doi: 10.1038/oby.2005.149. [DOI] [PubMed] [Google Scholar]
- 17.Mifflin M.D., St Jeor S.T., Hill L.A., Scott B.J., Daugherty S.A., Koh Y.O. A new predictive equation for resting energy expenditure in healthy individuals. Am. J. Clin. Nutr. 1990;51:241–247. doi: 10.1093/ajcn/51.2.241. [DOI] [PubMed] [Google Scholar]
- 18.Porter J., Ward L.C., Nguo K., Davidson Z., Gibson S., Prentice R., et al. Development and validation of new predictive equations for the resting metabolic rate of older adults aged ≥65 y. Am. J. Clin. Nutr. 2023;117:1164–1173. doi: 10.1016/j.ajcnut.2023.04.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Arvidsson D., Slinde F., Nordenson A., Larsson S., Hulthén L. Validity of the ActiReg system in assessing energy requirement in chronic obstructive pulmonary disease patients. Clin. Nutr. 2006;25:68–74. doi: 10.1016/j.clnu.2005.09.001. [DOI] [PubMed] [Google Scholar]
- 20.Batista L.D., De França N.A.G., Pfrimer K., Fontanelli M.M., Ferriolli E., Fisberg R.M. Estimating total daily energy requirements in community-dwelling older adults: validity of previous predictive equations and modeling of a new approach. Eur. J. Clin. Nutr. 2021;75:133–140. doi: 10.1038/s41430-020-00717-0. [DOI] [PubMed] [Google Scholar]
- 21.Blanc S., Schoeller D.A., Bauer D., Danielson M.E., Tylavsky F., Simonsick E.M., et al. Energy requirements in the eighth decade of life. Am. J. Clin. Nutr. 2004;79:303–310. doi: 10.1093/ajcn/79.2.303. [DOI] [PubMed] [Google Scholar]
- 22.Calabro M.A., Kim Y., Franke W.D., Stewart J.M., Welk G.J. Objective and subjective measurement of energy expenditure in older adults: a doubly labeled water study. Eur. J. Clin. Nutr. 2015;69:850–855. doi: 10.1038/ejcn.2014.241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Choquette S., Chuin A., Lalancette D.A., Brochu M., Dionne I.J. Predicting energy expenditure in elders with the metabolic cost of activities. Med. Sci. Sports Exerc. 2009;41:1915–1920. doi: 10.1249/MSS.0b013e3181a6164a. [DOI] [PubMed] [Google Scholar]
- 24.Colbert L.H., Matthews C.E., Havighurst T.C., Kim K., Schoeller D.A. Comparative validity of physical activity measures in older adults. Med. Sci. Sports Exerc. 2011;43:867–876. doi: 10.1249/MSS.0b013e3181fc7162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.de Carvalho Bastone A., Ferriolli E., Pfrimer K., de Souza Moreira B., Bergamaschine Mata Diz J., Marcos Domingues Dias J., et al. Energy expenditure in older adults who are frail: a doubly labeled water study. J. Geriatr. Phys. Ther. 2019;42:E135–E141. doi: 10.1519/JPT.0000000000000138. [DOI] [PubMed] [Google Scholar]
- 26.Farooqi N., Slinde F., Håglin L., Sandström T. Validation of SenseWear Armband and ActiHeart monitors for assessments of daily energy expenditure in free-living women with chronic obstructive pulmonary disease. Physiol. Rep. 2013;1 doi: 10.1002/phy2.150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Fassini P.G., Das S.K., Pfrimer K., Suen V.M.M., Sérgio Marchini J.S., Ferriolli E. Energy intake in short bowel syndrome: assessment by 24-h dietary recalls compared with the doubly labelled water method. Br. J. Nutr. 2018;119:196–201. doi: 10.1017/S0007114517003373. [DOI] [PubMed] [Google Scholar]
- 28.Frisard M.I., Fabre J.M., Russell R.D., King C.M., DeLany J.P., Wood R.H., et al. Physical activity level and physical functionality in nonagenarians compared to individuals aged 60–74 years. J. Gerontol. A Biol. Sci. Med. Sci. 2007;62:783–788. doi: 10.1093/gerona/62.7.783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Goran M.I., Poehlman E.T. Total energy expenditure and energy requirements in healthy elderly persons. Metabolism. 1992;41:744–753. doi: 10.1016/0026-0495(92)90315-2. [DOI] [PubMed] [Google Scholar]
- 30.Hagfors L., Westerterp K., Sköldstam L., Johansson G. Validity of reported energy expenditure and reported intake of energy, protein, sodium and potassium in rheumatoid arthritis patients in a dietary intervention study. Eur. J. Clin. Nutr. 2005;59:238–245. doi: 10.1038/sj.ejcn.1602064. [DOI] [PubMed] [Google Scholar]
- 31.Hertogh E.M., Monninkhof E.M., Schouten E.G., Peeters P.H., Schuit A.J. Validity of the modified Baecke questionnaire: comparison with energy expenditure according to the doubly labeled water method. Int. J. Behav. Nutr. Phys. Act. 2008;5:30. doi: 10.1186/1479-5868-5-30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ichihara N., Namba K., Ishikawa-Takata K., Sekine K., Takase M., Kamada Y., et al. Energy requirement assessed by doubly-labeled water method in patients with advanced amyotrophic lateral sclerosis managed by tracheotomy positive pressure ventilation. Amyotroph. Lateral Scler. 2012;13:544–549. doi: 10.3109/17482968.2012.699968. [DOI] [PubMed] [Google Scholar]
- 33.Kashiwazaki H., Dejima Y., Orias-Rivera J., Coward W.A. Energy expenditure determined by the doubly labeled water method in Bolivian Aymara living in a high altitude agropastoral community. Am. J. Clin. Nutr. 1995;62:901–910. doi: 10.1093/ajcn/62.5.901. [DOI] [PubMed] [Google Scholar]
- 34.Koea J.B., Wolfe R.R., Shaw J.H. Total energy expenditure during total parenteral nutrition: ambulatory patients at home versus patients with sepsis in surgical intensive care. Surgery. 1995;118:54–62. doi: 10.1016/s0039-6060(05)80010-8. [DOI] [PubMed] [Google Scholar]
- 35.Lopes de Pontes T., Pinheiro Amador Dos Santos Pessanha F., Freire Junior R.C., Pfrimer K., da Cruz Alves N.M., Fassini P.G., et al. Total energy expenditure and functional status in older adults: a doubly labelled water study. J. Nutr. Health Aging. 2021;25:201–208. doi: 10.1007/s12603-020-1482-5. [DOI] [PubMed] [Google Scholar]
- 36.Morino K., Kondo K., Tanaka S., Nishida Y., Nakae S., Yamada Y., et al. Total energy expenditure is comparable between patients with and without diabetes mellitus: clinical evaluation of energy requirements in patients with diabetes mellitus (CLEVER-DM) study. BMJ Open Diabetes Res. Care. 2019;7 doi: 10.1136/bmjdrc-2019-000648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Moshfegh A.J., Rhodes D.G., Baer D.J., Murayi T., Clemens J.C., Rumpler W.V., et al. The US Department of Agriculture Automated Multiple-Pass Method reduces bias in the collection of energy intakes. Am. J. Clin. Nutr. 2008;88:324–332. doi: 10.1093/ajcn/88.2.324. [DOI] [PubMed] [Google Scholar]
- 38.Neuhouser M.L., Tinker L., Shaw P.A., Schoeller D., Bingham S.A., Horn L.V., et al. Use of recovery biomarkers to calibrate nutrient consumption self-reports in the Women’s Health Initiative. Am. J. Epidemiol. 2008;167:1247–1259. doi: 10.1093/aje/kwn026. [DOI] [PubMed] [Google Scholar]
- 39.Nishida Y., Nakae S., Yamada Y., Kondo E., Yamaguchi M., Shirato H., et al. Validity of one-day physical activity recall for estimating total energy expenditure in elderly residents at long-term care facilities: Clinical Evaluation of Energy Requirements Study (CLEVER Study) J. Nutr. Sci. Vitaminol. (Tokyo) 2019;65:148–156. doi: 10.3177/jnsv.65.148. [DOI] [PubMed] [Google Scholar]
- 40.Ostendorf D.M., Caldwell A.E., Creasy S.A., Pan Z., Lyden K., Bergouignan A., et al. Physical activity energy expenditure and total daily energy expenditure in successful weight loss maintainers. Obesity (Silver Spring) 2019;27:496–504. doi: 10.1002/oby.22373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Pannemans D.L., Westerterp K.R. Energy expenditure, physical activity and basal metabolic rate of elderly subjects. Br. J. Nutr. 1995;73:571–581. doi: 10.1079/bjn19950059. [DOI] [PubMed] [Google Scholar]
- 42.Pfrimer K., Vilela M., Resende C.M., Scagliusi F.B., Marchini J.S., Lima N.K., et al. Under-reporting of food intake and body fatness in independent older people: a doubly labelled water study. Age Ageing. 2015;44:103–108. doi: 10.1093/ageing/afu142. [DOI] [PubMed] [Google Scholar]
- 43.Prentice A.M., Leavesley K., Murgatroyd P.R., Coward W.A., Schorah C.J., Bladon P.T., et al. Is severe wasting in elderly mental patients caused by an excessive energy requirement? Age Ageing. 1989;18:158–167. doi: 10.1093/ageing/18.3.158. [DOI] [PubMed] [Google Scholar]
- 44.Prentice R.L., Mossavar-Rahmani Y., Huang Y., Van Horn L., Beresford S.A., Caan B., et al. Evaluation and comparison of food records, recalls, and frequencies for energy and protein assessment by using recovery biomarkers. Am. J. Epidemiol. 2011;174:591–603. doi: 10.1093/aje/kwr140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Pullicino E., Coward A., Elia M. Total energy expenditure in intravenously fed patients measured by the doubly labeled water technique. Metabolism. 1993;42:58–64. doi: 10.1016/0026-0495(93)90172-k. [DOI] [PubMed] [Google Scholar]
- 46.Reilly J.J., Lord A., Bunker V.W., Prentice A.M., Coward W.A., Thomas A.J., Briggs R.S. Energy balance in healthy elderly women. Br. J. Nutr. 1993;69:21–27. doi: 10.1079/bjn19930005. [DOI] [PubMed] [Google Scholar]
- 47.Rollo M.E., Ash S., Lyons-Wall P., Russell A.W. Evaluation of a mobile phone image-based dietary assessment method in adults with type 2 diabetes. Nutrients. 2015;7:4897–4910. doi: 10.3390/nu7064897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Rothenberg E.M. Resting, activity and total energy expenditure at age 91–96 compared to age 73. J. Nutr. Health Aging. 2002;6:177–178. doi: 10.1007/s00592-003-0046-6. [DOI] [PubMed] [Google Scholar]
- 49.Rothenberg E.M., Bosaeus I.G., Steen B.C. Energy expenditure at age 73 and 78—a five year follow-up. Acta Diabetol. 2003;40(Suppl 1):S134–S138. doi: 10.1007/s00592-003-0046-6. [DOI] [PubMed] [Google Scholar]
- 50.Rothney M.P., Brychta R.J., Meade N.N., Chen K.Y., Buchowski M.S. Validation of the ActiGraph two-regression model for predicting energy expenditure. Med. Sci. Sports Exerc. 2010;42:1785–1792. doi: 10.1249/MSS.0b013e3181d5a984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Slinde F., Ellegård L., Grönberg A.M., Larsson S., Rossander-Hulthén L. Total energy expenditure in underweight patients with severe chronic obstructive pulmonary disease living at home. Clin. Nutr. 2003;22:159–165. doi: 10.1054/clnu.2002.0618. [DOI] [PubMed] [Google Scholar]
- 52.Sridharan S., Wong J., Vilar E., Farrington K. Comparison of energy estimates in chronic kidney disease using doubly-labelled water. J. Hum. Nutr. Diet. 2016;29:59–66. doi: 10.1111/jhn.12326. [DOI] [PubMed] [Google Scholar]
- 53.Subar A.F., Potischman N., Dodd K.W., Thompson F.E., Baer D.J., Schoeller D.A., et al. Performance and feasibility of recalls completed using the automated self-administered 24-hour dietary assessment tool in relation to other self-report tools and biomarkers in the interactive diet and activity tracking in AARP (IDATA) study. J. Acad. Nutr. Diet. 2020;120:1805–1820. doi: 10.1016/j.jand.2020.06.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Tooze J.A., Schoeller D.A., Subar A.F., Kipnis V., Schatzkin A., Troiano R.P. Total daily energy expenditure among middle-aged men and women: the OPEN study. Am. J. Clin. Nutr. 2007;86:382–387. doi: 10.1093/ajcn/86.2.382. [DOI] [PubMed] [Google Scholar]
- 55.Wang X., Bowyer K.P., Porter R.R., Breneman C.B., Custer S.S. Energy expenditure responses to exercise training in older women. Physiol. Rep. 2017;5 doi: 10.14814/phy2.13360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Yamada Y., Yokoyama K., Noriyasu R., Osaki T., Adachi T., Itoi A., et al. Light-intensity activities are important for estimating physical activity energy expenditure using uniaxial and triaxial accelerometers. Eur. J. Appl. Physiol. 2009;105:141–152. doi: 10.1007/s00421-008-0883-7. [DOI] [PubMed] [Google Scholar]
- 57.Seoane F., Abtahi S., Abtahi F., Ellegård L., Johannsson G., Bosaeus I., Ward L.C. Mean expected error in prediction of total body water: a true accuracy comparison between bioimpedance spectroscopy and single frequency regression equations. BioMed Res. Int. 2015;2015 doi: 10.1155/2015/656323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Frankenfield D., Roth-Yousey L., Compher C. Comparison of predictive equations for resting metabolic rate in healthy nonobese and obese adults: a systematic review. J. Am. Diet. Assoc. 2005;105:775–789. doi: 10.1016/j.jada.2005.02.005. [DOI] [PubMed] [Google Scholar]
- 59.Copay A.G., Subach B.R., Glassman S.D., Polly D.W., Schuler T.C. Understanding the minimum clinically important difference: a review of concepts and methods. Spine J. 2007;7:541–546. doi: 10.1016/j.spinee.2007.01.008. [DOI] [PubMed] [Google Scholar]
- 60.Ward L.C. Bioelectrical impedance analysis for body composition assessment: reflections on accuracy, clinical utility, and standardisation. Eur. J. Clin. Nutr. 2019;73:194–199. doi: 10.1038/s41430-018-0335-3. [DOI] [PubMed] [Google Scholar]
- 61.Warkentin L.M., Majumdar S.R., Johnson J.A., Agborsangaya C.B., Rueda-Clausen C.F., Sharma A.M., et al. Weight loss required by the severely obese to achieve clinically important differences in health-related quality of life: two-year prospective cohort study. BMC Med. 2014;12:175. doi: 10.1186/s12916-014-0175-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Joseph K.L., Dagfinrud H., Christie A., Hagen K.B., Tveter A.T. Criterion validity of the International Physical Activity Questionnaire-Short Form (IPAQ-SF) for use in clinical practice in patients with osteoarthritis. BMC Musculoskelet. Disord. 2021;22:232. doi: 10.1186/s12891-021-04069-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Hagströmer M., Oja P., Sjöström M. The International Physical Activity Questionnaire (IPAQ): a study of concurrent and construct validity. Public Health Nutr. 2006;9:755–762. doi: 10.1079/phn2005898. [DOI] [PubMed] [Google Scholar]
- 64.Rosenbaum S., Morell R., Abdel-Baki A., Ahmadpanah M., Anilkumar T.V., Baie L., et al. Assessing physical activity in people with mental illness: 23-country reliability and validity of the simple physical activity questionnaire (SIMPAQ) BMC Psychiatry. 2020;20(1):108. doi: 10.1186/s12888-020-2473-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Gerrior S., Juan W., Basiotis P. An easy approach to calculating estimated energy requirements. Prev. Chronic Dis. 2006;3(4):A129. PMID: 16978504. [PMC free article] [PubMed] [Google Scholar]
- 66.Zhai Y., Nasseri N., Pöttgen J., Gezhelbash E., Heesen C., Stellmann J.P. Smartphone accelerometry: a smart and reliable measurement of real-life physical activity in multiple sclerosis and healthy individuals. Front. Neurol. 2020;11:688. doi: 10.3389/fneur.2020.00688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Kfir A., Lahav Y., Gepner Y. Cross-validation of a new general population resting metabolic rate prediction equation based on body composition. Nutrients. 2023;15:80. doi: 10.3390/nu15040805. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data described in the manuscript, code book, and analytic code will not be made available because of the confidentiality clauses contained in the agreements to obtain many of the datasets obtained for this analysis.