Abstract
Synthetic droplets mimicking bio-soft matter droplets formed via liquid-liquid phase separation (LLPS) in living cells have recently been employed in nanobiotechnology for artificial cells, molecular robotics, molecular computing, etc. Temporally controlling the dynamics of synthetic droplets is essential for developing such bio-inspired systems because living systems maintain their functions based on the temporally controlled dynamics of biomolecular reactions and assemblies. This paper reports the temporal control of DNA-based LLPS droplets (DNA droplets). We demonstrate the timing-controlled division of DNA droplets via time-delayed division triggers regulated by chemical reactions. Controlling the release order of multiple division triggers results in order control of the multistep droplet division, i.e., pathway-controlled division in a reaction landscape. Finally, we apply the timing-controlled division into a molecular computing element to compare microRNA concentrations. We believe that temporal control of DNA droplets will promote the design of dynamic artificial cells/molecular robots and sophisticated biomedical applications.
Subject terms: DNA nanotechnology, Biophysics, Nanobiotechnology, Synthetic biology, miRNAs
Controlling the dynamics of synthetic liquid-liquid phase separation droplets is essential for various bioinspired systems. Here, authors demonstrate temporally-controlled multi-step division of DNA-based liquid droplets, and develop a molecular computation system to compare miRNA concentrations.
Introduction
Living cells exhibit well-organized dynamics in bio-soft matter assemblies, such as membrane deformation, cell division, and cell differentiation1, which are essential features that distinguish living systems from non-living matter. Recently, liquid-liquid phase separation (LLPS) droplets of bio-soft matter have been found in living cells, and their dynamic behaviors have attracted attention2,3, such as nucleolar assembly through non-equilibrium processes of rRNA transcription4, sol-gel transition5, and activation/inhibition of molecular reactions6. These examples show that precise temporal control of biological LLPS droplets via non-equilibrium chemical reactions realizes such dynamic behaviors.
Synthetic LLPS droplets have recently been explored in bottom-up synthetic biology for constructing artificial cells7,8, molecular robots9, molecular computers10,11, and biomedical nanodevices12. Various dynamic behaviors of synthetic LLPS droplets have been reported, such as sequestration of molecules13–15, motion9,16, and division17. More recently, non-equilibrium dynamics such as cyclic assembly/disassembly18,19 and transient shell-formation20 of synthetic coacervate droplets were achieved by coupling LLPS droplets with non-equilibrium chemical reactions such as phosphorylation/dephosphorylation21,22 and enzymatic synthesis of polynucleotide23. However, temporal control of LLPS droplet dynamics remains difficult. Programmable temporal control methods must be developed to mimic cell dynamics.
DNA is well known for its programmable structures24,25 and reactions26. DNA programmability also facilitates the temporal control of chemical reactions. For example, DNA computing reactions have been demonstrated, such as the chemical oscillation of DNA concentrations27–29, temporal logic circuit30, and timing-controlled generation of chemical signals31,32. Moreover, the programmability of DNA has been utilized not only for controlling chemical reactions but also for controlling the physical dynamics of mechanical DNA-based nanostructures33–35. Particularly, DNA-based coacervates36,37 (also referred to as DNA droplets) formed with branched DNA nanostructures17,38–45 can couple physical dynamics with chemical reactions in a programmable manner. DNA droplets divide autonomously with enzymatic17 and photo41 cleavage reactions and locomotion via enzymatic degradation16,46. Phase separation of DNA droplets based on molecular logic computation47 and reaction-diffusion pattern formation coupled with RNA transcription and diffusion48 have also been demonstrated. However, achieving the timing-controlled physical dynamics of DNA droplets coupled with chemical reactions remains challenging.
In the present study, we demonstrate the timing-controlled division dynamics of DNA droplet-based artificial cells by coupling them with chemical reactions exhibiting a transient non-equilibrium relaxation process, resulting in the pathway control of artificial cell division (Fig. 1). We use DNA droplets constructed by mixing two Y-shaped branched DNA nanostructures (YA and YB; called binary-mixed DNA droplets), in which 6-branched DNA linkers crosslinked YA and YB (Figs. 2a, b). Mixed DNA droplets are divided into YA- and YB-droplets by cleaving the DNA linkers through the hybridization with division trigger DNAs. Here, we couple the mixed DNA droplet with chemical reactions; the time-delayed release of division triggers (Fig. 1a) realizes timing and pathway control of DNA droplet division (Figs. 1b–d). We use temporal control of DNA reactions based on RNA degradation with a ribonuclease H (RNase H), which has been used in many dynamic DNA reactions such as DNA oscillators27, DNA bistable switch49, logic computation50, DNA walker51, and timers for DNA strand displacement reactions31,32; however, there is no report on temporal control of LLPS droplets with the RNase H reaction. Finally, we present a molecular computing element to compare the concentrations of microRNA (miRNA) sequences (called molecular comparators) as an application of the timing-controlled division of DNA-droplet-based artificial cells. Our results provide a method for chemically regulating the timing-controlled physical dynamics of LLPS droplets for artificial cell studies.
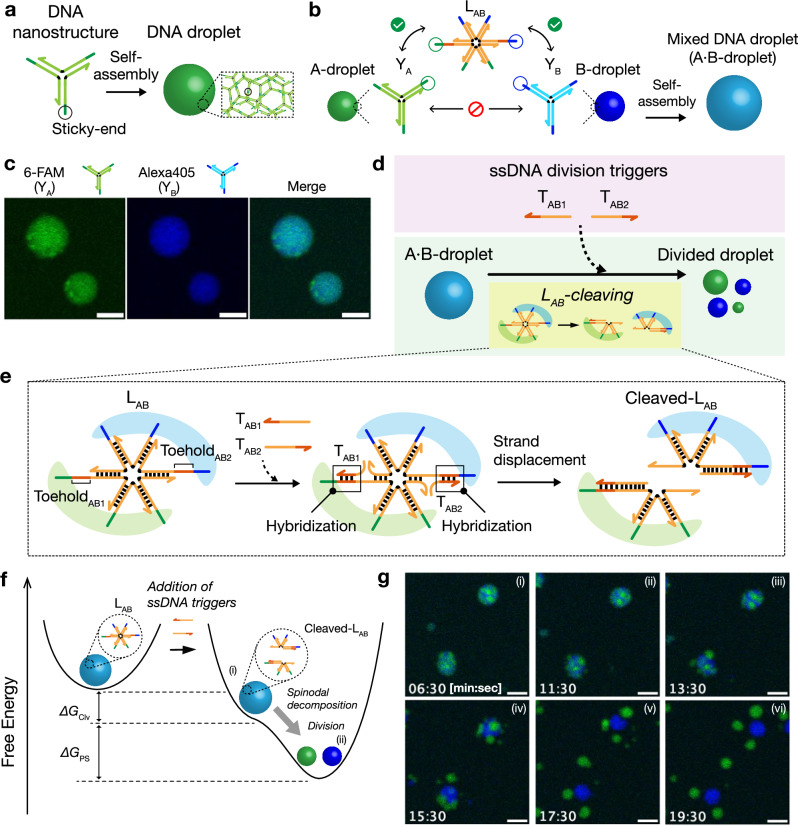
Fig. 1. Conceptual illustration of timing control of artificial cell division via chemical reactions.
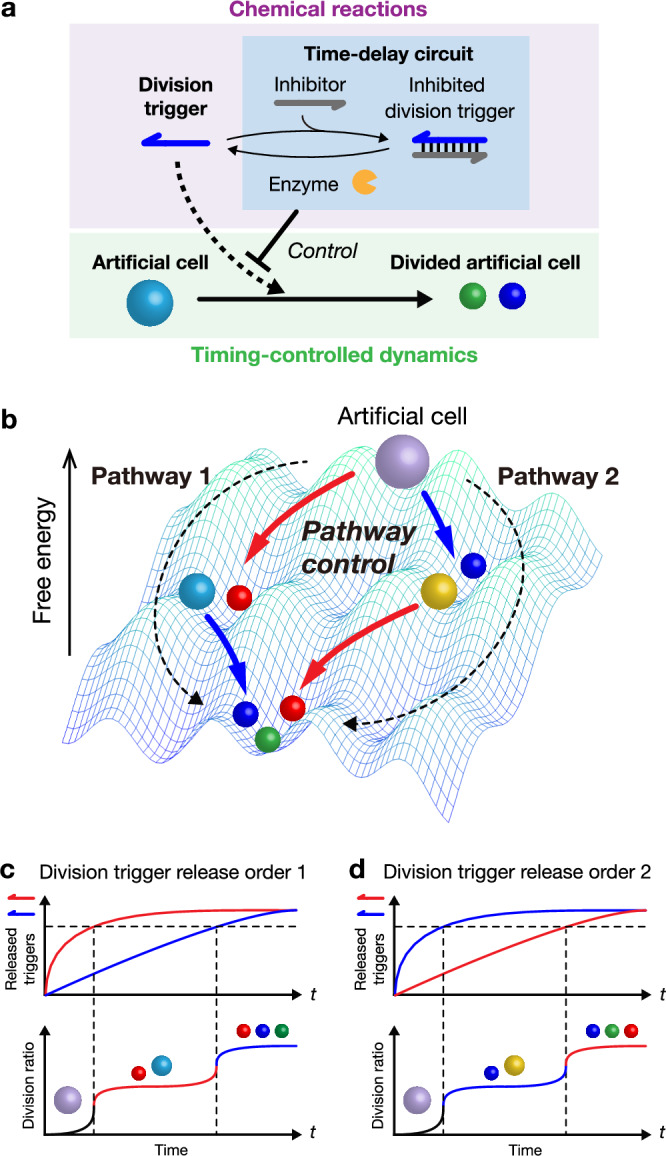
a Timing-controlled division of an artificial cell regulated by a time-delay circuit. b Pathway-controlled division of DNA droplet-based artificial cells. c, d Time-delay circuits control division pathways by changing the release order of different division triggers.
Fig. 2. Design of binary-mixed DNA droplets.
a Schematic of DNA droplet formation. Y-shaped branched DNA nanostructures self-assemble via binding of palindromic sticky ends, forming a DNA droplet. b Binary-mixed DNA droplet formation. Sticky ends of YA and YB are crosslinked by 6-branched DNA linker LAB. After the self-assembly of these DNA nanostructures, a binary-mixed DNA droplet (A·B-droplet) is formed. c CLSM images of A·B-droplets. Green: YA labeled with 6-carboxyfluorescein (6-FAM); Blue: YB labeled with Alexa Fluor® 405 (Alexa405). Co-localization of YA and YB was observed. Scale bars: 10 μm. Experiments were repeated three times independently with similar results. d, e Division of A·B-droplet via LAB cleavage. LAB is designed to be cleaved by a strand-displacement reaction with ssDNA division triggers (TAB1 and TAB2). f Description of the A·B-droplet division dynamics based on reaction landscapes. The ssDNA division triggers change the reaction landscape from a single-minimum shape: (i) A·B-droplet with ssDNA triggers but the A·B-droplet is not divided yet; (ii) A- and B-droplets are divided through the spinodal decomposition. ΔGClv and ΔGPS are Gibbs free energy changes for the linker cleavage reaction and the phase separation, respectively. g Time-lapse images of A·B-droplet division. Scale bars: 10 μm. Experiments were repeated three times independently with similar results.
Results
Autonomous division of binary-mixed DNA droplets using division trigger DNAs
Figure 2a shows the design of DNA droplets for artificial cells. Y-shaped branched DNA nanostructures self-assemble to form DNA droplets via hybridization of self-complementary sticky ends at their branches17. Because YA and YB have non-complementary sticky ends (Fig. 2b; detailed sequences are in Supplementary Table 1), the resultant A- and B-droplets do not fuse; however, a 6-branched DNA linker (LAB) (Fig. 2b; Supplementary Table 2) can crosslink YA and YB, forming a binary-mixed DNA droplet (A·B-droplet) (Fig. 2b). Here, ‘·’ (a single center dot) in ‘A·B’ indicates that one type of linker (LAB) crosslinks YA and YB in A·B-droplet. Figure 2c shows confocal laser scanning microscopy (CLSM) images of the A·B-droplet. The A·B-droplet can be divided by cleaving LAB into two portions (Fig. 2d). For LAB cleavage, we used a nucleic acid strand displacement reaction induced by single-stranded DNA (ssDNA) division triggers (TAB1 and TAB2) (Fig. 2e). This design is based on our previous study47. The division triggers hybridize to the toehold sequences (ToeholdAB1 and ToeholdAB2) in LAB and invade the branches of LAB via strand-displacement reactions (Fig. 2e, middle), cleaving LAB into two portions (Fig. 2e, right). After adding the division triggers, the cleaved-LAB is more stable than the initial LAB because of the Gibbs free energy change (ΔGClv) induced by division trigger hybridization and strand displacement reactions, leading to the droplet division (Fig. 2f). Figure 2g shows the time-lapse images of the division of the A·B-droplet after adding the division triggers. The A·B-droplet started to divide just after adding division triggers. The result agreed with the previous study47; although a slightly inhomogeneous area richer in YA or YB component was observed in the A·B-droplet, the inhomogeneity was not necessary for a droplet division.
Design of timing-control of DNA droplet division based on time-delay circuits
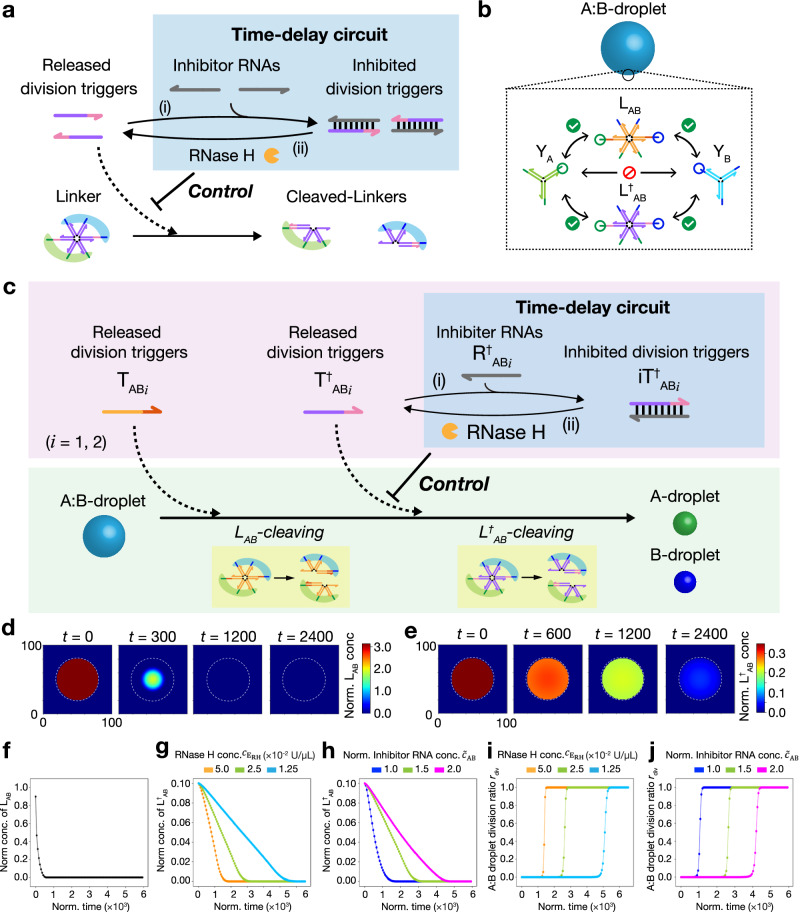
We hypothesized that inhibiting released division triggers causes the time delay of the linker cleavage, resulting in timing control over DNA droplet division. Figure 3a shows the design of a time-delay circuit comprising reactions (i) and (ii). (i) Released division triggers changed to inhibited division triggers by the hybridization of excess single-stranded RNAs (ssRNAs), named inhibitor RNAs. (ii) An RNase H degrades the inhibitor RNAs in the inhibited division triggers, thereby releasing released division triggers. These two reactions cause a time delay in the cleavage of the DNA linker.
Fig. 3. Numerical investigation of timing-controlled linker-cleavage for DNA droplet division.
a Schematics of time-delay circuit to regulate cleaving rate of a DNA linker. (i) Excess inhibitor RNAs hybridize with released division triggers, producing inhibited division triggers. (ii) Released division triggers are released from inhibited division triggers by RNase H reaction. Released division triggers hybridize with the DNA linker, cleaving the linker via strand displacement. b Compositions of a binary-mixed DNA droplet (A:B-droplet). c Schematic of the timing-controlled division of A:B-droplet using a time-delay circuit. LAB is initially cleaved using TABi followed by the cleaving of L†AB, resulting in the division of A:B-droplet. The time-delayed cleaving of L†AB is achieved by the release of T†ABi from iT†ABi. The degree of time delay of the T†ABi release decides the timing control of the droplet division. Linkers and triggers with “†” indicate those that can achieve a time-delay circuit if inhibitor RNAs and RNase H are added. d, e Snapshots of numerically calculated concentrations of LAB and L†AB in the A:B-droplet using the reaction-diffusion simulation. The white broken-line circle indicates the surface of the A:B-droplet. f Time course of LAB of the A:B-droplet in the numerical simulation. g, h Time courses of L†AB concentrations of the A:B-droplet in the numerical simulation via changing the RNase H concentration or inhibitor RNA concentration , respectively. Normalized initial total concentration of inhibitor RNA is defined as = (i = 1,2), where = is the initial total concentration of excess and hybridized inhibitor RNAs, and = is the initial total concentration of released and inhibited triggers. g = 1.25, 2.5, and 5.0 × 10−2 U/µL; = 1.5. h = 2.5 × 10−2 U/µL; = 1.0, 1.5, and 2.0. i, j Time courses of the division ratio rdiv in the reaction-diffusion simulation with changing the or , respectively. i = 1.25, 2.5, and 5.0 × 10−2 U/µL; = 1.5. j = 2.5 × 10−2 U/µL; = 1.0, 1.5, and 2.0. Source data are provided as a Source Data file.
To tune the time delay of the binary-mixed DNA droplet division, we introduced L†AB in addition to the original DNA linker, LAB (Fig. 3b). We describe this binary-mixed DNA droplet as “A:B-droplet,” where ‘:’ (double dots) indicates that YA and YB are crosslinked with two DNA linkers, LAB and L†AB. A:B-droplets divide only when both LAB and L†AB are cleaved. In addition, linkers and triggers with “†” indicate those that can achieve a time delay in the presence of inhibitor RNAs and RNase H (Fig. 3c). LAB is cleaved by the released division triggers TABi (i = 1, 2), while L†AB is cleaved by released division triggers T†ABi (i = 1, 2). Inhibitor RNAs R†ABi hybridize with T†ABi, and form inhibited division triggers iT†ABi, inducing the time delay of A:B-droplet division. This time-delay circuit was inspired by intracellular time-delay control via reaction suppression based on small RNA expression52. For such biological meaning and applications shown later, we used natural miRNA sequences, miR-6875-5p and miR-463447,53, for R†ABi sequences, respectively (Supplementary Table 3); that is, if either of the miRNAs exist, the A:B-droplet division is delayed.
Numerical investigations of timing-control of DNA droplet division
First, we numerically investigated the dependence of the cleaving rate of the DNA linker L†AB on the concentrations of RNase H and the inhibitor RNAs (; i = 1, 2) when the time-delay circuits work. By assuming that the phase separation dynamics follows the spatiotemporal DNA linker distribution in a mixed DNA droplet, we used a reaction-diffusion model based on the partial differential equations (details in Supplementary Note 1) to estimate the spatiotemporal distribution. The following equations denote the spatiotemporal change of the division triggers T†ABi (i = 1, 2) controlled by the time-delay circuit:
| 1 |
| 2 |
where is the concentration of molecule “X”; , , , …} is the vector of concentrations of molecules. The first term in Eq. (1) is the spatial diffusion of T†ABi; is the diffusion coefficient depending on the position x (x = “inside” or “outside” of A:B-droplet). The second term denotes the consumption of division triggers T†ABi via hybridization and strand displacement with the linker L†AB. The third term denotes the time-delay circuit reaction composed of the generation and inhibition of T†ABi, described in Eq. (2) in detail; and are the Michaelis-Menten parameters for the RNase H reaction; is the total RNase H concentration; are the hybridization rates of the division triggers with inhibitor RNAs; (i = 1, 2) are the initial concentrations of excess inhibitor RNAs. Thus, the time course of T†ABi is controlled by two important factors of the time-delay circuit: and .
Figures 3d and e show the distributions of LAB and L†AB, respectively, in an A:B-droplet at several normalized simulation time steps (the white broken-line circle indicates the surface of the A:B-droplet). In the present study, we fixed the percentages of LAB and L†AB to the total amount of linker DNA to 90% and 10%, respectively. We referred to previously reported kinetic parameters and diffusion coefficients50,54–57. The degradation of LAB occurs from the outside of the droplet towards the inside, while that of L†AB happens uniformly throughout the droplet. This would be because the reaction rate is faster than the diffusion rate for LAB, whereas the reaction rate is slower than the diffusion rate for L†AB due to the low amount of released division triggers. The results show that L†AB remains longer than LAB, although the percentage of L†AB is lower than that of LAB. This indicates that the decrease of L†AB becomes slower due to the time-delay circuit.
Figure 3f is the time course of DNA linker LAB cleavage, showing that LAB cleaves rapidly. Next, we investigated the dependence of the cleavage rate of DNA linkers L†AB on the total RNase H concentration () and the initial concentration of the excess inhibitor RNAs (; i = 1, 2) (Figs. 3g and h). The cleavage rate of the L†AB becomes slower by decreasing RNase H concentration (Fig. 3g) or increasing RNA concentration (Fig. 3h). By summing them up, the decreasing time courses of total linker concentrations are found to be delayed (Supplementary Fig. 1). Here, we assume that the division ratio of the A:B-droplets follows a sigmoidal cooperative function of the total concentration of uncleaved linkers w (Supplementary Note 1):
| 3 |
| 4 |
where K is the threshold concentration of the uncleaved linker for A:B-droplet division and n is a cooperativity coefficient that expresses the switch-like dependence of division on w. and are the maximum and minimum values of , respectively. The cooperative switch-like dependence expressed by the Hill-type function was observed by Gong et al. 47; cooperative nonlinear behavior is observed because the cleavage of most linkers is necessary for DNA droplet division. Figures 3i and j show the time courses of when changing RNase H concentration , and RNA concentration with K = 0.05 and n = 16 fixed. Consequently, the increases at a slower rate by decreasing or increasing . This trend did not change depending on values of K and n (Supplementary Fig. 2). Therefore, these results suggest that the timing of the division can be controlled by tuning the cleavage rate of L†AB.
Experimental investigations of timing-control of DNA droplet division
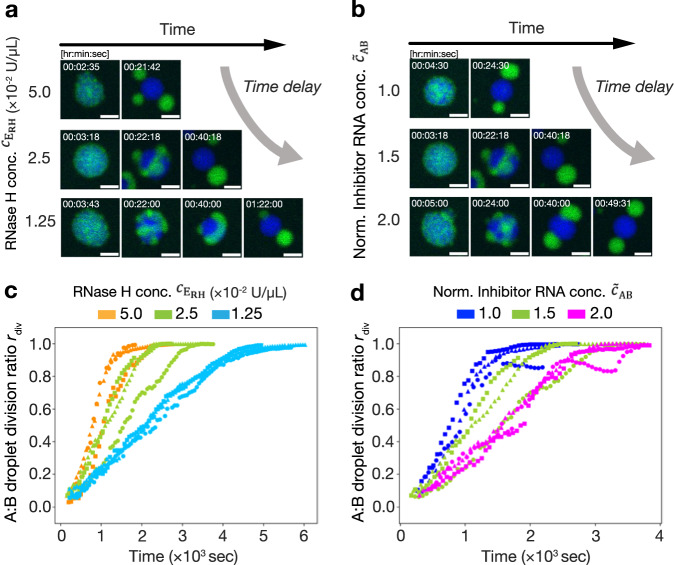
We performed the experiments shown in Fig. 3c for the timing-controlled division of the A:B-droplets. The droplet division reaction started by adding released triggers (TABi), inhibited triggers (iT†ABi), excess inhibitors (R†ABi), and RNase H into an A:B-droplet solution (Methods in detail). Figures 4a and b show time-lapse images of A:B-droplet division. The required time for the division was elongated with decreasing or increasing . Furthermore, we quantified the division ratio rdiv of the A:B-droplet using image processing (see Supplementary Note 3) (Fig. 4c, d). rdiv is 0 if the A- and B-droplets are fully mixed in the A:B-droplets, and 1 if the A:B-droplets are completely divided into A- and B-droplets. The results demonstrated that the increasing rate of rdiv became slower with decreasing or increasing , which is consistent with the numerical simulation results. The time courses of rdiv in the experiments were not as sharp as those in the simulation, probably because of the slow response of the B-droplet against linker cleavage. From the experimental results, we concluded that the timing-controlled division of DNA droplets was achieved using a time-delay circuit.
Fig. 4. Timing-controlled division of an A:B-droplet coupling with time-delay circuit.
a, b Time-lapse images of the division of A:B-droplets with changing the or (i = 1, 2) (see also Supplementary Movie 1–5). Scale bars: 10 μm. a = 1.25, 2.5, and 5.0 × 10−2 U/µL; = 1.5. b = 2.5 × 10−2 U/µL; = 1.0, 1.5, and 2.0. c, d Time courses of the division ratio rdiv with changing the or . Three repeated experiments in each condition are shown with the same color. c = 1.25, 2.5 and 5.0 × 10−2 U/µL; = 1.5. d = 2.5 × 10−2 U/µL; = 1.0, 1.5 and 2.0. All concentrations are at the final concentration of the observed samples. Source data are provided as a Source Data file.
Pathway control of droplet division
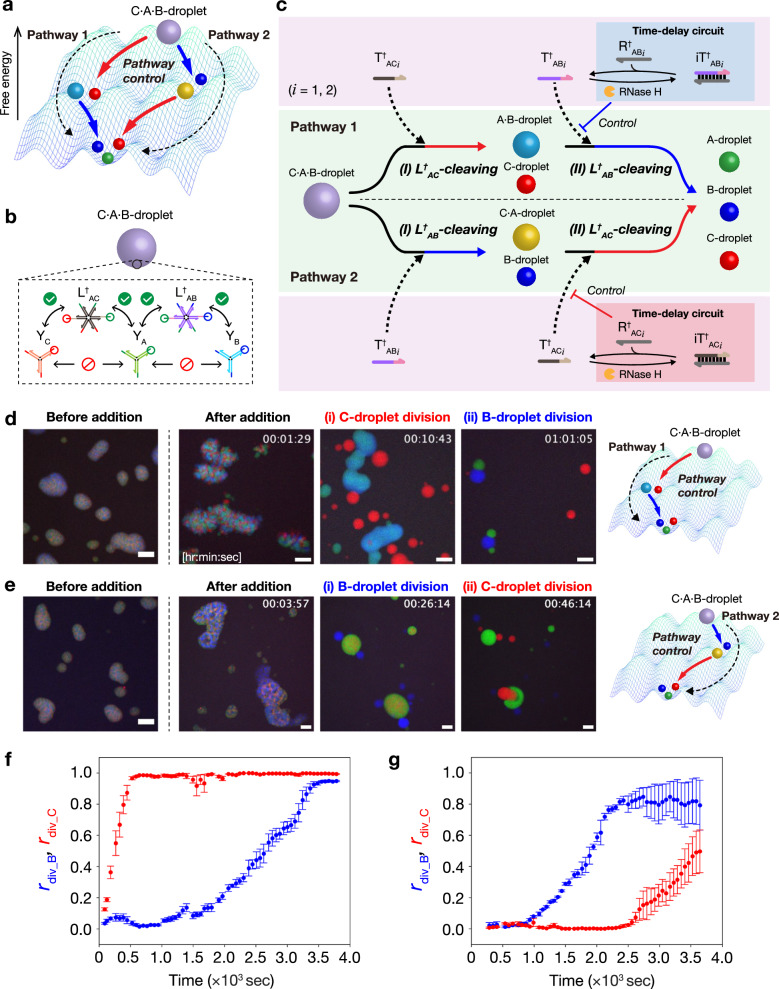
Next, we applied the time-delay circuit to control the pathway of DNA droplet division (Fig. 5a). We used a ternary-mixed C·A·B-droplet, comprising three types of Y-shaped branched DNA nanostructures (YC, YA, and YB) connected with two types of linkers (L†AC and L†AB) (Fig. 5b). YA, YB, and L†AB are the same as those used in the previously described experiment; L†AC was designed to crosslink YC and YA. From the viewpoint of the reaction landscape shown in Fig. 5a, the C·A·B-droplet has two different pathways (Pathways 1 and 2) for complete division into C-, A-, and B-droplets. Pathway control was achieved by changing the inhibited division triggers (Fig. 5c). In Pathway 1, the release of T†ABi is inhibited; only the C-droplet is divided from the C·A·B-droplet via cleaving L†AC earlier before the complete division. In Pathway 2, the release of T†ACi is inhibited; the B-droplet is divided from the C·A·B-droplet via cleaving L†AB earlier.
Fig. 5. Control of droplet division pathway.
a A reaction landscape of the division of ternary-mixed DNA droplets. The division pathway indicates the order of droplet division. b Formation of ternary-mixed DNA droplet (C·A·B-droplet) containing three types of Y-shaped DNA nanostructures and two types of DNA linkers. c Schematic of pathway-controlled division of C·A·B-droplet. The linker-cleavage reaction rates decide the order of droplet division, thereby changing the pathway of droplet division. d Time-lapse images of C·A·B-droplet division in Pathway 1 before and after adding T†ACi, iT†ABi, R†ABi, and RNase H. The detail of multistep division process is shown in Supplementary Movie 6. R†ABi (i = 1, 2): miR-6875-5p and miR-4634. Scale bars: 20 μm. e Time-lapse images of C·A·B-droplet division in Pathway 2 before and after adding T†ABi, iT†ACi, R†ACi, and RNase H. The detail of multistep division process is shown in Supplementary Movie 7. R†ACi (i = 1,2): miR-1246 and miR-1307-3p. Scale bars: 20 μm. f, g Time courses of division ratio rdiv_B (blue) and rdiv_C (red) during C·A·B-droplet division in Pathway 1 (f) and Pathway 2 (g), respectively. Data are presented as the mean ± standard error (SE) of three field of view of microscopy observation.
Figures 5d and e show time-lapse images before and after adding the division triggers. To achieve Pathway 1, we added released triggers T†ACi (for cleaving L†AC earlier); inhibited triggers iT†ABi, excess inhibitors R†ABi, and RNase H (for cleaving L†AB later). Supplementary Movie 6 shows that the order of the division of C- and B-droplets was successfully controlled, as follows. Ternary-mixed C·A·B-droplets (Fig. 5d, before addition) divided into C-droplets and binary-mixed A·B-droplets approximately 10 min after the addition (Fig. 5d (i)). After another 50 min, the A·B-droplets were divided into A- and B-droplets (Fig. 5d (ii)). This indicates that Pathway 1 was selected via the inhibition of T†ABi due to the presence of R†ABi (miR-6875-5p and miR-4634). Next, to achieve Pathway 2, we added released triggers T†ABi (for cleaving L†AB earlier); inhibited triggers iT†ACi, excess inhibitors R†ACi, and RNase H (for cleaving L†AC later). For R†ACi, miRNA sequences, miR-1246 and miR-1307-3p, were used (Supplementary Table 3). Supplementary Movie 7 shows that the order of the division of B- and C-droplets was also controlled well. The C·A·B-droplets were first divided into B-droplets and C·A-droplets approximately 30 min after the addition (Fig. 5e (i)). After another 20 min, the C·A-droplets were divided into A- and C-droplets (Fig. 5e (ii)). This indicates that Pathway 2 was selected because of the presence of R†ACi (miR-1246 and miR-1307-3p). Furthermore, we quantified the time courses of the division ratios of B- (rdiv_B) and C- (rdiv_C) droplets using the image processing method shown in Supplementary Note 3. The results showed that the increase of rdiv_B was slower than rdiv_C in Pathway 1 (Fig. 5f), while that of rdiv_C was slower than rdiv_B in Pathway 2 (Fig. 5g). Thus, the pathway-controlled division was achieved using time-delay circuits.
Molecular computation: application of pathway control of droplet division
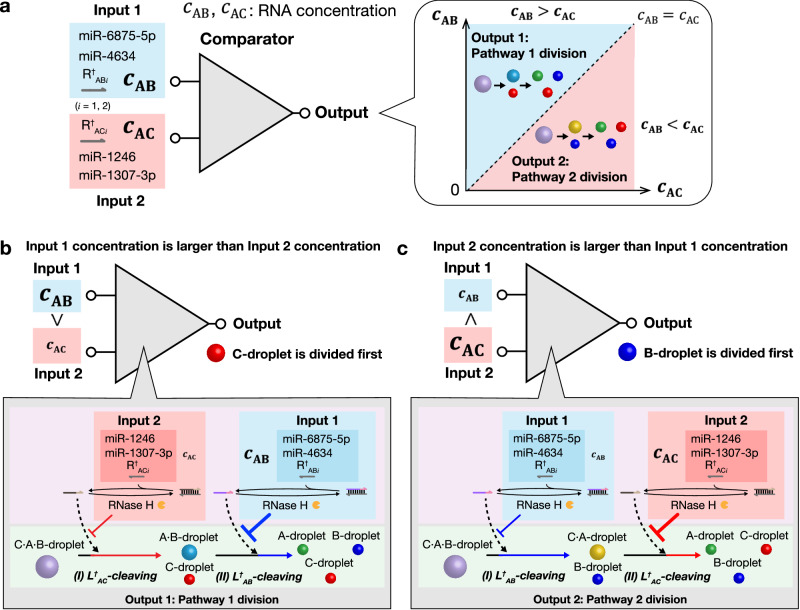
Finally, we applied the pathway control of droplet division to a molecular computing element “comparator” of RNA concentrations. Figure 6a shows the concept of the comparator using the division pathway of the C·A·B-droplet (details are explained below using Fig. 6b, c). In this comparator, Input is the initial total concentrations of miRNA sequences that are used as inhibitor RNAs in the time delay circuit. Specifically, Input 1 () is the concentration of R†ABi (i = 1, 2; miR-6875-5p and miR-4634) used in the time delay circuit for the delay of B-droplet division. Input 2 () is the concentration of R†ACi (i = 1, 2; miR-1246 and miR-1307-3p) used in the time delay circuit for the delay of C-droplet division. Output is the selection result of the division pathway depending on the differences two Inputs ( and ).
Fig. 6. Application of pathway control to a molecular comparator for miRNA concentrations.
a Concept of a molecular comparator of miRNA concentrations. The triangle is a symbol for a comparator element. miRNAs miR-6875-5p and miR-4634 were used for Input 1 for the comparator; miR-1246 and miR-1307-3p were used for the Input 2. The Output is the selection of the droplet division pathway, which changes depending on the difference between two initial total concentrations of miRNAs (working as inhibitor RNAs), and . This concentration comparison is achieved by the two time-delay circuits as shown in (b) and (c). b Pathway 1 is selected: if the Input 1 concentration is larger than the Input 2 concentration (), the L†AB cleavage delays longer than the L†AC because more R†ABi causes a longer time delay of the L†AB cleavage. Thus, C-droplet is divided first, and B-droplet is divided subsequently. c Pathway 2 is selected: if , the L†AC cleavage delays longer. Thus, B-droplet is divided first, and C-droplet is divided subsequently.
The details of the reaction scheme are shown in Fig. 6b, c. If (Fig. 6b), the L†AB cleavage delays longer than the L†AC because more R†ABi causes a longer time delay of the L†AB cleavage; then, C-droplet is divided first, and B-droplet is divided subsequently, which means that Pathway 1 is selected. On the other hand, if (Fig. 6c), the L†AC cleavage delays longer; then, B-droplet is divided first, and C-droplet is divided subsequently, which means that Pathway 2 is selected. Thus, the observation of the selected pathway indicates the result of the concentration comparison between Inputs, and .
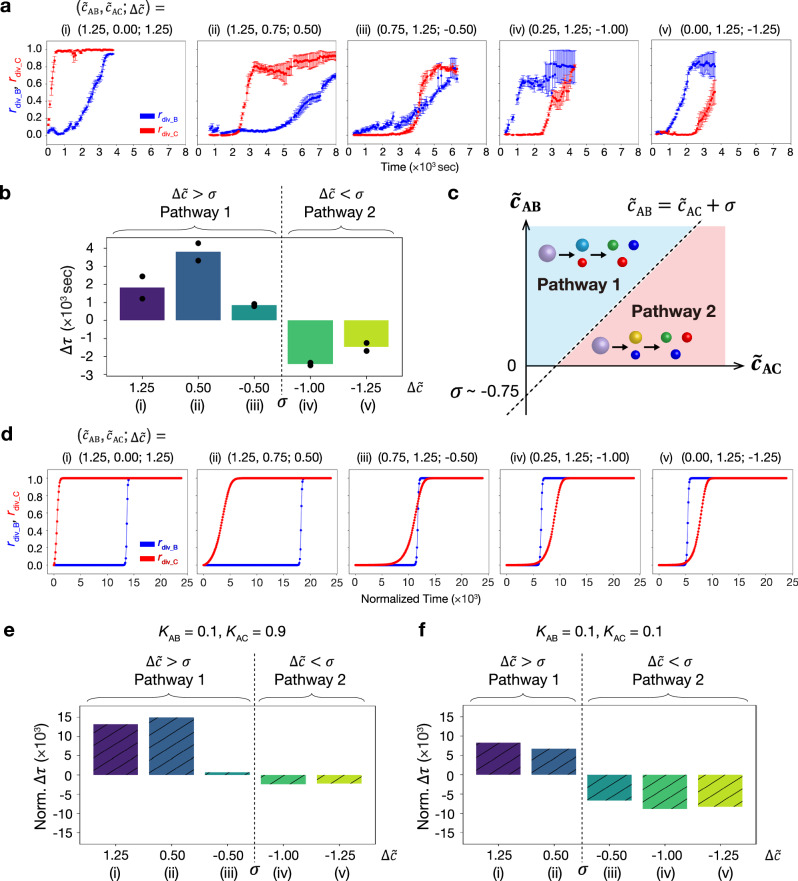
Comparator experiments were performed using several RNA concentrations. In the experiments, we used the same DNA nanostructures as those in Fig. 5b. Here, we define = , where and are normalized initial total concentrations of inhibitor RNAs ( = and (i = 1, 2) are defined in the same way (see Fig. 3 caption)). We investigated five types of conditions of the initial RNA concentrations shown in Fig. 7a: (i), (ii), (iii), (iv), and (v). Under conditions (i)–(iii), the C-droplet divided first, whereas the B-droplet divided first under conditions (iv) and (v) (Supplementary Fig. 3 and Supplementary Movies 6–10). Figure 7a shows the time courses of the division ratios of B- (rdiv_B) and C- (rdiv_C) droplets quantified using the image processing method shown in Supplementary Note 3. These results showed that with higher , C-droplet division was faster. Note that an increase in caused a delay in the overall reaction, probably because more RNA molecules induced competition in RNA degradation by RNase H in the condition of the same RNase H concentration.
Fig. 7. Experimental and simulation results of molecular concentration comparator.
a Time courses of rdiv_B (blue) and rdiv_C (red) at varying the two normalized initial total concentrations of inhibitor RNAs and in the experiment. = and (i = 1, 2), where the input initial total RNA concentrations are defined as [miR-6875-5p], [miR-4634], and ; [miR-1246], [miR-1307-3p], and . The () was varied at (i) 1.25, (ii) 0.50, (iii) 0.50, (iv) 1.00, and (v) 1.25. RNase H concentration was fixed at 0.25 U/µL in all experiments. The plots in conditions (i) and (v) are identical to those in Figs. 5f and 5g, respectively. Data are presented as the mean ± SE of three field of view of microscopy observation. b Time difference Δτ at each of five RNA conditions (i)-(v) in the experiment. Data are presented as the mean; more than four field of view of microscopy observation in two independent experiments. c Schematic of the pathway selection depending on the , , and offset concentration in the experiment. was estimated as 0.75, which is the average of between conditions (iii) and (iv). d Time courses of rdiv_B (blue) and rdiv_C (red) at varying inhibitor RNA concentrations in the reaction-diffusion simulation. The was varied at (i) 1.25, (ii) 0.50, (iii) 0.50, (iv) 1.00, and (v) 1.25. The hybridization rate and the strand displacement rate between T†ABi and L†AB were set 10 times lower than those between T†ACi and L†AC, respectively. Threshold parameters KAB and KAC were set as 0.1 and 0.9, respectively. n = 16. e, f Time difference Δτ at each of five RNA conditions (i)–(v) in the reaction-diffusion simulation. The hybridization rate and the strand displacement rate between T†ABi and L†AB were set 10 times lower than those between T†ACi and L†AC, respectively. KAB = 0.1 and KAC = 0.9 (). n = 16 (e). The hybridization rate and the strand displacement rate between T†ABi and L†AB were the same as those between T†ACi and L†AC, respectively. KAB = 0.1 and KAC = 0.1 (). n = 16 (f). Source data are provided as a Source Data file.
For quantitative estimation, we calculated the time difference Δτ between the division timings of B- and C-droplets (Fig. 7b): , where and are defined as the times when rdiv_B and rdiv_C were approximately 0.5, respectively. Large errors of rdiv were observed at the later stage (Fig. 7a), which would be because the slight dissolution of droplets made background noises. Since the errors were small around rdiv = 0.5, the errors did not significantly affect the determination of Δτ. As shown in Fig. 7b, Δτ > 0 was observed when the RNA concentration difference (i), (ii), and (iii), indicating that the division occurred through Pathway 1. Alternatively, Δτ < 0 was observed when (iv) and (v), indicating that Pathway 2 was selected. These results demonstrated that the division pathway changed depending on the RNA concentration differences, confirming that the concentration comparator for the miRNA sequences worked as expected.
Ideally, the sign of Δτ is expected to switch when (i.e., ). However, the results imply that the sign switches between (i.e., ). Here, we define an offset concentration of this molecular comparator, , at which the sign of Δτ switches, where the output of the comparator switches. Ideally, as shown in Fig. 6a, while our molecular comparator had a non-zero offset (); the value was estimated around since the sign of Δτ switches between (Fig. 7c). Generally, regular electrical comparators also have a non-zero offset voltage because of non-ideal circuit properties; similarly, our molecular comparator would have had non-ideal reaction properties. We guess that would be caused probably because B-droplet division took longer than that of the C-droplet for some reasons; for example, the DNA sequence difference induced the slower cleavage of L†AB than L†AC, or more linker cleavage is required for B-droplet division than C-droplet division. In future studies, may be tuned by sequence designing of DNAs.
To estimate the hypothesis for the mechanism of the non-zero offset, we performed numerical simulations using a reaction-diffusion model that considered differences in the cleavage rate of linker DNAs (see Supplementary Note 2). First, we changed the hybridization and the strand displacement rates for L†AB cleavage. Next, we varied the threshold parameters KAB and KAC for rdiv_B and rdiv_C (Eqs. S.90 and S.91 in Supplementary Note 2); the larger the threshold parameters, the faster the division.
We set the hybridization rate and the strand displacement rate between T†ABi and L†AB to be 10 times lower than that between T†ACi and L†AC. KAB and KAC are set to asymmetric values of 0.1, and 0.9, respectively. Figure 7d shows the time courses of rdiv_B and rdiv_C in the simulation results. As increased, the C-droplets tended to divide earlier. Additionally, as shown in Fig. 7e, the offset concentration was approximately 0.75, indicating that the trend is consistent with the experimental result. These results suggest that the differences in the cleavage rate between L†AB and L†AC and the required amount of linker cleavage for B-droplet and C-droplet divisions resulted in . Furthermore, numerical simulations were performed using different parameter values (Fig. 7f and Supplementary Figs. 4–7), producing different offset concentrations. These results suggest that changing DNA sequences could potentially control the offset concentration . Note that, when more , the simulation results reproduce the delay in the overall reaction as observed in experiments due to the competition in the RNase H reaction.
Discussion
We demonstrated the timing-controlled division dynamics of DNA droplets using a time-delay circuit. We developed the reaction-diffusion model and numerically investigated the strategy to control the division timing by controlling the cleavage rate of L†AB. Using this strategy, we experimentally demonstrated timing control of the division of an A:B-droplet by tuning the time-delay circuit parameters. Although the current simulation model focused on the spatiotemporal distribution of linker DNAs to estimate the time-delay circuit behavior, the model would be extended to a model explicitly considering the phase separation process by adding the Cahn-Hilliard term58. In addition, although our model suggested one of the possibilities of the cause of the offset concentration σ, this model is not perfect as discussed above; thus, further study on numerical modeling with experimental studies would be required.
Using the time-delay circuit, we realized the pathway control of the C·A·B-droplet division by changing the order of two types of linker DNA cleavage. Finally, the pathway control of the C·A·B-droplet division was employed for molecular computation. We achieved not only the detection of the presence/absence of miRNA sequences but also the comparison of the concentrations of miRNA sequences, which may be applied to a diagnosis based on the expressed miRNA concentrations. Based on these results, we revealed that the RNase H-based strategy could be applied to the control of the phase separation dynamics as well as the other DNA nanotechnologies in a bulk solution.
The RNA concentration comparator had non-zero offset () (Fig. 7b), and the simulation results suggested that changed depending on hybridization rates or strand displacement rates of linker DNAs (Fig. 7e, f and Supplementary Figs. 4–7). Because the hybridization and strand displacement rates of DNAs depend on their sequence and length55, these results suggest that the non-zero offset was probably due to the sequences of the linker DNA nanostructure. Previously, Nguyen et al. 59 and Sato et al. 57 have shown that differences in the sequences of DNA nanostructures changed the kinetic and thermodynamic properties of DNA droplets. To further control the DNA droplet dynamics, the influence of DNA sequences on the kinetic properties of DNA nanostructures must be clarified.
The present study demonstrated that chemical reactions could control DNA droplet dynamics such as droplet division. However, since the coupled chemical reactions were only a transient non-equilibrium relaxation process, far-from-equilibrium chemical reactions with sustained chemical energy supplies are required to achieve truly active systems. Moreover, in future, the control of chemical reactions via the physical dynamics of DNA droplets and the reversible control of DNA droplet dynamics should be explored. Such bidirectional control over more complex dynamics can help build artificial cells with more living cell-like functions, such as biochemical reactions controlled by the condensates of transcriptional factors and cell/organelle behaviors controlled by transcripts6,60. Moreover, enzymatic reactions regulated by synthetic protein-based coacervates61 can be combined with our DNA-based droplet system. We believe that this technology provides a strategy to create artificial cells and molecular robots with more sophisticated functions, such as timing-controlled self-replication, drug delivery, and diagnosis, with more accuracy and quantitative specifications.
Methods
Sequence design and oligo-nucleotides preparation
DNA and RNA sequences were designed using the Nucleic Acid Package (NUPACK)62. DNA sequences listed in Tables S1–S3 were purchased from Eurofins Genomics (Tokyo, Japan). The fluorescently labeled DNA was purified using high-performance liquid chromatography (HPLC), while the others were purified using an oligonucleotide purification cartridge (OPC). RNA sequences listed in Table S3 were purchased from Sangon Biotech (Shanghai, China) and purified using HPLC. The purchased oligonucleotide powders were diluted to 100 or 200 μM with ultra-pure water (Direct-QUV, Millipore, ZRQSVP030) and stored at −20 °C.
Preparation of mixed DNA droplets
We prepared three DNA droplets (A·B-droplet, A:B-droplet, C·A·B-droplet). In Figs. 2c, g, a sample solution for the A·B-droplet contained 5 μM YA, 5 μM YB, and 1.65 µM LAB in a reaction buffer (20 mM Tris-HCl [pH 8.0], 350 mM NaCl) was heated at 85 °C for 5 min and then cooled down from 85 °C to 25 °C at a rate of −1 °C/min to anneal the contained DNAs using a thermal cycler (Mastercycler® nexus X2, Eppendorf, Germany). In Figs. 4a, b, a sample solution for the A:B-droplet contained 5 μM YA, 5 μM YB, 1.485 µM LAB, and 0.165 µM L†AB in the reaction buffer was heated and cooled down in the same manner. In Fig. 5d, e, a sample solution for the C·A·B-droplet contained 1.0 μM YA, 1.0 μM YB, 1.0 μM YC, 2.0 µM L†AB, and 2.0 µM L†AC in the reaction buffer was heated and cooled down in the same manner. After annealing, the sample of the A·B-droplet and A:B-droplet were diluted twofold with the reaction buffer. The C·A·B-droplet was not diluted. The concentrations of each strand in the mixed DNA droplet after dilution and addition of the division trigger mixture are shown in Supplementary Tables 4–6. Tris-HCl (pH 8.0) (cat. #15568025) was purchased from Invitrogen (Carlsbad, CA), and NaCl (cat. #191-01665) was purchased from Wako (Japan), respectively.
Microscopy observation
To observe the autonomous division of the A·B-droplet samples and the timing-controlled division of the A:B-droplet samples, we used a confocal laser scanning microscopy (CLSM) (FV-1000, Olympus, Tokyo, Japan) and a stage heater (10021-PE120 system, Linkam, Fukuoka, Japan). To observe the pathway-controlled division of the C·A·B-droplet, we used fluorescent microscopy (IX-71, Olympus, Tokyo, Japan) equipped with a spinning-disk confocal system (CSU-X1, Yokogawa, Tokyo, Japan), an EM CCD camera (iXon X3, Andor), and the stage heater. Samples containing 6-FAM, Alexa 405, and Cy3 were visualized at excitation wavelengths of 473, 405, and 561 nm, respectively. Observation chambers were prepared for CLSM observation. Glass slides (dimensions: 30 × 40 mm, thickness: 0.17 mm, Matsunami, Kishiwada, Japan) were soaked in 5% bovine serum albumin (BSA) (cat. #019-15123, Wako, Japan) solution with 20 mM Tris-HCl (pH 8.0) for 30 min. After BSA coating, the glasses were washed with ultrapure water and dried. The 1-mm-thickness silicon sheet (cat. #107-0040202, Kokugo, Japan) with 5 mm-diameter holes was placed on the BSA-coated glass.
Autonomous division experiments of A·B-droplets
The A·B-droplet sample solution containing 5 μM YA, 5 μM YB, and 1.65 µM LAB in a reaction buffer (20 mM Tris-HCl [pH 8.0], 350 mM NaCl) was heated 85 °C for 5 min and then cooled down from 85 °C to 25 °C at a rate of −1 °C/min to anneal the contained DNAs using a thermal cycler. The trigger mixture comprised 2.5 µM TAB1 and 2.5 µM TAB2 in the reaction buffer. A·B-droplet sample solution (3 µL) was placed in the 5 mm hole of the observation chamber. The sample solutions were covered with mineral oil to prevent evaporation. The chamber was incubated on a stage heater at 60 °C for 30 min to increase the fluidity of the DNA droplets. After incubation, we added 3 µL of the trigger mixture to the sample solution in the chamber and observed it at 60 °C.
Timing-controlled division experiments of A:B-droplets by adding a division trigger solution
The A:B-droplet sample solution containing 5 μM YA, 5 μM YB, 1.485 µM LAB, and 0.165 µM L†AB in the reaction buffer was heated and cooled down in the same manner. The trigger mixture was prepared by mixing TAB solution, iT†AB solution, RNase H solution, and MgCl2 solutions. The TAB solution comprised 25 µM TAB1 and 25 µM TAB2 in the reaction buffer. To prepare the iT†AB solution, we mixed ssDNA triggers (T†AB1, T†AB2), and inhibitor RNAs (R†AB1 and R†AB2) in the reaction buffer. Here, the concentration of T†AB1 and T†AB2 (, (i = 1, 2)) was fixed at 1.0 μM, while that of R†AB1 and R†AB2 (, (i = 1, 2)) was changed to 1.0, 1.5, and 2.0 µM at a final concentration. Normalized initial total RNA concentration = is defined. The iT†AB solution was heated at 85 °C for 5 min and then cooled down from 85 °C to 25 °C at a rate of −1 °C/min to form RNA-DNA hybrids. The RNase H solution contained thermostable ribonuclease H (RNase H) (M0523S, New England Biolabs) in the reaction buffer. The concentrations of RNase H used were 0.125, 0.25, and 0.5 U/µL. The MgCl2 solution comprised 15 mM MgCl2 (20908-65, Nacalai Tesque, Japan) in the reaction buffer. To prepare the trigger mixture, the TAB solution, iT†AB solution, RNase H solution, and MgCl2 solution were mixed with the reaction buffer at the concentrations shown in Supplementary Table 7. The normalized initial total concentration of inhibitor RNA is defined as = (i = 1, 2), where is the concentration of R†ABi, and is the concentration of T†ABi.
A:B-droplet sample solution (3 µL) was placed in a 5 mm hole of the observation chamber. The sample solutions were covered with mineral oil to prevent evaporation. The chamber was incubated on a stage heater at 60 °C for 30 min to increase the fluidity of the DNA droplets. After incubation, we added 3 µL of the trigger mixture to the sample solution in the chamber and observed it at 60 °C. As shown in Supplementary Table 7, when the final concentration of was fixed at 2.5 × 10−2 U/µL, was varied as 1, 1.5, and 2. When was fixed at 1.5, was varied as 1.25 × 10−2, 2.5 × 10−2, and 5.0 × 10−2 U/µL. To calculate the division ratio, rdiv, we binarized the fluorescent images and analyzed them using Fiji63.
Pathway-controlled division experiments of C·A·B-droplets by adding a division trigger solution
To demonstrate the pathway-controlled division of C·A·B-droplets in Figs. 5d, e, we added the trigger mixture to the C·A·B-droplet sample solution. Trigger mixtures 1 and 2 were prepared for the division pathways 1 and 2, respectively. The trigger mixture 1 was prepared by mixing T†AC, iT†AB, RNase H, and MgCl2 solutions. The T†AC solution comprised 30 µM T†AC1 and 30 µM T†AC2 in the reaction buffer. To prepare the iT†AB solution, we mixed ssDNA triggers T†AB1 and T†AB2 (6 µM each) and inhibitor RNAs R†AB1 and R†AB2 (7.5 µM each) in the reaction buffer. The iT†AB solution was heated 85 °C for 5 min and then cooled down from 85 °C to 25 °C at a rate of −1 °C/min to form RNA-DNA hybrids. The RNase H solution contained 2.0 U/µL RNase H in the reaction buffer. The MgCl2 solution comprised 30 mM MgCl2 in the reaction buffer. To prepare the trigger mixture 1, the T†AC solution, the iT†AB solution, the RNase H solution, and the MgCl2 solution were mixed with the same buffer at the concentrations shown in Supplementary Table 8.
The trigger mixture 2 was prepared by mixing T†AB, iT†AC, RNase H, and MgCl2 solutions. The T†AB solution was composed of 30 µM T†AB1 and 30 µM T†AB2 in the reaction buffer. To prepare the iT†AC solution, we mixed ssDNA triggers T†AC1 and T†AC2 (6 µM each) and inhibitor RNAs R†AC1 and R†AC2 (7.5 µM each) in the reaction buffer. The iT†AC solution was heated 85 °C for 5 min and then cooled down from 85 °C to 25 °C at a rate of −1 °C/min to form RNA-DNA hybrids. The RNase H and MgCl2 solutions were the same as those used to prepare trigger mixture 1. To prepare the trigger mixture 2, the T†AB solution, the iT†AC solution, the RNase H solution, and the MgCl2 solution were mixed with the same buffer at the concentrations shown in Supplementary Table 9.
For the RNA concentration comparator experiments, we varied the RNA concentration in the trigger mixture. The trigger mixture was prepared by mixing the iT†AB solution, iT†AC solution, an RNase H solution, and an MgCl2 solution. The inhibitor RNA concentration of iT†AB solution and iT†AC solution were changed based on each experimental condition. The concentration of the trigger mixture after mixing it with the C·A·B-droplet sample at each experimental condition is shown in Supplementary Table 10. Normalized initial total concentration of inhibitor RNA is defined as = (i = 1,2), where is the concentration of R†ABi, and is the concentration of T†ABi. Normalized initial total concentration of inhibitor RNA is defined as = (i = 1,2), where is the concentration of R†ACi, and is the concentration of T†ACi.
C·A·B-droplet sample solution (2.4 µL) was placed in the 5 mm hole of the observation chamber. The sample solutions were covered with mineral oil to prevent evaporation. The chamber was incubated on a stage heater at 60 °C for 30 min and 63 °C for 15 min to increase the fluidity of the DNA droplets. After incubation, we added 3.6 µL of the trigger mixture to the sample solution in the chamber and observed it at 63 °C.
Statistics and reproducibility
Data are presented as means ± SE with the number of replicates indicated. No statistical methods were used to determine sample size.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Supplementary information
Description of Additional Supplementary Files
Source data
Acknowledgements
We thank Mr. Ryohei Furuichi, Dr. Hirotake Udono, Mr. Nozomi Tsumura, and Dr. Marcos K. Masukawa for fruitful discussions. This work was supported by MEXT/JSPS KAKENHI (Nos. JP20H05701, JP20H00619, JP20H05935, and JP24H00070) to M.T., Human Frontier Science Program (HFSP; RGP0016/2022-102) to M.T., and JSPS Research Fellowships for Young Scientists (DC1) (Nos. JP22KJ1346) to T.M.
Author contributions
M.T. provided the original concept. T.M. and M.T. performed all experiments. T.M., J.G., and M.T. design experiments. T.M. and M.T. wrote and revised the manuscript.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.
Data availability
The dataset of the main figures generated in this study is provided in the Supplementary Information, Supplementary Videos and Source Data files. Source data are provided with this paper.
Code availability
The source codes for numerical simulations are provided through GitHub (https://github.com/takinouelab/MaruyamaTakinoue2024)64.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-024-51299-5.
References
- 1.Alberts, B. et al. Molecular Biology of the Cell. 6th edn. (Garland Science, 2014).
- 2.Shin, Y. & Brangwynne, C. P. Liquid phase condensation in cell physiology and disease. Science357, eaaf4382 (2017). [DOI] [PubMed]
- 3.Banani, S. F., Lee, H. O., Hyman, A. A. & Rosen, M. K. Biomolecular condensates: organizers of cellular biochemistry. Nat. Rev. Mol. Cell Biol.18, 285–298 (2017). 10.1038/nrm.2017.7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Falahati, H., Pelham-Webb, B., Blythe, S. & Wieschaus, E. Nucleation by rRNA dictates the precision of nucleolus assembly. Curr. Biol.26, 277–285 (2016). 10.1016/j.cub.2015.11.065 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Brangwynne, C. P., Mitchison, T. J. & Hyman, A. A. Active liquid-like behavior of nucleoli determines their size and shape in Xenopus laevis oocytes. Proc. Natl. Acad. Sci. USA.108, 4334–4339 (2011). 10.1073/pnas.1017150108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sabari, B. R. et al. Coactivator condensation at super-enhancers links phase separation and gene control. Science361, eaar3958 (2018). [DOI] [PMC free article] [PubMed]
- 7.Martin, N. Dynamic synthetic cells based on liquid-liquid phase separation. Chembiochem20, 2553–2568 (2019). 10.1002/cbic.201900183 [DOI] [PubMed] [Google Scholar]
- 8.Lin, Z., Beneyton, T., Baret, J.-C. & Martin, N. Coacervate droplets for synthetic cells. Small Methods7, 2300496 (2023). [DOI] [PubMed]
- 9.Zhang, S. et al. Engineering motile aqueous phase-separated droplets via liposome stabilisation. Nat. Commun.12, 1673 (2021). 10.1038/s41467-021-21832-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Schuster, B. S. et al. Controllable protein phase separation and modular recruitment to form responsive membraneless organelles. Nat. Commun.9, 2985 (2018). 10.1038/s41467-018-05403-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Mu, W. et al. Membrane-confined liquid-liquid phase separation toward artificial organelles. Sci. Adv.7, eabf9000 (2021). [DOI] [PMC free article] [PubMed]
- 12.Liu, S. et al. Enzyme-mediated nitric oxide production in vasoactive erythrocyte membrane-enclosed coacervate protocells. Nat. Chem.12, 1165–1173 (2020). 10.1038/s41557-020-00585-y [DOI] [PubMed] [Google Scholar]
- 13.Tsumoto, K. et al. Does DNA exert an active role in generating cell-sized spheres in an aqueous solution with a crowding binary polymer? Life5, 459–466 (2015). 10.3390/life5010459 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lin, Y., Jing, H., Liu, Z., Chen, J. & Liang, D. Dynamic behavior of complex coacervates with internal lipid vesicles under nonequilibrium conditions. Langmuir36, 1709–1717 (2020). 10.1021/acs.langmuir.9b03561 [DOI] [PubMed] [Google Scholar]
- 15.Matsuo, M. & Kurihara, K. Proliferating coacervate droplets as the missing link between chemistry and biology in the origins of life. Nat. Commun.12, 5487 (2021). 10.1038/s41467-021-25530-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Saleh, O. A., Wilken, S., Squires, T. M. & Liedl, T. Vacuole dynamics and popping-based motility in liquid droplets of DNA. Nat. Commun.14, 3574 (2023). 10.1038/s41467-023-39175-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sato, Y., Sakamoto, T. & Takinoue, M. Sequence-based engineering of dynamic functions of micrometer-sized DNA droplets. Sci Adv6, eaba3471 (2020). 10.1126/sciadv.aba3471 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Donau, C. et al. Active coacervate droplets as a model for membraneless organelles and protocells. Nat. Commun.11, 5167 (2020). 10.1038/s41467-020-18815-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Späth, F. et al. Molecular design of chemically fueled peptide-polyelectrolyte coacervate-based assemblies. J. Am. Chem. Soc.143, 4782–4789 (2021). 10.1021/jacs.1c01148 [DOI] [PubMed] [Google Scholar]
- 20.Bergmann, A. M. et al. Liquid spherical shells are a non-equilibrium steady state of active droplets. Nat. Commun.14, 6552 (2023). 10.1038/s41467-023-42344-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Aumiller, W. M. Jr & Keating, C. D. Phosphorylation-mediated RNA/peptide complex coacervation as a model for intracellular liquid organelles. Nat. Chem.8, 129–137 (2016). 10.1038/nchem.2414 [DOI] [PubMed] [Google Scholar]
- 22.Nakashima, K. K., Baaij, J. F. & Spruijt, E. Reversible generation of coacervate droplets in an enzymatic network. Soft Matter14, 361–367 (2018). 10.1039/C7SM01897E [DOI] [PubMed] [Google Scholar]
- 23.Spoelstra, W. K., van der Sluis, E. O., Dogterom, M. & Reese, L. Nonspherical coacervate shapes in an enzyme-driven active system. Langmuir36, 1956–1964 (2020). 10.1021/acs.langmuir.9b02719 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hong, F., Zhang, F., Liu, Y. & Yan, H. DNA origami: scaffolds for creating higher order structures. Chem. Rev.117, 12584–12640 (2017). 10.1021/acs.chemrev.6b00825 [DOI] [PubMed] [Google Scholar]
- 25.Dong, Y. et al. DNA functional materials assembled from branched DNA: design, synthesis, and applications. Chem. Rev.120, 9420–9481 (2020). 10.1021/acs.chemrev.0c00294 [DOI] [PubMed] [Google Scholar]
- 26.Kieffer, C., Genot, A. J., Rondelez, Y. & Gines, G. Molecular computation for molecular classification. Adv. Biol.7, 2200203 (2023). [DOI] [PubMed]
- 27.Kim, J. & Winfree, E. Synthetic in vitro transcriptional oscillators. Mol. Syst. Biol.7, 465 (2011). 10.1038/msb.2010.119 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Montagne, K., Plasson, R., Sakai, Y., Fujii, T. & Rondelez, Y. Programming an in vitro DNA oscillator using a molecular networking strategy. Mol. Syst. Biol.7, 466 (2011). 10.1038/msb.2010.120 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Srinivas, N., Parkin, J., Seelig, G., Winfree, E. & Soloveichik, D. Enzyme-free nucleic acid dynamical systems. Science358, eaal2052 (2017). [DOI] [PubMed]
- 30.Lapteva, A. P., Sarraf, N. & Qian, L. DNA strand-displacement temporal logic circuits. J. Am. Chem. Soc.144, 12443–12449 (2022). 10.1021/jacs.2c04325 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bucci, J., Irmisch, P., Del Grosso, E., Seidel, R. & Ricci, F. Orthogonal enzyme-driven timers for DNA strand displacement reactions. J. Am. Chem. Soc. 144, 19791–19798 (2022). [DOI] [PMC free article] [PubMed]
- 32.Bucci, J., Irmisch, P., Del Grosso, E., Seidel, R. & Ricci, F. Timed pulses in DNA strand displacement reactions. J. Am. Chem. Soc.145, 20968–20974 (2023). 10.1021/jacs.3c06664 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Shin, J.-S. & Pierce, N. A. A synthetic DNA walker for molecular transport. J. Am. Chem. Soc.126, 10834–10835 (2004). 10.1021/ja047543j [DOI] [PubMed] [Google Scholar]
- 34.Andersen, E. S. et al. Self-assembly of a nanoscale DNA box with a controllable lid. Nature459, 73–76 (2009). 10.1038/nature07971 [DOI] [PubMed] [Google Scholar]
- 35.Pumm, A.-K. et al. A DNA origami rotary ratchet motor. Nature607, 492–498 (2022). 10.1038/s41586-022-04910-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Udono, H., Gong, J., Sato, Y. & Takinoue, M. DNA droplets: intelligent, dynamic fluid. Adv. Biol.7, 2200180 (2022). [DOI] [PubMed]
- 37.Takinoue, M. DNA droplets for intelligent and dynamical artificial cells: from the viewpoint of computation and non-equilibrium systems. Interface Focus13, 20230021 (2023). 10.1098/rsfs.2023.0021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Jeon, B.-J. et al. Salt-dependent properties of a coacervate-like, self-assembled DNA liquid. Soft Matter14, 7009–7015 (2018). 10.1039/C8SM01085D [DOI] [PubMed] [Google Scholar]
- 39.Jeon, B.-J., Nguyen, D. T. & Saleh, O. A. Sequence-controlled adhesion and microemulsification in a two-phase system of DNA. Liquid Droplets. J. Phys. Chem. B124, 8888–8895 (2020). 10.1021/acs.jpcb.0c06911 [DOI] [PubMed] [Google Scholar]
- 40.Sato, Y. & Takinoue, M. Capsule-like DNA hydrogels with patterns formed by lateral phase separation of DNA nanostructures. JACS Au2, 159–168 (2022). 10.1021/jacsau.1c00450 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Tran, M. P. et al. A DNA segregation module for synthetic cells. Small19, 2202711 (2022). [DOI] [PubMed]
- 42.Agarwal, S., Osmanovic, D., Klocke, M. A. & Franco, E. The growth rate of DNA condensate droplets increases with the size of participating subunits. ACS Nano16, 11842–11851 (2022). [DOI] [PubMed]
- 43.Lee, T., Do, S., Lee, J. G., Kim, D.-N. & Shin, Y. The flexibility-based modulation of DNA nanostar phase separation. Nanoscale13, 17638–17647 (2021). 10.1039/D1NR03495B [DOI] [PubMed] [Google Scholar]
- 44.Zhao, Q.-H., Cao, F.-H., Luo, Z.-H., Huck, W. T. S. & Deng, N.-N. Photoswitchable molecular communication between programmable DNA-based artificial membraneless organelles. Angew. Chem. Int. Ed Engl.61, e202117500 (2022). 10.1002/anie.202117500 [DOI] [PubMed] [Google Scholar]
- 45.Deng, J. & Walther, A. Programmable ATP-fueled DNA coacervates by transient liquid-liquid phase separation. Chem6, 3329–3343 (2020). 10.1016/j.chempr.2020.09.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Saleh, O. A., Jeon, B.-J. & Liedl, T. Enzymatic degradation of liquid droplets of DNA is modulated near the phase boundary. Proc. Natl. Acad. Sci. USA.117, 16160–16166 (2020). 10.1073/pnas.2001654117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Gong, J., Tsumura, N., Sato, Y. & Takinoue, M. Computational DNA droplets recognizing miRNA sequence inputs based on liquid–liquid phase separation. Adv. Funct. Mater. 32, 2202322 (2022).
- 48.Leathers, A. et al. Reaction–diffusion patterning of DNA-based artificial cells. J. Am. Chem. Soc. 144, 17468–17476 (2022). [DOI] [PMC free article] [PubMed]
- 49.Kim, J., White, K. S. & Winfree, E. Construction of an in vitro bistable circuit from synthetic transcriptional switches. Mol. Syst. Biol.2, 68 (2006). 10.1038/msb4100099 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Takinoue, M., Kiga, D., Shohda, K.-I. & Suyama, A. Experiments and simulation models of a basic computation element of an autonomous molecular computing system. Phys. Rev. E78, 041921 (2008). 10.1103/PhysRevE.78.041921 [DOI] [PubMed] [Google Scholar]
- 51.Wang, Y. et al. An RNase H-powered DNA walking machine for sensitive detection of RNase H and the screening of related inhibitors. Nanoscale12, 1673–1679 (2020). 10.1039/C9NR07550J [DOI] [PubMed] [Google Scholar]
- 52.Legewie, S., Dienst, D., Wilde, A., Herzel, H. & Axmann, I. M. Small RNAs establish delays and temporal thresholds in gene expression. Biophys. J.95, 3232–3238 (2008). 10.1529/biophysj.108.133819 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Shimomura, A. et al. Novel combination of serum microRNA for detecting breast cancer in the early stage. Cancer Sci.107, 326–334 (2016). 10.1111/cas.12880 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Hirano, N., Haruki, M., Morikawa, M. & Kanaya, S. Enhancement of the enzymatic activity of ribonuclease HI from Thermus thermophilus HB8 with a suppressor mutation method. Biochemistry39, 13285–13294 (2000). 10.1021/bi0015008 [DOI] [PubMed] [Google Scholar]
- 55.Zhang, D. Y. & Winfree, E. Control of DNA strand displacement kinetics using toehold exchange. J. Am. Chem. Soc.131, 17303–17314 (2009). 10.1021/ja906987s [DOI] [PubMed] [Google Scholar]
- 56.Lukacs, G. L. et al. Size-dependent DNA mobility in cytoplasm and nucleus. J. Biol. Chem. 275, 1625–1629 (2000). 10.1074/jbc.275.3.1625 [DOI] [PubMed] [Google Scholar]
- 57.Sato, Y. & Takinoue, M. Sequence-dependent fusion dynamics and physical properties of DNA droplets. Nanoscale Adv.5, 1919–1925 (2023). 10.1039/D3NA00073G [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Agarwal, S., Osmanovic, D., Dizani, M., Klocke, M. A. & Franco, E. Dynamic control of DNA condensation. Nat. Commun.15, 1915 (2024). 10.1038/s41467-024-46266-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Nguyen, D. T. & Saleh, O. A. Tuning phase and aging of DNA hydrogels through molecular design. Soft Matter13, 5421–5427 (2017). 10.1039/C7SM00557A [DOI] [PubMed] [Google Scholar]
- 60.Feric, M. et al. Coexisting liquid phases underlie nucleolar subcompartments. Cell165, 1686–1697 (2016). 10.1016/j.cell.2016.04.047 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Ura, T., Tomita, S. & Shiraki, K. Dynamic behavior of liquid droplets with enzyme compartmentalization triggered by sequential glycolytic enzyme reactions. Chem. Commun.57, 12544–12547 (2021). 10.1039/D1CC04596B [DOI] [PubMed] [Google Scholar]
- 62.Zadeh, J. N. et al. NUPACK: analysis and design of nucleic acid systems. J. Comput. Chem32, 170–173 (2011). 10.1002/jcc.21596 [DOI] [PubMed] [Google Scholar]
- 63.Schindelin, J. et al. Fiji: an open-source platform for biological-image analysis. Nat. Methods9, 676–682 (2012). 10.1038/nmeth.2019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Maruyama, T., Gong, J. & Takinoue, M. Numerical simulation codes for: temporally controlled multistep division of DNA droplets for dynamic artificial cells. Zenodo, 10.5281/zenodo.12741343 (2024). [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Description of Additional Supplementary Files
Data Availability Statement
The dataset of the main figures generated in this study is provided in the Supplementary Information, Supplementary Videos and Source Data files. Source data are provided with this paper.
The source codes for numerical simulations are provided through GitHub (https://github.com/takinouelab/MaruyamaTakinoue2024)64.