Long-term memory induced correction to Arrhenius law

Abstract

The Kramers escape problem is a paradigmatic model for the kinetics of rare events, which are usually characterized by Arrhenius law. So far, analytical approaches have failed to capture the kinetics of rare events in the important case of non-Markovian processes with long-term memory, as occurs in the context of reactions involving proteins, long polymers, or strongly viscoelastic fluids. Here, based on a minimal model of non-Markovian Gaussian process with long-term memory, we determine quantitatively the mean FPT to a rare configuration and provide its asymptotics in the limit of a large energy barrier E. Our analysis unveils a correction to Arrhenius law, induced by long-term memory, which we determine analytically. This correction, which we show can be quantitatively significant, takes the form of a second effective energy barrier $E^{\prime }<E$ and captures the dependence of rare event kinetics on initial conditions, which is a hallmark of long-term memory. Altogether, our results quantify the impact of long-term memory on rare event kinetics, beyond Arrhenius law.

Kinetics of rare events in chemical systems can be described by Arrhenius law, however this is less elaborated in systems displaying complex dynamics leading to long-lived memory effects. The authors propose an analytical framework that identifies the effects of long-lived memory on rare event kinetics in chemical systems

Introduction

Many physical and chemical processes are controlled by “rare” events, referring to events that are qualitatively unlikely, but nonetheless important because their realization has exceptional consequences^1,2. Such events are ubiquitous in the context of chemical physics, as exemplified at the molecular scale by the formation or rupture of bonds¹ (e.g. in force spectroscopy experiments^3–5 or adhesion kinetics⁶), protein folding⁷, molecular motor dynamics^8–10, or more generally nucleation events. Rare events are also relevant in other contexts, such as stock market crashes¹¹ or climate¹² or population^13,14 dynamics. The kinetics of such events, quantified by the first-passage time (FPT) to a target configuration, generally follows Arrhenius (also called Kramers, or Eyring–Kramers) law: the mean waiting time for a rare event is exponentially large with the energy barrier that has to be crossed to reach the target configuration¹. This picture is also valid in non-equilibrium systems with the definition of a pseudo-potential^15–18. In the weak-noise limit, the mean FPT is generally obtained by analyzing the dynamics at the top of the (pseudo-)potential barrier, by expanding around the most probable path leading to the target configuration. In this limit the waiting time for a rare event becomes larger than all relaxation times of the dynamics, and is thus independent of initial conditions.

While the effect of memory on first passage^19–25 and rare event kinetics^4,26–39 has been the object of recent studies, an important open question arises as to whether Arrhenius law is still valid for stochastic processes (or “reaction coordinates”) x(t) displaying infinite relaxation times, i.e. with correlation functions decaying as a power-law rather than exponentially:

$$\varphi \left(\tau \right)\equiv {\lim }_{t\to \infty }\frac{⟨x\left(t\right)x\left(t+\tau \right)⟩}{⟨x^2\left(t\right)⟩}\underset{\tau \to \infty }{\simeq }\frac{A}{{\tau }^{\alpha }},$$ 1

where A > 0, α > 0 and 〈x(t)〉 = 0 by convention. Stochastic processes possessing the property (1) will be called hereafter long-term memory processes^40,41 and arise when their dynamics results from the evolution of an infinite number of degrees of freedom. Examples of processes with long-term memory are provided by the dynamics of polymers⁴², proteins^43,44 or interfaces¹⁹, but also earthquakes⁴⁵ or rainfalls⁴⁶. It is known that long-term memory induces dispersed kinetics^47,48 and correlations between successive realizations of rare events^40,41,49; its impact on the kinetics of rare events however remains to be elucidated. In fact, this question was considered in ref. ³⁴ by means of a generalized Fokker–Planck equation, a controversial^4,50,51 method which leads to the notable prediction that the mean FPT to a rare configuration is infinite for a class of processes with long-term memory ; in ref. ³⁵, it was noted that the standard so-called “Wilemski-Fixman” approximation⁵² also predicts infinite mean FPTs when the exponent α defined in (1) satisfies α < 1 (note that in the non-equilibrium model of ref. ³⁵, the correlation function decays as 〈x(t)x(0)〉 ~ 1/t^α with α = 2 − 2H, where H is defined so that 〈x²〉 ∝ t^2H in the absence of potential. As a consequence, the long-term memory property α < 1 corresponds to H > 1/2, with an infinite mean FPT predicted by the Wilemski-Fixman approximation). Nevertheless, these predictions of infinite mean FPTs for processes with long-term memory seem inconsistent with numerical simulations^35,50,51 and the mathematical results of refs. ^53–55, which point to finite mean FPTs. Such contradiction shows that the above mentioned methods cannot be used to analyze the impact of long-term memory on rare event kinetics.

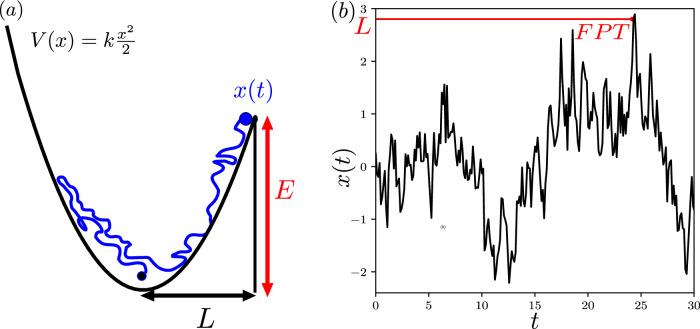
Here, on the basis of a simple model of a particle in a potential V(x) at finite temperature with retarded friction force, we resolve this issue and quantify the impact of long-term memory on the kinetics of rare events. We generalize to processes with long-term memory a formalism that was so far restricted to the analysis of either FPTs in large confining volumes with flat energy landscapes²⁴, or of rare events without long-term memory³⁷. Our theory predicts finite mean FPTs, and is supported quantitatively by numerical simulations. In the limit of large energy barriers—called hereafter rare events limit, we show that Arrhenius law does hold, with however sub-exponential corrections induced by the long-term memory, which we determine explicitly. We find that long-term memory effectively induces a second effective energy barrier of size $E^{\prime }=E\left(1-\alpha \right)$ (for α < 1), where E = V(L) − V(0) is the size of the real barrier (see Fig. 1). We find that the prefactor of this correction, which we explicitly calculate, is much larger than the prefactor of the leading order Arrhenius law, which implies that this correction is significant for a broad range of energy barriers.

Fig. 1. Sketch of the problem.

a Let x(t) be a random walker in a potential at temperature $\mathcal{T}$, submitted to a power-law friction kernel. In this example of long-term memory (meaning that the correlation function of x(t) decay as a power-law), what is the mean FPT to a target at x = L that can be reached only by overcoming an energy barrier E = V(L) − V(0). b Sketch of the FPT for a single stochastic trajectory of x(t).

RESULTS

Minimal model

We consider a minimal model of non-Markovian process x(t) with long-term memory at temperature $\mathcal{T}$, in a confining potential that is assumed harmonic, see Fig. 1a. We assume that x(t) obeys the overdamped Generalized Langevin Equation (GLE) :

$${\int }_0^{t}d{t}^{\prime }K\left(t-t^{\prime }\right)\stackrel{°}{x}\left(t^{\prime }\right)=-kx\left(t\right)+\xi \left(t\right).$$ 2

Here, the 1-dimensional random variable x(t) stands typically for the position of a particle, K(t) represents the friction kernel, k is the stiffness of the harmonic potential applied to the particle, and ξ(t) is a Gaussian thermal force with zero mean whose magnitude is set by the fluctuation dissipation theorem $⟨\xi \left(t\right)\xi \left(t^{\prime }\right)⟩=k_B\mathcal{T}K\left(\mid t-t^{\prime }\mid \right)$. With these definitions the process x(t) is Gaussian and its stationary probability density function (pdf) is $p_s\left(x\right)=e^{-\frac{k{x}^2}{2k_B\mathcal{T}}}/\sqrt{2\pi l^2}$, where $l=\sqrt{k_B\mathcal{T}/k}$ is the confinement length. Memory effects are encoded in the friction kernel K(t), and result typically from complex interactions of the variable x(t) with other, potentially hidden, degrees of freedom. The dynamics (2) describes a variety of physical processes: (i) the motion of a tracer particle in a viscoelastic fluid^56–58, (ii) the motion of a tagged particle attached to a polymer chain^42,59,60, (iii) the dynamics of the distance between two protein residues as experimentally observed⁴⁴. In the following we will mainly focus on scale invariant friction kernels:

$$K\left(t\right)=\frac{K_{\alpha }}{\mathrm{\Gamma }\left(1-\alpha \right)t^{\alpha }},$$ 3

where 0 < α < 1, K_α is a transport coefficient, and Γ( ⋅ ) is the gamma function. While the theory presented below could be applied to other kernels, this choice (3) is relevant to the physical examples (i),(ii),(iii) above. Furthermore, in absence of target, the correlation function defined in (1) is $\varphi \left(t\right)=E_{\alpha }\left[-{\left(t/{\tau }_d\right)}^{\alpha }\right]$^34,47 where ${\tau }_d={\left(K_{\alpha }/k\right)}^{1/\alpha }$ and E_α( ⋅ ) is the Mittag–Leffler function. Since E_α( −u) ~ 1/[Γ(1 − α)u] for large arguments, the choice of kernel (3) ensures that the process x(t) displays long-term memory as defined in (1): there is no finite relaxation time in the correlation function, and A = K_α/[Γ(1 − α)k] (SI, Section A).

If one imposes the initial condition x(0) = x₀, the average path $m_0\left(t\right)\equiv {⟨x\left(t\right)⟩}_{x\left(0\right)=x_0}$ and the covariance $\sigma \left(t,t^{\prime }\right)\equiv \mathrm{Cov}{\left(x\left(t\right),x\left(t^{\prime }\right)\right)}_{x\left(0\right)=x_0}$ conditional to x(0) = x₀ read⁶¹

$$m_0\left(t\right)=x_0\varphi \left(t\right),\sigma \left(t,t^{\prime }\right)=l^2\left[\varphi \left(\mid t-t^{\prime }\mid \right)-\varphi \left(t\right)\varphi \left(t^{\prime }\right)\right].$$ 4

We also define ψ(t) = σ(t, t) as the Mean Squared Displacement (MSD) of x(t). In absence of potential (k = 0), x(t) is the fractional Brownian motion of Hurst exponent H = α/2; for finite k this regime is realized at short times, when the harmonic force is negligible, as seen from the MSD:

$$\psi \left(t\right){\simeq }_{t\to 0}\kappa t^{2H},\kappa =\frac{2k_B\mathcal{T}}{K_{\alpha }\mathrm{\Gamma }\left(1+\alpha \right)},H=\frac{\alpha }{2}.$$ 5

Hereafter we study the mean FPT of the process x(t) defined by (2), (3) to a target threshold x = L, with an initial configuration either drawn from the equilibrium distribution or set by x(0) = x₀.

Numerical analysis

We have performed numerical simulations of the GLE (2) by using a modified version of the circulant matrix algorithm⁶² described in ref. ⁶³, which is an exact generator of x(t) at sampling times t_n = n × dt for any value of the time step dt. The used values of dt are indicated in the Supplementary Information (SI, Section D) and are always < 2 × 10⁻⁵τ_d. We used the two values of H = α/2 that are used in classical polymer models : either a semi-flexible chain (H = 3/8) or a flexible (Rouse) chain without hydrodynamic interactions (H = 1/4). For each trajectory {x(t_n)} we measured the FPT to L. The resulting survival probability S(t) (defined as the probability that the FPT is larger than t) is shown in Fig. 2. Our numerical results are consistent with the mathematical results of refs. ^53–55: an exponential decay of S(t) in the rare events limit L → ∞, and a stretched exponential behavior for L = 0. This numerical analysis thus further supports that the mean FPT is finite (see Fig. 3).

Fig. 2. Survival probabilities for the stochastic process defined by Eq. (2), as measured in numerical simulations.

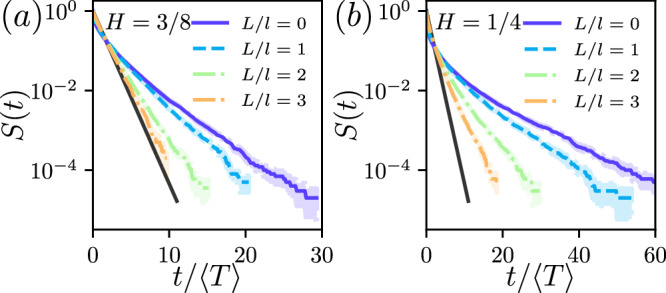
a H = 3/8 and b H = 1/4, Here, x₀ is drawn from the equilibrium distribution p_s(x). The black line represents S(t) = e^−t/〈T〉. Error bars represent 68% confidence intervals, due to statistical uncertainties.

Fig. 3. Mean FPT for the process described by Eq. (2) when the initial position is x₀ = 0.

a H = 3/8 and b H = 1/4. Symbols: numerical simulations; dots: numerical integration of Eqs. ((6), (8)); dashed red line: Arrhenius law at leading order, Eq. (10); orange full line: refined Arrhenius law (13), including the corrections due to long-term memory. We have used the values ν_3/8 = 5.26 and ν_1/4 = 5.0 calculated in ref. ³⁷.

General non-Markovian analysis

We now proceed to the theoretical determination of the mean FPT to x = L, denoted 〈T〉, with fixed initial condition x(0) = x₀ [the case of stationary initial conditions can be obtained by averaging over p_s(x₀)]. Our approach consists in generalizing the tools developed in refs. ^24,37,64, which, in the context of rare event kinetics, have been used so far only to analyze processes with a finite maximal relaxation time³⁷. We describe the main steps of the approach for completeness ; details can be found in SI (Section B). We start with the following general exact expression of the mean FPT, derived in ref. ²⁴:

$$⟨T⟩p_s\left(L\right)={\int }_0^{\infty }dt\left[p_{\pi }\left(L,t\right)-p\left(L,t\right)\right],$$ 6

where we have introduced p_π(x, t) as the pdf of the process x_π(t) ≡ x(t + T), where T is the FPT; x_π(t) is thus the process after a first-passage event. To characterize p_π(x, t), we assume that the process x_π(t) is Gaussian (as is x(t)), and thus fully characterized by its first moment m_π(t) = 〈x_π(t)〉, and covariance ${\sigma }_{\pi }\left(t,t^{\prime }\right)\simeq \sigma \left(t,t^{\prime }\right)$ that is assumed to be identical to that of the unconditioned process x(t). The validity of these hypotheses has been checked numerically [Fig. 4(a) and SI, Section D] and analytically for weakly non-Markovian processes (SI, Sections E). With these approximations, Eq. (6) becomes

$$⟨T⟩p_s\left(L\right)={\int }_0^{\infty }\frac{dt}{\sqrt{2\pi \psi \left(t\right)}}\left[e^{-\frac{{\left[m_{\pi }\left(t\right)-L\right]}^2}{2\psi \left(t\right)}}-e^{-\frac{{\left[x_0\varphi \left(t\right)-L\right]}^2}{2\psi \left(t\right)}}\right].$$ 7

The so far unknown quantity m_π(t) can then be determined self-consistently by analyzing a generalized version of the renewal equation (see SI, Section B), leading to

$${\int }_0^{\infty }dt\left\{\frac{e^{-\frac{{\left[m_{\pi }\left(t\right)-L\right]}^2}{2\psi \left(t\right)}}}{\sqrt{2\pi \psi \left(t\right)}}\left(m_{\pi }\left(t+\tau \right)-\left[m_{\pi }\left(t\right)-L\right]\frac{\sigma \left(t+\tau ,t\right)}{\sigma \left(t,t\right)}-L\varphi \left(\tau \right)\right)\right)-\left(\frac{e^{-\frac{{\left[x_0\varphi \left(t\right)-L\right]}^2}{2\psi \left(t\right)}}}{\sqrt{2\pi \psi \left(t\right)}}\left(x_0\varphi \left(t+\tau \right)-\left[x_0\varphi \left(t\right)-L\right]\frac{\sigma \left(t+\tau ,t\right)}{\sigma \left(t,t\right)}-L\varphi \left(\tau \right)\right)\right\}=0.$$ 8

This equation generalizes similar equations in refs. ^24,37, which were restricred on the determination of p_π(L, t) at short times and thus did not enable the analysis of long-term memory effects. This integral equation, together with the condition m_π(0) = L, allows to determine the only unknown m_π(t) : this finally gives access to 〈T〉 thanks to Eq. (7).

Fig. 4. Check of the approximations of the theory.

a Check of the stationary covariance approximation (i.e. ${\sigma }_{\pi }\left(t,t^{\prime }\right)\simeq \sigma \left(t,t^{\prime }\right)$): comparison between ψ_π(t) = Var(x_π(t)) measured in numerical simulations (symbols) and ψ(t) (dashed line: H = 3/8, full line H = 1/4). b Check of Eq. (9): comparison between the value m_π(t) in simulations (symbols) and x₀ϕ(t) (full line: x₀ = l/2 for H = 3/8; dashed line x₀ = l for H = 1/4). Note that m_π(t) ≃ x₀ϕ(t) is expected at large times only. c Check of the short-time scaling regime for H = 3/8. d Check of the long-time scaling regime (11) for H = 3/8. In a, c, d, the initial position is drawn from an equilibrium distribution, corresponding to our predictions for x₀ = 0. When present, error bars represent 68% confidence intervals.

General results

This approach first shows unambiguously that the mean FPT is finite. Indeed, we show in SI (Section B) that the solution to Eq. (8) satisfies at long times

$$m_{\pi }\left(t\right){\simeq }_{t\to \infty }{x}_0\varphi \left(t\right),$$ 9

which can be checked directly in numerical simulations, see figure 4b. This scaling, together with Eq. (6), shows that the mean FPT is finite. This contradicts the results obtained with the generalized Fokker–Planck equation³⁴ or with the Wilemski-Fixman approximation⁵². The latter amounts to assuming that the process is at all times in an equilibrium state, and would thus yield m_π(t) ≃ Lϕ(t), leading to an infinite mean FPT when α < 1 (as noted earlier in a similar, but out of equilibrium, situation³⁵). Beyond this proof of finiteness, our approach yields a quantitative determination of 〈T〉 by solving numerically the integral equation (8) for m_π(t) and next using Eq. (6); this shows quantitative agreement with numerical simulations in Fig. 3.

Rare events limit L → ∞

We now consider the rare event limit to determine explicitly the impact of long-term memory on rare events kinetics. The mean FPT obtained by the method of matched asymptotics which we sketch here; calculation details are provided in SI (Section C). The dynamics involves different time and length scales ; two can be readily identified: (i) the confinement length l and (ii) the length $l*=k_B\mathcal{T}/F$, where F = kL is the slope of the potential at L. The associated timescales are respectively (i) τ_d and (ii) the time t* at which the characteristic fluctuations $\sqrt{\kappa }{\left(t*\right)}^H$ of the trajectories near the target become comparable to l^*, this leads to $t*={\left(l*/\sqrt{\kappa }\right)}^{1/H}$. Note that in the rare events limit t* ≪ τ_d.

The leading order term $T_{\mathrm{RE}}$ of 〈T〉 in the L → ∞ limit results from the contribution of timescales t ~ t* ≪ τ_d only in (6). Indeed, after a time t ≫ t*, a particle initially at L has typically moved away from the target, so that p_π(L, t) is exponentially small, whereas p_π is of order 1 at very short times t ~ t*. In turn, if the starting position is typically not close from L, p(L, t) is exponentially small with L at all times. The above consideration suggests to look for solutions of the form m_π(t) ≃ L − l^*f(t/t*); inserting this ansatz in (8) and taking the rare event limit leads to an equation for f that depends only on H, justifying our ansatz. The mean FPT at leading order is then obtained as

$$⟨T⟩{~}_{L\to \infty }\frac{l^{\frac{2}{H}-1}{\nu }_H}{L^{\frac{1}{H}-1}{\kappa }^{\frac{1}{2H}}}\times e^{\beta E}\equiv T_{\mathrm{RE}},$$ 10

where ${\nu }_H={\int }_0^{\infty }\frac{du}{u^H}{e}^{-f^2\left(u\right)/2u^{2H}}$ depends only on H, E = kL²/2 is the energy barrier and $\beta =1/\left(k_B\mathcal{T}\right)$. This leading order result displays the usual Arrhenius factor e^βE, which is the hallmark of rare event kinetics, and is compatible with the mathematical results of Pickands⁵⁴. Of note, it is controlled only by the short-time behavior of the MSD ψ(t), and is independent of the long time relaxation of correlations, and thus of long-term memory. It is indeed identical to the results of ref. ³⁷ obtained for non-Markovian processes with the same MSD at short times but finite relaxation time. To prove this result self-consistently, we need to estimate the contributions to 〈T〉 in (6), that are induced by the behavior of the integrand at timescales t ≫ t *. These contributions are expected to be relevant in the case of long-term memory, due to the slow decay of correlation functions.

Here, the key point is to note that, in addition to the previously identified timescales τ_d and t*, a third relevant timescale for the dynamics of x_π(t) is the time $T_{\mathrm{RE}}$ itself. Indeed, we show in SI that m_π(t, L) can be written for t ≫ t* :

$$m_{\pi }\left(t\right)\simeq \left\{\begin{array}{cc}L{\varphi }_{\pi }\left(t\right)\hfill & \left(t*\ll t=\mathcal{O}\left({\tau }_d\right)\ll T_{\mathrm{RE}}\right)\hfill \\ \frac{LA}{T_{\mathrm{RE}}^{\alpha }}\chi \left(\frac{t}{T_{\mathrm{RE}}}\right)\hfill & \left({\tau }_d\ll t=\mathcal{O}\left(T_{\mathrm{RE}}\right)\right)\hfill \end{array}\right),$$ 11

where A is defined in (1) and χ and ϕ_π are scaling functions. The analysis of Eq. (8) at timescales τ_d and $T_{\mathrm{RE}}$, respectively, enables us to obtain equations for ϕ_π and χ that can be solved, leading to

$${\varphi }_{\pi }\left(t\right)=\varphi \left(t\right),\chi \left(y\right)=\alpha \left(1-\frac{x_0}{L}\right)\mathrm{\Gamma }\left(-\alpha ,y\right)e^y+\frac{x_0}{y^{\alpha }L},$$ 12

where $\mathrm{\Gamma }\left(s,y\right)={\int }_y^{\infty }{t}^{s-1}{e}^{-t}dt$ is the upper incomplete gamma function. Finally, inserting the scaling forms for m_π(t) into Eq. (6), we obtain

$$⟨T⟩\simeq T_{\mathrm{RE}}+T_{\mathrm{RE}}^{1-\alpha }\times \frac{A}{l^2}L\left(L-x_0\right)\mathrm{\Gamma }\left(1-\alpha \right).$$ 13

This is the central result of this Letter. It confirms the validity of the leading order term $T_{\mathrm{RE}}$, which is independent of long-term memory, and explicitly determines the subleading term, which is induced by long-term memory, as seen by the factor A that characterizes the long-time decay of fluctuations. Several remarks are in order: (i) Since $T_{\mathrm{RE}}\propto e^{\beta E}$, the correction due to long-term memory is of order $e^{\beta E^{\prime }}$ with an effective energy barrier $E^{\prime }=E\left(1-\alpha \right)$. The smaller the value of α the larger the value of $E^{\prime }$, so that the convergence to the rare event limit is expected to be slower for small α (where non-Markovian effects are stronger). (ii) Furthermore, the pre-exponential factor is clearly much larger for the corrective term than for the leading order term in the limit L → ∞, so that the corrective term can be quantitatively important. Indeed, as observed in figure 3, taking into account this correction is essential to predict the rare event kinetics for not-too-large values of L. (iii) Eq. (13) shows that the subleading correction depends on the initial position x₀: because of long-term memory, initial conditions can thus impact quantitatively rare event kinetics. (iv) As a further validation of our analysis, the expected scaling behaviors of m_π are given in Fig. 4c, d and hold in the large L limit, with discrepancies at small times in Fig. 4c due to limitations in the choice of the time step (see SI, Section D for additional parameters).

Discussion

We have proposed a theoretical analysis of the classical Kramers escape problem for non-Markovian processes with long-term memory. Although our approach is approximate, it captures the essence of memory effects and allows for a quantitative determination of the mean FPT to a target, which we unambiguously show is finite, whereas all existing theoretical approaches so far incorrectly predicted infinite mean FPTs (for α < 1). This comes from the assumption of a system at equilibrium at all times that is implicitly made in the methods that have been employed so far, namely the Wilemski-Fixman approximation or the generalized Fokker–Planck equation approach. Such hypothesis is too strong to take properly into account long-term memory effects. In our approach, the genuine non-equilibriumness of the system upon a first passage event manifests itself in the trajectory m_π(t), whose behavior at very long times is affected by long-term memory. In the rare event limit, we have explicitly determined the correction to Arrhenius laws, which is due to long-term memory. This takes the form of a second effective energy barrier o f size $E^{\prime }=E\left(1-\alpha \right)$, which we show can be quantitatively significant, and captures the dependence of the kinetics on initial conditions. It is known that Arrhenius laws can be identified for non-Gaussian models by considering the linearized dynamics around the target³⁷. Since our study reveals that the effect of long-term memory on rare event kinetics comes from the slow dynamics at the bottom of the potential only, we may expect that our main result (13) could be generalized to non-Gaussian models. Moreover, although we have focused here on a simple model of a particle with viscoelastic friction at equilibrium at constant temperature, it is clear that our arguments to identify the mean FPT could be adapted to active models where the fluctuation-dissipation theorem does not hold. Indeed, Eq. (7) and (8) would still be valid, and would involve similarly the properties of the process in absence of target (A, ϕ, p_s, κ, . . . ), which are in principle still accessible from the definition of the process in Eq. (2), even if the fluctuation-dissipation relation does not hold because of active effects³⁵. Last, because our approach puts forward deviations from Arrhenius law due to long-term memory, we also anticipate deviations from exponential laws for the distribution of FPTs, that could be studied by generalizing our approach to higher moments of the FPT, possibly giving access to the analytical study of extreme events clustering and dispersed kinetics. Altogether, our results shed light on the effect of long-term memory on rare event kinetics, beyond Arrhenius laws.

METHODS

Numerical methods

To generate stochastic trajectories x(t_n) satisfying the GLE (2) at sampling times t_n = n × dt, a modified version of the circulant matrix algorithm⁶² described in ref. ⁶³ was used. This algorithm enables one to generate trajectories of N points with a computational complexity $\mathcal{O}\left(N\log N\right)$. The value of the maximal time of the simulations and the time steps were systematically varied to check that the measured properties of the FPT do not depend on such values. Next, to determine the FPT, we have used a theory relying on the analysis of trajectories after the FPT, assumed to display Gaussian statistics with the same covariance function as the original stochastic process. The control of such approximations can be found in SI (Sections D for numerical check and E for a perturbative analysis for weakly non-Markovian processes). To obtain numerical predictions for the mean FPT, equations (7) and (8) were integrated numerically by evaluating the integrals over a non-uniform mesh (with more concentrated points near the origin) using the trapeze method; the number of points in the mesh and the maximal time were systematically varied to make sure that predictions do not depend on the properties of the mesh.

Author contributions

All authors contributed to analytical calculations. A.B. performed numerical computations. O.B., R.V., and T.G. conceived research and wrote the manuscript.

Peer review

Peer review information

Nature Communications thanks Roland Netz, and the other, anonymous, reviewers for their contribution to the peer review of this work. A peer review file is available.

Data availability

The simulation data of the first passage time which were used to plot Figs. 2-4 have been deposited in the figshare database [10.6084/m9.figshare.25817599].

Code availability

The code which has been used to generate the simulation data have been deposited in the figshare database [10.6084/m9.figshare.25817599].

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-50938-1.