Abstract
Introduction:
Developing alternative approaches to evaluating absolute efficacy of new HIV prevention interventions is a priority, as active-controlled designs, whereby individuals without HIV are randomized to the experimental intervention or an active control known to be effective, are increasing. With this design, however, the efficacy of the experimental intervention to prevent HIV acquisition relative to placebo cannot be evaluated directly.
Methods:
One proposed approach to estimate absolute prevention efficacy is to use an HIV exposure marker, such as incident rectal gonorrhea, to infer counterfactual placebo HIV incidence. We formalize a statistical framework for this approach, specify working regression and likelihood-based estimation approaches, lay out three assumptions under which valid inference can be achieved, evaluate finite-sample performance, and illustrate the approach using a recent active-controlled HIV prevention trial.
Results:
We find that in finite samples and under correctly specified assumptions accurate and precise estimates of counterfactual placebo incidence and prevention efficacy are produced. Based on data from the DISCOVER trial in men and transgender women who have sex with men, and assuming correctly specified assumptions, the estimated prevention efficacy for tenofovir alafenamide plus emtricitabine is 98.1% (95%CI: 96.4% to 99.4%) using the working model approach, and 98.1% (95% CI: 96.4% to 99.7%) using the likelihood-based approach.
Conclusions:
Careful assessment of the underlying assumptions, study of their violation, evaluation of the approach in trials with placebo arms, and advancement of improved exposure markers are needed before the HIV exposure marker approach can be relied upon in practice.
Keywords: Counterfactual placebo, HIV prevention, randomized controlled trial, rectal gonorrhea, trial design
Introduction
The last decade has seen dramatic success in HIV prevention1 with effective pre-exposure prophylaxis (PrEP) products.2–8 Despite these successes, HIV remains a major threat to global health.9 As considerable challenges to implementing existing prevention interventions exist,10,11 additional biomedical prevention interventions are needed.
A variety of new preventive interventions (e.g., alternative PrEP agents, vaccines, etc.) are in development.12 Placebo-controlled randomized trials that enroll individuals without HIV and follow them for incident HIV acquisition have historically been required for regulatory approval of new interventions. For new interventions in the same “class” as an intervention already proven effective, future trials will likely be “active-controlled”;13 participants without HIV are randomized to the experimental intervention or an existing “active control” intervention already proven effective. Even for new interventions in as-yet-unproven classes, e.g., vaccines, an active-controlled design may be necessary.
The fundamental challenge of an active-controlled trial is that absolute prevention efficacy, i.e., the reduction in HIV incidence for the intervention relative to placebo, cannot be evaluated based on the trial data alone. Instead, relative efficacy of the experimental and active control interventions is assessed. Yet absolute efficacy is arguably the parameter of most interest.14,15 A traditional approach to estimating efficacy is using data from a historical placebo-controlled trial of the active control to set a “margin” for establishing non-inferiority or superiority of the experimental intervention, based on the assumption that efficacy established in the historical trial can be carried over to the new trial.16,17 This approach is challenging in HIV prevention, since many interventions are highly user-dependent,18–20 and efficacy of vaccines and monoclonal antibodies depends on properties of the exposing virus;21–23 thus, efficacy in the historical trial may not apply to the current trial. In addition, non-inferiority trials generally require larger sample sizes than placebo-controlled trials, especially if the active control is highly effective. Therefore, developing alternative approaches to evaluating absolute efficacy of new HIV prevention interventions is a priority.
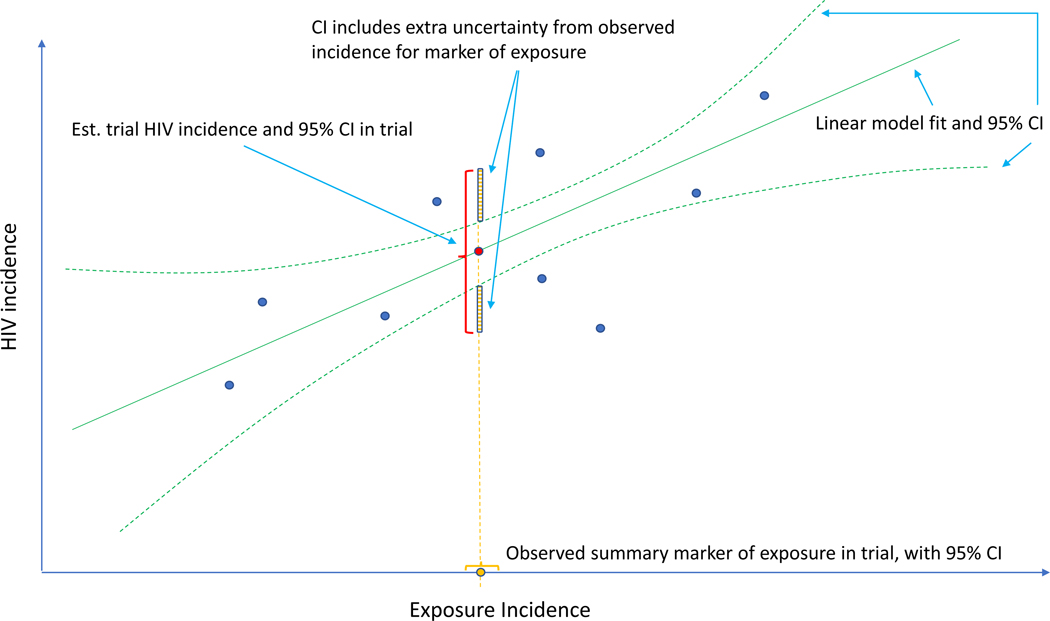
One approach proposed in concept24,25 and widely discussed in the HIV prevention field14,15,25–31 is to use a marker of HIV exposure as a proxy to infer “counterfactual placebo” HIV incidence, i.e., the incidence observed had a placebo arm been included in the active-controlled trial. This requires establishing the association between incidence of HIV and an HIV exposure marker in the absence of intervention, estimated based on historical data. Provided the intervention does not affect the HIV exposure marker, incidence of the marker in the active-controlled trial can be used to estimate counterfactual placebo HIV incidence. Figure 1 illustrates this concept. Incident rectal gonorrhea has been proposed as the HIV exposure marker for men who have sex with men, based on observational data suggesting that the incidence rates of these two sexually-transmitted infections are highly correlated.24 US Food and Drug Administration (FDA) advisory committees reviewing new PrEP agents support this approach,32 and the FDA endorsed the approach in guidance to industry. Yet, a formal statistical framework is lacking.
Figure 1.
Estimation of counterfactual HIV incidence based on an HIV exposure marker. Green solid and dashed curves correspond to the fitted model associating HIV and exposure marker incidences with an associated pointwise 95% confidence interval (CI), based on a set of external cohorts reporting HIV and exposure marker incidence rates (dark blue dots). Given the exposure marker incidence in the active-controlled trial (yellow dot), counterfactual placebo HIV incidence is estimated with use of the fitted model (red dot). The 95% CI for the counterfactual placebo incidence captures uncertainty due to the model fit and uncertainty in the exposure marker incidence.
Here, we: 1) articulate a statistical framework for inferring counterfactual placebo HIV incidence for an active-controlled trial using a marker of HIV exposure; 2) describe two estimation approaches and articulate the assumptions under which they produce unbiased estimates; 3) conduct a simulation study designed to closely mimic data on HIV and rectal gonorrhea and evaluate the performance of the methods under idealized conditions, i.e., when all assumptions are satisfied; and 4) apply the methodology to data from a recently conducted active-controlled HIV prevention trial.6 and highlight the limitations of the approach and implications for its use in future HIV prevention trials.
Methods
Setting and notation
Let indicate the HIV prevention intervention where denotes placebo, denotes experimental intervention, and denotes active-control intervention.
For an active-controlled trial, denotes the HIV diagnosis event time and denotes the HIV incidence rate for subjects randomized to for . Let denote the counterfactual HIV incidence for the trial population under placebo. Incidence rates are assumed constant over time. The quantity of primary interest is the prevention efficacy of the experimental intervention, given by
| (1) |
We formulate a general approach for evaluating , .
Remark 1.
Prevention efficacy is evaluated against a backdrop standard of HIV prevention for the target population, consisting of proven and available HIV prevention products.13 Therefore, , hereafter “placebo incidence”, is the counterfactual HIV incidence where trial participants are randomized to receive a placebo in addition to the standard of HIV prevention. Interpretation of and are specific to this standard of prevention.
In a randomized placebo-controlled trial for intervention , and are estimated directly. However, in an active-controlled trial, only can be estimated, and , and therefore , cannot be estimated directly. Instead, data from external cohorts are used to establish a relationship between HIV and an exposure marker, so as to infer .
Assumptions
Let denote the incidence of HIV exposure marker in the active-controlled trial population, given randomization to intervention . We assume is constant in time. We establish the relationship between and based on data from external cohorts, each of which is conducted under a specific standard of HIV prevention. We refer to these as “placebo” incidence rates for simplicity. For external cohort , let and be the incidences of HIV and the exposure marker, respectively.
We parameterize the relationship between HIV and the exposure marker incidences as
| (2) |
for , where and are the incidence parameters for the active-controlled trial population, and are known link functions appropriate for non-negative incidence parameters, e.g., logit or log links, is an invertible function, is an unknown regression function that can be either parametric or nonparametric, and is an i.i.d. mean-zero error term. Importantly, and are random variables: there is variability in the placebo incidence rates across cohorts due to different compositions of risk factors and differences in the standard of prevention for both HIV and the exposure marker.
We state the following assumptions.
Assumption 1.
Model (2) describes a general relationship between placebo HIV and exposure marker incidence rates that holds across external cohorts and the active-controlled trial population.
While HIV and exposure marker incidences may vary, the association between the incidence rates is assumed constant. To evaluate Assumption 1, one must consider carefully the background standard of HIV prevention for the active-controlled trial population, and whether any element of this prevention package influences the relationship between HIV and the exposure marker. For example, oral PrEP is known to reduce HIV but does not have a biological effect on rectal gonorrhea or other non-HIV sexually transmitted infections,6 even though it may have an effect in terms of behavioral “risk disinhibition”.33 Therefore, if the trial standard of HIV prevention does not include oral PrEP, the external cohorts should be drawn from populations without access to oral PrEP. Elements of the standard of HIV prevention (i.e., condoms and risk reduction counseling) may influence HIV and rectal gonorrhea incidences, but not to modify their association, and therefore may not be critical to consider in evaluating external cohorts. Effective biomedical prevention of non-HIV sexually transmitted infections is another potential effect modifier. Other potential effect modifiers include subject demographics, behaviors, and features of the local HIV epidemic, i.e., population prevalence of HIV and level of viral suppression for those living with HIV. Blinding may also influence the relationship between HIV and the exposure marker. While the counterfactual placebo arm is (conceptually) blinded, the external cohorts may not be. While Assumption 1 can be evaluated for the external cohorts, whether it holds for the trial population cannot be tested, given the absence of a placebo arm for the trial population.
Assumption 2.
An unbiased estimate of the parameters in can be obtained based on estimated incidences , , and their associated variances in the external cohorts. The estimate of after plugging in those parameter estimates is denoted by .
Assumption 2 indicates the relationship between HIV and exposure marker incidences can be consistently estimated using the observed incidence rates from the external cohorts. This assumption is specific to the estimation approach and will be discussed below.
Assumption 3.
The exposure marker incidence is not modified by randomization to active intervention , i.e., .
Assumption 3 stipulates that the incidence of the HIV exposure marker under is the same as that under placebo. In evaluating this assumption one must consider whether the intervention, or elements of the standard of HIV prevention, may modify the incidence of the exposure marker. Whether or not the active-controlled trial is blinded is also relevant, since knowledge of receipt of intervention may modify behavior. This assumption can be partially evaluated in the context of an historical randomized, placebo-controlled trial of the intervention with the exposure marker collected as an endpoint. However, the historical data do not inform on whether Assumption 3 holds for the trial population.
Under Assumptions 1–3, counterfactual placebo HIV incidence can be consistently estimated by
where is the observed exposure marker incidence in the trial arm randomized to intervention . Importantly, uncertainty in the estimated counterfactual placebo HIV incidence is comprised of the uncertainty due to fitting the regression model, , and the uncertainty in the exposure marker incidence, , as illustrated in Figure 1. Prevention efficacy, , can then be estimated by
where is the estimated HIV incidence among those randomized to intervention in the active-controlled trial.
Remark 2.
If the exposure marker incidence is not modified by either intervention in the active-controlled trial, the exposure marker incidence among all trial participants may be used to estimate counterfactual placebo HIV incidence. This provides a more precise estimate, relative to the estimate based on the exposure marker incidence among participants that received intervention .
Bivariate Linkage Model
To estimate , we focus on a special case of model (2) for which we discuss validity and violation of Assumption 2. We assume a bivariate normal distribution for the log-transformed HIV and exposure marker incidence rates, and . In particular,
| (3) |
for , where denotes a -dimensional multi-normal distribution with mean and variance matrix , and are means of and , respectively, and are variances of and , respectively, and is the correlation of and that measures the magnitude of association.
We assume the estimated incidence rates from the external cohorts, , are conditionally independent given the true incidence rates , for . The joint conditional distribution is given by
| (4) |
where , and and are the conditional variances of and given , respectively. Conditional independence is a common assumption in bivariate outcome meta-analysis,34,35 in part because conditional dependence is not commonly evaluated or reported in studies. We evaluate bias due to violation of the conditional independence assumption in simulations. Note that (4) is a model for the log-transformed incidence rates, but it does not stipulate a model for individual-level HIV and exposure marker outcomes.
Under the bivariate linkage model, the parameters can be estimated using a maximum likelihood approach given the observed external cohort data . Write as the estimates. The counterfactual placebo HIV incidence can therefore be estimated by
| (5) |
and prevention efficacy can be estimated by
| (6) |
See Supplementary Materials for details.
While maximum likelihood estimation yields consistent and efficient parameter estimates under correct model specification, it may not be stable when the number of external cohorts is small, e.g., , as suggested by our simulations. When is small, we suggest fitting a working regression model or “working model”:
| (7) |
In general, the working model is mis-specified. However, the estimated regression function based on working model estimates and denoted by , may approximate enough to provide adequate inference about counterfactual placebo HIV incidence. Using the working model, the counterfactual placebo HIV incidence is estimated by
| (8) |
and prevention efficacy is estimated by
| (9) |
See Supplementary Materials for details.
In summary, assuming the bivariate linkage model (3), the procedure for estimating counterfactual placebo HIV incidence and prevention efficacy is as follows:
Step 1. Given estimated incidences from external cohorts, fit the bivariate linkage model using either the maximum likelihood or working model approaches;
Step 2. Given the estimated incidence rate of the exposure marker from the active-controlled trial, estimate the counterfactual placebo HIV incidence , using either (5) for maximum likelihood, or (8) for the working model approaches;
Step 3. Given the estimated HIV incidence rate in the active-controlled trial, estimate using either (6) for the maximum likelihood, or (9) the working model approaches.
R code for implementation is available on Github (https://github.com/feigao1/CF_Exposuremarker).
Simulation studies
To evaluate the numerical performance of the counterfactual placebo incidence and prevention efficacy estimates, we examine the ideal scenario when all assumptions hold (with maximum likelihood estimation), and when Assumption 2 holds approximately (with working model estimation).
External cohorts
Incidences in the external cohort are generated from the bivariate linkage model (3) with log link functions where the parameter values are the maximum likelihood estimates based on published studies reporting both HIV and rectal gonorrhea incidence for men who have sex with men, summarized in Supplementary Table S1. The interquartile range of HIV and marker incidences in the cohorts are (2.5, 6.8) and (5.8,19.4) cases per 100 person-years, respectively. We also consider a bivariate linkage model (3) with logit link functions (see Supplementary Materials). Since the maximum likelihood estimate of the correlation is high (0.98), we also consider a moderate correlation scenario wherein . We set the number of external cohorts to or 20, as generally only a small number of external studies will be available with the required data. The person-times for the external cohorts, , are uniformly distributed between 200 and 5000 person-years. The number of HIV and exposure marker events, and , follow binomial distributions with expectations and , respectively. In each cohort , we estimate incidences by , ; standard deviations are estimated by and .
Active-controlled trial
We consider a single arm trial for conciseness, with a follow-up time of or 4000 person-years. Placebo HIV incidence is assumed to be 3, 4.5, or 6 cases per 100 person-years, and exposure marker incidence is generated based on the conditional distribution of given (see Supplementary Materials). Prevention efficacy is assumed to be 0.3, 0.6 or 0.75 and . The number of HIV and exposure marker events, and , follow binomial distributions with expectation and , respectively. Incidences are estimated by , .
Estimation methods and performance measures
We apply maximum likelihood and working model estimation approaches, following the procedure listed at the end of the Methods section. We evaluate the average bias, empirical standard deviation, and coverage probability of nominal 95% confidence intervals (CIs) for counterfactual placebo incidence and prevention efficacy estimates across 5,000 simulations.
Results
Simulation
Table 1 summarizes the performance of counterfactual placebo HIV incidence estimates across simulation scenarios. We show results with and 20 for the working model, and for likelihood-based estimation, as likelihood-based estimation requires sufficiently large to ensure numerical stability. For both estimation approaches, we find high correlation between HIV and the exposure marker yields accurate and precise estimation, as evidenced by low bias, reasonably low standard deviation, and CIs with close to nominal coverage. Even with modest correlation , low bias and nominal coverage rates are seen, although the standard deviation is larger than in the high correlation scenario. Performance is minimally impacted by the size of the trial’s active arm. Performance of the working model is comparable to that of likelihood-based estimation in settings with , while it performs worse for large , with CIs that are overly conservative (results not shown). Bias and coverage rates are similar under a logit-link bivariate linkage model (see Supplementary Table S2).
Table 1.
Bias, standard deviation, and empirical coverage for estimated counterfactual placebo HIV incidence, based on external cohorts used to estimate the association between HIV and an exposure biomarker with correlation . A total of person-years follow-up accrue in the active arm of the trial. Counterfactual placebo HIV incidence varies. Performance is shown for working model and likelihood-based estimation approaches, assuming log link function for marginal incidences.
| HIV incidence (cases per 100 person-years) | 3 | 4.5 | 6 | 3 | 4.5 | 6 | ||
| Exposure marker incidence (cases per 100 person-years) | 7.1 | 11.8 | 17.0 | 4.8 | 13.2 | 26.7 | ||
|
| ||||||||
| Working model approach | ||||||||
|
| ||||||||
| Bias × 100 | −0.01 | −0.02 | −0.03 | 0.13 | 0.07 | 0.26 | ||
| Standard deviation × 100 | 0.33 | 0.38 | 0.53 | 1.03 | 1.05 | 2.22 | ||
| Coverage (%) | 96.1 | 97.5 | 97.2 | 95.8 | 95.5 | 94.5 | ||
| Bias × 100 | −0.01 | −0.02 | −0.02 | 0.11 | 0.09 | 0.25 | ||
| Standard deviation × 100 | 0.30 | 0.36 | 0.49 | 1.00 | 1.09 | 2.12 | ||
| Coverage (%) | 95.4 | 96.5 | 96.8 | 95.4 | 95.4 | 95.7 | ||
|
| ||||||||
| Bias × 100 | −0.01 | −0.02 | −0.03 | 0.05 | 0.02 | 0.11 | ||
| Standard deviation × 100 | 0.27 | 0.31 | 0.39 | 0.64 | 0.71 | 1.39 | ||
| Coverage (%) | 95.2 | 96.0 | 97.3 | 95.0 | 95.9 | 95.1 | ||
| Bias × 100 | −0.02 | −0.02 | −0.03 | 0.04 | 0.03 | 0.07 | ||
| Standard deviation × 100 | 0.24 | 0.27 | 0.34 | 0.63 | 0.73 | 1.36 | ||
| Coverage (%) | 94.6 | 96.2 | 97.4 | 95.0 | 94.8 | 95.2 | ||
|
| ||||||||
| Likelihood-based approach | ||||||||
|
| ||||||||
| Bias × 100 | 0.03 | 0.02 | 0.04 | 0.11 | 0.08 | 0.20 | ||
| Standard deviation × 100 | 0.26 | 0.31 | 0.40 | 0.65 | 0.71 | 1.39 | ||
| Coverage (%) | 95.5 | 95.4 | 94.4 | 94.5 | 94.2 | 93.7 | ||
| Bias × 100 | 0.02 | 0.03 | 0.05 | 0.10 | 0.10 | 0.21 | ||
| Standard deviation × 100 | 0.22 | 0.26 | 0.35 | 0.64 | 0.71 | 1.42 | ||
| Coverage (%) | 95.1 | 95.2 | 93.5 | 94.3 | 94.3 | 93.1 | ||
The performance of estimates of prevention efficacy based on an active-controlled trial with are shown in Table 2. When is large, prevention efficacy can be estimated with low bias and CIs with near-nominal coverage, even with external cohorts. For example, when PE is 0.6 against a 4.5 cases per 100 person-years placebo HIV incidence, with 10 external cohorts the bias is less than 0.01 and the nominal 95% CI for prevention efficacy has 93.2% coverage. However, with modest , prevention efficacy is estimated with larger bias and CIs slightly under-cover with . Fixing , modest generally yields prevention efficacy estimates with larger standard deviation. With high , prevention efficacy can be estimated with better precision when the placebo HIV incidence rate is higher, because incidences can be more precisely estimated when there are more events. With modest , however, the standard deviation is larger when the placebo HIV incidence is 3 or 6 cases per 100 person-years compared to 4.5. This is because, with moderate , the variability of the prevention efficacy estimate is largely dominated by the variability of the estimated counterfactual placebo HIV incidence, which is larger when the placebo HIV incidence is further from the mean HIV incidence across the external cohorts (illustrated in Figure 1). With , the standard deviations are similar for the working model and likelihood-based estimation approaches, although the CIs from the working model approach have slightly lower coverage in some cases. Similar performance is observed with logit-link functions (see Supplementary Table S3). Performance based on a smaller active-controlled trial with person-years follow-up is shown in Supplementary Table S4; standard deviations are larger but coverage rates and bias are only minimally worse.
Table 2.
Bias, standard deviation, and empirical coverage for estimates of prevention efficacy (PE) based on external cohorts used to estimate the association between HIV and an exposure biomarker with correlation . A total of person-years follow-up accrue in the active arm of the trial. Counterfactual placebo HIV incidence and true PE vary. Performance is shown for working model and likelihood-based estimation approaches, assuming log link function for marginal incidences.
| PE estimate | ||||||||
|---|---|---|---|---|---|---|---|---|
| HIV incidence (cases per 100 person-years) | 3 | 4.5 | 6 | 3 | 4.5 | 6 | ||
| Exposure marker incidence (cases per 100 person-years) | 7.1 | 11.8 | 17.0 | 4.8 | 13.2 | 26.7 | ||
|
| ||||||||
| Working model approach | ||||||||
|
| ||||||||
| 10 | Bias × 100 | −1.42 | −0.83 | −0.96 | −3.72 | −2.28 | −4.88 | |
| Standard deviation × 100 | 14.49 | 11.45 | 10.20 | 28.78 | 19.50 | 28.72 | ||
| Coverage (%) | 93.0 | 93.4 | 93.2 | 92.2 | 92.7 | 90.1 | ||
| 20 | Bias × 100 | −1.09 | −0.77 | −0.63 | −1.93 | −1.20 | −1.88 | |
| Standard deviation × 100 | 13.55 | 10.58 | 9.20 | 19.89 | 14.38 | 18.24 | ||
| Coverage (%) | 92.5 | 93.4 | 93.1 | 93.0 | 94.4 | 92.7 | ||
|
| ||||||||
| 10 | Bias × 100 | −0.70 | −0.23 | −0.53 | −2.08 | −1.11 | −2.81 | |
| Standard deviation × 100 | 10.03 | 7.97 | 7.03 | 17.51 | 12.04 | 16.99 | ||
| Coverage (%) | 93.3 | 93.1 | 93.8 | 92.6 | 93.6 | 90.8 | ||
| 20 | Bias × 100 | −0.46 | −0.33 | −0.42 | −1.04 | −0.44 | −1.05 | |
| Standard deviation × 100 | 9.49 | 7.47 | 6.56 | 12.63 | 9.45 | 11.1 | ||
| Coverage (%) | 93.3 | 93.8 | 93.9 | 93.8 | 93.7 | 93.3 | ||
|
| ||||||||
| 10 | Bias × 100 | −0.33 | −0.21 | −0.22 | −1.14 | −0.62 | −1.19 | |
| Standard deviation × 100 | 7.48 | 5.95 | 5.29 | 11.80 | 8.30 | 10.38 | ||
| Coverage (%) | 93.3 | 93.9 | 93.6 | 93.0 | 92.9 | 91.9 | ||
| 20 | Bias × 100 | −0.17 | −0.17 | −0.20 | −0.53 | −0.36 | −0.48 | |
| Standard deviation × 100 | 7.18 | 5.80 | 5.03 | 8.91 | 6.65 | 7.49 | ||
| Coverage (%) | 93.4 | 93.7 | 93.7 | 94.0 | 94.3 | 93.6 | ||
|
| ||||||||
| Likelihood-based approach | ||||||||
|
| ||||||||
| 20 | Bias × 100 | 0.08 | −0.11 | 0.04 | −0.62 | −0.64 | −1.04 | |
| Standard deviation × 100 | 12.36 | 9.90 | 8.90 | 18.55 | 13.83 | 18.02 | ||
| Coverage (%) | 94.9 | 95.0 | 93.9 | 93.8 | 94.3 | 92.8 | ||
|
| ||||||||
| 20 | Bias × 100 | −0.20 | −0.29 | 0.10 | −0.31 | 0.04 | −0.26 | |
| Standard deviation × 100 | 8.83 | 7.27 | 6.30 | 11.80 | 9.06 | 10.92 | ||
| Coverage (%) | 95.3 | 94.8 | 94.5 | 94.3 | 94.6 | 93.0 | ||
|
| ||||||||
| 20 | Bias × 100 | −0.16 | 0.00 | −0.05 | −0.20 | −0.03 | −0.54 | |
| Standard deviation × 100 | 6.81 | 5.48 | 4.86 | 8.44 | 6.55 | 7.38 | ||
| Coverage (%) | 95.3 | 95.5 | 95.1 | 94.7 | 94.3 | 94.4 | ||
We evaluate power for testing prevention efficacy with this approach compared to a placebo-controlled trial (see Supplementary Figures S1 and S2 for simulation results. Surprisingly, we find power for the counterfactual approach may exceed that obtained from a placebo-controlled trial with the same active arm size. For example, 74% power to detect prevention efficacy of 0.6 can be obtained with 3 cases per 100 person-years placebo HIV incidence, active arm size of 2000 person-years, a highly correlated marker () and 10 external cohorts, while a standard 1:1 placebo-controlled trial with sample sizes of 2000 person-years for both experimental and placebo arms has less than 70% power. The reason is incidence of the exposure marker is much higher than that of HIV, so it can be estimated with better precision than HIV incidence. Therefore, with a highly correlated exposure marker, HIV incidence can be estimated more precisely by leveraging information in the higher-incidence exposure marker.
We evaluate scenarios where the conditional independence assumption in (4) is violated;the estimated incidences are correlated conditional on the true incidences. Performance is similar to that under the conditional independence model (4)(see Supplementary Materials). Further, we assess performance with external cohort data analyzed at the sub-cohort-level, reflecting that site-level data may be available for multi-center studies (Supplementary Tables S7). Given a fixed total sample size across external cohorts, more cohorts of smaller sizes are preferred to fewer cohorts of larger size.
Application
We apply the estimation to the DISCOVER trial, a randomised, double-blinded, double-dummy, active-controlled trial that compared the efficacy of coformulated tenofovir alafenamide plus emtricitabine and tenofovir disoproxil fumarate plus emtricitabine for preventing HIV in men and transgender women who have sex with men.6 The US FDA approved tenofovir alafenamide plus emtricitabine for men and transgender women who have sex with men based on the trial results.36 Rectal gonorrhea infections were captured in both arms.37 Collectively, 1313 rectal gonorrhea cases were observed over 6243 person-years, implying a rectal gonorrhea incidence of 21.0 cases per 100 person-years. Historical data suggest that oral anti-retrovirals do not have biological effects on rectal gonorrhea incidence.38
Table 3 contains point estimates and 95% CIs for counterfactual placebo HIV incidence using likelihood-based and working model estimation, assuming log and logit-link functions in the bivariate linkage model (2), based on previously-reported cohorts reporting both HIV and rectal gonorrhea incidence for men who have sex with men24 (see Supplementary Table S1). The estimated counterfactual placebo HIV incidences are approximately 7 cases per 100 person-years for both estimation approaches and link functions. A naive analysis that assumes an identity link and treats estimated HIV and rectal gonorrhea incidence rates as fixed and known, similar to what is done in the applied literature, gives a lower counterfactual HIV incidence estimate of 6.6 cases per 100 person-years.
Table 3.
Estimated counterfactual placebo HIV incidence (cases per 100 person-years), and corresponding 95% confidence intervals (CIs) for the DISCOVER study. Uncertainty is quantified by 95% confidence intervals except for Bayesian estimates where *95% and +80% credible intervals (CrIs) are reported.
| Link function | Estimation approach | Est. | 95% CI (CrI∗+) |
|---|---|---|---|
|
| |||
| Log | Likelihood-based | 7.10 | (5.02, 10.03) |
| Working model | 7.06 | (5.25, 9.49) | |
|
| |||
| Logit | Likelihood-based | 6.94 | (4.82, 9.88) |
| Working model | 6.87 | (5.08, 9.23) | |
|
| |||
| Identity | Naive approach24 | 6.60 | n.a. |
|
| |||
| Bayesian Gamma-Copula15 | 4.51 | (2.06, 7.36)∗ | |
| Bayesian case-cohort sampling39 | 3.4 | (1.9, 5.9)+ | |
We compare the results with those from15,39 who applied Bayesian approaches with Gamma-Copula models and case-cohort sampling adjustment to the DISCOVER study. Posterior estimates of counterfactual placebo HIV incidence from the two Bayesian approaches are much lower at 4.51 and 3.4 cases per 100 person-years. We conjecture that the lower estimates are due in part to the chosen prior HIV incidence rate (mean of 2.9 cases per 100 person-years) in,15 which was lower than the average incidence across the external cohort studies.
Another difference in the latter estimate is its reliance on an additional data source, namely historical estimates of efficacy.
Given the estimated 0.16 HIV diagnosis cases per 100 person-years from the tenofovir alafenamide plus emtricitabine arm,6 the estimated prevention efficacy for tenofovir alafenamide plus emtricitabine vs. counterfactual placebo is 98.1% (95% CI: 96.4% to 99.4%), based on the working model and log link, and 98.1% with the likelihood-based estimation (95% CI: 96.4% to 99.7%). This prevention efficacy inference is simple to interpret and supports tenofovir alafenamide plus emtricitabine effectiveness.
Conclusions
Advancing HIV prevention, and ultimately stemming the HIV pandemic, requires additional biomedical interventions. While active-controlled trials will likely be used in future trials evaluating candidate interventions, absolute efficacy of the experimental intervention cannot be evaluated based on the trial data alone. If a marker of HIV exposure is measured in the trial, and external data are leveraged to model the association between HIV and the exposure marker, under Assumptions 1–3 HIV incidence in a counterfactual placebo arm, and prevention efficacy of the experimental intervention relative to the counterfactual placebo, can be estimated reliably and precisely.
Importantly, we considered performance of the approach when Assumptions 1 and 3 hold, and Assumption 2 either holds or is slightly violated. These are strong and not fully testable assumptions that deserve careful attention. For one, correct specification of the model linking HIV incidence with the exposure marker is challenging. Mis-specification may be due to omission of covariates that modify the association, incorrect model form, or measurement error of variables. Recent work demonstrates that the rectal gonorrhea and HIV incidence association may differ across populations,40 and is difficult to model accurately across cohorts.14,29–31
While standard statistical methods may check for specific types of model mis-specification, with few external cohorts the power to detect model mis-specification is low. Given some of the assumptions are not fully testable, further research is needed into methods for incorporating uncertainty due to violation of these assumptions.
Our findings suggest that more cohorts of smaller size provide more precise inference than fewer cohorts of larger size. Accuracy and precision may be further improved with individual-level data. As well, with only study-level data from external cohorts the correlation between reported HIV and the exposure marker incidences in the external cohorts is rarely available. Accordingly, our estimation approaches assume conditional independence of HIV incidence and the exposure marker. Our simulation study suggests a degree of robustness to violation of this assumption, mainly because between-study variation dominated with-in study variation. Similar results were found for bivariate meta-analysis.41 However, as discussed in,41 ignoring within-study correlation is expected to yield estimates with inferior statistical properties. Given individual-level data from external cohorts, estimation of the conditional dependence parameter would be feasible and performance improved.
We call for additional research, with application held until such research is conducted. Evaluation of the approach’s performance in HIV prevention trials that included placebo arms is needed to gauge the ‘real world’ accuracy of the counterfactual placebo estimation. Individual- or trial-site-level data from recent HIV prevention trials, with incidence of other sexually transmitted infections captured, should be made public to enable further evaluation of the correlation between HIV and other sexually transmitted infections as potential exposure markers. Finally, HIV exposure markers that more readily satisfy the assumptions we detail should be pursued; markers more fundamentally linked to HIV exposure may be needed to realize the potential.
We did not find existing statistical frameworks that provided a good fit for our problem.42–44 The exposure marker we considered is different from a surrogate marker for which the effect of the intervention on the surrogate reflects the effect of the intervention on the primary endpoint..42,45 The framework we developed may have application to other clinical contexts where a proxy outcome is associated with the clinical outcome under the control condition, but is not impacted by the intervention, and a body of data is available for estimating the association between proxy and clinical outcome under the control condition.
Supplementary Material
Funding
This work was supported by the National Institutes of Health/National Institute of Allergy and Infectious Diseases (NIH/NIAID) through grants R01CA152089, R56AI143418 and UM1AI068635 to HJ, and R01AI143357 to DVG.
Footnotes
Declaration of conflicting interests
DVG has accepted fees from Gilead Sciences. Other author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
References
- 1.Saag MS, Gandhi RT, Hoy JF, et al. Antiretroviral Drugs for Treatment and Prevention of HIV Infection in Adults. JAMA 2020;324:1651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Chou R, Evans C, Hoverman A, et al. Preexposure Prophylaxis for the Prevention of HIV Infection. JAMA 2019;321:2214. [DOI] [PubMed] [Google Scholar]
- 3.Baeten JM, Palanee-Phillips T, Brown ER, et al. Use of a Vaginal Ring Containing Dapivirine for HIV-1 Prevention in Women. New England Journal of Medicine 2016;375:2121–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Nel A, Niekerk N van, Kapiga S, et al. Safety and Efficacy of a Dapivirine Vaginal Ring for HIV Prevention in Women. New England Journal of Medicine 2016;375:2133–43. [DOI] [PubMed] [Google Scholar]
- 5.Harel C, Coll J, Ruane P, et al. The Phase 3 Discover Study: Daily F/TAF or F/TDF for HIV Preexposure Prophylaxis. Abstract number 104 http://www.croiconference.org/sessions/phase-3-discover-study-daily-ftaf-or-ftdf-hiv-preexposure-prophylaxis 2019.
- 6.Mayer KH, Molina JM, Thompson MA, et al. Emtricitabine and tenofovir alafenamide vs emtricitabine and tenofovir disoproxil fumarate for HIV pre-exposure prophylaxis (DISCOVER): primary results from a randomised, double-blind, multicentre, active-controlled, phase 3, non-inferiority trial. Lancet 2020;396:239–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Landovitz RJ, Donnell D, Clement ME, et al. Cabotegravir for HIV Prevention in Cisgender Men and Transgender Women. New England Journal of Medicine 2021;385:595–608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Delany S. Long acting injectable cabotegravir is safe and effective in preventing HIV infection in cisgender women: interim results from HPTN 084. Abstract number HY01.02 https://programme.hivr4p.org/Abstract/Abstract/1479 2021.
- 9.The Joint United Nations Programme on HIV/AIDS. Global HIV and AIDS statistics — 2021 fact sheet. http://www.unaids.org/en/resources/fact-sheet 2021. (Cited Mar 2021).
- 10.Sugarman J. Bioethical Challenges with HIV Treatment as Prevention. Clin Infect Dis 2014;59:S32–S34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Knight R, Small W, Thomson K, et al. Implementation Challenges and Opportunities for HIV Treatment as Prevention (Tasp) among Young Men in Vancouver, Canada: A Qualitative Study. BMC Public Health 2016;15:262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.AIDS Vaccine Advocacy Coalition. The Future of ARV-Based Prevention and More. https://www.avac.org/infographic/future-arv-based-prevention 2022.
- 13.World Health Organization. Ethical considerations in HIV prevention trials. https://www.unaids.org/sites/default/files/media asset/ethical-considerations-hiv-prevention-trials_en.pdf 2021.
- 14.Glidden DV. Advancing Novel PrEP Products - Alternatives to Non-Inferiority. Stat Commun Infect Dis 2019;11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Glidden DV, Stirrup OT, and Dunn DT. A Bayesian averted infection framework for PrEP trials with low numbers of HIV infections: application to the results of the DISCOVER trial. The Lancet HIV 2020;7:e791–e796. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.James Hung HM, Wang SJ, Tsong Y, et al. Some Fundamental Issues with Non-inferiority Testing in Active Controlled Trials. Stat Med 2003;22:213–25. [DOI] [PubMed] [Google Scholar]
- 17.Fleming TR. Current Issues in Non-inferiority Trials. Stat Med 2008;27:317–32. [DOI] [PubMed] [Google Scholar]
- 18.Grobler AC and Abdool Karim SS. Design challenges facing clinical trials of the effectiveness of new HIV-prevention technologies. AIDS 2012;26:529–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Cutrell A, Donnell D, Dunn DT, et al. HIV prevention trial design in an era of effective pre-exposure prophylaxis. HIV Clin Trials 2017;18:177–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hanscom B, Hughes J, Williamson B, et al. Adaptive Non-inferiority Margins Under Observable Non-constancy. Statistical Methods in Medical Research 2019;28:3318–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Corey L, Gilbert PB, Juraska M, et al. Two Randomized Trials of Neutralizing Antibodies to Prevent HIV-1 Acquisition. New England Journal of Medicine 2021;384:1003–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Corey L, Gilbert PB, Tomaras GD, et al. Immune correlates of vaccine protection against HIV-1 acquisition. Science Translational Medicine 2015;7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Gilbert PB, Huang Y, deCamp AC, et al. Neutralization titer biomarker for antibody-mediated prevention of HIV-1 acquisition. Nature Medicine 2022;28:1924–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Mullick C and Murray J. Correlations between HIV infection and rectal gonorrhea incidence in men who have sex with men: Implications for future HIV pre-exposure prophylaxis trials. J. Infect. Dis 2019. [DOI] [PubMed] [Google Scholar]
- 25.Murray J. Regulatory Perspectives for Streamlining HIV Prevention Trials. Stat. Comm. Infect. Dis 2019;11. [Google Scholar]
- 26.Murray J. Regulatory perspective for streamlining HIV prevention trials. TUSY0502 https://programme.ias2019.org/Programme/Session/11 2019.
- 27.Janes H, Donnell D, and Nason M. Designing the Next Generation of HIV Prevention Efficacy Trials: Synopsis of a 2018 Symposium. Statistical Communications in Infectious Diseases 2019;11. [Google Scholar]
- 28.Follmann D. Tomorrow’s HIV Prevention Trials of Vaccines and Antibodies. Statistical Communications in Infectious Diseases 2019;11. [Google Scholar]
- 29.Cohen MS and Donnell D. Novel Approaches for Development of Human Immunodeficiency Virus Preexposure Prophylaxis Agents. The Journal of Infectious Diseases 2019;221:172–4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Glidden DV. Statistical approaches to accelerate the development of long-acting antiretrovirals for HIV pre-exposure prophylaxis. Curr Opin HIV AIDS 2020;15:56–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Collaborative Research TF for. Public Meeting Webinar 3– Protocol Design Considerations: Analyses for Efficacy. In-Depth Webinar Report. Journal Article 2021. URL: https://forumresearch.org/storage/documents/HIV_Forum/Public_Meeting_Webinar_3_Report_Final_211027.pdf.
- 32.US Food and Drug Administration. Minutes for the August 7, 2019 Meeting of the Antimicrobial Drugs Advisory Committee. https://www.fda.gov/media/131002/download 2018.
- 33.Traeger MW, Cornelisse VJ, Asselin J, et al. Association of HIV Preexposure Prophylaxis With Incidence of Sexually Transmitted Infections Among Individuals at High Risk of HIV Infection. JAMA 2019;321:1380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Van Houwelingen H, Arends L, and Stijnen T. Advanced methods in meta-analysis: multivariate approach and meta-regression. Stat Med 2002;21:589–624. [DOI] [PubMed] [Google Scholar]
- 35.Reitsma JB, Glas AS, Rutjes AW, et al. Bivariate analysis of sensitivity and specificity produces informative summary measures in diagnostic reviews. Journal of clinical epidemiology 2005;58:982–90. [DOI] [PubMed] [Google Scholar]
- 36.Voelker R. PrEP drug Is approved for some patients but not for others. JAMA 2019;322:1644–4. [DOI] [PubMed] [Google Scholar]
- 37.Hare CB, Coll J, Ruane P, et al. The phase 3 DISCOVER study: daily F/TAF or F/TDF for HIV preexposure prophylaxis. In: Conference on retroviruses and opportunistic infections. International Antiviral Society Seattle, Washington. 2019:4–7. [Google Scholar]
- 38.Grant RM, Lama JR, Anderson PL, et al. Preexposure Chemoprophylaxis for HIV Prevention in Men Who Have Sex With Men. N Engl J Med 2010;363:2587–99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Glidden DV, Das M, Dunn DT, et al. Using the adherence-efficacy relationship of emtricitabine and tenofovir disoproxil fumarate to calculate background hiv incidence: a secondary analysis of a randomized, controlled trial. Journal of the International AIDS Society 2021;24:e25744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Donnell D, Zewdie K, Ratna N, et al. Association between rectal gonorrhoea and HIV incidence in men who have sex with men: a meta-analysis. Sexually Transmitted Infections 2021:2021–55254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Riley RD. Multivariate meta-analysis: the effect of ignoring within-study correlation. Journal of the Royal Statistical Society: Series A (Statistics in Society) 2009;172:789–811. [Google Scholar]
- 42.Fleming TR and Powers JH. Biomarkers and surrogate endpoints in clinical trials. Statistics in Medicine 2012;31:2973–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Tchetgen ETT, Ying A, Cui Y, et al. An Introduction to Proximal Causal Learning. arXiv 2020;arXiv:2009.10982. [Google Scholar]
- 44.Arnold BF and Ercumen A. Negative Control Outcomes. JAMA 2016;316:2597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Temple R. A regulatory authority’s opinion about surrogate endpoints. Clinical measurement in drug evaluation 1995:1–22. [Google Scholar]
- 46.Nadarajah S and Dey DK. On the product and ratio of t random variables. Applied Mathematics Letters 2006;19:45–55. [Google Scholar]
- 47.Nadarajah S. On the ratio X/Y for some elliptically symmetric distributions. Journal of Multivariate Analysis 2006;97:342–58. [Google Scholar]
- 48.Morris SR, Klausner JD, Buchbinder SP, et al. Prevalence and incidence of pharyngeal gonorrhea in a longitudinal sample of men who have sex with men: the EXPLORE study. Clinical Infectious Diseases 2006;43:1284–9. [DOI] [PubMed] [Google Scholar]
- 49.Jin F, Prestage GP, Imrie J, et al. Anal sexually transmitted infections and risk of HIV infection in homosexual men. JAIDS Journal of Acquired Immune Deficiency Syndromes 2010;53:144–9. [DOI] [PubMed] [Google Scholar]
- 50.Molina JM, Capitant C, Spire B, et al. On-Demand Preexposure Prophylaxis in Men at High Risk for HIV-1 Infection. N Engl J Med 2015;373:2237–46. [DOI] [PubMed] [Google Scholar]
- 51.Castillo R, Konda KA, Leon SR, et al. HIV and sexually transmitted infection incidence and associated risk factors among high-risk MSM and male-to-female transgender women in Lima, Peru. JAIDS Journal of Acquired Immune Deficiency Syndromes 2015;69:567–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Kelley CF, Vaughan AS, Luisi N, et al. The effect of high rates of bacterial sexually transmitted infections on HIV incidence in a cohort of black and white men who have sex with men in Atlanta, Georgia. AIDS research and human retroviruses 2015;31:587–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.McGowan I, Cranston RD, Mayer KH, et al. Project gel a randomized rectal microbicide safety and acceptability study in young men and transgender women. PLoS One 2016;11:e0158310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.McCormack S, Dunn DT, Desai M, et al. Pre-exposure prophylaxis to prevent the acquisition of HIV-1 infection (PROUD): effectiveness results from the pilot phase of a pragmatic open-label randomised trial. The Lancet 2016;387:53–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Girometti N, Gutierrez A, Nwokolo N, et al. High HIV incidence in men who have sex with men following an early syphilis diagnosis: is there room for pre-exposure prophylaxis as a prevention strategy? Sexually Transmitted Infections 2017;93:320–2. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.