Abstract
Quantum reservoir computing (QRC) has been proposed as a paradigm for performing machine learning with quantum processors where the training takes place in the classical domain, avoiding the issue of barren plateaus in parameterized-circuit quantum neural networks. It is natural to consider using a quantum processor based on microwave superconducting circuits to classify microwave signals that are analog—continuous in time. However, while there have been theoretical proposals of analog QRC, to date QRC has been implemented using the circuit model—imposing a discretization of the incoming signal in time. In this paper we show how a quantum superconducting circuit comprising an oscillator coupled to a qubit can be used as an analog quantum reservoir for a variety of classification tasks, achieving high accuracy on all of them. Our work demonstrates processing of ultra-low-power microwave signals within our superconducting circuit, a step towards achieving a quantum sensing-computational advantage on impinging microwave signals.
Subject terms: Quantum information, Information theory and computation
Quantum reservoir computing might in principle give advantages in solving signal classification tasks, but current implementations usually incur in the digitalization bottleneck. Here, the authors demonstrate an implementation dealing directly with the analogue MW signals.
Introduction
Over the last decade, researchers in quantum information processing have broadly divided their efforts into two distinct but complementary directions. In one, the focus has been on realizing the building blocks for large-scale, fault-tolerant quantum processors1–3, which would enable running algorithms such as Shor’s or Grover’s at meaningful scale. In the other, there has been a push to realize quantum systems comprising tens to hundreds of qubits or qumodes, but without error correction, and to explore what can be done with such noisy, pre-fault-tolerance systems—often denoted as noisy, intermediate-scale, quantum (NISQ) devices4. Quantum computational supremacy with such NISQ devices has been demonstrated5,6, but there has been much less progress on achieving quantum advantage in practically relevant applications7. There have been many NISQ studies on quantum machine learning8, and in this area too, quantum advantage for problems of broad practical interest has remained elusive9,10. A key challenge in quantum neural networks realized with parameterized quantum circuits has been training the parameters when the optimization landscape suffers from barren plateaus11–14. A major open question is whether one can achieve any practically relevant advantage for machine learning with NISQ systems.
Inspired by the framework of reservoir computing15–18 in classical machine learning, quantum reservoir computing (QRC)19–24 has emerged as an approach to quantum machine learning that entirely avoids barren plateaus by performing all learning in a final, linear layer. They key idea of a QRC is that a quantum system (called a quantum reservoir) can generate nonlinear, high-dimensional features of inputs to it, and that these features can be used to perform machine-learning tasks purely by training a classical linear transformation. However, experimental demonstrations to date have been performed with digital quantum circuits25–31 that have limited the complexity of tasks that can be performed, in part due to an input bottleneck imposed by the use of discrete gates to input temporal data using a series of separate, imperfect gates.
In this work, we demonstrate a proof-of-principle for a new application of and approach to quantum machine learning with NISQ devices that overcomes or sidesteps the challenges in training and inputs noted above. We use the driven, continuous-time analog quantum nonlinear dynamics of a superconducting microwave circuit as a quantum reservoir to generate features for classifying weak, analog microwave signals (Fig. 1a). We use repeated measurements of the reservoir both to extract features that contain information about temporal correlations in the input data, as well as to induce non-unitary dynamics. Our use of a continuous-variable system in our quantum reservoir grants us access to a substantially larger Hilbert space than would be the case with a qubit-only system with equally many hardware components. Our approach is similar to proposals for analog NISQ processors and simulators32–34, which aim to avoid the overhead caused by imposing a discrete-time abstraction. Analog operation grants us an even more important ability however, which fundamentally distinguishes our work from prior experimental demonstrations of quantum machine learning on circuit-model quantum processors: it allows our device to directly, natively receive weak analog microwave signals, and to immediately leverage analog quantum information processing to extract relevant features of the signals for classification. Our experiments do not address the question of whether a QRC can achieve a quantum computational advantage, since our experimental device is small enough to be easily simulated classically. However, our demonstrations suggest a route to achieving a quantum advantage of a different kind: an advantage in the quantum detection and processing of weak microwave signals, allowing quantum hardware to extract complex information of interest from dim, analog signals in ways that would be noisier with a conventional classical approach. This type of quantum advantage, arising from a combination of quantum sensing with extraction of complex features about the sensed signal, is discussed in general terms as a route to quantum advantage with quantum machine learning in Ref. 10. Our work shows that when classical signals comprising just a few photons have entered an analog quantum reservoir, they can be classified using our QRC approach. The signals we classify are synthesized at room temperature and pass through 60 dB of attenuation before reaching our device. However, if instead one combines this analog quantum processing with a sensitive quantum detector of microwave radiation, as has already been previously demonstrated using superconducting circuits35–39, then one can construct a system that achieves a quantum advantage in the task of combined sensing and signal processing of ultra-low-power impinging microwave signals.
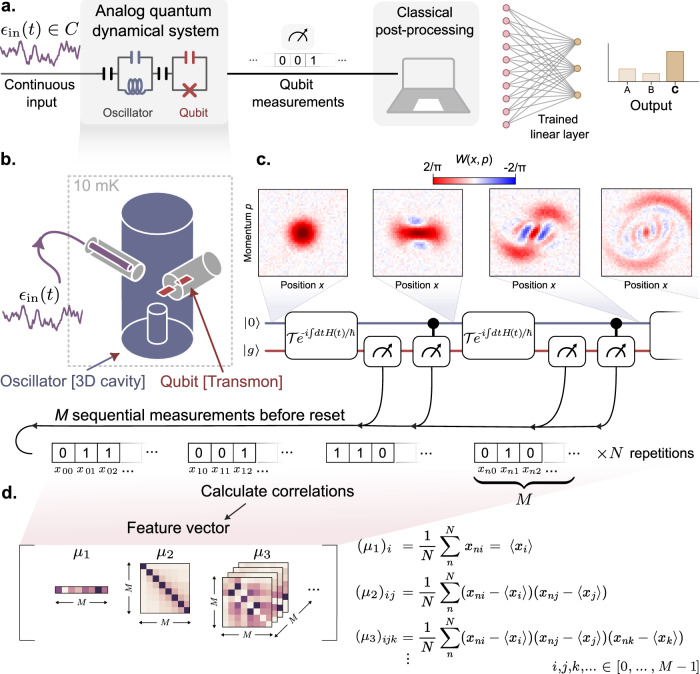
Fig. 1. Analog signal classification with a continuous-variable quantum reservoir computer (QRC) using measurement trajectories.
a We perform machine learning using a quantum system consisting of an oscillator coupled to a qubit. Analog signals are fed into our analog quantum dynamical system, continually displacing the oscillator mode while the qubit is projectively measured. The measurement trajectories provide complex features a digital linear layer can use to perform classification on a variety of tasks. b The signals interface directly with the qubit-oscillator system, composed of a 3D aluminum cavity (blue) hosting a transmon qubit (red) and a readout resonator (omitted for clarity; Supplementary Fig. 1). c Wigner tomography performed on the oscillator state through various stages of the reservoir dynamics. The dynamics include entanglement-generating unitary evolution, and projective measurements of both the qubit and oscillator. The back-action produced by the measurements add to the non-classical features generated by the entangling unitaries. The balance of measurements and unitaries, which do not commute with each other in our implementation, lead to complex correlations in the measurement trajectories. d The digital linear layer performs classification based on a feature vector, which we construct using the expectation values of the central moments μp (p = 1, 2, 3, …), which capture the essential correlations in the reservoir dynamics.
Results
Experimental setup and protocols
Our quantum reservoir, composed of a cavity resonator coupled to a transmon (Fig. 1b), can be modeled with the following qubit-oscillator Hamiltonian in the rotating-frame,
| 1 |
where and define the qubit subspace of the transmon, a is the photon annihilation operator of the oscillator mode, and χ is the nonlinear interaction strength (see Supplementary Note 2 for details). The third term of Eq. (1) describes the unitary control of the qubit with a time-dependent drive Ω(t), and the second term describes both the encoding of the input data ϵin(t), and unitary control of the oscillator mode, i.e., ϵ(t) = ϵin(t) + ϵcontrol(t). Equation (1) describes the unitary dynamics, which is complemented by non-unitary dynamics generated by the back-action from qubit measurements interspersed throughout the evolution.
The oscillator and qubit control drives used in this paper realize a reservoir that consists of a series of entangling unitaries interleaved with qubit and oscillator measurements (Fig. 1c). The analog input is sent resonantly to the cavity and results in a time varying conditional displacement of the oscillator, which streams in concurrently with control drives. The cavity resonator hosting the oscillator mode has a resonance frequency of 6 GHz and a 2-kHz linewidth. The combination of the input and control drives implement a unitary that encodes the input into the state of the oscillator and generates entanglement between the qubit and the oscillator. Following the unitary evolution, we perform a qubit measurement, and then a parity measurement of the oscillator state40,41 (see Supplementary Fig. 8). The parity measurement projects the oscillator state into super-positions of either even or odd Fock states, a highly non-Gaussian measurement allowing one to sense changes in the photon-number distribution. Additionally, the entangling dynamics between the measurements effectively implement a sequence of non-commuting measurements (see Supplementary Note 2), generating correlated measurement distributions that can then be used as complex output features. Finally, after four rounds of applying the unitary and the qubit-oscillator measurements, we reset the system before repeating the scheme so that we may collect many samples of the measurement trajectory. The reset, which occurs at a rate much faster than the decoherence rate of the oscillator, additionally ensures that our system remains coherent.
The measurement outcomes are used to construct output feature vectors to be fed into the linear layer, but this can be done in a few different ways. When performing repeated measurements on our system, we generate a sample bitstring of length M describing the quantum trajectory over M measurements. After M measurements are performed, we reset the system and repeat the procedure, each time generating a bitstring , where n refers to the nth sample (Fig. 1c). The outcomes can be counted to directly form a sample probability distribution over measurement trajectories, which can then be used as a high-dimensional output feature vector after obtaining a sufficient number of samples N. While this approach has the benefit of capturing all information in the measurement distribution31, it can generally suffer from poor scaling in sampling noise, requiring N ~ 2M shots in the worst case42.
Here, we construct an output feature vector from estimates of successive central moments μ1, μ2, μ3, … of the underlying distribution (Fig. 1d). For example, the first-order central moment μ1 is a M-dimensional vector representing the average over all measured bitstrings, i.e. μ1 = [〈xn0〉, 〈xn1〉, …], the second-order central moment μ2 is the covariance matrix with elements , and so on. Here, the expectation value is taken over the sample index n. This approach, inspired by Ref. 17, has the benefit of leveraging the hierarchy of noise in the central moments, while capturing the essential correlations in the dynamics to achieve high accuracy even in the few-sample regime. Furthermore, the output feature vector dimension only scales polynomially with the number of measurements, where the highest polynomial power is given by the order of the highest central moment, which we restrict to 3 for all tasks in this work. Finally, given finite memory in our reservoir, we further restrict the output vector by choosing to only calculate correlations between measurements at most 3 measurements apart. These truncated moments are then flattened and concatenated to construct our output feature vectors. In all, for the M = 8 measurements we use in this work, the resultant output feature vector size with this prescription is 94. For a detailed discussion of the construction of our reservoir output features with comparisons of different encodings, see Supplementary Note 4.
Classification of time-independent signals
To illustrate the scheme proposed in this work, we begin with an example classification using our quantum reservoir by performing binary classification task of time-independent signals. Figure 2a describes the control drives in more detail. For time-independent input data, the two-dimensional input data is encoded as the I and Q quadratures of an analog signal resonant with the cavity resonance frequency. In the rotating frame of the system (Eq. (1)), this is effectively a time-independent signal, i.e. ϵin(t) = ϵin = I + Q, which results in a displacement of the oscillator state. For such time-independent tasks, the signal bandwidth is set by its duration which, in general, can make the resultant displacement conditioned on the qubit state due to the cross-Kerr interaction (see first term of Eq. (1)).
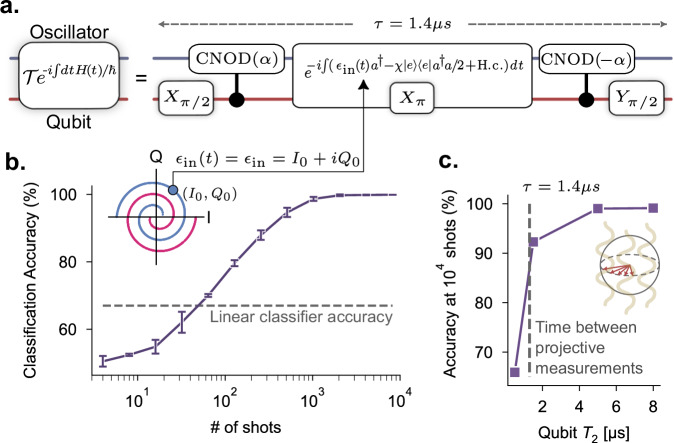
Fig. 2. Reservoir protocol overview with an example time-independent classification task.
a The unitary dynamics in our reservoir are generated by control pulses that serve to entangle the qubit with the oscillator before the analog input is received by the oscillator. For tasks where the analog data is time-independent, the dynamics are fully gate-based, and the oscillator is dis-entangled with the qubit before the qubit and oscillator measurements. For details of the motivation behind the particular unitaries implemented for our reservoir, see Supplementary Note 2. b (Inset) An illustrative machine learning example is the classification of time-independent signals from two arms of a Spiral distribution defined in the signal I − Q plane. For quantum machine learning, unlike classical, the performance is unavoidably impacted by sampling noise. Here, we plot the classification accuracy of the spiral task against an increasing number of shots. Also plotted is the performance of a linear layer acting directly on the two-dimensional I, Q data, indicating that non-linearity is required to perform this task with sufficient accuracy. c Classification accuracy at 104 shots as a function of qubit coherence time that we tune via resonator-induced dephasing during the classification (see Supplementary Fig. 9). The errorbars indicate the error in classification accuracy over the testing dataset. While we see a large drop in classification performance when the qubit coherence time is heavily suppressed and the system is completely disentangled, the performance only begins to suffer once the qubit T2 approaches the duration between measurements.
The unitary encoding the input displacement is complimented by control drives that entangle the qubit and oscillator via conditional displacements43 and qubit rotations (Fig. 2a). The entangling conditional displacements are applied before and after the unknown input is fed into the system, and the qubit is rotated by π or π/2 pulses before, during, and after the input. Due to the qubit-state-dependent shift of the oscillator frequency by − χ, these qubit rotations serve to make the oscillator sensitive to the input signal independent of the state of the qubit at the start of each round of input. Additionally, when combined with conditional displacements on the oscillator, the control and input scheme impart a geometric area enclosed by the oscillator trajectory onto the qubit, such that the phase of an unknown time-independent input signal can be extracted via a qubit measurement (see Supplementary Note 2 for details of this unitary). In Supplementary Note 7, we show the ability of the set of unitaries implemented here to be able to approximate any scalar function of the input signal when the signal is time-independent. For all results presented, we implement our reservoir unitary with these control drives across all tasks, with 4 applications of the unitary interleaved with qubit and oscillator-parity measurements.
The binary classification task we perform here is: Two distributions of time-independent signals, completely characterized by the signal’s in-phase (I) and quadrature (Q) components, are distributed along two separate “arms of a spiral” in the I − Q plane (Fig. 2b). Given a displacement described by the points I and Q sampled from either signal distribution, one must figure out which distribution the signal came from. The maximum amplitude of the input signal distribution (i.e. the points in the spiral arms furthest away from the origin in Fig. 2b) was chosen such that the amount of displacement of the oscillator state initialized in vacuum would result in a coherent state with photons per round of input ( ~ 1 μs). This input amplitude was needed in order to perform the classification with sufficient accuracy in a reasonable amount of shots. Our QRC solved the spiral classification task with > 97% accuracy at 103 shots (Fig. 2b). This simple task has the feature that, if one feeds in the inputs directly into a linear layer, the classification accuracy would reach no more than 67%—just above the random guessing accuracy of 50%. As a point of comparison with non-linear digital reservoirs, we found that a 64-dimensional, two-layer digital reservoir was needed to achieve the same performance as our quantum reservoir for this task (see Supplementary Note 8 for details of this comparison).
To probe the role of quantum coherence in our reservoir, we performed the same classification task, but with reduced coherence time in the qubit during the reservoir execution (Fig. 2c). This was achieved by populating the lossy readout resonator with photons that send the qubit to the center of the Bloch-sphere when the readout resonator is traced out (see Supplementary Fig. 9). With T2 → 0, we effectively removed all entanglement with the oscillator, and observed two things: a dramatic reduction in classification performance, and importantly, T2 only began affecting the performance once it was on the order of the reservoir duration, after which the qubit is projected to a pure state.
Classification of radio-frequency (RF) communication modulation schemes
Next, to highlight the ability to perform classification of higher dimensional data, we classified time-dependent radio-frequency (RF) signals. The microwave signals in this dataset encode digital information using one of 10 different digital modulation schemes, a standard benchmark task in RF machine learning44,45. Digital modulation schemes encode binary information in discrete ‘symbols’ encoding in sequential time-bins. For example, Binary Phase-Shift Keying (BPSK) encodes binary data in discrete phase jumps of a signal, such that a symbol 0 (1) maps to a phase flip of 0 (π). Other modulation schemes can encode more bits per symbol. BPSK and other encodings can be represented in a constellation diagram (Fig. 3a), which denotes the potential (I, Q) values a signal can take for each symbol. A given string of digital data can then be encoded in a time-domain signal by sequentially choosing points in the constellation diagram with a given symbol rate. For typical WiFi signals this is around 250 kHz per subchannel46.
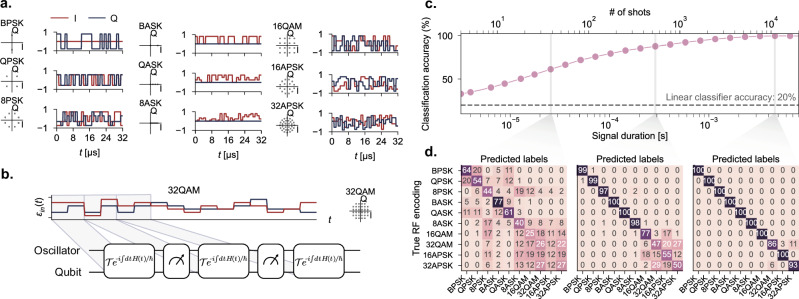
Fig. 3. Classification of radio-frequency (RF) communication modulation protocols.
a Description of the dataset for digital modulation schemes used in this experiment. In conventional digital modulation schemes, one encodes data in the amplitude and phase of the signal. The modulation schemes can be represented by a “constellation diagram” in (I, Q) space (left), where point represents one of the possible choice of (I, Q) values to encode a symbol, with example time traces (right). b These signals are broken up and fed into our reservoir. c The performance of the reservoir as a function of the shots taken in real time (see text). The top row contains the corresponding duration of the radio frequency signal required. As the number of shots increases, the fluctuations in the measurement distribution reduces, resulting in a higher classification accuracy. For context, a classical linear classifier applied directly on the input data achieves only 20% accuracy, independent of the duration of the signal. The error bars of the accuracy curve have been omitted here due to the fact they are too small. d Confusion matrix for the QRC at 32, 512, and 104 shots, showing that the reservoir confuses only a few classes at the highest shots.
For this task, we generated RF signals by encoding random digital strings into the 10 different modulation schemes with a fixed symbol rate of around 2 symbols per μs, or with a sampling rate of 2 MSps. The duration of these signals typically lasts much longer than the reset period of our system. Importantly, we did not repeat the same signal to artificially reduce the sampling noise associated with each input data, as this would not typically be applicable in a real-world setting. Instead, the measurement statistics were generated by sampling the signal in real time. Consequently, what we refer to as ‘shots’ in a real-time task does not correspond to identical repetitions of the experiment, but instead, is the number of resets we performed while acquiring the signal, which changed from shot to shot. In effect, each different encoding scheme produces a unique “fingerprint" distribution over measurement outcomes, and the goal of the linear layer is to separate these distributions with as high accuracy as possible.
Figure 3c shows the accuracy in classifying digitally modulated RF signals with increasing number of shots, compared with the performance of a linear classifier. We note that in less than a millisecond, or with less than 2000 symbols, the reservoir was able to classify which of the 10 classes a given signal belongs to with > 90% accuracy when using 8 qubit-oscillator measurements. A linear classifier can only achieve 20% classification accuracy for this task, even with infinite symbols. The confusion matrix between the different classes at 32, 512, and 104 shots is displayed in Fig. 3d, the latter two of which are nearly diagonal.
Classification of filtered noise
Finally, to demonstrate the performance of our QRC on continuous-time data, and with a task that requires both long-term and short-term memory in the quantum reservoir, we performed the following classification task: input data assumed to have come from a source of white noise is filtered using a moving-average filter having one of three filter shapes (Gaussian, Lorentzian and inverse-power-law), and one of two window widths (50 ns and 600 ns), and the task is to identify both the filter shape and window width (Fig. 4a). The resultant dataset consisting of six classes of noisy signals was designed to probe the ability of our QRC to process high dimensional data with bandwidths larger than the cavity linewidth. Additionally, this task allowed us to probe the memory of our QRC and its ability to be sensitive to fluctuations in time, a key feature that enable temporal signal processing in QRCs47,48. The filter functions were normalized so that the photon-number distributions generated by the time-dependent displacements are identical up to the filter width. This normalization was applied to ensure that the task is not trivially solvable by just measuring the mean photon number (see Supplementary Fig. 14).
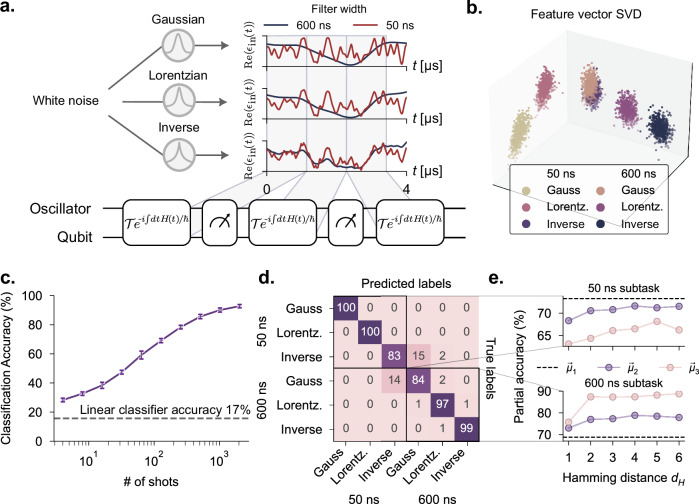
Fig. 4. Classification of filtered noise.
a We classify various fast and slow noisy signals by applying a moving average on stochastic white-noise signals. Three different filters are used for the moving averages: a Gaussian filter, a Lorentzian, and an inverse power law. For each filter, we generate stochastic analog signals based on both a 50 ns filter width, and a 600 ns filter width, with the latter being on the order of the measurement rate. Example time traces are given for the real part of an example stochastic white noise signal passed through each of the filters. We divide up these stochastic signals and send to the QRC to then distinguish the noise source. b Visualization of the high-dimensional output feature space using Singular Value Decomposition (SVD). Each point corresponds to a different signal over 2000 shots taken in real time (see text). c Classification accuracy as a function of the number of shots using third-order moments as the output feature. Our reservoir reaches 93% accuracy in about 2000 shots, corresponding to about 10 ms of the signal received. The errorbars here indicate the variation in the classification accuracy over the testing dataset. d Confusion matrix of the task taken at 2000 shots. e Participation of the mean and the off-diagonal elements of the second- and third-order moments in the classification accuracy within the subtasks of classifying different noise sources with fixed filter width. We see that for signals with long coherence times, higher-order measurement correlations are important, while for fast signals, the mean dominates in the performance contribution.
Because all the signals used in this dataset are noise with zero mean, a linear classifier would do no better than random guessing. By contrast, Fig. 4b visually shows (using Singular Value Decomposition (SVD) on the output feature space) that the quantum reservoir was able to peel apart the different noise distributions. On the task of classifying over six different sources of noise, we achieved 93% accuracy (Fig. 4c) in only 2000 shots. As seen in the confusion matrix in Fig. 4d, the primary confusion at 2000 shots was distinguishing between the 50-ns inverse-power-law noise class and the 600-ns Gaussian noise class, as expected from the overlap in the SVD of the feature space.
Finally, we compared the ability of our reservoir to understand long vs short correlations in input signals. For this, we deconstructed the 6-class classification task into two classification subtasks, where in each subtask, the QRC learned to distinguish noisy signals generated from among three different filter window types, but with fixed window widths. The two subtasks differ by the filter window width (see Fig. 4d, e). The class of signals with coherence length of 50 ns highlights the convenience of our input encoding scheme, i.e. feeding signals directly into the oscillator mode without the need to sample the signal discretely in time. Additionally, the ability for our quantum reservoir to distinguish between signals with correlation times on the order of 50 ns demonstrates the sensitivity to signals which vary on time-scales much faster than the measurement rate. In contrast, classification of the class of signals with coherence lengths of 600 ns requires correlations of the reservoir dynamics beyond that of the measurement rate. To highlight the advantage of our scheme, we simulated the performance of a reservoir with that of a recent gate-based protocol where the input was sampled discretely in time29. Our simulation results, in Supplementary Note 6, highlight the advantage of our protocol when the sampling rate of the input is slow, which can arise in experiment such as finite pulse durations and latency introduced by the FPGA classical comparison.
Figure 4e looks at the participation of the different moments μk of the measurements in the classification accuracy of the 50-ns subtask (top), and the 600-ns subtask (bottom). Here, the output features were constructed by the mean μ1, or the off-diagonal elements of the moments μ2 and μ3 as a function of the distance between measurements dH, allowing us to probe the contribution of the moments as a function of the locality of the correlations. For the 50-ns subtask, we see that the most important contribution is the mean, with the second-order moment being the next-most important contribution, and the third-order moment being relatively unimportant. In stark contrast, the third-order moment is most important for the 600-ns subtask, surprisingly yielding nearly 90% classification accuracy using non-local third-order correlations alone. The ability to distinguish stochastic signals among the combined six classes demonstrates the ability of our reservoir to capture both slow and fast features of microwave signals.
Discussion
In summary, we have experimentally realized an analog quantum reservoir computer (QRC) and demonstrated its ability to directly process microwave analog input signals without discretization, achieving high classification accuracy on three different tasks. Previous demonstrations of quantum reservoir computing have used multi-qubit, gate-based quantum reservoirs25–31. In contrast, we perform machine learning directly on analog signals fed into a single oscillator coupled to a transmon qubit. The superconducting-circuits platform not only allows us to leverage projective non-demolition (QND) non-Gaussian measurements to generate correlated output features, but is also well-matched to process microwave signals that can generally be continuous in time. In addition to demonstrating accurate classification of microwave signals in our experiments, we also performed a direct comparison with a state-of-the-art discrete-time, gate-based QRC approach in simulation, and found that a continuous-time reservoir outperforms a discrete-time reservoir when the input signals contain temporal variations fast relative to the discretization time (see Supplementary Fig. 16).
For any quantum neural network, including QRC approaches, a central concern is to what extent one can achieve high accuracy on a particular task without needing an impractical number of shots42. Ref. 31 recently reported that certain functions—termed eigentasks—can be constructed with low error from quantum reservoirs even when the number of shots is modest, giving evidence that for some tasks, sampling noise need not be overwhelming. In our experiments, we found that it was possible to achieve high accuracy for all the tasks we attempted while needing only 103–104 shots (depending on the task). There is important future work to be done in exploring the trade-offs between reservoir size (e.g., number of oscillators or qubits), number of measurements M between reservoir resets, feature-vector dimension (dependent both on M and the choice of order of correlators to include), and number of shots required for both training and inference.
With improved quantum hardware, we anticipate that it will be possible to carry out even more sophisticated tasks than what we have already demonstrated. Increasing the coherence time of the oscillator would enable us to perform many more measurements (the qubit’s coherence time is, favorably, less important in our scheme because our protocol involves repeatedly projectively measuring the qubit). While we analytically showed in Supplementary Note 7 the ability of our QRC to be able to approximate any scalar function of the input signal when the signal is time-independent, provided the number of measurements M performed is large enough, there remains the open theoretical question of the expressiveness of the QRC when the input signal is time-dependent. Generalizing our approach to spatial in addition to temporal inputs, as was explored in Ref. 24, would likely support more sophisticated computations. In Supplementary Note 6, we explore such extensions in simulations and find a marked improvement in classification accuracy.
It is an open question if QRC—using the type of reservoir we considered in this paper, or any other—can, when implemented with NISQ hardware, achieve a quantum computational advantage over the best classical machine learning approaches, just as it is unclear if any quantum-machine-learning method can10. We did not investigate the potential for purely computational quantum advantage: our quantum reservoir is small enough to be easily classically simulable. However, our work opens up the possibility to experimentally achieve a different type of quantum advantage than a purely computational one. If one performs quantum processing on data obtained by a quantum sensor, there is the potential for an advantage that is a hybrid of being due to the advantage of quantum sensing and of quantum computing10. Our work suggests the feasibility of concretely realizing this kind of hybrid quantum sensing-computational advantage, where the quantum sensor is a superconducting circuit that can detect classical microwave radiation with high quantum efficiency and low noise35–38. While the signals classified in this work originate at room temperature and are highly attenuated before reaching the device, our experiments have shown that it is possible to accurately classify signals using a superconducting circuit even when there are only a few photons of signal in the superconducting circuit within any single run. Combining this with a sensitive quantum detector could lead to quantum smart sensors—quantum versions of classical in-sensor processors49—that can reliably extract information from weak microwave signals in a way that exceeds the accuracy of any equivalent classical system.
Methods
Reservoir unitary
To design a good reservoir computer capable of performing machine learning on a variety of tasks, one needs to implement control drives that can efficiently capture important information of the input and perform a non-trivial and non-linear map to output features. Here, our reservoir is composed of alternating unitaries and measurements. The design of the former is motivated to harness the quantum properties of the dynamical system to generate entanglement and the design of the latter to generate non-linear operations on the state of our reservoir via measurement back-action. Here we summarize the control drives and measurements we use and their effect on the reservoir dynamics, both in the context of time-dependent and time-independent signals.
For time-independent signals, the unitary implemented in our reservoir (see Fig. 2b) can be approximated by the following set of unitaries (see Supplementary Note 2)
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
This combination of unitaries encloses a loop in the oscillator’s phase space. The area of this closed loop, which depends on the phase of the unknown displacement β, imparts a geometric phase onto the qubit. In this work, we perform this unitary directly after a qubit measurement without reset. The action of the combined unitary on the qubit prepared in the ground or excited state, and for an arbitrary oscillator state, is
| 9 |
| 10 |
| 11 |
where is the geometric phase enclosed by the oscillator trajectory, and dependent on the phase difference δ between a known displacement α, and the unknown displacement β. The probability of measuring the qubit in the excited state given it started out in the ground state, Pe∣g, and the probability of measuring excited given the qubit start in the excited state, Pe∣e are given by
| 12 |
The equation relates the qubit probability to the phase of the input displacement, which is otherwise challenging to extract in a setup with only qubit measurements.
For general time-dependent signals, the closed loop formed by Eqs. (2)–(8) is broken, and the system is entangled before the measurement. While this can be hard to study analytically in the general case, we take a look at a special case of time-dependent signals, namely those of Fig. 3. Here, the signal is time-dependent up to half the duration, so that the signal is effectively two time-independent signals combined. As a result, Eqs. (4) and (6) are no longer equal, but each still a time-independent displacement, and thus, the effects of the cross-Kerr, as discussed in Supplementary Note 2 do not hinder the interpretation of the effective gate-based model. For such input signals, the state of the system just before measurement is
| 13 |
where βi is the displacement just before the qubit flip (corresponding to Eq. (4) for this time-dependent set of tasks), and βj is the displacement after (Eq. (6)). Ai = αβi is the phase acquired after two non-orthogonal displacements. When βi = βj we recover the dynamics for time-independent signals.
Repeated measurements
The unitaries described above are followed by a qubit measurement, then a parity measurement. For time-independent signals, the qubit and oscillator are disentangled at the end of the unitary, and the effect of the unitary on the oscillator is just a displacement. Thus we can ignore any affects of the qubit measurement on the oscillator. The state of the oscillator after M repeated measurements and M time-independent displacements can be effectively described as
| 14 |
where is the projector of the nth parity measurement Π with measurement outcomes xn = { + , − }. In Supplementary Note 7, we show that by sampling the parity measurements alone combined with the linear layer, we can realize (but not limited to) the following vector space of funtions:
| 15 |
Output feature encoding & the linear layer
In reservoir computing, the outputs of a reservoir, called feature vectors, are sent to a trained linear layer. Here, we briefly outline the motivation and construction of the feature vectors and the training algorithms used in this manuscript.
In general, sampling over all possible measurement trajectory outcomes and generating a probability distribution contains all the information one can extract from a quantum system. However, not all the information plays an equal role for finite samples. Thus, for our work here, we use a physically motivated output feature vector that efficiently captures the relevant information for a linear layer. The output feature vectors for our reservoir are generated from computed correlations of measurement outcomes. The p-th order correlations are characterized by the p-th central moment μp of the underlying distribution of measurement trajectories. The elements of μp are
| 16 |
where xin is the nth repeated measurement outcome of observable xi for a total of Nshots repetitions, and 〈…〉 is the expectation value taken over repetitions. For the results presented in the main text, we use only up to third-order correlations. Additionally, due to the finite memory present in our reservoir, we only keep correlations between nearest, next-nearest, and next-next-nearest measurements. See Supplementary Note 4 for details and motivation behind this choice.
For machine learning with reservoir computing, the only component of the reservoir that is trained is a linear layer applied to the above feature vectors. The linear layer is an R × C matrix Wtrain and applied to the R-dimensional feature vector x, and biased with a C-dimensional vector vtrain:
| 17 |
Here C is equal to the number of classes in the data set. The largest elements of y corresponds to the class that the reservoir predicts the given input data point x belongs to. To train the weight matrix Wtrain, we either use a pseudo-inverse method to minimize the mean squared error (MSE) between Wtrainx and y, or backpropagation to minimize the MSE after a softmax function. Both methods are described in more detail in Supplementary Note 4. In the main manuscript, we present results for whichever performed the best.
Supplementary information
Acknowledgements
We would like to thank Hakan Türeci, Shyam Shankar, Saeed A. Khan, Haohai Shi, William P. Banner, Shi-Yuan Ma, and Maxwell Anderson for helpful discussions and comments. We would also like to thank Bradley Cole, Clayton Larson, Britton Plourde, Eric Yelton, and Luojia Zhang for the fabrication of the transmon and on-chip resonator, Chris Wang for the design of the transmon, the on-chip resonator and the 3D superconducting cavity (using pyEPR50), and Nord Quantique for the fabrication of the 3D superconducting cavity. We gratefully acknowledge MIT Lincoln Laboratory for supplying the Josephson traveling-wave parametric amplifier (TWPA) used in our experiments. This paper is based upon work supported by the Air Force Office of Scientific Research under award number FA9550-22-1-0203. We gratefully acknowledge a DURIP award with AFOSR award number FA9550-22-1-0080 for equipment used in this work. We wish to thank NTT Research for their financial and technical support. P.L.M. acknowledges membership in the CIFAR Quantum Information Science Program as an Azrieli Global Scholar. Y.C. and X.W. were supported by the Air Force Office of Scientific Research under Grant No. FA9550211005, NSF CCF-1942837 (CAREER), and a Sloan Research Fellowship.
Author contributions
A.S. designed and carried out the hardware experiments and performed the data analysis. S.P. performed the numerical simulations of the quantum system and helped to optimize the experimental protocol with early contribution from J.K.. V.K. performed the numerical simulations of the classicalized quantum system, and performed the comparisons with classical machine-learning methods. V.F. oversaw the design and creation of the superconducting device by S.R. and others. A.S. and V.F. set up the cryogenic and microwave apparatus. S.R. calibrated the superconducting device with A.S. and V.F.. Y.C. and X.W. performed the theoretical analysis of the expressivity in Supplementary Note 7. T.O., L.G.W. and P.L.M. conceived the project, and T.O. and J.K. performed initial numerical simulations to validate the concept. A.S., S.P. and P.L.M. wrote the manuscript with input from all authors. P.L.M. supervised the project.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Data availability
All data generated used in this work is available at: 10.5281/zenodo.10432778.
Code availability
All code used in this work is available at: 10.5281/zenodo.10432778.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Alen Senanian, Email: As3656@cornell.edu.
Peter L. McMahon, Email: pmcmahon@cornell.edu
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-024-51161-8.
References
- 1.Ladd, T. D. et al. Quantum computers. Nature464, 45–53 (2010). 10.1038/nature08812 [DOI] [PubMed] [Google Scholar]
- 2.Jones, N. C. et al. Layered architecture for quantum computing. Phys. Rev. X2, 031007 (2012). [Google Scholar]
- 3.Campbell, E. T., Terhal, B. M. & Vuillot, C. Roads towards fault-tolerant universal quantum computation. Nature549, 172–179 (2017). 10.1038/nature23460 [DOI] [PubMed] [Google Scholar]
- 4.Preskill, J. Quantum computing in the nisq era and beyond. Quantum2, 79 (2018). 10.22331/q-2018-08-06-79 [DOI] [Google Scholar]
- 5.Arute, F. et al. Quantum supremacy using a programmable superconducting processor. Nature574, 505–510 (2019). 10.1038/s41586-019-1666-5 [DOI] [PubMed] [Google Scholar]
- 6.Zhong, H.-S. et al. Quantum computational advantage using photons. Science370, 1460–1463 (2020). 10.1126/science.abe8770 [DOI] [PubMed] [Google Scholar]
- 7.Mohseni, M. et al. Commercialize quantum technologies in five years. Nature543, 171–174 (2017). 10.1038/543171a [DOI] [PubMed] [Google Scholar]
- 8.Biamonte, J. et al. Quantum machine learning. Nature549, 195–202 (2017). 10.1038/nature23474 [DOI] [PubMed] [Google Scholar]
- 9.Schuld, M. & Killoran, N. Is quantum advantage the right goal for quantum machine learning? PRX Quantum3, 030101 (2022). 10.1103/PRXQuantum.3.030101 [DOI] [Google Scholar]
- 10.Cerezo, M., Verdon, G., Huang, H.-Y., Cincio, L. & Coles, P. J. Challenges and opportunities in quantum machine learning. Nat. Comput. Sci.2, 567–576 (2022). 10.1038/s43588-022-00311-3 [DOI] [PubMed] [Google Scholar]
- 11.McClean, J. R., Boixo, S., Smelyanskiy, V. N., Babbush, R. & Neven, H. Barren plateaus in quantum neural network training landscapes. Nat. Commun.9, 4812 (2018). 10.1038/s41467-018-07090-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wang, S. et al. Noise-induced barren plateaus in variational quantum algorithms. Nat. Commun.12, 6961 (2021). 10.1038/s41467-021-27045-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Marrero, C. O., Kieferová, M. & Wiebe, N. Entanglement-induced barren plateaus. PRX Quantum2, 040316 (2021). 10.1103/PRXQuantum.2.040316 [DOI] [Google Scholar]
- 14.Arrasmith, A., Holmes, Z., Cerezo, M. & Coles, P. J. Equivalence of quantum barren plateaus to cost concentration and narrow gorges. Quantum Sci. Technol.7, 045015 (2022). 10.1088/2058-9565/ac7d06 [DOI] [Google Scholar]
- 15.Lukoševičius, M. & Jaeger, H. Reservoir computing approaches to recurrent neural network training. Computer Sci. Rev.3, 127–149 (2009). 10.1016/j.cosrev.2009.03.005 [DOI] [Google Scholar]
- 16.Schrauwen, B., Verstraeten, D. & Van Campenhout, J. An overview of reservoir computing: theory, applications and implementations (2007).
- 17.Khan, S. A., Hu, F., Angelatos, G. & Türeci, H. E. Physical reservoir computing using finitely-sampled quantum systems (2021). 2110.13849.
- 18.Gauthier, D. J., Bollt, E., Griffith, A. & Barbosa, W. A. S. Next generation reservoir computing. Nat. Commun.1210.1038/s41467-021-25801-2 (2021). [DOI] [PMC free article] [PubMed]
- 19.Fujii, K. & Nakajima, K.Quantum Reservoir Computing: A Reservoir Approach Toward Quantum Machine Learning on Near-Term Quantum Devices, 423–450 (Springer Singapore, Singapore, 2021). 10.1007/978-981-13-1687-6_18.
- 20.Fujii, K. & Nakajima, K. Harnessing disordered-ensemble quantum dynamics for machine learning. Phys. Rev. Appl.8, 024030 (2017). 10.1103/PhysRevApplied.8.024030 [DOI] [Google Scholar]
- 21.Ghosh, S., Opala, A., Matuszewski, M., Paterek, T. & Liew, T. C. H. Quantum reservoir processing. npj Quant. Inf.5 (2019). 10.1038/s41534-019-0149-8.
- 22.Govia, L. C. G., Ribeill, G. J., Rowlands, G. E., Krovi, H. K. & Ohki, T. A. Quantum reservoir computing with a single nonlinear oscillator. Phys. Rev. Res.3, 013077 (2021). 10.1103/PhysRevResearch.3.013077 [DOI] [Google Scholar]
- 23.Kalfus, W. D. et al. Hilbert space as a computational resource in reservoir computing. Phys. Rev. Res.4, 033007 (2022). 10.1103/PhysRevResearch.4.033007 [DOI] [Google Scholar]
- 24.Spagnolo, M. et al. Experimental photonic quantum memristor. Nat. Photon.16, 318–323 (2022). 10.1038/s41566-022-00973-5 [DOI] [Google Scholar]
- 25.Pfeffer, P., Heyder, F. & Schumacher, J. Hybrid quantum-classical reservoir computing of thermal convection flow. Phys. Rev. Res.4 (2022). 10.1103/PhysRevResearch.4.033176.
- 26.Chen, J., Nurdin, H. I. & Yamamoto, N. Temporal information processing on noisy quantum computers. Phys. Rev. Appl.14, 024065 (2020). 10.1103/PhysRevApplied.14.024065 [DOI] [Google Scholar]
- 27.Kubota, T. et al. Quantum noise-induced reservoir computing (2022). 2207.07924.
- 28.Mlika, Z., Cherkaoui, S., Laprade, J. F. & Corbeil-Letourneau, S. User trajectory prediction in mobile wireless networks using quantum reservoir computing (2023). 2301.08796.
- 29.Yasuda, T. et al. Quantum reservoir computing with repeated measurements on superconducting devices (2023). 2310.06706.
- 30.Suzuki, Y., Gao, Q., Pradel, K. C., Yasuoka, K. & Yamamoto, N. Natural quantum reservoir computing for temporal information processing. Sci. Rep.12 (2022). 10.1038/s41598-022-05061-w. [DOI] [PMC free article] [PubMed]
- 31.Hu, F. et al. Tackling sampling noise in physical systems for machine learning applications: fundamental limits and eigentasks. Phys. Rev. X13, 041020 (2023). [Google Scholar]
- 32.Parra-Rodriguez, A., Lougovski, P., Lamata, L., Solano, E. & Sanz, M. Digital-analog quantum computation. Phys. Rev. A101, 022305 (2020). 10.1103/PhysRevA.101.022305 [DOI] [Google Scholar]
- 33.García-Molina, P., Martin, A., de Andoin, M. G. & Sanz, M. Noise in digital and digital-analog quantum computation (2021). 2107.12969.
- 34.Daley, A. J. et al. Practical quantum advantage in quantum simulation. Nature607, 667–676 (2022). 10.1038/s41586-022-04940-6 [DOI] [PubMed] [Google Scholar]
- 35.Wang, Z. et al. Quantum microwave radiometry with a superconducting qubit. Phys. Rev. Lett.126, 180501 (2021). 10.1103/PhysRevLett.126.180501 [DOI] [PubMed] [Google Scholar]
- 36.Wang, W. et al. Quantum-enhanced radiometry via approximate quantum error correction. Nat. Commun.13, 3214 (2022). 10.1038/s41467-022-30410-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Backes, K. M. et al. A quantum enhanced search for dark matter axions. Nature590, 238–242 (2021). 10.1038/s41586-021-03226-7 [DOI] [PubMed] [Google Scholar]
- 38.Assouly, R., Dassonneville, R., Peronnin, T., Bienfait, A. & Huard, B. Quantum advantage in microwave quantum radar. Nat. Phys.19, 1418–1422 (2023). 10.1038/s41567-023-02113-4 [DOI] [Google Scholar]
- 39.Dixit, A. V. et al. Searching for dark matter with a superconducting qubit. Phys. Rev. Lett.126, 141302 (2021). 10.1103/PhysRevLett.126.141302 [DOI] [PubMed] [Google Scholar]
- 40.Wang, C. S. et al. Efficient multiphoton sampling of molecular vibronic spectra on a superconducting bosonic processor. Phys. Rev. X10, 021060 (2020). [Google Scholar]
- 41.Heeres, R. W. et al. Cavity state manipulation using photon-number selective phase gates. Phys. Rev. Lett.115 (2015). 10.1103/PhysRevLett.115.137002. [DOI] [PubMed]
- 42.Wright, L. G. & McMahon, P. L. The capacity of quantum neural networks (2019). 1908.01364.
- 43.Diringer, A. A., Blumenthal, E., Grinberg, A., Jiang, L. & Hacohen-Gourgy, S. Conditional-not displacement: Fast multioscillator control with a single qubit. Phys. Rev. X14, 011055 (2024). [Google Scholar]
- 44.O’Shea, T. J., Roy, T. & Clancy, T. C. Over-the-air deep learning based radio signal classification. IEEE J. Sel. Top. Signal Process.12, 168–179 (2018). 10.1109/JSTSP.2018.2797022 [DOI] [Google Scholar]
- 45.Jagannath, A. & Jagannath, J. Dataset for modulation classification and signal type classification for multi-task and single task learning. Comput. Netw.199, 108441 (2021). 10.1016/j.comnet.2021.108441 [DOI] [Google Scholar]
- 46.Jones, A., Chapman, D., Donelan, H., Dooley, L. & Poulton., A. Exploring communications technology – open university (2017). https://www.open.edu/openlearn/digital-computing/exploring-communications-technology/content-section-4.7.
- 47.Sannia, A., Martínez-Peña, R., Soriano, M. C., Giorgi, G. L. & Zambrini, R. Dissipation as a resource for Quantum Reservoir Computing. Quantum8, 1291 (2024). 10.22331/q-2024-03-20-1291 [DOI] [Google Scholar]
- 48.Martínez-Peña, R., Giorgi, G. L., Nokkala, J., Soriano, M. C. & Zambrini, R. Dynamical phase transitions in quantum reservoir computing. Phys. Rev. Lett.127, 100502 (2021). 10.1103/PhysRevLett.127.100502 [DOI] [PubMed] [Google Scholar]
- 49.Zhou, F. & Chai, Y. Near-sensor and in-sensor computing. Nat. Electron.3, 664–671 (2020). 10.1038/s41928-020-00501-9 [DOI] [Google Scholar]
- 50.Minev, Z. K. et al. pyepr: The energy-participation-ratio (epr) open-source framework for quantum device design (2021).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data generated used in this work is available at: 10.5281/zenodo.10432778.
All code used in this work is available at: 10.5281/zenodo.10432778.