Abstract
Characterizing the nature of hydrodynamical transport properties in quantum dynamics provides valuable insights into the fundamental understanding of exotic non-equilibrium phases of matter. Experimentally simulating infinite-temperature transport on large-scale complex quantum systems is of considerable interest. Here, using a controllable and coherent superconducting quantum simulator, we experimentally realize the analog quantum circuit, which can efficiently prepare the Haar-random states, and probe spin transport at infinite temperature. We observe diffusive spin transport during the unitary evolution of the ladder-type quantum simulator with ergodic dynamics. Moreover, we explore the transport properties of the systems subjected to strong disorder or a tilted potential, revealing signatures of anomalous subdiffusion in accompany with the breakdown of thermalization. Our work demonstrates a scalable method of probing infinite-temperature spin transport on analog quantum simulators, which paves the way to study other intriguing out-of-equilibrium phenomena from the perspective of transport.
Subject terms: Quantum simulation, Qubits
Quantum devices offer the potential to simulate quantum phenomena, which are otherwise computationally intractable. Here, Shi, Sun, Wang and coauthors use a superconducting quantum simulator to study spin-transport at infinite temperature.
Introduction
Transport properties of quantum many-body systems driven out of equilibrium are of significant interest in several active areas of modern physics, including the ergodicity of quantum systems1–4 and quantum magnetism5–7. Understanding these properties is crucial to unveil the non-equilibrium dynamics of isolated quantum systems8,9. One essential property of transport is the emergence of classical hydrodynamics in microscopic quantum dynamics, which shows the power-law tail of autocorrelation functions8. The rate of the power-law decay, referred as to the transport exponent, characterizes the universal classes of hydrodynamics. In d-dimensional quantum systems, in addition to generally expected diffusive transport with the exponent d/2 in non-integrable systems10–12, more attention has been attracted by the anomalous superdiffusive5,13–16 or subdiffusive transport2,3,17–19, with the exponent larger or smaller than d/2, respectively.
Over the last few decades, considerable strides have been made in enhancing the scalability, controllability, and coherence of noisy intermediate-scale quantum (NISQ) devices based on superconducting qubits20–23. With these advancements, several novel phenomena in non-equilibrium dynamics of quantum many-body systems have been observed, such as quantum thermalization24,25, ergodicity breaking26–29, time crystal30–32, and information scrambling33,34. More importantly, in this platform, the beyond-classical computation has been demonstrated by sampling the final Haar-random states of randomized sequences of gate operations35–39. Recently, a method of measuring autocorrelation functions at infinite temperature based on the Haar-random states has been proposed, which opens up a practical application of pseudo-random quantum circuits for simulating hydrodynamics on NISQ devices40,41.
In this work, using a ladder-type superconducting quantum simulator with up to 24 qubits, we first demonstrate that in addition to the digital pseudo-random circuits35–41, a unitary evolution governed by a time-independent Hamiltonian, i.e., an analog quantum circuit, can also generate quantum states randomly chosen from the Haar measure, i.e., the Haar-random states, for measuring the infinite-temperature autocorrelation functions42–44. Subsequently, we study the properties of spin transport on the superconducting quantum simulator via the measurement of autocorrelation functions by using the Haar-random states. Notably, we observe a clear signature of the diffusive transport on the qubit ladder, which is a non-integrable system11,12,25.
Upon subjecting the qubit ladder to disorder, a transition from delocalized phases to many-body localization (MBL) occurs as the strength of the disorder increases45. By measuring the autocorrelation functions, we experimentally probe an anomalous subdiffusive transport with intermediate values of the disorder strength. The observed signs of subdiffusion are consistent with recent numerical results and can be explained as a consequence of a Griffth-like region on the delocalized side of the MBL transition2,3,46–49.
Finally, we explore spin transport on the qubit ladder with a linear potential, and it is expected that Stark MBL occurs when the potential gradients are sufficiently large28,50–54. With a large gradient, the conservation of the dipole moment emerges28,54, associated with the phenomena known as the Hilbert space fragmentation55–57. Recent theoretical works reveal a subdiffusion in the dipole-moment conserving systems17,19. In this experiment, we present evidence of a subdiffusive regime of spin transport in the tilted qubit ladder.
Results
Experimental setup and protocol
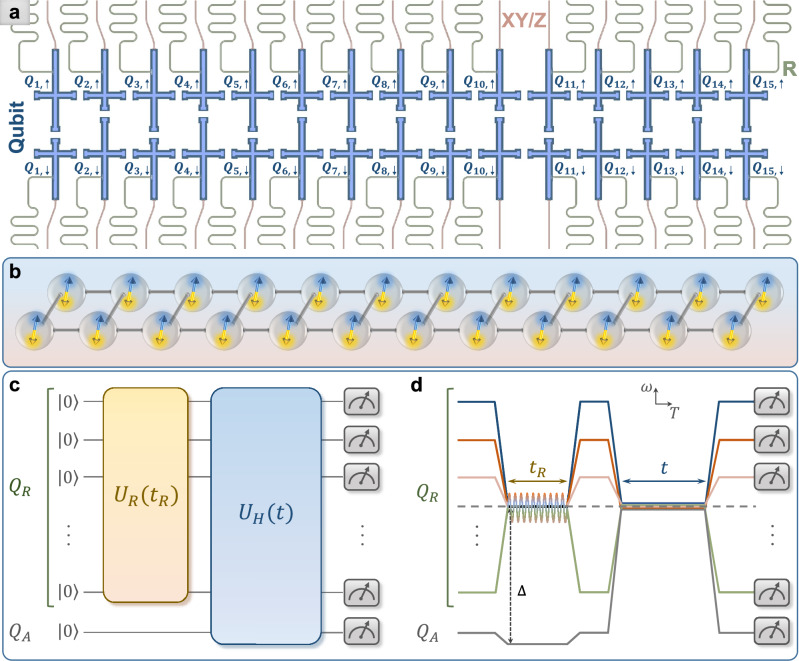
Our experiments are performed on a programmable superconducting quantum simulator consisting of 30 transmon qubits with the geometry of a two-legged ladder, see Fig. 1a, b. The nearest-neighbor qubits are coupled by a fixed capacitor, and the effective Hamiltonian of capacitive interactions can be written as22,23 (also see Supplementary Note 1)
| 1 |
where ℏ = h/2π, with h being the Planck constant (in the following, we set ℏ = 1), L is the length of the ladder, () is the raising (lowering) operator for the qubit Qj,m, and () refers to the rung (intrachain) hopping strength. For this device, the averaged rung and intrachain hopping strength are and , respectively. The XY and Z control lines on the device enable us to realize the drive Hamiltonian , and the on-site potential Hamiltonian , respectively. Here, Ωj,m and ϕj,m denote the driving amplitude and the phase of the microwave pulse applied on the qubit Qj,m, and wj,m is the effective on-site potential.
Fig. 1. Superconducting quantum simulator and experimental pulse sequences.
a The schematic showing the ladder-type superconducting quantum simulator, consisting of 30 qubits (the blue region), labeled Q1,↑ to Q15,↑, and Q1,↓ to Q15,↓. Each qubit is coupled to a separate readout resonator (the green region), and has an individual control line (the red region) for both the XY and Z controls. b Schematic diagram of the simulated 24 spins coupled in a ladder. The blue and yellow double arrows represent the infinite-temperature spin hydrodynamics without preference for spin orientations. c Schematic diagram of the quantum circuit for measuring the autocorrelation functions at infinite temperature. All qubits are initialized at the state . Subsequently, an analog quantum circuit acts on the set of qubits QR to generate Haar-random states. This is followed by a time evolution of all qubits, i.e., with being the Hamiltonian of the system, in which the properties of spin transport are of our interest. d Experimental pulse sequences corresponding to the quantum circuit in (c) displayed in the frequency (ω) versus time (T) domain. To realize , qubits in the set QR are tuned to the working point (dashed horizontal line) via Z pulses, and simultaneously, the resonant microwave pulses represented as the sinusoidal line are applied to QR through the XY control lines. Meanwhile, the qubit QA is detuned from the working point with a large value of the frequency gap Δ. To realize the subsequent evolution with the Hamiltonian (1), all qubits are tuned to the working point.
To study spin transport and hydrodynamics, we focus on the equal-site autocorrelation function at infinite temperature, which is defined as
| 2 |
where is a local observable at site , and D is the Hilbert dimension of the Hamiltonian . Here, for the ladder-type superconducting simulator, we choose (r = 1)12, and the autocorrelation function can be rewritten as
| 3 |
with (subscripts μ and ν denote the qubit index 1 ↑ or 1, ↓).
The autocorrelation functions (2) at infinite temperature can be expanded as the average of over different in z-basis. In fact, the dynamical behavior of an individual is sensitive to the choice of under some circumstances (see Supplementary Note 7 for the dependence of on in the qubit ladder with a linear potential as an example). To experimentally probe the generic properties of spin transport at infinite temperature, one can obtain (2) by measuring and averaging with different 15. Alternatively, we employ a more efficient method to measure (2) without the need of sampling different . Based on the results in ref. 40 (also see “Methods”), the autocorrelation function cμ;ν can be indirectly measured by using the quantum circuit as shown in Fig. 1c, i.e.,
| 4 |
where with , and being a unitary evolution generating Haar-random states. For example, to experimentally obtain c1,↓;1,↑, we choose Q1,↑ as QA, and the remainder qubits as the QR. After performing the pulse sequences as shown in Fig. 1d, we measure the qubit Q1,↓ at z-basis to obtain the expectation value of the observable .
Observation of diffusive transport
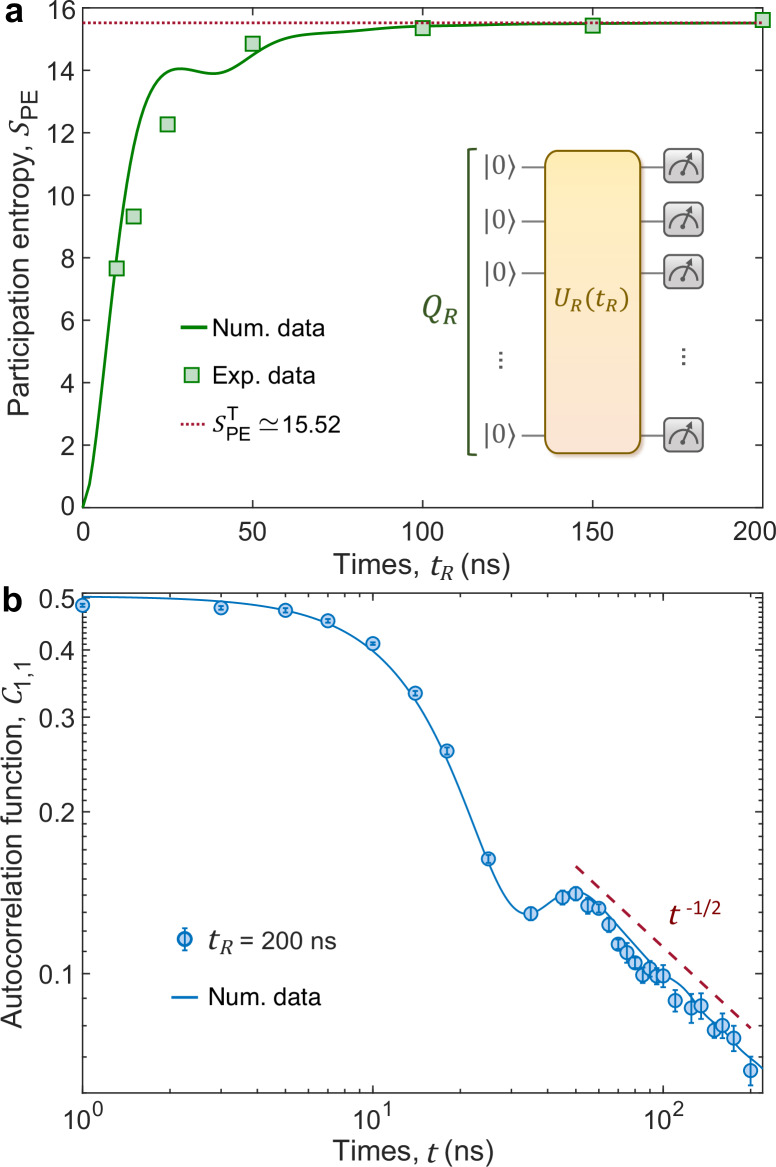
In this experiment, we first study spin transport on the 24-qubit ladder consisting of Q1,↑, …, Q12,↑ and Q1,↓, …, Q12,↓, described by the Hamiltonian (1). For a non-integrable model, one expects that diffusive transport C1,1 ∝ t−1/2 occurs12. To measure the autocorrelation function C1,1 defined in Eq. (3), we should first perform a quantum circuit generating the required Haar-random states . Instead of using the digital pseudo-random circuits in refs. 35–41, here we experimentally realize the time evolution under the Hamiltonian , where the parameters Ωj,m and ϕj,m in have site-dependent values with the average () and (see “Methods” and Supplementary Note 3 for more details), i.e., , which is more suitable for our analog quantum simulator. To benchmark that the final state can approximate the Haar-random states, we measure the participation entropy , with D being the dimension of Hilbert space, pk = ∣〈k∣ψR〉∣2, and being a computational basis. Figure 2a shows the results of SPE with different evolution times tR. For the 23-qubit system, the probabilities pk are estimated from the single-shot readout with a number of samples Ns = 3 × 107. It is seen that the SPE tends to the value for Haar-random states, i.e., with N = 23 being the number of qubits and γ ≃ 0.577 as the Euler’s constant36. Moreover, for the final state with tR = 200 ns, the distribution of probabilities pk satisfies the Porter-Thomas distribution (see Supplementary Note 4).
Fig. 2. Observation of diffusive transport.
a Experimental verification of preparing the states via the time evolution of participation entropy. Here, we chose QR = {Q1,↑, Q2,↑, …, Q12,↑, Q2,↓, Q3,↓, …, Q12,↓} with total 23 qubits. The inset of (a) shows the corresponding quantum circuit. The dotted horizontal line represents the participation entropy for Haar-random states, i.e., . b Experimental results of the autocorrelation function C1,1(t) for the qubit ladder with L = 12, which are measured by performing the quantum circuit shown in Fig. 1c, d. Here, we consider the state generated from with tR = 200 ns, which is approximate to a Haar-random state. Markers are experimental data. The solid line is the numerical simulation of the correlation function C1,1 at infinite temperature. The dashed line represents a power-law decay t−1/2. Error bars represent the standard deviation.
In Fig. 2b, we show the dynamics of the autocorrelation function C1,1 measured via the quantum circuit in Fig. 1c with tR = 200 ns. The experimental data satisfies C1,1 ∝ t−α, with a transport exponent α ≃ 0.5067, estimated by fitting the data in the time window t ∈ [50 ns, 200 ns]. Our experiments clearly show that spin diffusively transports on the qubit ladder (1), and demonstrate that the analog quantum circuit with tR = 200 ns can provide sufficient randomness to measure the autocorrelation function defined in Eq. (2) and probe infinite-temperature spin transport. We also discuss the influence of tR in Supplementary Note 4, numerically showing that the results of C1,1 do not substantially change for longer tR > 200 ns. Moreover, in Supplementary Note 4, we show that for a shortly evolved time tR ≃ 15 ns, the values of the observable defined in Eq. (4) are incompatible with the infinite-temperature autocorrelation functions. Given that the chosen initial state for generating the Haar-random state exhibits a high effective temperature associated with the Hamiltonian , the state would asymptotically converge to the Haar-random state with a sufficiently extended tR. However, with tR ≃ 15 ns, the time scale is too small to get rid of the coherence, and the value of SPE for the state is much smaller than the (see Fig. 2a), suggesting that with tR ≃ 15 ns is far away from the Haar-random state, and cannot be employed to measure the infinite-temperature autocorrelation function (2). In the following, we fix tR = 200 ns, and study spin transport in other systems with ergodicity breaking.
Subdiffusive transport with ergodicity breaking
After demonstrating that the quantum circuit shown in Fig. 1c can be employed to measure the infinite-temperature autocorrelation function C1,1, we study spin transport on the superconducting qubit ladder with the disorder, whose effective Hamiltonian can be written as , with wj,m drawn from a uniform distribution [ − W, W], and W is the strength of disorder. For each disorder strength, we consider 10 disorder realizations and plot the dynamics of averaged C1,1 with different W are plotted in Fig. 3a. With the increasing of W, and as the system approaches the MBL transition, C1,1 decays more slowly. Moreover, the oscillation in the dynamics of C1,1 becomes more obvious with larger W, which is related to the presence of local integrals of motion in the deep many-body localized phase58.
Fig. 3. Subdiffusive transport on the superconducting qubit ladder with disorder.
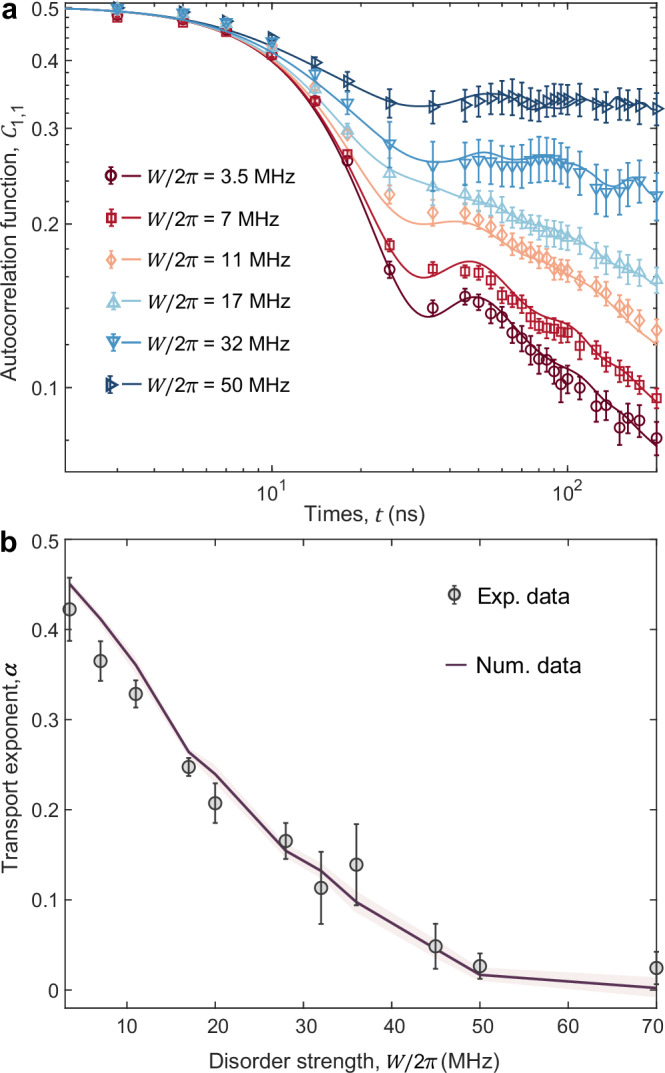
a The time evolution of autocorrelation function C1,1(t) for the qubit ladder with L = 12 and different values of disorder strength W, ranging from W/2π = 35 MHz () to W/2π = 70 MHz (). Markers (lines) are experimental (numerical) data. b Transport exponent α as a function of W obtained from fitting the data of C1,1(t). Error bars (experimental data) and shaded regions (numerical data) represent the standard deviation.
We then fit both the experimental and numerical data with the time window t ∈ [50 ns, 200 ns] by adopting the power-law decay C1,1 ∝ t−α. As shown in Fig. 3b, we observe an anomalous subdiffusive region with the transport exponent α < 1/2. For the strength of disorder W/2π ≳ 50 MHz, the transport exponent α ~ 10−2 indicates the freezing of spin transport and the onset of MBL on the 24-qubit system2. Here, we emphasize that the estimated transition point between the subdiffusive regime and MBL is a lower bound since, with longer evolved time, the exponent α obtained from the power-law fitting becomes slightly larger (see Supplementary Note 6).
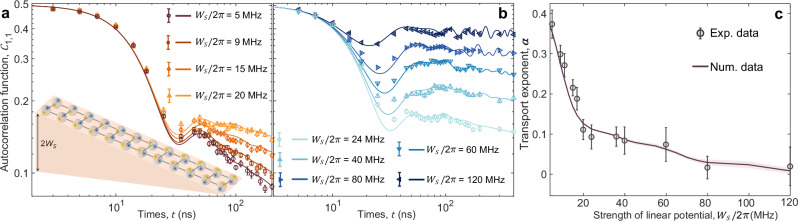
Next, we explore the transport properties on a tilted superconducting qubit ladder, which is subjected to the linear potential , with Δ = 2WS/(L − 1) being the slope of the linear potential (see the tilted ladder in the inset of Fig. 4a). Thus, the effective Hamiltonian of the tilted superconducting qubit ladder can be written as . Different from the aforementioned breakdown of ergodicity induced by the disorder, the non-ergodic behaviors induced by the linear potential arise from strong Hilbert-space fragmentation55–57. The ergodicity breaking in the disorder-free system is known as the Stark MBL28,50–54.
Fig. 4. Subdiffusive transport on the superconducting qubit ladder with linear potential.
a Time evolution of autocorrelation function C1,1(t) for the tilted qubit ladder with L = 12 and WS/2π≤20 MHz. b is similar to (a) but for the data with WS/2π≥24 MHz. Markers (lines) are experimental (numerical) data. c Transport exponent α as a function of WS. For WS/2π≤20 MHz and WS/2π≥24 MHz, the exponent α is extracted from fitting the data of C1,1(t) with the time window t ∈ [50 ns, 200 ns] and t ∈ [100 ns, 400 ns], respectively. Error bars (experimental data) and shaded regions (numerical data) represent the standard deviation.
We employ the method based on the quantum circuit shown in Fig. 1c to measure the time evolution of the autocorrelation function C1,1 with different slopes of the linear potential. The results are presented in Fig. 4a, b. Similar to the system with the disorder, the dynamics of C1,1 still satisfies C1,1 ∝ t−α with α < 0.5, i.e., subdiffusive transport. Figure 4c displays the transport exponent α with different strengths of the linear potential, showing that α asymptotically drops as WS increases.
Two remarks are in order. First, by employing the same standard for the onset of MBL induced by disorder, i.e., α ~ 10−2, the results in Fig. 4c indicate that the Stark MBL on the tilted 24-qubit ladder occurs when WS/2π ≳ 80 MHz (Δ/2π ≳ 14.6 MHz). Second, on the ergodic side (WS/2π < 80 MHz and W/2π < 50 MHz for the tilted and disordered systems, respectively), the transport exponent α exhibits rapid decay with increasing WS up to WS/2π ≃ 20 MHz in the tilted system. Subsequently, as WS continues to increase, the decay of z becomes slower. In contrast, for the disordered system, α consistently decreases with increasing disordered strength W. We note that the impact of the emergence of dipole-moment conservation with increasing the slope of linear potential on the spin transport, and its distinction from the transport in disordered systems remains unclear and deserve further theoretical studies.
Discussion
Based on the novel protocol for simulating the infinite-temperature spin transport using the Haar-random state40, we have experimentally probed diffusive transport on a 24-qubit ladder-type programmable superconducting processor. Moreover, when the qubit ladder is subject to sufficiently strong disorder, we observe the signatures of subdiffusive transport, accompanied by the breakdown of ergodicity due to MBL.
It is worthwhile to emphasize that previous experimental studies of the Stark MBL mainly focus on the dynamics of imbalance50,59,60. Different from the disorder-induced MBL with a power-law decay of imbalance observed in the subdiffusive Griffith-like region61, for the Stark MBL, there is no experimental evidence for the power-law decay of imbalance50,59,60. Here, by measuring the infinite-temperature autocorrelation function, we provide solid experimental evidence for the subdiffusion in tilted systems, which is induced by the emergence of strong Hilbert-space fragmentation55–57. Theoretically, it has been suggested that for a thermodynamically large system, non-zero tilted potentials, i.e., Δ > 0, will lead to a subdiffusive transport with α ≃ 1/417,62. In finite-size systems, both results, as shown in Fig. 4 and the cold atom experiments on the tilted Fermi-Hubbard model63 demonstrate a crossover from the diffusive regime to the subdiffusive one. Investigating how this crossover scales with increasing system size is a further experimental task, which requires quantum simulators with a larger number of qubits.
Ensembles of Haar-random pure quantum states have several promising applications, including benchmarking quantum devices42,64 and demonstrating beyond-classical computation35–39. Our work displays a practical application of the randomly distributed quantum state, i.e., probing the infinite-temperature spin transport. In contrast to employing digital random circuits, where the number of imperfect two-qubit gates is proportional to the qubit number36–41, the scalable analog circuit adopted in our experiments can also generate multi-qubit Haar-random states useful for simulating hydrodynamics. The protocol employed in our work can be naturally extended to explore the non-trivial transport properties on other analog quantum simulators, including the Rydberg atoms42,65–67, quantum gas microscopes68,69, and the superconducting circuits with a central resonance bus, which enables long-range interactions21,70,71.
Methods
Derivation of Eq. 4
Here, we present the details of the deviation of Eq. (4), which is based on the typicality12,40,72. According to Eq. (2), , with D = 2N. We define , and then . By using , we have . We note that is an operator which projects the state of the ν-th qubit to the state .
According to the typicality12,40,72, the trace of an operator can be approximated as the expectation value averaged by the pure Haar-random state , i.e.,
| 5 |
with N being the number of qubits. It indicates that the infinite-temperature expectation value can be better estimated by the expectation value for the Haar-random state . Thus, for multi-qubit systems. Based on the definition of the projector is a Haar-random state for the whole system except for the ν-th qubit, and in the experiment, only a (N − 1)-qubit Haar-random state is required.
Numerical simulations
Here, we present the details of the numerical simulations. We calculate the unitary time evolution by employing the Krylov method49. The Krylov subspace is panned by the vectors defined as . Then, the Hamiltonian in the Krylov subspace becomes a m-dimensional matrix , where H denotes the Hamiltonian in the matrix form, and Km is the matrix whose columns contain the orthonormal basis vectors of the Krylov space. Finally, the unitary time evolution can be approximately simulated in the Krylov subspace as . In our numerical simulations, the dimension of the Krylov subspace m is adaptively adjusted from m = 6 to 30, making sure the numerical errors are smaller than 10−14.
For the numerical simulation of the in Fig. 1c, based on the experimental data of the XY drive, the parameters in are Ωj,m/2π = 10.4 ± 1.6 MHz, and ϕj,m ∈ [ − π/10, π/10].
Details of generating Haar-random states
In this section, we present more details about the generation of faithful Haar-random states. The analog quantum circuit employed to generate Haar-random states is , where is given by Eq. (1) and is the drive Hamiltonian.
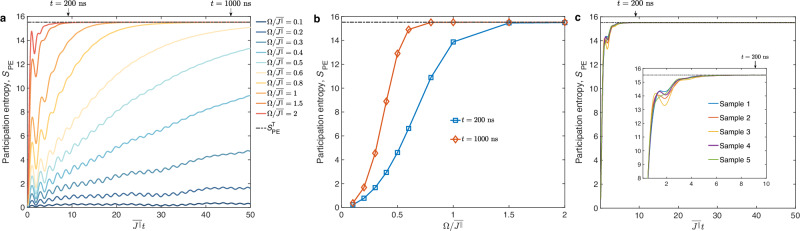
Here, we first numerically study the influence of the driving amplitude Ωj,m. For convenience, we consider ϕj,m = 0, and isotropic driving amplitude, i.e., Ω = Ωj,m for all (j, m). We chose QR = {Q1,↑, Q2,↑, …, Q12,↑, Q2,↓, Q3,↓, …, Q12,↓} with total 23 qubits. The dynamics of participation entropy SPE for different values of Ω are plotted in Fig. 5a, and the values of SPE with the evolved time t = 200 ns and 1000 ns are displayed in Fig. 5b. It is seen that for small Ω, the growth of SPE is slow and with increasing Ω, it becomes more rapid. In this experiment, we chose because the participation entropy can achieve with a relatively short evolved time t ≃ 200 ns. As Ω further increases, the time when is reached does not significantly become shorter. Based on the above discussions, is an appropriate choice of the driving amplitude.
Fig. 5. Impact of driving amplitude and phases of microwave pulse on the generation of Haar-random states.
a The time evolution of the participation entropy SPE for different driving amplitude Ω. b The value of SPE at two evolved times t = 200 ns and 1000 ns, as a function of Ω. c The dynamics of SPE with the phases of the microwave pulse drawn from [ − π, π]. Here, we present the numerical data of 5 different samples of the phases. The inset shows the dynamics in a shorter time interval. The horizontal dashed line represents the participation entropy for Haar-random states .
Next, we numerically study the influence of the randomness for the phases of driving microwave pulse ϕj,m. In this experiment, by using the correction of crosstalk, the randomness of the phases is small, i.e., ϕj,m ∈ [ − π/10, π/10]. Here, we consider the phases with large randomness, i.e., ϕj,m ∈ [ − π, π]. The numerical results for the time evolution of SPE with 5 samples of ϕj,m are plotted in Fig. 5c. With ϕj,m ∈ [ − π, π], the participation entropy can still tend to around 200 ns. Only the short-time behaviors are slightly different from each other for the 5 samples (see the inset of Fig. 5c).
Supplementary information
Acknowledgements
We thank Hai-Long Shi and H. S. Yan for their helpful discussions. Z.X., D.Z., K.X., and H.F. are supported by the Beijing Natural Science Foundation (Grant No. Z200009), National Natural Science Foundation of China (Grants Nos. 92265207, T2121001, 12122504, 12247168, 11934018, T2322030), Innovation Program for Quantum Science and Technology (Grant No. 2021ZD0301800), Beijing Nova Program (Nos. 20220484121, 2022000216). Y.-H.S. acknowledges the support of the Postdoctoral Fellowship Program of CPSF (Grant No. GZB20240815). Z.-A.W. acknowledges the support of the China Postdoctoral Science Foundation (Grant No. 2022TQ0036).
Author contributions
H.F. supervised the project. Z.-H.S. proposed the idea. Y.-H.S. conducted the experiment with the help of K.H. and K.X. Z.-H.S., Y.-Y.W., and Y.-H.S. performed the numerical simulations. Z.X. and D.Z. fabricated the ladder-type sample. X.S., G.X., and H.Y. provided the Josephson parametric amplifiers. W.-G.M., H.-T.L., K.Z., J.-C.S., G.-H.L., Z.-Y.M., J.-C.Z., H.L., and C.-T.C. helped the experimental setup. Z.-A.W., Y.-R.Z., J.W., K.X., and H.F. discussed and commented on the manuscript. Z.-H.S., Y.-H.S., Y.-Y.W., Y.-R.Z., and H.F. co-wrote the manuscript. All authors contributed to the discussions of the results and development of the manuscript.
Peer review
Peer review information
Nature Communications thanks Amir Karamlou, and the other anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Data availability
The authors declare that the data supporting the findings of this study are available within the paper and its Supplementary Information files. Should any raw data files be needed in another format, they are available from the corresponding author upon reasonable request. Source data are provided in this paper.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Yun-Hao Shi, Zheng-Hang Sun, Yong-Yi Wang.
Contributor Information
Kaixuan Huang, Email: huangkx@baqis.ac.cn.
Zhongcheng Xiang, Email: zcxiang@iphy.ac.cn.
Kai Xu, Email: kaixu@iphy.ac.cn.
Heng Fan, Email: hfan@iphy.ac.cn.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-024-52082-2.
References
- 1.Nandkishore, R. & Huse, D. A. Many-body localization and thermalization in quantum statistical mechanics. Annu. Rev. Condens. Matter Phys.6, 15–38 (2015). 10.1146/annurev-conmatphys-031214-014726 [DOI] [Google Scholar]
- 2.Agarwal, K., Gopalakrishnan, S., Knap, M., Müller, M. & Demler, E. Anomalous diffusion and griffiths effects near the many-body localization transition. Phys. Rev. Lett.114, 160401 (2015). 10.1103/PhysRevLett.114.160401 [DOI] [PubMed] [Google Scholar]
- 3.Žnidarič, M., Scardicchio, A. & Varma, V. K. Diffusive and subdiffusive spin transport in the ergodic phase of a many-body localizable system. Phys. Rev. Lett.117, 040601 (2016). 10.1103/PhysRevLett.117.040601 [DOI] [PubMed] [Google Scholar]
- 4.Ljubotina, M., Desaules, J.-Y., Serbyn, M. & Papić, Z. Superdiffusive energy transport in kinetically constrained models. Phys. Rev. X13, 011033 (2023). [Google Scholar]
- 5.Scheie, A. et al. Detection of Kardar–Parisi–Zhang hydrodynamics in a quantum Heisenberg spin-1/2 chain. Nat. Phys.17, 726–730 (2021). 10.1038/s41567-021-01191-6 [DOI] [Google Scholar]
- 6.Žnidarič, M. Spin transport in a one-dimensional anisotropic heisenberg model. Phys. Rev. Lett.106, 220601 (2011). 10.1103/PhysRevLett.106.220601 [DOI] [PubMed] [Google Scholar]
- 7.Dupont, M., Sherman, N. E. & Moore, J. E. Spatiotemporal crossover between low- and high-temperature dynamical regimes in the quantum Heisenberg magnet. Phys. Rev. Lett.127, 107201 (2021). 10.1103/PhysRevLett.127.107201 [DOI] [PubMed] [Google Scholar]
- 8.Bertini, B. et al. Finite-temperature transport in one-dimensional quantum lattice models. Rev. Mod. Phys.93, 025003 (2021). 10.1103/RevModPhys.93.025003 [DOI] [Google Scholar]
- 9.Eisert, J., Friesdorf, M. & Gogolin, C. Quantum many-body systems out of equilibrium. Nat. Phys.11, 124–130 (2015). 10.1038/nphys3215 [DOI] [Google Scholar]
- 10.Peng, P., Ye, B., Yao, N. Y., and Cappellaro, P. Exploiting disorder to probe spin and energy hydrodynamics. Nat. Phys.10.1038/s41567-023-02024-4 (2023).
-
11.Steinigeweg, R., Heidrich-Meisner, F., Gemmer, J., Michielsen, K. & De Raedt, H. Scaling of diffusion constants in the spin-
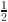 XX ladder. Phys. Rev. B90, 094417 (2014). 10.1103/PhysRevB.90.094417 [DOI] [Google Scholar]
XX ladder. Phys. Rev. B90, 094417 (2014). 10.1103/PhysRevB.90.094417 [DOI] [Google Scholar] - 12.Schubert, D. et al. Quantum versus classical dynamics in spin models: Chains, ladders, and square lattices. Phys. Rev. B104, 054415 (2021). 10.1103/PhysRevB.104.054415 [DOI] [Google Scholar]
- 13.Ljubotina, M., Žnidarič, M. & Prosen, Tomaž. Spin diffusion from an inhomogeneous quench in an integrable system. Nat. Commun.8, 16117 (2017). 10.1038/ncomms16117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wei, D. et al. Quantum gas microscopy of Kardar-Parisi-Zhang superdiffusion. Science376, 716–720 (2022). 10.1126/science.abk2397 [DOI] [PubMed] [Google Scholar]
- 15.Joshi, M. K. et al. Observing emergent hydrodynamics in a long-range quantum magnet. Science376, 720–724 (2022). 10.1126/science.abk2400 [DOI] [PubMed] [Google Scholar]
- 16.Rosenberg, E. et al. Dynamics of magnetization at infinite temperature in a Heisenberg spin chain. Science384, 48–53 (2024). 10.1126/science.adi7877 [DOI] [PubMed] [Google Scholar]
- 17.Feldmeier, J., Sala, P., De Tomasi, G., Pollmann, F. & Knap, M. Anomalous diffusion in dipole- and higher-moment-conserving systems. Phys. Rev. Lett.125, 245303 (2020). 10.1103/PhysRevLett.125.245303 [DOI] [PubMed] [Google Scholar]
- 18.De Nardis, J., Gopalakrishnan, S., Vasseur, R. & Ware, B. Subdiffusive hydrodynamics of nearly integrable anisotropic spin chains. Proc. Natl. Acad. Sci. USA119, e2202823119 (2022). 10.1073/pnas.2202823119 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gromov, A., Lucas, A. & Nandkishore, R. M. Fracton hydrodynamics. Phys. Rev. Res.2, 033124 (2020). 10.1103/PhysRevResearch.2.033124 [DOI] [Google Scholar]
- 20.Ma, R. et al. A dissipatively stabilized Mott insulator of photons. Nature566, 51–57 (2019). 10.1038/s41586-019-0897-9 [DOI] [PubMed] [Google Scholar]
- 21.Zhang, X., Kim, E., Mark, D. K., Choi, S. & Painter, O. A superconducting quantum simulator based on a photonic-bandgap metamaterial. Science379, 278–283 (2023). 10.1126/science.ade7651 [DOI] [PubMed] [Google Scholar]
- 22.Xiang, Zhong-Cheng et al. Simulating Chern insulators on a superconducting quantum processor. Nat. Commun.14, 5433 (2023). 10.1038/s41467-023-41230-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Gu, X., Kockum, AntonFrisk, Miranowicz, A., Liu, Yu-xi & Nori, F. Microwave photonics with superconducting quantum circuits. Phys. Rep.718-719, 1–102 (2017). 10.1016/j.physrep.2017.10.002 [DOI] [Google Scholar]
- 24.Chen, F. et al. Observation of strong and weak thermalization in a superconducting quantum processor. Phys. Rev. Lett.127, 020602 (2021). 10.1103/PhysRevLett.127.020602 [DOI] [PubMed] [Google Scholar]
- 25.Zhu, Q. et al. Observation of thermalization and information scrambling in a superconducting quantum processor. Phys. Rev. Lett.128, 160502 (2022). 10.1103/PhysRevLett.128.160502 [DOI] [PubMed] [Google Scholar]
- 26.Roushan, P. et al. Spectroscopic signatures of localization with interacting photons in superconducting qubits. Science358, 1175–1179 (2017). 10.1126/science.aao1401 [DOI] [PubMed] [Google Scholar]
- 27.Guo, Q. et al. Observation of energy-resolved many-body localization. Nat. Phys.17, 234–239 (2021). 10.1038/s41567-020-1035-1 [DOI] [Google Scholar]
- 28.Guo, Q. et al. Stark many-body localization on a superconducting quantum processor. Phys. Rev. Lett.127, 240502 (2021). 10.1103/PhysRevLett.127.240502 [DOI] [PubMed] [Google Scholar]
- 29.Zhang, P. et al. Many-body Hilbert space scarring on a superconducting processor. Nat. Physics19, 120–125 (2023). 10.1038/s41567-022-01784-9 [DOI] [Google Scholar]
- 30.Zhang, X. et al. Digital quantum simulation of Floquet symmetry-protected topological phases. Nature607, 468–473 (2022). 10.1038/s41586-022-04854-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Mi, X. et al. Time-crystalline eigenstate order on a quantum processor. Nature601, 531–536 (2022). 10.1038/s41586-021-04257-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Frey, P. & Rachel, S. Realization of a discrete time crystal on 57 qubits of a quantum computer. Sci. Adv.8, eabm7652 (2022). 10.1126/sciadv.abm7652 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Mi, X. et al. Information scrambling in quantum circuits. Science374, 1479–1483 (2021). 10.1126/science.abg5029 [DOI] [PubMed] [Google Scholar]
- 34.Braumüller, J. et al. Probing quantum information propagation with out-of-time-ordered correlators. Nat. Phys.18, 172–178 (2022). 10.1038/s41567-021-01430-w [DOI] [Google Scholar]
- 35.Neill, C. et al. A blueprint for demonstrating quantum supremacy with superconducting qubits. Science360, 195–199 (2018). 10.1126/science.aao4309 [DOI] [PubMed] [Google Scholar]
- 36.Boixo, S. et al. Characterizing quantum supremacy in near-term devices. Nat. Phys.14, 595–600 (2018). 10.1038/s41567-018-0124-x [DOI] [Google Scholar]
- 37.Arute, F. et al. Quantum supremacy using a programmable superconducting processor. Nature574, 505–510 (2019). 10.1038/s41586-019-1666-5 [DOI] [PubMed] [Google Scholar]
- 38.Wu, Y. et al. Strong quantum computational advantage using a superconducting quantum processor. Phys. Rev. Lett.127, 180501 (2021). 10.1103/PhysRevLett.127.180501 [DOI] [PubMed] [Google Scholar]
- 39.A., Morvan et al. Phase transition in random circuit sampling. Preprint at 10.48550/arXiv.2304.11119 (2023).
- 40.Richter, J. & Pal, A. Simulating hydrodynamics on noisy intermediate-scale quantum devices with random circuits. Phys. Rev. Lett.126, 230501 (2021). 10.1103/PhysRevLett.126.230501 [DOI] [PubMed] [Google Scholar]
- 41.Keenan, N., Robertson, N. F., Murphy, T., Zhuk, S. & Goold, J. Evidence of Kardar-Parisi-Zhang scaling on a digital quantum simulator. Npj Quantum Inf.9, 72 (2023). 10.1038/s41534-023-00742-4 [DOI] [Google Scholar]
- 42.Choi, J. et al. Preparing random states and benchmarking with many-body quantum chaos. Nature613, 468–473 (2023). 10.1038/s41586-022-05442-1 [DOI] [PubMed] [Google Scholar]
- 43.Karamlou, A. H. et al. Probing entanglement in a 2D hard-core Bose-Hubbard lattice. Nature629, 561–566 (2024). 10.1038/s41586-024-07325-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Yanay, Y., Braumüller, J., Gustavsson, S., Oliver, W. D. & Tahan, C. Two-dimensional hard-core Bose–Hubbard model with superconducting qubits. Npj Quantum Inf.6, 58 (2020). 10.1038/s41534-020-0269-1 [DOI] [Google Scholar]
- 45.Sun, Z.-H., Cui, J. & Fan, H. Characterizing the many-body localization transition by the dynamics of diagonal entropy. Phys. Rev. Res.2, 013163 (2020). 10.1103/PhysRevResearch.2.013163 [DOI] [Google Scholar]
- 46.Khait, I., Gazit, S., Yao, N. Y. & Auerbach, A. Spin transport of weakly disordered heisenberg chain at infinite temperature. Phys. Rev. B93, 224205 (2016). 10.1103/PhysRevB.93.224205 [DOI] [Google Scholar]
- 47.Gopalakrishnan, S., Agarwal, K., Demler, E. A., Huse, D. A. & Knap, M. Griffiths effects and slow dynamics in nearly many-body localized systems. Phys. Rev. B93, 134206 (2016). 10.1103/PhysRevB.93.134206 [DOI] [Google Scholar]
- 48.Setiawan, F., Deng, D.-L. & Pixley, J. H. Transport properties across the many-body localization transition in quasiperiodic and random systems. Phys. Rev. B96, 104205 (2017). 10.1103/PhysRevB.96.104205 [DOI] [Google Scholar]
- 49.Luitz, D. J. & Lev, Y. B. The ergodic side of the many-body localization transition. Ann. Phys.529, 1600350 (2017). 10.1002/andp.201600350 [DOI] [Google Scholar]
- 50.Morong, W. et al. Observation of Stark many-body localization without disorder. Nature599, 393–398 (2021). 10.1038/s41586-021-03988-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Schulz, M., Hooley, C. A., Moessner, R. & Pollmann, F. Stark Many-Body Localization. Phys. Rev. Lett.122, 040606 (2019). 10.1103/PhysRevLett.122.040606 [DOI] [PubMed] [Google Scholar]
- 52.van Nieuwenburg, E., Baum, Y. & Refael, G. From bloch oscillations to many-body localization in clean interacting systems. Proc. Natl. Acad. Sci.116, 9269–9274 (2019). 10.1073/pnas.1819316116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Wang, Y.-Y., Sun, Z.-H. & Fan, H. Stark many-body localization transitions in superconducting circuits. Phys. Rev. B104, 205122 (2021). 10.1103/PhysRevB.104.205122 [DOI] [Google Scholar]
- 54.Taylor, S. R., Schulz, M., Pollmann, F. & Moessner, R. Experimental probes of Stark many-body localization. Phys. Rev. B102, 054206 (2020). 10.1103/PhysRevB.102.054206 [DOI] [PubMed] [Google Scholar]
- 55.Doggen, E. V. H., Gornyi, I. V. & Polyakov, D. G. Stark many-body localization: Evidence for Hilbert-space shattering. Phys. Rev. B103, L100202 (2021). 10.1103/PhysRevB.103.L100202 [DOI] [Google Scholar]
- 56.Khemani, V., Hermele, M. & Nandkishore, R. Localization from hilbert space shattering: From theory to physical realizations. Phys. Rev. B101, 174204 (2020). 10.1103/PhysRevB.101.174204 [DOI] [Google Scholar]
- 57.Sala, P., Rakovszky, T., Verresen, R., Knap, M. & Pollmann, F. Ergodicity breaking arising from hilbert space fragmentation in dipole-conserving hamiltonians. Phys. Rev. X10, 011047 (2020). [Google Scholar]
- 58.Serbyn, M., Papić, Z. & Abanin, D. A. Local conservation laws and the structure of the many-body localized states. Phys. Rev. Lett.111, 127201 (2013). 10.1103/PhysRevLett.111.127201 [DOI] [PubMed] [Google Scholar]
- 59.Scherg, S. et al. Observing non-ergodicity due to kinetic constraints in tilted Fermi-Hubbard chains. Nat. Commun.12, 4490 (2021). 10.1038/s41467-021-24726-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Kohlert, T. et al. Exploring the regime of fragmentation in strongly tilted fermi-hubbard chains. Phys. Rev. Lett.130, 010201 (2023). 10.1103/PhysRevLett.130.010201 [DOI] [PubMed] [Google Scholar]
- 61.Bordia, P. et al. Probing slow relaxation and many-body localization in two-dimensional quasiperiodic systems. Phys. Rev. X7, 041047 (2017). [DOI] [PubMed] [Google Scholar]
- 62.Nandy, S. et al. Emergent dipole moment conservation and subdiffusion in tilted chains. Phys. Rev. B109, 115120 (2024). 10.1103/PhysRevB.109.115120 [DOI] [Google Scholar]
- 63.Guardado-Sanchez, E. et al. Subdiffusion and heat transport in a tilted two-dimensional fermi-hubbard system. Phys. Rev. X10, 011042 (2020). [Google Scholar]
- 64.Cross, A. W., Bishop, L. S., Sheldon, S., Nation, P. D. & Gambetta, J. M. Validating quantum computers using randomized model circuits. Phys. Rev. A100, 032328 (2019). 10.1103/PhysRevA.100.032328 [DOI] [Google Scholar]
- 65.Saffman, M., Walker, T. G. & Mølmer, K. Quantum information with rydberg atoms. Rev. Mod. Phys.82, 2313–2363 (2010). 10.1103/RevModPhys.82.2313 [DOI] [Google Scholar]
- 66.Browaeys, A. & Lahaye, T. Many-body physics with individually controlled Rydberg atoms. Nat. Phys.16, 132–142 (2020). 10.1038/s41567-019-0733-z [DOI] [Google Scholar]
- 67.Henriet, L. et al. Quantum computing with neutral atoms. Quantum4, 327 (2020). 10.22331/q-2020-09-21-327 [DOI] [Google Scholar]
- 68.Kaufman, A. M. et al. Quantum thermalization through entanglement in an isolated many-body system. Science353, 794–800 (2016). 10.1126/science.aaf6725 [DOI] [PubMed] [Google Scholar]
- 69.Gross, C. & Bloch, I. Quantum simulations with ultracold atoms in optical lattices. Science357, 995–1001 (2017). 10.1126/science.aal3837 [DOI] [PubMed] [Google Scholar]
- 70.Xu, K. et al. Probing dynamical phase transitions with a superconducting quantum simulator. Sci, Adv.6, 10.1126/sciadv.aba4935 (2020). [DOI] [PMC free article] [PubMed]
- 71.Xu, K. et al. Metrological characterization of non-gaussian entangled states of superconducting qubits. Phys. Rev. Lett.128, 150501 (2022). 10.1103/PhysRevLett.128.150501 [DOI] [PubMed] [Google Scholar]
- 72.Jin, F. et al. Random state technology. J. Phys. Soc. Jpn.90, 012001 (2020). 10.7566/JPSJ.90.012001 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The authors declare that the data supporting the findings of this study are available within the paper and its Supplementary Information files. Should any raw data files be needed in another format, they are available from the corresponding author upon reasonable request. Source data are provided in this paper.