GradICON: Approximate Diffeomorphisms via Gradient Inverse Consistency

Abstract

We present an approach to learning regular spatial transformations between image pairs in the context of medical image registration. Contrary to optimization-based registration techniques and many modern learning-based methods, we do not directly penalize transformation irregularities but instead promote transformation regularity via an inverse consistency penalty. We use a neural network to predict a map between a source and a target image as well as the map when swapping the source and target images. Different from existing approaches, we compose these two resulting maps and regularize deviations of the Jacobian of this composition from the identity matrix. This regularizer – GradICON – results in much better convergence when training registration models compared to promoting inverse consistency of the composition of maps directly while retaining the desirable implicit regularization effects of the latter. We achieve state-of-the-art registration performance on a variety of real-world medical image datasets using a single set of hyperparameters and a single non-dataset-specific training protocol. Code is available at https://github.com/uncbiag/ICON.

1. Introduction

Image registration is a key component in medical image analysis to estimate spatial correspondences between image pairs [14, 53]. Applications include estimating organ motion between treatment fractions in radiation therapy [25, 37], capturing disease progression [64], or allowing for localized analyses in a common coordinate system [19].

Many different registration algorithms have been proposed over the last decades in medical imaging [10, 41, 44, 63, 64] and in computer vision [21, 33]. Contributions have focused on different transformation models (i.e., what types of transformations are considered permissible), similarity measures (i.e., how “good alignment” between image pairs is quantified), and solution strategies (i.e., how transformation parameters are numerically estimated). The respective choices are generally based on application requirements as well as assumptions about image appearance and the expected transformation space. In consequence, while reliable registration algorithms have been developed for transformation models ranging from simple parametric models (e.g., rigid and affine transformations) to significantly more complex nonparametric formulations [41, 44, 63] that allow highly localized control, practical applications of registration typically require many choices and rely on significant parameter tuning to achieve good performance. Recent image registration work has shifted the focus from solutions based on numerical optimization for a specific image pair to learning to predict transformations based on large populations of image pairs via neural networks [10, 15, 17, 34, 35, 56, 57, 68]. However, while numerical optimization is now replaced by training a regression model which can be used to quickly predict transformations at test time, parameter tuning remains a key challenge as loss terms for these two types of approaches are highly related (and frequently the same). Further, one also has additional choices regarding network architectures. Impressive strides have been made in optical flow estimation as witnessed by the excellent performance of recent approaches [34] on Sintel [7]. However, our focus is medical image registration, where smooth and often diffeomorphic transformations are desirable; here, a simple-to-use learning-based registration approach, which can adapt to different types of data, has remained elusive. In particular, nonparametric registration approaches require a balance between image similarity and regularization of the transformation to assure good matching at a high level of spatial regularity, as well as choosing a suitable regularizer. This difficulty is compounded in a multi-scale approach where registrations at multiple scales are used to avoid poor local solutions.

Instead of relying on a complex spatial regularizer, the recent ICON approach [23] uses only inverse consistency to regularize the sought-after transformation map, thereby dramatically reducing the number of hyperparameters to tune. While inverse consistency is not a new concept in image registration and has been explored to obtain transformations that are inverses of each other when swapping the source and the target images [11], ICON [23] has demonstrated that a sufficiently strong inverse consistency penalty, by itself, is sufficient for spatial regularity when used with a registration network. Further, as ICON does not explicitly penalize spatial gradients of the deformation field, it does not require pre-registration (e.g., rigid or affine), unlike many other related works. However, while conceptually attractive, ICON suffers from the following limitations: 1) training convergence is slow, rendering models costly to train; and 2) enforcing approximate inverse consistency strictly enough to prevent folds becomes increasingly difficult at higher spatial resolutions, necessitating a suitable schedule for the inverse consistency penalty, which is not required for GradICON.

Our approach is based on a surprisingly simple, but effective observation: penalizing the Jacobian of the inverse consistency condition instead of inverse consistency directly¹ applies zero penalty for inverse consistent transform pairs but 1) yields significantly improved convergence, 2) no longer requires careful scheduling of the inverse consistency penalty, 3) results in spatially regular maps, and 4) improves registration accuracy. These benefits facilitate a unified training protocol with the same network structure, regularization parameter, and training strategy across registration tasks.

Our contributions are as follows:

• We develop GradICON (Gradient Inverse CONsistency), a versatile regularizer for learning-based image registration that relies on penalizing the Jacobian of the inverse consistency constraint and results, empirically and theoretically, in spatially well-regularized transformation maps.

• We demonstrate state-of-the-art (SOTA) performance of models trained with GradICON on three large medical datasets: a knee magnetic resonance image (MRI) dataset of the Osteoarthritis Initiative (OAI) [46], the Human Connectome Project’s collection of Young Adult brain MRIs (HCP) [60], and a computed tomography (CT) inhale/exhale lung dataset from COPDGene [47].

2. Related work

Nonparametric transformation models & regularization.

There are various ways of modeling a transformation between image pairs. The most straightforward nonparametric approach is via a displacement field [59]. Different regularizers for displacement fields have been proposed [32], but they are typically only appropriate for small displacements [44] and cannot easily guarantee diffeomorphic transformations [2], which is our focus here for medical image registration. Fluid models, which parameterize a transformation by velocity fields instead, can capture large deformations and, given a suitably strong regularizer, result in diffeomorphic transformations. Popular fluid models are based on viscous fluid flow [12, 13], the large deformation diffeomorphic metric mapping (LDDMM) model [5], or its shooting variant [41, 63]. Simpler stationary fluid approaches, such as the stationary velocity field (SVF) approach [1, 61], have also been developed. While diffeomorphic transformations are not always desirable, they are often preferred due to their invertibility, which allows mappings between images to preserve object topologies and prevent foldings that are physically implausible. These models have initially been developed for pair-wise image registration where solutions are determined by numerical optimization, but have since, with minimal modifications, been integrated with neural networks [4, 52, 68]. In a learning-based formulation, the losses are typically the same as for numerical-optimization approaches, but one no longer directly optimizes over the parameters of the chosen transformation model but instead over the parameters of a neural network which, once trained, can quickly predict the transformation model parameters.

Fluid registration models are computationally complex as they require solving a fluid equation (either greedily or via direct numerical integration [42], or via scaling and squaring [1]), but can guarantee diffeomorphic transformations. In contrast, displacement field models are computationally cheaper but make it more difficult to obtain diffeomorphic transformations. Solution regularity can be obtained for displacement field models by adding appropriate constraints on the Jacobian [24]. Alternatively, invertibility can be encouraged by adding inverse consistency losses, either for numerical optimization approaches [11] or in the context of registration networks as is the case for ICON [23]. Similar losses have also been used in computer vision to encourage cycle consistencies [6, 22, 67, 69] though they are, in general, not focused on spatial regularity. Most relevant to our approach, ICON [23] showed that inverse consistency alone is sufficient to approximately obtain diffeomorphic transformations when the displacement field is predicted by a neural network. Our work extends this approach by generalizing the inverse consistency loss to a gradient inverse consistency loss, which results in smooth transformations, faster convergence, and more accurate registration results.

Multi-scale image registration.

Finding good solutions for the optimization problems of image registration is challenging, and one might easily get trapped in an unfavorable local minimum. In particular, this might happen for self-similar images, such as lung vessels, where incorrect vessel alignment might be locally optimal. Further, if there is no overlap between vessels, a similarity measure might effectively be blind to misalignment, which is why it is important for a similarity measure to have a sufficient capture range².

Multi-scale approaches have been proposed for optimization-based registration models [39, 55, 58, 70] to overcome these issues. For these approaches, the loss function is typically first optimized at a coarse resolution, and the image warped via the coarse transformation then serves as the input for the optimization at a finer resolution. This helps to avoid poor local optima, as solutions computed at coarser resolutions effectively increase capture range and focus on large-scale matching first rather than getting distracted by fine local details. Multi-scale approaches have also been used for learning-based registration [16, 18, 29, 36, 45, 52] and generally achieve better results than methods that only consider one scale [4]. These methods all use sub-networks operating at different scales but differ in how the multi-scale strategy is incorporated into the network structure and the training process. A key distinction is if source images are warped as they pass through the different sub-networks [16, 23, 29, 45] or if sub-networks always start from the unwarped, albeit downsampled, source image [18]. The former approach simplifies capturing large deformations as sub-networks only need to refine a transformation rather than capturing it in its entirety. However, these methods compute the similarity measure and the regularizer losses at all scales, which requires balancing the weights of the losses across all scales and for each scale between the similarity measure and the regularizer. Hence, there are many parameters that are difficult to tune. To side-step the tuning issue, it is common to rely on a progressive training protocol to avoid tuning the weights between losses at all scales. We find that our multi-resolution approach trains well when the loss and regularizer are applied only at the highest scale: the coarser components are effectively trained by gradients propagating back through the multi-scale steps.

3. Gradient Inverse Consistency (GradICON)

3.1. Preliminaries

We denote by $I^A:\Omega \to \mathbb{R}$ and $I^B:\Omega \to \mathbb{R}$ the source and the target images in our registration problem. By ${\Phi }^{AB}:{\mathbb{R}}^d\to {\mathbb{R}}^d$ we denote a transformation map with the intention that $I^A\circ {\Phi }^{AB}~I^B$. The map ${\Phi }^{AB}$ is a diffeomorphism if it is differentiable, bijective and its inverse is differentiable as well³. Optimization-based image registration approaches typically solve the optimization problem

$${\tau }^{*}=\text{arg}\underset{\tau }{\text{min}}{ℒ}_{\text{sim}}\left(I^A\circ {\phi }_{\tau }^{-1},I^B\right)+\lambda {ℒ}_{\text{reg}}\left(\tau \right),$$ (1)

where ${ℒ}_{\text{sim}}(\cdot ,\cdot )$ is the similarity measure, ${ℒ}_{\text{reg}}(\cdot )$ is a regularizer, $\tau$ are the transformation parameters, and $\lambda \ge 0$. In learning-based registration, one does not directly optimize over the transformation parameters of ${\phi }^{-1}$, but instead over the parameters $\theta$ of a neural network ${\Phi }_{\theta }$ that predicts ${\phi }^{-1}$ given the source and target images. Such a network is trained over a set of image pairs $I={\left\{\left(I_i^A,I_i^B\right)\right\}}_{i=1}^N$ by solving

$${\theta }^{*}=\text{arg}\underset{\theta }{\text{min}}\frac{1}{N}{\sum }_{i=1}^N{ℒ}_{\text{sim}}\left(I_i^A\circ {\Phi }_{\theta ,i}^{AB},I_i^B\right)+\lambda {ℒ}_{\text{reg}}\left({\Phi }_{\theta ,i}^{AB}\right)$$ (2)

with ${\Phi }_{\theta ,i}^{AB}$ as shorthand for ${\Phi }_{\theta }\left[I_i^A,I_i^B\right]$ denoting the output of the network given the $i$-th input image pair. By training with $\left(I_i^A,I_i^B\right)$ and $\left(I_i^B,I_i^A\right)$ the loss is symmetric in expectation. For ease of notation, we omit the subscripts $i$ or $\theta$ in cases where the dependency is clear from the context.

3.2. Regularization

Picking a good regularizer ${ℒ}_{\text{reg}}$ is essential as it implicitly expresses the class of transformations one considers plausible for a registration. Ideally, the space of plausible transformations should be known (e.g., based on physical principles) or learned from the data. As nonparametric image registration (at least for image pairs) is an ill-posed problem [20], regularization is required to obtain reasonable solutions.

Regularizers frequently involve spatial derivatives of various orders to discourage spatial non-smoothness [32]. This typically requires picking a type of differential operator (or, conversely, a smoothing operator) as well as all its associated parameters. Most often, this regularizer is chosen for convenience and not learned from data. Instead of explicitly penalizing spatial non-smoothness, ICON [23] advocates using inverse consistency as a regularizer, which amounts to learning a transformation space from data in the class of (approximately) invertible transforms. When implementing inverse consistency, there is a choice of loss. The ICON approach penalizes the sum-of-squares difference between the identity and the composition of the maps between images $\left(I^A,I^B\right)$ and $\left(I^B,I^A\right)$, i.e., the regularizer has the form ${ℒ}_{\text{reg}}^{\mathtt{\text{ICON}}}={∥{\Phi }_{\theta }^{AB}\circ {\Phi }_{\theta }^{BA}-\mathrm{I}\mathrm{d}∥}_2^2$, where Id denotes the identity transform. In [23], it is shown that this loss has an implicit regularization effect, similar to a sum-of-squares on the gradient of the transformation, i.e., an $H^1$ type of norm. In fact, it turns out that regular invertible maps can be learned without explicitly penalizing spatial gradients. Inspired by this observation, we propose to use the Jacobian $(\nabla )$ of the composition of the maps instead, i.e.,

$${ℒ}_{\text{reg}}^{\mathtt{\text{GradICON}}}={‖\nabla \left[{\Phi }_{\theta }^{AB}\circ {\Phi }_{\theta }^{BA}\right]-I‖}_F^2,$$ (3)

where $\mathbf{I}$ the identity matrix, and $\parallel \cdot {\parallel }_F^2$ is the squared Frobenius norm integrated over $\Omega$. As we will see in Sec. 5, this loss equally leads to regular maps by exerting another form of implicit regularization, which we analyze in Sec. 3.3. To understand the implicit regularization of the ICON loss, one makes the modeling choice ${\Phi }_{\theta }^{AB}={\Phi }^{AB}+\epsilon n^{AB}$ such that ${\Phi }^{BA}\left({\Phi }^{AB}\right)=\mathrm{I}\mathrm{d}$, i.e., the output of the network is inverse consistent up to a white noise term $n$ with parameter $\epsilon >0$ (artificially introduced to make the discussion clear). This white noise can be used to prove that the resulting maps are regularized via the square of a first-order Sobolev (semi-) norm. Further, [23] empirically showed that an approximate diffeomorphism can be obtained without the white noise when used in the context of learning a neural registration model: if inverse consistency is not exactly enforced, as suggested above, the inconsistency can be modeled by noise, and the observed smoothness is explained by the theoretical result. In our analysis, we follow a conceptually similar idea.

3.3. Analysis

Implicit ${\mathit{H}}^1$ type regularization.

Since the GradICON loss of Eq. (3) is formulated in terms of the gradient, it is a natural assumption to put the white noise on the Jacobians themselves rather than on the maps, i.e., $\nabla {\Phi }_{\theta }^{AB}=\nabla {\Phi }^{AB}+\epsilon N$ where $N$ is a white noise. This model of randomness is motivated by the stochastic gradient scheme on the global population that drives the parameters of the networks. At the level of maps, we write ${\Phi }_{\theta }^{AB}={\Phi }^{AB}+\epsilon n$ where $N=\nabla n$. Since integration is a low-pass filter, the noise $n$ applies to the low frequencies of ${\Phi }_{\theta }^{AB}$. In addition, we expect the low frequencies of the noise to be dampened by the similarity measure between $I^A\circ {\Phi }^{AB}$ and $I^B$. Hence, we hypothesize that $\parallel n\parallel \ll \parallel \nabla n\parallel$, which will be used only once in our analysis. This comparison means that our estimates of the gradient $\nabla n$ and $n$ on our grid satisfy this inequality. We assess this hypothesis Appendix A.1. We start by rewriting the GradICON regularizer, by applying the chain rule, as

$$\begin{gathered} {ℒ}_{\text{reg}}^{\mathtt{\text{GradICON}}}=\parallel \left(\nabla {\Phi }^{AB}\right.\left.\left({\Phi }_{\theta }^{BA}\right)+\epsilon \nabla n^{AB}\left({\Phi }_{\theta }^{BA}\right)\right). \\ \left(\nabla {\Phi }^{BA}+\epsilon \nabla n^{BA}\right)-I{\parallel }_F^2, \end{gathered}$$ (4)

using $\nabla {\Phi }_{\theta }^{AB}=\nabla {\Phi }^{AB}+\epsilon \nabla n^{AB}$ and still omitting the integral sign. We now Taylor expand the loss w.r.t. $\epsilon$ and in particular expand the $\nabla {\Phi }^{AB}(\left.{\Phi }_{\theta }^{BA}\right)$ term from Eq. (4) as

$$\nabla {\Phi }^{AB}\left({\Phi }_{\theta }^{BA}\right)=\nabla {\Phi }^{AB}\left({\Phi }^{BA}\right)+\epsilon {\nabla }^2{\Phi }^{AB}\left({\Phi }^{BA}\right)n^{BA}+o\left(\epsilon \right).$$ (5)

where $\parallel n\parallel \ll \parallel \nabla n\parallel$ implies that the approximation

$$\nabla {\Phi }^{AB}\left({\Phi }_{\theta }^{BA}\right)=\nabla {\Phi }^{AB}\left({\Phi }^{BA}\right)+o\left(\epsilon \right)$$ (6)

holds as it is only compared with $\nabla n$ in the expansion. Using the first-order approximation $\nabla n^{AB}\left({\Phi }_{\theta }^{BA}\right)\approx \nabla n^{AB}\left({\Phi }^{BA}\right)$, see Appendix A.1, and simplifying Eq. (4), we obtain

$${ℒ}_{\text{reg}}^{\mathtt{\text{GradICON}}}\approx {\epsilon }^2{‖\nabla n^{AB}\left({\Phi }^{BA}\right)\nabla {\Phi }^{BA}+\nabla {\Phi }^{AB}\left({\Phi }^{BA}\right)\nabla n^{BA}‖}_F^2,$$ (7)

as $\nabla {\Phi }^{AB}\left({\Phi }^{BA}\right)={\left[\nabla {\Phi }^{BA}\right]}^{-1}$ (and selecting the first-order coefficients in $\epsilon$). Expanding the square then yields

$${ℒ}_{\text{reg}}^{\mathtt{\text{GradICON}}}\approx {\epsilon }^2\left({‖\nabla n^{AB}\left({\Phi }^{BA}\right)\nabla {\Phi }^{BA}‖}_F^2+{‖{\left[\nabla {\Phi }^{BA}\right]}^{-1}\nabla n^{BA}‖}_F^2\right.\left.+2{〈\nabla n^{AB}\left({\Phi }^{BA}\right)\nabla {\Phi }^{BA},{\left[\nabla {\Phi }^{BA}\right]}^{-1}\nabla n^{BA}〉}_F\right).$$ (8)

Under the assumption of independence of the white noises $\nabla n^{AB}$ and $\nabla n^{BA}$, the contribution of the last term in Eq. (8) vanishes in expectation. We are left with the following loss, at order ${\epsilon }^2$, now taking expectation,

$$\mathbb{E}\left[{ℒ}_{\text{reg}}^{\mathtt{\text{GradICON}}}\right]\approx {\epsilon }^2\mathbb{E}[{‖\nabla n^{AB}\left({\Phi }^{BA}\right)\nabla {\Phi }^{BA}‖}_F^2+{‖{\left[\nabla {\Phi }^{BA}\right]}^{-1}\nabla n^{BA}‖}_F^2].$$ (9)

Note that the expectation is explicit due to the white noise assumption; thus, Eq. (9) can be further simplified to

$$\mathbb{E}\left[{ℒ}_{\text{reg}}^{\mathtt{\text{GradICON}}}\right]\approx {\epsilon }^2\left({‖{\left[\nabla {\Phi }^{AB}\right]}^{-1}\sqrt{\text{Det}\left(\nabla {\Phi }^{AB}\right)}‖}_F^2\right.\left.+{‖{\left[\nabla {\Phi }^{BA}\right]}^{-1}‖}_F^2\right).$$ (10)

Eq. (10) amounts to an $L^2$ regularization of the inverse of the Jacobian maps on ${\Phi }^{AB}$ and ${\Phi }^{BA}$ which explains why we call it $H^1$ type of regularization, see Appendix A.1; yet, strictly speaking, it is not the standard $H^1$ norm [40].

Comparison with ICON [23].

Interestingly, our analysis shows that GradICON is an $H^1$ type of regularization as for ICON, although we could have expected a second-order regularization from the model. Such higher-order terms appear when taking into account the magnitude of the noise $n$ in the expansion. While there are several assumptions that can be formulated differently, such as the form of the noise and the fact that it is white noise for given pairs of images $\left(I^A,I^B\right)$, we believe that Eq. (10) is a plausible explanation of the observed regularity of the maps in practice. Importantly, since this regularization is implicit, GradICON, as well as ICON can learn based on a slightly more informative prior than this $H^1$ regularization which relies on simplifying assumptions.

Why GradICON performs better than ICON.

In practice, we observe that learning a registration model via the GradICON regularizer of Eq. (3) shows a faster convergence than using the ICON regularizer, not only in the toy experiment of Sec. 5.4 but also on real data. While we do not yet have a clear explanation for this behavior, we provide insight based on the following key differences between the two variants.

First, a difference by a translation is not penalized in the GradICON formulation, but implicitly penalized in the similarity measure, assuming images are not periodic. Second, using the Jacobian in Eq. (3) correlates the composition of the map between neighboring voxels. In a discrete (periodic) setting, this can be seen by expanding the squared norm. To shorten notations, define $\psi \left(x\right):={\Phi }^{AB}\left({\Phi }^{BA}\left(x\right)\right)–\text{Id}$ considered as a discrete vector. Then, Eq. (3) is the sum over voxels ${\sum }_i\frac{{\left|\psi \left(x_i+\delta \right)-\psi \left(x_i\right)\right|}^2}{{\delta }^2}$, which can be rewritten as

$${ℒ}_{\text{reg}}^{\mathtt{\text{GradICON}}}=\frac{2\Vert \psi {\Vert }_{L^2}^2}{{\delta }^2}\left(1-\frac{〈\psi \left(\cdot \right),\psi \left(\cdot +\delta \right)〉}{\Vert \psi {\Vert }_{L^2}^2}\right),$$ (11)

where $\delta$ is the (hyper-)parameter for the finite difference estimation of the gradient. This shows that the GradICON regularizer includes more correlation than the ICON regularizer, which would only contain the first factor in Eq. (11). Lastly, it is known [9] that gradient descent on an $H^1$ energy rather than $L^2$ energy is a preconditioning of the gradient flow, emphasizing high-frequencies over low-frequencies. In our case, however, high-frequencies are the dominant cause of folds. Consequently, as GradICON penalizes high frequencies but allows low frequencies of the composition of the maps to deviate from identity, this is beneficial to avoid folds⁴. Overall, GradICON is more flexible than ICON while retaining the non-folding behavior of the resulting maps.

4. Implementation

To learn a registration model under Eq. (3), we use a neural network that predicts the transformation maps. In particular, we implement a multi-step (i.e., multiple steps within a forward pass), multi-resolution approach trained with a two-stage process, followed by optional instance optimization at test time. We will discuss these parts next.

4.1. Network structure

To succinctly describe our network structure, we hence-forth omit $\theta$ and represent a registration neural network as $\Phi$ (or e.g. $\Psi$). The notation ${\Phi }^{AB}$ (shorthand for $\Phi \left[I^A,I^B\right]$) represents the output of this network (a transform from ${\mathbb{R}}^d\to {\mathbb{R}}^d$) for input images $I^A$ and $I^B$. To combine such registration networks into a multistep, multiscale approach, we rely on the following combination operators from [23]:

$$\mathtt{\text{Down}}\left\{\Phi \right\}\left[I^A,I^B\right]:=\Phi \left[\mathtt{\text{AvgPool}}\left(I^A,2\right),\mathtt{\text{AvgPool}}\left(I^B,2\right)\right]$$

$$\mathtt{\text{TS}}\{\Phi ,\Psi \}\left[I^A,I^B\right]:=\Phi \left[I^A,I^B\right]\circ \Psi \left[I^A\circ \Phi \left[I^A,I^B\right],I^B\right]$$

The downsample operator (Down) is for predicting the warp between two high-resolution images using a network that operates on low-resolution images, and the two-step operator (TS) is for predicting the warp between two images in two steps, first capturing the coarse transform via $\Phi$ and then the residual transform via $\Psi$. We use these operators to realize a multi-resolution, multi-step network, see Fig. 2, via

$$\begin{gathered} \mathtt{\text{Stage}}1=\mathtt{\text{TS}}\left\{\mathtt{\text{Down}}\left\{\mathtt{\text{TS}}\left\{\mathtt{\text{Down}}\left\{{\Psi }_1\right\},{\Psi }_2\right\}\right\},{\Psi }_3\right\} \\ \mathtt{\text{Stage}}2=\mathtt{\text{TS}}\left\{\mathtt{\text{Stage}}1,{\Psi }_4\right\} \end{gathered}$$ (12)

Our atomic (i.e., not composite) registration networks ${\Psi }_i$ are each represented by a UNet instance⁵ from [23] taking as input two images and returning a displacement field $D$. These displacement fields are converted to functions $x\mapsto x+\mathtt{\text{interpolate}}(D,x)$ since the above operators are defined on networks that return functions from ${\mathbb{R}}^d$ to ${\mathbb{R}}^d$.

Figure 2.

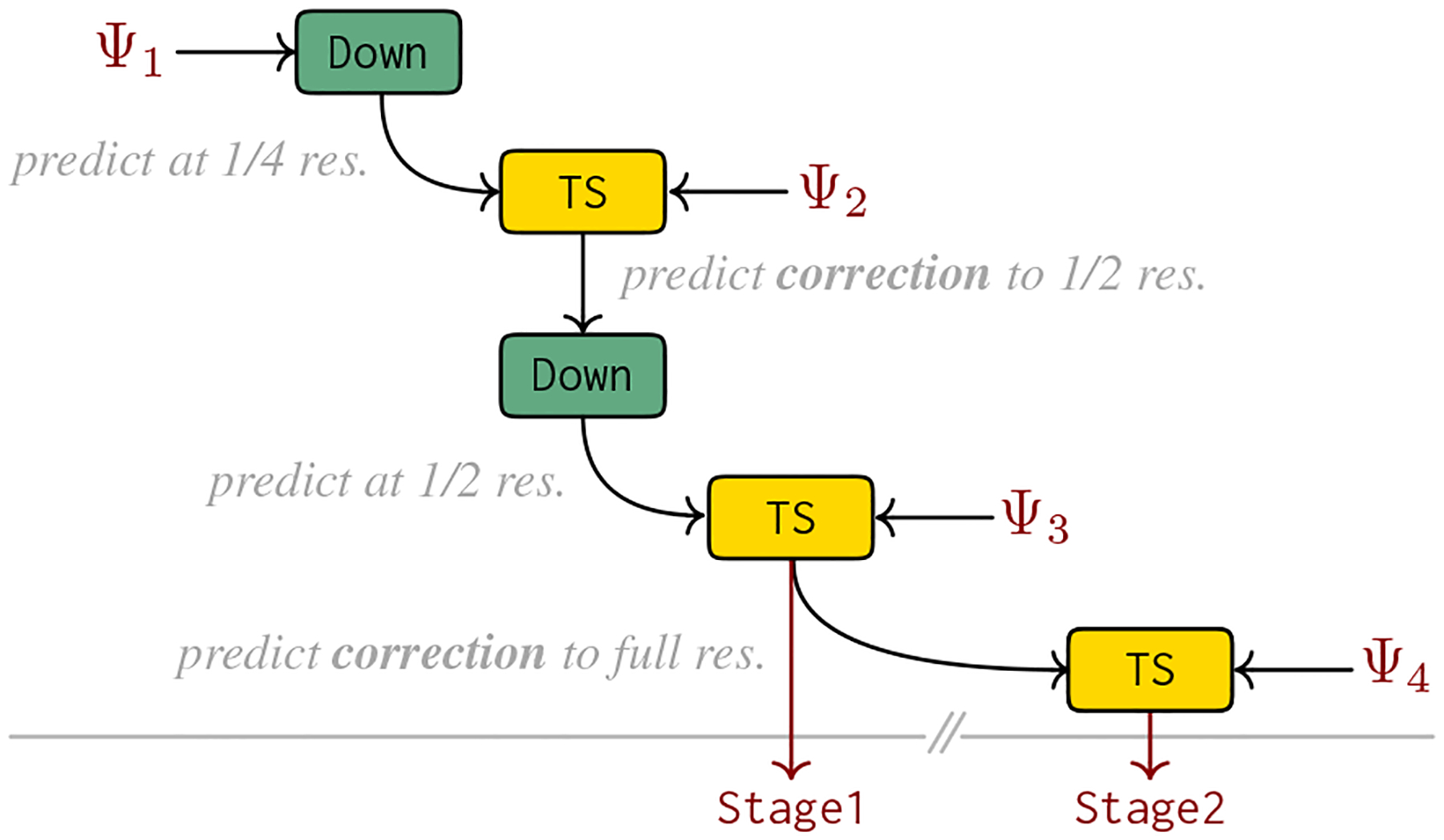
Illustration of the combination steps to create our registration network, see Eq. (12), from the atomic registration networks (${\Psi }_i$) via the downsample (Down) and the two-step (TS) operator.

4.2. Training

We define a single training protocol that is applied to train a network on all the registration tasks of Sec. 5. For preprocessing, each image has its intensity clipped and rescaled to [0, 1], with clipping intensities appropriate for the modality and anatomy being registered. For modalities with region of interest (ROI) annotations (brain and lung), all values outside the region of interest are set to zero. For intra-subject registration, we have many fewer pairs to train on⁶, so we perform augmentation via random flips along axes and small affine warps (see Appendix A.2). In all experiments, the image similarity measure is combined with the GradICON regularizer to yield the overall loss

$$\begin{gathered} ℒ={ℒ}_{\text{sim}}\left(I^A\circ \Phi \left[I^A,I^B\right],I^B\right)+ \\ {ℒ}_{\text{sim}}\left(I^B\circ \Phi \left[I^B,I^A\right],I^A\right)+ \\ +\lambda {‖\nabla \left(\Phi \left[I^A,I^B\right]\circ \Phi \left[I^B,I^A\right]\right)-I‖}_F^2. \end{gathered}$$ (13)

In our implementation, $\nabla \left({\Phi }^{AB}\circ {\Phi }^{BA}\right)$ is computed using one-sided finite differences with $\Delta x=1\mathrm{e}-3,\parallel \cdot {\parallel }_F^2$ is computed by (uniform) random sampling over $\Omega$ with number of samples equal to the number of voxels in the image $/2^d$, and we use coordinates where $\Omega =[0,1{]}^3$.

Multi-stage training.

We train in two stages. Stage1: we train the multi-resolution network defined in Eq. (12) with the loss from Eq. (13). Stage2: we train with the same loss, jointly optimizing the parameters of Stage1 and ${\Psi }_4$.

Instance optimization.

We optionally optimize the loss of Eq. (13) for 50 iterations at test time [66]. This typically improves performance but also increases runtime.

Unless noted otherwise, we use LNCC (local normalized cross-correlation) with a Gaussian kernel (std. of 5 voxels), computed as in [65], and GradICON with balancing parameter $\lambda =1.5$. Stage1 and Stage2 are trained using ADAM at a learning rate of 5e-5 for 50,000 iterations each. This protocol remains fixed across all datasets, and any result obtained by exactly this protocol is marked by †; if instance optimization is included, results are marked by ‡.

5. Experiments

Ethics.

We use one 2D synthetic (Triangles and Circles), one real 2D (DRIVE), and four real 3D datasets (OAI, HCP, COPDGene, DirLab). Acquisitions for all real datasets were approved by the respective Institutional Review Boards.

5.1. Datasets

Triangles and Circles.

A synthetic 2D dataset introduced in [23] where images are either triangles or circles. We generate 2000 hollow images with size 128 × 128 which consist of the shape edges and use them as the training set.

DRIVE [54].

This 2D dataset contains 20 retina images and the corresponding vessel segmentation masks. We use the segmentation masks to define a synthetic registration problem. In particular, we take downsampled segmentations as the source (/target) image and warp them with random deformations generated by ElasticDeform⁷ to obtain the corresponding target (/source) image. We generate 20 pairs per image, leading to 400 pairs at size 292×282 in total.

OAI [46].

We use a subset of 2532 images from the full corpus of MR images of the Osteoarthritis Initiative (OAI⁸) for training and 301 pairs of images for testing. The images are normalized so that the 1th percentile and the 99th percentile of the intensity are mapped to 0 and 1, respectively. Then we clamp the normalized intensity to be in [0, 1]. We follow the train-test split⁹ used in [23, 52]. We downsample images from 160×384×384 to 80×192×192

HCP [60].

We use a subset of T1-weighted and brain-extracted images of size 260×311×260 from the Human Connectome Project’s (HCP) young adult dataset to assess inter-patient brain registration performance. We downsample images to 130×155×130 for training but evaluate the average Dice score for 28 manually segmented subcortical brain regions [49, 50]¹⁰ at the original resolution. We train on 1076 images, excluding the 44 images we use for testing.

COPDGene [47].

We use a subset of¹¹ 999 inspiratory-expiratory lung CT pairs from the COPDGene study¹² [47] with provided lung segmentation masks for training. The segmentation masks are computed automatically¹³. CT images are first resampled to isotropic spacing (2 mm) and cropped/padded evenly along each dimension to obtain a 175×175×175 volume. Hounsfield units are clamped within [−1000, 0] and scaled linearly to [0, 1]. Then, the lung segmentations are applied to the images to extract the lung region of interest (ROI). Among the processed data, we use 899 pairs for training and 100 pairs for validation.

DirLab [8].

This dataset is only used to evaluate a trained network. It contains 10 pairs of inspiration-expiration lung CTs with 300 anatomical landmarks per pair, manually identified by an expert in thoracic imaging. We applied the same preprocessing and lung segmentation as for COPDGene.

5.2. Ablation study

In Table 1, we investigate 1) which UNet structure should be used and 2) how multi-resolution, multi-stage training, instance optimization, and data augmentation affect the registration results. To this end, we train on COPDGene and evaluate on DirLab using the same similarity measure, regularizer weight $\lambda$, and number of iterations. We report the mean target registration error (mTRE) on landmarks (in mm) and the percentage of voxels with negative Jacobian $\left(\%\right|J\left|\right)$. First, we observe that the UNet from [23] performs better than the UNet from [4]. Hence, in all experiments, we adopt the former as our backbone. Notably, this model has considerably more parameters than the variant from [4] (≈ 17M vs. 300k, see Appendix A.6), but uses less V-RAM as it concentrates parameters in the heavily downsampled layers of the architecture. Second, we find that the multi-resolution approach, including Stage2 training, clearly improves performance, reducing the mTRE from 5.176mm to 3.478mm (1 vs. 3 res.) and further down to 3.153mm (with Stage2). In this setting, there is also a noticeable benefit of (affine) data augmentation, with the mTRE dropping to 1.258mm. This is not unexpected, though, as we only have 899 pairs of training images for this (inter-patient) registration task. While this is considered a large corpus for medical imaging standards, it is small from the perspective of training a large neural network. Finally, we highlight that adding instance optimization yields the overall best results, but the benefits are less noticeable in combination with augmentation.

Table 1.

Ablation results for training on COPDGene and evaluating on Dirlab. We assess the effect of the backbone network, the number of resolutions (Res.), including Stage2 training (2nd), instance optimization (Opt.), and affine augmentation (Aug.).

Backbone	Res.	2nd	Opt.	Aug.	mTRE (in mm)	%|J|
UNet from [4]	1				16.21	0.01440
	1				5.176	0.00014
	3				3.478	0.00109
	3			✓	1.756	0.00032
UNet from [23]	3	✓			3.153	0.00042
	3	✓	✓		0.865	0.00021
	3	✓		✓	1.258†	0.00026
	3	✓	✓	✓	0.955‡	0.00023

5.3. Comparison to other regularizers

We study different regularizers in terms of the trade-off between transform regularity and image similarity on the training set when varying $\lambda$. We use Stage1 from Eq. (12) for all experiments, setting the regularizer to either Bending Energy $\left({ℒ}_{\text{reg}}={\sum }_i{∥{\nabla }^2\left({\left({\Phi }^{AB}-\mathrm{I}\mathrm{d}\right)}_i\right)∥}_F^2\right)$, Diffusion $\left({ℒ}_{\text{reg}}={∥\nabla \left({\Phi }^{AB}-\mathrm{I}\mathrm{d}\right)∥}_F^2\right)$, ICON, or GradICON. Specifically, we pick ${\lambda }_0$ for each regularizer such that $\mathrm{\%}\left|J\right|$ is kept at roughly the same level and train multiple networks with $\lambda =\left\{{\lambda }_0\cdot 2^i\mid i\in [-6,6],i\in \mathbb{Z}\right\}$ for the same number of iterations. Fig. 3 shows results on Triangles and Circles and DRIVE. We observe that all the regularizers lose a certain level of accuracy when increasing $\lambda$ and GradICON in general has the least sacrifice in similarity. This is presumably because of the possible magnitude of deformation each regularizer allows. More results can be found in Appendix A.3.

Figure 3.

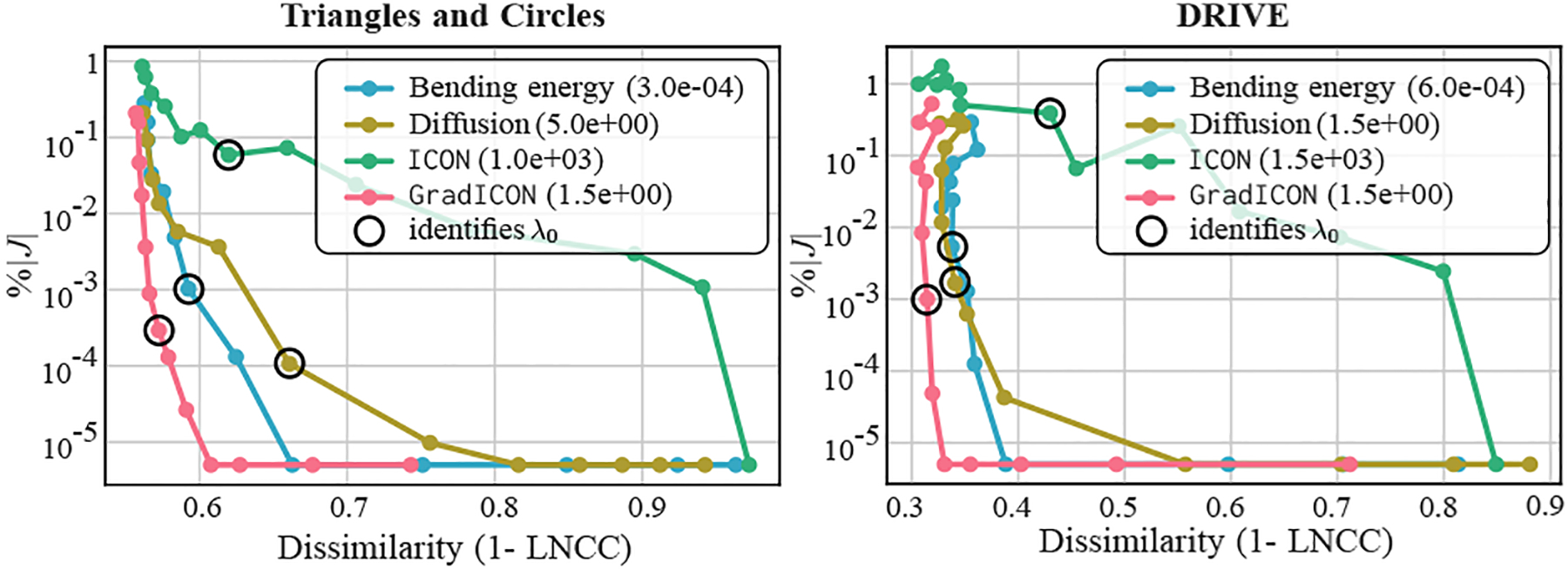
GradICON vs. other regularization techniques.

5.4. Empirical convergence analysis

To demonstrate improved convergence when training models with our GradICON regularizer vs. models trained with the ICON regularizer of [23], we assess the corresponding loss curves under the same network architecture, in particular, the network described in Sec. 4. We are specifically interested in (training) convergence behavior when both models produce a similar level of map regularity. To this end, we choose $\lambda$ to approximately achieve the same similarity loss under both regularizers and plot the corresponding curves for $\%\left|J\right|$, see Fig. 4, for Triangles and Circles and DRIVE.

Figure 4.

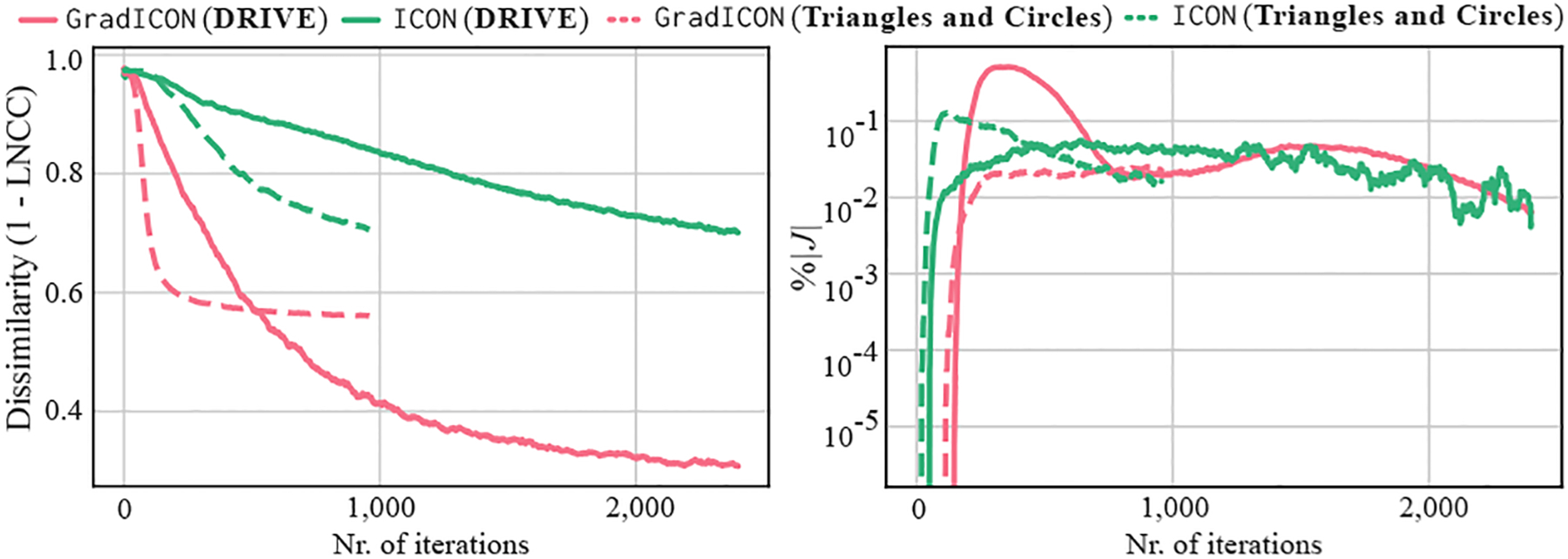
Comparison of the convergence speed (left), visualized as 1-LNCC (i.e., dissimilarity), for ICON and GradICON when $\lambda$ is set to produce a similar level of map regularity (right).

Overall, we see that GradICON converges significantly faster than ICON. We hypothesize that this is due to the fact that maps produced by GradICON contain larger motions than maps produced by ICON. I.e., for the same level of regularity, ICON more strongly limits deformations, effectively slowing down and resulting in less accurate image alignments.

5.5. Inter-patient registration

We evaluate inter-patient registration performance of our model with GradICON regularization on OAI and HCP. We report $\left|\%J\right|$ (as in Sec. 5.2) and the mean DICE score between warped and target image for the segmentations of the femoral and tibial cartilage (OAI), and of a set of 28 subcortical brain regions (HCP). Both measures, averaged over the evaluation data, are listed in Table 2. In particular, we compare GradICON to the methods reported in [52] and [23] on OAI, and compare to ANTs SyN [3] and SynthMorph [31]¹⁴ (sm-shapes/brains) on HCP. Segmentations are not used during training and allow quantifying if the network yields semantically meaningful registrations. Table 2 shows that on the OAI dataset GradICON can significantly outperform the state-of-the-art with minimal parameter tuning and, just as ICON, without the need for affine pre-alignment (i.e., a step needed by many registration methods on OAI). On HCP, GradICON performs better than the standard non-learning approach (SyN) and matches SynthMorph while not requiring affine pre-alignment and producing much less folds.

Table 2.

Results on OAI, HCP and DirLab. † and ‡ indicate results obtained using our standard training protocol (Sec. 4.2), w/o (†) and w/ (‡) instance optimization (Opt.). Only when GradICON is trained with MSE do we set $\lambda =0.2$. Results marked with * are obtained using the official source code; otherwise, values are taken from the literature (see A.5). Top and bottom table parts denote non-learning and learning-based methods, resp. For DirLab, results are shown in the common inspiration→expiration direction. A: affine pre-registration, BE: bending energy, MI: mutual information, TB: Tukey’s biweight, DV: displacement vector of sparse key points, TV: total variation, Curv: curvature regularizer, VCC: volume change control, NGF: normalized gradient flow, TVD: sum of squared tissue volume difference, VMD: sum of squared vesselness measure difference, Diff: diffusion, VF: velocity field, SVF: stationary VF, DVF: displacement vector field. PLOSL₅₀: 50 iterations of instance optimization with PLOSL.

Method	Trans.	${\mathcal{L}}_{\text{reg}}$	${\mathcal{L}}_{\text{sim}}$	DICE ↑	%|J| ↓
OAI
Initial				7.6
Demons [62]	A,DVF	Gaussian	MSE	63.5	0.0006
SyN [3]	A,VF	Gaussian	LNCC	65.7	0.0000
NiftyReg [43]	A,B-Spline	BE	NMI	59.7	0.0000
NiftyReg [43]	A,B-Spline	BE	LNCC	67.9	0.0068
vSVF-opt [52]	A,vSVF	m-Gauss	LNCC	67.4	0.0000
VM [4]	SVF	Diff.	MSE	46.1	0.0028
VM [4]	A,SVF	Diff.	MSE	66.1	0.0013
AVSM [52]	A,vSVF	m-Gauss	LNCC	68.4	0.0005
ICON* [23]	DVF	ICON	MSE	65.1	0.0040
Ours (MSE, λ=0.2)	DVF	GradICON	MSE	69.5	0.0000
Ours (MSE, λ=0.2, Opt.)	DVF	GradICON	MSE	70.5	0.0001
Ours (std. protocol)	DVF	GradICON	LNCC	70.1†	0.0261
	DVF	GradICON	LNCC	71.2‡	0.0042
HCP
Initial				53.4
FreeSurfer-Affine* [48]	A	—	TB	62.1	0.0000
SyN* [3]	A,VF	Gaussian	MI	75.8	0.0000
sm-shapes* [31]	A,SVF	Diff.	DICE	79.8	0.2981
sm-brains* [31]	A,SVF	Diff.	DICE	78.4	0.0364
Ours (std. protocol)	DVF	GradICON	LNCC	78.7†	0.0012
	DVF	GradICON	LNCC	80.5‡	0.0004
DirLab
Method	Trans.	${ℒ}_{\text{reg}}$	${ℒ}_{\text{sim}}$	mTRE ↓ (in mm)	%|J| ↓
Initial				23.36
SyN [3]	A,VF	Gaussian	LNCC	1.79	—
Elastix [38]	A,B-Spline	BE	MSE	1.32	—
NiftyReg [43]	A,B-Spline	BE	MI	2.19	—
PTVReg [65]	DVF	TV	LNCC	0.96	—
RRN [28]	DVF	TV	LNCC	0.83	—
VM* [4]	A,SVF	Diff.	NCC	9.88	0.0000
LapIRN* [45]	SVF	Diff.	NCC	2.92	0.0000
LapIRN* [45]	DVF	Diff.	NCC DICE	4.24	0.0105
Hering et al. [30]	DVF	Curv+VCC	+KP+NGF	2.00	0.0600
GraphRegNet [26]	DV	—	MSE	1.34	—
PLOSL [66]	DVF	Diff.	TVD+VMD	3.84	0.0000
PLOSL50 [66]	DVF	Diff.	TVD+VMD	1.53	0.0000
ICON* [23]	DVF	ICON	LNCC	7.04	0.3792
Ours (std. protocol)	DVF	GradICON	LNCC	1.26†	0.0003
	DVF	GradICON	LNCC	0.96‡	0.0002

5.6. Intra-patient registration

We demonstrate the ability of our model with GradICON regularization to predict large deformations between lung exhale (source)/inhale (target) pairs (within patient) from COPDGene. This dataset is challenging as deformations are complex and large. Motion is primarily visually represented by the deformation of lung vessels, which form a complex tree-like structure that creates capture-range and local minima challenges for registration. As in our ablation study (Sec. 5.2), we report $\%\left|J\right|$ and the mTRE (in mm) for manually annotated lung vessel landmarks [8] averaged over all 10 DirLab image pairs. We assess GradICON against traditional optimization-based methods and state-of-the-art (SOTA) learning-based methods. Table 2 shows that our approach with instance optimization (0.96mm) yields a mTRE very close to the SOTA techniques and exceeds the SOTA for learning-based approaches of any sort. Further, our performance (1.26mm) in a single forward pass is the best of any one-forward-pass neural method.

6. Conclusion

We introduced and theoretically analyzed GradICON, a new regularizer to train deep image registration networks. In contrast to ICON [23], GradICON penalizes the Jacobian of the inverse consistency constraint. This has profound effects: we obtain dramatically faster training convergence, higher registration accuracy, do not require scale-dependent regularizer tuning, and retain desirable implicit regularization effects resulting in approximately diffeomorphic transformations. Remarkably, this allows us to train registration networks using GradICON regularization with one standard training protocol for a range of different registration tasks. In fact, using this standard training protocol, we match or outperform state-of-the-art registration methods on three challenging and diverse 3D datasets. This uniformly good performance without the need for dataset-specific tuning takes the pain out of training deep 3D registration networks and makes our approach highly practical.

Limitations and future work.

We only explored first-order derivatives of the inverse-consistency constraint and intensity-based registration. This might have limited registration performance. Studying higher-order derivatives, more powerful image similarity measures (e.g., based on deep features), as well as extensions to piecewise diffeomorphic transformations would be interesting future work.

Figure 1.

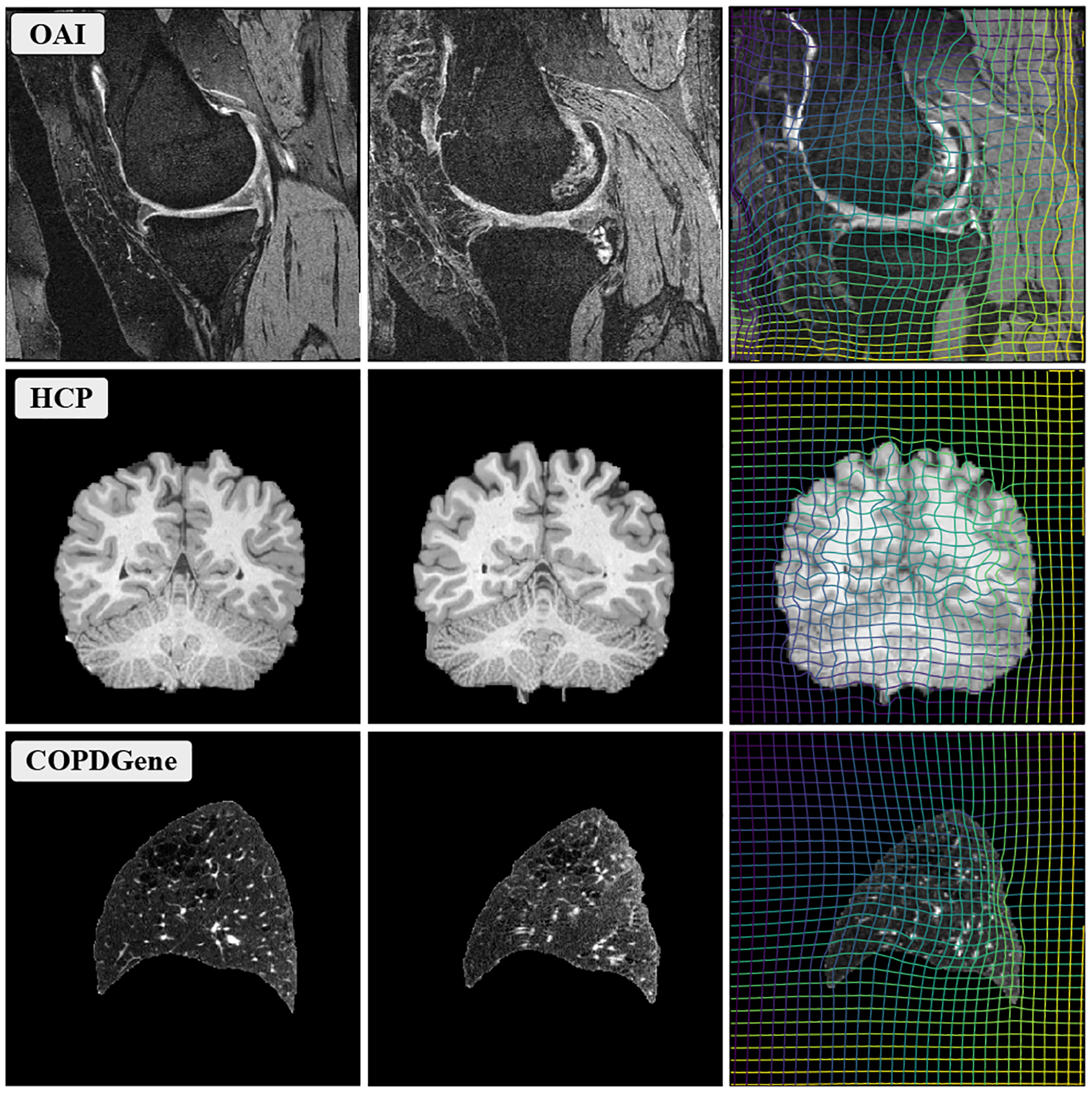
Example source (left), target (middle) and warped source (right) images obtained with our method, trained with a single protocol, using the proposed GradICON regularizer.