ST-GEARS: Advancing 3D downstream research through accurate spatial information recovery

Abstract

Three-dimensional Spatial Transcriptomics has revolutionized our understanding of tissue regionalization, organogenesis, and development. However, existing approaches overlook either spatial information or experiment-induced distortions, leading to significant discrepancies between reconstruction results and in vivo cell locations, causing unreliable downstream analysis. To address these challenges, we propose ST-GEARS (Spatial Transcriptomics GEospatial profile recovery system through AnchoRS). By employing innovative Distributive Constraints into the Optimization scheme, ST-GEARS retrieves anchors with exceeding precision that connect closest spots across sections in vivo. Guided by the anchors, it first rigidly aligns sections, next solves and denoises Elastic Fields to counteract distortions. Through mathematically proved Bi-sectional Fields Application, it eventually recovers the original spatial profile. Studying ST-GEARS across number of sections, sectional distances and sequencing platforms, we observed its outstanding performance on tissue, cell, and gene levels. ST-GEARS provides precise and well-explainable ‘gears’ between in vivo situations and in vitro analysis, powerfully fueling potential of biological discoveries.

Existing 3D Spatial Transcriptomics reconstruction approaches often overlook spatial information or experiment-induced distortions. Here, authors propose ST-GEARS to bridge the gap between in vivo cell locations and in vitro analysis, accurately recovering spatial profiles.

Introduction

Spatial transcriptomics (ST) is an omics technology that fuels biological research based on measuring gene expression on each position-recorded spot across sliced tissues^1–3. Notably, a range of methods has been developed. In vivo sequencing (ISS)⁴ platforms such as Barcoded Anatomy Resolved by Sequencing (BARseq)⁵ and Spatially-resolved Transcript Amplicon Readout Mapping (STARmap)⁶ rely on amplification, hybridization and imaging process to capture gene expression information. Next Generation Sequencing (NGS)⁷ platform such as Visium¹, Stereo-seq⁸ and Slide-Seq2⁹ uses spatial barcoding and capturing in their implementations. These methods offer various sequencing resolutions ranging from 100 µm^10,11 to 500 nm⁸, and can measure thousands⁵ to tens of thousands⁸ of genes simultaneously.

Single-slice ST studies have unleashed discoveries, and facilitated our understanding in diverse biological and medical fields^9,12–15. Consequently, numerous processing pipelines and analysis models have been developed for ST data on a single section^16–21. However, to truly capture transcriptomics in the real-world context, three-dimensional (3D) ST was designed to recover biological states and processes in real-world dimensions, without restriction of the isolated planes in single sectional ST studies. Various research has utilized the power of 3D ST to uncover insights in homeostasis, development, and diseases. Among them, Wang et al. ²² uncovered spatial cell state dynamics of Drosophila larval testis and revealed potential regulons of transcription factors. Mohenska et al. ²³ revealed complex spatial patterns in Murine heart and identified novel markers for cardiac subsections. And Vickovic et al. ²⁴ explored cell type localizations in Human rheumatoid arthritis synovium. The vast and large variety of downstream 3D research has posted the need for a reliable and automatic recovery method of in vivo spatial profile.

However, the collection process of ST data casts significant challenges onto the accurate reconstruction of 3D ST and the situation has not been overcome by current explorations. Specifically, in 3D ST experiments, individual slices are cross sectioned in a consistent direction, then manually placed on different chips or slides^14,25. This operation introduces varying geospatial reference systems of distinct sections, and coordinates are distorted compared to their in vivo states. The distortions occur due to squeezing and stretching effects during the picking, holding, and relocation of the sections. Such different geospatial systems and distortions complicates the recovery of in vivo 3D profile. Among current recovery approaches, STUtility²⁶ realizes multi-section alignment through the registration of histology images, without considering either geospatial or molecular profile of mRNA, which leads to compromised accuracies. Recently published method PASTE²⁷, and its second version PASTE2²⁸ achieve alignment using both gene expression and coordinate information, through optimization of mapping between individual spots across sections. These methods cause inaccurate mappings and produces rotational misalignments due to the nonadaptive regularization factors, and their uniform sum of probability assigned to all spots upon presence of spots without actual anchors. All above approaches only consider rigid alignment, yet neglect the correction of shape distortions, resulting in shape inconsistency across registered sections. Published method Gaussian Process Spatial Alignment (GPSA)²⁹ considers shape distortions in its alignment, yet it doesn’t involve structural consistency in its loss function, which can cause the model to overfit to local gene expression similarities, leading to mistaken distortions of spatial information. Moreover, its hypothesis space involves readout prediction in addition to coordinates alignment, causing uncertainty in direction of gradient descent, and vulnerabilities to input noises. Another alignment approach, Spatial-linked alignment tool (SLAT)³⁰ also focuses on anchors construction between sections, yet it doesn’t provide a methodology to construct 3D transcriptomics profile. Other tools focus on analysis and visualization of 3d data, such as Spateo³¹, VT3D³² and StereoPy³³.

To address these limitations, we introduce ST-GEARS, a 3D geospatial profile recovery approach designed for ST experiments. By formulating the problem using the framework of Fused Gromov-Wasserstein (FGW) Optimal Transport (OT)³⁴, ST-GEARS incorporates both gene expression and structural similarity into the Optimization process to retrieve cross-sectional mappings of spots with the same in vivo planar positions, also referred to as ‘anchors’. During this process, we introduce innovative Distributive Constraints that allow for different emphasis on distinct spot groups. The strategy addresses importance of expression consistent groups and suppresses inconsistent groups from imposing disturbances to optimization. Hence it increases anchor accuracy compared to current approaches. ST-GEARS utilizes the retrieved anchors to initially perform rigid alignment of sections. Subsequently, it introduces Elastic Field guided by the anchors to represent the deformation and knowledge to correct it according to each spot’s location. To enhance the quality of the field, Gaussian Smoothing is applied for denoising purposes. ST-GEARS then applies Bi-sectional Application to correction of each section’s spatial profile based on its denoised fields calculated with its neighboring sections. With validity proved mathematically, Bi-sectional Application eliminates distortions of sections, resulting in the successful recovery of a 3D in vivo spatial profile.

To understand effects of ST-GEARS, we first studied its counterparts with innovations including anchors retrieval and elastic registration, respectively on Human dorsolateral prefrontal cortex (DLPFC)³⁵, and Drosophila larva²². We found an advanced anchors accuracy of ST-GEARS compared to other available methods involving anchor’s concept and unveiled Distributive Constraints as reason behind the advancement. We validated the effectiveness of elastic registration process of ST-GEARS on both tissue shape smoothness and cross-sectional consistency. Then, we studied output of ST-GEARS and other methods on their reconstruction of Mouse hippocampus tissues³⁶, Drosophila embryo individual²² and a complete Mouse brain³⁷. The result was studied on morphological, cell and gene levels. ST-GEARS was found to be the only method that correctly reconstruct on all cases despite of cross-sectioning distance, number of sections, and sequencing platforms, and it was found to output the most accurate spatial information under both annotation type or clustering information, and hybridization evidence.

Results

ST-GEARS algorithm

ST-GEARS uses ST data as its inputs, including mRNA expression, spatial coordinates as well as approximate grouping information such as clustering or annotation of each observation. Then it recovers 3D geospatial profile in following steps (Fig. 1).

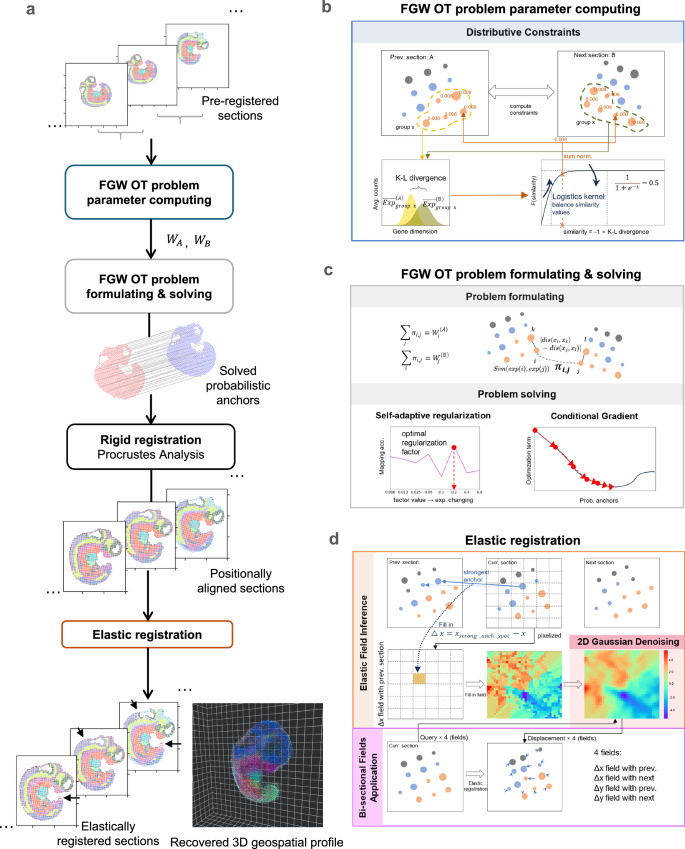
Fig. 1. Three-Dimensional (3D) Spatial Transcriptomics (ST) Geospatial profile recovery with ST-GEARS.

a The automatic pipeline of ST-GEARS which recovers ST-GEARS 3D in vivo spatial information by ordered steps including Fused Gromov Wasserstein (FGW) Optimal Transport (OT) problem parameter computing, problem formulating and solving which outputs probabilistic anchors across sections, rigid registration through Procrustes Analysis which solves optimal positional alignment using the anchors, and finally elastic registration. The input of the method is Unique molecular identifier (UMI) counts and location of each spot measured by ST technology, along with their annotations or cross-section clustering result. And the output of the method is recovered 3D in vivo spatial information of the experimented tissue, or sample. b FGW OT problem parameter computing, which assigns nonuniform weights to spots in preparation for future problem formulating, based on cross-sectional similarity of annotation types or clusters. c FGW OT problem formulating, whose setting aims to solve probabilistic anchors joining spots with highest in vivo proximity, through optimizing the combination of gene expression and structural similarity³⁴. FGW OT problem solving, which is implemented based on Conditional Gradient (CG) method, leading to retrieved probabilistic anchors. d Elastic registration, which utilizes the anchors again to compute and denoise distortion fields which guides the elimination of distortions, then applies the fields bi-sectionally to positionally aligned sections, leading to the recovered 3D in vivo spatial information.

(1) Optimization problem formulation under scheme of FGW OT with enhancement of Distributive Constraints. FGW OT formulation is established to enable solving of ‘anchors’, which are the joining of pair of spots with same in vivo planar positions. Noticeably, each solved anchor is equipped with a probability that describes its strength of connection, and each spot is solved to have zero to multiple anchors. Among each two sections, section-specific groups of spots, and genes are initially excluded from the formulation to avoid causing disturbances to anchors computing. Considering that connected spots are more spatially approximate, and more similar in gene expression because of shared cell identity^38,39, FGW was adopted to combine the gene expression and structural terms in optimization, enabling highest gene expression similarity between mapped spots, at the same time keeping similar spot positions relative to their sections. Moreover, an innovative Distributive Constraints setting is designed and integrated into FGW OT’s formulation, to assign higher emphasis on spots or cells whose annotation or cluster express high similarity across section, and vice versa. Distributive Constraints leads registration to rely more on expression-consistent regions of sections, hence largely enhancing both accuracy of anchors and precision of following rigid and elastic registration.

(2) Optimization problem solving utilizing self-adaptive regularization and conditional gradient descent. Our designed Self-adaptive Regularization strategy automatically determines the relative importance between gene expression and structural terms in the optimization problem. This strategy leads to an optimal regularization factor across different section distances, spot sizes, extent of distortions, and data quality such as level of diffusion. Conditional Gradient³⁴ is adopted as optimizer, which updates anchors iteratively towards higher expression and structural similarity with each iteration. The efficacy of Conditional Gradient has been demonstrated through its convergence to a local optimal point⁴⁰, thereby ensuring the robustness and effectiveness of our approach.

(3) Rigid registration by Procrustes Analysis⁴¹. After filtering out anchors with relatively low probabilities, the optimal transformation and rotation of each section are analytically solved through Procrustes Analysis, which minimizes summed spatial distances of spots anchored to each other. With the transformation and rotation applied, sections are positionally aligned.

(4) Elastic registration guided by anchors. Based on rigid registration result and anchors solved by FGW OT, elastic registration is implemented through the process including elastic field inference, 2D Gaussian denoising, and bi-sectional fields application. Based on each rigidly registered section, elastic fields is inferred leveraging the location difference between its own spots and its anchored spots on anterior and posterior neighbor sections. An elastic field is a 2D displacement distribution, describing how displacement values are distributed across different locations. Making use of continuity of deformation at local scales, 2D Gaussian Denoising convolutes all over the fields to reduce noises. With denoised fields, our designed Bi-sectional Fields Application corrects each section’s deformation according to its fields calculated with anterior and posterior neighbor sections. The bi-sectional correction method is mathematically proved to approximately recover each section’s spatial profile to its original state.

Enhancement of anchor retrieval accuracy through distributive constraints

As was unfolded, ST-GEARS is an algorithm flow jointly constituted of probabilistic anchor computation and spatial information recovery. Hence, to validate the effectiveness of our method and demonstrate its underlying design philosophy, we conducted comprehensive studies on the two counterparts using real-world data. To begin, we utilized the DLPFC dataset³⁵ to study our anchors retrieving accuracy with emphasis on the effect of Distributive Constraints design.

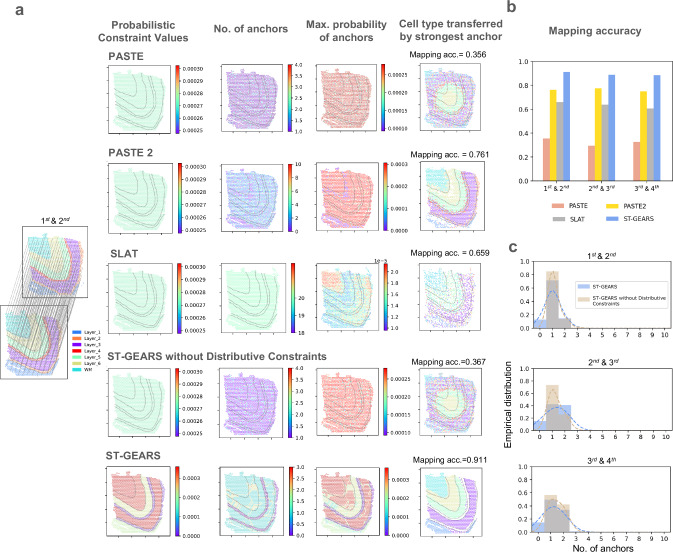
To assess the effects of Distributive Constraints on anchor accuracy, we compared ST-GEARS with and without this setting, and with other constraints involving methods including PASTE, PASTE2 and SLAT. We investigated constraint values assigned by these methods, as well as their solved number of anchors and maximum anchor probability of each spot. Furthermore, we examined the annotation types that were considered connected based on the computed anchors to assess accuracy of anchors. Among the methods we compared, ST-GEARS with Distributive Constraints was found to assign different constraint values to spots within different neuron layers, while the others assigned uniform constraints to all layers (Fig. 2a, Supplementary Fig. 1). The results of ST-GEARS showed that both number of anchors and the anchors’ maximum probabilities for each spot were lower in Layer 2 and Layer 4 compared to the thicker layers. However, this pattern was not observed in methods without Distributive Constraints setting (Fig. 2a, Supplementary Fig. 1). To illustrate the impact of this strategy on anchor accuracy, we tagged each spot with annotation of its connected spot by anchor with highest probability. We then compared this result to the tagged spot’s original annotation (Fig. 2a, Supplementary Fig. 1). Under Distributive Constraints, ST-GEARS achieved a significantly higher proximity between annotations compared to PASTE and our method without Distributive Constraints. PASTE2 also led to approximate annotations, but it anchored multiple spots to spots from neighboring layers, particularly those near layer boundaries. SLAT also mapped multiple spots to spots from different tissue layers, particularly of spots located on layer 2, 4 and 6.

Fig. 2. Anchors generated by ST-GEARS and their accuracy study.

a (from left to right) 1st and 2nd human dorsolateral prefrontal cortex (DLPFC) section of patient #3 by Maynard et al.³⁵ with their provided annotations and our anchors showcase, (of the same section pair) probabilistic constraints settings in Optimal Transport (OT) problem formulating, no. of anchors computed on each spot, max. anchor probability value computed of each spot, and annotation type mapped back to spots through computed anchors; (from top to bottom) respectively by PASTE, PASTE2, SLAT, ours without distributive constraints setting, and ours. The distinction of different annotation types on the 1st section is marked by dotted lines. Mapping accuracy is used to measure accuracy of anchors and is marked alongside respective annotation type mapping visualizations. b Mapping accuracy measured on anchors of sections pairs used in (b) by PASTE, PASTE2, SLAT, and ST-GEARS. c Comparison of no. of anchors histograms between ST-GEARS and ST-GEARS without distributive constraints, of sections pairs of 1st and 2nd, 2nd and 3rd, and 3rd and 4th sections. The Probability Density Function (PDF) estimated by Gaussian kernel was plotted in dotted lines with the same color of histograms, to highlight the distribution differences. Source data are provided as a Source Data file.

To evaluate the precision of anchors, we conducted a comparison with the Mapping accuracy index introduced by PASTE²⁷. This index measures the weighted percentage ${\sum }_{i,j,l\left(i\right)=l\left(j\right)}{\pi }_{ij}$ of anchors that connect spots with same annotation. As a result, ST-GEARS outperformed PASTE2 and SLAT, and reached a score that was over 0.5 (out of 1) higher than both PASTE and our method without Distributive Constraints (Fig. 2a, b, Supplementary Fig. 1).

To uncover the reasons behind the aforementioned phenomena, as the functional area in between thicker neocortical layers, thinner neocortical layers have comparable transcriptomic similarity with their adjacent layers in gene expression, than with its own annotation type^1,35. This implies that, in contrast to thicker layers, thinner layers tend to introduce more disturbances during anchor computation. However, the Distributive Constraints imposed suppression on these annotation types by assigning a smaller sum of probability to each of their spots. The suppression was reflected in above results where each spot in Layer 2 and Layer 4 has fewer assigned anchors and a lower maximum probability (Fig. 2a, Supplementary Fig. 1). Further analysis on all spots in the DLPFC reveals that a certain percentage of spots were suppressed in anchor generation due to the Distributive Constraints (Fig. 2c, Supplementary Fig. 2).

Recovery of in vivo shape profile through elastic registration

We then utilized Drosophila larva data to investigate the spatial profile recovery effect of ST-GEARS, with an emphasis on our innovated elastic registration. We first applied rigid registration to Drosophila larva sections and observed a visually aligned configuration of individual sections (Supplementary Fig. 3). By further mapping cell annotations back to their previous sections, according to the strongest anchors of each spot, the projected annotations are visually in match with original ones (Supplementary Fig. 4). The accuracy of the mapping matching between annotations was quantified by Mapping accuracy (Supplementary Fig. 5). The above findings validated that ST-GEARS produced reliable anchors and accurately aligned sections through rigid registration. However, when stacking the sections together, we observed an inconsistency on the edge of lateral cross-section of the rigid result (Supplementary Fig. 6). This inconsistency doesn’t conform to the knowledge of intra-tissue and overall structural continuity of Drosophila larvae.

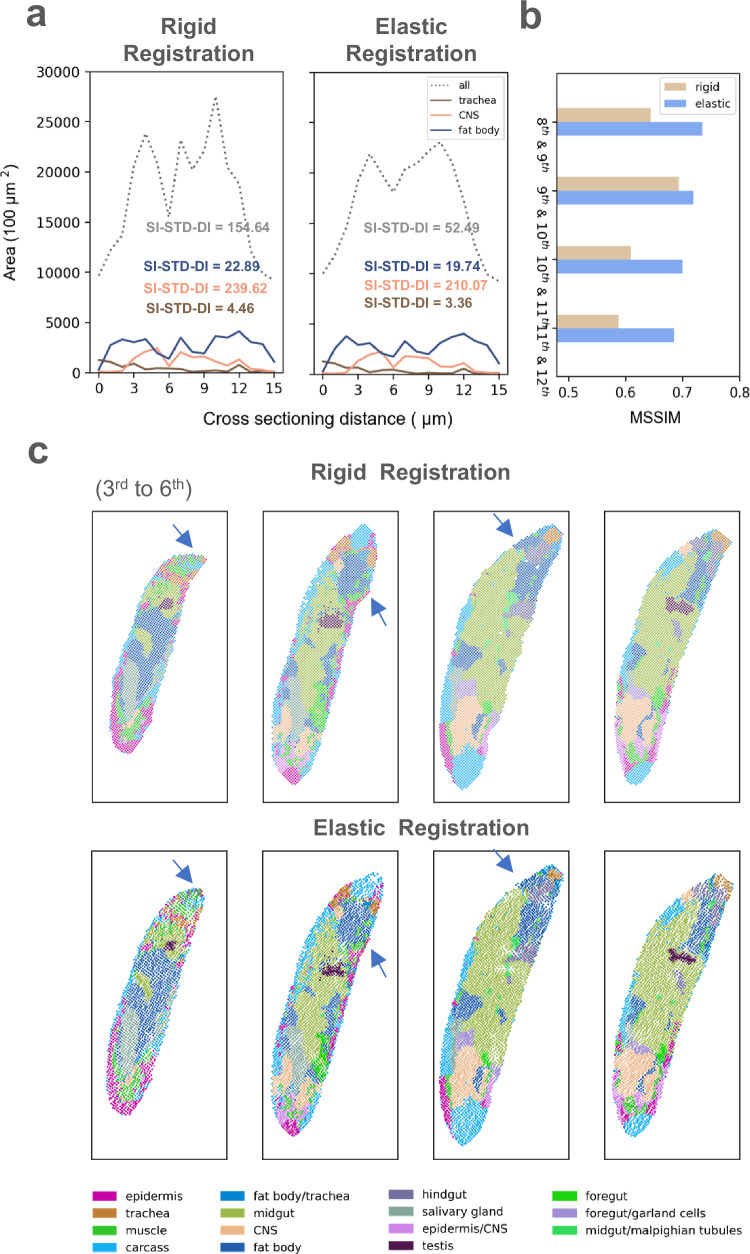
After applying elastic registration to the rigidly-aligned larva, we observed a notable improvement in the continuity of the cross section above, indicating a closer-to-real spatial information being retrieved. To further understand the effect of elastic operation on the dataset, we compared the changes in area of the complete body and three individual tissues (trachea, central nervous system (CNS), and fat body) on all sections. We observed an enhanced smoothness in the curves of elastically registered sections, which aligns with the continuous morphology of the larva as expected by theoretical knowledge. To quantify the smoothing effect, we calculated Scale-independent Standard Deviation of Differences ($SI-STD-DI=STD\left(\left\{s_i-s_{i-1}:i\in \left[\mathrm{1,\; 2},...,I-1\right]\right\}\right)/\mid mean\left(\left\{s_i-s_{i-1}:i\in \left[\mathrm{1,\; 2},...,I-1\right]\right\}\right)\mid$) onto the curves, which measures the smoothness of area changes along the sectioning direction (Fig. 3a and Methods). A decrease of SI-STD-DI on all tissues and the body provided empirical evidence for the improved smoothness. To further investigate the recovery of internal structures, we introduced Mean Structural Similarity (MSSIM). MSSIM takes structurally consistent sections as input, and measures pairwise internal similarity of reconstructed result using annotations or clustering information (Supplementary Fig. 7). (See Methods for details). An improved MSSIM was noticed on all 4 sections, indicating that elastic registration further recovers internal geospatial continuity on basis of rigid operation(Fig. 3b). By comparing registration effect of individual sections, we also observed that the elastic process successfully rectified a bending flaw along the edge of the third section, (Fig. 3c). The shape fixing highlighted that ST-GEARS not only yielded a more structurally consistent 3D volume, but also provided a more accurate morphology for single sections. The improved smoothness, the recovered structural continuity, and the shape fixing collectively demonstrate that elastic registration effectively recovers geospatial profile.

Fig. 3. Distortion correction effect by elastic registration of ST-GEARS.

a A comparison of area changes of 3 tissues and complete body of Drosophila Larva, between result of rigid registration and result of elastic registration appended to rigid registration. The areas are calculated based on recovered spot position of different tissues along cross-sectioning direction. Standard Deviation of Differences (SI-STD-DI) quantifying the smoothness is marked alongside each curve. b A comparison of structural accuracy, measured by Mean Structural Similarity (MSSIM), of selected section pairs from Drosophila Larva (L3), between result of rigid registration only and result of elastic registration appended to rigid registration. The chosen section pairs are the structurally consistent ones. c Comparison of individual sections recovered by rigid registration only and by elastic registration appended to rigid registration, of 1st to 5th section of Drosophila Larva (L3). Shape correction of bended area in the 3^rd section, and increased cross-sectional consistency on the 4th and 5th section were highlighted by blue arrows. Source data are provided as a Source Data file.

With elastic process validated and applied onto rigid registration result, the recovery of spatial information was completed. Stacking individual sections of the elastic result, a complete geospatial profile of the larva was generated (Supplementary Fig. 8), visualizing the ST-GEARS’ ability of in vivo spatial information recovery.

Application to sagittal sections of Mouse hippocampus

After validating the component phases of ST-GEARS, we proceeded to apply the method to multiple real-world problems to recover geospatial profiles. We first focused on two sagittal sections of Mouse hippocampus³⁶ (Supplementary Fig. 9) that were 10 μm apart, accounting for 1–2 layers of Cornu Ammonis (CA) 1 neurons⁴². Considering the proximity of these sections, we assumed no structural differences between them.

To compare the differences of registration effect among methods, we extracted CA fields and dentate gyrus (DG) beads (Supplementary Fig. 10), then stacked the two sections for a more obvious contrast (Fig. 4a). PASTE2 failed in performing the registration, leaving the sections unaligned. By GPSA, the sections’ positions were aligned, yet the 2nd section were squeezed into a narrower region than first one, leading to a contradiction of region’s location. The ‘narrowing’ phenomena may be caused by the overfitting of GPSA model on gene expression similarity, since it doesn’t involve structural similarity between registered sections in loss function. The scale on horizontal and vertical axis was distorted due to the equal scale range strategy adopted in GPSA’s preprocessing. STalign also misaligned the sections, leaving an obvious angle between two slices in registration result. This may be due to the method’s processing of ST data into images which completely relies on gene expression abundance to decide pixel intensities. On the sagittal section of Mouse hippocampus, the abundance difference between regions may not provide sufficient structural information required by registration. In the comparison between PASTE and ST-GEARS, our method demonstrates a more accurate centerline overlapping of CA fields and DG compared to PASTE. This indicated an enhanced recovery of spatial structure consistency and an improved registration effect. To quantitatively evaluate these findings, we utilized the MSSIM index as a measure of structural consistency and compared it among PASTE, PASTE2, GPSA, STalign and ST-GEARS (Fig. 4b). Consistent with the results of centerline, ST-GEARS achieved a higher MSSIM score than GPSA and PASTE, surpassing PASTE2 and STalign by >0.2 out of 1. By comparing memory efficiency across all methods, ST-GEARS and PASTE used ~1 GB less memory than PASTE2, GPSA and STalign, and the peak memory across ST-GEARS and PASTE was almost the same (Supplementary Fig. 11). In perspective of time efficiency, registration utilizing ST-GEARS, STalign, GPSA and PASTE was much faster than PASTE2.

Fig. 4. Registration of Mouse hippocampus, respectively by PASTE, PASTE2, GPSA, STalign and ST-GEARS.

a Stacked projections of Cornu Ammonis (CA) fields and dentate gyrus (DG), of pre-registered and registered result of Mouse hippocampus sagittal sections with 10 µm distance, respectively by PASTE, PASTE2, GPSA, STalign and ST-GEARS. b A comparison of both MSSIM measuring structural accuracy and Mapping accuracy measuring anchor accuracy of the 2 registered sections, across PASTE, PASTE2, GPSA, STalign and ST-GEARS. c Stacked projections of region-specific annotation types including DG, Neurogenesis, subiculum, CA1, CA2 and CA3, registered by ST-GEARS. Each column highlights the stacked projection of a single annotation type. Source data are provided as a Source Data file.

To understand reasons behind our enhancement, we thoroughly examined the anchors generated by PASTE, PASTE2 and ST-GEARS, as well as the effects of our elastic registration. By mapping cluster information of the 2nd section to the 1st, and the 1st to the 2nd through anchors, we found correspondences between the projected and original annotations (Supplementary Fig. 12). Accordingly, our Mapping accuracy was over 0.25 higher than PASTE and over 0.45 than PASTE2 (Fig. 4a), indicating our exceptional anchor accuracy. To understand and further substantiate this advantage, we visualized the probabilistic constraints and its resulted anchors probabilities (Supplementary Fig. 13a). It is worth noting that ST-GEARS implemented Distributive Constraints, in contrast to the uniform distributions used by PASTE. As a result, a certain percentage of spots were found to be suppressed in anchors connection by ST-GEARS (Supplementary Fig. 13b) compared to PASTE, leaving the registration to rely more on spots with higher cross-sectional similarity and less computational disturbances, and hence lead to a higher anchor accuracy. We excluded Distributive Constraints from ST-GEARS, and noticed an obvious decrease of mapping accuracy on the hippocampus dataset (Supplementary Fig. 14), indicating the contribution of Distributive Constraints on anchors accuracy. In the study of elastic effect, we found an increased overlapping of centerlines by elastic registration than by rigid operation only when overlapping CA fields and DG (Fig. 4b). Quantitively by MSSIM, the cross-sectional similarity was found to be increased by elastic registration (Supplementary Fig. 15). These findings suggest that the combination of Distributive Constraints and elastic process contributed to the enhanced registration of the Mouse hippocampus.

To explore the potential effect of impact of our registration on downstream analysis, we extracted region-specific annotation types from the sections, and analyzed their overlapping through stacking registered sections together (Fig. 4c). In all annotation types including DG, Neurogenesis, subiculum, CA1, CA2 and CA3, the distribution regions from both sections were nearly identical. The overlapping result unveils that ST-GEARS integrated the spatial profile of same cell subpopulations, enabling a convenient and accurate downstream analysis of multiple sections.

Application to 3D reconstruction of Drosophila embryo

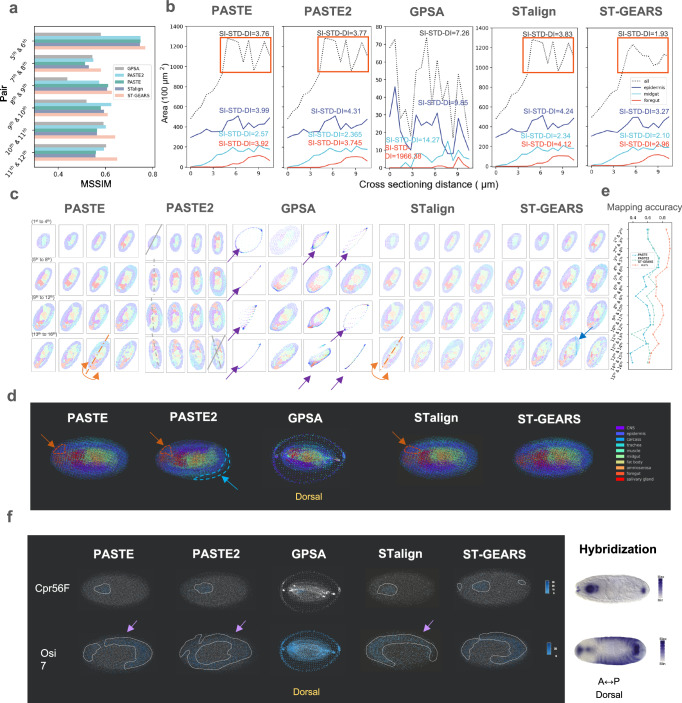
Besides tissue level registration of Mouse hippocampus, to evaluate the performance of ST-GEARS in reconstructing individual with multiple sections, we further tested it on a Drosophila embryo. The transcriptomics of embryo was measured by Stereo-seq, with 7 μm cross-sectioning distance²². By quantifying the registration effect of spatial information recovery and comparing it to PASTE, PASTE2, GPSA and STalign, we found that ST-GEARS achieved the highest MSSIM in five out of the six structurally consistent pairs (Fig. 5a). On the pair where ST-GEARS did not result in highest MSSIM, it surpassed PASTE, and achieved a similar score to PASTE2. By comparing area changes with SI-STD-DI quantification of the complete section, and three individual tissues including epidermis, midgut and foregut, ST-GEARS yielded higher smoothness on all regions than all other approaches, both visually and quantitatively (Fig. 5b).

Fig. 5. Three-Dimensional (3D) reconstruction of Drosophila Embryo, respectively by PASTE, PASTE2, GPSA, STalign and ST-GEARS.

a A comparison of Mean Structural Similarity (MSSIM) measuring structural similarity, of section pairs that are structurally consistent from Drosophila Embryo (E14-16h), between reconstruction results of PASTE, PASTE2, GPSA, STalign and ST-GEARS. b A comparison of area changes of 3 tissues and complete body of Drosophila Embryo, along cross-sectioning direction, between reconstruction result of PASTE, PASTE2, GPSA, STalign and ST-GEARS. Standard Deviation of Differences (SI-STD-DI) which measures structural consistency is marked alongside each curve to quantify the smoothness. The smoothness difference of ST-GEARS compared to PASTE, PASTE2 and STalign are highlighted by orange rectangles. c Reconstructed individual sections with recovered spatial location of each spot. In result of PASTE, the incorrect flipping on the 15th section was highlighted in orange. In result of PASTE2, gradual rotations were marked by the 1st, 5th, 9th, 13th and 16th sections’ approximate symmetry axis whereas symmetry axis of the 1st section was replicated onto the 16th for angle comparison. In result of GPSA, mistakenly distorted sections were marked by purple arrows. In result of STalign, the incorrect flipping on the 13th section was highlighted in orange. In result of ST-GEARS, the fix of dissecting area on the 15th section was marked by a blue arrow. d Dorsal view of 3D reconstructed Drosophila embryo by PASTE, PASTE2, GPSA, STalign and ST-GEARS. The inaccurate regionalization of midgut was circled and pointed with arrow in orange. The resulted extruding part of single section by PASTE2 was circled and pointed in blue. e Mapping accuracy of all section pairs by PASTE, PASTE2 and ST-GEARS. f By dorsal view, regionalization of marker gene Cpr56F and Osi7 by PASTE, PASTE2, GPSA, STalign and ST-GEARS, and their comparison with hybridization result from Berkeley Drosophila Genome Project (BDGP) database. The gathering expression regions were highlighted by dotted lines. Source data are provided as a Source Data file.

To compare the reconstruction effect, we studied both registered individual section, and reconstructed 3D volume. Among the methods compared, PASTE produced a wrong flipping on the 15^th section along A-P axis (Fig. 5c). Stacking sections back to 3D and investigating on dorsal view, the wrong flipping caused a false regionalization of foregut circled in orange (Fig. 5d). Along the first to last section registered by PASTE2, a gradual rotation was witnessed (Fig. 5c), leading to over 20 degrees of angular misalignment between the first and the last section. Similar to PASTE, this misalignment also caused the wrong regionalization of foregut in 3D map (Fig. 4d). Equally induced by the rotation, sections were found to extrude in the 3D result circled in blue, breaking the round overall morphology of the embryo. GPSA caused false distortion of 8 out of 16 sections as pointed by purple arrows (Fig. 5c) and the stacked sections formed a dorsal view of an isolated circle and an inner region (Fig. 5d). The phenomena may be due to its overfitting onto expressions, which is caused by the contradiction between its hypothesis of consistent readout across sections, and the large readout variation across 16 sections in this application. Similar to PASTE, STalign also produced a wrong flipping, on the 13^th section along A-P axis (Fig. 5c). Stacking the projections back to 3D, a mistaken regionalization of foregut, caused by the wrong flipping, was circled in orange (Fig. 5d). In contrast, ST-GEARS avoided all of these mistakes in its results (Fig. 5c). From the perspective of individual section profiles, noticeably in the 15^th section, we observed a significant reduction in the dissecting region between two parallel lines, indicating the successful fixation of flaws in the session. By comparing time usage across all methods, ST-GEARS achieved the 2nd lowest time consumption in registration (Supplementary Fig. 11). In terms of memory consumption, ST-GEARS, PASTE and STalign used much less memory than PASTE2 and GPSA. The three most memory efficient methods used almost identity peak memory, with the value fluctuation of <7%.

To comprehend the rationale behind our improvement, we analyzed the anchors generated by the three methods and the impact of our elastic registration. In the investigation of anchor accuracy, we discovered that ST-GEARS achieves the highest mapping accuracy among all section pairs (Fig. 5e), suggesting its advanced ability to generate precise anchors, which forms the basis for precise spatial profile recovery. To understand this advancement, probabilistic constraints and its resulted anchors distributions (Supplementary Fig. 16, Supplementary Fig. 17) were studied. With Distributive Constraints (Supplementary Fig. 16a), ST-GEARS generated different maximum probabilities on different annotation types (Supplementary Fig. 16b), which indicates that annotation types with higher cross-sectional consistency were prioritized in anchor generation. This selection led to reduced computational disturbances, and hence higher accuracy of anchors. We also compared anchor accuracy with and without Distributive Constraints adopted, and noticed an increase of mapping accuracy on each pair of sections (Supplementary Fig. 18). In final registration result, ST-GEARS without Distributive Constraints failed to fix the experimental flaw on the 15^th section (Supplementary Fig. 19), in contrast to effect upon the setting adopted (Fig. 5c). Above findings validate the contributive effect of Distributive Constraints in our method. In study of elastic registration in shape smoothness, we witnessed an increased level of smoothness of tissue epidermis, foregut, and midgut, as well as the complete section, through area changes quantified by SI-STD-DI index (Supplementary Fig. 20). In internal structure aspect, an increased MSSIM of structural consistent pairs were noticed (Supplementary Fig. 21). An experimental flaw on the 15^th section was also fixed by elastic registration (Supplementary Fig. 22). Above findings point that the enhancement of registration accuracy on Drosophila embryo was induced by Distributive Constraints and elastic process.

By mapping spots back to 3D space, we further investigated the effect of different method on downstream analysis, in the perspective of genes expression (Fig. 5f). Cpr56F and Osi7 were selected as marker genes, which were found to respectively highly express in foregut, and foregut plus epidermis region²². Investigating Cpr56F expression by ST-GEARS from dorsal view, we noticed three highly expressing regions, at anterior end, front region, and posterior end of the embryo. The finding matches the hybridization result of stage 13-16 Drosophila embryo extracted from Berkeley Drosophila Genome Project (BDGP) database. In contrast, none of PASTE, PASTE2, GPSA and STalign presented high expression at all three locations. When analyzing the distribution of Osi7 by PASTE, PASTE2 and STalign, we noticed a sharp decrease in expression from inner region to the outer layer marked by purple arrows, contradicting the prior knowledge of high expression in the epidermis. This is probably because PASTE and PASTE2 do not consider distortion correction as part of their methods, leaving section edges un-coincided and marker genes not obviously highly expressed on the outermost region. Though involving distortion correction, STalign lost certain amount of structural information by transforming ST data to image utilizing only information of regional gene expression abundance. The registration did not adequately correct distortion without support of enough structural messages. Similarly, PASTE2 failed to capture expression in outer layers and instead revealed a high expression in one inter-connected area, which did not correspond to the separate expression regions observed in hybridization result. No spatial pattern was witnessed when analyzing distribution of Osi7 by GPSA, which forms an obvious contrast to its hybridization evidence. Comparably, none of the violations was shown in the result of ST-GEARS. The comparison of spatial distribution indicated our potential capability to better enhance the process of downstream gene-related analysis.

Application to Mouse brain reconstruction

The design of 3D experiments involves various levels of sectioning distances^22,36,37. To further investigate the applicability of ST-GEARS on ST data with larger slice intervals, we applied the method to a complete Mouse brain hemisphere dataset, which consists of 40 coronal sections (Supplementary Fig. 23a), with a sectioning distance of 200 μm³⁷. The transcriptomics data was measured by BARseq, which includes sequencing data and its cross-modal histology images. Each observation represents captured transcriptomics surrounded by the boundary of a cell.

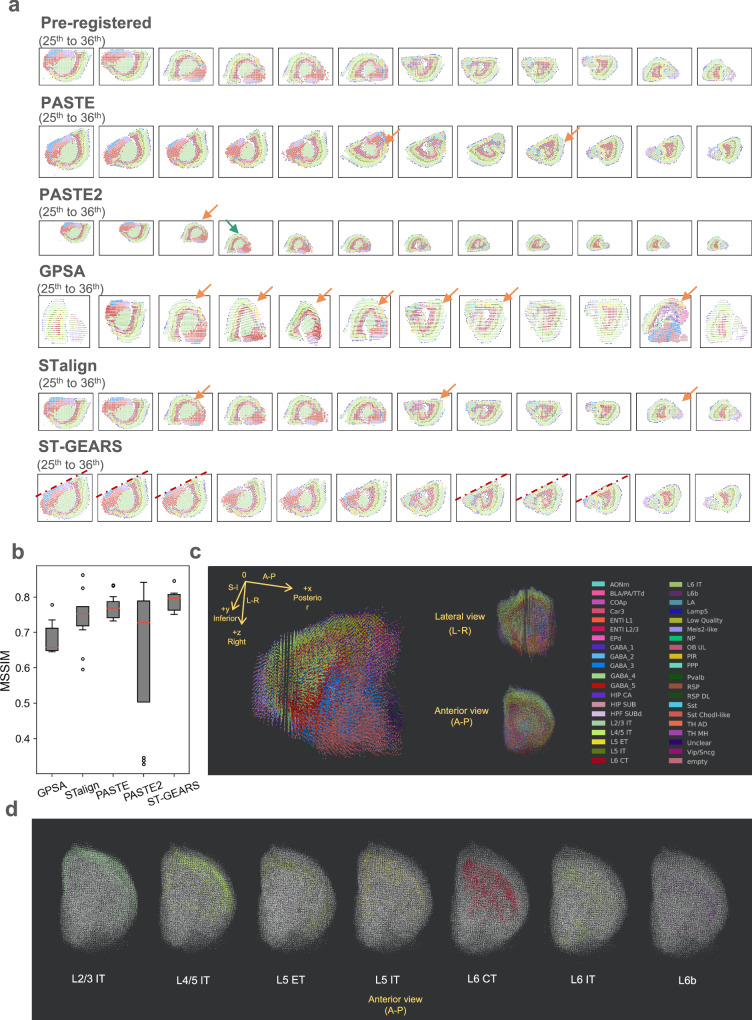
Through respectively applying PASTE, PASTE2, GPSA, STalign and ST-GEARS onto the dataset, we observed multiple misaligned sections produced by approaches including PASTE, PASTE2, GPSA and STalign (Supplementary Fig. 23b, Supplementary Fig. 23c, Supplementary Fig. 23d, Fig. 6a). In PASTE, these misalignments include 2 sections with ~ 180° angular misalignment (Supplementary Fig. 23b). By PASTE2, 4 rotational misalignments and 8 positional misalignments were noticed (Supplementary Fig. 23d). By GPSA, 12 sections were observed to be rotationally misaligned, and 3 sections were mistakenly distorted (Supplementary Fig. 23b), probably due to its overfitting onto expressions discussed in analysis of Drosophila embryo. The scale on horizontal and vertical axis was distorted maybe due to the similar reason analyzed in Mouse hippocampus. And by STalign, 7 rotational misalignments were generated (Supplementary Fig. 23e). As a clear contrast, our algorithm correctly aligned all 40 sections with 200 μm intervals (Supplementary Fig. 23f). To more accurately assess the result of our registration, we employed the direction of the cutting lines induced during tissue processing³⁷, and compared the consistency of tilt angles of these lines in the 20th, 25th, 26th, 27th, 33rd, 34th and 37th slices where these lines are visible. Notably, neither visual angle differences nor cutting line curving were observed, indicating that the sections were properly aligned by ST-GEARS (Fig. 6a, Supplementary Fig. 23f). To quantify the registration accuracy in aspect of structural continuity, we calculated MSSIM scores of 11 section pairs that are structural consistent (Fig. 6b). Consistent with the visual observations, PASTE2 presented a much larger score range than other methods, which reflects its instability across sections in this dataset, and GPSA exhibited the lowest median MSSIM score indicating its suboptimal average performance. By comparison, PASTE yielded a higher median score and a smaller variation, while ST-GEARS resulted in the highest median score and the smallest variation among all methods. In terms of computational efficiency, ST-GEARS achieved the 2nd lowest time consumption and lowest peak memory consumption across all methods (Supplementary Fig. 11).

Fig. 6. Three-Dimensional (3D) reconstruction of Mouse Brain, respectively by PASTE, PASTE2, GPSA, STalign and ST-GEARS.

a Reconstructed individual sections with recovered spatial location of each spot from the 25th to 36th section. Positional misalignments are marked by arrows of green, and angular misalignments are marked by arrows of orange. Visible cutting lines by ST-GEARS are marked by dotted lines. b A comparison of Mean Structural Similarity (MSSIM) score of 11 section pairs that are structurally consistent, between result of PASTE, PASTE2, GPSA, STalign and our method. The 11 biological replicates were studied, which were derived from different closest section pairs with each section pair representing smallest unit of study. Non control group was used as a MSSIM close to 1 is assumed to the idealized similarity value of the structurally similar pairs, hence a higher MSSIM value indicates higher reconstruction accuracy. The red lines positions show median score; the box extends from the first quartile (Q1) to the third quartile (Q3) of scores; the lower whisker is at the lowest datum above Q1 − 0.5 * (Q3-Q1), and the upper whisker is at the highest datum below Q3 + 0.5*(Q3-Q1); scores out of whiskers range are marked by circles. c Perspective, Lateral and Anterior view of reconstructed Mouse brain hemisphere. d Anterior view of layer annotation types distribution of reconstructed Mouse brain hemisphere. Source data are provided as a Source Data file.

To understand the reasons behind our progress, we examined anchor accuracy changes with regularization factors during ST-GEARS computation (Supplementary Fig. 24). Out of 39 section pairs, we observed a change in mapping accuracy >0.1 (out of 1) in 12 pairs. By Self-adaptive Regularization which was designed to face varying data characteristics which also includes varying section distances, regularization factor that leads to optimal mapping accuracy was selected, leading to an increased anchors accuracy in the 12 section pairs. Notably, among these 12 pairs, pairs 29th & 30th, 31st & 32nd and 32nd & 33rd were correctly aligned by ST-GEARS but misaligned by PASTE, which doesn’t adopt any self-adaptive regularization strategy.

After validating the registration result, we investigated the recovered cell-types’ distribution in the 3D space to assess the effectiveness of the reconstruction and its impact on further analysis. We observed that the complete morphology of hemisphere was recovered by ST-GEARS, with clear distinction of different tissues on perspective, lateral and anterior views (Fig. 6c). We further studied the distribution of separate annotation types within cortex layers and found that 3D regionalization of each annotation type was recovered by ST-GEARS (Fig. 6d). The reconstructed result indicated the adaptability of ST-GEARS across various scales of sectioning intervals, and its applicability on both bin-level, and cell-level datasets on which histology information is incorporated.

Discussion

We introduce ST-GEARS, a 3D geospatial profile recovery approach for ST experiments. Leveraging the formulation of FGW OT, ST-GEARS utilizes both gene expression and structural similarities to retrieve cross-sectional mappings of spots with same in vivo planar coordinates, referred to as ‘anchors’. To further enhance accuracy, it uses our innovated Distributive Constraints to enhance the accuracy. Then it rigidly aligns sections utilizing the anchors, before finally eliminating section distortions using Gaussian-denoised Elastic Fields and its Bi-sectional Application.

We validate counterpart of ST-GEARS including anchors retrieval and elastic registration, respectively on DLPFC and Drosophila larva dataset. In the validation of anchors retrieval, through Mapping accuracy evaluation of retrieved anchors, ST-GEARS consistently outperformed PASTE and PASTE2 across all section pairs. We show Distributive Constraints as reasons behind its distinguished performance, which effectively suppressed the generation of anchors between spot groups with low cross-sectional similarity while enhances their generation among groups with higher similarity. To investigate the effectiveness of the elastic registration process, we evaluate the effects of tissue area changes and cross-sectional similarity using the Drosophila larvae dataset. Both smoother tissue area curves and higher similarity observed between structurally consistent sections confirm the efficacy of the elastic process of ST-GEARS.

We demonstrate ST-GEARS’s advanced accuracy of reconstruction compared to current approaches including PASTE, PASTE2 and GPSA, and its positive impact on downstream analysis compared to existing approaches. Our evaluation encompasses diverse application cases, including registration of two adjacent sections of Mouse hippocampus tissue measured by Slide-seq, reconstruction of 16 sections of Drosophila embryo individual measured by Stereo-seq, and reconstruction of a complete Mouse brain measured by BARseq, including 40 sections with sectioning interval as far as 200 μm. Among the methods, registered result by ST-GEARS exhibited the highest intra-structural consistency measured by MSSIM for two hippocampus sections separated by a single layer of neurons. On 16 sections of a Drosophila embryo individual, our method’s outstanding accuracy is indicated by both MSSIM and smoothness of tissue area changes. Importantly, ST-GEARS provides more reliable embryo morphology, precise tissue regionalization, and accurate marker gene distribution under hybridization evidence compared to existing approaches. This suggests that ST-GEARS provides higher quality tissues, cells, and genes information. On Mouse brain sections with large intervals of 200 μm, ST-GEARS avoided positional and angular misalignments that occur in result of PASTE and PASTE2. The improvement was quantified by a higher MSSIM. Both hemisphere morphology and cortex layer regionalization were reflected in the result of 3D reconstruction by ST-GEARS. The successful representation of important structural and functional features in the aforementioned studies collectively underscores ST-GEARS’ reliability and capability for advancing 3D downstream research, enabling more comprehensive and insightful analysis of complex biological systems.

To further enhance and extend our method, opportunities in various aspects are anticipated to be explored. Firstly, algorithm aspects including hyperparameter sensitivity and scalability can be further explored for a more enhanced method performance. Though recommended values are provided for two of its hyperparameters, method performance is still affected by parameter values, raising the potential issue of overfitting and sensitivity which can be further studied. In scalability aspect, ST-GEARS introduces obvious computational cost increasement when dealing with large-scale datasets. Though strategy of Granularity adjusting is innovated to down-grade complexity, opportunity of improving robustness on increasing scale of data is expected to be further explored. Secondly, tasks aimed at improving data preprocessing, including but not limited to batch effect removal and diffusion correction, are expected to be integrated into our method, considering their coupling property with registration task itself: inaccuracies in input data introduce perturbations to anchors optimization, while recovered spatial information of our method may assist data quality enhancement by providing registered sections. Thirdly, the ST-GEARS’ Distributive Constraint takes rough grouping information as its input, which may potentially introduce computational burden during the reconstruction process. To address this, an automatic step is expected to be developed to reliably cluster spots while maintaining computational efficiency of the overall process. This step can be integrated into our method either as preprocessing, or as a coupling task, similarly to our expectation of data quality enhancement. Finally, we envision incorporating a wider scope of anchors applications into our existing framework. such as information integration of sections across time, across modalities and even across species. With interpretability, robustness and accuracy provided by ST-GEARS, we anticipate its applications and extension in various areas of biological and medical research. We believe that our method can help address a multitude of questions regarding growth and development, disease mechanisms, and evolutionary processes.

Methods

FGW OT description

Fused Gromov Wasserstein (FGW) Optimal Transport (OT) is the modeling of spot-wise or cell-wise similarity between two sections, with the purpose of solving optimal mappings between the spots or cells, with mappings also called ‘anchors’. By FGW OT, the optimal group of mappings enables highest gene expression similarity between mapped spots, at the same time keeping similar positions relative to their located sections.

The required input of FGW OT includes genes expression, spot or cell locations before registration, and constraint values which assigns different weight to the optimization on different spots or cells. For gene expression, we introduce $\mathbf{A}\in R^{n_A,m}$ for section A, to describe normalized count of unique molecular identifiers (UMIs) of different genes of each cell or spot, thereinto n_A denotes number of spots in slice A, and m denotes number of genes that are captured in both sections. Similarly, we describe gene expression on section B as $\mathbf{B}\in R^{n_B,m}$, with genes arranged in the same order as in A. For spot or cell locations, we introduce ${\mathbf{X}}_{\mathbf{A}}\in R^{n_A,2}$ to describe spots locations of section A, with the 1st column storing horizontal coordinates and the 2nd storing vertical coordinates. Similarly, we have ${\mathbf{X}}_{\mathbf{B}}\in R^{n_B,2}$ to describe spots locations in section B. Spots are arranged in the same order in gene expression and location matrices. Constraint values are discussed in section of Distributive Constraints.

FGW OT solves:

$$\mathit{\pi }=argmi{n}_{\mathit{\pi }\in \Pi \left(a,b\right)}⟨\left(1-\alpha \right){\mathbf{M}}_{\mathbf{AB}}^{\mathbf{2}}+\alpha L^2\left({\mathbf{C}}_{\mathbf{A}},{\mathbf{C}}_{\mathbf{B}}\right)\otimes \mathit{\pi },\mathit{\pi }⟩=argmi{n}_{\mathit{\pi }\in \Pi \left(a,b\right)}\left(\left(1-\alpha \right)⟨{\mathbf{M}}_{\mathbf{AB}}^{\mathbf{2}},\pi ⟩+\alpha ⟨L^2\left({\mathbf{C}}_{\mathbf{A}},{\mathbf{C}}_{\mathbf{B}}\right)\otimes \mathit{\pi },\mathit{\pi }⟩\right)$$

$$s.t.{\sum }_j{\mathit{\pi }}_{\mathbf{i},\mathbf{j}}={\mathbf{W}}_{\mathbf{i}}^{\left(\mathbf{A}\right)},{\sum }_i{\mathit{\pi }}_{\mathbf{i},\mathbf{j}}={\mathbf{W}}_{\mathbf{j}}^{\left(\mathbf{B}\right)}$$ 1

Thereinto, ${\mathbf{M}}_{\mathbf{AB}}\in R^{n_A,n_B}$ describes the similarity of each pair of spots respectively on section A and B, formulated as ${\mathbf{M}}_{\mathbf{i},\mathbf{j}}^{\left(\mathbf{AB}\right)}=KL\left(A_{i,:},B_{j,:}\right)$. Be noted that ${\mathrm{M}}_{\mathrm{i},\mathrm{j}}^{\left(\mathrm{AB}\right)}$ still indicates spot-wise similarity M_AB, with section code AB being moved to superscript and added parenthesis for clarity, since subscript location are taken by spot index i, j. KL denotes Kullback-Leibler (KL) divergence⁴³. ${\mathbf{C}}_{\mathbf{A}}\in R^{n_A,n_A}$ describes spot-wise distance within section A, with ${\mathbf{C}}_{\mathbf{i},\mathbf{j}}^{\left(\mathbf{A}\right)}=dis\left({\mathbf{X}}_{\mathbf{i},:}^{\left(\mathbf{A}\right)},{\mathbf{X}}_{\mathbf{j},:}^{\left(\mathbf{A}\right)}\right)$, and dis denoting Euclidean distance measure. Be noted that ${\mathrm{X}}_{\mathrm{i},:}^{\left(\mathrm{A}\right)}$ and ${\mathrm{X}}_{\mathrm{j},:}^{\left(\mathrm{A}\right)}$ still indicate spot locations X_A, with section code A being moved to superscript and added parenthesis for clarity, since subscript location are taken by spot index i and j. ${\mathrm{C}}_{\mathrm{i},\mathrm{j}}^{\left(\mathrm{A}\right)}$ refers to spot-wise distance C_A for the same reason. Similarly, ${\mathbf{C}}_{\mathbf{B}}\in R^{n_B,n_B}$ describes spot-wise distance of section B. $\mathbf{L}\in R^{n_A,n_B,n_A,n_B}$ defines the difference between all spot pair distance respectively on section A and B, with ${\mathrm{L}}_{\mathrm{i},\mathrm{j},\mathrm{k},\mathrm{l}}=\mid {\mathrm{C}}_{\mathrm{i},\mathrm{k}}^{\left(\mathrm{A}\right)}-{\mathrm{C}}_{\mathrm{j},\mathrm{l}}^{\left(\mathrm{B}\right)}\mid$. ⊗ denotes Kronecker product of two matrices; 〈,〉 denotes matrix multiplication.

Adjacency matrix $\mathbf{\pi }\in R^{\left(n_A,n_B\right)}$ to be optimized stores strength of anchors between spots from the two sections, with row index representing spots on section A, and column index representing spots on section B. Sum of elements of π is 1. With $⟨{\mathbf{M}}_{\mathbf{AB}}^{\mathbf{2}},\mathbf{\pi }⟩$, the similarity of mapped spots are measured. With $⟨{\mathbf{L}}^{\mathbf{2}}\left({\mathbf{C}}_{\mathbf{A}},{\mathbf{C}}_{\mathbf{B}}\right)\times \mathbf{\pi },\mathbf{\pi }⟩$, similarity between distance of spot pairs on section A, with its anchored spot pairs on section B, is measured. $⟨{\mathbf{L}}^{\mathbf{2}}\left({\mathbf{C}}_{\mathbf{A}}l,{\mathbf{C}}_{\mathbf{B}}\right)\otimes \mathbf{\pi },\mathbf{\pi }⟩$ describes similarity between spatial structures under the anchors’ connection. α ∈ [0,1] denotes regularization factor, which specifies the relative importance of structure similarity compared to expression similarity. W_A and W_B are constraint values that are introduced in section of Distributive Constraints.

With the formulation above, FGW OT solves optimal anchors between the spots, or cells, which enables maximum weighted combination of gene expression similarity and position similarity of mapped spots or cells.

Distributive constraints

As adopted by constraint values in FGW OT, we introduce Distributive Constraints, to assign different emphasis to spots or cells in the optimization. Distributive Constraints utilizes cell type component information to differentiate the emphasis: if an annotation or cluster express high similarity across sections, its corresponding spots or cells will be placed relatively high sum of probability, and vice versa. With higher sum of probability, more anchors and anchors with higher strength are generated, while less anchors are produced on spots with lower sum of probability. This operation leads registration to rely more on expression-consistent regions of sections, hence largely enhancing both accuracy of anchors and precision of following rigid and elastic registration.

The required inputs of Distributive Constraints include ${\mathbf{G}}_{\mathbf{A}}\in R^{n_A}$ and ${\mathbf{G}}_{\mathbf{B}}\in R^{n_B}$, which store the grouping information such as annotation type or cluster of each spot in section A and B. We then summarize the repeated annotations or clusters from G_A and G_B, and put the unique values in $\mathbf{g}\in R^{n_{group}}$. n_group is the number of unique annotation type or clusters. Then implemented in ST-GEARS, for each annotation type or cluster g_i, we calculate the average gene expression across spots:

$$\begin{array}{c}\hfill \mathbf{av}{\mathbf{g}}_{\mathbf{A}}=\frac{1}{\mid {\mathbf{I}}_{\mathbf{A}}\mid }{\mathbf{1}}_{{\mathbf{n}}_{\mathbf{A}}}{\mathbf{A}}_{\mathbf{i}\in {\mathbf{I}}_{\mathbf{A}},:}\hfill \\ \hfill \mathbf{av}{\mathbf{g}}_{\mathbf{B}}=\frac{1}{\mid {\mathbf{I}}_{\mathbf{B}}\mid }{\mathbf{1}}_{{\mathit{n}}_{\mathit{B}}}{\mathit{B}}_{\mathit{i}\in {\mathit{I}}_{\mathit{B}},:}\hfill \end{array}$$

where

$$\begin{array}{c}\hfill {\mathbf{I}}_{\mathbf{A}}=\left\{i^{\prime }\in \left\{1,2,...,n_A\right\}\mid {\mathbf{G}}_{{\mathbf{i}}^{\prime }}^{\left(\mathbf{A}\right)}={\mathbf{g}}_{\mathbf{i}}\right\}\hfill \\ \hfill {\mathbf{I}}_{\mathbf{B}}=\left\{i^{\prime }\in \left\{1,2,...,n_B\right\}\mid {\mathbf{G}}_{{\mathbf{i}}^{\prime }}^{\left(\mathbf{B}\right)}={\mathbf{g}}_{\mathbf{i}}\right\}\hfill \end{array}$$

Be noted that ${\mathbf{G}}_{{\mathbf{i}}^{\prime }}^{\left(\mathbf{A}\right)}$ and ${\mathbf{G}}_{{\mathbf{i}}^{\prime }}^{\left(\mathbf{B}\right)}$ still indicate grouping information G_A and G_B, with section code A and B being moved to superscript and added parenthesis for clarity, since subscript location are taken by spot index i′ and j′. And ${\mathbf{1}}_{{\mathbf{n}}_{\mathbf{A}}}$ and ${\mathbf{1}}_{{\mathbf{n}}_{\mathbf{B}}}$ are both row vectors of ones.

With average gene expression of each annotation type or cluster, with the form of distribution, we measure its difference across sections by KL divergence. Then the calculated distance is mapped by logistic kernel, to further emphasize differences between relatively consistent annotations or clusters.

$$dis=KL\left(av{g}_A,av{g}_B\right)$$

$di{s}_{map}=f_{logistic}\left(dis\right)$, where $f_{logistic}\left(x\right)=\frac{1}{1+e^{-x}}-0.5$. Putting scaler value dis of each annotation or cluster together, we have a vector $\mathbf{DI}{\mathbf{S}}_{\mathbf{map}}\in R^{n_{celltype}}$. Finally, we transform the distance to similarity, map the similarity result back to each spot:

$$\begin{array}{c}\hfill \mathrm{sim}=-1\times \mathrm{DI}{\mathrm{S}}_{\mathrm{map}}\hfill \\ \hfill {\mathrm{W}\_\mathrm{raw}}_{\left\{\mathrm{i}\mid {\mathrm{C}}_{\mathrm{i}}^{\left(\mathrm{A}\right)}={\mathrm{c}}_{\mathrm{i}}\right\}}^{\left(\mathrm{A}\right)}=\mathrm{si}{\mathrm{m}}_{\mathrm{i}}\hfill \\ \hfill {\mathrm{W}\_\mathrm{raw}}_{\left\{\mathrm{i}\mid {\mathrm{C}}_{\mathrm{i}}^{\left(\mathrm{B}\right)}={\mathrm{c}}_{\mathrm{i}}\right\}}^{\left(\mathrm{B}\right)}=\mathrm{si}{\mathrm{m}}_{\mathrm{i}}\hfill \end{array}$$

We further apply normalization on the result:

$$\begin{array}{c}\hfill {\mathbf{W}}_{\mathbf{A}}=\frac{1}{\Sigma \mathbf{W}\_\mathbf{ra}{\mathbf{w}}^{\left(\mathbf{A}\right)}}\left(\mathbf{W}\_\mathbf{ra}{\mathbf{w}}^{\left(\mathbf{A}\right)}-\min \left(\mathbf{W}\_\mathbf{ra}{\mathbf{w}}^{\left(\mathbf{A}\right)}\right)\times {\mathbf{1}}_{{\mathbf{n}}_{\mathbf{A}}}\right)\hfill \\ \hfill {\mathbf{W}}_{\mathbf{B}}=\frac{1}{\mathrm{\Sigma }\mathbf{W}\_\mathbf{ra}{\mathbf{w}}^{\left(\mathbf{B}\right)}}\left(\mathbf{W}\_\mathbf{ra}{\mathbf{w}}^{\left(\mathbf{B}\right)}-\min \left(\mathbf{W}\_\mathbf{ra}{\mathbf{w}}^{\left(\mathbf{B}\right)}\right)\times {\mathbf{1}}_{{\mathbf{n}}_{\mathbf{B}}}\right)\hfill \end{array}$$

W_A and W_B are constraints values applied in (1). Since the values are computed based on similarity measure using cell composition information, weight of FGW OT is automatically redistributed, with higher emphasis on more consistent regions across sections, and less emphasis on less consistent area. Enhanced anchor accuracy hence registration accuracy is then achieved.

Self-adaptive regularization

In FGW OT formulation, a regularization factor is included to specify the relative importance of structural similarity compared to expression similarity during optimization. ST-GEARS includes a self-adaptive regularization method that determines the factor value, that induces highest overall accuracy of anchors despite of varying situations. Situations include but are not limited to section distances, spot sizes, extent of distortions, and data quality such as level of diffusion.

By practice, our method respectively adopts factors on multiple scales including 0.8, 0.4, 0.2, 0.1, 0.05, 0.025, 0.013, and 0.006. The candidate values vary exponentially, for ST-GEARS to find the optimal term regardless of scale differences between expression and structural term in (1). The accuracy of each set of optimized anchors by every regularization factor was evaluated, by measuring weighted percentage ${\sum }_{{\mathbf{G}}_{\mathbf{i}}^{\left(\mathbf{A}\right)}={\mathbf{G}}_{\mathbf{j}}^{\left(\mathbf{B}\right)}}{\mathit{\pi }}_{\mathbf{i},\mathbf{j}}$ of anchors that join spots with same annotation types or clusters. Be noted that ${\mathrm{G}}_{\mathrm{i}}^{\left(\mathrm{A}\right)}$ and ${\mathrm{G}}_{\mathrm{j}}^{\left(\mathrm{B}\right)}$ still indicate grouping information G_A and G_B, respectively, with section code A and B being moved to superscript and added parenthesis for clarity, since subscript location are taken by spot index i and j. The regularization factor value that achieves highest accuracy is then adopted by our method.

Elastic field inference

Finding spots with highest probability

After rigid registration, elastic fields are inferred based on the anchors with the highest probability for each spot or cell. For elastic field to be applied on each section, it is calculated using its anchors with closest sections, as well as spatial coordinates of sections after rigid registration. Along cross-sectioning order, each section in the middle has two closest sections, respectively on its anterior and posterior sides. Exceptionally, if a section is on anterior or posterior end, it has only one closest section.

Specifically for a section in the middle with N spots, we calculate ${\mathbf{I}}_{\mathbf{pre}}ϵZ^N$ and ${\mathbf{I}}_{\mathbf{next}}ϵZ^N$ which stores the mapped spots on anterior and posterior neighbor section for each of its spots. The calculation takes as input adjacency matrix π_pre, which stores anchors with the anterior neighbor section output by FGW OT, and π_next storing anchors with posterior section.

$$\begin{array}{c}\hfill {\mathbf{I}}_{\mathbf{pre}}^{\mathbf{n}}=argma{x}_{iϵ\left\{0,\dots ,N_{pre}-1\right\}}{\mathit{\pi }}_{:,\mathbf{n}}^{\left(\mathbf{pre}\right)}\hfill \\ \hfill {\mathbf{I}}_{\mathbf{next}}^{\mathbf{n}}=argma{x}_{jϵ\left\{0,...,N_{next}-1\right\}}{\mathit{\pi }}_{\mathbf{n},:}^{\left(\mathbf{next}\right)}\hfill \end{array}$$

Be noted that ${\mathrm{\pi }}_{:,\mathrm{n}}^{\left(\mathrm{pre}\right)}$ and${\mathrm{\pi }}_{\mathrm{n},:}^{\left(\mathrm{next}\right)}$ still indicate adjacency matrix π_pre and π_next, with direction code pre and next being moved to superscript and added parenthesis for clarity, since subscript location are taken by spot index n.

Notably, not every spot in a selected section has its own anchored spot, due to multiple strategies including distributive constraint and anchors filtration, hence their corresponding element in I_pre and I_next are null. For section located on posterior end, only I_next is applicable; and for section located on anterior end, only ${\mathbf{I}}_{\mathrm{pre}}^{\mathrm{n}}$ is applicable.

Elastic field establishment

After specifying spots with highest probability, ST-GEARS calculates location displacements between the spots, then establishes elastic fields for each section. An elastic field is a 2D displacement distribution, describing how displacement values are distributed across different locations. And it is established to enable ST-GEARS to benefit from further denoising functions to reduce elastic operation outliers and improve elastic effect consistency across regions.

For each section located in the middle, 4 elastic fields are generated. Two of those represent the section’s horizontal and vertical displacement distribution compared to anterior neighbor section, denoted as 2D matrix F^(x_pre) and F^(y_pre), while the other two represent its horizontal and vertical displacement distribution compared to posterior neighbor, denoted as F^(x_next) and F^(y_next). To initialize F^(x_pre), F^(y_pre), F^(x_next) and F^(y_next) for the section, the shape of the matrix is first decided. Its height denoted by Height and width denoted by Width are calculated by gridding the spot locations using a fixed step. Height and Width are shared across the 4 matrices:

$$\begin{array}{c}\hfill Height=\lceil \left(ma{x}_{iϵ\left\{0,...,N\right\}}{\mathbf{X}}_{\mathbf{i},\mathbf{0}}-mi{n}_{iϵ\left\{0,...,N\right\}}{\mathbf{X}}_{\mathbf{i},\mathbf{0}}\right)/psize\rceil \hfill \\ \hfill Width=\lceil \left(ma{x}_{iϵ\left\{0,...,N\right\}}{\mathbf{X}}_{\mathbf{i},\mathbf{1}}-mi{n}_{iϵ\left\{0,...,N\right\}}{\mathbf{X}}_{\mathbf{i},\mathbf{1}}\right)/psize\rceil \hfill \end{array}$$

For its input, $\mathbf{X}\in R^{N,2}$ denotes spots location of current section after rigid registration. For a single section, we prepare ${\mathbf{X}}^{\left(\mathbf{pre}\right)}ϵR^{N\_pre,2}$ and ${\mathbf{X}}^{\left(\mathbf{next}\right)}ϵR^{N\_next,2}$ as spots location of its anterior and posterior section after rigid alignment, respectively. psize represents average distance between closest spot or cell centers, and it is to be input by users. The matrix has no filled values to this step.

To fill in the fields, we first transform spot locations into the coordinate system of field. With $\mathbf{X}\_\mathbf{shifted}ϵR^{N,2}$ and $\mathbf{X}\_\mathbf{pixel}ϵR^{N,2}$:

$$\begin{array}{c}\hfill {\mathbf{X}\_\mathbf{shifted}}_{\mathbf{i},:}={\mathbf{X}}_{\mathbf{i},:}-{\left[mi{n}_{iϵ\left\{0,...,N\right\}}{\mathbf{X}}_{\mathbf{i},\mathbf{0}},mi{n}_{iϵ\left\{0,...,N\right\}}{\mathbf{X}}_{\mathbf{i},\mathbf{1}}\right]}^T\hfill \\ \hfill {\mathbf{X}\_\mathbf{pixel}}_{\mathbf{i},\mathbf{j}}=\lceil {\mathbf{X}\_\mathbf{shifted}}_{\mathbf{i},\mathbf{j}}/psize\rceil \hfill \end{array}$$

We then calculate location displacements between each of its spots and their anchored spots with highest probability, on both anterior and posterior neighbors. With $\mathbf{X}\_\mathbf{corres}ϵR^{N,2}$ and $\mathbf{X}\_\mathbf{delta}ϵR^{N,2}$:

$$\begin{array}{c}\hfill {\mathrm{X}\_\mathrm{corres}}_{\mathrm{n},:}^{\left(\mathrm{pre}\right)}={\mathrm{X}}_{{\mathrm{I}}_{\mathrm{pre}}^{\mathrm{n}},:}^{\left(\mathrm{pre}\right)}\hfill \\ \hfill {\mathrm{X}\_\mathrm{corres}}_{\mathrm{n},:}^{\left(\mathrm{next}\right)}={\mathrm{X}}_{{\mathrm{I}}_{\mathrm{next}}^{\mathrm{n}},:}^{\left(\mathrm{next}\right)}\hfill \\ \hfill \begin{array}{c}\hfill {\mathrm{X}\_\mathrm{delta}}_{\mathrm{n},:}^{\left(\mathrm{pre}\right)}={\mathrm{X}\_\mathrm{corres}}_{\mathrm{n},:}^{\left(\mathrm{pre}\right)}{-\mathrm{X}}_{\mathrm{n},:}\hfill \\ \hfill {\mathrm{X}\_\mathrm{delta}}_{\mathrm{n},:}^{\left(\mathrm{next}\right)}={\mathrm{X}\_\mathrm{corres}}_{\mathrm{n},:}^{\left(\mathrm{next}\right)}{-\mathrm{X}}_{\mathrm{n},:}\hfill \end{array}\hfill \end{array}$$

With the spot locations in field coordinates and the displacement values above, we fill in corresponding elements of the elastic field:

$$\begin{array}{c}\hfill {\mathrm{F}}^{\left(\mathrm{x}\_\mathrm{pre}\right)}\left[\mathrm{X}\_\mathrm{pixel}\right]={\mathrm{X}\_\mathrm{delta}}_{:,0}^{\left(\mathrm{pre}\right)}\hfill \\ \hfill {\mathrm{F}}^{\left(\mathrm{y}\_\mathrm{pre}\right)}\left[\mathrm{X}\_\mathrm{pixel}\right]={\mathrm{X}\_\mathrm{delta}}_{:,1}^{\left(\mathrm{pre}\right)}\hfill \\ \hfill {\mathrm{F}}^{\left(\mathrm{x}\_\mathrm{next}\right)}\left[\mathrm{X}\_\mathrm{pixel}\right]={\mathrm{X}\_\mathrm{delta}}_{:,0}^{\left(\mathrm{next}\right)}\hfill \end{array}$$

$${\mathrm{F}}^{\left(\mathrm{y}\_\mathrm{next}\right)}\left[\mathrm{X}\_\mathrm{pixel}\right]={\mathrm{X}\_\mathrm{delta}}_{:,1}^{\left(\mathrm{next}\right)}$$ 2

By the end of Eqs. (2), 4 elastic fields for each section in the middle is established. However, some elements in the matrix are still empty, because of absence of spots or cells located in the grid of location. To address this problem, 2d nearest interpolation method⁴⁴ was adopted, which fills in every empty element, with the displacement value of its neighboring elements:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathbf{F}}^{\left(\mathbf{x}\_\mathbf{pre}\right)}=f_{interp\_grid}\left(\mathbf{X}\_\mathbf{pixel},{\mathbf{X}\_\mathbf{delta}}_{:,\mathbf{0}}^{\left(\mathbf{pre}\right)},\mathbf{mes}{\mathbf{h}}_{\mathbf{trans}}\right)\hfill \\ \hfill {\mathbf{F}}^{\left(\mathbf{y}\_\mathbf{pre}\right)}=f_{interp\_grid}\left(\mathbf{X}\_\mathbf{pixel},{\mathbf{X}\_\mathbf{delta}}_{:,\mathbf{1}}^{\left(\mathbf{pre}\right)},\mathbf{mes}{\mathbf{h}}_{\mathbf{trans}}\right)\hfill \end{array}\hfill \\ \hfill {\mathbf{F}}^{\left(\mathbf{x}\_\mathbf{next}\right)}=f_{interp\_grid}\left(\mathbf{X}\_\mathbf{pixel},{\mathbf{X}\_\mathbf{delta}}_{:,\mathbf{0}}^{\left(\mathbf{next}\right)},\mathbf{mes}{\mathbf{h}}_{\mathbf{trans}}\right)\hfill \\ \hfill {\mathbf{F}}^{\left(\mathbf{y}\_\mathbf{next}\right)}=f_{interp\_grid}\left(\mathbf{X}\_\mathbf{pixel},{\mathbf{X}\_\mathbf{delta}}_{:,\mathbf{1}}^{\left(\mathbf{next}\right)},\mathbf{mes}{\mathbf{h}}_{\mathbf{trans}}\right)\hfill \end{array}$$

thereinto $\mathbf{mes}{\mathbf{h}}_{\mathbf{trans}}ϵN^{n_{grids}\times 2}$ denotes grid coordinates of the designed field, with $n_{grids}=Height\times Width$. And f_{interp_grid} denotes the nearest interpolation method.

For section located on posterior end, only F^(x_next) and F^(y_next) are applicable; and for section located on anterior end, only F^(x_pre) and F^(y_pre) are applicable.

2D Gaussian denoising

As caused by exerted force, the displacement or elastic field is expected to have static or smoothly changing values across different locations^45–47. ST-GEARS makes use of this property, to smoothen the field and to reduce errors in the field caused by any upper stream process, such as raw data noises and inaccuracy in anchor computation. Gaussian filtering^48,49 is adopted to implement the denoising, similarly to image denoising processes^50,51. Denoised elastic fields are then generated.

It calculates weighted average across the neighboring region of each element to replace its value:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathbf{F}}^{\left(\mathbf{x}\_\mathbf{pre}\right)}=f_{gaussian\_filter}\left({\mathbf{F}}^{\left(\mathbf{x}\_\mathbf{pre}\right)}\right)\hfill \\ \hfill {\mathbf{F}}^{\left(\mathbf{y}\_\mathbf{pre}\right)}=f_{gaussian\_filter}\left({\mathbf{F}}^{\left(\mathbf{y}\_\mathbf{pre}\right)}\right)\hfill \end{array}\hfill \\ \hfill {\mathbf{F}}^{\left(\mathbf{x}\_\mathbf{next}\right)}=f_{gaussian\_filter}\left({\mathbf{F}}^{\left(\mathbf{x}\_\mathbf{next}\right)}\right)\hfill \\ \hfill {\mathbf{F}}^{\left(\mathbf{y}\_\mathbf{next}\right)}=f_{gaussian\_filter}\left({\mathbf{F}}^{\left(\mathbf{y}\_\mathbf{next}\right)}\right)\hfill \end{array}$$

where f_{gaussian_filter} denotes the method of Gaussian filtering.

Bi-sectional fields application

Bi-sectional fields application plan

With elastic fields generated and denoised, ST-GEARS uses the fields as a guidance to correct distortion for each section. Through querying the elastic fields with spatial location of each spot, the displacement to be implemented is returned. For a section in the middle, its elastic fields calculated with both anterior and posterior neighbor sections are queried, and guidance provided by both anterior and posterior sections are applied on the rigid aligned result, called ‘Bi-sectional Fields Application’. After the application, the distortion of the section is corrected, and the elastic registration result is generated.

Specifically, the denoised elastic fields are first queried, returning the displacement to be implemented:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill X{\_delta}_{i,0}^{\left(pre\_final\right)}=F_{X_{i,0}^{\left(pixel\right)}}^{\left(x\_pre\right)}\hfill \\ \hfill {X\_delta}_{i,1}^{\left(pre\_final\right)}=F_{X_{i,1}^{\left(pixel\right)}}^{\left(y\_pre\right)}\hfill \end{array}\hfill \\ \hfill {X\_delta}_{i,0}^{\left(next\_final\right)}=F_{X_{i,0}^{\left(pixel\right)}}^{\left(x\_next\right)}\hfill \\ \hfill {X\_delta}_{i,1}^{\left(next\_final\right)}=F_{X_{i,1}^{\left(pixel\right)}}^{\left(y\_next\right)}\hfill \end{array}$$

Next, average displacement returned by both anterior and posterior sections are applied on the rigid registration result, leading to final elastic registration result $\mathbf{X}\_\mathbf{final}\in R^{N,2}:$

$$\mathrm{X}\_\mathrm{final}=\mathrm{X}+\frac{1}{2}{\mathrm{X}\_\mathrm{delta}}^{\left(\mathrm{pre}\_\mathrm{final}\right)}+\frac{1}{2}{\mathrm{X}\_\mathrm{delta}}^{\left(\mathrm{next}\_\mathrm{final}\right)}$$

For section located on posterior end,

$$\mathrm{X}\_\mathrm{final}=\mathrm{X}+{\mathrm{X}\_\mathrm{delta}}^{\left(\mathrm{pre}\_\mathrm{final}\right)}$$

For section located on anterior end,

$$\mathrm{X}\_\mathrm{final}=\mathrm{X}+{\mathrm{X}\_\mathrm{delta}}^{\left(\mathrm{next}\_\mathrm{final}\right)}$$

The validity of this plan is proved in the section: Proof of validity of Bi-sectional Fields Application.

Proof of validity of Bi-sectional fields application

Bi-sectional Fields Application accurately recovers the spatial profile before distortion, by averaging and applying displacement value guided by both anterior and posterior neighbor section. The effect is approved mathematically as following:

Take section A, B, and C as an example of a sequence of sections, with X_A, X_B and X_C denoting their spots’ spatial information after rigid alignment, and X_{A_insitu}, X_{B_insitu} and X_{C_insitu} denoting their in vivo spatial information. The distortion occurred to the slices during experiments are denoted as X_{A_dis}, X_{B_dis} and X_{C_dis}.

According to Bi-sectional Fields Application, the corrected spatial information is:

$${\mathbf{X}}_{\mathbf{B}\_\mathbf{cor}}={\mathbf{X}}_{\mathbf{B}}+\frac{1}{2}\left({\mathbf{X}}_{\mathbf{A}}-{\mathbf{X}}_{\mathbf{B}}\right)+\frac{1}{2}\left({\mathbf{X}}_{\mathbf{c}}-{\mathbf{X}}_{\mathbf{B}}\right)=\frac{1}{2}\left({\mathbf{X}}_{\mathbf{A}}+{\mathbf{X}}_{\mathbf{c}}\right)$$

Thereinto,

$${\mathbf{X}}_{\mathbf{A}}={\mathbf{X}}_{\mathbf{A}\_\mathbf{insitu}}+{\mathbf{X}}_{\mathbf{A}\_\mathbf{dis}}$$

$${\mathbf{X}}_{\mathbf{C}}={\mathbf{X}}_{\mathbf{C}\_\mathbf{insitu}}+{\mathbf{X}}_{\mathbf{C}\_\mathbf{dis}}$$

Hence,

$${\mathbf{X}}_{\mathbf{B}\_\mathbf{cor}}=\frac{1}{2}{\mathbf{X}}_{\mathbf{A}\_\mathbf{insitu}}+\frac{1}{2}{\mathbf{X}}_{\mathbf{C}\_\mathbf{insitu}}+\frac{1}{2}\left({\mathbf{X}}_{\mathbf{A}\_\mathbf{dis}}+{\mathbf{X}}_{\mathbf{C}\_\mathbf{dis}}\right)$$ 3

Based on the in vivo morphological consistency across sections, spatial information of section B can be approximated by an average of information of A and C, written as

$${\mathbf{X}}_{\mathbf{B}\_\mathbf{insitu}}=\frac{1}{2}\left({\mathbf{X}}_{\mathbf{A}\_\mathbf{insitu}}+{\mathbf{X}}_{\mathbf{C}\_\mathbf{insitu}}\right)$$ 4

Given that X_{A_dis} and X_{C_dis} can be seen as independent and identically distributed sets of variables,

$${\mathbf{X}}_{\mathbf{A}\_\mathbf{dis}}+{\mathbf{X}}_{\mathbf{C}\_\mathbf{dis}}=N\left({\mathit{\mu }}_{\mathbf{ABC}},{\mathit{\Sigma }}_{\mathbf{ABC}}\right)$$ 5

where μ_ABC is the universal mean, and Σ_ABC is the variance of the 2d displacement information.

Inserting the terms (4) and (5) back to Eq. (3) gives

$${\mathbf{X}}_{\mathbf{B}\_\mathbf{cor}}={\mathbf{X}}_{\mathbf{B}\_\mathbf{insitu}}+\frac{1}{2}N\left({\mathit{\mu }}_{\mathbf{ABC}},{\mathit{\Sigma }}_{\mathbf{ABC}}\right)={\mathbf{X}}_{{\mathbf{B}}_{\mathbf{insitu}}}+o\left({\mathbf{X}}_{{\mathbf{B}}_{\mathbf{insitu}}}\right)\to {\mathbf{X}}_{\mathbf{B}\_\mathbf{insitu}}$$

indicating the proximity of corrected spatial information to in vivo spatial information.

Evaluation metrix

We evaluated the accuracy of anchors by index of Mapping Accuracy, and measured the reconstruction effect by MSSIM and SI-STD-DI, in both elastic effect study and overall methodology comparison.

Mapping accuracy

Designed and adopted by PASTE²⁷, Mapping Accuracy calculates the weighted percentage of anchors joining spots with same annotation.

$$\mathrm{Mapping}\mathrm{Accuracy}={\sum }_{i,j,\mathbf{l}\left(\mathbf{i}\right)=\mathbf{l}\left(\mathbf{j}\right)}{\mathit{\pi }}_{\mathbf{ij}}$$

MSSIM index

MSSIM measures the accuracy of registration, based on the assumption that in some sectioning positions, tissue morphology remains almost consistent across slices. The method quantifies the accuracy, by measuring the similarity of annotation type distribution of such section pairs.

To implement the quantification, first, structurally consistent section pairs are selected among all sections arranged in sequence.

Next, on each section from the pair, transformation from individual spots to a complete image is implemented, by gridding the rectangular area that surrounds the tissue, and assigning each grid of a value that represents the annotation type which occurs most frequently in the grid. The resulted image describes the annotation type distribution of the section.

Finally, similarity between each pair of images is measured, by index of MSSIM⁵². The method generates a window with fixed size, slides the window simultaneously on both images, and compares the two framed parts by windows on their intensity, contrast, and structures. Among those, the intensity difference is measured by difference of average pixel values, the contrast difference is measured by comparing variance of the two sets of framed pixel values, and the structure difference is measured by comparing their covariances. A Structural Similarity of Images (SSIM) index is calculated for each position of the window using $SSIM\left(X,Y\right)=\frac{\left(2{\mu }_x{\mu }_y\right)\left(2{\sigma }_{xy}+c_2\right)}{\left({\mu }_x^2+{\mu }_y^2+c_1\right)\left({\sigma }_x^2+{\sigma }_y^2+c_2\right)}$, where μ_x and μ_y denote average pixel values of the frames, σ_x and σ_y denote variances of the frames, and σ_xy denotes covariances of the two frames. c₁ and c₂ are constants to avoid 0 value of the divisor. Averaging the SSIM value across all windows gives the final MSSIM result of the two sections.

SI-STD-DI

SI-STD-DI measures smoothness of area changing across sections along a fixed axis, by calculating the standard deviation of area changes on each pair of adjacent sections and scale the result by dividing it by average area.

$$\mathrm{SI}-\mathrm{STD}-\mathrm{DI}=STD\left(\left\{s_i-s_{i-1}:i\in \left[1,2,...,I-1\right]\right\}\right)/\left(\mid mean\left(\left\{s_i-s_{i-1}:i\in \left[1,2,...,I-1\right]\right\}\right)\mid \right)$$

Software and code

Data analysis

All software used to analyze data in this study are open-sourced Python packages, including anndata = 0.9.2, numpy = 1.22.4, pandas = 1.4.3, scipy = 1.10.1, matplotlib = 3.5.2, k3d = 2.15.3.

Statistics and reproducibility

No statistical method was used to predetermine sample size. No data were excluded from the analyses. The experiments were not randomized. The Investigators were not blinded to allocation during experiments and outcome assessment.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Author contributions

Tianyi Xia was responsible of method design, analysis design and implementation, as well as drafting of this manuscript. Dr. Luni Hu participated in structure design of the applications. Lulu Zuo was in part of 3D visualizations design, and she helps maintain our online repository. Tianyi Xia, Lei Cao, Lulu Zuo and Dr. Luni Hu conducted experiments and analysis for reply to peer review. Dr. Yunjia Zhang provided insights in anchors results interpretation of DLPFC dataset, and in accuracy analysis of mouse brain dataset. Dr. Mengyang Xu revised this article. Lei Zhang and Bowen Ma offered numerous suggestions to enhance computational efficiency, in both memory and time. Taotao Pan and Chuan Chen provided suggestions in data preprocessing. Qin Lu, Bohan Zhang, Junfu Guo, Chang Shi and Mei Li provided suggestions for this study. Dr. Shuangsang Fang supervised this study in structure and analysis design, and she revised this article. Chao Liu, Yuxiang Li and Yong Zhang supervised this study.

Peer review

Peer review information

Nature Communications thanks Jun Ding, Xiangyu Luo and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Data availability

All data used in this research were collected from published sources. DLPFC data was obtained from the research: Transcriptome-scale Spatial Gene Expression in the Human Dorsolateral Prefrontal Cortex, with data downloading link of http://research.libd.org/spatialLIBD/index.html; Drosophila embryo and Drosophila larva data were collected from High-resolution 3d Spatiotemporal Transcriptomic Maps of Developing Drosophila Embryos and Larvae, with the dataset link of https://db.cngb.org/stomics/datasets/STDS0000060. Mouse brain data was collected from research: Modular cell type organization of cortical areas revealed by in vivo sequencing. The download link is: https://data.mendeley.com/datasets/8bhhk7c5n9/1. All datasets were generated on Spatial Transcriptomics platform, with DLPFC data generated by Visium technology of 10x Genomics, Mouse brain data generated by BARseq of Cold Spring Harbor Laboratory, while Drosophila embryo and larva generated by Stereo-seq technology of BGI. Source data are provided with this paper.

Code availability

The methods of ST-GEARS is packaged, and distributed as an open-source, publicly available repository at https://github.com/STOmics/ST-GEARS⁵³.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-51935-0.