Abstract
Landau–Zener–Stückelberg–Majorana (LZSM) transitions occur between quantum states when parameters in the system’s Hamiltonian are varied continuously and rapidly. In magnetic resonance, losses in adiabatic rapid passage can be understood using the physics of LZSM transitions. Most treatments of LZSM transitions ignore the dephasing of coherences, however. Motivated by ongoing work in magnetic resonance force microscopy, we employ the Bloch equations, coordinate transformation, and the Magnus expansion to derive expressions for the final magnetization following a rapid field sweep at fixed irradiation intensity that include losses. Our derivation introduces an inversion-function, Fourier transform method for numerically evaluating highly oscillatory integrals. Expressions for the final magnetization are given for low and high irradiation intensity, valid in the limit. Analytical results are compared to numerical simulations and nuclear magnetic resonance experiments. Our relatively straightforward calculation reproduces semiquantitatively the well known LZSM result in the limit.
Keywords: Landau–Zener–Stückelberg–Majorana transition, Landau–Zener transition, Bloch equations, electron spin resonance, saturation, adiabatic rapid passage, magnetic resonance force microscopy, force-gradient detected magnetic resonance
Graphical Abstract
1. Introduction
The rapid detection and imaging of single electron spins would be a powerful tool for the atomic-scale characterization of samples ranging from emerging quantum computing materials to individual spin-labeled biomolecules. Applying single-spin imaging to nitroxide spin labels — widely employed to study globular proteins, membrane proteins, and nucleic acids — is an especially exciting prospect. Since pioneering experiments in the early 1990’s optically detected magnetic resonance in individual pentacene molecules [1, 2], more widely applicable magnetic resonance experiments have demonstrated the detection and imaging of individual electron spins. The two most generally applicable such experiments involve using magnetic resonance force microscopy to detect an individual defect in quartz [3] and employing a nitrogen-vacancy center in diamond to observe a single adventitious radical located nearby [4, 5].
Frustratingly, both these experiments observed essentially unpolarized spins and consequently required signal-averaging times of 13 hour/pt. in Ref. 3 and 40 min/pt. in Ref. 5 [6]. For imaging nitroxide-labeled proteins, magnetic resonance force microscopy (MRFM) is preferable to NV-center magnetometry because of the MRFM experiment’s superior depth of view. Moore and coworkers showed that small numbers of nitroxide spins could be observed as a cantilever frequency shift in an MRFM experiment [7]. Motivated by this breakthrough, Nguyen and Marohn proposed a single-spin MRFM experiment optimized to detect and image individual nitroxide spin labels using a magnet-tipped cantilever, with an estimated signal averaging time of only seconds per point [8]. In contrast with the spin-noise experiments of Refs. 3 and 5, the proposed experiment measures the average (i.e. thermal) spin polarization, greatly improving the signal-averaging statistics.
In the Ref. 8 proposal, spin magnetization is manipulated with short bursts of microwave irradiation applied in synchrony with cantilever motion. The resulting changes in spin magnetization are detected as a force-gradient-induced shift in cantilever frequency [7, 9]. Computing spin evolution in the Ref. 8 experiment is challenging. To detect spin-induced changes in cantilever frequency, the cantilever must be moving. Large time-dependent resonance offsets are experienced by electron spins below the moving magnet-tipped cantilever, and one is concerned that the resonance offset changes so rapidly that spins may not be in resonance with the applied microwaves long enough to invert or even saturate. The purpose of this manuscript is to assess the potential loss of signal due to this effect.
The magnetic resonance community is familiar with the problem of magnetization loss during an adiabatic rapid passage through resonance [10–18]. Adiabatic rapid passage is an example of a Landau–Zener–Stückelberg–Majorana (LZSM) transition [19] — wavefunction evolution that occurs when the Hamiltonian parameters are changed continuously. LZSM transitions are used to describe a wide range of phenomena beyond magnetic resonance — atomic collisions [20] chemical reaction rates [21, 22], population inversion in electronic states [23], and qubit control [24–27] for example. LZSM transitions have recently been used to describe the quantum dynamics of two coupled qubits [28, 29], qutrits [30–32], coupled qutrits [29], and quantum annealing protocols [33].
State-to-state transition probabilities following an LZSM transition can be calculated for a two-level system exactly using the Schrödinger equation [19, 26, 27, 34]. If the frequency of applied irradiation is swept through resonance too quickly, level populations are unaffected by the irradiation. If, on the other hand, the irradiation is swept through resonance slowly, i.e. adiabatically, then a population inversion is achieved. The Schrödinger-equation treatment of the LZSM transition is not obviously valid at low irradiation intensity and, moreover, neglects relaxation. Our nitroxide spin of interest has , comparable to or shorter than the time to sweep through resonance in a magnetic resonance force microscope experiment. Relaxation during a rapid passage through resonance is, therefore, a concern.
Assessing how relaxation modifies the transition probabilities during an LZSM transition is an area of active research. There are two issues to consider in magnetic resonance versions of the LZSM experiment. The first is computing spin relaxation during a perfectly adiabatic sweep through resonance; even when losses due to violation of the adiabatic condition are negligible, magnetization can still be lost due to relaxation. There is a large body of magnetic resonance literature treating relaxation from dipolar interactions and chemical exchange during an adiabatic, frequency-swept pulse [35–42]. This body of literature, however, neglects non-adiabatic losses.
The second issue is computing the final magnetization when the adiabatic condition is violated and relaxation is present. This is the issue considered here. One must take care assessing LZSM-transition studies, because, outside the magnetic resonance literature, non-adiabatic losses are often called “dissipation” despite their being due to neither nor relaxation. While numerous studies have modeled losses during an LZSM transition [23, 43–55], none of these studies obtain a simple and accurate closed-form solution for the -modified transition probabilities in the simple case of a linear energy-level sweep, and none consider both low- and high-intensity irradiation.
To address this deficiency, here we compute the magnetization evolution following a fast sweep through resonance in the limit using the Bloch equations [56–59], coordinate transformations, and the Magnus expansion [60, 61]. We consider both low-intensity and high-intensity limits and obtain approximate solutions for the magnetization following an LZSM transition that accounts for losses.
2. Theory
2.1. The connection between LZSM transitions and the Bloch equations
To see the connection between LZSM transitions and the Bloch equations, let us write out the LZSM problem in the language of magnetic resonance. Consider a spin with magnetic moment , with Planck’s constant, the spins’s gyromagnetic ratio, and the unitless angular momentum operator having components , and . This spin is placed in a magnetic field , formed from a longitudinal magnetic field of magnitude plus a transverse magnetic field of magnitude rotating about the axis at angular frequency . The Hamiltonian for the spin, , is given by
| (1) |
with the (time-dependent) Larmor frequency and the Rabi frequency. The eq. 1 Hamiltonian gives rise to LZSM transitions, instead of the usual Rabi oscillations, because in eq. 1 the longitudinal field amplitude is now time-dependent; a static field and time-dependent irradiation frequency also yields LSZM transitions.
Consider the resulting dynamics of a spin particle having two energy levels: a ground state and an excited state. In the eigenbasis of the operator, the spin’s wavefunction is given by
| (2) |
with and the ground-state and excited-state wavefunction coefficients, respectively. Plugging and into the Schrödinger equation gives a set of two coupled non-linear equations for and . These coupled equations can be simplified by applying a unitary, rotating-frame transformation with . The transformed wavefunction is governed by an effective Hamiltonian , leading to the following two coupled differential equations for the complex-valued coefficients of the wavefunction
| (3) |
| (4) |
Eliminating gives a second order differential equation for . For a linear sweep through resonance, and the coefficients in this differential equation are time dependent. Closed-form solutions for and , given and , can be written in terms of Weber functions [19].
According to the Feynman-Vernon-Hellwarth theorem [58], the dynamics of a two-level quantum system can be solved by following the time evolution of a real, three-dimensional vector whose components are
| (5) |
| (6) |
| (7) |
For the magnetic two-level system, the numbers , and are the components of the Bloch unit vector that points in the direction of spin’s magnetization. Recasting the LZSM problem in terms of the Bloch vector, we obtain the Bloch equations of the next section in the and limit. By recasting the LZSM problem as a modified set of Bloch equations, we can introduce saturation and dephasing effects by adding finite and .
2.2. Unitless Bloch equations
Defining a unitless magnetization vector as follows,
| (8) |
with the thermal-equilibrium magnetization, the Bloch equations in the rotating frame can be written as
| (9) |
with
| (10) |
a unitless time parameter created by multiplying time by the Rabi frequency , with the electron gyromagnetic ratio and the irradiation intensity in the rotating frame. The inverse Rabi frequency is chosen as the time basis because is held constant in experiments considered here. In eq. 9
| (11) |
and
| (12) |
are unitless relaxation-time parameters and
| (13) |
is a unitless resonance-offset parameter, with the resonance offset and the irradiation frequency. In experiments considered here, is constant, and is time-dependent due to tip motion in the MRFM experiment.
If we neglect the relaxation terms in the Bloch matrix, then eq. 9 is equivalent to with an effective magnetic field in the rotating frame and , and the rotating-frame unit vectors. The above equation describes the undamped precession of magnetization about the effective field in the rotating frame.
2.3. Breakdown of saturation when the resonance offset is time-dependent
Closed-form solutions to eq. 9 can be obtained when the intensity, , and resonance offset, , of the applied irradiation are both time-independent. In the presence of the moving tip in the MRFM experiment, however, spins experience a large time-dependent resonance offset. The evolution of magnetization in this situation requires the development of approximate solutions. Below we develop approximate solutions in a low- limit and a high- limit. The transition between the two limits occurs at a critical field
| (14) |
below which all the Bloch-matrix eigenvalues are real, and no Rabi oscillations are evident.
2.4. Breakdown in the low- limit
We are interested in spins with , i.e. . In this limit, the transverse magnetization quickly reaches a pseudo-equilibrium with the slowly evolving longitudinal magnetization. We can use this pseudo-equilibrium condition to develop a useful approximation for how the rate at which the longitudinal magnetization reaches equilibrium depends on irradiation intensity and resonance offset.
The Bloch equations describing the unitless transverse magnetization can be written
| (15) |
where we write to emphasize that the -axis magnetization is time dependent. Let us nevertheless treat in the above equation as if it was time-independent and solve for the steady-state transverse magnetization. The result is
| (16) |
We should regard in these equations as a slowly varying function of time that and respond to instantaneously. Substituting in the Bloch equation for , we obtain the differential equation
| (17) |
where the underbraced term is an effective relaxation rate . This rate is time-dependent if the resonance offset is time-dependent, as indicated. Changing the independent variable in eq. 17 from to we obtain a new differential equation , with
| (18) |
the effective relaxation rate in units of , now written in terms of time . The above treatment is valid when , which is true, assuming , when with
| (19) |
the homogeneous linewidth. In other words, the solution is valid in the low- limit.
Now consider an experiment in which the resonance offset is swept from above resonance (at time ) to below resonance (at time ). In this experiment, the unitless resonance offset can be expressed as follows
| (20) |
with
| (21) |
a unitless sweep-rate parameter. We are interested in the -magnetization at the end of the sweep. The exact solution to eq. 17 is
| (22) |
with ,
| (23) |
and . The argument of the arctan function in the above equation can be written
| (24) |
with the resonance offset at the end of the sweep.
In the limit that (a) and (b) the sweep time is fast compared to (i.e. ), the integrated relaxation rate simplifies to . Making these assumptions, and switching notation for clarity, the second term in eq. 22 can be neglected and
| (25) |
in the low- limit. When the field is swept slowly through resonance, , the final magnetization is zero, and the sample has been fully saturated. On the other hand, when the field is swept quickly through resonance, , and the magnetization is essentially unaffected by the irradiation.
2.5. Breakdown in the high- limit
For sufficiently high and sufficiently slow sweep rate, when is swept from well above resonance to well below resonance, the magnetization follows the effective field adiabatically. The initial unitless magnetization is . Ideally, if is suitably strong and the sweep suitably slow, then the final magnetization is . If these conditions are not met, then will deviate from −1.
Klein et al. [62] and Harrell et al. [63] have considered the loss of magnetization during adiabatic rapid passage in the context of magnetic resonance force microscope experiments. Following Harrell et al., the probability of a deleterious diabatic transition follows from the long-known LZSM result [34, 64],
| (26) |
with the unitless sweep-rate parameter given by eq. 21 above. We see that this parameter also governs the efficacy of the adiabatic rapid passage. The probability of not making a diabatic transition is
| (27) |
Assume the initial magnetization is . If the magnetization follows the effective field adiabatically, then final -component of magnetization is . If, on the other hand, a diabatic transition occurs, then the magnetization remains unchanged by the sweep and . To obtain the final magnetization, we should weight each of these two possible outcomes by their probabilities,
| (28) |
| (29) |
The adiabatic rapid passage is successful, , when (i.e. is large and is small).
While the LZSM result is a remarkably simple equation, the result comes from a limiting solution to the Schrödinger equation, so completely neglects relaxation. Our sample of interest has a short , so we are concerned about the validity of neglecting relaxation. We now use the Bloch equations to derive a result analogous to eq. 29. This approach opens a route to amending the Landau-Zener result to capture additional losses of magnetization due to relaxation during the rapid passage through resonance.
To describe the loss of magnetization during a rapid passage through resonance, let us first approximate eq. 9 by neglecting the inhomogeneous term,
| (30) |
With the resonance offset time-dependent, , let us work in a tilted coordinate system that keeps the effective field directed along the axis. We define a tilted magnetization as follows
| (31) |
with a coordinate-rotation matrix. The inverse relation is . Plugging eq. 31 into 30 we obtain the following differential equation governing the evolution of the rotated magnetization,
| (32) |
Using the intuition that tilting the rotating-frame around the axis will align with the axis, we choose to be a rotation around the axis:
| (33) |
with
| (34) |
At large positive resonance offset, is zero, is the diagonal matrix, and the axes are untilted. At large negative resonance offset, implements a rotation around the axis.
Using trigonometric relations,
| (35) |
| (36) |
Substituting Eqs. 33 through 36 into eq. 32 yields the following effective Bloch matrix in the tilted frame
| (37) |
For compactness, we have dropped the explicit time dependence of . Neglecting relaxation by setting and gives the approximate Bloch matrix
| (38) |
This Bloch matrix describes the precession of magnetization about an effective field
| (39) |
with and unit vectors in the tilted frame of reference defined by . Because is time dependent, the direction of is continuously changing, giving rise to complicated magnetization dynamics, even in the tilted frame of reference.
To simplify the evolution further, let us apply an additional rotation to our coordinate system. Let the magnetization in the new coordinate system be
| (40) |
with
| (41) |
a transformation designed to rotate the magnetization around , the axis in the tilted frame; below we will choose judiciously to simplify the effective Bloch matrix. The rotated magnetization is now governed by the differential equation
| (42) |
where the effective Bloch matrix is given by
| (43) |
which reduces to
| (44) |
For a linear field sweep, evolving from way above resonance to way below, is given by eq. 20. Here we have used eqs. 10, 13, and 21 to write the time-dependent resonance offset in unitless form.
We are interested in following magnetization from time to where we will ultimately take the limit . The effective Bloch matrix can be simplified by choosing the phase angle to be
| (45) |
This choice of phase makes the (1,2) and (2,1) matrix elements of vanish. Carrying out the above integral,
| (46) |
where, for simplicity, we have set the initial condition to be
| (47) |
Choosing this initial phase is required to obtain a phase of at , when the system has reached resonance.
To solve eq. 42 we use a 1st-order Magnus expansion [60, 61]. We are interested in the long-time solution, so will take the integration limits to be and . In integrating eq. 44 to obtain the 1st -order Magnus exponent below we used a change of variables ; the variable is the associated integration limit. We obtain
| (48) |
with
| (49) |
where the relevant integral can be written as follows
| (50) |
with
| (51) |
a unitless sweep-time parameter, and
| (52) |
In writing eq. 49 we have employed the convention that when the integral is written with a single argument, the integration limits are assumed to be , i.e. . In writing eq. 49 we have also used that the integral vanishes by symmetry.
By inspection, runs from 1 to 0 as the inverse-sweep-rate parameter runs from 0 to . However, the eq. 50 integrand is highly oscillatory, and is therefore challenging to compute both quickly and accurately at arbitrary . A fast numerical method for computing the eq. 50 integral is reported in Appendix A. The integral is plotted versus the parameter in Fig. A.8.
Taking into account eqs. 48 and 49 and eq. 31, the final magnetization in the rotating frame is given by
| (53) |
with given by eq. 51. The final magnetization is plotted versus the unitless sweep-rate in Fig. 1. The LZSM result, eq. 29, is plotted for comparison. We can see in Fig. 1 that eq. 53 predicts semiquantitatively the LZSM breakdown of adiabatic rapid passage through resonance at high .
Figure 1:
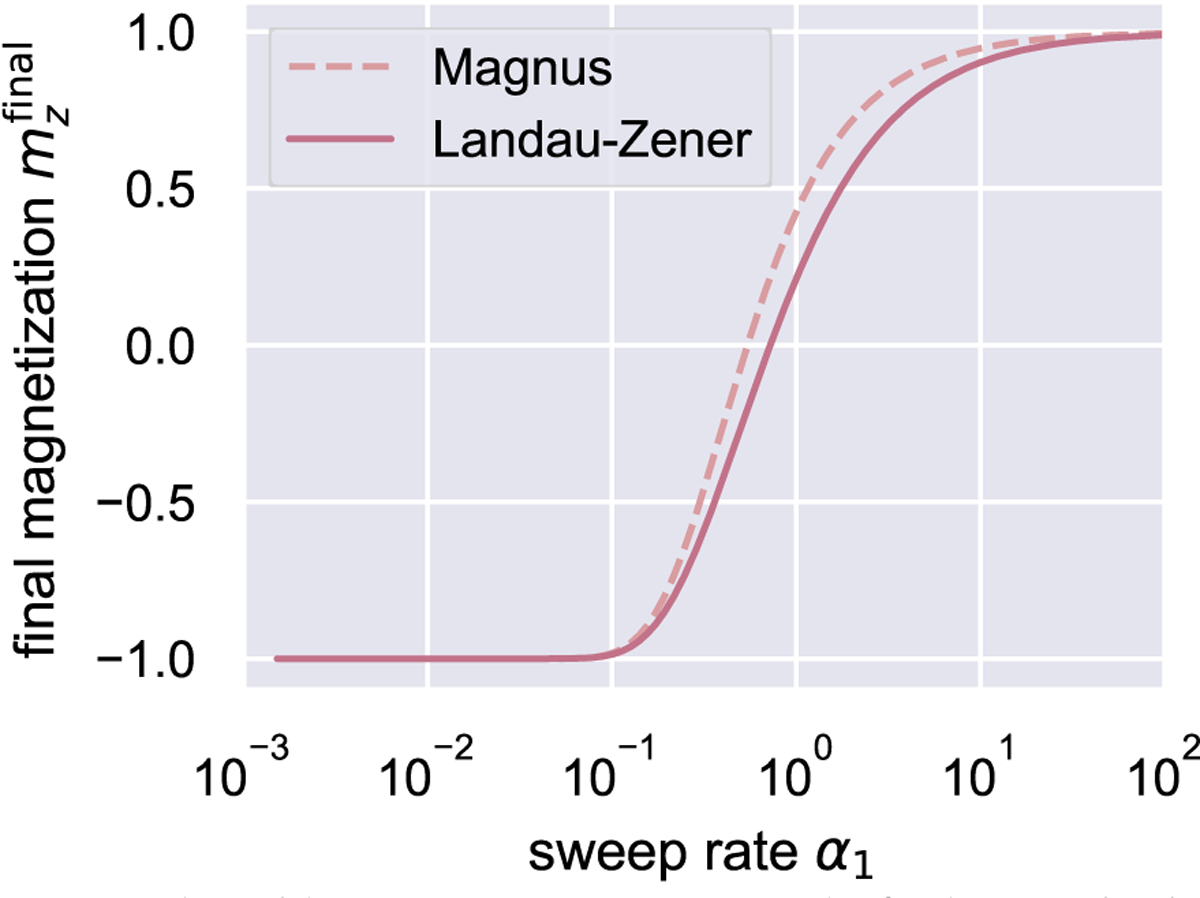
Final magnetization versus the unitless sweep-rate parameter. The final magnetization was computed, neglecting relaxation, using the Magnus expansion (dotted line, eq. 53) and the LZSM formula (solid line, eq. 29).
In summary, neglecting relaxation, we can recover Landau–Zener–Stückelberg–Majorana behavior from the Bloch equations using appropriately chosen coordinate transformations and the Magnus expansion.
We now expand our treatment to include -related magnetization losses during rapid passage. Returning to eq. 37, we set , retain , and recompute , eq. 44, setting the angle according to eq. 45. The result is
| (54) |
Integrating over to obtain the first-order Magnus exponent is now problematic, giving a divergent answer. To avoid this divergence, let us instead compute by integrating from as follows:
| (55) |
with
| (56) |
In the above equation, the integration limit is . The new integrals appearing in are , and
| (57) |
The integrals and are plotted versus the inverse sweep-rate parameter in Fig. A.8. Also appearing in is a second unitless sweep-rate parameter
| (58) |
We can see that eq. 49 is recovered from eq. 56 by taking the limit (i.e. setting and ). Comparing eqs. 21 and 58,
| (59) |
where is the homogeneous linewidth. We expect in the high- limit where .
Let us use eq. 56 as a starting point for developing an approximate expression that accounts for losses during the rapid passage. Developing this approximate expression is tricky because the Magnus expansion is not unconditionally convergent. The convergence condition for the Magnus expansion is an ongoing area of research [61, 65–68]. The convergence condition is usually formulated for a quantum-mechanical system undergoing unitary evolution, with relaxation neglected. The usually-given convergence condition is [61]
| (60) |
with shorthand for the 2-norm. At large integration times , the diagonal elements of the matrix become large and negative, violating the eq. 60 condition. However, in Ref. 67 it is noted that “one can easily construct examples showing that [eq. 60] is not necessary for the convergence of the expansion.” It would appear that our eqs. 42 and 54 are one such example. At long time, , the matrix is dominated by two large negative matrix elements at diagonal positions (1,1) and (2,2). In this limit, is bounded, and the Magnus expansion is convergent by inspection.
In the absence of a clearly applicable convergence criterion, how to proceed? To guarantee convergence, we will be conservative and assume , equivalent to requiring the total sweep time to be much shorter than , so that eq. 60 holds. At the same time, we would like to approximate the integrals in by their values. The integrands are of the form oscillating function. We surmise that the integrals will be approximately converged for . This is equivalent to requiring , which guarantees that the -related matrix elements in are suitably small. At very large , however, eq. 56 reverts to eq. 49 and is uninteresting; we expect interesting behavior as decreases towards 1.
When , and , we find that is well approximated by
| (61) |
When , the terms are negligible and
| (62) |
In this limit, magnetization losses are small when . Mathematically, this limit is achieved when is large, is small, or the sweep is fast. To avoid losses, we need the magnetization to spend as little time as possible “near” the plane, where “near” means when the resonance offset becomes comparable to . This behavior is somewhat counterintuitive, because adiabatic losses are small when is large and the sweep is slow. We conclude that some compromise might be required to limit both and adiabatic losses during rapid passage. Considering eqs. 62 and 29, we propose
| (63) |
as an approximate expression that captures both and fast-sweep losses during rapid passage at high .
3. Numerical simulations
Numerical simulations of magnetization versus time in a time-dependent offset experiment were carried out for the representative TEMPAMINE radical. Except where noted, the electron spin resonance parameters in Table 1 were used. Also shown in the table are useful reference fields: the saturation field , the critical Rabi frequency , and the homogeneous linewidth .
Table 1:
Electron spin resonance parameters for TEMPAMINE.
| variable | definition | numerical value |
|---|---|---|
| 1.3 ms | ||
The Bloch equations were numerically integrated in Python. To facilitate numerical integration, the equations were put in the following homogeneous form [69]:
| (64) |
with
| (65) |
an expanded 4-dimensional magnetization vector and
| (66) |
an expanded 4 × 4 Bloch matrix. In these equations is the equilibrium magnetization, is the spin-lattice relaxation rate, and is the spin dephasing rate. For numerical stability, time was expressed in units of , rates in units of , and fields in units of mT.
When the resonance offset is time-independent, eqs. 65 can be integrated to give . Implementing the matrix exponential using the SciPy package’s linalg.expm function, we verified that direct integration of eqs. 65 gives an exhibiting the expected magnetization evolution and decay, including spin-lattice relaxation, following pulses applied both on and off resonance.
When the resonance offset is a function of time,
| (67) |
with the time at which resonance was reached and the field derivative. Simulations were run from time 0 to , with . In this case eqs. 65 were numerically integrated using the scipy.integrate module’s odeint function to obtain .
3.1. Low-B simulations
To study the dependence of the final magnetization on in the low- regime, we fixed and varied . The Bloch equations were integrated with carefully chosen values of the sweep time and sweep rate. The numerical integration became unstable at long time if the sweep rate was too large. If the final time was shortened to avoid this instability, then steady state was not reached. So the largest sweep rate could not be too large and the final time could not be too long.
With , we evolved magnetization with between and ; the associated values ranged from to . Representative plots of versus time are shown in Fig. 2. From these plots a final magnetization was extracted as and plotted versus .
Figure 2:
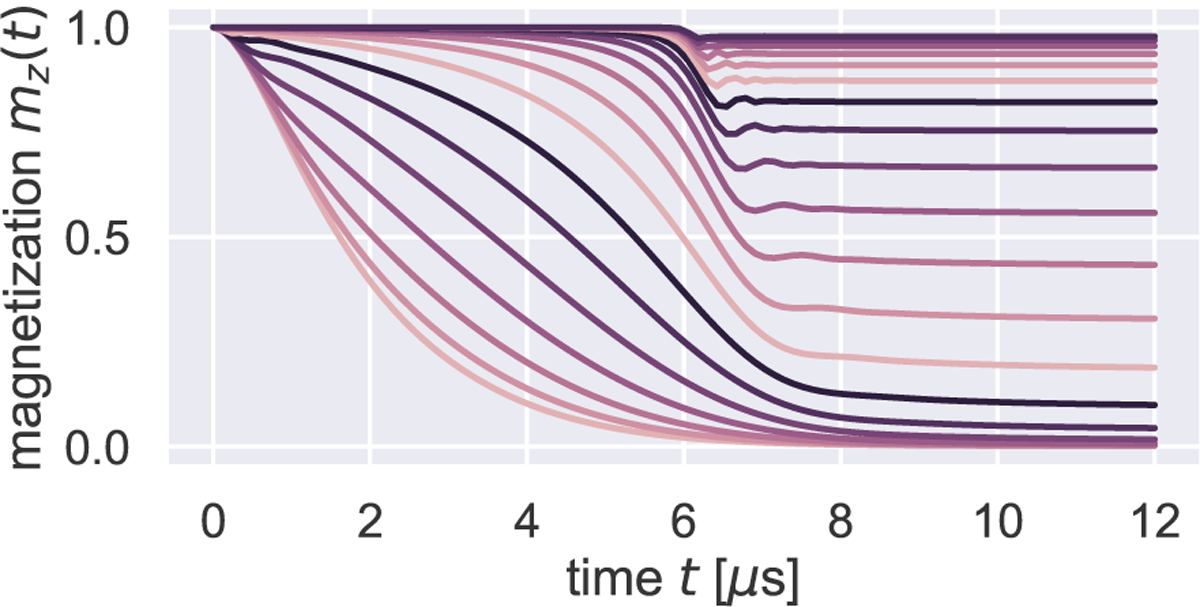
Calculated magnetization versus time in the low- regime. Simulation details: resonance parameters from Table 1; field intensity ; and, from bottom to top, 20 different sweep rates logarithmically distributed between (bottom) to (top).
3.2. High- simulations
To simulate magnetization dynamics in the high- regime, we set , and varied from 1.12 mT to ; the associated values ranged from to . As mentioned above, the simulation parameters were carefully chosen to meet the competing constraints of covering a five-order-of-magnitude variation in , reaching steady-state, and avoiding long-time instability in the numerical integration of the Bloch equations.
Simulations were carried out for , and . Representative plots of versus time are shown in Fig. 3 for the simulation. In contrast with the low- simulations of Fig. 2, large Rabi oscillations are now apparent. From such plots a final magnetization was extracted as and plotted versus . To compare to theory, eqs. 56 and 63, we also need to know . In an experiment in which is varied and is fixed, can be computed from as follows:
| (68) |
Figure 3:
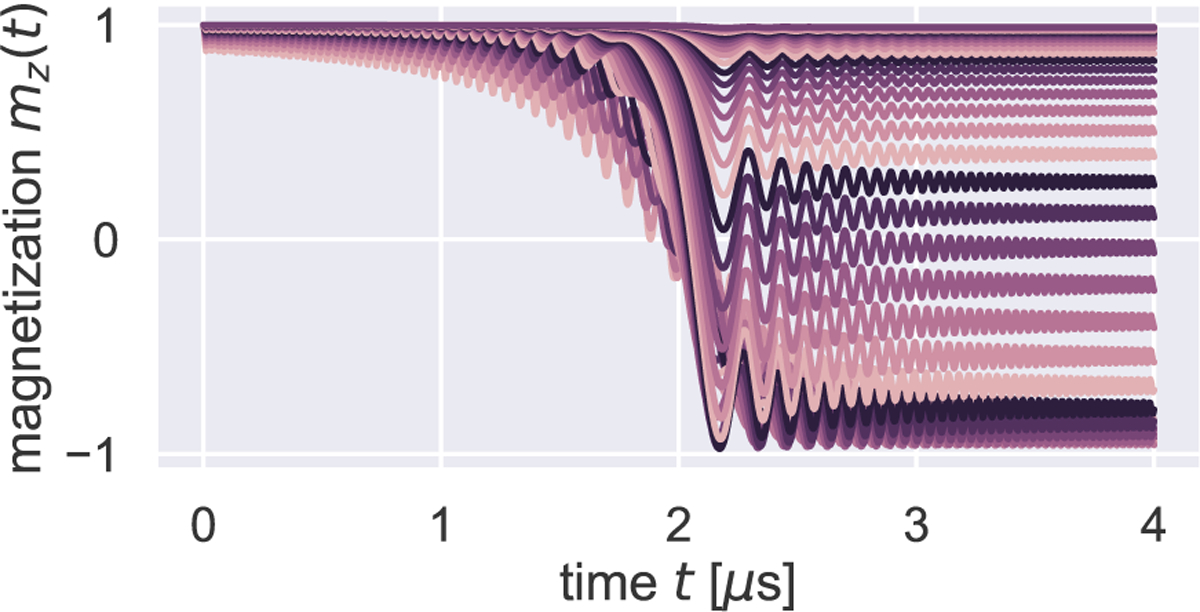
Calculated magnetization versus time in the high- regime. Simulation details: resonance parameters from Table 1, except sweep rate and, from bottom to top, 40 different values logarithmically distributed between 1.12 mT (bottom) to (top).
4. Experiments
Experimental studies of magnetization after an adiabatic rapid passage were carried out in a nuclear magnetic resonance experiment on polystyrene. The proton spins in polystyrene, like the unpaired electron spin in TEMPAMINE, have a and that differ by orders of magnitude [70, 71]. Atactic polystyrene (Sigma Aldrich, , lot no. 11326LH) was dissolved at 0.8% w/w in deuterated chloroform (Cambridge Isotopes, 99.8%, lot no. PR-33545/04142). No care was taken to remove dissolved oxygen from the solution. Liquid NMR experiments were performed at −60°C, slightly above the chloroform solvent freezing point, on a 500MHz Varian INOVA spectrometer equipped with an extended VT range Varian broadband probe; cooling the sample reduced . Shaped pulses were generated with Pbox, as implemented in VnmrJ 2.2D, using a hard 90° pulse as a reference (14.9 μs at 57 dB coarse power). The longitudinal relaxation time was measured with the Varian Chempack inversion recovery sequence (INVREC; hard and pulses, 8 time points, 2 s acquisition time and 8 s repetition time). The transverse relaxation time was acquired with the Varian Chempack Carr-Purcell-Meiboom-Gill (CPMGT2) sequence; the echo time was 1 ms giving a 2 ms time resolution between positive echos.
The polystyrene NMR spectrum consists of resonances from aliphatic backbone protons (0.975 to 1.686 ppm and 1.778 to 2.289 ppm) and aromatic protons (ortho and meta at 6.031 to 6.913 ppm and para at 6.922 to 7.254 ppm). These resonances have distinct values. Equation 63 was tested by producing, using a modified Varian s2pul sequence, a fixed-amplitude linear frequency sweep “chirped” pulse followed by a pulse; the interpulse delay was . The chirped pulse was between 25 and 100 ms long with a 47619 Hz sampling rate. For each measurement chirp was varied between and , corresponding to an sweep-rate parameter of to . Data were processed with MNova 14.3.2 (Mestrelab Research). The and measurement integrals were fit in Python using the lmfit package.
5. Results and discussion
Simulation results are shown in Fig. 4, where they are compared to theory.
Figure 4:
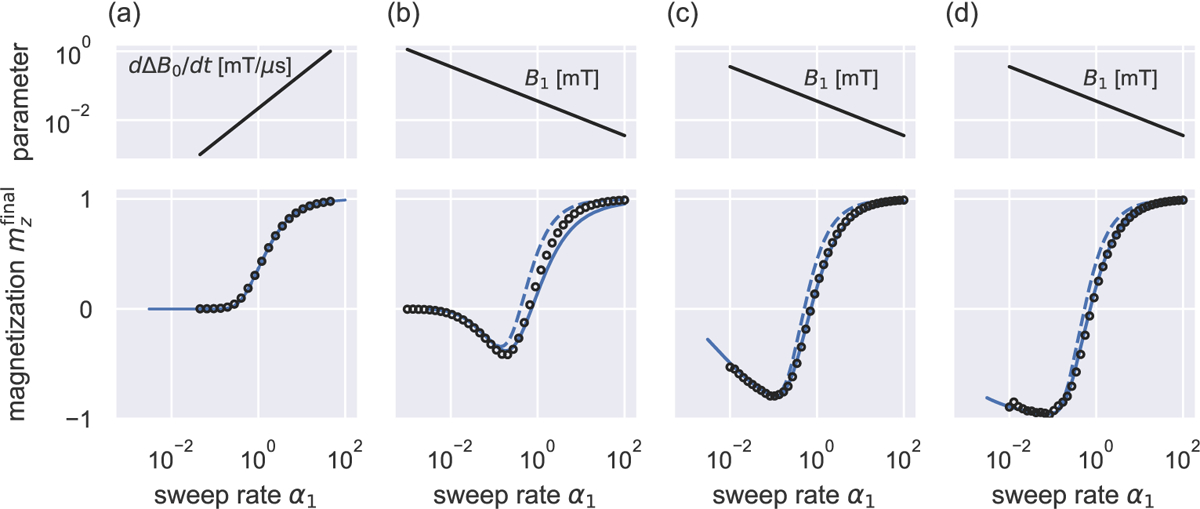
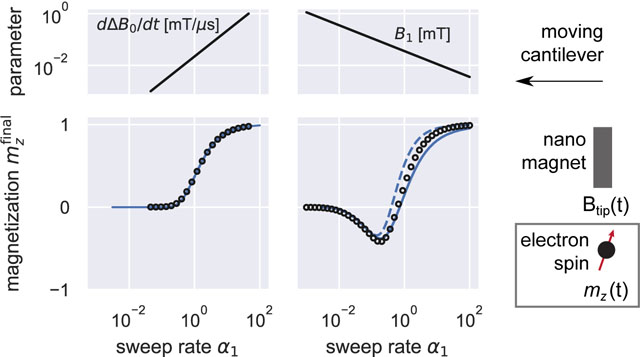
Simulated final magnetization , after a sweep through resonance, plotted versus the unitless sweep rate . The Bloch equations were numerically integrated at (a) low intensity (, , and variable ) and at (b-d) high intensity (, variable , and equal to (b) , (c) , and (d) ). In the top plots we graph the varied parameter, in (a) and in (b-d), versus , while on the bottom plots we graph the final magnetization. Open circles are the numerically computed magnetization. In (a), the solid line is eq. 25. In (b-d), the solid line is eq. 63 while the dotted line is the magnetization computed using the first-order Magnus expansion in eq. 56 taken in the , limit.
At low-, Fig. 4(a), we see that saturation is effective for slow sweeps (i.e. small ) but becomes ineffective for fast sweeps (i.e. large ). Equation 25 quantitatively predicts the numerically calculated final magnetization over a three-order-of-magnitude variation in .
At high-, the final magnetization depends on in a more complicated way. Consider the simulation in Fig. 4(b). At large , the irradiation is ineffective, as in the low- case. Now as is decreased, the magnetization becomes negative, indicating the onset of adiabatic inversion. Yet as is decreased further, adiabatic inversion fails, and the magnetization becomes merely saturated.
This counter-intuitive behavior can be understood as follows. During a suitably “slow” sweep (i.e. small ), the magnetization is effectively spin-locked along the direction of the effective field during an adiabatic passage through resonance. This situation corresponds to the magnetization remaining along the axis in the tilted frame defined by . According to eq. 37, the decay of the -axis magnetization is governed by the matrix element . Writing out the differential equation governing this spin-locked magnetization in terms of time ,
| (69) |
with
| (70) |
an effective relaxation rate. We see that the decay of spin-locked magnetization is -like (i.e. slow) far away from resonance but is -like (i.e. fast) near resonance. In the Fig. 4(b–d) simulations, is largest at small . At low , therefore, the magnetization spends a comparatively larger fraction of its evolution near resonance where losses are significant. The apparent reversion to saturation apparent at low in Fig. 4(b–d) is thus the result of a -related loss of magnetization. Consistent with this explanation, at fixed , these losses are smaller as is increased, as can be seen in Fig. 4(c) and Fig. 4(d).
At high , we used two curves to describe the simulated magnetization in Fig. 4(b–d) — the empirical eq. 63 (solid line) and the first-order Magnus expansion, eq. 56, taken in the limit (dotted line). Of the two, eq. 63 describes the simulated magnetization better. Although we derived it rigorously, eq. 56 agrees only semiquantitatively with the LZSM result in the limit, so it is perhaps not surprising that this equation describes the magnetization imperfectly in the finite- limit as well. While our proposed semi-empirical eq. 63 was not derived rigorously, our Sec. 2 derivation shows why it is physically plausible.
Equation 63 was tested experimentally using spins in polystyrene dissolved in deuterated chloroform. The chemical structure and NMR spectrum of the polystyrene sample are shown in Fig. 5(top); four groups of protons are spectroscopically resolvable. The measured relaxation times of the sample’s protons are tabulated in Table 2. The ratio ranged from 41 for the group 1 aromatic protons to 241 for the group 4 aliphatic protons. Since , the primary assumption underlying eq. 63 is valid for all groups of spins in the sample. For comparison, for electron spins in TEMPAMINE.
Figure 5:
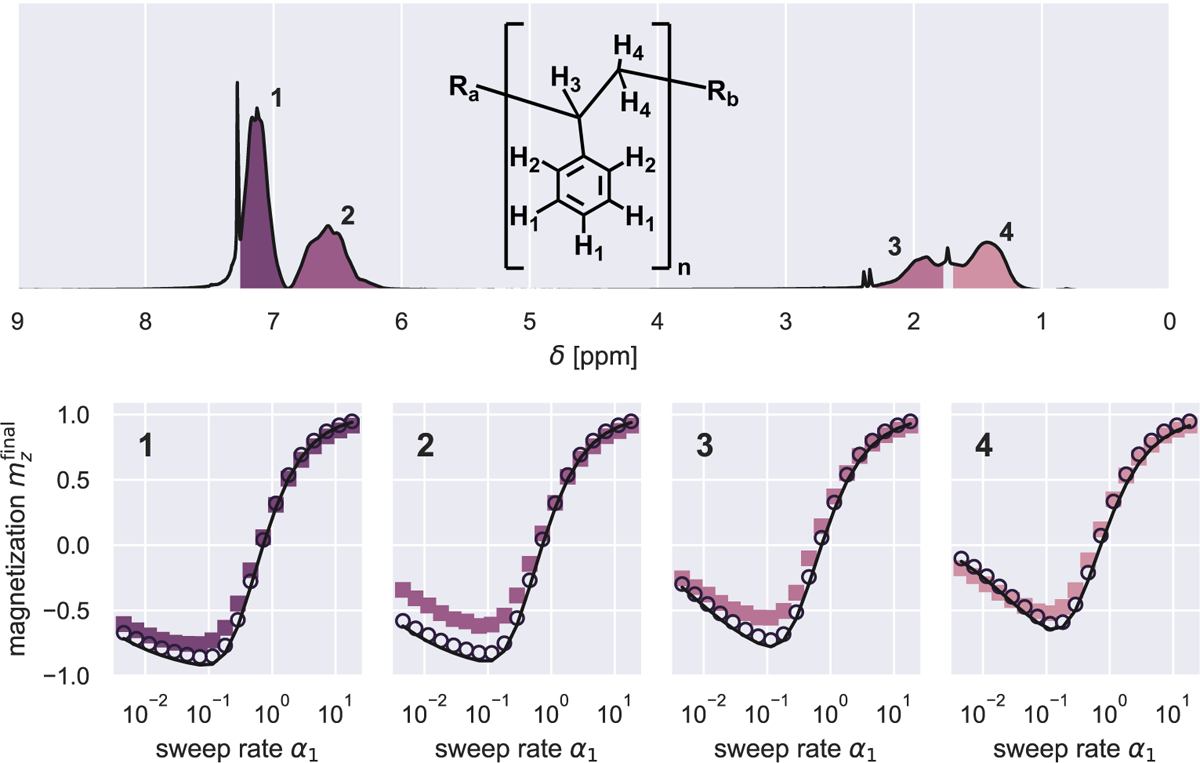
Experimental measurement of final magnetization after a sweep through resonance. Top: Solution NMR of 200k polystyrene in at and 500 MHz. The integrated NMR peaks used in the analysis are numbered and shaded in purple. Bottom: Final magnetization after a chirped pulse plotted . the sweep-rate parameter for the four numbered resonances (sweep rate , sweep time ). Colored squares are experimental data, black circles are numerical simulations, and black lines are eq. 63.
Table 2:
Relaxation times of polystyrene in deuterated chloroform at −60 °C and 500 MHz.
| spin | |||
|---|---|---|---|
| 1 | 1430 (10) | 35.1 (0.6) | 41 |
| 2 | 1393 (04) | 24.5 (0.2) | 57 |
| 3 | 1400 (10) | 10.4 (0.2) | 135 |
| 4 | 1370 (20) | 5.6 (0.2) | 241 |
The proton spectrum was acquired following an adiabatic rapid passage through all proton resonances in the sample. Rapid passages were carried out at a fixed sweep rate with varied. The final magnetization, normalized to the initial magnetization, was plotted versus ; see Fig. 5(bottom). The measured (colored squares), calculated (lines), and numerically computed (black circles) values of are in good agreement. For all four groups of spins, eq. 63 correctly predicts (a) the failure to invert or even saturate magnetization at low (i.e. large ), (b) the existence of a maximally inverted magnetization at intermediate (at an value between 0.1 and 1), and (c) and a reversion to saturation at high (i.e. small ). The group 4, aliphatic spins follow eq. 63 quantitatively while spin groups 1 through 3 follow eq. 63 only qualitatively. This discrepancy cannot be due to the breakdown of the infinite-time approximation, i.e. , because the numerical simulations (black circles) accounted for the finite sweep time. We surmise that the discrepancy is due to spins not behaving as isolated two-level systems, as our theory also assumes. The sweep time, 100 ms, is on the order of the inverse coupling, so interference effects during the sweep could be a complicating factor.
6. Conclusions
Our main findings are Eqs. 25 and 63, plotted against numerical simulations in Fig. 4. These simple analytical expressions for the final magnetization after a rapid passage through resonance, valid at low and high intensity, respectively, account for both the non-adiabatic and losses seen in exact numerical simulations over a wide range of irradiation intensities and field-sweep rates. Equation 63 was tested experimentally using nuclear spins and found to be in good agreement with experiment. The Appendix A method for numerically evaluating highly oscillatory integrals and the eq. 53 and 56 intermediate results are also noteworthy.
There is a large body of literature concerned with creating population inversions using adiabatic sweeps optimized for total power or operational bandwidth [10–18, 26, 27]. The most effective of these inversions employ sweeps in which both and the resonance offset are time-dependent. Although we assumed above that was time-independent, it is straightforward to modify the definition of in eqs. 35 and 36 to account for a time-dependent . Our approach can thus be applied to account for non-adiabatic and losses in these more sophisticated inversion protocols.
Prior studies addressing relaxation in LZSM transitions have employed a wide range of methods: formal perturbation expansion series [23], a sum over paths [43], Bloch equations [44, 46, 54], Linblad equations [46, 50, 54], an imaginary Hamiltonian [52], master equations [54], and a two-level system coupled to a bath of bosons [45, 47–49, 51, 53, 55] or other two-level systems [47] (e.g. spin-boson models). The spin-boson models generally include longitudinal (i.e. diagonal) bath couplings [49, 51, 55], to model -like dephasing of coherence, and may also include transverse (i.e. off-diagonal) bath couplings [45, 47, 48, 53], to model -like spin-lattice relaxation of population differences. Here we addressed relaxation in LZSM transitions using the Bloch equations, three coordinate transformations, and the Magnus expansion. There are only a few prior examples of using a Magnus expansion to treat LZSM transitions [33, 68], but these treatments neglected relaxation. Calculating the LZSM-transition probabilities in the dissipationless limit usually requires contour integration [34] or invoking opaque special-function solutions to a third-order differential equation [19]. It is therefore noteworthy that our relatively straightforward calculation reproduces semiquantitatively the well-known LZSM result (eq. 53, in the limit). Working in the limit, it was easy to include losses using our approach. In contrast with nearly all prior work, we obtained closed-form expressions for the final population difference that depend explicitly on and .
Our results agree with prior work. Some [23, 49], but not all [44], prior numerical studies of LZSM transitions including losses obtained behavior qualitatively similar to that seen in Fig. 4: the two-level system remains unperturbed at high sweep rate, imperfect adiabatic inversion is seen at intermediate sweep rate, and saturation is achieved at low sweep rate. Our low- result, eq. 25, reproduces eq. 15 in Ref. 72, derived via resumming a formal perturbation expansion series. Our high- result, eq. 63, has the same form as eq. 27 in Ref. 46, derived using an approach complimentary to ours.1 The Ref. 46 derivation employed an interaction representation diagonalizing the Bloch matrix, assumed the nondissipative propagator is known, assumed (without justification) that the nondissipative propagator commutes with the dissipation matrix in both the adiabatic and non-adiabatic limits, and obtained corrections to the known LZSM dynamics arising from dissipation. In contrast, we have derived a correction to LZSM dynamics from first principles, eq. 56, having made no ab initio assumptions about the nondissipative propagator.
Nevertheless, we make a number of uncontrolled approximations, and further work is needed to make our derivation more rigorous. The first such assumption requires . This condition seems unnecessarily conservative given (1) the obvious convergence of the Magnus expansion at long times, as discussed following eq. 60, and (2) the good agreement between eq. 63, numerical calculations, and experiments at times . To go beyond the requirement we need a Magnus-expansion convergence criterion applicable to the sort of real matrices considered here — a significant undertaking. The second uncontrolled approximation is computing the eq. 56 integrals only in the , infinite-time limit. We have not been able to generalize the Appendix A integration scheme to finite ; the integrals at finite can be computed numerically but this approach is prohibitively slow. The agreement between eq. 63, numerical Bloch-equation simulations, and experiments indicates that the eq. 56 integrals are close to their limit for the large-bandwidth, finite-time sweeps considered here.
Finally, we can use our results to design magnetic resonance force microscope experiments. Consider an experiment [73] employing a radius cobalt sphere (saturation magnetization ) operating at a tip-sample separation of . The sphere is magnetized along the direction and oscillates in the direction, moving parallel to a sample surface. To compute the time-dependent magnetic field experienced by the sample, it is helpful to know the tip field gradient [74]
| (71) |
where we have expressed the gradient in polar coordinates, with defined relative to defined relative to , and the radial distance relative to the center of the sphere. The gradient is zero directly beneath the tip. The gradient is maximized along the line (i.e. at an angle . At that location, using ,
| (72) |
The spherical magnet is attached to a cantilever whose position is time dependent: , with the zero-to-peak cantilever amplitude and the cantilever oscillation frequency. The peak time-dependent field experienced by a spin at angle and tip-sample separation is
| (73) |
where we have evaluated at the zero crossing where the derivative is maximum.
In the presence of the eq. 73 field sweep, eq. 21 tells us that achieving requires . One would naively think that to saturate the electron spin magnetization would require . The above analysis shows that, surprisingly, an irradiation intensity more than -fold larger than is actually required to fully saturate the electron spin in the presence of the moving tip.
Supplementary Material
Revised Highlights.
Accounting for dephasing losses during rapid-passage experiments is challenging
Treat with Bloch equations, coordinate transformations, and a Magnus expansion
Obtain analytic equations accounting for both adiabaticity and dephasing losses
Need a larger than expected in electron-spin magnetic resonance force microscopy
A compromise may be required to limit and adiabatic losses during passage
Acknowledgments
The authors would like to thank Christopher Klug of the U.S. Naval Research Laboratory for a careful reading of a preliminary version of this study. Research reported in this publication was supported by Cornell University, the Army Research Office under Award Number W911NF-17-1-0247, and the National Institute Of General Medical Sciences of the National Institutes of Health under Award Number R01GM143556. The content of this manuscript is solely the responsibility of the authors and does not necessarily represent the official views of Cornell University, the U.S. Army Research Office, the National Institutes of Health, the Department of the Army, the Department of Defense, or the U.S Government. The authors have no competing interests to declare.
John A. Marohn reports financial support was provided by US Army Research Office. John A. Marohn reports financial support was provided by National Institutes of Health. John A. Marohn reports financial support was provided by Cornell University.
Appendix A. Numerically integrating a highly oscillatory function
We wish to evaluate the integral
| (A.1) |
with
| (A.2) |
Figure A.6:
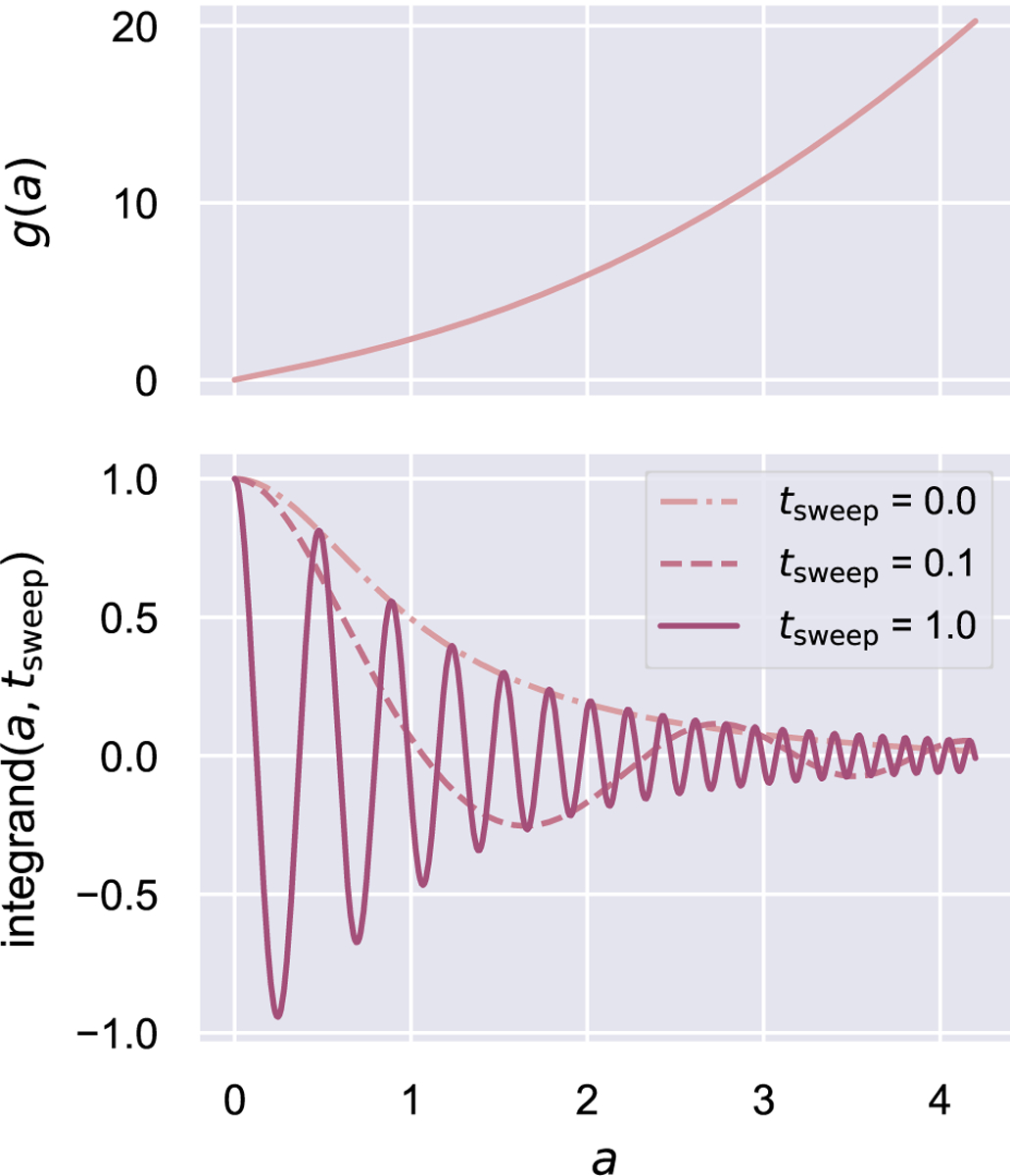
The Eq. A.1 integrand is highly oscillatory. (a) The Eq. A.2 function versus . (b) The Eq. A.1 integrand for various values of the parameter .
and
| (A.3) |
an inverse sweep-rate parameter. Other integrals of interest are
| (A.4) |
and
| (A.5) |
The function is plotted in Fig. A.6(a). The Eq. A.1 integrand is plotted in Fig. A.6(b) for selected values of the parameter . For large values of , the integration variable, . The Eq. A.1 integrand is highly oscillatory, with the oscillation frequency continuously increasing. This is true of the Eq. A.4 and A.5 integrands as well.
Computing the Eq. A.1 integral using standard integration packages is problematic and slow, especially when is large. When . Another useful reference value is . Mathematica returns without error in 85 ms. Mathematica is advertised as handling a wide range of one-dimensional and multidimensional integrals. Yet for , Mathematica returns the error NIntegrate failed to converge.
Computing using the Python function scipy.integrate.quad() returns 0.4925 ± 0.0036 in 35 ms with the message IntegrationWarning: The maximum number of subdivisions (50) has been achieved. Increasing the number of subdivisions to limit = 5000 returns , but the integration requires 2.2 s and still returns an IntegrationWarning error.
The Python function mpmath.quadosc() is specifically optimized to integrate oscillating functions. The function performs the Eq. A.1 integral well, provided it is fed an asymptotic formula for the integrand’s zeros. Evaluating using mpmath.quadosc () and integrating over the interval with the argument zeros=lambda n:mp.sqrt(mp.pi*n/0.0466475) returns 0.50000046 without error, but takes 2.5 s to do so. In our application, we need many thousands of integral evaluations. These evaluations require over 30 min using mpmath.quadosc(). We clearly need a faster way to evaluate integrals like Eq. A.1.
To carry out the above integrals, we adapted an inverse-function approach suggested by Evans [75, 76]. Let be the inverse function of . That is
| (A.6a) |
| (A.6b) |
| (A.6c) |
Substituting Eq. A.6b into Eq. A.1 and changing the integration variable from to using Eq. A.6c transforms Eq. A.1 to
| (A.7) |
By changing the integration variable, we have removed the variable-frequency oscillation from the integrand. However, at this point neither nor is known. We can actually derive a formula for , as follows. Substituting Eqs. A.6b and A.6c into Eq. A.2 we obtain
| (A.8) |
Differentiating both sides of this equation with respect to yields an implicit equation for , which may be solved to obtain
| (A.9) |
Substituting this result into Eq. A.7 gives
| (A.10) |
According to Eq. A.10, the integral and the function are Fourier transform pairs. We can therefore compute at an array of values rapidly using the fast Fourier transform (FFT) algorithm.
It remains to determine the inverse function . Given the complicated form of , Eq. A.2, there is unfortunately no analytic formula for the inverse function . Given a set of values, however, we can determine values of the inverse function numerically using an iterative algorithm, as follows.
Suppose we have a good guess for the inverse function. At large , which suggests as an approximate inverse function. Applied to , the approximate inverse function yields . If we have guessed the inverse function well, then will be close to . Employing a Taylor series, let us write
| (A.11) |
where is an error we can use to improve our estimate of the inverse function and . Solving for ,
| (A.12) |
We can create an updated estimate of the inverse function using
| (A.13) |
with convergence factor. We can apply Eqs. A.12 and A.13 iteratively to obtain a converged estimate of the value of the inverse function at . While the algorithm was just described for a single value, it can be carried out on an entire array of values simultaneously.
Representative results are shown in Fig. A.7. An array of values was created and the above algorithm was run for 75 iterations with , taking 2 s. The resulting inverse function is plotted in Fig. A.7(a). As an accuracy check, we can apply the original function to the inverse function . The result should be , a line with zero intercept and unit slope; this is observed, Fig. A.7(b). The relative error, , is plotted in Fig. A.7(c) with the point removed to avoid a division-by-zero error. The relative error is worst at small , but is no larger than approximately after as few as 75 iterations.
From the resulting values we computed an array values were computed from this array via FFT. Some thought is required to perform the FFT. The variables and are Fourier transform pairs, with and playing the role of frequency and time, respectively. Recall that . We are interested in computing the integral for values ranging from to , corresponding to values ranging from
We created an array of values using as the time step. Working in Python, the np.fft.fftfreq function was used to create an array of negative and positive values from the values. We created an array of inverse function values using the above algorithm and implemented the Eq. A.10 integral, using the np.fft.ifft function to obtain an array of values. Because of the even symmetry of the values, the resulting values are artificially symmetric; only values with indices are meaningful.
The and integrals were computed analogously. The resulting integrals are plotted versus in Fig. A.8.
Figure A.7:
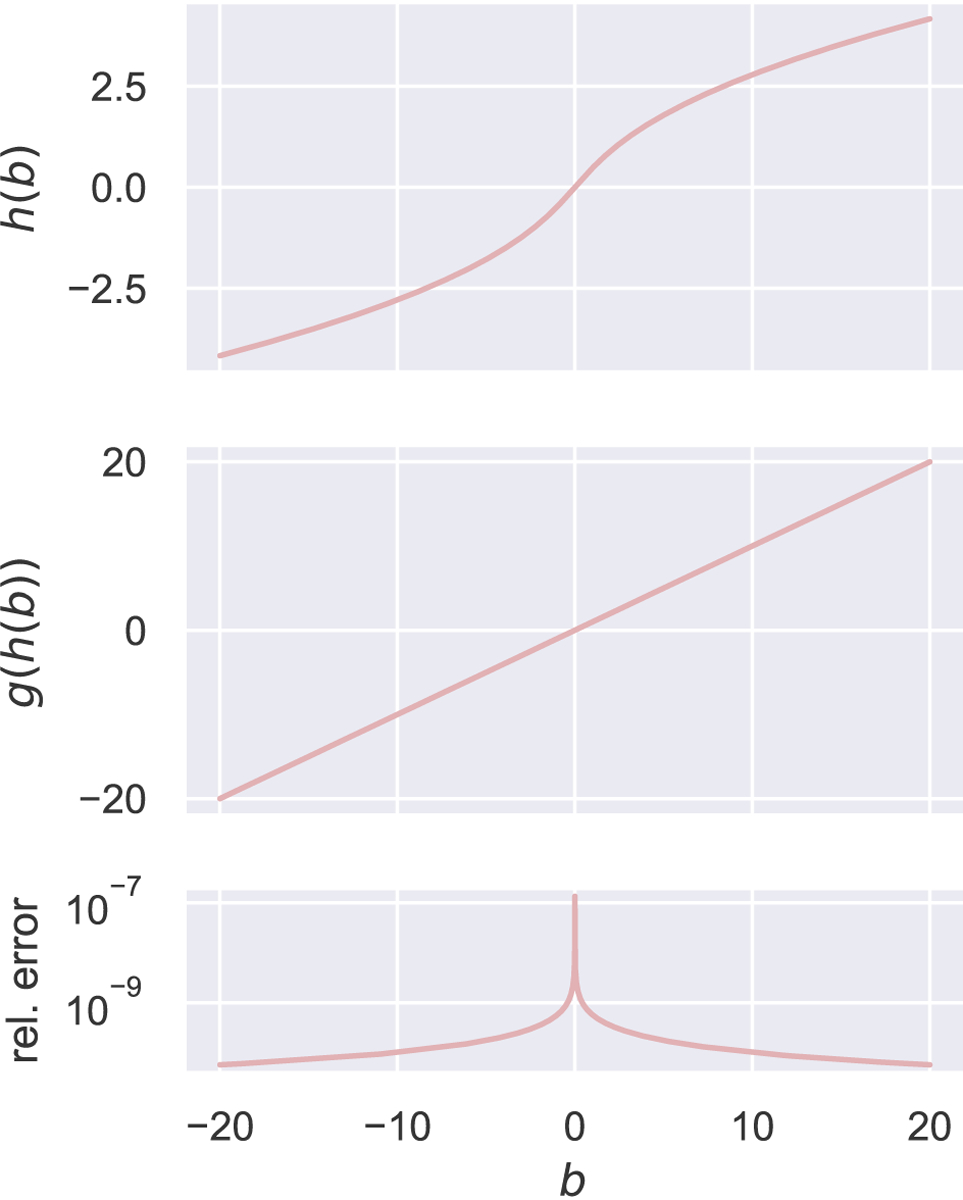
Iterative determination of the inverse function , Eq. A.6, using the algorithm described in the text. Upper: The resulting inverse function. Middle: An accuracy check. Bottom: The relative error.
Selected values of the integral were compared to mpmath.quadosc() results. The fractional error in was as large as at where , improved to at where , and deceased further at larger values. The associated error in magnetization at is nevertheless only because is a quadratic function near . The evaluation of the integral by the inverse-function/FFT method took only 0.5 s for 131072 points, compared to an extrapolated 80 h for the same number of points using mpmath.quadosc().
To create Fig. 1, a final magnetization, , was computed from the integral and plotted versus the array , with the point discarded.
Figure A.8:
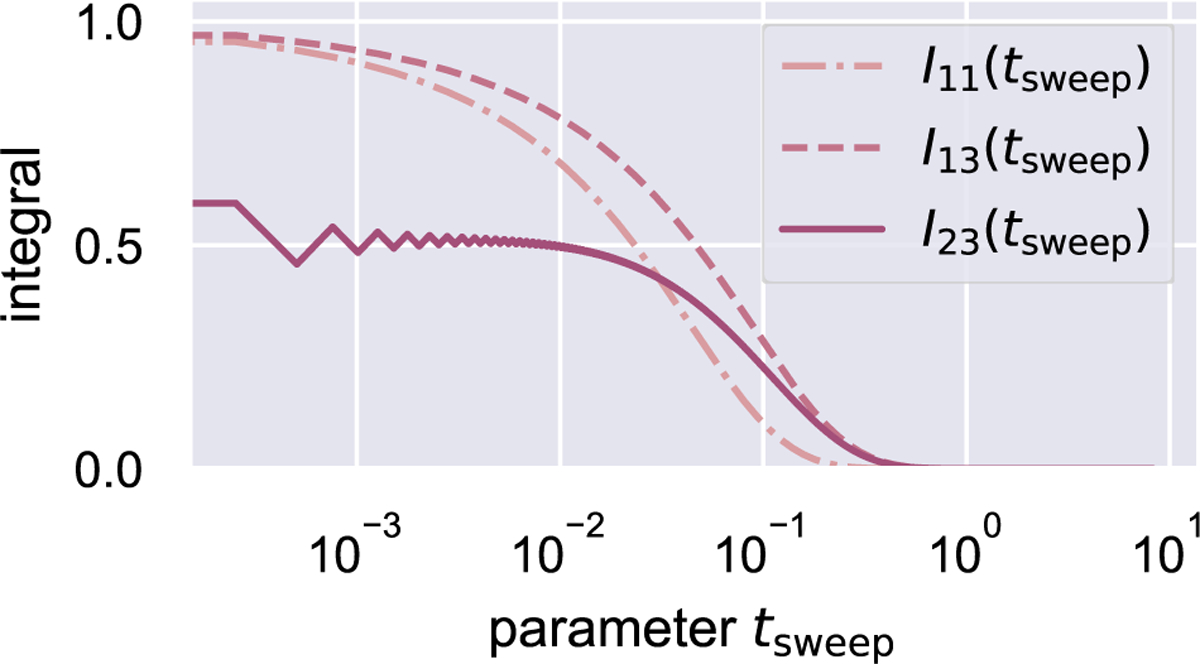
The integrals , and versus . Note the logarithmic axis (the point has been discarded). The integral was computed numerically using the inverse-function/FFT method described in the text. Declaration of Interest Statement (docx format)
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Supplementary material
Longitudinal relaxation time data and fits (peak integral vs. time, Fig. S1); transverse relaxation time data and fits (peak integral vs. time, Fig. S2); and additional measurements of final magnetization after a sweep through resonance, carried out at different sweep rates and sweep times (Figs. S3 and S4).
We caution that the exponential factor in the Ref. 46, eq. 15 formula contains a typographical error. In Ref. 46, the exponential factor in Table I, the Landau-Zener sweep case, is given by , which has incorrect units Reproducing the last steps in the Ref. 46 derivation of the exponential factor, we obtain , equal to in our notation.
References
- [1].Köhler J, Disselhorst JAJM, Donckers MCJM, Groenen EJJ, Schmidt J, Moerner WE, Magnetic resonance of a single molecular spin, Nature 363 (1993) 242–244. doi: 10.1038/363242a0. [DOI] [Google Scholar]
- [2].Wrachtrup J, von Borczyskowski C, Bernard J, Orrit M, Brown R, Optical-detection of magnetic-resonance in a single molecule, Nature 363 (1993) 244–245. doi: 10.1038/363244a0. [DOI] [Google Scholar]
- [3].Rugar D, Budakian R, Mamin HJ, Chui BW, Single spin detection by magnetic resonance force microscopy, Nature 430 (2004) 329–332. doi: 10.1038/nature02658. [DOI] [PubMed] [Google Scholar]
- [4].Grinolds MS, Hong S, Maletinsky P, Luan L, Lukin MD, Walsworth RL, Yacoby A, Nanoscale magnetic imaging of a single electron spin under ambient conditions, Nat. Phys 9 (2013) 215–219. doi:10/f4szjx. [Google Scholar]
- [5].Grinolds MS, Warner M, De Greve K, Dovzhenko Y, Thiel L, Walsworth RL, Hong S, Maletinsky P, Yacoby A, Subnanometre resolution in three-dimensional magnetic resonance imaging of individual dark spins, Nat. Nanotech 9 (2014) 279–284. doi: 10.1038/nnano.2014.30. [DOI] [PubMed] [Google Scholar]
- [6].Yacoby A, Personal communication, 2015.
- [7].Moore EW, Lee S-G, Hickman SA, Wright SJ, Harrell LE, Borbat PP, Freed JH, Marohn JA, Scanned-probe detection of electron spin resonance from a nitroxide spin probe, Proc. Natl. Acad. Sci. U.S.A 106 (2009) 22251–22256. doi: 10.1073/pnas.0908120106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Nguyen HL, Marohn JA, Reverse Monte Carlo reconstruction of electron spin-label coordinates from scanned-probe magnetic resonance microscope signals, arXiv:1802.07247 (2018). arXiv: 1802 .07247. [Google Scholar]
- [9].Garner SR, Kuehn S, Dawlaty JM, Jenkins NE, Marohn JA, Force-gradient detected nuclear magnetic resonance, Appl. Phys. Lett 84 (2004) 5091–5093. doi: 10.1063/1.1762700. [DOI] [Google Scholar]
- [10].Silver MS, Joseph RI, Hoult DI, Selective spin inversion in nuclear magnetic resonance and coherent optics through an exact solution of the Bloch-Riccati equation, Phys. Rev. A 31 (1985) 2753–2755. doi: 10.1103/PhysRevA.31.2753. [DOI] [PubMed] [Google Scholar]
- [11].Baum J, Tycko R, Pines A, Broadband and adiabatic inversion of a two-level system by phase-modulated pulses, Phys. Rev. A 32 (1985) 3435–3447. doi: 10.1103/PhysRevA.32.3435. [DOI] [PubMed] [Google Scholar]
- [12].Kupce E, Freeman R, Adiabatic pulses for wideband inversion and broadband decoupling, J. Magn. Reson., Ser. A 115 (1995) 273–276. doi: 10.1006/jmra.1995.1179. [DOI] [Google Scholar]
- [13].Kupce E, Freeman R, Stretched adiabatic pulses for broadband spin inversion, J. Magn. Reson., Ser. A 117 (1995) 246–256. doi: 10.1006/jmra.1995.0750. [DOI] [Google Scholar]
- [14].Tannús A, Garwood M, Improved performance of frequency-swept pulses using offset-independent adiabaticity, Journal of Magnetic Resonance, Series A 120 (1996) 133–137. doi: 10.1006/jmra.1996.0110. [DOI] [Google Scholar]
- [15].Tannús A, Garwood M, Adiabatic pulses, NMR Biomed. 10 (1997) 423–434. doi:. [DOI] [PubMed] [Google Scholar]
- [16].Garwood M, DelaBarre L, The return of the frequency sweep: Designing adiabatic pulses for contemporary NMR, J. Magn. Reson 153 (2001) 155–177. doi: 10.1006/jmre.2001.2340. [DOI] [PubMed] [Google Scholar]
- [17].Doll A, Jeschke G, Wideband frequency-swept excitation in pulsed EPR spectroscopy, J. Magn. Reson 280 (2017) 46–62. doi: 10.1016/j.jmr.2017.01.004. [DOI] [PubMed] [Google Scholar]
- [18].Gan Z, An analytical treatment of electron spectral saturation for dynamic nuclear polarization NMR of rotating solids, J. Chem. Phys 158 (2023) 024114. doi: 10.1063/5.0109077. [DOI] [PubMed] [Google Scholar]
- [19].Ivakhnenko OV, Shevchenko SN, Nori F, Nonadiabatic Landau–Zener–Stückelberg–Majorana transitions, dynamics, and interference, Physics Reports 995 (2023) 1–89. doi: 10.1016/j.physrep.2022.10.002. [DOI] [Google Scholar]
- [20].Rosen N, Zener C, Double Stern-Gerlach experiment and related collision phenomena, Phys. Rev 40 (1932) 502–507. doi: 10.1103/PhysRev.40.502. [DOI] [Google Scholar]
- [21].Frauenfelder H, Wolynes PG, Rate theories and puzzles of hemeprotein kinetics, Science 229 (1985) 337–345. doi: 10.1126/science.4012322. [DOI] [PubMed] [Google Scholar]
- [22].Garg A, Onuchic JN, Ambegaokar V, Effect of friction on electron transfer in biomolecules, J. Chem. Phys 83 (1985) 4491–4503. doi: 10.1063/1.449017. [DOI] [Google Scholar]
- [23].Kayanuma Y, Population inversion in optical adiabatic rapid passage with phase relaxation, Phys. Rev. Lett 58 (1987) 1934–1936. doi: 10.1103/PhysRevLett.58.1934. [DOI] [PubMed] [Google Scholar]
- [24].Economou SE, Sham LJ, Wu Y, Steel DG, Proposal for optical U(1) rotations of electron spin trapped in a quantum dot, Phys. Rev. B 74 (2006) 205415. doi: 10.1103/PhysRevB.74.205415. [DOI] [Google Scholar]
- [25].Poem E, Kenneth O, Kodriano Y, Benny Y, Khatsevich S, Avron JE, Gershoni D, Optically induced rotation of an exciton spin in a semiconductor quantum dot, Phys. Rev. Lett 107 (2011) 087401. doi: 10.1103/PhysRevLett.107.087401. [DOI] [PubMed] [Google Scholar]
- [26].Barnes E, Das Sarma S, Analytically solvable driven time-dependent two-level quantum systems, Phys. Rev. Lett 109 (2012) 060401. doi: 10.1103/PhysRevLett.109.060401. [DOI] [PubMed] [Google Scholar]
- [27].Barnes E, Analytically solvable two-level quantum systems and Landau-Zener interferometry, Phys. Rev. A 88 (2013) 013818. doi: 10.1103/PhysRevA.88.013818. [DOI] [Google Scholar]
- [28].Grimaudo R, Vitanov NV, Messina A, Coupling-assisted Landau-Majorana-Stückelberg-Zener transition in a system of two interacting spin qubits, Phys. Rev. B 99 (2019) 174416. doi: 10.1103/PhysRevB.99.174416. [DOI] [Google Scholar]
- [29].Grimaudo R, Nakazato H, Messina A, Vitanov NV, Dzyaloshinskii-Moriya and dipole-dipole interactions affect coupling-based Landau-Majorana-Stückelberg-Zener transitions, Phys. Rev. Res 2 (2020) 033092. doi: 10.1103/PhysRevResearch.2.033092. [DOI] [Google Scholar]
- [30].Grimaudo R, Vitanov NV, Messina A, Landau-Majorana-Stückelberg-Zener dynamics driven by coupling for two interacting qutrit systems, Phys. Rev. B 99 (2019) 214406. doi: 10.1103/PhysRevB.99.214406. [DOI] [Google Scholar]
- [31].Militello B, Three-state Landau-Zener model in the presence of dissipation, Phys. Rev. A 99 (2019) 033415. doi: 10.1103/PhysRevA.99.033415. [DOI] [Google Scholar]
- [32].Militello B, Detuning-induced robustness of a three-state Landau-Zener model against dissipation, Phys. Rev. A 99 (2019) 063412. doi: 10.1103/PhysRevA.99.063412. [DOI] [Google Scholar]
- [33].Munoz-Bauza H, Chen H, Lidar D, A double-slit proposal for quantum annealing, npj Quantum Inf 5 (2019) 1–11. doi: 10.1038/s41534-019-0160-0. [DOI] [Google Scholar]
- [34].Wittig C, The Landau–Zener formula J. Phys. Chem. B 109 (2005) 8428–8430. doi: 10.1021/jp040627u. [DOI] [PubMed] [Google Scholar]
- [35].Michaeli S, Sorce DJ, Idiyatullin D, Ugurbil K, Garwood M, Transverse relaxation in the rotating frame induced by chemical exchange, Journal of Magnetic Resonance 169 (2004) 293–299. doi: 10.1016/j.jmr.2004.05.010. [DOI] [PubMed] [Google Scholar]
- [36].Sorce DJ, Michaeli S, Garwood M, The time-dependence of exchange-induced relaxation during modulated radio frequency pulses, Journal of Magnetic Resonance 179 (2006) 136–139. doi: 10.1016/j.jmr.2005.11.001. [DOI] [PubMed] [Google Scholar]
- [37].Michaeli S, Sorce DJ, Springer CS, Ugurbil K, Garwood M, MRI contrast in the human brain: Modulation of the longitudinal rotating frame relaxation shutter-speed during an adiabatic RF pulse, Journal of Magnetic Resonance 181 (2006) 135–147. doi: 10.1016/j.jmr.2006.04.002. [DOI] [PubMed] [Google Scholar]
- [38].Mangia S, Liimatainen T, Garwood M, Michaeli S, Rotating frame relaxation during adiabatic pulses vs. conventional spin lock: simulations and experimental results at 4 T, Magn. Reson. Imaging 27 (2009) 1074–1087. doi: 10.1016/j.mri.2009.05.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Mangia S, Traaseth NJ, Veglia G, Garwood M, Michaeli S, Probing slow protein dynamics by adiabatic and NMR experiments, J. Am. Chem. Soc 132 (2010) 9979–9981. doi: 10.1021/ja1038787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Traaseth NJ, Chao F-A, Masterson LR, Mangia S, Garwood M, Michaeli S, Seelig B, Veglia G, Heteronuclear adiabatic relaxation dispersion ({HARD}) for quantitative analysis of conformational dynamics in proteins, Journal of Magnetic Resonance 219 (2012) 75–82. doi: 10.1016/j.jmr.2012.03.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Barbara TM, Nonadiabatic exchange dynamics during adiabatic frequency sweeps, Journal of Magnetic Resonance 265 (2016) 45–51. doi: 10.1016/j.jmr.2016.01.017 [DOI] [PubMed] [Google Scholar]
- [42].Chao F-A, Byrd RA, Geometric approximation: A new computational approach to characterize protein dynamics from nmr adiabatic relaxation dispersion experiments, J. Am. Chem. Soc 138 (2016) 7337–7345. doi: 10.1021/jacs.6b02786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Shimshoni E, Stern A, Dephasing of interference in Landau-Zener transitions, Phys. Rev. B 47 (1993) 9523–9536. doi: 10.1103/PhysRevB.47.9523. [DOI] [PubMed] [Google Scholar]
- [44].Ivanov PA, Vitanov NV, Adiabatic evolution amidst dephasing, Phys. Rev. A 71 (2005) 063407. doi: 10.1103/PhysRevA.71.063407. [DOI] [Google Scholar]
- [45].Wubs M, Saito K, Kohler S, Hänggi P, Kayanuma Y, Gauging a quantum heat bath with dissipative Landau-Zener transitions, Phys. Rev. Lett 97 (2006) 200404. doi: 10.1103/PhysRevLett.97.200404. [DOI] [PubMed] [Google Scholar]
- [46].Lacour X, Guérin S, Yatsenko LP, Vitanov NV, Jauslin HR, Uniform analytic description of dephasing effects in two-state transitions, Phys. Rev. A 75 (2007) 033417. doi: 10.1103/PhysRevA.75.033417. [DOI] [Google Scholar]
- [47].Saito K, Wubs M, Kohler S, Kayanuma Y, Hänggi P, Dissipative Landau-Zener transitions of a qubit: Bathspecific and universal behavior, Phys. Rev. B 75 (2007) 214308. doi: 10.1103/PhysRevB.75.214308. [DOI] [Google Scholar]
- [48].Pokrovsky VL, Sun D, Fast quantum noise in the Landau-Zener transition, Phys. Rev. B 76 (2007) 024310. doi: 10.1103/PhysRevB.76.024310. [DOI] [Google Scholar]
- [49].Nalbach P, Thorwart M, Landau-Zener transitions in a dissipative environment: Numerically exact results, Phys. Rev. Lett 103 (2009) 220401. doi: 10.1103/PhysRevLett.103.220401. [DOI] [PubMed] [Google Scholar]
- [50].Avron JE, Fraas M, Graf GM, Grech P, Landau-Zener tunneling for dephasing Lindblad evolutions, Commun. Math. Phys 305 (2011) 633–639. doi: 10.1007/s00220-011-1269-y. [DOI] [Google Scholar]
- [51].Orth PP, Imambekov A, Le Hur K, Nonperturbative stochastic method for driven spin-boson model, Phys. Rev. B 87 (2013) 014305. doi: 10.1103/PhysRevB.87.014305. [DOI] [Google Scholar]
- [52].Avishai Y, Band YB, Landau-Zener problem with decay and dephasing, Phys. Rev. A 90 (2014) 032116. doi: 10.1103/PhysRevA.90.032116. [DOI] [Google Scholar]
- [53].Xu C, Poudel A, Vavilov MG, Nonadiabatic dynamics of a slowly driven dissipative two-level system, Phys Rev. A 89 (2014) 052102. doi: 10.1103/PhysRevA.89.052102. [DOI] [Google Scholar]
- [54].Zlatanov KN, Vasilev GS, Ivanov PA, Vitanov NV, Exact solution of the Bloch equations for the nonresonant exponential model in the presence of dephasing, Phys. Rev. A 92 (2015) 043404. doi: 10.1103/PhysRevA.92.043404. [DOI] [Google Scholar]
- [55].Zhuang F, Zeng J, Economou SE, Barnes E, Noise-resistant Landau-Zener sweeps from geometrical curves, Quantum 6 (2022) 639. doi: 10.22331/q-2022-02-02-639. [DOI] [Google Scholar]
- [56].Bloch F, Nuclear induction, Phys. Rev 70 (1946) 460–474. doi: 10.1103/PhysRev.70.460. [DOI] [Google Scholar]
- [57].Torrey HC, Transient nutations in nuclear magnetic resonance, Phys. Rev 76 (1949) 1059–1068. doi: 10.1103/PhysRev.76.1059. [DOI] [Google Scholar]
- [58].Feynman RP, Vernon FL, Hellwarth RW, Geometrical representation of the Schrödinger equation for solving maser problems, J. Appl. Phys 28 (1957) 49–52. doi: 10.1063/1.1722572. [DOI] [Google Scholar]
- [59].Madhu PK, Kumar A, Bloch equations revisited: New analytical solutions for the generalized Bloch equations, Concepts Magn. Reson 9 (1997) 1–12. doi:. [DOI] [Google Scholar]
- [60].Magnus W, On the exponential solution of differential equations for a linear operator, Comm. Pure Appl. Math 7 (1954) 649–673. doi: 10.1002/cpa.3160070404. [DOI] [Google Scholar]
- [61].Blanes S, Casas F, Oteo J, Ros J, The Magnus expansion and some of its applications, Phys. Rep 470 (2009) 151–238. doi: 10.1016/j.physrep.2008.11.001. [DOI] [Google Scholar]
- [62].Klein O, Naletov V, Alloul H, Mechanical detection of nuclear spin relaxation in a micron-size crystal, Eur. Phys. J. B 17 (2000) 57–68. doi: 10.1007/s100510070160. [DOI] [Google Scholar]
- [63].Harrell LE, Thurber KR, Smith DD, Cantilever noise in off-cantilever-resonance force-detected nuclear magnetic resonance, J. Appl. Phys 95 (2004) 2577–2581. doi: 10.1063/1.1643780. [DOI] [Google Scholar]
- [64].Rubbmark JR, Kash MM, Littman MG, Kleppner D, Dynamical effects at avoided level crossings: A study of the Landau-Zener effect using Rydberg atoms, Phys. Rev. A 23 (1981) 3107–3117. doi: 10.1103/PhysRevA.23.3107. [DOI] [Google Scholar]
- [65].Fel’dman EB, On the convergence of the Magnus expansion for spin systems in periodic magnetic fields, Phys Lett. A 104 (1984) 479–481. doi: 10.1016/0375-9601(84)90027-6. [DOI] [Google Scholar]
- [66].Moan PC, Oteo JA, Convergence of the exponential Lie series, J. Math. Phys 42 (2001) 501–508. doi: 10.1063/1.1330198. [DOI] [Google Scholar]
- [67].Casas F, Sufficient conditions for the convergence of the Magnus expansion, J. Phys. A: Math. Theor 40 (2007) 15001. doi: 10.1088/1751-8113/40/50/006. [DOI] [Google Scholar]
- [68].Begzjav TK, Eleuch H, Magnus expansion applied to a dissipative driven two-level system, Results in Physics 17 (2020) 103098. doi: 10.1016/j.rinp.2020.103098. [DOI] [Google Scholar]
- [69].Bain AD, Anand CK, Nie Z, Exact solution to the Bloch equations and application to the Hahn echo, J. Magn. Reson 206 (2010) 227–240. doi: 10.1016/j.jmr.2010.07.012. [DOI] [PubMed] [Google Scholar]
- [70].Lauprêtre F, Noël C, Monnerie L, Dynamics of macromolecular chains. {VI}. carbon {13} and proton nuclear magnetic relaxation of polystyrene in solution, J. Polym. Sci. Polym. Phys. Ed 15 (1977) 2127–2142. doi: 10.1002/pol.1977.180151208. [DOI] [Google Scholar]
- [71].Heatley F, Nuclear magnetic relaxation of synthetic polymers in dilute solution, Prog. Nucl. Magn. Reson. Spectrosc 13 (1979) 47–85. doi: 10.1016/0079-6565(79)80013-8. [DOI] [Google Scholar]
- [72].Kayanuma Y, Phase coherence and nonadiabatic transition at a level crossing in a periodically driven two-leve system, Phys. Rev. B 47 (1993) 9940–9943. doi: 10.1103/PhysRevB.47.9940. [DOI] [PubMed] [Google Scholar]
- [73].Boucher MC, Isaac CE, Sun P, Borbat PP, Marohn JA, A non-perturbative, low-noise surface coating for sensitive force-gradient detection of electron spin resonance in thin films, ACS Nano 17 (2023) 1153–1165. doi: 10.1021/acsnano.2c08635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [74].Kempf JG, Marohn JA, Nanoscale fourier-transform imaging with magnetic resonance force microscopy, Phys. Rev. Lett 90 (2003) 087601. doi: 10.1103/PhysRevLett.90.087601. [DOI] [PubMed] [Google Scholar]
- [75].Evans GA, An alternative method for irregular oscillatory integrals over a finite range, Int. J. Comput. Math 52 (1994) 185–193. doi: 10.1080/00207169408804303. [DOI] [Google Scholar]
- [76].Evans GA, Webster JR, A comparison of some methods for the evaluation of highly oscillatory integrals, J. Comput. Appl. Math 112 (1999) 55–69. doi: 10.1016/S0377-0427(99)00213-7. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


