SADI: Similarity-Aware Diffusion Model-Based Imputation for Incomplete Temporal EHR Data

Abstract

Missing values are prevalent in temporal electronic health records (EHR) data and are known to complicate data analysis and lead to biased results. The current state-of-the-art (SOTA) models for imputing missing values in EHR primarily leverage correlations across time points and across features, which perform well when data have strong correlation across time points, such as in ICU data where high-frequency time series data are collected. However, this is often insufficient for temporal EHR data from non-ICU settings (e.g., outpatient visits for primary care or specialty care), where data are collected at substantially sparser time points, resulting in much weaker correlation across time points. To address this methodological gap, we propose the Similarity-Aware Diffusion Model-Based Imputation (SADI), a novel imputation method that leverages the diffusion model and utilizes information across dependent variables. We apply SADI to impute incomplete temporal EHR data and propose a similarity-aware denoising function, which includes a self-attention mechanism to model the correlations between time points, features, and similar patients. To the best of our knowledge, this is the first time that the information of similar patients is directly used to construct imputation for incomplete temporal EHR data. Our extensive experiments on two datasets, the Critical Path For Alzheimer’s Disease (CPAD) data and the PhysioNet Challenge 2012 data, show that SADI outperforms the current SOTA under various missing data mechanisms, including missing completely at random (MCAR), missing at random (MAR), and missing not at random (MNAR).

1. INTRODUCTION

Electronic health records (EHR) are comprehensive collections of patient health information that include demographic data, medical history, laboratory results, diagnoses, treatment, and more (Häyrinen et al., 2008). Rich data in EHR offer great promises in advancing research and improving patient care (Cowie et al., 2017; Jensen et al., 2012; Rajkomar et al., 2018b). For example, deep learning models trained on temporal EHR data can detect sepsis at an early stage (Khojandi et al., 2018; Lauritsen et al., 2020), potentially reducing mortality rates. However, EHR data are typically recorded with irregular time intervals and contain a significant amount of missing values(Wells et al., 2013; Steele et al., 2018), which present daunting challenges for many statistical and machine learning models that require structured, regularly sampled, and complete input data. More importantly, biases caused by missing data in EHR have been identified as a significant factor contributing to the unfairness of ML/AI models in medicine, which can perpetuate and exacerbate health inequities (Gianfrancesco et al., 2018; Rajkomar et al., 2018a). For example, patients with less access to healthcare, often people of color or with lower socioeconomic status, tend to have more incomplete data in their EHR (Getzen et al., 2023). Getzen et al. further demonstrate that incomplete data in EHR adversely impact the accuracy of prediction models which would unfairly harm under-served minority groups and exacerbate health inequities (Getzen et al., 2023). As such, it is of great value to develop robust methods for adequately addressing incomplete temporal EHR data.

Imputation is a widely used and effective approach for addressing the issue of missing data in EHR data. In recent years, there has been a growing body of literature on deep learning-based imputation models for time series EHR data (Cao et al., 2018; Fortuin et al., 2020; Tashiro et al., 2021). The current state-of-the-art (SOTA) models can generally be classified into two categories: RNN-based imputation models, such as those presented in Che et al. (2018); Yoon et al. (2018); Luo et al. (2018, 2019); Cao et al. (2018), and transformer-based imputation models, such as Suo et al. (2020); Shukla and Marlin (2021); Tashiro et al. (2021). For example, Multi-Directional Recurrent Neural Network (MRNN) (Yoon et al., 2018) leverages the power of a bi-directional recurrent neural network, and is composed of an interpolation block and an imputation block. It imputes missing values according to hidden states in both directions of RNN. Similar to MRNN, Bidirectional Recurrent Imputation for Time Series (BRITS) (Cao et al., 2018) also conducts imputation based on a bidirectional recurrent neural network. One difference is that BRITS treats missing values as variables in the model graph, and this change can lead to a more accurate estimation. However, all RNN-based imputation methods have an inherent weakness, which is RNN suffers from the short memory issue. Hence RNN-based imputation methods might not effectively model long-term dependencies. Transformer-based methods, which use a self-attention mechanism and are non-autoregressive, can generally overcome the short memory issue and lead to better imputation performance. For example, the Global and Local Time Series Imputation with Multi-directional Attention Learning (GLIMA) (Suo et al., 2020), which is a combination of RNN networks and transformer layers, imputes missing values by extracting local and global information from time series. The multi-Time Attention Networks for Irregularly Sampled Time Series (mTAND) (Shukla and Marlin, 2021) imputes missing values through an encoder-decoder framework, in which a newly designed attention mechanism is used to interpolate missing values. The Conditional Score-based Diffusion Model for Imputation (CSDI) (Tashiro et al., 2021) is a more recent SOTA imputation method that uses a 2D transformer to capture temporal and feature dependencies among EHR data.

It is important to note that all of the existing SOTA methods primarily leverage correlations across time points and across features to impute missing values. They use RNN or transformer layers to capture these dependencies. These models perform well when data have strong correlation across time points, such as in ICU data where high-frequency time series data are collected. However, this is often insufficient for temporal EHR data from non-ICU settings (e.g., outpatient visits for primary care or specialty care), where data are collected at substantially sparser time points, resulting in much weaker correlation across time points. In this case, it is crucial to also consider patient similarity in the imputation model. Intuitively, patients with similar characteristics and disease histories tend to have similar lab values, and the correlation between similar patients can also be leveraged for a more robust imputation model. In this paper, we propose a similarity-aware imputation model known as SADI (Similarity-Aware Diffusion model-based Imputation for incomplete temporal EHR data) to impute missing values by modeling the dependencies across three dimensions: time, feature and patient. Particularly, our contributions are summarized as the following:

• We propose a similarity-aware diffusion model-based imputation method named SADI. Then we apply SADI to temporal EHR data and design a similarity-aware denoising function that models correlations from all three perspectives (time, feature, and patient). Thus, our imputation model can directly borrow information from similar patients. To the best of our knowledge, this is the first time people have modeled the patient dependency.

• We conduct extensive experiments to quantitatively evaluate our proposed approach under different missing mechanisms. Our experiments show that the SADI outperforms existing SOTA imputation models under MCAR, MAR, and MNAR, particularly for temporal EHRs data from non-ICU settings.

2. NOTATIONS

To fix ideas, let ${\mathbf{X}}_{i,t}^d(i=1,\dots ,n;t=1,\dots ,T;d=1,\dots ,p$) denote the observation for the $i$-th patient at time $t$ for the $d$-th feature. Here $n$ represents the number of patients (samples), $T$ represents the length of the temporal EHR data, and $p$ represents the number of features. Without loss of generality, we focus on the case that each patient’s data has the same length $T$. For patients with fewer visits/time points, their EHR data will be extended through zeropadding, with these zeroes representing missing values. Denote the missing indicator of ${\mathbf{X}}_{i,t}^d$ as ${\mathbf{M}}_{i,t}^d$. If ${\mathbf{M}}_{i,t}^d=1$, then ${\mathbf{X}}_{i,t}^d$ is observed. Similarly, if ${\mathbf{M}}_{i,t}^d=0$, then ${\mathbf{X}}_{i,t}^d$ is missing. Additionally, ${\mathbf{X}}_i$ represents the full $p$-dimensional temporal EHR data for the $i$-th patient, and ${\mathbf{X}}_i^d=\left({\mathbf{X}}_{i,1}^d,\dots ,{\mathbf{X}}_{i,T}^d\right)$ represents the $d$-th feature of ${\mathbf{X}}_i$, which is one-dimensional EHR data. Plus, all the following norms $\Vert \cdot \Vert$ represent $l_2$ norm and $\left[K\right]$ represents list of positive integers from 1 to $K$.

3. PRELIMINARIES

3.1. Adapting diffusion models for imputation

Diffusion models are a class of powerful generative models that have been used in many applications (Song and Ermon, 2019; Niu et al., 2020; Ho et al., 2020; Song et al., 2020; Kong et al., 2020; Chen et al., 2020). They can also be leveraged to approximate conditional distribution given observed data (Song et al., 2020; Kadkhodaie and Simoncelli, 2020; Mittal et al., 2021). More recently, diffusion models have also been adapted for imputing missing time series data by Tashiro et al. (2021), known as the Conditional Score-based Diffusion Model for Imputation (CSDI).

In this section, we briefly review the application of diffusion models for estimating the conditional distribution of missing data given the observed data. Given a sample ${\mathbf{x}}_0$ with missing values, which is not limited to time series, we are interested in two parts of ${\mathbf{x}}_0$: the target part, represented by ${\mathbf{x}}_0^{ta}$, and the conditional part, represented by ${\mathbf{x}}_0^{co}$. Our goal is to estimate the true conditional distribution $q\left({\mathbf{x}}_0^{ta}\mid {\mathbf{x}}_0^{co}\right)$ by the model distribution $p_{\theta }\left({\mathbf{x}}_0^{ta}\mid {\mathbf{x}}_0^{co}\right)$ from a diffusion process. It is important to note that, in section 3.1, the subscript $s$ of variable $\mathbf{x}$ does not represent a particular patient or time step in the time series. Instead, it represents a step in the Markov process. The first subscript 0 represents variables ${\mathbf{x}}_0$ coming from the true data distribution.

At a high level, the diffusion model estimates the true conditional distribution through two processes: a forward process and a reverse process. The forward process adds noise to the target part until it resembles a sample from a white noise Gaussian distribution. This is done through a Markov chain that generates a sequence of latent variables ${\mathbf{x}}_1^{ta},\dots ,{\mathbf{x}}_S^{ta}$ as follows:

$$\begin{gathered} q\left({\mathbf{x}}_1^{ta},\dots ,{\mathbf{x}}_S^{ta}\mid {\mathbf{x}}_0^{ta}\right)=\prod _{s=1}^S q\left({\mathbf{x}}_s^{ta}\mid {\mathbf{x}}_{s-1}^{ta}\right) \\ \text{where}q\left({\mathbf{x}}_s^{ta}\mid {\mathbf{x}}_{s-1}^{ta}\right)=𝒩\left(\sqrt{1-{\beta }_s}{\mathbf{x}}_{s-1}^{ta},{\beta }_s\mathbf{I}\right) \end{gathered}$$ (1)

Here, ${\beta }_s\in (0,1)$ are hyperparameters that represent the noise level. The marginal distribution for ${\mathbf{x}}_s^{ta}$ can be calculated as

$$q\left({\mathbf{x}}_s^{ta}\mid {\mathbf{x}}_0^{ta}\right)=𝒩\left(\sqrt{{\bar{\alpha }}_s}{\mathbf{x}}_0^{ta},\left(1-{\bar{\alpha }}_s\right)\mathbf{I}\right)$$

where ${\alpha }_s:=1-{\beta }_s$ and ${\bar{\alpha }}_s:={\prod }_{i=1}^s {\alpha }_i$. The above equation is equivalent to

$${\mathbf{x}}_s^{ta}=\sqrt{{\bar{\alpha }}_s}{\mathbf{x}}_0^{ta}+\sqrt{1-{\bar{\alpha }}_s}\mathit{ϵ}$$ (2)

where $\mathit{ϵ}\sim 𝒩(0,\mathbf{I})$ is a Gaussian vector.

The reverse process removes noise from ${\mathbf{x}}_S^{ta}$ to recover the original data ${\mathbf{x}}_0^{ta}$. This is done through a learnable Markov chain defined by the following distribution:

$$\begin{array}{l}{p}_{\theta }\left({\mathbf{x}}_0^{ta},\dots ,{\mathbf{x}}_S^{ta}\mid {\mathbf{x}}_0^{co}\right)\\ =p\left({\mathbf{x}}_S^{ta}\right)\prod _{s=1}^S p_{\theta }\left({\mathbf{x}}_{s-1}^{ta}\mid {\mathbf{x}}_s^{ta},{\mathbf{x}}_0^{co}\right),\text{where}{\mathbf{x}}_S^{ta}\sim 𝒩(0,\mathbf{I})\\ p_{\theta }\left({\mathbf{x}}_{s-1}^{ta}\mid {\mathbf{x}}_s^{ta},{\mathbf{x}}_0^{co}\right)\\ & =𝒩\left({\mathbf{x}}_{s-1}^{ta};{\mathit{\mu }}_{\theta }\left({\mathbf{x}}_s^{ta},s\mid {\mathbf{x}}_0^{co}\right),{\sigma }_{\theta }\left({\mathbf{x}}_s^{ta},s\mid {\mathbf{x}}_0^{co}\right)\mathbf{I}\right)\end{array}$$ (3)

where $\theta$ represents model parameters. Note that all the terms are conditioned on ${\mathbf{x}}_0^{co}$ to exploit conditional observations. The conditional version of the Denoising Diffusion Probabilistic Model (DDPM) (Ho et al., 2020) is used in this method, which uses the following specific parameterization of $p_{\theta }\left({\mathbf{x}}_{s-1}^{ta}\mid {\mathbf{x}}_s^{ta},{\mathbf{x}}_0^{co}\right)$:

$$\begin{gathered} {\mathit{\mu }}_{\theta }\left({\mathbf{x}}_s^{ta},s\mid {\mathbf{x}}_0^{co}\right)=\frac{1}{{\alpha }_s}\left({\mathbf{x}}_s^{ta}-\frac{{\beta }_s}{\sqrt{1-{\alpha }_s}}{\mathit{ϵ}}_{\theta }\left({\mathbf{x}}_s^{ta},s\mid {\mathbf{x}}_0^{co}\right)\right) \\ {\sigma }_{\theta }\left({\mathbf{x}}_s^{ta},s\mid {\mathbf{x}}_0^{co}\right)=\left\{\begin{array}{ll}\sqrt{\frac{1-{\alpha }_{s-1}}{1-{\alpha }_s}{\beta }_s}& s>1\\ \sqrt{{\beta }_1}& s=1\end{array}\right. \end{gathered}$$ (4)

Here, ${\mathit{ϵ}}_{\theta }$ is a deep neural network with parameters $\theta$. Under this parameterization, the training of the reverse process is equivalent to solving the following optimization problem:

$$\begin{array}{l}\underset{\theta }{\mathrm{m}\mathrm{i}\mathrm{n}} ℒ(\theta )\\ :=\underset{\theta }{\mathrm{m}\mathrm{i}\mathrm{n}} {\mathbb{E}}_{{\mathbf{x}}_0\sim q\left({\mathbf{x}}_0\right),\mathit{ϵ}\sim 𝒩(0,\mathbf{I}),s\sim 𝒰\{1,S\}}{‖\mathit{ϵ}-{\mathit{ϵ}}_{\theta }\left({\mathbf{x}}_s^{ta},s\mid {\mathbf{x}}_0^{co}\right)‖}_2^2\end{array}$$ (5)

where ${\mathbf{x}}_s^{ta}=\sqrt{{\bar{\alpha }}_s}{\mathbf{x}}_0^{ta}+\sqrt{1-{\bar{\alpha }}_s}\mathit{ϵ}$. This can be interpreted as using the function ${\mathit{ϵ}}_{\theta }$ as a denoising function to estimate the noise added to its noisy input ${\mathbf{x}}_s^{ta}$. Once the model is trained, we can sample ${\mathbf{x}}_0^{ta}$ from the reverse process eq. (3). The model distribution $p_{\theta }\left({\mathbf{x}}_0^{ta}\mid {\mathbf{x}}_0^{co}\right)$ is then used to estimate the true conditional distribution $q\left({\mathbf{x}}_0^{ta}\mid {\mathbf{x}}_0^{co}\right)$.

Since we have no access to the ground truth of missing values, both ${\mathbf{x}}_0^{ta}$ and ${\mathbf{x}}_0^{co}$ are selected from observed values in the model training phase (Tashiro et al., 2021). During the imputation phase, ${\mathbf{x}}_0^{ta}$ consists of all missing values and ${\mathbf{x}}_0^{co}$ consists of all observed values, in order to make full use of observed information.

3.2. Time series clustering

To gain insights on patient similarities, it is common to group patients’ data into clusters. Numerous techniques have been proposed for clustering time series data, including the K-Means with Dynamic Time Warping (DTW) (Berndt and Clifford, 1994; Salvador and Chan, 2007), K-Shape algorithm (Paparrizos and Gravano, 2015), and K-Spectral Centroid algorithm (K-SC) (Yang and Leskovec, 2011; Ozer et al., 2020). The common idea behind these methods is to utilize an appropriate distance metric for time series data to define similarity between patients. All of them operate in an iterative manner, similar to the K-Means algorithm, and involve two steps: the assignment step and the refinement step. During the assignment step, each EHR time series is assigned to a centroid, with each centroid representing a cluster. The refinement step involves updating the centroids using the EHR data in their corresponding clusters. This process is repeated until the clusters are stable.

Algorithm 1.

Training of SADI

Input: distribution $q_k\left({\mathbf{x}}_0\right)$ and the corresponding weight $c_k$ for $k\in \left[K\right]$, target selection strategy, training epochs $N$, maximum number of diffusion steps $S$, noise level ${\left\{{\beta }_s\right\}}_{s=1}^S$
Output: Trained denoising function ${\mathit{ϵ}}_{\theta }$
1:	for $i\in \{1,\dots ,N\}$ do
2:	Sample $k\sim 𝒞\left\{c_1,c_2,\dots ,c_K\right\}$
3:	Sample $s\sim \mathrm{U}\mathrm{n}\mathrm{i}\mathrm{f}\{1,\dots ,S\}$, and ${\mathbf{x}}_0\sim q_k\left({\mathbf{x}}_0\right)$
4:	Separate observed values ${\mathbf{x}}_0$ into target part ${\mathbf{x}}_0^{ta}$ and conditional part ${\mathbf{x}}_0^{co}$ by the target selection strategy
5:	Sample $\mathit{ϵ}\sim 𝒩(0,\mathbf{I})$ where the dimension of $\mathit{ϵ}$ corresponds to ${\mathbf{x}}_0^{ta}$
6:	Calculate noisy targets ${\mathbf{x}}_s^{ta}=\sqrt{{\bar{\alpha }}_s}{\mathbf{x}}_0^{ta}+\sqrt{1-{\bar{\alpha }}_s}\mathit{ϵ}$
7:	Take gradient step on $\nabla {∥\mathit{ϵ}-{\mathit{ϵ}}_{\theta }\left({\mathbf{x}}_s^{ta},s\mid {\mathbf{x}}_0^{co}\right)∥}_2^2$
8:	end for

4. SIMILARITY-AWARE DIFFUSION MODEL-BASED IMPUTATION (SADI)

Consider a random variable ${\mathbf{x}}_0$, where the subscript $s$ represents a step in a Markov process. Here, $s=0$ specifically refers to the variables ${\mathbf{x}}_0$ originating from the true data distribution $q\left({\mathbf{x}}_0\right)$, which is our primary interest. We consider a setting where the data distribution is a mixture distribution with $K$ components that can be represented as

$$q\left({\mathbf{x}}_0\right)=c_1{q}_1\left({\mathbf{x}}_0\right)+\cdots +c_K{q}_K\left({\mathbf{x}}_0\right).$$ (6)

Each component corresponds to a group or class of the data, and the sum of the weights of each group $c_k$ equals 1.

In the traditional CSDI algorithm, a batch of random samples is drawn from the overall data distribution $q\left({\mathbf{x}}_0\right)$ at each optimization step. Consequently, each sample in the batch may come from different groups, limiting the amount of shared information across samples due to their dissimilarity. In contrast, the similarity-aware diffusion model utilizes the decomposition from eq. (6) and draws a batch of random samples from the same group $q_k\left({\mathbf{x}}_0\right)$ at each optimization step, ensuring that samples within the same batch are similar. This sample similarity introduces an additional source of information that the model can learn from, thereby enhancing imputation performance. We name the optimized imputation method as similarity-aware diffusion model-based imputation (SADI). For complex EHR time series data, defining groups and patient similarity can be challenging. To address this issue, we have developed a novel data-driven approach to evaluate group information and patient similarity, which is detailed in Section 5.1.

Algorithm 2.

Sampling/Imputation with SADI

Input: a data sample ${\mathbf{x}}_0$ from $q_k\left({\mathbf{x}}_0\right)$, maximum number of diffusion steps $S$, trained denoising function ${\mathit{ϵ}}_{\theta }$
Output: Imputed values
1:	Denote the observed values of ${\mathbf{x}}_0$ as ${\mathbf{x}}_0^{co}$, the missing part as ${\mathbf{x}}_0^{ta}$
2:	Sample ${\mathbf{x}}_S^{ta}\sim 𝒩(0,\mathbf{I})$ where ${\mathbf{x}}_S^{ta}$ has the shape as ${\mathbf{x}}_0^{ta}$
3:	for $s\in \{S,\dots ,1\}$ do
4:	Sample ${\mathbf{x}}_{s-1}^{ta}$ from the reverse process, see eq. (3).
5:	end for

We choose to use a diffusion model to approximate the conditional distribution $q\left({\mathbf{x}}_0^{ta}\mid {\mathbf{x}}_0^{co}\right)$. Specifically, the diffusion model contains one forward process eq. (1), and one reverse process eq. (3). Intuitively, the forward process defines a sequence of latent variables ${\mathbf{x}}_1^{ta},\dots ,{\mathbf{x}}_S^{ta}$ through a Markov chain (see eq. (1)). As the step $s$ increases, the determined part $\sqrt{{\bar{\alpha }}_s}{\mathbf{x}}_0^{ta}$ in the latent variable ${\mathbf{x}}_s^{ta}$ decreases, while the noise part $\sqrt{1-{\bar{\alpha }}_s}\mathit{ϵ}$ increases, as illustrated in eq. (2). Eventually, the last latent variable ${\mathbf{x}}_S^{ta}$ is approximately to be random noise. On the contrary, the reverse process aims to denoise ${\mathbf{x}}_S^{ta}$ and recover the original data ${\mathbf{x}}_0^{ta}$. The reverse process eq. (3) is defined by a learnable Markov chain, where the transition probability follows a normal distribution and the corresponding mean and variance are learned by models.

The diffusion model is usually trained by optimizing the variational bound on the negative log-likelihood (Sohl-Dickstein et al., 2015). By considering DDPM parameterization eq. (4), training the diffusion model is essentially training the denoising function ${\mathit{ϵ}}_{\theta }$ (Ho et al., 2020; Tashiro et al., 2021), which is represented by a deep neural network with parameter $\theta$. The loss function of similarity-aware diffusion model is

$$\begin{array}{l}\underset{\theta }{\mathrm{m}\mathrm{i}\mathrm{n}} ℒ(\theta )\\ :=\underset{\theta }{\mathrm{m}\mathrm{i}\mathrm{n}} {\mathbb{E}}_{k\sim 𝒞\left\{c_1,c_2,\dots ,c_K\right\},{\mathbf{x}}_0\sim q_k\left({\mathbf{x}}_0\right),\mathit{ϵ}\sim 𝒩(0,\mathbf{I}),s\sim 𝒰\{1,S\}}\\ {‖\mathit{ϵ}-{\mathit{ϵ}}_{\theta }\left({\mathbf{x}}_s^{ta},s\mid {\mathbf{x}}_0^{co}\right)‖}_2^2\end{array}$$ (7)

Here $𝒞\left\{c_1,c_2,\dots ,c_K\right\}$ represents a categorical distribution, and the group number $k$ is sampled from $\{1,2,\dots ,K\}$ with corresponding probability $\left\{c_1,c_2,\dots ,c_K\right\}$. As we can observe, the distinction between the SADI loss function eq. (7) and CSDI Equation (5) lies in the sampling approach. SADI first determines the group number and then samples data from the corresponding group distribution, whereas CSDI directly samples data from the entire distribution. Thus, when optimizing the model using a batch of samples, SADI draws a batch of similar samples at each optimization step, while in CSDI, samples may be dissimilar since they could be drawn from different groups.

As we mentioned in section 3.1, the target part should be known during the training phase to calculate the loss function. So the target part should be selected from observed values during training. Once the denoising function ${\mathit{ϵ}}_{\theta }$ is trained, we can sample imputations for ${\mathbf{x}}_0^{mis}$ from the reverse process eq. (3) by letting the target part be all the missing values and the conditional part be all the observed values. The training and sampling algorithms are presented in algorithm 1 and algorithm 2 respectively.

5. SADI for INCOMPLETE TEMPORAL EHR DATA

In this section, we describe the procedure of how to use SADI to impute incomplete temporal EHR data ${\left\{{\mathbf{X}}_i\right\}}_{i=1}^n$. The motivation for applying SADI is to effectively incorporate information across similar patients and model the correlations among them to further improve imputation performance.

5.1. The overall imputation pipeline of SADI

Due to the incompleteness of EHR data, it is challenging to access patient similarity directly. So we propose a procedure as shown in Figure 1, which entails four steps. The first step is to utilize an imputation method, such as MICE or CSDI, to perform an initial imputation and obtain the complete dataset ${\{{\overline{\mathbf{X}}}_i\}}_{i=1}^n$. The second step is to apply a time series clustering algorithm, such as the K-SC clustering method, to divide ${\{{\overline{\mathbf{X}}}_i\}}_{i=1}^n$ into $K$ groups ${\{{\overline{\mathbf{X}}}_i\}}_{i\in G_k}$ for $k=1,\dots ,K$.

Figure 1:

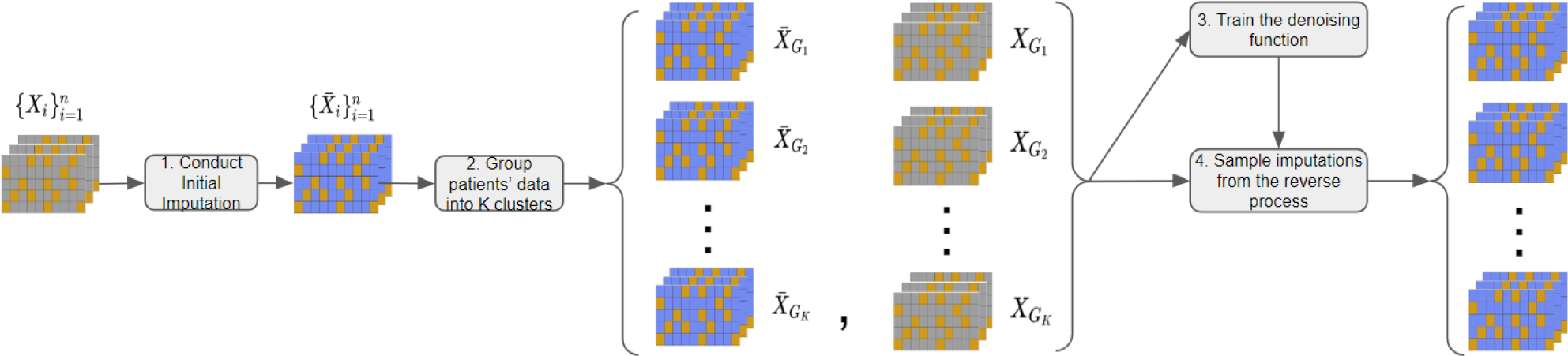
The procedure of temporal missing value imputation with SADI. Each table represents a patient’s EHR data, with gray cells indicating missing values, orange cells indicating observed values, and blue cells indicating imputed values. The process involves (1) conducting an initial imputation (e.g., using CSDI) on the entire dataset ${\left\{{\mathbf{X}}_i\right\}}_{i=1}^n$ to generate imputed data ${\{{\overline{\mathbf{X}}}_i\}}_{i=1}^n$, (2) applying a clustering algorithm (e.g., K-SC) to categorize imputed data ${\{{\overline{\mathbf{X}}}_i\}}_{i=1}^n$ into $\mathrm{K}$ clusters ${\{{\overline{\mathbf{X}}}_{G_k}\}}_{k=1}^K$ and acquiring the corresponding original data clusters ${\{{\mathbf{X}}_{G_k}\}}_{k=1}^K$, (3) training SADI on the $\mathrm{K}$ clustered datasets ${\{{\mathbf{X}}_{G_k}\}}_{k=1}^K$, and (4) sampling imputations for the data clusters using the reverse process of SADI.

Here, the number of groups $K$ is a predefined hyperparameter, and the goal of the second step is to obtain the group information $G_k$. We then partition the original dataset $\{\mathbf{X}{\}}_{i=1}^n$ into the corresponding groups ${\mathbf{X}}_{G_k}={\left\{{\mathbf{X}}_i\right\}}_{i\in G_k}$ for $k=1,\dots ,K$. Then we regard each group ${\mathbf{X}}_{G_k}$ containing samples from the distribution $q_k\left(x_0\right)$ defined in section 4 and the samples in the same group are similar. The third step is to leverage the SADI framework in section 5 for approximating the distribution of missing values conditioned on observed values. In this step, we propose a novel patient-similarity-aware denoising function ${\mathit{ϵ}}_{\theta }$ and train the denoising function ${\mathit{ϵ}}_{\theta }$ on groups ${\left\{{\mathbf{X}}_{G_k}\right\}}_{k=1}^K$. The fourth and last step is to utilize the trained denoising function ${\mathit{ϵ}}_{\theta }$ to sample imputation from the reverse process for missing data. Note that subscript $s$ in ${\mathbf{X}}_{i,s}$ represents the $s$-th step in the Markov process in the remainder of section 5, and ${\mathbf{X}}_{i,0}={\mathbf{X}}_i$ denotes data from the true data distribution.

5.2. Similarity-aware denoising function

We first specify the input and the structure of the patient-similarity-aware denoising function ${\mathit{ϵ}}_{\theta }$. Recall that the original denoising function ${\mathit{ϵ}}_{\theta }\left({\mathbf{x}}_s^{ta},s\mid {\mathbf{x}}_0^{co}\right)$ in section 3.1 takes noisy target part ${\mathbf{x}}_s^{ta}$, step $s$ and conditional part ${\mathbf{x}}_0^{co}$ as input and predicts the noise contained in the noisy target ${\mathbf{x}}_s^{ta}$. During the training phase, a random batch of training data from $q\left({\mathbf{x}}_0\right)$ is used to optimize the original denoising function. SADI refines this process to use information across similar patients. Specifically, the denoising function ${\mathit{ϵ}}_{\theta }\left({\mathbf{x}}_s^{ta},s\mid {\mathbf{x}}_0^{co}\right)$ takes a batch of samples from $q_k\left({\mathbf{x}}_0\right)$ as input. Since we have regarded each group data ${\mathbf{X}}_{G_k}$ as samples from $q_k\left({\mathbf{x}}_0\right)$ after the clustering step. So the denoising function ${\mathit{ϵ}}_{\theta }\left({\mathbf{x}}_s^{ta},s\mid {\mathbf{x}}_0^{co}\right)$ of SADI takes a batch of similar patients’ data ${\mathbf{X}}_B$ as input, where $B\subset G_k$ with batch size $\left|B\right|=b$. To handle the varying shapes of the target part ${\mathbf{X}}_{i,s}^{ta}$ and conditional part ${\mathbf{X}}_{i,0}^{co}$ of patients’ EHR data, zero padding is applied to both parts to ensure that they have the same shape $p\times T$. As such, a conditional mask ${\mathbf{M}}_i^{co}\in \{0,1{\}}^{p\times T}$ is also passed as input to indicate the position of conditional observations. We also apply zero padding to the outputs to keep the output also lying in the sample space ${\mathbb{R}}^{p\times T}$. Denote the stacked target parts, the stacked conditional parts, and the stacked masks of batched data from the $k$-th group by

$${\mathbf{X}}_{B,s}^{ta}=\mathrm{S}\mathrm{t}\mathrm{a}\mathrm{c}\mathrm{k}({\{{\mathbf{X}}_{i,s}^{ta}\}}_{i\in B})\in {\mathbb{R}}^{b\times p\times T}$$

$${\mathbf{X}}_{B,0}^{co}=\mathrm{S}\mathrm{t}\mathrm{a}\mathrm{c}\mathrm{k}({\{{\mathbf{X}}_{i,0}^{co}\}}_{i\in B})\in {\mathbb{R}}^{b\times p\times T}$$

$${\mathbf{M}}_B^{co}=\mathrm{S}\mathrm{t}\mathrm{a}\mathrm{c}\mathrm{k}({\{{\mathbf{M}}_i^{co}\}}_{i\in B})\in {\mathbb{R}}^{b\times p\times T}$$

Then the dimensions of the input and output of the denoising function ${\mathit{ϵ}}_{\theta }\left({\mathbf{X}}_{B,s}^{ta},s\mid {\mathbf{X}}_{B,0}^{co},{\mathbf{M}}_B\right)$ can be written as: $\left({\mathbb{R}}^{b\times p\times T}\times \mathbb{R}\mid {\mathbb{R}}^{b\times p\times T}\times {\mathbb{R}}^{b\times p\times T}\right)\to {\mathbb{R}}^{b\times p\times T}$. Note that the same diffusion step $s$ is applied to all the patients’ data in the same batch $B\subset G_k$. This is different from the training procedure of the original denoising function in section 3.1, where each training sample has its own diffusion step $s$.

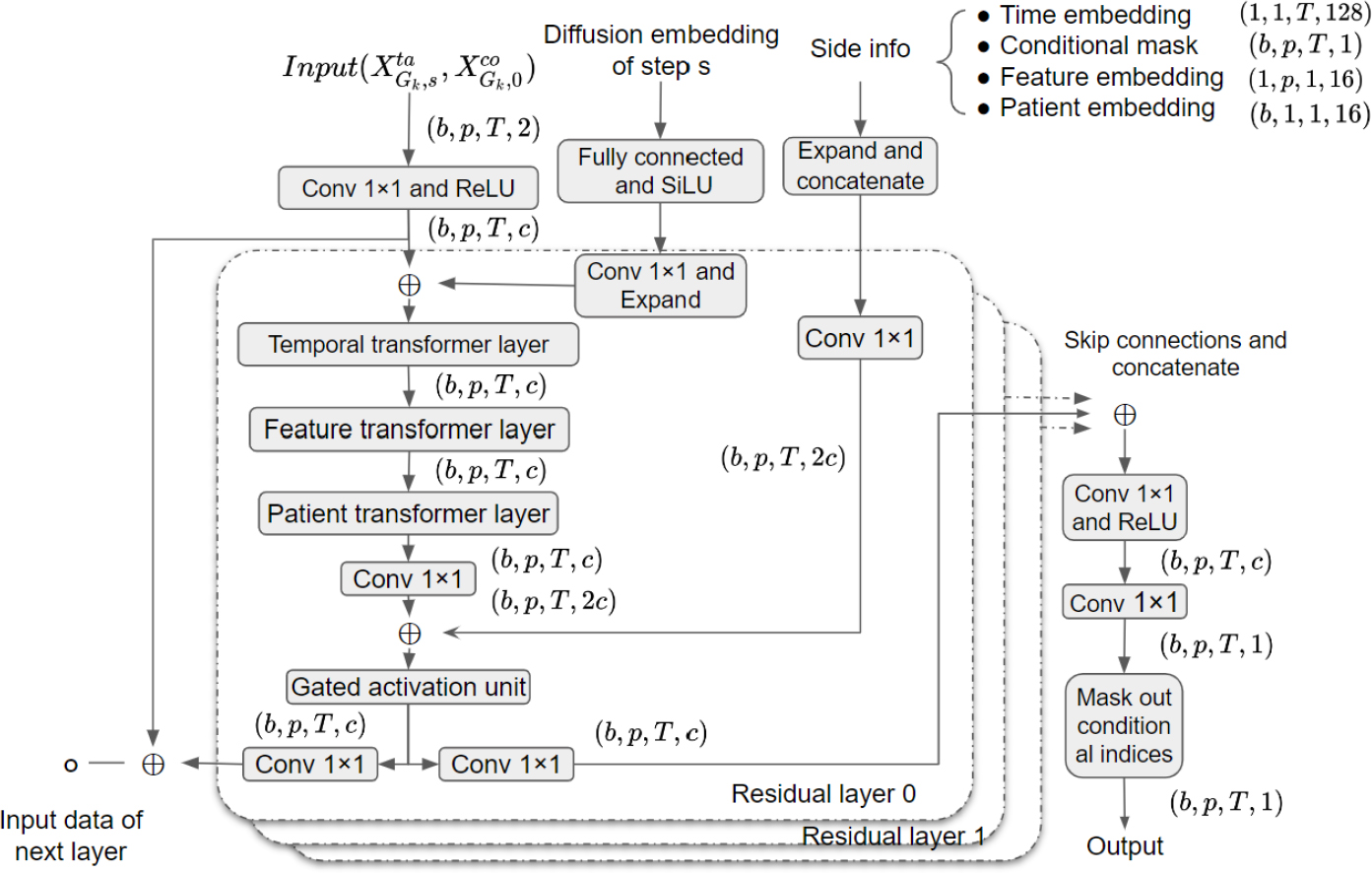
The structure of our patient-similarity-aware denoising function ${\mathit{ϵ}}_{\theta }$ is designed using techniques from DiffWave (Kong et al., 2020) and CSDI (Tashiro et al., 2021) which consist of multiple residual layers with $c$ residual channels. The details of the denoising function can be found in appendix A.3. Here we discuss the main difference from previous works, which is the use of a three-dimensional attention mechanism within each residual layer to learn the temporal, feature, and patient dependencies, as shown in Figure 2. This is achieved by incorporating three transformer layers, each with a single-layer transformer encoder. The first transformer layer captures temporal dependencies by processing input tensors for each feature and patient, where the length of each input sequence is $T$. The second transformer layer learns feature dependencies by operating on input tensors for each time point and patient. Lastly, the third transformer layer captures patient dependencies by processing input tensors for each time point and feature.

Figure 2:

Architecture of 3D attention mechanism. Given a tensor from the $k$-th group with $b$ patients, $p$ features, $T$ time points, and $c$ channels, the temporal transformer layer processes inputs of shape $(1,1,T,c)$ to learn temporal dependency. The feature transformer layer processes inputs of shape $(1,p,1,c)$ to learn feature dependency. The patient transformer layer processes inputs of shape $(b,1,1,c)$ to learn patient dependency.

6. EXPERIMENTS

6.1. Datasets

To evaluate the performance of SADI in comparison with the current SOTA, we conduct numerical experiments on two real-world EHR datasets: a dataset from The Critical Path For Alzheimer’s Disease (CPAD) consortium¹ (Sivakumaran et al., 2020) and the PhysioNet Challenge 2012² dataset (Silva et al., 2012). For both datasets, we run each experiment five times. Our main focus is on the CPAD dataset, a temporal EHR dataset collected from a non-ICU setting. The PhysioNet dataset, on the other hand, is a high-frequency time series dataset collected from ICUs. Both datasets have been anonymized and do not contain sensitive information.

The CPAD dataset consists of 36 sub-tables, including clinical events, lab results, imaging results, and other data domains collected over a period of up to four years. In our experiments, we focus on the lab result table and choose the most frequent 37 features. This table includes 11369 patients. We preprocess the dataset to monthly-based EHR data with 12 time points. Only the visit data within the first year after the initial visit are used to generate the EHR data. This evenly spaced EHR dataset has around 79% missing values in total.

The PhysioNet dataset contains 4000 patients’ clinical multivariate time series data from ICUs. Except for the general descriptors like age and gender, each multivariate time series has 35 features, including Glucose, DiasABP, and so on. Those features are irregularly sampled in the first 48 hours after admission to the ICU. We preprocess the original dataset to hourly-based time series with 48 time points. This evenly spaced time series dataset has around 80% missing values in total. The description of these two datasets are summarized in Table 1, and more details can be found in appendix A.1.

Table 1:

Description of two EHR datasets

	CPAD	PhysioNet Challenge 2012
Number of patients	11369	4000
Number of features	37	35
Number of time points	12	48
Percentage of missing values	79%	80%

Since there are no ground truths for missing values on the CPAD data and the PhysioNet data, we artificially mask out 10% of observed values as test data to evaluate model performance under three missing data mechanisms, MCAR, MAR, and MNAR (Little and Rubin, 2019). The remaining observed data are used as the training data, and we randomly select 10% of the training data as the validation data, as shown in Figure 3.

Figure 3:

An illustration of dividing a patient’s EHR data with 5 features and 10 time points into training, validation, and testing sets. Each row represents a feature and each column represents a time point. Missing values are shown in gray, while observed values are divided into orange (training), blue (validation), and purple (testing) segments.

6.2. Missing mechanism

Briefly, MCAR occurs when the missingness is independent of both the observed and missing values. MAR occurs when the missingness depends solely on the observed values. Lastly, MNAR occurs when the missingness is dependent on both observed and missing values. MCAR typically is not valid in EHR data, whereas MAR is more plausible. Imputing missing values in MNAR settings is more challenging than in MCAR and MAR settings. It is well known that one cannot test MAR vs MNAR using observed data. As such, to gain a comprehensive assessment of SADI in comparison with the current SOTA, we evaluate their performance under all three missing data mechanisms. The detailed description can be found in appendix A.2.

6.3. Methods to be compared

We evaluate our proposed SADI with both RNN-based and attention-based imputation models which are listed below. All models are trained with GPU RTX 2080. Experiment details can be found in appendix A.3. To conduct accurate imputation, SADI takes the median of 100 generated samples as the final imputation. RNN-based methods: (1) MRNN (Yoon et al., 2018) uses bidirectional LSTM to impute missing values and models both temporal and feature dependencies. (2) RITS (Cao et al., 2018) is a simplified version of BRITS and only models the temporal dependency. (3) BRITS (Cao et al., 2018) is similar to MRNN, and also uses bidirectional RNN to model both temporal and feature dependencies. Transformer-based methods: (4) CSDI (Tashiro et al., 2021) is based on diffusion models and utilizes two transformer layers to capture time and feature dependencies.

6.4. Performance metrics

We use three metrics to evaluate the imputation performance: mean absolute error (MAE), mean relative error (MRE) and root mean square error (RMSE). Suppose ${\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}_i$ is the ground truth for the $i$-th item and ${\mathrm{e}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}_i$ is the predictive value for the $i$-th item, and there are $N$ items in total. Then three metrics are defined as follows

$$\text{MAE}=\frac{\sum _i \mid {\text{estimation}}_i-{\text{target}}_i\mid }{N}$$

$$\text{MRE}=\frac{\sum _i \mid {\text{estimation}}_i-{\text{target}}_i\mid }{\sum _i \left|{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}_i\right|}$$

$$\text{RMSE}=\sqrt{\frac{\sum _i \mid {\text{estimation}}_i-{\left.{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}_i\right|}^2}{N}}$$

6.5. Experiment results

We first evaluate the performance of SADI and four other SOTA methods on the CPAD dataset (the non-ICU dataset) and compare their imputation performance. The results under MCAR, MAR, and MNAR settings are presented in Table 2. The best performance in each table is highlighted in bold. First, the three settings show similar results in terms of comparisons across the methods. Particularly, three RNN-based methods (MRNN, RITS, and BRITS) tend to perform worse than the two transformer-based methods (CSDI and SADI), suggesting that transformer layers are better suited for modeling sequence dependencies. Among the transformer-based methods, SADI significantly outperforms CSDI in all scenarios. Specifically, SADI reduces MAE, RMSE, and MRE by around 8%, 6%, and 7%, respectively, compared to CSDI in the MCAR setting. Similar improvements are also observed in the MAR setting and the MNAR setting, where SADI reduces the MAE, RMSE, and MRE by 6.5%, 2.5%, 8% and 6%, 2%, 6% respectively, compared to CSDI. This suggests that it is insufficient to only model temporal dependency and feature dependency on sparse temporal EHR data. Additionally, the consistent better performance of SADI over CSDI under all missing data mechanisms also highlights the importance of modeling dependency among similar patients, which makes the model more robust and able to handle different types of missing data mechanisms in EHR data. Ablation study on the CPAD dataset can be found in appendix A.4.

Table 2:

Performance comparison of methods on the CPAD dataset under MCAR, MAR, and MNAR mechanisms. We report the mean and standard error for five trials.

Methods	MCAR			MAR			MNAR
	MAE	RMSE	MRE	MAE	RMSE	MRE	MAE	RMSE	MRE
MRNN	0.233(0.001)	0.478(0.013)	33.5%(0.001)	0.233(0.001)	0.672(0.030)	38.5%(0.001)	0.246(0.001)	0.723(0.123)	44.4%(0.003)
RITS	0.259(0.001)	0.547(0.009)	40.3%(0.002)	0.252(0.001)	0.654(0.024)	41.8%(0.001)	0.265(0.002)	0.730(0.122)	47.7%(0.002)
BRITS	0.239(0.001)	0.532(0.008)	37.1%(0.001)	0.233(0.001)	0.629(0.019)	38.7%(0.001)	0.244(0.001)	0.710(0.117)	44.1%(0.003)
CSDI	0.206(0.006)	0.440(0.004)	30.2%(0.009)	0.207(0.002)	0.640(0.025)	34.3%(0.003)	0.219(0.001)	0.679(0.134)	39.5%(0.003)
SADI	0.190(0.001)	0.416(0.005)	28.0%(0.002)	0.194(0.002)	0.624(0.031)	32.1%(0.003)	0.206(0.002)	0.664(0.137)	37.1%(0.005)

Then we evaluate SADI in comparison with the other methods on the PhysioNet dataset (the ICU dataset) under MCAR, MAR, and MNAR mechanisms, as shown in Table 3. The results still show that the two transformer-based methods (CSDI and SADI) outperform the three RNN-based methods (MRNN, RITS, and BRITS). But the improvement of SADI over CSDI is more modest, at less than 2% in most cases. As discussed earlier, in the ICU setting, the strong temporal correlation between time points could provide sufficient information to achieve accurate imputation. In this case, borrowing information across similar patients only offers marginal improvement. Nevertheless, our proposed SADI still achieves the best or close to the best performance in all settings.

Table 3:

Performance comparison of methods on the PhysioNet dataset under MCAR, MAR, and MNAR mechanisms. We report the mean and standard error for five trials.

Methods	MCAR			MAR			MNAR
	MAE	RMSE	MRE	MAE	RMSE	MRE	MAE	RMSE	MRE
MRNN	0.381(0.001)	0.721(0.096)	54.6%(0.001)	0.377(0.001)	0.677(0.013)	48.3%(0.001)	0.389(0.001)	0.782(0.029)	47.8%(0.001)
RITS	0.322(0.001)	0.653(0.074)	44.9%(0.001)	0.323(0.001)	0.654(0.012)	39.9%(0.001)	0.329(0.001)	0.795(0.027)	40.3%(0.001)
BRITS	0.294(0.001)	0.632(0.056)	41.7%(0.001)	0.296(0.001)	0.621(0.008)	37.9%(0.001)	0.313(0.001)	0.764(0.019)	38.2%(0.001)
CSDI	0.242(0.001)	0.586(0.043)	34.3%(0.002)	0.243(0.001)	0.546(0.007)	31.0%(0.001)	0.252(0.001)	0.689(0.019)	30.7%(0.001)
SADI	0.241(0.001)	0.624(0.069)	34.3%(0.002)	0.241(0.001)	0.543(0.007)	30.8%(0.001)	0.248(0.001)	0.681(0.023)	30.1%(0.001)

7. CONCLUSION/DISCUSSION

In this work, we present a new imputation method, SADI, for imputing missing values in temporal EHR data. SADI enables borrowing information across similar patients, in addition to leverage information across time and across features, to fill in missing values. Our experiments show that SADI outperforms current SOTA EHR data imputation methods in temporal EHR data from non-ICU settings and still achieves the best or close to the best performance in EHR data from ICUs. One limitation of SADI is that the clustering step can be computationally expensive when applied to large datasets with a large number of patients. To mitigate this issue, a potential future research direction would be to generate embedding for EHR data and cluster the dataset based on embeddings (Nalmpantis and Vrakas, 2019; Shukla and Marlin, 2021).

A. Experiment details

A.1. Dataset details

Physinet 2012 dataset

35 features are selected: Albumin, ALP, ALT, AST, Bilirubin, BUN, Cholesterol, Creatinine, DiasABP, FiO2, GCS, Glucose, HCO3, HCT, HR, K, Lactate, Mg, MAP, Na, NI-DiasABP, NIMAP, NISysABP, PaCO2, PaO2, pH, Platelets, RespRate, SaO2, SysABP, Temp, TroponinI, TroponinT, Urine, WBC

Critical Path For Alzheimer’s Disease (CPAD) dataset

37 features are selected: Hemoglobin, Alkaline Phosphatase, Creatinine, Alanine Aminotransferase, Aspartate Aminotransferase, Potassium, Sodium, Gamma Glutamyl Transferase, Albumin, Cholesterol, Calcium, Leukocytes, Triglycerides, Blood Urea Nitrogen, Glucose, Bilirubin, Platelets, Eosinophils/Leukocytes, Lymphocytes/Leukocytes, Monocytes/Leukocytes, Basophils/Leukocytes, Neutrophils/Leukocytes, Hematocrit, Creatine Kinase, Bicarbonate, Prothrombin Intl. Normalized Ratio, Activated Partial Thromboplastin Time, C Reactive Protein, Chloride, Protein, Erythrocytes, Monocytes, Basophils, Lymphocytes, Neutrophils, Eosinophils, Indirect Bilirubin

A.2. Missing mechanism

For the MCAR setting, we set each observed entry to have the same probability of 0.1 to be masked out as a part of the test set. For the MAR and the MNAR settings, the specific details of how missingness is introduced are presented below.

Recall that the observations are denoted by ${\mathbf{X}}_{i,t}^d(i=1,\dots ,n;t=1,\dots ,T;d=1,\dots ,p$). We also denote the original missing indicator ${\mathbf{M}}_{i,t}^d$ as ${}_1{\mathbf{M}}_{i,t}^d$. Denote the missing indicator after masking out the test set as ${}_2{\mathbf{M}}_{i,t}^d$. Here we describe how to generate ${}_2{\mathbf{M}}_{i,t}^d$ based on ${}_1{\mathbf{M}}_{i,t}^d$. Specifically, if MAR mechanism is applied, ${}_2{\mathbf{M}}_{i,t}^d$ is generated through the following rules:

$$\begin{gathered} P\left({}_2{\mathbf{M}}_{i,t}^d=0\right) \\ =\left\{\begin{array}{ll}1,& \text{if}{}_1{\mathbf{M}}_{i,t}^d=0\\ \frac{p^t\cdot (\sum _{d^{\prime }=1}^D {}_1{\mathbf{M}}_{i,t}^{d^{\prime }})\cdot e^{-\sum _{t^{\prime }<t} {\omega }_{t^{\prime }}\cdot {\mathbf{x}}_{i,t^{\prime }}^d\cdot {}_2{\mathbf{M}}_{i,t^{\prime }}^d}}{\sum _{d^{\prime }=1}^D {}_1{\mathbf{M}}_{i,t}^{d^{\prime }}\cdot e^{-\sum _{t^{\prime }<t} {\omega }_{t^{\prime }}\cdot {\mathbf{X}}_{i,t^{\prime }}^{d^{\prime }}\cdot {}_2{\mathbf{M}}_{i,t^{\prime }}^{d^{\prime }}}},& \text{otherwise}\end{array}\right. \end{gathered}$$

Alternatively, if MNAR mechanism is applied, ${}_2{\mathbf{M}}_{i,t}^d$ is generated from ${}_1{\mathbf{M}}_{i,t}^d$ through the following rules:

$$\begin{gathered} P\left({}_2{\mathbf{M}}_{i,t}^d=0\right) \\ =\left\{\begin{array}{ll}1,& \text{if}{}_1{\mathbf{M}}_{i,t}^d=0\\ \frac{p^t\cdot (\sum _{d^{\prime }=1}^D {}_1{\mathbf{M}}_{i,t}^{d^{\prime }})\cdot e^{-\sum _{t^{\prime }\le t} {\omega }_{t^{\prime }}\cdot {\mathbf{x}}_{i,t^{\prime }}^d\cdot {}_2{\mathbf{M}}_{i,t^{\prime }}^d}}{\sum _{d^{\prime }=1}^D {}_1{\mathbf{M}}_{i,t}^{d^{\prime }}\cdot e^{-\sum _{t^{\prime }\le t} {\omega }_{t^{\prime }}\cdot {\mathbf{X}}_{i,t^{\prime }}^{d^{\prime }}\cdot {}_2{\mathbf{M}}_{i,t^{\prime }}^{d^{\prime }}}},& \text{otherwise}\end{array}\right. \end{gathered}$$

Here $p^t$ denotes the proportion of observed data that are masked out as the test dataset at time step $t$, and ${\omega }_{t^{\prime }}$ are sampled from $U(0,1)$ (but only sampled once for the entire dataset). In our experiments, $p^t$ is set to 10% for all $t$.

A.3. Implementation details

All experiments are repeated five times under the random seeds from 42 to 46. For RITS³, BRITS⁴, and CSDI⁵, we use the open-access implementations provided by their authors. For MRNN⁶, we use open-access implementations provided by the author of BRITS. We use the default or the recommended hyperparameters of RITS, BRITS, and MRNN in their papers on both the PhysioNet challenge 2012 data and CPAD data. For CSDI, we use the default parameter on the PhysioNet challenge 2012 data and fine-tune the batch size of CSDI based on validation MAE on the CPAD dataset for a fair comparison.

For SADI, we use CSDI with the default parameters to generate the initial imputation in the first step. Then we use the K-SC method with shift=5 to conduct the clustering step. We show the structure of the denoising function in Figure 4. The number of residual layers is 4, the batch size is 32 and the residual channel is 64. Each transformer layer used in Figure 4 is a 1-layer TransformerEncoder implemented in PyTorch (Paszke et al., 2019), and it consists of a multi-head attention layer, fully-connected layers, and layer normalization. The number of heads in each attention layer is 8. By following previous works (Vaswani et al., 2017; Kong et al., 2020; Tashiro et al., 2021), we use the following 128-dimensions embedding for the diffusion step $s$:

$$\begin{array}{r}{s}_{\text{embedding}}(s)=(\sin ({10}^{0\cdot 4/63}s),\dots ,\sin ({10}^{63\cdot 63/63}s),\\ \mathrm{c}\mathrm{o}\mathrm{s}({10}^{0\cdot 4/63}s),\dots ,\mathrm{c}\mathrm{o}\mathrm{s}({10}^{63\cdot 63/63}s))\end{array}$$

Similarly, we adopt the following 128-dimensions embedding for the time point $t$ as side information:

$$\begin{array}{r}{t}_{\text{embedding}}(t)=(\mathrm{s}\mathrm{i}\mathrm{n}(t/{\tau }^{0/64}),\dots ,\mathrm{s}\mathrm{i}\mathrm{n}(t/{\tau }^{63/64}),\\ \mathrm{c}\mathrm{o}\mathrm{s}(t/{\tau }^{0/64}),\dots ,\mathrm{c}\mathrm{o}\mathrm{s}(t/{\tau }^{63/64}))\end{array}$$

where $\tau =10000$.

Table 4:

Ablation study on the CPAD dataset under MNAR: In this table, a check mark indicates the inclusion of the corresponding transformer layer, while a cross mark denotes its exclusion. We report the mean and standard error for five trials.

Temporal	Feature	Patient	MAE	RMSE	MRE
✔	✔	✔	0.206(0.002)	0.664(0.137)	37.1%(0.005)
✘	✔	✔	0.294(0.001)	0.787(0.114)	53.0%(0.003)
✔	✘	✔	0.228(0.001)	0.700(0.126)	41.1%(0.002)
✔	✔	✘	0.220(0.004)	0.681(0.133)	39.7%(0.008)
✔	✘	✘	0.244(0.003)	0.731(0.125)	44.0%(0.006)
✘	✔	✘	0.352(0.020)	0.885(0.094)	63.4%(0.035)
✘	✘	✔	0.339(0.001)	0.843(0.104)	61.1%(0.002)

We set the number of training epochs as 200 and chose the Adam optimizer to update the parameters. The learning rate is 0.001 and decayed to 0.0001 and 0.00001 at 75% and 90% of the total epochs, respectively. We set the number of diffusion steps as $S=50$ and the noise level is increased from ${\beta }_1=0.0001$ to ${\beta }_S=0.5$. We adopt the quadratic schedule (Tashiro et al., 2021) for other noise levels:

$${\beta }_s=(\frac{S-s}{S-1}\sqrt{{\beta }_1}+\frac{s-1}{S-1}\sqrt{{\beta }_S})$$

A.4. Ablation study on CPAD dataset

In our implementation of the denoising function ${\mathit{ϵ}}_{\theta }$, we design a 3D attention mechanism to learn the temporal, feature, and patient dependencies. In this section, we explore the contribution of each transformer layer using ablation. We show the result in Table 4. It shows that all three transformer layers contribute to the best final performance. Even in non-ICU settings, the temporal correlation is still the most important source of information that the model can learn from. Compared the first and fourth lines of the table, adding a patient layer improves the MAE, RMSE, and MRE performance by 6%, 2.5%, and 7%, respectively.

Figure 4:

structure of ${\mathit{ϵ}}_{\theta }$