A high-dimensional omnibus test for set-based association analysis

Abstract

Set-based association analysis is a valuable tool in studying the etiology of complex diseases in genome-wide association studies, as it allows for the joint testing of variants in a region or group. Two common types of single nucleotide polymorphism (SNP)–disease functional models are recognized when evaluating the joint function of a set of SNP: the cumulative weak signal model, in which multiple functional variants with small effects contribute to disease risk, and the dominating strong signal model, in which a few functional variants with large effects contribute to disease risk. However, existing methods have two main limitations that reduce their power. Firstly, they typically only consider one disease–SNP association model, which can result in significant power loss if the model is misspecified. Secondly, they do not account for the high-dimensional nature of SNPs, leading to low power or high false positives. In this study, we propose a solution to these challenges by using a high-dimensional inference procedure that involves simultaneously fitting many SNPs in a regression model. We also propose an omnibus testing procedure that employs a robust and powerful P-value combination method to enhance the power of SNP-set association. Our results from extensive simulation studies and a real data analysis demonstrate that our set-based high-dimensional inference strategy is both flexible and computationally efficient and can substantially improve the power of SNP-set association analysis. Application to a real dataset further demonstrates the utility of the testing strategy.

Introduction

Genome-wide association studies (GWASs) have made significant progress in identifying genetic risk factors associated with complex disease traits. However, the variants identified so far can only account for a small proportion of heritability for many complex traits [1–3]. Several factors could contribute to the missing heritability, including rare variants, structural variants, and gene–gene interactions [4]. Furthermore, the missing heritability could be attributed to the inability to capture SNPs with weak effects [1]. In traditional GWAS analysis, SNP effects are usually analyzed and tested individually [4, 5]. Therefore, weak signals are less likely to be detected, leading to a failure to explain the heritability of complex traits, even for highly heritable traits such as body height [5]. This suggests that a single SNP-based analysis can be underpowered in GWAS studies [1]. To overcome the limitations of single SNP analysis, efforts have been made to infer the combined effects of SNPs. Set-based methods, including gene-, network-, or pathway-based association tests, have been shown to be powerful and promising alternatives to traditional single SNP-based marginal tests [6–8]. The set-based methods take the joint function of multiple variants in a set into account and have the potential to improve association power [9]. They serve as complementary approaches to single SNP-based analysis [10, 11]. While numerous gene-set analysis methods have been developed, the majority of these approaches primarily concentrate on GWAS summary statistics. These statistics, derived from marginal regressions, may produce biased parameter estimates when not considering linkage disequilibrium (LD) at the GWAS scale. For methods with individual-level data, SNP-Set Sequence Kernel Association Test (SKAT) has been one of the most popular approaches [12, 13]. For an in-depth exploration of gene-set analysis, readers are encouraged to consult the review papers authored by Wang et al. [14] and Das et al. [15].

When multiple SNPs in a set are jointly analyzed to assess the group effect, one popular and computationally efficient strategy is to combine individual SNP P-values to assess the SNP-set association, using a method like Fisher’s P-value combination. Since SNPs are marginally analyzed and then combined, this makes the P-value combination method computationally efficient. This method has been widely used, even for a large number of SNPs. However, when assessing a group effect, two types of genetic manifestation mechanisms could be observed: (i) only a small number of SNPs in a set but each with a large effect contributes to disease risk, as seen in age-related macular degeneration [16], and (ii) a large number of SNPs, each with a small effect, together contribute to disease risk, as seen in Crohn’s disease [17]. Any misspecification of the disease model could lead to power loss when combining P-values to assess a group effect.

When dealing with high-dimensional GWAS SNP data, it is inevitable to encounter correlations due to LD. Although various variable selection methods have been proposed for high-dimensional data, the presence of high correlations within regions or groups poses two major challenges: (i) instability in variable selection and (ii) low power, particularly when considering the multiplicity problem and working with small sample sizes [18]. To address these issues and increase power, an alternative approach is to test the effects of SNPs not at the individual SNP level, but rather at the level of regions or groups of highly correlated variables, such as an SNP set or gene [19]. Group structure arises naturally in many applications, and methods that can take it into account have been proposed from a variable selection perspective. Examples include group selection that produces sparse estimates at the group level, such as group LASSO [20], concave L2-norm group bridge, concave L2-norm group SCAD, and concave L2-norm group MCP [21]. Other methods include bi-level selection that produces sparse estimates at both the group and individual levels, such as the L1-norm group bridge [22], composite MCP [23], and other approaches based on additive penalties [24, 25].

Although the group lasso and its modified versions are effective for variable selection at the group level or both the group and individual levels, they are unable to provide a measure of uncertainty or statistical significance for individual or group variables. This limitation restricts their practical utility in many applications, where researchers require P-values or confidence intervals to make inferences, particularly when experimental validation is not feasible. Therefore, it is essential to quantify uncertainty in high-dimensional statistical inference procedures to ensure reliable scientific conclusions based on statistically sound results [26]. These practical concerns make it crucial to quantify uncertainty in real-world applications. To address these challenges, it is essential to employ high-dimensional statistical inference procedures.

In low-dimensional settings, regular regression models can be applied directly to obtain P-values or confidence intervals for regression coefficients. However, in high-dimensional setups, this becomes a challenging issue. Knight and Fu demonstrated that the asymptotic distribution of sparse LASSO estimators is non-Gaussian with a point mass at zero for fixed dimension as n → ∞, and the situation worsens for P → ∞ as n → ∞ [27]. This problem also applies to other sparse estimators. Due to the noncontinuous distribution of the estimators, regular bootstrap or subsampling methods cannot provide valid P-values or confidence intervals [18]. It was not until the work of Wasserman and Roeder that obtaining valid P-values in high-dimensional regression became possible [28]. Since then, significant efforts have been made to develop statistical methods for high-dimensional inference, including multisample splitting [18], projection-based estimations [29–31], and the desparsifying LASSO estimator [32]. These methods establish the theoretical foundation for high-dimensional inference methods to obtain P-values for individual variables and address the correlation issue, which is inevitable in high-dimensional data. This makes the high-dimensional inference procedure attractive since the individual P-values are obtained based on partial effect estimates, rather than on marginal estimates obtained by single SNP analysis. This is generally true for any regression analysis. When regression variables are completely independent, there should be no difference in the inference of regression coefficient estimates regardless of fitting a multiple regression or a marginal regression. However, when variables are correlated, inferences based on marginal regressions are typically biased. Therefore, group-wise testing based on P-values obtained by fitting a multiple regression model is expected to yield more meaningful results.

As previously mentioned, two genetic effect models can be assumed when evaluating an SNP-set effect: (i) multiple functional variants, each with a small effect in a set, collectively contribute to disease risk, referred to as the cumulative weak signal model (CWSM), and (ii) very few variants with large dominating effects in a set contribute to disease risk, referred to as the dominating strong signal model (DSSM). When applying the DSSM, the distribution of the largest statistic or smallest P-value is a natural choice to obtain the P-value of a group. This approach is also known as the minimum P-value (MinP) approach. However, the MinP method may not be well suited for the CWSM. In this case, a natural choice is to combine P-values to obtain a group P-value and assess group significance.

Methods for P-value combination have been extensively studied and the most typical methods include Fisher’s product test [33], truncated product method (TPM) [34], rank truncated product (RTP) [35], augmented RTP (ART) [36], adaptive ART (ART-A) [36], and the Cauchy combination test [37], to name a few. These P-value combination methods all have their own advantages and disadvantages; the details are given in the supplementary file. In view of the limitations of these methods, we proposed an improved version of ART-A, termed iART-A, by leveraging the Cauchy combination test [37].

As people usually have no prior knowledge about the true genetic effect in practice [38], it is of substantial interest to develop a robust and powerful test that can be adaptive to the two genetic models described above. The omnibus test, as the pick-the-winner method, is a robust and powerful strategy [9]. It borrows the strengths of multiple candidate methods by adaptively accommodating different genetic effects; thus, it is a robust choice in GWAS in the absence of prior knowledge [9]. A brief review of the omnibus test application is available in the supplemental file. To adaptively accommodate the two different genetic models we hypothesized earlier, we proposed a novel omnibus test method under the high-dimensional inference framework. We first obtained the P-values of individual variants using a desparsified (or debiased) LASSO algorithm which has nice asymptotic normality properties in a high-dimensional linear model. For the CWSM, we proposed to use the MinP to represent the set signal. For the DSSM, we used our proposed iART-A to get the combined P-value in a set. As no prior knowledge about the true disease model is known in practice, we proposed an omnibus testing strategy to integrate the two P-values obtained under the two disease model assumptions, using a Cauchy combination test. The Cauchy combination test is asymptotically optimal in a strong sparsity setting [37]. Furthermore, the Cauchy combination test is insensitive to correlations between P-values, making it a powerful tool to integrate the two P-values for a given gene set. We illustrated the idea with extensive simulation studies and application to a real dataset. Our method provides a unified approach for a set-based analysis under a high-dimensional setting.

Statistical methods

In a GWAS study, the number of SNPs is typically in the order of thousands or millions, termed ultrahigh dimensional data. A large proportion of SNPs have no relationship with a disease outcome. Such “noise” SNPs can undermine the power of any statistical methods in a disease–gene association study. Here, we propose to first reduce the data dimension from ultrahigh to high, then conduct the testing in a high-dimensional setup. The flowchart of the framework is summarized in Fig. 1.

Figure 1.

The flowchart of the SNP-set association test leveraging the DSSM and CWSM hypothesis.

Variable screening via high dimensional ordinary least squares projection

The high-dimensional ordinary least squares projection (HOLP) method is a simple and powerful method for variable screening in ultrahigh dimensional scenario [39]. To make this work self-contained, a brief introduction to the HOLP procedure is available in the supplemental file. After we get the HOLP estimator , we follow a very simple strategy by ranking the components of 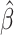and select the top ones [39]. More precisely, let 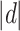be the number of SNP variables that are retained after screening. We choose a submodel 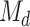as

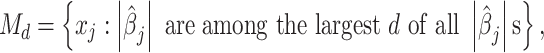where one can choose d with size n, n − 1, or n/log(n) [40, 41], or use extended BIC [42] to determine d [39]. To avoid selection bias in the screening stage, we borrowed the idea from Fan and Lv [40]: first, split samples into two halves, with the first half for variable screening via HOLP and the second half for further high-dimensional inference by desparsifying the LASSO estimator as described in the following.

SNP inference with the desparsified LASSO estimator

Focusing on the submodel 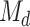, we apply the desparsified LASSO as the high-dimensional inference method to obtain individual P-values for testing individual SNPs, i.e. 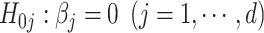, while fitting all the d SNPs as predictors in a multiple linear regression model as follows:

(1)

To make the work self-contained, again, we briefly describe the desparsified LASSO estimator and how we can use it to do testing. For further details, readers are referred to Zhang and Zhang [31] and van de Geer [43]. To save space, we have rendered the details about the desparsified LASSO process in the supplemental file. The asymptotic normality of the estimators can be established [31, 43] as,

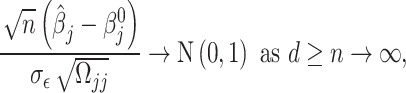(2)

where 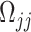can be computed from the data. From Equation (2), we can easily conduct hypothesis testing by plugging in an estimator 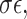which can be obtained based on the scaled LASSO [43]. In short, the aforementioned desparsified LASSO estimator is based on regular LASSO and yields a nonsparse estimator which follows a Gaussian distribution [43]. The asymptotic normality distribution allows us to assess the significance of each coefficient 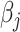[31] and compute P-values for testing the null, i.e. 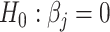in a high-dimensional regression setup [44].

Remark

Depending on how one defines a group (e.g. genes or pathways), our interest is to test the significance of group effect after fitting the d predictors simultaneously in a multiple regression model (the dimension d can still be large after the HOLP screening). This has two major advantages: (i) the coefficients of the d predictors are partial regression effects. When d is large or the d predictors are correlated, the ordinary least squares (OLS) estimates could be problematic, and (ii) simultaneously fitting d variables in a regression model is more advantageous than fitting them marginally one at a time. Imagine there are two highly correlated variables, if only one variable contributes to the response, a marginal regression will show the significance for both variables. On the other hand, fitting the two variables in one regression model will also lead to biased inference if the correlation is not properly taken care of. The issue can be worse when d is large. The desparsified LASSO inference procedure handles this issue well.

Inference under the dominating strong signal model assumption by minimum P-value approach

For the DSSM, we propose to use the minimum P-value to represent the group P-value for further inference. In general, the distribution of the minimum P-value relies on a resampling approach. Such a method is very time-consuming. In this work, utilizing the nice asymptotic results of the desparsified LASSO estimates, we propose a fast resampling method that does not need to refit the model. Suppose we are interested in testing a group hypothesis, i.e. , by using the following maximum statistic:

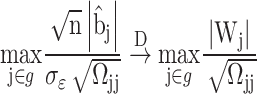(3)

where , where is the cardinality of the group 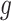, and one can obtain 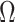by the following formula:

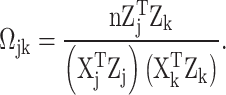(4)

Since the statistic converges in distribution to the maximum of a multivariate normal, i.e. 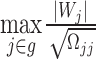, instead of getting the distribution of 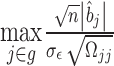by a resampling approach, we can get the distribution of by simulating from a multivariate Gaussian distribution with variance–covariance matrix . For example, we can sample 10 000 random draws from 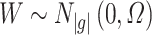and then scale the data by 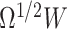. Then, we can get the empirical distribution of 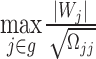by extracting the maximum element corresponding to the jth variable in the scaled data matrix. Next, we can take the minimum P-value (MinP) among the individual P-values in a group as the P-value of the group.

Inference under the cumulative weak signal model assumption by iART-A

For the CWSM, we developed an iART-A approach based on the ART-A method proposed by Vsevolozhskaya et al. [36]. The procedure of iART-A is as follows:

Decorrelation by orthogonal transformation

• The idea of decorrelation by orthogonal transformation (DOT) is to let all d correlated P-values (p₁, p₂, …, p_L) originate from a standard multivariate normal distribution, (u can be replaced with β in the desparsified LASSO), under . For two-sided P-values, the elements of u are squared. Elements of the vector of squared variables, 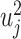, follow a one degree of freedom chi-square distribution with . Dependent variables can be transformed into independent variables by using eigen decomposition of Σ, such that Σ = QΛQ⁻¹, where Q is a square matrix, with ith column containing eigenvector q_i of Σ, and Λ is a diagonal matrix of eigenvalues λ₁, λ₂, …, λ_L. Next, define an orthogonal matrix H = QΛ^−1/2Q^T and u_e = H^Tu. Then, P-values are decorrelated by 1-Φ⁻¹(u_e). In our high-dimensional inference framework, P-values within a group, such as P-values of SNPs within a gene, can be decorrelated as follows [36, 45]:

• (1)We get the covariance matrix, of all d regression coefficients derived from the desparsified LASSO model and then get 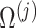for group j from 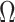by locating the jth group.
• (2)We convert 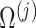to its corresponding correlation matrix .
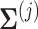• (3)We obtain the eigenvector matrix Q and eigenvalue matrix Λ from the eigen-decomposition of .
• (4)We define an orthogonal matrix H = QΛ^−1/2Q^T and get u_e = H^Tu.
• (5)We get the decorrelated P-value vector P_DOT by using 2 × (1-Φ⁻¹(|u_e |)), where, 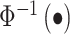is the inverse CDF of a standard normal distribution.
• (6)We sort P_DOT in ascending order.

Adaptative augmented rank truncation

We use the ART-A to combine the first k smallest P-values based on the product of the first smallest P-values. k can be determined by:

• (1) Transforming P_DOT to Z. The ith element, Z_i can be obtained as follows:

  

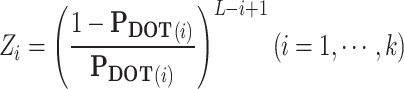
where .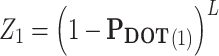

• (2) Define a partial sum as follows:

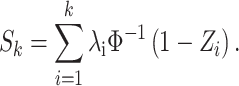Under the null hypothesis, S = (S₁, S₂, …, S_k)^T follows a multivariate normal distribution, i.e. , with 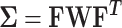, where

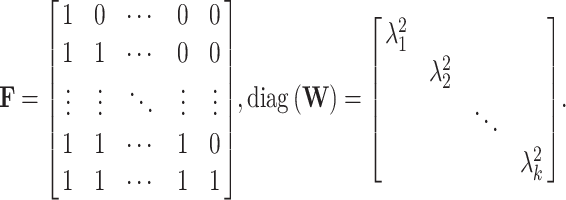• (3) Evaluate the adaptive ART (ART-A) P-value (P_ART-A). Standardize the vector S as 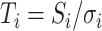, where 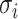is the diagonal element of Σ. The null distribution of S is used to evaluate P_ART-A, by calculating Pr(S_i/σ_i > s_i) from a multivariate normal distribution as follows: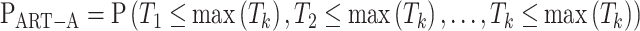

  

In R programming, we can use the function pmvnorm to get P_ART-A by specifying the vector of lower limits as (-Inf, k), the vector of upper limits as (-Inf, max (T_k)), and the covariance matrix as .

Improved adaptative augmented rank truncation

ART-A is still a method that evaluates the adaptive RTP based on the number of candidate values of truncation points, 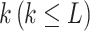which is prespecified. As discussed in Zaykin et al., the optimal value of k is usually lower than the actual number of real signals. However, a priori knowledge about the potential number of real signals is not easy to get; thus, a poor choice of k value will possibly affect the power of the group [46]. For convenience, one usually sets k as L, which may suffer from power loss. To boost the power of ART-A, we propose to calculate the P-value of ART-A via a Cauchy combination test [37] over k (ranging from 2 to L), i.e.

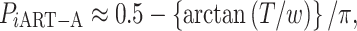where 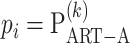. We call this procedure iART-A. The type I error and power of iART-A are shown in the simulation study of the Results section.

Omnibus test based on minimum P-value and iART-A

In practice, people generally lack prior knowledge about the underlying disease model. Here, we suggest integrating the two methods proposed under two genetic models (CWSW and DSSW) from an omnibus testing perspective. Specifically, we aim to construct an omnibus test for SNP sets utilizing the strength of MinP and iART-A to adaptively accommodate the two genetic models. To leverage the strength of the two complementary tests, we define an omnibus test statistic as,

Due to the high dependence between the two P-values, we borrow the idea of the Cauchy combination test [37] to obtain the analytical distribution of Min-O. Let

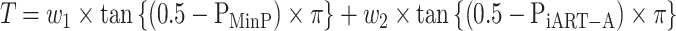where we set 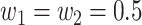(different weights can also be chosen based on prior information). Then, the P-value of the T can be simply approximated by .

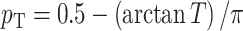Validation of the proposed method with simulation studies

We conducted extensive simulations to evaluate the performance of our proposed framework under different scenarios. We followed the procedure described by Morris et al. to report the simulation design [47].

Aims

In all the simulation scenarios, we aim to evaluate the type I error control under the null hypothesis that some set or group is not associated with the phenotype and assess the power of our proposed framework under different scenarios, including different sample sizes, different types of predictor, correlation within a group, and different gene action modes.

Case I: simulation for the small-scale discrete predictors

The details about the data-generating mechanisms are given in the supplementary file. We evaluated the performance of statistical inference for the two groups (e.g. genes) consisting of discrete predictors (e.g. SNP genotypes) in different scenarios. To borrow the LD information from real data, real SNP genotype data from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) project was used to assess the inference performance of the method at the gene level. The original genotype data can be accessed through their website https://adni.loni.usc.edu/.

Case II: simulation with the genome-wide SNP data

We evaluated the type I error control and power of the method under a high-dimensional setting and further compared our method with the SKAT method. The details about the simulation setting can be found in the supplemental file.

Case III: simulation with quantitative predictors

Our proposed framework is not limited to discrete SNP data; it extends to the analysis of quantitative predictors. For quantitative variables, this can be a pathway-based association study with gene expressions as predictors. Due to space limitations, we rendered the simulation design and results in the supplemental file.

Validation of the proposed method using real data

The Alzheimer’s Disease Neuroimaging Initiative data

Data used in the preparation of this article were obtained from the ADNI database (adni.loni.usc.edu)¹. The ADNI was launched in 2003 as a public–private partnership, led by Principal Investigator Michael W. Weiner, MD. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer’s disease (AD). We conducted a comparative analysis to evaluate the effectiveness of our proposed omnibus test in detecting genes associated with the volume of five brain regions, namely, ventricles, hippocampus, entorhinal cortex, fusiform gyrus, and middle temporal gyrus.

The preprocessing of the Alzheimer’s Disease Neuroimaging Initiative data

Preprocessing of the dataset involved several steps, including the removal of SNPs with call rate <0.95, HWE test P-value <1e-6, and minor allele frequency < 0.01. Individuals with missingness >0.1, sex discrepancy, and sex chromosome SNPs were also excluded, and the SNPs were mapped to genes based on GRCh37. We did not conduct LD pruning to remove SNPs, so the remaining SNPs can be correlated due to LD. After these steps, the dataset comprised of 299 763 SNPs. Missing genotypes were imputed using PLINK v1.9 software (https://www.cog-genomics.org/plink1.9/). Further quality control involved the removal of individuals with heterozygosity exceeding 3 SD and who have parent–offspring relationships. In total, 1043 samples, including cognitive normal, MCI, and AD patients, were included in the final analysis. The covariates considered in the analysis were age, gender, education, and APOE4 (Apolipoprotein E4 copy number), as outlined in Table S7 available online at http://bib.oxfordjournals.org/ in the supplemental file.

The birth weight data

We also analyzed a human birth weight dataset in the Thai population from the Gene Environment Association Studies initiative GENEVA founded by the trans-NIH (National Institute of Health) Genes, Environment, and Health Initiative (GEI). The dataset was obtained from dbGaP with the dbGaP accession number phs000096.v4.p1. The details can be found in the supplemental file due to space limitations.

Results

Results of simulation studies

We first conducted a series of simulation studies and compared the method’s performance with its counterparts. The simulation study included three cases that evaluate the performance of the method, considering small-scale discrete predictors, large-scale GWAS SNPs, and quantitative predictors (see the Statistical Methods section for the detailed simulation designs).

Results of Case I: simulation for the small-scale discrete predictors

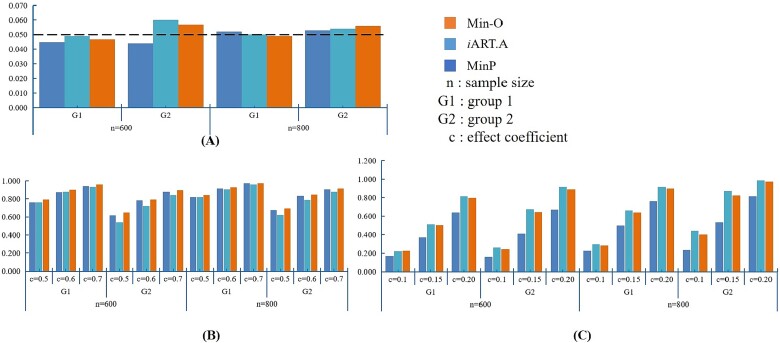
Figure 2A shows the type I error comparison between MinP, iART-A, and Min-O in Case I. The empirical type I error of Min-O can be effectively controlled in the two genes and across different sample sizes.

Figure 2.

Case I: empirical type I error and power comparison between iART-A, ART-A, and Min-O (omnibus test based on ART.A and MinP). (A) The type I error comparison between iART-A, ART-A, and Min-O; (B) the power comparison between iART-A, ART-A, and Min-O under the DSSM; and (C) the power comparison between iART-A, ART-A, and Min-O under the CWSM.

Figure 2B and C depicts the results of power comparison by MinP, iART-A, and Min-O. In the DSSW model, the power of the omnibus test, Min-O, is higher than that of MinP or iART-A and is similar to the most powerful one, iART-A, in the CWSM. The LD plot of CAMTA1 (G1: group1) reveals that 9 out of 15 signals are located within one block where there is a high correlation between SNPs. Consequently, the difference in power between MinP, iART-A, and Min-O is minimal, which aligns with the simulation results. However, the LD structure of the first 50 SNPs in CSMD1 (G2: group2) does not exhibit a strong correlation, resulting in a relatively larger difference in power between MinP, iART-A, and Min-O, compared to CAMTA1. To summarize, our proposed omnibus test, Min-O, is anticipated to yield comparable or superior performance to MinP and iART-A, likely depending on the LD structure between the SNPs and their effects [48]. This suggests that Min-O has practical applicability in real-world data analysis.

Results of Case II: simulation with the genome-wide SNP data

The comparison results of power between our proposed methods and SKAT are shown in Table 1. Overall, our method outperformed the SKAT, especially for the gene CSMD1 which is high dimensional (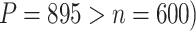. Interestingly, SKAT with the linear kernel has no power to detect the two genes, while SKAT with the IBS kernel has reasonable power to detect gene SGCZ (a relatively low-dimensional gene compared to CSMD1). In terms of computational time, our method is comparable with SKAT with the linear kernel but is much faster than SKAT with the IBS kernel. The simulation results demonstrate the benefit of our method in a high-dimensional setup.

Table 1.

The power comparison between our proposed methods and SKAT

Methods	c1 = 0.7 & c2 = 0.2a		c1 = 1.0 & c2 = 0.3		c1 = 1.5 & c2 = 0.5		Elapsed time* (minutes)
	CSMD1	SGCZ	CSMD1	SGCZ	CSMD1	SGCZ
MinP	0.224	0.309	0.763	0.956	0.998	1	4.5
iART.A	0.295	0.366	0.898	0.960	1	1
Min-O	0.303	0.380	0.898	0.974	1	1
SKAT (L)	0	0	0	0	0	0	2.4
SKAT (IBS)	0	0.014	0	0.482	0.002	1	70

L denotes the linear kernel, and IBS denotes the IBS kernel.

^ac₁ and c₂ refer to SNP effects for gene CSMD1 and SGCZ, respectively (see simulation Case II in the supplemental file for details).

^bElapsed time is the average time for a single simulation based on the genome-wide data.

Results of Case III: simulation with quantitative predictors

The detailed results for Case III can be found in the supplemental file. From the results, we can see that our proposed iART-A effectively controls the type I error rate and demonstrates higher power than ART-A across various scenarios and disease model assumptions. Thus, it is safe to apply iART-A in real-world applications.

In conclusion, the omnibus test simulation results indicate that the omnibus test consistently exhibits comparable or superior power compared to the best-performing individual method under the respective model, particularly when the within-group correlation is high (e.g. ρ = 0.9). These findings from the power simulation suggest that the omnibus approach can be reliably applied in practice, regardless of the underlying disease model.

Results from real data analyses

We applied our proposed method to two real data; one is obtained from the ADNI database (adni.loni.usc.edu) and the other is a human birth weight dataset in the Thai population from the Gene Environment Association Studies initiative GENEVA founded by the trans-NIH GEI. A detailed analysis of the birth weight data can be found in the supplemental file.

In the ADNI data, we chose the volume of ventricles as the response variable to demonstrate the implementation of our method. Initially, we selected the top 30 000 most significant predictors, including covariates and SNPs, using a HOLP screening procedure to address computational constraints. Next, we obtained the P-values of these 30 000 predictors using a desparsified LASSO approach. Subsequently, we identified two covariates, age (P = 3.83e-13) and gender (P = 6.97e-18), that were associated with the volume of ventricles. Furthermore, we mapped the remaining 29 998 candidate SNPs to 7170 genes and obtained the P-values of these genes using MinP, iART-A, and Min-O methods. Finally, we corrected the P-values of the 7170 genes using FDR at the gene level. We identified two significant genes ABCA1 and GRIP1 after the FDR adjustment (the Benjamini–Hochberg procedure). There are 18 SNPs in gene ABCA1 and two SNPs in GRIP1. For ABCA1, the FDR-adjusted P-values for MinP, iART-A, and Min-O are 1, 1e-16, and 1e-16, respectively, while for GRIP1, the respective FDR adjusted P-values are 1e-16, 1, and 1e-16. The list of the SNP ID in each gene along with their P-values using the desparsified LASSO and the decorrelation method is shown in Table 2. Within ABCA1, there are many significant SNPs that meet the CWSM assumption, whereas there is only one significant SNP within GRIP1 that meets the DSSW assumption. When only focusing on one method (MinP or iART-A), one gene will be missed. However, the omnibus test can identify both genes regardless of the underlying functional mechanism, showing the power and robustness of the omnibus testing procedure. This is also consistent with the simulation results.

Table 2.

List of genes and SNPs associated with the volume of ventricles

Gene (ensemble ID)	SNP ID	P DS-LASSO	P DOT
ABCA1 (ENSG00000165029)	rs4149339	0.4012	0.3914
	rs4149338	0.7020	0.8793
	rs2066716	0.7302	0.6412
	rs2254884	0.4389	0.4708
	rs2253304	0.4337	1e-16
	rs2253182	0.8662	0.5189
	rs2253175	0.9215	1e-16
	rs2253174	0.9215	1e-16
	rs2253172	0.8365	1.95e-07
	rs2230806(R219K)	0.5263	1e-16
	rs2243313	0.9586	1e-16
	rs2482420	0.9586	1e-16
	rs2487059	0.8355	0.6218
	rs2230805	0.7343	0.6511
	rs4149281	0.2917	0.3083
	rs2575878	0.2172	0.2254
	rs3905001	0.8760	0.9112
GRIP1 (ENSG00000155974)	rs7300761	0.1507	0.3179
	rs10878485	1.01e-04	1.47e-04

P _DS-LASSO: P-values of SNPs inferred via the desparsified-LASSO.

P _DOT: P-values of SNPs after decorrelation with the orthogonal transformation.

The same data were analyzed with SKAT, and we did not identify any significant genes after the FDR control. Methods for gene-level analysis with summary statistics have been proposed, e.g. MAGMA [49]. We also compared the performance of our omnibus test with these methods using summary statistics. We first did a marginal regression with each SNP as a regressor and recorded the summary statistics such as the effect size, standard error, and P-value. We then input these summary statistics into one of the popular software, MAGMA, to get the gene-level P-values. For the ADNI data, we analyzed the ventricle volume, resulting in P-values for all 299 763 SNPs. We then entered these SNP P-values into MAGMA and obtained the P-values for the 13 043 genes mapped by all 299 763 SNPs. We adjusted the P-values of the 13 043 genes using FDR at the gene level. We did not identify any significant genes using the MAGMA software as revealed by the gene-level Q-Q plot (see Fig. S6 available online at http://bib.oxfordjournals.org/ in the supplemental file).

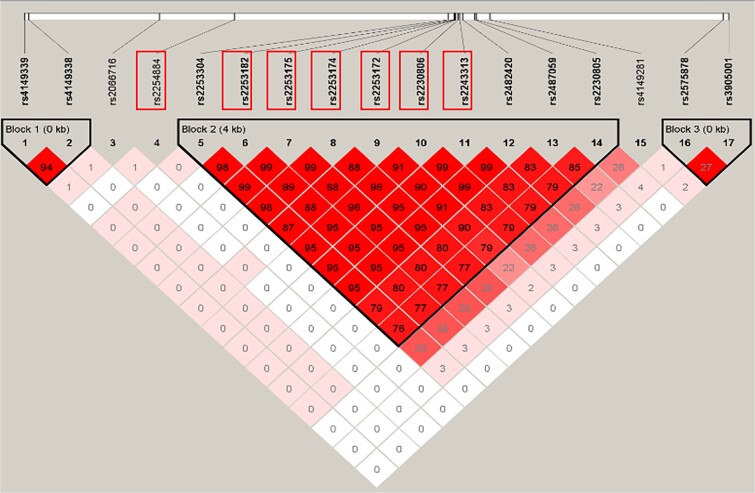
We examined the LD structure of the SNPs in gene ABCA1 to gain further insights into their significance. As shown in Fig. 3, the LD plot of the 17 SNPs in ABCA1 revealed strong correlations between SNPs in different blocks. As such, none of the SNPs were significant with the desparsified LASSO method. However, after applying decorrelation by orthogonal transformation, seven SNPs were found to be significant. These seven SNPs were all in block 2, which includes the R219K polymorphism (rs2230806) that has been reported to be associated with AD [50]. The rs2230806 (G) allele encodes arginine (R), while the (A) allele encodes lysine (K). This exonic polymorphism has been shown to influence cerebrospinal fluid cholesterol [51–54]. Previous studies have also reported a significant association with the G allele of rs2230806 in the absence of the ApoE4 allele [50], while the association with the A-allele of rs2230806 was significant in the presence of the APOE4 allele. The strong LD between the SNPs may explain why the desparsified LASSO method failed to produce significant results.

Figure 3.

LD plot of SNPs in ABCA1. The rectangle-highlighted SNPs are significant ones.

ABCA1 has been identified as a novel risk factor associated with AD [51–54]. Currently, ABCA1 and ApoE are the subject of intense research for AD treatment [55]. ABCA1 plays a role in cholesterol homeostasis and is involved in the pathophysiology of neurological diseases characterized by the accumulation of proteins in brain cells, such as traumatic brain injury, stroke sequelae, Parkinson’s disease, and AD [55].

The PDZ protein–protein interaction domain plays a crucial role in enabling efficient synaptic transmission in the brain. The dysfunction of synaptic transmission is believed to be the underlying cause of many neuropsychiatric and neurodegenerative disorders, including AD. Gene GRIP1 has been identified as one of the most important differentially expressed and topologically significant proteins in this protein–protein interaction network [56].

We also analyzed the volume of fusiform, entorhinal, and middle temporal gyrus, and the results are summarized in supplemental Tables S8–S10 available online at http://bib.oxfordjournals.org/.

Conclusion and discussion

Genome-wide association studies (GWASs) have become increasingly important in identifying genetic variants associated with complex diseases. However, analyzing GWAS data poses several challenges due to high-dimensional data, LDs between markers, and nonlinearity in the relationship between genotype and phenotype. In this work, we proposed an omnibus approach that overcomes some of these challenges by leveraging two disease models: CWSM and DSSM.

The proposed omnibus approach is designed to test gene set associations while being robust to the misspecification of analytical models. Specifically, we proposed an iART-A method, which is an improved version of the ART-A method and applicable to the CWSM model. This approach can overcome the limitations of the ART-A method by integrating P-values calculated under different threshold values based on the Cauchy transformation. Under the DSSM assumption, we proposed to use the minimum P-value method (MinP) while incorporating the desparsified LASSO method, which works under a high-dimensional regression framework. The MinP method can detect the overall association of a gene set by taking the minimum P-value among all the SNPs within the set. The desparsified LASSO can further reduce the bias of the estimated regression coefficients and provide better power in detecting the gene set association. To assess the significance of the minimum P-value, we leveraged the asymptotic normality results with the desparsified LASSO and developed a computationally efficient resampling approach.

We integrated the two approaches, iART-A and MinP, and developed an omnibus method, Min-O, to obtain a robust P-value, regardless of the underlying disease model. We evaluated the proposed omnibus testing framework through extensive simulation studies, which showed that it effectively controls the type I error rate and performs well in various simulation scenarios. Notably, in scenarios with extremely strong correlations within a group, the omnibus test outperformed the marginal approach, as observed under the DSSW model assumption. The results indicate that the proposed approach is robust and powerful in detecting gene set associations in high-dimensional data.

The impact of misspecifying a GWAS model can be significant, potentially resulting in reduced statistical power, as demonstrated in our simulation studies. This served as the impetus for proposing an omnibus test that aggregates information from different disease models in this work. Given the inherent uncertainty in identifying the true disease model during real data analysis, this approach offers a more robust solution. When sample populations are confounded by ancestry, the issue of related samples arises, posing a challenge to GWAS methods relying on the assumption of unrelated individuals. This confounding can manifest in various ways, leading to elevated false positives or false negatives in different scenarios. While the precise consequences of such confounding are not explicitly elucidated without extensive simulation studies, we acknowledge that this goes beyond the current study’s scope. To address these challenges, we suggest considering models built under quasi-likelihood rather than maximum likelihood, as they may offer a viable solution. This alternative approach holds promise in mitigating issues related to confounding and related samples, providing a potential avenue for refining GWAS analyses. We intend to explore and evaluate these effects in future research.

LASSO, also known as the L₁-norm regularization, is a commonly used method for variable selection in high-dimensional statistics. However, LASSO generates biased estimates due to shrinkage and hence cannot be directly used to quantify uncertainty. In contrast to LASSO, the regularized projection method, desparsified LASSO (or debiased LASSO), not only provides P-values for the penalized regression coefficients but also preserves the covariance matrix of these coefficients. This property allows us to efficiently adopt a DOT strategy in a high-dimensional setting, further improving the power of SNP-set analyses.

Both the HOLP screening procedure and the desparsified LASSO algorithm can handle a wider range of models beyond the one studied in this work. It is worth mentioning that the desparsified LASSO can be computationally expensive. Leveraging parallel computing with multiple cores has the potential to significantly enhance computational speed. In the simulation study (see the supplemental file) with GWAS SNP data, the run time for the desparsified LASSO after screening is quite scalable. The runtime of our proposed methods is ~4.5 min with n = 600 and the number of SNPs as 196 998, which is comparable with the SKAT method (their runtime with linear kernel and IBS kernel is 2.4 and 70 min, respectively). As for biobank-scale data, we are not sure about the computational cost associated with large samples. However, it is essential to note that the number of SNPs can be substantially reduced after the HOLP screening step. An alternative option to the LASSO projection is the ridge projection, which does not require any assumption on the fixed design (but does not reach the asymptotic Cramér–Rao efficiency bound) and is computationally less demanding than the desparsified LASSO [18]. The R package HDI also implements the bridge projection and bias correction under a high-dimensional setting.

In our proposed inference framework, the input data consists of individual-level genotype information, and the desired output is the P-value for each group (e.g. a gene or pathway). While summary statistics are commonly derived through marginal regression analysis (i.e. analyzing one SNP at a time), this approach may lead to biased estimations, particularly when LD is present between SNPs. To address this, we advocate for the use of multiple regression models, where the estimated SNP effect reflects the partial effect considering other SNPs in the model. Given the impracticality of fitting a multiple regression model with tens of thousands of SNPs, we suggest employing a screening procedure such as HOLP with a theoretically sure screening property to retain the true model. The number of SNPs can be substantially reduced after screening, allowing for the fitting of a multiple regression model with the remaining SNPs. However, due to LD and the dimension of the remaining SNPs, regular multiple regression may still yield inconsistent estimates. This issue can be addressed by fitting a desparsified LASSO regression model that addresses the bias issue and can obtain valid P-values and confidence intervals for statistical inference. The covariance matrix obtained through this procedure can be used in our decorrelation by orthogonal transformation (DOT) step to remove the effects caused by high LDs.

In practice, the relationship between a marker set and phenotype may not be linear. It is a challenging task to capture such nonlinear relationships. To address this challenge, we plan to incorporate kernel methods into our framework in the future. For instance, kernel principal component analysis can be utilized to extract kernel principal components for each marker set, and the inference of the marker set can be based on the P-values of these kernel principal components.

Key Points

• We focused on boosting the power of gene-set association analysis with high-dimensional SNP data and surveyed methods for ultrahigh dimensional feature screening, high-dimensional inference, P-value combination, and omnibus test.

• Focusing on two genetic effect theories of common variants, DSSM and CWSM, we developed an omnibus test under the high-dimensional inference procedure to assess gene-set association.

• The proposed improved augmented rank truncation (iART-A) test does not need to prespecify the threshold of truncation points and can automatically aggregate P-values.

• The proposed omnibus test approach (Min-O) further integrates the minimum P-value (MinP) and the iART-A method to achieve robust test results.

• The proposed method can be extended to other group-wise tests, such as pathway associations, and can incorporate weight information to further boost the testing power.

Funding

This work was supported, in part, by the National Natural Science Foundation of China (81872717 to H.Y.), the Education Department of Hebei Province (ZD2018022 to H.Y.), the Natural Science Foundation of Hebei province (H2019206558 to H.Y.), the opening foundation of Hebei Key Laboratory of Forensic Medicine (JYFY-23ZR013 to H.Y), and the Education Department of Hebei Province (ZD2022143 to X.G.).

Code availability

The code used for the analyses in this work is available on Github at https://github.com/HaitaoYang1978/Gene_set_HDI.