Abstract
This study employs computational chemistry to investigate the detailed mechanisms behind the dissolution of thermally activated clays, which are emerging as promising supplementary cementitious materials (SCM) for enhancing concrete properties and reducing carbon footprint. Specifically, the study employs a first-principles methodology for obtaining activation energies (ΔEa) involved in the dissolution of metakaolinite (MK) silicate units using NaOH and KOH activators. The investigation includes considerations of hydrolyzing oxo-bridging covalent bonds, van der Waals (vdW) interactions, and the influence of water molecules surrounding alkali cations. The study employs the enhanced dimer method within density functional theory (DFT) to propose four models for determining the activation energies required to break oxo-bridging bonds. The results demonstrate that KOH generally requires lower activation energies than NaOH, particularly when considering vdW interactions. They also highlight the lower activation energy required for commencing the dissolution of silicate units and emphasize the significance of the hydration shell around cations. The proposed methodology contributes to establishing a systematic database of atomistic activation energies, essential for atomistic kinetic Monte Carlo upscaling and mesoscopic forward dissolution rate calculations in clays. This holds relevance in understanding their reactivity within cementitious materials.
Introduction
Metakaolinite (MK) is the most important constituent of calcined clays due to its pozzolanic reactivity1,2 and is used in various applications in the construction industry.3−7 It is used as a supplementary cementitious material (SCM) for production of concrete and geopolymer-based8 materials. When used to replace from 5% up to 20% of the cement by weight, the resulting concrete is generally more cohesive and less likely to bleed, possesses higher compressive strength, reduces associated CO2 emissions and lowers porosity, and demonstrates greater resistance against attacks by sulfates, chlorides, and other aggressive substances such as minerals and organic acids. MK is derived from dehydroxylation (DHX) of kaolinite9 within a temperature range of 500–700 °C. These meta-clay-like materials and industrial byproducts are rich in reactive silica and aluminum, with their reactivity mainly governed by their dissolution rates. This is also driving the ecological efficiency in terms of optimized cement replacement and geopolymers for the lowest carbon footprint.
In cement-based and alkali activated geopolymer applications, MK exhibits higher initial pozzolan reactivity than other pozzolans, enhancing the performance of cementitious materials. However, the primary challenge in using calcined clay to partially replace cement or as alternative cement-free binders is managing the variation in their composition and its effect on hydration or geopolymerization reactivity. Hollanders et al.2 investigated the pozzolanic reactivity of eight reference clay samples (four kaolinitic, three smectitic, and one illitic) in cementitious materials, calcining them at temperatures between 500 and 900 °C. Kaolinitic clays (K1, K2, K3, and H1) showed high reactivity across a broad temperature range, with higher ordered kaolinites (K1 and K2) exhibiting lower reactivity at 500 °C compared to medium and low ordered kaolinites (K3 and H1). Na- and Ca-montmorillonite (S1 and S2) demonstrated optimum calcination temperature at 800 °C, with reactivity decreasing at higher temperatures (900 °C). The optimal activation temperature for illitic clay is 900 °C; however, even at this temperature, only partial amorphization occurs, limiting its reactivity. The pozzolanic activity ranking is as follows: kaolinitic clays > Ca-montmorillonite > Na-montmorillonite > illite > hectorite. Werling et al.10 reported on the amount of various phases formed during geopolymerization by measuring metakaolinite solubility and amorphous of SiO2 in NaOH solution at diverse concentrations. An increase in the solubility of metakaolinite calcined at 700 °C was observed with higher NaOH concentrations. In metakaolinite, Si solubility was below 5% after 24 h and even after 7 days in 0.01 and 0.1 mol/L NaOH solutions. However, in 10.79 mol/L NaOH, Si solubility for the identical metakaolinite reached 65% after 24 h and 80% after 7 days.
The atomistic computational approach has demonstrated its effectiveness in comprehending the microstructure of cement clinker,11,12 hydrated cement phases,13,14 and glasses,15 including atomistic configurations’ relationships to their reactivity. Density functional theory (DFT),16−20 molecular dynamic (MD),21−25 and ab initio molecular dynamics (MD) computations are widely used in chemistry and materials science to explore properties like reaction mechanisms and mechanical characteristics.26,27 Izadifar et al.12,14 explored the mesoscopic forward dissolution rate of β-C2S cement clinker and portlandite under far-from-equilibrium conditions. Their study relied on atomistic activation energies (ΔEa) obtained using the MetaD molecular dynamics (MD) computational method.11,13 In another study, Izadifar et al.28 examined the nucleation mechanism of alkaline aluminosilicate gels, including metakaolinite. They based their analysis on the binding energies of four different monomer species29 using the coarse-grained Monte Carlo (CGMC) approach. Martin et al.30 investigated the dissolution of quartz using a kinetic Monte Carlo (KMC) upscaling approach. They reported the formation of each pit, the mesoscopic dissolution rates, and the macroscopic activation energy dependence with ΔG. Most recently, Coopamootoo and Masoero31 investigated the dissolution of tricalcium silicate at screw dislocation within finite grains with various facet orientation combinations but without any crystallographic defects. They showed that dissolution occurs through the consumption of kink particles in a layer-by-layer manner, starting at low-coordinated sites found at the intersections of facets such as edges and corners, and that these sites exhibit similar dissolution rates. The dissolution rates of finite-sized crystals without crystallographic defects are linearly related to β, consistent with traditional transition state theory (TST). Chen et al.32 also carried out an integrated dissolution model for alite (tricalcium silicate)33 to deal with various hydrodynamics conditions on dissolution rates, ranging from low to high. They combined surface topography and ion transport using a kinetic Monte Carlo model, which addresses both dilute and near-saturated conditions. Their simulation results generally align well with the existing references. Valencia et al.34 recently used coarse-grained Monte Carlo simulations with octree cells to study geopolymer nucleation at different pH values. Schliemann and Churakov35,36 employed an ab initio simulation method to study the atomistic mechanisms of pyrophyllite dissolution on the (010) surface and the (110) edge surface. Kurganskaya and Luttge37 employed a kinetic Monte Carlo approach to investigate the dissolution of phyllosilicates, predicting the temporal surface evolution dynamics based on the kinetics of elementary surface reactions. Ayuela et al.38 provided compelling evidence of the crucial role certain ionic species play in forming silicate chains within cementitious materials through first-principles simulations. Their results indicated that adding nanosilicate can lead to the development of higher-performance cement-based materials. Dupius et al.39 also employed metadynamics to demonstrate that the depolymerization of cement silicate skeletons involves hydroxylation followed by bond-breaking, a finding confirmed in this study. Their research recommended that the dissolution of these minerals occurs via the formation of etch pits at opened screw dislocation cores through the movement and coalescence of stepwaves.
The dimer method is a method used to optimize transition states.40 In VASP calculations, the improved dimer method (IDM) by Heyden et al.41 is implemented, which is a technique employed for transition state optimization. The computed minimum energy pathway illustrates how atoms evolve between initial and final states, with the maximum potential energy along the dimer axis and minimized along all other directions representing the activation energy of the process under investigation. Izadifar et al.42 lately utilized the improved dimer method (IDM) and the transition-state theory (TST) through density functional theory (DFT) to compute the atomistic activation energies necessary for the dissolution of MK silicate tetrahedra units by water molecules, excluding the contribution of van der Waals (vdW) interactions under far-from-equilibrium conditions. It has been noted that the atomistic activation energy required to break the oxo-bridging bond to a silicate neighbor is greater than that to an aluminate neighbor, which is attributed to ionic interactions. It has been verified by a single imaginary frequency associated with the reaction coordinate to determine the atomistic activation energies (energy barrier) involved in the dissolution of silicate tetrahedra on the MK surfaces of 001 and 001̅. Cheng et al.43 recently employed the dimer method to identify transition states, which were subsequently confirmed to have only one imaginary vibrational frequency through DFT calculations. To identify the transition states of the reaction pathway for hydrogen evolution reactions (HERs) on pyrrolic-Ru, pyridinic-Ru (111), and carbon-Ru surfaces under both acidic and alkaline conditions at equilibrium, Chen et al.44 also employed the dimer method in DFT calculations.
Understanding the dissolution mechanism of metakaolin is crucial for optimizing its use as a supplementary cementitious material and/or as a cement-free geopolymer binder. Insights into this process enable the development of more efficient and sustainable construction materials, enhancing their technical and environmental performance. The following fundamental research questions need to be answered to enable understanding via a bottom-up computational approach: What are the atomistic energy barriers (activation energies, ΔEa) at the transition state for the hydrolysis reaction, elucidating NaOH vs KOH, vdW interactions, and hydration shell effects? How does the energy change in reaction enthalpy vary under far-from-equilibrium conditions for the hydrolysis reaction of silicate tetrahedra’s (SiO44–) dissolution in MK? The main objective of this study is to compute the atomistic ΔEa at the transition state for the hydrolysis reaction using the IDM method and to determine the energy change in the reaction enthalpy under far-from-equilibrium conditions. The computations, based on TST, aim to determine the atomistic reaction rates for silicate tetrahedra (SiO44–) dissolution in MK, incorporating two activators of NaOH and KOH with and without the contribution of vdW interactions and the hydration shell around cations. Moreover, to facilitate a comparison of the calculated ΔEa values derived from high-alkaline environments (NaOH and KOH), we have also computed the ΔEa values for the hydrolysis reaction, considering the presence of water molecules with the contribution of vdW interactions. The results from this study will fill the gap in data required for performing mesoscopic forward dissolution rate calculations, essential for the atomistic kinetic Monte Carlo (KMC) upscaling approach.
Methodology and Computational Models
Computational Details
The density functional theory (DFT)45 quantum mechanical modeling method was applied using the Vienna ab initio simulation package (VASP).46−50 Electron–ion interactions were defined using the projector augmented wave (PAW) method and pseudopotential.51 For electron exchange and correlation functionals, the generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) parametrization was used.52 The Brillouin zone sampling was conducted by a well-converged k-sampling equivalent to a 1 × 1 × 1 Monkhorst–Pack k-points mech-size for the entire system.53 Structural relaxations employed a well-converged plane-wave cutoff energy of 400 eV. The convergence criterion for electronic self-consistent cycles was set to 1 × 10–3 eV, and ions were relaxed until forces were below 1 × 10–3 eV/Å. van der Waals interactions were calculated using the Grimme DFT-D3 dispersion energy correction with a zero-damping function in the VASP package.54 Structural analyses of our models were performed using three-dimensional visualization software of VESTA.55
To effectively discover transition states in chemical reactions, a combination of interpolation methods and local saddle-point search algorithms is utilized. Interpolation methods, like the growing-string method and the nudged-elastic band, approximate the minimum-energy pathway and provide a good initial guess for transition states and the imaginary mode linking reactant and product states. However, interpolation methods often involve a limited number of configurations and show slow convergence near the minimum-energy pathway. Therefore, local methods such as partitioned rational function optimization or minimum-mode-following techniques (e.g., dimer or Lanczos methods) are essential to accurately reach the transition state. Henkelman and Jónnson40 proposed a modified version of the original dimer method, reducing the number of gradient calculations per cycle from six to four or three gradients and one energy calculation, thereby enhancing algorithm performance, especially on noisy quantum-chemical potential energy surfaces. Comparisons between this improved dimer method and the well-established partitioned rational function optimization methods for postinterpolation transition state identification showed that the improved dimer method is highly efficient for medium to large systems. It often succeeds where partitioned rational function optimization methods fail to converge.41
Structural Preparation
The surface energy (γ)21 for low Miller index facets has been computed for different surface orientations of 001, 010, and 100. The surface energies of 0.0057, 0.116, and 0.18 eV/Å were computed for the surface orientations of 001, 100, and 010, respectively. Therefore, it is evident that the surface orientation of 001 is the most exposed and reactive surface in layered clay-derived materials like MK. The presented metakaolinite (MK) structure belongs to the 001 and 001̅ surfaces of the crystal structure and has been simulated for dissolution of the silicate tetrahedra (SiO44–) including semiprotonated (hydrogen-bonded) oxygen ions bonded to the silicate neighbors, as illustrated in Figure 1. The dissolution of silicate tetrahedra on the MK 001 and 001̅ surfaces depends on different neighboring atoms, representing bonding via the bridging oxygen between silicate and aluminum units. It is essential to note that Figures 1A and 1B illustrate the contribution of NaOH and KOH activators without hydration shell contribution around each activator on the MK surfaces of 001 and 001̅. Figure 1C shows the initial structure of the reactant, including a water molecule as the absorbent on the MK surfaces of 001 and 001̅. Table 1 exhibits four models (models 1–4) for dissolution of the silicate tetrahedra (SiO44–), labeled as S0S0, A0S0, A0S1, and S0A1, respectively. Models 1 and 4, and models 2 and 3 represent the optimized geometric structures of reactants using NaOH or KOH activators on the MK surfaces of 001̅ and 001, respectively. Table 2 presents the total computations conducted to determine the energy barrier (activation energy) (ΔEa) of the hydrolysis reaction and the energy change of the reaction enthalpy (ΔH). These calculations consider both the presence and absence of the hydration shell surrounding cations as well as the contribution of van der Waals (vdW) interactions.
Figure 1.
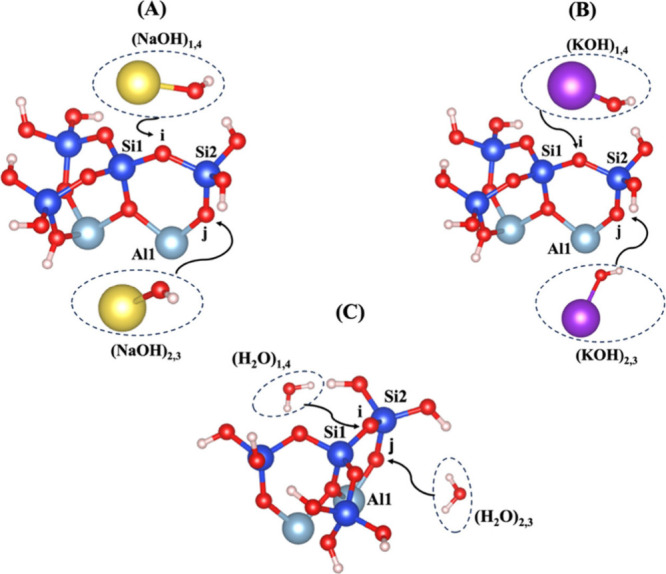
Illustration of different scenarios, resulting in dissolution of silicate tetrahedra (SiO44–) through (A) sodium hydroxide (NaOH), (B) potassium hydroxide (KOH), or (C) water (H2O), depending on the bridging oxygens bonded to the silicate and aluminate neighboring units. Silicon ions are shown in blue; aluminum cations, in light blue; oxygen ions, in red; hydrogen protons, in white; sodium cations, in yellow; potassium cations, in purple.
Table 1. Illustration of Four Scenarios Modeling Optimized Geometric Structures of Reactants Using NaOH and KOH Activatorsa.
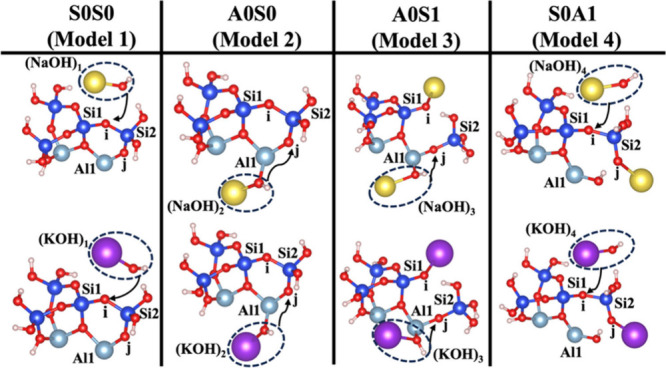
Models 1–4 are also labeled as S0S0, A0S0, A0S1, and S0A1, respectively.
Table 2. Total Various Computations Conducted Aimed to Determine ΔEa and ΔHa.
| DFT | vdW/hydration shell | vdW | hydration shell | excluding vdW/hydration shell |
|---|---|---|---|---|
| NaOH | yes | yes | yes | yes |
| KOH | yes | yes | yes | yes |
| H2O | no | yes | no | no |
These calculations utilized first-principles methods, including and excluding the influence of the hydration shells surrounding cations and the contribution of van der Waals (vdW) interactions. This analysis was applied to NaOH, KOH, and H2O as absorbents on the MK surfaces of 001 and 001̅, employed for all four models.
Results and Discussion
DFT Results without Contribution of Hydration Shell
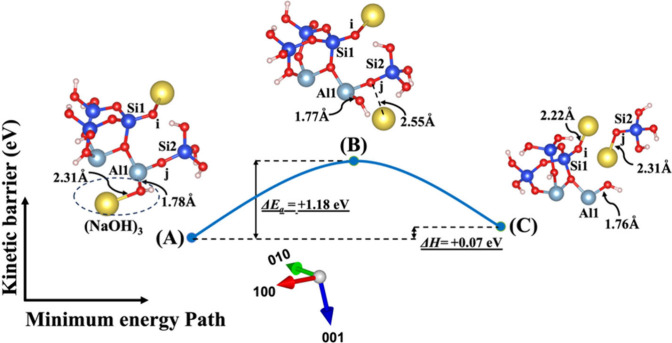
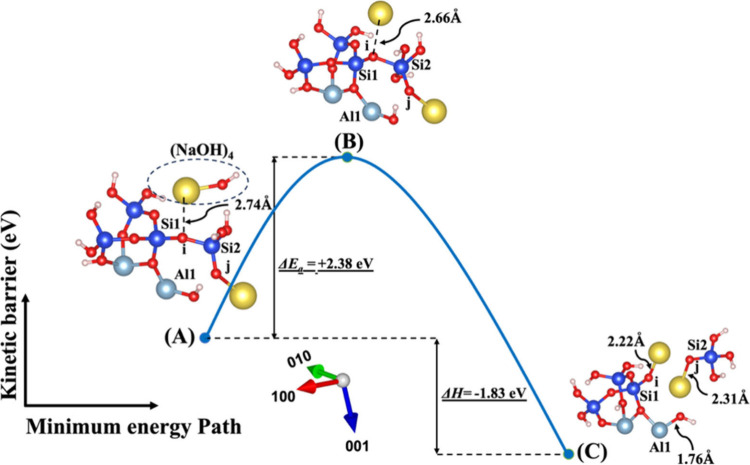
Dissolution of silicate tetrahedra (SiO44–) in MK depends on the nature of their neighboring units, which exhibit distinct bonding characteristics via bridging oxygen with neighboring silicate ions and aluminum cations, as illustrated in Figure 1. This process has been promoted using two activators, NaOH and KOH, both with and without the involvement of the vdW interaction, as shown in Figures 1A and 1B, respectively. Additionally, Figure 1C illustrates the impact of water molecules, which contribute solely through vdW interactions. As depicted in Figures 1A–1C, the initial scenario (model 1 or S0S0) occurs when the bridging oxygen (i), linked to the adjacent silicate neighbor (Si1), undergoes protonation due to the influence of cations from any activator, e.g., NaOH and KOH, as depicted in Figures 2 and 3, respectively. The second scenario (model 2 or A0S0) entails that the bridging oxygen (j) bonded to the neighboring silicate (Si2) is protonated by a cation, as shown in Figures 4 and 5. In the third scenario (model 3 or A0S1), the optimized geometry structure of the product obtained from the first scenario (model 1C) is used as an optimized geometry structure of reactant (model 3A), involving the dissolution of the silicate tetrahedra monomer through the protonation of the bridging oxygen (j) bonded to the silicate neighbor (Si2) by cations, as depicted in Figures 6 and 7. In the fourth and last scenario (model 4 or S0A1), the optimized geometry structure of the product obtained from the second scenario (model 2C) is exerted as an optimized geometry structure of the reactant (model 4A), involving the protonation of the bridging oxygen linked to the silicate neighbor (Si1) by a cation, as shown in Figures 8 and 9.
Figure 2.
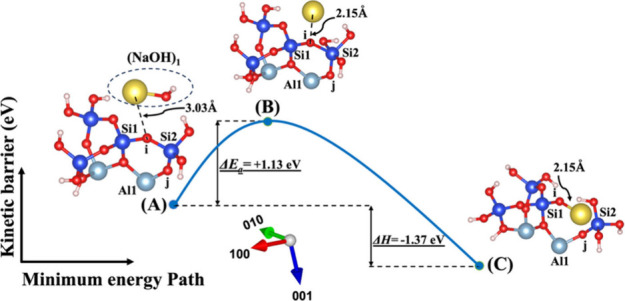
Model 1. (A) The optimized geometric structure of the reactant, including the (NaOH)1 molecule as the absorbent on the MK surface (001̅) with the contribution of vdW interactions (Table S1) for breaking of the bridging oxygen (i) bonded to the silicate neighbor (Si2). (B) The transition state was identified at the saddle point using the improved dimer method. (C) The optimized geometric structure of the product after full saturation of the bridging oxygen (i) with sodium cations (ionic bond) bonded to the silicate neighbor (Si1). The energy barrier (activation energy) of the hydrolysis reaction (ΔEa) and the energy change of reaction enthalpy (ΔH) were obtained from first-principles calculations.
Figure 3.
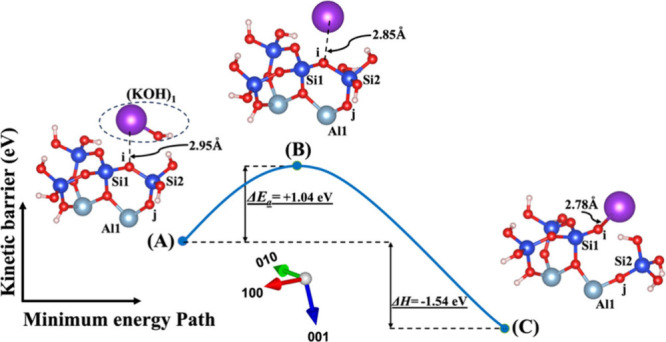
Model 1. (A) The optimized geometric structure of the reactant, including (KOH)1 molecules as the absorbent on the MK surface (001̅) with the contribution of vdW interactions (Table S3) for breaking of the bridging oxygen (i) bonded to the silicate neighbor (Si2). (B) The transition state was identified at the saddle point using the improved dimer method. (C) The optimized geometric structure of the product after full saturation of the bridging oxygen (i) with potassium cations (ionic bond) bonded to the silicate neighbor (Si1). The energy barrier (activation energy) of the hydrolysis reaction (ΔEa) and the energy change of reaction enthalpy (ΔH) were obtained from first-principles calculations.
Figure 4.
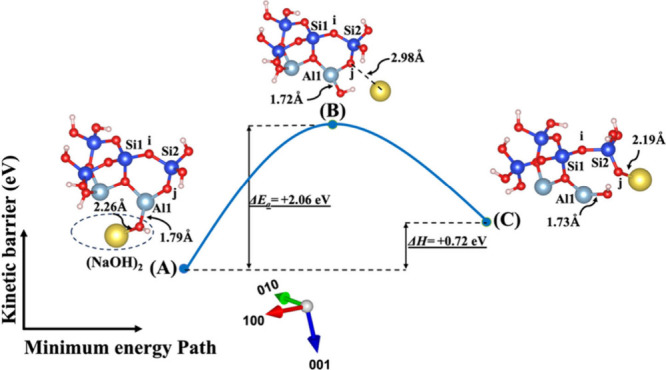
Model 2. (A) The optimized geometric structure of the reactant, including (NaOH)2 molecules as the absorbent on the MK surface (001) with the contribution of vdW interactions (Table S1) for breaking of the bridging oxygen (j) bonded to the aluminum neighbor (Al1). (B) The transition state was identified at the saddle point using the improved dimer method. (C) The optimized geometric structure of the product after full saturation of the bridging oxygen (j) with sodium cations (ionic bond) bonded to the silicate neighbor (Si2). The energy barrier (activation energy) of the hydrolysis reaction (ΔEa) and the energy change of the reaction enthalpy (ΔH) were obtained from first-principles calculations.
Figure 5.
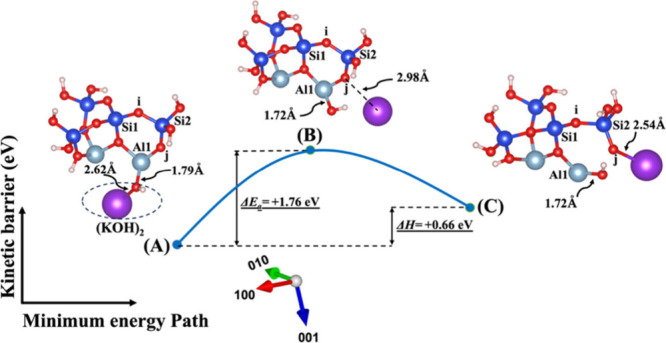
Model 2. (A) The optimized geometric structure of the reactant, including (KOH)2 molecules as the absorbent on the MK surface (001) with the contribution of vdW interactions (Table S3) for breaking of the bridging oxygen (j) bonded to the aluminum neighbor (Al1). (B) The transition state was identified at the saddle point using the improved dimer method. (C) The optimized geometric structure of the product after full saturation of the bridging oxygen (j) with potassium cations (ionic bond) bonded to the silicate neighbor (Si2). The energy barrier (activation energy) of the hydrolysis reaction (ΔEa) and the energy change of reaction enthalpy (ΔH) were obtained from first-principles calculations.
Figure 6.
Model 3. (A) The optimized geometric structure of the reactant, including (NaOH)3 molecules as the absorbent on the MK surface (001) obtained from model 1C (Figure 2) with the contribution of vdW interactions (Table S1) for breaking of the bridging oxygen (j) bonded to the aluminum neighbor (Al1). (B) The transition state was identified at the saddle point using the improved dimer method. (C) The optimized geometric structure of the product after full saturation of the bridging oxygens (i, j) with two sodium cations (ionic bond) bonded to the silicate neighbors (Si1, Si2). The energy barrier (activation energy) of the hydrolysis reaction (ΔEa) and the energy change of reaction enthalpy (ΔH) were obtained from first-principles calculations.
Figure 7.
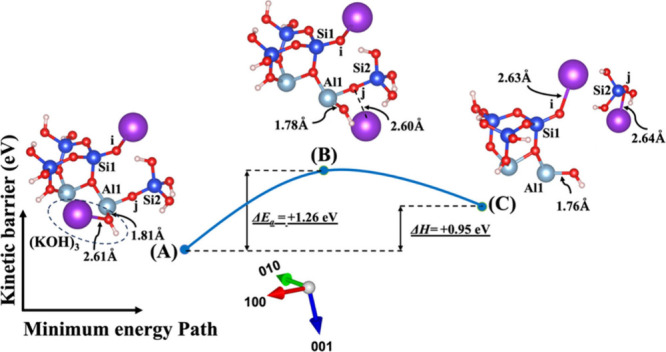
Model 3. (A) The optimized geometric structure of the reactant, including (KOH)3 molecules as the absorbent on the MK surface (001) obtained from model 1C (Figure 3) with the contribution of vdW interactions (Table S3) for breaking of the bridging oxygen (j) bonded to the aluminum neighbor (Al1). (B) The transition state was identified at the saddle point using the improved dimer method. (C) The optimized geometric structure of the product after full saturation of the bridging oxygen (i, j) with two potassium cations (ionic bond) bonded to the silicate neighbors (Si1, Si2). The energy barrier (activation energy) of the hydrolysis reaction (ΔEa) and the energy change of reaction enthalpy (ΔH) were obtained from first-principles calculations.
Figure 8.
Model 4. (A) The optimized geometric structure of the reactant, including (NaOH)4 molecules as the absorbent on the MK surface (001̅) obtained from model 2C (Figure 4) with the contribution of vdW interactions (Table S1) for breaking of the bridging oxygen (i) bonded to the silicate neighbor (Si2). (B) The transition state was identified at the saddle point using the improved dimer method. (C) The optimized geometric structure of the product after full saturation of the bridging oxygens (i, j) with two sodium cations (ionic bond) bonded to the silicate neighbors (Si1, Si2). The energy barrier (activation energy) of the hydrolysis reaction (ΔEa) and the energy change of reaction enthalpy (ΔH) obtained from first-principles calculations.
Figure 9.
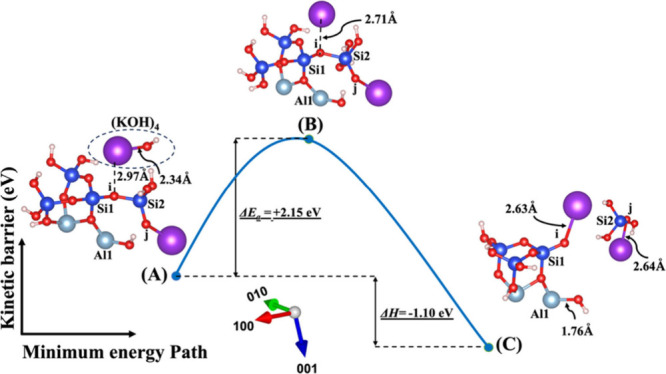
Model 4. (A) The optimized geometric structure of the reactant, including (KOH)4 molecules acting as the absorbent on the MK surface of (001̅) obtained from model 2C (Figure 5) with the contribution of vdW interactions (Table S3) for breaking of the bridging oxygen (i) bonded to the silicate neighbor (Si2). (B) The transition state was identified at the saddle point using the improved dimer method. (C) The optimized geometric structure of the product after full saturation of the bridging oxygen (i, j) with two potassium cations (ionic bond) bonded to the silicate neighbors (Si1, Si2). The energy barrier (activation energy) of the hydrolysis reaction (ΔEa) and the energy change of reaction enthalpy (ΔH) were obtained from first-principles calculations.
In recent study conducted by Liu et al.,56 it was observed that the oligomerization of poly silicic acid molecules occurs through lateral attacks accompanied by simultaneous proton transfer from the incoming molecule. This process leads to the formation of 5-coordinated silicon species as the transition state, ultimately leading to the release of a water molecule from the poly silicic acid structure. Hence, in our recent publication,42 we benchmarked our IDM against the results published by Liu et al., affirming the excellent repeatability of their findings. Our IDM implementation has proven to be an accurate method for evaluating the structure configurations and calculating the total energy of the new metakaolinite (MK) system at the saddle point. We have established four distinct models (scenarios) for the dissolution of silicate tetrahedra (SiO44–) in MK, each incorporating a different activator. The computation results have been reported in Tables S1–S5, corresponding to hydrolysis by NaOH and KOH activators with and without the inclusion of van der Waals (vdW) interactions as well as in the presence of water molecules as an activator with the contribution of vdW interactions, respectively. Based on the computed energies at the reactant, transition state (TS), and product for each model as outlined in the tables, the results include the ΔEa for the hydrolysis reaction in both eV and kJ/mol. Additionally, the tables provide ΔH reported in eV and kJ/mol for each respective scenario.
The first scenario represents model 1, depicted in Figures 2 and 3, including (NaOH)1 and (KOH)1 molecules as absorbents on the MK surface (001̅) with contribution of vdW interactions for the breaking of the bridging oxygen (i) bonded to the silicate neighbor (Si2). The initial optimized structure (Figure 2A), which incorporates NaOH as the activator, reveals that the sodium cation is positioned 0.08 Å farther away from the bridging oxygen of (i) in comparison to the potassium cation in the KOH activator (Figure 3A). In contrast, at the transition state, the sodium cation approaches the bridging oxygen (i) more closely compared to the potassium cation. Simultaneously, the hydroxyl (OH) from NaOH or KOH bonds to the neighboring silicate ion (Si2), leading to the creation of a trigonal-bipyramidal silicate structure with 5-fold coordination. Upon achieving the optimized geometric structure of the product, the bridging oxygen (i) breaks from Si2, resulting in the formation of silicate tetrahedra with 4-fold coordination for Si2. Additionally, the bridging oxygen (i) becomes saturated with the neighboring Na or K cations. In contrast to the initial structure, the ground state structure, obtained as the optimized geometry, reveals that the sodium cation (Figure 2A) is positioned 0.63 Å closer to the bridging oxygen (i) in comparison to the potassium cation in the KOH activator (Figure 3A).
Figures 4 and 5 illustrate the second scenario, referred to as model 2, which includes (NaOH)2 and (KOH)2 molecules as absorbents on the MK surface (001). This model considers the contribution of vdW to break the bridging oxygen (j) bonded to the aluminum neighbor (Al1). The distribution of electron density within the molecule, influenced by the electronegativity of the cations, potentially affects bond lengths, resulting in a shorter bond length for the Na cation (2.26 Å) due to its higher electronegativity with respect to OH compared to the K cation (2.62 Å) in the initial optimized structure. At the transition state, the OH group approaches Al1 by 0.07 Å (from 1.79 to 1.72 Å) for both systems, as depicted in Figures 4B and 5B. Additionally, both sodium and potassium cations approach the bridging oxygen (j) more closely. The optimized geometric structure of the product is achieved as the bridging oxygen (j) breaks from neighboring Al1, resulting in the formation of an ionic bond between the dangling oxygen (j) bonded to the silicate neighbor (Si2) and cations. Due to higher electronegativity, the Na cation also gets 0.35 Å closer to dangling oxygen (j) in comparison to the K cation.
The initial optimized structures are depicted in Figures 6A and 7A, representing the third scenario introduced as model 3, derived from model 1C in Figures 2 and 3, respectively. In both of these initial models, the Na cation exhibits a shorter bond length with OH due to higher electronegativity when compared to the K cation. Like model 2, at the transition state, the OH group approaches Al1, and both sodium and potassium cations draw closer to the bridging oxygen (j). The product’s optimized geometric structure is achieved as the bridging oxygen (j) debonded from the neighboring Al1, leading to the formation of an ionic bond between the dangling oxygen (j) bonded to the silicate neighbor (Si2) and the cation, along with the dissolution of SiO(OH)3– Na+. The fourth and final scenario presented as model 4, derived from model 2C in Figures 4 and 5, is denoted in Figures 8A and 9A, respectively. In this model, dissolution of SiO(OH)3– Na+ also takes place when the (NaOH)4 or (KOH)4 molecules as the absorbent break the bond between bridging oxygen (i) and Si2, leading to the full saturation of oxygen (i) with K or Na cations.
The ΔEa attained for the hydrolysis reaction in the presence of the KOH activator (precise values also presented in Tables S3 and S4) is more negative or less positive than NaOH (precise values also presented in Tables S1 and S2) in both systems, whether vdW interactions contribute or not. This indicates that the activation energy required for the KOH reactant to reach the transition state is lower than that for the NaOH reactant. In simpler terms, the KOH reactant undergoes the reaction more readily. In other words, it is kinetically more negative or less positive under certain conditions, compared to the NaOH reactant. The computed energy changes in reaction enthalpy (ΔH) indicate that model 1, which represents the breaking of the oxo-bridging bond to the silicate neighbor (Si2), and model 2, which represents the breaking of the oxo-bridging bond to the aluminum neighbor (Al1) in the presence of the KOH activator for both with and without the involvement of vdW interactions, exhibit more negative or less positive enthalpy energies in comparison to the NaOH reactant. On the other hand, models 3 and 4, representing the dissolution of SiO(OH)3–K+ in the presence of the KOH activator for both systems with and without vdW interactions (precise values also presented in Tables S3 and S4), demonstrate less negative or more positive enthalpy energies in comparison to the NaOH reactant (precise values also presented in Tables S1 and S2). Moreover, the highest (less negative or more positive) and lowest (more negative or less positive) ΔEa needed to initiate the reaction for breaking the bond are presented in models 4 and 1 with either an NaOH or KOH activator under conditions with and without the involvement of the vdW interactions (precise values also presented in Tables S1–S4), respectively. In contrast, models 4 and 1 with a water molecule under conditions with the involvement of vdW interactions, as presented in Table S5, exhibit the lowest (more negative or less positive) and the highest (less negative or more positive) activation energies, respectively.
DFT Results with Contribution of Hydration Shell
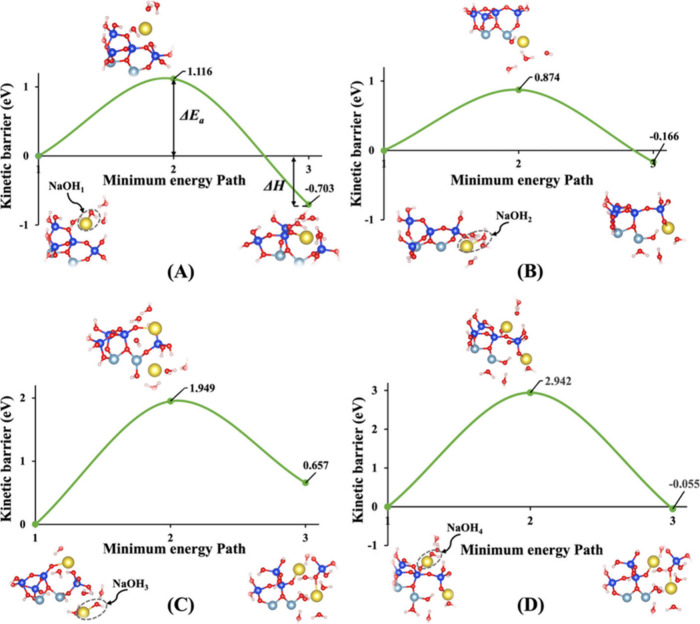
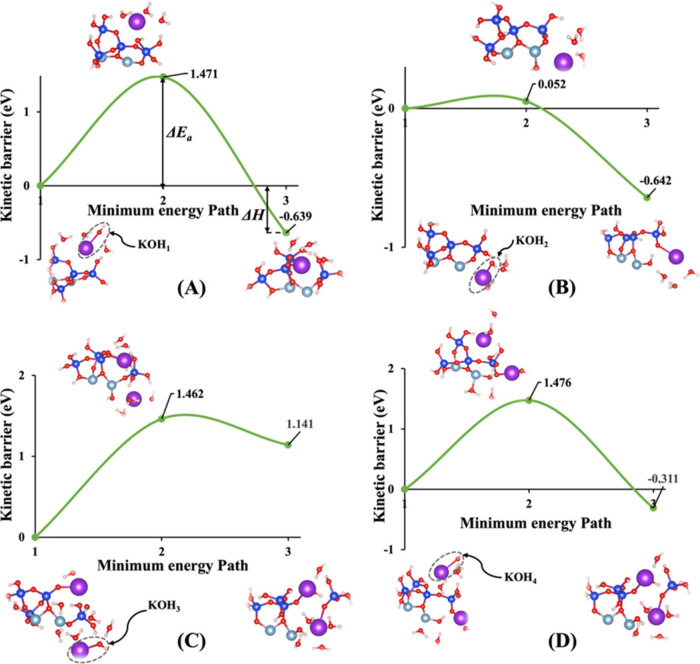
To thoroughly understand the impact of the hydration shell on both the activation energy (ΔEa) of a hydrolysis reaction and the energy change in reaction enthalpy (ΔH) computations, we focus on identical molecular structures depicted in Figures 1A and 1B. Each activator within these structures is surrounded by precisely three water molecules. This deliberate selection allows for a consistent comparison and assessment of the subtle nuances arising from the hydration shell’s influence. Irrespective of the considerations from model 1, our investigation reveals that the activation energies (ΔEa) obtained for the hydrolysis reaction in the presence of the KOH activator consistently exhibit greater favorability when compared to those with NaOH. Yao et al.57 and Hu et al.58 experimentally illustrated that the geopolymerization rate in KOH solution significantly outpaces that in NaOH solution, highlighting the heightened reactivity of KOH compared to NaOH. This trend holds true across both systems, whether vdW interactions are considered or not. The minimum energy path versus kinetic barrier representations in Figures 10, 11, S1, and S2 vividly illustrate this pattern, emphasizing the noteworthy advantage of KOH over NaOH in influencing the activation energy of the hydrolysis reaction. Upon meticulous examination of the data extracted from the figures, a distinctive trend emerges with respect to the enthalpy energies associated with the breaking of the oxo-bridging bond to the silicate neighbor (Si2) in model 3. It becomes evident that all values pertaining to both KOH and NaOH activators in this model 3 exhibit less negative or more positive enthalpy energies, indicative of an endothermic reaction. This nuanced observation sheds light on the intricate interplay between activators and the enthalpy changes during the breaking of specific bonds, offering valuable insights into the thermodynamic aspects of the hydrolysis reaction under consideration. Furthermore, it has been observed that in model 2, the majority of activation energies required to break the oxo-bridging bond to the aluminum neighbor (Al1) are lower than those in all other models across both systems and activators.
Figure 10.
(A–D) Minimum energy path for computation of the energy barrier (activation energy) of the hydrolysis reaction (ΔEa) along with the associated energy change in reaction enthalpy (ΔH), including (NaOH)1–4 absorbents surrounded by hydration shells with the contribution of vdW interactions as presented for four models (1–4), respectively.
Figure 11.
(A–D) Minimum energy path for computation of the energy barrier (activation energy) of the hydrolysis reaction (ΔEa) along with the associated energy change in reaction enthalpy (ΔH), including (KOH)1–4 absorbents surrounded by hydration shells with the contribution of vdW interactions as presented for four models (1–4), respectively.
Discussion
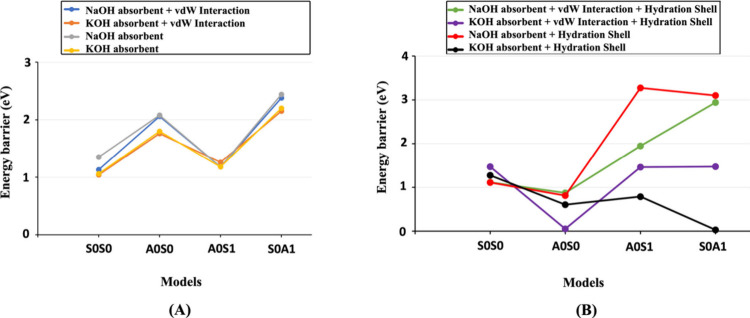
Figure 12 depicts various bond types without (A) and with (B) the hydration shell contribution. It also demonstrates the noticeable effect of water molecules around the cation and OH group, applied to the surface of MK exactly above the targeted oxo binding (−O−), where it will split during the hydrolysis reaction, emphasizing the importance of incorporating van der Waals interactions for water simulations. This emphasizes the necessity of accounting for the influence of liquid water with dissolved cations and OH groups, which can significantly impact the scenario. It is advisible to proceed with the lowest number of water molecules to compute the activation energy in a conservative manner because increasing the water shell around cations typically reduces the energy barrier or activation energy for dissolution processes. This is primarily due to the stabilizing effect of the hydration shell, which shields the cations and facilitates their interaction with the surrounding solvent molecules. By surrounding the cations with water molecules, the hydration shell effectively lowers the energy required for the cations to break away from the solid phase and enter the solution, thus reducing the overall activation energy of the dissolution reaction. It is evident that none of the four presented models exhibit ΔEa values lower than 1 eV (96.485 kJ/mol) in the absence of hydration shells around cations, as illustrated in Figure 12A. However, 37.5% of the ΔEa values with the influence of hydration shells around cations are less than 1 eV (96.485 kJ/mol), as shown in Figure 12B. Moreover, 50%, and 75% of the ΔEa values are observed for models lower than 1.55 eV (150 kJ/mol) in the absence and presence of hydration shells, respectively. Overall, it is clear that the presence of a hydration shell around cations leads to a less demanding ΔEa values compared with when hydration shells are absent around cations. Comparing our results with former studies, Pelmenschikov et al.59 reported that hydrolysis of the (OH)3Si–O–Si(OH)3 linkage of β-cristobalite by single water molecules in a cluster with Q1-Q1 configuration requires an activation energy of 71 kJ/mol. Moreover, for the cluster model of the siloxane bridge, the activation energy of 95 kJ/mol is required for hydrolysis of the Si–O–Si. Nangia and Garrison60 also computed the activation energy value of 157 kJ/mol for hydrolysis of the Si–O–Si bridge bond by an H2O activator in a quartz cluster with Q1-Q2 configuration using ab initio density functional theory calculations, which is almost identical to our computation (161.13 kJ/mol, as shown in Table S5). In another study, Nangia and Garrison61 also reported that the activation energy for the hydrolysis of the Si–O–Si bridge bond in a quartz cluster decreases at higher pH levels, a finding we have confirmed here. Recently, we demonstrated that our approach establishes a foundation for future studies of aluminosilicate dissolution mechanisms. This is based on a systematic database of atomistic activation energies derived from various scenarios using DFT (or MD) computational methods. Consequently, this facilitates mesoscopic forward dissolution rate calculations, which are essential for developing an atomistic kinetic Monte Carlo (KMC) upscaling model.
Figure 12.
Comparing ΔEa computed for four models with and without vdW interaction contributions, under the influence of NaOH or KOH activators, without (A) and with (B) hydration shells. Models 1–4 are also labeled as S0S0, A0S0, A0S1, and S0A1, respectively.
Conclusions
This work employs an improved dimer method (IDM) within the density functional theory (DFT) computational quantum mechanical modeling method to optimize transition states and calculate enthalpy activation energies for silicate dissolution mechanisms from metakaolinite (MK). Reaction mechanisms involve breaking oxo-bridging bonds between two silicates and silicate–aluminate MK units under far-from-equilibrium conditions. In this way, four distinct scenarios were presented, considering two different activators, NaOH and KOH, with and without the inclusion of van der Waals (vdW) interactions. Furthermore, it examines the influence of water molecules (hydration shell) surrounding alkali cations as well as incorporating vdW interactions to compute the activation energies required to break oxo-bridging bonds between silicate or aluminate units at the TST. The results revealed that the Na cation forms a shorter bond length with OH due to higher electronegativity when compared to the K cation. The optimal activation energy for initiating the reaction is identified during the breaking of the initial bridging oxygen bonded to the silicate neighbor. Conversely, the least favorable activation energy is observed when breaking the final bridging oxygen bonded to the silicate neighbor, as the bridging oxygen bonded to aluminum is already broken, leading to the dissolution of silica species SiO(OH)3– Na+. The obtained database of atomistic activation energies is crucial for scaling up dissolution rate computations using atomistic kinetic Monte Carlo (KMC) to obtain mesoscopic forward dissolution rates. Further research is needed to investigate other crystal surfaces to provide additional inputs for KMC upscaling.
Acknowledgments
The authors gratefully acknowledge the financial support provided by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) for the Priority Programme “Net-Zero Concrete” (SPP 2436), Project: “Supplementary Cementitious Materials Reactivity: Chemistry-Structure Relationships for Dissolution Kinetics by Upscaling Atomistic Modeling (SuperUptom)” under project number 541788011. The computational work for this research was carried out on the Lichtenberg High Performance Computer at TU Darmstadt.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.langmuir.4c00890.
Energy barrier (activation energy) for the hydrolysis reaction (ΔEa) and the energy change of reaction enthalpy (ΔH) computations for four presented models with contribution of vdW interactions, hydrolyzed by NaOH activator, Table S1; without contribution of vdW interaction, hydrolyzed by NaOH activator, Table S2; with contribution of vdW interaction, hydrolyzed by KOH activator, Table S3; without contribution of vdW interaction, hydrolyzed by KOH activator, Table S4; with contribution of vdW interaction, hydrolyzed by H2O activator, Table S5; minimum energy path for computation of energy barrier (activation energy) of the hydrolysis reaction (ΔEa), along with the associated energy change in reaction enthalpy (ΔH) without contribution of vdW interactions as presented for four models (1–4) surrounded by hydration shells, including (NaOH)1–4 absorbents, Figure S1; including (KOH)1–4 absorbents, Figure S2 (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Fernandez R.; Martirena F.; Scrivener K. L. The Origin of the Pozzolanic Activity of Calcined Clay Minerals: A Comparison between Kaolinite, Illite and Montmorillonite. Cem. Concr. Res. 2011, 41, 113–122. 10.1016/j.cemconres.2010.09.013. [DOI] [Google Scholar]
- Hollanders S.; Adriaens R.; Skibsted J.; Cizer Ö.; Elsen J. Pozzolanic Reactivity of Pure Calcined Clays. Appl. Clay Sci. 2016, 132–133, 552–560. 10.1016/j.clay.2016.08.003. [DOI] [Google Scholar]
- Kavitha O. R.; Shanthi V. M.; Arulraj G. P.; Sivakumar V. R. Microstructural Studies on Eco-Friendly and Durable Self-Compacting Concrete Blended with Metakaolin. Appl. Clay Sci. 2016, 124–125, 143–149. 10.1016/j.clay.2016.02.011. [DOI] [Google Scholar]
- Madandoust R.; Mousavi S. Y. Fresh and Hardened Properties of Self-Compacting Concrete Containing Metakaolin. Constr. Build. Mater. 2012, 35, 752–760. 10.1016/j.conbuildmat.2012.04.109. [DOI] [Google Scholar]
- Weise K.; Ukrainczyk N.; Koenders E. Pozzolanic Reactions of Metakaolin with Calcium Hydroxide: Review on Hydrate Phase Formations and Effect of Alkali Hydroxides, Carbonates and Sulfates. Mater. 2023, 231, 112062. 10.1016/j.matdes.2023.112062. [DOI] [Google Scholar]
- Ramezanianpour A. A.; Bahrami Jovein H. Influence of Metakaolin as Supplementary Cementing Material on Strength and Durability of Concretes. Constr. Build. Mater. 2012, 30, 470–479. 10.1016/j.conbuildmat.2011.12.050. [DOI] [Google Scholar]
- Hwalla J.; Saba M.; Assaad J. J. Suitability of Metakaolin-Based Geopolymers for Underwater Applications. Mater. Struct. 2020, 53, 119. 10.1617/s11527-020-01546-0. [DOI] [Google Scholar]
- Davidovits J. Geopolymers: Inorganic Polymeric New Materials. J. Therm. Anal. 1991, 37, 1633–1656. 10.1007/BF01912193. [DOI] [Google Scholar]
- Izadifar M.; Thissen P.; Steudel A.; Kleeberg R.; Kaufhold S.; Kaltenbach J.; Schuhmann R.; Dehn F.; Emmerich K. Comprehensive Examination of Dehydroxylation of Kaolinite, Disordered Kaolinite, and Dickite: Experimental Studies and Density Functional Theory. Clays Clay Miner. 2020, 68, 319–333. 10.1007/s42860-020-00082-w. [DOI] [Google Scholar]
- Werling N.; Dehn F.; Krause F.; Steudel A.; Schuhmann R.; Emmerich K. Solubility of Precursors and Carbonation of Waterglass-Free Geopolymers. Clays Clay Miner. 2020, 68, 524–531. 10.1007/s42860-020-00096-4. [DOI] [Google Scholar]
- Salah Uddin K. M.; Izadifar M.; Ukrainczyk N.; Koenders E.; Middendorf B. Dissolution of β-C2S Cement Clinker: Part 1 Molecular Dynamics (MD) Approach for Different Crystal Facets. Mater. 2022, 15, 6388. 10.3390/ma15186388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Izadifar M.; Ukrainczyk N.; Salah Uddin K. M.; Middendorf B.; Koenders E. Dissolution of β-C2S Cement Clinker: Part 2 Atomistic Kinetic Monte Carlo (KMC) Upscaling. Approach. Mater. 2022, 15, 6716. 10.3390/ma15196716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salah Uddin K. M.; Izadifar M.; Ukrainczyk N.; Koenders E.; Middendorf B. Dissolution of Portlandite in Pure Water: Part 1 Molecular Dynamics (MD) Approach. Mater. 2022, 15, 1404. 10.3390/ma15041404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Izadifar M.; Ukrainczyk N.; Salah Uddin K.; Middendorf B.; Koenders E. Dissolution of Portlandite in Pure Water: Part 2 Atomistic Kinetic Monte Carlo (KMC) Approach. Mater. 2022, 15, 1442. 10.3390/ma15041442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gong K.; White C. E. Predicting CaO-(MgO)-Al2O3-SiO2 Glass Reactivity in Alkaline Environments from Force Field Molecular Dynamics Simulations. Cem. Concr. Res. 2021, 150, 106588. 10.1016/j.cemconres.2021.106588. [DOI] [Google Scholar]
- Izadifar M.; Sekkal W.; Dubyey L.; Ukrainczyk N.; Zaoui A.; Koenders E. Theoretical Studies of Adsorption Reactions of Aluminosilicate Aqueous Species on Graphene-Based Nanomaterials: Implications for Geopolymer Binders. ACS Appl. Nano Mater. 2023, 6, 16318–16331. 10.1021/acsanm.3c02438. [DOI] [Google Scholar]
- Izadifar M.; Dolado J. S.; Thissen P.; Ukrainczyk N.; Koenders E.; Ayuela A. Theoretical Elastic Constants of Tobermorite Enhanced with Reduced Graphene Oxide through Hydroxyl vs Epoxy Functionalization: A First-Principles Study. J. Phys. Chem. C 2023, 127, 18117–18126. 10.1021/acs.jpcc.3c03893. [DOI] [Google Scholar]
- Izadifar M.; Dolado J. S.; Thissen P.; Ayuela A. Interactions between Reduced Graphene Oxide with Monomers of (Calcium) Silicate Hydrates: A First-Principles Study. Nanomate. 2021, 11, 2248. 10.3390/nano11092248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Izadifar M.; Natzeck C.; Emmerich K.; Weidler P. G.; Gohari S.; Burvill C.; Thissen P. Unexpected Chemical Activity of a Mineral Surface: The Role of Crystal Water in Tobermorite. J. Phys. Chem. C 2022, 126, 12405–12412. 10.1021/acs.jpcc.1c10151. [DOI] [Google Scholar]
- Izadifar M.; Königer F.; Gerdes A.; Wöll C.; Thissen P. Correlation between Composition and Mechanical Properties of Calcium Silicate Hydrates Identified by Infrared Spectroscopy and Density Functional Theory. J. Phys. Chem. C 2019, 123, 10868–10873. 10.1021/acs.jpcc.8b11920. [DOI] [Google Scholar]
- Sekkal W.; Izadifar M.; Zaoui A.; Ukrainczyk N.; Koenders E. Theoretical Investigation of Protective Graphene-Coated Metakaolin Geopolymer Interface under Moisture and Chemical Composition Effects. Powder Technol. 2023, 430, 119007. 10.1016/j.powtec.2023.119007. [DOI] [Google Scholar]
- Izadifar M.; Thissen P.; Abadi R.; Jam A. N.; Gohari S.; Burvill C.; Rabczuk T. Fracture Toughness of Various Percentage of Doping of Boron Atoms on the Mechanical Properties of Polycrystalline Graphene: A Molecular Dynamics Study. Phys. E Low-Dimens. Syst. Nanostruct. 2019, 114, 113614. 10.1016/j.physe.2019.113614. [DOI] [Google Scholar]
- Izadifar M.; Abadi R.; Nezhad Shirazi A. H.; Alajlan N.; Rabczuk T. Nanopores Creation in Boron and Nitrogen Doped Polycrystalline Graphene: A Molecular Dynamics Study. Phys. E Low-Dimens. Syst. Nanostruct. 2018, 99, 24–36. 10.1016/j.physe.2017.12.036. [DOI] [Google Scholar]
- Izadifar M.; Abadi R.; Jam A. N.; Rabczuk T. Investigation into the Effect of Doping of Boron and Nitrogen Atoms in the Mechanical Properties of Single-Layer Polycrystalline Graphene. Comput. Mater. Sci. 2017, 138, 435–447. 10.1016/j.commatsci.2017.06.038. [DOI] [Google Scholar]
- Jam A. N.; Jam N. N.; Izadifar M.; Rabczuk T. Molecular Dynamics Study on the Crack Propagation in Carbon Doped Polycrystalline Boron-Nitride Nanosheets. Comput. Mater. Sci. 2022, 203, 111066. 10.1016/j.commatsci.2021.111066. [DOI] [Google Scholar]
- Mortazavi B.; Cuniberti G.; Rabczuk T. Mechanical Properties and Thermal Conductivity of Graphitic Carbon Nitride: A Molecular Dynamics Study. Comput. Mater. Sci. 2015, 99, 285–289. 10.1016/j.commatsci.2014.12.036. [DOI] [Google Scholar]
- Zhang Q.; Mortazavi B.; Aldakheel F. Molecular Dynamics Modeling of Mechanical Properties of Polymer Nanocomposites Reinforced by C7N6 Nanosheet. Surfaces 2021, 4, 240–254. 10.3390/surfaces4030019. [DOI] [Google Scholar]
- Izadifar M.; Valencia N. C.; Xiao P.; Ukrainczyk N.; Koenders E. 3D Off-Lattice Coarse-Grained Monte Carlo Simulations for Nucleation of Alkaline Aluminosilicate Gels. Mater. 2023, 16, 1863. 10.3390/ma16051863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White C. E.; Provis J. L.; Proffen T.; van Deventer J. S. J. Molecular Mechanisms Responsible for the Structural Changes Occurring during Geopolymerization: Multiscale Simulation. AIChE J. 2012, 58, 2241–2253. 10.1002/aic.12743. [DOI] [Google Scholar]
- Martin P.; Gaitero J. J.; Dolado J. S.; Manzano H. New Kinetic Monte Carlo Model to Study the Dissolution of Quartz. ACS Earth Space Chem. 2021, 5, 516–524. 10.1021/acsearthspacechem.0c00303. [DOI] [Google Scholar]
- Coopamootoo K.; Masoero E. Simulations of Tricalcium Silicate Dissolution at Screw Dislocations: Effects of Finite Crystal Size and Mechanical Interaction Potentials. Cem. Concr. Res. 2024, 175, 107384. 10.1016/j.cemconres.2023.107384. [DOI] [Google Scholar]
- Chen J.; Martin P.; Xu Z.; Manzano H.; Dolado J. S.; Ye G. A Dissolution Model of Alite Coupling Surface Topography and Ions Transport under Different Hydrodynamics Conditions at Microscale. Cem. Concr. Res. 2021, 142, 106377. 10.1016/j.cemconres.2021.106377. [DOI] [Google Scholar]
- Manzano H.; Durgun E.; López-Arbeloa I.; Grossman J. C. Insight on Tricalcium Silicate Hydration and Dissolution Mechanism from Molecular Simulations. ACS Appl. Mater. Interfaces 2015, 7, 14726–14733. 10.1021/acsami.5b02505. [DOI] [PubMed] [Google Scholar]
- Valencia N. C.; Izadifar M.; Ukrainczyk N.; Koenders E. Coarse-Grained Monte Carlo Simulations with Octree Cells for Geopolymer Nucleation at Different pH Values. Mater. 2024, 17, 95. 10.3390/ma17010095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schliemann R.; Churakov S. V. Atomic Scale Mechanism of Clay Minerals Dissolution Revealed by Ab Initio Simulations. Geochim. Cosmochim. Acta 2021, 293, 438–460. 10.1016/j.gca.2020.10.026. [DOI] [Google Scholar]
- Schliemann R.; Churakov S. V. Pyrophyllite Dissolution at Elevated Pressure Conditions: An Ab Initio Study. Geochim. Cosmochim. Acta 2021, 307, 42–55. 10.1016/j.gca.2021.05.017. [DOI] [Google Scholar]
- Kurganskaya I.; Luttge A. A Comprehensive Stochastic Model of Phyllosilicate Dissolution: Structure and Kinematics of Etch Pits Formed on Muscovite Basal Face. Geochim. Cosmochim. Acta 2013, 120, 545–560. 10.1016/j.gca.2013.06.038. [DOI] [Google Scholar]
- Ayuela A.; Dolado J. S.; Campillo I.; De Miguel Y. R.; Erkizia E.; Sánchez-Portal D.; Rubio A.; Porro A.; Echenique P. M. Silicate Chain Formation in the Nanostructure of Cement-Based Materials. J. Chem. Phys. 2007, 127, 164710. 10.1063/1.2796171. [DOI] [PubMed] [Google Scholar]
- Dupuis R.; Dolado J. S.; Surga J.; Ayuela A. Doping as a Way To Protect Silicate Chains in Calcium Silicate Hydrates. ACS Sustain. Chem. Eng. 2018, 6, 15015–15021. 10.1021/acssuschemeng.8b03488. [DOI] [Google Scholar]
- Henkelman G.; Jónsson H. A Dimer Method for Finding Saddle Points on High Dimensional Potential Surfaces Using Only First Derivatives. J. Chem. Phys. 1999, 111, 7010–7022. 10.1063/1.480097. [DOI] [Google Scholar]
- Heyden A.; Bell A. T.; Keil F. J. Efficient Methods for Finding Transition States in Chemical Reactions: Comparison of Improved Dimer Method and Partitioned Rational Function Optimization Method. J. Chem. Phys. 2005, 123, 224101. 10.1063/1.2104507. [DOI] [PubMed] [Google Scholar]
- Izadifar M.; Ukrainczyk N.; Koenders E. Silicate Dissolution Mechanism from Metakaolinite Using Density Functional Theory. Nanomater. 2023, 13, 1196. 10.3390/nano13071196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng G.; Wang X.-X.; Zhang S.-H.; Zhu K.-K.; Sui Z.-J.; Zhou X.-G.; Chen D.; Zhu Y.-A. On the Product and Transition-State Shape Selectivities in 2-Heptene Isomerization. Chem. Phys. Lett. 2023, 812, 140263. 10.1016/j.cplett.2022.140263. [DOI] [Google Scholar]
- Chen X.; Wang K.; Xing X. Nitrogen-Coordinated Ruthenium on Porous Carbon Enhanced Hydrogen Evolution Reactions. Mater. Chem. Front. 2023, 8, 282–286. 10.1039/D3QM01082A. [DOI] [Google Scholar]
- Kohn W.; Sham L. J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. 10.1103/PhysRev.140.A1133. [DOI] [Google Scholar]
- Kresse G.; Hafner J. Ab Initio Molecular Dynamics for Liquid Metals. Phys. Rev. B 1993, 47, 558–561. 10.1103/PhysRevB.47.558. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Furthmüller J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Furthmüller J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. 10.1016/0927-0256(96)00008-0. [DOI] [PubMed] [Google Scholar]
- Mortazavi B. Structural, Electronic, Thermal and Mechanical Properties of C60-Based Fullerene Two-Dimensional Networks Explored by First-Principles and Machine Learning. Carbon 2023, 213, 118293. 10.1016/j.carbon.2023.118293. [DOI] [Google Scholar]
- Mortazavi B.Machine Learning Interatomic Potentials: Keys to First-Principles Multiscale Modeling. In Machine Learning in Modeling and Simulation; Rabczuk T., Bathe K.-J., Eds.; Computational Methods in Engineering & the Sciences; Springer International Publishing: Cham, 2023; pp 427–451. [Google Scholar]
- Kresse G.; Joubert D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59, 1758–1775. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
- Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- Monkhorst H. J.; Pack J. D. Special Points for Brillouin-Zone Integrations. Phys. Rev. B 1976, 13, 5188–5192. 10.1103/PhysRevB.13.5188. [DOI] [Google Scholar]
- Grimme S.; Antony J.; Ehrlich S.; Krieg H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
- Momma K.; Izumi F. It VESTA: A Three-Dimensional Visualization System for Electronic and Structural Analysis. J. Appl. Crystallogr. 2008, 41, 653–658. 10.1107/S0021889808012016. [DOI] [Google Scholar]
- Liu X.; Liu C.; Meng C. Oligomerization of Silicic Acids in Neutral Aqueous Solution: A First-Principles Investigation. Int. J. Mol. Sci. 2019, 20, 3037. 10.3390/ijms20123037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao X.; Zhang Z.; Zhu H.; Chen Y. Geopolymerization Process of Alkali-Metakaolinite Characterized by Isothermal Calorimetry. Thermochim. Acta 2009, 493, 49–54. 10.1016/j.tca.2009.04.002. [DOI] [Google Scholar]
- Hu N.; Bernsmeier D.; Grathoff G. H.; Warr L. N. The Influence of Alkali Activator Type, Curing Temperature and Gibbsite on the Geopolymerization of an Interstratified Illite-Smectite Rich Clay from Friedland. Appl. Clay Sci. 2017, 135, 386–393. 10.1016/j.clay.2016.10.021. [DOI] [Google Scholar]
- Pelmenschikov A.; Strandh H.; Pettersson L. G. M.; Leszczynski J. Lattice Resistance to Hydrolysis of Si-O-Si Bonds of Silicate Minerals: Ab Initio Calculations of a Single Water Attack onto the (001) and (111) β-Cristobalite Surfaces. J. Phys. Chem. B 2000, 104, 5779–5783. 10.1021/jp994097r. [DOI] [Google Scholar]
- Nangia S.; Garrison B. J. Ab Initio Study of Dissolution and Precipitation Reactions from the Edge, Kink, and Terrace Sites of Quartz as a Function of pH. Mol. Phys. 2009, 107, 831–843. 10.1080/00268970802665621. [DOI] [Google Scholar]
- Nangia S.; Garrison B. J. Reaction Rates and Dissolution Mechanisms of Quartz as a Function of pH. J. Phys. Chem. A 2008, 112, 2027–2033. 10.1021/jp076243w. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.