TARGETING UNDERREPRESENTED POPULATIONS IN PRECISION MEDICINE: A FEDERATED TRANSFER LEARNING APPROACH

Abstract

The limited representation of minorities and disadvantaged populations in large-scale clinical and genomics research poses a significant barrier to translating precision medicine research into practice. Prediction models are likely to underperform in underrepresented populations due to heterogeneity across populations, thereby exacerbating known health disparities. To address this issue, we propose FETA, a two-way data integration method that leverages a federated transfer learning approach to integrate heterogeneous data from diverse populations and multiple healthcare institutions, with a focus on a target population of interest having limited sample sizes. We show that FETA achieves performance comparable to the pooled analysis, where individual-level data is shared across institutions, with only a small number of communications across participating sites. Our theoretical analysis and simulation study demonstrate how FETA’s estimation accuracy is influenced by communication budgets, privacy restrictions, and heterogeneity across populations. We apply FETA to multisite data from the electronic Medical Records and Genomics (eMERGE) Network to construct genetic risk prediction models for extreme obesity. Compared to models trained using target data only, source data only, and all data without accounting for population-level differences, FETA shows superior predictive performance. FETA has the potential to improve estimation and prediction accuracy in underrepresented populations and reduce the gap in model performance across populations.

1. Introduction.

Precision medicine holds promises to improve individual health by integrating a person’s genetics, environment, and lifestyle information to determine the best approach to prevent or treat diseases (Ashley (2016)). Precision medicine research has attracted considerable interest and investment during the past few decades (Collins and Varmus (2015)). With the emergence of electronic health records (EHR) linked with biobank specimens, massive environmental data, and health surveys, we now have increasing opportunities to develop accurate personalized risk prediction models in a cost-effective way (Li et al. (2020)).

Despite the increasing availability of large-scale biomedical data, many demographic sub-populations are observed to be underrepresented in precision medicine research (Kraft et al. (2018), West, Blacksher and Burke (2017)). For example, a disproportionate majority (>75%) of participants in existing genomics studies are of European descent (Martin et al. (2019)). The UK Biobank, one of the largest biobanks, has more than 95% of European-ancestry participants (Sudlow et al. (2015)). Mounting evidence has shown that the transferability and generalizability of models trained in a particular population can be low due to a substantial amount of heterogeneity in underlying distributions of data across populations (Duncan et al. (2019), Kraft et al. (2018), Landry et al. (2018), West, Blacksher and Burke (2017)). For example, the performance of existing genetic risk prediction models in non-European populations has generally been found to be much poorer than in European-ancestry populations, most notably in African-ancestry populations (Duncan et al. (2019)). It remains challenging to optimize prediction model performance for underrepresented populations accounting for both the heterogeneity and the insufficient sample sizes. However, to advance precision medicine it is crucial to improve the performance of statistical and machine learning models in underrepresented populations so as not to exacerbate health disparities.

We propose to address the lack of representation and disparities in model performance through two data integration strategies: (1) leveraging the shared knowledge from diverse populations and (2) integrating larger bodies of data from multiple healthcare institutions. Data across multiple populations may share a certain amount of similarity that can be leveraged to improve the model performance in an underrepresented population (Cai et al. (2021)). However, conventional methods, where all data are combined and used indistinctly in training and testing, cannot tailor the prediction models to work well for a specific population; if using a population-specific training strategy, the sample size from an underrepresented population is usually not sufficient to train a model with reliable performance. To account for such heterogeneity and lack of representation, we propose to use transfer learning to transfer the shared knowledge learned from diverse populations to an underrepresented population so that comparable model performance can be reached with much less data for training (Weiss, Khoshgoftaar and Wang (2016)). In addition, multiinstitutional data integration can improve the sample size of the underrepresented populations and the diversity of data (McCarty et al. (2011)). In recent years, many research consortia and data networks have been built which provide infrastructures for multiinstitutional data integration. For example, the electronic Medical Records and Genomics (eMERGE) Network is a consortium of ten participating sites to investigate the use of EHR systems for genomic research (Gottesman et al. (2013)). In 2019, the Global Biobank Meta Initiative (GBMI) was founded which brings together 19 biobanks to work together to understand the genetic basis of human health and disease (Zhou, analysis Initiative et al. (2021)). We propose to use federated learning to unlock the multiinstitutional health records/biobank data, which overcomes two main barriers to institutional data integration. One is that the individual-level information can be highly sensitive and cannot be shared across institutions (van der Haak et al. (2003)). The other one is that the often-enormous size of the health records/biobanks data makes it infeasible or inefficient to pool all data together due to challenges in data storage, management, and computation (Kushida et al. (2012)). Therefore, as illustrated in Figure 1, we proposed a FEderated Transfer Algorithm (FETA) to incorporate data from diverse populations that are stored at multiple institutions to improve the model performance in a target underrepresented population.

Fig. 1.

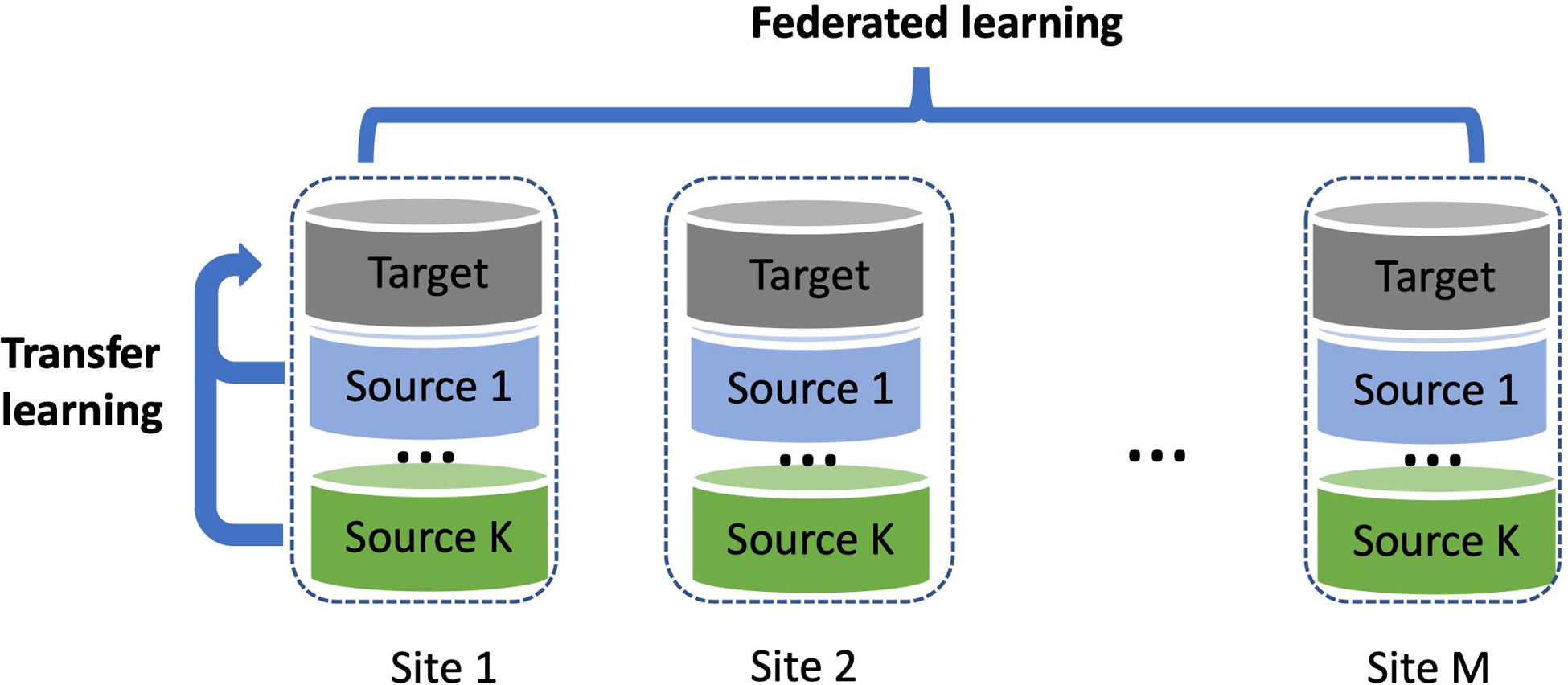
A schematic illustration of the federated transfer learning framework and the problem setting.

Existing transfer learning methods primarily focus on settings where individual-level data can be shared. For example, Cai and Wei (2021) study the minimax and adaptive methods for nonparametric classification in the transfer learning setting. Bastani (2020) studies estimation and prediction in high-dimensional linear models, and the sample size of the auxiliary study is larger than the number of covariates. Li, Cai and Li (2022) propose a transfer learning algorithm in high-dimensional linear models and studies the adaptation to the unknown similarity level. Li, Cai and Li (2020) study transfer learning in high-dimensional Gaussian graphical models with false discovery rate control. Tian and Feng (2021) study transfer learning under high-dimensional generalized linear models. These individual data-based methods cannot be directly extended to the federated settings due to data sharing constraints and the potential heterogeneity across sites.

Under data sharing constraints, most federated learning methods focus on settings where the true models are the same across studies. For example, many algorithms fit a common model to data from each institution and then aggregate these local estimates through a weighted average, for example, Chen and Xie (2014), Lee et al. (2017), Li, Lin and Li (2013), Wang et al. (2019a). To improve efficiency, surrogate likelihood approaches have been adopted in recently proposed distributed algorithms (Duan et al. (2019), Duan et al. (2020), Jordan, Lee and Yang (2019)) to approximate the global likelihood. These methods cannot be easily extended to the federated transfer learning setting where training a model for a target population is of interest and both data sharing constraints and heterogeneity are present. Recently, Liu et al., 2021 and Cai, Liu and Xia (2022) propose distributed multitask learning approaches, which jointly train site-specific regression parameters based on derived summary data. Different from their work which assumes site-level homogeneous populations, we consider that data in each site are from multiple populations, and the sample sizes can be highly unbalanced. Without making assumptions that model parameters across populations have the same support, our methods are robust to the cases where some populations differ significantly from the target.

To summarize, our work contributes to the current literature from the following perspectives: (1) adopting transfer learning ideas, FETA tackles an important issue in precision medicine where sample sizes from different populations can be highly unbalanced. We provide theoretical analysis, extensive numerical experiments, and real data analysis to demonstrate the improved accuracy and the robustness to the level of heterogeneity; (2) FETA enables federated model training across multiple datasets, which only require a small number of communications across participating sites and can achieve performance comparable to the pooled analysis. Our theoretical analysis and numerical experiments demonstrated how the estimation accuracy is influenced by communication budgets, privacy restrictions, and heterogeneity among populations, and (3) our real data application shows the promise of applying FETA to improve the risk prediction in underrepresented population using data from multicenter large-scale clinical/genomic datasets with communication-efficiency and privacy protection.

The rest of the paper is organized as follows. In Section 2 we introduce FETA with detailed discussions on potential options for initialization, tuning parameter selection, and reducing communication costs. In Sections 3 and 4, we provide theoretical guarantees and simulation studies, respectively, to evaluate the performance of the methods and how it is influenced by the communication constraints and level of heterogeneity across populations. In Section 5 we apply our methods to the construction of prediction models for extreme obesity, which is an emerging public health issue and an important risk factor for many complex diseases. We combine multicenter data from eMERGE Network and target the underrepresented African-ancestry population.

2. Method.

2.1. Problem setup and notation.

We build our federated transfer learning methods based on sparse high-dimensional regression models (Tibshirani (1996), Bickel, Ritov and Tsybakov (2009)). These models have been widely applied to precision medicine research for both association studies and risk prediction models, due to the benefits of simultaneous model estimation and variable selection, and the desirable interpretability (Qian et al. (2020)).

We assume there are $N$ subjects in total from $K+1$ populations. We treat the underrepresented population of interest as the target population, indexed by $k=0$, while the other $K$ populations are treated as source populations, indexed by $k=1,\dots K$. We assume data for the $N$ subjects are stored at $M$ different sites where, due to privacy constraints, no individual-level data are allowed to be shared across sites. We consider the case where $K$ is finite but $M$ is allowed to grow as the total sample size grows to infinity.

Let ${𝒩}^{(m,k)}$ be the index sets of the data from the $k$th population in the $m$th site and $n^{(m,k)}=\left|{𝒩}^{(m,k)}\right|$ denote the corresponding sample size, for $k=0,\dots ,K$ and $m=1,\dots M$. We assume the index sets are known and do not overlap with one another, that is, ${𝒩}^{(m,k)}\cap {𝒩}^{\left(m,k^{\mathrm{\text{'}}}\right)}=\varnothing$ for any $0\le k<k^{\mathrm{\text{'}}}\le K$. In precision medicine research, these index sets may be obtained from indicators of minority and disadvantaged groups, such as race, gender, and socioeconomic status. Denote $N^{\left(k\right)}={\sum }_{m=1}^M n^{(m,k)}$ and $N={\sum }_{k=0}^K N^{\left(k\right)}$. We are particularly interested in the challenging scenario $N^{\left(0\right)}\ll N$, where the underrepresentation is severe. However, at certain sites the relative sample compositions can be arbitrary. It is possible that some sites may not have data from certain populations, that is, $n^{(m,k)}=0$ for some but not all $m$ for $1\le m\le M$. We consider the high-dimensional setting where $p$ can be larger and much larger than $N^{\left(0\right)}$ and $N$.

For the $i$th subject, we observe an outcome variable $y_i\in \mathbb{R}$ and a set of $p$ predictors ${\mathit{x}}_i\in {\mathbb{R}}^p$, including the intercept term. We assume that the target data on the $m$th site, ${\left\{{\mathit{x}}_i,y_i\right\}}_{i\in {𝒩}^{(m,0)}}$, follow a generalized linear model

$$g\left\{\mathbb{E}\left(y_i\mid {\mathit{x}}_i\right)\right\}={\mathit{x}}_i^{\mathrm{\top }}\mathit{\beta }$$

with a canonical link function $g(\cdot )$ and a negative log-likelihood function

$$L^{(m,0)}\left(\mathit{\beta }\right)=\sum _{i\in {𝒩}^{(m,0)}} \left\{\psi \left({\mathit{x}}_i^{\mathrm{\top }}\mathit{\beta }\right)-y_i\cdot {\mathit{x}}_i^{\mathrm{\top }}\mathit{\beta }\right\}$$

for some unknown parameter $\mathit{\beta }\in {\mathbb{R}}^p$ and $\psi (\cdot )$ uniquely determined by $g(\cdot )$. Similarly, the data from the $k$th source population in the $m$th site are ${\left\{{\mathit{x}}_i,y_i\right\}}_{i\in {𝒩}^{(m,k)}}$, and they follow a generalized linear model

$$g\left\{\mathbb{E}\left(y_i\mid {\mathit{x}}_i\right)\right\}={\mathit{x}}_i^{\mathrm{\top }}{\mathit{w}}^{\left(k\right)}$$

with negative log-likelihood

$$L^{(m,k)}\left({\mathit{w}}^{\left(k\right)}\right)=\sum _{i\in {𝒩}^{(m,k)}} \left\{\psi \left({\mathit{x}}_i^{\mathrm{\top }}{\mathit{w}}^{\left(k\right)}\right)-y_i\cdot {\mathit{x}}_i^{\mathrm{\top }}{\mathit{w}}^{\left(k\right)}\right\}$$

for some unknown parameter ${\mathit{w}}^{\left(k\right)}\in {\mathbb{R}}^p$.

Our goal is to estimate $\mathit{\beta }$, using data from $K+1$ populations and $M$ sites. These data are heterogeneous at two levels: for data from different populations, differences may exist in terms of both the regression coefficients, which characterize the conditional distribution $f\left(y_i\mid {\mathit{x}}_i\right)$, as well as the underlying distribution of the covariates, also known as covariate shift in some related work (Guo (2020)). For data from a given population, the distribution of covariates might also be heterogeneous across sites. We assume the regression parameters to be distinct across populations. In addition, we consider the setting where only summary-level data can be shared across sites.

Despite the presence of between-population heterogeneity, it is reasonable to believe that the population-specific models may share some degree of similarity. For example, in genetic risk prediction models the genetic architectures, captured by regression coefficients, of many complex traits and diseases are found to be highly concordant across ancestral groups (Lam et al. (2019)). It is important to characterize and leverage such similarities so that knowledge can be transferred from the source to the target population.

Under our proposed modeling framework, we characterize the similarities between the $k$th source population and the target based on the difference between their regression parameters, ${\mathit{\delta }}^{\left(k\right)}={\mathit{w}}^{\left(k\right)}-\mathit{\beta }$. We consider the following parameter space:

$$\mathrm{\Theta }(s,h)=\left\{\mathit{\theta }=\left(\mathit{\beta },{\mathit{\delta }}^{\left(1\right)},\dots ,{\mathit{\delta }}^{\left(K\right)}\right):\parallel \mathit{\beta }{\parallel }_0\le s,\underset{1\le k\le K}{\mathrm{m}\mathrm{a}\mathrm{x}} {∥{\mathit{\delta }}^{\left(k\right)}∥}_0\le h\right\},$$

where $s$ and $h$ are the upper bounds for the support size of $\mathit{\beta }$ and ${\left\{{\mathit{\delta }}^{\left(k\right)}\right\}}_{k=1}^K$, respectively. Intuitively, a smaller $h$ indicates a higher level of similarity so that the source data can be more helpful for estimating $\mathit{\beta }$ in the target population. When $h$ is relatively large, incorporating data from source populations may be worse than only using data from the target population to fit the model, also known as negative transfer in the machine learning literature (Weiss, Khoshgoftaar and Wang (2016)). With unknown $s$ and $h$, in practice, we aim to devise an adaptive estimator to avoid negative transfer under unknown levels of heterogeneity across populations.

Throughout, for real-valued sequences $\left\{a_n\right\},\left\{b_n\right\}$, we write $a_n\lesssim b_n$, if $a_n\le c{b}_n$ for some universal constant $c\in (0,\mathrm{\infty })$, and $a_n\gtrsim b_n$, if $a_n\ge c^{\mathrm{\text{'}}}{b}_n$ for some universal constant $c^{\mathrm{\text{'}}}\in (0,\mathrm{\infty })$. We say $a_n\asymp b_n$ if $a_n\lesssim b_n$ and $a_n\gtrsim b_n$. We let $c,C,c_0,c_1,c_2,\dots$, denote some universal constants. For a vector $\mathit{v}\in {\mathbb{R}}^d$ and an index set $S\subseteq \left[d\right]$, we use ${\mathit{v}}_S$ to denote the subvector of $\mathit{v}$ corresponding to $S$. For any vector $\mathit{b}\in {\mathbb{R}}^p$, let ${\mathscr{H}}_k\left(\mathit{b}\right)$ be formed by setting all but the largest (in magnitude) $k$ elements of $\mathit{b}$ to zero.

2.2. The proposed algorithm.

To motivate our proposed FETA framework, we first consider the ideal case when site-level data can be shared. The transfer learning estimator of $\mathit{\beta }$ can be obtained via the following three-step procedure:

Step 1: Fit a regression model in each source population. For $k\in \{1,\dots ,K\}$, we obtain

$${\stackrel{\mathit{ˆ}}{\mathit{w}}}^{\left(k\right)}=\mathrm{a}\mathrm{r}\mathrm{g}\underset{\mathit{b}\in {\mathbb{R}}^p}{\mathrm{m}\mathrm{i}\mathrm{n}} \left\{\frac{1}{N^{\left(k\right)}}\sum _{m=1}^M L^{(m,k)}\left(\mathit{b}\right)+{\lambda }^{\left(k\right)}\parallel \mathit{b}{\parallel }_1\right\}.$$ (2.1)

Step 2: Adjust for differences using target data. For $k=1,\dots ,K$, we obtain

$${\stackrel{\mathit{ˆ}}{\mathit{\delta }}}^{\left(k\right)}=\mathrm{a}\mathrm{r}\mathrm{g}\underset{\mathit{b}\in {\mathbb{R}}^p}{\mathrm{m}\mathrm{i}\mathrm{n}} \left\{\frac{1}{N^{\left(0\right)}}\sum _{m=1}^M L^{(m,0)}\left({\stackrel{\mathit{ˆ}}{\mathit{w}}}^{\left(k\right)}+\mathit{b}\right)+{\lambda }_{\delta }\parallel \mathit{b}{\parallel }_1\right\}.$$ (2.2)

Threshold ${\stackrel{\mathit{ˆ}}{\mathit{\delta }}}^{\left(k\right)}\mathrm{v}\mathrm{i}\mathrm{a}{\check{\mathit{\delta }}}^{\left(k\right)}={\mathscr{H}}_{{\left(N^{\left(0\right)}/\mathrm{l}\mathrm{o}\mathrm{g}p\right)}^{1/2}}\left({\stackrel{\mathit{ˆ}}{\mathit{\delta }}}^{\left(k\right)}\right)$.

Step 3: Joint estimation using source and target data. We obtain

$$\stackrel{\mathit{ˆ}}{\mathit{\beta }}=\mathrm{a}\mathrm{r}\mathrm{g}\underset{\mathit{b}\in {\mathbb{R}}^p}{\mathrm{m}\mathrm{i}\mathrm{n}} \left\{\frac{1}{N}\sum _{m=1}^M L^{(m,0)}\left(\mathit{b}\right)+\frac{1}{N}\sum _{k=1}^K \sum _{m=1}^M L^{(m,k)}\left(\mathit{b}-{\check{\mathit{\delta }}}^{\left(k\right)}\right)+{\lambda }_{\beta }\parallel \mathit{b}{\parallel }_1\right\},$$ (2.3)

where ${\left\{{\lambda }^{\left(k\right)}\right\}}_{k=1}^K,{\lambda }_{\delta }$, and ${\lambda }_{\beta }$ are tuning parameters. Instead of learning $\mathit{\beta }$ directly from the target data with a limited sample size, we learn ${\mathit{w}}^{\left(k\right)}$ from the source populations and use them to “jumpstart” the model fitting in the target population. More specifically, we learn the difference ${\mathit{\delta }}^{\left(k\right)}$ by offsetting each ${\stackrel{\mathit{ˆ}}{\mathit{w}}}^{\left(k\right)}$. In Step 3 we pool all the data to jointly learn $\mathit{\beta }$, where the estimated differences ${\stackrel{\mathit{ˆ}}{\mathit{\delta }}}^{\left(k\right)}$ are adjusted for data from the $k$th source population. In contrast to the existing transfer learning methods based on generalized linear models, the above procedure has benefits in estimation accuracy and flexibility to be implemented in the federated setting. Compared to recent work (Tian and Feng (2021)), the above procedure has a faster convergence rate, which is, in fact, minimax optimal under mild conditions. Moreover, our method learns ${\mathit{w}}^{\left(k\right)}$ independently in Step 1 and Step 2, while in other related methods (Li, Cai and Li (2022), Tian and Feng (2021)), a pooled analysis is conducted with data from multiple populations. In a federated setting, finding a proper initialization for such a pooled estimator is challenging due to various levels of heterogeneity.

To generalize (2.1)–(2.3) to the federated setting, we consider an approximation of $L^{(m,k)}\left(\mathit{b}\right)$ by the second-order expansion of $L^{(m,k)}\left(\mathit{b}\right)$ at $\stackrel{\circ }{\mathit{b}}$. That is,

$${\tilde{L}}^{(m,k)}(\mathit{b};\stackrel{\circ }{\mathit{b}})=L^{(m,k)}\left(\stackrel{\circ }{\mathit{b}}\right)+\sum _{m=1}^M (\mathit{b}-\stackrel{\circ }{\mathit{b}}{)}^{\mathrm{\top }}\nabla L^{(m,k)}(\stackrel{\circ }{\mathit{b}})+\frac{1}{2}\sum _{m=1}^M {\nabla }^2{L}^{(m,k)}(\stackrel{\circ }{\mathit{b}}\left)\right(\mathit{b}-\stackrel{\circ }{\mathit{b}}{)}^{\otimes 2}.$$

The higher-order terms are omitted, given that the initial value $\stackrel{\circ }{\mathit{b}}$ is sufficiently close to the true parameter. Using these surrogate losses, the sites only need to share three sets of summary statistics, the current estimate $\stackrel{\circ }{\mathit{b}}$, the score vector $\nabla L^{(m,k)}\left(\stackrel{\circ }{\mathit{b}}\right)$, and the Hessian matrix ${\nabla }^2{L}^{(m,k)}\left(\stackrel{\circ }{\mathit{b}}\right)$. For $k=0,\dots ,K$, we define

$$\begin{array}{l}\nabla L^{\left(k\right)}\left(\mathit{b}\right)=\sum _{m=1}^M\nabla L^{\left(m,k\right)}\left(\mathit{b}\right),{\widehat{\mathit{H}}}^{\left(k\right)}\left(\mathit{b}\right)=\frac{1}{N^{\left(k\right)}}\sum _{m=1}^M{\nabla }^2{L}^{\left(m,k\right)}\left(\mathit{b}\right),\\ {\widehat{R}}^{\left(k\right)}\left(\mathit{b};\stackrel{\circ }{\mathit{b}}\right)=\frac{1}{2}{(\mathit{b}-\stackrel{\circ }{\mathit{b}})}^{\top }{\widehat{\mathit{H}}}^{\left(k\right)}\left(\stackrel{\circ }{\mathit{b}}\right)\left(\mathit{b}-\stackrel{\circ }{\mathit{b}}\right)+〈\mathit{b}-\stackrel{\circ }{\mathit{b}},\frac{1}{N^{\left(k\right)}}\nabla L^{\left(k\right)}\left(\stackrel{\circ }{\mathit{b}}\right)〉.\end{array}$$ (2.4)

The functions ${\widehat{R}}^{\left(k\right)}(\mathit{b};\stackrel{\circ }{\mathit{b}})$ are the combined surrogate log-likelihood functions for the $k$th population, based on the previous estimate $\stackrel{\circ }{\mathit{b}}$ and corresponding gradients obtained from the $M$ sites. We then follow similar strategies as (2.1)–(2.3) but replace the full likelihood with the surrogate losses to construct a federated transfer learning estimator for $\mathit{\beta }$, as detailed in Algorithm 1.

We discuss strategies for the initialization of $\mathit{\beta }$ and ${\left\{{\mathit{w}}^{\left(k\right)}\right\}}_{k=1}^K$ in Section 2.3. Algorithm 1 requires $T$ iterations, where within each iteration we collect the first- and second-order derivatives calculated at each site based on the current parameter values. In practice, when iterative communication across sites is not preferred, we can choose $T=1$. We show in Section 3 that additional iterations can improve the estimation accuracy.

Remark 1. A special case of Algorithm 1 concerns the linear regression models where $L^{(m,k)}\left(\mathit{b}\right)={\sum }_{i\in {𝒩}^{(m,k)}} {\left(y_i-{\mathit{x}}_i^{\mathrm{\top }}\mathit{b}\right)}^2$. In such a case, we can directly obtain summary statistics ${\mathit{s}}^{(m,k)}={\sum }_{i\in {𝒩}^{(m,k)}} {\mathit{x}}_i{y}_i$ and ${\mathit{H}}^{(m,k)}={\sum }_{i\in {𝒩}^{(m,k)}} {\mathit{x}}_i{\mathit{x}}_i^{\mathrm{\top }}/n^{(m,k)}$. We can reconstruct $L^{(m,k)}\left(\mathit{b}\right)/n^{(m,k)}$, using ${\mathit{s}}^{(m,k)}$ and ${\mathit{H}}^{(m,k)}$, as $L^{(m,k)}\left(\mathit{b}\right)\propto \frac{1}{2}{\mathit{b}}^{\mathrm{\top }}{\mathit{H}}^{(m,k)}\mathit{b}-⟨{\mathit{s}}^{(m,k)},\mathit{b}⟩$. Thus, each site only needs to transfer ${\mathit{s}}^{(m,k)}$ and ${\mathit{H}}^{(m,k)}$ to perform Steps 1–3 (in equations (2.1)–(2.3)), using summary statistics, and no iterative communication is needed.

For the proper choices of tuning parameters, we provide theoretical investigation in Section 3. In practical implementation, they can be chosen by cross-validation. In a federated setting, minimizing the communication cost of choosing tuning parameters is important, and we provide an efficient procedure in the following remark.

Remark 2. In a federated setting, cross-validation is preferred to be done locally, since otherwise the communication costs would be much higher if different models need to be fitted and validated in a federated way. To reduce communication costs, we suggest the following procedure. We first learn the best tuning parameter for each population using local data. For the $k$th population, we find $I_k=\mathrm{a}\mathrm{r}\mathrm{g}{\mathrm{m}\mathrm{a}\mathrm{x}}_{1\le m\le M} n^{(m,k)}$, which is the site with the largest sample size from the $k$th population. Using data at site $I_k$ from the $k$th population, we fit a local penalized GLM and use cross-validation to choose the best tuning parameter (denoted by ${\lambda }_k^{\mathrm{*}}$). With ${\lambda }_k^{\mathrm{*}}$, based on the theoretical conclusion (van de Geer (2008)), which suggests the best tuning parameter is roughly $C_k\sqrt{\mathrm{l}\mathrm{o}\mathrm{g}p/n^{\left(I_k,k\right)}}$, where $C_k$ is some positive constant not related to $p$ or $n^{\left(I_k,k\right)}$, we can obtain $C_k^{\mathrm{*}}={\lambda }_k^{\mathrm{*}}/\sqrt{\mathrm{l}\mathrm{o}\mathrm{g}p/n^{\left(I_k,k\right)}}$. When fitting FETA, we choose tuning parameters by rescaling the local best tuning parameters. More specifically, in equation (2.5) we choose ${\lambda }^{\left(k\right)}=C_k^{\mathrm{*}}\sqrt{\mathrm{l}\mathrm{o}\mathrm{g}p/N^{\left(k\right)}}$. In equation (2.6), we choose ${\lambda }_{\delta }=C_0^{\mathrm{*}}\sqrt{\mathrm{l}\mathrm{o}\mathrm{g}p/N^{\left(0\right)}}$. In equation (2.7) we choose ${\lambda }_{\beta }=C_0^{\mathrm{*}}\sqrt{\mathrm{l}\mathrm{o}\mathrm{g}p/N}$. This procedure is implemented in both our simulation study and real data application and is demonstrated to be effective. Most importantly, it does not increase the communication cost since tuning parameter selection is performed locally within a single site.

In practice, it is likely that some source models are substantially different from the target model. In such a case, excluding source populations that are highly different from the target may lead to better performance than including all source populations. In an extreme case, if all the source populations are not helpful, it is desired that our algorithm can at least maintain a comparable performance than the estimator obtained using the target data alone. We thus proposed to increase the robustness of the transfer learning by an aggregation step, based on a small target validation dataset in the leading site, which can guarantee that, loosely speaking, the aggregated estimator has prediction performance comparable to the best prediction performance among all the candidate estimators (Rigollet and Tsybakov (2011), Tsybakov (2014), Lecué and Rigollet (2014)). In the leading site (denoted as the $m^{\mathrm{*}}$th site), we denote the validation data to be ${\left\{{\stackrel{\circ }{y}}_i,{\stackrel{\circ }{\mathit{x}}}_i\right\}}_{i=1}^{\stackrel{\circ }{\mathit{n}}}$, with sample size $\stackrel{\circ }{n}=c{n}^{\left(m^{\mathrm{*}},0\right)}$ for some $c\in \left(\mathrm{0,1}\right)$, where $n^{\left(m^{\mathrm{*}},0\right)}$ is the sample size of the training data in the leading site from the target population. We hope to first obtain a ranking of the $K$ source populations based on their similarity to the target. We can then obtain candidate estimators obtained by only incorporating the top $k$ source populations, for $k=\mathrm{1,2},\dots ,K$. Using the validation data, we select the estimator with the best performance. We summarize the details of the above procedures in Algorithm 2.

In the aggregation step, ${\stackrel{\mathit{ˆ}}{\mathit{\eta }}}_t$ can be viewed as a weight vector for ${\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_{t,0},\dots ,{\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_{t,K}$. Through optimization (2.9) one can find the optimal combination which maximizes the log-likelihood in some validation samples, and existing work has shown that the performance of the optimal combination ${\hat{\beta }}_t^{\left(\text{agg}\right)}$ is no worse than any of the candidate estimators in $\widehat{B}$, when the sample size of the validation data is not too small (Rigollet and Tsybakov (2011), Tsybakov (2014), Lecué and Rigollet (2014)). Based on our simulation study and real data example, the size of the validation data can be relatively small, compared to the training data, and cross-fitting may be used to make full use of all the data. In practice, if there is strong prior knowledge indicating that the level of heterogeneity is low across populations, the aggregation step may be skipped.

Remark 3 (Avoid sharing Hessian matrices). Algorithm 1 requires each site to transmit Hessian matrices to the leading site, which may not be a concern when $p$ is relatively small. When $p$ is large, we provide possible options to reduce the communication cost of sharing Hessian matrices: (1) If the distributions of covariate variables $\mathit{x}$ are homogeneous across sites for a certain population, we propose to use Algorithm B.1 in Section B of the Supplementary Material (Li, Cai and Duan (2023)), which only requires the gradient vector from each site. (2) When the distributions of covariate variables are heterogeneous across sites, another possibility is to fit a density ratio model between each dataset and the target data in the leading site. Then we can still use the leading target data to approximate the Hessian matrices of the other datasets, through the density ratio tilting technique proposed in Duan, Ning and Chen, 2022. (3) We can leverage the sparsity structures of the population-level Hessian matrices, denoted by ${\mathit{H}}^{(m,k)}$, to reduce the communication cost. For example, when constructing polygenic risk prediction, the existing knowledge on the structures of linkage disequilibrium may infer similar block-diagonal structures of the Hessian matrices. In such cases we can apply thresholding to the Hessian matrices and only share the resulting blocks. (4) As demonstrated in our simulation study and real data application, our algorithm with one round of iteration $(T=1)$ already achieves comparable performance as the pooled analysis. Thus, if choosing $T=1$, each site will only need to share Hessian matrices once. If more iterations are allowed, we propose to only update the first-order gradients in the rest of the $T-1$ iterations.

2.3. Initialization strategies.

The initialization determines the convergence rate and the number of iterations that Algorithm 1 and Algorithm B.1 need to reach convergence. With data from more than one population, one needs to balance the sample sizes and similarities across populations.

Here we offer two initialization strategies, namely, the single-site initialization and the multisite initialization. The ideal scenario for initialization is that one site has relatively large sample sizes for all $K+1$ populations. In such a case, we initialize ${\mathit{w}}^{\left(k\right)}$ and $\mathit{\beta }$ using the single-site initialization. If we cannot find a site with enough data from all the $K+1$ populations, the multisite initialization can be used:

• Strategy 1: Single-site initialization. Find $m^{\mathrm{*}}\in \{1,\dots M\}$, such that the sample sizes satisfy $n^{\left(m^{\mathrm{*}},k\right)}\asymp {\mathrm{m}\mathrm{a}\mathrm{x}}_{1\le m\le M} n^{(m,k)}$ for all $k\in \{0,\dots K\}$. In site $m^{\mathrm{*}}$, we initialize ${\mathit{w}}^{\left(k\right)}$ and $\mathit{\beta }$ by applying the pooled transfer learning approach introduced in equations (2.1)–(2.3). For example, the All of Us Precision Medicine Initiative aims to recruit one million Americans, with estimates of early recruitment showing up to 75% of participants are from underrepresented populations (Sankar and Parker (2017)). Such a database can be treated as an initialization site or leading site.

• Strategy 2: Multisite initialization. We first find $I_k=\mathrm{a}\mathrm{r}\mathrm{g}{\mathrm{m}\mathrm{a}\mathrm{x}}_{1\le m\le M} n^{(m,k)}$, which is the site with the largest sample size from the $k$th population. In site $I_k$, if the sample size of the $k$th population is much smaller than the total sample size, we initialize ${\mathit{w}}^{\left(k\right)}$ by treating the $k$th population as the target and other populations as the source and apply the transfer learning approach introduced in equations (2.1)–(2.3). If the $k$th population is the dominating population, we can simply initialize ${\mathit{w}}^{\left(k\right)}$ using only its own data. The same procedure applies to the initialization of $\mathit{\beta }$. For example, when constructing polygenic prediction models, the UK Biobank has around 500,000 European-ancestry samples but only 3000 African-ancestry samples (Collins (2012)). Thus, if UK Biobank is selected for initialization of the European-ancestry population, it can be done by using only the European-ancestry samples. On the contrary, if the UK Biobank is selected for initialization of the African-ancestry population, a transfer learning approach is needed to improve the accuracy of initialization by incorporating both European-ancestry and African-ancestry samples.

In Section 3 we show that the convergence rates of Algorithm 1 depend on the accuracy of the initial estimators. For the above two strategies, we derive their corresponding convergence rates in the next section. The corresponding theoretical results for Algorithm B.1 can be found in Section D of the Supplementary Material.

3. Theoretical guarantees.

We denote the population Hessian matrices for the $k$th population at the $m$th site as ${\mathit{H}}^{(m,0)}=\mathbb{E}\left[{\mathit{x}}_i^{(m,0)}{\left({\mathit{x}}_i^{(m,0)}\right)}^{\mathrm{\top }}\ddot{\psi }\left({\left({\mathit{x}}_i^{(m,0)}\right)}^{\mathrm{\top }}\mathit{\beta }\right)\right]$ and ${\mathit{H}}^{(m,k)}=\mathbb{E}\left[{\mathit{x}}_i^{(m,k)}{\left({\mathit{x}}_i^{(m,k)}\right)}^{\mathrm{\top }}\ddot{\psi }\left({\left({\mathit{x}}_i^{(m,k)}\right)}^{\mathrm{\top }}{\mathit{w}}^{\left(k\right)}\right)\right]$. We denote the population Hessian matrices across all sites to be ${\mathit{H}}^{\left(k\right)}={\sum }_{m=1}^M n^{(m,k)}{\mathit{H}}^{(m,k)}/N^{\left(k\right)},k=0,\dots ,K$. We assume the following condition for the theoretical analysis.

Condition 1. The predictors ${\left\{{\mathit{x}}_i\right\}}_{i\in {𝒩}^{(m,k)}}$ are independent and uniformly bounded with mean zero and covariance ${\mathbf{\Sigma }}^{(m,k)}$ with

$$\underset{1\le m\le M,0\le k\le K}{\mathrm{m}\mathrm{a}\mathrm{x}} \underset{i\in {𝒩}^{(m,k)}}{\mathrm{m}\mathrm{a}\mathrm{x}} {∥{\mathit{x}}_i∥}_{\mathrm{\infty }}\le C<\mathrm{\infty }.$$

The covariance matrices ${\mathbf{\Sigma }}^{(m,k)}$ and the Hessian matrices ${\mathit{H}}^{(m,k)}$ are all positive definite for $m=1,\dots ,M$ and $k=1,\dots ,K$.

Condition 2 (Lipschitz condition of $\psi$). The random noises ${\left\{y_i-\dot{\psi }\left({\mathit{x}}_i^{\mathrm{\top }}{\mathit{w}}^{\left(k\right)}\right)\right\}}_{i\in {𝒩}^{\left(k\right)}}$ are independent sub-Gaussian with mean zero for $k=0,\dots ,K$. The second-order derivative $\ddot{\psi }$ is uniformly bounded and $|\mathrm{l}\mathrm{o}\mathrm{g}\ddot{\psi }(a+b)-\mathrm{l}\mathrm{o}\mathrm{g}\ddot{\psi }(a\left)\right|\le C\left|b\right|$ for any $a,b\in \mathbb{R}$.

Condition 1 assumes uniformly bounded designs with positive definite covariance matrices. The distribution of ${\mathit{x}}_i^{(m,k)}$ can be different for different $m$ and $k$. This assumption is more realistic in practical settings than the homogeneity assumptions in, say, Jordan, Lee and Yang (2019). In fact, the heterogeneous covariates are allowed because the Hessian matrices from different sites are transmitted in Algorithm 1. In contrast, Algorithm B.1, which only requires transmitting the gradients across sites, would require a stricter version of Condition 1, as stated in Condition B.1 in the Supplementary Material. On the other hand, the positive definiteness assumption is only required for the Hessian matrices involved in the initialization and the pooled Hessian matrix ${\mathit{H}}^{\left(k\right)}$. Moreover, when having unbounded covariates, one may consider relaxing the uniformly bounded designs to sub-Gaussian designs. We comment that our theoretical analysis still carries through with sub-Gaussian designs, but the convergence rate will be inflated with some factors of log $p$. Condition 2 assumes a Lipschitz condition on the link function which holds for linear, logistic, and multinomial models.

For the tuning parameters, we take

$$\begin{array}{l}{\lambda }^{\left(k\right)}=c_0{\left(\frac{\text{log}p}{N^{\left(k\right)}}\right)}^{1/2},\hspace{1em}{\lambda }_{\delta }=c_0{\left(\frac{\text{log}p}{N^{\left(0\right)}}\right)}^{1/2},\\ {\lambda }_{\beta }=c_0{\left(\frac{\text{log}p}{N}\right)}^{1/2}+\frac{h\text{log}p}{N^{\left(0\right)}}\text{and}{c}_n=2c_{1}s\end{array}$$

for some constants $c_0>0$ and $c_1\ge 1$. We set $c_n$ at the magnitude of $s$ to simplify the theoretical analysis. Indeed, $c_n$ can be chosen as ${\mathrm{m}\mathrm{i}\mathrm{n}}_{1\le k\le K} c_0{\left(n^{\text{(init,}k)}/\mathrm{l}\mathrm{o}\mathrm{g}p\right)}^{1/2}$, where $n^{\left(\text{init,}k\right)}$ is the sample size for the $k$th population at its initialization site. In practice, a common practice is to select the tuning parameters by cross-validation, as in Remark 2.

We first show the convergence rate of the pooled transfer learning estimator $\beta$ in the following lemma.

Lemma 1 (Pooled transfer learning estimator). Assume Conditions 1 and 2, $h\le s,N^{\left(0\right)}\mathrm{l}\mathrm{o}\mathrm{g}p\le {\mathrm{m}\mathrm{i}\mathrm{n}}_{1\le k\le K} {\left(N^{\left(k\right)}\right)}^2$, and ${\mathrm{m}\mathrm{a}\mathrm{x}}_{0\le k\le K} s\mathrm{l}\mathrm{o}\mathrm{g}p/N^{\left(k\right)}+hs\mathrm{l}\mathrm{o}\mathrm{g}p/N^{\left(0\right)}=o\left(1\right)$. Then for $\stackrel{\mathit{ˆ}}{\mathit{\beta }}$ defined in (2.3) and some constant $c_1>0$,

$$\underset{\mathrm{\Theta }(s,h)}{\mathrm{s}\mathrm{u}\mathrm{p}} \mathbb{P}\left(\parallel \stackrel{\mathit{ˆ}}{\mathit{\beta }}-\mathit{\beta }{\parallel }_2^2\gtrsim \frac{s\mathrm{l}\mathrm{o}\mathrm{g}p}{N}+\frac{h\mathrm{l}\mathrm{o}\mathrm{g}p}{N^{\left(0\right)}}\right)\le \mathrm{e}\mathrm{x}\mathrm{p}\left(-c_1\mathrm{l}\mathrm{o}\mathrm{g}p\right).$$

Lemma 1 demonstrates that the pooled estimator $\stackrel{\mathit{ˆ}}{\mathit{\beta }}$ has optimal rates under mild conditions. Its convergence rate is faster than the target-only minimax rate $s\mathrm{l}\mathrm{o}\mathrm{g}p/N^{\left(0\right)}$ when $N^{\left(0\right)}\ll N$ and $h\ll s$. The sample size condition of Lemma 1 is relatively mild. First, $N\ge K{N}^{\left(0\right)}$ is reasonable, as our target population is underrepresented. The condition $s=o\left({\mathrm{m}\mathrm{i}\mathrm{n}}_{0\le k\le K} N^{\left(k\right)}/\mathrm{l}\mathrm{o}\mathrm{g}p\right)$ suggests that it is beneficial to exclude too-small samples as source data. The condition that $hs=o\left(N^{\left(0\right)}/\mathrm{l}\mathrm{o}\mathrm{g}p\right)$ and $h\le s$ requires that the similarity among different populations is sufficiently high.

Lemma 1 also shows the benefits of our two data integration strategies. When we integrate data across multiple sites, $N^{\left(k\right)}$ becomes larger, which relaxes the sparsity conditions and improves the convergence rate. On the other hand, when we incorporate data from diverse populations, the total sample size $N$ is increased, which also improves the convergence rate.

In the federated setting, we first provide in Theorem 3.1 a general conclusion that describes how the convergence rate of Algorithm 1 relies on the initial values. We then provide the convergence rates of Algorithm 1 under initialization Strategies 1 and 2 in Corollaries 1 and 2, respectively.

Theorem 3.1 (Error contraction of Algorithm 1). Assume Conditions 1 and 2 and the true parameters are in the parameter space $\mathrm{\Theta }(s,h)$. Assume that $h\le s\le c\surd N^{\left(0\right)}$ and ${\mathrm{m}\mathrm{a}\mathrm{x}}_{1\le k\le K} s\mathrm{l}\mathrm{o}\mathrm{g}p/N^{\left(k\right)}+hs\mathrm{l}\mathrm{o}\mathrm{g}p/N^{\left(0\right)}=o\left(1\right)$. If event $E_0$ in (C.16) in the Supplementary Material holds for the initial estimators ${\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_0$ and ${\left\{{\stackrel{\mathit{ˆ}}{\mathit{w}}}_0^{\left(k\right)}\right\}}_{k=1}^K$, then with probability at least $1-\mathrm{e}\mathrm{x}\mathrm{p}\left(-c_2\mathrm{l}\mathrm{o}\mathrm{g}p\right)$, for any finite $t\ge 1$,

$${∥{\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_t-\mathit{\beta }∥}_2^2\lesssim \frac{s\mathrm{l}\mathrm{o}\mathrm{g}p}{N}+\frac{h\mathrm{l}\mathrm{o}\mathrm{g}p}{N^{\left(0\right)}}+{\left(\underset{1\le k\le K}{\mathrm{m}\mathrm{a}\mathrm{x}} {∥{\stackrel{\mathit{ˆ}}{\mathit{w}}}_0^{\left(k\right)}-{\mathit{w}}^{\left(k\right)}∥}_2+{∥{\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_0-\mathit{\beta }∥}_2\right)}^{4t}.$$ (3.1)

Theorem 3.1 establishes the convergence rate of ${\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_t$ under certain conditions on the initializations. As the conditions in event $E_0$ guarantee that ${∥{\stackrel{\mathit{ˆ}}{\mathit{w}}}_0^{\left(k\right)}-{\mathit{w}}^{\left(k\right)}∥}_2=o\left(1\right)$ for all $1\le k\le K$ and ${∥{\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_0-\mathit{\beta }∥}_2=o\left(1\right),{\stackrel{\mathit{ˆ}}{\mathit{w}}}_t^{\left(k\right)}$ and ${\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_t$ converge to ${\mathit{w}}^{\left(k\right)}$ and $\mathit{\beta }$ in ${\ell }_2$-norm, respectively. For large enough $t$, the convergence rate of ${\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_t$ is $s\mathrm{l}\mathrm{o}\mathrm{g}p/N+h\mathrm{l}\mathrm{o}\mathrm{g}p/N^{\left(0\right)}$, which is the minimax rate for estimating $\mathit{\beta }$ in $\mathrm{\Theta }(s,h)$. Hence, the FETA estimators converge to the global minimax estimators. With proper initialization the number of iterations for convergence can be very small. Detailed analysis based on the initialization strategies, proposed in Section 2.3, is provided in the sequel.

Comparing Theorem 3.1 with Lemma 1, we see some important trade-offs in federated learning. First, the larger estimation error of ${\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_t$ with small $t$ in comparison to the pooled version $\stackrel{\mathit{ˆ}}{\mathit{\beta }}$ is a consequence of leveraging summary information rather than the individual data. Second, while the accuracy of ${\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_t$ improves as $t$ increases, the communication cost also increases. A balance between communication efficiency and estimation accuracy needs to be determined based on the practical constraints.

To better understand the convergence rate, we investigate the initialization strategies proposed in Section 2.3. Under the single-site strategy, we have the following conclusion.

Corollary 1 (Algorithm 1 with single-site initialization). We compute ${\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_0$ and ${\stackrel{\mathit{ˆ}}{\mathit{w}}}_0^{\left(k\right)}$ via (2.1)–(2.3) based on the individual data in site $m^{\mathrm{*}}$. Assume Conditions 1 and 2 and the true parameters are in the parameter space $\mathrm{\Theta }(s,h)$. Assume that $N\ge K{N}^{\left(0\right)},N^{\left(m^{\mathrm{*}}\right)}\ge K{n}^{\left(m^{\mathrm{*}},0\right)},h\le s$, and

$$\underset{1\le k\le K}{\mathrm{m}\mathrm{a}\mathrm{x}} s^2\mathrm{l}\mathrm{o}\mathrm{g}p/n^{\left(m^{\mathrm{*}},k\right)}+sh\mathrm{l}\mathrm{o}\mathrm{g}p/n^{\left(m^{\mathrm{*}},0\right)}=o\left(1\right).$$

Then with probability at least $1-\mathrm{e}\mathrm{x}\mathrm{p}\left(-c_2\mathrm{l}\mathrm{o}\mathrm{g}p\right)$, for any fixed $T\ge 1$,

$${∥{\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_T-\mathit{\beta }∥}_2^2\vee {\mathbb{E}}_{{\mathit{x}}_{\mathrm{*}}}\left[{\left|{\mathit{x}}_{\mathrm{*}}^{\mathrm{\top }}\left({\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_T-\mathit{\beta }\right)\right|}^2\right]\lesssim \frac{s\mathrm{l}\mathrm{o}\mathrm{g}p}{N}+\frac{h\mathrm{l}\mathrm{o}\mathrm{g}p}{N^{\left(0\right)}}+{\left\{\frac{s\mathrm{l}\mathrm{o}\mathrm{g}p}{N^{\left(m^{\mathrm{*}}\right)}}+\frac{h\mathrm{l}\mathrm{o}\mathrm{g}p}{n^{\left(m^{\mathrm{*}},0\right)}}\right\}}^{2T},$$

where ${\mathit{x}}_{\mathrm{*}}\in {\mathbb{R}}^p$ is an independent test sample with ${\mathrm{\Lambda }}_{\mathrm{m}\mathrm{a}\mathrm{x}}\left(\mathbb{E}\left[{\mathit{x}}_{\mathrm{*}}{\mathit{x}}_{\mathrm{*}}^{\mathrm{\top }}\right]\right)\le C<\mathrm{\infty }$.

Corollary 1 provides estimation and prediction errors for FETA after $T$ iterations. If the response is binary, then it is of more interest to bound the classification errors, which will be proved in Remark 4. Corollary 1 uses the results that ${∥{\stackrel{\mathit{ˆ}}{\mathit{w}}}_0^{\left(k\right)}-{\mathit{w}}^{\left(k\right)}∥}_2^2=O_P\left(\right(s+h)\left.\mathrm{l}\mathrm{o}\mathrm{g}p/n^{\left(m^{\mathrm{*}},k\right)}\right)$ and ${∥{\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_0-\mathit{\beta }∥}_2^2=O_P\left(s\mathrm{l}\mathrm{o}\mathrm{g}p/N^{\left(m^{\mathrm{*}}\right)}+h\mathrm{l}\mathrm{o}\mathrm{g}p/n^{\left(m^{\mathrm{*}},0\right)}\right)$ under the current conditions. We see that, after $O\left(\mathrm{l}\mathrm{n}N/\mathrm{l}\mathrm{n}{N}^{\left(m^{\mathrm{*}}\right)}+\mathrm{l}\mathrm{n}{N}^{\left(0\right)}/\mathrm{l}\mathrm{n}{n}^{\left(m^{\mathrm{*}},0\right)}\right)$ number of iterations, ${\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_t$ has the same convergence rate as the pooled estimator $\stackrel{\mathit{ˆ}}{\mathit{\beta }}$. If $N\asymp {\left(N^{\left(m^{\mathrm{*}}\right)}\right)}^{\alpha }$ and $N^{\left(0\right)}\asymp {\left(n^{\left(m^{\mathrm{*}},0\right)}\right)}^{{\alpha }^{\mathrm{\text{'}}}}$ for some finite $\alpha$ and ${\alpha }^{\mathrm{\text{'}}}$, then only constant number of iterations are needed.

Remark 4 (Classification error under logistic link). Assume the conditions of Corollary 1 and logistic model $\psi \left(\mu \right)=\mathrm{l}\mathrm{o}\mathrm{g}(1+\mathrm{e}\mathrm{x}\mathrm{p}\{-\mu \left\}\right)$. For an independent test sample ${\mathit{x}}_{\mathrm{*}}\in {\mathbb{R}}^p$, let ${\hat{y}}_{\mathrm{*}}=1\left({\mathit{x}}_{\mathrm{*}}^{\mathrm{\top }}{\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_T>0\right)$. If $\mathbb{P}\left({\left({\mathit{x}}_{\mathrm{*}}^{\mathrm{\top }}\mathit{\beta }\right)}^2\ge c_{1}s\mathrm{l}\mathrm{o}\mathrm{g}p/N+c_{1}h\mathrm{l}\mathrm{o}\mathrm{g}p/N^{\left(0\right)}\right)\ge 1-\mathrm{e}\mathrm{x}\mathrm{p}\left\{-c_2\mathrm{l}\mathrm{o}\mathrm{g}p\right\}$ and $T\ge \mathrm{m}\mathrm{a}\mathrm{x}\left\{\mathrm{l}\mathrm{o}\mathrm{g}N/\mathrm{l}\mathrm{o}\mathrm{g}{N}^{\left(m^{\mathrm{*}}\right)},\mathrm{l}\mathrm{o}\mathrm{g}{N}^{\left(0\right)}/\mathrm{l}\mathrm{o}\mathrm{g}{n}^{\left(m^{\mathrm{*}},0\right)}\right\}$, it holds that

$$\mathbb{P}\left({\hat{y}}_{\mathrm{*}}\ne \mathrm{s}\mathrm{g}\mathrm{n}\left({\mathit{x}}_{\mathrm{*}}^{\mathrm{\top }}\mathit{\beta }\right)\right)\le \mathrm{e}\mathrm{x}\mathrm{p}\left\{-c_3\mathrm{l}\mathrm{o}\mathrm{g}p\right\}$$

for some positive constants $c_1,c_2$, and $c_3$.

Remark 4 states that if the true signal $\left|x_{\mathrm{*}}^{\mathrm{\top }}\mathit{\beta }\right|$ is strong enough with high probability, then, under the conditions of previous theorems, the misclassification rate is $o\left(1\right)$.

Next, we study the performance of Algorithm 1 when using multisite initialization strategy. For simplicity, we study the case where $n^{\left(I_k,k\right)}\asymp N^{\left(I_k\right)}$. That is, the $k$th population is abundant in site $I_k$, and hence ${\mathit{w}}^{\left(k\right)}$ can be initialized based on the data from only the $k$th population in site $I_k$. Specifically,

$$\begin{array}{l}{\hat{\mathit{\beta }}}_0=\text{arg}\underset{b\in {ℝ}^p}{\text{min}}\left\{\frac{1}{n^{\left(I_0,0\right)}}{L}^{\left(I_0,0\right)}\left(\mathit{b}\right)+{\lambda }_{\beta ,0}\parallel \mathit{b}{\parallel }_1\right\},\\ {\hat{\mathit{w}}}_0^{\left(k\right)}=\text{arg}\underset{b\in {ℝ}^p}{\text{min}}\left\{\frac{1}{n^{\left(I_k,k\right)}}{L}^{\left(I_k,k\right)}\left(\mathit{b}\right)+{\lambda }_0^{\left(k\right)}\parallel \mathit{b}{\parallel }_1\right\},k=1,\dots ,K.\end{array}$$ (3.2)

Corollary 2 (Algorithm 1 with multisite initialization). We compute ${\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_0$ and ${\stackrel{\mathit{ˆ}}{\mathit{w}}}_0^{\left(k\right)}$ via (3.2) based using data in site $I_k$ for $k=0,\dots ,K$. We take ${\lambda }_{\beta ,0}=c_1{\left\{\mathrm{l}\mathrm{o}\mathrm{g}p/n^{\left(I_0,0\right)}\right\}}^{1/2}$ and ${\lambda }_0^{\left(k\right)}=c_1{\left\{\mathrm{l}\mathrm{o}\mathrm{g}p/n^{\left(I_k,0\right)}\right\}}^{1/2}$ with some large enough constant $c_1$. Assume Conditions 1 and 2 and the true parameters are in the parameter space $\mathrm{\Theta }(s,h)$. Assume that $N\ge K{N}^{\left(0\right)},h\le s$, and ${\mathrm{m}\mathrm{a}\mathrm{x}}_{1\le k\le K} s^2\mathrm{l}\mathrm{o}\mathrm{g}p/n^{\left(I_k,k\right)}+sh\mathrm{l}\mathrm{o}\mathrm{g}p/N^{\left(I_0\right)}=o\left(1\right)$. Then with probability at least $1-\mathrm{e}\mathrm{x}\mathrm{p}\left(-c_2\mathrm{l}\mathrm{o}\mathrm{g}p\right)$, for any fixed $T\ge 1$,

$${∥{\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_T-\mathit{\beta }∥}_2^2\vee {\mathbb{E}}_{{\mathit{x}}_{\mathrm{*}}}\left[{\left|{\mathit{x}}_{\mathrm{*}}^{\mathrm{\top }}\left({\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_T-\mathit{\beta }\right)\right|}^2\right]\lesssim \frac{s\mathrm{l}\mathrm{o}\mathrm{g}p}{N}+\frac{h\mathrm{l}\mathrm{o}\mathrm{g}p}{N^{\left(0\right)}}+\underset{0\le k\le K}{\mathrm{m}\mathrm{i}\mathrm{n}} {\left\{\frac{s\mathrm{l}\mathrm{o}\mathrm{g}p}{n^{\left(I_k,k\right)}}\right\}}^{2T},$$

where ${\mathit{x}}_{\mathrm{*}}\in {\mathbb{R}}^p$ is an independent test sample with ${\mathrm{\Lambda }}_{\mathrm{m}\mathrm{a}\mathrm{x}}\left(\mathbb{E}\left[{\mathit{x}}_{\mathrm{*}}{\mathit{x}}_{\mathrm{*}}^{\mathrm{\top }}\right]\right)\le C<\mathrm{\infty }$.

Corollary 2 uses the results that ${∥{\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_0-\mathit{\beta }∥}_2^2=O_P\left(s\mathrm{l}\mathrm{o}\mathrm{g}p/n^{\left(I_0,0\right)}\right)$ and ${∥{\stackrel{\mathit{ˆ}}{\mathit{w}}}^{\left(k\right)}-{\mathit{w}}^{\left(k\right)}∥}_2^2=O_P\left(s\mathrm{l}\mathrm{o}\mathrm{g}p/n^{\left(I_k,k\right)}\right)$, given the optimization (3.2). In this case, the number of iterations needed for ${\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_t$ to reach the same rate as the pooled estimator $\hat{\beta }$ is about $O\left({\mathrm{m}\mathrm{a}\mathrm{x}}_{0\le k\le K} \mathrm{l}\mathrm{n}N/\mathrm{l}\mathrm{n}{n}^{\left(I_k,k\right)}\right)$.

4. Simulation studies.

4.1. Predictive performance under different levels of heterogeneity when $K=1$.

Motivated from our real data application, which is introduced in Section 5, we first consider the setting where $K=1$. We generate data to mimic genetic risk prediction in a federated network with $M=5$ sites. In site $m\in \{1,\dots M\}$, we have $n^{(m,0)}=400$ samples from the target population and $n^{(m,1)}=2000$ samples from a source population. We set the dimension of ${\mathit{x}}_i$ to be $p=2000$ and generate ${\mathit{x}}_i$ to mimic the genotype data which take values (0, 1, and 2). The distribution of ${\mathit{x}}_i$ in the target population differs with the source population in terms of LD structures and minor allele frequencies; see Section E of the Supplementary Material for more details. For each subject we generate the binary outcome variable through a logistic regression model

$$\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}\left(\mathbb{E}\left\{y_i\mid {\mathit{x}}_i\right\}\right)={\mathit{x}}_i^{\mathrm{\top }}{\mathit{b}}_i,$$

where $\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}\left(t\right)=\mathrm{l}\mathrm{o}\mathrm{g}\{x/(1-x\left)\right\}$. The regression coefficients ${\mathit{b}}_i=\mathit{\beta }$ is subject $i$ is from the target population, otherwise ${\mathit{b}}_i={\mathit{w}}^{\left(1\right)}$. The regression-coefficient $\mathit{\beta }$ has $s=100$ nonzero entries which are generated from $U(-\mathrm{0.4,0.4})$. The source coefficient ${\mathit{w}}^{\left(1\right)}$ is generated from the following two settings:

(S1) $w_j^{\left(1\right)}={\beta }_j+\delta \mathbb{I}(j\in H)$, where $H$ is a random subset of $\left[p\right]$ with $\left|H\right|=h$ and $\delta$ is sampled from $\{-\mathrm{\Delta },\mathrm{\Delta }\}$ with $\mathrm{\Delta }>0$. This is corresponding to the setting that a small number of genetic variants have relatively large differences in effect sizes across populations.

(S2) $w_j^{\left(1\right)}={\beta }_j+{\delta }_j\mathbb{I}(j\in H)$ where $H$ is a random subset with $\left|H\right|=5h$. We generate ${\delta }_j{~}_{\mathrm{i.i.d.}}N(0,\mathrm{\Delta }/3)$. This is corresponding to the setting that a large number of genetic variants have relatively small differences in effect sizes across populations.

In both settings the level of heterogeneity increases with $h$ and $\mathrm{\Delta }$. We compare a list of methods including: (1) federated learning based on all the target data (target-only), (2) federated learning based on all the source data (source-only), (3) federated learning based on all data combing both the source and target (combined), (4) Algorithm 2 with $T=1$ (proposed $(T=1)$), (5) Algorithm 2 with $T=3$ (proposed $(T=3)$), and (6) the pooled transfer learning equations (2.1)–(2.3) method where data from all sites are pooled together (pooled). The methods are evaluated based on the out-sample area under the receiver operating characteristic curve (AUC), based on a randomly generated testing sample with sample size $n=1000$.

We present in Figures 2 the AUC over 200 replications under different simulation settings. In setting 1 with the increase of $\mathrm{\Delta }$ and $h$, the prediction performance of all methods decreases. This is consistent with our intuition that a source population more different to the target is less helpful. The estimator combining source and target data outperforms the source-only estimator in all scenarios, as it incorporates target samples. Our proposed estimators, even with only one round of communication $(T=1)$, achieve better performance than these benchmarks. With $T=3$, our methods can further improve the performance, especially when heterogeneity is high. Our estimators have comparable performance to the pooled estimator when $\mathrm{\Delta }$ or $h$ is small. When the level of heterogeneity is high, we see that the combining source and target data lead to worse performance than the target-only model, while the transfer learning and the proposed methods, due to the aggregation step, can prevent negative transfer from the source population, which is highly different from the target. Results from setting 2 convey similar conclusions. We see that numerically when $\parallel \mathit{\delta }{\parallel }_0$ is relatively large (even bigger than $s$), our methods still have improvement, given the magnitude of entries are small. We also evaluated the effect of aggregation by comparing the proposed estimator with $\stackrel{\mathit{ˆ}}{\mathit{\beta }}$ from Algorithm 1 (see Figures E.1 and E.2 in the Supplementary Material). Across all scenarios the proposed estimators with aggregation perform no worse than the estimators without aggregation. The improvement is substantial when the level of heterogeneity is moderate or large.

Fig. 2.

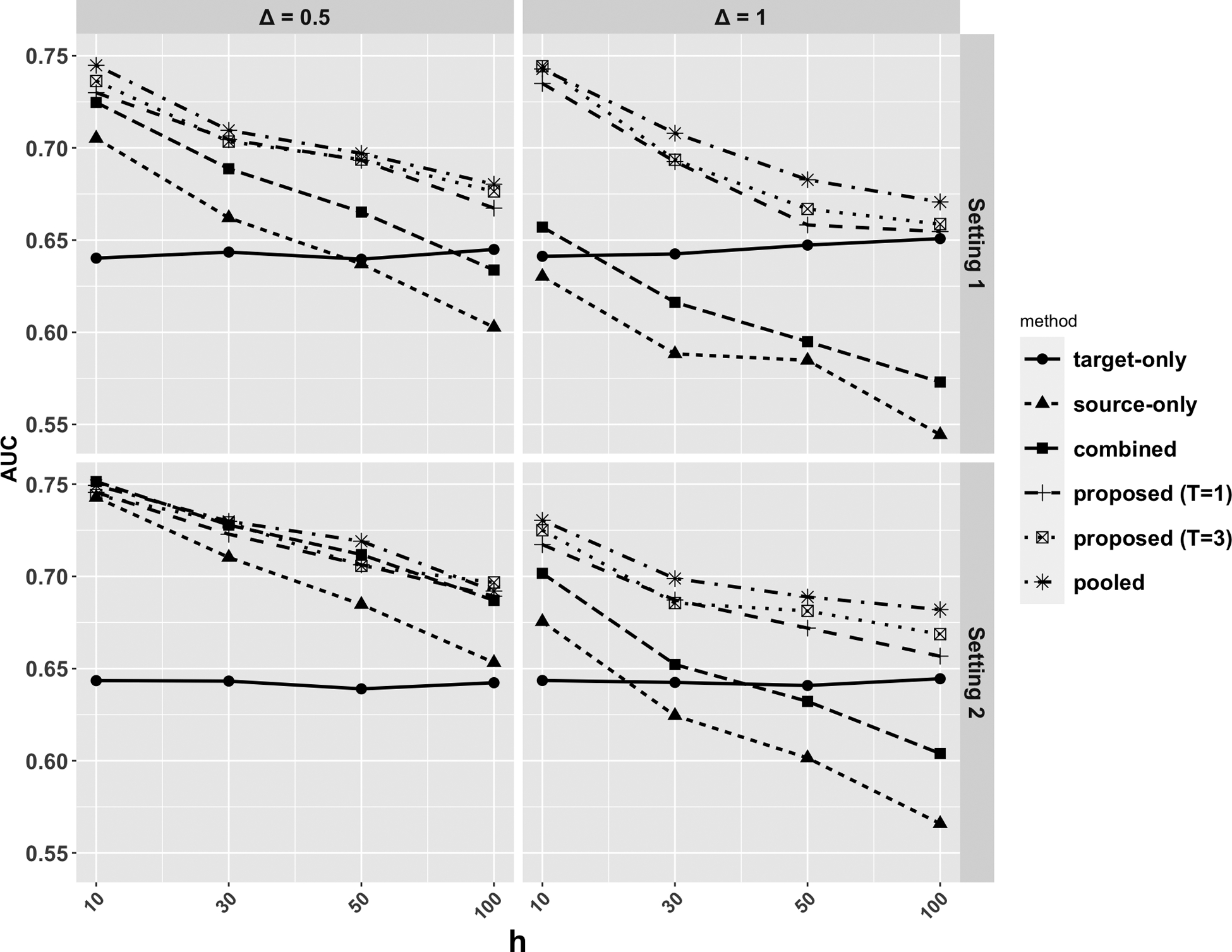
Comparison of AUC over 200 replications under simulation settings 1 and 2.

4.2. Robustness under different levels of heterogeneity when $K>1$.

We then consider the setting with multiple source populations and investigate the robustness of the proposed method when some source populations are more helpful than others. In particular, we choose $K=3$ and $M=5$, that is, data from three source populations and one target population are collected from five sites. We set $n^{(m,0)}=400,n^{(m,1)}=600,n^{(m,2)}=1000,n^{(m,3)}=2000$ for all $m\in \{\mathrm{1,2},\mathrm{3,4},5\}$. We generate $\mathit{\beta }$ in the same way, as described in Section 4.1. To generate ${\mathit{w}}^{\left(k\right)}$, we choose the same procedure described in setting (S1) of Section 4.1, where for a “good” source population, we choose $h=10$ and $\mathrm{\Delta }=1$ and for a “bad” source, we choose $h=100$ and $\mathrm{\Delta }=1$. We consider the following cases:

• Case 1: No bad source, that is, ${∥{\mathit{\delta }}^{\left(k\right)}∥}_0=10$ for $k=\mathrm{1,2},3$.

• Case 2: One bad source, that is, ${∥{\mathit{\delta }}^{\left(k\right)}∥}_0=10$ for $k=\mathrm{1,2}$, and ${∥{\mathit{\delta }}^{\left(3\right)}∥}_0=100$.

• Case 3: Two bad sources, that is, ${∥{\mathit{\delta }}^{\left(1\right)}∥}_0=10$ and ${∥{\mathit{\delta }}^{\left(k\right)}∥}_0=100$ for $k=\mathrm{2,3}$.

• Case 4: Three bad sources, that is, ${∥{\mathit{\delta }}^{\left(k\right)}∥}_0=100$ for $k=\mathrm{1,2},3$.

From Figure 3, when all the source populations are helpful (Case 1), the proposed method with $T=1$ and $T=3$ has nearly the same AUC as the pooled transfer learning method. The combined approach also performs well in Case 1, although it has slightly lower AUC than the proposed method. From Case 1 to Case 4, the number of helpful source populations increases, and the performance of the proposed method also decreases, but it has performance no worse than the target-only estimator across all four cases. In Case 4 all the source data are not helpful, and the combined approach has AUC lower than the target-only approach. The proposed method has nearly the same performance than the target-only model, while the pooled transfer learning method is slightly better than the target-only approach probably due to the loss of federated learning.

Fig. 3.

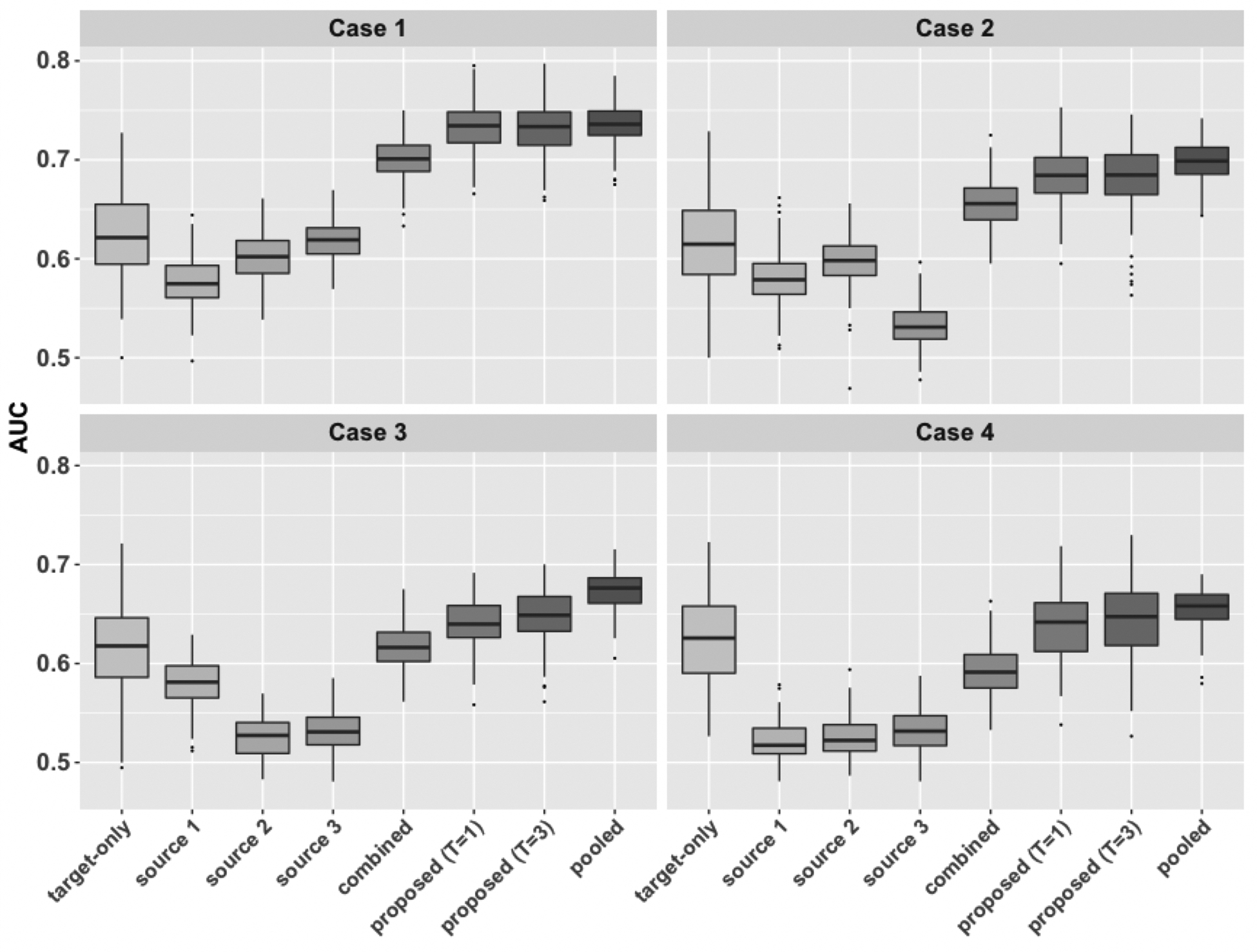
Comparison of AUC over 200 replications under Case 1 to Case 4, where we set $K=3$ and $M=5$. The number of helpful source populations decreases from Case 1 to Case 4.

In sum, the simulation studies demonstrate that our proposed methods have improved predictive accuracy compared to the benchmark methods. Compared to the ideal case where data are pooled together, FETA with only one iteration has comparable or slightly worst performance in most of the scenarios. When the level of heterogeneity is high, extra iterations can improve the accuracy and fill the gap between the federated analysis and the pooled analysis. In general, we recommend the aggregation step to ensure the robustness of the results and effectively leverage source data which are more helpful to the target.

5. Risk prediction of extreme obesity using data from the eMERGE network.

Obesity is one of the most significant risk factors for many complex human diseases, including hypertension, coronary heart disease, and type II diabetes (Kaplan (1989)). The prevalence of obesity among adults has more than doubled in the past three decades, and obesity continues to be a public health concern (Pan et al. (2011)). Many studies have suggested that genetics is likely to play a substantial role in the predisposition to obesity and may contribute up to 70% risk for the disease (Golden and Kessler (2020)). Over a hundred genes and gene variants related to excess weight have been discovered (Loos and Yeo (2022)), which has built the foundations for genetic risk prediction models. Similar as we have discussed in Section 1, existing genomics studies of obesity were mostly conducted in European ancestry populations (Zillikens et al. (2017)), raising concerns regarding the generalizability and transferibility of the study results.

5.1. Lack of representation of non-EA populations in eMERGE network.

To study this problem, we applied our proposed method to construct risk predication models using multicenter data from the eMERGE network, where EHR-derived phenotypes for 55,029 subjects from 10 participating sites were linked with DNA samples from biorepositories (Gottesman et al. (2013)). Among the 10 participating sites, three sites are children’s hospitals and are not included in this study. Trained EHR phenotyping algorithms are applied to derive the case-control status of extreme obesity, where participants are classified to either a “case,” a “control,” or “Unknown” (meaning the algorithm is not able to determine the case-control status based on the data available at the EHR system). In our study we exclude participants with unknown case-control status. We consider self-reported race as a population indicator, and Table 1 shows the sample size distribution across race and sites.

Table 1.

Sample sizes by self-reported races and sites.

	American Indian or Alaska Native	Asian	Black or African American	Unknown	White
Geisinger Health System	*	*	*	*	1023
Group Health Cooperative	*	*	*	*	252
Marshfield Clinic	*	*	*	*	1477
Mayo Clinic	*	*	*	47	1278
Mount Sinai	*	*	1148	343	185
Northwestern University	*	*	167	*	1306
Vanderbilt University	*	*	646	35	1472

^*indicates sample sizes less than 20.

A majority proportion of participants are White (>75%) across all seven sites, and in some sites, such as the Geisinger Health System, Marshfield Clinic, Mayo Clinic, more than 95% of the participant are White. There are around 20% of the participants who are Black or African American (AA), mostly coming from Mount Sinai, Northwestern University and Vanderbilt University. Except for Mount Sinai, White participants are overrepresented in all six sites. There are very few participants who are Asian (<1%), American Indian or Alaska Native (<1%), where all the sites have less than 20 participants in these racial groups.

In this application we treat the Black and AA population as our target population and treat the White population as the source. Due to the extremely small sample sizes from the other racial groups, a population-specific model is hard to be fitted, and we, therefore, incorporate them to the source population. As it is shown in Appendix F of the Supplementary Material, compared to a sensitivity which removes participants whose self-reported race is Asian, American Indian or Alaska Native, or unknown, the study results are consistent with the current findings, probably due to the extremely small sample sizes.

5.2. Data processing and feature selection.

Among the seven sites, Mount Sinai, Northwestern, and Vanderbilt have substantial target samples, while Geisinger, Group Health, Marshfield, and Mayo each has a target sample size less than 14, which may have only limited contributions to the model fitting and can increase the communication cost. Therefore, we exclude the target samples from Geisinger, Group Health, Marshfield, and Mayo.

To test the performance of the proposed method, we select three testing datasets each from Mount Sinai, Northwestern, and Vanderbilt, respectively. Specifically, from Vanderbilt and Northwestern we randomly select two internal testing datasets, each with size 300 target samples. We then choose all the target sample (n = 167) from Northwestern as an external testing dataset, whose data will be held out in the entire model training stage. We expect that this external testing dataset can help to evaluate the portability of the trained model when applied to a new dataset.

Predictors include age (coded as birth decades), gender, top 3 principal components (PCs) calculated from the genotypic data as well as top single nucleotide polymorphisms (SNPs), coded as 0,1, and 2 and selected by their marginal associations with the phenotypes. In particular, we applied regression between each phenotype and SNP controlling for age, gender, and 3 PCs and then select the top 2047 SNPs associated with each phenotype after filtering out SNPs with high LD, missing proportions and low minor allele frequency. The detailed filtering procedure and selected SNPs can be found in Section F of the Supplementary Material.

We applied our proposed method with a logistic regression. Similar as the simulation study, we choose the number of iterations to be $T=1$ and $T=3$ and compared them with the methods defined in Section 4. Methods are evaluated on the three testing datasets from Mount Sinai, Vanderbilt, and Northwestern. To account for sampling variability when selecting the testing datasets from Vanderbilt and Mount Sinai, we repeat the evaluation 20 times, and within each replication, prediction performance are evaluated separately on the three testing sets. Mount Sinai was chosen to be the leading site, whose individual-level data was used for the aggregation step.

5.3. Evidence for data heterogeneity between the source and the target populations.

We first investigate the heterogeneity of the distributions of the predictors between the target and the source populations. Using the genotypic data from the target and the source samples, we calculate the minor allele frequencies and pairwise correlations of the SNPs. For more clear presentation, we only plot the SNPs in chromosome 1 in Figure 4, while the comparisons of SNPs in chromosomes 2–22 lead to consistent conclusions.

Fig. 4.

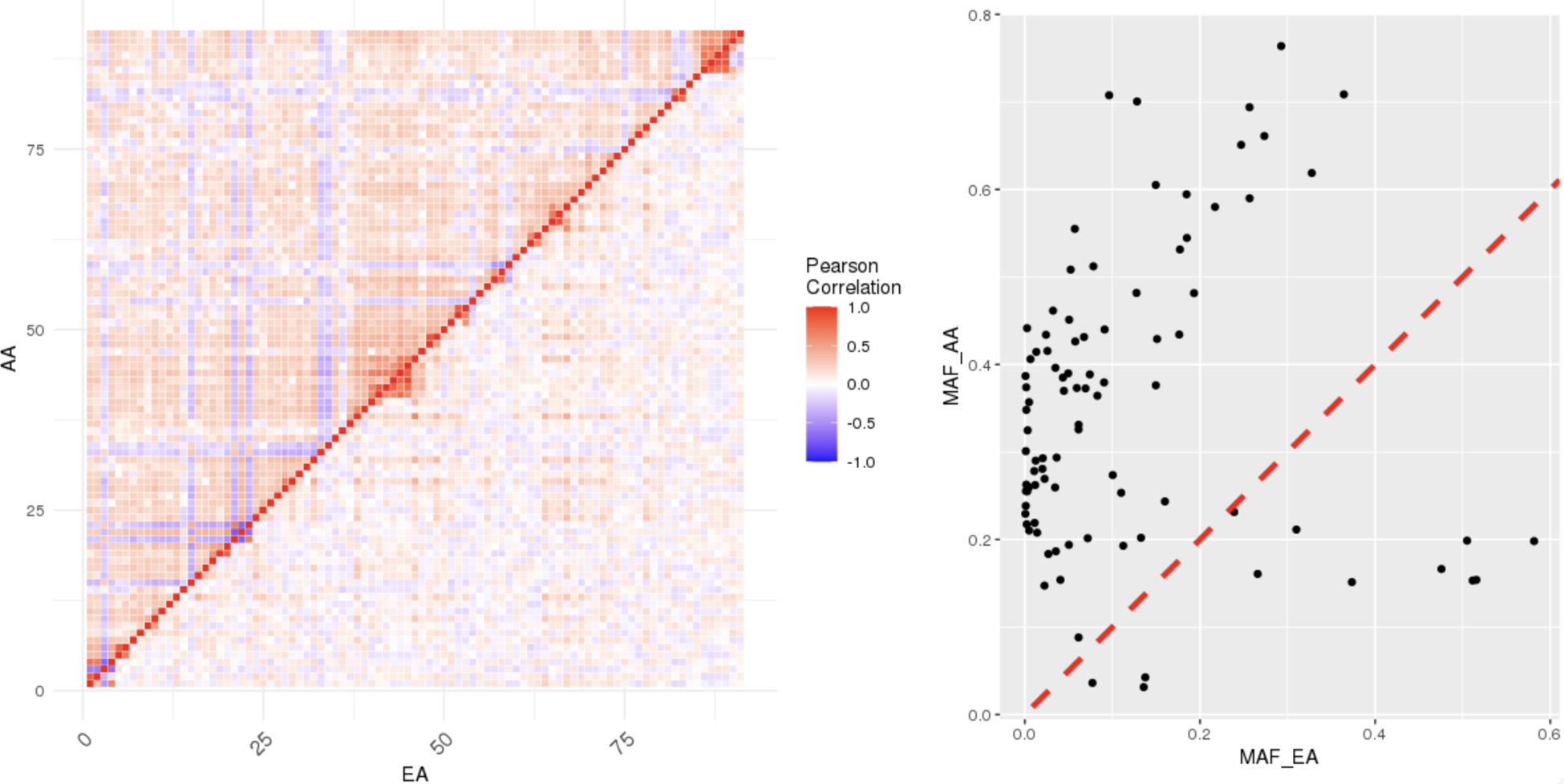
Comparisons of correlations and minor allele frequencies (MAFs) calculated from the source and the target populations. Among the 2047 selected SNPs, we show the SNPs on chromosome 1 for illustration purpose. The left panel shows the pairwise correlations between SNPs calculated from the source (the lower triangle) and the target (the upper triangle). The right panel compares the MAFs.

In the left panel of Figure 4, we compare the correlations of SNPs calculated from the target samples (the upper triangle) to the correlations calculated from the source samples (the lower triangle). Overall, the magnitude of correlations are larger and more structured in the target population than the source population. The weaker correlations, observed in the source population, are possibly due to the fact that we use the LD structure obtained from all data to remove SNPs with high correlations, which is closer to the LD structure of the White population due to the dominant sample size. In the right panel of Figure 4, we also observe that the MAFs of SNPs in the target population are highly different from the source population. Figure 4 is consistent with the existing findings, suggesting substantial differences in the LD structures and MAFs across different ancestral and ethnic groups (Martin et al. (2019)).

In addition, our method yields estimated values for the differences of the coefficients between the source and the target models, that is, $\stackrel{\mathit{ˆ}}{\mathit{\delta }}$, and Table 2 shows the SNPs with top differential effects between the two populations. Among the 25 SNPs, We found that most of them are in introns and intergenic regions. Existing literature found that rs6673201 is associated with interaction between insulin sensitivity index and BMI (Walford et al. (2016)); MEGF6 (multiple epidermal growth factor-like domains protein 6) was reported to contribute to the periotic mesenchyme and its derivatives, skin epidermis, certain cells in brain and ribs (Wang et al. (2019b)); HPSE2 was reported to be related to childhood BMI trajectory and adult lung function (Rathod et al. (2022)); ALOX5AP and TPD52 were reported to be associated with body weight (Kaaman et al. (2006)), and STK39 was shown to be a hypertension susceptibility gene (Wang et al. (2009)). Although there have not been enough multiethnic studies supporting the potentially heterogeneous effects of the above genes and SNPs on obesity across different ancestries, our analysis provides potential evidence for further investigations.

Table 2.

Top 25 SNPs having different effects in the source and the target populations

	SNPID	Gene name	Function
1	rs6673201	C1orf198	3_prime_UTR
2	rs41315290	MEGF6	intron
3	rs546147	HPSE2	intron
4	rs57588150	ALOX5AP	intergenic
5	rs13410278	AC016723.4	intergenic
6	rs10497334	STK39	intron
7	rs9975258	AP000233.4	intron
8	rs75401219	–	intergenic
9	rs845884	RP11–157J24.2	intergenic
10	rs7741633	TPD52L1	intron
11	rs4395726	TCTE3	intron
12	rs7763865	KIAA0319	intron
13	rs2143457	TMEM14C	intergenic
14	rs2485835	RP11–374I15.1	intergenic
15	rs11975134	NPY	intergenic
16	rs10282500	TBRG4	intergenic
17	rs7836712	ZFPM2	intron
18	rs11782183	PVT1	intron
19	rs55641476	LRRC6	intron
20	rs113235293	KHDRBS3	intron
21	rs672918	GLIS3	intron
22	rs10823830	CDH23	3_prime_UTR
23	rs8008067	RGS6	–
24	rs6747667	C2orf76	intron
25	rs4848615	AC018866.1	intergenic

5.4. Evaluation of the predictive performance.

Figure 5 presents the prediction performance of the compared methods. Due to the limited sample size, the target-only estimator has the lowest AUC among all the methods, where the average AUC is around 0.64–0.66, when evaluated across the three testing datasets. The variation of the target-only estimator across different random replications, however, is the largest, where the AUC can be as low as 0.51 and up to 0.85. The source-only estimator has better performance compared to the target-only estimator, having an average AUC around 0.71. Combining source and target data leads to better performance than using a population-specific training strategy, having an average AUC of 0.8. The pooled transfer learning estimator has the highest AUC which is around 0.85–0.89. With only one round of communication, FETA can achieve comparable performance to the pooled transfer learning estimator (ratios of AUC range from 88% to 107% with a median at 97%). With two additional rounds of communications, the AUC is nearly the same as the pooled estimator (ratios of AUC range from 92% to 102% with a median at 99%).

Fig. 5.

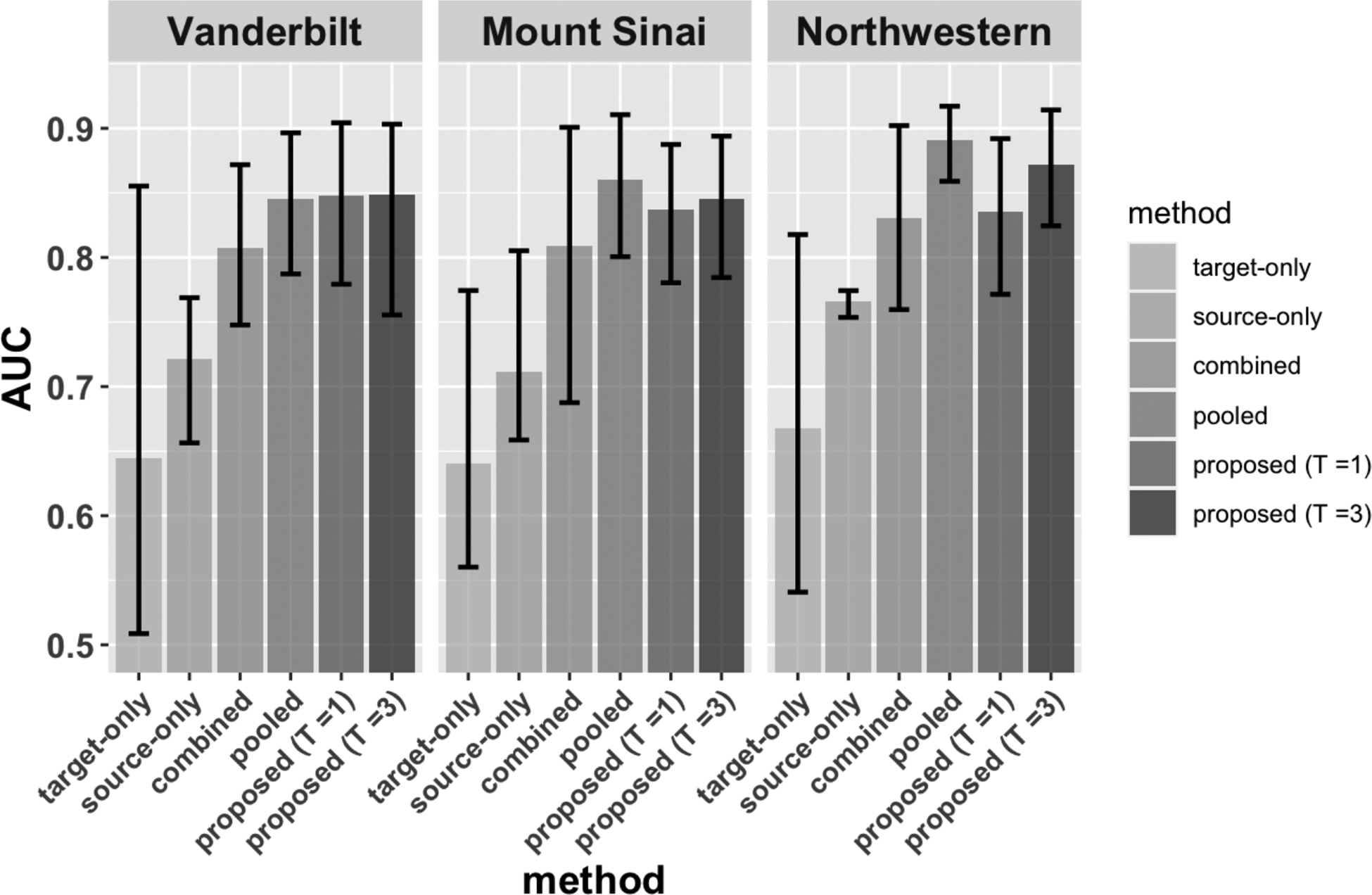
Comparisons of prediction performance across three testing datasets. Each colored bar denoted the average AUC over 20 replications, and the error bar indicates the highest and lowest performance.

Interestingly, the performance of FETA with $T=1$ and $T=3$ is similar when applied to the internal testing sets at Vanderbilt and Mount Sinai. When being evaluated at the external testing set from Northwestern University, FETA with $T=3$ is shown to perform better than $T=1$, indicating additional iterations might be helpful for the portability of the prediction models. Overall, the results from external evaluation are similar to the internal evaluation, indicating relatively low between-site heterogeneity. Depending on the goal of the prediction model, one can modify our method to treat a specific site as the target population and treat other sites as source data. We also perform sensitivity study in which we exclude participants who have unknown self-reported race or who are nonWhite from the source samples; the prediction performance is nearly the same as the current results. More details can be found in Appendix F of the Supplementary Material.

In sum, this application demonstrates the feasibility and the promise of our methods to be implemented in large heal data networks for the construction of risk prediction models. It may also be applied in other use cases, such as phenotyping or risk profiling, using multi-center data.

6. Discussion.

In this paper we propose federated transfer learning methods to improve the performance of estimation and prediction in underrepresented populations, which enables incorporating data from diverse populations that are stored at different institutions in a communication-efficient and individual-data protected manner. Our theoretical analysis and numerical experiments demonstrate the improved accuracy and robustness of the proposed methods compared with benchmark methods. The application to eMERGE network for constructing prediction models for extreme obesity in the African-ancestry population demonstrates the feasibility of applying our methods to large clinical/genomics consortia for improved risk prediction and stratification among underrepresented groups.

Our proposed FETA framework and the theoretical analyses are illustrated based on high-dimensional GLM with ${\ell }_1$-penalty, due to their wide application in biomedical applications (Morin et al. (2021), Wu, Roy and Stewart (2010), Lange et al. (2014)). However, the proposed framework can be extended to machine-learning methods with different penalty terms or model formulations. For example, if the difference of regression parameters between a source and the target population is nonsparse, we can change the ${\ell }_1$-penalty to the ${\ell }_2$-penalty or elastic net type of penalties. In addition, GLM can be replaced with other methods, such as the support vector machine which has been studied in the distributed setting (Stolpe, Bhaduri and Das (2016)). To account for the heterogeneity across populations, we can also allow a discrepancy term between the source and the target model parameters. However, some of the machine learning models may not be directly extended to the FETA framework. For instance, random forest has not been formally studied in the distributed setting as far as we know.

We account for population-level heterogeneity by allowing both the conditional distribution $f(y\mid \mathit{x})$ and the marginal distribution $f\left(\mathit{x}\right)$ to be different across sites. We use an aggregation method to improve the robustness of our methods to the level of heterogeneity. To account for site-level heterogeneity, our methods allow $f\left(\mathit{x}\right)$ to vary across sites, while $f(y\mid x)$ is assumed to be shared across sites, given a specific population. In practice, there might still be site-level heterogeneity that causes differences in $f(y\mid \mathit{x})$ and robust methods to account for such heterogeneity need to be incorporated, which we will consider in our future work.

Our proposed methods improve the fairness of statistical models by reducing the gap of estimation accuracy across populations due to lack of representation. Our theoretical conclusion provides insights for future data collection, as it reveals how the level of heterogeneity impacts the accuracy gain and the sample size from the target population needed to achieve comparable accuracy as the source populations. This is different from methods that impose constraints on model fitting to ensure that the prediction accuracy of an algorithm has to be at the same level across different populations (Mehrabi et al. (2021)). Since we are focusing on improving the performance of models in an underrepresented population, our work cannot guarantee complete fairness in prediction accuracy across all groups. In the future we can incorporate fairness corrections and constraints into our framework and in the meantime consider a wide variety of models in longitudinal and survival analysis, causal inference, to advance algorithmic fairness in precision medicine.